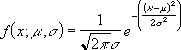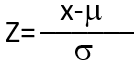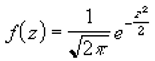Греческая строчная буква ро ρ
Значение символа
Греческая строчная буква ро. Греческое и коптское письмо.
Символ «Греческая строчная буква ро» был утвержден как часть Юникода версии 1.1 в 1993 г.
| Название в Юникоде | Greek Small Letter Rho |
| Номер в Юникоде | |
| HTML-код | |
| CSS-код | |
| Мнемоника | ρ |
| Разделы Юникода | Греческое и коптское письмо |
| Прописная | Ρ |
| Версия Юникода | 1.1 (1993) |
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03C1 |
| Простое изменение регистра | 03C1 |
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CF 81 | 207 129 | 53121 | 11001111 10000001 |
| UTF-16BE | 03 C1 | 3 193 | 961 | 00000011 11000001 |
| UTF-16LE | C1 03 | 193 3 | 49411 | 11000001 00000011 |
| UTF-32BE | 00 00 03 C1 | 0 0 3 193 | 961 | 00000000 00000000 00000011 11000001 |
| UTF-32LE | C1 03 00 00 | 193 3 0 0 | 3238199296 | 11000001 00000011 00000000 00000000 |
Похожие символы
Наборы с этим символом
ρ Греческая строчная буква ро
U+03C1
Нажмите, чтобы скопировать и вставить символ
Техническая информация
Значение символа
Греческая строчная буква ро. Греческое и коптское письмо.
Символ «Греческая строчная буква ро» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03C1 |
| Простое изменение регистра | 03C1 |
Похожие символы
Греческая строчная буква омега
Греческая строчная буква ню
Греческая строчная буква дельта
Греческая строчная буква эпсилон
Греческая строчная буква дзета
Греческая строчная буква эта
Греческая строчная буква тета
Греческая строчная буква йота
Греческая строчная буква каппа
Греческая строчная буква лямбда
Греческая строчная буква мю
Греческая строчная буква кси
Греческая строчная буква бета
Греческая строчная буква омикрон
Греческая строчная буква пи
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CF 81 | 207 129 | 53121 | 11001111 10000001 |
| UTF-16BE | 03 C1 | 3 193 | 961 | 00000011 11000001 |
| UTF-16LE | C1 03 | 193 3 | 49411 | 11000001 00000011 |
| UTF-32BE | 00 00 03 C1 | 0 0 3 193 | 961 | 00000000 00000000 00000011 11000001 |
| UTF-32LE | C1 03 00 00 | 193 3 0 0 | 3238199296 | 11000001 00000011 00000000 00000000 |
Наборы с этим символом:
© Таблица символов Юникода, 2012–2021.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.
Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее
Как в ворде набрать символ плотности (ро)
// PascalABC.NET 3.3, сборка 1583 от 25.11.2017
// Внимание! Если программа не работает, обновите версию!
begin
var (x,y,z):=ReadReal3(‘Введите через пробел три числа:’);
if (x+y>z) and (x+z>y) and (y+z>x) then Writeln(‘Треугольник существует’)
else Writeln(‘Треугольник не существует’)
end.
Примеры
Введите через пробел три числа: 2.34 5.18 9
Треугольник не существует
Введите через пробел три числа: 3 4 5
Треугольник существует
Как поставить знак приблизительно равно в Word и Excel
На клавиатуре отсутствует знак приблизительного равенства, а для вставки часто применяют копирование из другого места. Но есть и более удобные способы, которые помогут быстро напечатать символ в любом месте документа Word или Excel.
Конвертация кода в знак
Первый способ заключается в конвертации юникода символа в знак. В любом месте документа набираем 2248 и одновременно нажимаем «Alt» + «X».
- 2248 ➟ Alt + x = ≈
Вторая возможность связана с ASCII-кодом и преобразование идёт следующим чередом:
- зажимаем Alt ;
- вводим на правой цифровой клавиатуре 8776;
- отпускаем Alt и цифры превращаются в ≈.
Оба варианта работают в Word, Excel и других офисных программах.
Вставка символа без клавиатуры
В Word для вставки символа приблизительно равно можно воспользоваться функцией вставки. На вкладке «Вставка» открываем окно «Другие символы».
Выбираем шрифт «обычный текст» и набор «математические операторы». В первых рядах будет нужный знак.
Похожие знаки равенства
Кроме знака примерного равенства есть много похожих математических и геометрических операндов. Они часто используются в формулах и имеют разную смысловую нагрузку.
К ним также применимы способы вставки в офисных программах.
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Как построить график с нормальным распределением в Excel
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
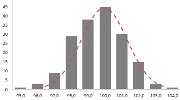
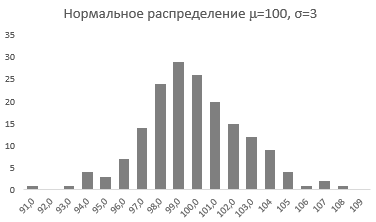
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
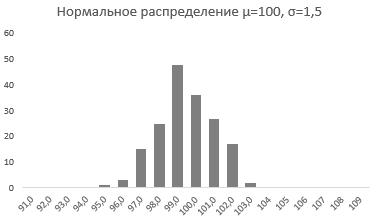
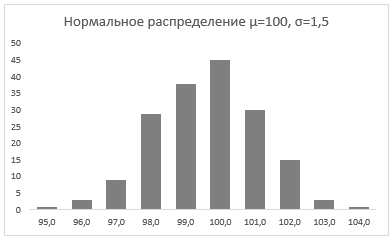
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
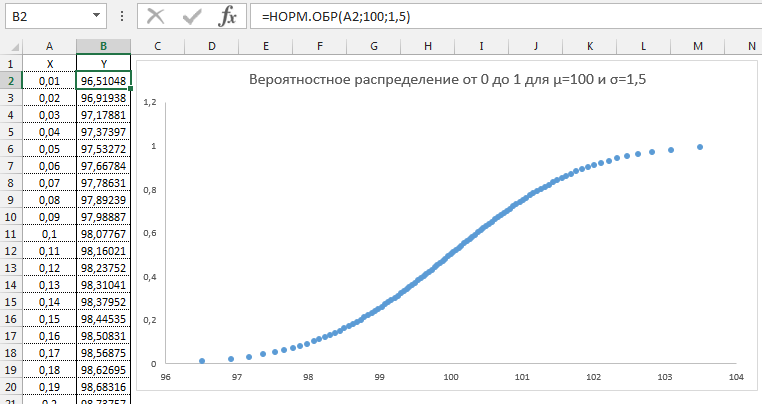
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
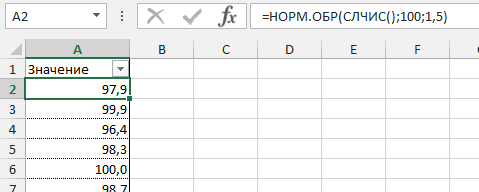
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
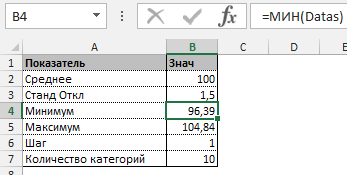
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
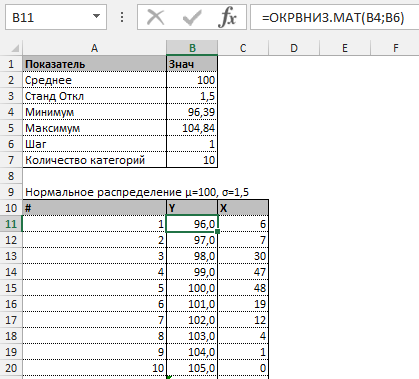
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
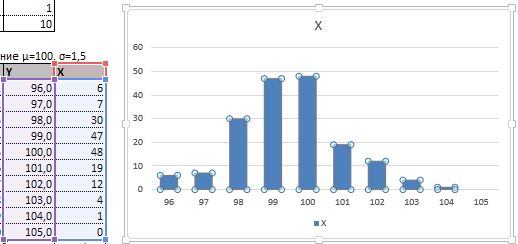
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Вам также могут быть интересны следующие статьи
12 комментариев
Ренат, добрый день.
Все несколько проще:
Данные->Анализ данных->Генерация случайных чисел (Распределение=Нормальное)
+
Данные->Анализ данных->Гистограмма->Галка на «вывод графика» («Карманы» можно даже не задавать)
Диаграмма нормального распределения (Гаусса) в Excel
Требуется построить диаграмму стандартного нормального распределения Гаусса (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.
1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).
2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.
3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.
4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.
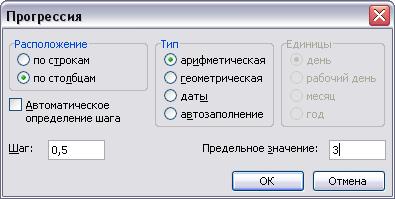
5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.
Функция НОРМРАСПР в EXCEL
6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.
7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.
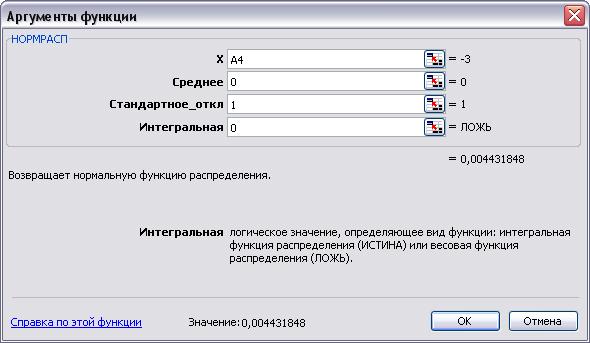
8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).
Диаграмма нормального интегрального распределения в EXCEL
9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.
10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.
11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .
НОРМРАСП (функция НОРМРАСП)
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.РАСП.
Аргументы функции НОРМРАСП описаны ниже.
x Обязательный. Значение, для которого строится распределение.
Среднее Обязательный. Среднее арифметическое распределения.
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Если аргумент «среднее» или «стандартное_откл» не является числом, функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!.
Если аргумент «стандартное_откл» меньше или равен 0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!.
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Нормальное распределение. Построение графика в Excel. Концепция шести сигм
Наверное, не все знают, что в Excel есть встроенная функция для построения нормального распределения. Графики нормального распределения часто используются для демонстрации идей статистической обработки данных.
Функция НОРМРАСП имеет следующий синтаксис:
НОРМРАСП (Х; среднее; стандартное_откл; интегральная)
Х — аргумент функции; фактически НОРМРАСП можно трактовать как y=f(x); при этом функция возвращает вероятность реализации события Х
Среднее (µ) — среднее арифметическое распределения; чем дальше Х от среднего, тем ниже вероятность реализации такого события
Стандартное_откл (σ) — стандартное отклонение распределения; мера кучности; чем меньше σ, тем выше вероятность у тех Х, которые расположены ближе к среднему
Интегральная — логическое значение, определяющее форму функции. Если «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения, тот есть суммарную вероятность всех событий для аргументов от -∞ до Х; если «интегральная» имеет значение ЛОЖЬ, возвращается вероятность реализации события Х, точнее говоря, вероятность событий находящихся в некотором диапазоне вокруг Х
Например, для µ=0 имеем:
Скачать заметку в формате Word, пример в формате Excel
Здесь по оси абсцисс единица измерения – σ, или (что то же самое), можно сказать, что график построен для σ = 1. То есть, «-2» на графике означает -2σ. По оси ординат шкала убрана умышленно, так как она лишена смысла. Точнее говоря, высота кривой зависит от плотности точек на оси абсцисс, по которым мы строим график. Например, если на интервал от 0 до 1σ приходится 10 точек, то высота в максимуме составит 4%, а если 20 точек – 2%. Здесь проценты означают вероятность попадания случайной величины в узкий диапазон окрестности точки на оси абсцисс. Зато имеет смысл площадь под кривой на определенном интервале. И эта площадь не зависит от плотности точек. Так, например, площадь под кривой на интервале от 0 до 1σ составляет 34,13%. Это значение можно интерпретировать следующим образом: с вероятностью 68,26% случайная величина Х попадет в диапазон µ ± σ.
Теперь, наверное, вам будет лучше понятен смысл выражения «качество шести сигм». Оно означает, что производство налажено таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазон µ ± 6σ, всё еще удовлетворяет техническим условиям (допускам). Это достигается за счет значительного уменьшения сигмы, то есть случайная величина Х очень близка к нормативному значению µ. На графике ниже представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества (уменьшению вариабельности, сужению сигма) доля брака сокращается:
На первом рисунке только 1,5σ попадают в границы допуска, то есть только 86,6% деталей являются годными. На втором рисунке уже 3σ попадают в границы допуска, то есть 99,75% являются годными. Но всё еще 25 деталей из каждых 10 000 произведенных являются браком. На третьем рисунке целых 6σ попадают в границы допуска, то есть в брак попадут только две детали на миллиард изготовленных!
Вообще-то говоря, измерение качества в терминах сигм использует не совсем нормальное распределение. Вот что пишет на эту тему Википедия:
Опыт показывает, что показатели процессов имеют тенденцию изменяться с течением времени. В результате со временем в промежуток между границами поля допуска будет входить меньше, чем было установлено первоначально. Опытным путём было установлено, что изменение параметров во времени можно учесть с помощью смещения в 1,5 сигма. Другими словами, с течением времени длина промежутка между границами поля допуска под кривой нормального распределения уменьшается до 4,5 сигма вследствие того, что среднее процесса с течением времени смещается и/или среднеквадратическое отклонение увеличивается.
Широко распространённое представление о «процессе шесть сигма» заключается в том, что такой процесс позволяет получить уровень качества 3,4 дефектных единиц на миллион готовых изделий при условии, что длина под кривой слева или справа от среднего будет соответствовать 4,5 сигма (без учёта левого или правого конца кривой за границей поля допуска). Таким образом, уровень качества 3,4 дефектных единиц на миллион готовых изделий соответствует длине промежутка 4,5 сигма, получаемых разницей между 6 сигма и сдвигом в 1,5 сигма, которое было введено, чтобы учесть изменение показателей с течением времени. Такая поправка создана для того, чтобы предупредить неправильною оценку уровня дефектности, встречающееся в реальных условиях.
С моей точки зрения, не вполне внятное объяснение. Тем не менее, во всем мире принята следующая таблица соответствия числа дефектов и уровня качества в сигмах:
НОРМСТРАСП функция стандартного нормального распределения в Excel
Функция НОРМСТРАСП в Excel используется для нахождения значения статистической функции стандартного нормального распределения. Рассмотрим примеры использования данной функции и самостоятельно составим таблицу нормального закона.
Алгоритм функции нормального стандартного распределения чисел в Excel
В новых версиях Microsoft Office была введена более универсальная функция =НОРМ.СТ.РАСП(), содержащая дополнительный аргумент, который принимает два возможных значения:
- ИСТИНА – для получения интегральной функции распределения;
- ЛОЖЬ – для получения весовой функции распределения.
Стандартное нормальное распределение (СНР) – специальная форма распределения, используемая в качестве эталона для оценки данных любого вида. Данный тип распределения по причине неудобства использования формулы общего нормального распределения на практике.
Главные особенности функции:
- Площадь участка, ограниченного кривой и осью абсцисс принята за 1.
- Стандартное отклонение считается равным 1.
- Среднее арифметическое значение принято равным 0.
- В функцию f(x) общего теоретического нормального распределения введена переменная z (стандартная нормальная).
Переменная z рассчитывается по формуле:
- X – значение некоторой случайной величины;
- µ — среднее значение;
- ó — значение стандартного отклонения.
Смысл переменной z – число стандартных отклонений, на которые отличается значение случайной величины от среднего значения.
Функция НОРМСТРАСП возвращает результат, рассчитанный на основе следующей формулы:
Именно так и выглядит алгоритм вычисления функции НОРМСТРАСП в Excel
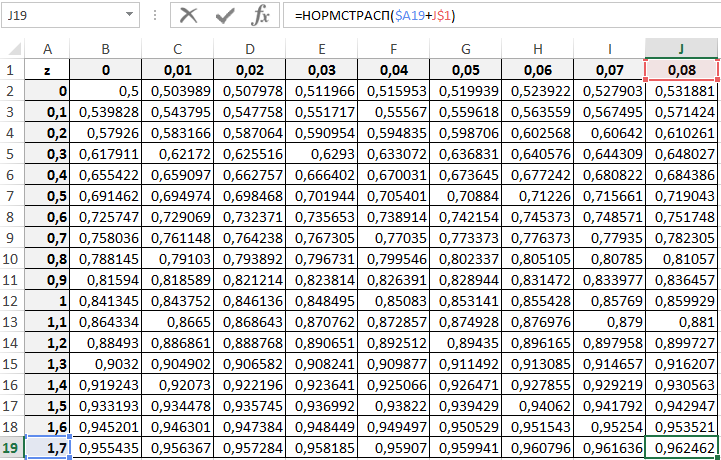
Таблица стандартного нормального распределения в Excel
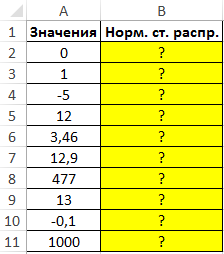
Пример 1. Найти стандартные нормальные распределения для числовых данных, указанных в таблице.
Вид таблицы данных:
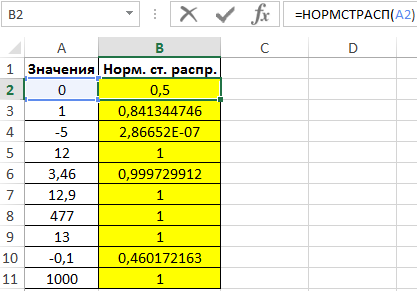
Для расчетов используем следующую формулу:
- A2:A11 – диапазон ячеек, содержащих значения переменной z.
С принципом действия функции мы ознакомились. Теперь ничто нам не мешает составить свою таблицу стандартного распределения в Excel. Для этого построим шаблон таблицы нормального закона и заполним ее ячейки формулой со смешанными ссылками:
Таким образом мы самостоятельно составили таблицу стандартного нормального распределения в Excel.
Расчет вероятности стандартным нормальным распределением в Excel
Пример 2. На заводе изготавливают лампочки. Средний период бесперебойной работы каждой лампы составляет 1000 ч. Стандартное отклонение от срока службы составляет 50 ч. Определить вероятность для каждого из указанных случаев:
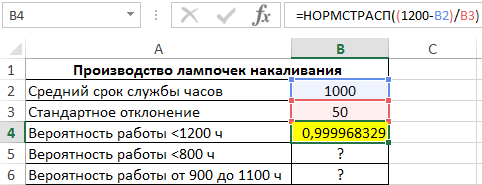
- Купленная лампа будет работать не более 1200 ч.
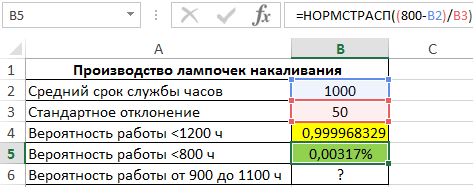
- Срок службы составит менее 800 ч.
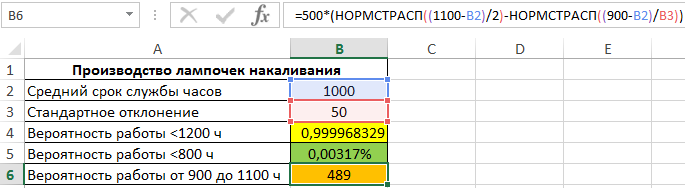
- Количество ламп в партии из 500 шт., которые проработают от 900 до 1100 часов.
Вид таблицы данных:
Для расчета вероятности срока службы менее 1200 ч используем следующую формулу:
(1200-B2)/B3 – выражение для расчета переменной z.
В результате вычислений получим следующее значение вероятности:
Аналогично рассчитаем вероятность того, что срок службы составит менее 800 часов:
Результат вычислений (получена слишком маленькая вероятность, поэтому для наглядности был установлен формат Проценты):
Нормальное распределение является симметричным относительно оси ординат, поэтому функция НОРМСТРАСП может вычислить значение даже для отрицательного z.
Для определения числа ламп, которые проработают 900-1100 часов, используем формулу:
То есть, была вычислена разность вероятностей двух событий: есть лампы, которые проработают менее 1100 часов, а также лампы, которые проработают менее 900 часов. Результат произведения полученной вероятности и общего числа ламп в партии является искомым значением.
Описание параметров функции НОРМСТРАСП в Excel
Функция НОРМСТРАСП имеет следующую синтаксическую запись:
- z – единственный аргумент, обязательный для заполнения, принимающий числовое значение стандартной нормальной переменной.
- В качестве аргумента z может быть передано числовое значение, преобразуемый в число текст, логическое значение (например, результат выполнения функции =НОРМСТРАСП(ИСТИНА) будет число 0,841, поскольку данная функция выполняет промежуточное преобразование логического ИСТИНА в число 1), ссылка на ячейку с числовыми данными.
- Если функция НОРМСТРАСП получила в качестве аргумента текст, не преобразуемый в числовые данные, она вернет код ошибки #ЗНАЧ!.
Содержание
- как в ворде набрать символ плотности (ро)
- Знак плотности в word
- Доступные наборы символов
- Формула плотности вещества
- Функция ФИ и плотность стандартного нормального распределения в Excel
- Значения функции плотности стандартного нормального распределения в Excel
- Пример расчета плотности стандартного нормального распределения в Excel
- Правила использования функции ФИ в Excel
- Как использовать наборы значков для представления значений в Microsoft Excel
- Применение набора значков быстрого условного форматирования
- Создание набора значков настраиваемого условного форматирования
как в ворде набрать символ плотности (ро)
Можно греческие буквы вставлять автозаменой. Причем настроить так, чтобы работало в ту и другую сторону.
Я делаю так:
— через Вставка/Символ из шрифта Times New Roman (не Symbol) вставляем все нужные греческие буквы, математические символы и hbar (Alt-0158) до кучи;
— по очереди выделяем и нажимаем Alt-F3;
— назначаем вменяемое имя (я сделал как латехе) alpha, beta, hbar, leq, geq, gg, ll, approx, propto, to, infty; большие греческие не получилось так сделать, так как автотекст в названии элемента автотекста не различает большие/маленькие буквы, сделал G → Γ, D → Δ, Y → Ψ, W → Ω.
— затем проделываем обратную операцию, пишем alpha;
— выделяем, нажимаем Alt-F3, назначаем имя в виде греческой буквы «α»;
— после всех этих операций желательно аккуратно закрыть ворд и снова его открыть, убедившись, что элементы автотекста сохранились (назначение автотекста и сочетаний клавиш хранятся в стандартном файле %appdata%MicrosoftШаблоныNormal.dot(m); если назначенные элементы автотекста не сохранились, то открывайте в ворде прямо Normal.dot или Normal.dotm для современных версий ворда от 2007 и выше, назначайте автозамену и сохраняйте файл шаблона Ctrl-S, тогда точно сохранится).
Все. Теперь, если написать в ворде alpha и сразу нажать F3, то получится греческая α, снова нажимаем F3, и α превращается в alpha.
Насчет «Symbol». Если надо сделать на скорую руку и далеко это не пойдет, то делаю так. Пишу латинскую a, выделяю, нажимаю Ctrl-Shift-Q, получается греческая α в шрифте «Symbol» и т. д. b → β, g → γ, c → χ, z → ζ. Последнее время стараюсь этого избегать, так как «Symbol» — это не юникодовский шрифт, и при вставке такого текста, скажем, в индизайн будут проблемы с греческими символами.
Источник
Знак плотности в word
Я делаю так:
— через Вставка/Символ из шрифта Times New Roman (не Symbol) вставляем все нужные греческие буквы, математические символы и hbar (Alt-0158) до кучи;
— по очереди выделяем и нажимаем Alt-F3;
— назначаем вменяемое имя (я сделал как латехе) alpha, beta, hbar, leq, geq, gg, ll, approx, propto, to, infty; большие греческие не получилось так сделать, так как автотекст в названии элемента автотекста не различает большие/маленькие буквы, сделал G → Γ, D → Δ, Y → Ψ, W → Ω.
— затем проделываем обратную операцию, пишем alpha;
— выделяем, нажимаем Alt-F3, назначаем имя в виде греческой буквы «α»;
— после всех этих операций желательно аккуратно закрыть ворд и снова его открыть, убедившись, что элементы автотекста сохранились (назначение автотекста и сочетаний клавиш хранятся в стандартном файле %appdata%MicrosoftШаблоныNormal.dot(m); если назначенные элементы автотекста не сохранились, то открывайте в ворде прямо Normal.dot или Normal.dotm для современных версий ворда от 2007 и выше, назначайте автозамену и сохраняйте файл шаблона Ctrl-S, тогда точно сохранится).
Все. Теперь, если написать в ворде alpha и сразу нажать F3, то получится греческая α, снова нажимаем F3, и α превращается в alpha.
Примечание: Мы стараемся как можно оперативнее обеспечивать вас актуальными справочными материалами на вашем языке. Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Просим вас уделить пару секунд и сообщить, помогла ли она вам, с помощью кнопок внизу страницы. Для удобства также приводим ссылку на оригинал (на английском языке).
В Word можно вставлять математические символы в уравнения и текст.
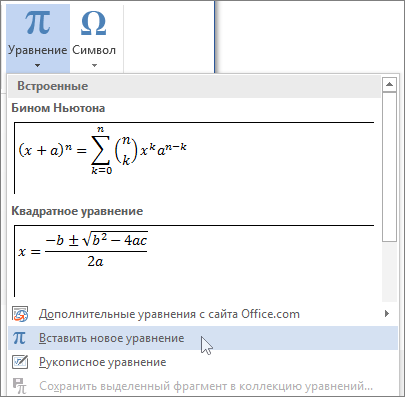
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
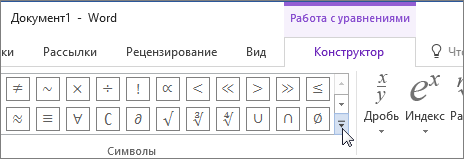
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов, а затем выберите набор символов, который вы хотите отобразить.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Формула плотности вещества
m
ρ = ——
V
ρ (ро) — плотность тела, m — масса тела, V — объем тела.
В Международной системе (СИ) плотность измеряют в килограммах на кубический метр или в граммах на кубический сантиметр (1 кг/м 3 или 1 г/см 3 ).
Источник
Функция ФИ и плотность стандартного нормального распределения в Excel
Функция ФИ в Excel предназначена для определения значения плотности вероятности величины, описанной законом стандартного нормального распределения, и возвращает соответствующее число.
Значения функции плотности стандартного нормального распределения в Excel
Если случайная величина распределена непрерывно, она может иметь любое значение, взятое из интервала, в котором она определена. Такое число значений стремится к бесконечности, следовательно, вероятность попадания в какую-либо определенную точку из данного интервала стремится к нулю (сумма вероятностей должна соответствовать числу 1). Поэтому, является возможным только определение вероятности нахождения некоторой величины в заданном интервале значений. С этой целью было введено понятие плотности вероятности – производная функции распределения. Для вычисления вероятности определяют площадь, образованную кривой графика, осью абсцисс и двумя вертикальными линиями, проведенными от точек, соответствующих граничным значениям исследуемого интервала.
Рассматриваемая функции вычисляет то же значение, которое возвращает функция НОРМ.СТ.РАСП, у которой второй аргумент принимает значение ЛОЖЬ.
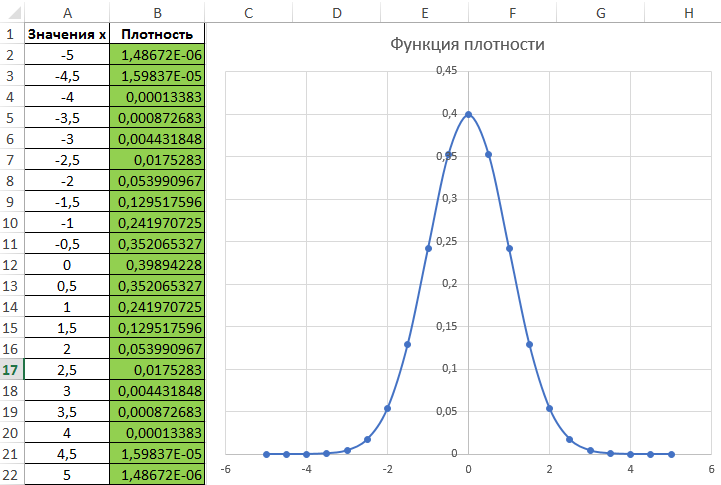
Пример 1. Построить график плотности вероятности для известных значений x, которые внесены в таблицу Excel.
Для построения графика определим значения плотности для известных значений x. Используем формулу, предварительно выделив ячейки в диапазоне B2:B22:
Используем полученные данные для построения графика:
Значение плотности вероятности имеет смысл при определении вероятности нахождения величины в некотором диапазоне. Ее используют для вычисления интеграла с указанными граничными значениями некоторой величины, в результате чего получают вероятность нахождения некоторого значения в диапазоне, заданного этими граничными значениями.
В Excel функция плотности используется преимущественно для построения графиков. Вероятность определяется функцией НОРМ.СТ.РАСП (для стандартного нормального распределение) с последним аргументом, принимающим значение ИСТИНА.
Пример расчета плотности стандартного нормального распределения в Excel
Пример 2. Определить максимальное значение плотности вероятности для ряда значений двумя различными способами.
Максимальное значение плотности вероятности для некоторой величины, распределенной по стандартному нормальному закону, можно определить с помощью функции МАКС, исследуя массив значений, возвращаемых функцией ФИ в формуле массива CTRL+SHIFT+Enter:
Другой способ – нахождение значения плотности для среднего значения известных величин. Однако, для начала необходимо стандартизировать имеющийся ряд значений с помощью функции НОРМАЛИЗАЦИЯ. Для нахождения используем формулу (вводить как формулу массива CTRL+SHIFT+Enter):
Небольшая разница в полученных значениях свидетельствует о том, что исследуемый ряд значений можно рассматривать как нормальное стандартное распределение некоторой величины.
Правила использования функции ФИ в Excel
Функция ФИ имеет следующую синтаксическую запись:
- x – обязательный, принимает число для некоторой величины, распределенной по стандартному нормальному закону, для которой необходимо определить значение плотности распределения.
- В качестве аргумента функции можно передавать ссылку на ячейку с числовыми данными или само число. Функция ФИ автоматические преобразует логические значения и текстовые строки, содержащие числа, к числовым значениям.
- Если аргумент функции принимает данные, не преобразуемые к числовым значениям, результатом выполнения ФИ будет код ошибки #ЗНАЧ!
- Для больших значений, значение плотности вероятности которых стремится к нулю, функция возвращает число 0. Например, =ФИ(100) вернет число 0.
Источник
Как использовать наборы значков для представления значений в Microsoft Excel
Если вы ищете уникальный способ представления данных в Microsoft Excel, подумайте об использовании наборов значков. Подобно цветовым шкалам, наборы значков принимают диапазон значений и используют визуальные эффекты для обозначения этих значений.
С помощью правила условного форматирования вы можете отображать значки, такие как светофор, звезды или стрелки, в зависимости от введенных вами значений. Например, вы можете показать пустую звезду для значения 10, частично заполненную звезду для 30 и заполненную заполненную звезду для 50.
Эта функция отлично подходит для таких вещей, как использование рейтинговой системы, отображение выполненных задач, представление продаж или отображение финансовых потоков.
Применение набора значков быстрого условного форматирования
Как и другие правила условного форматирования в Excel, такие как выделение значений с верхним или нижним рангом, у вас есть несколько быстрых вариантов на выбор. К ним относятся базовые наборы значков с использованием трех, четырех или пяти категорий с диапазоном предустановленных значений.
Выберите ячейки, к которым вы хотите применить форматирование, щелкнув первую ячейку и перетащив курсор через остальные.
Затем откройте вкладку «Главная» и перейдите в раздел «Стили» на ленте. Щелкните «Условное форматирование» и переместите курсор на «Наборы значков». Вы увидите список этих быстрых вариантов.
Когда вы наводите курсор на различные наборы значков, вы можете просмотреть их предварительно в своей электронной таблице. Это отличный способ узнать, какой набор иконок лучше всего подходит для вас.
Если вы заметили тот, который хотите использовать, просто щелкните по нему. Это применяет правило условного форматирования к выбранным ячейкам с выбранным набором значков. Как вы можете видеть на скриншоте ниже, мы выбрали звезды из нашего первоначального примера.
Создание набора значков настраиваемого условного форматирования
Как упоминалось ранее, к этим параметрам набора значков во всплывающем меню прилагаются предварительно заданные значения. Итак, если вам нужно настроить диапазоны, чтобы они соответствовали данным на вашем листе, вы можете создать собственное правило условного форматирования. И это проще, чем вы думаете!
Выберите ячейки, в которых вы хотите применить значки, перейдите на вкладку «Главная» и выберите «Новое правило» в раскрывающемся списке «Условное форматирование».
Когда откроется окно «Новое правило форматирования», выберите вверху «Форматировать все ячейки на основе их значений».
Внизу окна щелкните раскрывающийся список «Стиль формата» и выберите «Наборы значков». Затем вы настроите детали для правила.
В следующем раскрывающемся списке выберите стиль значка. Опять же, вы можете выбрать из трех, четырех или пяти категорий. Если вы предпочитаете, чтобы значки располагались в обратном порядке, нажмите «Обратный порядок значков».
Удобная особенность настраиваемого правила «Наборы значков» заключается в том, что вы не ограничиваетесь точным набором выбранных значков. Под раскрывающимся списком «Стиль значка» вы увидите поля для значков в группе. Это позволяет вам настроить точные значки для вашего правила. Так что если вы, например, хотите использовать звезду, флаг и стрелку вместо трех звезд, дерзайте!
Последняя часть настройки правила — это ввод значений для диапазона. Выберите «Больше» (>) или «Больше или равно» (> =) в первом раскрывающемся списке. Введите свое значение в следующее поле и выберите число, процент, формулу или процентиль. Это дает вам большую гибкость при настройке правила.
Теперь нажмите «ОК», чтобы применить правило.
Еще одна удобная функция, о которой стоит упомянуть, — это то, что вы можете отображать только значок. По умолчанию в Excel отображается как значок, так и введенное вами значение. Но могут быть случаи, когда вы планируете полагаться исключительно на значок. В этом случае установите флажок «Показывать только значок».
Вот потрясающий пример использования наборов значков, когда вы хотите отображать только значок.
Мы хотим отображать зеленые, желтые и красные значки светофора, чтобы указать, является ли наш заказ новым, выполняющимся или завершенным. Для этого мы просто введем цифры один, два или три. Как видите, в этом сценарии значения не важны. Они используются только для запуска значка, который мы и хотим видеть.
- Выберите наши значки светофора из трех категорий.
- Поменяйте порядок в обратном порядке (потому что мы хотим, чтобы наибольшее число было выделено красным).
- Введите наши значения «3» и «2» как «Числа».
- Установите флажок, чтобы отображался только значок.
Теперь все, что нам нужно сделать в нашем листе, — это ввести «1» для новых заказов, «2» для выполняемых и «3» для полных заказов. Когда мы нажимаем Enter, все, что мы видим, — это зеленый, желтый и красный индикаторы светофора.
Надеюсь, это руководство по использованию наборов значков в Microsoft Excel побудит вас воспользоваться этой замечательной функцией. И еще один способ использования условного форматирования: посмотрите, как создавать индикаторы выполнения в Excel.
Источник
Функция ФИ в Excel предназначена для определения значения плотности вероятности величины, описанной законом стандартного нормального распределения, и возвращает соответствующее число.
Значения функции плотности стандартного нормального распределения в Excel
Если случайная величина распределена непрерывно, она может иметь любое значение, взятое из интервала, в котором она определена. Такое число значений стремится к бесконечности, следовательно, вероятность попадания в какую-либо определенную точку из данного интервала стремится к нулю (сумма вероятностей должна соответствовать числу 1). Поэтому, является возможным только определение вероятности нахождения некоторой величины в заданном интервале значений. С этой целью было введено понятие плотности вероятности – производная функции распределения. Для вычисления вероятности определяют площадь, образованную кривой графика, осью абсцисс и двумя вертикальными линиями, проведенными от точек, соответствующих граничным значениям исследуемого интервала.
Рассматриваемая функции вычисляет то же значение, которое возвращает функция НОРМ.СТ.РАСП, у которой второй аргумент принимает значение ЛОЖЬ.
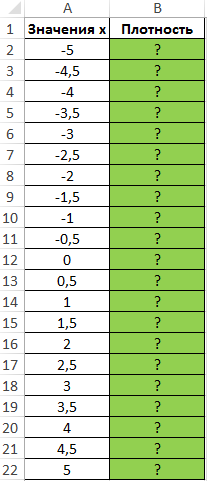
Пример 1. Построить график плотности вероятности для известных значений x, которые внесены в таблицу Excel.
Вид таблицы данных:
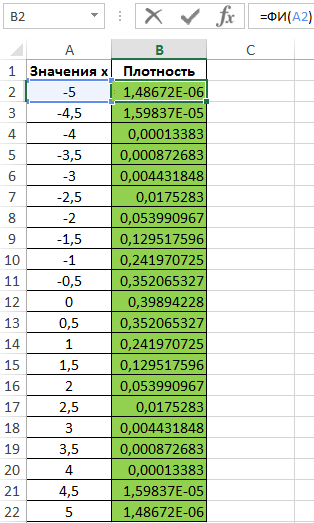
Для построения графика определим значения плотности для известных значений x. Используем формулу, предварительно выделив ячейки в диапазоне B2:B22:
=ФИ(A2)
Полученные значения:
Используем полученные данные для построения графика:
Значение плотности вероятности имеет смысл при определении вероятности нахождения величины в некотором диапазоне. Ее используют для вычисления интеграла с указанными граничными значениями некоторой величины, в результате чего получают вероятность нахождения некоторого значения в диапазоне, заданного этими граничными значениями.
В Excel функция плотности используется преимущественно для построения графиков. Вероятность определяется функцией НОРМ.СТ.РАСП (для стандартного нормального распределение) с последним аргументом, принимающим значение ИСТИНА.
Пример расчета плотности стандартного нормального распределения в Excel
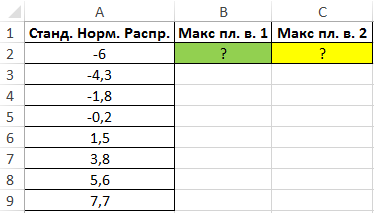
Пример 2. Определить максимальное значение плотности вероятности для ряда значений двумя различными способами.
Вид таблицы данных:
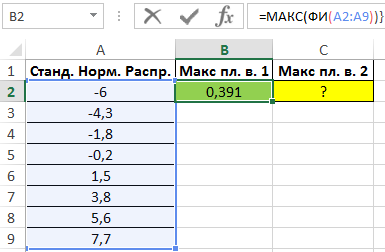
Максимальное значение плотности вероятности для некоторой величины, распределенной по стандартному нормальному закону, можно определить с помощью функции МАКС, исследуя массив значений, возвращаемых функцией ФИ в формуле массива CTRL+SHIFT+Enter:
=МАКС(ФИ(A2:A9))
Полученный результат:
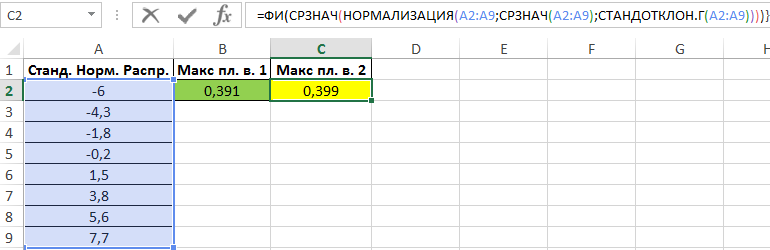
Другой способ – нахождение значения плотности для среднего значения известных величин. Однако, для начала необходимо стандартизировать имеющийся ряд значений с помощью функции НОРМАЛИЗАЦИЯ. Для нахождения используем формулу (вводить как формулу массива CTRL+SHIFT+Enter):
Полученное значение:
Небольшая разница в полученных значениях свидетельствует о том, что исследуемый ряд значений можно рассматривать как нормальное стандартное распределение некоторой величины.
Правила использования функции ФИ в Excel
Функция ФИ имеет следующую синтаксическую запись:
=ФИ(x)
- x – обязательный, принимает число для некоторой величины, распределенной по стандартному нормальному закону, для которой необходимо определить значение плотности распределения.
Примечания:
- В качестве аргумента функции можно передавать ссылку на ячейку с числовыми данными или само число. Функция ФИ автоматические преобразует логические значения и текстовые строки, содержащие числа, к числовым значениям.
- Если аргумент функции принимает данные, не преобразуемые к числовым значениям, результатом выполнения ФИ будет код ошибки #ЗНАЧ!
- Для больших значений, значение плотности вероятности которых стремится к нулю, функция возвращает число 0. Например, =ФИ(100) вернет число 0.