Значок лямбды в excel

Greek letters are commonly used in various areas, like mathematics and science as symbols for constants or variables, or even in the game industry to define phases of a product. They are also commonly used nowadays with naming new COVID-19 variants. If you need them in your worksheet, this article will show you how to use Greek Letters in Excel.

Download Workbook[/button

Copy & Paste

You can simply copy & paste the character from here:

α Α β Β γ Γ δ Δ ε Ε ζ Ζ η Η θ Θ ι Ι κ Κ λ Λ μ Μ ν Ν ξ Ξ ο Ο π Π ρ Ρ σ Σ τ Τ υ Υ φ Φ χ Χ ψ Ψ ω Ω

Enjoy. 🙂

Symbols

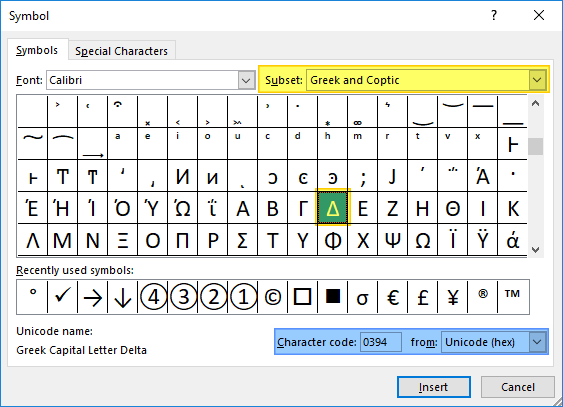
Excel (and Word) has a feature named Symbol which is a dialog that lists all supported characters in a single place. You can open the Symbol dialog by following INSERT > Symbols > Symbol path in the Ribbon.

In the Symbol dialog, choose Greek and Coptic in Subset dropdown and scroll down to find the Greek Letters. Select the letter you need and click the Insert button.

Alternatively, you can use the character code. First, select Unicode (hex) from dropdown and type the corresponding code into the Character code box.

Letter

Small Greek letter

Code

Capital Greek letter

Code

Letter

Small Greek letter

Code

Capital Greek letter

Code

Alpha

α

03B1

Α

391

Nu

ν

03BE

Ν

039D

Beta

β

03B2

Β

392

Xi

ξ

03BF

Ξ

039E

Gamma

γ

03B3

Γ

393

Omicron

ο

03C0

Ο

039F

Delta

δ

03B4

Δ

394

Pi

π

03C1

Π

03A0

Epsilon

ε

03B5

Ε

395

Rho

ρ

03C2

Ρ

03A1

Zeta

ζ

03B6

Ζ

396

Sigma

σ

03C3

Σ

03A3

Eta

η

03B7

Η

397

Tau

τ

03C4

Τ

03A4

Theta

θ

03B8

Θ

398

Upsilon

υ

03C5

Υ

03A5

Iota

ι

03B9

Ι

399

Phi

φ

03C6

Φ

03A6

Kappa

κ

03BA

Κ

039A

Chi

χ

03C7

Χ

03A7

Lambda

λ

03BB

Λ

039B

Psi

ψ

03C8

Ψ

03A8

Mu

μ

03BC

Μ

039C

Omega

ω

03C9

Ω

03A9

Symbol Font

Entire list of Greek Letter symbols is available in a font named Symbol. All you need to do is to change a cell’s font to Symbol and type the relevant character. For example, the capital «D» character returns the Δ symbol.

AutoCorrect

If you are frequently using one or a few Greek Letters in Excel, the AutoCorrect feature may become a life saver. The AutoCorrect is an essential Excel feature that corrects misspelled words automatically. An alternative use of this feature is its ability to insert symbols by typing keyboard friendly characters. For example, type (c) to get ©. You can add a new rule for a delta symbol as well.

1. Open Options window from File tab in the Ribbon.
2. Activate Proofing tab
3. Click AutoCorrect Options button
4. In the AutoCorrect dialog,
   1. enter a friendly text in Replace
   2. enter (copy/paste) a delta symbol in With
5. Click Add and OK buttons to apply rule and return back to worksheet
   

We chose the string «delta» as a friendly name. From now on, whenever we type «delta», Excel inserts a delta symbol.

Windows: 16.0.14729
Mac: 16.56 (сборка 211211)
Web: представлено 18 марта 2022 г.
iOS: 2.56 (сборка 211207)
Android: 16.0.14729

С помощью функции ЛЯМБДА можно создавать пользовательские функции для повторного использования и вызывать их по понятным именам. Новая функция доступна во всей книге и вызывается так же, как и основные функции Excel.

Вы можете создать функцию для часто используемой формулы, избавиться от необходимости копировать и вставлять эту формулу (что может приводить к ошибкам), а также эффективно добавлять собственные функции в основную библиотеку функций Excel. Кроме того, функция LAMBDA не требует VBA, макросов или JavaScript, поэтому ее могут использовать также пользователи, не являющиеся программистами. 

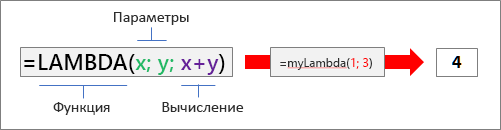
Синтаксис

=LAMBDA([параметр1; параметр2; …;] вычисление)    

Аргумент	Описание
параметр	Значение, которое вы хотите передать функции, например ссылку на ячейку, строку или число. Вы можете ввести до 253 параметров. Этот аргумент является необязательным.
вычисление	Формула, которую необходимо выполнить и вывести в качестве результата выполнения функции. Это должен быть последний аргумент и он должен возвращать результат. Это обязательный аргумент.

Замечания

• Имена и параметры функции LAMBDA соответствуют правилам синтаксиса Excel в отношении именования, за одним исключением: запрещено использовать точку (.) в имени параметра. Дополнительные сведения см. в статье Имена в формулах.

• При создании функции LAMBDA, как и в случае с любой основной формулой Excel, необходимо придерживаться рекомендаций, например, передавать правильное количество и тип аргументов, следить за соответствием открывающих и закрывающих скобок и вводить числа в неформатированном виде. Кроме того, при использовании команды Вычислить Excel немедленно возвращает результат функции LAMBDA, и вы не сможете выполнить ее пошагово. Дополнительные сведения см. в статье Обнаружение ошибок в формулах.

Ошибки

• В случае ввода более 253 параметров Excel возвращает ошибку «#ЗНАЧ!».

• В случае передачи функции LAMBDA неправильного количества аргументов Excel возвращает ошибку «#ЗНАЧ!».

• Если вы вызываете функцию LAMBDA из самой себя, и вызов является циклическим, Excel может вернуть #NUM! ошибка, если слишком много рекурсивных вызовов.

• Если создать функцию LAMBDA в ячейке, не вызвав ее также из самой ячейки, Excel возвращает ошибку «#ВЫЧИС!».

Создание функции LAMBDA

Ниже описана пошаговая процедура, выполнив которую, вы обеспечите правильную работу функции LAMBDA, которая будет выполняться аналогично основной функции Excel.

Убедитесь в правильности работы формулы, используемой вами при вычислении аргумента. Это крайне важно, так как при создании функции LAMBDA вам необходимо обеспечить, чтобы формула работала надлежащим образом, и в случае возникновения ошибок или непредвиденного поведения вы могли быть уверены, что не формула является тому причиной. Дополнительные сведения см. в статье Полные сведения о формулах в Excelи Создание простой формулы в Excel.

Рекомендуется создавать и испытывать свою функцию LAMBDA в ячейке, чтобы убедиться в правильности ее работы, включая определение и передачу параметров. Чтобы избежать ошибки #CALC!, добавьте вызов функции LAMBDA, чтобы немедленно вернуть результат:

=функция LAMBDA ([параметр1; параметр2; …];вычисление) (вызов функции)

В приведенном ниже примере возвращается значение 2.

=LAMBDA(number, number + 1)(1)

Завершив создание функции LAMBDA, переместите ее в диспетчер имен для окончательного определения. Таким образом вы сможете присвоить функции LAMBDA понятное имя, добавить описание и обеспечить возможность ее повторного использования в любой ячейке книги. Вы также можете управлять функцией LAMBDA точно так же, как и любым именем, например, строковой константы, диапазона ячеек или таблицы.

Последовательность действий

1. Выполните одно из указанных ниже действий.

   • В Excel для Windows выберите Формулы > Диспетчер имен.

   • В Excel для Mac выберите Формулы > Задать имя.

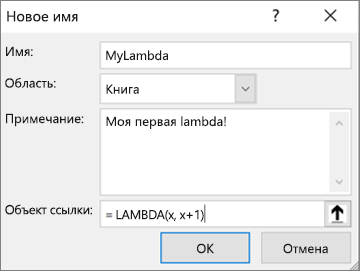
2. Выберите Новое, а затем введите необходимые данные в диалоговом окне Новое имя: 
    

   Имя:	Введите имя функции LAMBDA.
   Область:	Книга указывается по умолчанию. Также можно выбрать отдельные листы.
   Примечание:	Необязательно, но настоятельно рекомендуется. Введите до 255 знаков. Кратко опишите назначение функции, укажите правильное количество и тип аргументов. Отображается в диалоговом окне Вставить функцию и в виде подсказки (вместе с аргументом Вычисление ) при вводе формулы и использовании функции Автозаполнение формул (Intellisense).
   Объект ссылки:	Введите функцию LAMBDA.

   Например:

   

3. Чтобы создать функцию LAMBDA, нажмите ОК.

4. Чтобы закрыть диалоговое окно Диспетчер имен, нажмите Закрыть.

Дополнительные сведения см. в статье Использование Диспетчера имен.

Примеры

Определите в Диспетчере имен следующие данные:

Имя:	ToCelsius
Область:	Книга
Примечание:	Преобразование градусов по Фаренгейту в градусы Цельсия
Объект ссылки:	=LAMBDA(temp; (5/9) * (Temp-32))

Скопируйте данные примера из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
104
86
68
50
32
Формула	Результат
=TOCELSIUS(A2)	40
=TOCELSIUS(A3)	30
=TOCELSIUS(A4)	20
=TOCELSIUS(A5)	10
=TOCELSIUS(A6)	0

Определите в Диспетчере имен следующие данные:

Имя:	Гипотенуза
Область:	Книга
Примечание:	Возвращает длину гипотенузы прямоугольного треугольника
Объект ссылки:	=LAMBDA(a; b; КОРЕНЬ((a^2+b^2)))

Скопируйте данные примера из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
3	4
5	12
7	24
9	40
Формула	Результат
=HYPOTENUSE(A2,B2)	5
=HYPOTENUSE(A3,B3)	13
=HYPOTENUSE(A4,B4)	25
=HYPOTENUSE(A5,B5)	41

Определите в Диспетчере имен следующие данные:

Имя:	CountWords
Область:	Книга
Примечание:	Возвращает количество слов в текстовой строке
Объект ссылки:	=LAMBDA(текст; ДЛСТР(СЖПРОБЕЛЫ(текст)) — ДЛСТР(ПОДСТАВИТЬ(СЖПРОБЕЛЫ(текст); » «; «»)) + 1)

Скопируйте данные примера из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Что-то злое к нам спешит.
Пришел, увидел, победил.
Съешь же еще этих мягких французских булок, да выпей чаю.
Используй Силу, Люк!
Формула	Результат
=COUNTWORDS(A2)	5
=COUNTWORDS(A3)	6
=COUNTWORDS(A4)	9
=COUNTWORDS(A5)	4

Определите в Диспетчере имен следующие данные:

Имя:	ThanksgivingDate
Область:	Книга
Примечание:	Возвращает дату Дня Благодарения в США в текущем году
Объект ссылки:	=LAMBDA(год; ТЕКСТ(ДАТА(год; 11; ВЫБОР(ДЕНЬНЕД(ДАТА(год; 11; 1)); 26; 25; 24; 23; 22; 28; 27)); «mm/dd/yyyy»))

Скопируйте данные примера из таблицы ниже и вставьте их в ячейку A1 нового листа Excel. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
2020
2021
2022
2023
2024
Формула	Результат
=THANKSGIVINGDATE(A2)	11/26/2020
=THANKSGIVINGDATE(A3)	11/25/2021
=THANKSGIVINGDATE(A4)	11/24/2022
=THANKSGIVINGDATE(A5)	11/23/2023
=THANKSGIVINGDATE(A6)	11/28/2024

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Функция «LET»

Создание пользовательских функций в Excel

На данный момент в Microsoft Excel имеется почти пять сотен функций рабочего листа, доступных через окно Мастера функций — кнопка fx в строке формул. Это весьма приличный набор, но, тем не менее, почти каждый пользователь рано или поздно сталкивается с ситуацией, когда в этом списке не оказывается нужной ему функции — просто потому, что её нет в Excel.

До сих пор единственным способом решить эту проблему были макросы, т.е. написание своей пользовательской функции (UDF = User Defined Function) на Visual Basic, что требует соответствующей программистской квалификации и бывает, порой, совсем непросто. Однако, с последними обновлениями Office 365 ситуация изменилась в лучшую сторону — в Excel была добавлена специальная «обёрточная» функция LAMBDA. С её помощью задача по созданию собственных функций теперь решается легко и красиво.

Давайте рассмотрим принцип её использования на следующем примере.

Как вы, скорее всего, знаете в Excel есть несколько функции для разборки даты позволяющие определить номер дня, месяца, недели и года для указанной даты. Но почему-то нет функции, определяющий номер квартала, который тоже часто нужен, правда? Давайте исправим этот недостаток и создадим с помощью LAMBDA собственную новую функцию для решения этой задачи.

Шаг 1. Пишем формулу

Начём с того, что вручную привычным образом напишем формулу в ячейке листа, которая вычисляет то, что нам нужно. В случае с номером квартала это можно сделать, например, так:

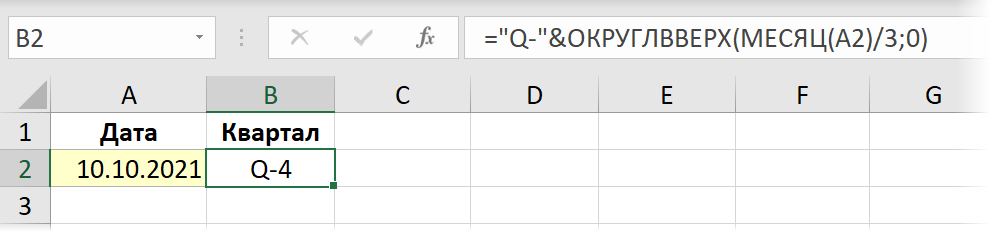
Шаг 2. Заворачиваем в LAMBDA и тестируем

Теперь пришло время применить новую функцию LAMBDA и завернуть в неё нашу формулу. Синтаксис у функции следующий:

=LAMBDA(Переменная1; Переменная2; … ПеременнаяN ; Выражение)

где сначала перечисляются имена одной или нескольких переменных, а последним аргументом всегда идёт формула или вычисляемое выражение, которое их использует. Имена переменных не должны быть похожи на адреса ячеек и не должны содержать точки.

В нашем случае переменная будет только одна — дата, для которой мы считаем номер квартала. Переменную для неё давайте назовем, допустим, d. Тогда завернув нашу формулу в функцию LAMBDA и подменив адрес исходной ячейки A2 на придуманное имя переменной, мы получим:

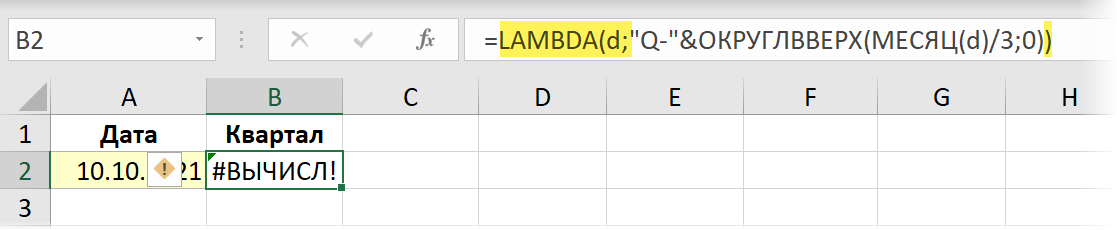
Обратите внимание, что после такого преобразования наша формула (по сути — правильная!) стала выдавать ошибку, т.к. теперь в неё не передается исходная дата из ячейки А2. Для тестирования и уверенности, можно передать ей аргументы, дописав их после функции LAMBDA в круглых скобках:

Шаг 3. Создаем имя

Теперь самая легкая и приятная часть. Открываем Диспетчер имен на вкладке Формулы (Formulas — Name Manager) и создаём новое имя кнопкой Создать (Create). Придумываем и вводим имя для нашей будущей функции (например, НОМКВАРТАЛА), а в поле Ссылка (Reference) аккуратно копируем из строки формул и вставляем нашу функцию LAMBDA, только без последнего аргумента (А2):

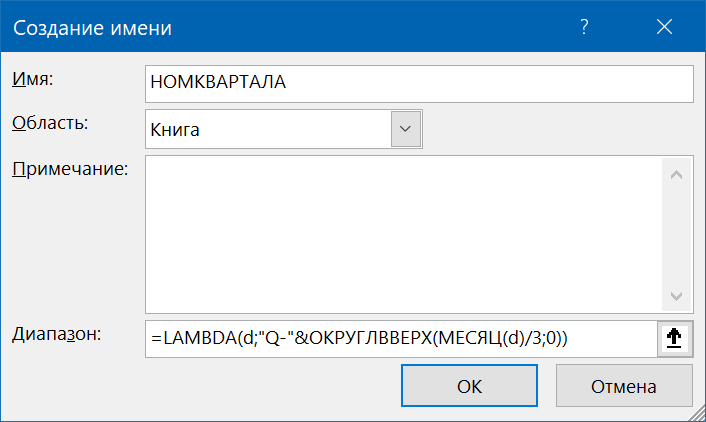
Всё. После нажатия на ОК созданную функцию можно использовать в любой ячейке на любом листе этой книги:

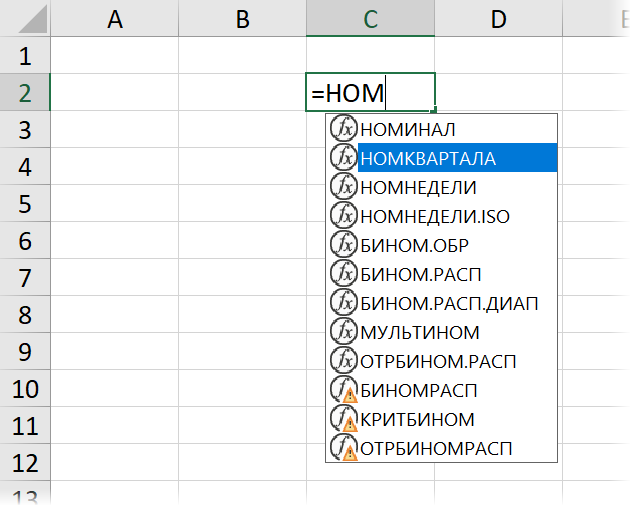
Использование в других книгах

Поскольку созданные с помощью LAMBDA пользовательские функции представляет из себя, по сути, именованные диапазоны, то можно легко сделать их доступными не только в текущей книге. Достаточно будет скопировать ячейку с функцией и вставить в любое место листа другого файла.

LAMBDA и динамические массивы

Пользовательские функции, создаваемые с помощью функции LAMBDA успешно поддерживают работу с новыми динамическими массивами и их функциями (ФИЛЬТР, УНИК, СОРТ), добавленными в Microsoft Excel в 2020 году.

Допустим, мы хотим создать новую пользовательскую функцию, которая сравнивала бы два списка и выдавала разницу между ними — те элементы из первого списка, которые отсутствуют во втором. Жизненная задача, не правда ли? Раньше для такого использовали либо функции а-ля ВПР (VLOOKUP), либо сводные таблицы, либо запросы Power Query. Теперь же можно обойтись одной формулой:

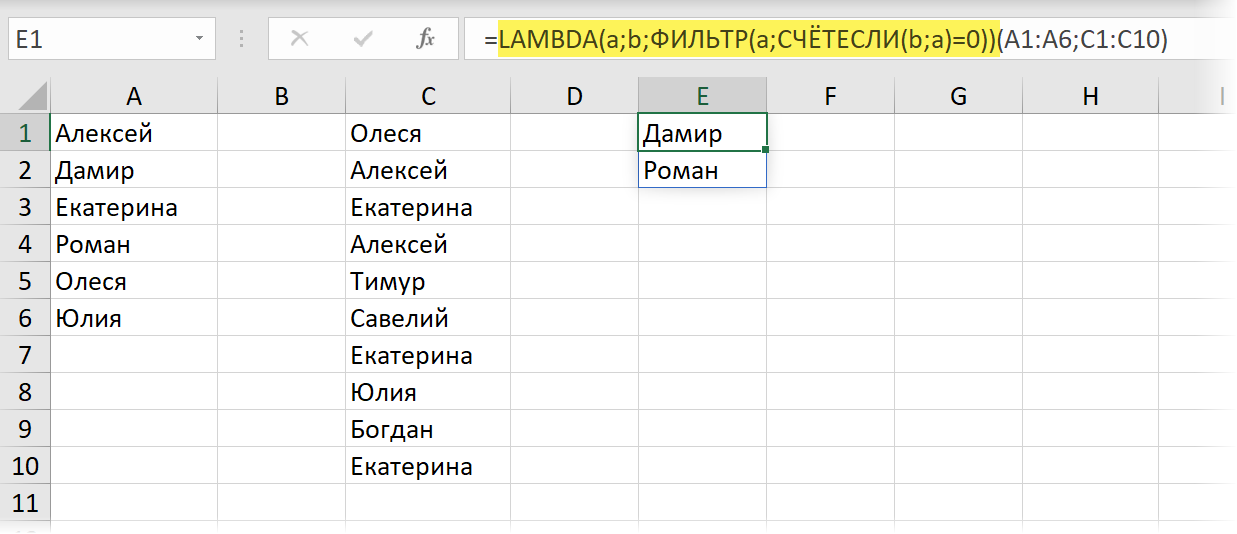
В английской версии это будет:

=LAMBDA(a;b;ФИЛЬТР(a;СЧЁТЕСЛИ(b;a)=0))(A1:A6;C1:C10)

Здесь функция СЧЁТЕСЛИ подсчитывает количество вхождений каждого элемента первого списка во второй, а затем функция ФИЛЬТР отбирает только те из них, у кого этих вхождений не оказалось. Завернув эту конструкцию в LAMBDA и создав на её основе именованный диапазон с названием, например, ПОИСКОТЛИЧ — мы получим удобную функцию, выдающую результат сравнения двух списков в виде динамического массива:

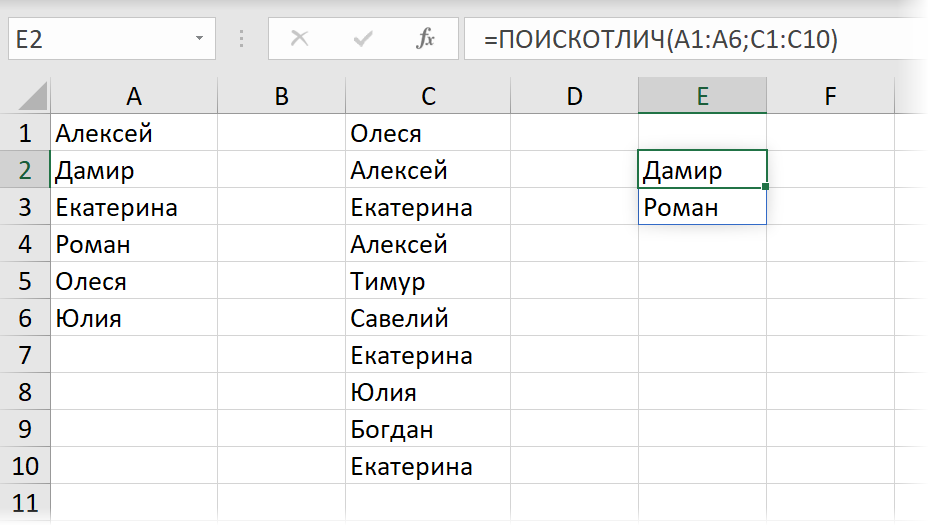
Если в качестве исходных данных будут не обычные, а «умные» таблицы — наша функция тоже справится без проблем:

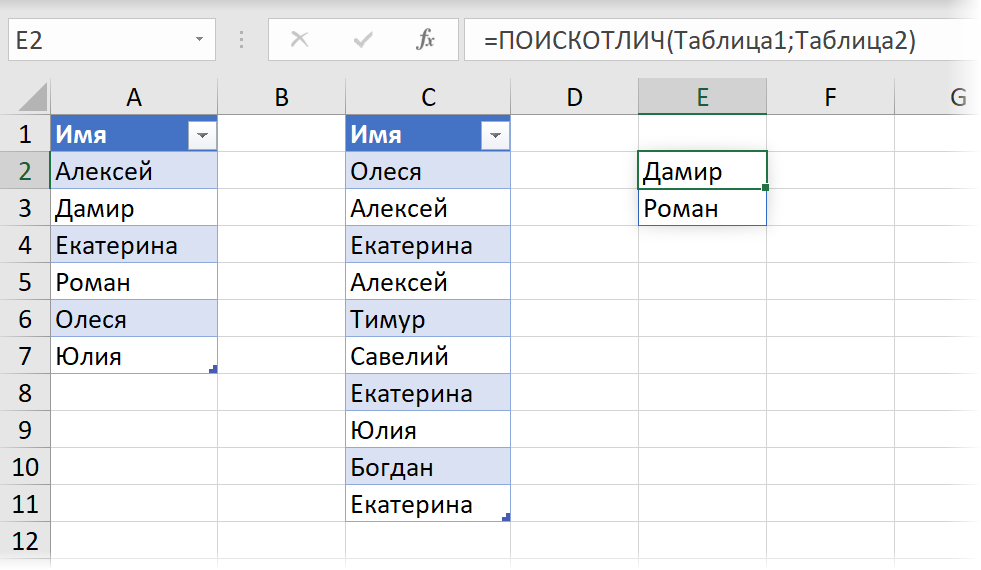
Другой пример — динамическое разделение текста путём превращения его в XML и последующего разбора по ячейкам с помощью функции ФИЛЬТР.XML, которое мы недавно разбирали. Чтобы не воспроизводить эту сложную формулу каждый раз вручную, проще будет завернуть её в LAMBDA и создать на её основе динамический диапазон, т.е. новую компактную и удобную функцию, назвав её, например, РАЗДТЕКСТ:

Первым аргументом этой функции будет ячейка с исходным текстом, а вторым — символ-разделитель, в возвращать результат она будет в виде горизонтального динамического массива. Код функции при этом будет следующим:

=LAMBDA(t;d; ТРАНСП(ФИЛЬТР.XML(«<x><y>»&ПОДСТАВИТЬ(t;d;»</y><y>»)&»</y></x>»;»//y»)))

Список примеров можно продолжать бесконечно — в любой ситуации, где вам часто приходится вводить одну и ту же длинную и громоздкую формулу функция LAMBDA сделает жизнь ощутимо проще.

Рекурсивный перебор символов

Все предыдущие примеры демонстрировали только одну, наиболее очевидную, сторону функции LAMBDA — её применение в качестве «обёртки» для заворачивания в неё длинных формул и упрощения их ввода. На самом деле, у LAMBDA есть ещё одна, гораздо более глубокая, сторона, превращающая её почти что в полноценный язык программирования.

Дело в том, что принципиально важной особенностью LAMBDA-функций является возможность реализации в них рекурсии — логики вычислений, когда в процессе расчета функция вызывает сама себя. С непривычки, возможно, звучит жутковато, но в программировании рекурсия — обычное дело. Даже в макросах на Visual Basic можно её реализовать, а теперь, вот, как видите, дошло и до Excel. Давайте попробуем разобраться в этой технике на практическом примере.

Предположим, нам требуется создать пользовательскую функцию, которая удаляла бы из исходного текста все заданные символы. Полезность такой функции, думаю, доказывать вам не нужно — с её помощью было бы очень удобно очищать замусоренные входные данные, правда?

Однако, по сравнению с предыдущими, нерекурсивными примерами, нас ожидают две сложности.

1. Нам придётся придумать название для нашей функции до того, как мы начнём писать её код, т.к. в нём это название уже будет использоваться для вызова функцией самой себя.
2. Ввести такую рекурсивную функцию в ячейку и отлаживать её, указав после LAMBDA аргументы в скобках (как мы делали ранее) не получится. Придётся создавать функцию сразу «с нуля» в Диспетчере Имен (Name Manager).

Назовём нашу функцию, допустим, ОЧИСТКА и хотелось бы, чтобы у неё было два аргумента — текст, который нужно почистить и список исключаемых символов в виде текстовой строки:

Создадим, как делали ранее, на вкладке Формулы в Диспетчере имён именованный диапазон, назовём его ОЧИСТКА и введём в поле Диапазон следующую конструкцию:

=LAMBDA(t;d;ЕСЛИ(d=»»;t;ОЧИСТКА(ПОДСТАВИТЬ(t;ЛЕВСИМВ(d);»»);ПСТР(d;2;255))))

Здесь переменная t — это исходный очищаемый текст, а d — список символов на удаление.

Работает всё это следующим образом:

Итерация 1

Фрагмент ПОДСТАВИТЬ(t;ЛЕВСИМВ(d);»»), как легко догадаться, заменяет в исходном тексте t первый слева символ из удаляемого набора d на пустую текстовую строку, т.е. удаляет букву «А». В качестве промежуточного результата получаем:

Вш зкз н 125 руб.

Итерация 2

Затем функция вызывает сама себя и в качестве входных данных (первый аргумент) получает уже то, что осталось после очистки на предыдущем шаге, а вторым аргументом задавая строку исключаемых символов начиная не с первого, а со второго символа, т.е. «БВГДЕЁЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,» без начальной «А» — это делает функция ПСТР. Как и до этого, функция берет первый слева символ из оставшихся (Б) и заменяет его в данном ей тексте (Зкз н 125 руб.) на пустую строку — получаем в качестве промежуточного результата:

Вш зкз н 125 ру.

Итерация 3

Функция опять вызывает сама себя, получая в качестве первого аргумента то, что осталось от зачищаемого текста на предыдущей итерации (Вш зкз н 125 ру.), а в качестве второго — урезанный слева ещё на один символ набор исключаемых знаков, т.е. «ВГДЕЁЖЗИКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯ.,» без начальной «Б». Затем опять берёт из этого набора первый символ слева (В) и удаляет его из текста — получаем:

ш зкз н 125 ру.

И так далее — надеюсь, вы ухватили идею. С каждой итерацией список удаляемых символов будет обрезаться слева и мы будем искать и заменять на пустоту очередной символ из набора.

Когда все символы закончатся нам необходимо будет выйти из цикла — эту роль как раз и выполняет функция ЕСЛИ (IF), в которую завернута наша конструкция. Если символов для удаления не осталось (d=»»), то функция не должна больше вызывать саму себя, а просто должна вернуть зачищаемый текст (переменная t) в его финальном виде.

Рекурсивный перебор ячеек

Похожим образом можно реализовать и рекурсивный перебор ячеек в заданном диапазоне. Предположим, что мы хотим создать лямбда-функцию с именем ЗАМЕНАПОСПИСКУ для оптовой замены фрагментов в исходном тексте по заданному списку-справочнику. Выглядеть всё это в результате должно так:

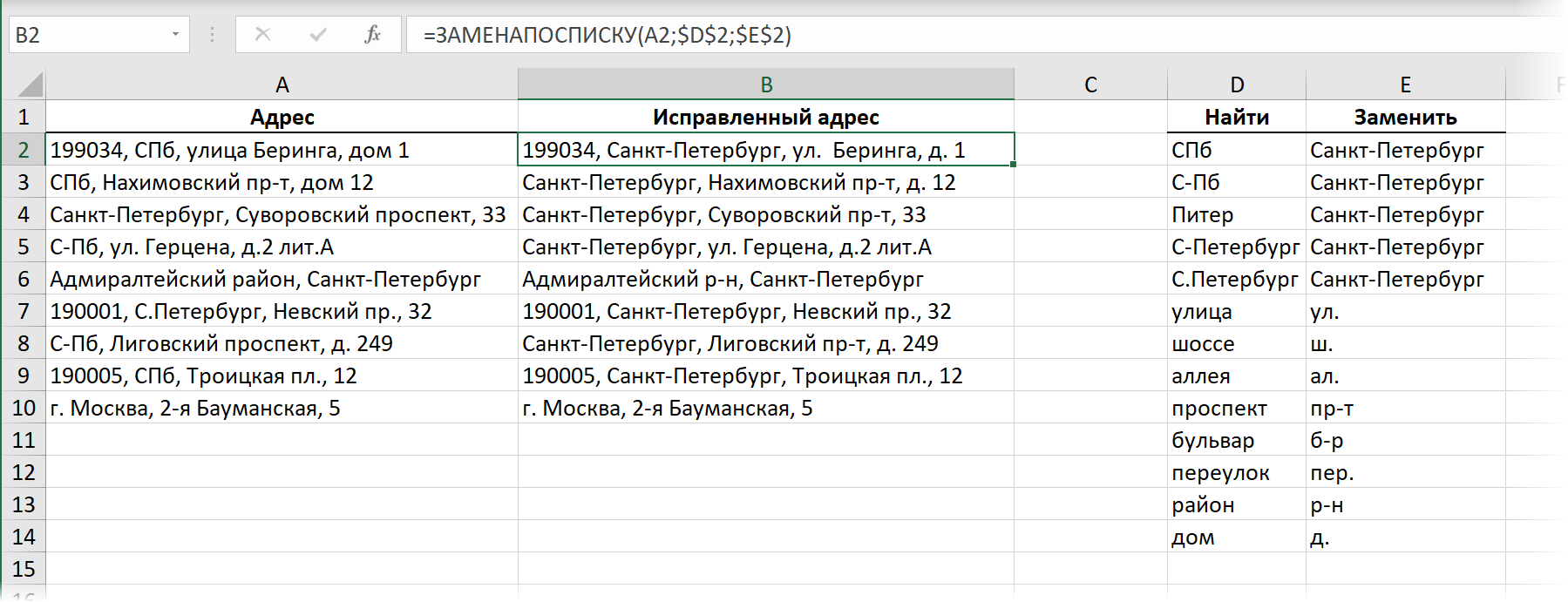
Т.е. у нашей функции ЗАМЕНАПОСПИСКУ будет три аргумента:

1. ячейка с текстом для обработки (исходный адрес)
2. первая ячейка столбца со значениями для поиска из справочника
3. первая ячейка столбца со значениями на замену из справочника

Функция должна проходить сверху-вниз по справочнику и заменять последовательно все варианты из левого столбца Найти на соответствующие варианты из правого столбца Заменить. Реализовать такое можно следующей рекурсивной лямбда-функцией:

Здесь в переменной t хранится исходный текст из очередной ячейки столбца Адрес, а переменные n и z указывают на первые ячейки в столбцах Найти и Заменить, соответственно.

Как и в предыдущем примере, сначала эта функция заменяет в исходном тексте с помощью функции ПОДСТАВИТЬ (SUBSTITUTE) данные по первой строке справочника (т.е. СПб на Санкт-Петербург), а затем вызывает сама-себя, но со сдвигом по справочнику вниз на следующую строку (т.е. заменяет С-Пб на Санкт-Петербург). Затем вызывает себя ещё раз со сдвигом вниз — и заменяет уже Питер на Санкт-Петербург и т.д.

Сдвиг вниз на каждой итериации реализован стандартной экселевской функцией СМЕЩ (OFFSET), у которой в данном случае три аргумента — исходный диапазон, сдвиг по строкам (1) и сдвиг по столбцам (0).

Ну, и как только мы достигаем конца справочника (n=»»), то должны закончить рекурсию — прекращаем вызывать сами себя и выводим то, что накопилось после всех выполненных замен в переменной исходного текста t.

Вот и всё. Никаких хитрых макросов или запросов Power Query — вся задача решается одной функцией.

Ссылки по теме

• Как использовать новые функции динамических массивов Excel: ФИЛЬТР, СОРТ, УНИК
• Замена и зачистка текста функцией ПОДСТАВИТЬ
• Создание макросов и пользовательских функций (UDF) на VBA

The LAMBDA function provides a way to create a custom function in Excel. Once defined and named, a LAMBDA function can be used anywhere in a workbook. LAMBDA functions can be very simple, or quite complex, stringing together many Excel functions into one formula. A custom LAMBDA function does not require VBA or macros.

Example 1 | Example 2 | Example 3 | More examples

In computer programming, the term LAMBDA refers to an anonymous function or expression. An anonymous function is a function defined without a name. In Excel, the LAMBDA function is first used to create a generic (unnamed) formula. Once a generic version has been created and tested, it is ported to the Name Manager, where it is formally defined and named.

One of the key benefits of a custom LAMBDA function is that the logic contained in the formula exists in just one place. This means there is just one copy of code to update when fixing problems or updating functionality, and changes will automatically propagate to all instances of the LAMBDA function in a workbook.

The LET function is often used together with the LAMBDA function. LET provides a way to declare variables and assign values in a formula. This makes more complicated formulas easier to read by reducing redundant code. The LET function can also improve performance by reducing the number of calculations performed by a formula.

By default, all arguments in a LAMBDA function are required. To create optional arguments, see the ISOMITTED function.

Creating a LAMBDA function

LAMBDA functions are typically created and debugged in the formula bar on a worksheet, then moved into the name manager to assign a name that can be used anywhere in a workbook. 

There are four basic steps to creating and using a custom LAMBDA function:

1. Verify the logic you will use with a standard formula
2. Create and test a generic (unnamed) LAMBDA version of the formula
3. Name and define the LAMBDA formula with the name manager
4. Call the new custom function with the defined name

The examples below discuss these steps in more detail.

Example 1 — basic example

To illustrate how LAMBDA works, let’s begin with a very simple formula:

=x*y // multiply x and y

In Excel, this formula would use typically use cell references like this:

=B5*C5 // with cell references

As you can see, the formula works fine, so we are ready to move on to creating a generic LAMBDA formula (unnamed version). The first thing to consider is if the formula requires inputs (parameters). In this case, the answer is «yes» – the formula requires a value for x, and a value for y. With that established, we start off with the LAMBDA function, and add the required parameters for user input:

=LAMBDA(x,y  // begin with input parameters

Next, we need to add the actual calculation, x*y:

=LAMBDA(x,y,x*y)

If you enter the formula at this point, you’ll get a #CALC! error. This happens because the formula has no input values to work with since there are no longer any cell references. To test the formula, we need to use a special syntax like this:

=LAMBDA(x,y,x*y)(B5,C5) // testing syntax

This syntax, where parameters are supplied at the end of a LAMBDA function in a separate set of parentheses, is unique to LAMBDA functions. This allows the formula to be tested directly on the worksheet before the LAMBDA is named. In the screen below, you can see that the generic LAMBDA function in F5 returns exactly the same result as the original formula in E5:

We are now ready to name the LAMBDA function with the Name Manager. First, copy the formula, not including the testing parameters at the end. Next, open the Name Manager with the shortcut Control + F3, and click New.

In the New Name dialog, enter the name  «XBYY», leave the scope set to workbook, and paste the formula you copied into the «Refers to» input area. (Tip: Use the tab key to navigate to the «Refers to» field).

Make sure the formula begins with an equals sign (=). Now that the LAMBDA formula has a name, it can be used in the workbook like any other function. In the screen below the formula in G5, copied down, is:

=XBYY(B5,C5)

The screen below shows how things look in the workbook:

The new custom function returns the same result as the other two formulas.

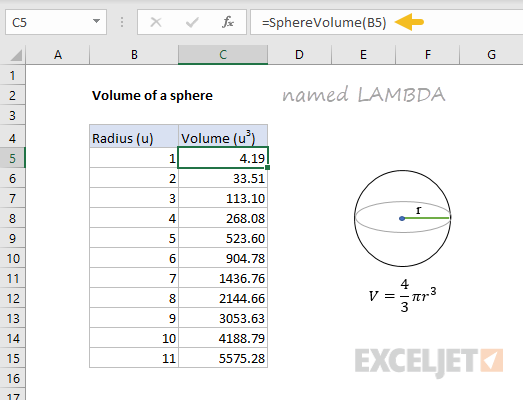
Example 2 — volume of sphere

In this example, we’ll convert a formula to calculate the volume of a sphere into a custom LAMBDA function. The general Excel formula for calculating the volume of a sphere is:

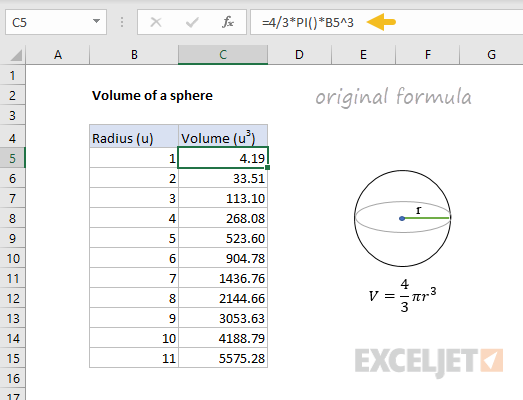
=4/3*PI()*A1^3 // volume of sphere

where A1 represents radius. The screen below shows this formula in action:

Notice this formula only requires one input (radius) to calculate volume, so our LAMBDA function will only need one parameter (r), which will appear as the first argument. Here is the formula converted to LAMBDA:

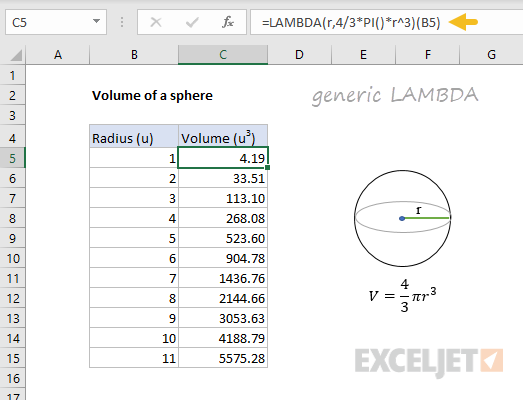
=LAMBDA(r,4/3*PI()*r^3) // generic lambda

Back in the worksheet, we’ve replaced the original formula with the generic LAMBDA version. Notice we are using the testing syntax, which allows us to plug in B5 for radius:

The results from the generic LAMBDA formula are exactly the same as the original formula, so the next step is to define and name this LAMBDA formula with the Name Manager, as explained above. The name used for a LAMBDA function can be any valid Excel name. In this case, we’ll name the formula «SphereVolume».

Back in the worksheet, we’ve replaced the generic (unnamed) LAMBDA formula with the named LAMBDA version, and entered B5 for r. Notice the results returned by the custom SphereVolume function are exactly the same as previous results.

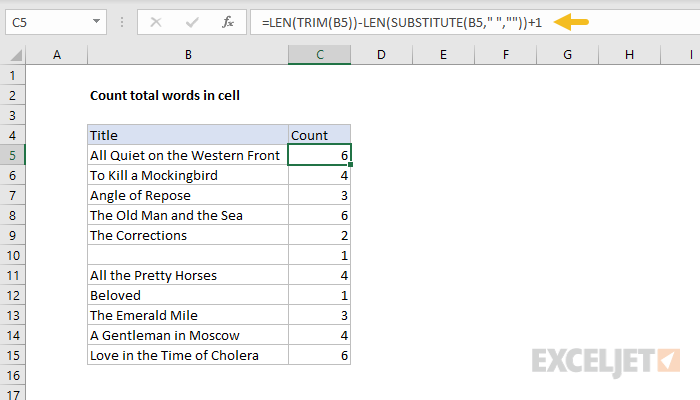
Example 3 — count words

In this example, we’ll create a LAMBDA function to count words. Excel doesn’t have a function for this purpose, but you can count words with a cell with a custom formula based on the LEN and SUBSTITUTE functions like this:

=LEN(TRIM(A1))-LEN(SUBSTITUTE(A1," ",""))+1

Read the detailed explanation here. Here is the formula in action in a worksheet:

Notice we are getting an incorrect count of 1 when the formula is given an empty cell (B10). We’ll address this problem below.

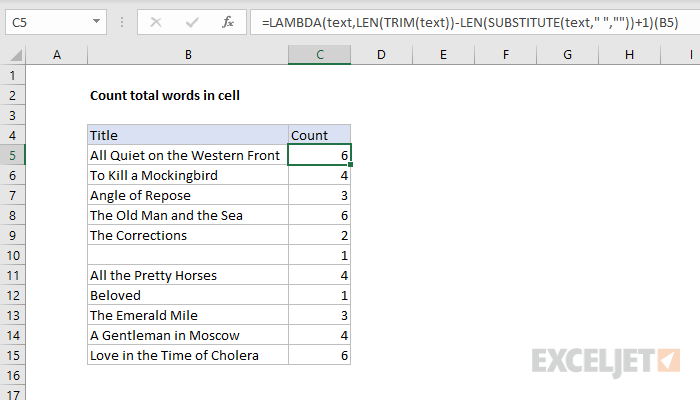
This formula only requires one input, which is the text that contains words. In our LAMBDA function, we’ll name this argument «text». Here is the formula converted to LAMBDA:

=LAMBDA(text,LEN(TRIM(text))-LEN(SUBSTITUTE(text," ",""))+1)

Notice «text» appears as the first argument, and the calculation is the second and final argument. In the screen below, we’ve replaced the original formula with the generic LAMBDA version. Notice we are using the testing syntax, which allows us to plug in B5 for text:

=LAMBDA(text,LEN(TRIM(text))-LEN(SUBSTITUTE(text," ",""))+1)(B5)

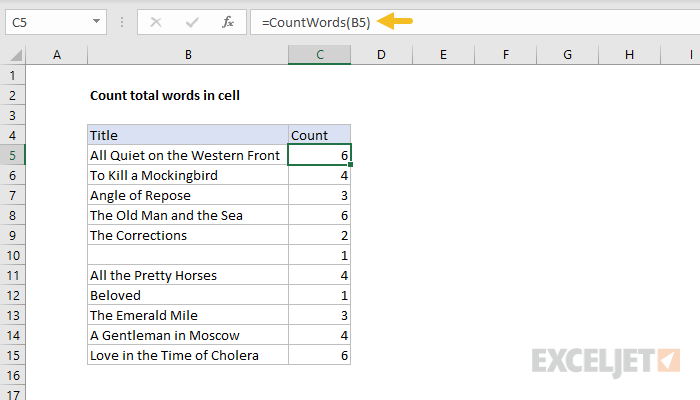
The results from the generic LAMBDA formula are the same as the original formula, so the next step is to define and name this LAMBDA formula with the Name Manager, as explained previously. We’ll name this formula «CountWords».

Below, we’ve replaced the generic (unnamed) LAMBDA formula with the named LAMBDA version, and entered B5 for text. Notice we get exactly the same results.

The formula used in the Name Manager to define CountWords is the same as above, without the testing syntax:

=LAMBDA(text,LEN(TRIM(text))-LEN(SUBSTITUTE(text," ",""))+1)

Fixing the empty cell problem

As mentioned above, the formula above returns an incorrect count of 1 when a cell is empty. This problem can be fixed by replacing +1 with the code below:

=LEN(TRIM(B5))-LEN(SUBSTITUTE(B5," ",""))+(LEN(TRIM(B5))>0)

Full explanation here. To update the existing named LAMBDA formula, we again need to use the Name Manager:

1. Open the Name Manager
2. Select the name «CountWords» and click «Edit»
3. Replace the «Refers to» code with this formula:

=LAMBDA(text,LEN(TRIM(text))-LEN(SUBSTITUTE(text," ",""))+(LEN(TRIM(text))>0))

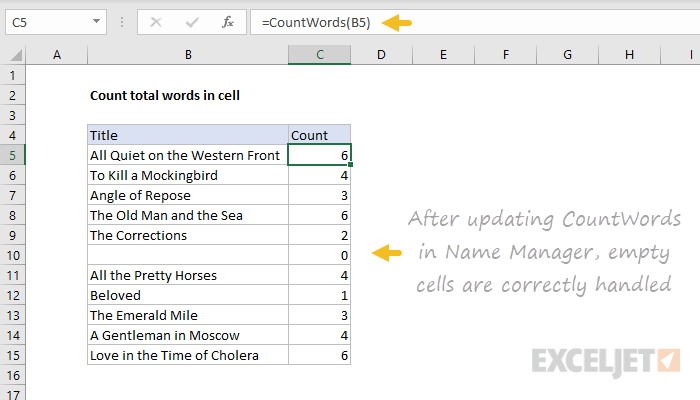
Once the Name Manager is closed, the CountWords works correctly on empty cells, as seen below:

Note: by updating the code once in the Name Manager, all instances of the CountWords formula are updated at once. This is a key benefit of custom functions created with LAMBDA –formula updates can be managed in one place.

LAMBDA is a new function available in Excel 365 only.

Как написать лямбду в ворде? Какой код Лямбда в ворде?

В программе ворд можно поставить разнообразные символы, в т.ч. лямбду. Так как с её написанием нередко возникают вопросы, то рассмотрим подробную инструкцию, как написать лямбду в программе ворд.

Первый шаг. Выберем на листе место, куда поставим символ лямбды, после перейдем на верхней панели настроек в закладку «Вставка» и нажмем в блоке «Символы» на иконку с аналогичным названием.

Второй шаг. В появившемся меню, нажмите на самую последнюю строчку «Другие символы».

Третий шаг. Появится подробное меню выбора различных символов, в строке набор из выпадающего списка, необходимо выбрать «греческие и коптские символы». Там можно найти маленькую и большую лямбду.

В итоге мы поставили в программе символы лямбда.

Некоторые пользователи вставляют символы через коды. Чтобы поставить символ большая лямбда, нужно вести код «039B», а для маленькой «03BB». Для преобразования кода в символ, поле его введения, нужно нажать сочетания клавиш «ALT+X».

Источник

Знак лямбда в ворде

Лямбда — 11-я буква греческого алфавита (использовалась также в коптском). В ионийской системе счисления соответствовала значению 30. Произошла от финикийской буквы Ламд. От самой лямбды произошли многие буквы, такие как L или Л.

Строчная лямбда широко используется в научной нотации. Лямбдой обозначается длина волны, постоянная распада, удельная теплота плавления, плотность заряда, а также многие другие переменные. λ-зонд — датчик остаточного кислорода в выхлопных газах. λ-фаг — название одного из бактериофагов.

Этот текст также доступен на следующих языках: English;

В программе ворд можно поставить разнообразные символы, в т.ч. лямбду. Так как с её написанием нередко возникают вопросы, то рассмотрим подробную инструкцию, как написать лямбду в программе ворд.

Первый шаг. Выберем на листе место, куда поставим символ лямбды, после перейдем на верхней панели настроек в закладку «Вставка» и нажмем в блоке «Символы» на иконку с аналогичным названием.

Второй шаг. В появившемся меню, нажмите на самую последнюю строчку «Другие символы».

Третий шаг. Появится подробное меню выбора различных символов, в строке набор из выпадающего списка, необходимо выбрать «греческие и коптские символы». Там можно найти маленькую и большую лямбду.

В итоге мы поставили в программе символы лямбда.

Некоторые пользователи вставляют символы через коды. Чтобы поставить символ большая лямбда, нужно вести код «039B», а для маленькой «03BB». Для преобразования кода в символ, поле его введения, нужно нажать сочетания клавиш «ALT+X».

Что такое альт код? Alt-код — это символы, которые выводятся при нажатии комбинации клавиш на клавиатуре Alt + X, где X это набор цифр (определенного числа) на NumPad’е. NumPAd это блок цифр на клавиатуре как правило расположенных справа. Символы альт на ПК с операционными системами Windows не доступны при использовании обычной клавиатуры. Их можно вызывать только при помощи дополнительных команд. Зажимаем кнопку ALT и набираем число в десятичной системе счисления. Надеюсь здесь все понятно. Таблица Alt кодов поможет вам сориентироваться и найти нужный символ.

Внимание! Цифры набирайте на боковой Num-pad клавиатуре.

Источник

Как поставить знак лямбда в ворде

Вставка математических знаков

В Word можно вставлять математические символы в уравнения и текст.

На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.

В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.

Щелкните стрелку рядом с именем набора символов, а затем выберите набор символов, который вы хотите отобразить.

Щелкните нужный символ.

Доступные наборы символов

В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.

Основные математические символы

Часто используемые математические символы, такие как > и

Как создать сайт в программе Frontpage — Уроки Frontpage

Как в word вставить лямбду

Как написать лямбду в ворде? Какой код Лямбда в ворде?

В программе ворд можно поставить разнообразные символы, в т.ч. лямбду. Так как с её написанием нередко возникают вопросы, то рассмотрим подробную инструкцию, как написать лямбду в программе ворд.

Первый шаг. Выберем на листе место, куда поставим символ лямбды, после перейдем на верхней панели настроек в закладку «Вставка» и нажмем в блоке «Символы» на иконку с аналогичным названием.

Второй шаг. В появившемся меню, нажмите на самую последнюю строчку «Другие символы».

Третий шаг. Появится подробное меню выбора различных символов, в строке набор из выпадающего списка, необходимо выбрать «греческие и коптские символы». Там можно найти маленькую и большую лямбду.

В итоге мы поставили в программе символы лямбда.

Некоторые пользователи вставляют символы через коды. Чтобы поставить символ большая лямбда, нужно вести код «039B», а для маленькой «03BB». Для преобразования кода в символ, поле его введения, нужно нажать сочетания клавиш «ALT+X».

Смотрите дополнительно:

Бесплатный видеокурс по работе в программе эксель для начинающих.

Горячие клавиши для вставки греческих символов в уравнение

альфа	каппа	varrho
beta	лямбда	сигма
чи	му	varsigma
дельта	nu	тау
эпсилон	о	ипсилон
варепсилон	pi	омега
фи	varpi	xi
varphi	тета	фунтов / кв. Дюйм
гамма	vartheta	zeta
eta	rho

См. Горячие клавиши для вставки символов и шаблонов в уравнение, чтобы часто находить другие использованные символы.

Чтобы вставить заглавную букву греческого алфавита, просто введите + Имя символа , начиная с с большой буквы:

Delta	Phi	Гамма
Лямбда	му	Pi
Тета	Sigma	Ипсилон
Омега	Hi	пси

Как вставлять другие символы и шаблоны в уравнение, см. Горячие клавиши для вставки символов и шаблонов в уравнение.

См. Также этот совет на французском: Raccourcis клавир для ввода греческих символов в уравнениях.

c # — Добавить подходящее слово в список с лямбда-выражением

Горячие клавиши для вставки символов и шаблонов в уравнение

Некоторые из часто используемых символов:

leq — меньше или равно

geq — больше или равно

partial — Частичный дифференциал

prod — Знак продукта

subset — Содержится в

cup — Союз (если хотите увидеть большой символ, введите bigcup )

приблизительно — Почти равно (асимптотически)

экв — идентично (эквивалент)

oint — Контур интегральный

См. Также этот совет на французском: Клавишный Раккурсис для ввода символов и моделей в уравнениях.

λ Греческая строчная буква лямбда

U+03BB

Нажмите, чтобы скопировать и вставить символ

Техническая информация

Значение символа

Лямбда — 11-я буква греческого алфавита (использовалась также в коптском). В ионийской системе счисления соответствовала значению 30. Произошла от финикийской буквы Ламд. От самой лямбды произошли многие буквы, такие как L или Л.

Строчная лямбда широко используется в научной нотации. Лямбдой обозначается длина волны, постоянная распада, удельная теплота плавления, плотность заряда, а также многие другие переменные. λ-зонд — датчик остаточного кислорода в выхлопных газах. λ-фаг — название одного из бактериофагов.

Символ «Греческая строчная буква лямбда» был утвержден как часть Юникода версии 1.1 в 1993 г.

Этот текст также доступен на следующих языках: English;

Источник

λ-исчисление. Часть первая: история и теория

Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.

UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.

Вступление

Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)

Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.

Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.

Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…

λ-исчисление: основные понятия

Синтаксис

В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.

Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.

Процесс вычисления

Рассмотрим следующий терм-применение:

Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:

который для простоты можно переписать как

(напомним, что id — это функция тождества вида λx.x )

В этом терме содержится три редекса:

Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение

(λx.λy. x) z ((λx.x x)(λx.x x))

Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.

На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.

Источник

C++0x (С++11). Лямбда-выражения

Буквально на днях случайно наткнулся на Хабре на статью о лямбда-выражениях из нового (будущего) стандарта C++. Статья хорошая и даёт понять преимущества лямбда-выражений, однако, мне показалось, что статья недостаточно полная, поэтому я решил попробовать более детально изложить материал.

Вспомним основы

Лямбда-выражения — одна из фич функциональных языков, которую в последнее время начали добавлять также в императивные языки типа C#, C++ etc. Лямбда-выражениями называются безымянные локальные функции, которые можно создавать прямо внутри какого-либо выражения.

В прошлой статье лямбда-выражения сравнивали с указателями на функции и с функторами. Так вот первое, что следует уяснить: лямбда-выражения в C++ — это краткая форма записи анонимных функторов. Рассмотрим пример:

Фактически данный код целиком соответствует такому:

Вывод соответственно будет следующим:

На что здесь стоит обратить внимание. Во-первых, из Листинга 1 мы видим, что лямбда-выражение всегда начинается с [] (скобки могут быть непустыми — об этом позже), затем идет необязательный список параметров, а затем непосредственно тело функции. Во-вторых, тип возвращаемого значения мы не указывали, и по умолчанию лямбда возвращает void (далее мы увидим, как и зачем можно указать возвращаемый тип явно). В-третьих, как видно по Листингу 2, по умолчанию генерируется константный метод (к этому тоже еще вернемся).

Не знаю, как вам, но мне for_each, записанный с помощью лямбда-выражения, нравится гораздо больше. Попробуем написать немного усложненный пример:

В данном случае лямбда играет роль унарного предиката, то есть тип возвращаемого значения bool, хотя мы нигде этого не указывали. При наличии одного return в лямбда-выражении, компилятор вычисляет тип возвращаемого значения самостоятельно. Если же в лямбда-выражении присутствует if или switch (или другие сложные конструкции), как в приведенном ниже коде, то на компилятор полагаться уже нельзя:

Код из Листинга 4 не компилируется, а, к примеру, Visual Studio пишет ошибку на каждый return такого содержания:

Компилятор не может самостоятельно вычислить тип возвращаемого значения, поэтому мы должны его указать явно:

Теперь компиляция проходит успешно, а вывод, как и ожидалось, будет следующим:

Единственное, что мы добавили в Листинге 5, это тип возвращаемого значения для лямбда-выражения в виде -> double. Синтаксис немного странноват и смахивает больше на Haskell, чем на C++. Но указывать возвращаемый тип «слева» (как в функциях) не получилось бы, потому что лямбда должна начинаться с [], чтобы компилятор смог её различить.

Захват переменных из внешнего контекста

Все лямбда-выражения, приведенные выше, выглядели как анонимные функции, потому что не хранили никакого промежуточного состояния. Но лямбда-выражения в C++ — это анонимные функторы, а значит состояние они хранить могут! Используя лямбда-выражения, напишем программу, которая выводит количество чисел, попадающих в заданный пользователем интервал [lower; upper):

Наконец, мы добрались до того момента, когда лямбда-выражение начинается не с пустых скобок. Как видно в Листинге 6, внутри квадратных скобок могут указываться переменные. Это называется… эээм… «список захвата» (capture list). Для чего это нужно? На первый взгляд может показаться, что внешней областью видимости для лямбда-выражения является функция main() и мы можем беспрепятственно использовать переменные, объявленные в ней, внутри тела лямбда-выражения, однако это не так. Почему? Потому что фактически тело лямбды — это тело перегруженного operator()() (как бы это назвать… оператора функционального вызова что ли) внутри анонимного функтора, то есть для кода из Листинга 6 компилятор неявно сгенерирует примерно такой код:

Листинг 7 немного всё разъясняет. Наша лямбда превратилась в функтор, внутри тела которого мы не можем напрямую использовать переменные, объявленные в main(), так как это непересекающиеся области видимости. Для того чтобы доступ к lowerBound и upperBound все-таки был, эти переменные сохраняются внутри самого функтора (происходит тот самый «захват»): конструктор их инициализирует, а внутри operator()() они используются. Я специально дал этим переменным имена, начинающиеся с префикса «m_», чтобы подчеркнуть различие.

Если мы попытаемся изменить «захваченные» переменные внутри лямбды, нас ждет неудача, потому что по умолчанию генерируемый operator()() объявлен как const. Для того чтобы это обойти, мы можем указать спецификатор mutable, как в следующем примере:

Ранее я упоминал, что список параметров лямбды можно опускать, когда он пустой, однако для того чтобы компилятор правильно распарсил применение слова mutable, мы должны явно указать пустой список параметров.
При выполнении программы из Листинга 8 получаем следующее:

Как видим, благодаря ключевому слову mutable, мы можем менять значение «захваченной» переменной внутри тела лямбда-выражения, но, как и следовало ожидать, эти изменения не отражаются на локальной переменной, так как захват происходит по значению. C++ позволяет нам захватывать переменные по ссылке и даже указывать «режим захвата», используемый по умолчанию. Что это означает? Мы можем не указывать каждую переменную в списке захвата по отдельности: вместо этого можно просто указать режим по умолчанию для захвата, и тогда все переменные из внешнего контекста, которые используются внутри лямбды, будут захвачены компилятором автоматически. Для указания режима захвата по умолчанию существует специальный синтаксис: [=] или [&] для захвата по значению и по ссылке соответственно. При этом для каждой переменной можно указать свой режим захвата, однако режим по умолчанию, естественно, указывается только единожды, причем в самом начале списка захвата. Вот варианты использования:

Следует отметить, что синтаксис наподобие &out в данном случае не означает взятие адреса. Его следует читать скорее как SomeType & out, то есть это просто передача параметра по ссылке. Рассмотрим пример:

В этот раз вместо явного захвата переменной init, я указал режим захвата по умолчанию: [&]. Теперь когда компилятор встречает внутри тела лямбды переменную из внешнего контекста, он автоматически захватывает её по ссылке. Вот эквивалентный Листингу 9 код:

И соответственно вывод будет следующим:

Теперь вам главное не запутаться, что, где и когда передавать по ссылке. Фактически, если мы указываем [&] и не указываем mutable, то все равно сможем менять значение захваченной переменной и это отразится на локальной, потому что operator()() const подразумевает, что мы не можем менять, на что указывает ссылка, а это и так невозможно.

Я так понял, что выполнить захват «по константной ссылке» невозможно. Ну, может, оно нам и не надо.

А что будет, если мы напишем такое, слегка надуманное лямбда-выражение внутри метода класса:

Несмотря на все наши ожидания, код не будет скомпилирован, так как компилятор не сможет захватить m_val и m_power: эти переменные вне области видимости. Вот что говорит на это Visual Studio:

Как же быть? Чтобы получить доступ к членам класса, в capture-list нужно поместить this:

Данная программа делает именно то, чего мы ожидали:

1 2 4 8 16 32 64 128 256 512 1024

Следует заметить, что this можно захватить только по значению, и если вы попытаетесь произвести захват по ссылке, компилятор выдаст ошибку. Даже если вы в коде из Листинга 12 напишете [&] вместо [this], то this будет все равно захвачен по значению.

Прочее

Помимо всего вышеперечисленного, в заголовке лямбда-выражения можно указать throw-list — список исключений, которые лямбда может сгенерировать. Например, такая лямбда не может генерировать исключения:

А такая генерирует только bad_alloc:

Естественно, если его не указывать, то лямбда может генерировать любое исключение.

К счастью, в финальном варианте стандарта throw-спецификации объявлены устаревшими. Вместо этого оставили ключевое слово noexcept, которое говорит, что функция не должна генерировать исключение вообще.

Таким образом, общий вид лямбда-выражения следующий (сорри за такой «вольный вид» грамматики):

Повторное использование лямбда-выражений. Генерация лямбда-выражений.

Все вышеперечисленное довольно удобно, но основная мощь лямбда-выражений приходится на то, что мы можем сохранить лямбду в переменной или передавать как параметр в функцию. В Boost для этого есть класс Function, который, если я не ошибаюсь, войдет в новый стандарт STL (возможно, в немного измененном виде). На данный момент уже можно поюзать фичи из обновленного STL, однако, пока что эти фичи находятся в подпространстве имен std::tr1.

Возможность сохранения лямбда-выражений позволяет нам не только повторно использовать лямбды, но и писать функции, которые генерируют лямбда-выражения, и даже лямбды, которые генерируют лямбды.

Рассмотрим следующий пример:

Данная программа выводит:

0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 11

Рассмотрим подробнее. Вначале у нас инициализируется вектор с помощью generate_n(). Тут всё просто. Далее мы создаем переменную traceLambda типа function (то есть функция, принимающая int и возвращающая void) и присваиваем ей лямбда-выражение, которое выводит на консоль значение и пробел. Далее мы используем только что сохраненную лямбду для вывода всех элементов вектора.

После этого мы видим немаленькое объявление lambdaGen, которая является лямбда-выражением, принимающим один параметр int и возвращающим другую лямбду, принимающую int и возвращающую int.

Следом за этим мы ко всем элементам вектора применяем transform(), в качестве мутационной функции для которого указываем lambdaGen(2). Фактически lambdaGen(2) возвращает другую лямбду, которая прибавляет к переданному параметру число 2 и возвращает результат. Этот код, естественно, немного надуманный, ибо то же самое можно было записать как

однако в качестве примера довольно показательно.

Затем мы снова выводим значения всех элементов вектора, используя для этого сохраненную ранее лямбду traceLambda.

На самом деле, данный код можно было записать еще короче. В новом стандарте C++ значение ключевого слова auto будет заменено. Если раньше auto означало, что переменная создается в стеке, и подразумевалось неявно в случае, если вы не указали что-либо другое (register, к примеру), то сейчас это такой себе аналог var в C# (то есть тип переменной, объявленной как auto, определяется компилятором самостоятельно на основе того, чем эта переменная инициализируется).
Следует заметить, что auto-переменная не сможет хранить значения разных типов в течение одного запуска программы. C++ как был, так и остается статически типизированным языком, и указание auto лишь говорит компилятору самостоятельно позаботиться об определении типа: после инициализации сменить тип переменной будет уже нельзя.

Кроме того что ключевое слово auto весьма полезно при работе с циклами вида

его очень удобно использовать с лямбда-выражениями. Теперь код из Листинга 13 можно переписать так:

Пожалуй, на этом я закончу описание лямбда-выражений. Если будут вопросы, поправки или замечания, с удовольствием выслушаю.

ETA (20.02.2012): Оказалось, что для кого-то эта статья до сих пор актуальна, поэтому поправил подсветку синтаксиса и подкорректировал информацию про throw-списки в объявлении лямбд. Помимо непосредственно лямбда-выражений другие фичи из нового стандарта С++11 (например, списки инициализации контейнеров) решил не добавлять, так что статья осталась практически в первозданном виде.

Источник