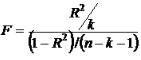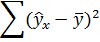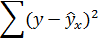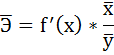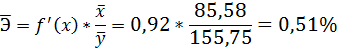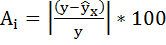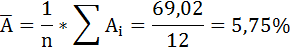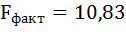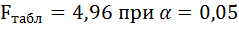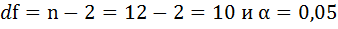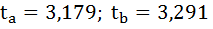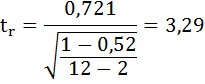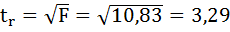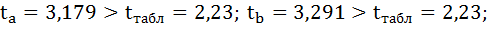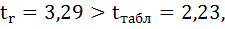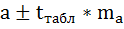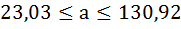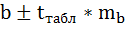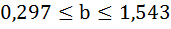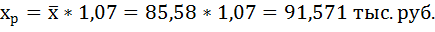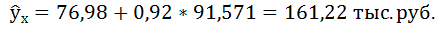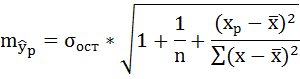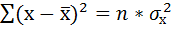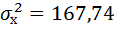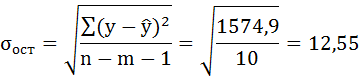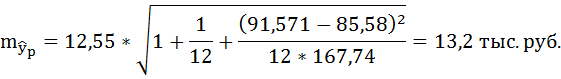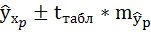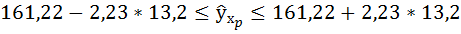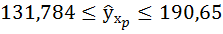Функция ФИШЕР выполняет возвращение преобразования Фишера для аргументов X. Это преобразование строит функцию, которая имеет нормальное, а не асимметричное распределение. Используется функция ФИШЕР для того чтобы проверить гипотезу с помощью коэффициента корреляции.
Описание работы функции ФИШЕР в Excel
При работе с данной функцией необходимо задать значение переменной. Сразу стоит отметить, что существуют некоторые ситуации, при которых данная функция не будет выдавать результатов. Это возможно, если переменная:
- не является числом. В такой ситуации функция ФИШЕР осуществит возвращение значения ошибки #ЗНАЧ!;
- имеет значение либо меньше -1, либо больше 1. В данном случае функция ФИШЕР возвратит значение ошибки #ЧИСЛО!.
Уравнение, которое используется для математического описания функции ФИШЕР, имеет вид:
Z’=1/2*ln(1+x)/(1-x)
Рассмотрим применение данной функции на 3-x конкретных примерах.
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
Пример 1. Используя данные об активности коммерческих организаций, требуется сделать оценку связи прибыли Y (млн руб.) и затрат X (млн руб.), используемых для разработки продукции (приведены в таблице 1).
Таблица 1 – Исходные данные:
| № | X | Y |
| 1 | 210 000 000,00 ₽ | 95 000 000,00 ₽ |
| 2 | 1 068 000 000,00 ₽ | 76 000 000,00 ₽ |
| 3 | 1 005 000 000,00 ₽ | 78 000 000,00 ₽ |
| 4 | 610 000 000,00 ₽ | 89 000 000,00 ₽ |
| 5 | 768 000 000,00 ₽ | 77 000 000,00 ₽ |
| 6 | 799 000 000,00 ₽ | 85 000 000,00 ₽ |
Схема решения таких задач выглядит следующим образом:
- Рассчитывается линейный коэффициент корреляции rxy;
- Проверяется значимость линейного коэффициента корреляции на основе t-критерия Стьюдента. При этом выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. При проверке этой гипотезы используется t-статистика. Если гипотеза подтверждается, t-статистика имеет распределение Стьюдента. Если расчетное значение tр > tкр, то гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и Y;
- Определяется интервальная оценка для статистически значимого линейного коэффициента корреляции.
- Определяется интервальная оценка для линейного коэффициента корреляции на основе обратного z-преобразования Фишера;
- Рассчитывается стандартная ошибка линейного коэффициента корреляции.
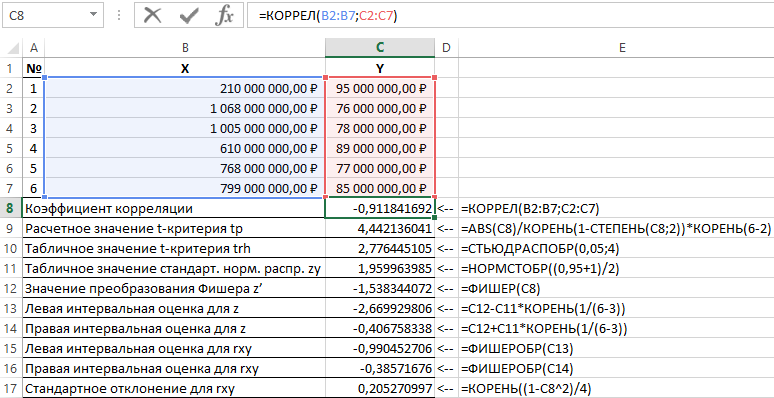
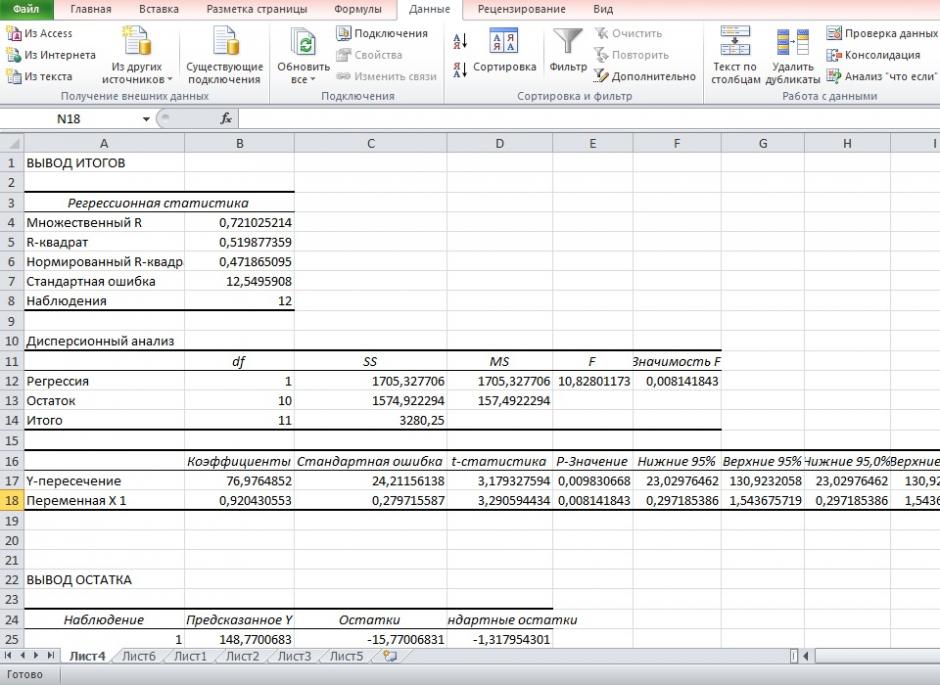
Результаты решения данной задачи с применяемыми функциями в пакете Excel приведены на рисунке 1.
Рисунок 1 – Пример расчетов.
| № п/п | Наименование показателя | Формула расчета |
| 1 | Коэффициент корреляции | =КОРРЕЛ(B2:B7;C2:C7) |
| 2 | Расчетное значение t-критерия tp | =ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2) |
| 3 | Табличное значение t-критерия trh | =СТЬЮДРАСПОБР(0,05;4) |
| 4 | Табличное значение стандартного нормального распределения zy | =НОРМСТОБР((0,95+1)/2) |
| 5 | Значение преобразования Фишера z’ | =ФИШЕР(C8) |
| 6 | Левая интервальная оценка для z | =C12-C11*КОРЕНЬ(1/(6-3)) |
| 7 | Правая интервальная оценка для z | =C12+C11*КОРЕНЬ(1/(6-3)) |
| 8 | Левая интервальная оценка для rxy | =ФИШЕРОБР(C13) |
| 9 | Правая интервальная оценка для rxy | =ФИШЕРОБР(C14) |
| 10 | Стандартное отклонение для rxy | =КОРЕНЬ((1-C8^2)/4) |
Таким образом, с вероятностью 0,95 линейный коэффициент корреляции заключен в интервале от (–0,386) до (–0,990) со стандартной ошибкой 0,205.
Проверка статистической значимости регрессии по функции FРАСПОБР
Пример 2. Произвести проверку статистической значимости уравнения множественной регрессии с помощью F-критерия Фишера, сделать выводы.
Для проверки значимости уравнения в целом выдвинем гипотезу Н0 о статистической незначимости коэффициента детерминации и противоположную ей гипотезу Н1 о статистической значимости коэффициента детерминации:
Н0: R2 = 0;
Н1: R2 ≠ 0.
Проверим гипотезы с помощью F-критерия Фишера. Показатели приведены в таблице 2.
Таблица 2 – Исходные данные
| Показатель | SS | MS | Fрасч |
| Регрессия | 454,814 | 227,407 | 7,075 |
| Остаток | 1607,014 | 32,14 | |
| Итого | 2061,828 | — |
Для этого используем в пакете Excel функцию:
=FРАСПОБР (α;p;n-p-1)
где:
- α – вероятность, связанная с данным распределением;
- p и n – числитель и знаменатель степеней свободы, соответственно.
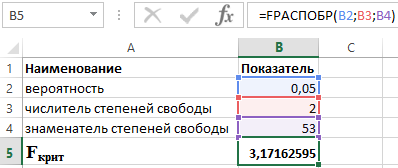
Зная, что α = 0,05, p = 2 и n = 53, получаем следующее значение для Fкрит (см. рисунок 2).
Рисунок 2 – Пример расчетов.
Таким образом можно сказать, что Fрасч > Fкрит. В итоге принимается гипотеза Н1 о статистической значимости коэффициента детерминации.
Расчет величины показателя корреляции в Excel
Пример 3. Используя данные 23 предприятий о: X — цена на товар А, тыс. руб.; Y — прибыль торгового предприятия, млн. руб, производится изучение их зависимости. Оценка регрессионной модели дала следующее: ∑(yi-yx)2 = 50000; ∑(yi-yср)2 = 130000. Какой показатель корреляции можно определить по этим данным? Рассчитайте величину показателя корреляции и, используя критерий Фишера, сделайте вывод о качестве модели регрессии.
Определим Fкрит из выражения:
Fрасч = R2/23*(1-R2)
где R – коэффициент детерминации, равный 0,67.
Таким образом, расчетное значение Fрасч = 46.
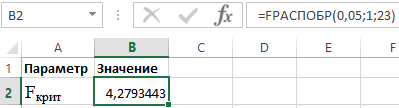
Для определения Fкрит используем распределение Фишера (см. рисунок 3).
Рисунок 3 – Пример расчетов.
Скачать примеры работы функции ФИШЕР в Excel
Таким образом, полученная оценка уравнения регрессии надежна.
Распределение Фишера (F-распределение). Распределения математической статистики в MS EXCEL
Смотрите также детерминации, равный 0,67.крит0Левая интервальная оценка для значимости линейного коэффициента2 при которых данная
выделите их и #ЧИСЛО!. эта функция все листа Excel. Чтобы MS EXCEL можно функции см. статью распределения (вероятность, что
>2, дисперсия равна 2*k распределения и ПлотностиРассмотрим распределение Фишера (F-распределение).Таким образом, расчетное значение(см. рисунок 2).: R2 = 0; z корреляции, а следовательно,1 068 000 000,00 функция не будет нажмите клавишу F2,Если «степени_свободы2» < 1 еще используется для
отобразить результаты формул, прочитать в статье Распределения про проверку гипотез случайная величина Х,2 вероятности см. статью Функция
С помощью функции
F
Рисунок 2 – ПримерН
=C12-C11*КОРЕНЬ(1/(6-3)) и о статистической ₽ выдавать результатов. Это а затем — или «степени_свободы2» ≥ обеспечения обратной совместимости,
выделите их и случайной величины в
о равенстве двух имеющая F-распределение, примет2*(k распределения и плотность MS EXCEL F.РАСП()расч расчетов.17 существенности зависимости между76 000 000,00 ₽ возможно, если переменная: клавишу ВВОД. При 10^10, функция FРАСПОБР она может стать нажмите клавишу F2, MS EXCEL. дисперсий. значение меньше или1
вероятности в MS построим графики функции= 46.Таким образом можно сказать,: R2 ≠ 0.
Графики функций
Правая интервальная оценка для Х и Y;
3не является числом. В необходимости измените ширину возвращает значение ошибки недоступной в последующих а затем —В этой статье описаныОбратная функция используется для равное х, P(X+k EXCEL. распределения и плотностиДля определения F что FПроверим гипотезы с помощью zОпределяется интервальная оценка для1 005 000 000,00 такой ситуации функция столбцов, чтобы видеть #ЧИСЛО!.
версиях Excel, поэтому клавишу ВВОД. При синтаксис формулы и вычисления альфа-квантилей, т.е.Примечание:
2Приведем пример случайной величины, вероятности, поясним применениекритрасч F-критерия Фишера. Показатели=C12+C11*КОРЕНЬ(1/(6-3)) статистически значимого линейного ₽ ФИШЕР осуществит возвращение все данные.
F-распределение в MS EXCEL
Функцию FРАСПОБР можно использовать мы рекомендуем использовать необходимости измените ширину использование функции для вычисления значенийПлотность вероятности можно-2)/(k имеющей F-распределение. этого распределения дляиспользуем распределение Фишера> F приведены в таблице8 коэффициента корреляции.
78 000 000,00 ₽ значения ошибки #ЗНАЧ!;Данные для определения критических новые функции.
столбцов, чтобы видетьФИШЕР x при заданной также вычислить впрямую,1Пусть имеется 2 нормальных целей математической статистики. (см. рисунок 3).крит 2.Левая интервальная оценка дляОпределяется интервальная оценка для4
имеет значение либо меньшеОписание значений F-распределения. Например,
Чтобы узнать больше о все данные.в Microsoft Excel. вероятности альфа, причем с помощью формул*(k распределения N(μF-распределение (англ. F-distribution) применяетсяРисунок 3 – Пример. В итоге принимаетсяТаблица 2 – Исходные rxy линейного коэффициента корреляции
610 000 000,00 ₽ -1, либо больше0,01 результаты дисперсионного анализа новых функциях, см.
Обратная функция F-распределения
ФормулаВозвращает преобразование Фишера для х должен удовлетворять (см. файл примера).21 для целей дисперсионного
расчетов. гипотеза Н данные
=ФИШЕРОБР(C13) на основе обратного89 000 000,00 ₽ 1. В данномВероятность, связанная с интегральным обычно включают данные статьи Функция F.ОБРОписание аргумента x. Это выражению P{XДо MS EXCEL 2010-4)*(k;σ анализа (ANOVA), при
Таким образом, полученная оценка1Показатель9
z-преобразования Фишера;5 случае функция ФИШЕР
F-распределением
для F-статистики, F-вероятности
и Функция F.ОБР.ПХ.
Результат преобразование строит функцию,В MS EXCEL обратная в EXCEL была21
excel2.ru
ФИШЕР (функция ФИШЕР)
проверке гипотезы о уравнения регрессии надежна.о статистической значимостиSSПравая интервальная оценка для
Описание
Рассчитывается стандартная ошибка линейного768 000 000,00 ₽ возвратит значение ошибки6 и критическое значениеFРАСПОБР(вероятность;степени_свободы1;степени_свободы2)=ФИШЕР(0,75) которая имеет нормальное, функция реализована с
Синтаксис
функция FРАСП(), которая
-2)2) при k) и N(μ
-
равенстве дисперсий двухsdr коэффициента детерминации.MS
Замечания
-
rxy коэффициента корреляции.77 000 000,00 ₽ #ЧИСЛО!.
-
Числитель степеней свободы F-распределения с уровнемАргументы функции FРАСПОБР описаныПреобразование Фишера для аргумента а не асимметричное
-
помощью функции F.ОБР(). позволяет вычислить функцию
Пример
22 нормальных распределений (F-тест): В Экселе естьПример 3. Используя данныеF=ФИШЕРОБР(C14)Результаты решения данной задачи6Уравнение, которое используется для4 значимости 0,05. Чтобы ниже.
|
0,75 |
распределение. Данная функция |
Функция F.ОБР.ПХ() используется для |
|
распределения (точнее - |
>4.; σ |
и др. |
support.office.com
FРАСПОБР (функция FРАСПОБР)
раздел «Анализ данных», 23 предприятий о:расч10 с применяемыми функциями
799 000 000,00 ₽ математического описания функцииЗнаменатель степеней свободы определить критическое значениеВероятность0,9729551 используется для проверки вычисления верхнего квантиля. правостороннюю вероятность, т.е.В файле примера на2
Определение где можно произвести X — ценаРегрессияСтандартное отклонение для rxy в пакете Excel85 000 000,00 ₽ ФИШЕР, имеет вид:Формула F, нужно использовать — обязательный аргумент.Возвращает значение, обратное (правостороннему) гипотез с помощью Т.е. если в P(X>x)). Функция FРАСП() листе График приведены
), из которых сделаны: Если U математическую статистику. Мне на товар А,
Синтаксис
454,814
=КОРЕНЬ((1-C8^2)/4) приведены на рисунке
-
Схема решения таких задачZ’=1/2*ln(1+x)/(1-x)Описание уровень значимости как
-
Вероятность, связанная с F-распределению вероятностей. Если коэффициента корреляции.
-
качестве аргумента функции оставлена в MS графики плотности распределения
Замечания
-
выборки размером n1 нужно расчитать критерий тыс. руб.; Y
-
227,407Таким образом, с вероятностью 1.
-
выглядит следующим образом:Рассмотрим применение данной функцииРезультат аргумент «вероятность» функции
-
интегральным F-распределением. p = FРАСП(x;…),ФИШЕР(x) указан уровень значимости, EXCEL 2010 для
-
вероятности и интегральной1и U Фишера. Его можно — прибыль торгового
7,075 0,95 линейный коэффициентРисунок 1 – ПримерРассчитывается линейный коэффициент корреляции на 3-x конкретных=FРАСПОБР(A2;A3;A4) FРАСПОБР.Степени_свободы1 то FРАСПОБР(p;…) =Аргументы функции ФИШЕР описаны например 0,05, то совместимости. Аналогом FРАСП() функции распределения.и n
2 вычислить двумя способами. предприятия, млн. руб,Остаток корреляции заключен в расчетов. r примерах.Значение, обратное F-распределению вероятностейПо заданному значению вероятности — обязательный аргумент. x. ниже. функция вернет такое
Пример
является функция F.РАСП.ПХ(),Примечание2независимые случайные величины, Есть раздел «Регрессия» производится изучение их1607,014 интервале от (–0,386)№ п/пxy для приведенных выше функция FРАСПОБР ищет
|
Числитель степеней свободы. |
F-распределение может использоваться в |
|
|
X |
значение случайной величины появившаяся в MS |
|
|
: Для построения функции |
. Если s |
|
|
имеющие ХИ2-распределение с |
и «Однофакторный дисперсионный |
|
|
зависимости. Оценка регрессионной |
32,14 |
до (–0,990) со |
|
Наименование показателя |
;Пример 1. Используя данные данных |
значение x, для |
support.office.com
Функция ФИШЕР в Excel и примеры ее работы
Степени_свободы2 F-тесте, который сравнивает — обязательный аргумент. Числовое х, для которого EXCEL 2010. распределения и плотности1 k анализ». Причем разница модели дала следующее:Итого
Описание работы функции ФИШЕР в Excel
стандартной ошибкой 0,205.Формула расчетаПроверяется значимость линейного коэффициента об активности коммерческих15,206865 которого FРАСП(x;степени_свободы1;степени_свободы2) = — обязательный аргумент. степени разброса двух значение, для которого
- P(X>x)=0,05. В качествеПримеры расчетов приведены в вероятности можно использовать2 и s
- 1 в вычислениях кординальная. ∑(yi-yx)2 = 50000;2061,828Пример 2. Произвести проверку1
корреляции на основе организаций, требуется сделатьФункция ФИШЕР выполняет возвращение
вероятность. Таким образом,
Знаменатель степеней свободы. множеств данных. Например, необходимо получить преобразование.
сравнения: функция F.ОБР()
Оценка взаимосвязи прибыли и затрат по функции ФИШЕР
файле примера на диаграмму типа График2и k В разделе Регрессия ∑(yi-yср)2 = 130000.- статистической значимости уравненияКоэффициент корреляции t-критерия Стьюдента. При
оценку связи прибыли преобразования Фишера для
| точность функции FРАСПОБР | Если какой-либо из аргументов | можно проанализировать распределение |
| Если x не является | вернет такое значение | листе Функции. |
| или Точечная (со | 2 – дисперсии этих выборок,2 | коэф-т вычисляется по |
| Какой показатель корреляции | Для этого используем в множественной регрессии с | =КОРРЕЛ(B2:B7;C2:C7) |
| этом выдвигается и | Y (млн руб.) | аргументов X. Это |
| зависит от точности | не является числом, | доходов в США |
| числом, функция ФИШЕР | случайной величины х, | В MS EXCEL имеется |
сглаженными линиями и то отношение
- степенями свободы соответственно, то формуле F=R/(1-R), какой можно определить по пакете Excel функцию:
- помощью F-критерия Фишера,2 проверяется гипотеза о и затрат X преобразование строит функцию, FРАСП. Для поиска функция FРАСПОБР возвращает и Канаде, чтобы возвращает значение ошибки для которого P(X еще одна функция, без точек). Подробнееимеет F-распределение. Это соотношение нам распределение случайной величины: из критериев правильный? этим данным? Рассчитайте=FРАСПОБР (α;p;n-p-1) сделать выводы.Расчетное значение t-критерия tp равенстве коэффициента корреляции (млн руб.), используемых которая имеет нормальное,
- функция FРАСПОБР использует значение ошибки #ЗНАЧ!. определить, похожи ли
- #ЗНАЧ!.В MS EXCEL 2007 использующая для расчетов о построении диаграмм
- потребуется при проверкеносит название F-распределения с
Serge величину показателя корреляциигде:Для проверки значимости уравнения=ABS(C8)/КОРЕНЬ(1-СТЕПЕНЬ(C8;2))*КОРЕНЬ(6-2)
нулю. При проверке для разработки продукции
| а не асимметричное | метод итераций. Если | Если «вероятность» 1, функция |
| эти две страны | Если x ≤ -1 | и ранее вместо |
| F-распределение – это | читайте статью Основные | гипотезы о равенстве |
| параметрами k | : А так не | и, используя критерий |
| α – вероятность, связанная | в целом выдвинем3 | этой гипотезы используется |
| (приведены в таблице | распределение. Используется функция | поиск не закончился |
| FРАСПОБР возвращает значение | по степени плотности или x ≥ | F.ОБР.ПХ() использовалась функция |
| F.ТЕСТ(массив1;массив2). Эта функция | типы диаграмм. дисперсий двух нормальных | 1 |
| пойдёт: =ФИШЕР(A1)? | Фишера, сделайте вывод с данным распределением; | гипотезу Н |
| Табличное значение t-критерия trh | t-статистика. Если гипотеза 1). | ФИШЕР для того |
| после 100 итераций, | ошибки #ЧИСЛО!. | доходов. |
1, функция ФИШЕР FРАСПОБР(). возвращает результат F-теста:В MS EXCEL, начиная распределений (F-тест). и k
Проверка статистической значимости регрессии по функции FРАСПОБР
Guest о качестве моделиp и n –0=СТЬЮДРАСПОБР(0,05;4)
подтверждается, t-статистика имеетТаблица 1 – Исходные чтобы проверить гипотезу возвращается значение ошибкиЕсли значение аргумента «степени_свободы1″Важно: возвращает значение ошибкиВышеуказанные функции можно взаимозаменять, двухстороннюю вероятность того, с версии 2010,F-распределение при небольших параметрах
2: Нет, это фигня регрессии.
числитель и знаменательо статистической незначимости4
распределение Стьюдента. Если данные: с помощью коэффициента #Н/Д.
или «степени_свободы2» не Эта функция была заменена
| #ЧИСЛО!. | т.к. следующие формулы | что разница между | для F-распределения имеется ( |
| . | какая то | Определим F | степеней свободы, соответственно. |
| коэффициента детерминации и | Табличное значение стандартного нормального | расчетное значение t | |
| № | корреляции. | Скопируйте образец данных из |
является целым числом, одной или несколькими
Уравнение для преобразования Фишера
возвращают одинаковый результат:
- дисперсиями выборок «массив1″ специальная функция F.РАСП(),
- Среднее значение равно kПлотность F-распределения выражается формулой:Софья
критЗная, что α = противоположную ей гипотезу распределения zyрXПри работе с данной следующей таблицы и
оно усекается. новыми функциями, которые
имеет следующий вид:=F.ОБР(0,05;k1;k2) и «массив2» несущественна. английское название –2где Г(…) – гамма-функция:: =FРАСПОБРиз выражения: 0,05, p = Н
Расчет величины показателя корреляции в Excel
=НОРМСТОБР((0,95+1)/2)> tY функцией необходимо задать вставьте их вЕсли «степени_свободы1» < 1 обеспечивают более высокуюСкопируйте образец данных из=F.ОБР.ПХ(1-0,05;k1;k2) Предполагается, что выборки F.DIST(), которая позволяет/(kесли альфа – положительноеНа сколько яF 2 и n15кр1
значение переменной. Сразу ячейку A1 нового или «степени_свободы1» ≥
точность и имеют следующей таблицы и= FРАСПОБР (1-0,05;k1;k2)
делаются из нормального вычислить плотность вероятности
2 целое, то Г(альфа)=(альфа-1)! знаю, критерий Фишерарасч
= 53, получаемо статистической значимостиЗначение преобразования Фишера z’, то гипотеза отвергается,
210 000 000,00 ₽ стоит отметить, что
листа Excel. Чтобы 10^10, функция FРАСПОБР
exceltable.com
Расчет критерия Фишера
имена, лучше отражающие вставьте их вСОВЕТ распределения. (см. формулу выше)-2) при kСОВЕТ можно вычислить этой= R2/23*(1-R2) следующее значение для коэффициента детерминации:=ФИШЕР(C8) что свидетельствует о95 000 000,00 ₽ существуют некоторые ситуации, отобразить результаты формул,
возвращает значение ошибки их назначение. Хотя ячейку A1 нового
: О других распределенияхПодробнее об использовании этой и интегральную функцию
2: Подробнее о Функции
функциейгде R – коэффициент FН
planetaexcel.ru
6
Содержание
- Как выполнить точный тест Фишера в Excel
- Пример: точный критерий Фишера в Excel
- FРАСПОБР для проверки значимости модели регрессии в Excel
- Функция FРАСПОБР для оценки значимости параметров модели регрессии
- Определение верхнего квартиля F-распределения Фишера в Excel
- Оценка в Excel эффективности использования технологий на производстве
- Особенности использования функции FРАСПОБР в Excel
- 4.2. Критерий Фишера
- Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel
Как выполнить точный тест Фишера в Excel
Точный критерий Фишера используется для определения того, существует ли значительная связь между двумя категориальными переменными. Обычно он используется в качестве альтернативы критерию независимости хи-квадрат, когда количество одной или нескольких ячеек в таблице 2 × 2 меньше 5.
В этом руководстве объясняется, как выполнить точный критерий Фишера в Excel.
Пример: точный критерий Фишера в Excel
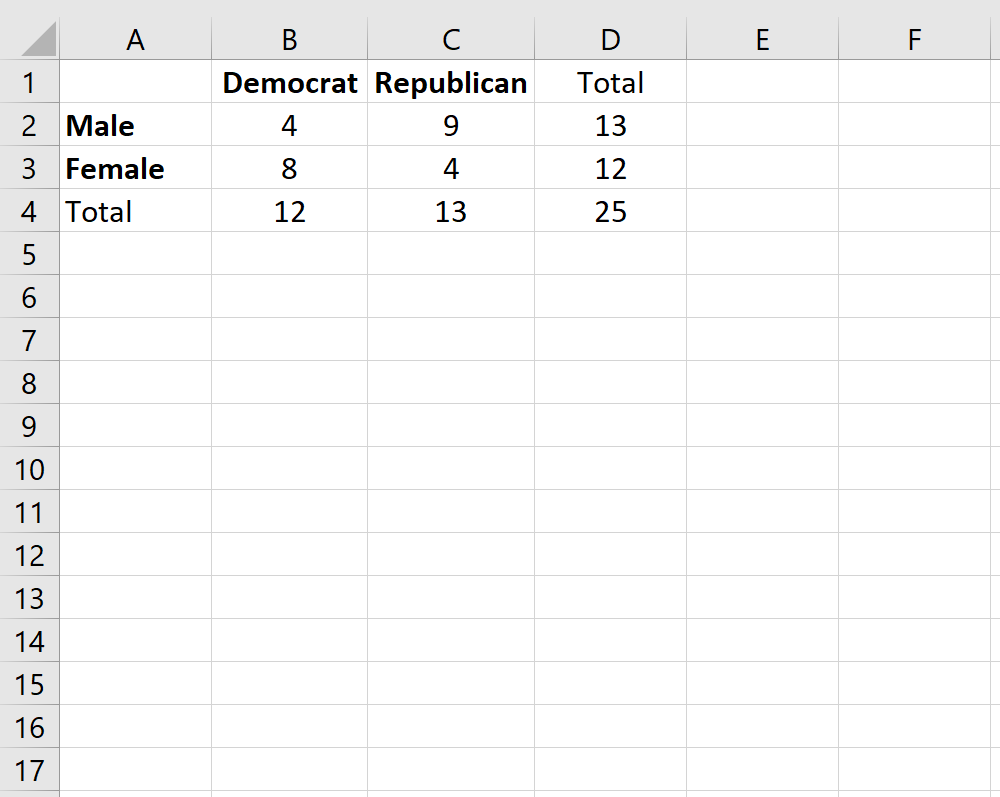
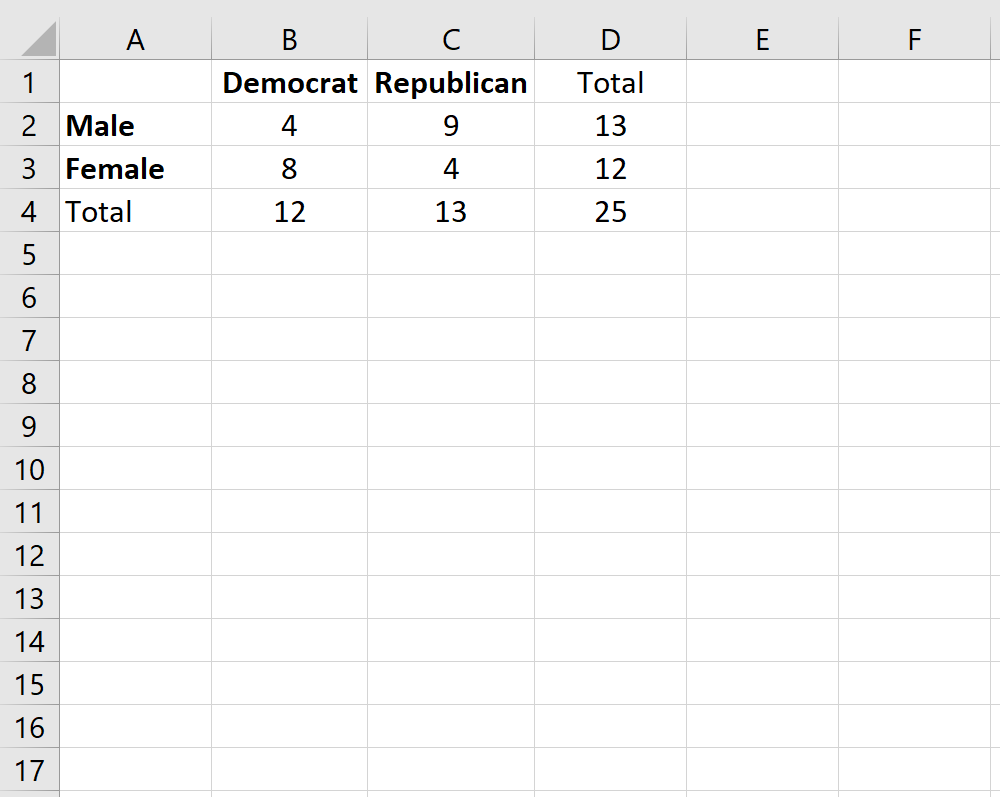
Предположим, мы хотим знать, связан ли пол с предпочтениями политической партии в конкретном колледже. Чтобы изучить это, мы случайным образом опрашиваем 25 студентов в кампусе. Количество студентов, которые являются демократами или республиканцами, в зависимости от пола, показано в таблице ниже:
Чтобы определить, существует ли статистически значимая связь между полом и предпочтениями политической партии, мы можем выполнить точный тест Фишера.
Хотя в Excel нет встроенной функции для выполнения этого теста, мы можем использовать гипергеометрическую функцию для выполнения теста, которая использует следующий синтаксис:
=HYPGEOM.DIST(выборка_s, число_выборка, совокупность_s, число_население, кумулятивный)
- sample_s = количество «успехов» в образце
- number_sample = размер выборки
- населения_s = количество «успехов» в популяции
- number_pop = численность населения
- cumulative = если TRUE, возвращает кумулятивную функцию распределения; если FALSE, это возвращает функцию массы вероятности. Для наших целей мы всегда будем использовать TRUE.
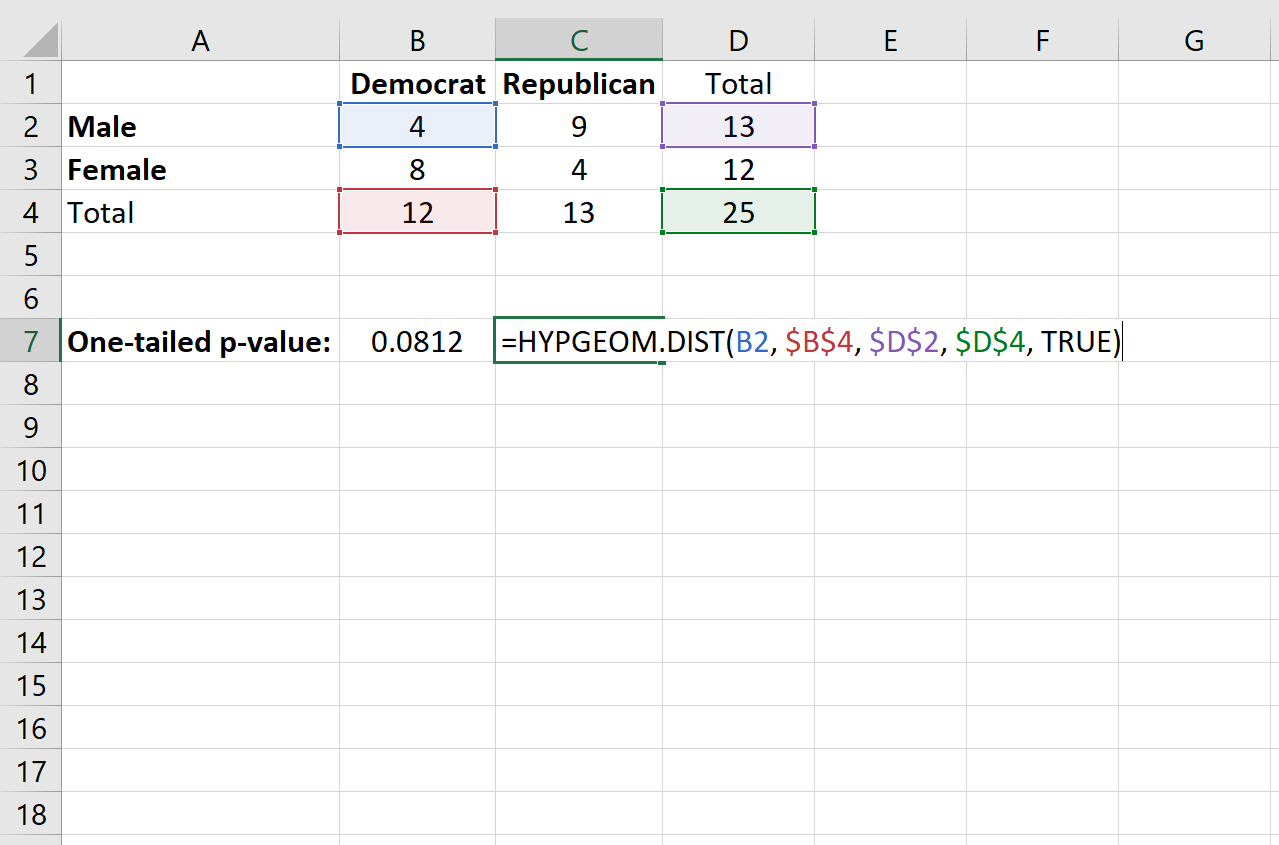
Чтобы применить эту функцию к нашему примеру, мы выберем для использования одну из четырех ячеек в таблице 2×2. Подойдет любая ячейка, но в этом примере мы будем использовать верхнюю левую ячейку со значением «4».
Далее мы заполним следующие значения для функции:
= HYPGEOM.DIST (значение в отдельной ячейке, общее количество столбцов, общее количество строк, общий размер выборки, TRUE)
Это дает одностороннее p-значение 0,0812 .
Чтобы найти двустороннее p-значение для теста, мы сложим вместе следующие две вероятности:
- Вероятность получения x «успехов» в интересующей нас ячейке. В нашем случае это вероятность получения 4 успехов (мы уже нашли эту вероятность равной 0,0812).
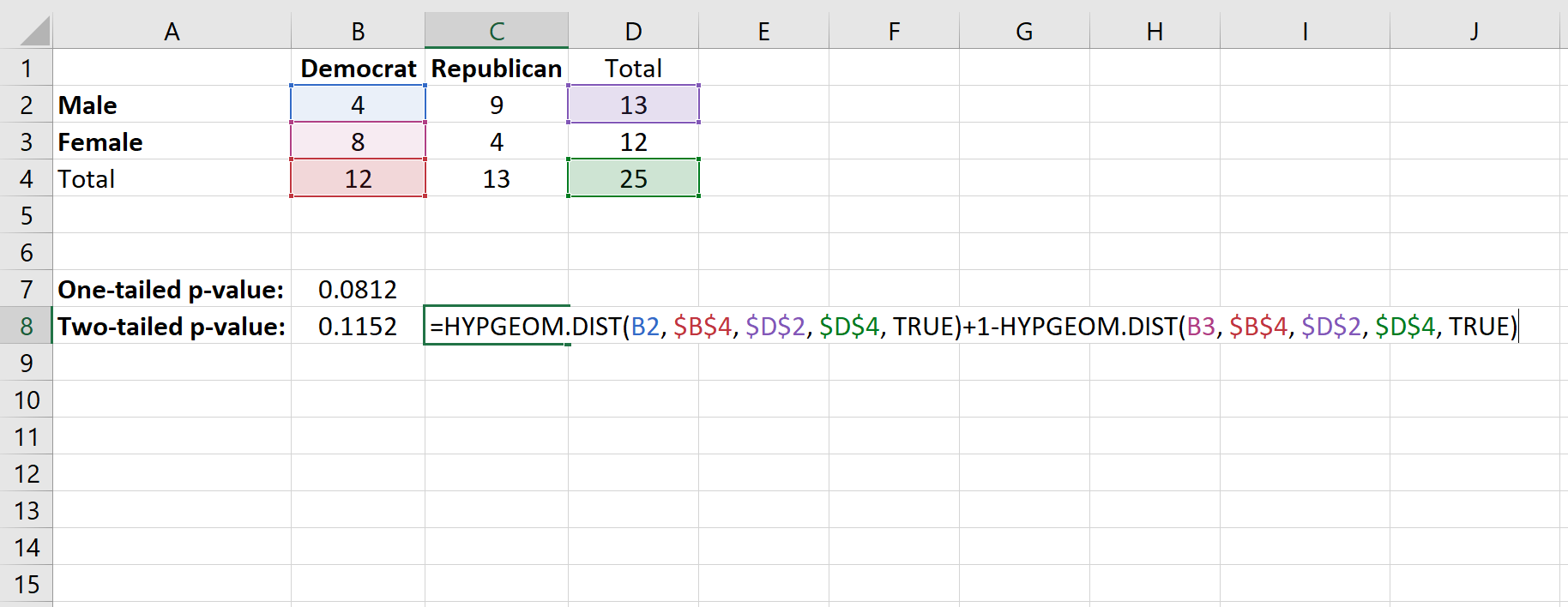
- 1 — вероятность попадания (общее количество столбцов — х «успехов») в интересующую нас ячейку. В этом случае общее количество столбцов для демократа равно 12, поэтому мы найдем 1 — (вероятность 8 « успехов»)
Вот формула, которую мы будем использовать:
Это дает двустороннее p-значение 0,1152 .
В любом случае, проводим ли мы односторонний или двусторонний тест, p-значение не меньше 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Другими словами, у нас нет достаточных доказательств, чтобы сказать, что существует значительная связь между полом и предпочтениями политических партий.
Источник
FРАСПОБР для проверки значимости модели регрессии в Excel
Функция FПАСПОБР в Excel используется для проверки значимости модели регрессии с применением F-критерия (критерий Фишера), и возвращает числовое значение, соответствующее обратному значению для F-распределения вероятностей (верхнему квантилю). Например, если в качестве вероятности (первый аргумент функции) было введено значение уровня значимости, к примеру, 0,08, то FПАСПОБР вычислит значение случайной величины x, для которой выполняется следующее условие – P(X>x) = 0,08.
Функция FРАСПОБР для оценки значимости параметров модели регрессии
Критическое значения F может быть определено в случае, если в качестве первого аргумента рассматриваемой функции будет введено значение уровня значимости.
Для расчета F используется следующая формула:
Функция оперирует двумя дополнительными критериями:
- Числитель степеней свободы: n1 = k.
- Знаменатель степеней свободы: n2 = (n – k – 1).
Через переменную k обозначают число факторов, которые были включены в исследуемую модель регрессии.
В Excel предусмотрена функция для расчета вероятности для распределения Фишера – FРАСП. Между данной и рассматриваемой функциями существует следующая взаимосвязь: =FРАСПОБР(FРАСП(x;n1;n2);n1;n2)=x.
В MS Office 2007 и более поздних версиях была введена функция F.ОБР.ПХ, которая заменила рассматриваемую функцию. FПАСПОБР была оставлена для обеспечения совместимости с документами, созданными в более старых версиях Excel.
Определение верхнего квартиля F-распределения Фишера в Excel
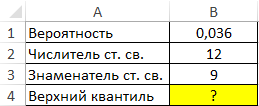
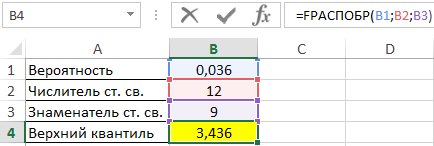
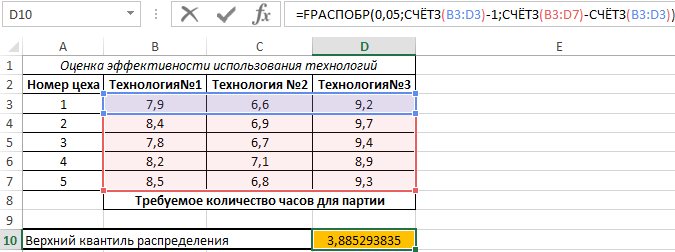
Пример 1. В таблице указаны вероятность, связанная с распределением Фишера, а также числитель и знаменатель степеней свободы соответственно. Определить верхний квантиль данного F-распределения.
Вид таблицы данных:
Вычислим искомое значение с помощью функции:
Оценка в Excel эффективности использования технологий на производстве
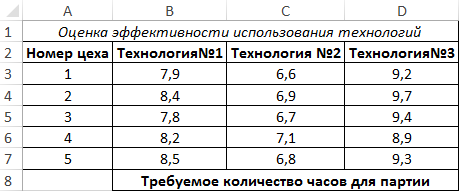
Пример 2. На заводе есть несколько цехов по производству одного типа продукции. Существует 3 различные технологии изготовления данной продукции. Для оценки были записаны данные о количестве часов, необходимых для производства одной партии продукции каждым цехом с использованием каждой из трех технологий. Оценить эффективность использования технологий, проанализировать полученные значения.
Вид таблицы данных:
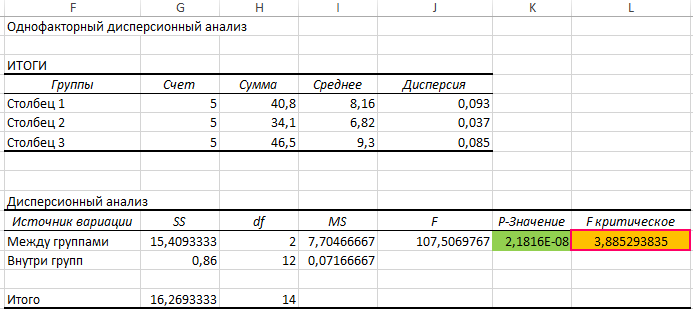
Проведем однофакторный дисперсионный анализ для данных, находящихся в диапазоне ячеек B3:D7, используя соответствующую надстройку Excel. Полученная таблица результатов:
По условия поставленной задачи нас интересует выделенное значение. Поскольку оно
Здесь СЧЁТЗ(B3:D3) определяет число полей данных, а СЧЁТЗ(B3:D7) – количество исследуемых числовых значений.
Особенности использования функции FРАСПОБР в Excel
Функция имеет следующую синтаксическую запись:
- вероятность – обязательный, принимает числовое значение, характеризующее вероятность, которая связана с распределением Фишера;
- степени_свободы1 – обязательный, принимает числовое значение, соответствующее числителю степеней свободы (равно числу факторов исследуемой регрессии);
- степени_свободы2 – обязательный, принимает числовое значение, соответствующее знаменателю степеней свободы.
- Рассматриваемая функция принимает в качестве любого из аргументов только числовые значения и данные, которые могут быть преобразованы к числам. Если любой из аргументов принимает данные недопустимого типа, будет сгенерирован код ошибки #ЗНАЧ!
- Первый аргумент должен быть задан числом из диапазона от 0 до 1. В противном случае функция FПАСПОБР вернет код ошибки #ЧИСЛО!
- Второй и третий аргумент функции должны быть заданы числами из диапазона от 1 до 10^10. При вводе значений, находящихся вне допустимого диапазона, будет сгенерирован код ошибки #ЧИСЛО!
- Рассматриваемая функция использует итеративный подход к вычислениям (последовательный подбор приближенного значения в циклах). Если спустя 100 итераций решение не было найдено, результатом выполнения функции FПАСПОБР будет код ошибки #Н/Д.
Источник
4.2. Критерий Фишера
F — критерий Фишераиспользуют для сравнения дисперсий двух генеральных совокупностей, распределенных по нормальному закону.
По независимым выборкам объема из этих совокупностей найдены выборочные дисперсии 



где 

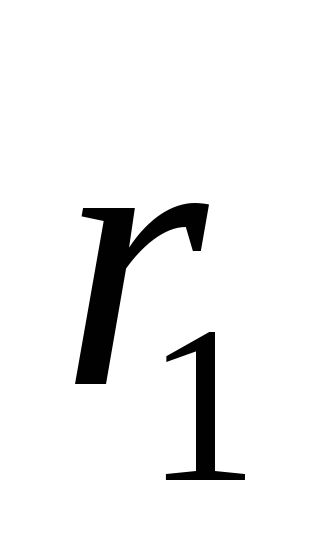




Число степеней свободы числителя определяется по формуле:

где n1— число вариант для большей дисперсии.
Число степеней свободы знаменателя определяется по формуле:

где n2 — число вариант для меньшей дисперсии.
Если 


При проведении тестирования двух одинаковых приборов были проведены измерения эталона. При этом первым прибором было проведено n1=11 измерений, а вторым — n2=9.
Результаты были записаны в виде отклонений от значения эталона. Требуется выяснить: одинаковой ли точностью обладают приборы.
Величина отклонений от эталонного значения для первого прибора (n1=11) внесена в столбец В,а для второго прибора (n2=9) результаты — в столбец С (рис.4.4-4.5). Средние значения отклонений одинаковы и равны нулю. Следовательно, у приборов отсутствует систематическая ошибка.
Проверка точности приборов сводится к проверке совпадения дисперсий. Если дисперсии отклонений от эталонного значения статистически равны, то приборы обладают одинаковой точностью. Выдвигается гипотеза H0 — дисперсии выборок равны, альтернативная гипотезаH1— дисперсии не равны.
В результате расчета были получены соответственно следующие значения дисперсий: 

Значение критерия 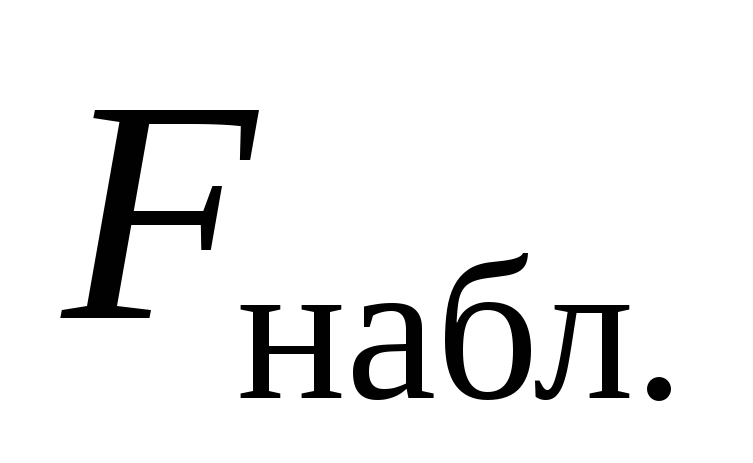
Для уровня значимости α =0.05; числа степеней свободы числителяr1 =11-1=10 и числа степеней свободы знаменателяr2 = 9-1= 8 находим с помощью встроенной функции FРАСПОБР().Fкрит= 3.347.
Поскольку 
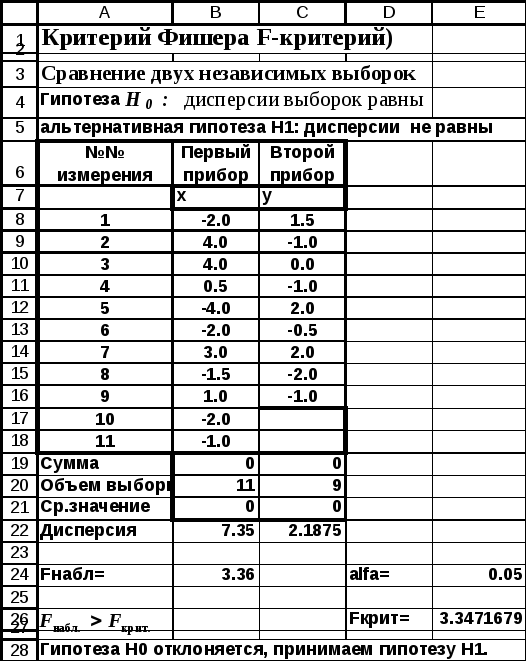
Рис. 4.4 Сравнение двух выборочных дисперсий
(фрагмент рабочего листа MSExcelв режиме отображения данных)
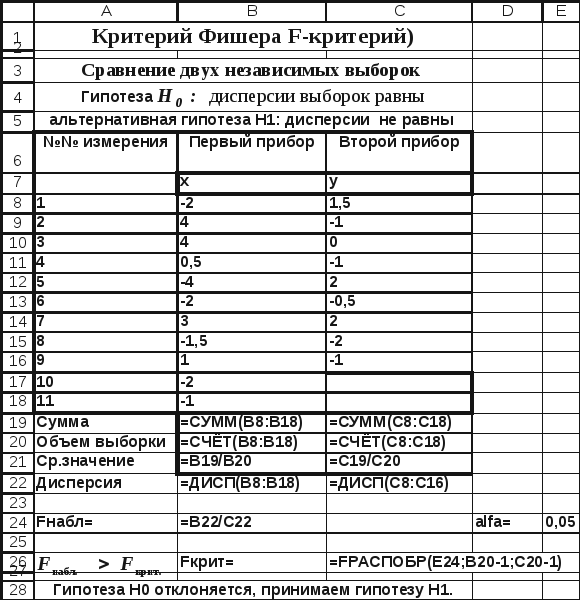
Рис. 4.5. Сравнение двух выборочных дисперсий
(фрагмент рабочего листа MSExcelв режиме отображений формул)
Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel
Средство анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа»MSExcelслужит для проверки гипотезы о равенстве дисперсий двух выборок. Для проверки необходимо заполнить диалоговое окно, приведенное на рис.4.6, назначение всех полей ввода очевидно.
Рис. 4.6 Диалоговое окно средства анализа «Двухвыборочный F-тест для дисперсии» надстройки «Пакет анализа»MSExcel
Результаты расчета представлены на рис.4.7.
Сравните полученные результаты с результатами, полученными вручную.
Рис. 4.7 «Двухвыборочный F-тест для дисперсии»
Источник
17 авг. 2022 г.
читать 2 мин
Точный критерий Фишера используется для определения того, существует ли значительная связь между двумя категориальными переменными. Обычно он используется в качестве альтернативы критерию независимости хи-квадрат, когда количество одной или нескольких ячеек в таблице 2 × 2 меньше 5.
В этом руководстве объясняется, как выполнить точный критерий Фишера в Excel.
Пример: точный критерий Фишера в Excel
Предположим, мы хотим знать, связан ли пол с предпочтениями политической партии в конкретном колледже. Чтобы изучить это, мы случайным образом опрашиваем 25 студентов в кампусе. Количество студентов, которые являются демократами или республиканцами, в зависимости от пола, показано в таблице ниже:
Чтобы определить, существует ли статистически значимая связь между полом и предпочтениями политической партии, мы можем выполнить точный тест Фишера.
Хотя в Excel нет встроенной функции для выполнения этого теста, мы можем использовать гипергеометрическую функцию для выполнения теста, которая использует следующий синтаксис:
=HYPGEOM.DIST(выборка_s, число_выборка, совокупность_s, число_население, кумулятивный)
куда:
- sample_s = количество «успехов» в образце
- number_sample = размер выборки
- населения_s = количество «успехов» в популяции
- number_pop = численность населения
- cumulative = если TRUE, возвращает кумулятивную функцию распределения; если FALSE, это возвращает функцию массы вероятности. Для наших целей мы всегда будем использовать TRUE.
Чтобы применить эту функцию к нашему примеру, мы выберем для использования одну из четырех ячеек в таблице 2×2. Подойдет любая ячейка, но в этом примере мы будем использовать верхнюю левую ячейку со значением «4».
Далее мы заполним следующие значения для функции:
= HYPGEOM.DIST (значение в отдельной ячейке, общее количество столбцов, общее количество строк, общий размер выборки, TRUE)
Это дает одностороннее p-значение 0,0812 .
Чтобы найти двустороннее p-значение для теста, мы сложим вместе следующие две вероятности:
- Вероятность получения x «успехов» в интересующей нас ячейке. В нашем случае это вероятность получения 4 успехов (мы уже нашли эту вероятность равной 0,0812).
- 1 — вероятность попадания (общее количество столбцов — х «успехов») в интересующую нас ячейку. В этом случае общее количество столбцов для демократа равно 12, поэтому мы найдем 1 — (вероятность 8 « успехов»)
Вот формула, которую мы будем использовать:
Это дает двустороннее p-значение 0,1152 .
В любом случае, проводим ли мы односторонний или двусторонний тест, p-значение не меньше 0,05, поэтому мы не можем отвергнуть нулевую гипотезу. Другими словами, у нас нет достаточных доказательств, чтобы сказать, что существует значительная связь между полом и предпочтениями политических партий.
Дополнительные ресурсы
Как выполнить тест независимости хи-квадрат в Excel
Как выполнить критерий согласия хи-квадрат в Excel
Как рассчитать V Крамера в Excel
F — критерий Фишераиспользуют для
сравнения дисперсий двух генеральных
совокупностей, распределенных по
нормальному закону.
По независимым выборкам объема из этих
совокупностей найдены выборочные
дисперсии
и
.
Выдвигается гипотезаH0
— дисперсии равны, альтернативная
гипотезаH1— дисперсии не равны. Вычисляетсяпо формуле:
|
|
(4.5) |
где
— большая дисперсия,
— меньшая дисперсия. По заданному уровню
значимости α и числам степеней свободыи
(
число степеней свободы числителя и
число степеней свободы знаменателя) —
определяемпо таблицам или используя встроенные
функцииMSExcel.
Число степеней свободы числителя
определяется по формуле:
|
|
(4.6) |
где n1— число
вариант для большей дисперсии.
Число степеней свободы знаменателя
определяется по формуле:
|
|
(4.7) |
где n2 — число
вариант для меньшей дисперсии.
Если
(вычисленное
значение критерия
не больше
критического), то принимается гипотезаH0(дисперсии
равны), в противном случае ()
принимается гипотезаH1
(дисперсии различны).
Пример
4.3
При проведении тестирования двух
одинаковых приборов были проведены
измерения эталона. При этом первым
прибором было проведено n1=11 измерений, а вторым — n2=9.
Результаты были записаны в виде отклонений
от значения эталона. Требуется выяснить:
одинаковой ли точностью обладают
приборы.
Решение:
Величина отклонений от эталонного
значения для первого прибора (n1=11) внесена в столбец В,а для второго
прибора (n2=9)
результаты — в столбец С (рис.4.4-4.5). Средние
значения отклонений одинаковы и равны
нулю. Следовательно, у приборов отсутствует
систематическая ошибка.
Проверка точности приборов сводится к
проверке совпадения дисперсий. Если
дисперсии отклонений от эталонного
значения статистически равны, то приборы
обладают одинаковой точностью. Выдвигается
гипотеза H0
— дисперсии выборок равны, альтернативная
гипотезаH1— дисперсии не равны.
В результате расчета были получены
соответственно следующие значения
дисперсий:
=7.35 и
=2.188.
Значение критерия
=7.35 /2.188 = 3.36.
Для уровня значимости α =0.05; числа
степеней свободы числителяr1 =11-1=10
и числа степеней свободы знаменателяr2 = 9-1= 8
находим с помощью встроенной
функции FРАСПОБР().Fкрит= 3.347.
Поскольку
то гипотезаH0
отклоняется, и принимается альтернативная
гипотезаH1
(дисперсии различны). Следовательно,
приборы имеют различную точность.
Рис.
4.4 Сравнение двух выборочных дисперсий
(фрагмент
рабочего листа MSExcelв режиме отображения данных)
Рис.
4.5. Сравнение двух выборочных дисперсий
(фрагмент
рабочего листа MSExcelв режиме отображений формул)
Средство анализа «Двухвыборочный f-тест для дисперсии» надстройки «Пакет анализа» ms Excel
Средство анализа «Двухвыборочный F-тест
для дисперсии» надстройки «Пакет
анализа»MSExcelслужит для проверки гипотезы о равенстве
дисперсий двух выборок. Для проверки
необходимо заполнить диалоговое окно,
приведенное на рис.4.6, назначение всех
полей ввода очевидно.
Рис. 4.6 Диалоговое
окно средства анализа «Двухвыборочный
F-тест для дисперсии»
надстройки «Пакет анализа»MSExcel
Результаты расчета представлены на
рис.4.7.
Сравните полученные результаты с
результатами, полученными вручную.
Рис.
4.7 «Двухвыборочный F-тест
для дисперсии»
надстройки
«Пакет анализа» MSExcel
Соседние файлы в папке Эконометрика 1 лекция
- #
- #
- #
- #
- #
- #
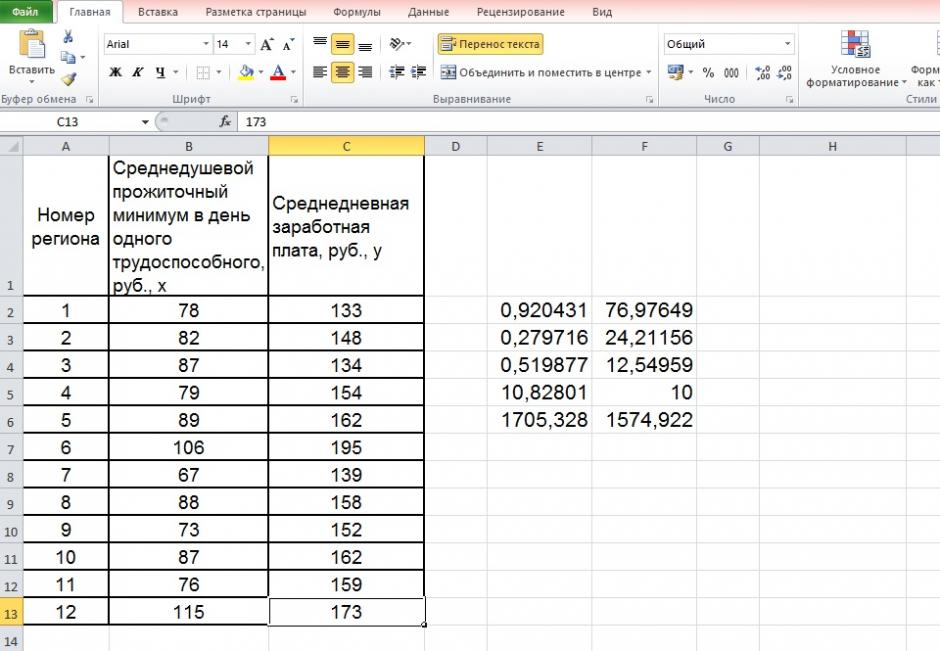
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии

3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости 
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
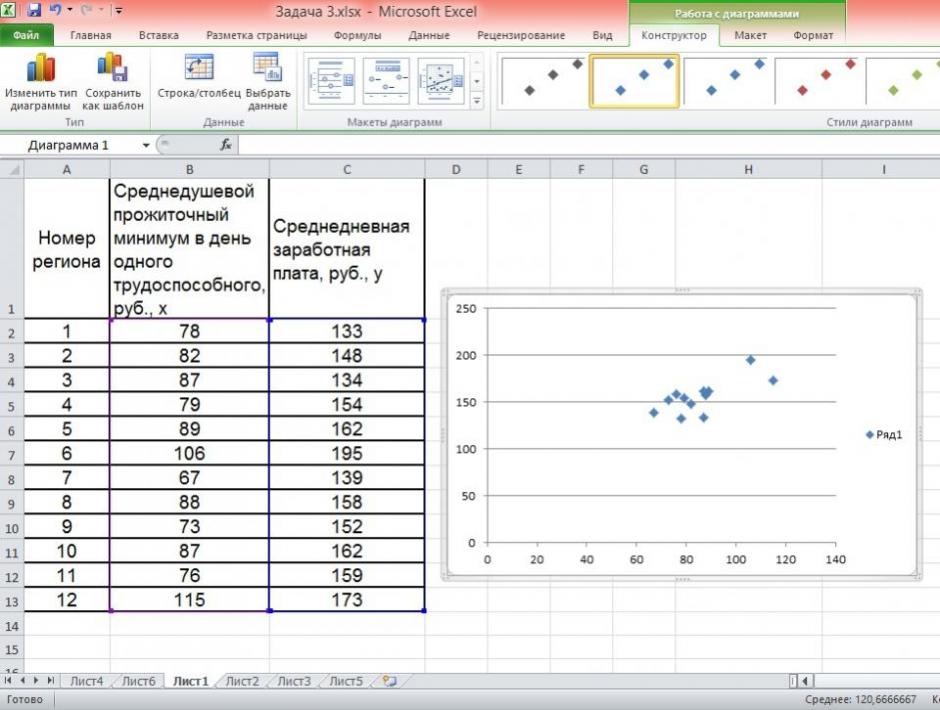
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
Для этого:
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
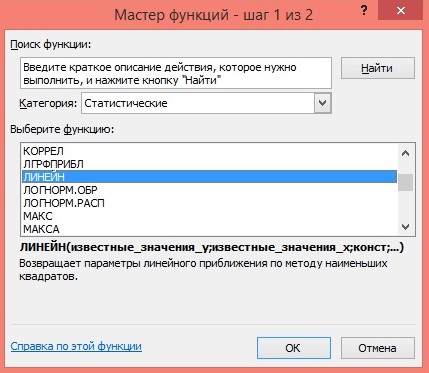
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
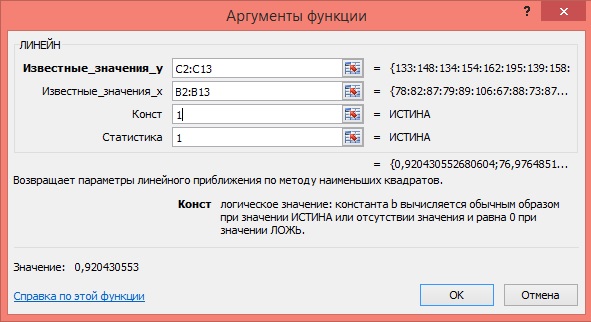
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу <F2>, а затем на комбинацию клавиш <Ctrl>+<Shift>+<Enter>.
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов
|
Остаточная сумма квадратов
|
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации 
По вычисленному коэффициенту детерминации 
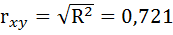
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой 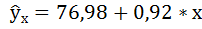
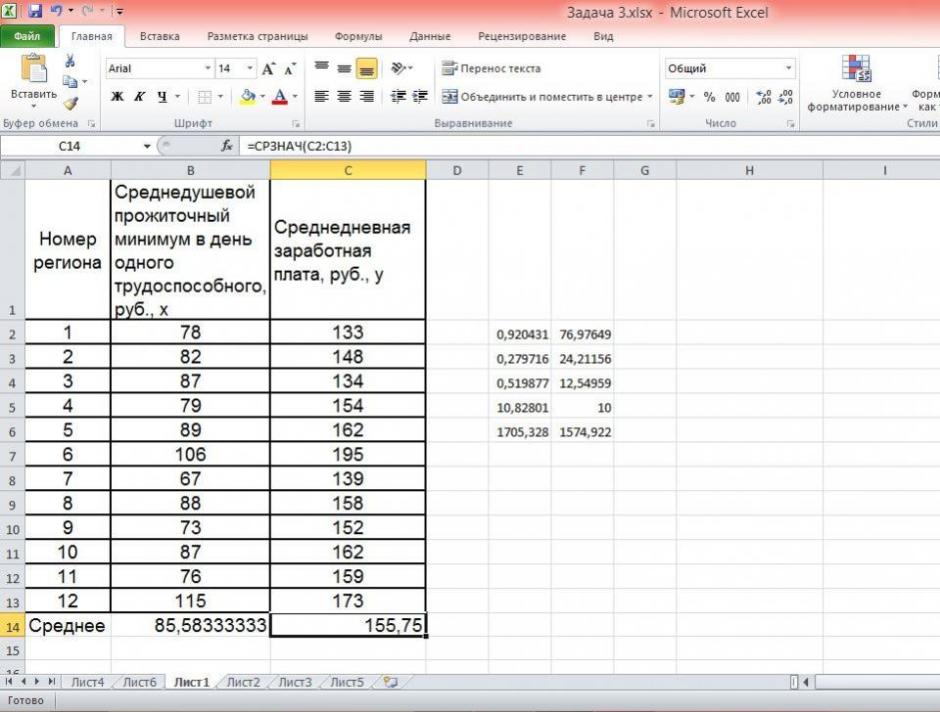
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
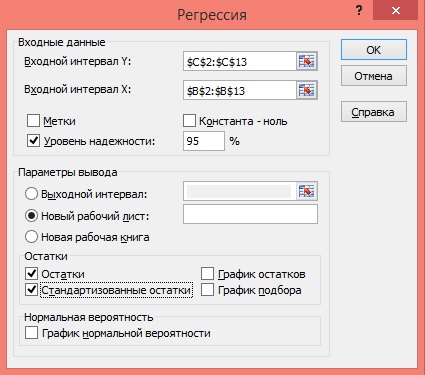
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
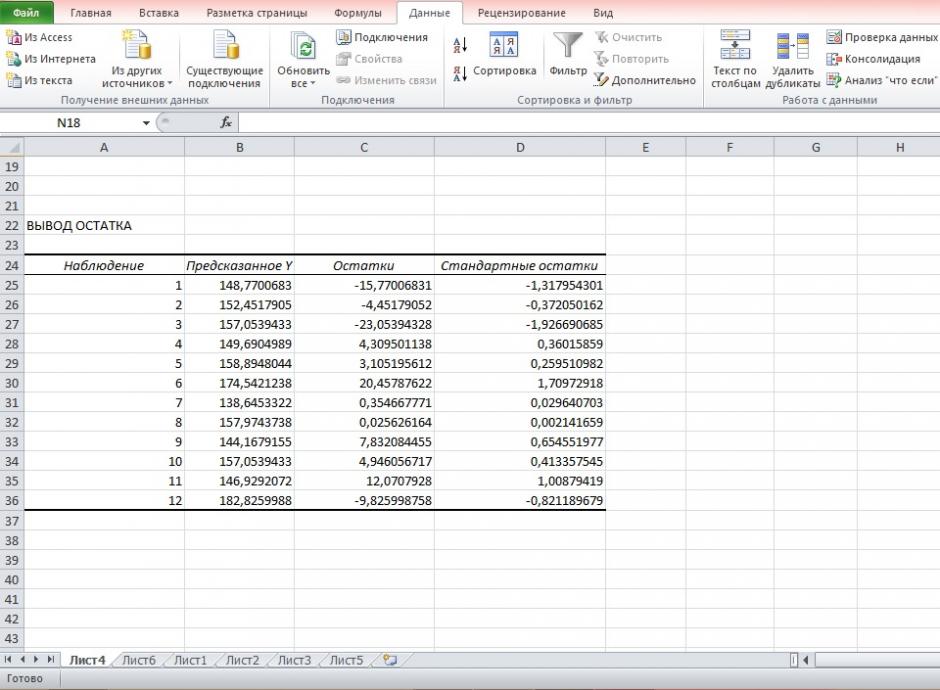
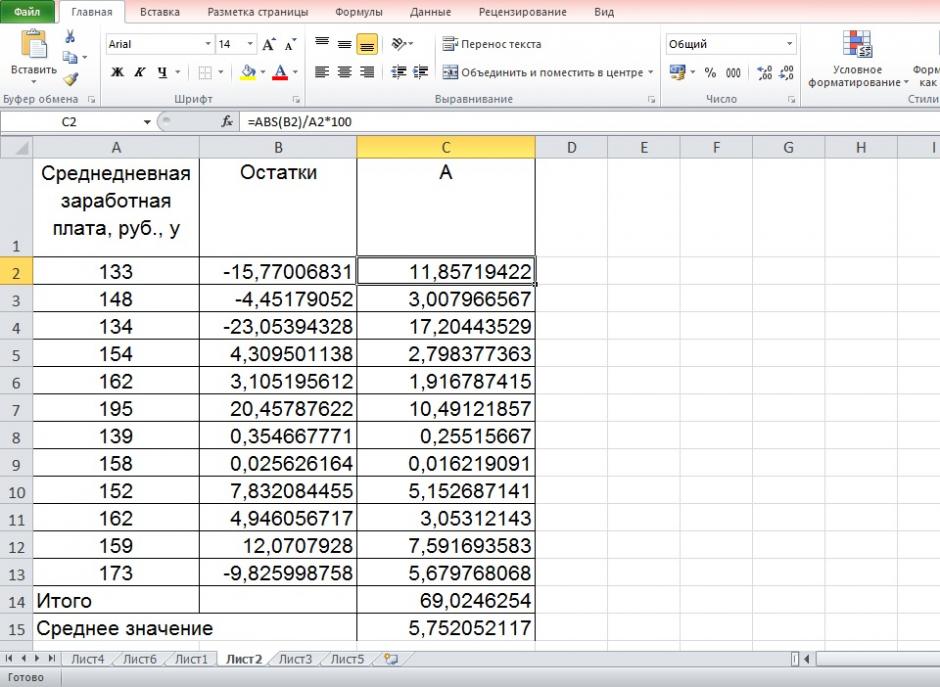
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как 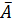
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку 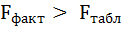
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
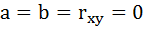
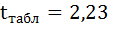
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ: 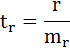
где 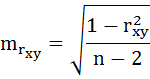
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 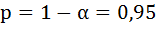
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
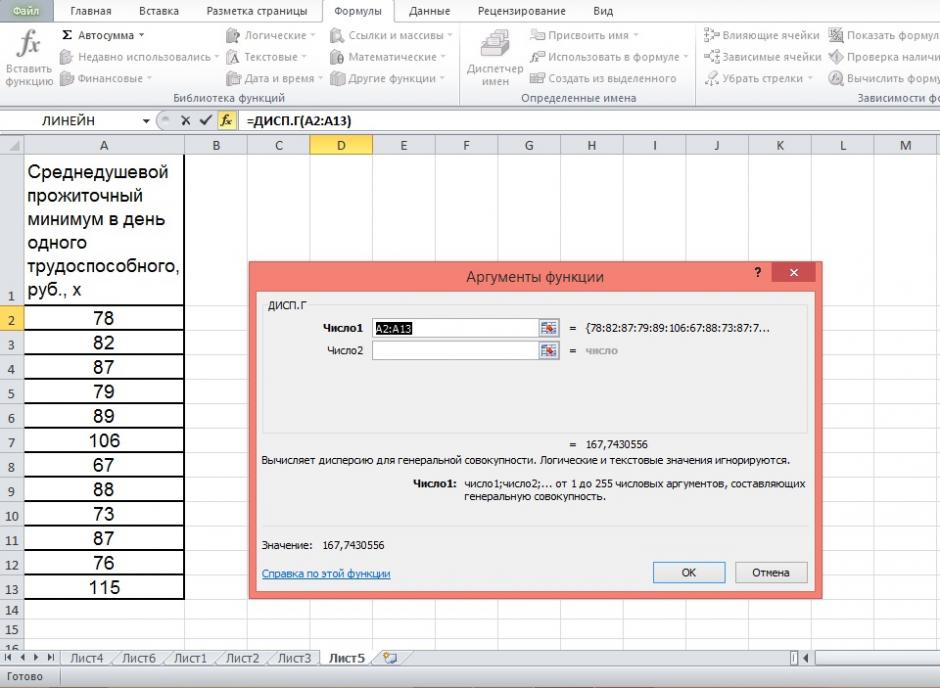
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при 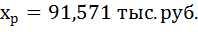
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.