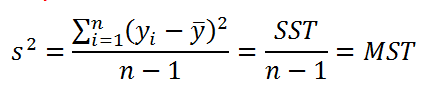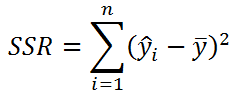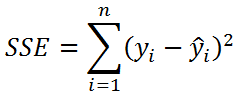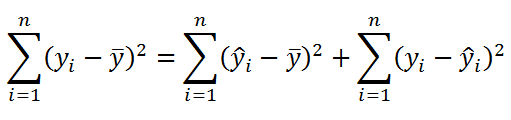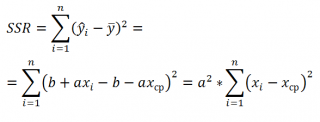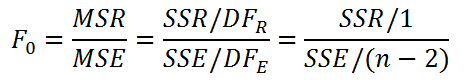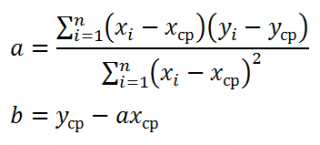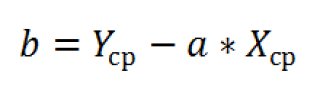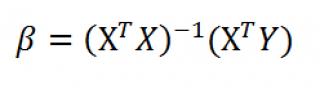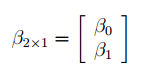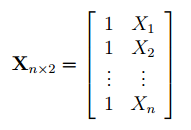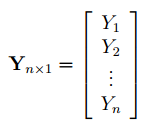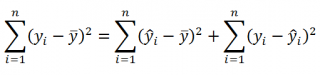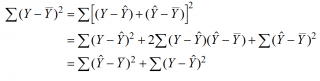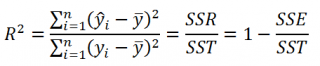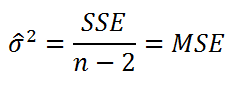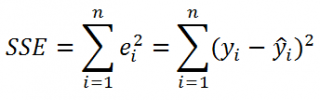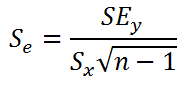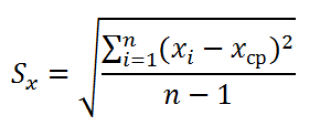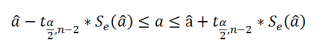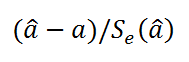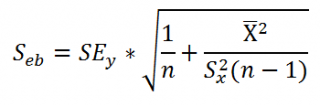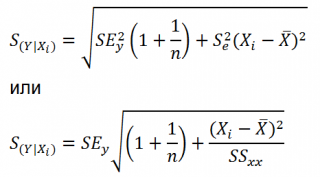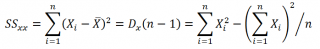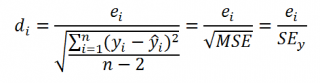- Авторы
- Резюме
- Файлы
- Ключевые слова
- Литература
Курзаева Л.В.
1
1 ФГБОУ ВО «Магнитогорский государственный технический университет им. Г.И. Носова»
Аналитическая статистика – одиниз самых сложных разделов анализа данных в плане изучения, при этом регрессионный анализ является одним из самых информативных. Такой анализ производится при решения следующих задач: установление и оценка взаимосвязи признаков; прогнозирование и предсказание; управление процессами. Существует два вида анализа двумерных данных, представленных переменными: корреляционный и регрессионныйанализ, последнийпозволяет определить форму взаимосвязи между признаками. В статье описывается простой способ проведения регрессионного анализа в MicrosoftExcel. Материалы данной статьи представляют методическую и практическую ценность для преподавателей, занимающихся вопросами повышения эффективности обучения в области основ анализа данных с информационных технологий, и осуществляющие реализацию образовательного процесса в вузах и на курсах повышения квалификаций.
Ключевыеслова: анализ данных
электронные таблицы
1. Овчинникова И.Г., Варфоломеева Т.Н., Гусева Е.Н. Учебно-методическое пособие для подготовки к вступительным экзаменам по информатике. -Магнитогорск, 2002. -С. 119
2. Овчинникова И.Г., Варфоломеева Т.Н., Корнещук Н.Г. Учебное пособие для подготовки к централизованному тестированию по информатике. -Магнитогорск, 2002. -С.205
3. Курзаева Л.В. Дистанционный курс «Основы математической обработки информации»: электронный учебно-методический комплекс // Хроники объединенного фонда электронных ресурсов Наука и образование. — 2014. -Т. 1. — № 12 (67). — С. 117
4. Курзаева Л.В. Введение в теорию систем и системный анализ: учеб. пособие/Л.В. Курзаева. -Магнитогорск: МаГУ, 2015. -211 с.
5. Курзаева Л.В. Введение в методы и средства получения и обработки информации для задач управления социальными и экономическими системами: учеб. пособие/Л.В. Курзаева, И.Г. Овчинникова, Г.Н. Чусавитина. -Магнитогорск:Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016. -118 с.
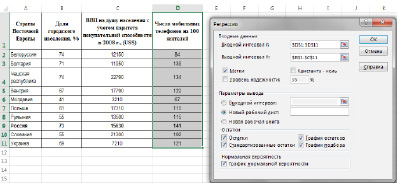
Для реализации процедуры Регрессия необходимо: выбрать в меню Сервис команду Анализ данных. В появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать строку Регрессия.
Рис.1. Окно «Регрессия»
В появившемся диалоговом окне (рис.1) задать:
Входной интервал Y– диапазон (столбец), содержащий данные со значениями объясняемой переменной;
Входной интервал Х– диапазон (столбцы), содержащий данные с заголовками.
Метки – флажок, который указывает, содержат ли первые элементы отмеченных диапазонов названия переменных (столбцов) или нет;
Константа-ноль– флажок, указывающий на наличие или отсутствие свободного члена в уравнении (а);
Уровень надежности– уровень значимости, (например, 0,05);
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона, в котором будет сохранен отчет по построению модели;
Новый рабочий лист– поставить значок и задать имя нового листа (Отчет – регрессия), в котором будет сохранен отчет.
Если необходимо получить значения и график остатков, а также график подбора (чтобы визуально проверить отличие экспериментальных точек от предсказанных по регрессионной модели), установите соответствующие флажки в диалоговом окне.
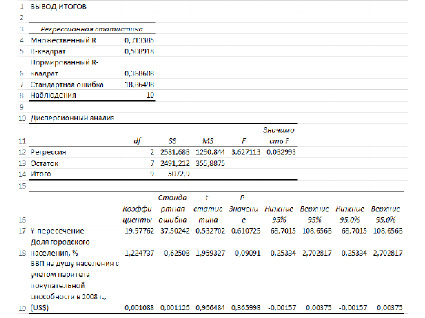
Рассмотрим результаты регрессионного анализа (рис. 2, 3).
Рис. 2. Вывод итогов регрессионного анализа
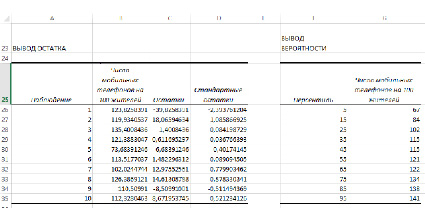
Рис. 3. Вывод остатков и вероятности по результатам регрессионного анализа
Множественный R – коэффициент корреляции
R-квадрат – это коэффициент линейной детерминации. Коэффициент является одной из наиболее эффективных оценок адекватности регрессионной R2модели, мерой качества уравнения регрессии в целом (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям.
Если R-квадрат > 0,95, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,8 до 0,95, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна и модель требует улучшения (введения новых независимых переменных, учета нелинейностей и т. д.).
Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
Недостатком коэффициента детерминации R-квадратявляется то, что он увеличивается при добавлении новых объясняющих переменных, хотя это и не обязательно означает улучшение качества регрессионной модели. В этом смысле предпочтительнее использовать нормированный, который в отличие от R-квадрат может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенное влияние на зависимую переменную.
Наблюдения – число наблюдений (в нашем случае 10 стран).
Df– число степеней свободы связано с числом единиц совокупности и с числом определяемых по ней констант.
F и Значимость F позволяют проверить значимость уравнения регрессии, т.е. установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
SS – Сумма квадратов отклонений значений признака Y.
MS – Дисперсия на одну степень свободы.
F – Наблюдаемое (эмпирическое) значение статистики F, по которой проверяется гипотеза равенства нулю одновременно всех коэффициентов модели. Значимость F – теоретическая вероятность того, что при гипотезе равенства нулю одновременно всех коэффициентов модели F-статистика больше эмпирического значения F.
На уровне значимости α=0,05 гипотеза H0:b1=0отвергается, если Значимость F<0.05, и принимается, если Значимость F
Значения коэффициентов регрессии находятся в столбце Коэффициенты и соответствуют:
У-пересечение – a;
переменная XI – b1;
переменная Х2 – b2 и т. Д.
Таким образом, получена следующая модель регрессии:
Y=1.2247X1+0.00108X2+19.9776
t-статистика соответствующего коэффициента.
P-Значение – вероятность, позволяющая определить значимость коэффициента регрессии. В случаях, когда Р-Значение>0,05, коэффициент может считаться нулевым, что означает, что соответствующая независимая переменная практически не влияет на зависимую переменную.
В нашем случае оба коэффициента оказались «нулевыми», а значит обе независимые переменные не влияют на модель.
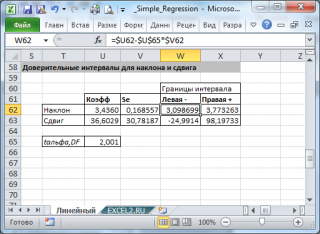
Нижние 95% – Верхние 95% – доверительный интервал для параметра , т.е. с надежностью 0.95 этот коэффициент лежит в данном интервале. Поскольку коэффициент регрессии в исследованиях имеют четкую интерпретацию, то границы доверительного интервала для коэффициента регрессии не должны содержать противоречивых результатов. Так, например, «Доля городского населения, в %» не может лежать в интервале -0,25≥b1≥2,7. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Предсказанное Y — теоретические (расчетные) значения результативного признака.
Остатки – остатки по модели регрессии.
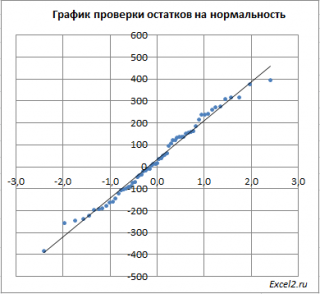
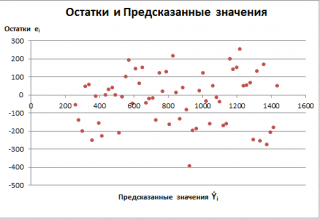
На основе данных об остатках модели регрессии был построен график остатков (рис. 4) и график подбора – поле корреляции фактических и теоретических (расчетных) значений результативной переменной (рис.5).
Рис. 4. График остатков по значениям признака «Доля городского населения, %»
Рис. 5. График подбора для признаков «Доля городского населения, %» и «Число мобильных телефонов на 100 жителей»
Рассмотрение графиков подбора позволяет предположить, что, возможно, качество модели можно усовершенствовать, исключив данные по Белоруссии как аномальные значения.
Библиографическая ссылка
Курзаева Л.В. РЕГРЕССИОННЫЙ АНАЛИЗ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ // Международный журнал прикладных и фундаментальных исследований. – 2016. – № 12-7.
– С. 1234-1238;
URL: https://applied-research.ru/ru/article/view?id=11019 (дата обращения: 15.04.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Для
оценки существенности, значимости
коэффициента корреляции используется
t-критерий
Стьюдента.
Находится средняя
ошибка коэффициента корреляции по
формуле:
На
основе ошибки рассчитываетсяt-критерий:
Рассчитанное
значение t-критерия
сравнивают с табличным, найденным в
таблице распределения Стьюдента при
уровне значимости 0,05 или 0,01 и числе
степеней свободы n-1.
Если расчетное значение t-критерия
больше табличного, то коэффициент
корреляции признается значимым.
При
криволинейной связи для оценки значимости
корреляционного отношения и уравнения
регрессии применяется F-критерий.
Он вычисляется по формуле:
или
где
η – корреляционное отношение; n
– число наблюдений; m
– число параметров в уравнении регрессии.
Рассчитанное
значение F
сравнивается с табличным для принятого
уровня значимости α (0,05 или 0,01) и чисел
степеней свободы к1=m-1
и k2=n-m.
Если расчетное значение F
превышает табличное, связь признается
существенной.
Значимость
коэффициента регрессии устанавливается
с помощью t-критерия Стьюдента,
который вычисляется по формуле:
где
σ2аi
— дисперсия коэффициента регрессии.
Она
вычисляется по формуле:
где
к – число факторных признаков в уравнении
регрессии.
Коэффициент
регрессии признается значимым, если
ta1≥tкр.
tкр
отыскивается в таблице критических
точек распределения Стьюдента при
принятом уровне значимости и числе
степеней свободы k=n-1.
4.3.Корреляционно-регрессионный анализ в Excel
Проведём
корреляционно-регрессионный анализ
взаимосвязи урожайности и затрат труда
на 1 ц зерна. Для этого открываем лист
Excel,
в ячейки А1:А30 вводим значения факторного
признака –
урожайности зерновых культур, в ячейки
В1:В30 значения результативного признака
– затрат труда
на 1 ц зерна. В меню Сервис выберем опцию
Анализ данных. Щелкнув левой кнопкой
мыши по этому пункту, откроем инструмент
Регрессия. Щелкаем по кнопке OK,
на экране появляется диалоговое окно
Регрессия. В поле Входной интервал У
вводим значения результативного признака
(выделяя ячейки В1:В30), в поле Входной
интервал Х вводим значения факторного
признака (выделяя ячейки А1:А30). Отмечаем
уровень вероятности 95%, выбираем Новый
рабочий лист. Щелкаем по кнопке OK.
На рабочем листе появляется таблица
«ВЫВОД ИТОГОВ», в которой даны результаты
вычисления параметров уравнения
регрессии, коэффициента корреляции и
другие показатели, позволяющие определить
значимость коэффициента корреляции и
параметров уравнения регрессии.
|
ВЫВОД |
||||||||
|
Регрессионная |
||||||||
|
Множественный |
0,853301 |
|||||||
|
R-квадрат |
0,728123 |
|||||||
|
Нормированный |
0,718413 |
|||||||
|
Стандартная |
0,112121 |
|||||||
|
Наблюдения |
30 |
|||||||
|
Дисперсионный |
||||||||
|
df |
SS |
MS |
F |
Значимость |
||||
|
Регрессия |
1 |
0,942676 |
0,942676 |
74,9876 |
2,09E-09 |
|||
|
Остаток |
28 |
0,351991 |
0,012571 |
|||||
|
Итого |
29 |
1,294667 |
||||||
|
Коэффициенты |
Стандартная |
t-статистика |
P-Значение |
Нижние |
Верхние |
Нижние |
Верхние |
|
|
Y-пересечение |
2,836242 |
0,200011 |
14,18042 |
2,64E-14 |
2,426538 |
3,245947 |
2,426538 |
3,245947 |
|
Переменная |
-0,06654 |
0,007684 |
-8,65954 |
2,09E-09 |
-0,08228 |
-0,0508 |
-0,08228 |
-0,0508 |
В
данной таблице «Множественный R»
— это коэффициент корреляции, «R-квадрат»
— коэффициент детерминации. «Коэффициенты:
Y-пересечение»
— свободный член уравнения регрессии
2,836242; «Переменная Х1» – коэффициент
регрессии -0,06654. Здесь имеются также
значения F-критерия
Фишера 74,9876, t-критерия
Стьюдента 14,18042, «Стандартная ошибка
0,112121», которые необходимы для оценки
значимости коэффициента корреляции,
параметров уравнения регрессии и всего
уравнения.
На
основе данных таблицы построим уравнение
регрессии: ух=2,836-0,067х.
Коэффициент регрессии а1=-0,067
означает, что с повышением урожайности
зерновых на 1 ц/га затраты труда на 1 ц
зерна уменьшаются на 0,067 чел.-ч.
Коэффициент
корреляции r=0,85>0,7,
следовательно, связь между изучаемыми
признаками в данной совокупности тесная.
Коэффициент детерминации r2=0,73
показывает, что 73% вариации результативного
признака (затрат труда на 1 ц зерна)
вызвано действием факторного признака
(урожайности зерновых).
В
таблице критических точек распределения
Фишера — Снедекора найдём критическое
значение F-критерия
при уровне значимости 0,05 и числе степеней
свободы к1=m-1=2-1=1
и k2=n-m=30-2=28,
оно равно 4,21. Так как рассчитанное
значение критерия больше табличного
(F=74.9896>4,21),
то уравнение регрессии признаётся
значимым.
Для
оценки значимости коэффициента корреляции
рассчитаем t-критерий
Стьюдента:
Втаблице критических точек распределения
Стьюдента найдём критическое значениеt-критерия
при уровне значимости 0,05 и числе степеней
свободы n-1=30-1=29,
оно равно 2,0452. Так как расчётное значение
больше табличного, то коэффициент
корреляции является значимым.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
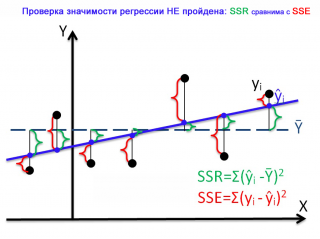
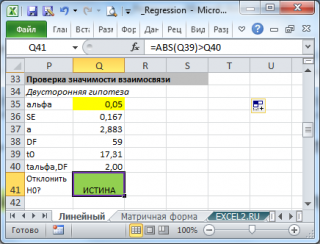
Проведем проверку значимости простой линейной регрессии с помощью процедуры
F
-тест.
Disclaimer
: Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей
Регрессионного анализа.
Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения
Регрессии
– плохая идея.
Проверку значимости взаимосвязи переменных в рамках модели
простой линейной регрессии
можно провести разными, но эквивалентными между собой, способами:
Проверку значимости взаимосвязи переменных в рамках модели простой линейной регрессии можно провести разными, но эквивалентными между собой, способами:
-
проверка гипотезы о равенстве 0 коэффициента регрессии
, т.е. наклона;
-
проверка статистической значимости коэффициента корреляции
;
-
с использованием дисперсионного анализа (процедура
F
-тест
).
Процедуру
F
-теста
рассмотрим на примере
простой линейной регрессии
, когда прогнозируемая переменная Y зависит только от одной переменной Х.
Чтобы определить может ли предложенная модель
линейной регрессии
быть использована для адекватного описания значений переменной Y,
дисперсию
наблюдаемых данных анализируют методом
Дисперсионного анализа (ANOVA for Simple Regression)
.
Дисперсия
данных разбивается на компоненты, которые затем используются в
F
-тесте
для определения значимости регрессии.
F
-тест для проверки значимости регрессии
НЕ относится к простым и интуитивно понятным процедурам. Вероятно, это связано с тем, что для проведения
F
-теста
требуется быть знакомым с определенным количеством статистических понятий и нужно неплохо разбираться в связанных с ними статистических методах. Нам потребуются понятия из следующих разделов статистики:
-
регрессионный анализ
;
-
процедура проверки гипотез
;
-
статистики и выборочные распределения
;
-
распределение Фишера
;
-
уровень значимости
.
Можно, конечно, рассмотреть
F
-тест
формально:
-
вычислить на основании выборки значение
тестовой
F
статистики;
-
сравнить полученное значение со значением, соответствующему заданному
уровню значимости
;
-
в зависимости от соотношения этих величин принять решение о значимости вычисленной
линейной регрессии
В этой статье ставится более амбициозная задача – разобраться в самом подходе, на котором основан
F
-тест
. Сначала введем несколько определений, которые используются в процедуре
F
-теста
, затем рассмотрим саму процедуру.
Примечание
: Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к
вычислительной части
.
Определения, необходимые для
F
-теста
Согласно
определению дисперсии
,
дисперсия выборки
прогнозируемой переменной Y определяется формулой:
В формуле используется ряд сокращений:
- SST (Total Sum of Squares) – это просто компактное обозначение Суммы Квадратов отклонений от среднего (такое сокращение часто используется в зарубежной литературе).
- MST (Total Mean Square) – Среднее Суммы Квадратов отклонений (еще одно общеупотребительное сокращение).
Примечание
: Необходимо иметь в виду, что с одной стороны величины MST и SST являются случайными величинами, вычисленными на основании выборки, т.е.
статистиками
. Однако с другой стороны, при проведении
регрессионного анализа
по данным имеющейся выборки вычисляются их конкретные значения. В этом случае величины MST и SST являются просто числами.
Значение n-1 в вышеуказанной формуле равно
числу степеней свободы (
DF
)
, которое относится к
дисперсии выборки
(одна
степень свободы
у
n
величин yi потеряна в результате наличия ограничения
, связывающего все значения выборки). Число
степеней свободы
у величины SST также имеет специальное обозначение: DFT (DF Total).
Как видно из формулы, отношение величин SST и DFT обозначается как MST. Эти 3 величины обычно выдаются в таблице результатов
дисперсионного анализа
в различных прикладных статистических программах (в том числе и в
надстройке Пакет анализа, инструмент Регрессия
).
Значение SST, характеризующую
общую
изменчивость переменной
Y, можно разбить на 2 компоненты:
Изменчивость объясненную моделью
(Explained variation), обозначается SSR
Необъясненную изменчивость
(Unexplained variation), обозначается SSЕ
Известно
, что справедливо равенство:
SST
=
SSR
+
SSE
Величинам
SSR
и
SSE
также сопоставлены
степени свободы
. У
SSR
одна
степень свободы
, т.к. она однозначно определяется одним параметром – наклоном
линии регрессии
a
(напомним, что мы рассматриваем
простую линейную регрессию
). Это очевидно из формулы:
Примечание:
Очевидность наличия только одной
степени свободы
проистекает из факта, что переменная Х – контролируемая (не является случайной величиной).
Число степеней свободы
величины
SSR
имеет специальное обозначение:
DFR
(для простой регрессии DFR=1, т.к. число независимых переменных Х равно 1)
.
По аналогии с MST, отношение этих величин также часто обозначают
MSR
=
SSR
/
DFR
.
У
SSE
число степеней свободы
равно
n
-2
, которое обозначается как
DFE
(или
DFRES
— residual degrees of freedom).
Двойка вычитается, т.к. изменчивость переменной yi имеет 2 ограничения, связанные с оценкой 2-х параметров линейной модели (
а
и
b
): ŷi=a*xi+b
Отношение этих величин также часто обозначают
MSE
=
SSE
/
DFE
.
MSR и MSE имеют размерность дисперсий, хотя корректней их называть средними значениями квадратов отклонений. Тем не менее, ниже мы их будем «дисперсиями», т.к. они отображают меру разброса: MSE – меру разброса точек наблюдений относительно линии регрессии, MSR показывает насколько линия регрессии совпадает с горизонтальной линией среднего значения Y.
Примечание
: Напомним, что MSE (Mean Square of Errors) является оценкой
дисперсии
s
2
ошибки, подробнее см. статью про
линейную регрессию
, раздел
Стандартная ошибка регрессии
.
Число степеней свободы
обладает свойством аддитивности:
DFT
=
DFR
+
DFE
.
В этом можно убедиться, составив соответствующее равенство
n
-1=1+(
n
-2)
Наконец, определившись с определениями, переходим к рассмотрению самой процедуры
F
-тест
.
Процедура
F
-теста
Сущность
F
-теста
при проверке значимости регрессии заключается в том, чтобы сравнить 2
дисперсии
:
объясненную
моделью (MSR) и
необъясненную
(MSE). Если эти
дисперсии
«примерно равны», то
регрессия незначима
(построенная модель не позволяет объяснить поведение прогнозируемой Y в зависимости от значений переменной Х). Если
дисперсия,
объясненная
моделью (MSR) «существенно больше», чем необъясненная, то
регрессия значимая
.
Примечание
: Чтобы быстрее разобраться с процедурой
F
-теста
рекомендуется вспомнить процедуру проверки статистических гипотез о равенстве дисперсий 2-х
нормальных распределений
(т.е.
двухвыборочный F-тест для дисперсий
).
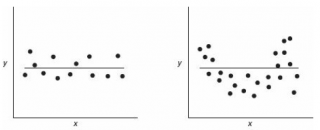
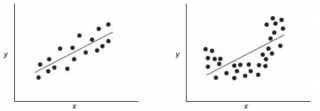
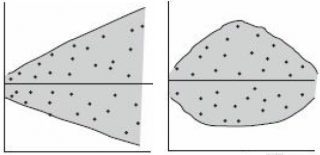
Чтобы пояснить вышесказанное изобразим на
диаграммах рассеяния
2 случая:
- регрессия значима (в этом случае имеем значительный наклон прямой) и
- регрессия незначима (линия регрессии близка к горизонтальной прямой).
На первой диаграмме показан случай, когда регрессия значима:
- Зеленым цветом выделены расстояния от среднего значения до линии регрессии , вычисленные для каждого хi. Сумма квадратов этих расстояний равна SSR;
- Красным цветом выделены расстояния от линии регрессии до соответствующих точек наблюдений . Сумма квадратов этих расстояний равна SSЕ.
Из диаграммы видно, что в случае значимой регрессии, сумма квадратов «зеленых» расстояний, гораздо больше суммы квадратов «красных». Понятно, что их отношение будет гораздо больше 1. Следовательно, и отношение дисперсий MSR и MSE будет гораздо больше 1 (не забываем, что SSE нужно разделить еще на соответствующее количество степеней свободы n-2).
В случае значимой регрессии точки наблюдений будут находиться вдоль линии регрессии. Их разброс вокруг этой линии описываются ошибками регрессии, которые были минимизированы посредством
процедуры МНК
. Очевидно, что разброс точек относительно линии регрессии значительно меньше, чем относительно горизонтальной линии, соответствующей среднему значению Y.
Совершенно другую картину мы можем наблюдать в случае незначимой регрессии.
Очевидно, что в этом случае, сумма квадратов «зеленых» расстояний, примерно соответствует сумме квадратов «красных». Это означает, что объясненная дисперсия примерно соответствует величине необъясненной дисперсии (MSR/MSE будет близко к 1).
Если ответ о значимости регрессии практически очевиден для 2-х вышеуказанных крайних ситуаций, то как сделать правильное заключение для промежуточных углов наклона линии регрессии?
Понятно, что если вычисленное на основании выборки значение MSR/MSE будет существенно больше некоторого критического значения, то регрессия значима, если нет, то не значима. Очевидно, что это значение должно быть больше 1, но
как определить это критическое значение статистически обоснованным методом
?
Вспомним, что для формулирования статистического вывода (т.е. значима регрессия или нет) используют
проверку гипотез
. Для этого формулируют 2 гипотезы: нулевую
Н
0
и альтернативную
Н
1
. Для проверки значимости регрессии в качестве
нулевой гипотезы
Н
0
принимают, что связи нет, т.е. наклон прямой a=0. В качестве альтернативной гипотезы
Н
1
принимают, что a <>0.
Примечание
: Даже если связи между переменными нет (a=0), то вычисленная на основании данных выборки оценка
наклона
— величина
а
, из-за случайности выборки будет близка, но все же отлична от 0.
По умолчанию принимается, что нулевая гипотеза верна – связи между переменными нет. Если это так, то:
- MSR/MSE будет близко к 1;
-
Случайная величина F = MSR/MSE будет иметь
F-распределение
со степенями свободы
1 (в числителе) и n-2 (знаменателе). F является
тестовой статистикой
для проверки значимости регрессии.
Примечание
: MSR и MSE являются случайными величинами (т.к. они получены на основе случайной выборки). Соответственно, выражение F=MSR/MSE, также является случайной величиной, которая имеет свое распределение,
среднее значение
и
дисперсию
.
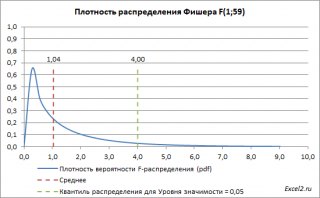
Ниже приведен
график плотности вероятности F-распределения
со степенями свободы
1 (в числителе) и 59 (знаменателе). 59=61-2, 61 наблюдение минус 2 степени свободы.
Если нулевая гипотеза верна, то значение F
0
=MSR/MSE, вычисленное на основании выборки, должно быть около ее
среднего значения
(т.е. около 1,04). Если F
0
будет существенно больше 1 (чем больше F0 отклоняется в сторону больших значений, тем это маловероятней), то это будет означать, что F не имеет
F-распределение
, а, следовательно, нулевую гипотезу нужно отклонить и принять альтернативную, утверждающую, что связь между переменными есть (значима).
Обычно предполагают, что если вероятность, того что
F
-статистика
приняла значение F0 составляет менее 5%, то это событие маловероятно и нулевую гипотезу необходимо отклонить. 5% — это
заданный
исследователем
уровень значимости
, который может быть, например, 1% или 10%.
Значение статистики F0 может быть вычислено на основании выборки:
Вычисления в
MS
EXCEL
В MS EXCEL критическое значение для заданного
уровня значимости
F1-альфа, 1, n-2 можно вычислить по формуле =
F.ОБР(1- альфа;1; n-2)
или =
F.ОБР.ПХ(альфа;1; n-2)
. Другими словами требуется вычислить
верхний альфа-квантиль F-распределения
с соответствующими
степенями свободы
.
Таким образом, при значении статистики F0> F1-альфа, 1, n-2 мы имеем основание для отклонения нулевой гипотезы.
Значение F
0
можно вычислить на основании значений выборки по вышеуказанной формуле или с
помощью функции
ЛИНЕЙН()
:
=
ИНДЕКС(ЛИНЕЙН($C$23:$C$83;$B$23:$B$83;;ИСТИНА);4;1)
В случае простой регрессии значение F0 также равно квадрату t-статистики, которую мы использовали при проверке двусторонней гипотезе
о равенстве 0 коэффициента регрессии
.
Проверку значимости регрессии можно также осуществить через вычисление p-значения. В этом случае вычисляют вероятность того, что случайная величина F примет значение F0 (это и есть p-значение), затем сравнивают p-значение с заданным
уровнем значимости
. Если p-значение больше
уровня значимости,
то нулевую гипотезу нет оснований отклонить, и регрессия незначима.
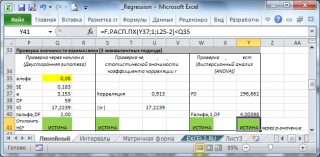
В MS EXCEL для проверки гипотезы используя
p
-значение
используйте формулу =
F.РАСП.ПХ(F0;1;n-2)
< альфа
Если формула вернет ИСТИНА, то регрессия значима. Если формула вернет ЛОЖЬ, то у нас нет оснований отклонить нулевую гипотезу, т.е. «скорее всего» параметр модели a равен 0 (см.
файл примера
, где показано эквивалентность всех подходов проверки значимости регрессии).
В программах статистики результаты процедуры
F
-теста
выводят с помощью стандартной таблицы
дисперсионного анализа
. В
файле примера
такая таблица приведена на листе Таблица, которая построена на основе результатов, возвращаемых
инструментом Регрессия надстройки Пакета анализа MS EXCEL
.
Множественная линейная регрессия является одним из наиболее часто используемых методов во всей статистике.
В этом руководстве объясняется, как интерпретировать каждое значение в выходных данных модели множественной линейной регрессии в Excel.
Пример: интерпретация выходных данных регрессии в Excel
Предположим, мы хотим знать, влияет ли количество часов, потраченных на учебу, и количество сданных подготовительных экзаменов на балл, который студент получает на определенном вступительном экзамене в колледж.
Чтобы исследовать эту взаимосвязь, мы можем выполнить множественную линейную регрессию, используя часы обучения и подготовительные экзамены, взятые в качестве переменных-предикторов, и экзаменационный балл в качестве переменной ответа.
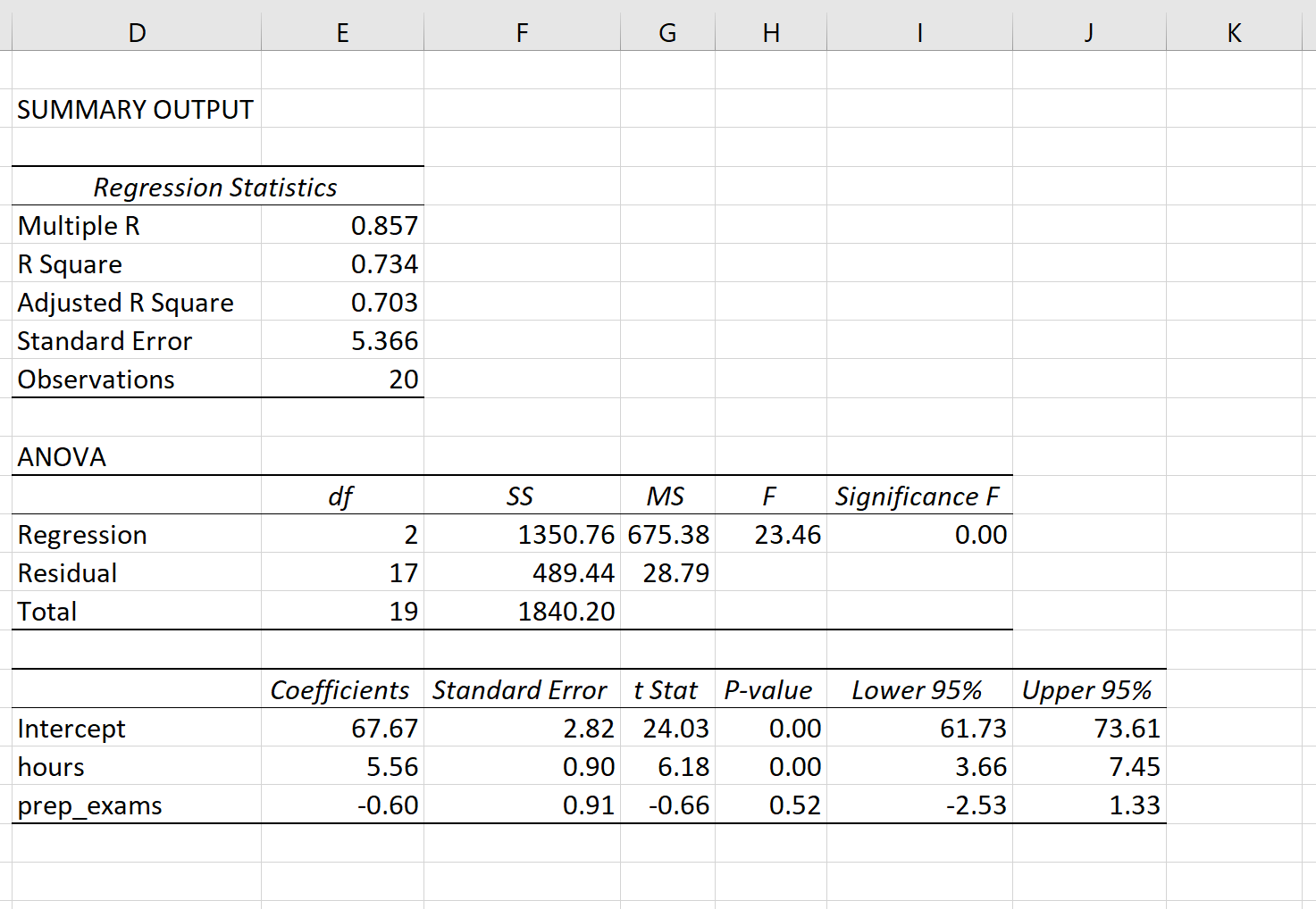
На следующем снимке экрана показаны выходные данные регрессии этой модели в Excel:
Вот как интерпретировать наиболее важные значения в выводе:
Несколько R: 0,857.Это представляет собой множественную корреляцию между переменной ответа и двумя переменными-предикторами.
R-квадрат: 0,734.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющими переменными. В этом примере 73,4% вариаций в экзаменационных баллах можно объяснить количеством часов обучения и количеством сданных подготовительных экзаменов.
Скорректированный квадрат R: 0,703.Это представляет собой значение R-квадрата, скорректированное с учетом количества переменных-предикторов в модели.Это значение также будет меньше, чем значение для R Square, и наказывает модели, которые используют в модели слишком много переменных-предикторов.
Стандартная ошибка: 5,366.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,366 единицы.
Наблюдения: 20.Общий размер выборки набора данных, используемого для создания регрессионной модели.
Ф: 23,46.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель в целом статистически значимой.
В этом случае p-значение меньше 0,05, что указывает на то, что независимые переменные количество часов обучения и количество сданных подготовительных экзаменов вместе имеют статистически значимую связь с экзаменационным баллом .
Коэффициенты: коэффициенты для каждой независимой переменной говорят нам о среднем ожидаемом изменении переменной отклика при условии, что другая независимая переменная остается постоянной.
Например, ожидается, что за каждый дополнительный час, потраченный на учебу, средний экзаменационный балл увеличится на 5,56 при условии, что количество сданных подготовительных экзаменов останется неизменным.
Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится ноль часов и сдает нулевые подготовительные экзамены, составляет 67,67 .
P-значения. Отдельные p-значения говорят нам, является ли каждая независимая переменная статистически значимой. Мы можем видеть, что изученные часы статистически значимы (p = 0,00), в то время как пройденные подготовительные экзамены (p = 0,52) не являются статистически значимыми при α = 0,05.
Как написать оценочное уравнение регрессии
Мы можем использовать коэффициенты из выходных данных модели, чтобы создать следующее оценочное уравнение регрессии:
Экзаменационный балл = 67,67 + 5,56*(часы) – 0,60*(подготовительные экзамены)
Мы можем использовать это оценочное уравнение регрессии, чтобы рассчитать ожидаемый балл экзамена для учащегося на основе количества часов, которые он изучает, и количества подготовительных экзаменов, которые он сдает.
Например, студент, который занимается три часа и сдает один подготовительный экзамен, должен получить 83,75 балла:
Экзаменационный балл = 67,67 + 5,56*(3) – 0,60*(1) = 83,75
Имейте в виду, что, поскольку пройденные подготовительные экзамены не были статистически значимыми (p = 0,52), мы можем решить удалить их, поскольку они не улучшают общую модель.
В этом случае мы могли бы выполнить простую линейную регрессию, используя только часы изучения в качестве независимой переменной.
Дополнительные ресурсы
Введение в простую линейную регрессию
Введение в множественную линейную регрессию
Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для работы необходима надстройка Пакет анализа
, которую необходимо включить в пункте меню СервисНадстройки
В Excel 2007 для включения пакета анализа надо нажать перейти в блок Параметры Excel
, нажав кнопку в левом верхнем углу, а затем кнопку «Параметры Excel
» внизу окна:
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия
. (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/ Регрессия
). Появится диалоговое окно, которое нужно заполнить:
1) Входной интервал Y
¾ содержит ссылку на ячейки, которые содержат значения результативного признака y
. Значения должны быть расположены в столбце;
2) Входной интервал X
¾ содержит ссылку на ячейки, которые содержат значения факторов . Значения должны быть расположены в столбцах;
3) Признак Метки
ставится, если первые ячейки содержат пояснительный текст (подписи данных);
4) Уровень надежности
¾ это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;
5) Признак Константа-ноль
включается, если необходимо построить уравнение, в котором свободная переменная ;
6) Параметры вывода
определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист
;
7) Блок Остатки
позволяет включать вывод остатков и построение их графиков.
В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика
, Дисперсионный анализ
, Вывод остатка
. Рассмотрим их подробнее.
1. Регрессионная статистика
:
множественный R
определяется формулой (коэффициент корреляции Пирсона
);
R

);
Нормированный R
-квадрат вычисляется по формуле 
Стандартная ошибка S
вычисляется по формуле 
Наблюдения ¾ это количество данных n
.
2. Дисперсионный анализ
, строка Регрессия
:
Параметр df
равен m
(количество наборов факторов x
);
Параметр SS
определяется формулой ;
Параметр MS
определяется формулой ;
Статистика F
определяется формулой ;
Значимость F
. Если полученное число превышает , то принимается гипотеза (нет линейной взаимосвязи), иначе принимается гипотеза (есть линейная взаимосвязь).
3. Дисперсионный анализ
, строка Остаток
:
Параметр df
равен ;
Параметр SS
определяется формулой 
Параметр MS
определяется формулой .
4. Дисперсионный анализ
, строка Итого
содержит сумму первых двух столбцов.
5. Дисперсионный анализ
, строка Y-пересечение
содержит значение коэффициента , стандартной ошибки и t
-статистики .
P
-значение ¾ это значение уровней значимости, соответствующее вычисленным t
-статистикам. Определяется функцией СТЬЮДРАСП(t
-статистика; ). Если P
-значение превышает , то соответствующая переменная статистически незначима и ее можно исключить из модели.
Нижние 95%
и Верхние 95%
¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.
6. Дисперсионный анализ
, строки содержат значения коэффициентов, стандартных ошибок, t
-статистик, P
-значений и доверительных интервалов для соответствующих .
7. Блок Вывод остатка
содержит значения предсказанного y
(в наших обозначениях это ) и остатки .
28 Окт
Добрый день, уважаемые читатели блога! Сегодня мы поговорим о нелинейных регрессиях. Решение линейных регрессий можно посмотреть по ССЫЛКЕ .
Данный способ применяется, в основном, в экономическом моделировании и прогнозировании. Его цель – пронаблюдать и выявить зависимости между двумя показателями.
Основными типами нелинейных регрессий являются:
- полиномиальные (квадратичная, кубическая);
- гиперболическая;
- степенная;
- показательная;
- логарифмическая.
Также могут применяться различные комбинации. Например, для аналитики временных рядов в банковской сфере, страховании, демографических исследованиях используют кривую Гомпцера, которая является разновидностью логарифмической регрессии.
В прогнозировании с помощью нелинейных регрессий главное выяснить коэффициент корреляции, который покажет нам есть ли тесная взаимосвязь меду двумя параметрами или нет. Как правило, если коэффициент корреляции близок к 1, значит связь есть, и прогноз будет довольно точен. Ещё одним важным элементом нелинейных регрессий является средняя относительная ошибка (А
), если она находится в промежутке <8…10%, значит модель достаточно точна.
На этом, пожалуй, теоретический блок мы закончим и перейдём к практическим вычислениям.
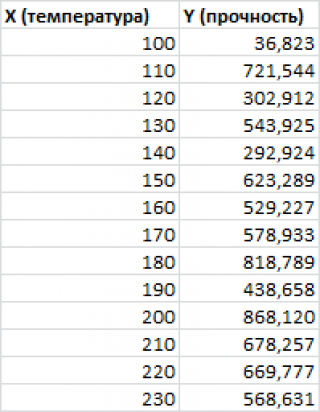
У нас имеется таблица продаж автомобилей за промежуток 15 лет (обозначим его X), количество шагов измерений будет аргумент n, также имеется выручка за эти периоды (обозначим её Y), нам нужно спрогнозировать какова будет выручка в дальнейшем. Построим следующую таблицу:
Для исследования нам потребуется решить уравнение (зависимости Y от X): y=ax 2 +bx+c+e. Это парная квадратичная регрессия. Применим в этом случае метод наименьших квадратов, для выяснения неизвестных аргументов — a, b, c. Он приведёт к системе алгебраических уравнений вида:
Для решения этой системы воспользуемся, к примеру, методом Крамера. Видим, что входящие в систему суммы являются коэффициентами при неизвестных. Для их вычисления добавим в таблицу несколько столбцов (D,E,F,G,H) и подпишем соответственно смыслу вычислений — в столбце D возведём x в квадрат, в E в куб, в F в 4 степень, в G перемножим показатели x и y, в H возведём x в квадрат и перемножим с y.
Получится заполненная нужными для решения уравнения таблица вида.
Сформируем матрицу A
системы, состоящую из коэффициентов при неизвестных в левых частях уравнений. Поместим её в ячейку А22 и назовём «А=
«. Следуем той системе уравнений, которую мы избрали для решения регрессии.
То есть, в ячейку B21 мы должны поместить сумму столбца, где возводили показатель X в четвёртую степень — F17. Просто сошлёмся на ячейку — «=F17». Далее нам необходима сумма столбца где возводили X в куб — E17, далее идём строго по системе. Таким образом, нам необходимо будет заполнить всю матрицу.
В соответствии с алгоритмом Крамера наберём матрицу А1, подобную А, в которой вместо элементов первого столбца должны размещаться элементы правых частей уравнений системы. То есть сумма столбца X в квадрате умноженная на Y, сумма столбца XY и сумма столбца Y.
Также нам понадобятся ещё две матрицы — назовём их А2 и А3 в которых второй и третий столбцы будут состоять из коэффициентов правых частей уравнений. Картина будет такова.
Следуя избранному алгоритму, нам нужно будет вычислить значения определителей (детерминантов, D) полученных матриц. Воспользуемся формулой МОПРЕД. Результаты разместим в ячейках J21:K24.
Расчёт коэффициентов уравнения по Крамеру будем производить в ячейках напротив соответствующих детерминантов по формуле: a
(в ячейке M22) — «=K22/K21»; b
(в ячейке M23) — «=K23/K21»; с
(в ячейке M24) — «=K24/K21».
Получим наше искомое уравнение парной квадратичной регрессии:
y=-0,074x 2 +2,151x+6,523
Оценим тесноту линейной связи индексом корреляции.
Для вычисления добавим в таблицу дополнительный столбец J (назовём его y*). Расчёта будет следующей (согласно полученному нами уравнению регрессии) — «=$m$22*B2*B2+$M$23*B2+$M$24».
Поместим её в ячейку J2. Останется протянуть вниз маркер автозаполнения до ячейки J16.
Для вычисления сумм (Y-Y усредненное) 2 добавим в таблицу столбцы K и L с соответствующими формулами. Среднее по столбцу Y посчитаем с помощью функции СРЗНАЧ.
В ячейке K25 разместим формулу подсчёта индекса корреляции — «=КОРЕНЬ(1-(K17/L17))».
Видим, что значение 0,959 очень близко к 1, значит между продажами и годами есть тесная нелинейная связь.
Осталось оценить качество подгонки полученного квадратичного уравнения регрессии (индекс детерминации). Он рассчитывается по формуле квадрата индекса корреляции. То есть формула в ячейке K26 будет очень проста — «=K25*K25».
Коэффициент 0,920 близок к 1, что свидетельствует о высоком качестве подгонки.
Последним действием будет вычисление относительной ошибки. Добавим столбец и внесём туда формулу: «=ABS((C2-J2)/C2), ABS — модуль, абсолютное значение. Протянем маркером вниз и в ячейке M18 выведем среднее значение (СРЗНАЧ), назначим ячейкам процентный формат. Полученный результат — 7,79% находится в пределах допустимых значений ошибки <8…10%. Значит вычисления достаточно точны.
Если возникнет необходимость, по полученным значениям мы можем построить график.
Файл с примером прилагается — ССЫЛКА !
Категории:
/
/
от
28.10.2017
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Мы рады, что смогли помочь Вам в решении проблемы.
Задайте свой вопрос в комментариях, подробно расписав суть проблемы. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
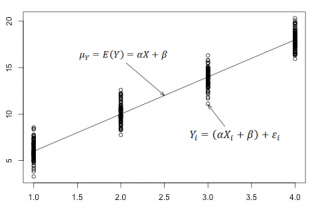
Метод линейной регрессии позволяет нам описывать прямую линию, максимально соответствующую ряду упорядоченных пар (x, y). Уравнение для прямой линии, известное как линейное уравнение, представлено ниже:
ŷ — ожидаемое значение у при заданном значении х,
x — независимая переменная,
a — отрезок на оси y для прямой линии,
b — наклон прямой линии.
На рисунке ниже это понятие представлено графически:
На рисунке выше показана линия, описанная уравнением ŷ =2+0.5х. Отрезок на оси у — это точка пересечения линией оси у; в нашем случае а = 2. Наклон линии, b, отношение подъема линии к длине линии, имеет значение 0.5. Положительный наклон означает, что линия поднимается слева направо. Если b = 0, линия горизонтальна, а это значит, что между зависимой и независимой переменными нет никакой связи. Иными словами, изменение значения x не влияет на значение y.
Часто путают ŷ и у. На графике показаны 6 упорядоченных пар точек и линия, в соответствии с данным уравнением
На этом рисунке показана точка, соответствующая упорядоченной паре х = 2 и у = 4. Обратите внимание, что ожидаемое значение у в соответствии с линией при х
= 2 является ŷ. Мы можем подтвердить это с помощью следующего уравнения:
ŷ = 2 + 0.5х =2 +0.5(2) =3.
Значение у представляет собой фактическую точку, а значение ŷ — это ожидаемое значение у с использованием линейного уравнения при заданном значении х.
Следующий шаг — определить линейное уравнение, максимально соответствующее набору упорядоченных пар, об этом мы говорили в предыдущей статье, где определяли вид уравнения по методу наименьших квадратов.
Использование Excel для определения линейной регрессии
Для того, чтобы воспользоваться инструментом регрессионного анализа встроенного в Excel, необходимо активировать надстройку Пакет анализа
. Найти ее можно, перейдя по вкладке Файл –> Параметры
(2007+), в появившемся диалоговом окне Параметры
Excel
переходим во вкладку Надстройки.
В поле Управление
выбираем Надстройки
Excel
и щелкаем Перейти.
В появившемся окне ставим галочку напротив Пакет анализа,
жмем ОК.
Во вкладке Данные
в группе Анализ
появится новая кнопка Анализ данных.
Чтобы продемонстрировать работу надстройки, воспользуемся данными с предыдущей статьи, где парень и девушка делят столик в ванной. Введите данные нашего примера с ванной в столбцы А и В чистого листа.
Перейдите во вкладку Данные,
в группе Анализ
щелкните Анализ данных.
В появившемся окне Анализ данных
выберите Регрессия
, как показано на рисунке, и щелкните ОК.
Установите необходимыe параметры регрессии в окне Регрессия
, как показано на рисунке:
Щелкните ОК.
На рисунке ниже показаны полученные результаты:
Эти результаты соответствуют тем, которые мы получили путем самостоятельных вычислений в предыдущей статье.
Регрессионный анализ — это статистический метод исследования, позволяющий показать зависимость того или иного параметра от одной либо нескольких независимых переменных. В докомпьютерную эру его применение было достаточно затруднительно, особенно если речь шла о больших объемах данных. Сегодня, узнав как построить регрессию в Excel, можно решать сложные статистические задачи буквально за пару минут. Ниже представлены конкретные примеры из области экономики.
Виды регрессии
Само это понятие было введено в математику Фрэнсисом Гальтоном в 1886 году. Регрессия бывает:
- линейной;
- параболической;
- степенной;
- экспоненциальной;
- гиперболической;
- показательной;
- логарифмической.
Пример 1
Рассмотрим задачу определения зависимости количества уволившихся членов коллектива от средней зарплаты на 6 промышленных предприятиях.
Задача. На шести предприятиях проанализировали среднемесячную заработную плату и количество сотрудников, которые уволились по собственному желанию. В табличной форме имеем:
Для задачи определения зависимости количества уволившихся работников от средней зарплаты на 6 предприятиях модель регрессии имеет вид уравнения Y = а0 + а1×1 +…+аkxk, где хi — влияющие переменные, ai — коэффициенты регрессии, a k — число факторов.
Для данной задачи Y — это показатель уволившихся сотрудников, а влияющий фактор — зарплата, которую обозначаем X.
Использование возможностей табличного процессора «Эксель»
Анализу регрессии в Excel должно предшествовать применение к имеющимся табличным данным встроенных функций. Однако для этих целей лучше воспользоваться очень полезной надстройкой «Пакет анализа». Для его активации нужно:
- с вкладки «Файл» перейти в раздел «Параметры»;
- в открывшемся окне выбрать строку «Надстройки»;
- щелкнуть по кнопке «Перейти», расположенной внизу, справа от строки «Управление»;
- поставить галочку рядом с названием «Пакет анализа» и подтвердить свои действия, нажав «Ок».
Если все сделано правильно, в правой части вкладки «Данные», расположенном над рабочим листом «Эксель», появится нужная кнопка.
Линейная регрессия в Excel
Теперь, когда под рукой есть все необходимые виртуальные инструменты для осуществления эконометрических расчетов, можем приступить к решению нашей задачи. Для этого:
- щелкаем по кнопке «Анализ данных»;
- в открывшемся окне нажимаем на кнопку «Регрессия»;
- в появившуюся вкладку вводим диапазон значений для Y (количество уволившихся работников) и для X (их зарплаты);
- подтверждаем свои действия нажатием кнопки «Ok».
В результате программа автоматически заполнит новый лист табличного процессора данными анализа регрессии. Обратите внимание! В Excel есть возможность самостоятельно задать место, которое вы предпочитаете для этой цели. Например, это может быть тот же лист, где находятся значения Y и X, или даже новая книга, специально предназначенная для хранения подобных данных.
Анализ результатов регрессии для R-квадрата
В Excel данные полученные в ходе обработки данных рассматриваемого примера имеют вид:
Прежде всего, следует обратить внимание на значение R-квадрата. Он представляет собой коэффициент детерминации. В данном примере R-квадрат = 0,755 (75,5%), т. е. расчетные параметры модели объясняют зависимость между рассматриваемыми параметрами на 75,5 %. Чем выше значение коэффициента детерминации, тем выбранная модель считается более применимой для конкретной задачи. Считается, что она корректно описывает реальную ситуацию при значении R-квадрата выше 0,8. Если R-квадрата tкр, то гипотеза о незначимости свободного члена линейного уравнения отвергается.
В рассматриваемой задаче для свободного члена посредством инструментов «Эксель» было получено, что t=169,20903, а p=2,89Е-12, т. е. имеем нулевую вероятность того, что будет отвергнута верная гипотеза о незначимости свободного члена. Для коэффициента при неизвестной t=5,79405, а p=0,001158. Иными словами вероятность того, что будет отвергнута верная гипотеза о незначимости коэффициента при неизвестной, равна 0,12%.
Таким образом, можно утверждать, что полученное уравнение линейной регрессии адекватно.
Задача о целесообразности покупки пакета акций
Множественная регрессия в Excel выполняется с использованием все того же инструмента «Анализ данных». Рассмотрим конкретную прикладную задачу.
Руководство компания «NNN» должно принять решение о целесообразности покупки 20 % пакета акций АО «MMM». Стоимость пакета (СП) составляет 70 млн американских долларов. Специалистами «NNN» собраны данные об аналогичных сделках. Было принято решение оценивать стоимость пакета акций по таким параметрам, выраженным в миллионах американских долларов, как:
- кредиторская задолженность (VK);
- объем годового оборота (VO);
- дебиторская задолженность (VD);
- стоимость основных фондов (СОФ).
Кроме того, используется параметр задолженность предприятия по зарплате (V3 П) в тысячах американских долларов.
Решение средствами табличного процессора Excel
Прежде всего, необходимо составить таблицу исходных данных. Она имеет следующий вид:
- вызывают окно «Анализ данных»;
- выбирают раздел «Регрессия»;
- в окошко «Входной интервал Y» вводят диапазон значений зависимых переменных из столбца G;
- щелкают по иконке с красной стрелкой справа от окна «Входной интервал X» и выделяют на листе диапазон всех значений из столбцов B,C, D, F.
Отмечают пункт «Новый рабочий лист» и нажимают «Ok».
Получают анализ регрессии для данной задачи.
Изучение результатов и выводы
«Собираем» из округленных данных, представленных выше на листе табличного процессора Excel, уравнение регрессии:
СП = 0,103*СОФ + 0,541*VO – 0,031*VK +0,405*VD +0,691*VZP – 265,844.
В более привычном математическом виде его можно записать, как:
y = 0,103*x1 + 0,541*x2 – 0,031*x3 +0,405*x4 +0,691*x5 – 265,844
Данные для АО «MMM» представлены в таблице:
Подставив их в уравнение регрессии, получают цифру в 64,72 млн американских долларов. Это значит, что акции АО «MMM» не стоит приобретать, так как их стоимость в 70 млн американских долларов достаточно завышена.
Как видим, использование табличного процессора «Эксель» и уравнения регрессии позволило принять обоснованное решение относительно целесообразности вполне конкретной сделки.
Теперь вы знаете, что такое регрессия. Примеры в Excel, рассмотренные выше, помогут вам в решение практических задач из области эконометрики.
Пакет MS Excel
позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.
Для построения модели регрессии необходимо выбрать пункт СервисАнализ данныхРегрессия (в Excel 2007
этот режим находится в блоке Данные/Анализ данных/Регрессия). Затем полученные результаты скопировать в блок для анализа.
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
Регрессия бывает:
· линейной (у = а + bx);
· параболической (y = a + bx + cx 2);
· экспоненциальной (y = a * exp(bx));
· степенной (y = a*x^b);
· гиперболической (y = b/x + a);
· логарифмической (y = b * 1n(x) + a);
· показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
У = а 0 + а 1 х 1 +…+а к х к.
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
В таблице Дисперсионный анализ оценивается общее качество полученной модели:
ее достоверность по уровню значимости критерия Фишера — р, который должен быть
меньше, чем 0,05 (строка Регрессия, столбец Значимость F).
Значение R-квадрат описывает степень точности описания моделью процесса
(вторая строка сверху в таблице Регрессионная статистика).
Далее определяем значения коэффициентов модели.
Они определяютя из таблицы в столбце Коэффициенты — в строке Y-пересечение — свободный член,
в строках соответствующих переменных — значения коэффициентов при этих переменных.
В столбце р-значение приводится достоверность отличия соответствующих коэффициентов от нуля.
В случае, когда р>0,05, коэффициент может считаться нулевым.
Это означает, что соответствующая независимая переменная практически не влияет на зависимую
переменную и коэффициент может быть убран из уравнения.
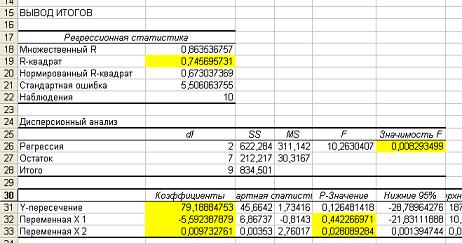
Именно поэтому в данной задаче дается такая интерпретация:
Достоверность по уровню значимости критерия Фишера (Значимость F) значительно меньше 0,05, значит модель значима.
Степень точности описания моделью процесса R-квадрат равен 0,75, что говорит о высокой точности аппроксимации (модель хорошо описывает процесс).
p-значение для коэффициента х1 больше 0,05, значит этот коэффициент может считаться нулевым.
p-значение для коэффициента х2 меньше 0,05, значит этот коэффициент может считаться не нулевым.
Значение свободного члена (Y-пересечение) 79,19.
Отсюда уравнение для расчета выхода телят на 100 коров (y) от среднегодового потребления кормовых единиц (x2) и среднего возраста стада (x1) будет иметь вид y=0,0097x2+79,19 с достоверностью R2=75%.
Простая линейная регрессия в EXCEL
history 26 января 2019 г.
-
Группы статей
- Статистический анализ
Регрессия позволяет прогнозировать зависимую переменную на основании значений фактора. В MS EXCEL имеется множество функций, которые возвращают не только наклон и сдвиг линии регрессии, характеризующей линейную взаимосвязь между факторами, но и регрессионную статистику. Здесь рассмотрим простую линейную регрессию, т.е. прогнозирование на основе одного фактора.
Disclaimer : Данную статью не стоит рассматривать, как пересказ главы из учебника по статистике. Статья не обладает ни полнотой, ни строгостью изложения положений статистической науки. Эта статья – о применении MS EXCEL для целей Регрессионного анализа. Теоретические отступления приведены лишь из соображения логики изложения. Использование данной статьи для изучения Регрессии – плохая идея.
Статья про Регрессионный анализ получилась большая, поэтому ниже для удобства приведены ее разделы:
Примечание : Если прогнозирование переменной осуществляется на основе нескольких факторов, то имеет место множественная регрессия .
Чтобы разобраться, чем может помочь MS EXCEL при проведении регрессионного анализа, напомним вкратце теорию, введем термины и обозначения, которые могут отличаться в зависимости от различных источников.
Примечание : Для тех, кому некогда, незачем или просто не хочется разбираться в теоретических выкладках предлагается сразу перейти к вычислительной части — оценке неизвестных параметров линейной модели .
Немного теории и основные понятия
Пусть у нас есть массив данных, представляющий собой значения двух переменных Х и Y. Причем значения переменной Х мы можем произвольно задавать (контролировать) и использовать эту переменную для предсказания значений зависимой переменной Y. Таким образом, случайной величиной является только переменная Y.
Примером такой задачи может быть производственный процесс изготовления некого волокна, причем прочность этого волокна (Y) зависит только от рабочей температуры процесса в реакторе (Х), которая задается оператором.
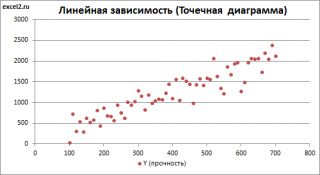
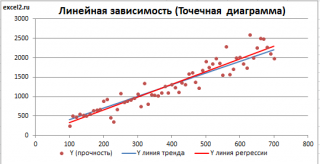
Построим диаграмму рассеяния (см. файл примера лист Линейный ), созданию которой посвящена отдельная статья . Вообще, построение диаграммы рассеяния для целей регрессионного анализа де-факто является стандартом.
СОВЕТ : Подробнее о построении различных типов диаграмм см. статьи Основы построения диаграмм и Основные типы диаграмм .
Приведенная выше диаграмма рассеяния свидетельствует о возможной линейной взаимосвязи между Y от Х: очевидно, что точки данных в основном располагаются вдоль прямой линии.
Примечание : Наличие даже такой очевидной линейной взаимосвязи не может являться доказательством о наличии причинной взаимосвязи переменных. Наличие причинной взаимосвязи не может быть доказано на основании только анализа имеющихся измерений, а должно быть обосновано с помощью других исследований, например теоретических выкладок.
Примечание : Как известно, уравнение прямой линии имеет вид Y = m * X + k , где коэффициент m отвечает за наклон линии ( slope ), k – за сдвиг линии по вертикали ( intercept ), k равно значению Y при Х=0.
Предположим, что мы можем зафиксировать переменную Х ( рабочую температуру процесса ) при некотором значении Х i и произвести несколько наблюдений переменной Y ( прочность нити ). Очевидно, что при одном и том же значении Хi мы получим различные значения Y. Это обусловлено влиянием других факторов на Y. Например, локальные колебания давления в реакторе, концентрации раствора, наличие ошибок измерения и др. Предполагается, что воздействие этих факторов имеет случайную природу и для каждого измерения имеются одинаковые условия проведения эксперимента (т.е. другие факторы не изменяются).
Полученные значения Y, при заданном Хi, будут колебаться вокруг некого значения . При увеличении количества измерений, среднее этих измерений, будет стремиться к математическому ожиданию случайной величины Y (при Х i ) равному μy(i)=Е(Y i ).
Подобные рассуждения можно привести для любого значения Хi.
Чтобы двинуться дальше, воспользуемся материалом из раздела Проверка статистических гипотез . В статье о проверке гипотезы о среднем значении генеральной совокупности в качестве нулевой гипотезы предполагалось равенство неизвестного значения μ заданному μ0.
В нашем случае простой линейной регрессии в качестве нулевой гипотезы предположим, что между переменными μy(i) и Хi существует линейная взаимосвязь μ y(i) =α* Х i +β. Уравнение μ y(i) =α* Х i +β можно переписать в обобщенном виде (для всех Х и μ y ) как μ y =α* Х +β.
Для наглядности проведем прямую линию соединяющую все μy(i).
Данная линия называется регрессионной линией генеральной совокупности (population regression line), параметры которой ( наклон a и сдвиг β ) нам не известны (по аналогии с гипотезой о среднем значении генеральной совокупности , где нам было неизвестно истинное значение μ).
Теперь сделаем переход от нашего предположения, что μy=a* Х + β , к предсказанию значения случайной переменной Y в зависимости от значения контролируемой переменной Х. Для этого уравнение связи двух переменных запишем в виде Y=a*X+β+ε, где ε — случайная ошибка, которая отражает суммарный эффект влияния других факторов на Y (эти «другие» факторы не участвуют в нашей модели). Напомним, что т.к. переменная Х фиксирована, то ошибка ε определяется только свойствами переменной Y.
Уравнение Y=a*X+b+ε называют линейной регрессионной моделью . Часто Х еще называют независимой переменной (еще предиктором и регрессором , английский термин predictor , regressor ), а Y – зависимой (или объясняемой , response variable ). Так как регрессор у нас один, то такая модель называется простой линейной регрессионной моделью ( simple linear regression model ). α часто называют коэффициентом регрессии.
Предположения линейной регрессионной модели перечислены в следующем разделе.
Предположения линейной регрессионной модели
Чтобы модель линейной регрессии Yi=a*Xi+β+ε i была адекватной — требуется:
- Ошибки ε i должны быть независимыми переменными;
- При каждом значении Xi ошибки ε i должны быть иметь нормальное распределение (также предполагается равенство нулю математического ожидания, т.е. Е[ε i ]=0);
- При каждом значении Xi ошибки ε i должны иметь равные дисперсии (обозначим ее σ 2 ).
Примечание : Последнее условие называется гомоскедастичность — стабильность, гомогенность дисперсии случайной ошибки e. Т.е. дисперсия ошибки σ 2 не должна зависеть от значения Xi.
Используя предположение о равенстве математического ожидания Е[ε i ]=0 покажем, что μy(i)=Е[Yi]:
Е[Yi]= Е[a*Xi+β+ε i ]= Е[a*Xi+β]+ Е[ε i ]= a*Xi+β= μy(i), т.к. a, Xi и β постоянные значения.
Дисперсия случайной переменной Y равна дисперсии ошибки ε, т.е. VAR(Y)= VAR(ε)=σ 2 . Это является следствием, что все значения переменной Х являются const, а VAR(ε)=VAR(ε i ).
Задачи регрессионного анализа
Для проверки гипотезы о линейной взаимосвязи переменной Y от X делают выборку из генеральной совокупности (этой совокупности соответствует регрессионная линия генеральной совокупности , т.е. μy=a* Х +β). Выборка будет состоять из n точек, т.е. из n пар значений .
На основании этой выборки мы можем вычислить оценки наклона a и сдвига β, которые обозначим соответственно a и b . Также часто используются обозначения â и b̂.
Далее, используя эти оценки, мы также можем проверить гипотезу: имеется ли линейная связь между X и Y статистически значимой?
Первая задача регрессионного анализа – оценка неизвестных параметров ( estimation of the unknown parameters ). Подробнее см. раздел Оценки неизвестных параметров модели .
Вторая задача регрессионного анализа – Проверка адекватности модели ( model adequacy checking ).
Примечание : Оценки параметров модели обычно вычисляются методом наименьших квадратов (МНК), которому посвящена отдельная статья .
Оценка неизвестных параметров линейной модели (используя функции MS EXCEL)
Неизвестные параметры простой линейной регрессионной модели Y=a*X+β+ε оценим с помощью метода наименьших квадратов (в статье про МНК подробно описано этот метод ).
Для вычисления параметров линейной модели методом МНК получены следующие выражения:
Таким образом, мы получим уравнение прямой линии Y= a *X+ b , которая наилучшим образом аппроксимирует имеющиеся данные.
Примечание : В статье про метод наименьших квадратов рассмотрены случаи аппроксимации линейной и квадратичной функцией , а также степенной , логарифмической и экспоненциальной функцией .
Оценку параметров в MS EXCEL можно выполнить различными способами:
Сначала рассмотрим функции НАКЛОН() , ОТРЕЗОК() и ЛИНЕЙН() .
Пусть значения Х и Y находятся соответственно в диапазонах C 23: C 83 и B 23: B 83 (см. файл примера внизу статьи).
Примечание : Значения двух переменных Х и Y можно сгенерировать, задав тренд и величину случайного разброса (см. статью Генерация данных для линейной регрессии в MS EXCEL ).
В MS EXCEL наклон прямой линии а ( оценку коэффициента регрессии ), можно найти по методу МНК с помощью функции НАКЛОН() , а сдвиг b ( оценку постоянного члена или константы регрессии ), с помощью функции ОТРЕЗОК() . В английской версии это функции SLOPE и INTERCEPT соответственно.
Аналогичный результат можно получить с помощью функции ЛИНЕЙН() , английская версия LINEST (см. статью об этой функции ).
Формула =ЛИНЕЙН(C23:C83;B23:B83) вернет наклон а . А формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) — сдвиг b . Здесь требуются пояснения.
Функция ЛИНЕЙН() имеет 4 аргумента и возвращает целый массив значений:
ЛИНЕЙН(известные_значения_y; [известные_значения_x]; [конст]; [статистика])
Если 4-й аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН() возвращает только оценки параметров модели: a и b .
Примечание : Остальные значения, возвращаемые функцией ЛИНЕЙН() , нам потребуются при вычислении стандартных ошибок и для проверки значимости регрессии . В этом случае аргумент статистика должен иметь значение ИСТИНА.
Чтобы вывести сразу обе оценки:
- в одной строке необходимо выделить 2 ячейки,
- ввести формулу в Строке формул
- нажать CTRL+SHIFT+ENTER (см. статью про формулы массива ).
Если в Строке формул выделить формулу = ЛИНЕЙН(C23:C83;B23:B83) и нажать клавишу F9 , то мы увидим что-то типа <3,01279389265416;154,240057900613>. Это как раз значения a и b . Как видно, оба значения разделены точкой с запятой «;», что свидетельствует, что функция вернула значения «в нескольких ячейках одной строки».
Если требуется вывести параметры линии не в одной строке, а одном столбце (ячейки друг под другом), то используйте формулу = ТРАНСП(ЛИНЕЙН(C23:C83;B23:B83)) . При этом выделять нужно 2 ячейки в одном столбце. Если теперь выделить новую формулу и нажать клавишу F9, то мы увидим что 2 значения разделены двоеточием «:», что означает, что значения выведены в столбец (функция ТРАНСП() транспонировала строку в столбец ).
Чтобы разобраться в этом подробнее необходимо ознакомиться с формулами массива .
Чтобы не связываться с вводом формул массива , можно использовать функцию ИНДЕКС() . Формула = ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);1) или просто ЛИНЕЙН(C23:C83;B23:B83) вернет параметр, отвечающий за наклон линии, т.е. а . Формула =ИНДЕКС(ЛИНЕЙН(C23:C83;B23:B83);2) вернет параметр b .
Оценка неизвестных параметров линейной модели (через статистики выборок)
Наклон линии, т.е. коэффициент а , можно также вычислить через коэффициент корреляции и стандартные отклонения выборок :
= КОРРЕЛ(B23:B83;C23:C83) *(СТАНДОТКЛОН.В(C23:C83)/ СТАНДОТКЛОН.В(B23:B83))
Вышеуказанная формула математически эквивалентна отношению ковариации выборок Х и Y и дисперсии выборки Х:
И, наконец, запишем еще одну формулу для нахождения сдвига b . Воспользуемся тем фактом, что линия регрессии проходит через точку средних значений переменных Х и Y.
Вычислив средние значения и подставив в формулу ранее найденный наклон а , получим сдвиг b .
Оценка неизвестных параметров линейной модели (матричная форма)
Также параметры линии регрессии можно найти в матричной форме (см. файл примера лист Матричная форма ).
В формуле символом β обозначен столбец с искомыми параметрами модели: β0 (сдвиг b ), β1 (наклон a ).
Матрица Х равна:
Матрица Х называется регрессионной матрицей или матрицей плана . Она состоит из 2-х столбцов и n строк, где n – количество точек данных. Первый столбец — столбец единиц, второй – значения переменной Х.
Матрица Х T – это транспонированная матрица Х . Она состоит соответственно из n столбцов и 2-х строк.
В формуле символом Y обозначен столбец значений переменной Y.
Чтобы перемножить матрицы используйте функцию МУМНОЖ() . Чтобы найти обратную матрицу используйте функцию МОБР() .
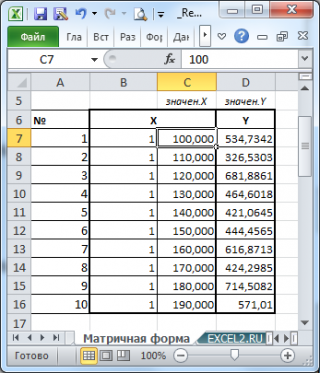
Пусть дан массив значений переменных Х и Y (n=10, т.е.10 точек).
Слева от него достроим столбец с 1 для матрицы Х.
и введя ее как формулу массива в 2 ячейки, получим оценку параметров модели.
Красота применения матричной формы полностью раскрывается в случае множественной регрессии .
Построение линии регрессии
Для отображения линии регрессии построим сначала диаграмму рассеяния , на которой отобразим все точки (см. начало статьи ).
Для построения прямой линии используйте вычисленные выше оценки параметров модели a и b (т.е. вычислите у по формуле y = a * x + b ) или функцию ТЕНДЕНЦИЯ() .
Формула = ТЕНДЕНЦИЯ($C$23:$C$83;$B$23:$B$83;B23) возвращает расчетные (прогнозные) значения ŷi для заданного значения Хi из столбца В2 .
Примечание : Линию регрессии можно также построить с помощью функции ПРЕДСКАЗ() . Эта функция возвращает прогнозные значения ŷi, но, в отличие от функции ТЕНДЕНЦИЯ() работает только в случае одного регрессора. Функция ТЕНДЕНЦИЯ() может быть использована и в случае множественной регрессии (в этом случае 3-й аргумент функции должен быть ссылкой на диапазон, содержащий все значения Хi для выбранного наблюдения i).
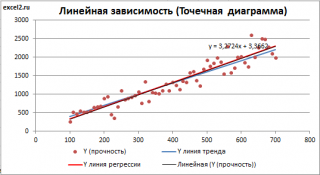
Как видно из диаграммы выше линия тренда и линия регрессии не обязательно совпадают: отклонения точек от линии тренда случайны, а МНК лишь подбирает линию наиболее точно аппроксимирующую случайные точки данных.
Линию регрессии можно построить и с помощью встроенных средств диаграммы, т.е. с помощью инструмента Линия тренда. Для этого выделите диаграмму, в меню выберите вкладку Макет , в группе Анализ нажмите Линия тренда , затем Линейное приближение. В диалоговом окне установите галочку Показывать уравнение на диаграмме (подробнее см. в статье про МНК ).
Построенная таким образом линия, разумеется, должна совпасть с ранее построенной нами линией регрессии, а параметры уравнения a и b должны совпасть с параметрами уравнения отображенными на диаграмме.
Примечание: Для того, чтобы вычисленные параметры уравнения a и b совпадали с параметрами уравнения на диаграмме, необходимо, чтобы тип у диаграммы был Точечная, а не График , т.к. тип диаграммы График не использует значения Х, а вместо значений Х используется последовательность 1; 2; 3; . Именно эти значения и берутся при расчете параметров линии тренда . Убедиться в этом можно если построить диаграмму График (см. файл примера ), а значения Хнач и Хшаг установить равным 1. Только в этом случае параметры уравнения на диаграмме совпадут с a и b .
Коэффициент детерминации R 2
Коэффициент детерминации R 2 показывает насколько полезна построенная нами линейная регрессионная модель .
Предположим, что у нас есть n значений переменной Y и мы хотим предсказать значение yi, но без использования значений переменной Х (т.е. без построения регрессионной модели ). Очевидно, что лучшей оценкой для yi будет среднее значение ȳ. Соответственно, ошибка предсказания будет равна (yi — ȳ).
Примечание : Далее будет использована терминология и обозначения дисперсионного анализа .
После построения регрессионной модели для предсказания значения yi мы будем использовать значение ŷi=a*xi+b. Ошибка предсказания теперь будет равна (yi — ŷi).
Теперь с помощью диаграммы сравним ошибки предсказания полученные без построения модели и с помощью модели.
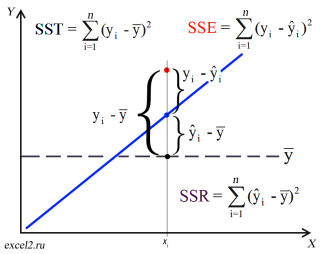
Очевидно, что используя регрессионную модель мы уменьшили первоначальную (полную) ошибку (yi — ȳ) на значение (ŷi — ȳ) до величины (yi — ŷi).
(yi — ŷi) – это оставшаяся, необъясненная ошибка.
Очевидно, что все три ошибки связаны выражением:
(yi — ȳ)= (ŷi — ȳ) + (yi — ŷi)
Можно показать, что в общем виде справедливо следующее выражение:
или в других, общепринятых в зарубежной литературе, обозначениях:
Total Sum of Squares = Regression Sum of Squares + Error Sum of Squares
Примечание : SS — Sum of Squares — Сумма Квадратов.
Как видно из формулы величины SST, SSR, SSE имеют размерность дисперсии (вариации) и соответственно описывают разброс (изменчивость): Общую изменчивость (Total variation), Изменчивость объясненную моделью (Explained variation) и Необъясненную изменчивость (Unexplained variation).
По определению коэффициент детерминации R 2 равен:
R 2 = Изменчивость объясненная моделью / Общая изменчивость.
Этот показатель равен квадрату коэффициента корреляции и в MS EXCEL его можно вычислить с помощью функции КВПИРСОН() или ЛИНЕЙН() :
R 2 принимает значения от 0 до 1 (1 соответствует идеальной линейной зависимости Y от Х). Однако, на практике малые значения R2 вовсе не обязательно указывают, что переменную Х нельзя использовать для прогнозирования переменной Y. Малые значения R2 могут указывать на нелинейность связи или на то, что поведение переменной Y объясняется не только Х, но и другими факторами.
Стандартная ошибка регрессии
Стандартная ошибка регрессии ( Standard Error of a regression ) показывает насколько велика ошибка предсказания значений переменной Y на основании значений Х. Отдельные значения Yi мы можем предсказывать лишь с точностью +/- несколько значений (обычно 2-3, в зависимости от формы распределения ошибки ε).
Теперь вспомним уравнение линейной регрессионной модели Y=a*X+β+ε. Ошибка ε имеет случайную природу, т.е. является случайной величиной и поэтому имеет свою функцию распределения со средним значением μ и дисперсией σ 2 .
Оценив значение дисперсии σ 2 и вычислив из нее квадратный корень – получим Стандартную ошибку регрессии. Чем точки наблюдений на диаграмме рассеяния ближе находятся к прямой линии, тем меньше Стандартная ошибка.
Примечание : Вспомним , что при построении модели предполагается, что среднее значение ошибки ε равно 0, т.е. E[ε]=0.
Оценим дисперсию σ 2 . Помимо вычисления Стандартной ошибки регрессии эта оценка нам потребуется в дальнейшем еще и при построении доверительных интервалов для оценки параметров регрессии a и b .
Для оценки дисперсии ошибки ε используем остатки регрессии — разности между имеющимися значениями yi и значениями, предсказанными регрессионной моделью ŷ. Чем лучше регрессионная модель согласуется с данными (точки располагается близко к прямой линии), тем меньше величина остатков.
Для оценки дисперсии σ 2 используют следующую формулу:
где SSE – сумма квадратов значений ошибок модели ε i =yi — ŷi ( Sum of Squared Errors ).
SSE часто обозначают и как SSres – сумма квадратов остатков ( Sum of Squared residuals ).
Оценка дисперсии s 2 также имеет общепринятое обозначение MSE (Mean Square of Errors), т.е. среднее квадратов ошибок или MSRES (Mean Square of Residuals), т.е. среднее квадратов остатков . Хотя правильнее говорить сумме квадратов остатков, т.к. ошибка чаще ассоциируется с ошибкой модели ε, которая является непрерывной случайной величиной. Но, здесь мы будем использовать термины SSE и MSE, предполагая, что речь идет об остатках.
Примечание : Напомним, что когда мы использовали МНК для нахождения параметров модели, то критерием оптимизации была минимизация именно SSE (SSres). Это выражение представляет собой сумму квадратов расстояний между наблюденными значениями yi и предсказанными моделью значениями ŷi, которые лежат на линии регрессии.
Математическое ожидание случайной величины MSE равно дисперсии ошибки ε, т.е. σ 2 .
Чтобы понять почему SSE выбрана в качестве основы для оценки дисперсии ошибки ε, вспомним, что σ 2 является также дисперсией случайной величины Y (относительно среднего значения μy, при заданном значении Хi). А т.к. оценкой μy является значение ŷi = a * Хi + b (значение уравнения регрессии при Х= Хi), то логично использовать именно SSE в качестве основы для оценки дисперсии σ 2 . Затем SSE усредняется на количество точек данных n за вычетом числа 2. Величина n-2 – это количество степеней свободы ( df – degrees of freedom ), т.е. число параметров системы, которые могут изменяться независимо (вспомним, что у нас в этом примере есть n независимых наблюдений переменной Y). В случае простой линейной регрессии число степеней свободы равно n-2, т.к. при построении линии регрессии было оценено 2 параметра модели (на это было «потрачено» 2 степени свободы ).
Итак, как сказано было выше, квадратный корень из s 2 имеет специальное название Стандартная ошибка регрессии ( Standard Error of a regression ) и обозначается SEy. SEy показывает насколько велика ошибка предсказания. Отдельные значения Y мы можем предсказывать с точностью +/- несколько значений SEy (см. этот раздел ). Если ошибки предсказания ε имеют нормальное распределение , то примерно 2/3 всех предсказанных значений будут на расстоянии не больше SEy от линии регрессии . SEy имеет размерность переменной Y и откладывается по вертикали. Часто на диаграмме рассеяния строят границы предсказания соответствующие +/- 2 SEy (т.е. 95% точек данных будут располагаться в пределах этих границ).
В MS EXCEL стандартную ошибку SEy можно вычислить непосредственно по формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))
или с помощью функции ЛИНЕЙН() :
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
Стандартные ошибки и доверительные интервалы для наклона и сдвига
В разделе Оценка неизвестных параметров линейной модели мы получили точечные оценки наклона а и сдвига b . Так как эти оценки получены на основе случайных величин (значений переменных Х и Y), то эти оценки сами являются случайными величинами и соответственно имеют функцию распределения со средним значением и дисперсией . Но, чтобы перейти от точечных оценок к интервальным , необходимо вычислить соответствующие стандартные ошибки (т.е. стандартные отклонения ).
Стандартная ошибка коэффициента регрессии a вычисляется на основании стандартной ошибки регрессии по следующей формуле:
где Sx – стандартное отклонение величины х, вычисляемое по формуле:
где Sey – стандартная ошибка регрессии, т.е. ошибка предсказания значения переменой Y ( см. выше ).
В MS EXCEL стандартную ошибку коэффициента регрессии Se можно вычислить впрямую по вышеуказанной формуле:
= КОРЕНЬ(СУММКВРАЗН(C23:C83; ТЕНДЕНЦИЯ(C23:C83;B23:B83;B23:B83)) /( СЧЁТ(B23:B83) -2))/ СТАНДОТКЛОН.В(B23:B83) /КОРЕНЬ(СЧЁТ(B23:B83) -1)
или с помощью функции ЛИНЕЙН() :
Формулы приведены в файле примера на листе Линейный в разделе Регрессионная статистика .
Примечание : Подробнее о функции ЛИНЕЙН() см. эту статью .
При построении двухстороннего доверительного интервала для коэффициента регрессии его границы определяются следующим образом:
где — квантиль распределения Стьюдента с n-2 степенями свободы. Величина а с «крышкой» является другим обозначением наклона а .
Например для уровня значимости альфа=0,05, можно вычислить с помощью формулы =СТЬЮДЕНТ.ОБР.2Х(0,05;n-2)
Вышеуказанная формула следует из того факта, что если ошибки регрессии распределены нормально и независимо, то выборочное распределение случайной величины
является t-распределением Стьюдента с n-2 степенью свободы (то же справедливо и для наклона b ).
Примечание : Подробнее о построении доверительных интервалов в MS EXCEL можно прочитать в этой статье Доверительные интервалы в MS EXCEL .
В результате получим, что найденный доверительный интервал с вероятностью 95% (1-0,05) накроет истинное значение коэффициента регрессии. Здесь мы считаем, что коэффициент регрессии a имеет распределение Стьюдента с n-2 степенями свободы (n – количество наблюдений, т.е. пар Х и Y).
Примечание : Подробнее о построении доверительных интервалов с использованием t-распределения см. статью про построение доверительных интервалов для среднего .
Стандартная ошибка сдвига b вычисляется по следующей формуле:
В MS EXCEL стандартную ошибку сдвига Seb можно вычислить с помощью функции ЛИНЕЙН() :
При построении двухстороннего доверительного интервала для сдвига его границы определяются аналогичным образом как для наклона : b +/- t*Seb.
Проверка значимости взаимосвязи переменных
Когда мы строим модель Y=αX+β+ε мы предполагаем, что между Y и X существует линейная взаимосвязь. Однако, как это иногда бывает в статистике, можно вычислять параметры связи даже тогда, когда в действительности она не существует, и обусловлена лишь случайностью.
Единственный вариант, когда Y не зависит X (в рамках модели Y=αX+β+ε), возможен, когда коэффициент регрессии a равен 0.
Чтобы убедиться, что вычисленная нами оценка наклона прямой линии не обусловлена лишь случайностью (не случайно отлична от 0), используют проверку гипотез . В качестве нулевой гипотезы Н 0 принимают, что связи нет, т.е. a=0. В качестве альтернативной гипотезы Н 1 принимают, что a <>0.
Ниже на рисунках показаны 2 ситуации, когда нулевую гипотезу Н 0 не удается отвергнуть.
На левой картинке отсутствует любая зависимость между переменными, на правой – связь между ними нелинейная, но при этом коэффициент линейной корреляции равен 0.
Ниже — 2 ситуации, когда нулевая гипотеза Н 0 отвергается.
На левой картинке очевидна линейная зависимость, на правой — зависимость нелинейная, но коэффициент корреляции не равен 0 (метод МНК вычисляет показатели наклона и сдвига просто на основании значений выборки).
Для проверки гипотезы нам потребуется:
- Установить уровень значимости , пусть альфа=0,05;
- Рассчитать с помощью функции ЛИНЕЙН() стандартное отклонение Se для коэффициента регрессии (см. предыдущий раздел );
- Рассчитать число степеней свободы: DF=n-2 или по формуле = ИНДЕКС(ЛИНЕЙН(C24:C84;B24:B84;;ИСТИНА);4;2)
- Вычислить значение тестовой статистики t 0 =a/S e , которая имеет распределение Стьюдента с числом степеней свободы DF=n-2;
- Сравнить значение тестовой статистики |t0| с пороговым значением t альфа ,n-2. Если значение тестовой статистики больше порогового значения, то нулевая гипотеза отвергается ( наклон не может быть объяснен лишь случайностью при заданном уровне альфа) либо
- вычислить p-значение и сравнить его с уровнем значимости .
В файле примера приведен пример проверки гипотезы:
Изменяя наклон тренда k (ячейка В8 ) можно убедиться, что при малых углах тренда (например, 0,05) тест часто показывает, что связь между переменными случайна. При больших углах (k>1), тест практически всегда подтверждает значимость линейной связи между переменными.
Примечание : Проверка значимости взаимосвязи эквивалентна проверке статистической значимости коэффициента корреляции . В файле примера показана эквивалентность обоих подходов. Также проверку значимости можно провести с помощью процедуры F-тест .
Доверительные интервалы для нового наблюдения Y и среднего значения
Вычислив параметры простой линейной регрессионной модели Y=aX+β+ε мы получили точечную оценку значения нового наблюдения Y при заданном значении Хi, а именно: Ŷ= a * Хi + b
Ŷ также является точечной оценкой для среднего значения Yi при заданном Хi. Но, при построении доверительных интервалов используются различные стандартные ошибки .
Стандартная ошибка нового наблюдения Y при заданном Хi учитывает 2 источника неопределенности:
- неопределенность связанную со случайностью оценок параметров модели a и b ;
- случайность ошибки модели ε.
Учет этих неопределенностей приводит к стандартной ошибке S(Y|Xi), которая рассчитывается с учетом известного значения Xi.
где SS xx – сумма квадратов отклонений от среднего значений переменной Х:
В MS EXCEL 2010 нет функции, которая бы рассчитывала эту стандартную ошибку , поэтому ее необходимо рассчитывать по вышеуказанным формулам.
Доверительный интервал или Интервал предсказания для нового наблюдения (Prediction Interval for a New Observation) построим по схеме показанной в разделе Проверка значимости взаимосвязи переменных (см. файл примера лист Интервалы ). Т.к. границы интервала зависят от значения Хi (точнее от расстояния Хi до среднего значения Х ср ), то интервал будет постепенно расширяться при удалении от Х ср .
Границы доверительного интервала для нового наблюдения рассчитываются по формуле:
Аналогичным образом построим доверительный интервал для среднего значения Y при заданном Хi (Confidence Interval for the Mean of Y). В этом случае доверительный интервал будет уже, т.к. средние значения имеют меньшую изменчивость по сравнению с отдельными наблюдениями ( средние значения, в рамках нашей линейной модели Y=aX+β+ε, не включают ошибку ε).
Стандартная ошибка S(Yср|Xi) вычисляется по практически аналогичным формулам как и стандартная ошибка для нового наблюдения:
Как видно из формул, стандартная ошибка S(Yср|Xi) меньше стандартной ошибки S(Y|Xi) для индивидуального значения .
Границы доверительного интервала для среднего значения рассчитываются по формуле:
Проверка адекватности линейной регрессионной модели
Модель адекватна, когда все предположения, лежащие в ее основе, выполнены (см. раздел Предположения линейной регрессионной модели ).
Проверка адекватности модели в основном основана на исследовании остатков модели (model residuals), т.е. значений ei=yi – ŷi для каждого Хi. В рамках простой линейной модели n остатков имеют только n-2 связанных с ними степеней свободы . Следовательно, хотя, остатки не являются независимыми величинами, но при достаточно большом n это не оказывает какого-либо влияния на проверку адекватности модели.
Чтобы проверить предположение о нормальности распределения ошибок строят график проверки на нормальность (Normal probability Plot).
В файле примера на листе Адекватность построен график проверки на нормальность . В случае нормального распределения значения остатков должны быть близки к прямой линии.
Так как значения переменной Y мы генерировали с помощью тренда , вокруг которого значения имели нормальный разброс, то ожидать сюрпризов не приходится – значения остатков располагаются вблизи прямой.
Также при проверке модели на адекватность часто строят график зависимости остатков от предсказанных значений Y. Если точки не демонстрируют характерных, так называемых «паттернов» (шаблонов) типа вор о нок или другого неравномерного распределения, в зависимости от значений Y, то у нас нет очевидных доказательств неадекватности модели.
В нашем случае точки располагаются примерно равномерно.
Часто при проверке адекватности модели вместо остатков используют нормированные остатки. Как показано в разделе Стандартная ошибка регрессии оценкой стандартного отклонения ошибок является величина SEy равная квадратному корню из величины MSE. Поэтому логично нормирование остатков проводить именно на эту величину.
SEy можно вычислить с помощью функции ЛИНЕЙН() :
Иногда нормирование остатков производится на величину стандартного отклонения остатков (это мы увидим в статье об инструменте Регрессия , доступного в надстройке MS EXCEL Пакет анализа ), т.е. по формуле:
Вышеуказанное равенство приблизительное, т.к. среднее значение остатков близко, но не обязательно точно равно 0.
Регрессионный анализ в Microsoft Excel
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
-
Перемещаемся во вкладку «Файл».
Переходим в раздел «Параметры».
В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Линейная регрессия в программе Excel
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк . В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.
Помимо этой статьи, на сайте еще 12771 полезных инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Корреляционно-регрессионный анализ в Excel: инструкция выполнения
Регрессионный и корреляционный анализ – статистические методы исследования. Это наиболее распространенные способы показать зависимость какого-либо параметра от одной или нескольких независимых переменных.
Ниже на конкретных практических примерах рассмотрим эти два очень популярные в среде экономистов анализа. А также приведем пример получения результатов при их объединении.
Регрессионный анализ в Excel
Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.
Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.
- линейной (у = а + bx);
- параболической (y = a + bx + cx 2 );
- экспоненциальной (y = a * exp(bx));
- степенной (y = a*x^b);
- гиперболической (y = b/x + a);
- логарифмической (y = b * 1n(x) + a);
- показательной (y = a * b^x).
Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.
Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.
Модель линейной регрессии имеет следующий вид:
Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.
В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).
В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».
Активируем мощный аналитический инструмент:
- Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
- Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
- Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.
После активации надстройка будет доступна на вкладке «Данные».
Теперь займемся непосредственно регрессионным анализом.
- Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
- Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
- После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).
В первую очередь обращаем внимание на R-квадрат и коэффициенты.
R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».
Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.
Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.
Корреляционный анализ в Excel
Корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Например, между временем работы станка и стоимостью ремонта, ценой техники и продолжительностью эксплуатации, ростом и весом детей и т.д.
Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого.
Коэффициент корреляции обозначается r. Варьируется в пределах от +1 до -1. Классификация корреляционных связей для разных сфер будет отличаться. При значении коэффициента 0 линейной зависимости между выборками не существует.
Рассмотрим, как с помощью средств Excel найти коэффициент корреляции.
Для нахождения парных коэффициентов применяется функция КОРРЕЛ.
Задача: Определить, есть ли взаимосвязь между временем работы токарного станка и стоимостью его обслуживания.
Ставим курсор в любую ячейку и нажимаем кнопку fx.
- В категории «Статистические» выбираем функцию КОРРЕЛ.
- Аргумент «Массив 1» — первый диапазон значений – время работы станка: А2:А14.
- Аргумент «Массив 2» — второй диапазон значений – стоимость ремонта: В2:В14. Жмем ОК.
Чтобы определить тип связи, нужно посмотреть абсолютное число коэффициента (для каждой сферы деятельности есть своя шкала).
Для корреляционного анализа нескольких параметров (более 2) удобнее применять «Анализ данных» (надстройка «Пакет анализа»). В списке нужно выбрать корреляцию и обозначить массив. Все.
Полученные коэффициенты отобразятся в корреляционной матрице. Наподобие такой:
Корреляционно-регрессионный анализ
На практике эти две методики часто применяются вместе.
- Строим корреляционное поле: «Вставка» — «Диаграмма» — «Точечная диаграмма» (дает сравнивать пары). Диапазон значений – все числовые данные таблицы.
- Щелкаем левой кнопкой мыши по любой точке на диаграмме. Потом правой. В открывшемся меню выбираем «Добавить линию тренда».
- Назначаем параметры для линии. Тип – «Линейная». Внизу – «Показать уравнение на диаграмме».
- Жмем «Закрыть».
Теперь стали видны и данные регрессионного анализа.
источники:
http://lumpics.ru/regression-analysis-in-excel/
http://exceltable.com/otchety/korrelyacionno-regressionnyy-analiz
Содержание
- Подключение пакета анализа
- Виды регрессионного анализа
- Линейная регрессия в программе Excel
- Разбор результатов анализа
- Вопросы и ответы
Регрессионный анализ является одним из самых востребованных методов статистического исследования. С его помощью можно установить степень влияния независимых величин на зависимую переменную. В функционале Microsoft Excel имеются инструменты, предназначенные для проведения подобного вида анализа. Давайте разберем, что они собой представляют и как ими пользоваться.
Подключение пакета анализа
Но, для того, чтобы использовать функцию, позволяющую провести регрессионный анализ, прежде всего, нужно активировать Пакет анализа. Только тогда необходимые для этой процедуры инструменты появятся на ленте Эксель.
- Перемещаемся во вкладку «Файл».
- Переходим в раздел «Параметры».
- Открывается окно параметров Excel. Переходим в подраздел «Надстройки».
- В самой нижней части открывшегося окна переставляем переключатель в блоке «Управление» в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «Перейти».
- Открывается окно доступных надстроек Эксель. Ставим галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
Теперь, когда мы перейдем во вкладку «Данные», на ленте в блоке инструментов «Анализ» мы увидим новую кнопку – «Анализ данных».
Виды регрессионного анализа
Существует несколько видов регрессий:
- параболическая;
- степенная;
- логарифмическая;
- экспоненциальная;
- показательная;
- гиперболическая;
- линейная регрессия.
О выполнении последнего вида регрессионного анализа в Экселе мы подробнее поговорим далее.
Внизу, в качестве примера, представлена таблица, в которой указана среднесуточная температура воздуха на улице, и количество покупателей магазина за соответствующий рабочий день. Давайте выясним при помощи регрессионного анализа, как именно погодные условия в виде температуры воздуха могут повлиять на посещаемость торгового заведения.
Общее уравнение регрессии линейного вида выглядит следующим образом: У = а0 + а1х1 +…+акхк. В этой формуле Y означает переменную, влияние факторов на которую мы пытаемся изучить. В нашем случае, это количество покупателей. Значение x – это различные факторы, влияющие на переменную. Параметры a являются коэффициентами регрессии. То есть, именно они определяют значимость того или иного фактора. Индекс k обозначает общее количество этих самых факторов.
- Кликаем по кнопке «Анализ данных». Она размещена во вкладке «Главная» в блоке инструментов «Анализ».
- Открывается небольшое окошко. В нём выбираем пункт «Регрессия». Жмем на кнопку «OK».
- Открывается окно настроек регрессии. В нём обязательными для заполнения полями являются «Входной интервал Y» и «Входной интервал X». Все остальные настройки можно оставить по умолчанию.
В поле «Входной интервал Y» указываем адрес диапазона ячеек, где расположены переменные данные, влияние факторов на которые мы пытаемся установить. В нашем случае это будут ячейки столбца «Количество покупателей». Адрес можно вписать вручную с клавиатуры, а можно, просто выделить требуемый столбец. Последний вариант намного проще и удобнее.
В поле «Входной интервал X» вводим адрес диапазона ячеек, где находятся данные того фактора, влияние которого на переменную мы хотим установить. Как говорилось выше, нам нужно установить влияние температуры на количество покупателей магазина, а поэтому вводим адрес ячеек в столбце «Температура». Это можно сделать теми же способами, что и в поле «Количество покупателей».
С помощью других настроек можно установить метки, уровень надёжности, константу-ноль, отобразить график нормальной вероятности, и выполнить другие действия. Но, в большинстве случаев, эти настройки изменять не нужно. Единственное на что следует обратить внимание, так это на параметры вывода. По умолчанию вывод результатов анализа осуществляется на другом листе, но переставив переключатель, вы можете установить вывод в указанном диапазоне на том же листе, где расположена таблица с исходными данными, или в отдельной книге, то есть в новом файле.
После того, как все настройки установлены, жмем на кнопку «OK».
Разбор результатов анализа
Результаты регрессионного анализа выводятся в виде таблицы в том месте, которое указано в настройках.
Одним из основных показателей является R-квадрат. В нем указывается качество модели. В нашем случае данный коэффициент равен 0,705 или около 70,5%. Это приемлемый уровень качества. Зависимость менее 0,5 является плохой.
Ещё один важный показатель расположен в ячейке на пересечении строки «Y-пересечение» и столбца «Коэффициенты». Тут указывается какое значение будет у Y, а в нашем случае, это количество покупателей, при всех остальных факторах равных нулю. В этой таблице данное значение равно 58,04.
Значение на пересечении граф «Переменная X1» и «Коэффициенты» показывает уровень зависимости Y от X. В нашем случае — это уровень зависимости количества клиентов магазина от температуры. Коэффициент 1,31 считается довольно высоким показателем влияния.
Как видим, с помощью программы Microsoft Excel довольно просто составить таблицу регрессионного анализа. Но, работать с полученными на выходе данными, и понимать их суть, сможет только подготовленный человек.