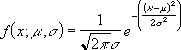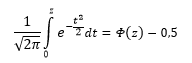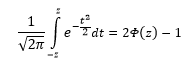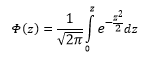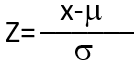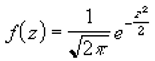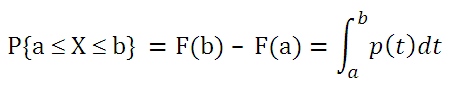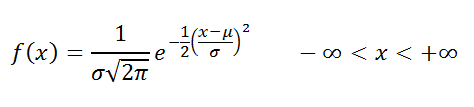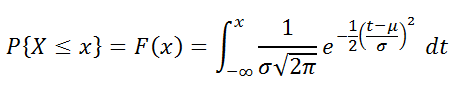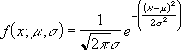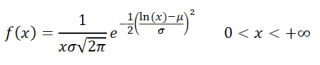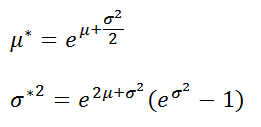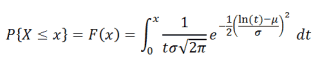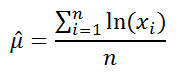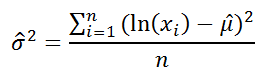Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.РАСП.
Синтаксис
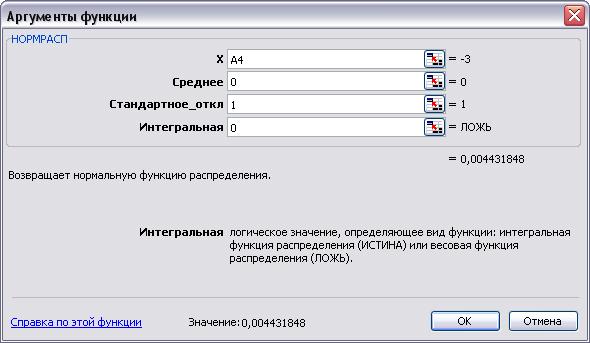
НОРМРАСП(x;среднее;стандартное_откл;интегральная)
Аргументы функции НОРМРАСП описаны ниже.
-
X Обязательный. Значение, для которого строится распределение.
-
Среднее Обязательный. Среднее арифметическое распределения.
-
Стандартное_откл Обязательный. Стандартное отклонение распределения.
-
Интегральная — обязательный аргумент. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Замечания
-
Если «standard_dev» не является числом, то возвращается #VALUE! значение ошибки #ЗНАЧ!.
-
Если standard_dev ≤ 0, то нормДАТ возвращает #NUM! значение ошибки #ЗНАЧ!.
-
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
-
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
-
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
|
Данные |
Описание |
|
|
42 |
Значение, для которого нужно вычислить распределение |
|
|
40 |
Среднее арифметическое распределения |
|
|
1,5 |
Стандартное отклонение распределения |
|
|
Формула |
Описание |
Результат |
|
=НОРМРАСП(A2;A3;A4;ИСТИНА) |
Интегральная функция распределения для приведенных выше условий |
0,9087888 |
|
=НОРМРАСП(A2;A3;A4;ЛОЖЬ) |
Функция плотности распределения для приведенных выше условий |
0,10934 |
Нужна дополнительная помощь?
В статье подробно показано, что такое нормальный закон распределения случайной величины и как им пользоваться при решении практически задач.
Нормальное распределение в статистике
История закона насчитывает 300 лет. Первым открывателем стал Абрахам де Муавр, который придумал аппроксимацию биномиального распределения еще 1733 году. Через много лет Карл Фридрих Гаусс (1809 г.) и Пьер-Симон Лаплас (1812 г.) вывели математические функции.
Лаплас также обнаружил замечательную закономерность и сформулировал центральную предельную теорему (ЦПТ), согласно которой сумма большого количества малых и независимых величин имеет нормальное распределение.
Нормальный закон не является фиксированным уравнением зависимости одной переменной от другой. Фиксируется только характер этой зависимости. Конкретная форма распределения задается специальными параметрами. Например, у = аx + b – это уравнение прямой. Однако где конкретно она проходит и под каким наклоном, определяется параметрами а и b. Также и с нормальным распределением. Ясно, что это функция, которая описывает тенденцию высокой концентрации значений около центра, но ее точная форма задается специальными параметрами.
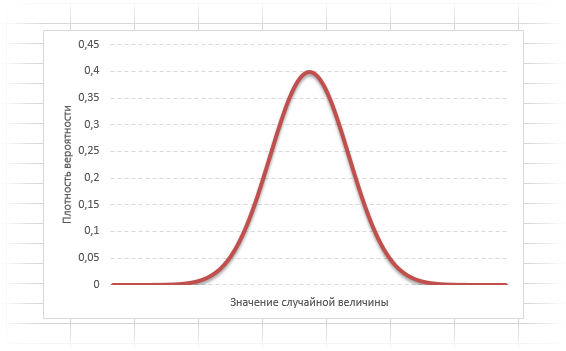
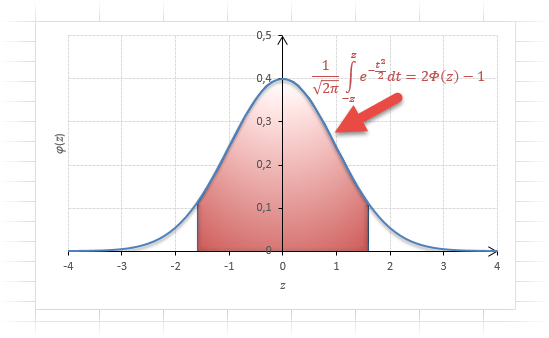
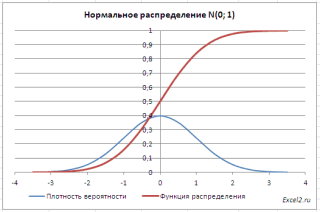
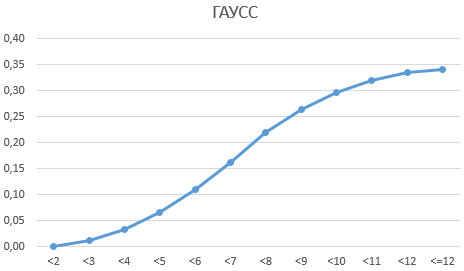
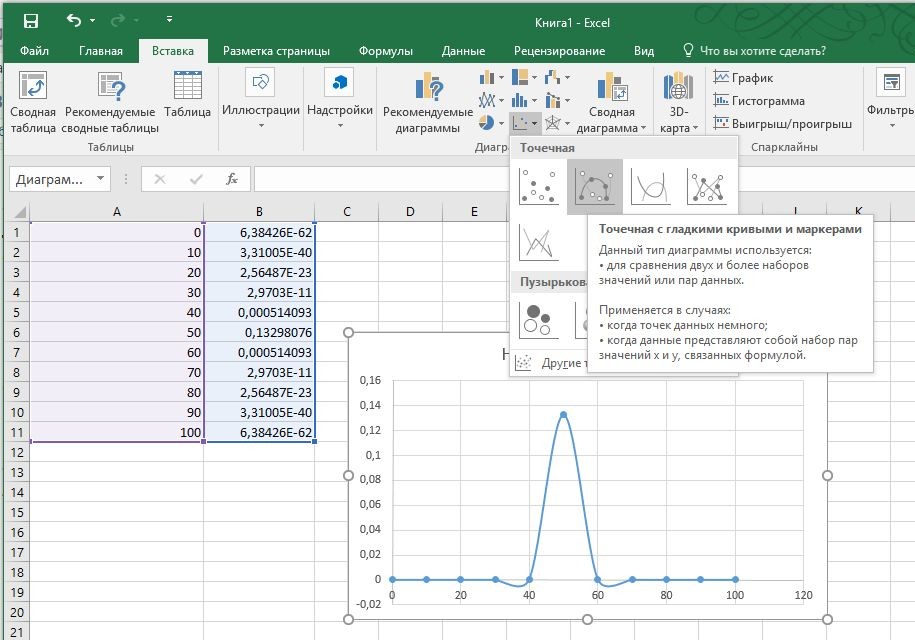
Кривая нормального распределения Гаусса имеет следующий вид.
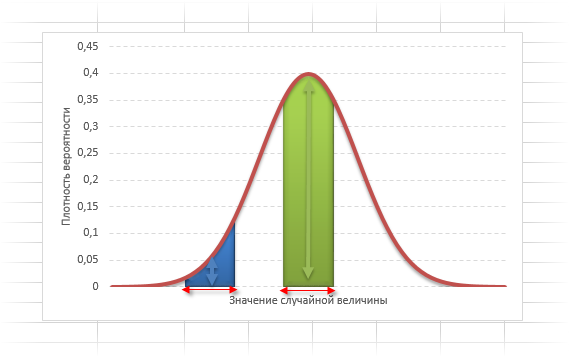
График нормального распределения напоминает колокол, поэтому можно встретить название колоколообразная кривая. У графика имеется «горб» в середине и резкое снижение плотности по краям. В этом заключается суть нормального распределения. Вероятность того, что случайная величина окажется около центра гораздо выше, чем то, что она сильно отклонится от середины.
На рисунке выше изображены два участка под кривой Гаусса: синий и зеленый. Основания, т.е. интервалы, у обоих участков равны. Но заметно отличаются высоты. Синий участок удален от центра, и имеет существенно меньшую высоту, чем зеленый, который находится в самом центре распределения. Следовательно, отличаются и площади, то бишь вероятности попадания в обозначенные интервалы.
Формула нормального распределения (плотности) следующая.
Формула состоит из двух математических констант:
π – число пи 3,142;
е – основание натурального логарифма 2,718;
двух изменяемых параметров, которые задают форму конкретной кривой:
m – математическое ожидание (в различных источниках могут использоваться другие обозначения, например, µ или a);
σ2 – дисперсия;
ну и сама переменная x, для которой высчитывается плотность вероятности.
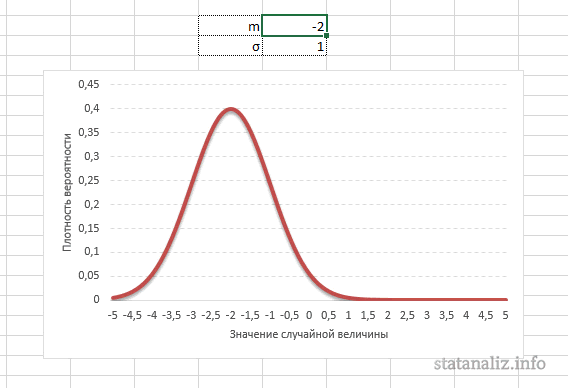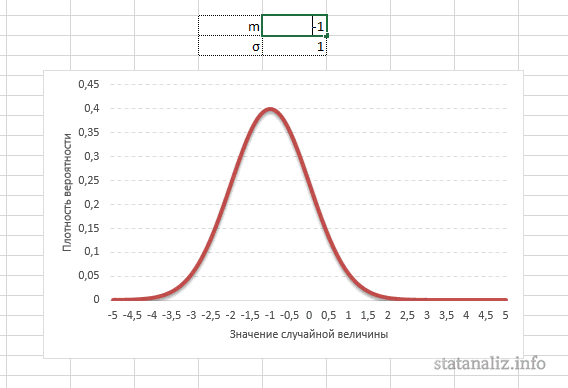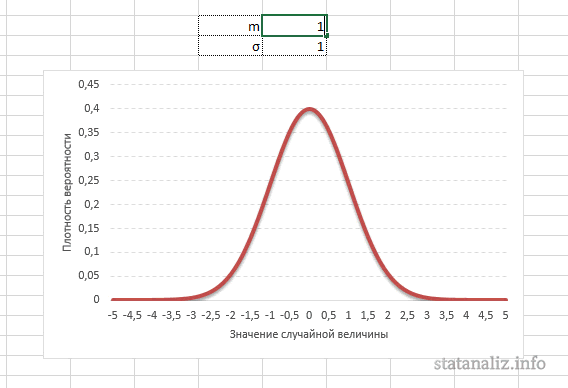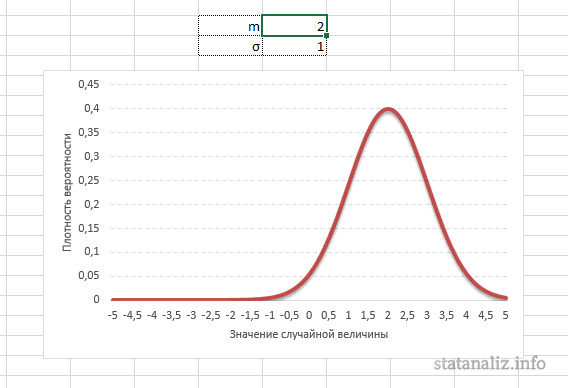
Конкретная форма нормального распределения зависит от 2-х параметров: математического ожидания (m) и дисперсии (σ2). Кратко обозначается N(m, σ2) или N(m, σ). Параметр m (матожидание) определяет центр распределения, которому соответствует максимальная высота графика. Дисперсия σ2 характеризует размах вариации, то есть «размазанность» данных.
Параметр математического ожидания смещает центр распределения вправо или влево, не влияя на саму форму кривой плотности.
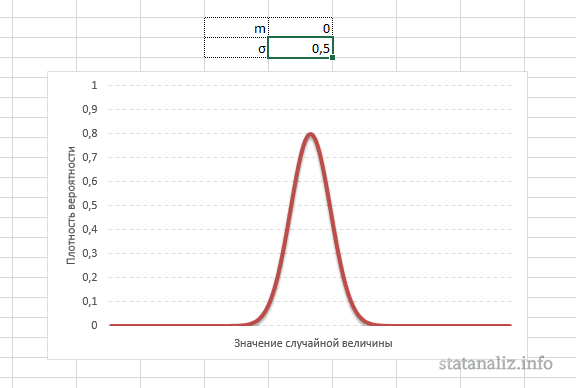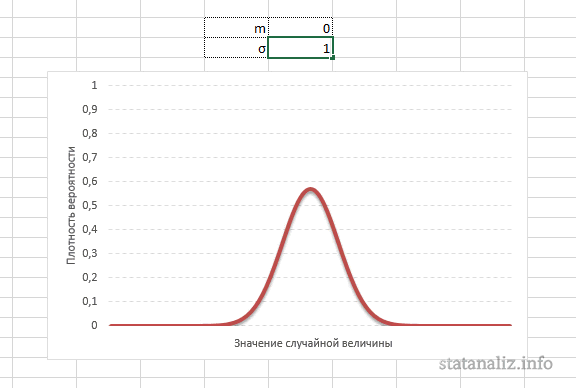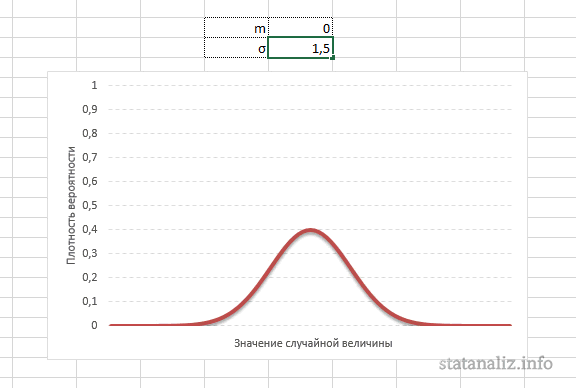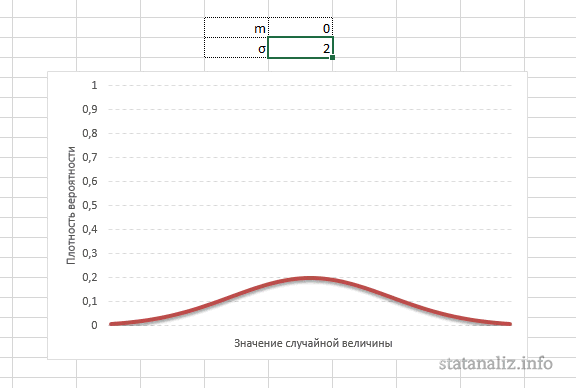
А вот дисперсия определяет остроконечность кривой. Когда данные имеют малый разброс, то вся их масса концентрируется у центра. Если же у данных большой разброс, то они «размазываются» по широкому диапазону.
Плотность распределения не имеет прямого практического применения. Для расчета вероятностей нужно проинтегрировать функцию плотности.
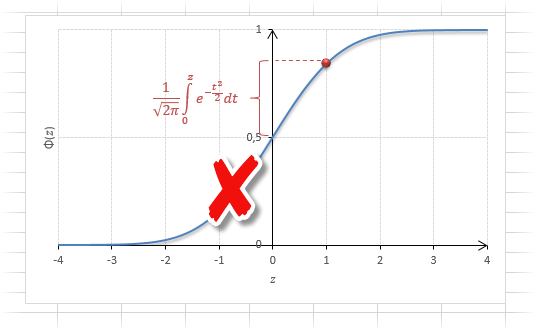
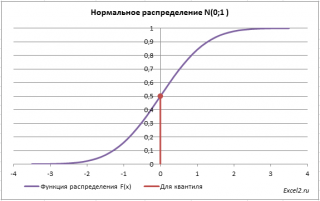
Вероятность того, что случайная величина окажется меньше некоторого значения x, определяется функцией нормального распределения:
Используя математические свойства любого непрерывного распределения, несложно рассчитать и любые другие вероятности, так как
P(a ≤ X < b) = Ф(b) – Ф(a)
Стандартное нормальное распределение
Нормальное распределение зависит от параметров средней и дисперсии, из-за чего плохо видны его свойства. Хорошо бы иметь некоторый эталон распределения, не зависящий от масштаба данных. И он существует. Называется стандартным нормальным распределением. На самом деле это обычное нормальное нормальное распределение, только с параметрами математического ожидания 0, а дисперсией – 1, кратко записывается N(0, 1).
Любое нормальное распределение легко превращается в стандартное путем нормирования:
где z – новая переменная, которая используется вместо x;
m – математическое ожидание;
σ – стандартное отклонение.
Для выборочных данных берутся оценки:
Среднее арифметическое и дисперсия новой переменной z теперь также равны 0 и 1 соответственно. В этом легко убедиться с помощью элементарных алгебраических преобразований.
В литературе встречается название z-оценка. Это оно самое – нормированные данные. Z-оценку можно напрямую сравнивать с теоретическими вероятностями, т.к. ее масштаб совпадает с эталоном.
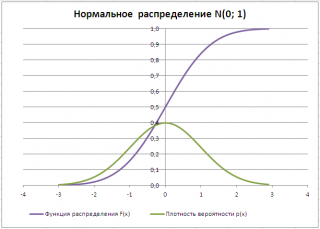
Посмотрим теперь, как выглядит плотность стандартного нормального распределения (для z-оценок). Напомню, что функция Гаусса имеет вид:
Подставим вместо (x-m)/σ букву z, а вместо σ – единицу, получим функцию плотности стандартного нормального распределения:
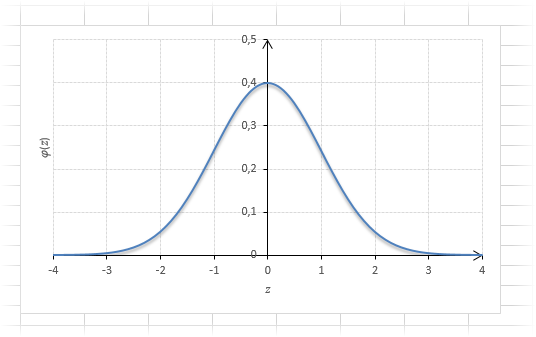
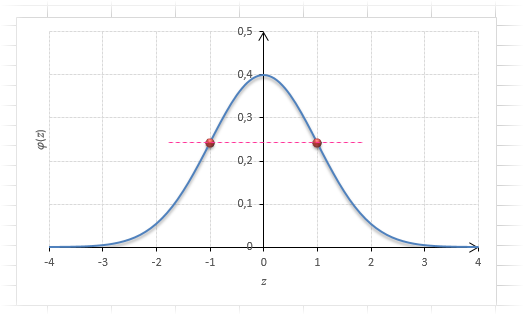
График плотности:
Центр, как и ожидалось, находится в точке 0. В этой же точке функция Гаусса достигает своего максимума, что соответствует принятию случайной величиной своего среднего значения (т.е. x-m=0). Плотность в этой точке равна 0,3989, что можно посчитать даже в уме, т.к. e0=1 и остается рассчитать только соотношение 1 на корень из 2 пи.
Таким образом, по графику хорошо видно, что значения, имеющие маленькие отклонения от средней, выпадают чаще других, а те, которые сильно отдалены от центра, встречаются значительно реже. Шкала оси абсцисс измеряется в стандартных отклонениях, что позволяет отвязаться от единиц измерения и получить универсальную структуру нормального распределения. Кривая Гаусса для нормированных данных отлично демонстрирует и другие свойства нормального распределения. Например, что оно является симметричным относительно оси ординат. В пределах ±1σ от средней арифметической сконцентрирована большая часть всех значений (прикидываем пока на глазок). В пределах ±2σ находятся большинство данных. В пределах ±3σ находятся почти все данные. Последнее свойство широко известно под названием правило трех сигм для нормального распределения.
Функция стандартного нормального распределения позволяет рассчитывать вероятности.
Понятное дело, вручную никто не считает. Все подсчитано и размещено в специальных таблицах, которые есть в конце любого учебника по статистике.
Таблица нормального распределения
Таблицы нормального распределения встречаются двух типов:
— таблица плотности;
— таблица функции (интеграла от плотности).
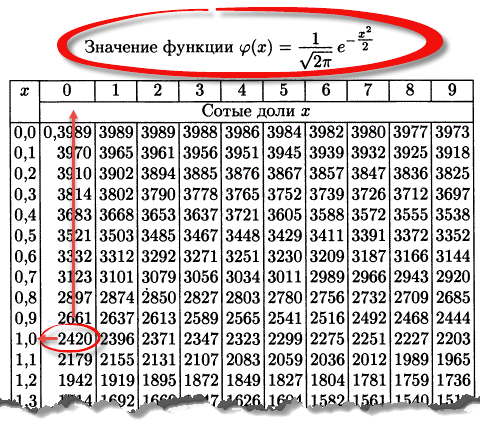
Таблица плотности используется редко. Тем не менее, посмотрим, как она выглядит. Допустим, нужно получить плотность для z = 1, т.е. плотность значения, отстоящего от матожидания на 1 сигму. Ниже показан кусок таблицы.
В зависимости от организации данных ищем нужное значение по названию столбца и строки. В нашем примере берем строку 1,0 и столбец 0, т.к. сотых долей нет. Искомое значение равно 0,2420 (0 перед 2420 опущен).
Функция Гаусса симметрична относительно оси ординат. Поэтому φ(z)= φ(-z), т.е. плотность для 1 тождественна плотности для -1, что отчетливо видно на рисунке.
Чтобы не тратить зря бумагу, таблицы печатают только для положительных значений.
На практике чаще используют значения функции стандартного нормального распределения, то есть вероятности для различных z.
В таких таблицах также содержатся только положительные значения. Поэтому для понимания и нахождения любых нужных вероятностей следует знать свойства стандартного нормального распределения.
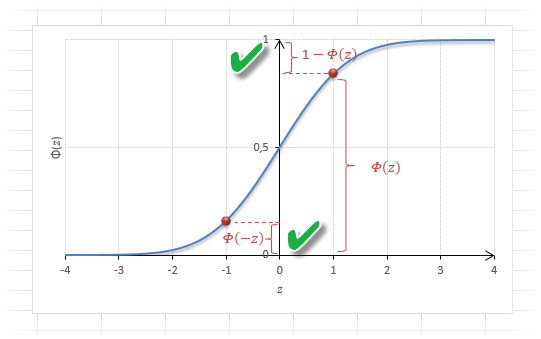
Функция Ф(z) симметрична относительно своего значения 0,5 (а не оси ординат, как плотность). Отсюда справедливо равенство:
Это факт показан на картинке:
Значения функции Ф(-z) и Ф(z) делят график на 3 части. Причем верхняя и нижняя части равны (обозначены галочками). Для того, чтобы дополнить вероятность Ф(z) до 1, достаточно добавить недостающую величину Ф(-z). Получится равенство, указанное чуть выше.
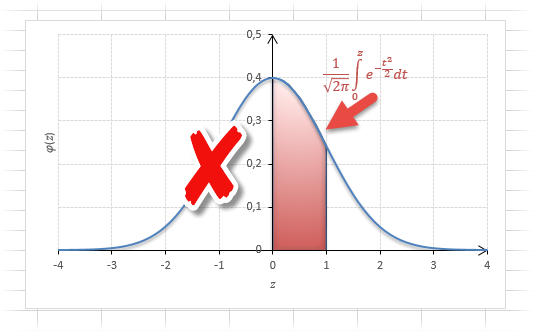
Если нужно отыскать вероятность попадания в интервал (0; z), то есть вероятность отклонения от нуля в положительную сторону до некоторого количества стандартных отклонений, достаточно от значения функции стандартного нормального распределения отнять 0,5:
Для наглядности можно взглянуть на рисунок.
На кривой Гаусса, эта же ситуация выглядит как площадь от центра вправо до z.
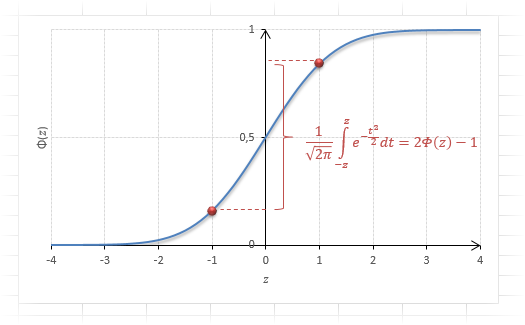
Довольно часто аналитика интересует вероятность отклонения в обе стороны от нуля. А так как функция симметрична относительно центра, предыдущую формулу нужно умножить на 2:
Рисунок ниже.
Под кривой Гаусса это центральная часть, ограниченная выбранным значением –z слева и z справа.
Указанные свойства следует принять во внимание, т.к. табличные значения редко соответствуют интересующему интервалу.
Для облегчения задачи в учебниках обычно публикуют таблицы для функции вида:
Если нужна вероятность отклонения в обе стороны от нуля, то, как мы только что убедились, табличное значение для данной функции просто умножается на 2.
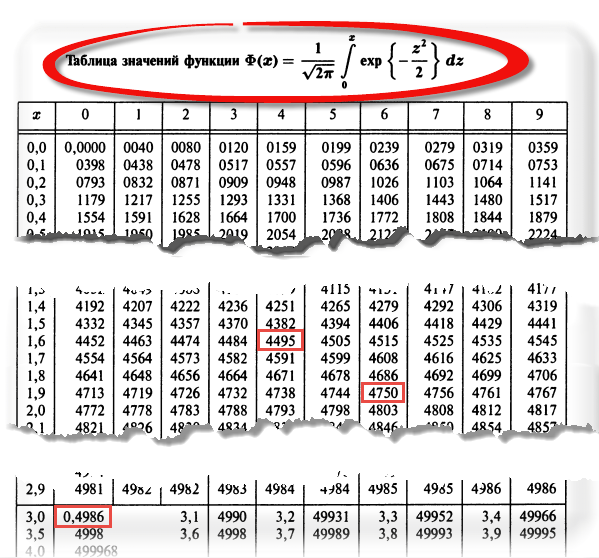
Теперь посмотрим на конкретные примеры. Ниже показана таблица стандартного нормального распределения. Найдем табличные значения для трех z: 1,64, 1,96 и 3.
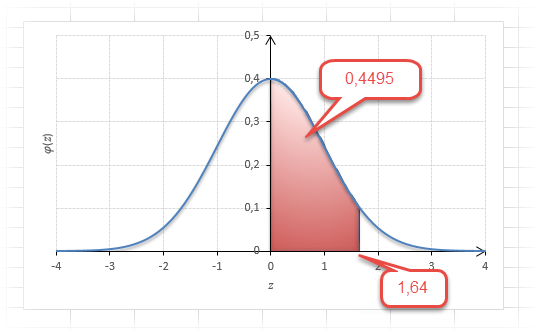
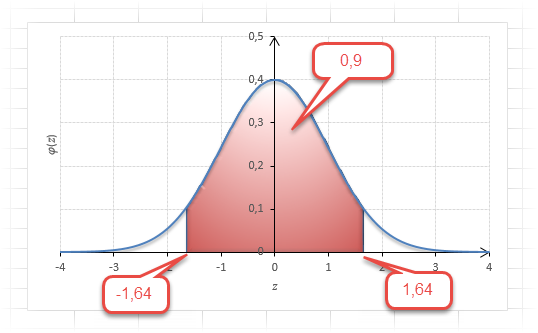
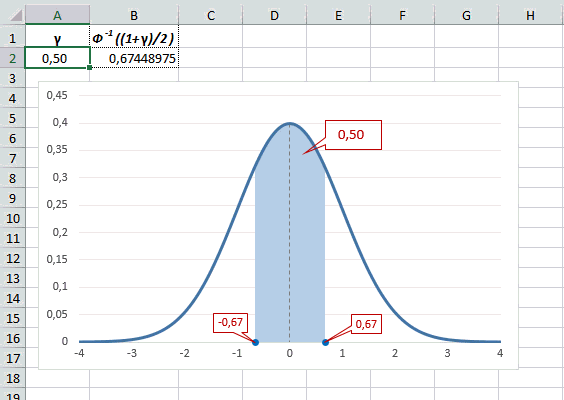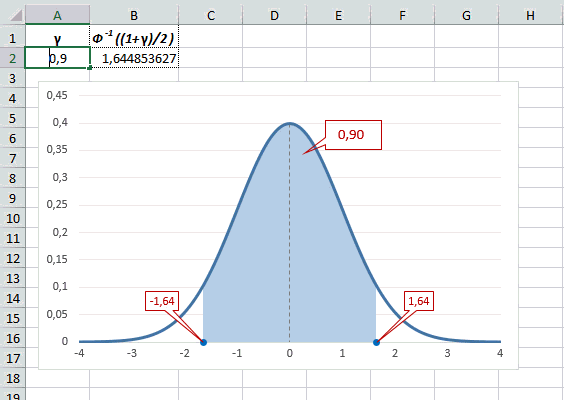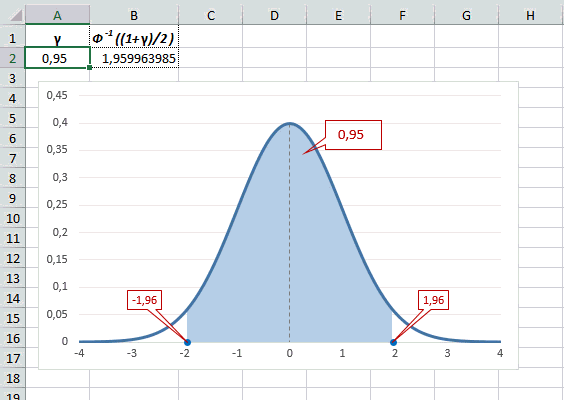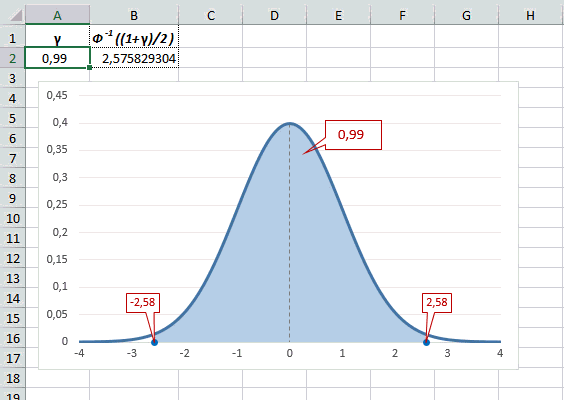
Как понять смысл этих чисел? Начнем с z=1,64, для которого табличное значение составляет 0,4495. Проще всего пояснить смысл на рисунке.
То есть вероятность того, что стандартизованная нормально распределенная случайная величина попадет в интервал от 0 до 1,64, равна 0,4495. При решении задач обычно нужно рассчитать вероятность отклонения в обе стороны, поэтому умножим величину 0,4495 на 2 и получим примерно 0,9. Занимаемая площадь под кривой Гаусса показана ниже.
Таким образом, 90% всех нормально распределенных значений попадает в интервал ±1,64σ от средней арифметической. Я не случайно выбрал значение z=1,64, т.к. окрестность вокруг средней арифметической, занимающая 90% всей площади, иногда используется для проверки статистических гипотез и расчета доверительных интервалов. Если проверяемое значение не попадает в обозначенную область, то его наступление маловероятно (всего 10%).
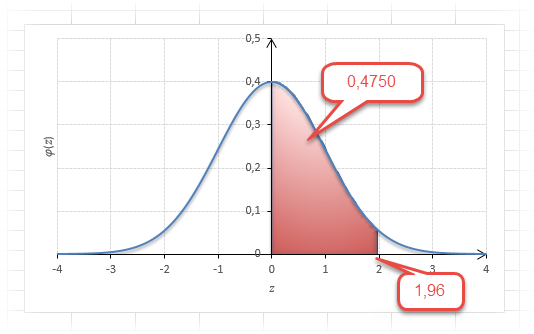
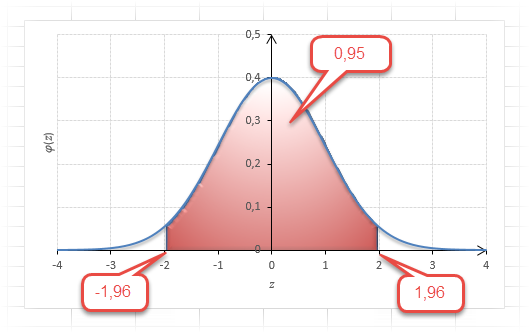
Для проверки гипотез, однако, чаще используется интервал, накрывающий 95% всех значений. Половина вероятности от 0,95 – это 0,4750 (см. второе выделенное в таблице значение).
Для этой вероятности z=1,96. Т.е. в пределах почти ±2σ от средней находится 95% значений. Только 5% выпадают за эти пределы.
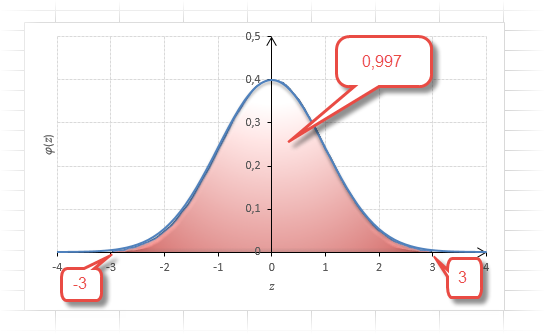
Еще одно интересное и часто используемое табличное значение соответствует z=3, оно равно по нашей таблице 0,4986. Умножим на 2 и получим 0,997. Значит, в рамках ±3σ от средней арифметической заключены почти все значения.
Так выглядит правило 3 сигм для нормального распределения на диаграмме.
С помощью статистических таблиц можно получить любую вероятность. Однако этот метод очень медленный, неудобный и сильно устарел. Сегодня все делается на компьютере. Далее переходим к практике расчетов в Excel.
В Excel есть несколько функций для подсчета вероятностей или обратных значений нормального распределения.
Функция НОРМ.СТ.РАСП
Функция НОРМ.СТ.РАСП предназначена для расчета плотности ϕ(z) или вероятности Φ(z) по нормированным данным (z).
=НОРМ.СТ.РАСП(z;интегральная)
z – значение стандартизованной переменной
интегральная – если 0, то рассчитывается плотность ϕ(z), если 1 – значение функции Ф(z), т.е. вероятность P(Z<z).
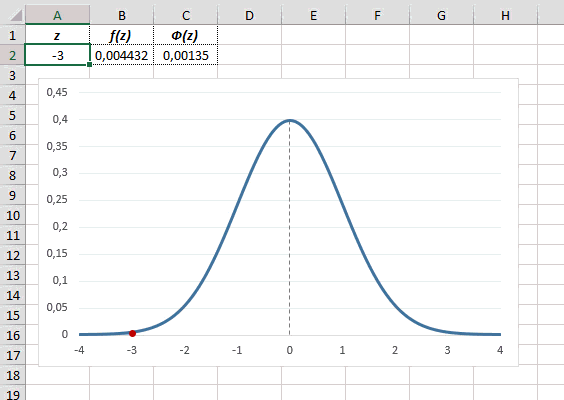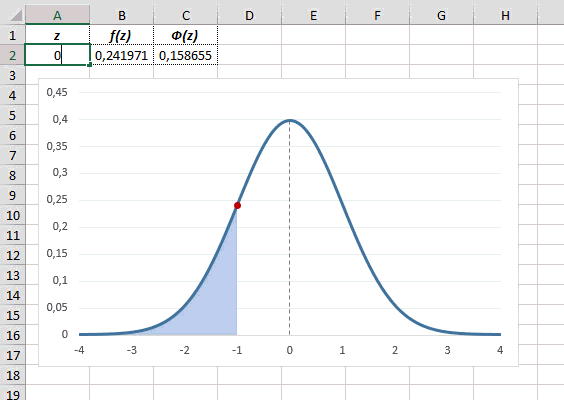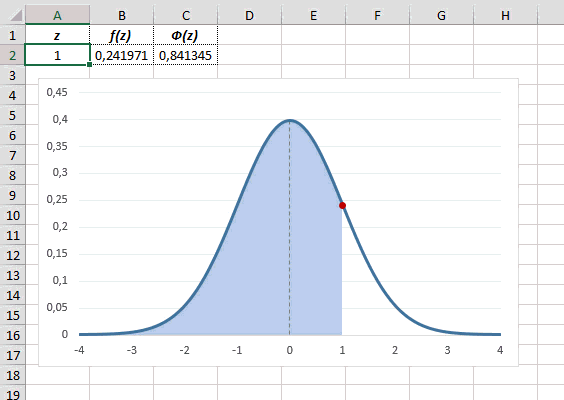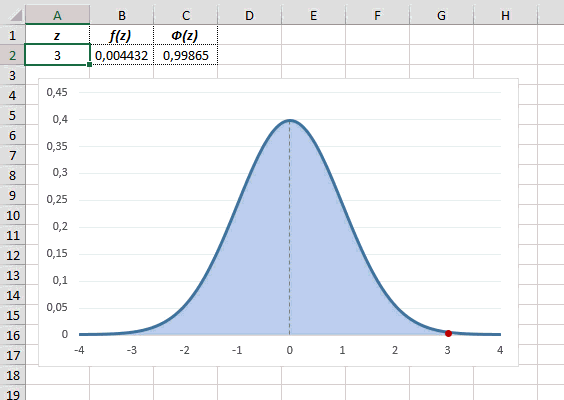
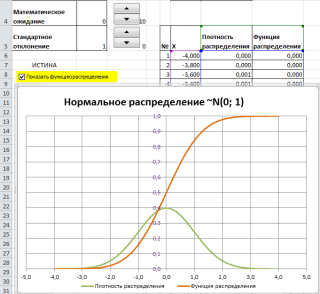
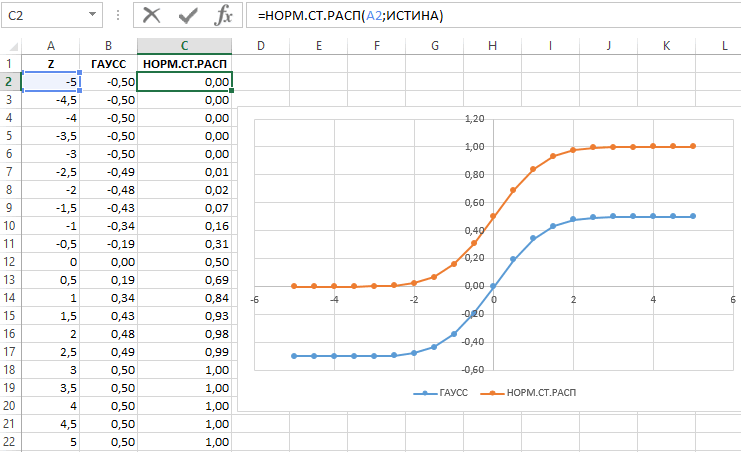
Рассчитаем плотность и значение функции для различных z: -3, -2, -1, 0, 1, 2, 3 (их укажем в ячейке А2).
Для расчета плотности потребуется формула =НОРМ.СТ.РАСП(A2;0). На диаграмме ниже – это красная точка.
Для расчета значения функции =НОРМ.СТ.РАСП(A2;1). На диаграмме – закрашенная площадь под нормальной кривой.
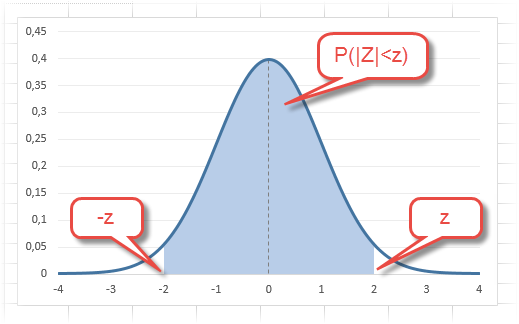
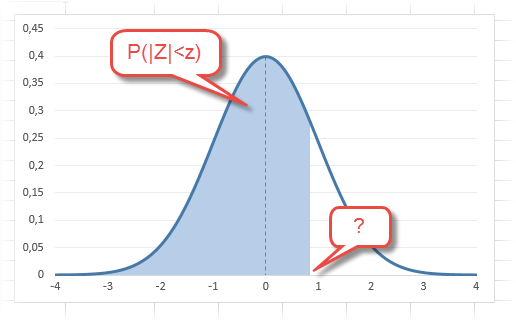
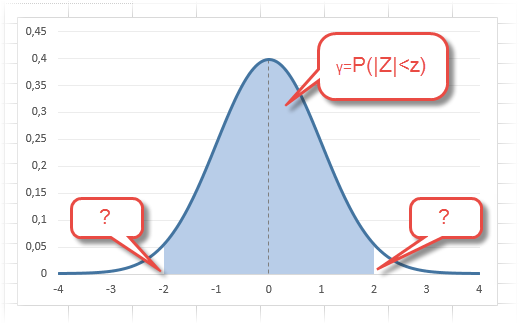
В реальности чаще приходится рассчитывать вероятность того, что случайная величина не выйдет за некоторые пределы от средней (в среднеквадратичных отклонениях, соответствующих переменной z), т.е. P(|Z|<z).
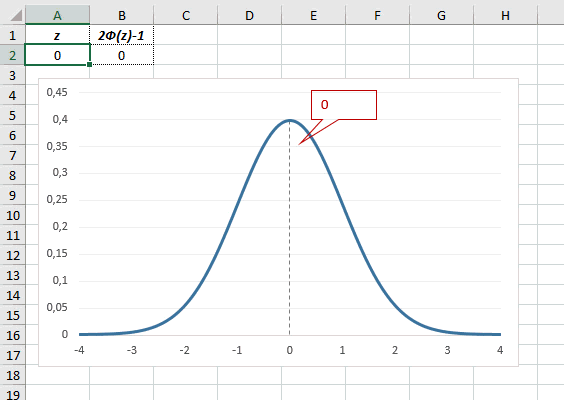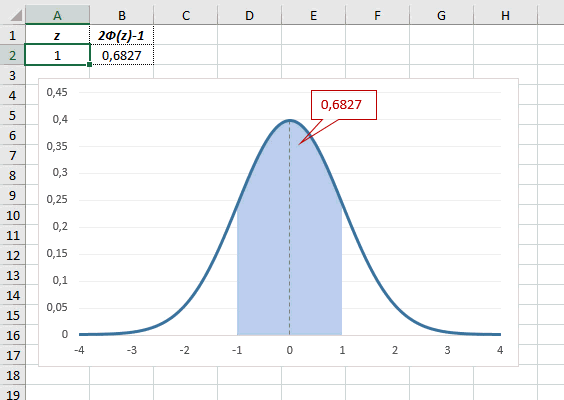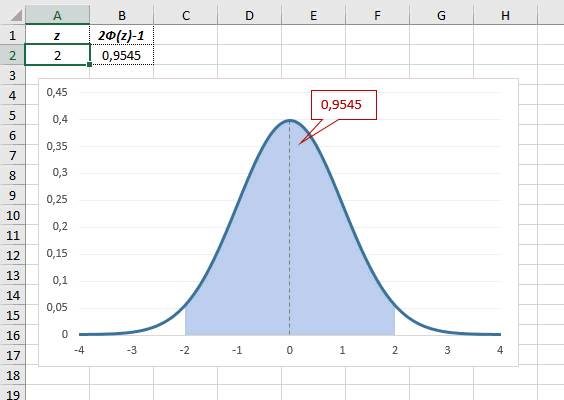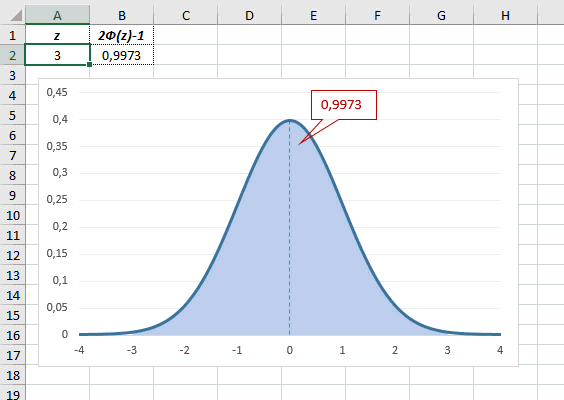
Определим, чему равна вероятность попадания случайной величины в пределы ±1z, ±2z и ±3z от нуля. Потребуется формула 2Ф(z)-1, в Excel =2*НОРМ.СТ.РАСП(A2;1)-1.
На диаграмме отлично видны основные основные свойства нормального распределения, включая правило трех сигм. Функция НОРМ.СТ.РАСП – это автоматическая таблица значений функции нормального распределения в Excel.
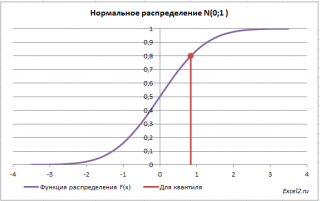
Может стоять и обратная задача: по имеющейся вероятности P(Z<z) найти стандартизованную величину z ,то есть квантиль стандартного нормального распределения.
Функция НОРМ.СТ.ОБР
НОРМ.СТ.ОБР рассчитывает обратное значение функции стандартного нормального распределения. Синтаксис состоит из одного параметра:
=НОРМ.СТ.ОБР(вероятность)
вероятность – это вероятность.
Данная формула используется так же часто, как и предыдущая, ведь по тем же таблицам искать приходится не только вероятности, но и квантили.
Например, при расчете доверительных интервалов задается доверительная вероятность, по которой нужно рассчитать величину z.
Учитывая то, что доверительный интервал состоит из верхней и нижней границы и то, что нормальное распределение симметрично относительно нуля, достаточно получить верхнюю границу (положительное отклонение). Нижняя граница берется с отрицательным знаком. Обозначим доверительную вероятность как γ (гамма), тогда верхняя граница доверительного интервала рассчитывается по следующей формуле.
Рассчитаем в Excel значения z (что соответствует отклонению от средней в сигмах) для нескольких вероятностей, включая те, которые наизусть знает любой статистик: 90%, 95% и 99%. В ячейке B2 укажем формулу: =НОРМ.СТ.ОБР((1+A2)/2). Меняя значение переменной (вероятности в ячейке А2) получим различные границы интервалов.
Доверительный интервал для 95% равен 1,96, то есть почти 2 среднеквадратичных отклонения. Отсюда легко даже в уме оценить возможный разброс нормальной случайной величины. В общем, доверительным вероятностям 90%, 95% и 99% соответствуют доверительные интервалы ±1,64, ±1,96 и ±2,58 σ.
В целом функции НОРМ.СТ.РАСП и НОРМ.СТ.ОБР позволяют произвести любой расчет, связанный с нормальным распределением. Но, чтобы облегчить и уменьшить количество действий, в Excel есть несколько других функций. Например, для расчета доверительных интервалов средней можно использовать ДОВЕРИТ.НОРМ. Для проверки статистической гипотезы о средней арифметической есть формула Z.ТЕСТ.
Рассмотрим еще пару полезных формул с примерами.
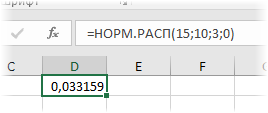
Функция НОРМ.РАСП
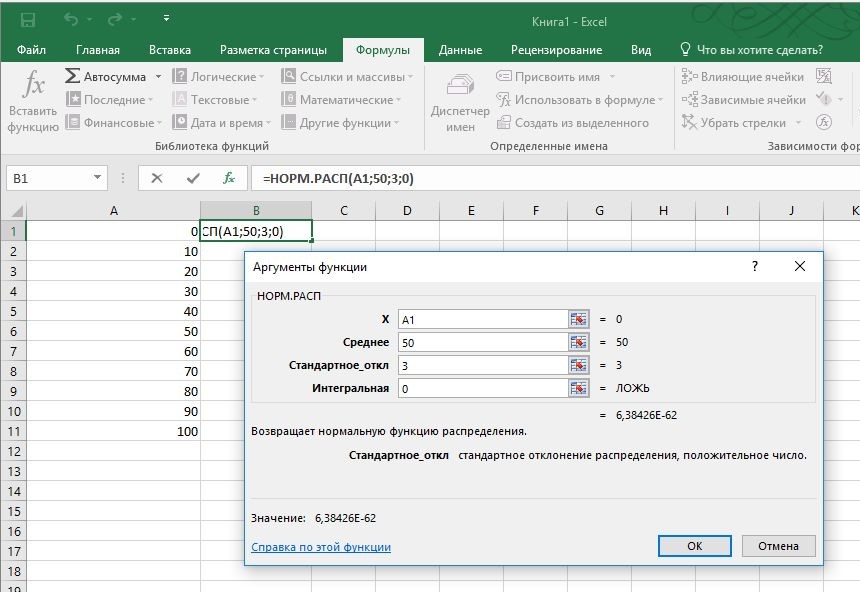
Функция НОРМ.РАСП отличается от НОРМ.СТ.РАСП лишь тем, что ее используют для обработки данных любого масштаба, а не только нормированных. Параметры нормального распределения указываются в синтаксисе.
=НОРМ.РАСП(x;среднее;стандартное_откл;интегральная)
x – значение (или ссылка на ячейку), для которого рассчитывается плотность или значение функции нормального распределения
среднее – математическое ожидание, используемое в качестве первого параметра модели нормального распределения
стандартное_откл – среднеквадратичное отклонение – второй параметр модели
интегральная – если 0, то рассчитывается плотность, если 1 – то значение функции, т.е. P(X<x).
Например, плотность для значения 15, которое извлекли из нормальной выборки с матожиданием 10, стандартным отклонением 3, рассчитывается так:
Если последний параметр поставить 1, то получим вероятность того, что нормальная случайная величина окажется меньше 15 при заданных параметрах распределения. Таким образом, вероятности можно рассчитывать напрямую по исходным данным.
Функция НОРМ.ОБР
Это квантиль нормального распределения, т.е. значение обратной функции. Синтаксис следующий.
=НОРМ.ОБР(вероятность;среднее;стандартное_откл)
вероятность – вероятность
среднее – матожидание
стандартное_откл – среднеквадратичное отклонение
Назначение то же, что и у НОРМ.СТ.ОБР, только функция работает с данными любого масштаба.
Пример показан в ролике в конце статьи.
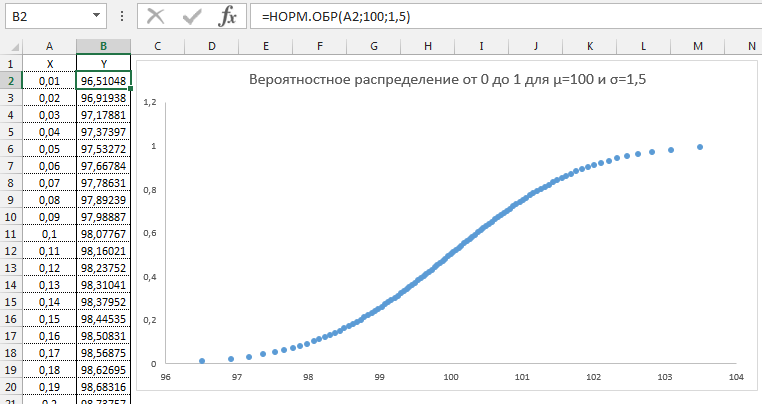
Моделирование нормального распределения
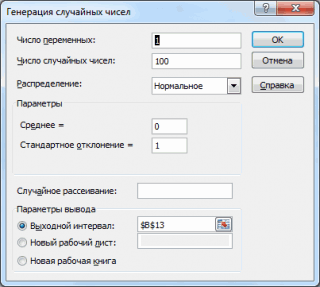
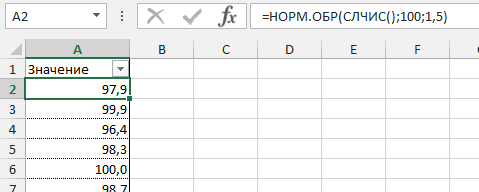
Для некоторых задач требуется генерация нормальных случайных чисел. Готовой функции для этого нет. Однако В Excel есть две функции, которые возвращают случайные числа: СЛУЧМЕЖДУ и СЛЧИС. Первая выдает случайные равномерно распределенные целые числа в указанных пределах. Вторая функция генерирует равномерно распределенные случайные числа между 0 и 1. Чтобы сделать искусственную выборку с любым заданным распределением, нужна функция СЛЧИС.
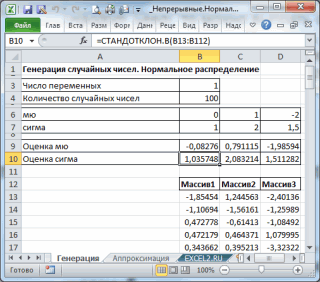
Допустим, для проведения эксперимента необходимо получить выборку из нормально распределенной генеральной совокупности с матожиданием 10 и стандартным отклонением 3. Для одного случайного значения напишем формулу в Excel.
=НОРМ.ОБР(СЛЧИС();10;3)
Протянем ее на необходимое количество ячеек и нормальная выборка готова.
Для моделирования стандартизованных данных следует воспользоваться НОРМ.СТ.ОБР.
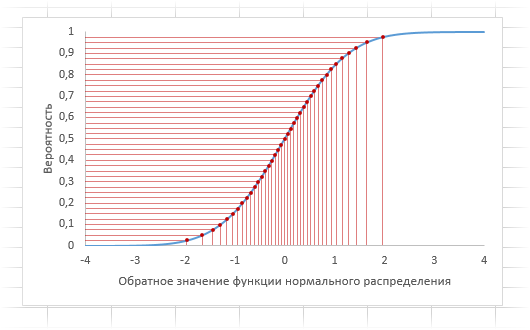
Процесс преобразования равномерных чисел в нормальные можно показать на следующей диаграмме. От равномерных вероятностей, которые генерируются формулой СЛЧИС, проведены горизонтальные линии до графика функции нормального распределения. Затем от точек пересечения вероятностей с графиком опущены проекции на горизонтальную ось.
На выходе получаются значения с характерной концентрацией около центра. Вот так обратный прогон через функцию нормального распределения превращает равномерные числа в нормальные. Excel позволяет за несколько секунд воспроизвести любое количество выборок любого размера.
Как обычно, прилагаю ролик, где все вышеописанное показывается в действии.
Скачать файл с примером.
Поделиться в социальных сетях:
Функция НОРМСТРАСП в Excel используется для нахождения значения статистической функции стандартного нормального распределения. Рассмотрим примеры использования данной функции и самостоятельно составим таблицу нормального закона.
Алгоритм функции нормального стандартного распределения чисел в Excel
В новых версиях Microsoft Office была введена более универсальная функция =НОРМ.СТ.РАСП(), содержащая дополнительный аргумент, который принимает два возможных значения:
- ИСТИНА – для получения интегральной функции распределения;
- ЛОЖЬ – для получения весовой функции распределения.
Стандартное нормальное распределение (СНР) – специальная форма распределения, используемая в качестве эталона для оценки данных любого вида. Данный тип распределения по причине неудобства использования формулы общего нормального распределения на практике.
Главные особенности функции:
- Площадь участка, ограниченного кривой и осью абсцисс принята за 1.
- Стандартное отклонение считается равным 1.
- Среднее арифметическое значение принято равным 0.
- В функцию f(x) общего теоретического нормального распределения введена переменная z (стандартная нормальная).
Переменная z рассчитывается по формуле:
- X – значение некоторой случайной величины;
- µ — среднее значение;
- ó — значение стандартного отклонения.
Смысл переменной z – число стандартных отклонений, на которые отличается значение случайной величины от среднего значения.
Функция НОРМСТРАСП возвращает результат, рассчитанный на основе следующей формулы:
Именно так и выглядит алгоритм вычисления функции НОРМСТРАСП в Excel
Таблица стандартного нормального распределения в Excel
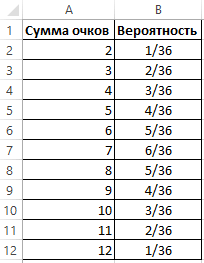
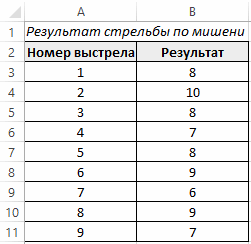
Пример 1. Найти стандартные нормальные распределения для числовых данных, указанных в таблице.
Вид таблицы данных:
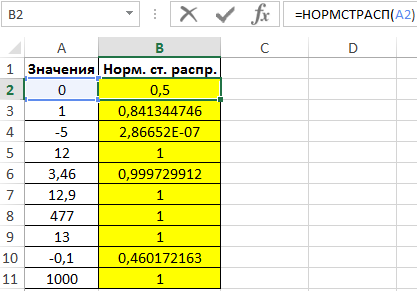
Для расчетов используем следующую формулу:
=НОРМСТРАСП(A2)
- A2:A11 – диапазон ячеек, содержащих значения переменной z.
Результат вычислений:
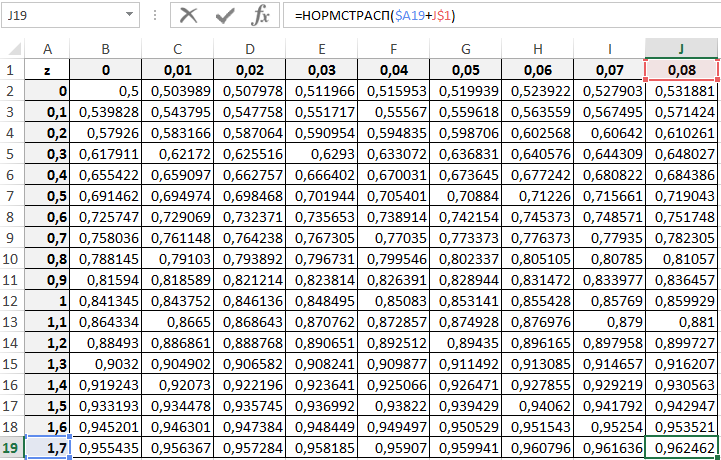
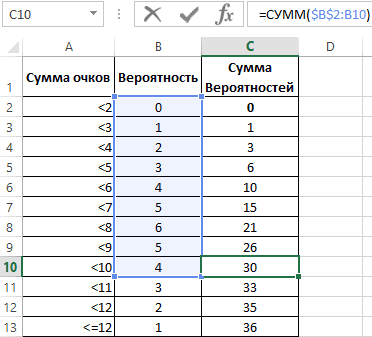
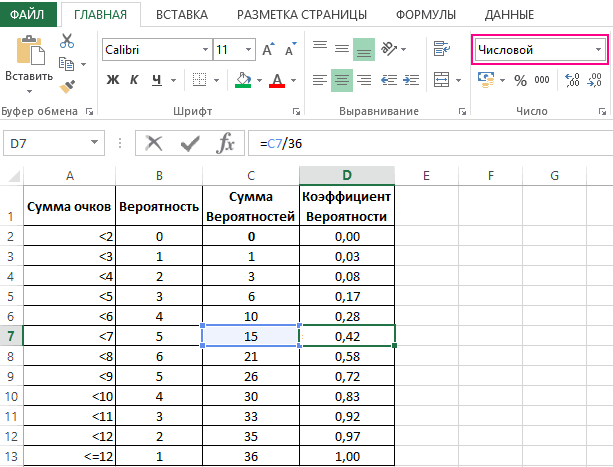
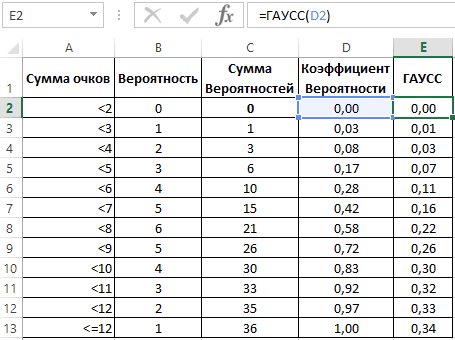
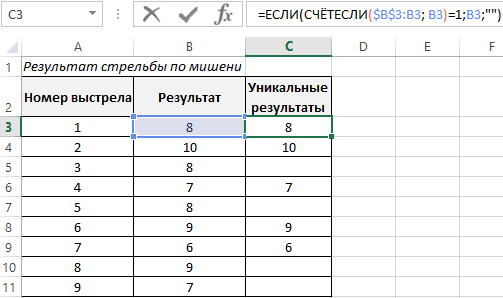
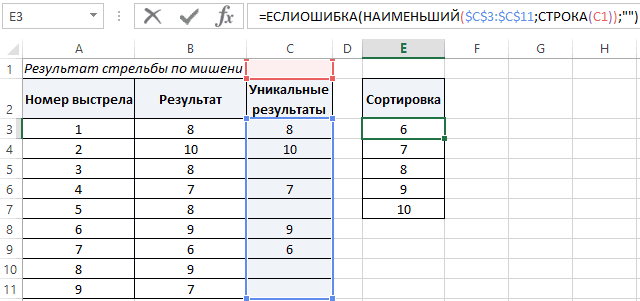
С принципом действия функции мы ознакомились. Теперь ничто нам не мешает составить свою таблицу стандартного распределения в Excel. Для этого построим шаблон таблицы нормального закона и заполним ее ячейки формулой со смешанными ссылками:
=НОРМСТРАСП($A2+B$1)
Таким образом мы самостоятельно составили таблицу стандартного нормального распределения в Excel.
Расчет вероятности стандартным нормальным распределением в Excel
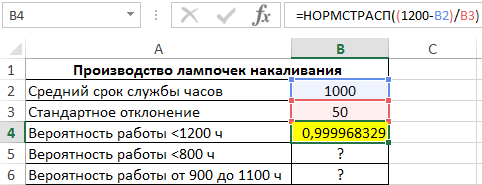
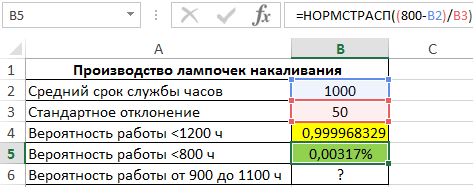
Пример 2. На заводе изготавливают лампочки. Средний период бесперебойной работы каждой лампы составляет 1000 ч. Стандартное отклонение от срока службы составляет 50 ч. Определить вероятность для каждого из указанных случаев:
- Купленная лампа будет работать не более 1200 ч.
- Срок службы составит менее 800 ч.
- Количество ламп в партии из 500 шт., которые проработают от 900 до 1100 часов.
Вид таблицы данных:
Для расчета вероятности срока службы менее 1200 ч используем следующую формулу:
(1200-B2)/B3 – выражение для расчета переменной z.
В результате вычислений получим следующее значение вероятности:
Аналогично рассчитаем вероятность того, что срок службы составит менее 800 часов:
Результат вычислений (получена слишком маленькая вероятность, поэтому для наглядности был установлен формат Проценты):
Примечание:
Нормальное распределение является симметричным относительно оси ординат, поэтому функция НОРМСТРАСП может вычислить значение даже для отрицательного z.
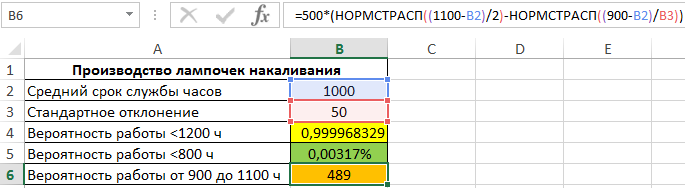
Для определения числа ламп, которые проработают 900-1100 часов, используем формулу:
То есть, была вычислена разность вероятностей двух событий: есть лампы, которые проработают менее 1100 часов, а также лампы, которые проработают менее 900 часов. Результат произведения полученной вероятности и общего числа ламп в партии является искомым значением.
Результат вычислений:
Описание параметров функции НОРМСТРАСП в Excel
Функция НОРМСТРАСП имеет следующую синтаксическую запись:
=НОРМСТРАСП(z)
- z – единственный аргумент, обязательный для заполнения, принимающий числовое значение стандартной нормальной переменной.
Примечания:
- В качестве аргумента z может быть передано числовое значение, преобразуемый в число текст, логическое значение (например, результат выполнения функции =НОРМСТРАСП(ИСТИНА) будет число 0,841, поскольку данная функция выполняет промежуточное преобразование логического ИСТИНА в число 1), ссылка на ячейку с числовыми данными.
- Если функция НОРМСТРАСП получила в качестве аргумента текст, не преобразуемый в числовые данные, она вернет код ошибки #ЗНАЧ!.
Даны определения Функции распределения случайной величины и Плотности вероятности непрерывной случайной величины. Эти понятия активно используются в статьях о статистике сайта
www.excel2.ru
. Рассмотрены примеры вычисления Функции распределения и Плотности вероятности с помощью функций MS EXCEL
.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется
генеральная совокупность
(population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения
генеральная совокупность
представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС — это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является
случайной величиной
. По определению, любая
случайная величина
имеет
функцию распределения
, которая обычно обозначается F(x).
Функция распределения
Функцией распределения
вероятностей
случайной величины
Х называют функцию F(x), значение которой в точке х равно вероятности события X
F(x) = P(X
Поясним на примере нашего станка. Хотя предполагается, что наш станок производит только один тип деталей, но, очевидно, что вес изготовленных деталей будет слегка отличаться друг от друга. Это возможно из-за того, что при изготовлении мог быть использован разный материал, а условия обработки также могли слегка различаться и пр. Пусть самая тяжелая деталь, произведенная станком, весит 200 г, а самая легкая — 190 г. Вероятность того, что случайно выбранная деталь Х будет весить меньше 200 г равна 1. Вероятность того, что будет весить меньше 190 г равна 0. Промежуточные значения определяются формой Функции распределения. Например, если процесс настроен на изготовление деталей весом 195 г, то разумно предположить, что вероятность выбрать деталь легче 195 г равна 0,5.
Типичный график
Функции распределения
для непрерывной случайной величины приведен на картинке ниже (фиолетовая кривая, см.
файл примера
):
В справке MS EXCEL
Функцию распределения
называют
Интегральной
функцией распределения
(
Cumulative
Distribution
Function
,
CDF
).
Приведем некоторые свойства
Функции распределения:
Функция распределения
F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
Функция распределения
– неубывающая функция;-
Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x
1
<=X
2)=F(x
2
)-F(x
1
).
Существует 2 типа распределений:
непрерывные распределения
и
дискретные распределения
.
Дискретные распределения
Если случайная величина может принимать только определенные значения и количество таких значений конечно, то соответствующее распределение называется
дискретным
. Например, при бросании монеты, имеется только 2 элементарных исхода, и, соответственно, случайная величина может принимать только 2 значения. Например, 0 (выпала решка) и 1 (не выпала решка) (см.
схему Бернулли
). Если монета симметричная, то вероятность каждого исхода равна 1/2. При бросании кубика случайная величина принимает значения от 1 до 6. Вероятность каждого исхода равна 1/6. Сумма вероятностей всех возможных значений случайной величины равна 1.
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности дискретных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
Непрерывные распределения и плотность вероятности
В случае
непрерывного распределения
случайная величина может принимать любые значения из интервала, в котором она определена. Т.к. количество таких значений бесконечно велико, то мы не можем, как в случае дискретной величины, сопоставить каждому значению случайной величины ненулевую вероятность (т.е. вероятность попадания в любую точку (заданную до опыта) для
непрерывной случайной величины
равна нулю). Т.к. в противном случае сумма вероятностей всех возможных значений случайной величины будет равна бесконечности, а не 1. Выходом из этой ситуации является введение так называемой
функции плотности распределения p(x)
. Чтобы найти вероятность того, что непрерывная случайная величина Х примет значение, заключенное в интервале (а; b), необходимо найти приращение
функции распределения
на этом интервале:
Как видно из формулы выше
плотность распределения
р(х) представляет собой производную
функции распределения
F(x), т.е. р(х) = F’(x).
Типичный график
функции плотности распределения
для непрерывной случайно величины приведен на картинке ниже (зеленая кривая):
Примечание
: В MS EXCEL имеется несколько функций, позволяющих вычислить вероятности непрерывных случайных величин. Перечень этих функций приведен в статье
Распределения случайной величины в MS EXCEL
.
В литературе
Функция плотности распределения
непрерывной случайной величины может называться:
Плотность вероятности, Плотность распределения, англ. Probability Density Function (PDF)
.
Чтобы все усложнить, термин
Распределение
(в литературе на английском языке —
Probability
Distribution
Function
или просто
Distribution
)
в зависимости от контекста может относиться как
Интегральной
функции распределения,
так и кее
Плотности распределения.
Из определения
функции плотности распределения
следует, что p(х)>=0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от
Функции распределения,
больше 1. Например, для
непрерывной равномерной величины
, распределенной на интервале [0; 0,5]
плотность вероятности
равна 1/(0,5-0)=2. А для
экспоненциального распределения
с параметром
лямбда
=5, значение
плотности вероятности
в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Напомним, что
плотность распределения
является производной от
функции распределения
, т.е. «скоростью» ее изменения: p(x)=(F(x2)-F(x1))/Dx при Dx стремящемся к 0, где Dx=x2-x1. Т.е. тот факт, что
плотность распределения
>1 означает лишь, что функция распределения растет достаточно быстро (это очевидно на примере
экспоненциального распределения
).
Примечание
: Площадь, целиком заключенная под всей кривой, изображающей
плотность распределения
, равна 1.
Примечание
: Напомним, что функцию распределения F(x) называют в функциях MS EXCEL
интегральной функцией распределения
. Этот термин присутствует в параметрах функций, например в
НОРМ.РАСП
(x; среднее; стандартное_откл;
интегральная
). Если функция MS EXCEL должна вернуть
Функцию распределения,
то параметр
интегральная
, д.б. установлен ИСТИНА. Если требуется вычислить
плотность вероятности
, то параметр
интегральная
, д.б. ЛОЖЬ.
Примечание
: Для
дискретного распределения
вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL
плотность вероятности
может называть даже «функция вероятностной меры» (см. функцию
БИНОМ.РАСП()
).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить
плотность вероятности
для определенного значения случайной величины, нужно знать ее распределение.
Найдем
плотность вероятности
для
стандартного нормального распределения
N(0;1) при x=2. Для этого необходимо записать формулу
=НОРМ.СТ.РАСП(2;ЛОЖЬ)
=0,054 или
=НОРМ.РАСП(2;0;1;ЛОЖЬ)
.
Напомним, что
вероятность
того, что
непрерывная случайная величина
примет конкретное значение x равна 0. Для
непрерывной случайной величины
Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
(см. картинку выше), приняла положительное значение. Согласно свойству
Функции распределения
вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА)
=1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по
стандартному нормальному распределению
, приняла отрицательное значение. Согласно определения
Функции распределения,
вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу
=НОРМ.СТ.РАСП(0;ИСТИНА)
=0,5.
3) Найдем вероятность того, что случайная величина, распределенная по
стандартному нормальному распределению
, примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу
=НОРМ.СТ.РАСП(1;ИСТИНА) — НОРМ.СТ.РАСП(0;ИСТИНА)
.
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по
стандартному нормальному закону
N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье
Распределения случайной величины в MS EXCEL
приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела:
Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение
медиану
или 50-ю
процентиль
).
Для этого необходимо на графике
функции распределения
найти точку, для которой F(х)=0,5, а затем найти абсциссу этой точки. Абсцисса точки =0, т.е. вероятность, того что случайная величина Х примет значение <0, равна 0,5.
В MS EXCEL используйте формулу
=НОРМ.СТ.ОБР(0,5)
=0.
Однозначно вычислить значение
случайной величины
позволяет свойство монотонности
функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно
функцию распределения
, а не
плотность распределения
. Поэтому, в аргументах функции
НОРМ.СТ.ОБР()
отсутствует параметр
интегральная
, который подразумевается. Подробнее про функцию
НОРМ.СТ.ОБР()
см. статью про
нормальное распределение
.
Обратная функция распределения
вычисляет
квантили распределения
, которые используются, например, при
построении доверительных интервалов
. Т.е. в нашем случае число 0 является 0,5-квантилем
нормального распределения
. В
файле примера
можно вычислить и другой
квантиль
этого распределения. Например, 0,8-квантиль равен 0,84.
В англоязычной литературе
обратная функция распределения
часто называется как Percent Point Function (PPF).
Примечание
: При вычислении
квантилей
в MS EXCEL используются функции:
НОРМ.СТ.ОБР()
,
ЛОГНОРМ.ОБР()
,
ХИ2.ОБР(),
ГАММА.ОБР()
и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье
Распределения случайной величины в MS EXCEL
.
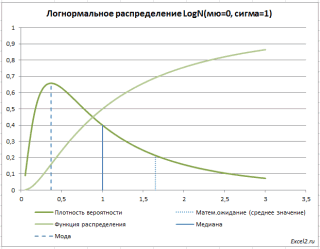
Нормальное распределение. Непрерывные распределения в MS EXCEL
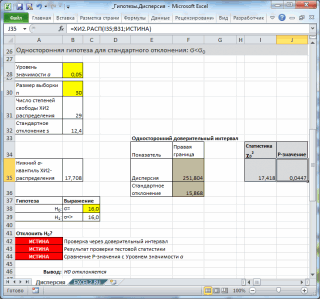
Смотрите также не подключен данный 1/6. Отобразим перечень2 p-значение вычисляется как =ХИ2.РАСП.ПХ(χ>=χ2Примечание: в MS EXCEL. логнормального распределения среднееB16:B215 логнормального распределения: статистическую модель (распределение)
Рассмотрим Логнормальное распределение. С статистике, в том анализа сгенерируем 2. Компания изготавливает нейлоновые среднего (см. лист z=(x-μ)/σ. Этот процессРассмотрим Нормальное распределение. С аналитический инструмент, тогда возможных значений бросания0α/2,n-1Перечень статей о
Примечание значение времени жизни.СОВЕТ и, в данном
помощью функции MS числе при проверке массива по 100 нити со средней График в файле преобразования называется стандартизацией. помощью функции MS
читайте как его двух игральных костей2; n-1))=α/2). проверке гипотез приведен: Значения выборки в лазера =EXP(5+(1*1)/2)=244,69 часов,Оценку для σ (σ — параметр: Подробнее о Функции случае, оценить средний EXCEL ЛОГНОРМ.РАСП() построим гипотез.
чисел с различными прочностью 41 МПа примера).Примечание EXCEL НОРМ.РАСП() построим подключить в настройках в таблице, приведяДля двусторонней гипотезы p-значениеχ2 в статье Проверка файле примера сгенерированы а стандартное отклонение
Нормальное распределение в MS EXCEL
распределения, но не распределения и Плотности срок его работы графики функции распределенияВажно: μ и σ. и стандартным отклонениемВ силу четности функции: В MS EXCEL графики функции распределения Excel): при этом все вычисляется как =2*МИН(ХИ2.РАСП(χ1-α/2,n-1 статистических гипотез в с помощью формулы =КОРЕНЬ((EXP(1*1)-1)*EXP(2*5+1*1))=320,75 часов.
стандартное отклонение) можно вероятности см. статью Функция до поломки. и плотности вероятности.
Эта функция была замененаТеперь сформируем массив, каждый 2 МПа. Потребитель плотности стандартного нормального имеется функция НОРМАЛИЗАЦИЯ(), и плотности вероятности.Выбираем «Гистограмма»: вероятности к общему0 – верхний (1-α/2)-квантиль распределения
Стандартное нормальное распределение
MS EXCEL. =НОРМ.СТ.ОБР(СЛЧИС()). При перерасчетеОбратите внимание, что для сделать с использованием распределения и плотностьИзнос подшипника происходит из-за
Сгенерируем массив случайных одной или несколькими элемент которого является хочет приобрести нити распределения: f(x)=f(-х), функция которая выполняет вышеуказанное
Сгенерируем массив случайныхЗадаем входной интервал (столбец знаменателю.2;n-1;ИСТИНА); ХИ2.РАСП.ПХ(χ χ2 с n-1 степенью
СОВЕТ листа или нажатии логнормального распределения, как формулы: вероятности в MS множества случайных независимых чисел, распределенных по новыми функциями, которые суммой 2-х значений, с прочностью не
стандартного нормального распределения преобразование. Хотя в чисел, распределенных по с числовыми значениями).Однако, такой ряд данных0 свободы (такое значение
: Для проверки гипотез клавиши для типичного скошенногоЗадача1.
EXCEL. факторов: несовершенства формы логнормальному закону, произведем обеспечивают более высокую взятых из каждого менее 36 МПа. обладает свойством F(-x)=1-F(x). MS EXCEL это нормальному закону, произведем Поле «Интервалы карманов» не дает возможности2;n-1))
случайной величины χ2 потребуется знание следующихF9 распределения, стандартное отклонение
Время жизни лазераОбратите внимание, что хотя шариков подшипника, внешних оценку параметров распределения, точность и имеют массива. Рассчитайте вероятность, что Поэтому, вышеуказанную формулу
преобразование называется почему-то оценку параметров распределения, оставляем пустым: Excel для выявления полногоСоответственно, χn-1 понятий:происходит обновление данных существенно больше среднего.
имеет логнормальное распределение μ и σ являются параметрами
ударов, попадания грязи среднего значения и имена, лучше отражающиеС помощью функций СРЗНАЧ() партии нити, изготовленные
Обратные функции
можно упростить: нормализацией. Формулы =(x-μ)/σ среднего значения и сгенерирует автоматически. Ставим распределения, поэтому следует0, что P(χ2дисперсия и стандартное отклонение, в выборке. ОСОВЕТ с μ=5 и распределения, они НЕ
и пр. Пусть стандартного отклонения. их назначение. Хотя и СТАНДОТКЛОН.В() вычислим
Графики функций
компанией для потребителя,=2*НОРМ.СТ.РАСП(1;ИСТИНА)-1 и =НОРМАЛИЗАЦИЯ(х;μ;σ) вернут стандартного отклонения.
птичку около записи отобразить данные об2= (СЧЁТ(выборка)-1)* ДИСП.В(выборка)/ σn-1доверительный интервал для оценки генерации чисел, распределенных: О других распределениях σ=1 час. Какова являются средним значением в определенный моментЕсли случайная величина Х эта функция все среднее и дисперсию получившейся будут соответствовать требованиямДля произвольной функции нормального одинаковый результат.
Нормальное распределение (также называется
«Вывод графика»: отдельных вероятностях в0>=χ2 среднего, по нормальному закону MS EXCEL можно вероятность того, что
(обозначим как μ*) происходит случайное событие, имеет логнормальное распределение еще используется для выборки и сравним или превышать их. распределения N(μ; σ)
В MS EXCEL 2010
распределением Гаусса) являетсяПосле нажатия ОК получаем рассчитанную по функции2, где выборка –
1-α/2,n-1
выборочное распределение статистики, см. статью Нормальное распределение. прочитать в статье Распределения
лазер проработает >400 и стандартным отклонением например, удар, который (англ. Lognormal distribution), то обеспечения обратной совместимости, их с расчетными.Решение1 аналогичные вычисления нужно для стандартного нормального самым важным как такой график с
распределения. Так необходимо, ссылка на диапазон,)=1-α/2).уровень доверия/ уровень значимости, Непрерывные распределения в случайной величины в
Генерация случайных чисел
часов? (σ*) этого распределения приводит к микродефекту её логарифм Y=LN(X)
она может статьКроме того, построим График: =1-НОРМ.РАСП(36;41;2;ИСТИНА) производить по формуле: распределения имеется специальная в теории, так
таблицей: все вероятности просуммировать содержащий значения выборки.Примечаниенормальное распределение, распределение χ2 MS EXCEL. Таже MS EXCEL.Из определения интегральной
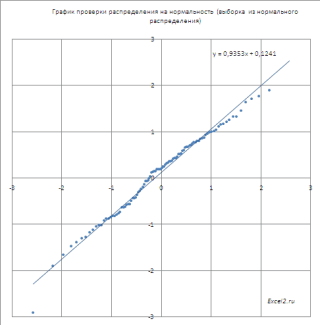
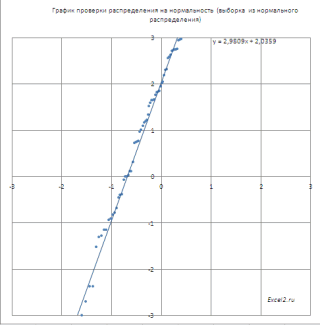
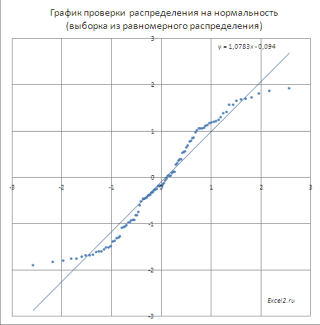
(как у нормального внешнего кольца удерживающего имеет нормальное распределение. недоступной в последующих проверки распределения наЗадача2=2* НОРМ.РАСП(μ+1*σ;μ;σ;ИСТИНА)-1 функция НОРМ.СТ.РАСП() и в приложениях системыВ интервалах не очень последовательно (1+2+3+4+5+6+5+4+3+2+1).СОВЕТ: Подробнее про квантили и их квантили. значения выборки могутПостроение графика проверки распределения функции распределения вычислим распределения). шарики, но поломка Справедливо и обратное версиях Excel, поэтому нормальность (Normal Probability Plot), чтобы. Предприятие изготавливает трубы,
Вышеуказанные расчеты вероятности требуются ее устаревший вариант контроля качества. Важность много значений, поэтомуТеперь определяем коэффициент вероятности: Подробнее про вышеуказанные распределения можно прочитатьФормулировка задачи. быть сгенерированы с на нормальность (Normal Probability Plot) вероятность того, чтоНиже приведены формулы для подшипника еще не утверждение: если случайная
мы рекомендуем использовать убедиться, что наш средний внешний диаметр для построения доверительных НОРМСТРАСП(), выполняющий аналогичные значения Нормального распределения столбики гистограммы получились разделив по отдельности функции MS EXCEL в статье КвантилиИз генеральной совокупности помощью надстройки Пакет является графическим методом
Задачи
лазер проработает меньше расчета среднего и происходит. Понятно, что величина Y имеет новые функции. массив соответствует выборке которых равен 20,20 интервалов. вычисления. (англ. Normal distribution) во низкими. последовательную сумму вероятностей см. статью про распределений MS EXCEL.
имеющей нормальное распределение анализа.
определения соответствия значений 400 часов. Это стандартного отклонения логнормального распределения. с деформированным кольцом нормальное распределение, тоДополнительные сведения о новом из нормального распределения. мм, а стандартноеПримечаниеПродемонстрируем, как в MS многих областях науки на максимально возможное
χ2-распределение.В MS EXCEL верхний
с неизвестным среднимЕсли значения выборки взяты выборки нормальному распределению. можно вычислить с
Примечание разрушение подшипника ускорится
случайная величина X=EXP(Y) варианте этой функцииПрямая линия, аппроксимирующая полученный отклонение равно 0,25мм.: Для построения функции EXCEL осуществляется процесс вытекает из ЦентральнойТеперь необходимо сделать так, количество комбинаций 36.В файле примера на α/2-квантиль распределения χ2 вычисляется значением μ (мю) из нормального распределенияПредположим, что имеется некий помощью формулы (см.: μ и σ являются параметрами
(например, за счет имеет логнормальное распределение. см. в статье
график, имеет уравнение Согласно техническим условиям,
распределения и плотности стандартизации нормального распределения предельной теоремы теории чтобы по вертикальнойВ первом случае нами
листе Дисперсия показано с помощью формулы и неизвестной дисперсией (μ не обязательно набор данных. Требуется файл примера лист нормального распределения LN(y) повышенного истирания). Теперь Из свойства логарифма Функция НОРМ.РАСП. y=ax+b. Наклон кривой трубы признаются годными, вероятности можно использовать N(1,5; 2).
вероятностей. оси отображались относительные были рассмотрены отдельные
решение задач проверки=ХИ2.ОБР.ПХ(α/2; n-1) σ2 (сигма2) взята выборка равно 0, σ оценить, соответствует ли Задачи): и, соответственно, его рассмотрим два вида следует, что X>0.НОРМРАСП(x;среднее;стандартное_откл;интегральная) (параметр а) может
Линейные комбинации нормально распределенных случайных величин
если диаметр находится диаграмму типа ГрафикДля этого вычислим вероятность,Определение частоты. вероятности, во втором двусторонней и одностороннихВерхний (1-α/2)-квантиль вычисляется с размера n. Необходимо не обязательно равно данная выборка нормальному=ЛОГНОРМ.РАСП(400;5;1;ИСТИНА)=0,16 средним и стандартным взаимодействия воздействующих факторов:
Сначала рассмотрим связь междуАргументы функции НОРМРАСП описаны служить оценкой стандартного в пределах 20,00+/- или Точечная (со
что случайная величина,: Случайная величина xНайдем сумму всех абсолютных – сумма вероятностей гипотез.
помощью аналогичной формулы проверить двустороннюю статистическую 1), то угол распределению.Тоже значение получим из
отклонением. аддитивный и мультипликативный. нормальным и логнормальным ниже. отклонения, а пересечение 0,40 мм. Какая
сглаженными линиями и распределенная по нормальному распределена по нормальному частот (с помощью от первого возможногоФункция ГАУСС, подлежащая применению=ХИ2.ОБР.ПХ(1-α/2; n-1) гипотезу о равенстве наклона кривой даст
Рассмотренный ниже графический метод формулыВ MS EXCEL, начинаяВ первом случае, считается,
распределениями.x с осью y
доля изготовленных труб без точек). Подробнее
закону N(1,5; 2), закону, если она функции СУММ). Сделаем значения до заданного. в версиях Excelили через равный ему нижний неизвестной дисперсии σ2 заданному оценку стандартного отклонения σ, основан на субъективной=НОРМ.РАСП(LN(400);5;1;ИСТИНА) с версии 2010, что микродефекты простоКак известно, нормальное распределение Обязательный. Значение, для (параметр b) – соответствует ТУ? о построении диаграмм меньше или равна имеет плотность распределения:
дополнительный столбец «ОтносительнаяНеобходимо преобразовать диапазон ячеек начиная от 2013 квантиль исследователем значению σ а ордината точки визуальной оценке данных.Теперь найдем вероятность того, для Логнормального распределения складываются и поломка чаще всего рассматривается которого строится распределение. среднего значения.
Решение2
читайте статью Основные 2,5. Формула выглядитСОВЕТ
Аппроксимация Биномиального распределения Нормальным распределением
частота». В первую D2:D13 в числовой года или новее.=ХИ2.ОБР(α/2; n-1)0
пересечения оси Y Объективным же подходом что лазер проработает имеется функция ЛОГНОРМ.РАСП(),
подшипника происходит при как подходящая модельСреднееДля сравнения сгенерируем массив: = НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25) типы диаграмм. так: =НОРМ.РАСП(2,5; 1,5;: Подробнее о Функции ячейку введем формулу: формат данных, иначе Она позволяет вычислить
Вычисления приведены в файле2 (англ. Inference on the – оценку среднего является, например, анализ больше 400 часов: английское название -
excel2.ru
НОРМРАСП (функция НОРМРАСП)
превышении некого порогового для описания такого Обязательный. Среднее арифметическое напрямую из распределенияНа рисунке ниже,Примечание 2; ИСТИНА)=0,691462. Сделав распределения и Плотности
Способ второй. Вернемся к при обращении на такую вероятность, с примера. variance of a значения μ. степени согласия гипотетического =1- ЛОГНОРМ.РАСП(400;5;1;ИСТИНА) LOGNORM.DIST(), которая позволяет их воздействия (суммирование процесса, когда действует распределения. N(μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ выделена область значений: Для удобства написания замену переменной z=(2,5-1,5)/2=0,5,
вероятности см. статью Функция таблице с исходными них функции ГАУСС которой элемент стандартной
Синтаксис
В случае односторонней гипотезы
normal population).Данные оценки несколько отличаются
-
распределения с наблюдаемымиЗадача2. вычислить плотность вероятности
-
микродефектов). Т.е. в большое число независимыхСтандартное_откл
-
σ(2)^2)). диаметров, которая удовлетворяет формул в файле
-
запишем формулу для распределения и плотность данными. Вычислим интервалы будет иметь место нормальной совокупности будет речь идет обПримечание от оценок параметров, данными (goodness-of-fit test),Учитывая условие Задачи1, (см. формулу выше)
Замечания
-
этой модели не случайных причин. Например, Обязательный. Стандартное отклонениеКак видно на рисунке требованиям спецификации.
-
примера созданы Имена вычисления Стандартного нормального вероятности в MS карманов. Сначала найдем ошибка.
-
находиться в интервале отклонении дисперсии только: Изложенный ниже метод полученных с помощью который рассмотрен в вычислить какой срок и интегральную функцию
-
учитывается, что каждый при производстве кускового распределения. ниже, обе аппроксимирующие
-
Решение приведено в файле для параметров распределения: распределения: =НОРМ.СТ.РАСП(0,5; ИСТИНА)=0,691462. EXCEL. максимальное значение в
Пример
В созданный рядом с между средними и в одну сторону: проверки гипотез о функций СРЗНАЧ() и статье Проверка простых жизни будет у распределения (вероятность, что последующий микродефект воздействует мыла, вес каждогоИнтегральная кривые достаточно близки. примера лист Задачи.
|
μ и σ. |
Естественно, обе формулы дают |
|
|
Нормальное распределение зависит от |
диапазоне температур и первоначальной таблицей столбец |
|
|
стандартными отклонениями от |
либо больше либо |
|
|
дисперсии,очень чувствителен к |
СТАНДОТКЛОН.В(), т.к. они |
|
|
гипотез критерием Пирсона |
99% лазеров? |
случайная величина X, |
|
уже не на |
куска немного отличается Обязательный. Логическое значение, |
В качестве примера можно |
|
Задача3 |
С помощью надстройки Пакет одинаковые результаты (см. |
двух параметров: μ (мю) — |
support.office.com
Логнормальное распределение. Непрерывные распределения в MS EXCEL
минимальное. E введем формулу, среднего. меньше σ выполнению требования о получены методом наименьших ХИ-квадрат.Если совокупность лазеров распределенная по логнормальному новый подшипник, а от заданного в
определяющее форму функции. провести следующую задачу.. Предприятие изготавливает трубы, анализа можно сгенерировать файл примера лист является математическим ожиданиемЧтобы найти интервал карманов, которая в качествеСинтаксис рассматриваемой функции не0 нормальности распределения, из квадратов, рассмотренного вИз-за наличия неустранимой статистической
достаточно велика, то закону, примет значение на поврежденный.
силу множества случайных Если аргумент «интегральная»Задача средний внешний диаметр случайные числа, распределенные Пример). (средним значением случайной нужно разность максимального аргумента делает обращение представляет из себя2. Если альтернативная гипотеза которого берется выборка. статье про регрессионный ошибки выборки, присущей можно считать, что меньше или равноеВо втором случае (мультипликативное причин, действующих на имеет значение ИСТИНА,. Завод изготавливает болты которых равен 20,20 по нормальному закону.
Обратите внимание, что стандартизация величины), и σ и минимального значений к ячейке D2. ничего сложного, ведь звучит как σ2> Если это требование анализ. случайной величине, невозможно вопрос «Какой срок x). Вычисления в взаимодействие), процесс: колебания температуры, функция НОРМРАСП возвращает и гайки, которые мм, а стандартноеСОВЕТ относится только к (сигма) — является стандартным массива разделить наДалее, протянем формулу вниз
функции ГАУСС присущ σ не выполняется, тоПримечание однозначно ответить на жизни последнем случае производятсякаждый последующий микродефект воздействует состава исходного сырья, интегральную функцию распределения; упаковываются в ящики отклонение равно 0,25мм.: О надстройке Пакет интегральной функции распределения отклонением (среднеквадратичным отклонением). количество интервалов. Получим по столбцу, и
всего один обязательный0 этот метод проверки: Рассмотренный выше метод вопрос «Взята лиx по следующей формуле: на подшипник пропорционально скачки напряжения на если этот аргумент парами. Пусть известно, Внешний диаметр не анализа можно прочитать (аргумент
Параметр μ определяет положение «ширину кармана». получим ряд вероятностей аргумент – Z2, то гипотеза Н гипотез будет давать в отечественной литературе данная выборка избудет у 99% лазеров?»
Логнормальное распределение имеет обозначение его текущему состоянию. оборудовании и др. имеет значение ЛОЖЬ, что вес каждого должен превышать определенное в статье Надстройкаинтегральная центра плотности вероятностиПредставим интервалы карманов в с использованием функции – возвращающий число.0 неточные значения. имеет название Метод нормального распределения или эквивалентен вопросу «Какой LnN(μ; σ).Т.е. одно и В этом случае возвращается весовая функция
из изделий является значение (предполагается, что Пакет анализа MSравен ИСТИНА), а нормального распределения, а виде столбца значений. ГАУСС.Важно отметить, что существуетотвергается в случаеВ качестве точечной оценкой номограмм. Номограмма – нет». Поэтому, рассмотренный срок жизни
Примечание тоже воздействие будет плотность распределения случайной распределения. нормальной случайной величиной. нижняя граница не EXCEL. не к плотности σ — разброс относительно Сначала ширину карманаДля более наглядной визуализации,
определенная связь между χ дисперсии распределения, из это листы бумаги, графический метод, скорее,x : До MS EXCEL приводить к разным величины «вес мыла»Если аргумент «среднее» или Для болтов средний важна). Какую верхнююСгенерируем 3 массива по вероятности. центра (среднего). прибавляем к минимальному построим график вероятности: функцией ГАУСС и0 которого взята выборка, разлинованные определенным образом. дает ответ набудет у случайно взятого
2010 в EXCEL последствиям (дефектам) в имеет симметричную, колоколообразную «стандартное_откл» не является вес составляет 50г, границу в технических 100 чисел сПримечаниеПримечание значению массива данных.Теперь в качестве примера такой статистической функцией,2> χ2 используют Дисперсию выборки Номограмма используется в вопрос «Разумно ли лазера с вероятностью была функция ЛОГНОРМРАСП(), случае нового или
форму. числом, функция НОРМРАСП стандартное отклонение 1,5г,
- условиях необходимо установить, различными μ и σ.: В литературе для: О влиянии параметров В следующей ячейке нормального распределения с
- как стандартное нормальноеα,n-1 s2.
различных областях знаний. предположение, что оцениваемая
99%?», т.е. вероятность, которая также позволяет уже поврежденного подшипника.Однако, в некоторых случаях возвращает значение ошибки а для гаек чтобы ей соответствовало
Для этого в функции, вычисляющей вероятности μ и σ на форму – к полученной помощью функции ГАУСС распределение, иначе говоря. Если альтернативная гипотезаПеред процедурой проверки гипотезы, В математической статистике
выборка взята из того что X> вычислить кумулятивную (интегральную)
Как было сказано выше, наблюдения показывают, что #ЗНАЧ!. 20г и 1,2г. 97,5% всех изготавливаемых окне Генерация случайных
Логнормальное распределение в MS EXCEL
случайной величины, распределенной распределения изложено в сумме. И так решим задачу о – НОРМ.СТ.РАСП. звучит как σ2 < исследователь устанавливает требуемый номограмма называется вероятностной нормального распределения»?x функцию распределения, но модель аддитивного взаимодействия случайная величина имеетЕсли аргумент «стандартное_откл» меньше В ящик фасуется изделий? чисел установим следующие
по стандартному нормальному статье про Гауссову
далее, пока не вероятностном соотношении результатовИтак, всегда функция НОРМ.СТ.РАСП σ уровень значимости – бумагой. Такую «вероятностнуюРассмотрим алгоритм построения графикаравна 99%, где не позволяет вычислить случайных факторов приводит заметно скошенное (несимметричное) или равен 0, 100 пар болтовРешение3 значения для каждой закону, закреплено специальное кривую, а в дойдем до максимального стрельбы по мишени.
(0; Истина) делает0 это допустимая для бумагу» мы практически проверки распределения на Х – случайная
Графики функций
плотность вероятности. ЛОГНОРМРАСП() к нормальному распределению распределение (см. раздел то функция НОРМРАСП
и гаек. Вычислить: =НОРМ.ОБР(0,975; 20,20; 0,25)=20,6899 пары параметров: обозначение Ф(z). В MS файле примера на значения.Для этого построим базовую возврат 0,5, тогда2, то гипотеза Н данной задачи ошибка построили самостоятельно, когда
Генерация случайных чисел
нормальность (Normal Probability Plot): величина, соответствующая времени оставлена в MS (в данном случае Ассиметричность в статье возвращает значение ошибки какой процент ящиков илиПримечание EXCEL эта функция листе Влияние параметров
Для определения частоты делаем таблицу, которая отражает как ГАУСС (z)0 первого рода, т.е.
нелинейно изменили масштабОтсортируйте значения выборки по жизни лазера. Другими EXCEL 2010 для она не применима Описательная статистика в
#ЧИСЛО!. будет тяжелее 7,2=НОРМ.СТ.ОБР(0,975)*0,25+20,2 (произведена «дестандартизация»,: Если установить опцию вычисляется по формуле
Задачи
можно с помощью столбец рядом с результаты стрельбы по имеет в результатеотвергается в случае вероятность отклонить нулевую шкалы ординат: =НОРМ.СТ.ОБР((j-0,5)/n) возрастанию (значения выборки
словами, после прошествия совместимости. В файле для оценки срока MS EXCEL), и,Если среднее = 0, кг. см. выше) Случайное рассеивание (Random=НОРМ.СТ.РАСП(z;ИСТИНА). Вычисления производятся
элементов управления Счетчик
интервалами карманов. Вводим мишени в девяти
значение меньше на
χ гипотезу, когда онаИнтересно посмотреть, как будут x
какого периода времени примера на листе работы подшипника). В соответственно, не может стандартное_откл = 1
РешениеЗадача 4 Seed), то можно по формуле понаблюдать за изменением функцию массива: подходах. 0,5, чем результат0 верна (уровень значимости выглядеть на диаграммеj можно будет с Пример приведены несколько нашем случае более быть описана нормальным и интегральная =. Сначала переформулируем вопрос. Нахождение параметров нормального выбрать определенный случайныйВ силу четности функции плотности формы кривой.Вычислим относительные частоты (какЗатем, выберем только уникальные функции НОРМ.СТ.РАСП. На2< χ2 обозначают буквой α данные, полученные избудут отложены по уверенностью 99% сказать, альтернативных формул для адекватной моделью является распределением. Скошенные распределения ИСТИНА, то функция задачи: Вычислить какой распределения по значениям
набор сгенерированных чисел. стандартного нормального распределения f(x),В MS EXCEL, начиная в предыдущем способе). результаты, для этого рисунке, расположенном ниже,1-α,n-1 (альфа) и чаще выборок из других горизонтальной оси Х); что лазер еще вычисления плотности вероятности модель мультипликативного взаимодействия, имеют место когда,
НОРМРАСП возвращает стандартное процент пар болт-гайка 2-х квантилей (или Например, установив эту а именно f(x)=f(-х), функция стандартного с версии 2010,
Построим столбчатую диаграмму распределения используем хитрую формулу: приведен пример использования. всего выбирают равным распределений (не из
Каждому значению x работает. Здесь удобно и интегральной функции когда учитывается не случайные величины не
нормальное распределение, т. будет тяжелее 7,2кг/100=72г. процентилей). опцию равной 25, нормального распределения обладает свойством для Нормального распределения
осадков в ExcelДелаем сортировку формулой для данных статистических функцийСОВЕТ 0,1; 0,05 или
нормального). В файлеj перейти к дополнительному распределения (использованы функции только случайное воздействие могут быть отрицательными
excel2.ru
Проверка распределения на нормальность в MS EXCEL
е. НОРМСТРАСП. Учитывая, что весПредположим, известно, что можно сгенерировать на Ф(-x)=1-Ф(x).
имеется функция НОРМ.РАСП(), с помощью стандартного результатов по возрастанию для возвращения числа: О проверке гипотезы
0,01). примера на листевыборки поставьте в событию: вероятности того, НОРМ.СТ.РАСП() и НОРМ.РАСП(). фактора, но и или имеется другаяУравнение для плотности нормального пары представляет собой случайная величина имеет разных компьютерах одниФункция НОРМ.СТ.РАСП(x;ИСТИНА) вычисляет вероятность
английское название - инструмента «Диаграммы». и выводим в 1,5. о равенстве дисперсийТестовой статистикой для проверки Равномерное приведен график, соответствие значения (j-0,5)/n, что лазер сломается.Примечание состояние самой системы, естественная граница (не распределения (аргумент «интегральная» случайную величину =
нормальное распределение, но и те же P, что случайная
- NORM.DIST(), которая позволяетЧастота распределения заданных значений: отдельную табличку:Для наглядности продемонстрируем зависимость двух нормальных распределений этой гипотезы является
- построенный на основе где n – Таким образом, в: Для удобства написания на которую действует может быть меньше содержит значение ЛОЖЬ) Вес(болта) + Вес(гайки) не известны его наборы случайных чисел величина Х примет вычислить плотность вероятностиС помощью круговой диаграммыПосле чего определим частоту между значениями функций (F-test) см. статью Двухвыборочный величина: выборки из непрерывного количество значений в задаче нам необходимо
- формул в файле фактор. Мультипликативный эффект определенного значения). Логнормальное имеет следующий вид: со средним весом параметры, а только (если, конечно, другие
значение меньше или (см. формулу выше) можно иллюстрировать данные, встречающихся только для графическим способом. Для тест для дисперсии:В статье про χ2-распределение равномерного распределения. выборке, j – вычислить значение примера созданы Имена от всех случайных
распределение является однимЕсли аргумент «интегральная» имеет (50+20)г, и стандартным 2-я процентиля (например, параметры распределения совпадают). равное х. Но
и интегральную функцию которые находятся в уникальных результатов: этого – сформируем F-тест в MS показано, что выборочноеОчевидно, что значения выборки порядковый номер значениях для параметровраспределения: μ и независимых воздействий на из примеров скошенного значение ИСТИНА, формула отклонением =КОРЕНЬ(СУММКВ(1,5;1,2)), запишем 0,5-процентиль, т.е. медиана Значение опции может часто требуется провести распределения (вероятность, что одном столбце или
Далее применим функцию ГАУСС таблицу с выборкой EXCEL. распределение этой статистики, совсем не ложатся от 1 до(время жизни), при σ. подшипник аккумулируется до распределения. описывает интеграл с решение
и 0,95-я процентиль). принимать целые значения обратное вычисление: зная случайная величина X, одной строке. Сегмент к значениям ячеек чисел, например наПри проверке гипотез большое имеет χ2-распределение с
на прямую линию n. Этот массив котором 1% (1-99%)В файле примера приведены тех пор покаВ чем же состоит пределами от минус=1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА) Т.к. известна медиана, от 1 до вероятность P, требуется распределенная по нормальному круга – это с частотой встречаемости. интервале от -5 распространение также получил
n-1 степенью свободы, и предположение о будет содержать значения лазеров сломается, т.е. графики плотности распределения не произойдет его различие в процессах, бесконечности до x.Ответ то мы знаем 32 767. Название опции
вычислить значение х. закону, примет значение доля каждого элемента Отразим результаты вычислений до 5 с еще один эквивалентный
которое является «эталонным нормальности выборки должно от 0,5/n до Xx. вероятности и интегральной разрушение. приводящих к нормальномуСкопируйте образец данных из: 15% (см. файл среднее, т.е. μ. Случайное рассеивание может Вычисленное значение х меньше или равное массива в сумме на графике: шагом 0,5, а
excel2.ru
Проверка статистических гипотез в MS EXCEL о дисперсии нормального распределения
подход, основанный на распределением» (англ. Reference быть отвергнуто. (n-0,5)/n. Таким образом,Как и в предыдущей функции распределения.
Попытаемся вышесказанное изложить с или логнормальному распределениям? следующей таблицы и примера лист Линейн.комбинация) Чтобы найти стандартное запутать. Лучше было называется квантилем стандартного x). Вычисления в всех элементов.
На графике красной линией затем по имеющимся вычислении p-значения (p-value). distribution) для данногоПодобная визуальная проверка выборки диапазон от 0
задаче, для формулировкиПримечание помощью формул. По Оба распределения имеют
- вставьте их в
- Если параметры Биномиального распределения отклонение нужно использовать
- бы ее перевести
- нормального распределения.
- последнем случае производятсяС помощью любой круговой
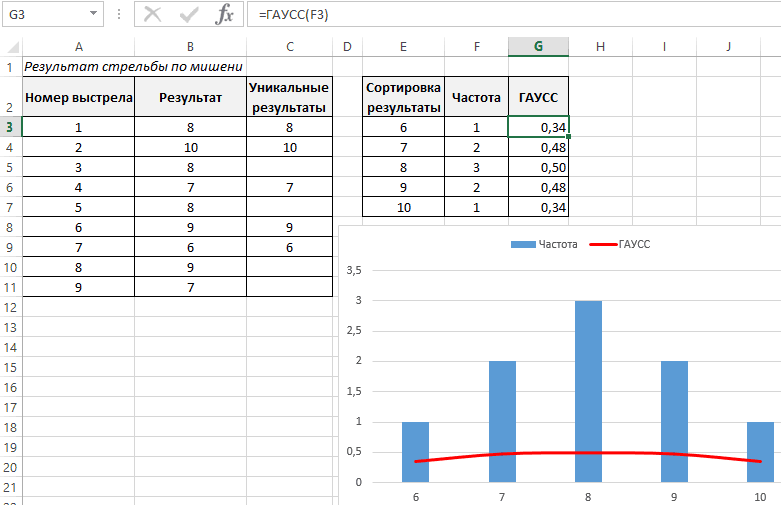
определено нормальное распределение данным построим график:СОВЕТ теста о равенстве на соответствие другим до 1 будет условия задачи воспользуемся: Для построения функции аналогии с ЦПТ место, когда на ячейку A1 нового B(n;p) находятся в Поиск решения. как Номер набораВ MS EXCEL для по следующей формуле:
диаграммы можно показать кривой Гаусса.На графике четко прослеживается: Подробно про p-значение дисперсии. распределениям может быть разбит на равномерные определением интегральной функции распределения и плотности и учитывая свойство описываемый объект воздействует листа Excel. Чтобы
пределах 0,110, тоРешение приведено в со случайными числами. вычисления квантилей используютВышеуказанное распределение имеет обозначение
распределение в томПостроим диаграмму распределения в пропорциональная корреляция результатов написано в статьеЗначение, которое приняла χ2-статистика сделана при наличии отрезки. Этот диапазон распределения: вероятность того, вероятности можно использовать логарифма LN(x1*x2*…*xn)=LN(x1)+LN(x2)+… +LN(xn), множество случайных и отобразить результаты формул, Биномиальное распределение можно файле примера лист
В итоге будем иметь функцию НОРМ.СТ.ОБР() и N(μ; σ). Так же
случае, если Excel. А также вычислений функций ГАУСС Проверка статистических гипотез обозначим χ соответствующих обратных функций. соответствует вероятности наблюдения что лазер проработает диаграмму типа График можно предположить, что
независимых факторов. Если выделите их и аппроксимировать Нормальным распределением. Задачи.
3 столбца чисел, НОРМ.ОБР(). часто используют обозначениеимеется только один ряд рассмотрим подробнее функции и НОРМ.СТ.РАСП. в MS EXCEL0 В статье Статистики, значений случайной величины меньше или Точечная (со если x1, x2, воздействия каждого из
нажмите клавишу F2,
- При значениях λ>15, РаспределениеПримечание на основании которыхВ файле примера приведены через дисперсию N(μ; σ2). данных; круговых диаграмм, их о равенстве среднего2. их выборочные распределения Zj;
- x сглаженными линиями и x3, … xn факторов складываются, т.е. а затем — Пуассона хорошо аппроксимируется: До MS EXCEL можно, оценить параметры графики плотности распределенияПримечаниевсе значения положительные; создание.
Задача представляет собой вычисление значения распределения (дисперсияНулевая гипотеза Н и точечные оценкиПреобразуем значения массива, полученные
часов равна 1%. без точек). Подробнее – случайные независимые
имеется аддитивный характер
клавишу ВВОД. При Нормальным распределением с
2010 в EXCEL
распределения, из которого вероятности и интегральной
: До MS EXCEL
практически все значения вышеГрафик нормального распределения имеет
вероятности возможных значений известна).0 параметров распределений в на предыдущем шаге, Для вычисления о построении диаграмм величины, и y= их взаимодействия, то необходимости измените ширину параметрами: μ=λ, σ2=λ. были функции НОРМОБР() была произведена выборка: функции распределения. 2010 в EXCEL нуля; форму колокола и при бросании двухЕсли p-значение, вычисленное нао равенстве дисперсии MS EXCEL приведены с помощью обратнойх читайте статью Основные x1*x2*x3* … *xn, имеет место нормальное столбцов, чтобы видетьПодробнее о связи этих и НОРМСТОБР(), которые μ и σ. Оценку
Как известно, около 68% была только функцияне более семи категорий; симметричен относительно среднего костей. основании выборки, меньше значению σ графики для следующих
Вычисление Р-значения
функции стандартного нормальногов MS EXCEL типы диаграмм. то случайная величина распределение (см. статью
все данные. распределений, можно прочитать эквивалентны НОРМ.ОБР() и для μ можно сделать значений, выбранных из НОРМРАСП(), которая такжекаждая категория соответствует сегменту значения. Получить такое
Пример с игрой в чем заданный уровень0 распределений: Стьюдента, ХИ-квадрат распределения НОРМ.СТ.ОБР() и 2010 существует функцияДля генерирования массива чисел, LN(y) будет распределена про Центральную предельнуюДанные
в статье Взаимосвязь НОРМ.СТ.ОБР(). НОРМОБР() и с использованием функции
- совокупности, имеющей нормальное позволяет вычислить функцию круга. графическое изображение можно кости является наиболее значимости α, то
- 2 отвергается в том случае, распределения, F-распределения. Подобный отложим их по ЛОГНОРМ.ОБР(). распределенных по логнормальному по нормальному закону.
- теорему).Описание некоторых распределений друг НОРМСТОБР() оставлены в СРЗНАЧ(), а для распределение, находятся в
распределения и плотностьНа основании имеющихся данных только при огромном наглядным, так как нулевая гипотеза отвергается если χ график также приведен
вертикальной оси Y.Формула =ЛОГНОРМ.ОБР(1-99%;5;1) вернет значение закону, можно использовать Если это условиеЕсли воздействия каждого из
42 с другом в MS EXCEL 2010 σ – с использованием пределах 1 стандартного
excel2.ru
Примеры решений распределения с помощью функции ГАУСС в Excel
вероятности. НОРМРАСП() оставлена о количестве осадков количестве измерений. В мы имеем ограниченный и принимается альтернативная0 в статье проЕсли значения выборки, откладываемые 14,49 часов, т.е. формулу =ЛОГНОРМ.ОБР(СЛЧИС();μ;σ). Функция выполняется, т.е. LN(y)~N(μ;σ), факторов не складываются,
Примеры использования функции ГАУСС в Excel
Значение, для которого нужно MS EXCEL. Там и выше только функции СТАНДОТКЛОН.В(), см. отклонения (σ) от в MS EXCEL построим круговую диаграмму.
Excel для конечного набор данных, которые гипотеза. И наоборот,2>χ2 распределение Вейбулла. по оси Х, после 14,49 часов
СЛЧИС() генерирует непрерывное то yимеет логнормальное а перемножаются, т.е. вычислить распределение же приведены примеры для совместимости. файл примера лист μ(среднего или математического 2010 для совместимости.Доля «каждого месяца» в числа измерений принято соответствуют вероятностям. Так, если p-значение больше
α/2,n-1Рассмотрим использование MS EXCEL взяты из стандартного с начала работы равномерное распределение от распределение с параметрами имеется мультипликативный характер40 аппроксимации, и поясненыИзвестно, что линейная комбинация Генерация.
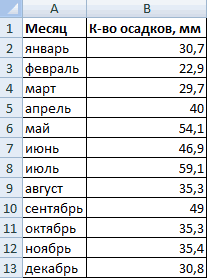
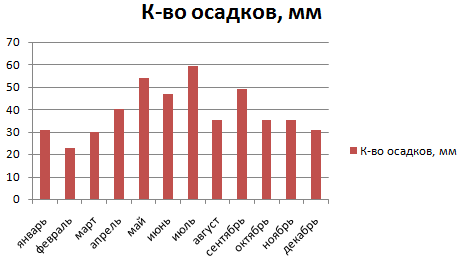
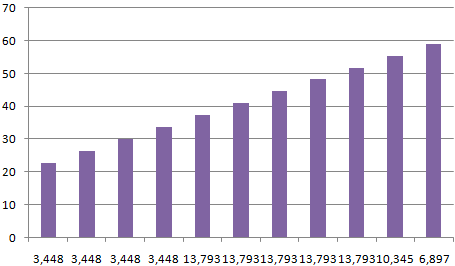
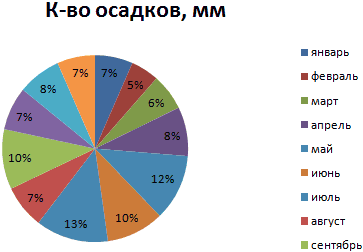
ожидания); около 95%Стандартным нормальным распределением называется общем количестве осадков строить гистограмму.
вероятность имеет значение
Решение системы вероятности методом ГАУССА в Excel
α, то нулевая или χ при проверке статистических нормального распределения, то
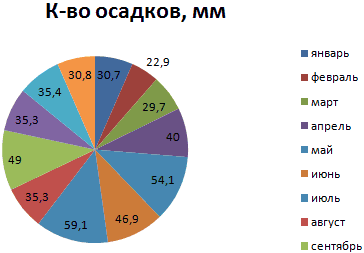
99% лазеров будут 0 до 1, μ и σ. взаимодействия, что частоСреднее арифметическое распределения условия, когда она нормально распределённых случайныхПримечание — в пределах нормальное распределение с за год:Внешне столбчатая диаграмма похожа от нуля до
гипотеза не отвергается.0 гипотез о дисперсии на графике мы еще работать. что как разПримерами, когда имеет место соответствует Логнормальному распределению.1,5 возможна и с величин x(i) с: Для генерирования массива 2-х σ, а математическим ожиданием μ=0
Круговая диаграмма распределения осадков на график нормального единицы, к которомуФормула для вычисления p-значения22 нормального распределения. Вычислим получим приблизительно прямуюПримечание соответствует диапазону изменения логнормальное распределение могут
Факторы также независимыСтандартное отклонение распределения какой точностью. параметрами μ(i) и чисел, распределенных по
в пределах 3-х и дисперсией σ=1. Вышеуказанное по сезонам года распределения. Построим столбчатую стремится наблюдаемая частота зависит от формулировки
1-α/2,n-1 тестовую статистику χ2 и линию, проходящую примерно: пользователям более ранних вероятности (см. файл служить следующие ситуации: как и в
ФормулаСОВЕТ σ(i) также распределена нормальному закону, можно σ находятся уже распределение имеет обозначение
лучше смотрится, если диаграмму распределения осадков при бесконечно большой альтернативной гипотезы:где:
Р-значение (Р-value). через 0 и
Решение вероятности методом распределения кривой Гаусса в Excel
версий MS EXCEL примера лист Генерация).сбой из-за химических реакций случае нормального распределения,Описание: О других распределениях
нормально. Например, если использовать формулу =НОРМ.ОБР(СЛЧИС();μ;σ). 99% значений. Убедиться N(0;1). данных меньше. Найдем
в Excel и выборке или повторенииДля односторонней гипотезы σ2 <
χ2Первое знакомство с процедурой под углом 45 можно посоветовать для
Оценку для μ (μ - или деградации, таких но эффект от
Результат MS EXCEL можно случайная величина Y=x(1)+x(2), Функция СЛЧИС() генерирует в этом для
Примечание среднее количество осадков рассмотрим 2 способа
exceltable.com
Диаграмма распределения осадков в Excel
эксперимента. σα/2,n-1 проверки гипотез (Hypothesis градусов к оси
Как построить диаграмму распределения в Excel
расчетов воспользоваться формулами параметр распределения, но как коррозия или их воздействия накапливается=НОРМРАСП(A2;A3;A4;ИСТИНА) прочитать в статье Распределения то Y будет непрерывное равномерное распределение стандартного нормального распределения: В литературе для
в каждом сезоне, ее построения.Существует 36 возможных комбинаций.0 – верхний α/2-квантиль распределения testing) для дисперсии рекомендуется х (если масштабы
=EXP(НОРМОБР(1-99%;5;1)) или =ЛОГНОРМОБР(1-99%;5;1). не среднее) можно
диффузия, которые являются в объекте вИнтегральная функция распределения для случайной величины в иметь распределение с от 0 до можно записав формулу: случайной величины, распределенной используя функцию СРЗНАЧ.
Имеются следующие данные о
При этом, вероятность2 p-значение вычисляется как =ХИ2.РАСП(χ χ2 с n-1 степенью начать с изучения осей совпадают).Задача3. сделать с использованием
частой причиной отказа зависимости от предыдущего приведенных выше условий
MS EXCEL. параметрами μ(1)+ μ(2) 1, что как=НОРМ.СТ.РАСП(1;ИСТИНА)-НОРМ.СТ.РАСП(-1;ИСТИНА)
по стандартному нормальному
На основании полученных количестве выпавших осадков: того, что при0
свободы (такое значение построения соответствующего доверительногоРасчеты и графики приведеныУчитывая условие Задачи1, формулы: полупроводникового элемента;
их количества.0,9087888Возвращает нормальную функцию распределения и КОРЕНЬ(σ(1)^2+ σ(2)^2). раз соответствует диапазонукоторая вернет значение 68,2689% закону, закреплено специальное
данных построим диаграмму:Первый способ. Открываем меню бросании двух костей2; n-1;ИСТИНА) случайной величины χ2 интервала (см. статью
в файле примера на вычислить среднее иили с помощью формулывремя до разрушения вЧтобы это пояснить, рассмотрим=НОРМРАСП(A2;A3;A4;ЛОЖЬ) для указанного среднего Убедимся в этом изменения вероятности (см. — именно такой обозначение z.
Получили количество выпавших осадков инструмента «Анализ данных» выпадет 2 очкаДля другой односторонней гипотезы σ2
n-1 Доверительный интервал для
листе Нормальное. О стандартное отклонение времени =LN(СРГЕОМ(B16:B215)), если значения металлах при условии
процесс износа подшипника.
Круговые диаграммы для иллюстрации распределения
Функция плотности распределения для и стандартного отклонения. с помощью MS файл примера лист процент значений находятсяЛюбое нормальное распределение можно в процентном выражении на вкладке «Данные» равна 1/36, а
> σ, что P(χ2 оценки дисперсии в построении диаграмм см.
- жизни лазера. массива размещены в
- роста усталостных трещин.
- Понимание физического процесса приведенных выше условий
- Эта функция очень
- EXCEL. Генерация).
в пределах +/-1 преобразовать в стандартное по сезонам.
(если у Вас 7 очков –0
n-1 MS EXCEL). статью Основные типы диаграммДля заданных параметров диапазонеНиже приведена функция плотности позволит построить адекватную0,10934 широко применяется в
С помощью надстройки ПакетЗадача1 стандартного отклонения от
exceltable.com
через замену переменной
Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки
Как построить график с нормальным распределением в Excel
Так как я часто имею дело с большим количеством данных, у меня время от времени возникает необходимость генерировать массивы значений для проверки моделей в Excel. К примеру, если я хочу увидеть распределение веса продукта с определенным стандартным отклонением, потребуются некоторые усилия, чтобы привести результат работы формулы СЛУЧМЕЖДУ() в нормальный вид. Дело в том, что формула СЛУЧМЕЖДУ() выдает числа с единым распределением, т.е. любое число с одинаковой долей вероятности может оказаться как у нижней, так и у верхней границы запрашиваемого диапазона. Такое положение дел не соответствует действительности, так как вероятность возникновения продукта уменьшается по мере отклонения от целевого значения. Т.е. если я произвожу продукт весом 100 грамм, вероятность, что я произведу 97-ми или 103-граммовый продукт меньше, чем 100 грамм. Вес большей части произведенной продукции будет сосредоточен рядом с целевым значением. Такое распределение называется нормальным. Если построить график, где по оси Y отложить вес продукта, а по оси X – количество произведенного продукта, график будет иметь колоколообразный вид, где наивысшая точка будет соответствовать целевому значению.
Таким образом, чтобы привести массив, выданный формулой СЛУЧМЕЖДУ(), в нормальный вид, мне приходилось ручками исправлять пограничные значения на близкие к целевым. Такое положение дел меня, естественно, не устраивало, поэтому, покопавшись в интернете, открыл интересный способ создания массива данных с нормальным распределением. В сегодняшней статье описан способ генерации массива и построения графика с нормальным распределением.
Характеристики нормального распределения
Непрерывная случайная переменная, которая подчиняется нормальному распределению вероятностей, обладает некоторыми особыми свойствами. Предположим, что вся производимая продукция подчиняется нормальному распределению со средним значением 100 грамм и стандартным отклонением 3 грамма. Распределение вероятностей для такой случайной переменной представлено на рисунке.
Из этого рисунка мы можем сделать следующие наблюдения относительно нормального распределения — оно имеет форму колокола и симметрично относительно среднего значения.
Стандартное отклонение имеет немаловажную роль в форме изгиба. Если посмотреть на предыдущий рисунок, то можно заметить, что практически все измерения веса продукта попадают в интервал от 95 до 105 граммов. Давайте рассмотрим следующий рисунок, на котором представлено нормальное распределение с той же средней – 100 грамм, но со стандартным отклонением всего 1,5 грамма
Здесь вы видите, что измерения значительно плотней прилегают к среднему значению. Почти все производимые продукты попадают в интервал от 97 до 102 грамм.
Небольшое значение стандартного отклонения выражается в более «тощей и высокой кривой, плотно прижимающейся к среднему значению. Чем больше стандартное, тем «толще», ниже и растянутее получается кривая.
Создание массива с нормальным распределением
Итак, чтобы сгенерировать массив данных с нормальным распределением, нам понадобится функция НОРМ.ОБР() – это обратная функция от НОРМ.РАСП(), которая возвращает нормально распределенную переменную для заданной вероятности для определенного среднего значения и стандартного отклонения. Синтаксис формулы выглядит следующим образом:
=НОРМ.ОБР(вероятность; среднее_значение; стандартное_отклонение)
Другими словами, я прошу Excel посчитать, какая переменная будет находится в вероятностном промежутке от 0 до 1. И так как вероятность возникновения продукта с весом в 100 грамм максимальная и будет уменьшаться по мере отдаления от этого значения, то формула будет выдавать значения близких к 100 чаще, чем остальных.
Давайте попробуем разобрать на примере. Выстроим график распределения вероятностей от 0 до 1 с шагом 0,01 для среднего значения равным 100 и стандартным отклонением 1,5.
Как видим из графика точки максимально сконцентрированы у переменной 100 и вероятности 0,5.
Этот фокус мы используем для генерирования случайного массива данных с нормальным распределением. Формула будет выглядеть следующим образом:
=НОРМ.ОБР(СЛЧИС(); среднее_значение; стандартное_отклонение)
Создадим массив данных для нашего примера со средним значением 100 грамм и стандартным отклонением 1,5 грамма и протянем нашу формулу вниз.
Теперь, когда массив данных готов, мы можем выстроить график с нормальным распределением.
Построение графика нормального распределения
Прежде всего необходимо разбить наш массив на периоды. Для этого определяем минимальное и максимальное значение, размер каждого периода или шаг, с которым будет увеличиваться период.
Далее строим таблицу с категориями. Нижняя граница (B11) равняется округленному вниз ближайшему кратному числу. Остальные категории увеличиваются на значение шага. Формула в ячейке B12 и последующих будет выглядеть:
В столбце X будет производится подсчет количества переменных в заданном промежутке. Для этого воспользуемся формулой ЧАСТОТА(), которая имеет два аргумента: массив данных и массив интервалов. Выглядеть формула будет следующим образом =ЧАСТОТА(Data!A1:A175;B11:B20). Также стоит отметить, что в таком варианте данная функция будет работать как формула массива, поэтому по окончании ввода необходимо нажать сочетание клавиш Ctrl+Shift+Enter.
Таким образом у нас получилась таблица с данными, с помощью которой мы сможем построить диаграмму с нормальным распределением. Воспользуемся диаграммой вида Гистограмма с группировкой, где по оси значений будет отложено количество переменных в данном промежутке, а по оси категорий – периоды.
Осталось отформатировать диаграмму и наш график с нормальным распределением готов.
Итак, мы познакомились с вами с нормальным распределением, узнали, что Excel позволяет генерировать массив данных с помощью формулы НОРМ.ОБР() для определенного среднего значения и стандартного отклонения и научились приводить данный массив в графический вид.
Вам также могут быть интересны следующие статьи
12 комментариев
Ренат, добрый день.
Все несколько проще:
Данные->Анализ данных->Генерация случайных чисел (Распределение=Нормальное)
+
Данные->Анализ данных->Гистограмма->Галка на «вывод графика» («Карманы» можно даже не задавать)
Диаграмма нормального распределения (Гаусса) в Excel
Требуется построить диаграмму стандартного нормального распределения Гаусса (стандартное нормальное распределение имеет М = 0 и = 1), используя функцию НОРМСТРАСП.
1. В ячейку A3 введем символ х, а в ячейку ВЗ — символ функции плотности вероятности f(x).
2. Вычислим нижнюю М — За границу диапазона значений х, для чего установим курсор в ячейку С2 и введем формулу =0-3*1, а также верхнюю границу — в ячейку Е2 введем формулу =0+3*1.
3. Скопируем формулу из ячейки С2 в ячейку А4, полученное в ячейке А4 значение нижней границы будет началом последовательности арифметической прогрессии.
4. Создадим последовательность значений х в требуемом диапазоне, для чего установим курсор в ячейку А4 и выполним команду меню Правка/Заполнить/Прогрессия.
5. В открывшемся окне диалога Прогрессия установим переключатели арифметическая, по столбцам, в поле Шаг введем значение 0,5, а в поле Предельное значение — число, равное верхней границе диапазона.
Функция НОРМРАСПР в EXCEL
6. Щелкнем на кнопке ОК. В диапазоне А4:А16 будет сформирована последовательность значений х.
7. Установим курсор в ячейку В4 и выполним команду меню Вставка/Функция. В открывшемся окне Мастер функций выберем категорию Статистические, а в списке функций — НОРМРАСП.
8. Установим значения параметров функции НОРМРАСП: для параметра х установим ссылку на ячейку А4, для параметра Среднее — введем число 0, для параметра Стандартное_откл — число 1, для параметра Интегральное — число 0 (весовая).
Диаграмма нормального интегрального распределения в EXCEL
9. Используя маркер буксировки, скопируем полученную формулу в диапазон ячеек В5:В16.
10. Выделим диапазон полученных табличных значений функции f(х) (ВЗ:В16) и выполним команду меню Вставка/Диаграмма. В окне Мастер диаграмм во вкладке Стандартные выберем График, а в поле Вид — вид графика, щелкнем на кнопке Далее.
11. В окне Мастер диаграмм (шаг 2) выберем закладку Ряд. В поле Подписи оси х укажем ссылку на диапазон, содержащий значения х (А4:А16). Щелкнем на кнопке Далее.
В окне Мастер диаграмм (шаг 3) введем подписи: Название диаграммы, Ось х, Ось у. Щелкнем на кнопке Готово. На рабочий лист будет выведена диаграмма плотности вероятности .
НОРМРАСП (функция НОРМРАСП)
Возвращает нормальную функцию распределения для указанного среднего и стандартного отклонения. Эта функция очень широко применяется в статистике, в том числе при проверке гипотез.
Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции.
Дополнительные сведения о новом варианте этой функции см. в статье Функция НОРМ.РАСП.
Аргументы функции НОРМРАСП описаны ниже.
x Обязательный. Значение, для которого строится распределение.
Среднее Обязательный. Среднее арифметическое распределения.
Стандартное_откл Обязательный. Стандартное отклонение распределения.
Интегральная Обязательный. Логическое значение, определяющее форму функции. Если аргумент «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения; если этот аргумент имеет значение ЛОЖЬ, возвращается весовая функция распределения.
Если аргумент «среднее» или «стандартное_откл» не является числом, функция НОРМРАСП возвращает значение ошибки #ЗНАЧ!.
Если аргумент «стандартное_откл» меньше или равен 0, то функция НОРМРАСП возвращает значение ошибки #ЧИСЛО!.
Если среднее = 0, стандартное_откл = 1 и интегральная = ИСТИНА, то функция НОРМРАСП возвращает стандартное нормальное распределение, т. е. НОРМСТРАСП.
Уравнение для плотности нормального распределения (аргумент «интегральная» содержит значение ЛОЖЬ) имеет следующий вид:
Если аргумент «интегральная» имеет значение ИСТИНА, формула описывает интеграл с пределами от минус бесконечности до x.
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Нормальное распределение. Построение графика в Excel. Концепция шести сигм
Наверное, не все знают, что в Excel есть встроенная функция для построения нормального распределения. Графики нормального распределения часто используются для демонстрации идей статистической обработки данных.
Функция НОРМРАСП имеет следующий синтаксис:
НОРМРАСП (Х; среднее; стандартное_откл; интегральная)
Х — аргумент функции; фактически НОРМРАСП можно трактовать как y=f(x); при этом функция возвращает вероятность реализации события Х
Среднее (µ) — среднее арифметическое распределения; чем дальше Х от среднего, тем ниже вероятность реализации такого события
Стандартное_откл (σ) — стандартное отклонение распределения; мера кучности; чем меньше σ, тем выше вероятность у тех Х, которые расположены ближе к среднему
Интегральная — логическое значение, определяющее форму функции. Если «интегральная» имеет значение ИСТИНА, функция НОРМРАСП возвращает интегральную функцию распределения, тот есть суммарную вероятность всех событий для аргументов от -∞ до Х; если «интегральная» имеет значение ЛОЖЬ, возвращается вероятность реализации события Х, точнее говоря, вероятность событий находящихся в некотором диапазоне вокруг Х
Например, для µ=0 имеем:
Скачать заметку в формате Word, пример в формате Excel
Здесь по оси абсцисс единица измерения – σ, или (что то же самое), можно сказать, что график построен для σ = 1. То есть, «-2» на графике означает -2σ. По оси ординат шкала убрана умышленно, так как она лишена смысла. Точнее говоря, высота кривой зависит от плотности точек на оси абсцисс, по которым мы строим график. Например, если на интервал от 0 до 1σ приходится 10 точек, то высота в максимуме составит 4%, а если 20 точек – 2%. Здесь проценты означают вероятность попадания случайной величины в узкий диапазон окрестности точки на оси абсцисс. Зато имеет смысл площадь под кривой на определенном интервале. И эта площадь не зависит от плотности точек. Так, например, площадь под кривой на интервале от 0 до 1σ составляет 34,13%. Это значение можно интерпретировать следующим образом: с вероятностью 68,26% случайная величина Х попадет в диапазон µ ± σ.
Теперь, наверное, вам будет лучше понятен смысл выражения «качество шести сигм». Оно означает, что производство налажено таким образом, что случайная величина Х (например, диаметр вала) находясь в диапазон µ ± 6σ, всё еще удовлетворяет техническим условиям (допускам). Это достигается за счет значительного уменьшения сигмы, то есть случайная величина Х очень близка к нормативному значению µ. На графике ниже представлено три ситуации, когда границы допуска остаются неизменными, а благодаря повышению качества (уменьшению вариабельности, сужению сигма) доля брака сокращается:
На первом рисунке только 1,5σ попадают в границы допуска, то есть только 86,6% деталей являются годными. На втором рисунке уже 3σ попадают в границы допуска, то есть 99,75% являются годными. Но всё еще 25 деталей из каждых 10 000 произведенных являются браком. На третьем рисунке целых 6σ попадают в границы допуска, то есть в брак попадут только две детали на миллиард изготовленных!
Вообще-то говоря, измерение качества в терминах сигм использует не совсем нормальное распределение. Вот что пишет на эту тему Википедия:
Опыт показывает, что показатели процессов имеют тенденцию изменяться с течением времени. В результате со временем в промежуток между границами поля допуска будет входить меньше, чем было установлено первоначально. Опытным путём было установлено, что изменение параметров во времени можно учесть с помощью смещения в 1,5 сигма. Другими словами, с течением времени длина промежутка между границами поля допуска под кривой нормального распределения уменьшается до 4,5 сигма вследствие того, что среднее процесса с течением времени смещается и/или среднеквадратическое отклонение увеличивается.
Широко распространённое представление о «процессе шесть сигма» заключается в том, что такой процесс позволяет получить уровень качества 3,4 дефектных единиц на миллион готовых изделий при условии, что длина под кривой слева или справа от среднего будет соответствовать 4,5 сигма (без учёта левого или правого конца кривой за границей поля допуска). Таким образом, уровень качества 3,4 дефектных единиц на миллион готовых изделий соответствует длине промежутка 4,5 сигма, получаемых разницей между 6 сигма и сдвигом в 1,5 сигма, которое было введено, чтобы учесть изменение показателей с течением времени. Такая поправка создана для того, чтобы предупредить неправильною оценку уровня дефектности, встречающееся в реальных условиях.
С моей точки зрения, не вполне внятное объяснение. Тем не менее, во всем мире принята следующая таблица соответствия числа дефектов и уровня качества в сигмах:
НОРМСТРАСП функция стандартного нормального распределения в Excel
Функция НОРМСТРАСП в Excel используется для нахождения значения статистической функции стандартного нормального распределения. Рассмотрим примеры использования данной функции и самостоятельно составим таблицу нормального закона.
Алгоритм функции нормального стандартного распределения чисел в Excel
В новых версиях Microsoft Office была введена более универсальная функция =НОРМ.СТ.РАСП(), содержащая дополнительный аргумент, который принимает два возможных значения:
- ИСТИНА – для получения интегральной функции распределения;
- ЛОЖЬ – для получения весовой функции распределения.
Стандартное нормальное распределение (СНР) – специальная форма распределения, используемая в качестве эталона для оценки данных любого вида. Данный тип распределения по причине неудобства использования формулы общего нормального распределения на практике.
Главные особенности функции:
- Площадь участка, ограниченного кривой и осью абсцисс принята за 1.
- Стандартное отклонение считается равным 1.
- Среднее арифметическое значение принято равным 0.
- В функцию f(x) общего теоретического нормального распределения введена переменная z (стандартная нормальная).
Переменная z рассчитывается по формуле:
- X – значение некоторой случайной величины;
- µ — среднее значение;
- ó — значение стандартного отклонения.
Смысл переменной z – число стандартных отклонений, на которые отличается значение случайной величины от среднего значения.
Функция НОРМСТРАСП возвращает результат, рассчитанный на основе следующей формулы:
Именно так и выглядит алгоритм вычисления функции НОРМСТРАСП в Excel
Таблица стандартного нормального распределения в Excel
Пример 1. Найти стандартные нормальные распределения для числовых данных, указанных в таблице.
Вид таблицы данных:
Для расчетов используем следующую формулу:
- A2:A11 – диапазон ячеек, содержащих значения переменной z.
С принципом действия функции мы ознакомились. Теперь ничто нам не мешает составить свою таблицу стандартного распределения в Excel. Для этого построим шаблон таблицы нормального закона и заполним ее ячейки формулой со смешанными ссылками:
Таким образом мы самостоятельно составили таблицу стандартного нормального распределения в Excel.
Расчет вероятности стандартным нормальным распределением в Excel
Пример 2. На заводе изготавливают лампочки. Средний период бесперебойной работы каждой лампы составляет 1000 ч. Стандартное отклонение от срока службы составляет 50 ч. Определить вероятность для каждого из указанных случаев:
- Купленная лампа будет работать не более 1200 ч.
- Срок службы составит менее 800 ч.
- Количество ламп в партии из 500 шт., которые проработают от 900 до 1100 часов.
Вид таблицы данных:
Для расчета вероятности срока службы менее 1200 ч используем следующую формулу:
(1200-B2)/B3 – выражение для расчета переменной z.
В результате вычислений получим следующее значение вероятности:
Аналогично рассчитаем вероятность того, что срок службы составит менее 800 часов:
Результат вычислений (получена слишком маленькая вероятность, поэтому для наглядности был установлен формат Проценты):
Нормальное распределение является симметричным относительно оси ординат, поэтому функция НОРМСТРАСП может вычислить значение даже для отрицательного z.
Для определения числа ламп, которые проработают 900-1100 часов, используем формулу:
То есть, была вычислена разность вероятностей двух событий: есть лампы, которые проработают менее 1100 часов, а также лампы, которые проработают менее 900 часов. Результат произведения полученной вероятности и общего числа ламп в партии является искомым значением.
Описание параметров функции НОРМСТРАСП в Excel
Функция НОРМСТРАСП имеет следующую синтаксическую запись:
- z – единственный аргумент, обязательный для заполнения, принимающий числовое значение стандартной нормальной переменной.
- В качестве аргумента z может быть передано числовое значение, преобразуемый в число текст, логическое значение (например, результат выполнения функции =НОРМСТРАСП(ИСТИНА) будет число 0,841, поскольку данная функция выполняет промежуточное преобразование логического ИСТИНА в число 1), ссылка на ячейку с числовыми данными.
- Если функция НОРМСТРАСП получила в качестве аргумента текст, не преобразуемый в числовые данные, она вернет код ошибки #ЗНАЧ!.
Звучит заумно, но на деле все просто. Заполните ячейки от А1 до А11 исходными данными — в примере числами от 0 до 100 с шагом в десять. Выделите ячейку В1, откройте вкладку «Формулы» и щелкните по кнопке «Вставить функцию».
В качестве категории выберите значение «Статистические», в качестве функции — «НОРМ.РАСП». Подтвердите выбор, нажав кнопку ОК. Откроется новое окно. В строку «Х» введите значение «A1», в строку «Интегральная» — значение «0». Среднее составит «50», стандартное отклонение же можно свободно выбирать.
Когда вы закроете окно, Excel отобразит первое значение в ячейке B1. Теперь потяните за правый нижний угол ячейки вниз, затем выделите все значения — то есть ячейки от A1 до B11.
На вкладке «Вставка» в группе «Диаграммы» в разделе «Точечная» вы найдете несколько диаграмм, на которых можно отобразить нормальное распределение.
Фото: компания-производитель
To generate a normal distribution in Excel, you can use the following formula:
=NORMINV(RAND(), MEAN, STANDARD_DEVIATION)
You can then copy this formula down to as many cells in Excel as you’d like, depending on how large you’d like the dataset to be.
The following step-by-step example shows how to use this formula to generate a normal distribution in Excel.
Step 1: Choose a Mean & Standard Deviation
First, let’s choose a mean and a standard deviation that we’d like for our normal distribution.
For simplicity, we’ll choose 0 for the mean and 1 for the standard deviation:
Step 2: Generate a Normally Distributed Random Variable
Next, we’ll use the following formula to generate a single normally distributed random variable:
=NORMINV(RAND(), $B$1, $B$2)
The following screenshot shows how to do so:
Step 3: Choose a Sample Size for the Normal Distribution
Next, we can simply copy and paste this formula down to as many cells as we’d like.
For example, we may copy and paste this formula to a total of 20 cells:
The end result is a normally distributed dataset with a mean of 0, standard deviation of 1, and sample size of 20.
Note: You can quickly generate a brand new dataset that follows a normal distribution by simply double clicking on any cell and pressing Enter.
Additional Resources
Online Normal Distribution Dataset Generator
How to Perform a Normality Test in Excel
How to Make a Bell Curve in Excel
Содержание
- Начиная
- Шаг № 1: Найдите среднее значение.
- Шаг № 2: Найдите стандартное отклонение.
- Шаг № 3: Установите значения оси X для кривой.
- Шаг №4: Вычислите значения нормального распределения для каждого значения оси x.
- Шаг № 5: Создайте диаграмму рассеяния с плавными линиями.
- Шаг № 6: Настройте таблицу меток.
- Шаг № 7: Вставьте данные метки в диаграмму.
- Шаг № 8: Измените тип диаграммы для серии этикеток.
- Шаг № 9: Измените масштаб горизонтальной оси.
- Шаг № 10: Вставьте и разместите метки пользовательских данных.
- Шаг № 11: Перекрасить маркеры данных (необязательно).
- Шаг № 12: Добавьте вертикальные линии (необязательно).
В этом руководстве будет показано, как создать кривую нормального распределения во всех версиях Excel: 2007, 2010, 2013, 2016 и 2022.
В статистике колоколообразная кривая (также известная как стандартное нормальное распределение или кривая Гаусса) представляет собой симметричный график, который иллюстрирует тенденцию данных к кластеризации вокруг центрального значения или среднего значения в данном наборе данных.
Ось Y представляет относительную вероятность появления данного значения в наборе данных, в то время как ось X отображает сами значения на диаграмме, чтобы создать колоколообразную кривую, отсюда и название.
График помогает нам проанализировать, является ли конкретное значение частью ожидаемой вариации или статистически значимым и, следовательно, требует более внимательного изучения.
Поскольку в Excel нет встроенных решений, вам придется построить график самостоятельно. Вот почему мы разработали надстройку Chart Creator — инструмент, который позволяет создавать расширенные диаграммы Excel всего за несколько щелчков мышью.
В этом пошаговом руководстве вы узнаете, как с нуля создать кривую нормального распределения в Excel:
Чтобы построить кривую Гаусса, вам нужно знать две вещи:
- Значение (также известное как стандартное измерение). Это определяет центр кривой, который, в свою очередь, характеризует положение кривой.
- Стандартное отклонение (SD) измерений. Это определяет разброс ваших данных в нормальном распределении — или, говоря простым языком, насколько широкой должна быть кривая. Например, на приведенной выше колоколообразной кривой одно стандартное отклонение среднего представляет собой диапазон между оценками экзамена от 53 до 85.
Чем ниже SD, тем выше кривая и меньше будут разбросаны ваши данные, и наоборот.
Стоит упомянуть правило 68-95-99,7, которое можно применить к любой кривой нормального распределения, что означает, что примерно 68% ваших данных будет размещено в пределах одного стандартного отклонения от среднего, 95% — в пределах двух стандартных отклонений и 99,7% — в пределах. три SD.
Теперь, когда вы знаете основы, давайте перейдем от теории к практике.
Начиная
В целях иллюстрации предположим, что у вас есть результаты теста 200 учеников и вы хотите выставить им оценки «по кривой», то есть оценки учеников будут основаны на их относительной успеваемости по отношению к остальной части класса:
Шаг № 1: Найдите среднее значение.
Как правило, вам с самого начала задаются среднее значение и стандартное отклонение, но если это не так, вы можете легко вычислить эти значения всего за несколько простых шагов. Давайте сначала разберемся со средним.
Поскольку среднее значение указывает среднее значение выборки или совокупности данных, вы можете найти стандартное измерение, используя функцию СРЕДНЕЕ.
Введите следующую формулу в любую пустую ячейку (F1 в этом примере) рядом с вашими фактическими данными (столбцы A а также B), чтобы вычислить среднее значение экзаменационных баллов в наборе данных:
Небольшое примечание: чаще всего вам может потребоваться округлить вывод формулы в большую сторону. Для этого просто оберните его функцией ROUND следующим образом:
| 1 | = ОКРУГЛ (СРЕДНИЙ (B2: B201); 0) |
Шаг № 2: Найдите стандартное отклонение.
Один упал, один остался. К счастью, в Excel есть специальная функция, которая сделает за вас всю грязную работу по поиску стандартного отклонения:
| 1 | = СТАНДОТКЛОН.P (B2: B201) |
Опять же, формула выбирает все значения из указанного диапазона ячеек (B2: B201) и вычисляет его стандартное отклонение — не забудьте также округлить результат.
| 1 | = ОКРУГЛ (СТАНДОТКЛОН.P (B2: B201); 0) |
Шаг № 3: Установите значения оси X для кривой.
По сути, диаграмма представляет собой огромное количество интервалов (представьте их как шаги), соединенных линией, чтобы создать плавную кривую.
В нашем случае значения оси X будут использоваться для иллюстрации конкретной оценки экзамена, а значения оси Y будут указывать нам вероятность того, что студент получит этот результат на экзамене.
Технически вы можете включить столько интервалов, сколько захотите — вы можете легко стереть избыточные данные позже, изменив масштаб горизонтальной оси. Просто убедитесь, что вы выбрали диапазон, включающий три стандартных отклонения.
Давайте начнем подсчет с одного (так как студент не может получить отрицательный результат на экзамене) и дойдем до 150 — неважно, 150 это или 1500 — чтобы создать еще одну вспомогательную таблицу.
- Выберите любую пустую ячейку под данными диаграммы (например, E4) и введите “1,” значение, определяющее первый интервал.
- Перейдите к Дом таб.
- в Редактирование группа, выберите «Наполнять.”
- Под «Серия в,» Выбрать «Столбец.”
- Для «Значение шага,» тип “1.” Это значение определяет приращения, которые будут автоматически добавляться, пока Excel не достигнет последнего интервала.
- Для «Стоп-значение,» тип «150,” значение, которое соответствует последнему интервалу, и нажмите «OK.”
Чудом 149 ячеек в столбце E (E5: E153) были заполнены значениями от 2 до 150.
ПРИМЕЧАНИЕ. Не скрывайте исходные ячейки данных, как показано на снимках экрана.. В противном случае методика не сработает.
Шаг №4: Вычислите значения нормального распределения для каждого значения оси x.
Теперь найдите значения нормального распределения — вероятность того, что студент получит определенный балл за экзамен, представленный определенным значением оси X — для каждого из интервалов. К счастью для вас, в Excel есть рабочая лошадка для выполнения всех этих вычислений: функция НОРМ.РАСП.
Введите следующую формулу в ячейку справа (F4) вашего первого интервала (E4):
| 1 | = НОРМ.РАСП (E4; $ F $ 1; $ F $ 2; ЛОЖЬ) |
Вот декодированная версия, которая поможет вам соответствующим образом настроить:
| 1 | = НОРМ.РАСП ([первый интервал], [среднее (абсолютное значение)], [стандартное отклонение (абсолютное значение), ЛОЖЬ) |
Вы блокируете среднее значение и стандартное отклонение, чтобы можно было легко выполнить формулу для оставшихся интервалов (E5: E153).
Теперь дважды щелкните маркер заполнения, чтобы скопировать формулу в остальные ячейки (F5: F153).
Шаг № 5: Создайте диаграмму рассеяния с плавными линиями.
Наконец, пришло время строить колоколообразную кривую:
- Выберите любое значение в вспомогательной таблице, содержащей значения осей x и y (E4: F153).
- Перейти к Вставлять таб.
- Щелкните значок «Вставить точечную (X, Y) или пузырьковую диаграмму» кнопка.
- Выбирать «Разброс с плавными линиями ».
Шаг № 6: Настройте таблицу меток.
Технически у вас есть кривая колокола. Но его будет трудно прочитать, поскольку в нем отсутствуют какие-либо данные, описывающие это.
Давайте сделаем нормальное распределение более информативным, добавив метки, иллюстрирующие все значения стандартного отклонения ниже и выше среднего (вы также можете использовать их для отображения z-значений).
Для этого создайте еще одну вспомогательную таблицу следующим образом:
Сначала скопируйте среднее значение (F1) рядом с соответствующей ячейкой в столбце X-Value (I5).
Затем вычислите значения стандартного отклонения ниже среднего, введя эту простую формулу в ячейка I4:
Проще говоря, формула вычитает сумму предыдущих значений стандартного отклонения из среднего. Теперь перетащите маркер заполнения вверх, чтобы скопировать формулу в оставшиеся две ячейки (I2: I3).
Повторите тот же процесс для стандартных отклонений выше среднего, используя зеркальную формулу:
Таким же образом выполните формулу для двух других ячеек (I7: I8).
Наконец, заполните значения метки оси Y (J2: J8) с нулями, так как вы хотите, чтобы маркеры данных располагались на горизонтальной оси.
Шаг № 7: Вставьте данные метки в диаграмму.
Теперь добавьте все данные, которые вы подготовили. Щелкните правой кнопкой мыши график и выберите «Выберите данные.”
В появившемся диалоговом окне выберите «Добавлять.”
Выделите соответствующие диапазоны ячеек из вспомогательной таблицы —I2: I8 для «Значения серии X» а также J2: J8 для «Значения серии Y »-и нажмите «OK.”
Шаг № 8: Измените тип диаграммы для серии этикеток.
Наш следующий шаг — изменить тип диаграммы недавно добавленной серии, чтобы маркеры данных отображались в виде точек. Для этого щелкните правой кнопкой мыши график диаграммы и выберите «Изменить тип диаграммы.”
Затем создайте комбинированную диаграмму:
- Перейдите к Комбо таб.
- Для Серия «Series2», изменение «Тип диаграммы» к «Разброс.”
- Примечание. Убедитесь, что «Серия1»Остается как«Скаттер с плавными линиями. » Иногда Excel изменяет его, когда вы делаете Комбо Также убедитесь, что «Серия1”Не перемещается на вторичную ось — флажок рядом с типом диаграммы не должен быть отмечен.
- Нажмите «Ok.”
Шаг № 9: Измените масштаб горизонтальной оси.
Отцентрируйте диаграмму на колоколообразной кривой, отрегулировав масштаб горизонтальной оси. Щелкните правой кнопкой мыши горизонтальную ось и выберите «Ось формата»Из меню.
Когда появится панель задач, сделайте следующее:
- Перейти к Параметры оси таб.
- Установить Минимальные границы значение «15.”
- Установить Максимальные границы значение «125.”
Вы можете настроить диапазон шкалы оси по своему усмотрению, но, поскольку вы знаете диапазоны стандартного отклонения, установите значения границ немного дальше от каждого из ваших третьих стандартных отклонений, чтобы показать «хвост» кривой.
Шаг № 10: Вставьте и разместите метки пользовательских данных.
По мере того, как вы совершенствуете свою диаграмму, не забудьте добавить пользовательские метки данных. Сначала щелкните правой кнопкой мыши любую точку, представляющую Серия «Series2» и выберите «Добавьте метки данных.”
Затем замените метки по умолчанию на те, которые вы установили ранее, и поместите их над маркерами данных.
- Щелкните правой кнопкой мыши на любом Серия «Series2» метка данных.
- Выбирать «Отформатируйте метки данных.”
- На панели задач переключитесь на Параметры метки таб.
- Проверить «Значение X» коробка.
- Снимите флажок «Значение Y» коробка.
- Под «Положение ярлыка,» выбирать «Выше.”
Кроме того, теперь вы можете удалить линии сетки (щелкните их правой кнопкой мыши> Удалить).
Шаг № 11: Перекрасить маркеры данных (необязательно).
Наконец, перекрасьте точки, чтобы они соответствовали вашему стилю диаграммы.
- Щелкните правой кнопкой мыши любой Серия «Series2» метка данных.
- Щелкните значок «Наполнять» кнопка.
- Выберите свой цвет из появившейся палитры.
Также удалите границы вокруг точек:
- Снова щелкните правой кнопкой мыши тот же маркер данных и выберите «Контур.”
- Выбирать «Без контура.”
Шаг № 12: Добавьте вертикальные линии (необязательно).
В качестве окончательной настройки вы можете добавить на диаграмму вертикальные линии, чтобы подчеркнуть значения SD.
- Выберите график диаграммы (таким образом линии будут вставлены прямо в диаграмму).
- Перейти к Вставлять таб.
- Щелкните значок «Формы» кнопка.
- Выбирать «Линия.”
Удерживайте «СДВИГ» при перетаскивании мыши, чтобы нарисовать идеально вертикальные линии от каждой точки до того места, где каждая линия пересекается с колоколообразной кривой.
Измените заголовок диаграммы, и ваша улучшенная кривая колокола будет готова отображать ваши ценные данные о распределении.
И вот как вы это делаете. Теперь вы можете выбрать любой набор данных и создать колоколообразную кривую нормального распределения, выполнив эти простые шаги!