В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
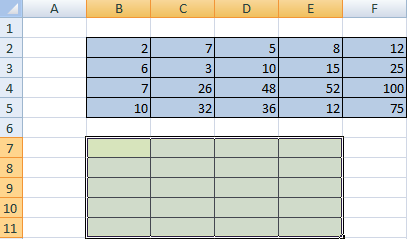
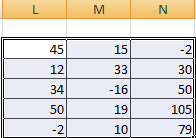
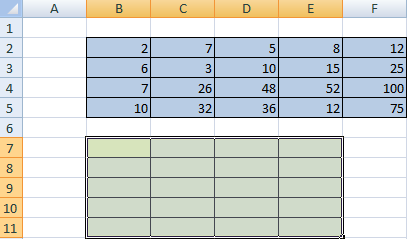
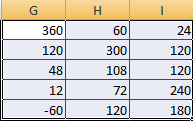
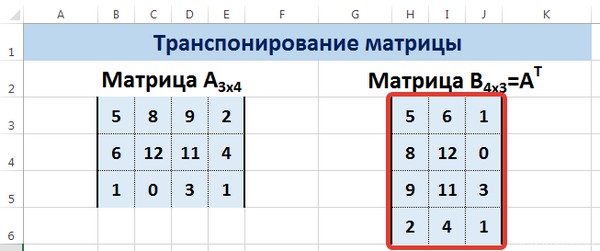
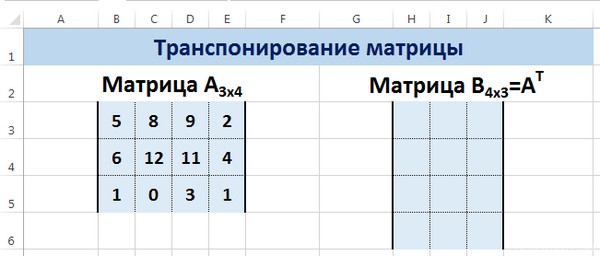
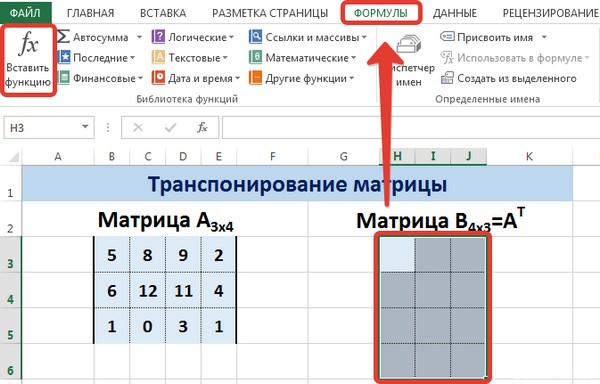
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
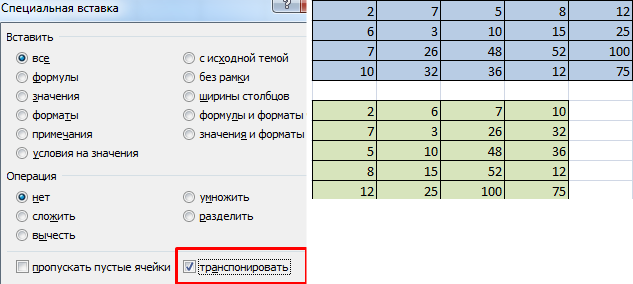
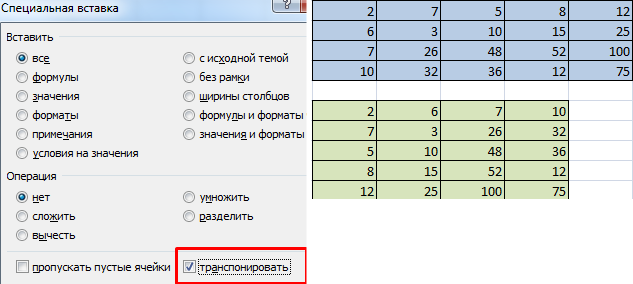
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
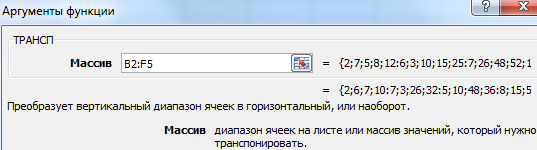
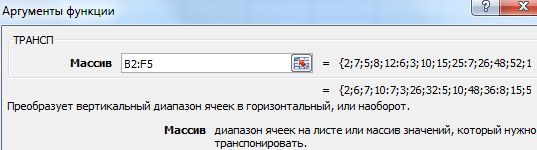
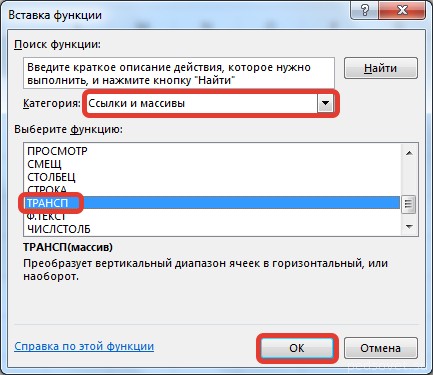
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
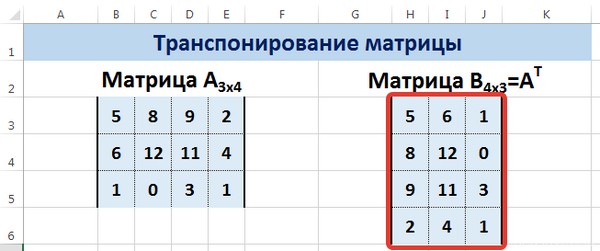
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
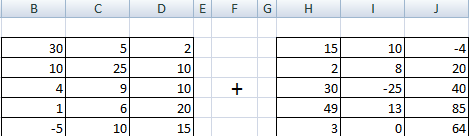
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
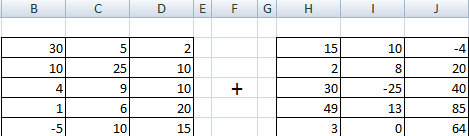
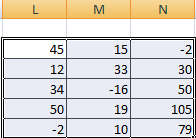
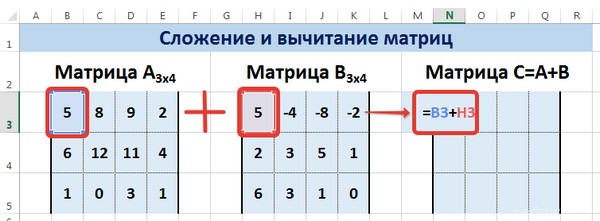
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
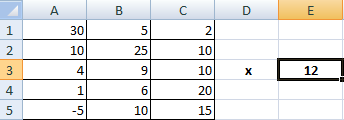
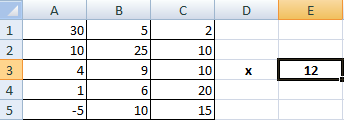
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
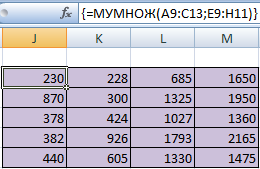
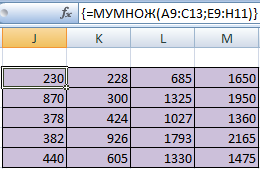
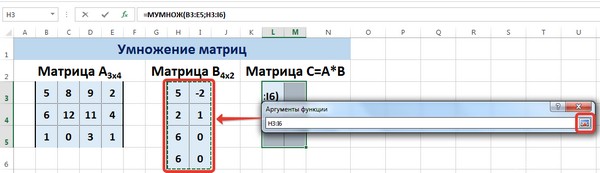
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
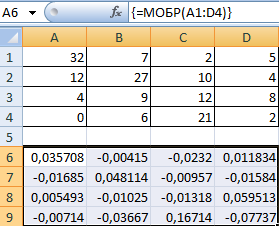
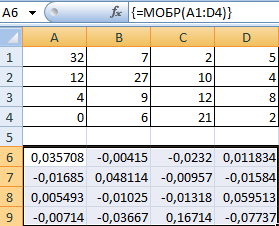
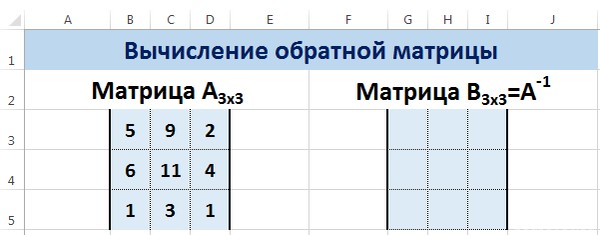
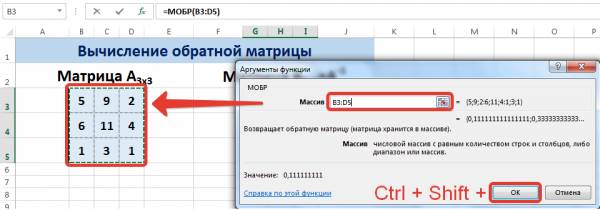
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
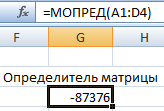
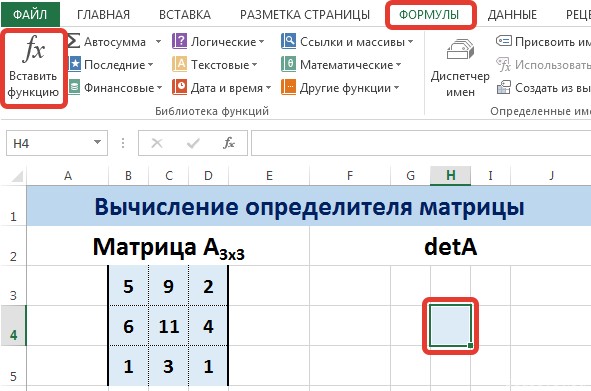
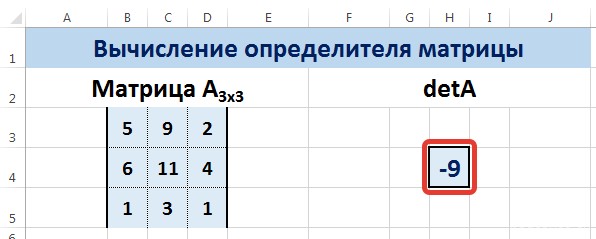
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
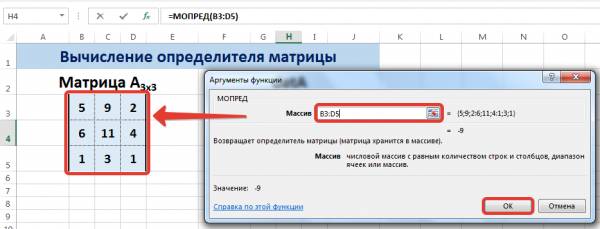
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Под матрицей подразумевается набор ячеек, расположенных непосредственно друг возле друга и которые образуют вместе прямоугольник. Не требуется особых навыков, чтобы выполнять различные действия с матрицей, достаточно тех же, какие используются во время работы с классическим диапазоном.
Каждая матрица имеет свой адрес, записывающийся аналогичным диапазону способом. Первая составная часть – первая ячейка диапазона (расположенная в верхнем левом углу), а второй – последняя ячейка, которая находится в нижнем правом углу.
Содержание
- Формулы массива
- Что можно делать с матрицами
- Транспонирование
- Сложение
- Умножение
- Обратная матрица
- Поиск определителя матрицы
- Несколько примеров
- Умножение и деление
- Метод 1
- Метод 2
- Сложение и вычитание
- Метод 1
- Метод 2
- Пример транспонирования матрицы
- Поиск обратной матрицы
- Выводы
Формулы массива
В подавляющем количестве задач при работе с массивами (а матрицы и являются таковыми) используются формулы соответствующего типа. Базовое их отличие от обычных заключается в том, что последние выводят всего одно значение. Для применения формулы массива необходимо осуществить несколько действий:
- Выделить набор ячеек, где будут выводиться значения.
- Непосредственно введение формулы.
- Нажатие последовательности клавиш Ctrl + Shift + Ввод.
После осуществления этих простых действий в поле ввода отображается формула массива. Ее можно отличить от обычной по фигурным скобкам.
Для редактирования, удаления формул массива, надо выделить требуемый диапазон и сделать то, что нужно. Чтобы редактировать матрицу, нужно использовать ту же комбинацию, что и для ее создания. При этом нет возможности редактировать отдельный элемент массива.
Что можно делать с матрицами
В целом, есть огромное количество действий, применение которых возможно для матриц. Давайте каждое из них рассмотрим более подробно.
Транспонирование
Многие люди не понимают значения этого термина. Представьте, что вам нужно поменять строки и колонки местами. Вот это действие и называется транспонированием.
Перед тем, как это осуществить, необходимо выделить отдельную область, которая имеет такое же количество строчек, сколько столбцов есть у исходной матрицы и такое же количество столбцов. Чтобы более наглядно понять, как это работает, посмотрите на этот скриншот.
Далее есть несколько методов, как можно осуществить транспонирование.
Первый способ следующий. Для начала нужно выделить матрицу, после чего скопировать ее. Далее выделяется диапазон ячеек, куда должен быть вставлен транспонированный диапазон. Далее открывается окно «Специальная вставка».
Там есть множество операций, но нам нужно найти радиокнопку «Транспонировать». После совершения этого действия нужно подтвердить его нажатием клавиши ОК.
Есть еще один способ, с помощью которого можно транспонировать матрицу. Сперва надо выделить ячейку, расположенную в верхнем левом углу диапазона, отведенного под транспонированную матрицу. Далее открывается диалоговое окно с функциями, где есть функция ТРАНСП. Ниже в примере вы более подробно узнаете, как это сделать. В качестве параметра функции используется диапазон, соответствующий изначальной матрице.
После нажатия кнопки ОК сначала будет показано, что вы допустили ошибку. Ничего в этом страшного нет. Все потому, что вставленная нами функция не определена, как формула массива. Поэтому нам нужно совершить такие действия:
- Выделить набор ячеек, отведенных под транспонированную матрицу.
- Нажать клавишу F2.
- Нажать на горячие клавиши Ctrl + Shift + Enter.
Главное достоинство метода заключается в способности транспонированной матрицы сразу корректировать содержащуюся в ней информацию, как только вносятся данные в изначальную. Поэтому рекомендуется использовать именно данный способ.
Сложение
Эта операция возможна лишь применительно к тем диапазонам, количество элементов которых такое же самое. Проще говоря, у каждой из матриц, с которыми пользователь собирается работать, должны быть одинаковые размеры. И приводим скриншот для наглядности.
В матрице, которая должна получиться, нужно выделить первую ячейку и ввести такую формулу.
=Первый элемент первой матрицы + Первый элемент второй матрицы
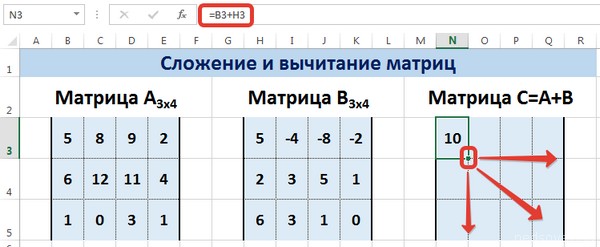
Далее подтверждаем ввод формулы с помощью клавиши Enter и используем автозаполнение (квадратик в правом нижнем углу), чтобы скопировать все значения на новую матрицу.
Умножение
Предположим, у нас есть такая таблица, которую следует умножить на 12.
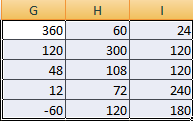
Догадливый читатель может легко понять, что метод очень похож на предыдущий. То есть, каждая из ячеек матрицы 1 должна умножаться на 12, чтобы в итоговой матрице каждая ячейка содержала значение, умноженное на этот коэффициент.
При этом важно указывать абсолютные ссылки на ячейки.
Итого, получится такая формула.
=A1*$E$3
Дальше методика аналогична предыдущей. Нужно это значение растянуть на необходимое количество ячеек.
Предположим, что необходимо перемножить матрицы между собой. Но есть лишь одно условие, при котором это возможно. Надо, чтобы количество столбцов и строк у двух диапазонов было зеркально одинаковое. То есть, сколько столбцов, столько и строк.
Чтобы было более удобно, нами выделен диапазон с результирующей матрицей. Надо переместить курсор на ячейку в верхнем левом углу и ввести такую формулу =МУМНОЖ(А9:С13;Е9:H11). Не стоит забыть нажать Ctrl + Shift + Enter.
Обратная матрица
Если наш диапазон имеет квадратную форму (то есть, количество ячеек по горизонтали и вертикали одинаковое), то тогда получится найти обратную матрицу, если в этом есть такая необходимость. Ее величина будет аналогичной исходной. Для этого используется функция МОБР.
Для начала следует выделить первую ячейку матрицы, в какую будет вставляться обратная. Туда вводится формула =МОБР(A1:A4). В аргументе указывается диапазон, для какого нам надо создать обратную матрицу. Осталось только нажать Ctrl + Shift + Enter, и готово.
Поиск определителя матрицы
Под определителем подразумевается число, находящееся матрицы квадратной формы. Чтобы осуществить поиск определителя матрицы, существует функция – МОПРЕД.
Для начала ставится курсор в какой-угодно ячейке. Далее мы вводим =МОПРЕД(A1:D4)
Несколько примеров
Давайте для наглядности рассмотрим некоторые примеры операций, которые можно осуществлять с матрицами в Excel.
Умножение и деление
Метод 1
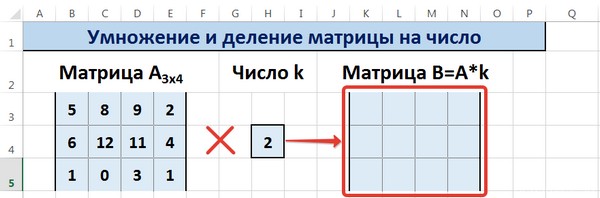
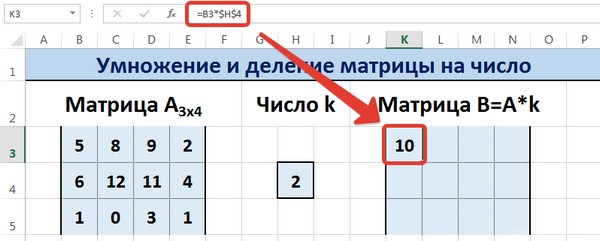
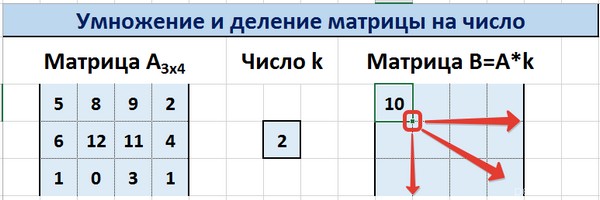
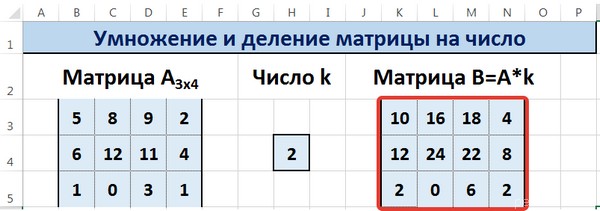
Предположим, у нас есть матрица A, имеющая три ячейки в высоту и четыре – в ширину. Также есть число k, которое записывается в другой ячейке. После выполнения операции умножения матрицы на число появится диапазон значений, имеющий аналогичные размеры, но каждая ее часть умножается на k.
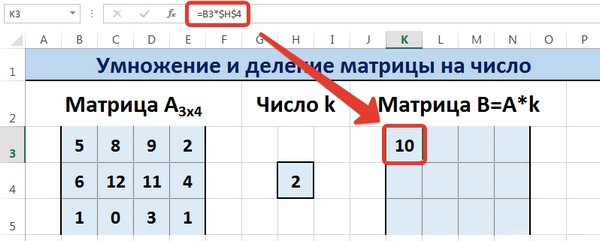
Диапазон B3:E5 – это исходная матрица, которая будет умножаться на число k, которое в свою очередь расположено в ячейке H4. Результирующая матрица будет находиться в диапазоне K3:N5. Исходная матрица будет называться A, а результирующая – B. Последняя образуется путем умножения матрицы А на число k.
Далее вводится =B3*$H$4 в ячейку K3, где В3 — элемент A11 матрицы А.
Не стоит забывать о том, ячейку H4, где указано число k необходимо вводить в формулу с помощью абсолютной ссылки. Иначе значение будет изменяться при копировании массива, и результирующая матрица потеряет работоспособность.
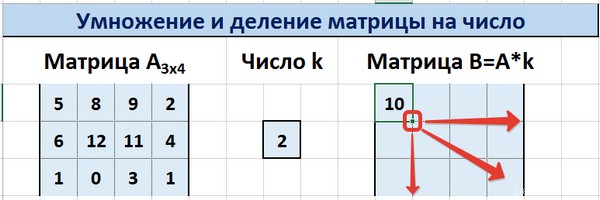
Далее маркер автозаполнения (тот самый квадратик в правом нижнем углу) используется для того, чтобы скопировать значение, полученное в ячейке K3, во все другие ячейки этого диапазона.
Вот у нас и получилось умножить матрицу A на определенное число и получить на выходе матрицу B.
Деление осуществляется аналогичным образом. Только вводить нужно формулу деления. В нашем случае это =B3/$H$4.
Метод 2
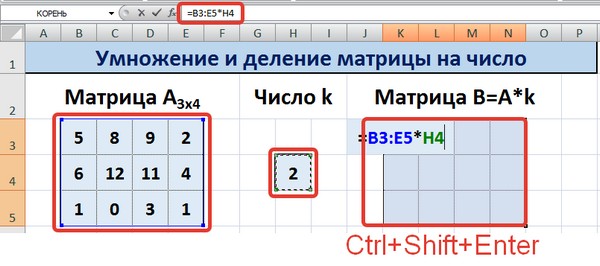
Итак, основное отличие этого метода в том, в качетве результата выдается массив данных, поэтому нужно применить формулу массива, чтобы заполнить весь набор ячеек.
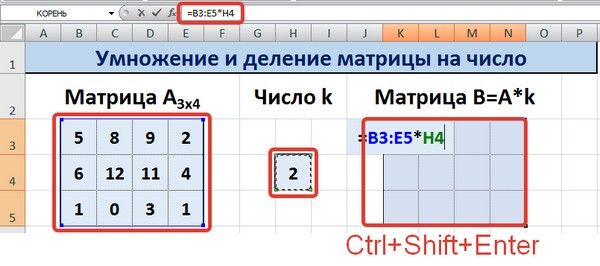
Необходимо выделить результирующий диапазон, ввести знак равно (=), выделить набор ячеек, с соответствующими первой матрице размерами, нажать на звездочку. Далее выделяем ячейку с числом k. Ну и чтобы подтвердить свои действия, надо нажать на вышеуказанную комбинацию клавиш. Ура, весь диапазон заполняется.
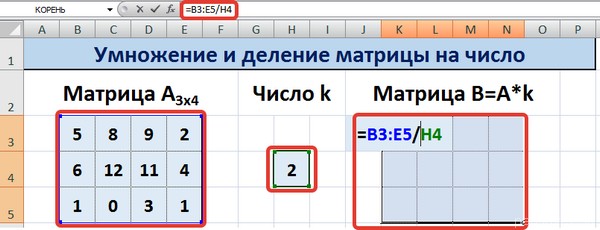
Деление осуществляется аналогичным образом, только знак * нужно заменить на /.
Сложение и вычитание
Давайте опишем несколько практических примеров использования методов сложения и вычитания на практике.
Метод 1
Не стоит забывать, что возможно сложение лишь тех матриц, размеры которых одинаковые. В результирующем диапазоне все ячейки заполняются значением, являющим собой сумму аналогичных ячеек исходных матриц.
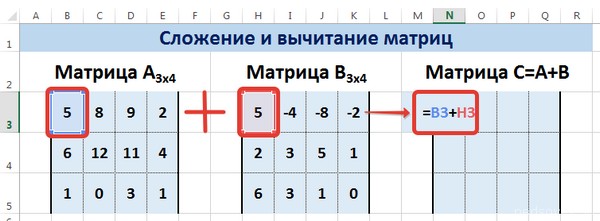
Предположим, у нас есть две матрицы, имеющие размеры 3х4. Чтобы вычислить сумму, следет в ячейку N3 вставить такую формулу:
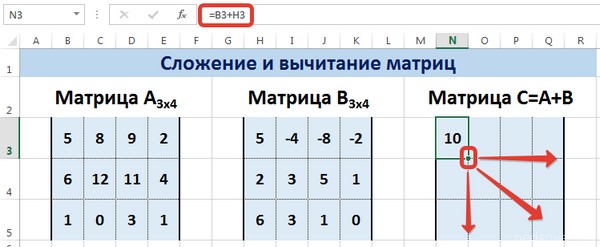
=B3+H3
Тут каждый элемент являет собой первую ячейку матриц, которые мы собрались складывать. Важно, чтобы ссылки были относительными, поскольку если использовать абсолютные, не будут отображаться правильные данные.
Далее, аналогично умножению, с помощью маркера автозаполнения распространяем формулу на все ячейки результирующей матрицы.
Вычитание осуществляется аналогично, за тем лишь исключением, что используется знак вычитания (-), а не сложения.
Метод 2
Аналогично методу сложения и вычитание двух матриц, этот способ подразумевает использование формулы массива. Следовательно, в качестве ее результата будет выдаваться сразу набор значений. Поэтому нельзя редактировать или удалять какие-то элементы.
Сперва надо выделить диапазон, отделенный под результирующую матрицу, а потом нажать на «=». Затем надо указать первый параметр формулы в виде диапазона матрицы А, нажать на знак + и записать второй параметр в виде диапазона, соответствующему матрице B. Подтверждаем свои действия нажатием комбинации Ctrl + Shift + Enter. Все, теперь вся результирующая матрица заполнена значениями.
Пример транспонирования матрицы
Допустим, нам надо создать матрицу АТ из матрицы А, которая у нас есть изначально методом транспонирования. Последняя имеет, уже по традиции, размеры 3х4. Для этого будем использовать функцию =ТРАНСП().
Выделяем диапазон для ячеек матрицы АТ.
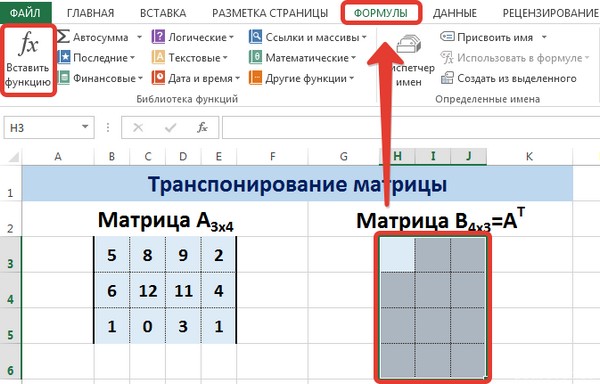
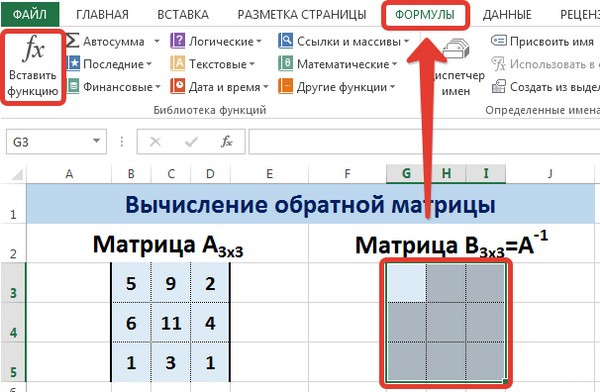
Для этого надо перейти на вкладку «Формулы», где выбрать опцию «Вставить функцию», там найти категорию «Ссылки и массивы» и найти функцию ТРАНСП. После этого свои действия подтверждаются кнопкой ОК.
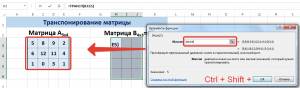
Далее переходим в окно «Аргументы функции», где вводится диапазон B3:E5, который повторяет матрицу А. Далее надо нажать Shift + Ctrl, после чего кликнуть «ОК».
Важно. Нужно не лениться нажимать эти горячие клавиши, потому что в ином случае будет рассчитано только значение первой ячейки диапазона матрицы АТ.
В результате, у нас получается такая транспонированная таблица, которая изменяет свои значения вслед за исходной.
Поиск обратной матрицы
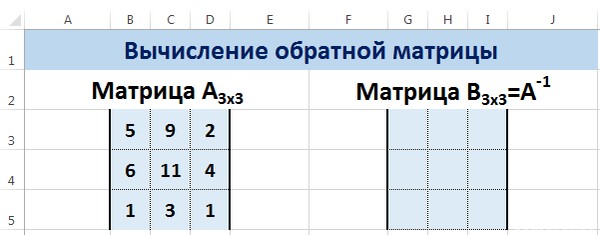
Предположим, у нас есть матрица А, которая имеет размеры 3х3 ячеек. Мы знаем, что для поиска обратной матрицы необходимо использовать функцию =МОБР().
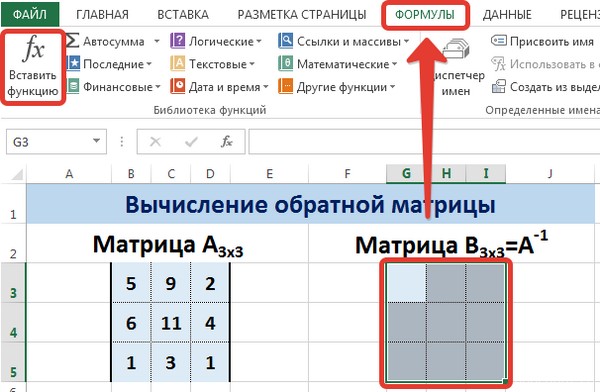
Теперь опишем, как это делать на практике. Сначала необходимо выделить диапазон G3:I5 (там будет располагаться обратная матрица). Необходимо найти на вкладке «Формулы» пункт «Вставить функцию».
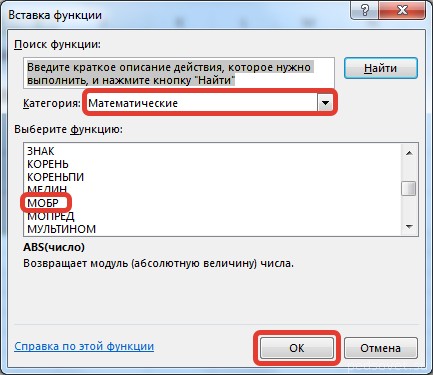
Откроется диалог «Вставка функции», где нужно выбрать категорию «Математические». И там в перечне будет функция МОБР. После того, как мы ее выберем, нужно нажать на клавишу ОК. Далее появляется диалоговое окно «Аргументы функции», в котором записываем диапазон B3:D5, который соответствует матрице А. Далее действия аналогичные транспонированию. Нужно нажать на комбинацию клавиш Shift + Ctrl и нажать ОК.
Выводы
Мы разобрали некоторые примеры, как можно работать с матрицами в Excel, а также описали теорию. Оказывается, что это не так страшно, как может показаться на первый взгляд, не так ли? Это только звучит непонятно, но на деле с матрицами среднестатистическому пользователю приходится иметь дело каждый день. Они могут использоваться почти для любой таблицы, где есть сравнительно небольшое количество данных. И теперь вы знаете, как можно себе упростить жизнь в работе с ними.
Оцените качество статьи. Нам важно ваше мнение:
Умножение и деление матрицы на число в Excel
Способ 1
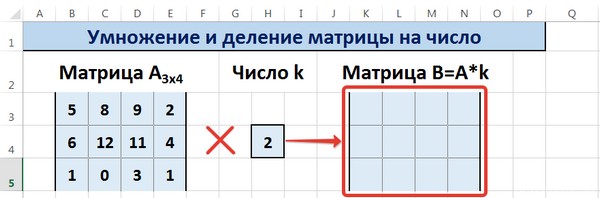
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
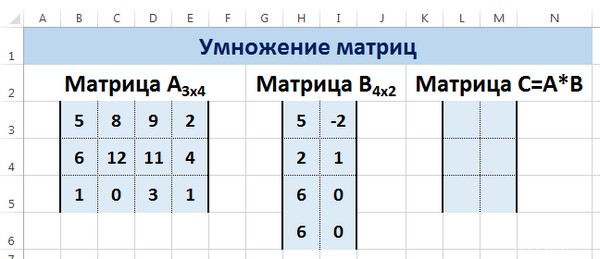
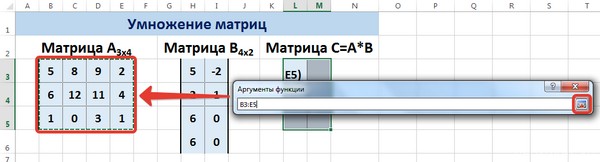
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
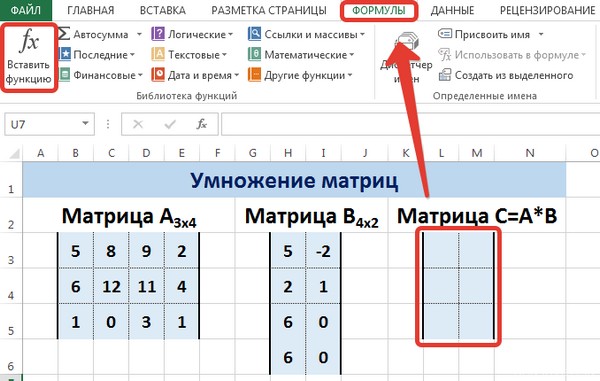
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
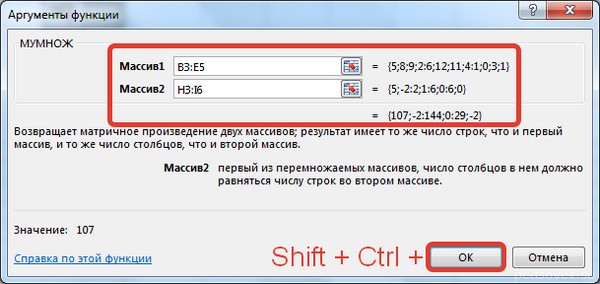
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
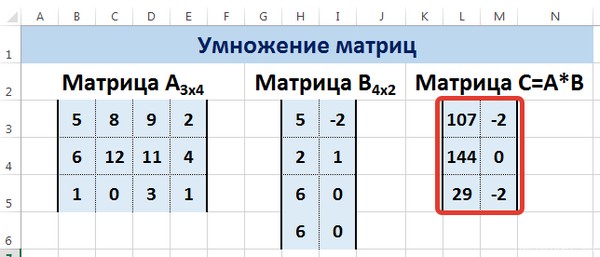
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу АТ.
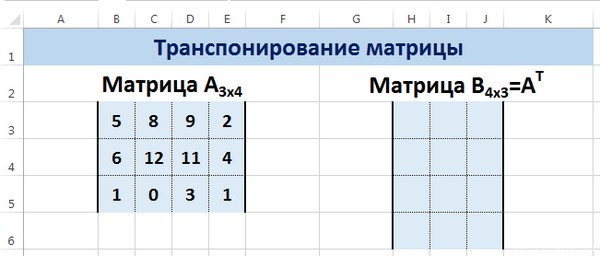
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу АТ, причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы АТ.
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А-1 называется обратной для матрицы А, если АА-1=А-1А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А-1.
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
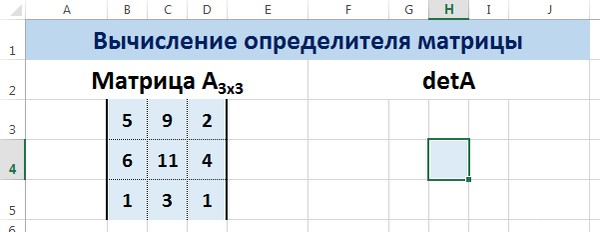
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
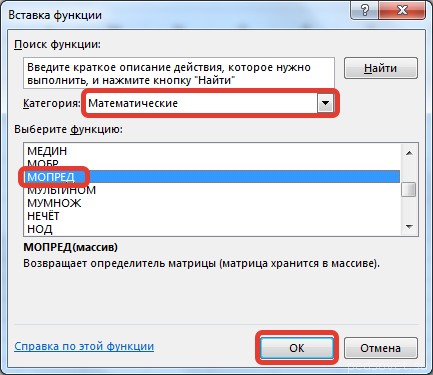
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Содержание
- Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
- Умножение и деление матрицы на число в Excel
- Способ 1
- Способ 2
- Сложение и вычитание матриц в Excel
- Способ 1
- Способ 2
- Умножение матриц в Excel
- Транспонирование матрицы в Excel
- Нахождение обратной матрицы в Excel
- Нахождение определителя матрицы в Excel
- Как найти определить матрицы в Excel
- Видеоурок
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
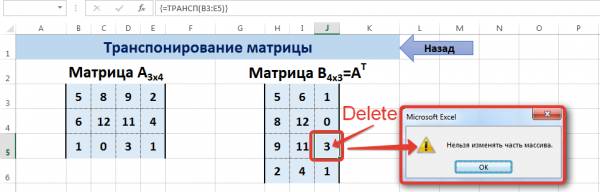
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Источник
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
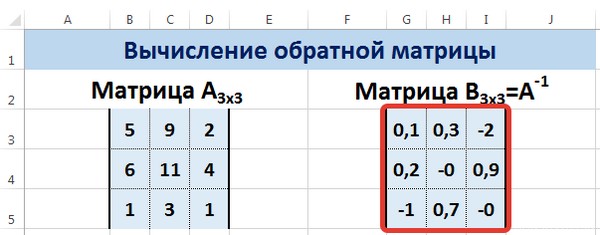
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А – В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .

Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АА -1 =А -1 А=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .

Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.

Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.

Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Матрица БКГ – уникальная матрица, которая помогает на основе исходных данных построить диаграмму и провести анализ всех сегментов рынка. Создана была матрица Бостонской консалтинговой группой, откуда и получила свое название.
Она дает возможность математические правильно проанализировать рынок и избрать необходимые меры для дальнейшего развития разных товаров в будущем.
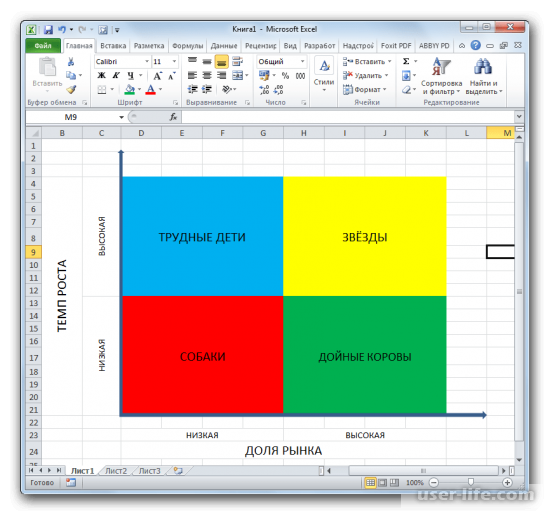
Звучит немного запутано, но на самом деле все немного проще чем кажется на первый взгляд. Стратегия матрицы предполагает, что все товары относятся лишь к четырем группам:
· «собаки» – товары, которые представляют незначительную долю рынка в своем сегменте низкого темпа роста; эти товары являются менее перспективными, поэтому производство данного сегмента не будет иметь успеха;
· «трудные дети» – товары, которые могут быстро выбиться в перспективный сегмент, но при этом еще занимают малую часть всего рынка; товары с хорошими темпами развития, но требующие финансовых и инвестиций;
· «дойные коровы» – сегмент рынка с постоянным, но незначительным доходом, которые при этом не требуют никаких инвестиций; их доля значительная, но в слабо растущем сегменте рынка;
· «звезды» – товары с существенной доле быстроразвивающегося рынка, которые имеют наибольший успех; с первых дней приносят хороший доход, а будущие вложения в данный сегмент смогут лишь увеличить прибыль.
Отношение темпа роста относительно сегментов рынка можно отобразить:
Суть массива БКГ – найти определенный сегмент рыка, к которой можно отнести исходную группу или единичный товар.
Попробуем на практике осуществить данную процедуру через функционал Excel:
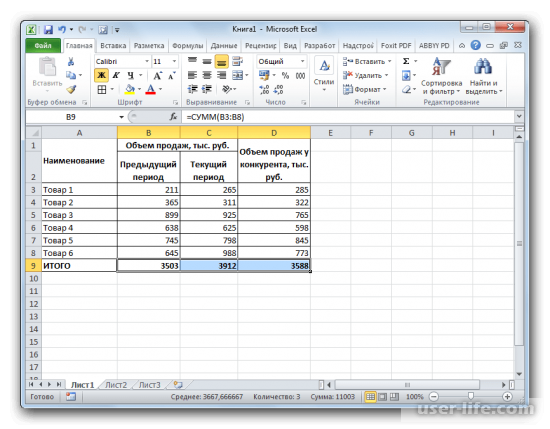
1. Создадим таблицу, в которой отобразим исходные товары с информацией о количестве продаж текущего месяца и прошлого, а также наименьшую цену этих товаров у конкурента.
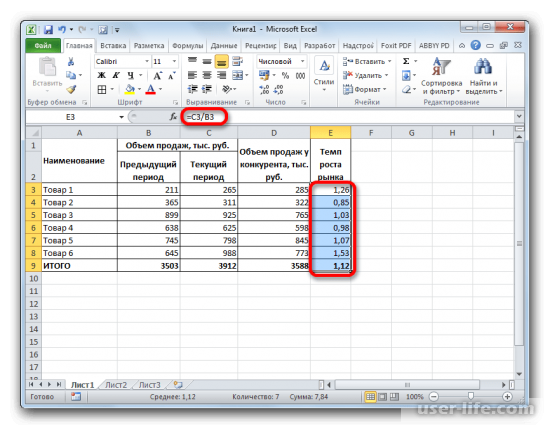
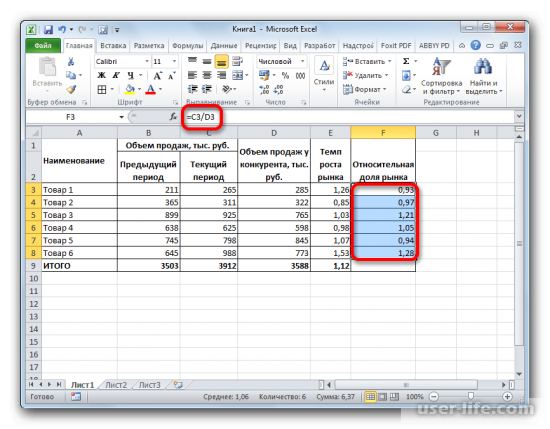
2. Рассчитываем темпы роста этих товаров на рыке и их относительную долю. Разделим количество продаж за текущий период на количество за прошлый период, и соответственно, величину продаж текущего периода на продажи у конкурентов.
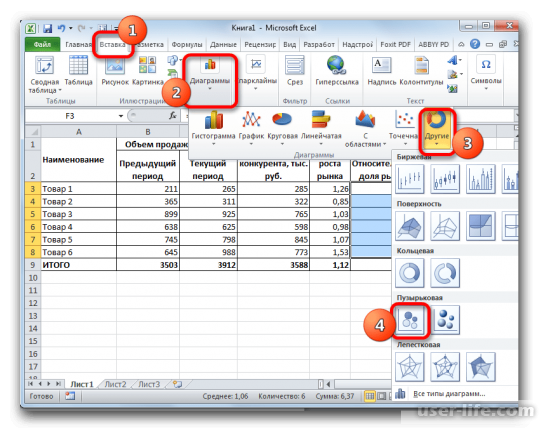
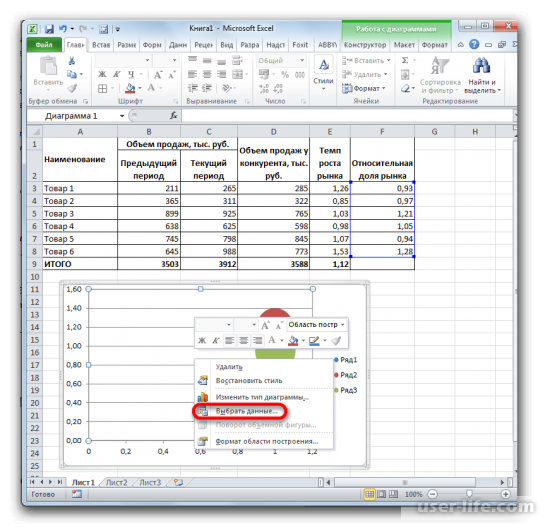
3. Следующим шагом будет построение диаграммы на основе полученной информации. Используем диаграмму пузырькового типа – «Вставка» – «Диаграмма» – «Другие» – «Пузырьковая».
4. Выберем необходимые вводные. Откроем функции и укажем на пункт «Выбрать данные».
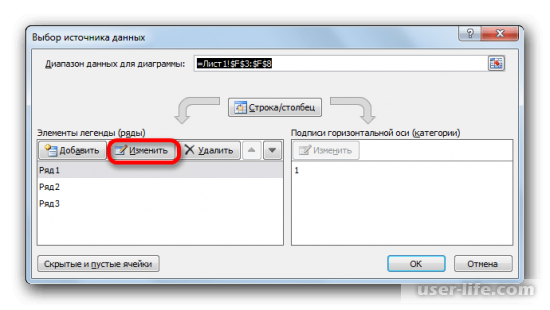
5. В окне выбора данных нажимаем на «Изменить» и начинаем заполнять изменения ряда пузырьковой диаграммы.
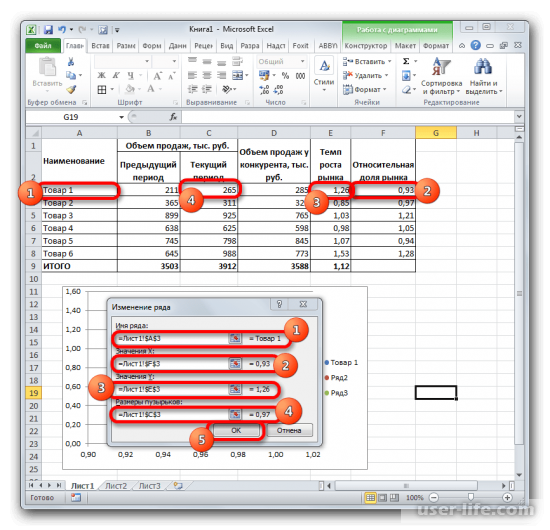
6. В «Имя ряда» устанавливаем ячейку «Наименование». «Значения Х» будут подтягиваться со столбца «Относительная доля рынка», в «Значения Y» – «Темп роста рынка». «Размеры пузырьков» будут браться со диапазона «Текущий период». На этом ввод значений завершаем и сформировать диаграмму.
7. Проведем подобные действия для всех групп и получаем итоговую пузырьковую диаграмму. Осталось лишь корректно настроить оси.
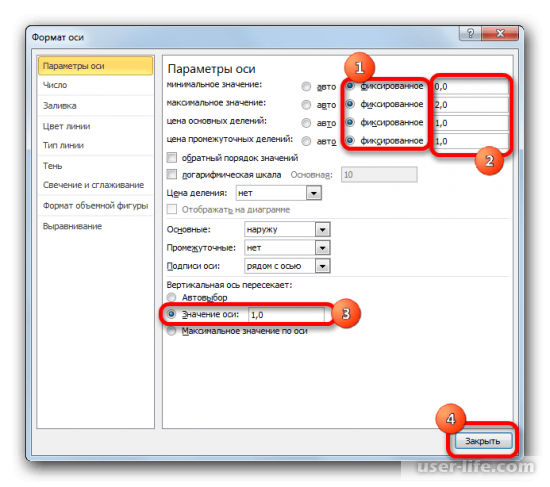
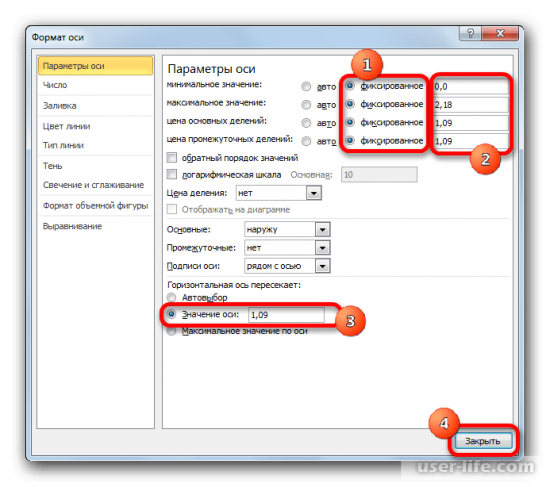
8. Нужно немного подкорректировать оси. Для начала в горизонтальных осях изменяем «Минимальное значение» на «0», «Максимальное» – на «2», а «Деления» на «1».
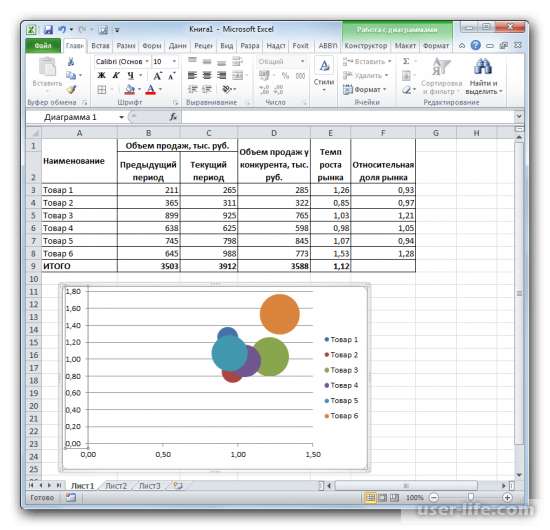
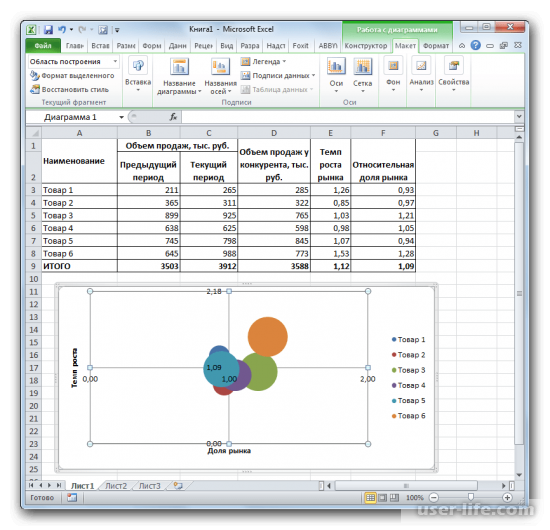
9. В настройках вертикальных осей устанавливаем «Минимальное» на 0, «Максимальное» на «2.18», а деления на «1.09». Эти показатели высчитываются из среднего показателя относительной доли рынка, который необходимо умножить на 2. «Деления» также устанавливаем «1.09». Последнее что укажем – «Значение оси» – «1.09» соответственно.
10. Осталось подписать наши оси и можно приступать к непосредственному анализу матрицы БКГ.
Матрица БКГ дает возможность провести быстрый и корректный анализ сегментов рынка.
В нашем случае мы видим, что:
«Товар 2» и «Товар 5» относятся к группе товаров «Собаки» – они не приносят прибыль. Они не имеют популярности на рынке, поэтому они в дальнейшем стратегии продаж нам больше не интересны.
«Товар 1» является представителем группы «Трудные дети», а это значит, что товар, при должном развитии и финансировании может приносить прибыль, но это будет происходить не в ближайшее время.
«Товар 3» и «Товар 4» – «Дойные коровы» – отличная выручка дает возможность развивать другие категории, при этом не вкладывая инвестиции в данный сегмент.
«Товар 6» – единственный, который полностью относится к категории «Звезды» – его отличная возможность приносить прибыль держит весь бизнес, а дополнительные инвестиции в этот сегмент помогут лишь улучшить финансовое положение.
Таким образом, можно провести существенный анализ сегментов рынка и получить необходимы выводы для каждой группы товаров с помощью матрицы БКГ. Построение матрицы не должно вызывать особых трудностей, но стоит учесть, что нужны проверенные исходные данные и показатели, ведь именно они являются основой матрицы.
Компьютерные пользователи пользуются программой Microsoft Excel не только для создания квартальных и годовых отчетов, но и еще в качестве многофункционального калькулятора. Например, вычислить матрицу в Excel несложно, достаточно лишь правильно использовать поля книги и инструменты.
Как умножить матрицы в Excel
Электронный редактор позволяет нам открыть мощный табличный диапазон утилит и параметров. Благодаря чему мы получаем возможность быстро создавать расчеты. Каждому пользователю известно, что перемножать можно лишь те матрицы, которые имеют одинаковое количество строк и столбцов.
Если матрица имеет пустые элементы, то перемножать ее тоже нельзя, поэтому использовать для расчетов в Excel можно не все виды математических условий.
Как пользоваться функцией МУМНОЖ для вычисления матрицы
Функция МУМНОЖ имеет возможность производить перемножение двух матричных массивов. Для этой операции используется специальный синтаксис, в котором недопустимо делать ошибки. Предлагаем на примере рассмотреть, как производится решение матриц в электронной таблице.
- Предположим, имеется пример двух матриц. Чтобы их перемножить, их необходимо сначала внести в свободные ячейки листа в Excel.
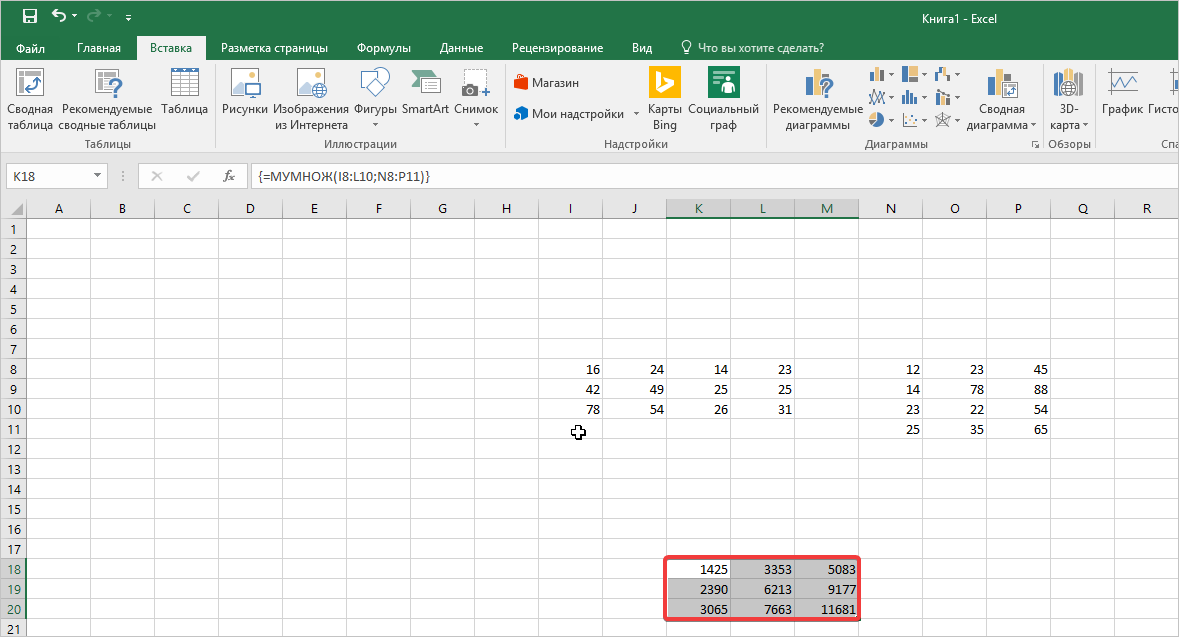
- Далее переходим в другую свободную зону. Здесь выделяем диапазон ячеек, который должен вмещать все ответы после перемножения, то есть в нашем случае результат должен занимать три строчки и два столбика. После выделения нажимаем на кнопку «Вставить функцию».
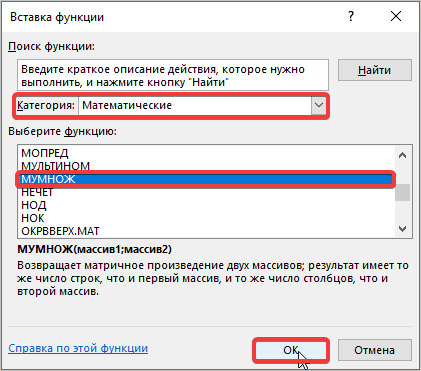
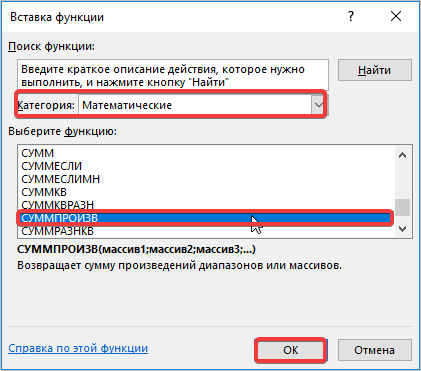
- Мы попадаем в мастер функций. Здесь в поле «Категория» выбираем «Математические», листаем до середины и находим «МУМНОЖ». Выбираем ее и нажимаем кнопку «ОК».
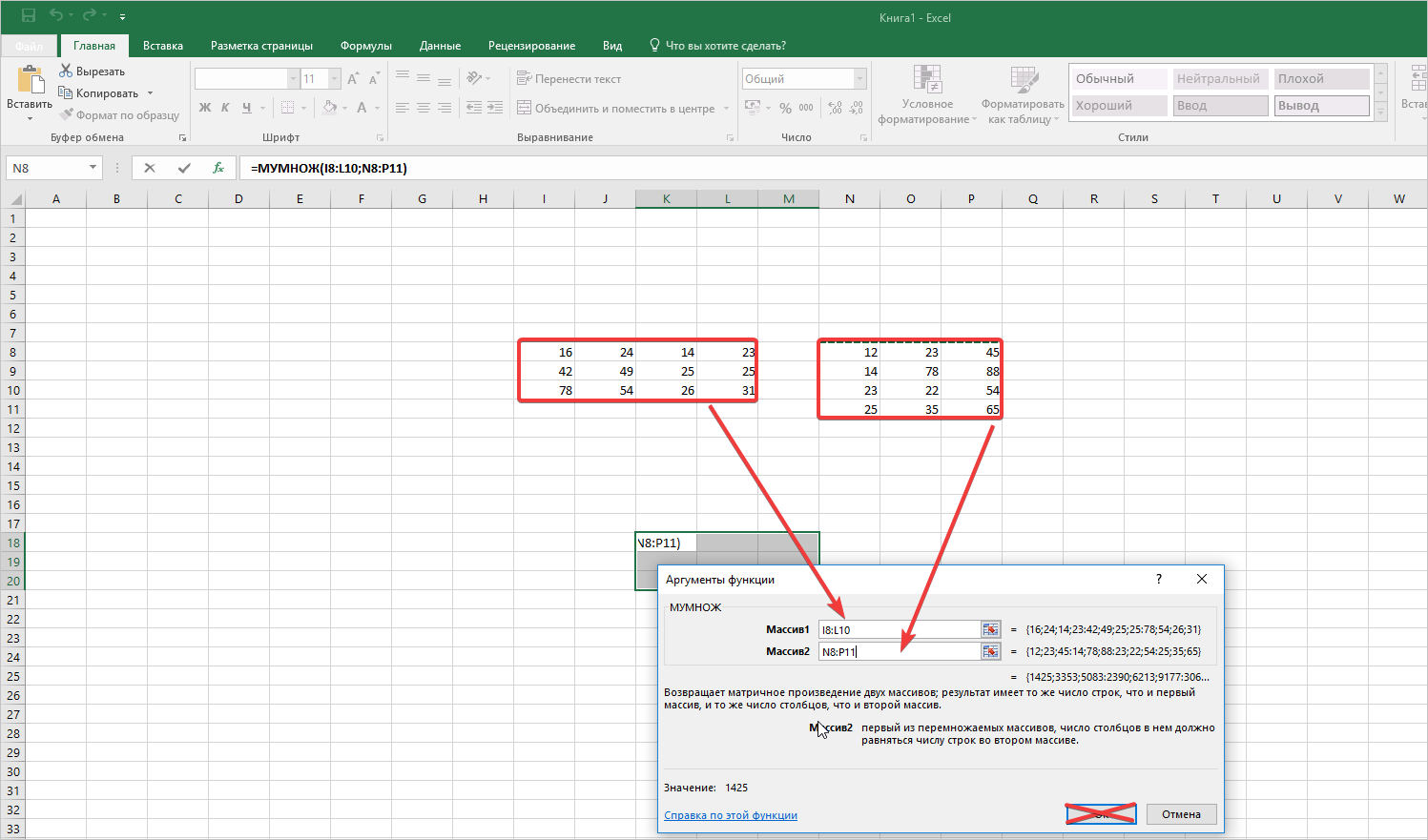
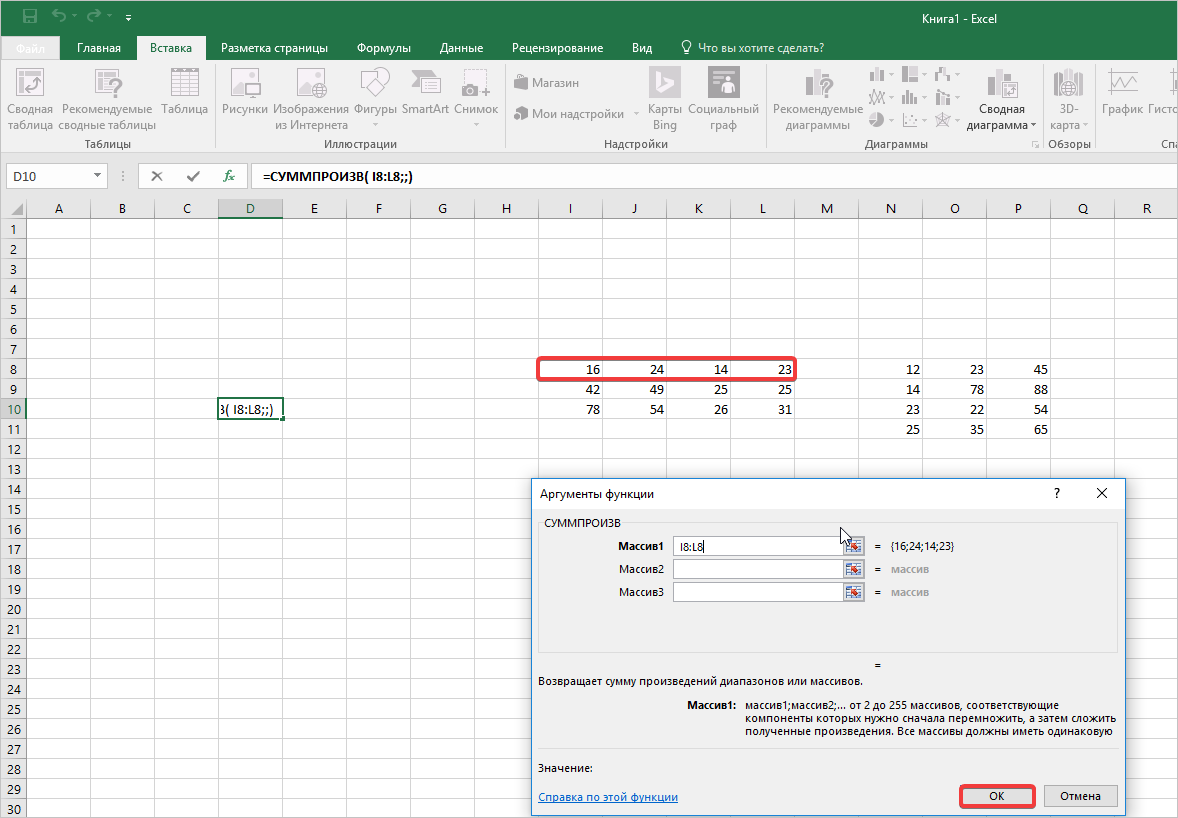
- В появившемся окне вводим аргументы массивов. В первый массив прописываем координаты первой матрицы, а во второй — второй, соответственно. Обратите внимание, что в полях проставились адреса этих объектов, затем нажмите комбинацию клавиш Ctrl+Shift+Enter.
Перед выводом результата в выделенный диапазон ячеек не нужно нажимать кнопку ОК. Это не даст результата, а только лишь выведет ошибку на экран. Так как здесь формула перемножения массива, необходимо использовать комбинацию кнопок, указанную выше.
Использование сборной формулы для решения
Если по какой-то причине первый вариант перемножения у вас не получился либо считаете его слишком простым, рекомендуем ознакомится с еще одним способом, который послужит дополнительным навыком в работе с матрицами в электронных таблицах.
- Начнем с выделения одной свободной ячейки на листе. Затем нажимаем кнопку «Вставить функцию».
- Открывается окно с набором функций, выбираем категорию «Математические», где в нижнем списке находим значение «СУММПРОИЗВ». Нажимаем кнопку ОК.
- Затем в появившемся окне, где нужно в пустые поля прописать диапазон ячеек, участвующих в вычислениях. В первое поле заносим ссылки на первую строчку первой матрицы.
- Именно со вторым полем могут возникнуть сложности. Поэтому дочитайте инструкцию до конца. Активируйте поле «Массива 2», затем перейдите к группе функций.
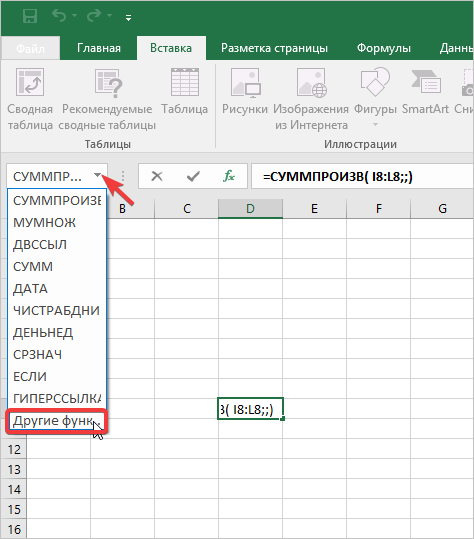
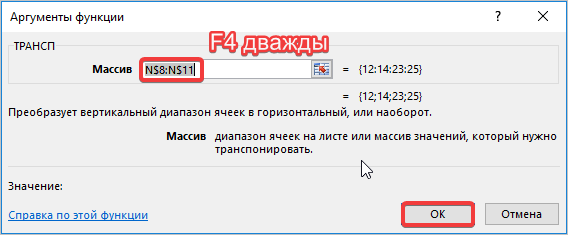
- Открываем категорию «Ссылки и массивы», затем выбираем функцию «ТРАНСП». Следом нажмите кнопку ОК. Во вновь открывшемся окне в пустое поле вводим диапазон первого столбика второй матрицы.
- Затем выделите фоном указанные адреса, после чего нажмите два раза клавишу F4. Это поможет проставить знак доллара к цифровым символам, что делает их привязанными. Затем также нажмите комбинацию клавиш Ctrl+Shift+Enter, как в предыдущем способе.
- Как видим у нас заполнилась только одна ячейка, чтобы изменить это и увидеть расчеты для оставшихся чисел, необходимо активировать маркер автозаполнения. Для этого наведите на правый нижний угол ячейки и протяните на количество строчек и количество столбцов. В нашем случае 3х3.
Таким образом вы можете использовать до двух вариантов работы с матрицами. Однако если необходимо быстро справиться с задачей, следует воспользоваться первым способом.
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Создание матрицы в excel
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Формулы массива
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
Решение матриц в Excel
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Программа Microsoft Office Excel позволяет выполнять операции с матрицами с помощью встроенных функций и формул. Рассмотрим основные операции над матрицами:
- умножение и деление матрицы на число;
- сложение, вычитание и умножение матриц;
- транспонирование матрицы;
- нахождение обратной матрицы;
- вычисление определителя.
Введем условные обозначения. Матрица А размерностью i x j — это прямоугольная таблица чисел, состоящая из i строк и j столбцов, аij — элемент матрицы.
Умножение и деление матрицы на число в Excel
Способ 1
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4. В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k. Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц. Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно. При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А – В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
Мы получим результат умножения матриц А и В.
Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу А Т .
Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу А Т , причем размерность этой матрицы будет 4х3.
Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А Т .
Нажмите для увеличения
Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А -1 называется обратной для матрицы А, если АžА -1 =А -1 žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А -1 .
Нажмите для увеличения
Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
Нажмите для увеличения
Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц). В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Нажмите для увеличения
Мы можем удалить только все элементы этой матрицы.
Видеоурок
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Есть мнение?
Оставьте комментарий
Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст
Матрица БКГ – уникальная матрица, которая помогает на основе исходных данных построить диаграмму и провести анализ всех сегментов рынка. Создана была матрица Бостонской консалтинговой группой, откуда и получила свое название.
Она дает возможность математические правильно проанализировать рынок и избрать необходимые меры для дальнейшего развития разных товаров в будущем.
Звучит немного запутано, но на самом деле все немного проще чем кажется на первый взгляд. Стратегия матрицы предполагает, что все товары относятся лишь к четырем группам:
· «собаки» – товары, которые представляют незначительную долю рынка в своем сегменте низкого темпа роста; эти товары являются менее перспективными, поэтому производство данного сегмента не будет иметь успеха;
· «трудные дети» – товары, которые могут быстро выбиться в перспективный сегмент, но при этом еще занимают малую часть всего рынка; товары с хорошими темпами развития, но требующие финансовых и инвестиций;
· «дойные коровы» – сегмент рынка с постоянным, но незначительным доходом, которые при этом не требуют никаких инвестиций; их доля значительная, но в слабо растущем сегменте рынка;
· «звезды» – товары с существенной доле быстроразвивающегося рынка, которые имеют наибольший успех; с первых дней приносят хороший доход, а будущие вложения в данный сегмент смогут лишь увеличить прибыль.
Отношение темпа роста относительно сегментов рынка можно отобразить:
Суть массива БКГ – найти определенный сегмент рыка, к которой можно отнести исходную группу или единичный товар.
Попробуем на практике осуществить данную процедуру через функционал Excel:
1. Создадим таблицу, в которой отобразим исходные товары с информацией о количестве продаж текущего месяца и прошлого, а также наименьшую цену этих товаров у конкурента.
2. Рассчитываем темпы роста этих товаров на рыке и их относительную долю. Разделим количество продаж за текущий период на количество за прошлый период, и соответственно, величину продаж текущего периода на продажи у конкурентов.
3. Следующим шагом будет построение диаграммы на основе полученной информации. Используем диаграмму пузырькового типа – «Вставка» – «Диаграмма» – «Другие» – «Пузырьковая».
4. Выберем необходимые вводные. Откроем функции и укажем на пункт «Выбрать данные».
5. В окне выбора данных нажимаем на «Изменить» и начинаем заполнять изменения ряда пузырьковой диаграммы.
6. В «Имя ряда» устанавливаем ячейку «Наименование». «Значения Х» будут подтягиваться со столбца «Относительная доля рынка», в «Значения Y» – «Темп роста рынка». «Размеры пузырьков» будут браться со диапазона «Текущий период». На этом ввод значений завершаем и сформировать диаграмму.
7. Проведем подобные действия для всех групп и получаем итоговую пузырьковую диаграмму. Осталось лишь корректно настроить оси.
8. Нужно немного подкорректировать оси. Для начала в горизонтальных осях изменяем «Минимальное значение» на «0», «Максимальное» – на «2», а «Деления» на «1».
9. В настройках вертикальных осей устанавливаем «Минимальное» на 0, «Максимальное» на «2.18», а деления на «1.09». Эти показатели высчитываются из среднего показателя относительной доли рынка, который необходимо умножить на 2. «Деления» также устанавливаем «1.09». Последнее что укажем – «Значение оси» – «1.09» соответственно.
10. Осталось подписать наши оси и можно приступать к непосредственному анализу матрицы БКГ.
Матрица БКГ дает возможность провести быстрый и корректный анализ сегментов рынка.
В нашем случае мы видим, что:
«Товар 2» и «Товар 5» относятся к группе товаров «Собаки» – они не приносят прибыль. Они не имеют популярности на рынке, поэтому они в дальнейшем стратегии продаж нам больше не интересны.
«Товар 1» является представителем группы «Трудные дети», а это значит, что товар, при должном развитии и финансировании может приносить прибыль, но это будет происходить не в ближайшее время.
«Товар 3» и «Товар 4» – «Дойные коровы» – отличная выручка дает возможность развивать другие категории, при этом не вкладывая инвестиции в данный сегмент.
«Товар 6» – единственный, который полностью относится к категории «Звезды» – его отличная возможность приносить прибыль держит весь бизнес, а дополнительные инвестиции в этот сегмент помогут лишь улучшить финансовое положение.
Таким образом, можно провести существенный анализ сегментов рынка и получить необходимы выводы для каждой группы товаров с помощью матрицы БКГ. Построение матрицы не должно вызывать особых трудностей, но стоит учесть, что нужны проверенные исходные данные и показатели, ведь именно они являются основой матрицы.
Как возвести матрицу в степень в excel
В этой статье рассмотрены операции умножения матриц с помощью функции МУМНОЖ() или англ.MMULT и с помощью других формул, а также свойства ассоциативности и дистрибутивности операции умножения матриц. Примеры решены в MS EXCEL.
Операция умножения двух матриц А и В определена только для случаев, когда число столбцов матрицы А равно числу строк матрицы В.
Произведение матрицы А порядка P x N и матрицы В порядка N x Q — это такая матрица С порядка P x Q, у которой каждый элемент равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В , то есть:
Для умножения матриц в MS EXCEL существует специальная функция МУМНОЖ() , которую нужно вводить как формулу массива .
Рассмотрим сначала умножение квадратных матриц 2 х 2.
Разместим матрицы в диапазонах А8:В9 и D8:E9 (см. файл примера ).
Результат, также матрицу 2 х 2, будем вводить в диапазон H8:I9 .
- выделите указанный диапазон H8:I9
- поставьте курсор в Строку формул (или нажмите клавишу F2 )
- введите формулу =МУМНОЖ(A8:B9;D8:E9)
- нажмите CTRL+SHIFT+ENTER
Выделенный диапазон заполнится элементами матрицы. В принципе можно выделить заведомо б о льший диапазон, в этом случае лишние ячейки будут заполнены ошибкой #Н/Д.
Удалить отдельный элемент матрицы А*В не удастся — только все элементы сразу (выделите весь диапазон и нажмите клавишу DEL ).
Чтобы изменить значения аргументов функции (например, поменять матрицы местами), выделите любую ячейку матрицы, нажмите F2 , исправьте формулу и нажмите CTRL+SHIFT+ENTER .
Альтернативной формулой для перемножения матриц является формула массива =СУММПРОИЗВ($A8:$B8;ТРАНСП(D$8:D$9)) . Введите формулу в верхнюю левую ячейку диапазона и нажмите CTRL+SHIFT+ENTER . Затем скопируйте ее вниз и вправо на нужное количество ячеек.
Если попытаться перемножить матрицы неподходящей размерности (когда число столбцов матрицы А НЕ равно числу строк матрицы В), то функция МУМНОЖ() вернет ошибку #ЗНАЧ!
В файле примера также продемонстрированы свойства ассоциативности и дистрибутивности операции умножения матриц.
Возведение числа в степень в Microsoft Excel
Возведение числа в степень является стандартным математическим действием. Оно применяется в различных расчетах, как в учебных целях, так и на практике. У программы Excel имеются встроенные инструменты для подсчета данного значения. Давайте посмотрим, как ими пользоваться в различных случаях.
Возведение чисел
В Excel существует одновременно несколько способов возвести число в степень. Это можно сделать при помощи стандартного символа, функции или применив некоторые, не совсем обычные, варианты действий.
Способ 1: возведение с помощью символа
Самый популярный и известный способ возведения в степень числа в Экселе – это использование стандартного символа «^» для этих целей. Шаблон формулы для возведения выглядит следующим образом:
В этой формуле x – это возводимое число, n – степень возведения.
- Например, чтобы возвести число 5 в четвертую степень мы в любой ячейке листа или в строке формул производим следующую запись:
Если возведение является составной частью более сложного расчета, то порядок действий производится по общим законам математики. То есть, например, в примере 5+4^3 сразу Excel выполняет возведение в степень числа 4, а потом уже сложение.
Кроме того, с помощью оператора «^» можно возводить не только обычные числа, но и данные, содержащиеся в определенном диапазоне листа.
Возведем в шестую степень содержимое ячейки A2.
- В любое свободное место на листе записываем выражение:
Жмем на кнопку Enter. Как видим, расчет был выполнен корректно. Так как в ячейке A2 находилось число 7, то результат вычисления составил 117649.
Как видим, все значения нужного интервала были возведены в указанную степень.
Данный способ максимально прост и удобен, и поэтому так популярен у пользователей. Именно он применяется в подавляющем большинстве случаев вычислений.
Способ 2: применение функции
В Экселе имеется также специальная функция для проведения данного расчета. Она так и называется – СТЕПЕНЬ. Её синтаксис выглядит следующим образом:
Рассмотрим её применение на конкретном примере.
- Кликаем по ячейке, куда планируем выводить результат расчета. Жмем на кнопку «Вставить функцию».
Открывается Мастер функций. В списке элементов ищем запись «СТЕПЕНЬ». После того как находим, выделяем её и жмем на кнопку «OK».
Вслед за этим результат вычисления данной функции выводится в место, которое было выделено ещё в первом шаге описываемых действий.
Кроме того, окно аргументов можно вызвать, перейдя во вкладку «Формулы». На ленте следует нажать кнопку «Математические», расположенную в блоке инструментов «Библиотека функций». В открывшемся списке доступных элементов нужно выбрать «СТЕПЕНЬ». После этого запустится окно аргументов этой функции.
Пользователи, которые имеют определенный опыт, могут не вызывать Мастер функций, а просто вводить формулу в ячейку после знака «=», согласно её синтаксису.
Данный способ более сложный, чем предыдущий. Его применение может быть обосновано, если расчет нужно произвести в границах составной функции, состоящей из нескольких операторов.
Способ 3: возведение в степень через корень
Конечно, данный способ не совсем обычный, но к нему тоже можно прибегнуть, если нужно возвести число в степень 0,5. Разберем этот случай на конкретном примере.
Нам нужно возвести 9 в степень 0,5 или по-другому — ½.
- Выделяем ячейку, в которую будет выводиться результат. Кликаем по кнопке «Вставить функцию».
В открывшемся окне Мастера функций ищем элемент КОРЕНЬ. Выделяем его и жмем на кнопку «OK».
Открывается окно аргументов. Единственным аргументом функции КОРЕНЬ является число. Сама функция выполняет извлечение квадратного корня из введенного числа. Но, так как квадратный корень тождественен возведению в степень ½, то нам данный вариант как раз подходит. В поле «Число» вводим цифру 9 и жмем на кнопку «OK».
Но, конечно, к данному способу расчета прибегают довольно редко, используя более известные и интуитивно понятные варианты вычислений.
Способ 4: запись числа со степенью в ячейке
Этот способ не предусматривает проведения вычислений по возведению. Он применим только тогда, когда нужно просто записать число со степенью в ячейке.
- Форматируем ячейку, в которую будет производиться запись, в текстовый формат. Выделяем её. Находясь во вкладке em«Главная» на ленте в блоке инструментов «Число», кликаем по выпадающему списку выбора формата. Жмем по пункту «Текстовый».
В одной ячейке записываем число и его степень. Например, если нам нужно написать три во второй степени, то пишем «32».
Ставим курсор в ячейку и выделяем только вторую цифру.
Нажатием сочетания клавиш Ctrl+1 вызываем окно форматирования. Устанавливаем галочку около параметра «Надстрочный». Жмем на кнопку «OK».
Внимание! Несмотря на то, что визуально в ячейке будет отображаться число в степени, Excel воспринимает его как обычный текст, а не числовое выражение. Поэтому для расчетов такой вариант применять нельзя. Для этих целей используется стандартная запись степени в этой программе – «^».
Как видим, в программе Excel существует сразу несколько способов возведения числа в степень. Для того, чтобы выбрать конкретный вариант, прежде всего, нужно определиться, для чего вам нужно выражение. Если вам нужно произвести возведение для записи выражения в формуле или просто для того, чтобы вычислить значение, то удобнее всего производить запись через символ «^». В отдельных случаях можно применить функцию СТЕПЕНЬ. Если вам нужно возвести число в степень 0,5, то существует возможность воспользоваться функцией КОРЕНЬ. Если же пользователь хочет визуально отобразить степенное выражение без вычислительных действий, то тут на помощь придет форматирование.
Мы рады, что смогли помочь Вам в решении проблемы.
Помимо этой статьи, на сайте еще 11905 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.
Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.
Построение матрицы средствами Excel в большинстве случаев требует использование формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (диапазон чисел).
Порядок применения формулы массива:
- Выделить диапазон, где должен появиться результат действия формулы.
- Ввести формулу (как и положено, со знака «=»).
- Нажать сочетание кнопок Ctrl + Shift + Ввод.
В строке формул отобразится формула массива в фигурных скобках.
Чтобы изменить или удалить формулу массива, нужно выделить весь диапазон и выполнить соответствующие действия. Для введения изменений применяется та же комбинация (Ctrl + Shift + Enter). Часть массива изменить невозможно.
С матрицами в Excel выполняются такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение обратной матрицы и ее определителя.
Транспонирование
Транспонировать матрицу – поменять строки и столбцы местами.
Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.
- 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.
- 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.
Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.
Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.
Сложение
Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.
В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.
Умножение матриц в Excel
Условие задачи:
Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).
Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.
В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.
Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.
Обратная матрица в Excel
Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).
Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.
Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:
Нахождение определителя матрицы
Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.
Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).
Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Источник: https://exceltable.com/funkcii-excel/funkcii-dlya-raboty-s-matricami
Матрицы в Excel: операции (умножение, деление, сложение, вычитание, транспонирование, нахождение обратной матрицы, определителя)
Рассмотрим матрицу А размерностью 3х4. Умножим эту матрицу на число k. При умножении матрицы на число получается матрица такой же размерности, что и исходная, при этом каждый элемент матрицы А умножается на число k.
Введем элементы матрицы в диапазон В3:Е5, а число k — в ячейку Н4.
В диапазоне К3:N5 вычислим матрицу В, полученную при умножении матрицы А на число k: В=А*k.
Для этого введем формулу =B3*$H$4 в ячейку K3, где В3 — элемент а11 матрицы А.
Примечание: адрес ячейки H4 вводим как абсолютную ссылку, чтобы при копировании формулы ссылка не менялась.
С помощью маркера автозаполнения копируем формулу ячейки К3 вниз и вправо на весь диапазон матрицы В.
Таким образом, мы умножили матрицу А в Excel и получим матрицу В.
Для деления матрицы А на число k в ячейку K3 введем формулу =B3/$H$4 и скопируем её на весь диапазон матрицы В.
Способ 2
Этот способ отличается тем, что результат умножения/деления матрицы на число сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий исходную матрицу А, нажимаем на клавиатуре знак умножить (*) и выделяем ячейку с числом k. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Для выполнения деления в данном примере в диапазон вводим формулу =B3:E5/H4, т.е. знак «*» меняем на «/».
Сложение и вычитание матриц в Excel
Способ 1
Следует отметить, что складывать и вычитать можно матрицы одинаковой размерности (одинаковое количество строк и столбцов у каждой из матриц). Причем каждый элемент результирующей матрицы С будет равен сумме соответствующих элементов матриц А и В, т.е. сij = аij + bij.
Рассмотрим матрицы А и В размерностью 3х4. Вычислим сумму этих матриц.
Для этого в ячейку N3 введем формулу =B3+H3, где B3 и H3 – первые элементы матриц А и В соответственно.
При этом формула содержит относительные ссылки (В3 и H3), чтобы при копировании формулы на весь диапазон матрицы С они могли измениться.
С помощью маркера автозаполнения скопируем формулу из ячейки N3 вниз и вправо на весь диапазон матрицы С.
Для вычитания матрицы В из матрицы А (С=А — В) в ячейку N3 введем формулу =B3 — H3 и скопируем её на весь диапазон матрицы С.
Способ 2
Этот способ отличается тем, что результат сложения/вычитания матриц сам является массивом. В этом случае нельзя удалить элемент массива.
Для деления матрицы на число этим способом выделяем диапазон, в котором будет вычислен результат, вводим знак «=», выделяем диапазон, содержащий первую матрицу А, нажимаем на клавиатуре знак сложения (+) и выделяем вторую матрицу В. После ввода формулы нажимаем сочетание клавиш Ctrl+Shift+Enter, чтобы значениями заполнился весь диапазон.
Умножение матриц в Excel
Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.
Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.
- В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.
В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.
- Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.
Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.
- Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.
В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С.
- Мы получим результат умножения матриц А и В.
- Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.
Транспонирование матрицы в Excel
Транспонирование матрицы — операция над матрицей, при которой столбцы заменяются строками с соответствующими номерами. Обозначим транспонированную матрицу АТ.
- Пусть дана матрица А размерностью 3х4, с помощью функции =ТРАНСП() вычислим транспонированную матрицу АТ, причем размерность этой матрицы будет 4х3.
- Выделим диапазон Н3:J6, в который будут введены значения транспонированной матрицы.
- На вкладке Формулы выберем Вставить функцию, выберем категорию Ссылки и массивы — функция ТРАНСП — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:Е5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы АТ.
- Нажмите для увеличения
- Мы получили транспонированную матрицу.
Нахождение обратной матрицы в Excel
Матрица А-1 называется обратной для матрицы А, если АžА-1=А-1žА=Е, где Е — единичная матрица. Следует отметить, что обратную матрицу можно найти только для квадратной матрицы (одинаковое количество строк и столбцов).
- Пусть дана матрица А размерностью 3х3, найдем для неё обратную матрицу с помощью функции =МОБР().
- Для этого выделим диапазон G3:I5, который будет содержать элементы обратной матрицы, на вкладке Формулы выберем Вставить функцию.
- В диалоговом окне Вставка функции выберем категорию Математические — функция МОБР — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.
ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы А-1.
- Нажмите для увеличения
- Мы получили обратную матрицу.
Нахождение определителя матрицы в Excel
Определитель матрицы — это число, которое является важной характеристикой квадратной матрицы.
Как найти определить матрицы в Excel
- Пусть дана матрица А размерностью 3х3, вычислим для неё определитель с помощью функции =МОПРЕД().
- Для этого выделим ячейку Н4, в ней будет вычислен определитель матрицы, на вкладке Формулы выберем Вставить функцию.
- В диалоговом окне Вставка функции выберем категорию Математические — функция МОПРЕД — ОК.
В диалоговом окне Аргументы функции указываем диапазон массива В3:D5, содержащего элементы матрицы А. Нажимаем ОК.
- Нажмите для увеличения
- Мы вычислили определитель матрицы А.
В заключение обратим внимание на важный момент. Он касается тех операций над матрицами, для которых мы использовали встроенные в программу функции, а в результате получали новую матрицу (умножение матриц, нахождение обратной и транспонированной матриц).
В матрице, которая получилась в результате операции, нельзя удалить часть элементов. Т.е. если мы выделим, например, один элемент матрицы и нажмём Del, то программа выдаст предупреждение: Нельзя изменять часть массива.
Источник: http://pedsovet.su/excel/6080_operacii_s_matricami
Вычисление обратной матрицы в Microsoft Excel
Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
-
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
-
- Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
-
- Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
- Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.
Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
-
- Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
-
- В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
-
- В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
-
- Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
- Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго.
Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи.
Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Источник: https://lumpics.ru/the-inverse-matrix-in-excel/
Действия с матрицами в Excel
Сегодня мы научимся работать с матрицами в Excel. Особенно актуальным этот пост будет для студентов, которые в данный момент изучают математику (линейную алгебру или высшую математику).
Выполняя действия с матрицами, вам постоянно приходится сталкиваться со следующими операциями:
1. Транспонирование — когда строки матрицы заменяются ее столбцами и наоборот;
2. Сложение матриц;
3. Умножение матрицы на число или умножение матриц между собой;
4. Нахождение обратной матрицы;
5. Нахождение определителя матрицы.
1. Транспонирование матрицы. Поместим на рабочем листе Excel в ячейках B2:H5 исходную матрицу, которую нужно транспонировать и заполним ее произвольными числами.
Транспонирование матриц в Excel можно выполнять двумя способами:
- используя встроенную функцию =ТРАНСП();
- воспользовавшись буфером обмена, можно скопировать исходную матрицу и вставив ее специальным образом, сразу транспонировать.
Соответственно, результат транспонирования исходной матрицы первым способом разместим в ячейках В8:Е14, а вторым способом — в ячейках В17:Е23, как показано на рисунке.
Каждый рисунок можно увеличить щелчком левой кнопки мыши на нем
Итак, устанавливаем курсор мыши в ячейке В8 и используя мастер функций вводим в нее формулу: =ТРАНСП(B2:H5)
При использовании функции =ТРАНСП() возникает один интересный момент. Как только мы вводим формулу и нажимаем на клавиатуре клавишу «ENTER», то вместо результата вычисления получаем ошибку «#ЗНАЧ!». В чем же дело?
Как вы знаете, результатом транспонирования исходной матрицы является тоже матрица! При этом, число ее строк равно числу столбцов исходной, а число столбцов — числу строк исходной матрицы. Но когда мы вводим формулу =ТРАНСП(B2:H5) и нажимаем «ENTER», то получаем одно значение! И это как раз наше сообщение об ошибке. Как заставить функцию вернуть не одно значение, а массив?
Для этого устанавливаем курсор мыши в ячейке В8 и удерживая левую кнопку мыши, растягиваем область выделения до ячейки Е14. Таким образом, мы выделили диапазон ячеек, куда должна вернуться транспонированная матрица. Далее, не снимая выделения, нажимаем на клавиатуре клавишу , а затем одновременно комбинацию кнопок ++. Чудо произошло! Весь выделенный диапазон заполнится нужными значениями!
Этот же прием мы будем неоднократно использовать ниже, во время умножения матриц друг на друга, а также нахождения обратной матрицы. И, как обещал, еще один, очень быстрый способ транспонирования с помощью буфера обмена.
Сначала выделяем диапазон ячеек В2:Н5 с исходной матрицей и во вкладке «Главная» нажимаем кнопку «Копировать». Затем устанавливаем курсор мыши в ячейку, начиная с которой мы хотим получить транспонированную матрицу. В нашем случае это ячейка В17. Во вкладке «Главная» нажимаем кнопку «Вставить», «Специальная вставка». В открывшемся окне выделяем флаг «Транспонировать», как показано на рисунке, и нажимаем кнопку «ОК».


Если исходная матрица в ячейках В2:Н5 изменится, то транспонированная матрица в ячейках В8:Е14 пересчитается автоматически, так как сработает функция =ТРАНСП(). А вот в ячейках В17:Е23 матрица останется без изменений, обратите на это внимание!
Сложение матриц. Здесь нет никакой хитрости, все очень просто. Сложение выполняется для двух матриц одинаковой размерности. Каждый элемент суммарной матрицы равен сумме соответствующих элементов двух исходных матриц.

Умножение матриц. Как было сказано выше, мы можем умножать матрицу на число или перемножать матрицы между собой.
В случае умножения исходной матрицы на число, мы должны каждый ее элемент умножить на это число, как показано на рисунке:

Не все матрицы можно перемножать между собой. Для этого они должны соответствовать определенному правилу: количество столбцов первой матрицы должно равняться количеству строк второй матрицы. Если это равенство не соблюдается, такие матрицы перемножаться не могут.
В результате перемножения мы тоже должны получить матрицу, число строк которой равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.
Учитывая все вышесказанное, получим:

Обратная матрица. Нахождение обратной матрицы связано с использованием встроенной функции =МОБР() и также имеет ограничение:
Нахождение обратной матрицы возможно только тогда, когда число строк матрицы равняется числу ее столбцов. То есть, только когда матрица квадратная. Кроме того, исходная матрица не должна быть вырожденной. То есть, ее определитель не должен быть равен нулю.

Определитель матрицы. Определитель матрицы будем находить с помощью встроенной функции =МОПРЕД(). Как и в случае с обратной матрицей, определитель мы будем находить только для квадратной матрицы.

В данном случае функция возвращает единственное число, а не массив значений, поэтому никаких дополнительных действий не требуется.
Как сообщалось на нашем сайте ранее, с помощью встроенной функции Excel ТЕНДЕНЦИЯ() вы можете с легкостью строить линейные прогнозы для исходных показателей динамики.
Источник: https://videolections.blogspot.com/2015/09/excel_28.html
Вычисление обратной матрицы в MS EXCEL
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE.
- Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
- СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
- Матрица А-1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А-1*А=Е и А*А-1=Е, где Е единичная матрица порядка n.
- Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР().
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера):
- выделить диапазон 2 х 2, который не пересекается с исходным диапазоном А8:В9, например, Е8:F9
- в Cтроке формул ввести формулу =МОБР(A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР({5;4: 3;2}).
Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией.
Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон.
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ()), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР().
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
В качестве проверки можно перемножить исходную и обратную матрицы. В результате должна получиться единичная матрица.
Источник: https://excel2.ru/articles/vychislenie-obratnoy-matricy-v-ms-excel
Татьяна Шкляр
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Excel – это созданная корпорацией Microsof программа, предназначенная для работы с электронными таблицами.
Введение
Матрица представляет собой комплект ячеек, которые располагаются последовательно одна за другой и отображаются как прямоугольник. Операции с матрицами в Excel выполняются аналогично работе со стандартным диапазоном памяти. Все матрицы обладают отдельным адресом, который записывается так же, как и диапазон. Сначала указывается адрес первой ячейки диапазона, которая располагается вверху в левом углу. Далее записывается адрес последней ячейки, расположенной в нижнем правом углу.
Формулы массива
Матрица, по сути, является массивом и для работы с ними применяются соответствующие формулы. Главным их отличием от стандартных формул считается то, что обычные стандартные формулы могут вывести только одну величину. Чтобы использовать формулы работы с массивами, следует выполнить такой набор операций:
- Осуществить выделение участка ячеек, куда следует вывести значения.
- Задать требуемую формулу для вычислений.
- Нажать клавишный набор Ctrl + Shift +Enter.
По завершению этих процедур в поле для ввода отобразится формула массива. Она отличается от стандартной формулы наличием фигурных скобок. Чтобы отредактировать или удалить формулу работы с массивом, нужно сделать выделение нужного диапазона и выполнить коррекцию. Для редактирования самой матрицы применяются те же комбинации клавиш, что и при её формировании.
Операции с матрицами
Операция замены местами строк и столбцов называется транспонированием. Перед началом этой процедуры, надо выполнить выделение отдельной зоны, имеющей число строк равное числу столбцов преобразуемой матрицы, и то же самое относительно столбцов. Существует два способа выполнения транспонирования. Согласно первому способу надо выполнить следующие действия:
- Нужно выполнить выделение матрицы и сделать её копию.
- Выполнить выделение диапазона ячеек для вставки транспонируемого диапазона.
- Открыть окно «Специальная вставка».
- Выбрать кнопку «Транспонировать» и нажать ОК.
«Матрица в Excel» 👇
Второй способ заключается в следующем. Нужно выполнить выделение ячейки, находящейся в левом верхнем углу диапазона, выделенного для транспонируемой матрицы. Далее следует открыть диалоговое окно с набором функций и выбрать функцию ТРАНСП.
Рисунок 1. Окно программы. Автор24 — интернет-биржа студенческих работ
В качестве параметра функции используется диапазон, соответствующий изначальной матрице. Но после того, как будет нажата клавиша ОК, появится сообщение об ошибке, поскольку вставляемая функция не определена в качестве формулы массива. То есть далее надо сделать следующее:
- Выполнить выделение комплекта ячеек, предназначенных для транспонируемой матрицы.
- Нажать кнопку F2.
- Нажать набор клавиш Ctrl + Shift + Enter.
Основным преимуществом такого способа является то, что транспонированная матрица сразу способна корректировать заложенную в неё информацию, по мере внесения коррекций в исходную матрицу.
Далее рассмотрим операцию сложения. Эта операция допустима только для тех диапазонов, которые имеют одинаковое число компонентов. Иначе говоря, матрицы, подлежащие сложению, обязаны иметь один и тот же размер. Пример представлен на рисунке ниже:
Рисунок 2. Пример. Автор24 — интернет-биржа студенческих работ
В итоговой матрице необходимо сделать выделение первой ячейки и задать следующую формулу:
= Начальный компонент первой матрицы + Начальный компонент второй матрицы
Затем следует подтвердить задание формулы клавишей Enter и применить функцию авто заполнения (квадрат в нижнем правом углу) для копирования всех величин в новую матрицу. Итог приведён на рисунке ниже:
Рисунок 3. Итог. Автор24 — интернет-биржа студенческих работ
Далее рассмотрим операцию умножения. Имеется следующая таблица, все элементы которой необходимо умножить на двенадцать:
Рисунок 4. Таблица. Автор24 — интернет-биржа студенческих работ
Суть метода умножения аналогична сложению, но здесь нужно все ячейки матрицы умножить на двенадцать и итог также отразить в отдельной матрице. Необходимо помнить об указании абсолютных ссылок на ячейки. В итоге получаем формулу:
=A1*$E$3
И результирующую матрицу:
Рисунок 5. Результирующая матрица. Автор24 — интернет-биржа студенческих работ
Рассмотрим пример перемножения матриц. Это возможно только при соблюдении одного условия. Необходимо, чтобы число строк и столбцов у этих матриц являлось зеркально одинаковым, то есть число столбцов равнялось числу строк.
Рисунок 6. Перемножение матриц. Автор24 — интернет-биржа студенческих работ
Для удобства можно выделить диапазон итоговой матрицы. Следует поместить курсор на ячейку в левом верхнем углу и задать следующую формулу:
=МУМНОЖ(А9:С13;Е9:H11).
Далее следует нажать комбинацию клавиш Ctrl + Shift + Enter, чтобы увидеть итог:
Рисунок 7. Итог. Автор24 — интернет-биржа студенческих работ
Далее рассмотрим пример обратной матрицы. Если матрица (её диапазон) квадратной формы, то есть число ячеек по вертикали равно числу ячеек по горизонтали, то значит, при необходимости, можно определить обратную матрицу. Это можно сделать при помощи функции МОБР. Сначала нужно сделать выделение первой ячейки матрицы, куда будет вставлена обратная матрица. В неё нужно ввести формулу:
=МОБР(A1:A4).
В качестве аргумента нужно указать диапазон, для которого следует сформировать обратную матрицу. Далее нужно использовать комбинацию клавиш Ctrl + Shift + Enter.
Рисунок 8. Окно программы. Автор24 — интернет-биржа студенческих работ
Далее рассмотрим нахождение определителя матрицы. Определителем матрицы является число, определяемое для квадратной матрицы по заданной формуле. Для этой цели в программе Excel есть специальная функция МОПРЕД. Необходимо установить курсор на любую ячейку матрицы и задать функцию:
=МОПРЕД(A1:D4).
Далее рассмотрим ещё один пример вычислений. Имеется матрица А, размером три на четыре. Есть, так же, некоторое число k, записанное вне матрицы. Когда будет выполнена операция умножения матрицы на это число, возникнет диапазон величин, который имеет такие же размеры, но все его компоненты умножены на k:
Рисунок 9. Окно программы. Автор24 — интернет-биржа студенческих работ
Диапазон B3:E5 является исходной матрицей, подлежащей умножению на число k, расположенному в клетке H4. Итоговая матрица будет располагаться в диапазоне K3:N5. Исходная матрица обозначается как А, а итоговая как В. Итоговая матрица В будет образована умножением матрицы А на величину k. Формула для вычислений записывается в ячейку К3:
=B3*$H$4.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме