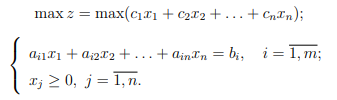Структура сценария вставляется в виде отдельного
листа непосредственно перед активным листом. Если отчеты по сценарию
создавались несколько раз, названия листов автоматически нумеруются («Структура
сценария 1», «Структура сценария 2» и т.д.).
Рисунок 37 – Диалоговое окно «Диспетчер сценариев»
Полученное решение также может быть сохранено в виде
сценария. Таким образом, можно запомнить результаты решения задачи для
различных вариантов исходных данных, провести вариантный анализ.
Рисунок 38 – Диалоговое окно «Отчет по сценарию»
После сохранения сценария продолжается работа в том
же окне, из которого это сохранение осуществлялось («Текущее состояние поиска
решения» или «Результаты поиска решения»).
С помощью соответствующих кнопок в «Диспетчере
сценариев» сохраненные сценарии можно изменять и удалять; можно добавлять новые
(при этом необходимо указать изменяемые ячейки, и их значения, которые
необходимо запомнить); объединять список сценариев со сценариями, находящимися
на другом листе; выводить сохраненные значения изменяемых ячеек на рабочий лист
(в те же ячейки).
6.5 Результаты решения задачи
После окончания работы «Поиска решения» оптимальный
план и оптимум, если они получены, находятся в тех ячейках, которые были
выбраны в качестве влияющих и целевой.
В рассмотренном примере (см. таблицу 26, раздел 6.2)
после нажатия кнопки «Выполнить» в ячейке В6 появится число 266,7 (х1
= 266,7), в С6 – 1173,3 (х2 = 1173,3), а в В11 – 193066,7
(оптимальное значение прибыли).
Кроме того, выводится диалоговое окно «Результаты
поиска решения», представленное на рисунке 39.
Рисунок 39 — Диалоговое окно «Результаты поиска решения»
С помощью переключателей в этом окне по желанию
пользователя найденное решение может быть сохранено в соответствующих ячейках,
либо в них восстанавливаются исходные значения (в примере из раздела 6.2 –
нулевые). По умолчанию при нажатии кнопки «ОК» решение сохраняется, а если
закрыть окно или воспользоваться «Отменой», будут восстановлены исходные
значения.
Поле «Тип отчета» служит для того, чтобы
пользователь мог получить отчеты о решении задачи (см. раздел 6.6). Для этого
необходимые типы отчетов надо выделить до нажатия кнопки «ОК». Каждый отчет
размещается на отдельном листе книги Microsoft Excel (как и «Структура сценария»).
Эти листы программа также вставляет непосредственно перед активным листом. Если
«Поиск решения» использовался несколько раз, и при этом создавались отчеты,
названия отчетов автоматически нумеруются. Если решение не было найдено,
обратиться к «Типу отчета» невозможно. Кроме того, для целочисленных задач не
выдаются отчеты по устойчивости и пределам.
Нажатием кнопки «Сохранить сценарий» полученное
решение может быть сохранено в виде сценария.
Первые строки окна результатов занимает итоговое
сообщение, которое может быть различным по содержанию. При успешном окончании
процедуры поиска решения для линейной модели выдается сообщение: «Решение найдено.
Все ограничения и условия оптимальности выполнены» (см. рисунок 38). Если поиск
не получил оптимального решения, выдается одно из сообщений, приведенных в
таблице 28.
Таблица 28 – Итоговые
сообщения «Поиска решения»
|
Итоговое сообщение |
Характеристика результата поиска |
Рекомендуемые действия (для линейной задачи) |
|
|
Поиск |
Время, |
Следует увеличить |
|
|
Поиск |
Произведено |
Следует увеличить |
|
|
Значения |
Целевая |
Если необходимо поставить |
|
|
Поиск |
Нажата кнопка “Стоп” в окне |
||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
В этой статье обсуждается использование надстройки Microsoft Excel «Решение», которая позволяет анализировать «что если» для определения оптимального сочетания продуктов.
Как определить ежемесячный набор продуктов, который позволяет повысить прибыльность?
Компаниям часто требуется определять количество каждого продукта, который будет создаваться ежемесячно. В простейшей форме проблема в наборе продуктов состоит в том, как определить объем каждого продукта, который должен быть произведен в течение месяца, чтобы максимально увеличить прибыль. Сочетание продуктов обычно должно соответствовать следующим ограничениям:
-
Сочетание продуктов не может использовать больше ресурсов, чем доступно.
-
Потребность в каждом продукте ограничена. В течение месяца мы не можем создать больше продукции, чем это диктует потребность в продукции, так как в нее нагребают лишние продукты (например, избежаемый продукт).
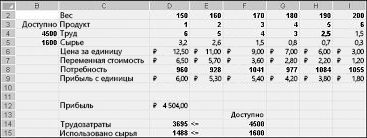
Теперь рассмотрим пример проблемы со сочетанием продуктов. Решение этой проблемы можно найти в файле Prodmix.xlsx, как показано на рисунке 27-1.
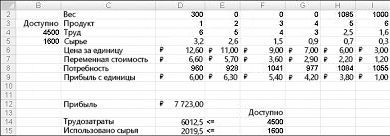
Предположим, что мы работаем в компании, которая производит шесть различных продуктов на своем заводе. Для производства каждого продукта требуются трудовые и необработанные материалы. В строке 4 на рисунке 27-1 показано количество часов труда, необходимое для получения фунта каждого товара, а в строке 5 — фунт необработанных материалов, необходимых для получения фунта каждого товара. Например, для получения фунта продукта 1 требуется 6 часов труда и 3,2 фунта неотработанных материалов. Цена за фунт для каждого фунта задается в строке 6, цена за единицу за фунт — в строке 7, а доход за фунт — в строке 9. Например, товар 2 продается по 11,00 долларов США за фунт, за единицу стоит 5,70 долларов США за фунт и вклад в сумму 5,30 долларов США за фунт. Запрос за месяц для каждого подмайки выдается в строке 8. Например, потребность в продукте 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов необработанных материалов. Как эта компания может максимально увеличить ежемесячную прибыль?
Если бы нам не было известно ничего о надстройке Excel «Решение», мы могли бы решить эту проблему, построив на этом листах данные о прибылях и использовании ресурсов, связанных с этим сочетанием продуктов. Затем мы использовали пробные и ошибки, чтобы оптимизировать прибыль, не используя при этом больше ресурсов и необработанных материалов, чем доступно, и не изменяя при этом лишние продукты. Над решением этой процедуры мы используем только пробную стадию с ошибкой. По сути, «Поиск решения» — это механизм оптимизации, который безукоризненно выполняет поиск по пробным версиям и ошибкам.
Ключ к решению этой проблемы — эффективное вычисление использования ресурсов и прибыли, связанных с любым сочетанием продуктов. Для этого важно использовать функцию СУММПРОИDUCT. Функция СУММПРОИCT перемножает соответствующие значения в диапазонах ячеев и возвращает сумму этих значений. Каждый диапазон ячеок, используемый в оценке СУММПРОИДУCT, должен иметь одинаковые размеры, что подразумевает, что можно использовать суммпроидуц с двумя строками или двумя столбцами, но не с одной строкой и столбцом.
В качестве примера использования функции СУММПРОИПР в нашем примере мы постараемся вычислить использование ресурсов. Трудоемкие труды вычисляются по
(Количество трудовых единиц, использованных для одного фунта воды в секунду)*(1 фунт 1, произведено)+
(Трудоемка, используемая для одного фунта валюты 2)*(2 фунта, произведенного) + …
(Трудоемка, используемая для одного фунта валюты 6)*(6 фунтов в секунду)
Мы могли бы более утомительным образом вычислять использование труда, как D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4. Кроме того, использование необработанных материалов можно вычислять как D2*D5+E2*E5+F2*F5+G2*G5+H2*H5+I2*I5. Однако ввод этих формул на таблицу для шести продуктов отнимает много времени. Представьте, сколько времени займет работа с компанией, которая производит, например, 50 продуктов на своем заводе. Гораздо проще вычислять трудоемкие и необработанные данные, скопируя из D14 в D15 формулу СУММПРОИДУCT($D$2:$I$2;D4:I4). Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+H2*H4+I2*I4 (это наш рабочий процесс), но гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, чтобы при копировании формулы все равно записать сочетание продуктов из строки 2. Формула в ячейке D15 вычисляет использование необработанных материалов.
Аналогичным образом прибыль определяется с помощью
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Доход легко вычисляется в ячейке D12 с помощью формулы СУММПРОИКТ(D9:I9;$D$2:$I$2).
Теперь мы можем определить три компонента модели решения для всех продуктов.
-
Целевая ячейка. Наша цель — максимально увеличить прибыль (вычисленную в ячейке D12).
-
Изменяя ячейки. Количество фунта, произведенного каждым продуктом (в диапазоне ячеок D2:I2)
-
Ограничения. В этом примере есть следующие ограничения:
-
Не используйте больше трудовых или необработанных материалов, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
-
Не выполыв при этом больше средств, чем нужно. Это значит, что значения в ячейках D2:I2 (фунта, произведенного для каждого пациента) должны быть меньше или равны требованию для каждого пациента (в ячейках D8:I8).
-
Мы не можем привести к отрицательным последствиям любых проблем с наркотиками.
-
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в «Найти решение». Все, что вам нужно сделать, — это нажать кнопку «Найти решение», чтобы найти набор товаров, который максимально увеличить прибыль!
Для начала на вкладке «Данные» в группе «Анализ» нажмите кнопку «Найти решение».
Примечание: Как объяснялось в главе 26 «Введение в оптимизацию с помощью надстройки Excel «Решение», надстройка «Решение» устанавливается с помощью кнопки Microsoft Office, а затем параметров Excel и надстройки. В списке «Управление» щелкните «Надстройки Excel», выберите поле «Найти решение» и нажмите кнопку «ОК».
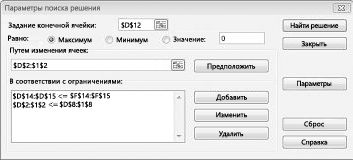
Появится диалоговое окно «Параметры решения», как показано на рисунке 27–2.
Щелкните поле «Установить целевую ячейку» и выберите ячейку прибыли (ячейка D12). Щелкните поле «Изменяя ячейки», а затем найдите диапазон D2:I2, содержащий количество отсюдоха каждого пациента. Диалоговое окно будет выглядеть как «Рисунок 27-3».
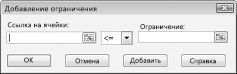
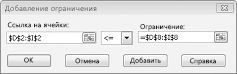
Теперь можно добавить ограничения в модель. Нажмите кнопку «Добавить». На рисунке 27–4 показано диалоговое окно «Добавить ограничение».
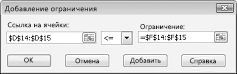
Чтобы добавить ограничения использования ресурсов, щелкните поле «Ссылка на ячейку» и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле ограничения, а затем выберите диапазон ячеев F14:F15. Диалоговое окно «Добавить ограничение» должно выглядеть так: «Рисунок 27-5».
Теперь, когда «Найти решение» пытается использовать другие значения для изменяющихся ячеек, будут учитываться только сочетания, которые удовлетворяют как D14<=F14 (трудоемка меньше или равна доступной работе), так и D15<=F15 (используемый необработаный материал меньше или равен доступному неоцененному). Нажмите кнопку «Добавить», чтобы ввести ограничения по запросу. Заполните поле в диалоговом окне «Добавить ограничение», как показано на рисунке 27–6.
Добавление этих ограничений гарантирует, что при попытках «Найти решение» для изменяемого значения ячейки будут учитываться только сочетания, которые удовлетворяют следующим параметрам:
-
D2<=D8 (количество произведенного средства 1 не превышает потребность в этом средстве)
-
E2<=E8 (количество произведенного средства 2 не превышает или равно запросу на доступ к более 2).
-
F2<=F8 (количество произведенного средства 3 не превышает потребность в этом средстве)
-
G2<=G8 (количество произведенного средства 4 не превышает или равно запросу на доступ к наркотиками 4)
-
H2<=H8 (количество произведенного средства 5 не превышает или равно запросу на доступ к более 5).
-
I2<=I8 (количество произведенного средства 6 не превышает потребность в этом средстве)
В диалоговом окне «Добавить ограничение» нажмите кнопку «ОК». Окно «Решение» должно выглядеть так: «Рисунок 27-7».
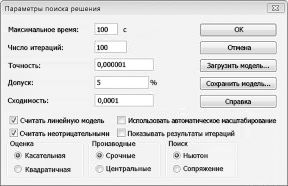
В диалоговом окне «Параметры решения» введите ограничение на то, что изменяющиеся ячейки не должны быть отрицательными. Нажмите кнопку «Параметры» в диалоговом окне «Параметры решения». Проверьте окне «Предполагаемая линейная модель» и «Нео отрицательная», как показано на рисунке 27–8 на следующей странице. Нажмите кнопку «ОК».
При проверке значения «Предположим, неохожим» над решением будут учитываться только сочетания изменяющихся ячеек, в которых каждая из изменяющихся ячеек принимает нео отрицательное значение. Мы проверили поле «Предполагаемая линейная модель», так как проблема с сочетанием продуктов — это особый тип решения, называемый линейной моделью. По сути, модель «Поиск решения» является линейной в следующих условиях:
-
Целевая ячейка вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа).
-
Каждое ограничение соответствует «требованиям к линейной модели». Это означает, что каждое ограничение вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой.
Почему эта проблема «Поиск решения» линейный? Целевая ячейка (прибыль) вычисляется как
(Доход от 1 дохода на фунт)*(1 фунт произведен) +
(Доход от 2 дохода на фунт)*(2 фунта произведено) + …
(6 доход на фунт)*(произведено 6 фунтов)
Эта вычисление вычисляется по шаблону, в котором вычисляется значение конечной ячейки путем с суммирования терминов формы (изменяемой ячейки)*(константа).
Наше ограничение на работу вычисляется путем сравнения значения, полученного из (Количество, используемого в фунте по 1)*(1 фунта влияния) + (Количество, используемого для одного фунта в фунте до 2)*(Фунт 2, полученный в качестве 2 фунта)+ (Трудоемкие мыed per pound of Drug 6)*(Pound 6 pound produced) to the labor available.
Следовательно, ограничение трудоемких ресурсов вычисляется путем с совокупности терминов формы (изменяемой ячейки)*(константа) и сравнения сумм с константой. Ограничение трудоемких ресурсов и ограничение в необработанных материалах отвечают требованиям к линейной модели.
Наши ограничения запроса принимают форму
(От 1 досье 1)<=(Потребность в наркотиками 1)
(От 2 досье 2)<=(Потребность в наркотиками 2)
§
(от 6 досье 6)<=(Потребность в наркотиками 6)
Каждое ограничение запроса также соответствует требованию к линейной модели, поскольку каждое из них вычисляется путем свести вместе условия формы (изменяемая ячейка)*(константа) и сравнить суммы с константой.
Если вы показываете, что модель нашего продукта является линейной, почему это важно?
-
Если модель «Поиск решения» является линейной и выбран вариант «Предположим, линейный режим», «Поиск решения» гарантирован, что будет найдено оптимальное решение для модели «Поиск решения». Если модель «Поиск решения» не линейный, «Поиск решения» может не найти оптимальное решение.
-
Если модель «Поиск решения» является линейной и выбран вариант «Предполагаемая линейная модель», то для поиска оптимального решения модели используется очень эффективный алгоритм (метод простого решения). Если модель «Поиск решения» является линейной и не выбран вариант «Предполагаемая линейная модель», «Поиск решения» использует очень неэффективный алгоритм (метод ОГР2), что может затруднить поиск оптимального решения модели.
После нажатия кнопки «ОК» в диалоговом окне «Параметры решения» вернимся в главное диалоговое окно «Решение», показанное ранее на рисунке 27–7. При нажатии кнопки «Поиск решения» «Поиск решения» вычисляет оптимальное решение (если оно существует) для модели микса продуктов. Как было сказано в главе 26, оптимальным решением для модели набора продуктов является набор изменяемых значений ячеок (фунта, произведенного каждым продуктом), который позволяет максимально увеличить прибыль в наборе всех возможных решений. В этом же, целесообразное решение — это набор изменяющихся значений ячеок, удовлетворяющий всем ограничениям. Изменяющиеся значения ячеок, показанные на рисунке 27–9, являются допустимым решением, поскольку все производственные уровни неоценимы, производственные уровни не превышают потребность, а использование ресурсов не превышает доступных ресурсов.
Изменяемые значения ячеек, показанные на рисунке 27–10 на следующей странице, являются неизменяемым решением по следующим причинам:
-
Мы выпускаем больше 5, чем за него требуются.
-
Мы используем больше трудоемких ресурсов, чем доступно.
-
Мы используем больше необработанных материалов, чем доступно.
Нажав кнопку «Поиск решения», «Поиск решения» быстро найдет оптимальное решение, показанное на рисунке 27–11. Вам нужно выбрать «Сохранить решение для решения проблемы», чтобы сохранить оптимальные значения решения на работе.
Наша организация, которая занимается наркотиками, может увеличить ежемесячную прибыль в размере 6 625,20 долларов США, выполив 596,67 фунта 4, 1084 фунта для подавлили 5 рублей и ни одного другого фунта! Мы не можем определить, можно ли достичь максимальной прибыли в 6 625,20 долларов США другими способами. Все, что мы можем быть уверены, что из-за ограниченных ресурсов и требований в этом месяце нельзя внести больше 6 627,20 долларов США.
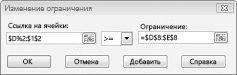
Предположим, что потребность в каждом продукте должна быть выполнены. (См. таблицу «Нет реального решения» в Prodmix.xlsx.) Затем нам нужно изменить ограничения по запросу с D2:I2<=D8:I8 на D2:I2>=D8:I8. Для этого откройте «Решение», выберите ограничение D2:I2<=D8:I8 и нажмите кнопку «Изменить». Появится диалоговое окно «Изменение ограничения», показанное на рисунке 27–12.
Выберите >=, а затем нажмите кнопку «ОК». Теперь над решением можно изменить только значения ячеок, которые соответствуют всем запросам. При нажатии кнопки «Найти решение» отобразилось сообщение «Поиск решения не удалось найти целесообразное решение». Это сообщение не означает, что мы допустили ошибку в модели, а о том, что из-за ограниченных ресурсов мы не сможем выполнить потребность во всех товарах. Надстройка «Решение» просто сообщает нам, что если мы хотим удовлетворить потребность в каждом продукте, нам нужно добавить больше труда, дополнительных необработанных материалов или и тех, и других.
Давайте посмотрим, что произойдет, если разрешить неограниченную потребность в каждом продукте и разрешить отрицательные количества каждого товара. (Эта проблема возникает в области «Набор значений не сходится» на Prodmix.xlsx.) Чтобы найти оптимальное решение в этой ситуации, откройте «Поиск решения», нажмите кнопку «Параметры» и откроем поле «Неохритимые». В диалоговом окне «Параметры решения» выберите ограничение запроса D2:I2<=D8:I8, а затем нажмите кнопку «Удалить», чтобы удалить это ограничение. При нажатии кнопки «Найти решение» возвращается сообщение «Установить значение ячейки не сходится». Это сообщение означает, что если нужно развернуть целевую ячейку (как в нашем примере), существуют допустимые решения, в том числе и для суммарных значений целевых ячеок. (Если целевая ячейка должна быть свернута, сообщение «Установить значения ячейки не сходятся» означает, что существуют возможные решения с небольших целевых значений, заверяемого в третейском деле.) В нашем случае, разрешив негативное производство в случае злоупотреблений, мы фактически создадим ресурсы, которые можно использовать для вывода в произвольное количество других средств. С учетом нашего неограниченного запроса это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечно. Если вы видите сообщение «Установить значения не сходятся», это означает, что в модели есть ошибка.
-
Предположим, в нашей компании в течение часа можно приобретать до 500 часов работы на 100 рублей больше, чем за текущие трудоемкие расходы. Как максимально увеличить прибыль?
-
На изготовителе микросхем четыре технических специалиста (A, B, C и D) выпускают три продукта («Товары 1», «2» и «3»). В этом месяце изготовитель микросхемы может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Специалист А может делать только продукты 1 и 3. Специалист Б может делать только продукты 1 и 2. Специалист C может сделать только продукт 3. Специалист D может сделать только продукт 2. Для каждого произведенного товара внести следующую прибыль: Товар 1; 600 рублей; Товар 2; 7000 рублей; и товар 3, 1000 рублей. Время (в часах) каждого технических специалиста, необходимое для производства продукта, должно быть следующим:
Продукт
Специалист А
Специалист Б
Специалист C
Специалист Д
1
2
2,5
Не удается сделать
Не удается сделать
2
Не удается сделать
3
Не удается сделать
3,5
3
3
Не удается сделать
4
Не удается сделать
-
Каждый специалист может работать до 120 часов в месяц. Как изготовитель микросхем может максимально увеличить ежемесячную прибыль? Предположим, что можно получить лишь дробное количество единиц.
-
Компьютерный завод производит мыши, клавиатуры и игровые joysticks. Доход за единицу, за единицу трудоемких ресурсов, ежемесячная потребность и за единицу машинного времени даются в следующей таблице:
Мыши
Клавиатуры
Joysticks
Прибыль/единица
8 $
11 $
9 $
Использование трудов и единицы
0,2 часа
0,3 часа
0,24 часа
Машинное время/единица
0,04 ч
0,055 ч.
0,04 ч
Ежемесячный запрос
15 000
27,000
11,000
-
Каждый месяц доступно 13 000 часов труда и 3000 часов машинного времени. Как изготовитель может максимально увеличить ежемесячный взнос в прибыль от растения?
-
Допустим, необходимо устранить проблему с этой проблемой при условии, что должны быть выполнены минимальные требования к 200 единицам для каждого из них.
-
Он делает ромбовидные ромбои, окаймлы и затейные. Он хочет работать не более 160 часов в месяц. У него 800 ромбов. Ниже дается прибыль, время труда и количество ромбов, необходимых для получения каждого товара. Если потребность в каждом продукте не ограничена, как Максим может увеличить прибыль?
Продукт
Прибыль за единицу
Трудоемкие часы на единицу
Ромбы на единицу
Лексема
300р.
.35
1,2
Кулигов
200 ₽
.15
.75
Кулигов
100р.
0,05
.5
-
Tags:
- Составление математических моделей
- экономических задач
- Решение оптимизационных задач
- с помощью электронных таблиц
- Молоко поставляется
- формат Денежный
- Установить целевую ячейку
- Установить целевую ячейку
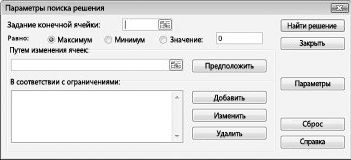
- Параметры поиска решения
Лабораторная работа. Составление математических моделей экономических задач. Решение оптимизационных задач с помощью электронных таблиц
Прочитайте Задание к лабораторной работе. Если вам необходимо вспомнить тему Поиск решения, выполните упражнения
Поиск решения
Подготовка к работе
Для выполнения упражнений и заданий необходимо наличие надстройки Поиск решения.
· Выполните команду Сервис/Поиск решения…
· Для загрузки надстройки выполните команду Сервис/Надстройки…
· В диалоговом окне Надстройки (рис. 11.1) установите флажок Поиск решения. OK.
Рис. 11.1
Упражнение № 11. SEQ Упражнение_№_*. * ARABIC 1
Частная фирма занимается переработкой молока на нескольких заводах, расположенных в разных районах Москвы. Молоко поставляется объединениями фермеров, расположенными в городах Московской области. Стоимость молока одинакова, однако перевозка от объединения фермеров на завод зависит от расстояния и отличается для каждого объединения и завода. Потребность заводов в молоке различна. Объем молока в каждом объединении ограничен.
Потребителей (молокоперерабатывающие заводы) назовем по наименованию районов Москвы, в которых они расположены, а поставщиков (объединения фермеров) – по названиям городов Подмосковья.
Потребность перерабатывающих заводов в молоке.
|
Лужники |
Сокол |
Измайлово |
Юго-Запад |
|
240 |
115 |
280 |
370 |
Возможности объединений в доставке молока.
|
Наро-Фоминск |
Солнечногорск |
Домодедово |
Балашиха |
Ногинск |
|
300 |
240 |
170 |
120 |
320 |
Для минимизации общих затрат на перевозку требуется определить, сколько поставлять молока, от какого объединения и на какой завод.
Затраты на перевозку тонны молока от объединения X к заводу, расположенному в районе Y, указаны в таблице.
|
Y X |
Лужники |
Сокол |
Измайлово |
Юго-Запад |
|
Наро-Фоминск |
4700 |
4150 |
4500 |
3265 |
|
Солнечногорск |
3900 |
3230 |
3800 |
4100 |
|
Домодедово |
2365 |
2730 |
2100 |
1800 |
|
Балашиха |
1950 |
1940 |
900 |
2400 |
|
Ногинск |
3900 |
3600 |
2750 |
4400 |
Решение
· Удалите все листы, кроме первого.
· Сохраните файл под именем Транспортная задача.
· Составьте модель задачи.
§ Заполните 1-ю строку и столбец A (рис. 11.11).
§ Запросы заводов на поставку молока занесите в диапазон ячеек C2:F2.
§ Возможный объем поставки молока объединениями фермеров занесите в диапазон ячеек B12:B16.
§ Общий объем молока, поставляемый каждым объединением фермеров, разместите в диапазоне ячеек B5:B9. Выделите ячейку B5 и введите формулу =СУММ(C5:F5). Скопируйте формулу в диапазон ячеек B6:B9.
§ В диапазон ячеек С12:F16 занесите стоимость перевозки тонны молока, используя данные из таблицы. Для ячеек указанного диапазона установите формат Денежный с двумя знаками после запятой.
§ Решение задачи (объем молока для перевозки) будет расположено в диапазоне ячеек C5:F9.
Рис. 11.11
§ Полная стоимость перевозки молока по маршруту Наро-Фоминск – Лужники вычисляется по формуле =C5*C12.
§ Общая стоимость перевозок на завод в Лужники составит =C5*C12+C6*C13+C7*C14+C8*C15+C9*C16. Введите эту формулу в ячейку С17.
§ Для подсчета общей стоимости перевозок на другие перерабатывающие заводы скопируйте формулу из ячейки С17 в диапазон ячеек D17:F17.
§ Для подсчета итоговой стоимости всех перевозок введите в ячейку B17 формулу =СУММ(C17:F17).
§ Выделите диапазон ячеек B17:F17 и установите для этих ячеек формат Денежный с двумя знаками после запятой.
· Выполните команду Сервис/ Поиск решения…
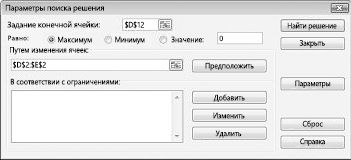
· В диалоговом окне Поиск решения установите значения (рис. 11.12).
— Поле Установить целевую ячейку: служит для указания целевой ячейки, значение которой необходимо максимизировать, минимизировать или установить равным заданному числу. Эта ячейка должна содержать формулу. По условию задачи необходимо минимизировать расходы на перевозку, поэтому в поле Установить целевую ячейку: введите ячейку $B$17.
— Поле Равной: служит для выбора варианта оптимизации значения целевой ячейки. Установите переключатель в режим минимальному значению.
— Поле Изменяя ячейки: служит для указания ячеек, значения которых изменяются в процессе поиска решения до тех пор, пока не будут выполнены наложенные ограничения и условие оптимизации значения ячейки, указанной в поле Установить целевую ячейку. Установите диапазон ячеек $C$5:$F$9, так как необходимо определить, от какого производителя, на какой склад и сколько продукции следует перевезти.
Рис. 11.12
— Кнопка Предположить используется для автоматического поиска ячеек, влияющих на формулу, ссылка на которую дана в поле Установить целевую ячейку. Результат поиска отображается в поле Изменяя ячейки.
— Список Ограничения: служит для отображения списка граничных условий поставленной задачи. Добавьте ограничения.
|
Ограничение |
Причина |
|
B5:B9<=B12:B16 |
объем поставок не может превышать имеющиеся запасы |
|
C4:F4>=C2:F2 |
запросы потребителей должны быть выполнены полностью |
|
C5:F9=целое |
количество перевозок не может быть дробным числом |
— Кнопка Параметры служит для отображения диалогового окна Параметры поиска решения (рис. 11.13), в котором можно загрузить или сохранить оптимизируемую модель и указать предусмотренные варианты поиска решения. Значения и состояния элементов управления окна, используемые по умолчанию, подходят для решения большинства задач.
§ Поле Максимальное время: служит для ограничения времени, отпускаемого на поиск решения задачи. В поле можно ввести время (в секундах), не превышающее число 32767.
§ Поле Предельное число итераций: служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести время (в секундах), не превышающее число 32767.
§ Поле Относительная погрешность служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать десятичную дробь от 0 (нуля) до 1. Чем больше десятичных знаков в задаваемом числе, тем выше точность. Например, число 0,0001 представлено с более высокой точностью, чем 0,01.
Рис. 11.13
§ Поле Допустимое отклонение служит для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. При указании большего допуска поиск решения заканчивается быстрее.
§ Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Сходимость применяется только к нелинейным задачам, условием служит дробь из интервала от 0 (нуля) до 1. Лучшую сходимость характеризует большее количество десятичных знаков. Например, 0,0001 соответствует меньшему относительному изменению по сравнению с 0,01. Лучшая сходимость требует больше времени на поиск оптимального решения.
§ Элемент управления Линейная модель служит для ускорения поиска решения линейной задачи оптимизации.
§ Элемент управления Показывать результаты итераций служит для приостановки поиска решения для просмотра результатов отдельных итераций. Установите флажок Показывать результаты итераций.
§ Элемент управления Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине. Например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
§ Элемент управления Неотрицательные значения позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых она не была указана в поле Ограничение диалогового окна Добавить ограничение. Установите флажок Неотрицательные значения.
— Кнопка Закрыть служит для выхода из окна диалога без запуска поиска решения поставленной задачи. При этом сохраняются установки, сделанные в окнах диалога, появлявшихся после нажатий на кнопки Параметры, Добавить, Изменить или Удалить.
— Кнопка Восстановить служит для очистки полей окна диалога и восстановления значений параметров поиска решения, используемых по умолчанию.
— Кнопка Выполнить служит для запуска поиска решения поставленной задачи. Щелкните по кнопке Выполнить.
· Появится диалоговое окно Текущее состояние поиска решения (рис. 11.14). Щелкните по кнопке Продолжить.
Рис. 11.14
· После каждой итерации на экране будет отображаться окно Текущее состояние поиска решения.
· После окончания поиска решения на экране появится окно Результаты поиска решения (рис. 11.15), сообщающее о том, что решение найдено.
Рис. 11.15
— Установите переключатель в значение Сохранить найденное решение.
— Раздел Тип отчета служит для указания типов отчета, которые могут быть добавлены в книгу.
§ Результаты. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях.
§ Устойчивость. Используется для создания отчета, содержащего сведения о чувствительности решения к малым изменениям в формуле (поле Установить целевую ячейку, диалоговое окно Поиск решения) или в формулах ограничений. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. В случае нелинейных моделей отчет содержит данные для градиентов и множителей Лагранжа. В отчет по нелинейным моделям включаются ограниченные затраты, фиктивные цены, объективный коэффициент (с некоторым допуском), а также диапазоны ограничений справа.
§ Ограничения. Используется для создания отчета, состоящего из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей, значения в которых ограничены множеством целых чисел. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения остальных влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно, верхним пределом называется наибольшее значение.
· Щелкните по кнопке OK.
Ответ
Минимальная сумма затрат на перевозки при соблюдении всех условий составит 2.795.450 рублей. Предлагается выполнять перевозки по следующим маршрутам:
|
Потребители: Предприятия: |
Лужники |
Сокол |
Измайлово |
Юго-Запад |
|
Наро-Фоминск |
0 |
0 |
0 |
300 |
|
Солнечногорск |
20 |
115 |
0 |
0 |
|
Домодедово |
100 |
0 |
0 |
70 |
|
Балашиха |
120 |
0 |
0 |
0 |
|
Ногинск |
0 |
0 |
280 |
0 |
 |
Примечание
При записи ограничения С5:F9=целое в окне Ссылка на ячейку: укажите диапазон ячеек С5:F9, в следующем окне – цел. В окне Ограничение: будет выведено – целое. OK.
Упражнение № 11. SEQ Упражнение_№_*. * ARABIC 2
Предположим, что фабрика производит зимние сапоги двух разных фасонов. Продукция обоих типов поступает в оптовую продажу. Для производства сапог используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 60 и 80 единиц соответственно. Расходы продуктов А и В на одну пару сапог приведены в таблице.
|
Исходный продукт |
Расход продукта |
Максимально возможный запас |
|
|
фасон1 |
фасон2 |
||
|
А |
1 |
2 |
60 |
|
В |
2 |
1 |
80 |
Изучение рынка сбыта показало, что суточный спрос на сапоги второго фасона никогда не превышает спроса на сапоги первого фасона более чем на одну пару. Кроме того установлено, что спрос на сапоги второго фасона никогда не превышает двух пар в сутки. Оптовые цены одной пары сапог равны 1500 руб. для сапог первого фасона и 1000 руб. для сапог второго фасона. Какое количество сапог каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Решение
· Составим математическую модель задачи.
Обозначим переменной X суточный объём производства сапог первого фасона, переменной Y – второго фасона. Тогда суммарная суточная прибыль от производства сапог обоих типов составит 1500*X+1000*Y (функция цели).
Задача состоит в определении всех допустимых значений X и Y таким образом, чтобы суммарная суточная прибыль была максимальна и выполнялись следующие условия:
, так как количество продуктов типа А и В на фабрике ограничено и соответствует данным таблицы
, так как суточный спрос на сапоги второго фасона никогда не превышает спроса на сапоги первого фасона более чем на одну пару
, так как спрос на сапоги второго фасона никогда не превышает двух пар в сутки
, так как количество не может быть отрицательным числом
· Перенесем построенную модель на лист Microsoft Excel (рис. 11.16).
Рис. 11.16
— Задайте ячейке B1 имя X, а ячейке B2 – Y.
— Стоимость сапог первого фасона составляет 1500 руб., а стоимость сапог второго фасона – 1000 руб., поэтому суммарная суточная прибыль от сапог обоих фасонов вычисляется по формуле =1500*X+1000*Y. Введите эту формулу в ячейку B4 (рис. 11.16).
— В диапазон ячеек B7:C10 введите ограничения, наложенные условием задачи (рис. 11.16).
· Для поиска оптимального решения выполните команду Сервис/Поиск решения…
· Найдите максимальную прибыль от производства сапог.
— Установите целевую ячейку B4.
— Равной: максимальному значению.
— Изменяя ячейки: B1:B2 (количество сапог первого и второго фасонов).
— Ограничения: B7:B10<=C7:C10 (данные ячеек B7:B10 должны быть меньше либо равны данным, находящимся в ячейках C7:C10).
— Щелкните по кнопке Параметры. Установите флажок Неотрицательные значения (так как количество сапог не может быть отрицательным числом). OK.
— Щелкните по кнопке Выполнить (рис. 11.17).
Рис. 11.17
Ответ
Максимальная суточная прибыль будет получена при производстве 39 пар сапог первого фасона и двух пар сапог второго фасона и составит 60500 руб.
Итоговые сообщения процедуры поиска решения
Если поиск решения успешно завершен, в диалоговом окне Результаты поиска решения выводится одно из следующих сообщений.
· Решение найдено. Все ограничения и условия оптимальности выполнены.
Все ограничения соблюдены с точностью, установленной в диалоговом окне Параметры поиска решения и найдено заданное значение целевой ячейки.
· Поиск свелся к текущему решению. Все ограничения выполнены.
Относительное изменение значения в целевой ячейке за последние пять итераций стало меньше установленного значения параметра Сходимость в диалоговом окне Параметры поиска решения. Чтобы найти более точное решение, установите меньшее значение параметра Сходимость, но это займет больше времени.
Если поиск не может найти оптимальное решение, в диалоговом окне Результаты поиска решения выводится одно из следующих сообщений.
· Поиск не может улучшить текущее решение. Все ограничения выполнены.
В процессе поиска решения нельзя найти такой набор значений влияющих ячеек, который был бы лучше текущего решения. Приблизительное решение найдено, но либо дальнейшее уточнение невозможно, либо погрешность, заданная в диалоговом окне Параметры поиска решения, слишком высока. Измените погрешность на меньшее число и запустите процедуру поиска решения снова.
· Поиск остановлен (истекло заданное на поиск время).
Время, отпущенное на решение задачи, исчерпано, но достичь удовлетворительного решения не удалось. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или Сохранить сценарий.
· Поиск остановлен (достигнуто максимальное число итераций).
Произведено разрешенное число итераций, но достичь удовлетворительного решения не удалось. Увеличение числа итераций может помочь, однако следует рассмотреть результаты, чтобы понять причины остановки. Чтобы при следующем запуске процедуры поиска решения не повторять выполненные вычисления, установите переключатель Сохранить найденное решение или нажмите кнопку Сохранить сценарий.
· Значения целевой ячейки не сходятся.
Значение целевой ячейки неограниченно увеличивается (или уменьшается), даже если все ограничения соблюдены. Возможно, следует в задаче снять одно ограничение или сразу несколько. Изучите процесс расхождения решения, проверьте ограничения и запустите задачу снова.
· Поиск не может найти подходящего решения.
В процессе поиска решения нельзя сделать итерацию, которая удовлетворяла бы всем ограничениям при заданной точности. Вероятно, ограничения противоречивы. Исследуйте лист на предмет возможных ошибок в формулах ограничений или в выборе ограничений.
· Поиск остановлен по требованию пользователя.
Нажата кнопка Стоп в диалоговом окне Текущее состояние поиска решения после прерывания поиска решения в процессе выполнения итераций.
· Условия для линейной модели не удовлетворяются.
Установлен флажок Линейная модель, однако итоговый пересчет порождает такие значения, которые не согласуются с линейной моделью. Это означает, что решение недействительно для данных формул листа. Чтобы проверить линейность задачи, установите флажок Автоматическое масштабирование и повторно запустите задачу. Если это сообщение опять появится на экране, снимите флажок Линейная модель и снова запустите задачу.
· При поиске решения обнаружено ошибочное значение в целевой ячейке или в ячейке ограничения.
При пересчете значений ячеек обнаружена ошибка в одной формуле или в нескольких сразу. Найдите целевую ячейку или ячейку ограничения, порождающие ошибку, и измените их формулы так, чтобы они возвращали подходящее числовое значение.
Набрано неверное имя или формула в окне Добавить ограничение или в окне Изменить ограничение, либо в поле Ограничение было задано целое или двоичное ограничение. Чтобы ограничить значения ячейки множеством целых чисел, выберите оператор целого ограничения в списке условных операторов. Чтобы установить двоичное ограничение, выберите оператор для двоичного ограничения.
· Мало памяти для решения задачи.
Система не смогла выделить память, необходимую для поиска решения. Закройте некоторые файлы или приложения и попытайтесь снова выполнить процедуру поиска решения.
Задание к лабораторной работе
Для каждой задачи составьте математическую модель задачи. Найдите ответ поиском решения.
Подготовьте и сдайте отчет (распечатанный электронный документ, не рукописный, с указанием № группы, Ф.И.О.)
Задача 1
Рацион для питания животных на ферме состоит из двух видов кормов I и II. Содержание веществ в килограмме корма представлено в таблице:
|
Корм I |
Корм II |
|
|
Жиры |
1 |
3 |
|
Белки |
3 |
1 |
|
Углеводы |
1 |
8 |
|
Нитраты |
2 |
4 |
|
Цена 1 кг |
20 руб |
10 руб |
Составить наиболее дешевый рацион питания, обеспечивающий жиров не менее 6 единиц, белков не менее 9 единиц, углеводов не менее 8 единиц, нитратов не более 16 единиц.
Задача 2
Для производства телевизоров необходимо 4 вида деталей. Количество деталей, необходимых для производства одного телевизора, представлено в таблице.
|
I деталь |
II деталь |
III деталь |
IV деталь |
|
|
Витязь |
4 |
0 |
2 |
2 |
|
Рекорд |
3 |
2 |
0 |
3 |
Прибыль от реализации одного телевизора марки Витязь – 3 у.е., Рекорд – 2 у.е.Со склада этих деталей привозят: I вида не менее 120, II вида – не более 100, III вида не более 133, IV вида не более 222. Сколько телевизоров и какого вида нужно производить, чтобы прибыль была наибольшей?
Задача 3
Задача об экономии химического сырья. На химическом предприятии оказалось возможным отходы производства возвращать в установки и использовать как добавку к исходному сырью. Установка давала за смену 50 т продукции, потребляя 84 т сырья. Выделенные отходы в количестве 34 т состояли из трех видов: первый вид –12 т, второй вид – 8 т, третий вид – 14 т. При меньшем потреблении сырья отходы выделяются в тех же пропорциях. Отходы до использования должны пройти соответствующую обработку. При этом для обработки первого и третьего видов отходов может быть использован старый, но находящийся в хорошем состоянии двухсекционный агрегат, устроенный таким образом, что в нем могут обрабатываться (в разных секциях) сразу два вида отходов. При обработке этих отходов в агрегате вырабатывается тепло в следующих количествах: для первого вида – 187 ккал/т, для третьего вида – 95 ккал/т.
Обе секции агрегата имеют систему охлаждения, устойчивая работа которых возможна только в том случае, если разность между выделяемым теплом в обеих секциях по абсолютной величине не превышает 500 ккал.
При обработке отходов в агрегате имеют место некоторые потери, составляющие для первого вида 20% отходов, для третьего вида 40% отходов. Для обработки отходов второго вида требуется простой агрегата и тепло в количестве 120 ккал/т. Это тепло может быть получено от первого агрегата, если охлаждающую воду после ее нагрева в этом агрегате направить во второй. В результате предварительного расчета установлено, что использование одной тонны отходов каждого вида дает следующую экономию: первый вид – 4000 руб., второй вид – 2000 руб., третий вид – 5000 руб.
В каких количествах использовать отходы, чтобы обеспечить максимально возможную экономию?
Задача 4
В течение каждого квартала на четырех строительствах требуется соответственно 5, 10, 20 и 15 вагонов материалов. Возможности различных заводов по производству строительных материалов соответственно равны 10, 15 и 25 вагонам в квартал.
Стоимость перевозки одного вагона приведена в таблице. Определите такой план перевозок, при котором стоимость последних была бы минимальна.
|
Строительство № Завод № |
1 |
2 |
3 |
4 |
|
1 |
8 |
3 |
5 |
2 |
|
2 |
4 |
1 |
6 |
7 |
|
3 |
1 |
9 |
4 |
3 |
-
Tags:
- Составление математических моделей
- экономических задач
- Решение оптимизационных задач
- с помощью электронных таблиц
- Молоко поставляется
- формат Денежный
- Установить целевую ячейку
- Установить целевую ячейку
- Параметры поиска решения
,
(1.3)
,
.
Эта
система показана на рис. 1.13, из которого
видно – область допустимых решений не
ограничена сверху. В таком случае при
максимизации целевой функции (например,
F
= 2x1
+ 3x2)
решение получено быть не может, т.к.
целевая функция, как и область допустимых
решений, не ограничена сверху.
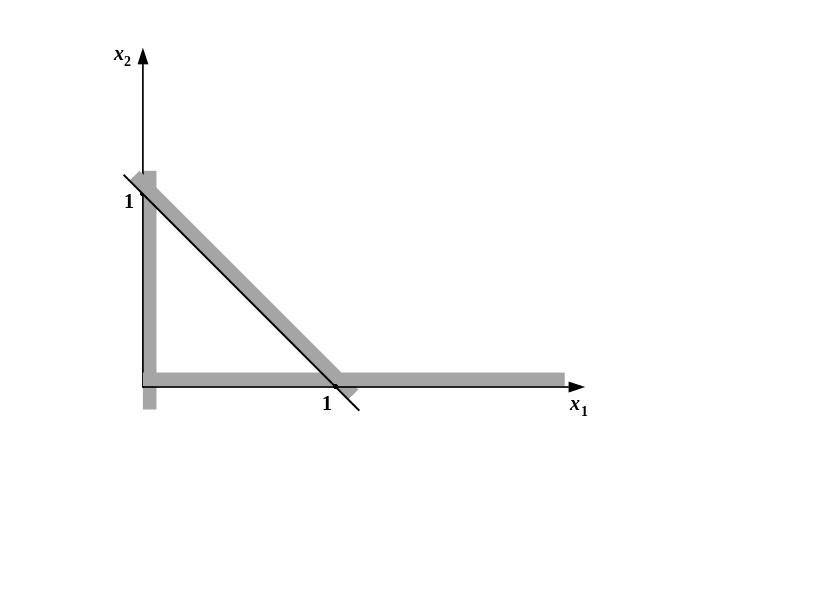
Рис. 1.13
Неограниченность
целевой функции – это следствие ошибки
в математической модели. Чтобы избежать
таких ошибок, надо выполнять следующие
правила:
1.
При максимизации целевой функции она
должна быть ограничена сверху с помощью
ограничений, при этом модель с точки
зрения содержания должна иметь вид:
(1.4)
2.
При минимизации целевой функции она
соответственно должна быть ограничена
снизу, как это показано в (1.5):
(1.5)
Итак,
уважаемый читатель, вот Вы и получили
тот необходимый минимум теоретических
сведений, который необходимо знать при
решении оптимизационных задач
экономического анализа с использованием
надстройки MS
Excel «Поиск решения». Но вместе с тем
Вы, наверное, и сами это чувствуете, что
в нашем изучении остался один очень
существенный пробел – мы не показали
примеры практического решения задач.
А это – все равно что учиться плавать
на берегу. Невозможно научиться решать
задачи, не решая их. Поэтому, не откладывая
в долгий ящик, советуем Вам переходить
к изучению следующей главы.
2.1.2. Транспортная задача
Настоящий
параграф посвящен вопросам разработки
в MS
Excel компьютерных моделей транспортного
типа. Такие модели используются для
составления наиболее экономичных планов
перевозки продукции из нескольких
пунктов отправления (например, склады)
в несколько пунктов назначения (например,
магазины). Транспортную модель можно
также применять и при рассмотрении ряда
других практических ситуаций, связанных
с управлением запасами, составлением
сменных графиков, назначением исполнителей
по рабочим местам, оборотом наличного
капитала и многими другими. Кроме того,
модель можно видоизменять, с тем чтобы
она учитывала перевозку нескольких
видов продукции.
Широкое
практическое приложение транспортной
задачи обусловило её обязательное
рассмотрение в курсе математического
программирования высших учебных
заведений. Можно предположить, что для
многих читателей линейное программирование
ассоциируется именно с решением
транспортной задачи, рассмотрению
которой уделено достаточно внимания в
книгах по исследованию операций,
экономико-математическому моделированию,
логистике, экономическому анализу и
некоторых других. Поэтому мы не будем
подробно останавливаться на теоретических
аспектах решения транспортной задачи,
а сфокусируем свое внимание на вопросах
разработки её компьютерной модели и
последующего анализа различных
практических ситуаций.
В
качестве примера транспортной задачи
рассмотрим задачу перевозки горюче-смазочных
материалов (ГСМ).
Содержательная
постановка задачи
Компанией
разрабатывается план обеспечения
потребителей горюче-cмазочными
материалами. Исходные данные о запасах
ГСМ в хранилищах, заявках на ГСМ в центрах
распределения и стоимости перевозки 1
т ГСМ от хранилищ к центрам распределения
представлены в нижеследующей таблице.
|
Хранилища ГСМ |
Центры распределения |
Запасы ГСМ в хранилищах, |
||||
|
Центр1 |
Центр2 |
Центр3 |
Центр4 |
Центр5 |
||
|
Хранилище1 |
4 |
6 |
7 |
9 |
1 |
350 |
|
Хранилище2 |
6 |
4 |
1 |
2 |
2 |
200 |
|
Хранилище3 |
5 |
8 |
7 |
4 |
9 |
450 |
|
Хранилище4 |
2 |
3 |
8 |
5 |
7 |
350 |
|
Потребность в |
350 |
400 |
250 |
100 |
250 |
Требуется
разработать такой план доставки ГСМ
от хранилищ к центрам распределения,
чтобы общая стоимость перевозок была
минимальной.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Цитата |
|---|
| daredavil написал: то есть каждая ячейка должна содержать формулу? |
Нет такого требования, а есть требования, которое я уже публиковал:
Для поиска решения формула целевой ячейки обязательно должна зависеть от значений изменяемых надстройкой ячеек
У Вас следующие ошибки:
1. Нет формул в столбце G, а должны быть.
2. Неправильно записаны 4 нижних ограничения (см. методичку)
Чтобы исключить опечатки лучше использовать именно те ячейки, которые приведены в методичке.
Перед началом расчета нужно задать начальные значения количества бумаг в портфеле (единичное по методичке)
Эволюционный метод решения можно продолжить после сообщения о достижении максимального времени и остановить в любой момент по ESC.
Текущее значение отображается в статусной строке — посматривайте на него и остановите, когда значение будет достаточно оптимальным (можно сравнивать с тем, что в методичке). В приложении — исправленный вариант с результатом, лучшим (5.02%), чем в методичке (4.73%). С Вас — оценка не ниже 5.02 за лабораторную
Решение задач линейного программирования с помощью надстройки «Поиск решения» в Microsoft Excel , страница 5
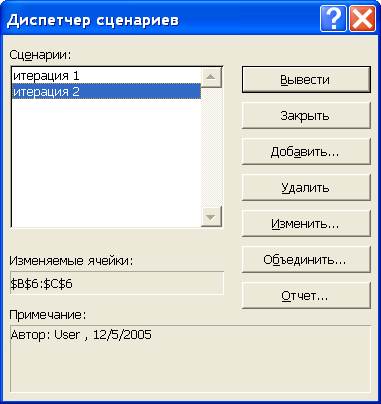
Структура сценария вставляется в виде отдельного листа непосредственно перед активным листом. Если отчеты по сценарию создавались несколько раз, названия листов автоматически нумеруются («Структура сценария 1», «Структура сценария 2» и т.д.).
Рисунок 37 – Диалоговое окно «Диспетчер сценариев»
Полученное решение также может быть сохранено в виде сценария. Таким образом, можно запомнить результаты решения задачи для различных вариантов исходных данных, провести вариантный анализ.
Рисунок 38 – Диалоговое окно «Отчет по сценарию»
После сохранения сценария продолжается работа в том же окне, из которого это сохранение осуществлялось («Текущее состояние поиска решения» или «Результаты поиска решения»).
С помощью соответствующих кнопок в «Диспетчере сценариев» сохраненные сценарии можно изменять и удалять; можно добавлять новые (при этом необходимо указать изменяемые ячейки, и их значения, которые необходимо запомнить); объединять список сценариев со сценариями, находящимися на другом листе; выводить сохраненные значения изменяемых ячеек на рабочий лист (в те же ячейки).
6.5 Результаты решения задачи
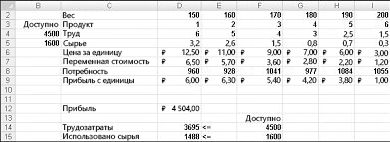
После окончания работы «Поиска решения» оптимальный план и оптимум, если они получены, находятся в тех ячейках, которые были выбраны в качестве влияющих и целевой.
В рассмотренном примере (см. таблицу 26, раздел 6.2) после нажатия кнопки «Выполнить» в ячейке В6 появится число 266,7 (х1 = 266,7), в С6 – 1173,3 (х2 = 1173,3), а в В11 – 193066,7 (оптимальное значение прибыли).
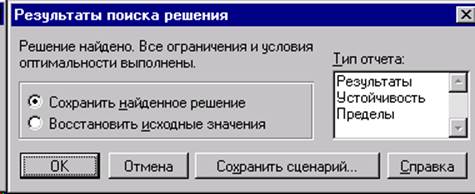
Кроме того, выводится диалоговое окно «Результаты поиска решения», представленное на рисунке 39.
Рисунок 39 — Диалоговое окно «Результаты поиска решения»
С помощью переключателей в этом окне по желанию пользователя найденное решение может быть сохранено в соответствующих ячейках, либо в них восстанавливаются исходные значения (в примере из раздела 6.2 – нулевые). По умолчанию при нажатии кнопки «ОК» решение сохраняется, а если закрыть окно или воспользоваться «Отменой», будут восстановлены исходные значения.
Поле «Тип отчета» служит для того, чтобы пользователь мог получить отчеты о решении задачи (см. раздел 6.6). Для этого необходимые типы отчетов надо выделить до нажатия кнопки «ОК». Каждый отчет размещается на отдельном листе книги Microsoft Excel (как и «Структура сценария»). Эти листы программа также вставляет непосредственно перед активным листом. Если «Поиск решения» использовался несколько раз, и при этом создавались отчеты, названия отчетов автоматически нумеруются. Если решение не было найдено, обратиться к «Типу отчета» невозможно. Кроме того, для целочисленных задач не выдаются отчеты по устойчивости и пределам.
Нажатием кнопки «Сохранить сценарий» полученное решение может быть сохранено в виде сценария.
Первые строки окна результатов занимает итоговое сообщение, которое может быть различным по содержанию. При успешном окончании процедуры поиска решения для линейной модели выдается сообщение: «Решение найдено. Все ограничения и условия оптимальности выполнены» (см. рисунок 38). Если поиск не получил оптимального решения, выдается одно из сообщений, приведенных в таблице 28.
Таблица 28 – Итоговые сообщения «Поиска решения»
Характеристика результата поиска
(для линейной задачи)
Поиск остановлен (истекло заданное на поиск время).
Время, отпущенное на решение задачи, исчерпано, но достичь удовлетворительного решения не удалось.
Следует увеличить максимальное время.
Поиск остановлен (достигнуто максимальное число итераций).
Произведено разрешенное число итераций, но достичь удовлетворительного решения не удалось.
Следует увеличить предельное число итераций.
Значения целевой ячейки не сходятся.
Целевая функция задачи не ограничена.
Если необходимо поставить задачу так, чтобы она была разрешима, следует изменить и/или добавить ограничения и запустить задачу снова. Возможно (исходя из смысла задачи), ошибка допущена и при построении целевой функции.
Поиск остановлен по требованию пользователя.
Нажата кнопка “Стоп” в окне диалога «Текущее состояние поиска решения» после прерывания поиска решения или в процессе пошагового выполнения итераций (которое устанавливается через «Параметры» «Поиска решения»).
Поиск решения MS EXCEL. Каноническая задача линейного программирования
Стандартная задача линейного программирования (ограничения на переменные выражены неравенствами) решена нами с помощью Поиска решения в предыдущей статье. Пример записи ограничений в такой задаче приведен ниже:
Как видно из картинки выше в задаче задано 3 ограничения (неравенства). Есть еще 4 ограничения (по числу переменных) — все переменные должны больше 0.
Примечание: В стандартной задаче все переменные больше 0. На то она и стандартная.
В этой статье сведем стандартную задачу к каноническому виду и решим ее с помощью Поиска решения (Solver) в MS EXCEL.
Дадим определение.
Канонической называется задача линейного программирования, которая состоит в нахождении максимального или минимального значения целевой функции при условии, что все ограничения являются равенствами.
Примечание: Каноническая форма необходима для решения задачи симплекс методом (SIMPLEX LP).
Теперь задача.
Примечание: Ограничения задачи заданы выше.
Для приведения задачи к канонической форме введем дополнительные (свободные) переменные (т.е. произведем эквивалентные преобразования). Так как у нас три ограничения, то и дополнительных переменных должно быть 3. Введение этих переменных позволяет избавиться от неравенств в ограничениях и заменить их на равенства.
Совет: для знакомства с Поиском решения см. эту статью.
Решение
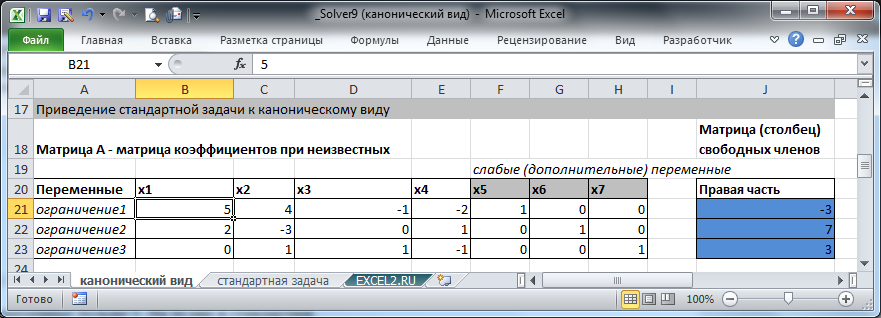
Сначала на лист EXCEL поместим все коэффициенты из 3-х неравенств (3х4) и добавим еще коэффициенты для 3-х свободных переменных (в форме единичной матрицы 3х3).
Также нужно заполнить столбец свободных членов (правая часть неравенств, синие ячейки).
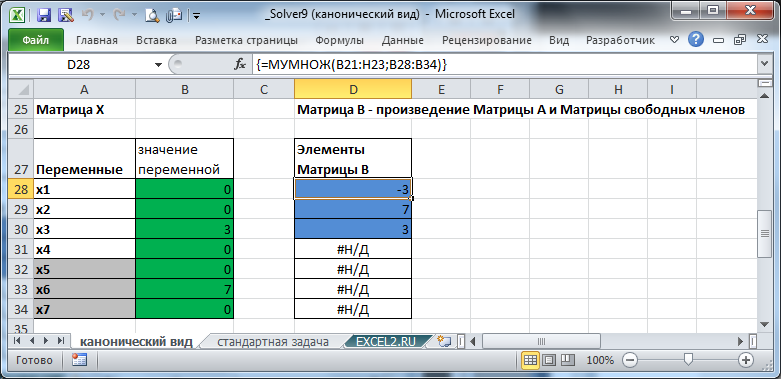
Теперь определим ячейки для хранения значений переменных х, выделим их зеленым цветом и расположим их в одном столбце (а не в строке). Значения этих ячеек Поиск решения будет изменять, чтобы максимизировать функцию F.
Напомним, что в задаче 4 переменных (x1, x2, x3, x4) и 3 дополнительных переменных (x5, x6, x7), необходимых для сведения задачи к каноническому виду, поэтому нам потребовалось 7 ячеек.
Теперь вычислим значения левых частей наших 3-х ограничений, то есть умножим коэффициенты Матрицы А на столбец переменных (Матрица Х, или просто столбец с переменными). Это можно сделать с помощью формулы = МУМНОЖ(B21:H23;B28:B34) , т.е. использовав умножение матриц. Формулу нужно вводить как формулу массива, возвращающим сразу несколько значений.
Примечание. Альтернативным и интуитивно более понятным подходом является использование формулы = СУММПРОИЗВ(B21:H21;ТРАНСП($B$28:$B$34)) Это реализовано в файле примера . Формулу тоже нужно ввести как формулу массива, т.к. СУММПРОИЗВ() работает с массивами (векторами), которые оба размещены по строкам или по столбцам. В нашем случае это не так: коэффициенты размещены в одной строке, а значения х в столбце, поэтому использована функция ТРАНСП() для транспонирования столбца с переменными. Можно, конечно, предварительно транспонировать столбец в строку, в этом случае функцию СУММПРОИЗВ() можно вводить как обычную формулу.
Итак, у нас полностью сформировалось 3 ограничения: левая часть выражения (элементы Матрицы В) и правая часть (дано). Выделим эти ячейки синим цветом, чтобы было удобнее вводить условия в окно Поиска решения. Т.к. мы ввели дополнительные переменные, то ограничения теперь заданы в виде равенств — это канонический вид.
Осталось задать целевую функцию, умножив коэффициенты на ячейки с переменными (дополнительные переменные использовать не нужно). Это проще всего сделать формулой = СУММПРОИЗВ(B40:B43;B28:B31)
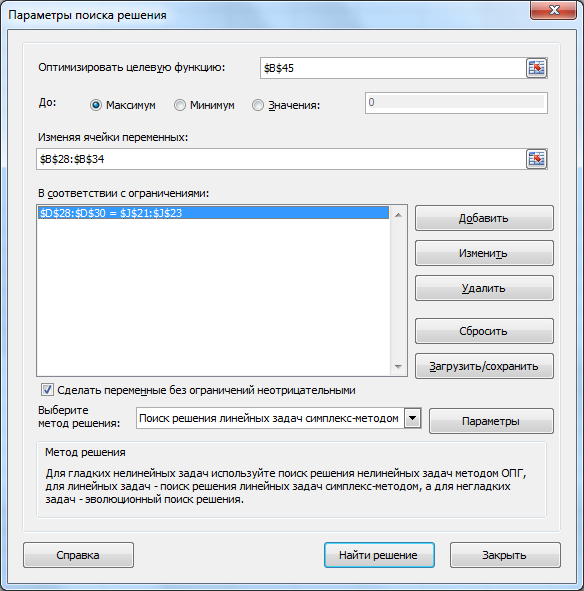
В окне Поиска решения задайте параметры оптимизации.
Совет: О том как установить Поиск решения см. эту статью.
Поиск решения сам предложил решить задачу Симплекс-методом, а также сделать переменные неотрицательными.
После запуска Поиска решения решение будет найдено и оно, конечно, совпадет с решением задачи, которая была решена в стандартной форме.
Методические указания по содержанию и организации выполнения курсовой работы по дисциплине «Маркетинг» для студентов всех форм обучения специальности 060800 Экономика и управление на предприятии
Для целевой функции (ЦФ): курсор в G5; активизировать Мастер функций; в Категории вызвать Математические; в Функциях найти и вызвать СУММПРОИЗВ. Далее. После этого должно появиться новое диалоговое окно: в 1-е окно (массив 1) ввести адреса ячеек оптимальных переменных (А, Б, В, Г, Д) — B$2:F$2; во 2-е окно (массив 2) ввести адреса ячеек целевой функции – B5:F5. Знак $ описывает переменную величину. Готово. В результате в ячейке G5 (результат расчета целевой функции) должна появиться следующая формула: =СУММАПРОИЗВ(B$2:F$2;B5:F5)
Для левых частей ограничений: курсор в G5; Копировать в буфер; курсор в G8; Вставить из буфера. На экране в ячейке G8 должна появиться следующая формула: =СУММАПРОИЗВ(B$2:F$2;B8:F8)
Чтобы ввести расчетные формулы (аналогичные той, что введена в ячейку G8) для других ресурсов достаточно произвести Копирование содержимого ячейки G8 в соответствующие адреса G9, G10, G12, G13, G14, G15, G17, G18, G19, G20.
в) Поиск решения
Для нахождения оптимального решения необходимо в МЕНЮ Excel Сервис вызвать Поиск решения. На экране монитора появится окно — Поиск решения. Ввести адрес в окно Поиск решения ($G$5). После этого задать направление поиска — Максимальное значение. Ввести адреса искомых переменных $B$2:$F$2 в окне Изменяя ячейки. Остается ввести граничные условия на переменные и на ограничения. Активизировать в этом окне клавишу Добавить. Появится новое окно Добавление ограничений.
Ввести граничные условия на переменные (B2=B3, C2=>C3, D2 E3, E2 F3). Для этого в окне Ссылка на ячейку ввести $B$2, затем указать тип ограничения = и ввести $B$3. Добавить. Аналогично вводятся остальные граничные условия: $C$2=>$C$3, $D$2 $E3$, $F$2=>$F$3.
|
Поиск решения не проходит через ячейку с функцией «если» |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |