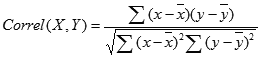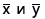Содержание
- Суть корреляционного анализа
- Расчет коэффициента корреляции
- Способ 1: определение корреляции через Мастер функций
- Способ 2: вычисление корреляции с помощью пакета анализа
- Вопросы и ответы
Корреляционный анализ – популярный метод статистического исследования, который используется для выявления степени зависимости одного показателя от другого. В Microsoft Excel имеется специальный инструмент, предназначенный для выполнения этого типа анализа. Давайте выясним, как пользоваться данной функцией.
Суть корреляционного анализа
Предназначение корреляционного анализа сводится к выявлению наличия зависимости между различными факторами. То есть, определяется, влияет ли уменьшение или увеличение одного показателя на изменение другого.
Если зависимость установлена, то определяется коэффициент корреляции. В отличие от регрессионного анализа, это единственный показатель, который рассчитывает данный метод статистического исследования. Коэффициент корреляции варьируется в диапазоне от +1 до -1. При наличии положительной корреляции увеличение одного показателя способствует увеличению второго. При отрицательной корреляции увеличение одного показателя влечет за собой уменьшение другого. Чем больше модуль коэффициента корреляции, тем заметнее изменение одного показателя отражается на изменении второго. При коэффициенте равном 0 зависимость между ними отсутствует полностью.
Расчет коэффициента корреляции
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.
Способ 1: определение корреляции через Мастер функций
Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).
- Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.
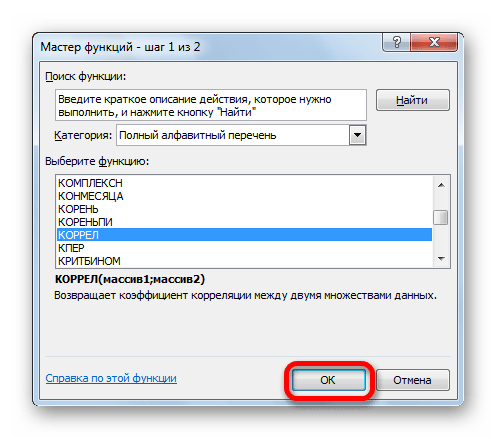
- В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».
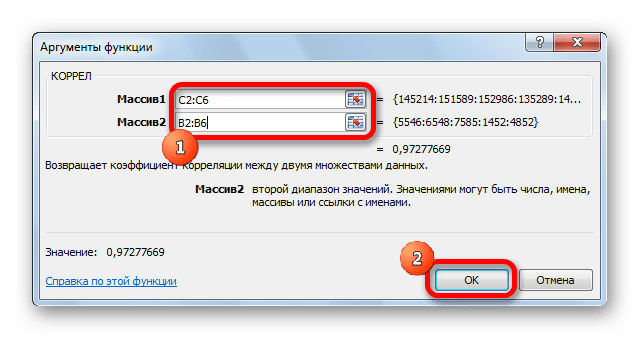
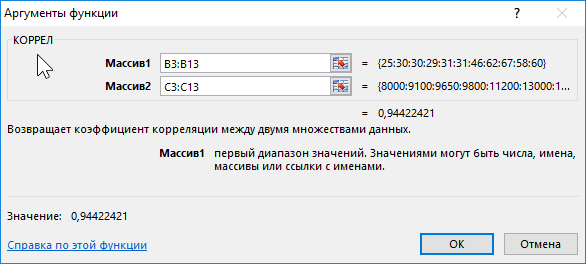
- Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.
В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.
Жмем на кнопку «OK».
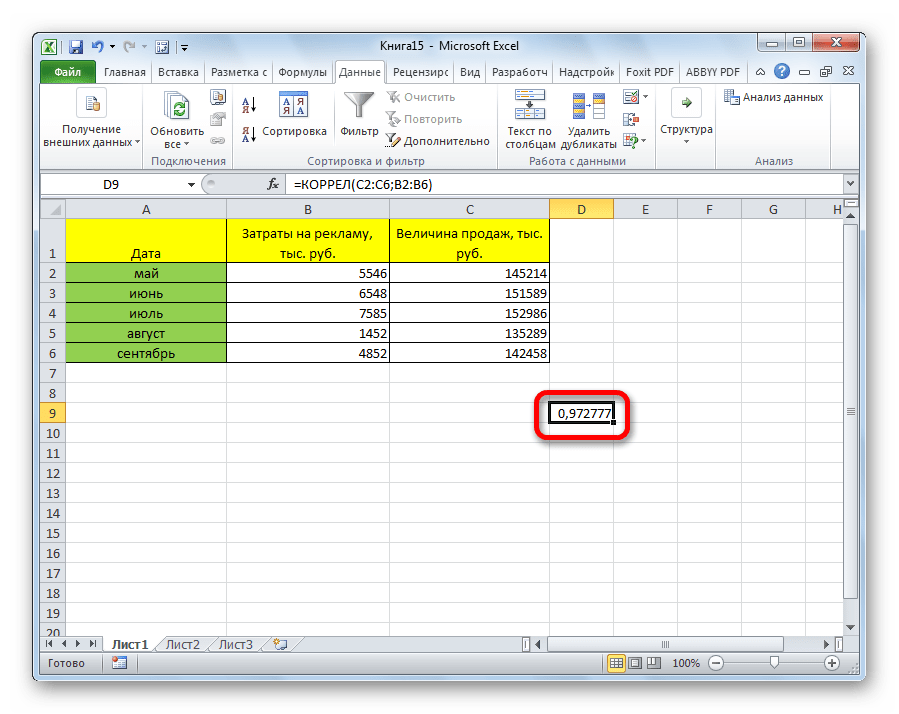
Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.
Способ 2: вычисление корреляции с помощью пакета анализа
Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.
- Переходим во вкладку «Файл».
- В открывшемся окне перемещаемся в раздел «Параметры».
- Далее переходим в пункт «Надстройки».
- В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».
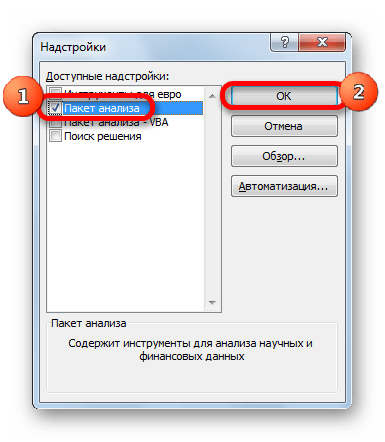
- В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».
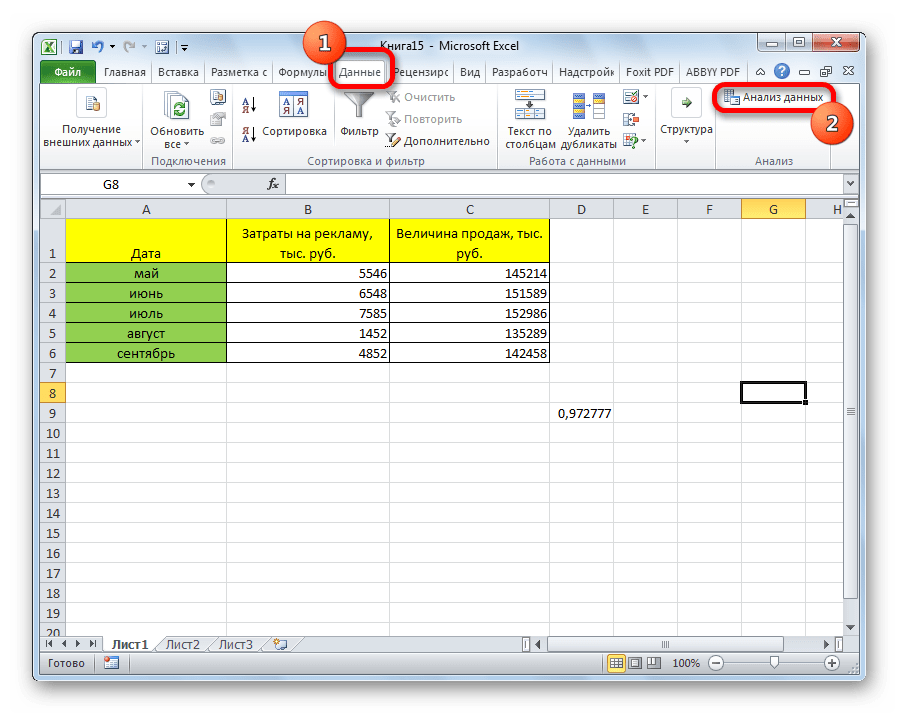
- После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.
- Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».
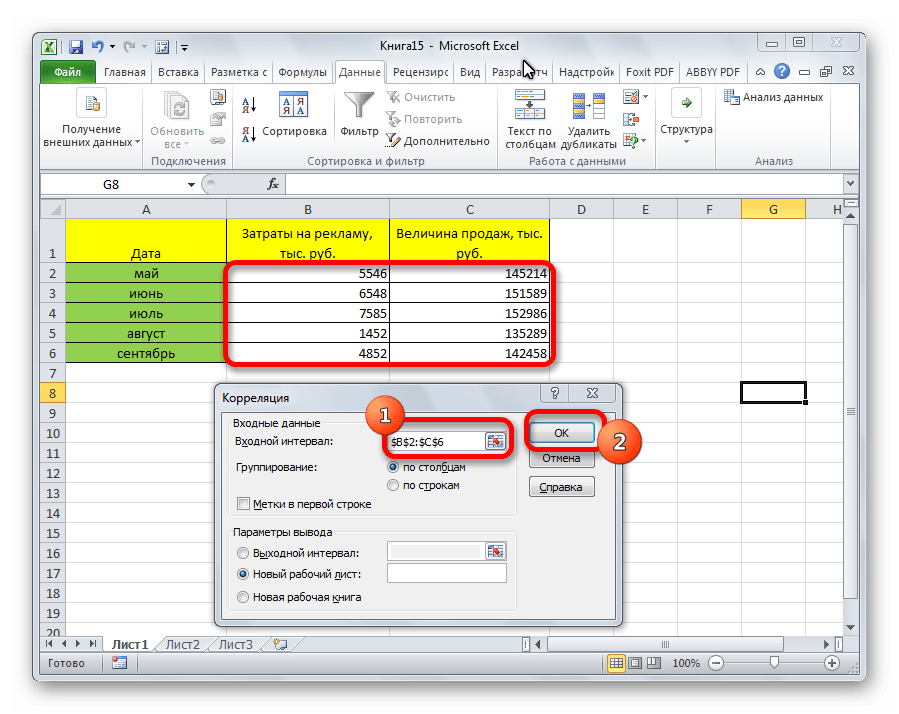
- Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».
Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».
В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).
Когда все настройки установлены, жмем на кнопку «OK».
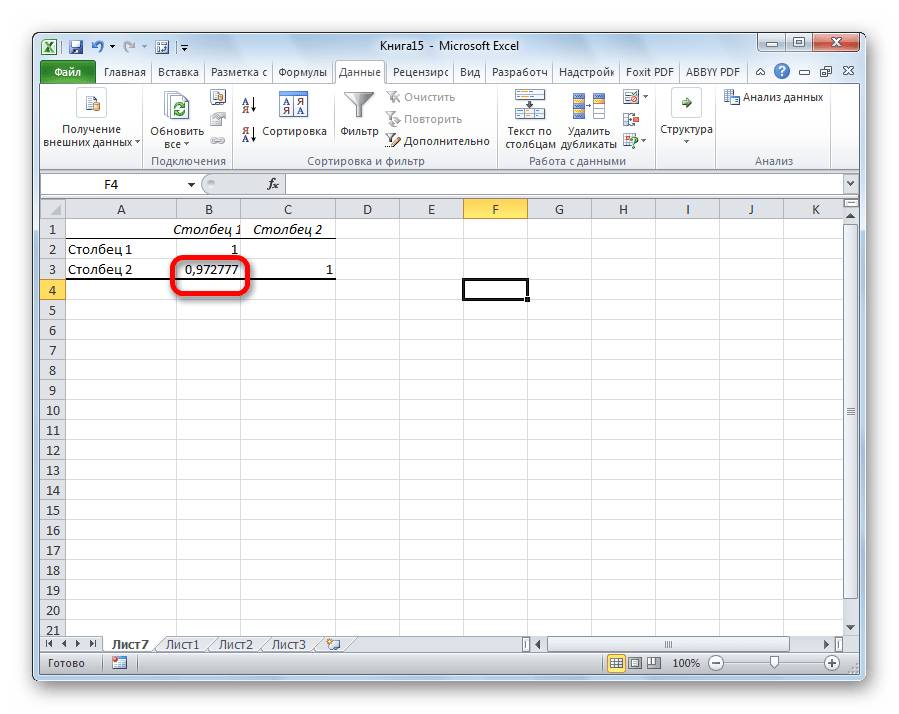
Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.
Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.
Еще статьи по данной теме:
Помогла ли Вам статья?
Функция КОРРЕЛ в Excel используется для расчета коэффициента корреляции между для двух исследуемых массивов данных и возвращает соответствующее числовое значение.
Примеры использования функции КОРРЕЛ в Excel
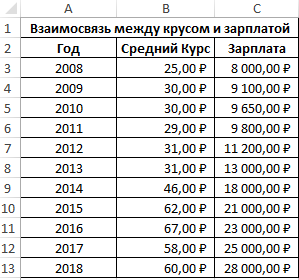
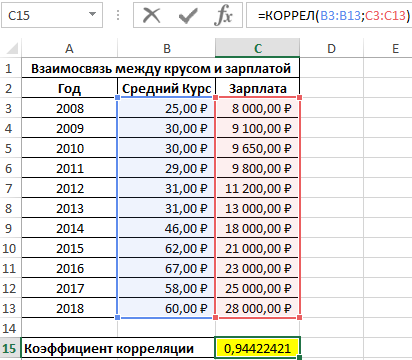
Пример 1. В таблице Excel содержатся данные о курсе доллара и средней зарплате сотрудников фирмы на протяжении нескольких лет. Определить взаимосвязь между курсом валюты и средней зарплатой.
Таблица данных:
Формула для расчета:
Описание аргументов:
- B3:B13 – диапазон ячеек, в которых хранятся данные о среднем курсе доллара;
- C3:C13 – диапазон ячеек со значениями средней зарплаты.
Результат расчетов:
Полученный результат близок к 1 и свидетельствует о сильной прямой взаимосвязи между исследуемыми величинами. Однако прямо пропорциональной зависимости между ними нет, то есть на увеличение средней зарплаты оказывали влияние и прочие факторы.
Определение коэффициента корреляции влияния действий на результат
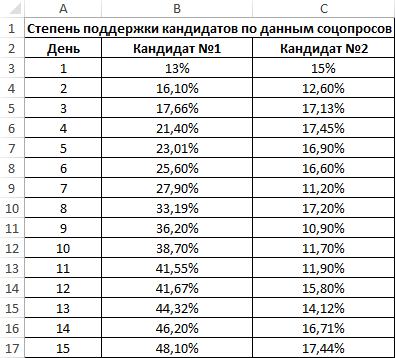
Пример 2. Два сильных кандидата на руководящий пост воспользовались услугами двух различных пиар-агентств для запуска предвыборной компании, которая длилась 15 дней. Ежедневно проводился соцопрос независимыми исследователями, которые определяли процент поддержки одного и второго кандидата. Респонденты могли отдавать предпочтение первому, второму кандидату или выступать против обоих. Определить, насколько влияла каждая предвыборная кампания на степень поддержки кандидатов, какая из них оказалась более эффективной?
Исходные данные:
Произведем расчет коэффициентов корреляции с помощью формул:
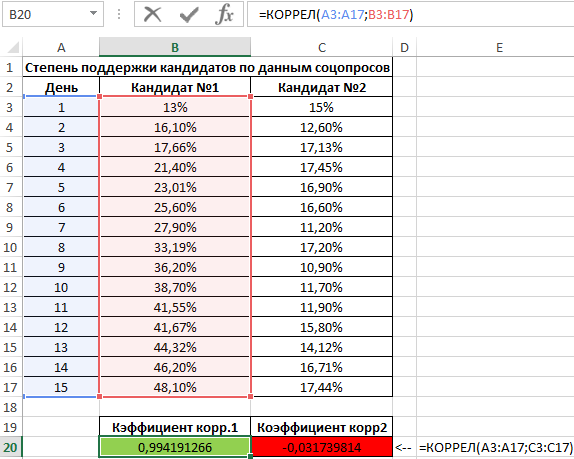
=КОРРЕЛ(A3:A17;B3:B17)
=КОРРЕЛ(A3:A17;C3:C17)
Описание аргументов:
- A3:A17 – массив ячеек, содержащий номера дней предвыборной кампании;
- B3:B17 и C3:C17 – диапазон ячеек, содержащие данные о проценте поддержки первого и второго кандидатов соответственно.
Полученные результаты:
Как видно, уровень поддержки первого кандидата увеличивался с каждым днем кампании, поэтому коэффициент корреляции в первом случае стремится к единице. На старте кампании второй кандидат имел больший процент поддержки, и это значение на протяжении первых пяти дней демонстрировало положительную динамику изменений. Однако затем уровень поддержки стал снижаться, и к 15-му дню упал ниже начального значения. Отрицательное значение коэффициента корреляции свидетельствует о негативном эффекте кампании. Однако на события могли оказывать влияние различные факторы, например, опубликованные компрометирующие материалы. В связи с этим полагаться только на значение коэффициента корреляции в данном случае нельзя. То есть, коэффициент корреляции не характеризует причинно-наследственную связь.
Анализ популярности контента по корреляции просмотров и репостов видео
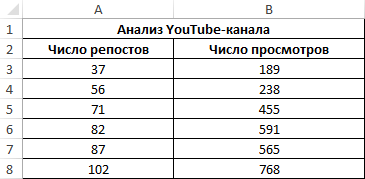
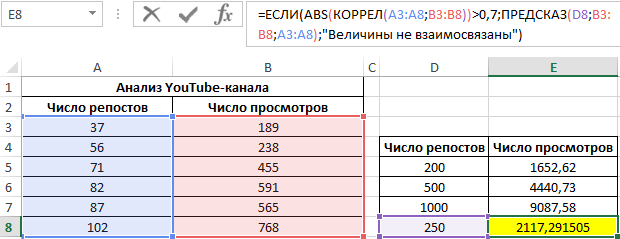
Пример 3. Владелец канала YouTube использует социальную сеть для рекламы своих роликов. Он заметил, что между числом просмотров и количеством репостов в социальной сети существует некоторая взаимосвязь. Можно ли спрогнозировать виральность контента канала в Excel? Определить целесообразность использования уравнения линейной регрессии для предсказания количества просмотров роликов в зависимости от числа репостов.
Исходные данные:
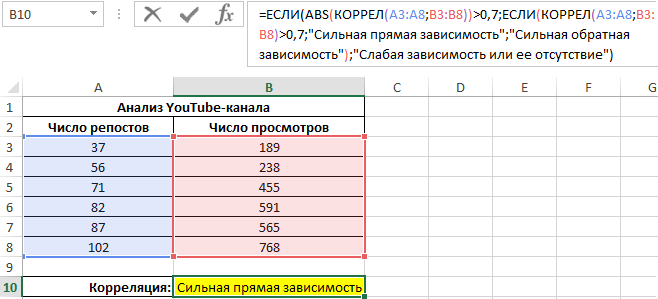
Определим наличие взаимосвязи между двумя параметрами по формуле:
Если модуль коэффициента корреляции больше 0,7, считается рациональным использование функции линейной регрессии (y=ax+b) для описания связи между двумя величинами. В данном случае:
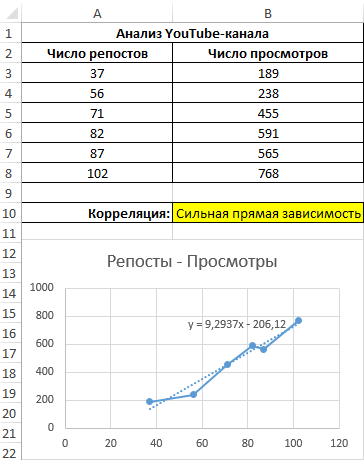
Построим график зависимости числа просмотров от количества репостов, отобразим линию тренда и ее уравнение:
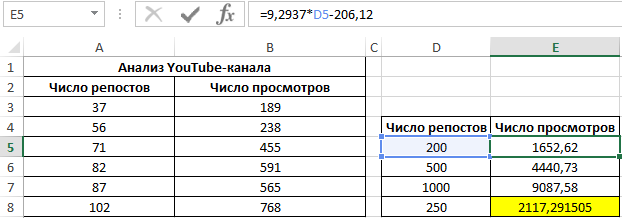
Используем данное уравнение для определения количества просмотров при 200, 500 и 1000 репостов:
=9,2937*D4-206,12
Полученные результаты:
Аналогичное уравнение использует функция ПРЕДСКАЗ. То есть, чтобы найти количество просмотров в случае, если было сделано, например, 250 репостов, можно использовать формулу:
Полученный результат:
Коэффициент корреляции – один из множества статистических критериев определения наличия взаимосвязи между двумя рядами значений. Для построения точных статистических моделей рекомендуется использовать дополнительные параметры, такие как коэффициент детерминации, стандартная ошибка и другие.
Особенности использования функции КОРРЕЛ в Excel
Функция КОРРЕЛ имеет следующий синтаксис:
=КОРРЕЛ(массив1;массив2)
Описание аргументов:
- массив1 – обязательный аргумент, содержащий диапазон ячеек или массив данных, которые характеризуют изменения свойства какого-либо объекта.
- массив2 – обязательный аргумент (диапазон ячеек либо массив), элементы которого характеризуют изменение свойств второго объекта.
Примечания 1:
- Функция КОРРЕЛ не учитывает в расчетах элементы массива или ячейки из выбранного диапазона, в которых содержатся данные текстового или логического типов. Пустые ячейки также игнорируются. Текстовые представления числовых значений учитываются.
- Если необходимо учесть логические ИСТИНА или ЛОЖЬ в качестве числовых значений 1 или 0 соответственно, можно выполнить явное преобразование данных используя двойное отрицание «—».
- Размерности массив1 и массив2 или количество ячеек, переданных в качестве этих двух аргументов, должны совпадать. Если аргументы содержат разное количество точек данных, например, =КОРРЕЛ({1;2;3};{4;6;8;10}), результатом выполнения функции будет код ошибки #Н/Д.
- Если один из аргументов представляет собой пустой массив или массив нулевых значений, функция КОРРЕЛ вернет код ошибки #ДЕЛ/0!. Аналогичный результат выполнения данной функции будет достигнут в случае, если стандартное отклонение распределения величин в одном из массивов (массив1, массив2) равно 0 (нулю).
- Функция КОРРЕЛ производит расчет коэффициента корреляции по следующей формуле:
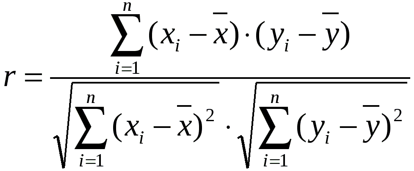
Примечание 2: Коэффициент корреляции представляет собой количественную характеристику степени взаимосвязи между двумя свойствами объектов. Этот коэффициент может принимать значения из диапазона от -1 до 1, при этом:
- Если значение коэффициента приближается к 1 или -1, между двумя исследуемыми свойствами существует сильная прямая или обратная взаимосвязи соответственно.
- Если значение коэффициента стремится к 0,5 или -0,5, два свойства слабо прямо или обратно взаимосвязаны друг с другом соответственно.
- Если коэффициент корреляции близок к 0 (нулю), между двумя исследуемыми свойствами отсутствует прямая либо обратная взаимосвязи.
Примечание 3: Для понимания смысла коэффициента корреляции можно привести два простых примера:
- При нагреве вещества количество теплоты, содержащееся в нем, будет увеличиваться. То есть, между температурой и количеством теплоты (физическая величина) существует прямая взаимосвязь.
- При увеличении стоимости продукции спрос на нее уменьшается. То есть, между ценой и покупательной способностью существует обратная взаимосвязь.
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
Функция КОРРЕЛ возвращает коэффициент корреляции двух диапазонов ячеев. Коэффициент корреляции используется для определения взаимосвязи между двумя свойствами. Например, можно установить зависимость между средней температурой в помещении и использованием кондиционера.
Синтаксис
КОРРЕЛ(массив1;массив2)
Аргументы функции КОРРЕЛ описаны ниже.
-
массив1 — обязательный аргумент. Диапазон значений ячеок.
-
массив2 — обязательный аргумент. Второй диапазон значений ячеев.
Замечания
-
Если аргумент массива или ссылки содержит текст, логические значения или пустые ячейки, эти значения игнорируются; однако ячейки с нулевыми значениями включаются.
-
Если массив1 и массив2 имеют различное количество точек данных, то correl возвращает #N/A.
-
Если массив1 или массив2 пуст или если s (стандартное отклонение) их значений равно нулю, то corREL возвращает значение #DIV/0! ошибку «#ВЫЧИС!».
-
Так как коэффициент корреляции ближе к +1 или -1, он указывает на положительную (+1) или отрицательную (-1) корреляцию между массивами. Положительная корреляция означает, что при увеличении значений в одном массиве значения в другом массиве также увеличиваются. Коэффициент корреляции, который ближе к 0, указывает на отсутствие или неабную корреляцию.
-
Уравнение для коэффициента корреляции имеет следующий вид:
где
являются средними значениями выборок СРЗНАЧ(массив1) и СРЗНАЧ(массив2).
Пример
В следующем примере возвращается коэффициент корреляции двух наборов данных в столбцах A и B.
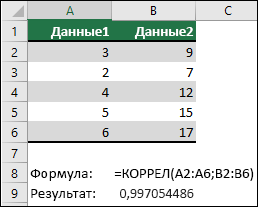
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Нужна дополнительная помощь?
Содержание:
- Что такое коэффициент корреляции?
- Расчет коэффициента корреляции в Excel
- Использование формулы CORREL
- Использование пакета инструментов анализа данных
- Включение пакета инструментов анализа данных
- Расчет коэффициента корреляции с помощью пакета Data Analysis Toolpak
Excel — это мощный инструмент, обладающий удивительными функциями и возможностями при работе со статистикой.
Поиск корреляции между двумя рядами данных — один из наиболее распространенных статистических расчетов при работе с большими наборами данных.
Несколько лет назад я работал финансовым аналитиком, и, хотя мы не принимали активного участия в статистических данных, обнаружение корреляции было тем, что нам все же приходилось делать довольно часто.
В этом уроке я покажу вам два действительно простых способа рассчитать коэффициент корреляции в Excel. Для этого уже есть встроенная функция, и вы также можете использовать Data Analysis Toolpak.
Итак, приступим!
Что такое коэффициент корреляции?
Поскольку это не статистический класс, позвольте мне вкратце объяснить, что такое коэффициент корреляции, а затем мы перейдем к разделу, где рассчитываем коэффициент корреляции в Excel.
Коэффициент корреляции — это значение, которое показывает, насколько тесно связаны два ряда данных.
Часто используемый пример — это вес и рост 10 человек в группе. Если мы рассчитаем коэффициент корреляции для данных о росте и весе этих людей, мы получим значение от -1 до 1.
Значение меньше нуля указывает на отрицательную корреляцию, что означает, что если рост увеличивается, то вес уменьшается, или если вес увеличивается, тогда рост уменьшается.
А значение больше нуля указывает на положительную корреляцию, что означает, что если рост увеличивается, то увеличивается вес, а если рост уменьшается, то вес уменьшается.
Чем ближе значение к 1, тем сильнее положительная корреляция. Таким образом, значение 0,8 будет означать, что данные о росте и весе сильно коррелированы.
Примечание. Существуют разные типы коэффициентов корреляции и статистики, но в этом руководстве мы рассмотрим наиболее распространенный из них — коэффициент корреляции Пирсона.
Теперь давайте посмотрим, как рассчитать этот коэффициент корреляции в Excel.
Расчет коэффициента корреляции в Excel
Как я уже упоминал, есть несколько способов рассчитать коэффициент корреляции в Excel.
Использование формулы CORREL
CORREL — это статистическая функция, представленная в Excel 2007.
Предположим, у вас есть набор данных, показанный ниже, где вы хотите рассчитать коэффициент корреляции между ростом и весом 10 человек.
Ниже приведена формула, которая сделает это:
= КОРРЕЛЬ (B2: B12; C2: C12)
Вышеупомянутая функция CORREL принимает два аргумента — серию с точками данных роста и серию с точками данных веса.
И это все!
Как только вы нажмете клавишу ВВОД, Excel выполнит все вычисления в серверной части и выдаст вам один единственный коэффициент корреляции Пирсона.
В нашем примере это значение немного больше 0,5, что указывает на довольно сильную положительную корреляцию.
Этот метод лучше всего использовать, если у вас есть две серии и все, что вам нужно, — это коэффициент корреляции.
Но если у вас есть несколько рядов, и вы хотите узнать коэффициент корреляции всех этих рядов, вы также можете рассмотреть возможность использования пакета инструментов анализа данных в Excel (рассматривается далее).
Использование пакета инструментов анализа данных
В Excel есть пакет инструментов для анализа данных, который можно использовать для быстрого расчета различных значений статистики (включая получение коэффициента корреляции).
Но пакет инструментов анализа данных в Excel по умолчанию отключен. Итак, первым шагом было бы снова включить инструмент анализа данных, а затем использовать его для расчета коэффициента корреляции Пирсона в Excel.
Включение пакета инструментов анализа данных
Ниже приведены шаги по включению пакета инструментов анализа данных в Excel:
- Перейдите на вкладку Файл.
- Нажмите на Параметры
- В открывшемся диалоговом окне «Параметры Excel» щелкните параметр «Надстройки» на боковой панели.
- В раскрывающемся списке «Управление» выберите надстройки Excel.
- Щелкните Go. Откроется диалоговое окно надстроек.
- Отметьте опцию Analysis Toolpak
- Нажмите ОК
Вышеупомянутые шаги добавят новую группу на вкладке «Данные» на ленте Excel под названием «Анализ». В этой группе у вас будет опция анализа данных
Расчет коэффициента корреляции с помощью пакета Data Analysis Toolpak
Теперь, когда инструмент анализа снова доступен на ленте, давайте посмотрим, как с его помощью рассчитать коэффициент корреляции.
Предположим, у вас есть набор данных, как показано ниже, и вы хотите выяснить корреляцию между тремя рядами (рост и вес, рост и доход, вес и доход).
Ниже приведены шаги для этого:
- Перейдите на вкладку «Данные».
- В группе «Анализ» выберите параметр «Анализ данных».
- В открывшемся диалоговом окне «Анализ данных» нажмите «Корреляция».
- Щелкните ОК. Откроется диалоговое окно «Корреляция».
- Для диапазона ввода выберите три серии, включая заголовки.
- Убедитесь, что для параметра «Сгруппировано по» выбрано «Столбцы».
- Выберите вариант — «Ярлык в первой строке». Это гарантирует, что в результирующих данных будут одинаковые заголовки, и будет намного легче понять результаты.
- В параметрах вывода выберите, где вы хотите получить результирующую таблицу. Я собираюсь использовать ячейку G1 на том же листе. Вы также можете получить результаты на новом листе или в новой книге.
- Нажмите ОК.
Как только вы это сделаете, Excel вычислит коэффициент корреляции для всех серий и выдаст вам таблицу, как показано ниже:
Обратите внимание, что результирующая таблица является статической и не будет обновляться в случае изменения какой-либо точки данных в вашей таблице. В случае каких-либо изменений вам придется повторить вышеуказанные шаги еще раз, чтобы сгенерировать новую таблицу коэффициентов корреляции.
Итак, это два быстрых и простых метода расчета коэффициента корреляции в Excel.
Надеюсь, вы нашли этот урок полезным!
17 авг. 2022 г.
читать 2 мин
В статистике мы часто используемкоэффициент корреляции Пирсона для измерения линейной зависимости между двумя переменными. Однако иногда нам интересно понять взаимосвязь между двумя переменными , контролируя при этом третью переменную .
Например, предположим, что мы хотим измерить связь между количеством часов, отработанных учащимся, и полученной им итоговой оценкой на экзамене, контролируя текущую оценку учащегося в классе. В этом случае мы могли бы использовать частичную корреляцию для измерения взаимосвязи между часами обучения и итоговой оценкой на экзамене.
В этом руководстве объясняется, как рассчитать частичную корреляцию в Excel.
Пример: Частичная корреляция в Excel
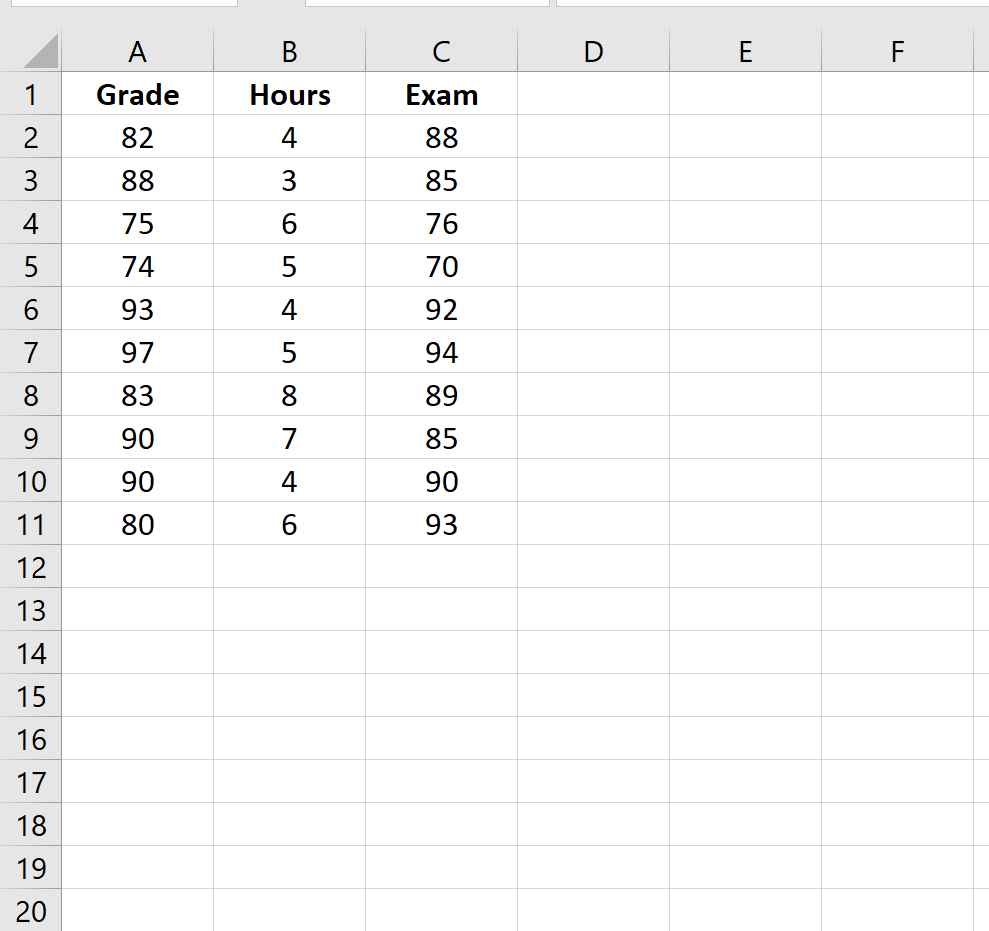
Предположим, у нас есть набор данных, который показывает следующую информацию для 10 студентов:
- Текущая оценка в классе
- Количество часов, потраченных на подготовку к выпускному экзамену
- Итоговый балл за экзамен
Используйте следующие шаги, чтобы найти частичную корреляцию между часами обучения и экзаменационными баллами при контроле текущей оценки.
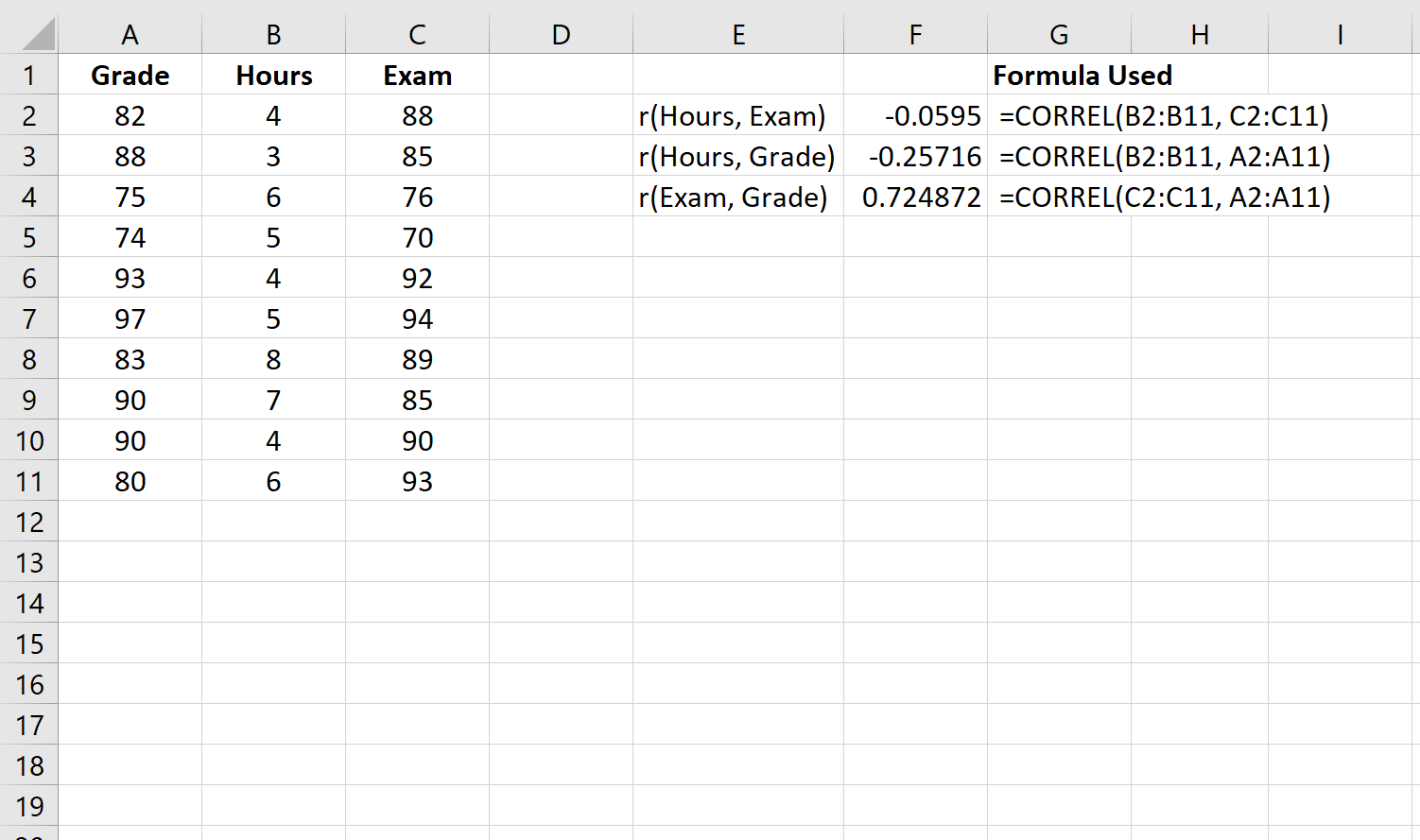
Шаг 1: Рассчитайте каждую попарную корреляцию.
Во-первых, мы рассчитаем корреляцию между каждой парной комбинацией переменных:
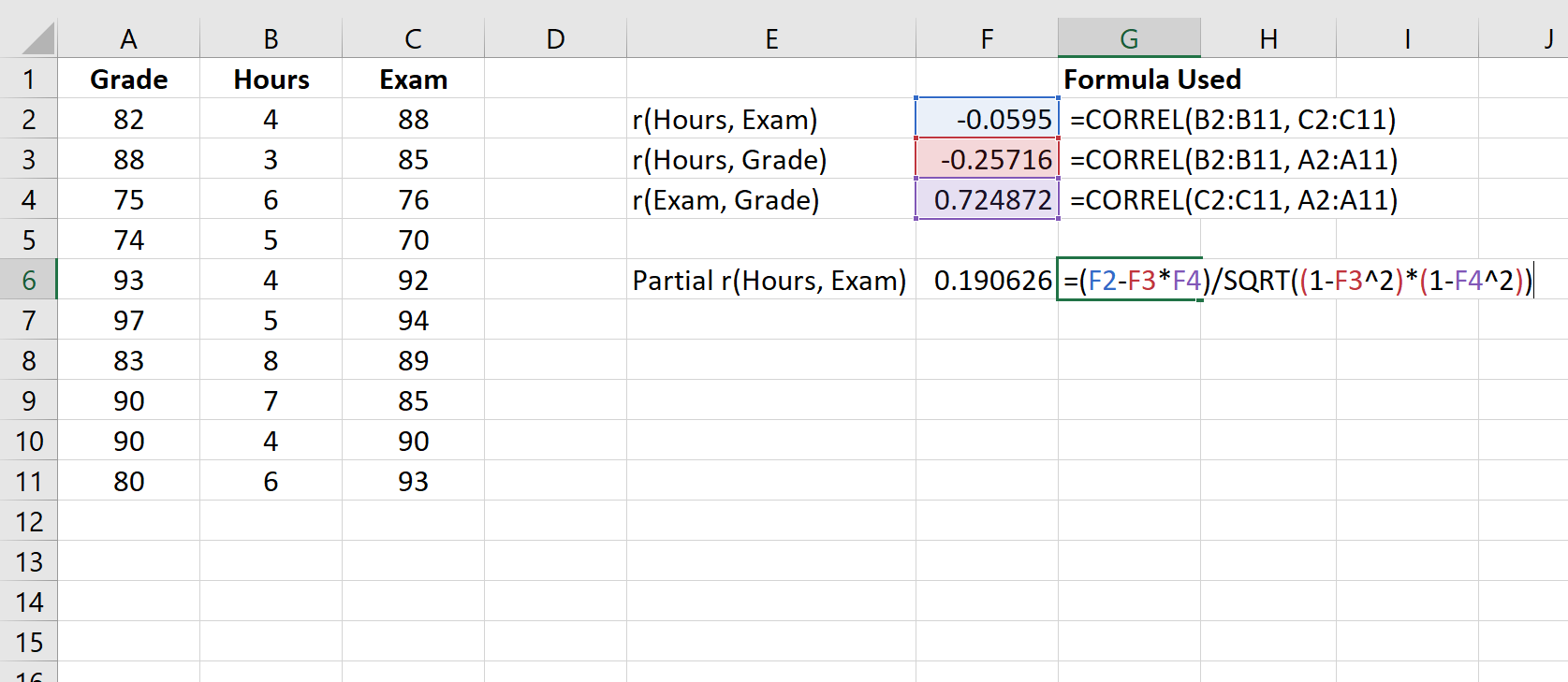
Шаг 2: Рассчитайте частичную корреляцию между часами и экзаменационным баллом.
Формула для расчета частичной корреляции между переменной A и переменной B при контроле переменной C выглядит следующим образом:
Частная корреляция = (r A,B – r A,C *r B,C ) / √((1-r 2 A,B )(1-r 2 B,C ))
На следующем снимке экрана показано, как использовать эту формулу для расчета частичной корреляции между часами и экзаменационным баллом с учетом текущей оценки:
Частная корреляция составляет 0,190626.Чтобы определить, является ли эта корреляция статистически значимой, мы можем найти соответствующее значение p.
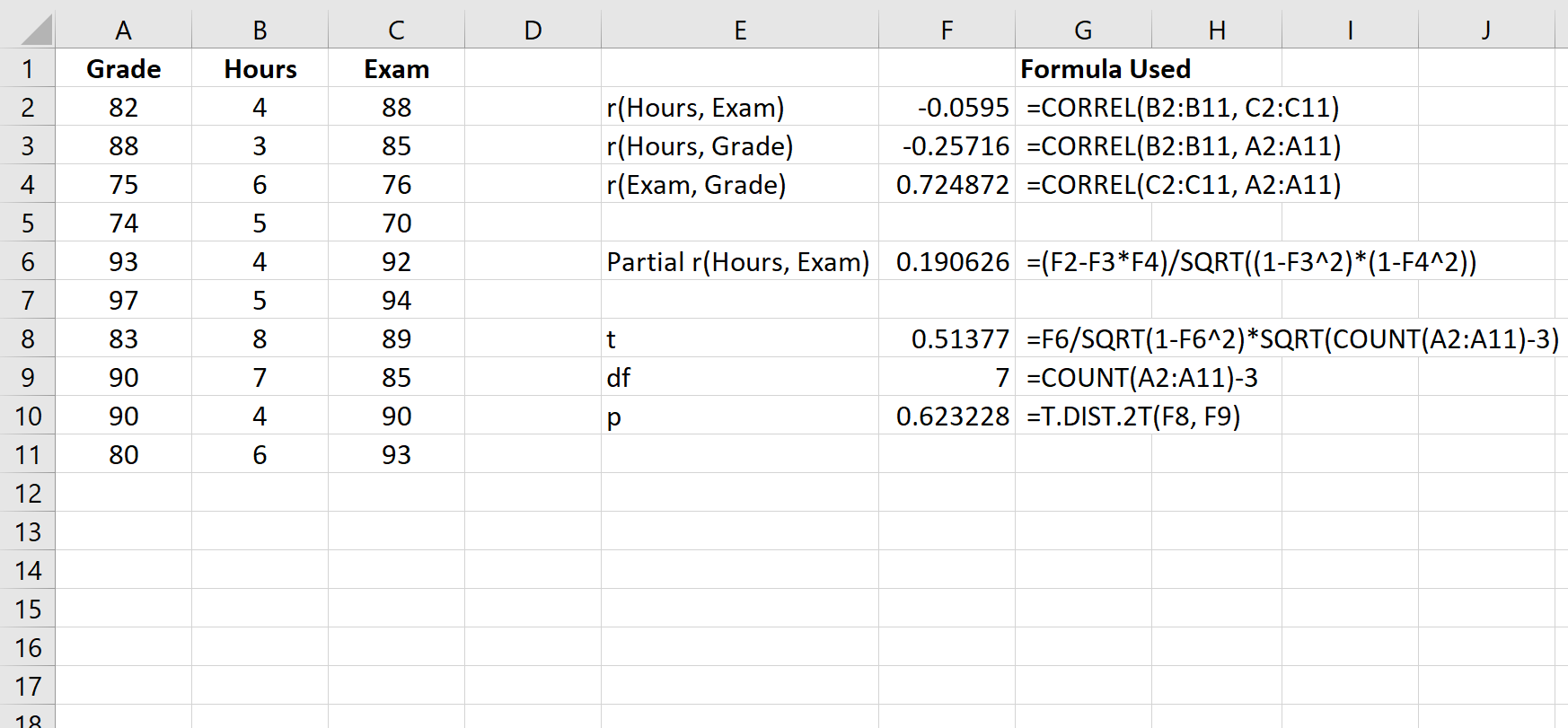
Шаг 3: Рассчитайте p-значение частной корреляции.
Тестовая статистика t может быть рассчитана как:
т = г √ (n-3) / √ (1-г 2 )
На следующем снимке экрана показано, как использовать эту формулу для расчета статистики теста и соответствующего значения p:
Тестовая статистика t равна 0,51377.Всего степеней свободы n-3 = 10-3 = 7.Соответствующее значение p равно 0,623228.Поскольку это значение не меньше 0,05, это означает, что частичная корреляция между часами и экзаменационным баллом не является статистически значимой.