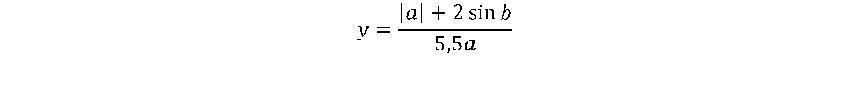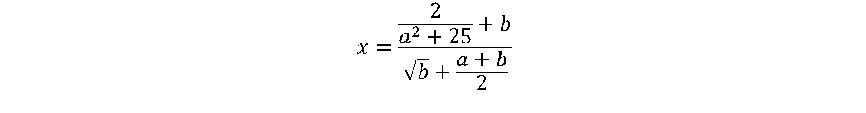Задачи на использование математических функций
Операцию возведения в степень не использовать
-
Известна сторона квадрата. Подготовить лист для расчета его площади.
|
A |
B |
C |
|
|
1 |
Задайте сторону квадрата |
||
|
2 |
Площадь квадрата равна: |
||
|
3 |
|||
|
4 |
-
Известна площадь квадрата. Оформить лист для расчета его стороны.
-
Известна площадь круга. Оформить лист для определения его диаметра.
-
Даны катеты прямоугольного треугольника. Подготовить лист для расчета его гипотенузы. Решение оформить в виде:
|
A |
B |
C |
|
|
1 |
|||
|
2 |
Задайте первый катет |
||
|
3 |
Задайте второй катет |
||
|
4 |
Гипотенуза равна: |
-
Даны стороны прямоугольника. Оформить лист для расчета его диагонали.
-
Известна длина стороны равностороннего треугольника. Оформить лист для определения его высоты.
-
Оформить лист для расчета среднего геометрического двух заданных целых чисел.
-
Даны стороны прямоугольного параллелепипеда. Оформить лист для определения его диагонали.
-
Считая, что Земля – идеальная сфера с радиусом R≈6350 км, определить расстояние от точки, с заданной высотой над Землей до линии горизонта.
-
Оформить лист для расчета периметра прямоугольного треугольника по известным катетам.
-
Известна площадь квадрата. Оформить лист для расчета его диагонали.
-
Даны стороны треугольника. Оформить лист для определения его площади.
-
Известны координаты двух точек на плоскости. Оформить лист для вычисления расстояния между ними.
-
Даны основания и высота равнобедренной трапеции. Подготовить лист для вычисления ее периметра.
-
Треугольник задан координатами своих вершин. Подготовить лист для вычисления его периметра и площади.
-
Подготовить лист для расчета синуса, косинуса, тангенса и котангенса угла, значение которого будет вводиться в одну из ячеек. Рассмотреть 2 варианта:
-
значение угла указывается в радианах;
-
значение угла указывается в градусах.
-
-
Подготовить лист для определения абсолютной величины числа, значение которого будет вводиться в одну из ячеек.
-
Известна диагональ квадрата. Оформить лист для расчета его площади и периметра.
-
Подготовить лист для определения площади ромба по известной длине его стороны и значению внутреннего угла в градусах.
-
Даны стороны параллелограмма и значение одного из внутренних углов (в градусах). Подготовить лист для определения площади параллелограмма.
-
Даны стороны треугольника и угол между ними (в градусах). Подготовить лист для определения площади треугольника.
-
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для определения периметра треугольника. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Известны размеры большего основания и боковой стороны равнобедренной трапеции, а также угол при большем основании. Подготовить лист для определения периметра трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для вычисления площади треугольника.
-
Подготовить лист для определения угла по известному значению его:
-
Синуса;
-
Косинуса;
-
Тангенса;
-
Котангенса.
-
Во всех случаях определить величину угла в радианах и градусах.
-
Известны длины сторон равнобедренного треугольника. Подготовить лист для вычисления его внутренних углов (в градусах).
-
Известны размеры оснований и боковой стороны равнобедренной трапеции. Подготовить лист для вычисления угла (в градусах) при большем основании.
-
Даны стороны a, b, c треугольника. Подготовить лист для вычисления его углов (в градусах) по теореме косинусов:
A=arcos(b2 + c2 – a2)/2bc
-
Даны катеты прямоугольного треугольника. Подготовить лист для вычисления острых углов треугольника (в градусах).
-
Даны основание и высота равнобедренного треугольника. Подготовить лист для вычисления угла (в градусах) при основании.
-
Известны размеры диагоналей ромба. Подготовить лист для вычисления его внутренних углов (в градусах).
-
Даны координаты на плоскости двух точек. Подготовить лист для вычисления угла наклона к оси абсцисс прямой, соединяющей эти точки.
-
Подготовить лист для нахождения десятичного логарифма числа, которое будет указываться в одной из ячеек.
-
Подготовить лист для нахождения натурального логарифма числа, которое будет указываться водной из ячеек.
-
Подготовить лист для вычисления значений eπ и πe.
-
Дана гипотенуза прямоугольного треугольника, а также один из его острых углов (в градусах). Подготовить лист для вычисления катетов этого треугольника.
-
Известна длина диагонали прямоугольника, а также угол ее наклона к большей стороне прямоугольника. Оформить лист для расчета площади и периметра прямоугольника.
-
Известны размеры большего основания и боковой поверхности равнобедренной трапеции, а также угол при большем основании. Подготовить лист для вычисления периметра и площади трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
-
Оформить лист для расчета значения функций
при данных значениях a и b
-
Считая, что Земля – идеальная сфера с радиусом R ≈ 6350 км, подготовить лист для определения расстояния до линии горизонта от точки с высотой над Землей, равной 1, 2, …, 10 км.
-
Получить на листе 10 первых чисел Евклида. Числа Евклида вычисляются по формуле:
Ek = 2k-1(2k-1), k = 1, 2, 3, …
-
Получить на листе 8 первых чисел ферма. Числа Ферма вычисляются следующим образом:
Fk = 2A+1, A = 2k+1, k = 1, 2, 3, …
-
Подготовить на листе таблицу значений функции y = sin(x), где х меняется от 0 до 6,5 радиан с шагом 0,5.
-
Получить на листе таблицу значений sin2, sin3, …, sin20 (значения углов указаны в радианах.
-
Получить на листе таблицу значений tg5, tg6, …, tg15 (значения углов указаны в радианах).
-
Получить на листе таблицу значений тригонометрических функций y = sin(x/2),
y = sin(2x), y = cosx для x, равного 00, 200, 400, …, 7200.
-
Пусть функция y(x) задана таблицей:
|
x |
y |
|
x1 |
y1 |
|
x2 |
y2 |
|
… |
… |
|
xn |
yn |
Значения аргумента х расположены в порядке возрастания, но не обязательно равномерно. Предположим, что точки (хi, уi) последовательно соединены отрезками прямых линий. Угловым коэффициентом каждого отрезка называется дробь:
(yi-1 — yi)/ (xi-1 — xi)
Оформить лист, на котором для каждого отрезка определить:
-
Его угловой коэффициент;
-
Угол наклона к горизонтали (в градусах).
-
Около стены наклонно стоит палка длиной 4,5 м. Один ее конец находится на расстоянии 3 м от стены. Нижний коней палки начинает скользить в плоскости, перпендикулярной стене. Оформить на листе таблицу для определения значения угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0,2 м.
-
Плотность воздуха убывает с высотой по закону p=p0e—bz, где p – плотность на высоте b метров, p0 =1,29 кг/м3, z=1,25*10-4. Получить на листе таблицу зависимости плотности от высоты для значений от 0 до 1000 м через каждые 100 м.
-
Получить на листе значения sin1, sin1+sin2, sin1+ sin2+sin3, …, sin1+sin2+…+ sin10. Значения получить в ячейках B2:B11, введя формулу только в одну ячейку и распространив (скопировав) ее на остальные ячейки диапазона.
A
B
C
1
2
1
0,841471
3
2
1,750768
4
3
1,891888
5
4
1,135086
6
5
0,176162
7
6
-0,10325
8
7
0,553733
9
8
1,543091
10
9
1,955209
11
10
1,411188
12
-
Получить на листе значения 1/ sin1, 1/( sin1+sin2), …, 1/(sin1+sin2+…+ sin10).
-
Значения получить С2:С11, введя формулу только в ячейки В2 и С2 и распространив (скопировав) их на остальные ячейки диапазона В2:С11.
|
A |
B |
C |
D |
|
|
1 |
||||
|
2 |
1 |
1,188395 |
||
|
3 |
2 |
0,571178 |
||
|
4 |
3 |
0,528572 |
||
|
5 |
4 |
0,880991 |
||
|
6 |
5 |
5,676604 |
||
|
7 |
6 |
-9,68487 |
||
|
8 |
7 |
1,805925 |
||
|
9 |
8 |
0,64805 |
||
|
10 |
9 |
0,511454 |
||
|
11 |
10 |
0,708623 |
||
|
12 |
-
Получить на листе значения cos1/sin1, (cos1+ cos2, )/ (sin1+sin2), …,( cos1+…+ cos15)/( sin1+…+ sin15).
Значения получить в ячейках F2:F11, введя формулы только в ячейки второй строки и распространив (скопировав) их на остальные ячейки диапазона В2: F11.
|
A |
B |
C |
D |
E |
F |
G |
|
|
1 |
|||||||
|
2 |
1 |
0,642093 |
|||||
|
3 |
2 |
0,070915 |
|||||
|
4 |
3 |
-0,45766 |
|||||
|
5 |
4 |
-1,33865 |
|||||
|
6 |
5 |
-7,01525 |
|||||
|
7 |
6 |
2,669616 |
|||||
|
8 |
7 |
0,863691 |
|||||
|
9 |
8 |
0,215641 |
|||||
|
10 |
9 |
-0,29581 |
|||||
|
11 |
10 |
-1,00444 |
|||||
|
12 |
Литература:
Д.М. Златопольский. Задачник по Excel, 2002, №24. Информатика
По теме: методические разработки, презентации и конспекты
Практическая работа на тему «Построение графиков функций средствами Microsoft Excel»
Задание и готовый пример практической работы на тему «Построение графиков функций средствами Microsoft Excel»…
Практическое задание по информатике 9 класс EXCEL условная функция
Дана таблица заработной платы некоторого предприятия…
Практическая работа «Использование функций в расчетах MS Excel 2007»
Дидактический материал практическая работа по теме «Использование функций в расчетах MS Excel 2007» предназначена для учащихся 8 класса .Для выполнения работы используется прогр…
Практическая работа по теме «Использование статистических функций в расчетах MS Excel 2007
Дидактический материал практическая работа по теме «Использование статистических функций в расчетах MS Excel 2007» предназначена для учеников 8 класса .Для выполнения работы использует…
Практическая работа «Встроенные функции в EXCEL»
При выполнении этой работы ученики научатся пользоваться различными группами функций при работе со статистическими данными. Находить максимальные и минимальные значения среди данных….
Практическая работа «Построение таблиц истинности логических функций в MS Excel» 9 класс
В данной работе дана пошагая инструкция по созданию ЭТ в MS Excel…
Практическая работа «Построение графиков математических функций в Excel»
Excel позволяет строить не только обычные графики, но и даже графики различных математических функций. Вот шаги, которые необходимо предпринять для построения графика функции в Excel: &bull…
Решение различных
математических задач, используя надстройки
«Подбор параметра» и «Поиск решения» в MS Excel.
Цель работы. Изучить:
· надстройку «Подбор параметра» для нахождения корней нелинейных
уравнений;
· надстройку «Поиск решения» для нахождения корней систем уравнений.
Пользуясь приемами выполнения простейших
расчетов и построения графиков функций в Excel, можно
находить решение различных математических задач. Рассмотрим это на примере
наиболее часто встречающихся задач нахождения корней нелинейных уравнений и
решения систем линейных уравнений. Указанные математические задачи легко
решаются с помощью надстроек Excel Поиск решения и Подбор параметра.
Подбор параметра
Надстройка Microsoft Excel Подбор параметра служит для нахождения
оптимального желаемого решения за счет изменения одного из параметров. С
формальной точки зрения такие задачи описываются уравнением с одной переменной,
которое в общем случае можно представить в следующем каноническом виде:
F(x) = 0,
где функция F(x) определена и непрерывна на интервале [a, b]. Таким образом, можно сказать, что
инструмент Подбор параметра служит для нахождения корня уравнения x. В этой надстройке реализован алгоритм метода
половинного деления.
Пример 1. Решим
уравнение x2 – 3 =
0, используя надстройку Подбор параметра.
В ячейку А1 вводится начальное приближение
для поиска одного из корней уравнения. Лучше найти его графически, хотя можно подставить и произвольное значение (например,
ноль). В ячейку В2 записывается в виде формулы левая часть решаемого уравнения.
Диалоговое окно данного инструмента вызывается через меню Данные
/ Что-если / Подбор параметра и имеет
следующий вид (рис. 2.7.1, 2.7.2):
Рис. 2.7.1. Надстройка Подбор параметра
В поле Установить в ячейке вводится
ссылка на ячейку, содержащую левую часть уравнения. В поле Значение
непосредственно (т.е. без ссылок на ячейки) вводится правая часть уравнения.
Причем правая часть уравнения должна обязательно представлять собой конкретное
числовое значение. Если правая часть уравнения содержит переменную или
какое-либо выражение, то такое уравнение должно быть предварительно
преобразовано к равносильному виду (в общем случае, к каноническому виду F(x) = 0). Нажав кнопку ОК, получаем в
ячейке А1 значение искомого корня: 1,731856.
Рис. 2.7.2. Надстройка Подбор параметра
Поиск решения
Нелинейные
уравнения также можно решать, используя надстройку Поиск решения. Для
того чтобы ее подключить, следует в меню Office (рис. 2.7.3) выбрать пункт Параметры Excel (рис. 2.7.4) и в раскрывшемся списке войти в меню Надстройки,
далее активировать Поиск решения, установив флажок против пункта Поиск
решения (рис. 2.7.5).
Рис. 2.7.3 Кнопка Office
Рис. 2.7.4. Меню Office
Рис. 2.7.5. Надстройки
После нажатия кнопки ОК
соответствующий значок появится во вкладке Данные (рис. 2.7.6).
Рис. 2.7.6. значок Поиск решения
Пример 2. Решим
уравнение x2 – 3 =
0, используя надстройку Поиск решения.
В ячейку А1
заносится начальное приближение корня, в ячейку В1 – левая
часть уравнения в виде формулы. Для предыдущего примера она имеет вид =А1*А1-3.
Далее из вкладки меню Данные
запускается надстройка Поиск решения.
В открывшемся диалоговом окне Поиск
решения устанавливается целевая ячейка $B$1, равная
нулевому значению. В текстовом поле Изменяя ячейки устанавливается адрес
$А$1 и нажимается кнопка Выполнить (рис. 2.7.7).
Рис. 2.7.7. Надстройка Поиск
решения
В ячейке А1 получается значение корня
1,732051 (рис. 2.7.8).
Рис. 2.7.8. Результаты работы
надстройки Поиск решения
Как видим, оно совпало с точностью до 0,001
с найденным ранее значением.
Обращает на
себя внимание неточность решения. Мы получаем очень близко приближающиеся к
точным, но все же неточные корни уравнения. Это происходит потому, что решение
уравнений на вычислительной технике происходит не аналитическими методами, как
это делает человек, а специально разработанными методами, получившими название
численных. В отличие от аналитических (точных) методов численные методы
обладают определенной погрешностью. В Excel с целью повышения точности решения
пользователь может уменьшить погрешность вычислений, но при этом может
потребоваться увеличение количества итераций. При этом надо помнить, что тем
самым увеличивается время на поиск решения. Установленные по умолчанию значения подходят для большинства практических задач, относительная
погрешность вычислений составляет 0,001 (рис. 2.7.9).
Рис. 2.7.9. Изменение
погрешности
Следует отметить, что найден только один из
двух корней данного уравнения. Для нахождения второго корня, следует в ячейку
А1 ввести новое приближение, близкое ко второму корню, и повторить поиск
решения.
Пример 3. Решим
систему уравнений, используя надстройку Поиск решения.
Для того, чтобы использовать рассматриваемую
надстройку Поиск решения для нахождения решения системы линейных
алгебраических уравнений, следует ввести в
столбец А начальное приближение для значений всех неизвестных. Пусть это будут
нули. В столбец В ввести формулы, описывающие левые части уравнений. В столбец
С вводят значения правых частей уравнений. Курсор ставят на ячейку В1 и
запускают надстройку Поиск решения. Значение целевой ячейки $B$1устанавливают равным значению ячейки С1. Изменяют значения ячеек
столбца А. К ограничениям добавляют все уравнения, кроме первого. Для системы
уравнений:
настроенный на
показ формул лист Excel с диалоговым окном Поиск решения
будут выглядеть так, как это показано на рисунках 2.7.10, 2.7.11.
Рис. 2.7.10. добавление ограничения
Рис. 2.7.11. Поиск решения
системы уравнений
Нажав кнопку Выполнить, получается в
столбце А значение неизвестных (рис. 2.7.12):
Как видно, надстройка Поиск решения
очень удобна для решения рассмотренных задач. Однако следует помнить, что
алгоритмы, реализованные в ней, предназначались не для них, а для решения задач
оптимизации. Поэтому возможны сбои в работе надстройки, и к полученным
результатам необходимо подходить критически.
.
Рис. 2.7.12. Результаты
работы с надстройкой Поиск решения
Задания для выполнения
Варианты заданий для работы приведены в
таблице 2.7.1, 2.7.2.
Задание1.
1.
Используя надстройку «Подбор параметра», найти все
корни уравнения (по вариантам) на отрезке [-2; +2] (табл. 2.7.1).
Таблица 2.7.1
Варианты заданий
|
№ |
Задание |
№ |
Задание |
|
1 |
|
11 |
|
|
2 |
|
12 |
|
|
3 |
|
13 |
|
|
4 |
|
14 |
|
|
5 |
|
15 |
|
|
6 |
|
16 |
|
|
7 |
|
17 |
|
|
8 |
|
18 |
|
|
9 |
|
19 |
|
|
10 |
|
20 |
|
Задание 2.
1.
Используя надстройку «Поиск решения», решить
систему линейных уравнений AX = B (по вариантам) (табл. 2.7.2)
и проверить правильность решения в Excel, подставив найденные значения неизвестных в систему уравнений. A – матрица коэффициентов при x1, x2, x3, x4. В- матрица свободных членов уравнений.
Таблица 2.7.2
Варианты заданий
|
№ |
Задание |
№ |
Задание |
|
1 |
2 |
3 |
4 |
|
1 |
|
9 |
|
|
2 |
|
10 |
|
|
3 |
|
11 |
|
|
4 |
|
12 |
|
|
5 |
|
13 |
|
|
6 |
|
14 |
|
|
7 |
|
15 |
|
|
8 |
|
16 |
|
Задание. Создать таблицу с
использованием математических функций,
которая рассчитывает значения функции
y=sin(2x/ 3)*cos(x/2)
на интервале значений х от -
до +2 с шагом 0,1, вычисляет максимальное
и минимальное значения функции на данном
интервале области определения, а также
строит график данной функции.
-
Запустите программу Excel и для получения
подсказки о синтаксисе тригонометрических
функций в окне справки Excel на вкладке
Содержание выберите раздел Справка
по функциям, тема Математические
функции. Для просмотра информации
щелкните по ссылкам SIN, COS и ПИ. Для
возврата к предыдущему окну справки
щелкайте кнопку «Назад».
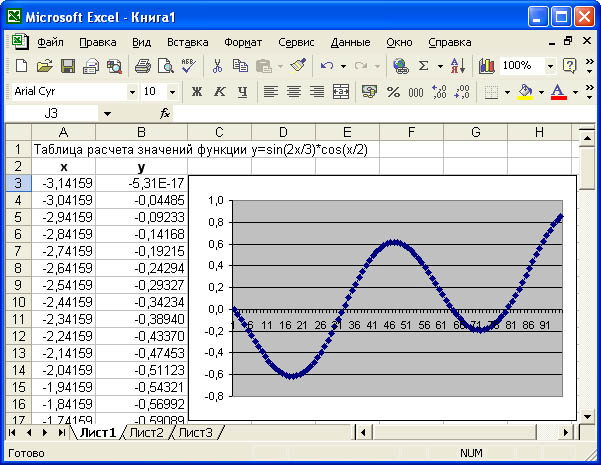
Рис. 1. Таблица расчета значений функции
y=sin(2x/3)*cos(x/2)
После просмотра справки закройте окно
справки любым из стандартных способов.
-
В ячейку А1 введите заголовок таблицы
«Таблица значений функции
y=sin(2x/3)*cos(x/2). Задайте в ячейке А2 формулу
= -ПИ() для ввода начального значения х.
В ячейке A3 задайте формулу = А2+0,1 для
вычисления следующего значения х,
изменяющегося с шагом 0,1. Скопируйте
формулу из A3 в диапазон (А4:А97).
-
В ячейку В2 введите формулу расчета
значения функции =SIN(2*A3/3)*COS(A3/2). Затем
скопируйте формулу из ячейкиВ2 в диапазон
(ВЗ:В97). -
В ячейку С2 введите формулу определения
минимума функции =МИН(В2:В97), а в ячейку
СЗ — формулу определения максимума
функции =МАКС(В2:В97).
В результате получится таблица, фрагмент
которой показан на рис. 1.
-
Для построения графика функции выделите
диапазон ячеек (В2:В97) и, щелкнув кнопку
на
панели инструментов Стандартная,
вызовите Мастер диаграмм. На первом
шаге диалога с Мастером диаграмм
выберите тип диаграмм График и
щелкните кнопку «Далее». На втором шаге
определите, что данные для построения
диаграммы берутся из ряда в столбце и
уточните значение диапазона В2:В97.
Щелкнув кнопку «Далее», определите
параметры диаграммы: заголовки, подписи
данных, положение легенды, линии сетки
и т.д. На последнем шаге определите
положение диаграммы на имеющемся листе
и щелкните кнопку «Готово». -
Сохраните полученную таблицу, выбрав
в меню Файл команду Сохранить
как, а затем в диалоговом окне
Сохранение документа, открыв нужную
папку, задайте в поле имя файла SIN_COS
и щелкните кнопку «Сохранить». -
Для просмотра вида таблицы на бумаге
выберите в меню Файл команду
Предварительный просмотр. Для
перехода к другим страницам щелкните
клавиши Далее или Назад. Для
печати таблицы на бумаге выберите
команду Печать в меню Файл. В
окне Печать укажите номера печатаемых
страниц и количество копий, после чего
щелкните кнопку «ОК» для начала печати. -
Закройте окно Excel.
Лабораторная работа 2. Использование логических функций
Задание. Создать таблицу,
которая формирует ведомость на выплату
зарплаты с прогрессивной шкалой
подоходного налога.
Пусть налог исчисляется по прогрессивной
шкале следующим образом: с зарплаты, не
превышающей 1000 руб., налог составляет
12%, а с части зарплаты, превышающей 1000
руб., взыскивается налог 20% от этой части.
1. Вначале определим исходные
данные задачи: фамилии работников
(текст) и размер зарплаты (число с двумя
цифрами в дробной части).
Установим, что мы должны рассчитать в
задаче величины подоходного налога и
получаемой каждым работником суммы.
2. Для выполнения расчетов
запустите Excel, опишите структуру таблицы
и введите исходные данные следующим
образом.
|
А |
В |
С |
D |
|
|
1 |
Расчет зарплаты с прогрессивной |
|||
|
2 |
Фамилия |
Зарплата |
Налог |
Получить |
|
3 |
Иванов |
1234,56 |
||
|
4 |
Петров |
1000 |
||
|
5 |
Сидоров |
1563,35 |
||
|
6 |
Фролов |
986,54 |
||
|
7 |
Итого |
4784,45 |
||
|
8 |
3. В ячейку СЗ поместите формулу
расчета величины подоходного налога,
вычисляемого по прогрессивной шкале.
Для этого выделите ячейку СЗ и введите
формулу =ЕСЛИ(ВЗ<=1000;
ВЗ*0,12;1000*0,12+(ВЗ-1000)*0,2). В этой формуле
проверяется условие В3<=1000. Если условие
соблюдается, то налог вычисляется по
формуле В3*0,12. Если условие ложно, то
налог вычисляется по формуле
1000*0,12+(ВЗ-1000)*0,2 (12% от суммы зарплаты в
1000 руб. + 20% от суммы, превышающей 1000
руб.).
4. В ячейку D3 введите формулу
=ВЗ-СЗ для определения суммы разности
зарплаты и налога.
5. Скопируйте формулы из
диапазона C3:D3 в диапазон C4:D6. В ячейку
В7 введите формулы суммирования результата
по столбцу В, для чего, выделив ячейки
ВЗ:В6, щелкните кнопку «Автосумма» в
панели инструментов Стандартная.
Скопируйте формулу вычисления суммы
столбца из В7 в C7:D7.
6. Оформите таблицу, выделив
диапазон A2:D7 и выбрав команду Автоформат
в меню Формат. В диалоговом окне
Автоформат из списка форматов
выберите вариант Финансовый 3 и щелкните
кнопку «ОК». Измените формат отображения
значений в ячейках B3:D7, для чего, выделив
этот диапазон, выберите в меню Формат
команду ячейки, затем в диалоговом окне
Формат ячеек выберите Финансовый
формат, в поле Число десятичных
знаков задайте отображение двух цифр
в дробной части, в поле Обозначение
выберите р и щелкните кнопку «ОК»
для применения заданного формата ячеек.
После этого таблица будет иметь следующий
вид .
|
А |
В |
С |
D |
|
|
1 |
Расчет зарплаты с прогрессивной |
|||
|
2 |
Фамилия |
Зарплата |
Налог |
Получить |
|
3 |
Иванов |
1234,56р. |
166,91р. |
1067,65р. |
|
4 |
Петров |
1000,00р. |
120,00р. |
880,00р. |
|
5 |
Сидоров |
1563,35р. |
232,67р. |
1330,68р. |
|
6 |
Фролов |
986,54р. |
118,38р. |
868,16р. |
|
7 |
Итого |
4784,45р. |
637,97р. |
4146,48р. |
7. Сохраните таблицу под именем
Расчет зарплаты. Для этого в меню
Файл выберите команду Сохранить
как, затем в диалоговом окне Сохранение
файла выберите папку, задайте имя
файла и щелкните кнопку «Сохранить».
8. Завершите работу приложения
Microsoft Excel одним из стандартных способов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Плашкова конкурсная работа Москва.docx, Курсовая работа Наружная реклама.docx, Практическая работа №5 (2).docx, Практическая работа 2.doc, Практическая работа №1.doc, Практическая работа под номером 7 (1).docx, Практическая работа №1.docx, Практическая работа № 8.docx, Исследовательская работа «Влияние социальных сетей на социализац, ороший вт Практическая работа № 1 Сравнение содержания обновленн
Практическая работа 1
Вычисления по формулам с использованием встроенных математических функций MS ExcelЦель работы:
- изучить принципы построения и синтаксис математических формул в Excel;
- изучить встроенные математические функции Excel, соответствующие основным элементарным функциям;
- освоить различные технологии ввода формул;
- применить полученные знания к решению элементарных вычислительных математических задач;
- развить навыки форматирования таблиц.
1. ОСНОВНЫЕ ПОНЯТИЯ
1.1. ФОРМУЛЫ
Формула задает правило для вычисления нового значения через исходные значения. Формула должна подчиняться определенным правилам записи, т.е. синтаксису. В Excel запись формулы всегда начинают со знака равенства. Часть формулы, следующая за знаком равенства, называется выражением.
Формулой в Excel называется последовательность, содержащая следующие элементы:
- знак равенства (=) – признак формулы в Excel;
- операнды (числа, текст, ссылки на ячейки, ссылки на массивы ячеек, встроенные функции);
- знаки операций (иногда их называют операторами);
- круглые скобки, причем число открывающих скобок должно быть равно числу закрывающих.
В первой работе уже приводились примеры вычисления по формулам, в которых выполнялись арифметические операции над числами. Числа в них задавались либо непосредственно в формуле, либо в виде ссылок на ячейки. Сейчас мы расширили это определение, включив в формулы функции в качестве операндов. Будем рассматривать только встроенные функции Excel.
1.2. ВСТРОЕННЫЕ ФУНКЦИИ EXCEL
Встроенные функции Excel – это функции, вычисление которых выполняется по определенным алгоритмам, содержащимся в приложении Excel. Вызов встроенной функции происходит при вычислении по формуле, содержащей эту функцию. Запись функции в формуле Excel аналогична записи функций в математике. Она имеет вид , где f – имя функции,
— аргументы. В общем случае аргументами функций могут быть данные любого вида, но для конкретной функции возможные аргументы определяются ее синтаксисом. Аргументы отделяются друг от друга точкой с запятой. Существуют встроенные функции, не содержащие аргументов, например, число π вычисляется с помощью функции ПИ(). Как видим, в этом случае после имени функции нужно ставить скобки, которые и являются признаком функции в записи. Встроенные функции Excel разбиты на категории. Каждая категория функций предназначена для определенных целей, например, имеются математические, логические, статистические функции и т.д. В данной лабораторной работе рассмотрим математические функции, причем только те, которые соответствуют элементарным функциям в математике. Они перечислены в табл. 1.
Таблица 1
| Математическая
функция |
Встроенная функция Excel | Тип
аргументов |
Пояснение |
| |x| | ABS(x) | Любое число | Абсолютная величина x
(модуль x) |
| arccos x | ACOS(x) | “ | Значение функции выражено в радианах |
| arcsin x | ASIN{x) | “ | Аналогично предыдущему |
| arctg x | ATAN(x) | “ | “ |
| cos x | COS(x) | “ | Косинус величины x, выраженной в радианах |
| EXP(x) | “ | Экспонента от x | |
| ln x | LN(x) | “ | Натуральный логарифм x |
| logax | LOG(x;a) | “ | Логарифм x по основанию a |
| lg x | LOG10(x) | “ | Десятичный логарифм x |
| sin x | SIN(x) | “ | Синус величины x, выраженной в радианах |
| tg x | TAN(x) | “ | Тангенс величины x, выраженной в радианах |
| КОРЕНЬ(x) | “ | Квадратный корень | |
| π | ПИ() | Без аргумента | Число π |
| xa | СТЕПЕНЬ(x;a) | Любые числа | x в степени a |
Замечание. При наборе формул с клавиатуры безразлично, набираются строчные или прописные буквы, но нужно соблюдать соответствие языка имени функции. Ссылки на ячейки записываются только латинскими буквами. При указании типа аргумента не рассматриваются ограничения на область определения функций, но, разумеется, их нужно соблюдать.
1.3. ОПЕРАЦИИ
Операции (арифметические и некоторые другие действия) в формулах записываются с помощью специальных символов, называемых знаками операций. Полный список операций Excel приведен в табл. 2.
Таблица 2
| Знак
операции |
Операция | Пример записи |
| Арифметические операции | ||
| + | сложение | =А1+2 |
| — | вычитание | =4-С4 |
| * | умножение | =А3*С6 |
| / | деление | B3/5 |
| % | процент | =10% (равно 0,01) |
| ^ | возведение в степень | =2^3 (равно  |
| Операции сравнения | ||
| = | равно | A5=0 |
| < | меньше | A5<1 |
| > | больше | B3>100 |
| <= | меньше или равно | 3<=2*A10 |
| >= | больше или равно | A10>=0 |
| < > | не равно | A10< >5 |
| Операция связывания ячеек | ||
| : | Диапазон | =СУММ(А1:С10) |
| Текстовый оператор соединения | ||
| & | соединение текстов | =”Ответственный”&” Иванов И.П.” |
Операции выполняются над некоторыми данными (операндами). Операндом может быть число, ссылка на ячейку, ссылка на диапазон ячеек, функция, выражение, взятое в скобки. Рассмотрим формулы Excel:
1) =4-5,2+3,68 2) =2*5+12*6,2
Порядок действий в первой формуле следующий: вычитание, затем сложение. Во второй формуле сначала вычисляется 2*5, затем 12*6,2, после этого выполняется сложение ранее вычисленных чисел. Порядок выполнения операций определяется приоритетом операций. Для изменения порядка действий нужно использовать скобки.
Порядок вычисления значения по формуле Excel:
- вычисляются значения функций, входящих в формулу;
- вычисляются выражения в скобках;
- выполняются операции слева направо с учетом приоритета.
Приоритет арифметических операций в формулах Excel указан в табл. 3.
Таблица 3
| Знак
операции |
Операция | Свойства | Приоритет |
| — | Изменение знака | Унарная | 1 |
| ^ | Возведение в степень | Бинарная | 2 |
| * , / | Умножение, деление | Бинарная | 3 |
| + , — | Сложение, вычитание | Бинарная | 4 |
Комбинировать арифметические операции с прочими не рекомендуется (за исключением связывания массива).
Примеры
1. Порядок вычислений по формуле: =3+5*COS(B4)-2*A2:
- COS(B4)
- 5*COS(B4)
- 2*A2
- 3+ 5*COS(B4)
- 3+5*COS(B4)-2*A2
2. Порядок вычислений по формуле =(3+A2^3/2)*3/5:
- A2^3
- A2^3/2
- 3+ A2^3/2
- (3+ A2^3/2)*3
- (3+ A2^3/2)*3/5
Замечания
1. При наборе сложной формулы легко сделать ошибку, поэтому надо хорошо знать синтаксис формул, чтобы в случае необходимости скорректировать формулу набором символов с клавиатуры.
2. Иногда Excel выводит подсказку пользователю, предлагая внести исправления в формулу. Их можно принять или отвергнуть после анализа предложения.
3. Если формула не может быть вычислена, в ячейке появляется сообщение об ошибке, которое начинается символом #.
4. Если MS Excel обнаружил ошибки в формуле, то вам может быть предложено исправить их автоматически.
Сообщения об ошибках.
#ДЕЛ/0! — деление на нуль
#ЧИСЛО! – недопустимый аргумент числовой функции
#ЗНАЧ! – недопустимое значение аргумента или операнда
#ИМЯ? – неверное имя ссылки или функции
#Н/ Д! – неопределенные данные
#ССЫЛКА! – ссылка на несуществующие ячейки
При обнаружении ошибки следует перейти в режим редактирования и исправить формулу. В случае затруднений надо провести синтаксический анализ формулы и ввести ее заново.
2. ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
Пример 1. с основанием R и высотой h. Значения R и h заданы. Положить R=1 м , h=3 м. Отчет представить в виде распечатки рабочих листов, содержащих условие задачи, расчетные формулы, расчеты в Excel в режиме отображения данных и формул.
Решение:
1. Расчетные формулы. (Формулы рекомендуется предварительно записать в тетрадь):
2. Создание рабочего листа с заданием и расчетными формулами. Порядок действий рекомендуется следующий:
- создать новый файл и сохранить его в личной папке под именем Конус.xls;
- в ячейку A1 ввести тему работы; в нижележащие ячейки (например, A3, A4) ввести номер примера и текст задачи;
- в отдельные ячейки A6:A7 и A10:A14 ввести обозначения размеров конуса с пояснениями; ввести данные: значения 1 и 3 для R и h соответственно в B6, B7;
- выполнить вставку расчетных формул с помощью приложения MS Equation 3.0.
3. Выполнение расчетов в Excel.
В ячейки E10:E14 последовательно ввести формулы:
=КОРЕНЬ(B6*B6+B7*B7)
=ПИ()*B7*B7
=ПИ()*B7*E10
=E11+E12
=E11*B6/3.
4. Форматирование таблицы.
- Установить в таблице шрифт Times New Roman, размер 10.
- Расположить текст по образцу, используя диалоговое окно Формат ячеек, вызываемого правой кнопкой мыши при выделении необходимых ячеек (вкладка Выравнивание, флажки — Объединить ячейки и Переносить по словам). Если весь текст не виден в объединенных ячейках, нужно увеличить высоту строки.
- Выполнить подчеркивание заголовка, используя команду Подчеркивание вкладки Шрифт диалогового окна Формат ячеек — одинарное по значению.
Фрагмент рабочего листа Excel после форматирования представлен на рис. 1.
Рисунок 1- Фрагмент рабочего листа Excel после форматирования
Пример 2. Вычислить по заданным формулам величины:
Рис. 2.1 Фрагмент рабочего листа Excel для примера 1
Решение
Решение выполним на одном рабочем листе с примером 1. Порядок действий аналогичен предыдущему примеру:
- введем услов`ие задачи с формулами для вычислений;
- введем в отдельные ячейки обозначения и значения исходных данных m, c, t, b (см. рис. 2.2);
- в ячейки для результатов введем формулы:
=(A33*TAN(C33)+ABS(B33*SIN(C33)))^0,5
=LOG(A33;2)*COS(D33*C33)*EXP(C33+B33);
- форматируем таблицу.
Фрагмент рабочего листа с решением примера 2 представлен на рис.2.2.
Рисунок 2- Фрагмент рабочего листа для примера 2
При вводе формул, необходим тщательный анализ порядка действий и аккуратный набор всех символов. Возможно, количество ошибок сократится, если применить ряд приемов:
- при вставке ссылки на ячейку нужно щелкнуть мышью по этой ячейке;
- при вставке функции нужно вызвать Мастер функций по команде Вставить функцию вкладки Формулы, который позволяет выполнить вставку функции за два шага: первый шаг – выбор категории функции и выбор функции, второй шаг – задание аргументов функции.
Опишем эту технологию подробнее на примере первой формулы:
- для возведения в степень используем знак операции ^, поэтому основание степени нужно взять в скобки; соответственно, наберем =(
- введем значение m щелчком по ячейке A33 и знак умножения *
- вызовем Мастер функций, при этом появится диалоговое окно первого шага, представленное на рис.3, выберем категорию функций Математические и в появившемся списке функций укажем TAN

Рисунок 3 — Диалоговое окно Мастера функций (первый шаг)
- при нажатии OK появится окно второго шага Мастера функций (см. рис. 4). В поле Число введем аргумент щелчком по ячейке со значением t C33. При нажатии OK или клавиши Enter ввод функции заканчивается, заканчивается и ввод формулы в ячейку.
Рисунок 4 — Диалоговое окно Мастера функций (второй шаг)
- вставим функцию ABS. При задании аргумента наберем B33* и снова вызовем Мастер функций;
- функция от функции выбирается в списке функций в строке формул. Если требуемой функции нет в списке, нужно выбрать из списка вариант Другие функции, что приведет к повторному вызову Мастера функций. После знака умножения вставим функцию SIN. После задания аргумента нужно щелкнуть в строке формул (нажатие OK или клавиши Enter приведет к окончанию набора, а предложенный вариант вернет нас к окну внешней функции);
- после окончания ввода внешней функции ABS закончим ввод формулы, набрав закрывающую скобку и возведение в степень 0,5 – символы — )^0,5 или )^(1/2). Можно было также использовать функцию КОРЕНЬ, но это привело бы к тройному вложению функций в формуле и усложнению ее набора.
Практическая работа
Задание 1.
Представленная ниже таблица должна помочь администрации института определить
количество студентов заслуживших получать стипендию по результатам сессии. Используйте
следующие критерии: менее 18—ти баллов — стипендию не получает, от 23,5 баллов включительно —
повышенная стипендия.
Задание 2.
Протабулируйте функцию на отрезке [—10;4] с шагом 1 в Excel, используя функцию ЕСЛИ.
Задание 3*.
Подготовьте таблицу, с помощью которой вам достаточно будет вести последние показания
счетчика, а таблица рассчитает расход электроэнергии и сумму оплаты. Сумма оплаты зависит от
категории плиты. Если плита электрическая, то 1 кВт ч стоит 125 руб., а если плита газовая 1 кВт ч
стоит 180 руб.
В ячейку D3 введите категорию плиты: 1 будет
означать, что плита в квартире электрическая, а цифра
2, что плита газовая.
1. Для заполнения столбца названиями месяцев,
введите первый месяц и, выделив ячейку,
протяните маркер заполнения вниз.
2. Для заполнения столбца «Дата» введите 2
первых значения, выделите обе ячейки и
протяните маркер заполнения вниз.
3. В столбце «Расход кВтч» введите формулу
«расход электроэнергии» = «последние показания счетчика» — «предыдущие».
4. В столбец «Сумма» вводится формула с функцией ЕСЛИ. Если «категория плиты»=1
(электроплита), то сумма равна: «расход» * 125 (D1), иначе «расход» * 180 (D2), для газовой
плиты.
5. Примените к ячейке «Денежный» формат числа без обозначений, с числом знаков после
запятой
Цель урока: продолжить формирование
навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания,
редактирования, форматирования и выполнения
простейших вычислений в электронных таблицах. - развивающие: расширить представления
учащихся о возможных сферах применения
электронных таблиц; развивать навыки
аналитического мышления, речи и внимания. - воспитательные: формировать и воспитывать
познавательный интерес; прививать навыки
самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
Ход урока
1. Организационный момент.
Сообщить тему урока, сформулировать цели и
задачи урока.
Сегодня мы вновь окажемся в гостях у маленького
великана Васи в Сказочной стране. Ему, как всегда,
требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы
вам известны? - Как задается имя ячейки (строки, столбца) в
электронной таблице? - Что может быть содержимым ячейки?
- Число 1 находится в столбце …, в строке …, в
ячейке с адресом … - Число 4 находится в ячейке с адресом …
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в
ячейке С1? - Чему равно значение, вычисляемое по формуле, в
ячейке D2?
2) Какой результат будет получен в ячейках с
формулами?
| А | В | |
| 1 | 25 | 4 |
| 2 | 2 | =A1*B1/2 |
| 3 |
Ответ: 25*4/2=50
| A | B | C | D | |
| 1 | 5 | 2 | 1 | |
| 2 | 6 | 8 | 3 | |
| 3 | 8 | 3 | 4 | |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил
домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований |
|||||||
| Среднее время участников соревнований |
|||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится
как среднее арифметическое трех его заплывов. - В ячейку «Лучшее время» записывается
минимальный результат из 3 заплывов. - В ячейку «Лучший результат соревнований»
записывается минимальное время из столбца. - В столбец «Отклонение» записывается
разность между лучшим временем спортсмена и
лучшим результатом соревнований. - В ячейку «Максимальное отклонение»
записывается максимальное значение столбца.
| Результаты соревнований по плаванию |
|||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований |
3,16 | ||||||
| Среднее время участников соревнований |
3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать
забор вокруг своего огорода и вскопать его под
посадку овощей (наступила очередная весна),
разметить грядки прямоугольной формы. Для работы
ему потребовалось найти длину забора и площадь
участка. Но ведь в школе он никогда не учился.
Поможем Васе.
№ 1. Вычислить периметр и площадь
прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для
следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно
решает следующую задачу и представляет свое
решение учащимся (через проектор).
№ 2. Маленький великан Вася решил
подсчитать, через сколько дней в его копилке
будет 100 руб., если ежедневно он стал класть туда
на 5 руб. больше, чем в предыдущий день. Помогите
Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению
следующей.
Один ученик показывает, как работать с
формулами, другой – как использовать функцию
суммирования, числовой формат (общий, денежный) и
т.д. (Таблица уже готова, ученикам предстоит
ввести формулы, использовать суммирование и
получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли
Васе 150 рублей, чтобы купить все продукты, которые
ему заказала мама, и хватит ли на чипсы за 10
рублей? Сдачу мама разрешила положить в копилку.
Сколько рублей попадет в копилку?
Предполагаемое решение:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
|
Итого: |
=СУММ(E2:E5) | |||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется |
=D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у
жителей Цветочного города.
Собираясь на пляж, веселые человечки решили
запастись прохладительными напитками. Незнайка
взял с собой 2 литра кваса, 1 литр газировки и 1
литр малинового сиропа, Пончик – 3 литра
газировки и 2 литра малинового сиропа, Торопыжка
– 2 литра газировки, доктор Пилюлькин – 1 литр
кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все
человечки вместе? - Сколько всего литров напитков взял с собой
каждый из человечков? - Сколько всего литров напитков взяли все
человечки вместе?
Оформите таблицу произвольно и сохраните в
своей личной папке.
Результат работы.
| Веселые человечки. Напитки. |
|||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны
еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе
стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр
малинового сиропа – 6 монет, 1 литр касторки – 2
монеты.
- Сколько монет истратил на покупку напитков
каждый человечек? - Сколько монет затрачено на покупку напитков
каждого вида? - Сколько потрачено денег всеми человечками
вместе?
Литература
- Информатика. Задачник-практикум в 2 т. /Под ред.
И.Г.Семакина, Е.К.Хеннера – М.: Лаборатория
Базовых Знаний, 2010. - Ефимова О. Курс компьютерной технологии с
основами информатики. – М.: ООО “издательство
АСТ”; АВF, 2005.
Презентация