Содержание
- 10 популярных финансовых функций в Microsoft Excel
- Выполнение расчетов с помощью финансовых функций
- ДОХОД
- ПРПЛТ
- СТАВКА
- ЭФФЕКТ
- Лабораторная работа №7: Экономические расчеты в MS Excel. Финансовые функции MS Excel
- Дистанционные курсы для педагогов
- Разговоры о важном
- «Финансовые функции в Excel» практическая работа
10 популярных финансовых функций в Microsoft Excel
Excel имеет значительную популярность среди бухгалтеров, экономистов и финансистов не в последнюю очередь благодаря обширному инструментарию по выполнению различных финансовых расчетов. Главным образом выполнение задач данной направленности возложено на группу финансовых функций. Многие из них могут пригодиться не только специалистам, но и работникам смежных отраслей, а также обычным пользователям в их бытовых нуждах. Рассмотрим подробнее данные возможности приложения, а также обратим особое внимание на самые популярные операторы данной группы.
Выполнение расчетов с помощью финансовых функций
В группу данных операторов входит более 50 формул. Мы отдельно остановимся на десяти самых востребованных из них. Но прежде давайте рассмотрим, как открыть перечень финансового инструментария для перехода к выполнению решения конкретной задачи.
Переход к данному набору инструментов легче всего совершить через Мастер функций.
- Выделяем ячейку, куда будут выводиться результаты расчета, и кликаем по кнопке «Вставить функцию», находящуюся около строки формул.
В Мастер функций также можно перейти через вкладку «Формулы». Сделав переход в неё, нужно нажать на кнопку на ленте «Вставить функцию», размещенную в блоке инструментов «Библиотека функций». Сразу вслед за этим запустится Мастер функций.
Имеется в наличии также способ перехода к нужному финансовому оператору без запуска начального окна Мастера. Для этих целей в той же вкладке «Формулы» в группе настроек «Библиотека функций» на ленте кликаем по кнопке «Финансовые». После этого откроется выпадающий список всех доступных инструментов данного блока. Выбираем нужный элемент и кликаем по нему. Сразу после этого откроется окно его аргументов.
ДОХОД
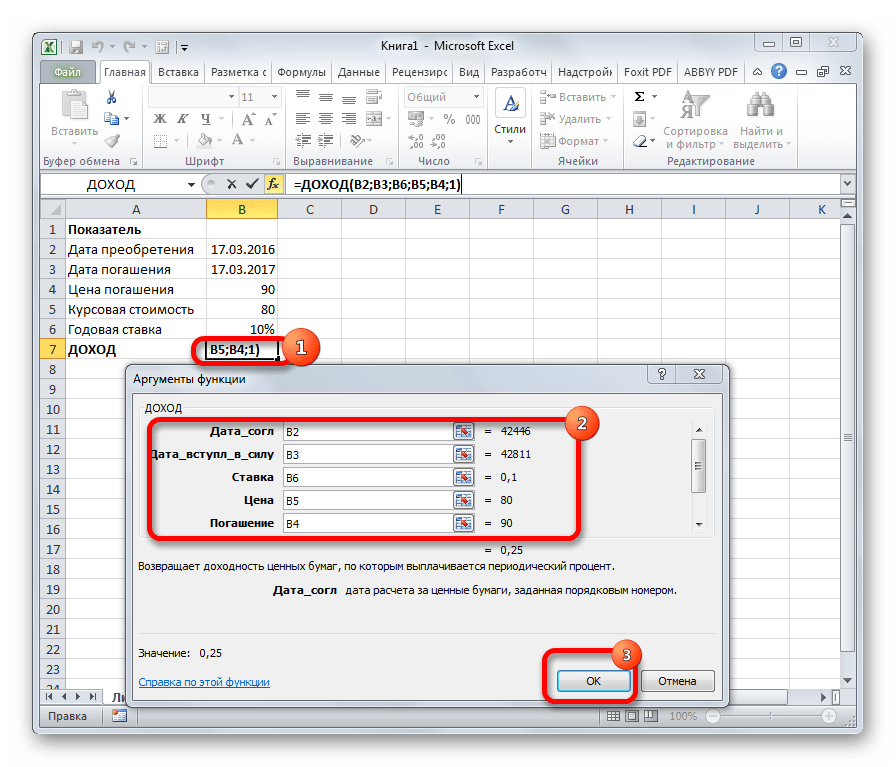
Одним из наиболее востребованных операторов у финансистов является функция ДОХОД. Она позволяет рассчитать доходность ценных бумаг по дате соглашения, дате вступления в силу (погашения), цене за 100 рублей выкупной стоимости, годовой процентной ставке, сумме погашения за 100 рублей выкупной стоимости и количеству выплат (частота). Именно эти параметры являются аргументами данной формулы. Кроме того, имеется необязательный аргумент «Базис». Все эти данные могут быть введены с клавиатуры прямо в соответствующие поля окна или храниться в ячейках листах Excel. В последнем случае вместо чисел и дат нужно вводить ссылки на эти ячейки. Также функцию можно ввести в строку формул или область на листе вручную без вызова окна аргументов. При этом нужно придерживаться следующего синтаксиса:
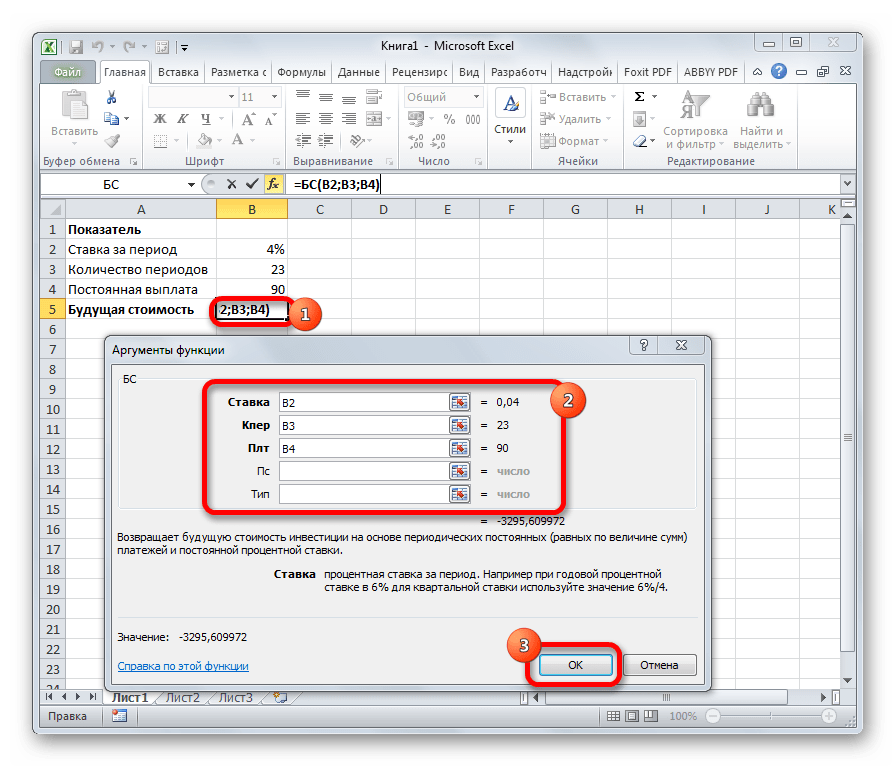
Главной задачей функции БС является определение будущей стоимости инвестиций. Её аргументами является процентная ставка за период («Ставка»), общее количество периодов («Кол_пер») и постоянная выплата за каждый период («Плт»). К необязательным аргументам относится приведенная стоимость («Пс») и установка срока выплаты в начале или в конце периода («Тип»). Оператор имеет следующий синтаксис:
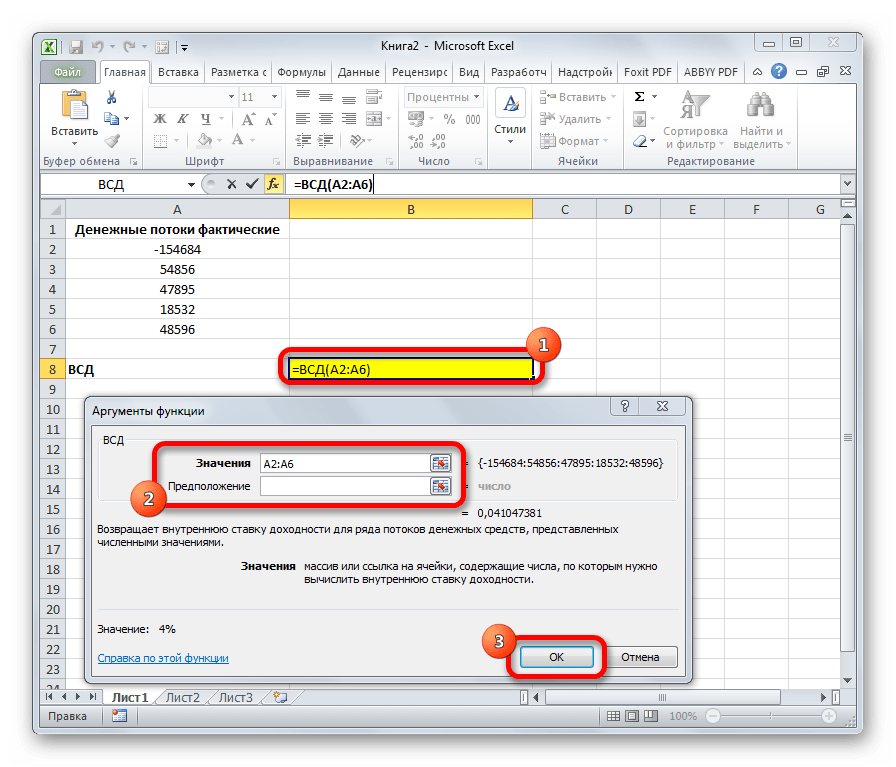
Оператор ВСД вычисляет внутреннюю ставку доходности для потоков денежных средств. Единственный обязательный аргумент этой функции – это величины денежных потоков, которые на листе Excel можно представить диапазоном данных в ячейках («Значения»). Причем в первой ячейке диапазона должна быть указана сумма вложения со знаком «-», а в остальных суммы поступлений. Кроме того, есть необязательный аргумент «Предположение». В нем указывается предполагаемая сумма доходности. Если его не указывать, то по умолчанию данная величина принимается за 10%. Синтаксис формулы следующий:
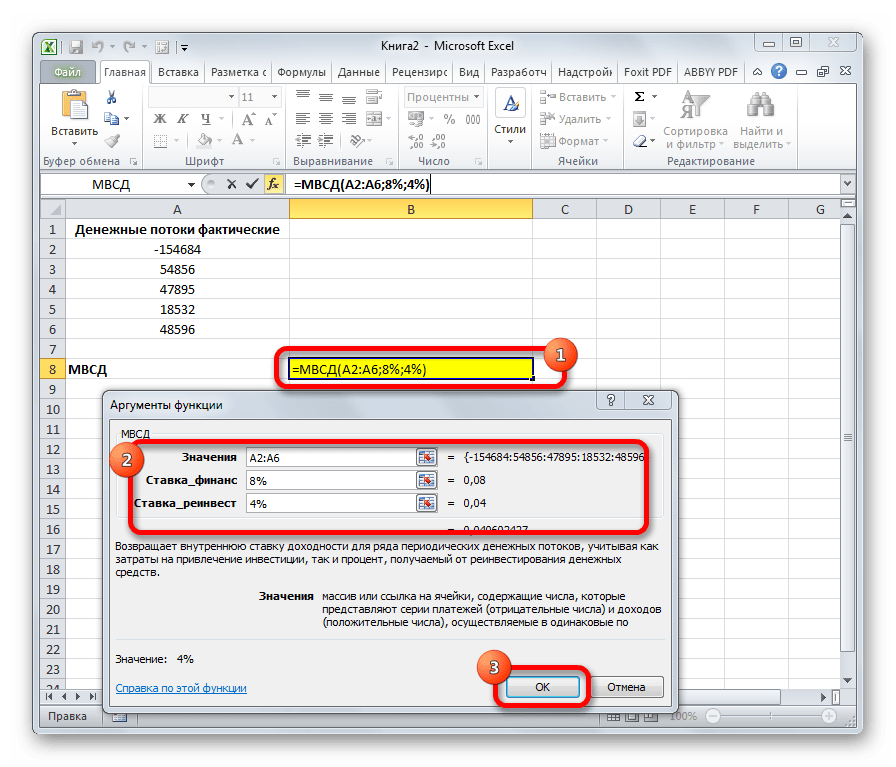
Оператор МВСД выполняет расчет модифицированной внутренней ставки доходности, учитывая процент от реинвестирования средств. В данной функции кроме диапазона денежных потоков («Значения») аргументами выступают ставка финансирования и ставка реинвестирования. Соответственно, синтаксис имеет такой вид:
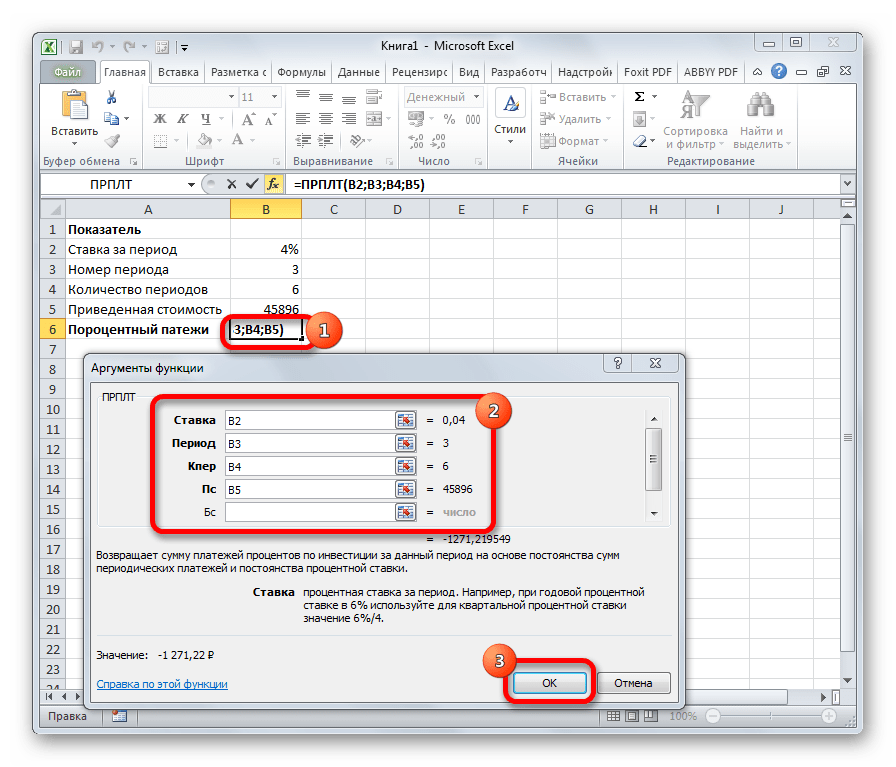
ПРПЛТ
Оператор ПРПЛТ рассчитывает сумму процентных платежей за указанный период. Аргументами функции выступает процентная ставка за период («Ставка»); номер периода («Период»), величина которого не может превышать общее число периодов; количество периодов («Кол_пер»); приведенная стоимость («Пс»). Кроме того, есть необязательный аргумент – будущая стоимость («Бс»). Данную формулу можно применять только в том случае, если платежи в каждом периоде осуществляются равными частями. Синтаксис её имеет следующую форму:
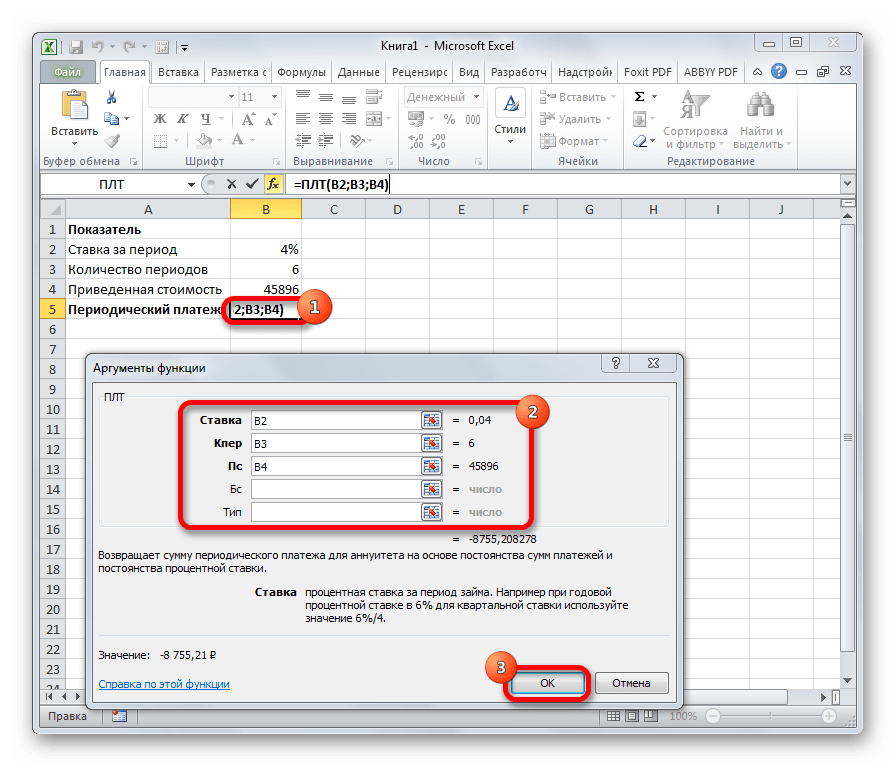
Оператор ПЛТ рассчитывает сумму периодического платежа с постоянным процентом. В отличие от предыдущей функции, у этой нет аргумента «Период». Зато добавлен необязательный аргумент «Тип», в котором указывается в начале или в конце периода должна производиться выплата. Остальные параметры полностью совпадают с предыдущей формулой. Синтаксис выглядит следующим образом:
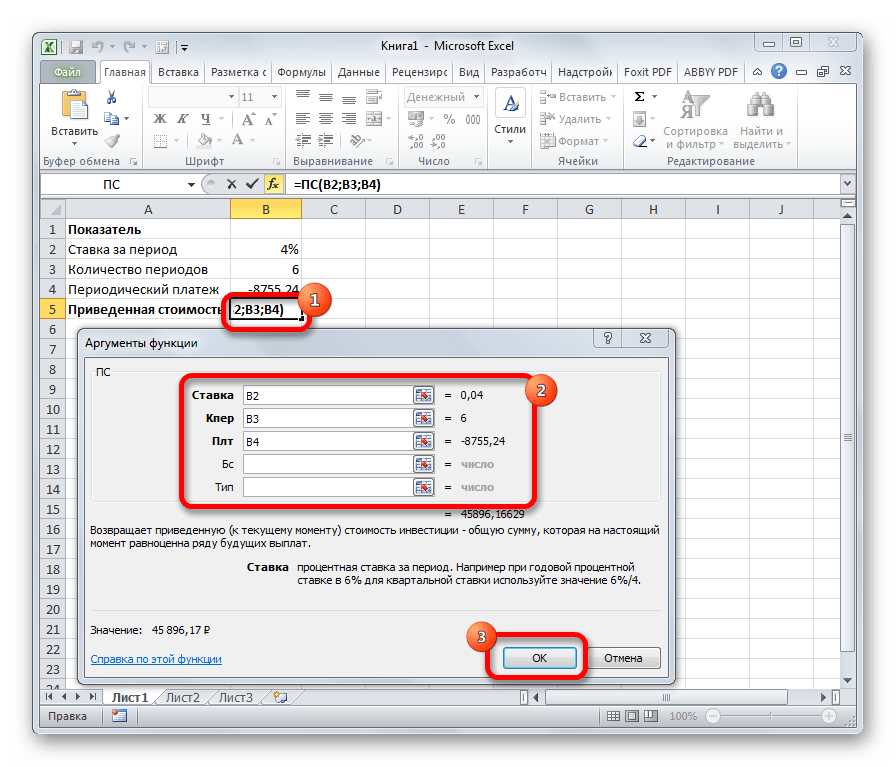
Формула ПС применяется для расчета приведенной стоимости инвестиции. Данная функция обратная оператору ПЛТ. У неё точно такие же аргументы, но только вместо аргумента приведенной стоимости («ПС»), которая собственно и рассчитывается, указывается сумма периодического платежа («Плт»). Синтаксис соответственно такой:
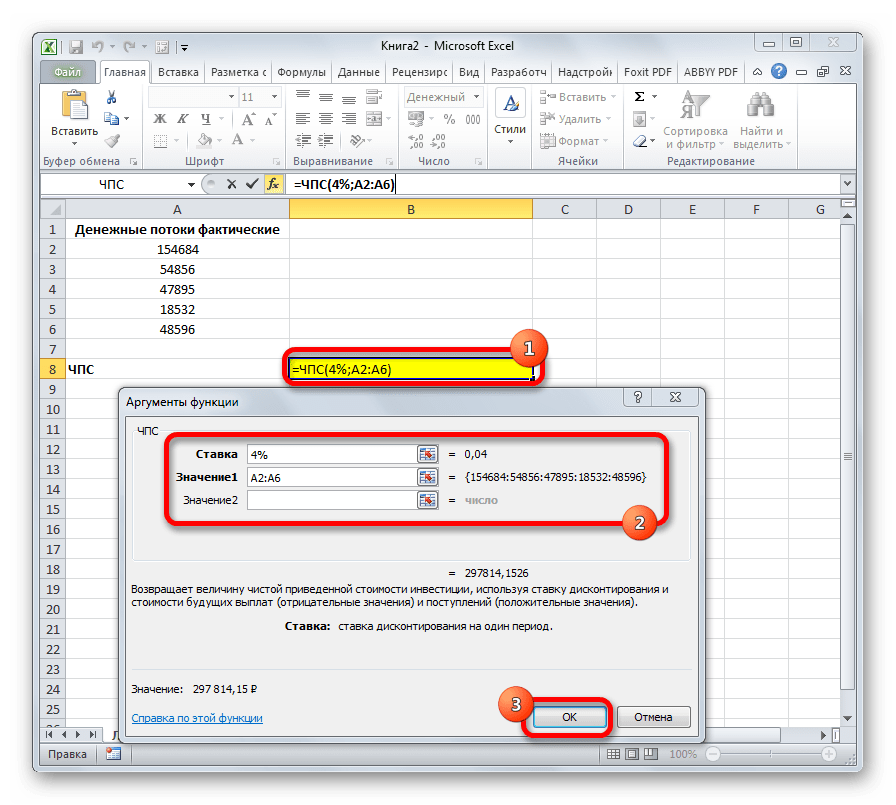
Следующий оператор применяется для вычисления чистой приведенной или дисконтированной стоимости. У данной функции два аргумента: ставка дисконтирования и значение выплат или поступлений. Правда, второй из них может иметь до 254 вариантов, представляющих денежные потоки. Синтаксис этой формулы такой:
СТАВКА
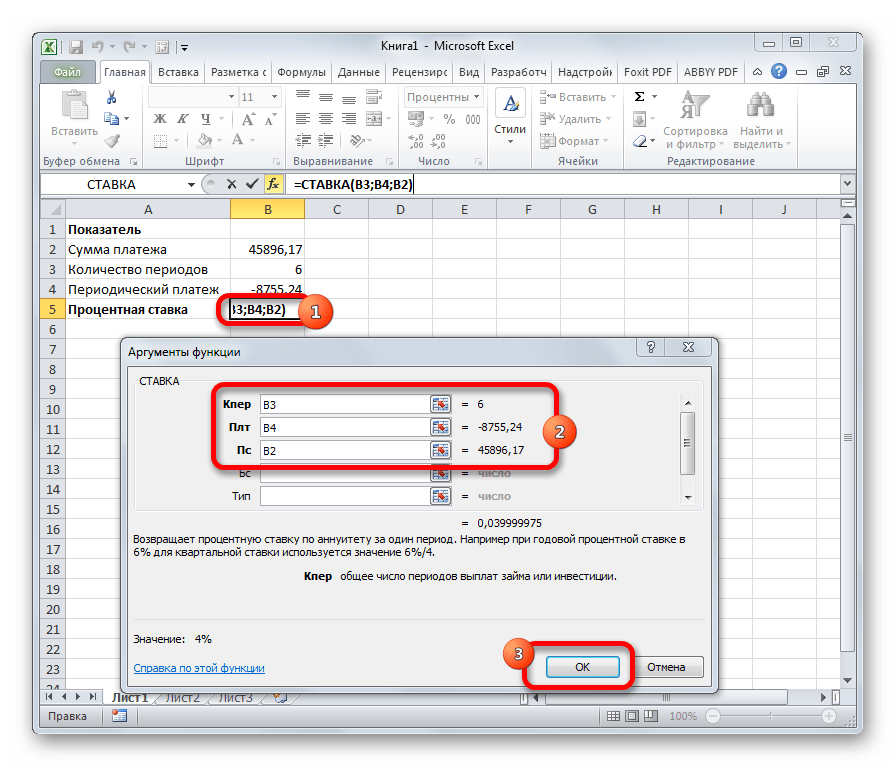
Функция СТАВКА рассчитывает ставку процентов по аннуитету. Аргументами этого оператора является количество периодов («Кол_пер»), величина регулярной выплаты («Плт») и сумма платежа («Пс»). Кроме того, есть дополнительные необязательные аргументы: будущая стоимость («Бс») и указание в начале или в конце периода будет производиться платеж («Тип»). Синтаксис принимает такой вид:
ЭФФЕКТ
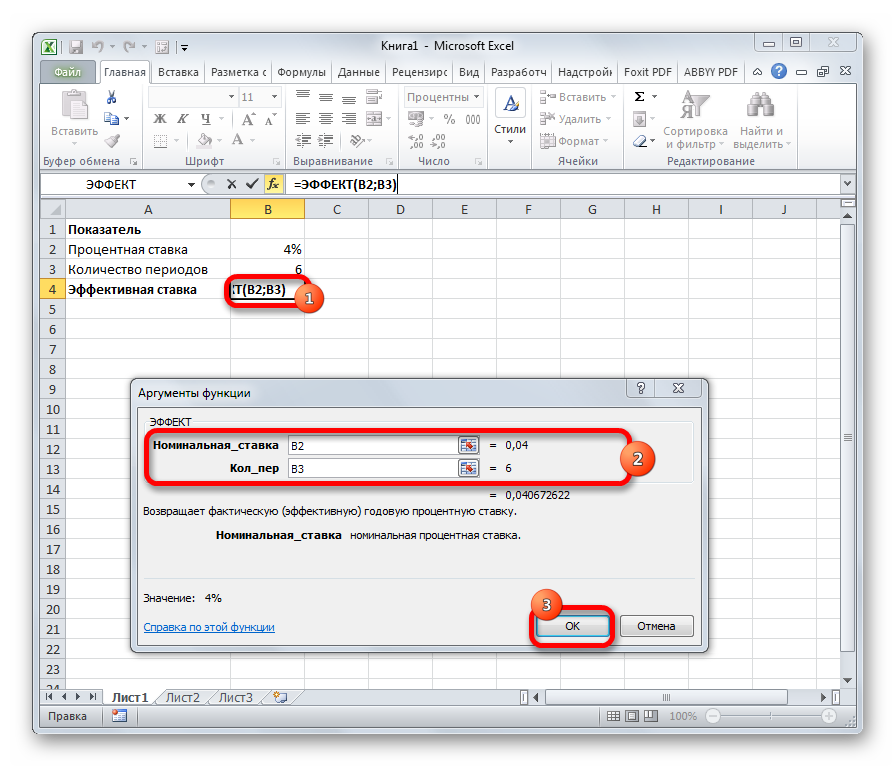
Оператор ЭФФЕКТ ведет расчет фактической (или эффективной) процентной ставки. У этой функции всего два аргумента: количество периодов в году, для которых применяется начисление процентов, а также номинальная ставка. Синтаксис её выглядит так:
Нами были рассмотрены только самые востребованные финансовые функции. В общем, количество операторов из данной группы в несколько раз больше. Но и на данных примерах хорошо видна эффективность и простота применения этих инструментов, значительно облегчающих расчеты для пользователей.
Источник
Лабораторная работа №7: Экономические расчеты в MS Excel. Финансовые функции MS Excel
Лабораторная работа №7:
Экономические расчеты в MS Excel. Финансовые функции MS Excel
Встроенные экономические функции MS Excel служат для проведения соответствующих расчетов (например, нахождение платы по процентам, расчет регулярных выплат по займу, оценка эффективности капиталовложений и т. д.).
Работа с финансовыми функциями MS Excel предполагает использование следующей методики:
1. Подготовить на рабочем листе значения основных аргументов функции.
2. Перейти к ячейке, в которую вводится формула, использующая встроенную финансовую функцию.
3. Вызвать мастер функций командой Вставка | Функция | категория Финансовые и в списке функций выбрать необходимую финансовую функцию.
Определить величину основного платежа за четвертый год, если выдана ссуда размером 1 сроком на 5 лет под 12% годовых.
Для основных платежей по займу, который погашается равными платежами в конце или начале каждого расчетного периода, в MS Excel XP используется функция:
ОСПЛТ(Ставка, Период, Кпер, Пс, Бс)
В нашем случае функция ОСПЛТ имеет вид:
Ввод данных и расчеты производятся в соответствии с рисунком 7.1.
Рисунок 7.1 — Расчет основных платежей по займу
В ячейку В8 вводится формула:
Рассчитать 20-летнюю ипотечную ссуду со ставкой 10% годовых при начальном взносе 25% и ежемесячной (ежегодной) выплате.
Для вычисления величины постоянной периодической выплаты ренты (например, регулярных платежей по займу) при постоянной процентной ставке используется функция ПЛТ:
ПЛТ (Ставка; Клер; Бс; Пс; Тип)
В нашем случае функция ПЛТ имеет вид:
а) ПЛТ(10%/12;20*12; -(350000*(1-25%))) — ежемесячные выплаты;
б) ПЛТ(10%;20,-(350000*(1-25%))) — ежегодные выплаты. Решение задачи приведено на рисунках 7.2 и 7.3.
Рисунок 7.3 — Формулы для расчета ипотечной суды
Определить, какая сумма окажется на банковском счете, еслирублей положены на 20 лет под 11% годовых. Проценты начисляются ежемесячно.
Для расчета будущей стоимости единой суммы вклада используются сложные проценты, а расчетная формула основана на функции БС:
БС(Ставка; Кпер; Плт; Пс; Тип)
Для нашей задачи функция БС примет вид:
Решение задачи приведено на рисунке 7.4, а формула для ячейки В8:
Аналогичным образом можно использовать встроенные функции MS Excel и для других финансовых расчетов. Приведем еще несколько примеров.
Ожидается, что ежегодные доходы от реализации проекта составятруб. Рассчитать срок окупаемости проекта, если инвестиции к началу поступления доходов составят руб., а норма дисконтирования 7,67%.
Для определения срока платежа используется функция
КПЕР(Ставка; Плт; Пс; Бс; Тип),
которая в нашей задаче выглядит следующим образом:
Рисунок 7.4 — Расчет будущей стоимости вклада
Облигация номиналом руб. выпущена на 7 лет. Предусматривается следующий порядок начисления процентов: в первый год — 11%, последующие три года — по 16%, в оставшиеся три года — по 20%. Рассчитать будущую (наращенную) стоимость облигации по сложной процентной ставке.
Для расчета наращенной стоимости облигации по сложной процентной ставке используется функция:
Для нашей задачи функция принимает вид:
Решение приведено на рисунке 7.5, а формула для расчета в ячейке В67:
Рисунок 7.5 — Расчет наращенной стоимости облигации по сложной процентной ставке
Затраты по проекту составят 600 млн. руб. Ожидаемые доходы в течение последующих 5 лет составят, соответственно, 50, 100, 300, 200, 300 млн. руб. Оценить экономическую целесообразность проекта по скорости оборота инвестиции, если рыночная норма дохода 15%.
Для вычисления внутренней скорости оборота инвестиции (внутренней нормы доходности) используется функция ВСД:
ВСД (Значения; Предположения)
В нашем случае функция для решения задачи использует только аргумент Значения, один из которых обязательно отрицателен. Если внутренняя скорость оборота инвестиций будет больше рыночной нормы доходности, то проект считается экономически целесообразным. В противном случае проект должен быть отвергнут.
Решение приведено на рис. 7.6. Формулы для расчета:
=ЕСЛИ(B12>B11;»Проект экономически целесообразен»; «Проект необходимо отвергнуть»)
Рисунок 7.6 — Расчет внутренней скорости оборота инвестиций
1. Вычислить 7-годичную ипотечную ссуду для покупки дома зарублей с годовой ставкой 7% и начальным взносом 10%. Расчеты произвести для ежемесячных и ежегодных выплат. Воспользоваться функцией ПЛТ (либо ППЛАТ).
2. Вычислить 3-годичную ипотечную ссуду для покупки мебели за рублей с годовой ставкой 6% и начальным взносом 14%. Расчеты произвести для ежемесячных и ежегодных выплат. Воспользоваться функцией ПЛТ (либо ПЛАТ).
3. Определить, какая сумма окажется на счете, если вклад размером 1 руб. положен под 8% годовых на 10 лет, а проценты начисляются ежеквартально. Воспользоваться функцией ВС (либо БЗ).
4. Какая сумма должна быть выплачена, если четыре года назад была выдана ссуда руб. под 20% годовых с ежемесячным начислением процентов. Воспользоваться функцией ВС (либо БЗ).
5. Сколько лет потребуется, чтобы платежи размером 1 руб. в конце каждого года достигли значения 10,897 млн. руб., если ставка процента 14,5%? Воспользоваться функцией КПЕР.
6. Через сколько лет вклад размером руб. достигнет 1 руб. при ежемесячном начислении процентов и ставке 35,18% годовых? Воспользоваться функцией КПЕР.
Источник
Дистанционные курсы для педагогов
650 курсов повышения квалификации от 590 руб.
253 курса профессиональной переподготовки от 2190 руб.
Входим в перечень Министерства просвещения Российской Федерации
Разговоры о важном
Рекомендуем всем учителям 1-11 классов
Ценности гуманной педагогики
Сертификаты всем участникам!
Войти с помощью:
«Финансовые функции в Excel» практическая работа
Самостоятельная практическая работа по теме:
КПЕР – общее число периодов выплат займа или инвестиций
ПЛТ – выплата, производимая в каждый период и не меняющаяся за все время выплаты займа или инвестиций
ПС – приведенная (нынешняя) стоимость – общая сумма, равноценная на настоящий момент серии будущих платежей
БС – будущая стоимость, или баланс наличности, который нужно достичь после последней выплаты (при отсутствии значения БС принимается равной 0)
ТИП – логическое значение (0 или 1), обозначающая, должна ли производиться выплата в конце периода (0 или отсутствие значения) или в начале периода (1)
СТАВКА – возвращает процентную ставку за один период. Например, при годовой процентной ставке в 6 % для квартальной ставки используется значение 6%/4.
ПС (ставка; кпер; плт; бс; тип);
ПРПЛТ(ставка; период; кпер; пс; бс);
АСЧ(нач_стоимость; ост_стоимость; время_эксплуатации; период);
ФУО(нач_стоимость; ост_стоимость; время_эксплуатации; период; месяцы);
ОСПЛТ(ставка; период; кпер; пс; бс; тип);
ДДОБ(нач_стоимость; ост_стоимость; время_эксплуатации; период; коэффициент).
Ваше предприятие рекламирует свою деятельность с использованием четырех источников массовой информации: телевидения, радио, газет и расклейки объявлений. Анализ рекламной деятельности в прошлом показал, что вложенные в рекламу средства приводят к увеличению прибыли на 10 руб., 5 руб., 7 руб. и 4 руб. соответственно в расчете на 1 руб., затраченный на рекламу. На рекламу выделено 50 000 руб., причем руководство намерено тратить на телевидение не более 50% выделенной суммы, на радио — не более 20%, на газеты — не более 35%, на расклейку объявлений — не более 30%. С помощью Поиска решения рассчитайте объем вложений в каждый вид рекламы, чтобы получить максимальную прибыль от рекламной кампании.
Для решения задачи: «Кредит в 45 000 руб. дается под 12% годовых со сроком погашения 5 лет. Какую сумму будут составлять ежемесячные выплаты?» — заполнили таблицу.
Столбец А – комментарии к данным, столбец В – необходимые для вычислений данные. Запишите содержимое ячеек диапазона А1:В3, ячейка ответа В4, содержит формулу: =ОКРУГЛ(ПЛТ(B3/12;B2*12;B1;0;0);2).
«Пусть начальная стоимость оборудования составляет 45 000 руб., срок полной амортизации, когда стоимость оборудования станет нулевой — 5 лет. Определите сумму, ежегодно подлежащую списанию»
Источник
Практическая работа №9
ФИНАНСОВЫЕ ФУНКЦИИ MS EXCEL В
ЭКОНОМИЧЕСКИХ РАСЧЕТАХ
Цель:
научиться использовать финансовые функции для экономических расчётов.
Задания:
|
1. |
Функции даты и времени для финансовых |
Время – один из важнейших факторов в
финансовых операциях и сделках. Для проведения финансовых расчетов необходимо
находить срок между начальной и конечной датами операции, обычно заданный в
днях или годах.
Если рассчитывается точное число дней, то
надо просто вычесть из конечной даты (даты завершения операции) начальную
дату.
Однако в финансовой практике есть правило,
согласно которому в месяце считается 30 дней, а в году 360. В этом случае
используется функция ДНЕЙ360. Ее назначение – расчет количества дней между
двумя датами на основе 360-дневного года (12 30-дневных месяцев), аргументы:
нач_дата – начальная дата сделки; кон_дата – конечная дата сделки; метод –
логическое значение, если отсутствует, есть «ЛОЖЬ».
Аргументы «нач_дата» и «кон_дата» могут
быть введены как текстовые строки в двойных кавычках или в числовом формате,
могут также использоваться ссылки на ячейки, в которых заданы даты в формате
дата. Если аргумент «метод» принимает значение «ЛОЖЬ» или опущен, то
используется американский метод определения приближенного числа дней между
двумя датами, а если «ИСТИНА» – то европейский (эти два метода различаются,
только если конечная дата – 31-е число месяца).
Для определения срока между датами в годах
надо использовать функцию ДОЛЯГОДА с аргументами (нач_дата, кон_дата,
базис).
Первые два аргумента имеют то же значение,
что и у функции ДНЕЙ360. Аргумент «базис» может принимать пять различных
значений в зависимости от правила, установленного для расчета срока в годах:
0
или опущен – правило 30/360 (приближенный срок между
датами в днях
(американский метод расчета), приближенное
число дней в году);
1
– АСТ/АСТ (точный срок между датами в днях, точное
число дней в году);
2
– АСТ/360 (точный срок между датами в днях,
приближенное число дней в году);
3
– АСТ/365 (точный срок между датами в днях, но в любом
году 365 дней);
4
– 30/360 европейский (приближенный срок между датами в
днях (европейский метод
расчета), приближенное число дней в году).
Пример.
Дата
получения кредита – 15 января 2008 г., дата погашения – 15 марта того же года.
Найти срок кредита в днях и годах.
Решение выполнить на Листе 1.
Откройте Лист 1 и переименуйте его в
Задание 1.
Точное число дней = «15/03/2008» –
«15/01/2008» = 59.
Приближенное число дней =
ДНЕЙ360(«15/01/2008», «15/03/2008») = 60. Срок кредита в годах по правилу
АСТ/АСТ = ДОЛЯГОДА(«15/01/2008»,
«15/03/2008») = 0,161644.
Расчет
ипотечной ссуды осуществляются с использованием финансовой функции ПЛТ
Функция ПЛТ вычисляет величину постоянной
периодической выплаты ренты (например, регулярных платежей по займу) при
постоянной процентной ставке.
Синтаксис: ПЛТ(Ставка;Кпер;Пс;Бс;Тип).
Аргументы:
§ Ставка
– процентная ставка по ссуде,
§ Кпер
– общее число выплат по ссуде,
§ Пс
– приведенная к текущему моменту стоимость, или общая сумма, которая на текущий
момент равноценна ряду будущих платежей, называемая также основной суммой,
§ Бс
– требуемое значение будущей стоимости, или остатка средств после последней
выплаты.
Если
аргумент Бс опущен, то он полагается равным 0 (нулю), т.е. для займа, например,
значение Бс равно 0, Тип – число 0 (нуль) или 1, обозначающее, когда должна
производиться выплата.
Отметим, что очень важно быть
последовательным в выборе единиц измерения для задания аргументов Ставка и
Кпер.
Например,
если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12
%
годовых, то для задания аргумента Ставка используйте 12 %/12, а для задания
аргумента Кпер – 4*12. Если вы делаете ежегодные платежи по тому же займу, то
для задания аргумента Ставка используйте 12 %, а для задания аргумента Кпер –
4.
Для нахождения общей суммы, выплачиваемой
на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на
величину Кпер. Интервал выплат – это последовательность постоянных денежных
платежей, осуществляемых за непрерывный период.
Например, заем под автомобиль или заклад
являются интервалами выплат. В функциях, связанных с интервалами выплат,
выплачиваемые вами деньги, такие как депозит на накопление, представляются
отрицательным числом, а деньги, которые вы получаете, такие как чеки на
дивиденды, представляются положительным числом.
Например,
депозит в банк на сумму 1000 руб. представляется аргументом – 1000, если вы
вкладчик,
и аргументом -1000, если вы – пpeдставитель банка.
Пример
1. Вычислить 30-летнюю ипотечную ссуду покупки квартиры за 201900 руб. с
годовой ставкой 8% и начальным взносом 20%. Сделать расчет для ежемесячных и
ежегодных выплат (табл. 1).
Решение:
1.
Откройте Лист 2 и переименуйте его в
Задание 2.
2.
Введите в ячейки A1:B6 данные,
представленные на рис. 1.
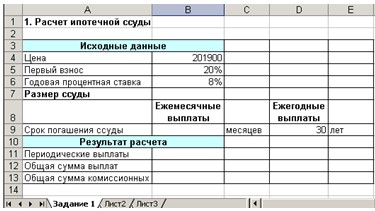
Рис.
1. Форма для расчета ипотечной ссуды
3.
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.
2.
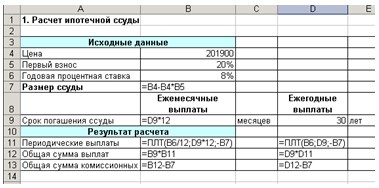
Рис.
2. Формулы для расчета ипотечной ссуды
4.
Результаты расчеты должны быть следующими
(рис. 3):
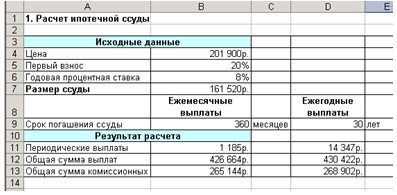
Рис.
3. Расчет ипотечной ссуды
3.
Функции для расчета годовой процентной ставки
Функция ЧПС возвращает чистый текущий
объем вклада, вычисляемый на основе ряда последовательных поступлений наличных
денег и нормы амортизации.
Чистый текущий объем вклада – это
сегодняшний объем будущих платежей (отрицательные значения) и поступлений
(положительные значения).
Например, вам предлагают следующую сделку.
У вас берут в долг некоторую сумму денег и предлагают через k1 лет вернуть
сумму, равную Рk1, через k2 лет – Рk2 и т. д. и, наконец, через kn лет – Рkn.
Кроме данной сделки, у вас есть альтернативный способ использования ваших
денег, например, положить их в банк под i процентов годовых. Тогда чистым
текущим объемом вклада является та сумма денег, которой вам нужно располагать
начальный год, чтобы, положив их в банк под i % годовых, получили предлагаемую
прибыль.
Синтаксис:
ЧПС(Ставка;Значение1;Значение2;…..) Аргументы:
§ ставка
– ставка дисконтирования за один период;
§ значение
1, значение 2, – от 1 до 29 аргументов, представляющих расходы и доходы:
• значение 1,
значение 2, … должны быть равномерно распределены во времени, выплаты должны
осуществляться в конце каждого периода.
ЧПС использует порядок аргументов значение
1, значение 2, … для определения порядка поступлений и платежей. Убедитесь в
том, что ваши платежи и поступления введены в правильном порядке.
Считается, что инвестиция, значение
которой вычисляет функция ЧПС, начинается за один период до даты денежного
взноса 1-го значения и заканчивается с последним денежным взносом в списке.
Вычисления функции ЧПС базируются на
будущих денежных взносах. Если первый денежный взнос приходится на начало
первого периода, то первое значение следует добавить к результату функции ЧПС,
но не включать в список аргументов.
Функция ЧПС
связана с функцией ВСД (внутренняя скорость оборота). ВСД – это скорость
оборота, для которой ЧПС равняется нулю:
ЧПС(ВСД(…);…)=0.
Функция ВСД возвращает внутреннюю скорость
оборота для ряда последовательных операций с наличными деньгами,
представленными числовыми значениями. Объемы операций не обязаны быть
регулярными, как в случае ренты.
Внутренняя скорость оборота – это
процентная ставка дохода, полученного от инвестиций, состоящих из выплат
(отрицательные значения) и поступлений (положительные значения), которые
происходят в регулярные периоды времени.
Синтаксис: ВСД (Значения;Предположение).
Аргументы:
§
значения – массив или ссылка на ячейки, содержащие
числовые величины, для которых вычисляется внутренняя ставка доходности.
Значения должны включать, по крайней мере, одно положительное значение и одно
отрицательное значение, для того чтобы можно было вычислить внутреннюю скорость
оборота.
Функция ВСД
использует порядок значений для интерпретации порядка денежных выплат или
поступлений, поэтому нужно следить, чтобы значения выплат и поступлений
вводились в правильном порядке.
§
предположение – величина, о которой предполагается,
что она близка к результату ВСД.
Для вычисления ВСД Excel использует метод
итераций. Начиная со значения прогноз, функция ВСД выполняет циклические
вычисления, пока не получит результат с точностью 0,00001. Если функция ВСД не
может получить результат после 20 попыток, то возвращается значение ошибки
#ЧИСЛО!
В большинстве случаев нет необходимости
задавать прогноз для вычислений с помощью функции ВСД. Если прогноз опущен, то
он полагается равным 0,1 (10 %).
Если
ВСД выдает значение ошибки #ЧИСЛО! Или результат далек от ожидаемого, можно
попытаться
выполнить вычисления еще раз, но уже с другим значением аргумента прогноз.
Пример
3. Вас просят в долг 10000 руб. и обещают вернуть через год 2000 руб., через
два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной
ставке эта сделка выгодна?
Решение.
1. Откройте Лист 3 и
переименуйте его в Задание 3. 2. Введите в ячейки A1:B7 данные, представленные
на рис. 4.
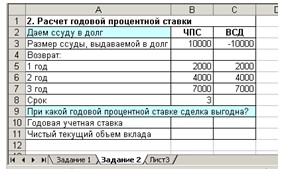
Рис. 4. Форма для расчета годовой
процентной ставки
3.
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.
5.
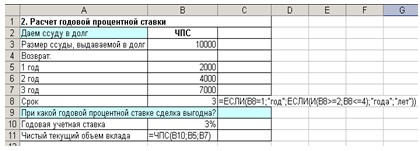
Рис. 5. Формулы для расчета годовой
процентной ставки
4.
Первоначально в ячейку В10 введите
произвольный процент, например 3 %.
В ячейку В11 введите формулу
=ЧПС(В10;В5:В7) (см. рис. 5).
5.
В ячейку С8 введите формулу:
=ЕСЛИ(В8=1;»год»;ЕСЛИ(И(В8>=2;B8<=4)
;»года»;»лет»)) В результате должно получиться (см. рис. 6):
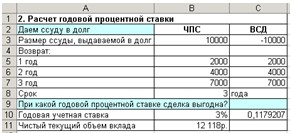
Рис. 6. Расчет чистого текущего объема
вклада
6.
Затем выбираем команду Сервис / Подбор
параметра и заполняем открывшееся
диалоговое окно Подбор параметра, как
показано на рис. 7.
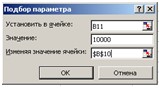
Рис. 7. Диалоговое окно Подбор параметра
при расчете годовой процентной ставки
7.
В поле Установить в ячейке: укажите ссылку
на ячейку В11, в которой вычисляется чистый текущий объем вклада по формуле:
=ЧПС(B10;B5:B7).
В поле Значение установить 10000 – размер
ссуды.
В
поле Изменения значения ячейки укажите ссылку на ячейку В10, в которой
вычисляется годовая процентная ставка.
После
нажатия кнопки ОК средство подбора параметров определит, при какой годовой
процентной ставке чистый текущий объем вклада равен 10000 руб. Результат
вычисления выводится в ячейку В10.
8.
В нашем случае годовая учетная ставка
равна 11,79 %.
Вывод:
если банки предлагают большую годовую процентную ставку, то предлагаемая сделка
не выгодна. 9. Результаты расчеты должны быть следующими:
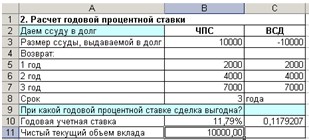
Рис. 8. Расчет годовой процентной ставки
4.  Функции для расчета
Функции для расчета
эффективности капиталовложений
Расчет
эффективности капиталовложений осуществляется с помощью функции ПС.
Функция ПС возвращает текущий объем вклада
на основе постоянных периодических платежей.
Функция ПС аналогична функции ЧПС.
Основное различие между ними заключается в том, что функция ПС допускает, чтобы
денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в
отличие от функции ЧПС, денежные взносы в функции ПС должны быть постоянными на
весь период инвестиции.
Синтаксис:
ПС(Ставка;Кпер;Плт;Бс;Тип) Аргументы:
§
Ставка – процентная ставка за период,
§
Кпер – общее число периодов платежей по аннуитету,
§
Плт – выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов,
§
Бс – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент опущен, он полагается равным 0
(будущая стоимость займа, например, равна 0),
§
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.
Пример
4. У вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 7
лет. Будет ли выгодна эта сделка при годовой ставке 7 %?
Решение:
1.
Откройте Лист 4 и переименуйте его в
Задание 4.
2.
Введите в ячейки A1:B6 данные,
представленные на рис. 9.
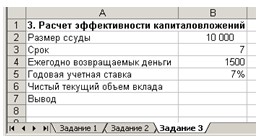
Рис. 9. Форма расчета эффективности
капиталовложений
3.
В ячейку В6 введите формулу:
=ПС(В5;В3;-В4)
4.
В ячейку С3 введите формулу:
=ЕСЛИ(В3=1;
«год»;ЕСЛИ(И(В3>=2;В3<=4); «года»;»лет»))
5. В ячейку В7:
=ЕСЛИ (В2<В6; «Выгодно дать деньги
в долг»; ЕСЛИ(В6=В2; «Варианты равносильны»;
«Выгоднее деньги положить под
проценты»))
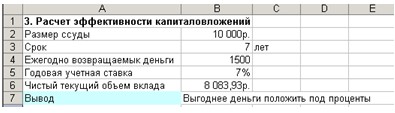
Рис. 10. Расчет эффективности
капиталовложений
5.  Функции для расчета основных
Функции для расчета основных
платежей и платы по процентам
Основные платежи и платы по процентам
вычисляются с помощью формул или финансовых функций ОСПЛТ и ПРПЛТ.
Функция ПРПЛТ возвращает платежи по
процентам за данный период на основе периодических постоянных выплат и
постоянной процентной ставки.
Синтаксис: ПРПЛТ (Ставка; Период; Кпер;
Пс; Бс; Тип).
Функция ОСПЛТ возвращает величину выплаты
за данный период на основе периодических постоянных платежей и постоянной
процентной ставки.
Синтаксис: ОСПЛТ(Ставка; Период; Кпер; Пс;
Бс; Тип).
Аргументы функций ПРПЛТ: и ОСПЛТ:
§
Ставка – процентная ставка за период,
§
Период – задает период, значение должно быть в
интервале от 1 до «Кпер»,
§
Кпер – общее число периодов выплат годовой ренты,
§
Пс – приведенная стоимость, то есть общая сумма,
которая равноценна ряду будущих платежей,
§
Бс – требуемое значение будущей стоимости, или остатка
средств после последней выплаты.
Если аргумент Бс
опущен, то он полагается равным 0 (нулю), то есть для займа, например, значение
Бс равно 0.
§
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.
Функции
ПРПЛТ и ОСПЛТ тесно связаны между собой, а именно ПЛПj= i Bj-1, ОСНПj = А —
ПЛПj,
Bj = Вj-1 — ОСНПj при j ∈[0,
n], где j – номер периода, п – КПЕР,
ПЛПj,
ОСНПj и Bj – это ПРПЛТ, ОСПЛТ и остаток долга, соответственно, за j-й период,
ПЛПо
= 0, ОСНПо = 0, Bо – Пс,
А – величина выплаты за один период
годовой ренты на основе постоянных выплат и постоянной процентной ставки,
вычисляемая с помощью функции ПЛТ.
Пример
5. Вычислить основные платежи, платы по процентам, общей ежегодной платы и
остатка долга на примере ссуды 100000 руб. на срок 5 лет при годовой ставке 2
%.
Решение:
1.
Откройте Лист 5 и переименуйте его в
Задание 5.
2.
Введите данные, представленные на рис. 13.
3.
Ежегодная плата вычисляется в ячейке В4 по
формуле: =ПЛТ(процент; срок; -размер_ссуды), где ячейки В2, В3 и В5 имеют
имена: процент, срок и размер_ссуды, соответственно.
4.
За первый год плата по процентам в ячейке
В8 вычисляется по формуле:
=D7*процент.
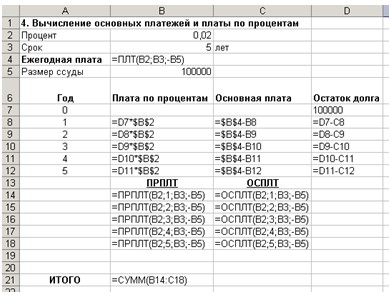
Рис. 13. Функции для вычисления основных
платежей и платы по процентам.
5.
Основная плата в ячейке С8 вычисляется по
формуле: =ежегодная_плата-В8, где ежегодная_плата – имя ячейки В4.
Остаток долга в ячейке D8
вычисляется по формуле: =D7-C8.
6.
В оставшиеся годы эти платы определяются с
помощью протаскивания маркера заполнения выделенного диапазона B8:D8 вниз по
столбцам.
7.
Данные результаты расчетов должны быть
следующими (рис. 14.):
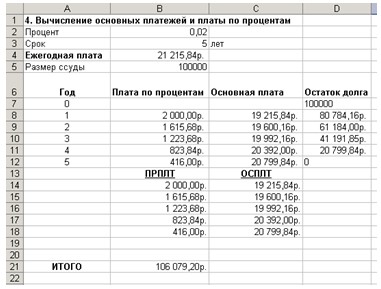
Рис. 14. Вычисление основных платежей и
платы по процентам
6. Функции для расчета
будущего значения вклада, процентной ставки и количества периодов выплаты долга
Функция БС вычисляет будущее значение
вклада на основе периодических постоянных платежей и постоянной процентной
ставки.
Функция
БС подходит для расчета итогов накоплений при ежемесячных банковских взносах. Синтаксис:
БС (Ставка; Кпер; Плт; Пс; Тип).
Аргументы:
§
Ставка – процентная ставка за период,
§
Кпер – общее число периодов выплат,
§
Плт – величина постоянных периодических платежей,
§
Пс – текущее значение, то есть общая сумма, которую
составят будущие платежи, § Тип – число 0 или 1,
обозначающее, когда должна производиться выплата.
Если
тип равен 0 или опущен, то оплата производится в конце периода, если 1 – в
начале
периода.
Если тип = 0 и БС = 0, то функция БС вычисляется по формуле (6):
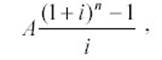
где
А – Плт; i – Ставка; n – Кпер.
Функция КПЕР вычисляет общее количество
периодов выплаты для данного вклада на основе периодических постоянных выплат и
постоянной процентной ставки.
Синтаксис: КПЕР(Ставка; Плт; Пс; БС; Тип).
Аргументы:
§
Ставка – процентная ставка за период,
§
Плт – величина постоянных периодических платежей,
§
Пс – текущее значение, т.е. общая сумма, которую
составят будущие платежи,
§
БС – будущая стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если аргумент БС опущен, он полагается
равным 0 (например, будущая стоимость займа равна 0), тип – число 0 или 1,
обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен,
то оплата производится в конце периода, если 1 – то в начале периода. Если тип
= 0 и БС = 0 функция КПЕР вычисляется по формуле (7):
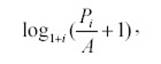
где
Р – ПС; i – Ставка; А – Плт.
Пример
6. Вы хотите зарезервировать деньги для специального проекта, который будет
осуществлен через год. Предположим, вы собираетесь вложить 1000 руб. при
годовой ставке 6 %. Вы собираетесь вкладывать по 100 руб. в начале каждого
месяца в течение года. Сколько денег будет на счете в конце 12 месяцев?
Решение:
1.
Откройте Лист 6 и переименуйте его в
Задание 6.
2.
Ведите данные в ячейки А1:С6 (см. рис.
15).
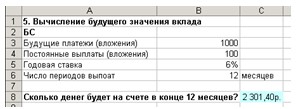
Рис. 15. Расчет будущего значения вклада
3.
В ячейку С8 введите формулу:
=БС(6 %/12; 12; -100;
-1000; 1) получаем ответ: 2 301,40 руб (см. рис. 16).
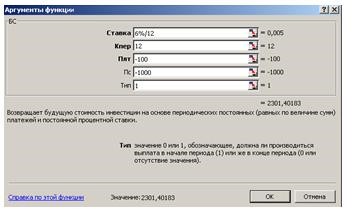
Рис. 16. Диалоговое окно Аргументы функции
БС
Пример
7. Вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать
по 100 руб. в год, Какое будет число выплат долга?
Решение:
1.
Откройте Лист 7 и переименуйте его в
Задание 7.
2.
Ведите данные в ячейки А1:В6 (см. рис.
17).
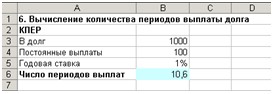
Рис. 17. Расчет количества периодов выплат
3.
В ячейку В6 введите формулу: =КПЕР(B5;
-B4; B3) В результате получаем ответ: ≈11. (см. рис. 18).
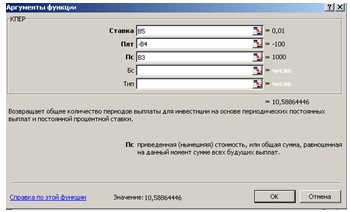
Рис. 18. Диалоговое окно Аргументы функции
КПЕР
Вычисление
процентной ставки
Функция СТАВКА вычисляет процентную
ставку, необходимую для получения определенной суммы в течение заданного срока
путем постоянных взносов, за один период.
Следует отметить, что функция СТАВКА
вычисляет процентную ставку методом итераций, поэтому решение может быть и не
найдено. Если после 20 итераций погрешность определения ставки превышает
0,0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО!
Синтаксис: СТАВКА(КПЕР; Плт; Пс; БС; Тип;
Предположение).
Аргументы:
§
КПЕР – общее число периодов платежей по аннуитету;
§
Плт – регулярный платеж (один раз в период), величина
которого остается постоянной в течение всего срока аннуитета. Обычно Плт состоит
из платежа основной суммы и платежа процентов, но не включает других сборов или
налогов. Если аргумент опущен, должно быть указано значение аргумента БС;
§
Пс – приведенная к текущему моменту стоимость или
общая сумма, которая на текущий момент равноценна ряду будущих платежей;
§
БС – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент БС опущен, то он полагается
равным 0 (например, БС для займа равно 0); тип – число 0 или 1, обозначающее,
когда должна производиться выплата; предположение – предполагаемая величина
ставки.
Если
БС = 0 и тип = 0, функция СТАВКА является корнем уравнения (8):
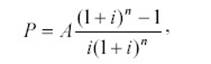
Пример
8. Определить процентную ставку для четырехлетнего займа размером в 8000 руб. с
ежемесячной выплатой 200 руб.
Решение:
1.
Откройте Лист 8 и переименуйте его в
Задание 8.
2.
Ведите данные в ячейки А1:В7 (см. рис.
19).
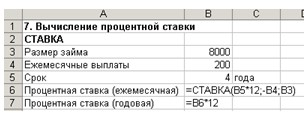
Рис. 19. Расчет процентной ставки
3.
В ячейку В6 введите формулу:
=СТАВКА(B5*12;-B4;B3).
4.
В ячейку В7 введите формулу: = В6*12.
В
результате получаем: месячная (так как период равен месяцу) процентная ставка
равна 0,77 %. Процентная ставка годовая равна 9 % см. рис 20).
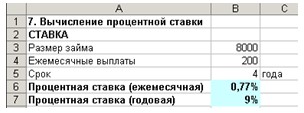
Рис.20. Результаты вычисления процентной
ставки
Контрольные вопросы:
1.
Как
рассчитать дату и временя с использованием финансовых функций?
2.
Каким
образом можно рассчитать ипотечную ссуду, годовую процентную ставку в Excel?
3.
Назовите
функции расчета постоянных рент.
В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Поможем с Excel, финансами и математикой 
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Помогаем с решением задач по финансовой математике
Может быть интересно:
|
|
ГОСУДАРСТВЕННОЕ
БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«КРАСНОЛУЧСКИЙ КОЛЛЕДЖ ПРОМЫШЛЕННОСТИ И СЕРВИСА»
МАТЕРИАЛ
для проведения открытого урока
Тема:
Работа с финансовыми функциями в Excel
Подготовила: преподаватель
Качмазова С.А.
Урок
Тема: Работа
с финансовыми функциями в Excel
Цель урока: выучить виды финансовых функций в редакторе электронных
таблиц, знать их назначение и правила использования.
Тип урока: Изучение новых
знаний.
ХОД
УРОКА
1.
Определение будущей стоимости
Финансовые функции EXCEL
предназначены для вычисления базовых величин, необходимых при проведении
сложных финансовых расчетов.
Будущая стоимость текущего значения вклада при
постоянной процентной ставке рассчитывается с помощью функции БС:
= БС (Ставка; Кпер; Плт; Пс; Тип),
где Ставка – процентная ставка за один
период;
Кпер (Число периодов ) – общее число периодов выплат;
Плт (Выплата) – это выплата, производимая в каждый период; значение Плт не
может меняться в течение всего периода выплат. Если аргумент Плт опущен, должно
быть указано значение аргумента Пс;
Пс (Вклад) – это приведенная к текущему моменту стоимость. Если аргумент опущен,
то он полагается равным 0. В этом случае должно быть указано значение аргумента
Плт;
Тип – это число 0 или 1, обозначающее, когда производится выплата (1 – в
начале периода, 0 – в конце периода). Если аргумент Тип опущен, то он полагается
равным 0. Параметр Тип нужно указывать, только если выплата не равна 0, т. е.
делаются взносы по периодам.
Таблица 2.1 – Расчет величин при внутригодовом
учете процента (на n лет при ставке k % в год)
|
Метод начисления процентов |
Общее число |
Ставка процента за период начисления |
|
Ежегодный |
n |
k |
|
Полугодовой |
n * 2 |
k / 2 |
|
Квартальный |
n * 4 |
k / 4 |
|
Месячный |
n * 12 |
k / 12 |
|
Ежедневный |
n * 365 |
k / 365 |
Пример выполнения.
На сберегательный счет вносятся ежеквартальные
платежи по 2500 грн. Рассчитайте, какая сумма окажется на счете через
4 года при ставке процента 9 % годовых.
Решение. Методика изучения и использования финансовых функций
EXCEL требует соблюдения определенной технологии.
1 На рабочем листе в отдельных ячейках
осуществляется подготовка значений основных аргументов функции (рис. 2.1).
В рассматриваемом примере для расчета
применяется функция БС, так как требуется найти будущее значения платежей. Так
как платежи вносятся ежеквартально, то согласно рис. 2.1 число периодов
начисления умножается на 4, а годовая ставка делится на 4. По условию Плт
= -2500. Это отрицательное число, означающее вложение денег. Информация о величине
вклада отсутствует – аргумент Пс = 0. Аргумент Тип = 0.
Рисунок 2.1– Расчет будущей стоимости вклада
(платежей)
2 Для расчета
результата финансовой функции EXCEL курсор устанавливается в новую ячейку для
ввода формулы, использующей встроенную финансовую функцию. В нашем примере
курсор устанавливаем в ячейку G3.
3 Осуществляется вызов Мастера функции с
помощью команды Вставка – Функция или нажатием одноименной кнопки на панели
инструментов Стандартная.

выбор категории Финансовые (рис. 2.2).
Рисунок 2.2 – Мастер
функций – шаг 1 из 2
В списке Выберите функцию содержится
полный перечень доступных функций выбранной категории. Для выбора функции
курсор устанавливается на имя функции. В нижней части окна приведен краткий
синтаксис и справка о назначении выбираемой функции. Кнопка Отмена прекращает
работу Мастера функций.
5 Выполняется выбор в списке требуемой
финансовой функции, в результате выбора появляется диалоговое окно для
ввода аргументов (рис. 2.3).
Для каждой финансовой функции существует
регламентированный по составу и формату значений перечень аргументов.
Рисунок 2.3
– Мастер функций – шаг 2 из 2
6 В поля ввода диалогового окна можно
вводить как ссылки на адреса ячеек, содержащих собственно значения аргументов,
так и сами значения аргументов.
7 Завершение ввода аргументов и запуск
расчета значения встроенной функции выполняется нажатием кнопки OK.
Затем формула копируется в ячейки G4:G6.
Строится гистограмма, отражающая рост вклада
по годам (рис. 2.4).
Рисунок 2.4 – Пример гистограммы
2. Определение текущей стоимости
Для расчета текущей стоимости (начального
значения) вклада (займа) используется функция ПС:
= ПС (Ставка;Кпер;Плт;Бс;Тип),
где Ставка – процентная ставка за один
период;
Кпер – общее число периодов выплат;
Плт (Выплата) – это выплата, производимая в каждый период;
Бс – будущая стоимость вклада, которую нужно достичь после последней
выплаты, если аргумент бс опущен, то он полагается равным 0;
Тип – это число 0 или 1, обозначающее, когда производится выплата (1 – в
начале периода, 0 – в конце периода), если аргумент Тип опущен, то он
полагается равным 0. Параметр Тип нужно указывать, только если выплата не равна
0, т. е. делаются взносы по периодам.
Пример выполнения.
Рассчитайте текущую стоимость вклада, который
через 5 лет составит 150 тыс. грн при ставке 9 % годовых. Построить таблицу и
диаграмму EXCEL, отражающую динамику роста вклада по годам.
Заносим в ячейки
исходные данные (рис.
2.5). Так как
проценты начисляются раз в год, то ставка и количество периодов остаются неизменными.
Аргумент Бс = -150000, соответственно, Плт = 0.
Устанавливаем курсор
в ячейку G3 и вызываем функцию ПС (Вставка
– Фукнция категория Финансовые). Вводим последовательно все аргументы
функции.

Рисунок 2.5 – Расчет текущей стоимости вклада
(платежей)
Результирующая
таблица и диаграмма будет иметь вид (рис. 2.6).
Рисунок 2.6
– Пример таблицы и диаграммы для расчета текущей
стоимости вклада
3 Определение платежа по сложным процентам
Функция ПРПЛТ служит
для расчета суммы платежей процентов по инвестиции за данный период при
постоянных суммах периодических платежей и постоянной процентной ставке.
= ПРПЛТ (Ставка; Период; Кпер; Пс;
Бс; Тип),
где Ставка –
процентная ставка за период;
Период – период, для которого нужно
определить сумм выплаты; должен быть в диапазоне от 1 до Кпер;
Кпер – общее число периодов выплат
инвестиции;
Пс – приведенная (нынешняя)
стоимость;
Бс – будущая стоимость, или наличный
баланс, который нужно достигнуть после последней выплаты. Если значение не
указано, Бс принимается равной 0;
Тип – это
число 0 или 1, обозначающее, когда производится выплата (1 – в начале периода,
0 – в конце периода). Если аргумент Тип опущен, то он полагается равным 0.
Параметр Тип нужно указывать, только если выплата не равна 0, т.е.
делаются взносы по периодам.
4. Определение выплат основной суммы
Функция ОСПЛТ возвращает
величину платежа в погашение основной суммы по инвестиции за данный период при
постоянных суммах периодических платежей и постоянной процентной ставке.
= ОСПЛТ (Ставка; Период; Кпер; Пс;
Бс; Тип),
где Ставка –
процентная ставка за период;
Период – период, для которого нужно
определить сумму выплаты; должен быть в диапазоне от 1 до Кпер;
Кпер – общее число периодов выплат
инвестиции;
Пс – приведенная (нынешняя)
стоимость, или общая сумма, равноценная на данный момент серии будущих выплат;
Бс – будущая стоимость, или наличный
баланс, который нужно достигнуть после последней выплаты. Если значение не
указано, Бс принимается равной 0;
Тип – это число 0 или 1,
обозначающее, когда производится выплата (1 – в начале периода, 0 – в конце
периода). Если аргумент Тип опущен, то он полагается равным 0. Параметр Тип
нужно указывать, только если выплата не равна 0, т.е. делаются взносы по
периодам.
5. Определение суммы ежегодного платежа
Фактически ежегодный платеж составляет сумму тела
кредита и выплаты процентов. Его сумма не изменяется на протяжении всего
периода выплат. Меняются пропорции соотношения выплат основной суммы и процентов.
В начале периода большую долю выплат занимают проценты, а в конце – выплата
основной суммы.
Если сумма основной выплаты или значения
выплат по процентам отсутствуют, то для вычисления ежегодного платежа можно
воспользоваться функцией ПЛТ.
= ПЛТ (Ставка; Кпер; Пс; Бс; Тип).
Аргументы этой функции такие же как и у осплт и ПРПЛТ.
Пример выполнения.
Рассчитать платеж по сложным процентам по шестигодичному
займу в 10000 грн из расчета 10 % годовых. Какую часть основного платежа занимают
выплаты основной суммы, а какую выплаты процентов. Построить гистограмму соотношения
выплат по процентам и основной суммы на протяжении всего периода выплат.
Таблица с расчетными формулами будет иметь вид
(рис. 2.7).
Рисунок 2.7 – Пример таблицы формул с расчетом
платежа, выплат
основной суммы и процентов
В ячейку С1 заносим ежегодный процент – 10 %,
в С2 – заносим размер ставки, в зависимости от периода начисления (см. табл. 2.1).
В нашем примере процент начисляется ежегодно, значит, ставка и количество
периодов начисления остается неизменными. В ячейку С4 заносим сумму займа – 10000
грн.
Далее по годам рассчитываем размер ежегодного
платежа, используя финансовую функцию ПЛТ (рис. 2.8).
Рисунок 2.8 – Аргументы функции ПЛТ
Таким образом, функция для вычисления
ежегодного платежа имеет вид: = ПЛТ (10 %; 6; 10000; 0; 0). Результат
вычисления равен -2296,07. Отрицательное значение означает вложение денег.
Значение платежа на протяжении всего периода
выплат остается неизменным (рис. 2.9).
Рисунок 2.9 – Пример расчетной таблицы платежа, выплат
основной суммы и процентов
Далее рассчитываем размер выплат основной
суммы, используя функцию ОСПЛТ (рис. 2.10).
Рисунок 2.10 – Аргументы функции ОСПЛТ
Расчет осуществляется по формуле:
= ОСПЛТ (Ставка; Период; Кпер; Пс; Бс; Тип).
При расчете следует обратить внимание на
разницу аргументов функции ОСПЛТ: Кпер – общее число периодов выплат (в нашем
примере 6 лет) и Период, для которого нужно определить сумму выплаты (для первого
года 1, для второго 2 и т.д).
Общий вид функции ОСПЛТ для первого года
начислений:
= ОСПЛТ (10 %; 1; 6; 10000; 0; 0). В
результате получим -2960,7.
Значение выплат основной суммы для всего
периода начислений представлено на рис. 2.9.
Далее рассчитываем размер выплат по процентам,
используя финансовую функцию ПРПЛТ (рис. 2.11).
Рисунок 2.11 – Аргументы функции ПРПЛТ
Расчет осуществляется по формуле:
= ПРПЛТ (Ставка; Период; Кпер;
Пс; Бс; Тип).
Общий вид функции ПРПЛТ для первого года
начислений:
= ПРПЛТ (10 %; 1; 6; 10000; 0; 0).
В результате получим значение -1000.
Значение выплат по процентам для всего периода
начислений представлено на рис. 2.9.
Можно сделать проверку – сумма выплат по
процентам и выплат основной суммы для каждого года составляет основной платеж (см.
рис. 2.9).
Для нахождения баланса на конец года находим
разницу баланса на начало года и выплатой основной суммы. Формула баланса
на конец первого года имеет вид:
= B7 — D8.
В результате получим значение 8703,93.
Так как выплата процентов и основной суммы
рассчитываются из остатка суммы, то баланс на конец первого года служит
балансом на начало второго года и так далее (см. рис. 2.9). Для заполнения
ячейки баланса на начало второго года (С8) нужно
скопировать значение (а не формулу) с ячейки баланса на конец первого
года (G7). Для этого:
1 Выделяем ячейку G7.
2 Меню: Правка – Копировать.
3 Ставим курсор в ячейку С8.
4 Меню: Правка – Специальная ставка –
Значения (рис. 2.12).
Рисунок 2.12 – Диалоговое окно Специальная ставка
Эта процедура повторятся для всего периода
начислений.
Завершаем анализ построением диаграммы,
которая наглядно отражает соотношение по годам выплат основной суммы и выплат
по процентам (рис. 2.13).
Рисунок 2.13 – Диаграмма соотношения выплат по
процентам
и основной суммы
практические задания
6. Расчет финансовых функций
Выполнить расчеты с использованием финансовых
функций. Оформите решение в виде таблицы и построить диаграмму, отражающую динамику
роста вклада по годам (тип диаграммы выбрать самостоятельно). Описать
используемые формулы, представить распечатку со значениями и с формулами.
Если в задаче не указано, в конце или в начале
расчетного периода производится выплата, считать, что выплата производится в
конце периода (аргумент Тип = 0).
В каждом варианте три
задачи. Например, для варианта 23 – задача 23.1, 23.2 и 23.3.
Варианты заданий представлены в таблице 5.1.
Таблица 6.1 – Варианты задания 1
|
Вариант |
Задачи |
|
1 |
1.1 Рассчитайте, какая сумма будет на счете, если сумма 1.2 Рассчитайте текущую стоимость вклада, который через 1.3 Определите |
|
2 |
2.1 Определите текущую стоимость платежей в начале 2.2 По вкладу размером 2000 тыс. грн начисляется 10 % 2.3 Банк |
Продолжение таблицы 6.1
|
3 |
3.1 На сберегательный счет вносятся платежи по 200 тыс. 3.2 Определите текущую 3.3 Какой |
|
4 |
4.1 Рассчитайте, какую сумму необходимо положить на депозит, 4.2 Определите, какая сумма окажется на счете, если 4.3 Рассчитайте |
|
5 |
5.1 Какая сумма должна быть выплачена, если шесть лет 5.2 5.3 Выдан |
|
6 |
6.1 Какую сумму необходимо положить на депозит под 16,5 % 6.2 6.3 Выдан |
Продолжение таблицы 6.1
|
7 |
7.1 7.2 7.3 |
|
8 |
8.1 Рассчитайте 8.2 8.3 Кредит |
|
9 |
9.1 На сберегательный счет вносятся 9.2 9.3 Определите |
|
10 |
10.1 Определите текущую стоимость ежемесячных платежей 10.2 10.3 Банк |
Продолжение таблицы 6.1
|
11 |
11.1 На сберегательный счет вносятся платежи по 50 тыс. 11.2 Рассчитайте, какую сумму надо положить на депозит, 11.3 |
|
12 |
12.1 Определите текущую стоимость ежеквартальных платежей 12.2 Рассчитайте, какая сумма будет на счете, если сумма 12.3 Рассчитайте |
|
13 |
13.1 Взносы на сберегательный счет составляют 100 тыс. 13.2 Рассчитайте 13.3 При |
|
14 |
14.1 Определите текущую стоимость ежеквартальных платежей 14.2 14.3 Выдан |
Продолжение таблицы 6.1
|
15 |
15.1 15.2 15.3 |
|
16 |
16.1 Рассчитайте, какую сумму необходимо положить на депозит, 16.2 16.3 |
|
17 |
17.1 На сберегательный счет вносятся ежеквартальные платежи 17.2 17.3 |
|
18 |
18.1 Какую сумму необходимо положить на депозит под 9,5 % 18.2 18.3 |
Продолжение таблицы 6.1
|
19 |
19.1 По вкладу размером 1500 тыс. грн начисляется 8 % 19.2 Определите 19.3 |
|
20 |
20.1 Рассчитайте текущую стоимость вклада, который через 20.2 20.3 |
|
21 |
21.1 Определите, какая сумма окажется на счете, если 21.2 21.3 |
|
22 |
22.1 Определите текущую стоимость ежемесячных платежей 22.2 22.3 |
Продолжение таблицы 6.1
|
23 |
23.1 Рассчитайте, какая сумма будет на счете, если вклад 23.2 Рассчитайте, какую сумму необходимо положить на депозит, 23.3 |
|
24 |
24.1 Определите текущую стоимость полугодовых платежей 24.2 Вклад размером 5000 грн положен под 14,5 % 24.3 |
|
25 |
25.1 На сберегательный счет в конце каждого месяца 25.2 Какую сумму необходимо положить на депозит под 16 % 25.3 Кредит размером 50000 грн взят на 2 года под 12 %. |
|
26 |
26.1 Рассчитайте, какая сумма будет на счете, если сумма 26.2 Рассчитайте текущую стоимость вклада, который через 26.3 Определите размер ежегодного платежа и выплат процентов |
Продолжение таблицы 6.1
|
27 |
27.1 Определите текущую стоимость платежей в начале каждого 27.2 По вкладу размером 2000 тыс. грн начисляется 10 % 27.3 Банк выдал кредит размером 54700 грн на 8 лет под 12,5 % |
|
28 |
28.1 На сберегательный счет вносятся платежи по 200 тыс. 28.2 Определите текущую стоимость ежемесячных платежей 28.3 Какой размер ежегодного платежа должен погашаться |
|
29 |
29.1 Рассчитайте, какую сумму необходимо положить на депозит, 29.2 Определите, какая сумма окажется на счете, если 29.3 Рассчитайте размер ежегодного платежа и выплат основной |
|
30 |
30.1 Какая сумма должна быть выплачена, если шесть лет 30.2 Определите текущую стоимость ежеквартальных платежей 30.3 При покупке домашнего кинотеатра был оформлен |
Финансовые функции Microsoft Excel
Функция БС
-
Необходимо определить будущую стоимость единовременного вклада с текущей стоимостью 20000 рублей, на который в течение 10 лет ежегодно начисляются сложные проценты по ставке 7 процентов годовых. Начисление процентов производится 1 раз в год.
-
Организация взяла заем размером 100000 рублей на срок 3 года под 30 процентов годовых. Необходимо определить сумму, подлежащую возврату.
-
Предположим, фирма собирается зарезервировать деньги для специального проекта, который будет осуществлен через год. Фирма открывает счет, единовременно на него вносятся 10000 рублей под 6% годовых (это составит в месяц 6/12, или 0,5%). Далее предполагается вносить 1000 рублей в начале каждого месяца в течение следующих 12 месяцев. Необходимо определить сумму денег на счете через год.
-
Есть два варианта инвестирования средств на 4 года. Первый вариант предполагает начисление 26 процентов годовых в начале каждого года. Второй вариант — начисление 38 процентов годовых в конце каждого года. Фирма имеет возможность ежегодно вносить 300000 рублей. Необходимо определить, какой вариант предпочтительнее.
Функция ПС
-
Рассматриваются два варианта покупки оборудования. Первый вариант предполагает, что сразу будет выплачена вся сумма 99000 рублей. Второй вариант — рассрочка на 15 лет при ежемесячной выплате по 940 рублей в конце каждого месяца. Годовая процентная ставка – 8 процентов. Необходимо определить, какой вариант предпочтительнее.
-
Организации потребуется 5000000 рублей через 12 лет. В настоящее время фирма располагает средствами и готова разместить деньги на депозит единым вкладом с тем, чтобы через 12 лет иметь необходимые деньги. Годовая процентная ставка — 12 процентов. Необходимо определить, сколько средств размещать на депозите.
Функция КПЕР
-
Для обеспечения будущих расходов фирмы создается фонд, величина которого должна составить 1000000 рублей. Деньги на создание фонда поступают ежегодно в конце года в виде фиксированных отчислений в 160000 рублей. На поступившие платежи начисляется 11,18% процентов годовых. Необходимо определить, через сколько лет будет накоплена необходимая сумма.
-
Фирма получила ссуду в размере 66000 рублей под 36 процентов годовых и предполагает рассчитываться ежемесячно по 6630 рублей в конце каждого месяца. Необходимо определить срок полного расчета по полученной ссуде.
Задачи для самостоятельного решения
-
Сумма 5000 руб. размещена на счете под 20 процентов годовых с начислением процентов 4 раза в год на срок 3 года. Какова будет величина вклада в конце периода?
-
На накопительный счет в начале каждого месяца вносится сумма 1000 руб. Определите, какая сумма окажется на счете через 3 года при ставке 12 процентов годовых.
-
Фирме предлагается инвестировать средства на 5 лет по одной из двух схем:
-
Первоначально инвестируется 100000 руб. и далее в конце каждого года – по 10000 руб. на вклад под 24 процента годовых, начисляемых в конце каждого года.
-
Ежеквартально в начале квартала инвестируется 10000 руб. под 32 процента годовых, и проценты начисляются в начале квартала.
-
Какая схема выгоднее?
-
Определите текущую стоимость ежеквартальных платежей размером 350 руб., осуществляемых в конце каждого квартала в течение 7лет при ставке 11 процентов годовых.
-
Фирма получила ссуду в размере 65000 рублей под 16% годовых и предполагает рассчитываться ежемесячно по 3500 рублей в конце каждого месяца. Необходимо определить срок полного расчета по полученной ссуде.
-
Для обеспечения будущих расходов предприятия создается фонд, величина которого должна составить 1900000 рублей. Деньги на создание фонда поступают ежегодно в начале года в виде фиксированных отчислений в 80000 рублей. На поступившие платежи начисляются 17% годовых. Необходимо определить через сколько лет будет накоплена необходимая сумма.