Задания по excel по логистике

Транспортная задача в Microsoft Excel

Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.

Общее описание транспортной задачи

Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.

Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.

Инструменты для решения транспортной задачи в Эксель

Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.

1. Делаем перемещение во вкладку «Файл».
2. Кликаем по подразделу «Параметры».

Пример решения транспортной задачи в Excel

Теперь давайте разберем конкретный пример решения транспортной задачи.

Условия задачи

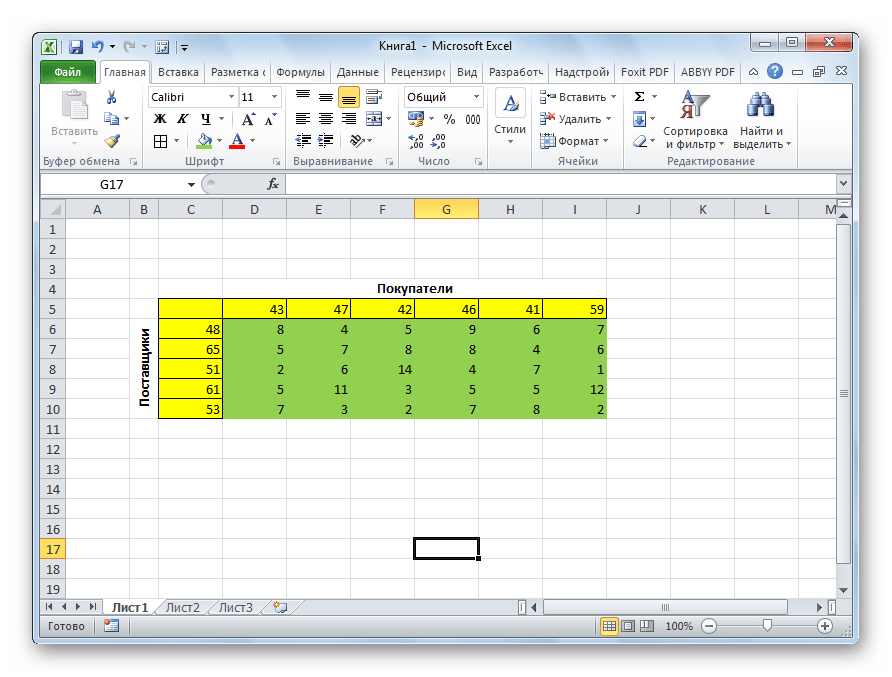
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.

Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.

Решение задачи

Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.

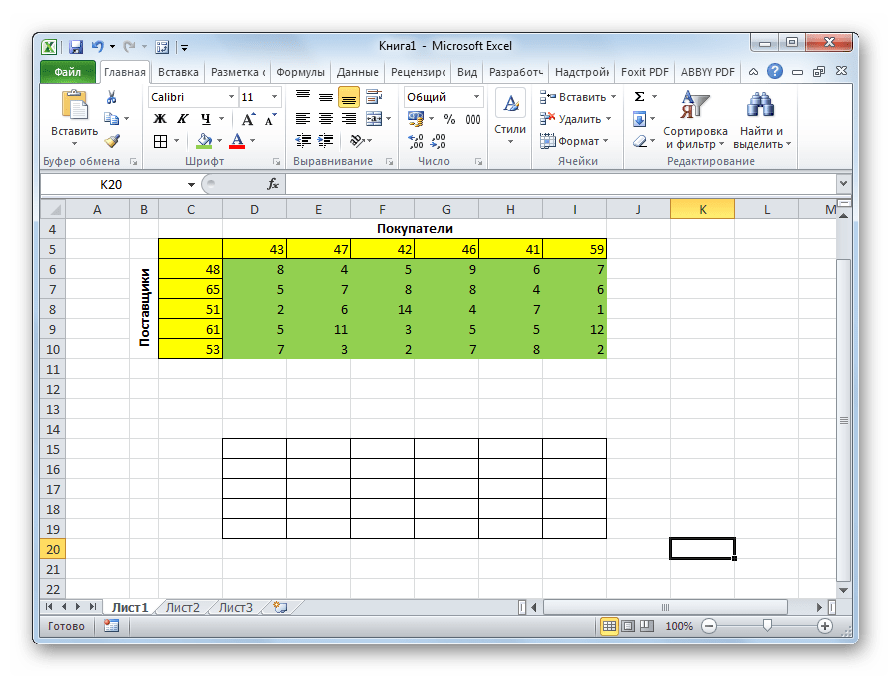
1. Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
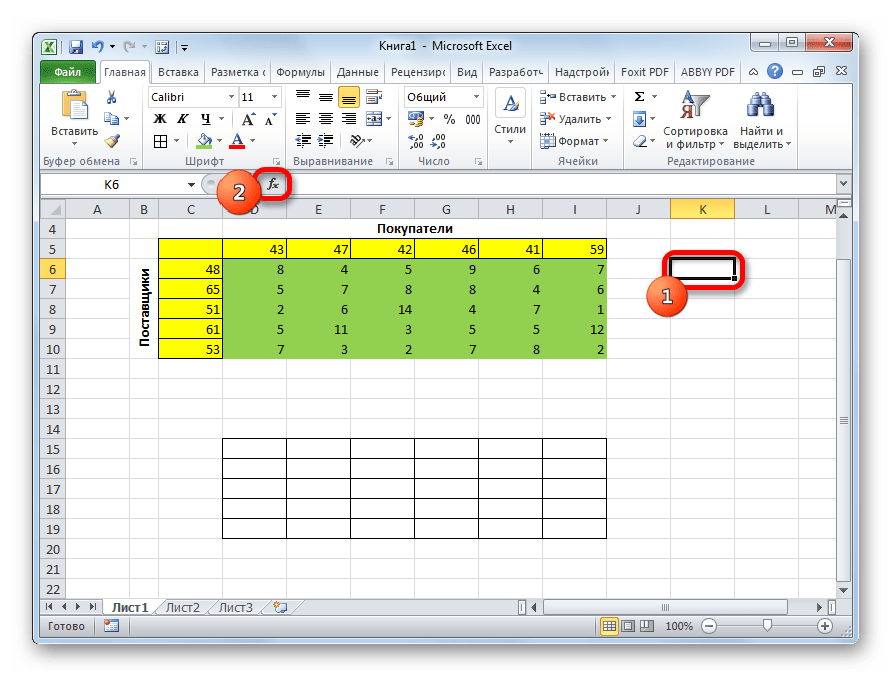
2. Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
3. Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
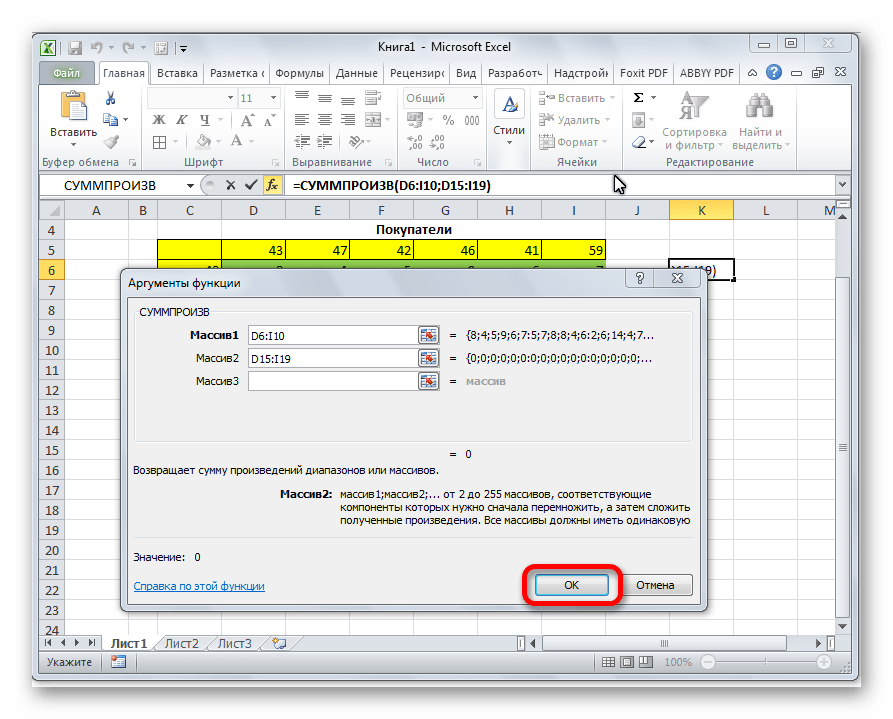
4. Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
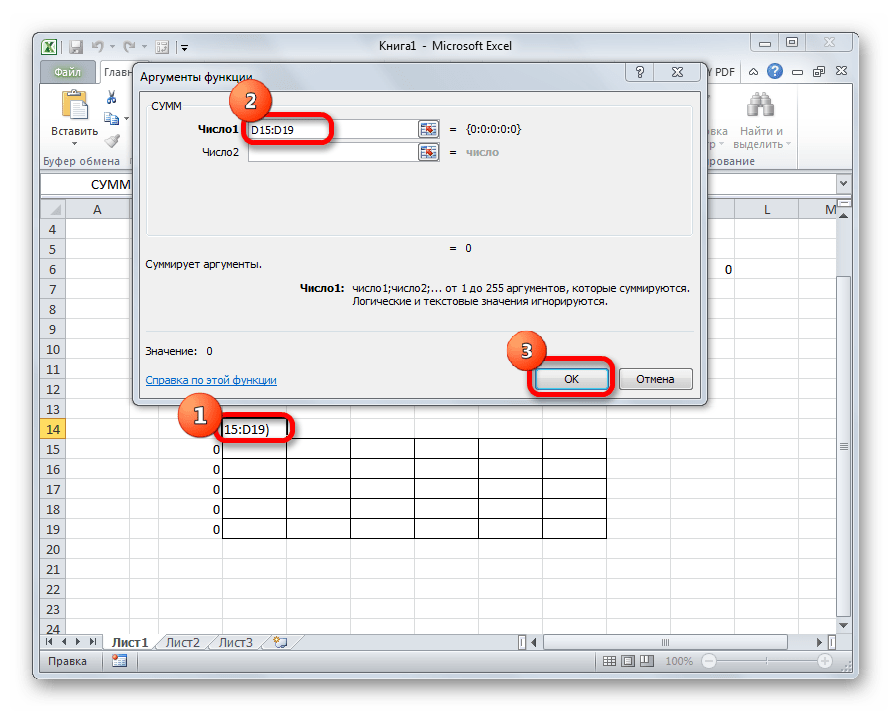
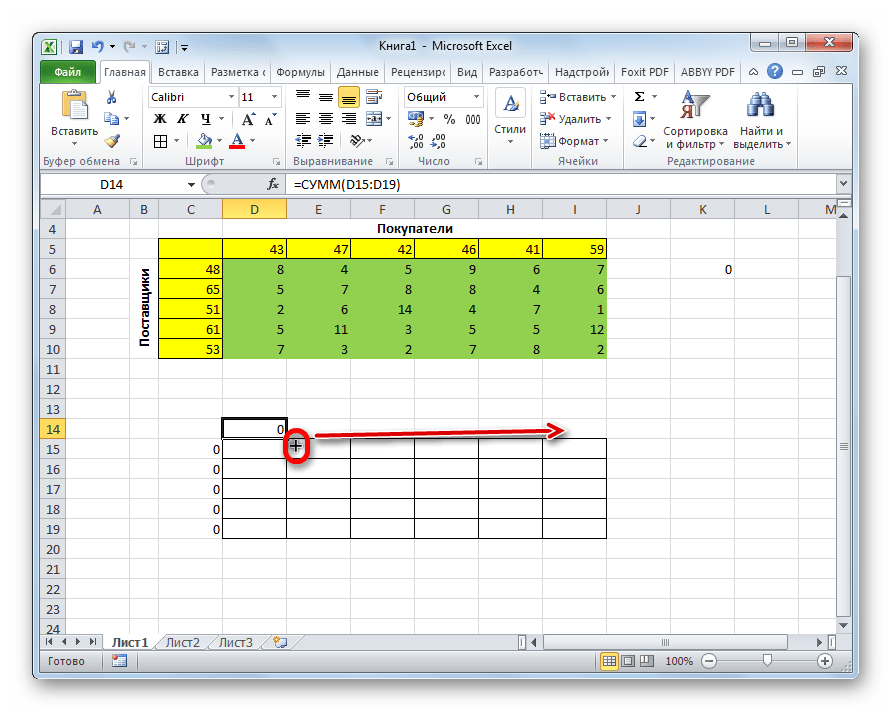
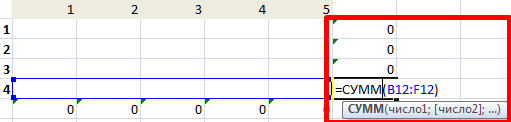
5. Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
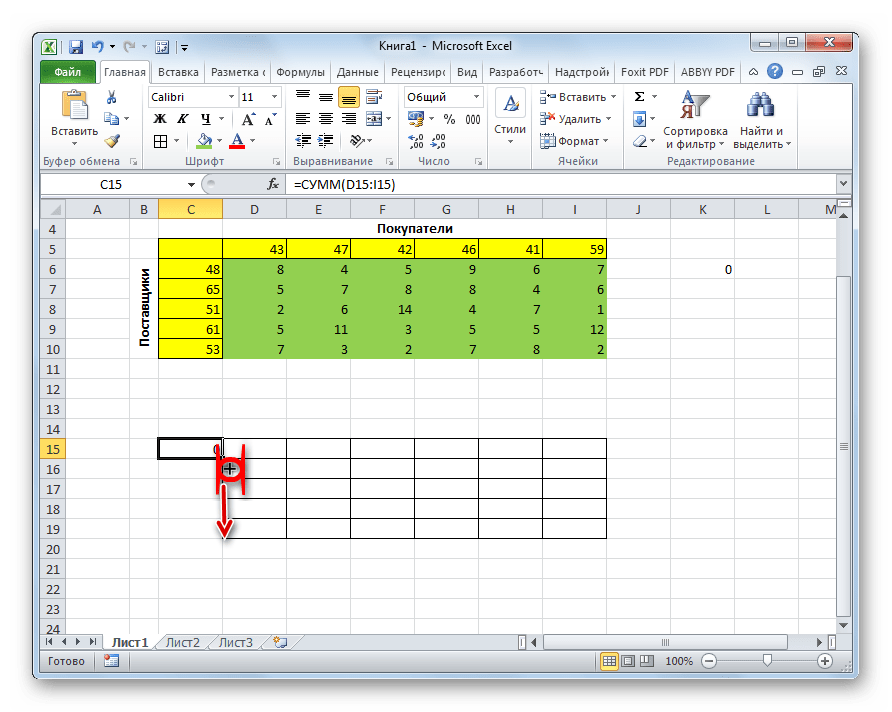
6. Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
7. Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
8. Копируем маркером заполнения формулу на всю строку.
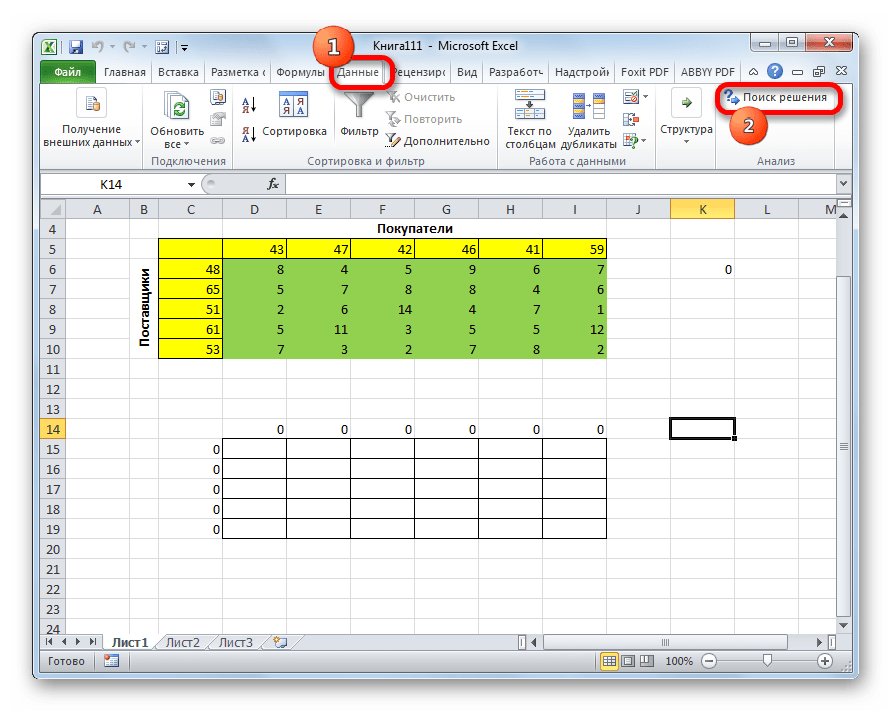
9. Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
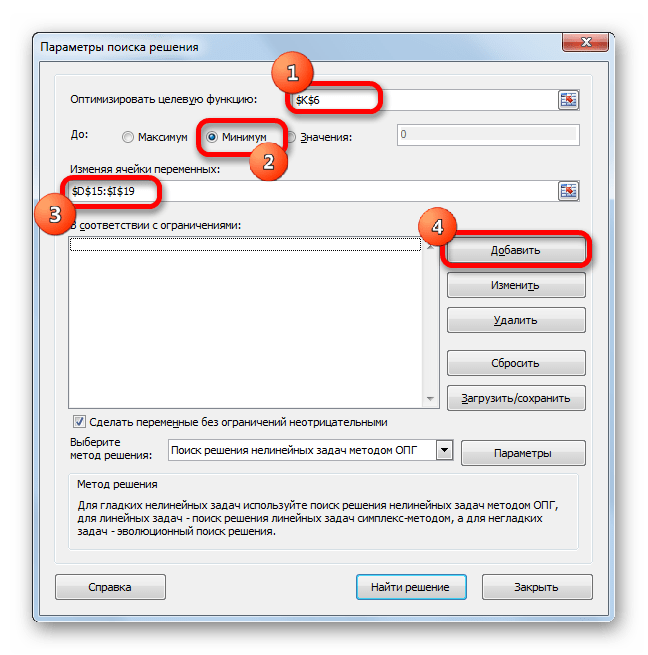
10. Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
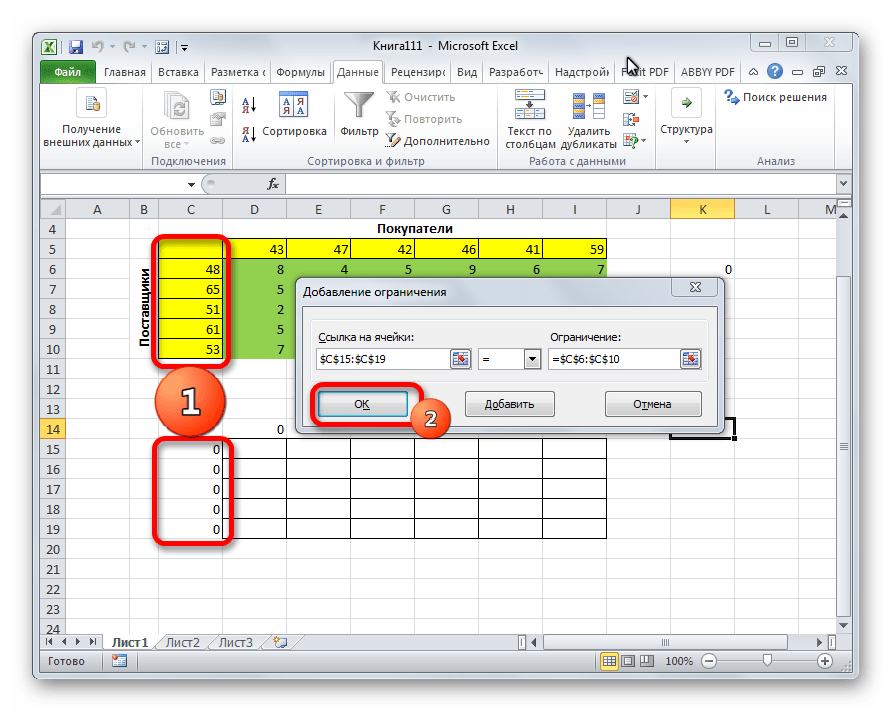
11. Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
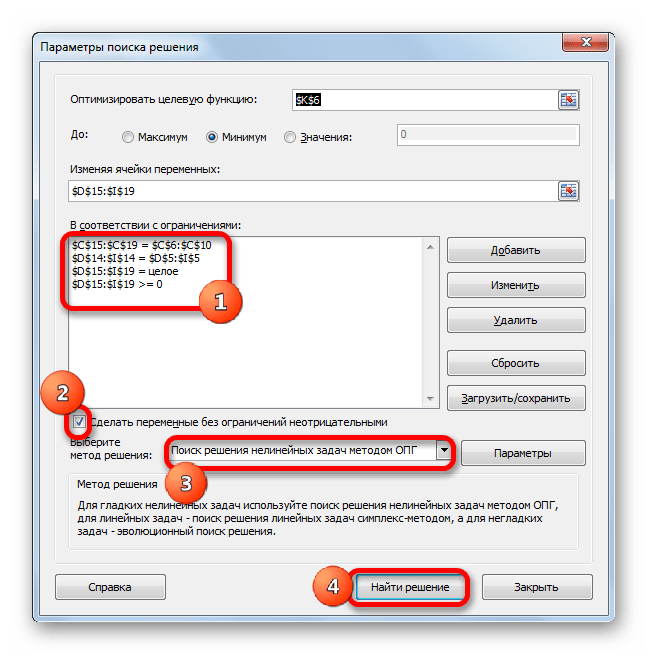
12. Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
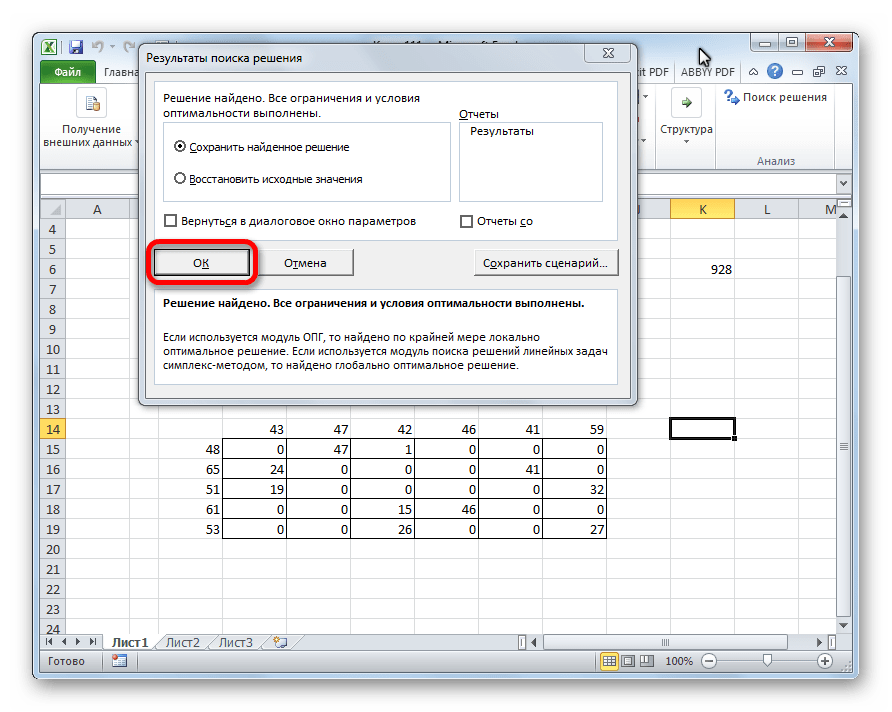
13. После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».

Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.

Источник

Решение транспортной задачи в Excel с примером и описанием

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

• открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
• закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.

Пример решения транспортной задачи в Excel

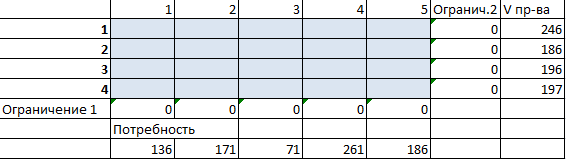
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

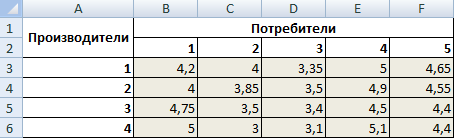
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
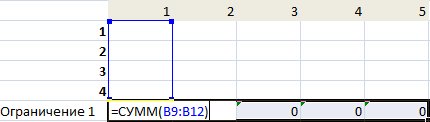
4. Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
5. Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
6. Вносим известные значения потребности в товаре и объема производства.
7. Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
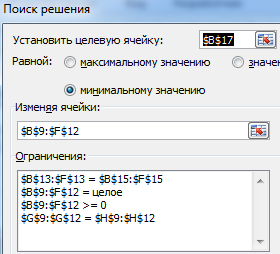
8. Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
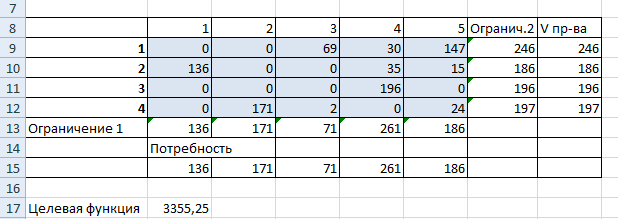
9. Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

• суммарный объем производства превышает суммарную потребность в товаре;
• суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Источник

Как решить транспортную задачу в Excel

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

• Закрытая – совокупное предложение продавца равняется общему спросу.
• Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

1. Открываем меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Источник

Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.

Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.

Виды транспортных задач

Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.

Условия транспортной задачи можно представить двумя способами:

• в виде схемы;
• в виде матрицы.

В процессе решения могут быть ограничения (либо задача решается без них).

По характеру условий различают следующие типы транспортных задач:

• открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
• закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).

Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.



Пример решения транспортной задачи в Excel

Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.

Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:

Производители	Потребители	Объем производства
	В1	В2	В3	В4	В5
А1	4,2	4	3,35	5	4,65	246
А2	4	3,85	3,5	4,9	4,55	186
А3	4,75	3,5	3,4	4,5	4,4	196
А4	5	3	3,1	5,1	4,4	197
Объем потребления	136	171	71	261	186

Задача: минимизировать транспортные расходы по перевозке продукции.

1. Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
2. Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
3. Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.



4. Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.



5. Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.



6. Вносим известные значения потребности в товаре и объема производства.



7. Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
8. Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.



9. Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.

Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.

Решение открытой транспортной задачи в Excel

При таком типе возможны два варианта развития событий:

• суммарный объем производства превышает суммарную потребность в товаре;
• суммарная потребность больше суммы запасов.

Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.

Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.

Единица перевозки груза для фиктивного участника равняется 0.

Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.

Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.

---

Подборка по базе: теорвер задача 1.docx, Решение задач — Паскаль.pdf, тема 10 задача 3.docx, 7 Анализ кадров Ethernet и просмотр сетевого трафика с помощью (, !Куда обратиться за помощью Алтайский край.pdf, Переделанные задачи.pdf, Презентация к докладу на тему _Типы и виды задач в начальной шко, Ситуационные задачи по ПМ 01 МДК 01.03 Сестринское дело в систем, Информатика решение.docx, БАНК ЗАДАЧ.docx

---

Типовые задачи (примеры и задания для самостоятельного решения)

Задача 1. Методом определения центра тяжести грузопотоков найти ориентировочное место для расположения склада, снабжающего магазины.

На территории района (рис.1) имеется 8 магазинов, торгующих продовольственными товарами.

Рисунок 1. Карта района обслуживания

У
4
словные обозначения:

— расстояние между обслуживаемыми магазинами — потребителями материального

потока, км;

6²⁰ — № магазина и его грузооборот (например, магазин № 6, грузооборот — 20 т/мес);

— автомобильные дороги.

Методические указания

В таблице 2 приведены координаты обслуживаемых магазинов (в прямоугольной системе координат), а также их месячный грузооборот.

Таблица 2. Грузооборот и координаты обслуживаемых магазинов

№ магазина	Координата X	Координата У	Грузооборот, т/мес.
1	10	10	15
2	23	41	10
3	48	59	20
4	36	27	5
5	60	34	10
6	67	20	20
7	81	29	45
8	106	45	30

Пользуясь приведенными в теоретических пояснениях к заданию формулами, необходимо найти координаты точ­ки (Х_склад, У_склад), в окрестностях которой рекомендуется организовать работу распределительного склада, а также указать эту точку на чертеже.

Прежде чем приступить к расчетам, необходимо вы­полнить чертеж к заданию. Для этого, желательно на мил­лиметровой бумаге, следует нанести координатные оси, а затем точки, в которых размещены магазины. Рекомендуе­мый масштаб: одно миллиметровое деление — один кило­метр (рис.2.).

Рисунок 2. Определение места расположения склада методом поиска центра тяжести грузовых потоков (рядом с номером магазина указан его месячый грузооборот)
На рисунке рядом с номером магазина указан ме­сячный грузооборот.

Координаты центра тяжести грузовых потоков (Х_склад,У_скяад), т.е. точки, в окрестностях которой может быть разме­щен распределительный склад, определяются по формулам:

где Г_i — грузооборот i-го потребителя;

Х_i, У_i — координаты i-го потребителя;

n — число потребителей.

Приведем в качестве примера расчет абсциссы центра тяжести грузовых потоков (Х_склад):

Ординату центра тяжести грузовых потоков предлага­ется рассчитать самостоятельно.

Точка территории, обеспечивающая минимум транспорт­ной работы по доставке, в общем случае не совпадает с найденным центром тяжести, но, как правило, находится где-то недалеко. Подобрать приемлемое место для склада позволит последующий анализ возможных мест размеще­ния в окрестностях найденного центра тяжести (в рамках данной работы не проводится). При этом необходимо оце­нить транспортную доступность местности, размер и кон­фигурацию возможного участка, а также планы местных властей в отношении намеченной территории.

Применение описанного метода имеет ограничение. На модели расстояние от пункта потребления материального потока до места размещения распределительного центра учитывается по прямой. В связи с этим моделируемый рай­он должен иметь развитую сеть дорог, так как в противном случае будет нарушен основной принцип моделирования — принцип подобия модели и моделируемого объекта.

Задача 2. Определить оптимальное месторасположение распределительного склада методом центра тяжести по тарифу

Три молочных комбината — Царицынский молочный комбинат, Лианозовский молочный комбинат, Завод детских молочных про­дуктов — вместе обслуживают 5 магазинов, расположенных в Мос­ковской области. В табл. 3. приведены координаты молочных ком­бинатов и обслуживаемых магазинов. Комбинаты осуществляют среднюю партию поставки соответственно в размерах 250 т; 275 т; 185 т. Партии поставок при реализации клиентам соответственно равны: К_А — 160 т; К_В — 110 т; К_С — 170 т; K_D — 150; К_Е — 120.

Необходимо определить месторасположение распределитель­ного центра, который может обеспечить сбыт продукции молочных заводов среди потребителей, если известно, что тариф для постав­щиков на перевозку продукции составляет 1 руб./т.км, а тарифы для клиентов на перевозку продукции равны: для К_А — 0,8 руб./т-км; К_В — 0,5 руб./т-км; К_С — 0,6 руб./т-км; K_D — 0,7 руб./т-км; К_Е — 0,5 руб./т.км.

Таблица 3.

Координаты расположения поставщиков и потребителей продукции

Коорди­ната	Поставщик	Клиент
Царицынский молочный комбинат	Лианозовский молочный комбинат	Завод детских молочных продуктов	КА	КВ	КС	KD	КЕ
X	20	50	70	55	15	35	40	46
Y	50	35	20	60	40	70	50	50

Решение рассматриваемой задачи основывает­ся на нахождении центра тяжести, который определяется по фор­муле

где M — центр массы, км;

R_ni— расстояние от начала осей координат до точки, обозначающей месторасположение поставщика, км;

R_ki — расстояние от начала координат до точки, обозначающей мес­торасположение потребителя,км;

T_ni— транспортный тариф для поставщика на перевозку груза, руб./ткм;

Т_ki— транспортный тариф для клиента на перевозку груза, руб./ткм;

Q_ni— объем груза, поставляемый i-м поставщиком, т;

Q_ki— объем груза, закупаемый i-м клиентом, т.
Пример решения задачи

1. Рассчитаем координаты центра тяжести грузовых потоков по оси X:

2. Рассчитаем координаты центра тяжести грузовых потоков по оси У:

Таким образом, оптимальное месторасположение склада нахо­дится в точке (43 км; 44 км).

Задача 3. Для самостоятельного решения
Торгово-посредническая компания «ТV» имеет 3 склада, которые обслуживаются 4 поставщиками. В табл. 4 приведены координаты месторасположения складов компании «ТV» и их поставщиков.

Поставщики осуществляют среднюю партию поставки в разме­рах: П_A — 75 т; П_B — 45 т; П_C -50 т; П_D — 30. Объемы заказов по складам равны: С_A — 70 т; С_B — 50 т; С_C — 80 т.

Для минимизации транспортных расходов компания «ТV» при­няла решение о строительстве распределительного центра в райо­не сбыта продукции. Необходимо определить место расположения распределительного центра, если известно, что тариф для постав­щиков на перевозку продукции составляет П_A — 1,25 руб./ткм; П_B — 1 руб./ткм; П_C -1,75 руб./ткм; П_D — 1 руб/ткм, а тарифы для складов на перевозку продукции равны: для К_A — 0,5 руб./ткм; К_B — 0,6 руб./ткм; К_C — 0,7 руб./ткм.

Таблица 4.

Координаты расположения поставщиков и складов торгово-посреднической компании «ТV» продукции

Координата	Клиент	Поставщик
СA	СB	СC	ПA	ПB	ПC	ПD
X	20	50	70	55	15	35	10
Y	5	35	20	60	40	70	20

Задача 4. Определение формы собственности склада
В связи с решением об увеличении объемов продаж перед тор­говой компанией «РИМ» встала проблема, что существующая собственная складская система не сможет поддерживать увеличе­ние объема продаж. Вследствие этого компания вынуждена вы­брать одну из двух альтернатив: приобрести склад в собственность или пользоваться услугами склада общего пользования.
Таблица 5.

Исходные данные задачи

Суммарная величина грузопотока, проходящего через склад	7000 т/год
Условно-постоянные затраты собственного склада	750 000 у.е./год
Удельная стоимость грузопереработки на собственном складе	3,5 у.е./т
Средняя цена закупки партии товара	4000 у.е./т
Средняя торговая надбавка при оптовой продаже товаров	8%
Коэффициент для расчета оплаты процентов за кредит	0,045
Тариф на услуги арендуемого склада	6 у.е./м2
Потребная площадь арендуемого склада	1211 м2

Пример решения задачи

1. Определим точку безубыточности деятельности склада, т. е. минимальный объем работы, ниже которого работа собственного склада компании «РИМ» становится убыточной при действующей системе расценок.

Точка безубыточности (Т_бу) — уровень грузооборота на складе, при котором доход от работы склада совпадает с общими издержками.

Точка безубыточности определяется по формуле

где С_пост — условно-постоянные затраты, размер которых напрямую не связан с грузооборотом (Q)на складе (амортизация, заработная пла­та персонала, страховые выплаты, проценты по долгам, затраты на рекламу, затраты на содержание помещений и прочее);

Д — прибыль на единицу груза от работы склада, рассчитывается по формуле

где N — средняя торговая надбавка при оптовой продаже товаров;

К — средняя цена закупки партии товара;

С_пер — переменные затраты, величина которых изменяется с измене­нием объема грузооборота складываются из процентов за кредит, взятого для оплаты партии товаров (С_кр) и стоимости грузопереработки (С_гр):

С_пер = С_кр + С_гр.

Размер процентов за кредит на единицу груза определяется по формуле

С_кр = k * R,

где k — коэффициент пропорциональности, зависящий от стоимости партии товаров и банковского процента.

Стоимость грузопереработки определяется объемом работ на складе и удельной стоимостью выполнения этих работ (С_уд).

Следовательно, в развернутом виде формулу точки безубыточ­ности можно представить как

Таким образом,

Иными словами, склад может работать безубыточно при грузо­обороте 5495 т/год, в то время как расчетный грузооборот компа­нии составляет 7000 т/год. Таким образом, компания «РИМ» может рассматривать вариант строительства собственного склада.

2. Рассчитаем суммарные затраты при условии использования собственного склада компанией «РИМ».

Зависимость затрат на грузопереработку на собственном скла­де от объема грузооборота рассчитывается исходя из того, что удельная стоимость грузопереработки на собственном складе со­ставит приблизительно 3,5 у.е. за 1 т/год.

Тогда С_сс =3,5 * Т + С_пост и С_сс = 3,5 * 70 000 + 750 000 = 774 500 у.е.

3. Рассчитаем суммарные затраты при условии использования услуг склада общего пользования.

Затраты на хранение товаров на складе общего пользования определяются по следующей формуле:

где — тариф на услуги арендуемого склада;

— потребная площадь арендуемого склада, в нашем случае 1211 м²;

365 — число дней хранения на наемном складе за год.

С_ас = 6 * 1211 * 365 = 2 652 090 у.е.

Таким образом, получаем, что при грузообороте склада 7000 т/год целесообразно иметь собственный склад, так как С_сс< С_ас.
Задача 5. Для самостоятельного решения

В связи с решением об увеличении объема продаж перед торго­вой компанией встал вопрос: приобрести склад в собственность или пользоваться услугами склада общего пользования.

На основе данных, приведенных в табл. 2, выберите и обоснуйте одну из альтернатив.

Таблица 6.

Исходные данные задачи

Суммарная величина грузопотока, проходящего через, склад	9000 т/год
Условно-постоянные затраты собственного склада	600 000 у.е./т
Удельная стоимость грузопереработки на собственном складе	3 у.е./т
Средняя цена закупки партии товара	2500 у.е./т
Средняя торговая надбавка при оптовой продаже товаров	8%
Коэффициент для расчета оплаты процентов за кредит	0,045
Тариф на услуги арендуемого склада	5,5 у.е./м2
Потребная площадь арендуемого склада	300 м2

Задача 6. Найти коэффициент неравномерности загрузки склада в отчет­ном и предыдущем году, а также темпы его изменения, используя сле­дующие данные:

Показатели	Месяцы года
1	2	3	4	5	6	7	8	9	10	11	12
Количество груза поступившего на склад, т	50	70	80	85	95	110	105	115	125	120	105	100

Решение:

1. Грузооборот склада — показатель, характеризующий мощность склада:

где Г — грузооборот склада;

Q — количество груза, поступившего на склад (или реализованного со склада) за период, т;

T — продолжительность периода времени.

1. Коэффициент неравномерности загрузки склада (К_н):

где Г_макс — грузооборот самого напряженного месяца;

Г_ср — среднемесячный грузооборот склада.

Г_ср = (50 + 70 + 80 + 85 + 95 +110+105+115+125+120+105+100) / 12 = 96,7т.

К_н = 125 т/96,7 т =1,29.

Задача 7. Для самостоятельного решения

Найти коэффициент неравномерности загрузки склада в отчет­ном и предыдущем году, используя сле­дующие данные:

Количество груза поступившего на склад, т	Месяцы года
1	2	3	4	5	6	7	8	9	10	11	12
Отчетный год	200	205	220	225	215	205	210	195	185	180	170	150
Предыдущий год	145	160	175	190	190	205	210	215	220	210	205	200

Задача 8. Компания «Модус продукт», занимающаяся реализацией продук­тов питания, решила приобрести склад для расширения рынка сбыта на юго-востоке Москвы. Она предполагает, что годовой грузооборот склада должен составить 16 тыс. т при среднем сроке хранения груза 25 дней. Оп­ределить необходимую емкость склада.

Решение:

Вместимость (емкость) склада определяется по формуле:

где Е — емкость склада, т;

Т_хр — средний срок хранения груза, дн.;

t — число поступлений грузов в год;

Q — годовой грузооборот, т.

Е=16000*(365/25)=1067

Задача 9. Найти показатель «готовность к поставке» и общие затраты фир­мы на логистику в стоимостном выражении. Если известно, что фактиче­ский объем поставок продукции в год составил 1440 т при 16 поставках, что характеризует товарооборот склада фирмы за год, при этом планиро­валось — 14 поставок, фактический объем поставляемой партии составил 75 % от запланированного. Затраты фирмы на логистику составили 2,5 млн. руб. Стоимость 1 т груза — 40000 руб.

Решение:

1. Готовность к поставке. Показатель используется как для оценки собст­венного уровня сервиса, так и для оценки уровня сервиса поставщика:

где Гп — готовность к поставке;

m — фактический объем поставок в количественном выражении;

М — запланированный объем в количественном выражении.

М = (1440/16)/75% * 100% * 14= 1680 т

Гп = 1440/1680 * 100% = 85,7%

1. Затраты на логистику, приходящиеся на единицу товарооборота:

где Дл — затраты на логистику, приходящиеся на единицу товарооборота;

С_л — затраты на логистику за период;

О — товарооборот за период.

О = 1440 * 40000 = 57,6 млн. руб.

Д_л = 2,5 млн. руб./ 57,6 млн. руб. * 100 % = 4,34 %

Задача 10. Для самостоятельного решения

Найти показатель готовность к поставке и общие затраты фирмы на логистику в стоимостном выражении. Известно, что фактический объем поставок продукции в год составил 1680 т при 14 поставках, что характе­ризует товарооборот склада фирмы за год, при этом планировалось 12 поставок, фактический объем поставляемой партии составил 80 % от запла­нированного. Затраты фирмы на логистику составили 3 % от стоимости поставляемой партии. Стоимость 1 т груза — 35000 руб.

Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.

Транспортная задача: описание

С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.

Транспортные задачи бывают двух типов:

• Закрытая – совокупное предложение продавца равняется общему спросу.
• Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).

Подготовительный этап: включение функции “Поиск решения”

Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:

1. Открываем меню “Файл”.
2. В перечне слева выбираем пункт “Параметры”.
3. В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
4. В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
5. В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.

Пример задачи и ее решение

Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.

Условия задачи

Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения

Итак, приступи к решению нашей задачи:

1. Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
2. Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
3. В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
4. На экране отобразится окно, в котором нужно заполнить аргументы:
   • в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
   • в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
   • по готовности жмем OK.
5. Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
6. На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
7. Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
8. В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
9. Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
10. Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
11. В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
12. С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
13. Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
14. Перед нами появится окно с параметрами функции:
    • в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
    • для параметра “До” выбираем вариант – “Минимум”.
    • в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
    • нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
15. Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
    • становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
    • затем выбираем знак “равно”.
    • в качестве значения для параметра “Ограничение” указываем координаты  аналогичного столбца в исходной таблице.
    • щелкаем OK по готовности.
16. Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
17. Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
    • больше или равно нулю;
    • целое число.
18. В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
19. В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
20. Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.

Заключение

Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.

Решить
задачу:

1.  установить
   параметры решения задачи
   (в окне «Поиск
   решения»);

2.  запустить
   задачу на решение
   (в окне «Поиск
   решения»);

3.  выбрать
   формат вывода решения
   (в окне «Результаты
   поиска решения»).

Рассмотрим пример
нахождения решения для следующей задачи
ЛП:

(1.1)

Ввод исходных данных

Создание экранной
формы и ввод в нее условия задачи

Экранная форма
для ввода условий задачи (1.1) вместе с
введенными в нее исходными данными
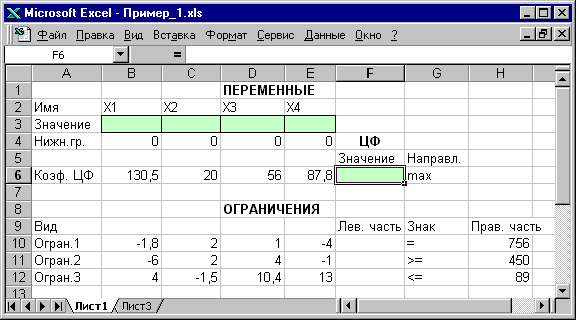
представлена на рис.1.1.

Рис.1.1. Экранная
форма задачи (1.1) (курсор в ячейке F6)

В экранной форме
на рис.1.1 каждой переменной и каждому
коэффициенту задачи поставлена в
соответствие конкретная ячейка в Excel.
Имя ячейки состоит из буквы, обозначающей
столбец, и цифры, обозначающей строку,
на пересечении которых находится объект
задачи ЛП. Так, например, переменным
задачи (1.1) соответствуют ячейки B3
(),C3
(),D3
(),E3
(),
коэффициентам ЦФ соответствуют ячейкиB6
(130,5),C6
(20),D6
(56),E6
(87,8),
правым частям ограничений соответствуют
ячейкиH10
(756),H11
(450),H12
(89)
и т.д.

Ввод зависимостей
из математической модели в экранную
форму

Зависимость для
ЦФ

В ячейку F6,
в которой будет отображаться значение
ЦФ, необходимо ввести формулу,
по которой это значение будет рассчитано.
Согласно (1.1) значение ЦФ определяется
выражением

.

(1.2)

Используя
обозначения соответствующих ячеек в
Excel (см. рис.1.1), формулу для расчета ЦФ
(1.2) можно записать как сумму
произведений
каждой из ячеек, отведенных для значений
переменных задачи (B3,
C3, D3, E3), на
соответствующую ячейку, отведенную для
коэффициентов ЦФ (B6,
C6, D6, E6), то
есть

.

(1.3)

Чтобы задать
формулу (1.3) необходимо в ячейку F6
ввести следующее выражение и нажать
клавишу «Enter»

=СУММПРОИЗВ(B$3:E$3;B6:E6),

(1.4)

где символ $
перед номером строки 3 означает, что при
копировании этой формулы в другие места
листа Excel номер строки 3 не изменится;

символ :
означает, что в формуле будут использованы
все
ячейки, расположенные между ячейками,
указанными слева и справа от двоеточия
(например, запись B6:E6
указывает на ячейки B6,
C6, D6 и E6).
После этого в целевой ячейке появится
0 (нулевое значение) (рис.1.2).

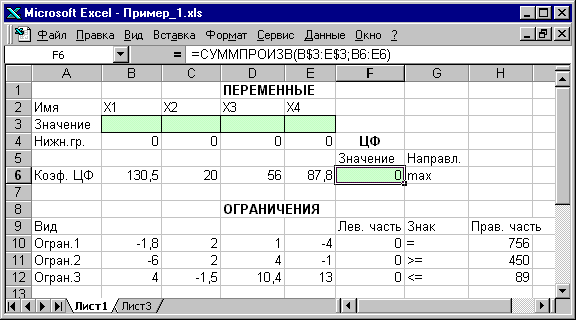
Рис.1.2. Экранная
форма задачи (1.1) после ввода всех
необходимых формул

(курсор в ячейке
F6)

Примечание 1.1.
Существует другой способ задания функций
в Excel с помощью режима «Вставка
функций»,
который
можно вызвать из меню «Вставка»
или при нажатии кнопки ««
на
стандартной панели инструментов. Так,
например, формулу (1.4) можно задать
следующим образом:

• курсор в поле F6;

• нажав кнопку ««,
  вызовите
  окно «Мастер
  функций – шаг 1 из 2»;

• выберите в окне
  «Категория»
  категорию
  «Математические»;

• в окне «Функция»
  выберите
  функцию
  СУММПРОИЗВ;

• в появившемся
  окне «СУММПРОИЗВ»
  в строку «Массив 1»
  введите выражение B$3:E$3,
  а в строку «Массив 2»
  – выражение B6:E6
  (рис.1.3);

• после ввода ячеек
  в строки «Массив 1»
  и «Массив 2»
  в окне «СУММПРОИЗВ»
  появятся числовые значения введенных
  массивов (см. рис.1.3), а в экранной
  форме в ячейке F6
  появится текущее значение, вычисленное
  по введенной формуле, то есть 0 (так как
  в момент ввода формулы значения
  переменных задачи нулевые).

Рис.1.3. Ввод формулы
для расчета ЦФ в окно «Мастер
функций»

Зависимости
для левых частей ограничений

Левые
части ограничений задачи (1.1) представляют
собой сумму
произведений
каждой из ячеек, отведенных для значений
переменных задачи (B3,
C3, D3, E3), на
соответствующую ячейку, отведенную для
коэффициентов конкретного ограничения
(B10, C10, D10, E10
– 1-е
ограничение;
B11, C11, D11, E11 –
2-е ограничение и B12,
C12, D12, E12 – 3-е
ограничение). Формулы, соответствующие
левым частям ограничений, представлены
в табл.1.1.

Таблица
1.1 — Формулы,
описывающие ограничения модели (1.1)

Левая часть ограничения	Формула Excel
или	=СУММПРОИЗВ(B$3:E$3;B10:E10)
или	=СУММПРОИЗВ(B$3:E$3;B11:E11)
или	=СУММПРОИЗВ(B$3:E$3;B12:E12)

Как видно из
табл.1.1, формулы, задающие левые части
ограничений задачи (1.1), отличаются друг
от друга и от формулы (1.4) в целевой ячейке
F6
только номером строки во втором массиве.
Этот номер определяется той строкой, в
которой ограничение записано в экранной
форме. Поэтому для задания зависимостей
для левых частей ограничений достаточно
скопировать формулу из целевой ячейки
в ячейки левых частей ограничений. Для
этого необходимо:

• поместить курсор
  в поле целевой ячейки F6
  и скопировать в буфер содержимое ячейки
  F6
  (клавишами «Ctrl-Insert»);

• помещать курсор
  поочередно в поля левой части каждого
  из ограничений, то есть в F10,
  F11 и
  F12, и вставлять
  в эти поля содержимое буфера (клавишами
  «Shift-Insert»)
  (при этом номер ячеек во втором массиве
  формулы будет меняться на номер той
  строки, в которую была произведена
  вставка из буфера);

• на экране в полях
  F10,
  F11 и F12
  появится 0 (нулевое значение) (см.
  рис.1.2).