Интегрированное занятие по биологии и
информационным технологиям “Изучение
статистических закономерностей живой природы
средствами MS Excel”. Занятие проводят 3 педагога
(практическую часть ведут преподаватели
информатики по подгруппам).
Задачи урока
Образовательные:
- расширить знания студентов о причинах,
свойствах и значении изменчивости на примере
ненаследственной изменчивости; о практическом
применении программы Excel. - сформировать умения и навыки работы в программе
Excel:- с данными типа Список на примере Сортировки;
- элементами автоматизации вычислений с
использованием статистических функций (max, min,
срзнач, счетесли); - с диаграммами и графиками;
- применительно к популяционно-статистическому
методу в генетических исследованиях.
Развивающие: продолжить формирование
умений:
- сравнивать на примере сравнения форм
изменчивости; - устанавливать причинно-следственные связи и
делать выводы на основе графического
представления зависимости между значением и
частотой встречаемости вариант.
Воспитательные:
- способствовать формированию научного
мировоззрения на основе познаваемости и
общности законов живой природы; - способности самостоятельно выполнять задания и
нести ответственность за результаты своего
труда.
Оборудование: персональный компьютер,
мультимедиа проектор, тексты индивидуальных
заданий, электронный шаблон для выполнения
отчета о проведенной работе.
Тип урока по основной образовательной
цели: урок изучения нового материала и
закрепление умений прикладного использования
программы MS Excel.
План урока.
1. Организационный этап.
2. Этап подготовки учащихся к активному и
сознательному усвоению новых знаний.
Электронная таблица – самая распространенная
и мощная технология для работы с числовыми
данными. Главное достоинство электронной
таблицы – возможность мгновенного
автоматического пересчета всех данных,
связанных формульными зависимостями, при
изменении значения любого компонента таблицы.
Excel в переводе с английского означает
“превосходить”.
В Excel вычислительные возможности объединены с
богатым набором функций, присущих текстовому,
графическому редакторам и другим приложениям
пакета Microsoft Office.
Табличный процессор Excel позволяет:
- Решать математические задачи: выполнять
табличные вычисления (в том числе как обычный
калькулятор), вычислять значения и исследовать функции,
строить графики функций (например: sin(х), cos(х), tg(х)
и др. ). - Проводить статистический анализ.
- Реализовывать функции базы данных – ввод,
поиск, сортировку. - Наглядно представлять данные в виде диаграмм
и графиков.
Беседа по вопросам и заданиям.
Какой раздел общей биологии мы изучаем?
Какие свойства организма являются предметом
изучения науки генетики?
Дайте определение наследственности и
изменчивости.
Как взаимосвязаны между собой эти свойства
организма?
(фенотип = генотип + условия внешней среды)
Какие две формы изменчивости вам известны?
3. Этап усвоения, закрепления и коррекции
знаний.
3. 1 Формулировка задач урока (слайд Приложение 1)
3. 2 Сообщение плана работы (слайд)
3. 3. Сущность, причины, значение
ненаследственной изменчивости (слайды).
Каждый организм развивается и обитает в
определенных внешних условиях и испытывает на
себе действие факторов внешней среды: колебаний
температуры, освещенности, влажности, количества
и качества пищи, вступает во взаимоотношения с
другими организмами. Все эти факторы могут
изменять морфологические и физиологические
свойства организма, то есть его фенотип. Поэтому
такую изменчивость называют фенотипической.
Причина: изменение условий среды, в результате
чего организм изменяется в пределах нормы
реакции, заданной генотипом.
Значение: адаптация – приспособление к данным
условиям среды, выживание, сохранение потомства.
Примеры: белокочанная капуста в условиях
жаркого климата не образует кочана. Породы
лошадей и коров, завезенных в горы, становятся
низкорослыми.
3.4 Свойства фенотипической изменчивости.
1. Ненаследуемость. (слайд)
У гималайского кролика наблюдается
неравномерное окрашивание шерсти:
темноокрашенны уши, лапы, хвост, остальная шерсть
– белая. Если у такого кролика выщипать шерсть на
спине и положить холодную повязку – на этом
месте вырастет черная шерсть. Если черную шерсть
удалить и наложить тёплую повязку – вырастет
вновь белая шерсть. При выращивании кроликов при
температуре 30 градусов вся шерсть будет белая. У
потомства двух таких белых кроликов, выращенного
в нормальных условиях будет обычное
распределение пигмента.
Вывод: изменения признаков, вызванные
действием факторов внешней среды, не
наследуются.
2. Групповой характер изменений. (Слайд)
Листья одного и того же растения могут иметь
разную форму листьев в зависимости от того, в
какой среде они находятся – в водной или
воздушной. У всех стрелолистов в воде будут
длинные тонкие листья, а у водяного лютика –
изрезанные. Также под воздействием
ультрафиолетовых лучей у всех людей возникает
загар – накопление в клетках кожи пигмента
меланина, хотя и в неодинаковой степени
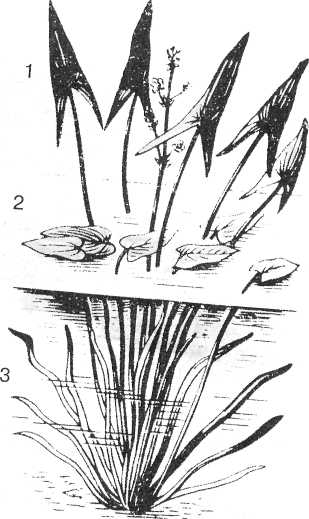
Стрелолист |
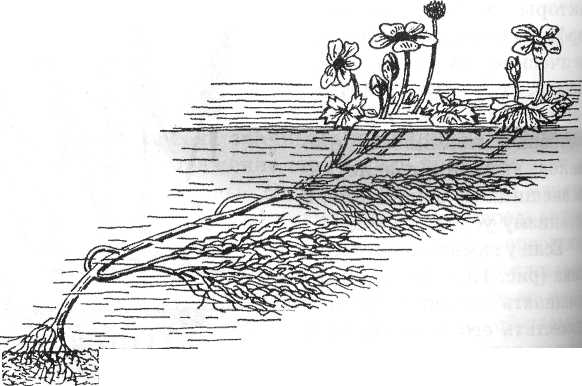
Водяной лютик |
Вывод: действие определенного фактора внешней
среды у каждого вида организмов вызывает
специфическую реакцию в виде изменения признака,
сходную у всех особей данного вида.
3. Обусловленность пределов изменчивости
генотипом, то есть хотя направленность изменений
и одинакова, степень выраженности изменения у
разных организмов различна. Степень
варьирования признака или пределы
модификационной изменчивости от минимального до
максимального значения признака называют нормой
реакции. Широта нормы реакции, то есть
разница между максимальным и минимальным
значением признака зависит от генотипа и
важности признака в жизнедеятельности
организма. Узкая норма реакции у таких признаков
как размеры сердца, головного мозга; у растений –
форма и размеры цветка. Широкая норма реакции у
таких признаков как количество жира в организме
млекопитающих, размеры листьев у растений ит. д.
3.5 Задания на закрепление.
1. Этот вид изменчивости имеет несколько
названий: ненаследственная,
модификационная, фенотипическая, определенная,
групповая. Объясните данные названия.
(Содержание ответа: возникает под влиянием,
какого либо фактора среды, действующего
одинаково на все особи сорта или породы и
изменяющего в определенном направлении; групповой
потому, что изменения происходят у всех
особей потомства в одном направлении
вследствие определенных условий (изменения
роста при изменении количества и качества пищи,
толщины кожи и густоты шерстного покрова от
изменения климата); ненаследственная, то есть у
потомков измененной группы при воздействии на
них других условий среды приобретенные
родителями признаки не наследуются;
изменения происходят в признаках, то есть в
фенотипе; особи группы имеют разные
значения одного признака, то есть модификации).
2. Дайте сравнительную характеристику
наследственной и ненаследственной изменчивости
по плану:
— объект изменения;
— подверженность изменениям хромосом, молекул
ДНК;
— возможность передачи изменений следующим
поколениям;
— значение для отдельной особи, вида;
— роль в эволюции.
Содержание ответа:
| Наследственная изменчивость | Ненаследственная изменчивость |
| Объектом изменения является генотип | Объектом изменения является фенотип в пределах нормы реакции. |
| Хромосомы изменяются в случае хромосомной мутации, а гены – при генной мутации. |
Хромосомы и гены не подвергаются изменениям. |
| Изменения передаются следующим поколениям |
Не наследуются |
| Полезные изменения приводят к победе в борьбе за существование отдельной особи, вредные – к гибели; может привести к появлению новых популяций, подвидов. |
Повышает или понижает продуктивность, жизнеспособность, способствует адаптации особей и выживанию вида. |
| Является материалом для естественного отбора. |
Приводит к приспособлениям организмов к конкретным условиям среды. |
3.6 Популяционно-статистические методы в
изучении ненаследственной изменчивости.
Для выявления нормы реакции организмов на
воздействие определенного признака используют
популяционно-статистический метод генетических
исследований, который заключается в:
— определении единичного значения признака (варианты
проявления признака) у каждого организма
выбранной группы;
— определении частоты встречаемости каждой
варианты;
— построении вариационного ряда,
отражающего постепенное увеличение значения
признака от минимального значения к
максимальному значению;
— построении вариационной кривой –
графической зависимости между значением вариант
и частотой их встречаемости;
— определении среднего значения признака и
нормы реакции генотипа на изменение окружающей
среды;
— выявлении полученных закономерностей.
Для проведения популяционно-статистических
исследований ненаследственной изменчивости
возможно использование компьютерной программы
Excel. И сейчас вам необходимо будет выполнить
задание с использованием этой программы.
3.7 Теоретический материал по дисциплине
“Информатика” (Приложение
2).
Типы данных в ячейках электронной таблицы
Ячейки рабочего листа электронной таблицы
могут содержать:
- исходные или первичные данные – константы;
- производные данные, которые рассчитываются
с помощью формул и функций.
В обычном режиме работы табличного процессора
в ячейках с вычислительными (производными)
данными отображаются значения, а формулы можно
увидеть лишь при активизации (выделении) ячейки в
строке ввода и редактирования.
Можно установить такой режим работы текстового
процессора, что в ячейках будут показываться (и
выводиться на печать) формулы, а не значения,
полученные в результате вычислений. Для этого
нужно использовать команду меню
СЕРВИС—>Параметры и в диалоговом окне
Параметры на вкладке Вид в поле Показывать
установить переключатель Формулы.
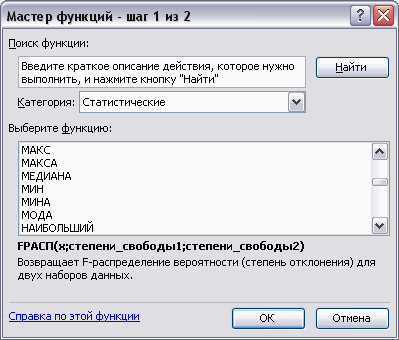
Категория функций Статистические
К уже известным типам данных (текст, число,
формула, дата) необходимо добавить функцию.
Функция представляет собой программу с
уникальным именем, для которой пользователь
должен задать конкретные значения аргументов.
Имена функций можно набирать на любом регистре –
верхнем или нижнем. После правильного ввода
функций буквы автоматически преобразовываются в
прописные. Для облегчения работы с встроенными
функциями используется Мастер функций.
Рисунок 1 Примеры статистических функций
Средства Excel для работы с данными
списка
Электронная таблица, все строки которой
содержат однородную информацию, рассматривается
как список или база данных.
К данным, организованным в виде списка (базы
данных), можно выполнять следующие операции:
— добавлять, изменять и удалять записи;
— находить записи;
— сортировать записи.
Сортировка данных
Для использования некоторых операций
автоматической обработки данных часто бывает
необходимо заранее расположить данные в таблице
(списке) в строго определенной
последовательности – выполнить сортировку
исходных данных.
Сортировка осуществляется “на месте” —
непосредственно в таблице.
В электронной таблице можно сортировать как
строки, так и столбцы. Строки можно отсортировать
по значениям ячеек одного столбца или
нескольких.
Строки, столбцы ли отдельные ячейки в процессе
сортировки переупорядочиваются в соответствии с
заданным пользователем порядком сортировки.
Списки можно сортировать в возрастающем порядке
(от 1 до 9, от А до Я) или в убывающем порядке (от 9 до
1, от Я до А).
По умолчанию Excel сортирует данные в алфавитном
порядке. Для сортировки в другом порядке,
например чтобы расположить месяцы дни недели в
соответствии с логическим, а не алфавитным
порядком, следует использовать пользовательский
порядок сортировки.
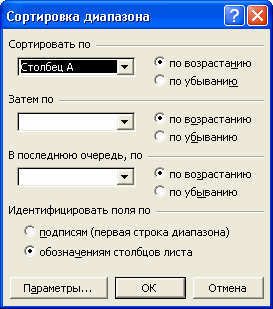
Сортировка данных в электронных таблицах
производится с помощью команд меню ДАННЫЕ >
Сортировка или с помощью кнопок на Стандартной
панели инструментов.
Рисунок 2 Пример сортировки данных
Построение диаграмм и графиков
Диаграмма представляет собой вставной объект,
внедренный на один из листов рабочей книги.
Диаграмма сохраняет связь с данными, на основе
которых она построена, и при обновлении этих
данных немедленно изменяет свой вид. Для
построения диаграммы обычно используется Мастер
диаграмм, запускаемый щелчком по кнопке Мастер
диаграмм на стандартной панели инструментов.
Работа мастера включает 4 шага.
Тип диаграммы. На первом этапе работы мастера
выбирают форму диаграммы. Доступные формы
перечислены в списке Тип на вкладке Стандартные.
Для выбранного типа диаграммы справа
указывается несколько вариантов представления
данных, из которых необходимо выбрать наиболее
подходящий.
Выбор данных. Второй этап работы мастера
служит для выбора данных в окне Источник данных
диаграммы, по которым будет строиться диаграмма.
Если диапазон данных был выбран заранее, то в
области предварительного просмотра окна мастера
появится приблизительное отображение будущей
диаграммы. Если данные образуют единый
прямоугольный диапазон, то их удобно выбирать
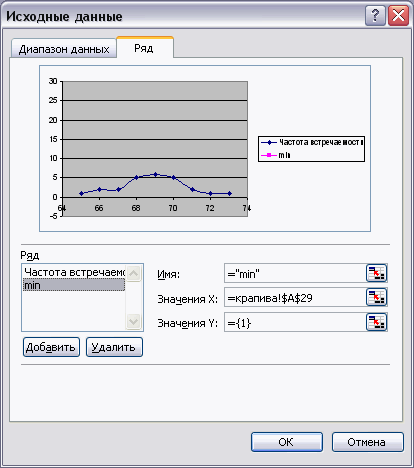
при помощи вкладки Диапазон данных. Если данные
не образуют единой группы, то информацию для
отдельных рядов задают на вкладке Ряд.
Рисунок 3 Пример добавления ряда в область
диаграммы
Оформление диаграммы. Третий этап работы
мастера (диалоговое окно Параметры диаграммы)
состоит в выборе оформления диаграммы. На
вкладках окна мастера задаются:
- название диаграммы, подписи осей (вкладка
Заголовки); - отображение и маркировка осей координат
(вкладка Оси); - описание построенных графиков (вкладка
Легенда); - отображение надписей, соответствующих
отдельным элементам данным на графике (вкладка
Подписи данных).
В зависимости от типа диаграммы некоторые из
перечисленных вкладок могут отсутствовать.
Размещение диаграммы. На последнем этапе
работы мастера указывается, следует ли
использовать для размещения диаграммы новый
рабочий лист или использовать один из имеющихся.
Обычно этот выбор важен только для последующей
печати документа, содержащего диаграмму.
3.8 Задания на закрепление в программе MS Excel в
проведении биологических исследований.
Цель практической части занятия: закрепить
умения прикладного использования программы MS Excel
на примере биологических исследований (Приложение 3).
4. Домашнее задание:
по биологии – стр. 148-151,ответить на контрольные
вопросы;
по информатике – отчет по лабораторной работе.
Пример выполненной работы
(Приложение 4)
Скачать материал

Скачать материал


- Сейчас обучается 616 человек из 76 регионов


- Сейчас обучается 82 человека из 37 регионов


- Сейчас обучается 122 человека из 48 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Решение задач
по информатике с биологической составляющей
Моделирование в Excel
Интегрированный урок биологии и информатики
в 9 ХБ классе
понедельник, 20 июня 2022 г.
МКОУ «Лицей №2» г. Нальчик, кафедра информатики и ИКТ. Учитель информатики Мащенко М.В. -
2 слайд
ДНК – это полимерная молекула состоящая из 2х комплементарных полинуклеотидных цепей соединенными водородными связями, имеют большие размеры и громадную молекулярную массу.
Структура молекулы ДНК
Расстояние между азотистыми основаниями = 0,34 нм -
3 слайд
Пиримидиновые основания являются производными пиримидина, а пуриновые основания – пурина.
В нуклеиновых кислотах встречаются
5 основных видов азотистых оснований:К пуриновым относятся:
К пиримидиновым относятся:
-
4 слайд
Правила Чаргаффа:
1. Сумма пуриновых нуклеотидов = сумме пиримидиновых нуклеотидов.2. Молярное содержание аденинов = молярному содержанию тиминов и их отношение =1.
3. Количество аденина = количеству цитозина, а количество гуанина = количеству тимина, сумма аденина и цитозина = сумме гуанина и тимина.
4. В ДНК из различных источников наблюдается не одинаковое соотношение нуклеотидов.
У одних видов преобладает .
Такую ДНК называют ДНК АТ типа ДНК ГЦ типаПур = Пир
А + Г = Т + ЦА + Ц = Т + Г
А + Т > Г + Ц -
-
6 слайд
Задача
1). По принципу комплементарности строим левую цепь ДНК:
правая цепь Г-Г-Г-Ц-А-Т-А-А-Ц-Г-Ц-Т- …
левая цепь Ц-Ц-Ц-Г-Т-А-Т-Т-Г-Ц-Г-А- …
2). Так как молекула ДНК двухцепочная, следовательно, ее длина равна длине одной цепи.
Один нуклеотид занимает в молекуле ДНК 0,34 нм. Отсюда длина данного фрагмента:
0,34 нм * 12 = 4,08 нмФрагмент правой цепи ДНК имеет следующий нуклеотидный состав: ГГГЦАТААЦГЦТ… Определите порядок чередования нуклеотидов в, левой цепи. Какова длина данного фрагмента молекулы ДНК? Определите процент содержания каждого нуклеотида в данном фрагменте.
3). Всего в данном фрагменте молекулы ДНК будет 24 нуклеотида.
Из них А = 5, или 20,8%
По правилу Чаргаффа А + Г = А+Ц, А = Т, Г=Ц
Тогда Т = 5 — 20,8%
Г + Ц = 24 — 10=14;
Г = Ц = 7, или 29,2%
Ответ: А = 20,8%; Т = 20,8%;
Г = 29,2%; Ц = 29,2%.Решение
ПОМНИТЕ!
Задача -
7 слайд
Задача дополненная вопросом
Дано:
Pa=Pт=20,8%
Pг=Рц=29,2% по данным и решению
Ка=Кт=5 биологической задачи
Кг=Кц=7
Найти: I-?Определить информационный объем данного фрагмента цепи ДНК?
Формулы для решения
P=1/N
N=2i
I=K*i
Решение информационной задачиPа=Рт=1/N →Nat=1/0,208~4,8
iat= 2,27 бит содержит сообщение о выпадении А или Т
Pг= Рц = 1/N→Ngc = 1/0,292~3,4
igc= 1,78 бит содержит сообщение о выпадении Г или Ц
Iа = Iт = 5* 2,27 = 11,35 бит
Iг = Iц = 7* 1,78 = 12,46 бит
I = 2 * (Iа + Iг) =2*(11,35 +12,46)=47,62
Ответ: 47,62 БИТ -
8 слайд
Что мыслимо — то возможно,
что возможно — то мыслимо.Г. Лейбниц
-
9 слайд
Сначала неизбежно идут:
мысль, фантазия, сказка.
За ними шествует научный расчет.
И уже, в конце концов,
исполнение венчает мысль.К. Э. Циолковский
-
10 слайд
Недостаточно знания,
необходимо также применение;
недостаточно хотеть,
надо и делать.И. Гёте
-
11 слайд
Практикум
Моделируем
в EXCELпонедельник, 20 июня 2022 г.
-
12 слайд
=ЕСЛИ(Адрес ячейки с данными=»значение1″;»значение2″;ЕСЛИ Адрес ячейки с данными=»значение1″;»значение2″; ЕСЛИ(Адрес ячейки с данными=»значение3″;»значение4″; «значение5»; и т.д. )))
Задание 1 -
13 слайд
АЗОТИСТЫЕ ОСНОВАНИЯ В НУКЛЕИНОВЫХ КИСЛОТАХ
2
3
5
6
7
1
4
Задание 2 -
14 слайд
ДНК: модель из бумаги
М
О
Д
Е
Л
И
Р
О
В
А
Н
И
Е
Задание3
-
15 слайд
Начало — половина целого
Пифагор
То, что мы знаем, — ограниченно,
а то, чего мы не знаем, — бесконечно.
П. Лаплас
Краткое описание документа:
класс 9
предмет Информатика
Презентация к интегрированному уроку информатики и биологии в 9 классе.
Рассматривается генетический код и находится информационный объем фрагмента цепи ДНК, в практической части предлагается рассмотреть, построить в Excel 5 основных видов азотных соединений и моделирование ДНК: модель из бумаги.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 210 479 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
-
Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
Другие материалы




- 05.09.2018
- 266
- 0




Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс профессиональной переподготовки «Информационные технологии в профессиональной деятельности: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Современные тенденции цифровизации образования»
Разработала Демержеева Т.В.
«Решение задач в Excel»
Открытый интегрированный урок информатики,
биологии, экологии
в 9 классе.
Цель:
- Показать учащимся разнообразие применения электронных таблиц Excel в решении нестандартных задач из таких областей человеческой деятельности как криминалистика, астрономия, астрология, биология, экология, экономика и др.
- Развивать у учащихся познавательный интерес.
- Воспитывать интерес к предмету.
Ход урока.
- Организационный момент.
Здравствуйте, ребята!
Помните, в начале изучения программы Excel, мы говорили о том, что эта программа позволяет решать задачи самого разного характера? Сегодняшний урок мы посвятим тому, чтобы отчасти доказать это и показать насколько широка область применения электронных таблиц. Основная цель урока — показать учащимся разнообразие применения электронных таблиц Excel в решении нестандартных задач из таких областей человеческой деятельности как криминалистика, астрономия, астрология, биология, экология, экономика и др.
Но в начале этой серьезной работы мы немного «разомнемся» и освежим в памяти навыки работы с электронными таблицами.
- Задание 1.
- Из чего состоит адрес клетки электронной таблицы?
- Сколько клеток входит в диапазон А5 : D8?
- Какие данные можно занести в клетку электронной таблицы?
- Запишите числовую константу 300 000 в экспоненциальном формате.
- Дан фрагмент ЭТ в режиме отображения формул:
|
А |
В |
|
|
1 |
1 |
5 |
|
2 |
=$A$1+2 |
=2*$B1 |
|
3 |
Какие формулы будут отображены в клетках А3 и В3, если в клетку А3 скопирована клетка В2, а в клетку В3 – клетка А2?
- Задание 2.
Для начала я предлагаю вам окунуться в такую науку как астрономия и решить следующую простую задачу:
Задача №1. Определите, пожалуйста, сколько земных дней длится год на других планетах Солнечной системы, если он составляет:
На компьютере, подключенном к проектору задачу решает один ученик.
- Задание 2.
Сейчас я предлагаю вам окунуться в такую науку как биология и решить следующую задачу. На компьютере, подключенном к проектору, задачу решает один ученик (просмотр презентации, с решением подзадач).
Задача №2. Ученые установили, что прирост какого-либо вида живых организмов за счет рождаемости прямо пропорционален их количеству, а убыль за счет смертности прямо пропорциональна квадрату их количества. Этот закон известен под названием закона Мальтуса.
Пусть в одном хозяйстве собираются разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчеты. Согласно закону Мальтуса, изменение числа рыб за один год вычисляется по формуле N=kN-qN2.
Здесь N – число карпов в начале года, k — коэффициент прироста, q- коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоема, наличие корма) k=1, q=0,001.
Вывести формулу математической модели процесса размножения рыб в водоеме. Провести компьютерный вычислительный эксперимент.
- Задание №3.
Ну а теперь, ребята, давайте попробуем стать на какое-то время экспертами-криминалистами. Каким бы странным не выглядело это предложение, но и в этой области человеческой деятельности возможно применение электронных таблиц. Итак, послушайте задание:На месте совершения преступления обнаружен след от обуви. Из протокола допроса свидетеля (показания бабушки 75 лет)
«… ой, милок, какой он рассказать точно не смогу. Хотя, запомнила, что он человек молодой и лет ему 26-28, не больше… Рост, ну не знаю, для меня уж очень большой … «.
Подтвердите показания свидетеля и предоставьте следователю как можно больше информации о человеке, совершившем преступление.
Примечание: По следу (отпечатку обуви) можно узнать: рост человека; определить длину шага; создать модель человека. Если известен примерный возраст, то рассчитать идеальную массу.
Я вам сейчас раздам образцы следов преступников, а вы попробуйте определить их основные параметры и помочь следствию.
Учащиеся решают задачи по полученным отпечаткам.
- Задание №4.
Сейчас я предлагаю вам окунуться в такую науку как тригонометрия и решить следующие задачи. (Один ученик решает, с демонстрацией на экране, а остальная группа по индивидуальным карточкам).
На отрезке [1,5; 2,5] c шагом 0,1 протабулировать функцию:
COS(2х)-SIN2(3х)+ и построить ее график.
Задание №5.
В кооперативе работают 10 рабочих. Собирают помидоры. Оплата производится по количеству собранных овощей, дневная норма сбора составляет N кг. Сбор 1 кг помидоров стоит M рублей. Сбор каждого килограмма сверх нормы оплачивается в 3 раза дороже. Сколько денег в день получит каждый рабочий за собранный урожай? (Один ученик решает, с демонстрацией на экране, а остальная группа по индивидуальным карточкам).
После окончания работы, представители от групп учащихся выходят к доске и отчитываются по проделанной работе, сравнивают полученные результаты (графики и диаграммы печатаются на принтере перед отчетом).
Домашнее задание.
Турист проплыл на байдарке за первый час 15 км. За каждый следующий час он проплывал на полкилометра меньше, чем за предыдущий. Сколько времени он потратил на путь, равный 127,5 км? Разработать модель решения задачи.
МБОУ Сосновская средняя школа № 1
Использование процессора электронных таблиц
Excel на уроке биологии
Материал подготовлен
учителем биологии
И.Ю. Тюриной
п. Сосновское
2019
Информационные и коммуникационные технологии
(ИКТ), поглубже химии простершие руки свои в
дела человеческие (по выражению Д.И. Менделе-
ева), вынуждают каждого учителя понять, принять,
оценить и применить их компоненты в повседнев-
ной урочной практике. Этот путь неповторим – и
обусловлен именно необходимостью авторизации
каждым учителем преподаваемого курса, перево-
да с абстрактного языка учебника в конкретный
мир ощущений и действий обучаемых, для которых
виртуальный мир компьютерных программ уже
стал не менее реальным, чем предметный и соци-
альный .
Тут уместно воспеть дифирамб нашему предмету:
биология – поистине уникальный предмет в плане
формирования многообразных общеучебных уме-
ний, жизненных компетенций и других слагаемых
информационной культуры. Ведь курс биологии
(и поддерживающие его задания и упражнения)
включает самые разные задания по работе с текс-
тами, математические (и физические, химические)
расчетные задачи, организацию визуальных рядов
и восприятие трехмерных моделей, что открывает
уникальные возможности сочетания заданий для
аудиалов, визуалов и кинестетиков, выполняющих
лабораторную или практическую работу в одной
группе. Кроме того, курс биологии включает ряд
специфических задач, не представленных в дру-
гих предметах: кодирование белков нуклеиновыми
кислотами (и общие свойства кодов), определители
разных типов, генетические задачи и многое другое.
Причем в большинстве случаев ИКТ не искусствен-
но привлекаются как дань моде, а вполне оправданы
решаемыми прикладными задачами, касающимися
непосредственно самого человека: будь то родос-
ловные, молекулы или пищевые рационы.
Математические задачи в курсе биологии тесно связаны с важнейшими жизненными компетенциями, связанными с размерами и мерами, представлением данных и их пониманием, а также границами применимости математических моделей.
Процессор электронных таблиц Microsoft Excel является мощным инструментом работы с числовыми данными, и использование его возможностей в разных задачах преподавания биологии достаточно широко: от расчетов и представления значений в виде диаграмм и графиков до математического моделирования, например, динамики популяций по уравнению Лотки-Вольтерры. Кроме того, они являются важным вступлением в более широкий класс программ математического моделирования сложных процессов и явлений (и соответствующих специализированных компьютерных программ), например, динамики изменения климата на земле или моделирования нервного импульса.
Использование процессора электронных таблиц
Excel на уроке связано с возможностями матема-
тического моделирования процессов и явлений, с
которыми полезно работать в классах с углублен-
ным изучением биологии и химии и/или матема-
тики. Важно отметить, что Excel позволяет перейти
от демонстрации закономерности (зависимости,
функции) к ее исследованию. И именно это ставит
очень сложные задачи перед учителем: мало зара-
нее знать ответ, нужно организовать деятельность
по поиску решений, а это уже больше менеджерские
функции, чем лекторские.
Рассмотрим эти изменения в содержании, мето-
дике и формах деятельности на примере лаборатор-
ной работы по изучению модификационной измен-
чивости с построением вариационного ряда и ва-
риационной кривой. Как изменится эта достаточно
рутинная задача, в основе которой – весьма важные
как в научном, так и в житейском плане понятии?
В аналоговом варианте львиную долю времени
занимает непосредственно само измерение и за-
полнение вариационного ряда – подсчет количест-
ва объектов в каждом из классов значений. Лимит
времени на уроке обычно ограничивает количество
объектов, что может отрицательно сказаться на ито-
говом виде вариационной кривой. Подсчет же боль-
шого количества объектов по классам требует большого внимания.
Выполнение лабораторной работы в Excel изме-
няет содержание работы. За счет снятия рутинных
операций можно поговорить о понятиях моды, ме-
дианы и среднего, среднего квадратичного откло-
нения, и дисперсии (их расчет можно показать в
заготовленном заранее файле Excel), а также обсу-
дить биологический смысл дисперсии и житейский
смысл различий в терминах, их использование для
манипуляций (на примере из книги выдающегося по-
пуляризатора математики Мартина Гарднера (пере-
сказано по Гарднер, 1984):
«Фирма «Гисмо продактс» владеет небольшой
фабрикой по производству супергисмо. В правле-
ние фирмы входят сам мистер Гисмо (заработок
4800 долл. в неделю), его брат (2000 долл.) и 6 родст-
венников (по 500 долл.). Рабочая сила состоит из
5 бригадиров (по 400 долл.) и 10 рабочих (по 200 долл.
в неделю). При приеме нового работника ему сооб-
щают, что средняя зарплата в фирме составляет 600
долл. в неделю. Через некоторое время сотрудник
приходит к боссу, т.к., поговорив с рабочими, уз-
нал, что их зарплата не превышает 200 долл. Тут-тои выясняется разница между средними значениями
(средним арифметическим: отношением суммы всех
заработков – 13 800 долл., к количеству сотрудни-
ков – 23 человека), медианой (400 долл. – значение,
расположенное посередине ряда всех зарплат) и мо-
дой («типичным случаем», наиболее часто встречаю-
щимся значением, равным, как убедился работник,
200 долл. в неделю).
Мода, медиана и среднее в случаях с нормальным
распределением случайных величин на больших вы-
борках будут приближаться друг к другу, а то и сов-
падать. Но там, где распределение не случайно (как
в примере с зарплатой), они могут весьма и весьма
различаться
А теперь вернёмся к задачам лабораторной работы, пос-
вященной модификационной изменчивости. Как
уже говорилось, выполнение работы в Excel позво-
лит решать не столько расчетные, сколько аналити-
ческие задачи. Рассмотрим на примере задачи.
Задача № 1
Количество щенков в помёте 70 серебристо — черных лисиц таково:
5, 4, 4, 4, 9, 3, 4, 4, 5,6, 6, 4, 5, 5, 4, 8, 4, 4, 5, 4, 4, 7, 3, 5, 5, 4, 3, 3, 3, 6, 4, 4, 5, 4, 4, 5, 5, 4, 6, 3, 4, 4, 3, 4, 4, 7, 4, 3, 5, 2, 5, 4, 7, 3, 2, 3, 1, 5, 4, 2, 6, 6, 4, 4, 6, 4, 8, 3, 5, 4.
Постройте вариационный ряд и вариационную кривую, найдите среднее значение, моду, и медиану. Рассчитайте среднее квадратичное отклонение.
1. Перенести данные в электронную таблицу
Excel . Если условие задачи приведено на
карточке, придется вводить вручную: удобно, если
работает пара учеников, один диктует, другой вно-
сит данные. Но можно и сэкономить время и подго-
товить файл (файлы с вариантами) заранее.
2. Построение вариационного ряда. Справа от
столбца со значениями (вариантами) строится ва-
риационный ряд, состоящий из двух строк: классы
(значения, которые принимает признак, в данном
случае – количество щенков, от 1 до 9), количество
объектов в каждом классе. Названия рядов таблицы
также желательно записать, например «Классы» в
ячейке С1, а «Количество» – в ячейке С2.
3. Подсчет количества объектов в каждом классе. Его можно выполнить вручную, а чтобы из-
бежать ошибок, можно ячейки каждого из классов
заливать своим цветом .
Можно процесс подсчета количества объектов в
каждом классе существенно упростить. Для этого
нужно выделить столбец со значениями и провести
сортировку по возрастанию (Данные – Сортиров-
ка ) После этого надо выделить классы (заливкой вы-
деленных ячеек, цветом шрифта или рамкой , причем в каждом из
случаев можно выбирать цвет или тип рамки в выпа-
дающих списках, появляющихся при нажатии на тре-
угольник справа от иконки. Теперь подсчитать будет
значительно проще. Останется внести значения ко-
личества объектов в каждом из классов в соответс-
твующие ячейки вариационного ряда. Не забудьте
порекомендовать провести проверку: посчитать об-
щее количество объектов (или просто посмотреть на
количество рядов со значениями) и сравнить с сум-
мой количества объектов по классам (можно посчи-
тать автосуммой: для этого выделить ячейку справа
от строки со значениями в вариационном ряде и
дважды нажать на знак Автосуммы .
4. Расчет среднего значения признака Х. Для
этого нужно сложить попарно произведения значе-
ния признака («Класс») на количество объектов в
классе («Количество») и полученную сумму разде-
лить на общее количество объектов. В ячейке С3 на-
бираем слово «Среднее», а в ячейку С4 записываем
формулу:
=(D2×D1+E2×E1+F2×F1+G2×G1+H2×H1+I2×I1+
+J2×J1+K2×K1+L2×L1)/M2 и нажимаем Enter.
Формулу можно вводить с клавиатуры (проверь-
те, чтобы была включена не русская, а английская
раскладка клавиатуры!), а можно вводить только
знаки арифметических действий, а ячейки указы-
вать при помощи мыши. Второй способ несравненно
удобнее, тем более что Excel вносит цветовую раз-
метку для разных ячеек, позволяющую визуально
контролировать процесс ввода формулы.
5. Расчет статистических характеристик
выборки при помощи функций. В Excel заложено
очень большое количество арифметических, статис-
тических, логических и т.п. функций, которые мож-
но использовать вместо формул. Например, чтобы
найти моду исследуемой выборки, надо в выбран-
ную ячейку вставить функцию. Это можно сделать
несколькими способами:
– Выбрать пункт меню Вставка – Функция и в
диалоговом окне Мастера функций найти нужную
(она входит в категорию статистических функций,
которую нужно выбрать в списке «Категории», и так
и называется – МОДА)5. На следующем шаге нужно
указать, к какому диапазону ячеек будет применена
функция: это можно сделать вручную, вводом диа-
пазона ячеек, или выделить нужный диапазон пря-
мо на листе и нажать ОК или [Enter].
– Впечатать в строке функций ее название и диа-
пазон =МОДА(А1:70) – или только =МОДА(), пос-
тавить курсор между скобками и при помощи мыши
выделить диапазон ячеек от А1 до А70.
Аналогично находим значения медианы =МЕ-
ДИАНА(А1:70); среднего =СРЗНАЧ(А1:70) – как
видим, для этого совершенно не обязательно было
вводить формулу (см. пункт 4) вручную, однако само-
умение составлять и вводить формулы самостоя-
тельно необходимо; и
среднее квадратичное (стандартное) отклонение
σ =СТАНДОТКЛОН(A1:70).
6. Построение вариационной кривой. Для этого
надо выделить на листе ячейки с представляемыми
значениями (D2:L2), и выбрать в меню програм-
мы Вставка – Диаграмма… или воспользоваться
кнопкой Мастер диаграмм на панели
инструментов. В Мастере диаграмм выбирается тип
диаграммы (лучше один из раздела График, но не
обязательно); на втором шаге можно, хотя здесь
это и не критично, указать «Значения по оси Х»,
выделив нужный диапазон ячеек (D1:L1); настраи-
ваются параметры диаграммы на шаге третьем (на-
пример, можно выбрать закладку Легенда и снять
«Добавить легенду») и сохранить диаграмму на этот
же лист рабочей книги.
Таким образом, время на выполнение лабораторной работы сокращается в 3 раза, обучающиеся применяют полученные знания на информатике на уроке биологии, прослеживаются межпредметные связи с экономикой, экологией, самостоятельно проводят исследование. К тому же, данное задание для сильных обучающихся можно усложнить, а именно закрасить области отклонения от среднего квадратичного в графическом редакторе Paint.
Чтобы успешно применять процессор электронных таблиц
Excel на уроке биологии, необходимо учителю освоить данную программу.
На это понадобиться терпение, время и самое главное желание. Но всё это
« окупиться», когда на Вас совершенно по другому посмотрят наши «современные» старшеклассники!
8
Биологические модели развития популяций
В биологии при исследовании развития биосистем строятся динамические модели изменения численности популяций различных живых существ (бактерий, рыб, зверей и т.д.) с учётом различных факторов.
Расчёт числа рыб в пруду с интервалом через год
Учёные установили, что прирост числа какого-либо вида живых организмов за счёт рождаемости прямо пропорционален их количеству, а убыль за счёт смертности прямо пропорциональна квадрату их количества. Этот закон известен под названием закона Мальтуса .
Задача.
В одном хозяйстве собираются разводить карпов. Прежде чем запускать мальков в пруд, решили провести расчёты. Согласно закону Мальтуса изменение числа рыб за один год вычисляется по формуле
∆ N=kN-qN 2 .
Здесь N — число карпов в начале года, k– коэффициент прироста, q – коэффициент смертности. Экспериментально установлено, что для данного вида рыб (карпы) и в данных условиях (состояние водоёма, наличие корма) k=1, q= 0,001.
Если первоначально в пруд запущено N 0 рыб, то из закона следует, что количество карпов через год будет таким:
N 1 = N 0 + (kN 0 – qN 0 2 ).
Через два года
N 2 = N 1 + (kN 1 – qN 1 2 )
и т.д. Можно написать общую формулу для вычисления количества рыб в i-том году после их запуска:
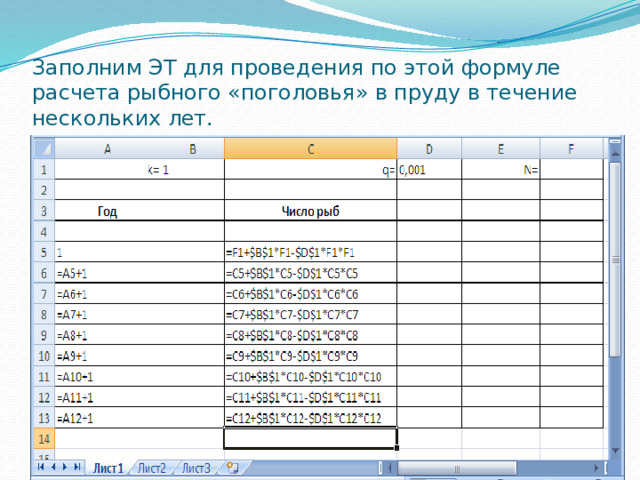
N i =N i-1 + (kN i-1 –qN i-1 2 ) для i= 1,2,3,…
Заполним ЭТ для проведения по этой формуле расчета рыбного «поголовья» в пруду в течение нескольких лет.
- Для получения результатов достаточно занести в ячейку F1 первоначальное число рыб.
- Из полученных результатов сделайте выводы.
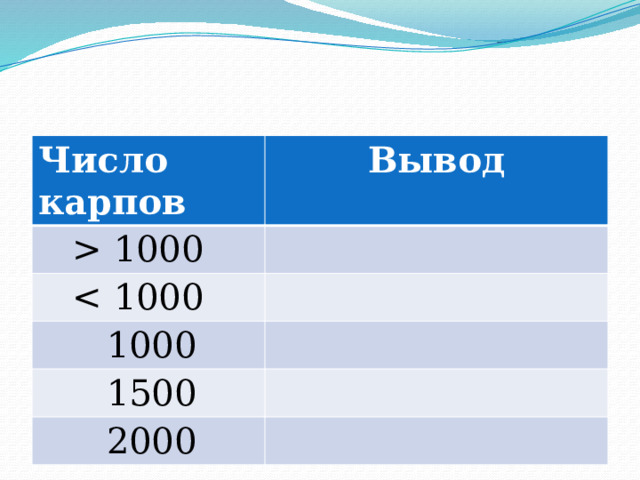
Число карпов
Вывод
1000
1000
1500
2000
Выводы:
- Невозможно иметь в пруду больше 1000 карпов.
- Если начальное число рыб меньше 1000, то оно постепенно будет расти до 1000 штук и далее не меняется.
- Если сразу запустить 1000 рыб, то это количество останется неизменным и в последующие годы.
- Если запустить сначала 1500 рыб, то через год их численность в два раза сократится, а затем все равно дойдёт до 1000.
- Если запустить в пруд 2000 рыб, то через год все они вымрут.