Тип урока: Обобщение, закрепление
пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического
способа решения уравнений; - закрепление навыков записи и
копирования формул, построения графиков
функций в электронных таблицах Excel 2007; - формирование и первичное закрепление
знаний о решении уравнений с
использованием возможностей электронных
таблиц Excel 2007; - формирование мышления, направленного на
выбор оптимального решения; - формирование информационной культуры
школьников.
Оборудование: персональные
компьютеры, мультимедиапроектор,
проекционный экран.
Материалы к уроку: презентация Power Point
на компьютере учителя (Приложение 1).
Ход урока
Организационный момент.
Слайд 1 из Приложения1 ( далее
ссылки на слайды идут без указания
Приложения1).
Объявление темы урока.
1. Устная работа (актуализация
знаний).
Слайд 2 — Соотнесите перечисленные
ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3)2; у = -(х — 4)2;
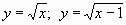
Рис. 1.
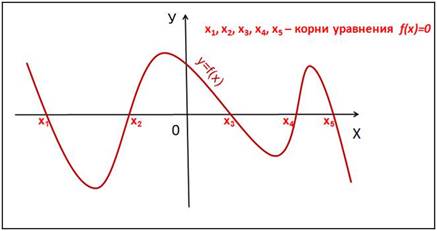
Слайд 3 Графический способ решения
уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются
значения х1, х2, … точек
пересечения графика функции y=f(x) с осью
абсцисс (Рис. 2).
Рис. 2.
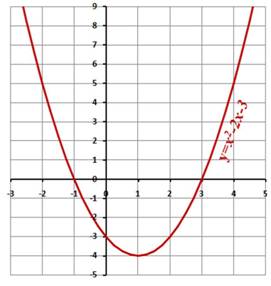
Слайд 4
Найдите корни уравнения х2-2х-3=0,
используя графический способ решения
уравнений (Рис.3).
Ответ: -1; 3.
Рис. 3.
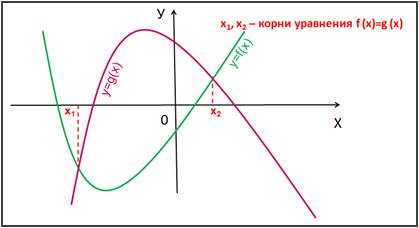
Слайд 5 Графический способ решения
уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются
значения х1, х2, … точек
пересечения графиков функций y=f(x) и у=g(x).
(Рис. 4):
Рис. 4.
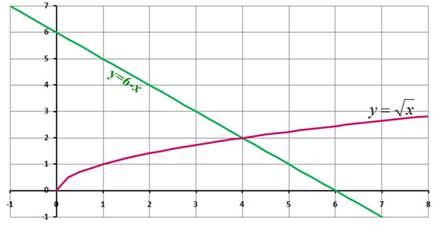
Слайд 6 Найдите корни уравнения 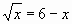
используя графический способ решения
уравнений (Рис. 5).
Ответ: 4.
Рис. 5.
2. Объяснение нового материала.
Практическая работа.
Решение уравнений графическим способом
требует больших временных затрат на
построение графиков функций и в
большинстве случаев дает грубо
приближенные решения. При использовании
электронных таблиц, в данном случае – Microsoft
Excel 2007, существенно экономится время на
построение графиков функций, и появляются
дополнительные возможности нахождения
корней уравнения с заданной точностью (метод
Подбор параметра).
I. Графический способ решения
уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в
Excel одновременно с учениками с подробными (при
необходимости) инструкциями и выводом
результатов на проекционный экран. Слайды
Приложения 1 используются для формулировки
задач и подведения промежуточных итогов.
Слайд 7
Пример1: Используя средства построения
диаграмм в Excel, решить графическим способом
уравнение —х2+5х-4=0.
Для этого: построить график функции у=-х2+5х-4
на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения
графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в
табличной форме (рис. 6):
Рис. 6.
Для этого:
- в ячейку А1 ввести текст Х, в
ячейку A2 — Y; - в ячейку В1 ввести число 0, в ячейку С1
– число 0,25; - выделить ячейки В1:С1, подвести
указатель мыши к маркеру выделения, и в
тот момент, когда указатель мыши примет
форму черного крестика, протянуть маркер
выделения вправо до ячейки V1 (Рис. 7).
Рис. 7.
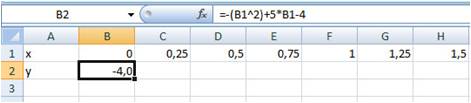
- в ячейку B2 ввести формулу =-(B1^2)+5*B1-4;
При вводе формулы можно
вводить адрес ячейки с клавиатуры (не
забыть переключиться на латиницу), а
можно просто щелкнуть мышью на ячейке с
нужным адресом.
После ввода формулы в ячейке
окажется результат вычисления по
формуле, а в поле ввода строки формул —
сама формула (Рис. 8):
Рис. 8.
- скопировать содержимое ячейки B2 в
ячейки C2:V2 за маркер выделения. Весь
ряд выделенных ячеек заполнится
содержимым первой ячейки. При этом ссылки
на ячейки в формулах изменятся
относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
Для этого:
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График
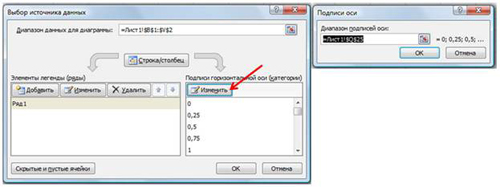
выбрать вид График; - на вкладке Конструктор|Выбрать данные
(Рис. 9) в открывшемся окне «Выбор
источника данных» щелкнуть по кнопке Изменить
в поле Подписи горизонтальной оси —
откроется окно «Подписи оси». Выделить в
таблице диапазон ячеек B1:V1 (значения
переменной х). В обоих окнах щелкнуть
по кнопкам ОК;
Рис. 9.
- на вкладке Макет|Оси|Основная
горизонтальная ось|Дополнительные
параметры основной горизонтальной оси
выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица
измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки
Тип
линии и Цвет линии);
- самостоятельно изменить ширину и цвет
линии для вертикальной оси; - на вкладке Макет|Сетка|Вертикальные
линии сетки по основной оси выбрать Основные
линии сетки.
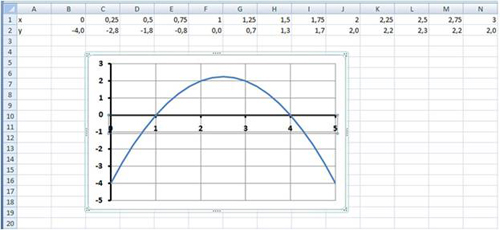
Примерный результат работы приведен на
рис. 10:
Рис. 10.
3 этап: Определение корней уравнения.
График функции у=-х2+5х-4
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня: х1=1; х2=4.
II. Графический способ решения уравнений
вида f(x)=g(x) в Excel.
Слайд 8
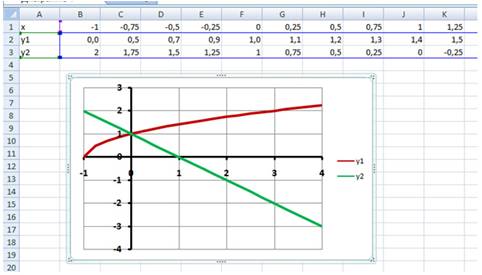
Пример 2: Решить графическим способом
уравнение 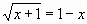
Для этого: в одной системе координат
построить графики функций у1=
и у2=1-х
на промежутке [ -1; 4 ] с шагом 0,25; найти значение х точки
пересечения графиков функций.
1 этап: Представление функций в
табличной форме (рис. 1):
- Перейти на Лист2.
- Аналогично Примеру 1, применив
приемы копирования, заполнить таблицу.
При табулировании функции у1=
воспользоваться встроенной функцией Корень
(Рис. 11).
Рис. 11.
2 этап: Построение диаграммы типа График.
- Выделить диапазон ячеек (А2:V3);
- Аналогично Примеру 1 вставить и
отформатировать диаграмму типа График,
выбрав дополнительно в настройках
горизонтальной оси: вертикальная ось
пересекает в категории с номером 5.
Примерный результат работы приведен на
Рис. 12:
Рис. 12.
3 этап: Определение корней уравнения.
Графики функций у1=
и у2=1-х пересекаются в одной
точке (0;1) и, следовательно, уравнение
имеет один корень – абсцисса этой точки: х=0.
III. Метод Подбор параметра.
Слайд 9
Графический способ решения уравнений
красив, но далеко не всегда точки
пересечения могут быть такими «хорошими»,
как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц
позволяют находить приближенные значения
коней уравнения с заданной точностью. Для
этого используется метод Подбор
параметра.
Слайд 10
Пример 3: Разберем метод Подбор
параметра на примере решения уравнения —х2+5х-3=0.
1 этап: Построение диаграммы типа График
для приближенного определения корней
уравнения.
Построить график функции у=—х2+5х-3,
отредактировав полученные в Примере 1
формулы.
Для этого:
- выполнить двойной щелчок по ячейке B2,
внести необходимые изменения; - с помощью маркера выделения
скопировать формулу во все ячейки
диапазона C2:V2.
Все изменения сразу отобразятся на
графике.
Примерный результат работы приведен на
Рис. 13:
Рис. 13.
2 этап: Определение приближенных
значений корней уравнения.
График функции у=-х2+5х-3
пересекает ось абсцисс в двух точках и,
следовательно, уравнение -х2+5х-4=0 имеет
два корня.
По графику приближенно можно
определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения
уравнения с заданной точностью методом Подбор
параметра.
1) Начать с поиска более точного
значения меньшего корня.
По графику видно, что ближайший
аргумент к точке пересечения графика с
осью абсцисс равен 0,75. В таблице
значений функции этот аргумент
размещается в ячейке E1.
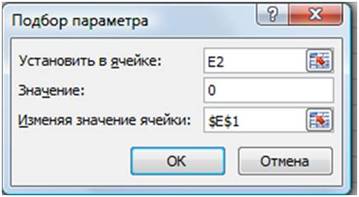
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор
параметра…;
В открывшемся диалоговом окне Подбор
параметра (Рис. 14) в поле Значение
ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки:
ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
Рис. 14.
Рис. 15.
- В окне Результат подбора (Рис. 15)
выводится информация о величине
подбираемого и подобранного значения
функции: - В ячейке E1 выводится подобранное
значение аргумента 0,6972 с требуемой
точностью (0,0001).
Установить точность можно путем
установки в ячейках таблицы точности
представления чисел – числа знаков
после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения
определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение
большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для
решения уравнений вида f(x)=g(x).
При использовании метода Подбор
параметров для решения уравнений вида f(x)=g(x)
вводят вспомогательную функцию y(x)=f(x)-g(x)
и находят с требуемой точностью значения х
точек пересечения графика функции y(x) с
осью абсцисс.
3. Закрепление изученного материала. Самостоятельная
работа.
Слайд 11
Задание: Используя метода Подбор
параметров, найти корни уравнения
с точностью до 0,001.
Для этого:
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с
шагом 0,25 (Рис. 16):
Рис. 16.
- найти приближенное значение х
точки пересечения графика функции с
осью абсцисс (х≈1,4); - найти приближенное решение уравнения с
точностью до 0,001 методом Подбор
параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной
работы.
Слайд 13 Повторение графического
способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического
способа решения уравнения вида f(x)=g(x).
Выставление оценок.
5. Домашнее задание.
Слайд 15 .
Используя средства построения диаграмм
в Excel и метод Подбор параметра, определите
корни уравнения х2-5х+2=0 с
точностью до 0,01.
Практическая работа «Графический метод решения уравнений в Excel»

Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Просмотр содержимого документа
«Практическая работа «Графический метод решения уравнений в Excel»»
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x 2 +5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с 2 и движение по оси OY можно считать равноускоренным;
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:


3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Координата x: =$B$1*COS($B$3*3,14/180)*A6 .
Координата y: =$B$2+$B$1*SIN($B$3*3,14/180)*A6-9,8*A6*A6/2.
Визуализируем модель построив график движения тела (зависимость y от x).
4) Исследуем модель и определим искомый угол.
Графический способ решения уравнений в среде Microsoft Excel 2007
Тип урока: Обобщение, закрепление пройденного материала и объяснение нового.
Цели и задачи урока:
- повторение изученных графиков функций;
- повторение и закрепление графического способа решения уравнений;
- закрепление навыков записи и копирования формул, построения графиков функций в электронных таблицах Excel 2007;
- формирование и первичное закрепление знаний о решении уравнений с использованием возможностей электронных таблиц Excel 2007;
- формирование мышления, направленного на выбор оптимального решения;
- формирование информационной культуры школьников.
Оборудование: персональные компьютеры, мультимедиапроектор, проекционный экран.
Материалы к уроку: презентация Power Point на компьютере учителя (Приложение 1).
Слайд 1 из Приложения1 ( далее ссылки на слайды идут без указания Приложения1).
Объявление темы урока.
1. Устная работа (актуализация знаний).
Слайд 2 — Соотнесите перечисленные ниже функции с графиками на чертеже (Рис. 1):
у = 6 — х; у = 2х + 3; у = (х + 3) 2 ; у = -(х — 4) 2 ; 
Слайд 3 Графический способ решения уравнений вида f(x)=0.
Корнями уравнения f(x)=0 являются значения х1, х2, … точек пересечения графика функции y=f(x) с осью абсцисс (Рис. 2).
Найдите корни уравнения х 2 -2х-3=0, используя графический способ решения уравнений (Рис.3).
Слайд 5 Графический способ решения уравнений вида f (x)=g (x).
Корнями уравнения f(x)=g(x) являются значения х1, х2, … точек пересечения графиков функций y=f(x) и у=g(x). (Рис. 4):
Слайд 6 Найдите корни уравнения 
2. Объяснение нового материала. Практическая работа.
Решение уравнений графическим способом требует больших временных затрат на построение графиков функций и в большинстве случаев дает грубо приближенные решения. При использовании электронных таблиц, в данном случае – Microsoft Excel 2007, существенно экономится время на построение графиков функций, и появляются дополнительные возможности нахождения корней уравнения с заданной точностью (метод Подбор параметра).
I. Графический способ решения уравнений вида f(x)=0 в Excel.
Дальнейшая работа выполняется учителем в Excel одновременно с учениками с подробными (при необходимости) инструкциями и выводом результатов на проекционный экран. Слайды Приложения 1 используются для формулировки задач и подведения промежуточных итогов.
Пример1: Используя средства построения диаграмм в Excel, решить графическим способом уравнение —х 2 +5х-4=0.
Для этого: построить график функции у=-х 2 +5х-4 на промежутке [ 0; 5 ] с шагом 0,25; найти значения х точек пересечения графика функции с осью абсцисс.
Выполнение задания можно разбить на этапы:
1 этап: Представление функции в табличной форме (рис. 6):
- в ячейку А1 ввести текст Х, в ячейку A2 — Y;
- в ячейку В1 ввести число 0, в ячейку С1 – число 0,25;
- выделить ячейки В1:С1, подвести указатель мыши к маркеру выделения, и в тот момент, когда указатель мыши примет форму черного крестика, протянуть маркер выделения вправо до ячейки V1 (Рис. 7).
При вводе формулы можно вводить адрес ячейки с клавиатуры (не забыть переключиться на латиницу), а можно просто щелкнуть мышью на ячейке с нужным адресом.
После ввода формулы в ячейке окажется результат вычисления по формуле, а в поле ввода строки формул — сама формула (Рис. 8):
- скопировать содержимое ячейки B2 в ячейки C2:V2 за маркер выделения. Весь ряд выделенных ячеек заполнится содержимым первой ячейки. При этом ссылки на ячейки в формулах изменятся относительно смещения самой формулы.
2 этап: Построение диаграммы типа График.
- выделить диапазон ячеек B2:V2;
- на вкладке Вставка|Диаграммы|График выбрать вид График;
- на вкладке Конструктор|Выбрать данные (Рис. 9) в открывшемся окне «Выбор источника данных» щелкнуть по кнопке Изменить в поле Подписи горизонтальной оси — откроется окно «Подписи оси». Выделить в таблице диапазон ячеек B1:V1 (значения переменной х). В обоих окнах щелкнуть по кнопкам ОК;
- на вкладке Макет|Оси|Основная горизонтальная ось|Дополнительные параметры основной горизонтальной оси выбрать:
Интервал между делениями: 4;
Интервал между подписями: Единица измерения интервала: 4;
Положение оси: по делениям;
Выбрать ширину и цвет линии (Вкладки Тип линии и Цвет линии);
- самостоятельно изменить ширину и цвет линии для вертикальной оси;
- на вкладке Макет|Сетка|Вертикальные линии сетки по основной оси выбрать Основные линии сетки.
Примерный результат работы приведен на рис. 10:
3 этап: Определение корней уравнения.
График функции у=-х 2 +5х-4 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня: х1=1; х2=4.
II. Графический способ решения уравнений вида f(x)=g(x) в Excel.
Пример 2: Решить графическим способом уравнение 
Для этого: в одной системе координат построить графики функций у1= 
1 этап: Представление функций в табличной форме (рис. 1):
 воспользоваться встроенной функцией Корень (Рис. 11).
воспользоваться встроенной функцией Корень (Рис. 11).2 этап: Построение диаграммы типа График.
Примерный результат работы приведен на Рис. 12:
3 этап: Определение корней уравнения.
Графики функций у1= 

III. Метод Подбор параметра.
Графический способ решения уравнений красив, но далеко не всегда точки пересечения могут быть такими «хорошими», как в специально подобранных примерах 1 и 2.
Возможности электронных таблиц позволяют находить приближенные значения коней уравнения с заданной точностью. Для этого используется метод Подбор параметра.
Пример 3: Разберем метод Подбор параметра на примере решения уравнения —х 2 +5х-3=0.
1 этап: Построение диаграммы типа График для приближенного определения корней уравнения.
Построить график функции у=—х 2 +5х-3, отредактировав полученные в Примере 1 формулы.
- выполнить двойной щелчок по ячейке B2, внести необходимые изменения;
- с помощью маркера выделения скопировать формулу во все ячейки диапазона C2:V2.
Все изменения сразу отобразятся на графике.
Примерный результат работы приведен на Рис. 13:
2 этап: Определение приближенных значений корней уравнения.
График функции у=-х 2 +5х-3 пересекает ось абсцисс в двух точках и, следовательно, уравнение -х 2 +5х-4=0 имеет два корня.
По графику приближенно можно определить, что х1≈0,7; х2≈4,3.
3 этап: Поиск приближенного решения уравнения с заданной точностью методом Подбор параметра.
1) Начать с поиска более точного значения меньшего корня.
По графику видно, что ближайший аргумент к точке пересечения графика с осью абсцисс равен 0,75. В таблице значений функции этот аргумент размещается в ячейке E1.
- Выделить ячейку Е2;
- перейти на вкладку Данные|Анализ «что-если»|Подбор параметра…;
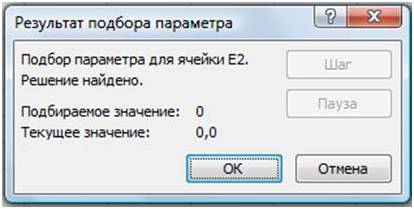
В открывшемся диалоговом окне Подбор параметра (Рис. 14) в поле Значение ввести требуемое значение функции: 0.
В поле Изменяя значение ячейки: ввести $E$1 (щелкнув по ячейке E1).
Щелкнуть по кнопке ОК.
- В окне Результат подбора (Рис. 15) выводится информация о величине подбираемого и подобранного значения функции:
- В ячейке E1 выводится подобранное значение аргумента 0,6972 с требуемой точностью (0,0001).
Установить точность можно путем установки в ячейках таблицы точности представления чисел – числа знаков после запятой (Формат ячеек|Число|Числовой).
Итак, первый корень уравнения определен с заданной точностью: х1≈0,6972.
2) Самостоятельно найти значение большего корня с той же точностью. (х2≈4,3029).
IV. Метод Подбор параметра для решения уравнений вида f(x)=g(x).
При использовании метода Подбор параметров для решения уравнений вида f(x)=g(x) вводят вспомогательную функцию y(x)=f(x)-g(x) и находят с требуемой точностью значения х точек пересечения графика функции y(x) с осью абсцисс.
3. Закрепление изученного материала. Самостоятельная работа.
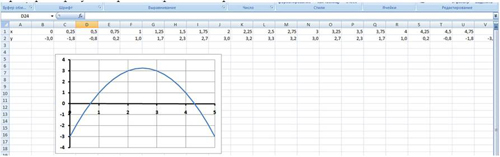
Задание: Используя метода Подбор параметров, найти корни уравнения 
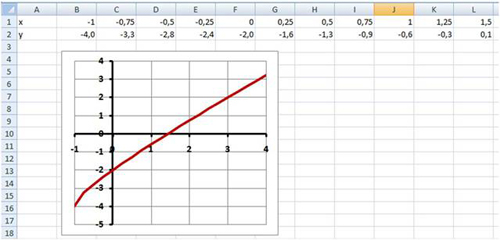
- ввести функцию у=
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
- найти приближенное значение х точки пересечения графика функции с осью абсцисс (х≈1,4);
- найти приближенное решение уравнения с точностью до 0,001 методом Подбор параметра (х≈1,438).
4. Итог урока.
Слайд 12 Проверка результатов самостоятельной работы.
Слайд 13 Повторение графического способа решения уравнения вида f(x)=0.
Слайд 14 Повторение графического способа решения уравнения вида f(x)=g(x).
5. Домашнее задание.
Используя средства построения диаграмм в Excel и метод Подбор параметра, определите корни уравнения х 2 -5х+2=0 с точностью до 0,01.
Практическая работа «Графическое решение уравнений»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 300 дидактических материалов для школьного и домашнего обучения
Приближенное решение уравнений графическим методом и с помощью метода «Подбор параметра»
Задача. Найти в электронных таблицах корень уравнения приближенным методами (графическим и численным).
Цель работы. Научиться в электронных таблицах при ближенно решать уравнения графическим методом и мето дом подбора параметра.
Задание 1. В электронных таблицах грубо приближенно графическим методом решить уравнение у = 
*3адание 2. Уточнить значения корней уравнения мето дом Подбор параметра.
Приближенное решение уравнения графическим методом
1. Запустить электронные таблицы OpenOffice Calc коман дой [Программы- OpenOffice -Электронные таблицы].
2. Представим функцию у = 
— В диапазон ячеек В1: J 1 ввести значения аргумента функции от -4,0 до 4,0 с шагом 1.
— В ячейку В2 ввести формулу для вычисления значений
функции (см рис.) и скопируем ее в диапазон яче ек В2: J 2 .
Для грубо приближенного определения корней уравне ния построить диаграмму типа График.
Построим график функции.
3. Ввести команду [Вставка- Диаграмма. ] и с помощью Мастера диаграмм постро ить диаграмму типа гра фик.
Приближенно можно опре делить, что график пересекает ось X в точках с координатами -2 и 2, т. е. уравнение имеет корни
Приближенное решение уравнения методом Подбор параметра
Для более точного приближенного решения уравнения методом Подбор параметра сначала необходимо установить требуемую точность представления чисел в ячейках (например, до 0,001).
1. Ввести команду [Формат — Формам ячеек. ].
В появившемся диалоговом окне Формат ячеек вы брать вкладку Число.
С помощью счетчика Число десятичных знаков установить необходимое количе ство знаков после запятой.

2. Таким значением является -0,4 в ячейке D 2. Выделить эту
ячейку и ввести команду [Данные – Анализ «что если» — Подбор параметра].
3. На панели Подбор параметра в поле Значение ввести
требуемое значение функции (в данном случае 0).
В поле Изменяемая ячейка ввести адрес ячейки $ D $1, в которой будет производиться подбор значения аргу мента. Щелкнуть по кнопке Да.


5. В ячейке аргумента D 1 появится подобранное значение
корня с заданной точностью -2,093.
Для уточнения значения второго корня уравнения методом Подбор параметра сначала необходимо выбрать ячей ку, в которой второе значение функции у наиболее близко к нулю.
6. Таким значением является -1,4 в ячейке Н2. Выделить
ячейку, ввести команду [Данные – Анализ «что если» — Подбор параметра]. и повторить пункты 3 — 4.
7. В ячейке аргумента H 1 появится подобранное значение
второго корня 2,349.
8. Таким образом, корни уравнения х1
2,349 найдены с точностью представления чисел в ячейках таблицы.
Задания для самостоятельного выполнения
1. Практическое задание. В электронных таблицах приближенно решить уравнение х — sinx = 0 графически и с помощью метода Подбор параметра.
2. 2. Практическое задание. В электронных таблицах приближенно решить уравнение х — cosx = 0 графически и с помощью мето да Подбор параметра
источники:
http://urok.1sept.ru/articles/564361
http://infourok.ru/prakticheskaya-rabota-graficheskoe-reshenie-uravneniy-2040762.html
Применение табличного процессора Microsoft Excel для
графического решения уравнений n-ой степени
·
Москалёва
Елена Александровна
·
Разделы: Математика, Информатика
Из курса математики
известно, что корнями уравнения являются значения точек пересечения графика
функции с осью абсцисс. Если же мы решаем систему уравнений, то ее решениями
будут координаты точек пересечения графиков функций. Этот метод нахождения
корней уравнения называется графическим. Мы уже знаем, что с помощью EXCEL
можно строить практически любые графики. Воспользуемся этими знаниями для
нахождения корней системы уравнений:
Преобразуем данную систему в приведенную:
Для оценки решений воспользуемся диаграммой, на которой
отобразим графики обеих функций. Сначала построим таблицу:
Первая строка – строка заголовков.
При заполнении столбца А: в ячейку А2 заносится начальное
значение аргумента Х = – 10, для автоматического заполнения всего столбца в
ячейку А3 занести формулу “= А2 + 1” и скопировать ее до ячейки А22.
При заполнении столбца В: в ячейку В2 заносится формула “= А2 *
А2”, которая затем копируется до ячейки В22.
При заполнении столбца С: в ячейку С2 заносится формула “ = 2 *
А2 + 9”, и также копируется до С22
Рисунок 1
С помощью Мастера диаграмм построим в одной координатной
плоскости графики заданных функций для первоначальной оценки решений/
Рисунок 2
На диаграмме видно, что оба графика имеют точки пересечения –
координаты этих точек и есть решения системы. Так как шаг изменения аргумента
достаточно велик, то мы получим приближенные значения решений.
Рисунок 3
Уточним их, построив два графика в интервалах от – 3 до 0, где
находится первое решение, и от 3 до 5, где находится второе решение. Составим
новые таблицы. Для первого решения – рисунок 4, для второго – рисунок 5.
Рисунок 4
Рисунок 5
Для более точного построения мы уменьшили шаг изменения
аргумента. Решением нашей системы будут координаты точек пересечения графиков:
Х1 = – 2,2; Y1 =
4,6; Х2 = 4,2; Y2 =
17,4. Как вы уже поняли, графическое решение системы дает приблизительные результаты.
Это можно сделать, построив график и определив координаты точек его пересечения
с осью OX, либо построив два графика: Y = X3;
Y = 2X2 + 4X – 12 и определив точки их пересечения.
Рисунок 6
Графический метод решения уравнений.
Найти графическим методом корень уравнения 10sin(x)-2x2+5=0.
Построим таблицу значений функции. Заполним столбец x значениями от -10 до 10. Значения y будем вычислять по формуле: =10*SIN(A2)-2*A2*A2+5 (формула для ячейки B2).
Построив график, найдем точки пересечения графика с осью OX. Это и есть приближенное решение.
Приближенное решение уравнения: -0.5 и 2.5.
Исследование физических моделей
Рассмотрим процесс решения задачи на конкретном примере: Тело брошено с некоторой высоты с начальной скоростью, направленной под углом к горизонту. Определить угол, при котором дальность полета будет максимальной.
Содержательная постановка задачи. В процессе тренировок теннисистов используются автоматы по бросанию мячика в определенное место площадки. Необходимо задать автомату необходимую скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
1) Описательная модель. Сначала построим качественную описательную модель процесса движения тела с использованием физических объектов, понятий и законов, то есть в данном случае идеализированную модель движения объекта. Из условия задачи можно сформулировать следующие основные предположения:
-
тело мало по сравнению с Землей, поэтому его можно считать материальной точкой;
-
изменение высоты тела не велико, поэтому ускорение свободного падения считать постоянной величиной g = 9,8 м/с2 и движение по оси OY можно считать равноускоренным;
-
скорость движения мала, поэтому сопротивлением воздуха можно пренебречь.
2) Формальная модель. Из курса физики известно, что описанное выше движение является равноускоренным. Координаты тела в любой момент времени можно найти по формулам:
Для формализации модели используем известные из курса физики формулы равномерного и равноускоренного движения. При заданных начальной скорости и и угле бросания а значения координат дальности полета х и высоты у от времени можно описать следующими формулами:
или
или
3) Компьютерная модель. Преобразуем формальную модель в компьютерную с использованием электронных таблиц. Выделим ячейки для ввода начальных данных: нач. скорость, нач. высота, угол. Построим таблицу для вычисления координат x и y.
Координата x: =$B$1*COS($B$3*3,14/180)*A6 .
Координата y: =$B$2+$B$1*SIN($B$3*3,14/180)*A6-9,8*A6*A6/2.
Визуализируем модель построив график движения тела (зависимость y от x).
4) Исследуем модель и определим искомый угол.
5) Проанализируем полученные результаты.
Конспект занятия
- Тема занятия: Графический способ решения уравнений и систем уравнений в среде Microsoft Excel.
- Тип занятия: Комбинированный
- Задача урока: Научиться графически решать уравнения и системы уравнений с помощью Мастера диаграмм.
- Цели занятия:
Воспитательная: Способствовать приобретению навыков сознательного и рационального использования компьютеров в учебной и производственной деятельности; способствовать развитию информационной культуры учащихся, способствовать воспитанию трудолюбия, культуры речи и общения учащихся.
Развивающая: развитие наглядно-образного мышления, памяти, внимания, умения сравнивать и анализировать, логически излагать мысли.
Обучающая:
сформировать представление учащихся о возможностях системной программы «Мастер диаграмм» при построении графиков и решении математических уравнений;
сформировать знания о способах построения графиков функций по алгоритму, о способах графического решения систем уравнений;
сформировать умения производить простейшие расчеты в электронной таблице с помощью формул и стандартных функций, строить графики различных функций в одной координатной плоскости по алгоритму построения диаграмм, применять электронные таблицы для решения задач, табулировать функцию с двумя изменяющимися аргументами, использовать средства автоматизации.
- Методы: словесный, наглядно – демонстрационный, практический, метод контроля.
- Оборудование: компьютерный класс, проектор, программное обеспечение Windows XP, Microsoft Office, файл-заготовка с входным тестом, карточка с заданием.
- Литература:
- А. А. Журин, И. А. Милютина Microsoft Office 97 для школьников и начинающих пользователей. / Учеб. пособие. / Под ред. А. А. Журина. – М.: Аквариум, К.: ГИППВ, 2000.
- Богумирский Б.С. Руководство пользователя ПЭВМ. Ч. 1,2. -С.-Питербург: «Печатный двор», 1994.
- Информатика. Еженедельная газета Издательского дома «Первое сентября».
- Лавренов С.М. «Excel. Сборник примеров и задач»
- Леонтьев В. П. Новейшая энциклопедия персонального компьютера 2001 год. – М.: ОЛМА-ПРЕСС, 2001.
- Фигурнов В.Э. IBM PC для пользователя. Изд. 7, перераб. и дополн. — М.: ИНФРА-М, 1997. — 640 с.
- Эффективный самоучитель работы на ПК: Пер. с англ. и нем./ А. Клименко, П. Нортон, Р. Вебер – К.: Издательство «ДиаСофт», 2001.-672 с.
- Ход занятия:
- План урока:
- Введение – 2 минуты;
- Решение теста – 10 минут;
- Повторение – 5 минут;
- Изучение новой темы – 25 минут;
- Подведение итогов – 3 минуты.
7.2. Краткое содержание:
1) Приветствие учащихся и гостей.
Все, с чем мы ежедневно сталкиваемся в жизни, скорее всего, зарегистрировано и хранится каким-либо образом. Для хранения и обработки данных используют базы данных, они же играют особую роль в современном мире.
Так как иметь дело с обширными таблицами приходится во многих областях жизни, то и информацию, представленную в них, необходимо осмыслить, проанализировать, выделить главное, не вникая в несущественное. В частности, это относится ко всем видам финансовой и учетной деятельности.
Включаются слайды 1,2
Способность электронных таблиц быстро и точно производить автоматические вычисления используют не только бухгалтеры. Без электронных таблиц не обходятся участники бирж, руководители брокерских контор, банков и другие финансовые менеджеры.
С помощью электронных таблиц можно моделировать реальные ситуации и оценивать получающиеся результаты. При работе с большими объемами данных важную роль играет их наглядность. Для этого, как Вы знаете, используют графики и диаграммы. Графическое представление помогает осмыслить закономерности, лежащие в основе больших объемов данных.
Включаются слайды:3
На предыдущем уроке Вы строили диаграммы для сравнения числовых данных в таблицах.
Сегодня Вы узнаете, как можно с помощью Мастера диаграмм строить графики функций и решать системы уравнений.
Итак, тема нашего урока «Графический способ решения уравнений и систем уравнений в среде Microsoft Excel».
Включаются слайды:4
Посмотрите на экран.
После этого урока Вы будете: Слайд 5
2) Прежде чем перейти к изучению материала урока, предлагаю ответить на вопросы теста.
У каждого из Вас на рабочем столе располагается тестовый файл «Электронные таблицы». Откройте его и ответьте на вопросы теста (В тесте нет возврата к предыдущему вопросу). На работу с тестом отводится 7 минут.
Включаются слайды:6
Сделали упражнение для отдыха глаз: на стене висят картинки с изображением птиц и дерева. Необходимо проводить глазами птицу из левого угла до дерева, а потом с дерева в правый угол и обратно.
После выполнения теста все учащиеся называют свою оценку преподавателю, который выставляет ее в свой журнал.
Молодцы. Сравните свои результаты с эталоном ответов. Включаются слайды 7-11.
3) В тесте было практическое задание. Вспомните, какое? Построить диаграмму.
Вспомните и дайте определение диаграммы. Учащиеся дают определение. Слайд 7
Расскажите, как можно с помощью программы MS Excel построить диаграмму.
(Учащиеся рассказывают алгоритм построения диаграмм.)
Алгоритм построения диаграмм:
1. Подготовить таблицу.
2. Выделить данные в таблице, которые надо включить в диаграмму.
3. С помощью Мастера диаграмм построить гистограмму.
Гистограмма – это разновидность диаграмм, представленная в виде столбиков.
Слайд 8.
Назовите способ выделения несмежных областей. С нажатой клавишей CTRL.
Назовите два способа вызова на экран Мастера диаграмм.
1 способ: меню Вставка – команда Диаграмма.
2 способ — соответствующая кнопка на панели инструментов.
Молодцы. Итак, правильно выполнив практическое задание, Вы получили следующую диаграмму. Слайд 9.
Из материала предыдущего урока Вы знаете, что работу Мастера диаграмм можно представить в виде следующей схемы (смотрим на экран): Слайд 10
Учащийся поясняет каждый этап, во время ответа ученика на экране появляются слайды с пошаговым построением диаграммы с помощью Мастера Диаграмм.
Итак, для того чтобы построить диаграмму, необходимо работать по алгоритму и воспользоваться помощью Мастера диаграмм. Слайд 11.
4) Итак, сегодня мы займемся созданием графиков с помощью Мастера диаграмм.
Рассмотрим пример построения графика функции у = х2 на промежутке [–7; 7] с шагом 1.
Составим таблицу значений функции у = х2 на промежутке [–7; 7] с шагом 1.
Таблица содержит две строки:
- В первой строке задаем значения переменной х на данном отрезке.
Напомните, как можно упростить ввод значений в первую строку таблицы.
Можно задать только два значения переменной х, например, -7 и -6, а затем использовать маркер заполнения. Слайд 12.
- Во второй строке задаем значения переменной y. Обратите внимание, что значения переменной y зависят от значений переменной х.
Назовите эту зависимость. у = х2.
Таким образом, значение переменной у задается формулой. Слайд 13.
Какая будет записана формула? =В1^2.
Можно ли упростить ввод значений во вторую строку таблицы? Аргументируйте свой ответ.
Да. Формулу вводим только в одну ячейку, а затем используем маркер заполнения.
Верно.
Итак, таблица построена. Что делаем дальше?
Выделяем подготовленную таблицу. Вызываем Мастер диаграмм.
Устанавливаем следующие параметры диаграммы: тип “Точечная”, легенда и линии сетки не нужны, заголовок “y=x2”, на имеющемся листе.
Так как большинство графиков готовится к деловым документам, то излишества здесь не нужны, и желательно придерживаться делового стиля в оформлении графика.
Назовите вид кривой, полученной в результате построения. Парабола. Слайд 14.
ЗАПОМНИТЕ:
Для построения графика функции с двумя изменяющимися аргументами необходимо:
- Задать функцию с определенным шагом,
- производить расчеты с помощью формул,
- использовать средства автоматизации ввода,
- воспользоваться помощью Мастера диаграмм.
Сделали упражнение для отдыха глаз: на стене висят картинки с изображением птиц и дерева. Необходимо проводить глазами птицу из левого угла до дерева, а потом с дерева в правый угол и обратно.
Слайд 15,16.
Перед Вами на столах лежат листы с практической работой, в них подробно рассмотрен предыдущий пример.
Для закрепления материала, выполните самостоятельно Задание1 (1 ряд) и Задание2 (2ряд) за компьютерами.
Проверка правильности выполненной работы Слайд 17
Молодцы.
Перейдем к следующему этапу урока. Слайд 18.
Рассмотрим пример, в котором требуется решить графически систему уравнений. Слайд 19.
Решить систему уравнений — это значит найти такие значения х и у, которые будут удовлетворять и первое уравнения и второе. Графически решить систему уравнений — в одной координатной плоскости построить графики уравнений системы и найти координаты точек их пересечения. Слайд 20.
А теперь давайте решим данную систему уравнений.
Итак, построим в одной координатной плоскости графики уравнений: у1 =x2-5 и у2 = 8-x2. Нам необходимо: Слайд 21.
1. Подготовить таблицу.
2. Выделить данные в таблице, которые надо включить в диаграмму.
3. С помощью Мастера диаграмм построить график.
Подумайте и скажите, сколько строк будет в таблице? Три строки.
Итак, смотрим на экран. Слайд 22.
Таблицу строим аналогично предыдущим заданиям, но в таблице будет уже три строки.
Обратите внимание: в первой строке задаем значения переменной х, во второй строке – значения переменной y1, и в третьей строке – значения y2.
Назовите зависимости, связывающие значения y1 и y2 с переменной х.
у1 =x2-5
у2 = 8-x2
С помощью Мастера диаграмм строим точечную диаграмму и получаем следующее решение.
ЗАПОМНИТЕ: Слайд 23.
Для того чтобы графически решить систему уравнений необходимо:
- построить графики функций из системы в одной координатной плоскости,
- найти точки пересечения графиков.
Сделали упражнение для отдыха глаз: на стене висят картинки с изображением птиц и дерева. Необходимо проводить глазами птицу из левого угла до дерева, а потом с дерева в правый угол и обратно.
5) Мы с Вами сегодня разобрали только два аспекта применения электронных таблиц, на самом деле их гораздо больше. Используя электронные таблицы, программисты создают обучающие программы, тесты и т.д.
Итак, чему же мы с вами сегодня научились? Ребята отвечают.
1) узнали о возможностях использования Мастера диаграмм при построении графиков и решении математических уравнений;
2 научились строить графики различных функций в одной координатной плоскости;
3) узнали новый способ графического решения систем уравнений с помощью электронных таблиц.
Давайте еще раз вспомним, как построить график функции и как решить графически систему уравнений. Ребята дают ответ, на экране появляется слайд 24.
Приложение 1
Входной тест
ВОПРОС 1.Принципиальное отличие электронной таблицы от обычной заключается в наличии . . .
- автоматического пересчета формул при изменении исходных данных.
ВОПРОС 2. На рисунке представлено рабочее окно табличного редактора MS Excel. Расставьте цифры, соответствующие следующим основным элементам рабочего окна.
|
Цифра |
Элемент рабочего окна |
|
1 |
строка заголовка рабочей книги |
|
9 |
системное меню |
|
2 |
панели инструментов |
|
6 |
строка формул |
|
7 |
поле имени ячейки |
|
4 |
заголовки столбцов ЭТ |
|
10 |
заголовки строк ЭТ |
|
8 |
ярлычки рабочих листов книги |
|
3 |
активная ячейка |
|
5 |
блок ячеек |
ВОПРОС 3. Каждая ячейка ЭТ имеет свой адрес, который состоит из . . .
- имени столбца и номера строки, на пересечении которых располагается ячейка.
ВОПРОС 4. Адрес активной ячейки дублируется в . . .
- поле имен ячеек.
ВОПРОС 5. Строка формул используется для . . .
- ввода и отображения любых значений активной ячейки.
ВОПРОС 6. Среди приведенных формул укажите формулу для электронной таблицы
- =A3*B8+12
ВОПРОС 7. Введите в выделенную ячейку формулу для электронной таблицы
- =5-(y^2+3)/(11+2*x)
ВОПРОС 8. Для наглядного представления числовых данных можно использовать . .
- Диаграмму.
ВОПРОС 9. Как выглядит маркер заполнения
- черный квадрат в правом нижнем углу активной ячейки.
ВОПРОС 10. Программа-помощник, которая предназначена для графического представления данных в таблице
- Мастер диаграмм.
ВОПРОС 11. Диаграмма, в которой отдельные значения представлены вертикальными столбцами различной высоты, называется . . .
- Гистограммой.
ВОПРОС 12. Дан фрагмент таблицы. Постройте диаграмму, отображающую продажу путевок за месяц Март.
Продажа путевок за год туроператором «Клеопатра»
|
НАПРАВЛЕНИЕ |
ЯНВАРЬ |
ФЕВРАЛЬ |
МАРТ |
АПРЕЛЬ |
МАЙ |
|
Египет |
100 |
45 |
34 |
22 |
45 |
|
Турция |
89 |
68 |
24 |
68 |
25 |
|
Италия |
46 |
45 |
98 |
15 |
35 |
|
Скандинавия |
45 |
53 |
5 |
25 |
21 |
Приложение 3
ТЕМА: ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
В СРЕДЕ MICROSOFT EXCEL
Цель работы: овладеть навыками обработки информации, представленной в виде таблиц, с помощью универсальной системы обработки данных Excel: организация рабочих страниц, формирование вычисляемых ячеек таблиц, установка рисунков и гистограмм, ввод текстового сопровождения, применение метода автозаполнения.
Ход урока:
Алгоритм построения диаграмм
- Составить таблицу.
- Выделить данные в таблице.
- С помощью Мастера диаграмм (ВСТАВКА-ДИАГРАММА) построить диаграмму:
- Шаг 1. Выбор типа и подтипа диаграммы
- Шаг 2. Проверка интервала данных. Ориентация данных. Подписи осей.
- Шаг 3. Оформление заголовка, легенды, оси, таблиц данных.
- Шаг 4. Определение листа для диаграммы
1) В своей личной папке создайте рабочую книгу под именем «ГРАФИКИ ФУНКЦИЙ». Выполняйте задания на разных листах.
ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
2) Рассмотрите пример и выполните его на первом листе, переименовав лист в “ПРИМЕР 1”.
ПРИМЕР 1. Построить график функции у = х2 на промежутке [-7;7] с шагом 1.
РЕШЕНИЕ:
- Составим таблицу значений функции у = х2 на промежутке [–7; 7] с шагом 1.
Для этого:
- В первой строке расположим все значения переменной х на данном отрезке. Достаточно ввести только два значения и использовать маркер заполнения.
- Во второй строке задаем соответствующие значения переменной y. Значения переменной y зависят от значений переменной х. Значения функции вычисляем, используя возможности Excel: итак, вводим в ячейку В2 формулу, отражающую зависимость переменной y от х; в данном случае это формула =В1^2.
- Формулу копируем на весь диапазон, используя маркер заполнения.
Получим следующую таблицу:
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
|
|
1 |
X |
-7 |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
Y |
49 |
36 |
25 |
16 |
9 |
4 |
1 |
0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
- Выделяем таблицу.
- Вызываем Мастер диаграмм (команда Вставка-Диаграмма).
Тип диаграммы: “Точечная”, легенда не нужна, линии сетки тоже, оформим заголовок “y= x2”, расположим диаграмму на имеющемся листе.
В результате получим график (сравните со своим результатом) |
|
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ
3) Переименуйте следующие листы соответственно в “ЗАДАНИЕ 1” и “ЗАДАНИЕ 2” и выполните их самостоятельно.
ЗАДАНИЕ 1. Построить график функции у =3х2— 4x+1 на промежутке [-6;6] с шагом 1.
ЗАДАНИЕ 2. Построить график функции у = х3 на промежутке [-5;5] с шагом 1.
РЕШЕНИЕ СИСТЕМЫ УРАВНЕНИЙ
2) Рассмотрите пример и выполните его на свободном листе, переименовав лист в “ПРИМЕР 2”.
ПРИМЕР 2. Решить систему уравнений на интервале [-5;6].
РЕШЕНИЕ: Построим в одной координатной плоскости графики уравнений: у1=x2— 5 и у2= 8 — x2.
На рабочем листе с именем “ПРИМЕР 2” построим таблицу.
Для этого:
- В строке 1 образуем прогрессию со значениями переменной х на интервале [-5;6], шаг изменения возьмем 0,5.
- В ячейку В2 вводим формулу =В1^2-5 и копируем её вправо.
- В ячейку В3 вводим формулу =8-В1^2 и копируем её вправо.
- Получим следующую таблицу:
- Выделяем таблицу и вызываем Мастер диаграмм. Тип диаграммы: “Точечная”, легенда не нужна, линии сетки тоже, сделайте заголовок “Решение системы уравнений”, расположите диаграмму на имеющемся листе.
- В результате получим график (сравните со своим результатом):
Ответ: Решением системы являются точки (-2,5;1,75) и (2,5;1,75)
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ
4) Переименуйте следующие листы соответственно в “ЗАДАНИЕ 3” и “ЗАДАНИЕ 4” и выполните их самостоятельно.
Решить системы уравнений: ЗАДАНИЕ 3.
ЗАДАНИЕ 4.
ИТОГОВЫЙ САМОКОНТРОЛЬ
5) Переименуйте следующие листы соответственно в “ЗАДАНИЕ 5” и “ЗАДАНИЕ 6” и выполните их самостоятельно.
ЗАДАНИЕ 5. Построить график функции у =sin(x) на промежутке [0;6,5] с шагом 0,5.
ЗАДАНИЕ 6. Решить графически систему уравнений на интервале (0;5).
ОТВЕТЫ
Решением системы являются
точки (0,8;0,7) и (3,9;-0,72)

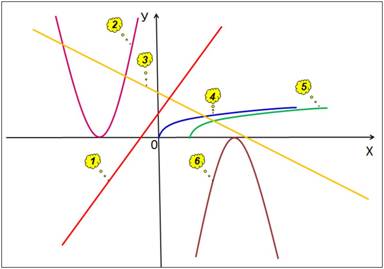


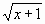

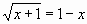
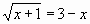
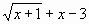


















 и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):
и построить ее график на промежутке [ -1; 4 ] с шагом 0,25 (Рис. 16):














