Содержание
- Трехмерные диаграммы (поверхности и изолинии) в EXCEL
- Поверхностная диаграмма в Excel и пример ее построения
- Построение поверхностной диаграммы в Excel
- Краткое описание примера
- Построение трехмерной поверхности в Excel
- Задание по excel 3 построение трехмерной поверхности
- §15. Excel. Построение поверхностей
Трехмерные диаграммы (поверхности и изолинии) в EXCEL
history 16 мая 2015 г.
Рассмотрим трехмерные диаграммы в MS EXCEL 2010. С помощью трехмерных диаграмм отображают поверхности объемных фигур (гиперболоид, эллипсоид и др.) и изолинии.
Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.
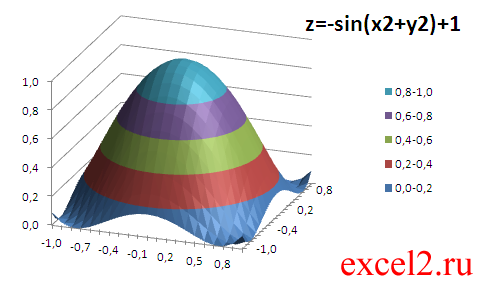
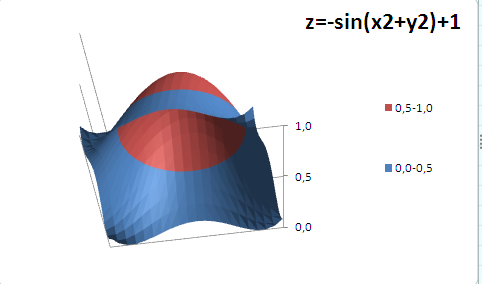
Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).
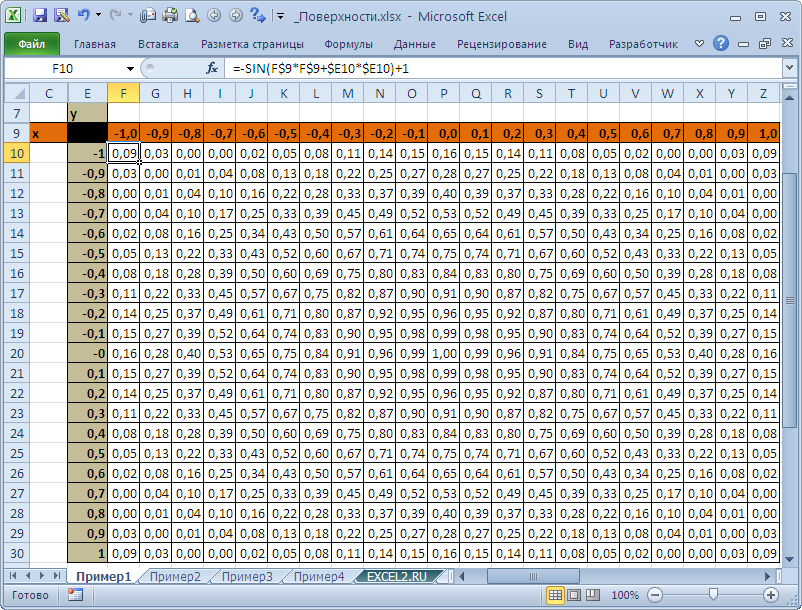
В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)
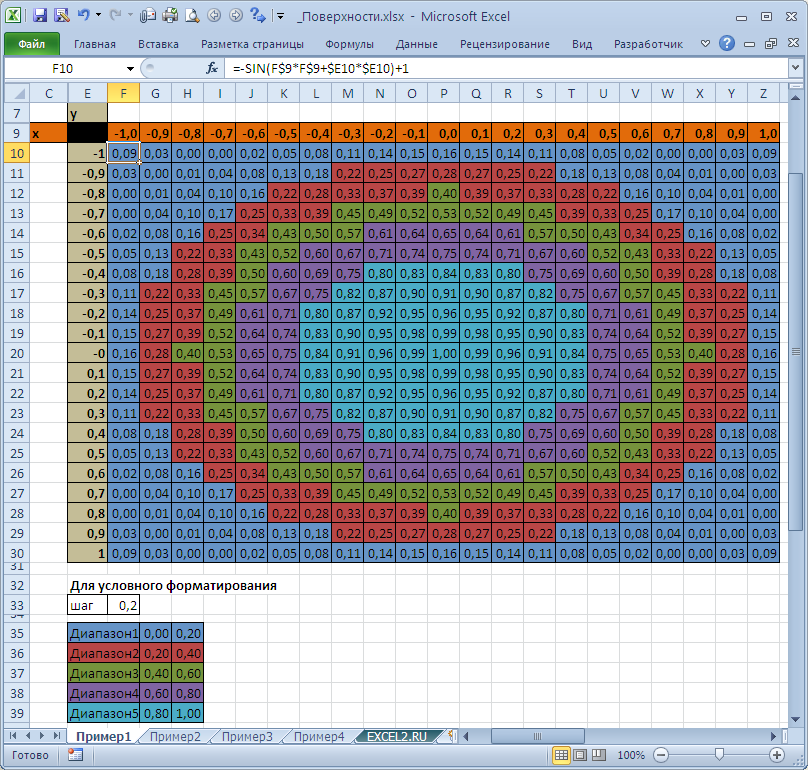
Чтобы значения Z были более информативны — можно использовать Условное форматирование .
Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.
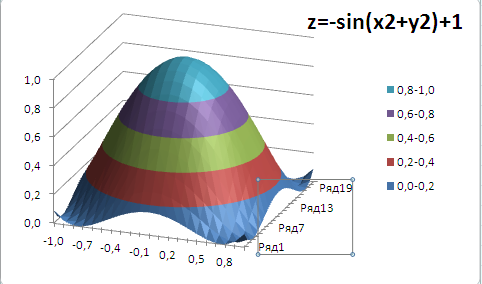
Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).
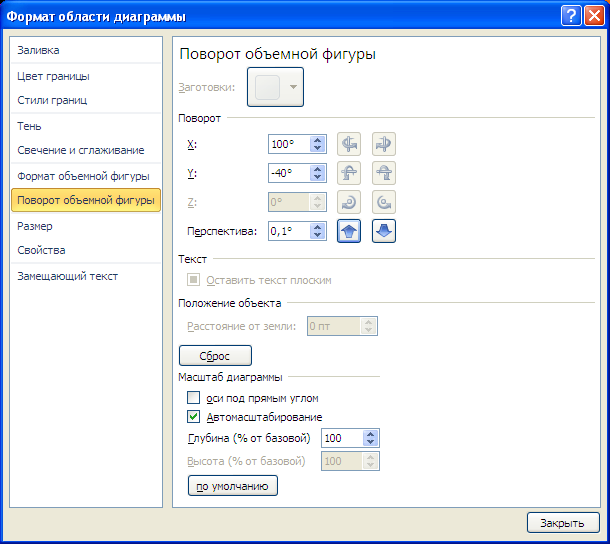
Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).
Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.
Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).
Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).
Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).
И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).
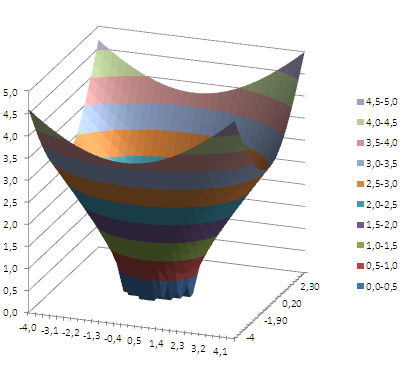
Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.
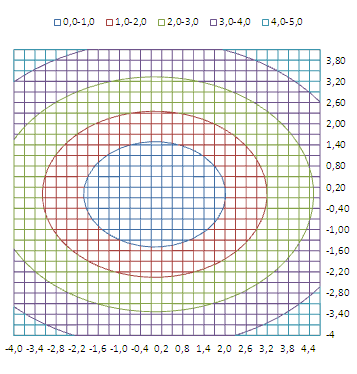
Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .
Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .
Источник
Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
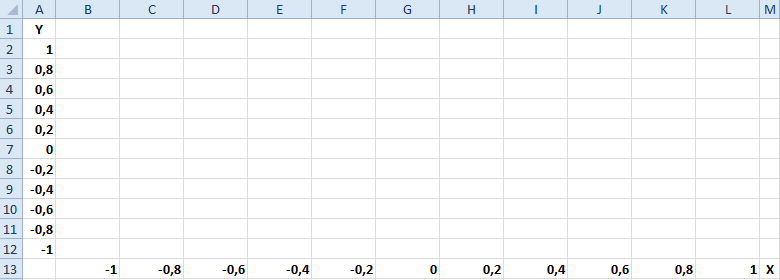
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
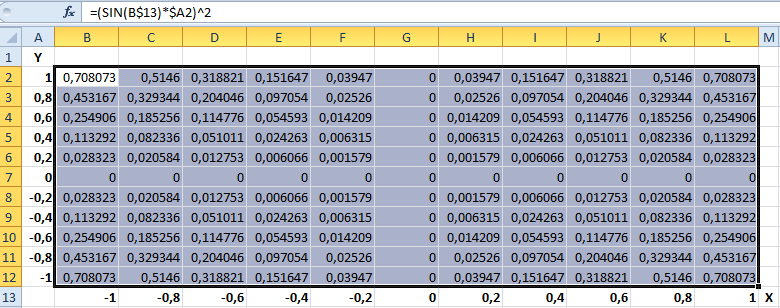
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
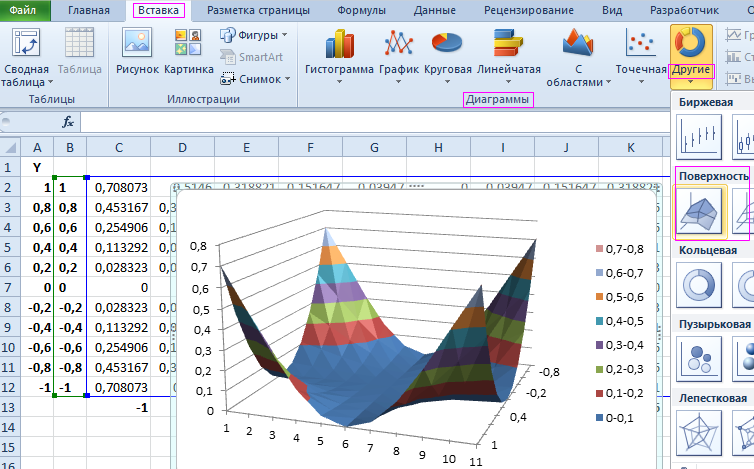
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
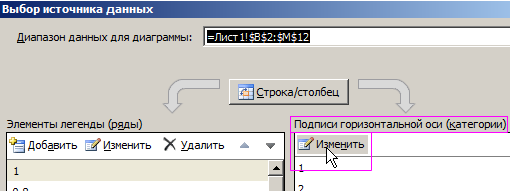
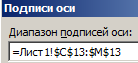
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
Источник
Построение трехмерной поверхности в Excel
1. Получить матрицу значений функции в виде двумерной таблицы. Для этого задать изменение двух аргументов функции в виде числовых рядов, расположенных под прямым углом друг к другу. Вычислить значение функции для каждой пары аргументов.
| xy | -5 | -4.5 | -4 | . |
| -5 | ||||
| -4.5 | Z(x,y) | |||
| … |
2. Внимание! Формула для вычисления значения функции должна быть набрана один раз, затем скопирована.
3. Выполнить построение трехмерной поверхности. Сравнить получившийся результат с образцом.
Вариант 1: 



С помощью автозаполнения заполнили столбец А и строку А значениями от 5 до -5 с шагом 0,5. В ячейку В2 занесли заданную формулу. Затем растянули формулу на все ячейки для вычисления в каждой точке. Выполнили построение трехмерной поверхности.
=(ABS(B$1-$A$1)-ABS($A2-$A$1))*КОРЕНЬ($A$1^2-B$1^2-$A2^2)
Поиск по сайту:
Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)
Источник
Задание по excel 3 построение трехмерной поверхности
В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
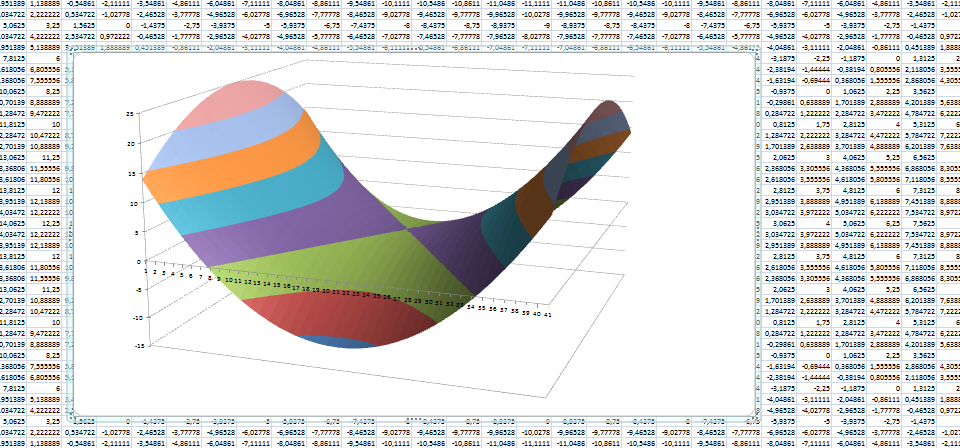
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
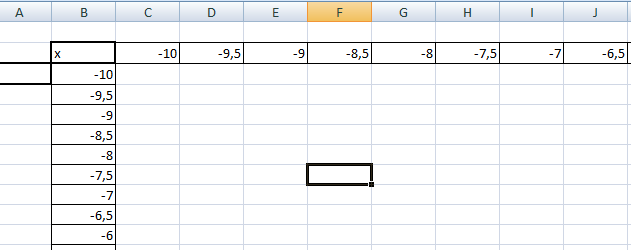
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
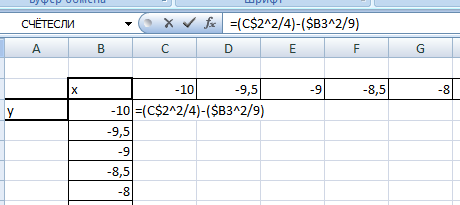
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Источник
§15. Excel. Построение поверхностей
Изучим графические возможности пакета Excel по построению графиков функций в трехмерном пространстве.
Пример 1. Построить верхнюю часть эллипсоида:
Для построения поверхности необходимо разрешить заданное уравнение относительно переменной z.
Так как в условии речь идет о верхней части эллипсоида, то рассмотрим ОДЗ положительной части уравнения:
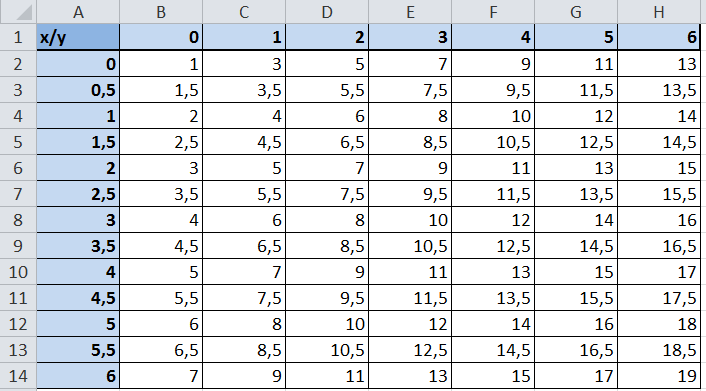
Приступим к построению поверхности. В диапазон B1:J1 введем последовательность значений переменной y: -4, -3, …,4, а в диапазон ячеек А2:А14 последовательность значений переменой x: -3, -2,5,…3.
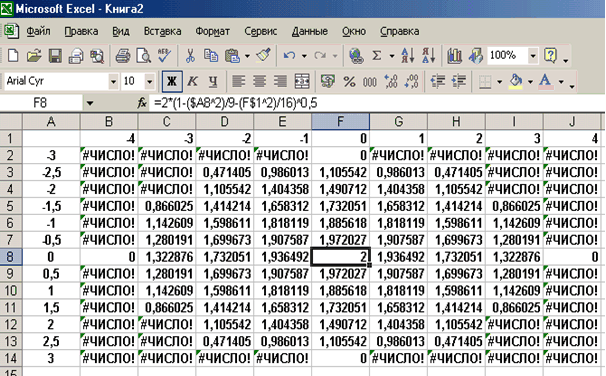
В ячейку В2 введем формулу = 2*(1-($A2^2)/9-(B$1^2)/16)^0,5.
Знак $, стоящий перед буквой в имени ячейки, дает абсолютную ссылку на столбец с данным именем, а знак $, стоящий перед цифрой — абсолютную ссылку на строку с этим именем. Поэтому при копировании формулы из ячейки В2 в ячейки диапазона B2:J14 в них будет найдено значение z при соответствующих значениях x, y. Т.о. создается таблица значений z.
Рис. 2.19. Образцы заполнения таблицы для построения поверхности
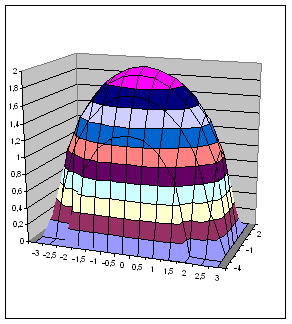
Перейдем к построению поверхности. Выделим диапазон ячеек A1:J14, содержащий таблицу значений функции и ее аргументов, вызовем Мастер диаграмм и тип диаграммы Поверхность, далее заполним диалоговые окна так как было описано в лабораторной работе по построению графиков функций. После нажатия кнопки Готово получим изображение заданной поверхности.
Рис. 2.20. Образцы построения поверхностей
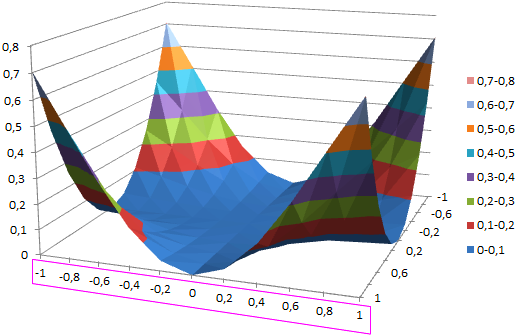
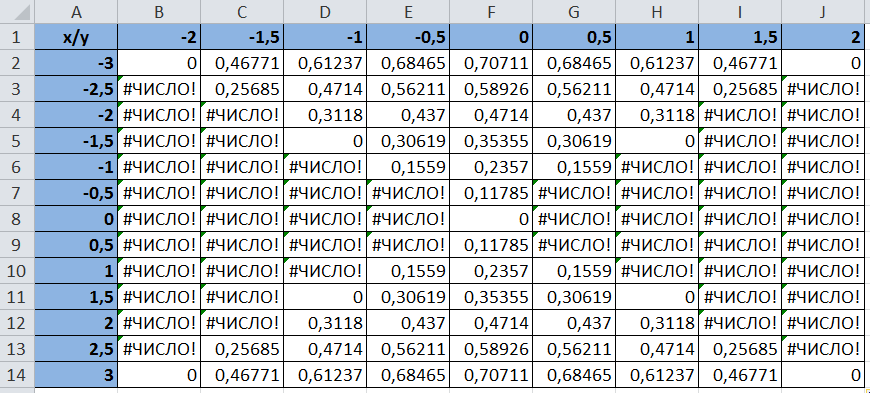
Пример 2. Построить поверхность z = x 2 -y 2 при x, y [-1;1].
В диапазон B1:L1 введем последовательность значений переменной x: -1, -0.8, …,1, а в диапазон ячеек А2:А12 последовательность значений переменой y. В ячейку В2 введем формулу = $A2^2-B$1^2 и скопируем ее в ячейки диапазона B2:L12. На рисунке 2 изображена заданная поверхность.
Задание 1. Построить верхнюю (четные варианты) или нижнюю (нечетные варианты) часть эллипсоида, заданного уравнением:
Источник
Построить
график кусочной функции на участке
[a;b]
с шагом 0,5.
|
№ Вар |
Функция |
[a;b] |
|
1. |
|
[-7;7] |
|
2. |
|
[-7;7] |
|
3. |
|
[-5;5] |
|
4. |
|
[-5;5] |
|
5. |
|
|
|
6. |
|
[-7;7] |
|
7. |
|
[-10;10] |
|
8. |
|
[-10;10] |
|
9. |
|
[-4;10] a-коэф-т |
|
10. |
|
[-10;10] |
|
11. |
|
[-5;8] с-коэф-т |
|
12. |
|
[-4;4] a-коэф-т |
|
13. |
|
[-4;4] |
|
14. |
|
[-10;10] с-коэф-т |
|
15. |
|
[-10;10] d-коэф-т |
|
16. |
|
[-7;7] |
|
17. |
|
[-7;7] |
|
18. |
|
[-30;30] |
|
19 |
|
[-30;30] |
|
20. |
|
|
|
21. |
|
[-10;10] |
|
22. |
|
[-3;3] |
|
23. |
|
[-10;10] |
|
24. |
|
[-10;10] |
|
25. |
|
[-5;6] a-коэф-т |
|
26. |
|
[-5;5] b-коэф-т |
|
27. |
|
[-10;10] |
|
28. |
|
[-8;8] d-коэф-т |
|
29. |
|
[-5;6] a-коэф-т |
|
30. |
|
[-7;7] d-коэф-т |
Задание по Excel № 3 «Построение трехмерной поверхности»
-
Получить
матрицу значений функции в виде двумерной
таблицы. Для этого задать изменение
двух аргументов функции в виде числовых
рядов, расположенных под прямым углом
друг к другу. Вычислить значение функции
для каждой пары аргументов. Шаг 0,1xy
-4
-3.5
-3
….
0
0.5
1
Z(x,y)
1.5
…
-
Внимание!
Формула для вычисления значения функции
должна быть набрана один раз, затем
скопирована. -
Выполнить
построение трехмерной поверхности.
Сравнить получившийся результат с
образцом.
|
№ |
Уравнение |
Вид |
№ |
Уравнение |
Вид |
|
1 |
x=[-5;5] y=[-5;5] a=2 b=7 |
|
8 |
x=[-2;2] y=[—2×p ; 2×p] a=2 |
|
|
2 |
x=[-5;5] y=[-5;5] a=2 b=5 |
|
9 |
x=[-1;1] y=[—2×p ; 2×p] a=10 b=2 |
|
|
3 |
x=[-5
y=[-2 ; a=1.5 b=0.5 |
|
10 |
x=[—p ; p] y=[—p ; p] a=2 |
|
|
4 |
x=[-5;5] y=[-5;5] a=0.7 |
|
11 |
x=[—p ; p] y=[—p ; p] a=0.5 |
|
|
5 |
x=[—2×p ; 2×p] y=[—2×p ; 2×p] a=2 b=5 |
|
12 |
x=[—p ; p] y=[—p ; p] a=4 |
|
|
6 |
x=[—p ; p] y=[—p ; p] a=3 |
|
13 |
x=[-2;2] y=[-2;2] a=0.5 |
|
|
7 |
x=[ —p ; p] y=[ —p ; p] a=3 |
|
14 |
x=[-2;2] y=[-2;2] a=2 |
|
|
15 |
x=[-2;2] y=[-2;2] a=2 |
|
22 |
x=[0.01 ; 2×p] y=[0.01 ; 2×p] a=200 |
|
|
16 |
x=[-5;5] y=[-5;5] a=2 b=1 |
|
23 |
x=[0.01 ; 2×p] y=[0.01 ; p] a=200 |
|
|
17 |
x=[-5;5] y=[-5;5] a=0.3 |
|
24 |
x=[-3’3] y=[-1;6] a=50 |
|
|
18 |
x=[-5;5] y=[-5;5] a=0.3 |
|
25 |
x=[-3;3] y=[-3;3] a=0.5 |
|
|
19 |
x=[-5;5] y=[-5;5] a=5 |
|
26 |
x=[-3;3] y=[-3;3] a=2 b=3 |
|
|
20 |
x=[-5;5] y=[-5;5] a=0.1 |
|
x=[—p/2
y=[—p/2 a=0.1 b=2 |
|
|
|
21 |
x[0.1;1] y[0.1;1] a=0.1 |
|
28 |
x[—p/4
y[—p/4 a=2 b=1 |
|
y=
Задание
№1 по MathCAD
«Двумерные графики, заданные в
параметрическом виде, и графики, заданные
в полярных координатах»
Задание:
1.
Построить
два графика;
2.
Вывести
таблицу значений функции, заданной в
параметрическом виде;
3.
При
сдаче работы уметь:
перевести
полярные координаты в декартовы;
отобразить
несколько зависимостей на одном графике.
Указания
к работе:
1.
Для
построения XY-графика,
заданного в параметрическом виде
необходимо:
указать
диапазон и шаг изменения параметра в
виде
.
Знак «:=»
вводится с помощью английского знака
«:».
Символ «..»
вводится с помощью символа «;»
|
№ Вар |
Функция, |
Функция, |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
|
9 |
|
|
|
10 |
|
|
|
11 |
|
|
|
12 |
|
|
|
13 |
|
|
|
14 |
|
|
|
15 |
|
|
|
16 |
|
|
|
17 |
|
|
|
18 |
|
|
|
19 |
|
|
|
20 |
|
|
|
21 |
|
|
|
22 |
|
|
|
23 |
|
|
|
24 |
|
|
|
26 |
|
|
|
27 |
|
|
|
28 |
|
|
|
29 |
|
|
задать
зависимость
;
“Graph”à
“Create
XY-Plot”.
2.
В
полярной системе координат каждая точка
задается углом и радиусом определенной
длины. Длина радиуса находится в
определенной зависимости от полярного
угла. Для построения графика, заданного
в полярных координатах необходимо:
указать
диапазон и шаг изменения полярного угла
в радианах , например
;
задать
зависимость
“Graph”à
“Create
Polar
Plot”.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Трехмерные диаграммы (поверхности и изолинии) в EXCEL
history 16 мая 2015 г.
-
Группы статей
- Диаграммы и графики
Рассмотрим трехмерные диаграммы в MS EXCEL 2010. С помощью трехмерных диаграмм отображают поверхности объемных фигур (гиперболоид, эллипсоид и др.) и изолинии.
Для начинающих пользователей EXCEL советуем прочитать статью Основы построения диаграмм в MS EXCEL , в которой рассказывается о базовых настройках диаграмм, а также статью об основных типах диаграмм .
При попытке построить диаграмму типа Поверхность на основе одного ряда данных, MS EXCEL может сказать, что ему требуется как минимум 2 ряда. На самом деле, для более или менее наглядной поверхности потребуется как минимум 10 рядов (лучше 20 – для сложных поверхностей). К счастью, ряды не нужно создавать в ручную – достаточно правильно сформировать таблицу с исходными данными.
Построим график функции z=-sin(x*х+y*y)+1 (см. файл примера ).
В качестве источника данных используем таблицу, в которой в верхней строке указаны значения Х, а в левом столбце Y. В остальных ячейках – значения Z для всех пар (Х,Y)
Чтобы значения Z были более информативны — можно использовать Условное форматирование .
Условное форматирование показывает некий вариант изолиний (см. ниже): близкие значения Z выделены одним цветом. Это также позволяет предварительно оценить вид создаваемой диаграммы.
Теперь выделите любую ячейку таблицы и постройте диаграмму типа Поверхность (вкладка Вставка , группа Диаграммы , Кнопка Другие ).
Полученную фигуру можно повращать (кнопка Поворот объемной фигуры на вкладке Макет ).
Для построения диаграммы используется 3 оси: горизонтальная ось (категорий), вертикальная ось (значений), ось Z (рядов значений). Все 3 названия осей требуют пояснения.
Во-первых, ось Z на самом деле является нашей осью Х и отображает имена рядов. Если имена рядов убрать, то изменятся и подписи оси (убрать имена рядов можно нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор ).
Этот факт роднит диаграмму Поверхность с Диаграммой График , где по Х отображаются лишь подписи. Т.е. при попытке построить поверхность с неравномерным шагом по Х (например, 1, 2, 5, 9, 77, 103, ..) получим искажения масштаба: значения по Х будут откладываться последовательно 1, 2, 3, … (конечно, Z будет рассчитаны правильно). Интересно, что формат подписей по оси Z можно настроить только изменяя формат ячеек, на которые ссылаются имена рядов (изменение формата на вкладке Число (в окне Формат Оси) ни к чему не приводит).
Во-вторых, по вертикальной оси (значений) на самом деле откладываются значения Z (это очевидно из рисунка).
И, наконец, в-третьих, горизонтальная ось (категорий) – это значения Y (на самом деле опять только подписи). Подписи, как и для Графика можно удалить или изменить нажав кнопку Изменить в окне Выбор источника данных , которое доступно через вкладку Конструктор (на этот раз нужно нажать кнопку расположенную справа).
Так как диаграмма Поверхность – это по сути трехмерный График , в котором одному Х соответствует один Y, то некоторые объемные фигуры отобразить на диаграмме Поверхность не удастся. Например, не удастся отобразить гиперболоид, т.к. каждой паре (Х;Y) на диаграмме Поверхность соответствует только один Z, а для гиперболоида это не так (каждой паре соответствует 2 значения Z). Поэтому, в MS EXCEL придется довольствоваться только половиной гиперболоида.
Как видно из диаграммы, близкие значения Z выделены одним цветом, которые указаны в Легенде. К сожалению, в MS EXCEL невозможно управлять этими уровнями (даже при повороте фигуры количество уровней и диапазоны значений существенно изменяются). Это приводит к тому, что построение изолиний ( линии уровня, контурный график, англ. Contour plot ) реализовано в MS EXCEL в достаточно ограниченном виде: невозможно указать на диаграмме значение изолинии (диапазоны цветов указаны на Легенде), разбиение на диапазоны по Z производится MS EXCEL автоматически и нет возможности на это повлиять. Ниже приведены изолинии для упомянутого выше гиперболоида. Это особый вид диаграммы – Проволочная контурная .
Практически такой же картинки можно добиться простым поворотом фигуры на диаграмме Поверхность .
Построение поверхностей второго порядка в excel
Построение поверхностей в трехмерном пространстве средствами MS Excel 2010.
Цель работы: Изучение графических возможностей пакета MS Excel 2010. Приобретение навыков построения поверхностей в трехмерном пространстве средствами пакета.
В этой лабораторной работе мы рассмотрим плоскость, а также поверхности второго порядка: эллипсоид, гиперболоид, параболоид и конус второго порядка.
Плоскость
Любое линейное уравнение определяет плоскость и, наоборот, уравнение любой плоскости есть уравнение первой степени.
называется общим уравнением плоскости.
Важные частные случаи уравнения плоскости возникают при равенстве нулю некоторых из коэффициентов А, В, С и D. Если D = О, то уравнение
определяет плоскость, проходящую через начало координат.
Если А=О, то уравнение
определяет плоскость, параллельную оси Ох; если А=D =, то уравнение
определяет плоскость, проходящую через ось Ох, если А=В=0, то уравнение
определяет плоскость, параллельную плоскости Оху; если А=В=D=0, то уравнение
Cz = 0 (или z = 0) определяет координатную плоскость Оху.
Существует также ряд уравнений, определяющих плоскости, обладающие специальными свойствами:
1. Уравнение плоскости в отрезках:
где а,b,с — отрезки, отсекаемые плоскостью на осях координат с учетом знака.
2. Уравнение плоскости, проходящей через заданную точку 
3. .Уравнение плоскости, проходящей через три точки
В MS Excel с помощью диаграмм можно построить плоскость. Необходимо ввести точки плоскости в рабочую таблицу, вставить диаграмму, задав ее тип, диапазоны данных и подписей оси х, ввести названия осей.
Пример1. Рассмотрим построение плоскости в Excel на примере уравнения 
Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере z = х + 2у + 1.
Введем значения переменной х в столбец А. Для этого в ячейку А1 вводим символ х. В ячейку А2 вводится первое значение аргумента — левая граница диапазона (0). В ячейку A3 вводится второе значение аргумента — левая граница диапазона плюс шаг построения (0,5). Затем, выделив блок ячеек А2:АЗ, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки А14).
Значения переменной у вводим в строку 1. Для этого в ячейку В1 вводится первое значение переменной — левая граница диапазона (0). В ячейку С1 вводится второе значение переменной — левая граница диапазона плюс шаг построения (1). Затем, выделив блок ячеек В1:С1, автозаполнением получаем все значения аргумента (за правый нижний угол блока протягиваем до ячейки H1).
Далее вводим значения переменной z. В ячейку В2 вводим ее уравнение — =$А2+2*В$1+1. Обращаем внимание, что символы $ предназначены для фиксации адреса столбца А — переменной x: и строки 1 — переменной у. Затем автозаполненнем (протягиванием вправо) копируем эту формулу вначале в диапазон В2:Н2, после чего — в диапазон ВЗ:Н14 (протягиванием вниз).
В результате должна быть получена следующая таблица (рис. 1).
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведите вид получившейся диаграммы как показано на рисунке:
Упражнения
1. Построить плоскость, параллельную плоскости Оху и пересекающую ось Oz в точке М(0, 0, 2). Диапазоны изменения переменных х и у.хÎ [0;6] с шагом = 0,5, уÎ [0; 6] с шагом = 1.
2. Построить плоскость, отсекающую на координатных осях отрезки а = 3, b= 2 и с = 1. Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1; 3] с шагом = 1.
3. Построить плоскость, проходящую через точки М(3,3,1), М2(2,3,2), М3(1,1,3). Диапазоны изменения переменных х и у: хÎ [-1; 4] с шагом = 0,5, у Î [-1;3] с шагом = 1.
Поверхности второго порядка в пространстве
Общее уравнение поверхностей второго порядка имеет вид уравнения второй степени:
Ах 2 + By 2 + Cz 2 + 2Dxy + 2Eyz + 2Fzx + 2Gx + 2Hy + 2Kz + L = 0.
Причем коэффициенты А, В, С, D, E, F немогут быть равны нулю одновременно.
Частными случаями уравнения являются основные поверхности второго порядка: эллипсоид, гиперболоид и параболоид.
Эллипсоид
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:
Это уравнение называется каноническим уравнением эллипсоида. Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии. Для построения эллипсоида в Excel каноническое уравнение необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример2. Рассмотрим построение эллипсоида в Excel на примере уравнения:
Пусть необходимо построить верхнюю часть эллипсоида, лежащую в диапазонах: х Î [-3; 3], у Î [-2; 2] с шагом = 0,5 для обеих переменных. Решение.Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1-$A2^2/9-B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Гиперболоид
Существует два вида гиперболоидов: однополостные и двухполостные.
Однополостным гиперболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горловины.
Двухполостным гиперболоидом называется поверхность, определяемая уравнением
Двухполостный гиперболоид представляет собой поверхность, состоящую из двух отдельных полостей, каждая из которых имеет вид бесконечной выпуклой чаши. Указанные уравнения называются каноническими уравнениями гиперболоидов. Для построения гиперболоида в Excel канонические уравнения, как и в случае с эллипсоидом, необходимо разрешить относительно переменной z (представить в виде z = f(x, у)).
Пример3. Рассмотрим построение двухполостного гиперболоида вида
Пусть необходимо построить верхнюю часть гиперболоида, лежащую в диапазонах: хÎ[-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение. Вначале необходимо разрешить уравнение относительно переменной z. В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ(1+$A2^2/9+B$1^2/4):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Параболоид
Существует два вида параболоидов: эллиптические и гиперболические.
Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.
Гиперболическим параболоидом называется поверхность, определяемая уравнением
Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида; числа р и q называются его параметрами.
Пример 4. Рассмотрим построение гиперболического параболоида вида
Пусть необходимо построить часть параболоида, лежащую в диапазонах: х Î [-3; 3], у Î[-2; 2] с шагом = 0,5 для обеих переменных.
Решение.Вначале необходимо разрешить уравнение относительно переменной z.В примере
Создайте таблицу значений данной зависимости, введя, а затем копируя, в ячейки B14:J26 формулу =КОРЕНЬ($A2^2/18-B$1^2/8):
Построим диаграмму. Выделим диапазон данных (без значений х и у). Выберем вкладку Вставка – Диаграммы – Другие – Проволочная поверхность.
Приведем вид получившейся диаграммы как показано на рисунке:
Конус второго порядка
Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением
Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.
В Excel построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.
Упражнения
1. Построить верхнюю часть эллипсоида:
Диапазоны изменения переменных х и у.хÎ[-2; 2] с шагом = 0,5; yÎ [-3; 3] с шагом = 1.
2. Построить верхнюю часть однополостного гиперболоида:
Диапазоны изменения переменных х и у.х Î[-3; 3] с шагом = 0,5,у Î[-4; 4] с шагом = 1.
3. Построить эллиптический параболоид:
Диапазоны изменения переменных х и у:х Î[-2; 2] с шагом = 0,5,у Î [-3; 3] с шагом = 1.
4. Построить верхнюю часть конуса
Диапазоны изменения переменных х и у. х Î [-2; 2] с шагом = 0,5, у Î[-3; 3] с шагом = 1.
| | | следующая лекция ==> |
| | | Решите задачи с использованием диаграммы Эйлера-Венна. |
Дата добавления: 2017-02-25 ; просмотров: 2062 | Нарушение авторских прав
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
by Ирина Кяршис
ГЛАВА 1. Возможности табличного процессора Microsoft Excel
1.1.Ввод данных в Excel
Электронная таблица – это программа, позволяющая автоматизировать табличные расчеты. Документ Microsoft Ехсел является рабочей книгой, состоящей из листов. Таблица состоит из 65536 строк и 256 столбцов. Строки нумеруются числами, столбцы – буквами латинского алфавита (А, В …, Z, АА, АВ …). На пересечении строки и столбца расположена ячейка, которая имеет адрес, состоящий из имени столбца и номера строки (А4). Одна из ячеек всегда является активной.
Прямоугольная группа смежных ячеек называется диапазоном ячеек. Примеры диапазонов – А2: С4, В2: К40.
Ячейки могут содержать данные трех типов:
1) Текстовые данные – это строка текста произвольной длины.
2) Числовые данные – это отдельное число. Может быть целым, дробным (зап.). Если ширина ячейки мала, то число записывается в экспоненциальной форме, например 125 000 000 → 1,25Е + 8 или вместо числа ставятся символы ###. При этом число сохраняется.
3) Формула – это арифметическое выражение. Он представляет собой последовательность чисел, ссылок на ячейки и функций, объединенных знаками арифметических операций: +, -, /, *. Excel предлагает несколько сотен встроенных функций, которые разделены на категории.
Ввод формулы в ячейку необходимо начинать со знака =. В ячейке вместо правильного результата, финансирования при ее вычислении.
Формулы можно копировать, использую относительную и абсолютную адресацию . Относительный адрес доступа к помещению, исходя из ее расстояния до другого ячейки столбца или строки. При копировании формулы, хранящиеся адреса, эти адреса изменяются в соответствии с новым положением формулы.
Абсолютный адрес ячейки описывает ее точные координаты. При копировании формулы, сохраненный адрес, эти адреса не изменяются. Запись абсолютных адресов содержит знаки доллара ($ A $ 2). Можно использовать смешанные адреса, которые задают столбец относительно, а строку абсолютно, или наоборот (A $ 5, $ D3).
1.2.Типы диаграмм
В зависимости от типа диаграммы данные отображаются на ней разным способом.
Можно отметить несколько стандартных типов:
1. Гистограмма . В этом типе диаграмм данные отображаются в виде вертикальных или горизонтальных столбцов. Высота каждого столбца соответствует отображаемому значению. Если отображается несколько согласованных рядов, то столбцы либо строятся рядом, либо один над другим.
2. Линейчатая . Создание и настройка Линейчатой диаграммы аналогично Гистограмме. Различие состоит в том, что столбцы расположены не вертикально, а горизонтально.
3. График . Диаграмма График создана для отображения графиков функций (одному значению Х соответствует только одно значение Y). В этих диаграммах точки соединяются линиями.
4. С областями . Диаграмма с областями похожа на график.
5. Круговая диаграмма . В этом типе диаграмм величины отражаются секторами круга. Чем больше величина, тем большую долю круга занимает ее отображение.
Диаграмма Круговая не похожа на другие типы диаграмм, прежде всего потому, что формально в ней не используются Оси.
6. Точечная . Визуально Точечная диаграмма похожа на диаграмму типа График (если у Точечной диаграммы точки соединены линиями)
7. Поверхность . Диаграмма, в которой ряды становятся линиями для некоторой поверхности в объеме.
8. Лепестковая диаграмма . Каждый ряд отображается как линия, соединяющая точки на радиусах.
Подробнее о типах диаграмм здесь
1.3 Основы построения диаграмм в Excel
Чтобы создать диаграмму в MS Excel, сначала необходимо создать таблицу с исходными данными.
Для построения диаграммы необходимо как минимум один столбец (строка) числовых данных.
Необходимо выделить необходимый диапазон данных в таблице. Далее на вкладке Вставка в группе Диаграммы выбрать тип диаграммы.
Практически у всех типов диаграмм есть следующие элементы:
1. Название диаграммы
2. Область диаграммы
3. Область построения
4. Ряд данных (может быть несколько)
5. Подписи данных (для каждого ряда)
6. Легенда (нужна при наличии нескольких рядов данных, позволяет отличить разные наборы данных на диаграмме)
7. Оси (вертикальная, горизонтальная, вспомогательные). Осей нет у круговой диаграммы.
Совокупность этих элементов определяет макет диаграммы.
Для настройки макета существует отдельная вкладка Макет. В этой вкладке, а также на вкладке Формат есть группа Текущий фрагмент, с помощью которой можно быстро выделить нужный элемент.
Разберем основные элементы макета.
1. Название диаграммы. При создании диаграммы на основе таблицы с одним числовым столбцом, заголовок столбца автоматически становится названием диаграммы и именем ряда.
Выделить название диаграммы можно просто кликнув на него левой кнопкой мыши (или можно выбрать пункт Название диаграммы).
Дважды кликнув по Названию диаграммы левой клавишей мыши, будет выведено окно его свойств. Можно настроить отображение названия в нужном стиле.
Основные настройки также можно сделать через вкладку Формат, группа Стили фигур и Стили WordArt или через вкладку Главная, группа Шрифт.
2. Область диаграммы – это прямоугольник, на котором располагаются все остальные элементы диаграммы. Область диаграммы можно отформатировать по своему усмотрению
Для каждого типа диаграмм в MS EXCEL 2010 существуют заранее созданные стили.
Применение стиля коснется формата всех элементов макета (названия, области диаграммы, подписей данных, осей, области диаграммы и др.), даже если они в данный момент не выделены (в отличие от Стилей фигур на вкладке Формат, которые применяются только к выделенному элементу диаграммы).
3. Область построения . Настройка формата Области построения аналогична настройке формата Области диаграммы.
4. Ряды данных . Каждая диаграмма должна содержать хотя бы 1 Ряд данных. В зависимости от типа диаграммы отображение Ряда данных и его настройка будут различными.
Чтобы выделить Ряд данных, нужно кликнуть левой клавишей мыши по одному из столбцов гистограммы (или линии на диаграмме типа График, или по кругу на круговой диаграмме и т.д.) Также можно выбрать нужный Ряд в выпадающем списке, который находится в группе Текущий фрагмент на вкладке Макет или Формат.
Если Ряд данных выделен, то на листе также выделяется диапазон ячеек, содержащий источник данных. Настроить формат Ряда данных можно с помощью вкладки Формат или с помощью Окна свойств.
Чтобы удалить Ряд данных: кликните на нужный ряд данных и нажмите на клавиатуре клавишу DELETE. Если будет удален последний ряд, то вместе с ним удалятся Оси, Легенда и Область построения, но останется Область диаграммы.
5. Подписи данных . Чтобы отобразить подписи данных, необходимо выделить нужный ряд данных, а затем во вкладке Макет в группе Подписи выбрать нужный вариант размещения подписи.
Подписи данных, как правило, представляют собой значения из исходной таблицы, на основании которых и была построена диаграмма. Дважды кликнув на одну из подписей левой клавишей мыши можно вызвать диалоговое окно для настройки свойств подписи.
В качестве подписи можно установить не только само значение, но и имя ряда и имя категории (для Точечной диаграммы – значения Х).
В окне Формат подписей данных имеется вкладка Число, через которую можно настроить отображение числовых значений.
В случае необходимости можно индивидуально отредактировать подпись к определенной точке ряда.
6. Легенда . Полезна только при наличии нескольких рядов данных, т.к. позволяет отличить их на диаграмме.
Чтобы отобразить Легенду, необходимо во вкладке Макет в группе Легенда выбрать нужный вариант размещения. В том же меню доступно диалоговое окно Формат легенды для настройки свойств. Через тоже меню можно удалить Легенду (или нажать на клавиатуре клавишу DELETE).
В случае необходимости можно удалить из Легенды отображение имени определенного ряда.
7. Оси . При создании Гистограммы, Графика или Точечной диаграммы создаются горизонтальная и вертикальная оси (основные).
Конкретные параметры оси зависят от типа диаграммы и от типа оси (вертикальная или горизонтальная). Диалоговое окно свойств оси можно вызвать, выбрав пункт Горизонтальная ось или Вертикальная ось в выпадающем списке, который находится в группе Оси на вкладке Макет или Формат.
Можно создать Названия для осей и линии сетки по основным и вспомогательным значениям оси.
Если необходимо изменить источник данных или добавить новый ряд данных, то для этого выделите диаграмму, на вкладке Конструктор в группе Данные нажмите пункт Выбрать данные.
ГЛАВА 2. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
2.1 Уравнения поверхностей второго порядка и их графики
Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.
Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2+z^2/c^2=1, где a, b, c – полуоси эллипсоида.
Если a = b = c, имеем сферу (шар): x^2+y^2+z^2=a^2.
Однополостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=1, где a и b – действительные полуоси, с – мнимая полуось.
Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется каноническим уравнением: x^2/a^2+y^2/b^2-z^2/c^2=-1,где с – действительная полуось, a и b – мнимые полуоси.
Поверхностная диаграмма в Excel и пример ее построения
Принцип построения поверхностных диаграмм в Excel можно сравнить с рельефными картами. Где положение пункта определяется не только долготой и широтой, но и третьей величиной – высотой.
Данное сравнение поможет понять, как создать на первый взгляд сложную поверхностную диаграмму в Excel и как ее использовать.
Построение поверхностной диаграммы в Excel
Практический пример применения и создания поверхностной диаграммы в Excel.
Напряжение излучения в квадратной комнате определено формулой z=[sin(x)*y] 2 . Начало осей координат расположено центру комнаты.
Визуально сложно определить место в комнате, где наиболее интенсивное излучение. Создадим графическое представление ситуации, которое будет читабельно даже для дилетантов.
Сначала выполним все необходимые расчеты и вычисления в таблице. А поверхностную диаграмму построим на основе уже полученных данных.
- Заполните таблицу как указано на рисунке.
- Выделите диапазон B2:L12 так, чтобы B2 активной ячейкой выделенного диапазона (выделяйте с верхнего левого угла B2 диапазона к нижнему правому углу до ячейки L12).
- Не снимая выделения, введите в строку формул: =(SIN(B$13)*$A2)^2 и нажмите комбинацию клавиш CTRL+Enter. Обратите внимание, как мы используем в аргументах формулы смешанные ссылки на ячейки.
- Между столбцами A и B вставьте новый столбец и заполните его вторую ячейку формулой: =» «&A2 (не забудьте поставить пробел между кавычками). Скопируйте эту формулу во все ячейки столбца до 12-ой строки (то есть заполните этой формулой диапазон ячеек B2:B12).
- Выделите диапазон: B2:M12 и выберите инструмент: «Вставка»-«Диаграммы»-«Другие»-«Поверхность».
Теперь четко видно на диаграмме что наибольшая интенсивность излучения находится в углах комнаты.
Чтобы правильно настроить горизонтальную ось X, щелкните по диаграмме, чтобы ее активировать и выберите инструмент: «Работа с диаграммами»-«Конструктор»-«Выбрать данные».
В появившемся окне «Выбор источника данных» в правом разделе «Подписи горизонтальной оси (категории)» щелкните на кнопку «Изменить».
В окне «Подписи оси» измените значение, выделив диапазон ячеек C13:M13 и на всех диалоговых окнах нажмите ОК.
Краткое описание примера
Стоит отметить! При создании поверхностной диаграммы мы изменили числовые значения столбца A в текстовые, поместив их в столбец B с помощью формулы . Если бы мы этого не сделали, то Excel воспринял бы эти числовые значения (столбца A) как данные для построения поверхностной диаграммы, а не как подписи данных.
Если бы мы просто присвоили текстовый формат для значений столбца A (вместо дополнительного столбца с формулами), тогда мы просто получили бы ошибку при расчетах.
Вот в такой нехитрый способ мы красиво сделали подписи для осей диаграммы и не допустили ошибок при расчетах.
источники:
http://4systems.ru/inf/postroenie-poverhnostej-vtorogo-porjadka-v-excel/
http://exceltable.com/grafiki/poverhnostnaya-diagramma


В продолжении темы о графиках функций в Excel расскажу о построении трехмерных графиков.
Трехмерный график функции — это график в трех измерениях. Соответственно каждая точка графика будет иметь три координаты (x, y. z).
Построим график функции, называемый гиперболический параболоид, в Excel.
Уравнение гиперболического параболоида (общий вид):
где x, y, z — переменные; a, b — константы.
Рассмотрим конкретный случай:
Как и для построения графика функции на плоскости нам потребуется таблица, на основании которой график и будет построен.
по горизонтали — значения х, по вертикали — значения у.
Значения z вычисляются по формуле (см. выше). Запишем формулу для вычисления z, где x=10, y = 10, a=2, b=3.
Для того, чтобы эта формула правильно копировалась с помощью маркера автозаполнения необходимо верно поставить знаки $ в формулу.
=(C$2^2/4)-($B3^2/9) , для ячейки со значением x фиксируем номер строки, для ячейки со значением y фиксируем букву столбца.
Используя маркер автозаполнения, копируем формулу для всех значений x и y.
Получим таблицу, в которой каждой паре (x, y) соответствует координата z.
Выделяем диапазон ячеек со значениями z, выбираем ВСТАВКА — ДРУГИЕ ДИАГРАММЫ — ПОВЕРХНОСТЬ
Скачать Гиперболический параболоид в Excel
Аналогично строятся другие поверхности:
1) Эллиптический параболоид
2) Однополостный гиперболоид
3) Двухполостный гиперболоид
См. также «Построение графиков функций на плоскости в Excel»
Вы можете оставить комментарий, или ссылку на Ваш сайт.
Оставить комментарий
В мир информатики # 82 (1-15 ноября). Трехмерные графики в Microsoft Excel
Л.Н. Медведев,
Москва
Как вам, очевидно, известно, одной из
основных задач, решаемых с помощью программы
Microsoft Excel, является построение диаграмм и
графиков (наряду с решением расчетных задач, в
которых информация представлена в виде таблицы).
А можно ли построить в Microsoft Excel трехмерное
изображение? Например, поверхность, называемую
“параболоидом вращения” (ее вид показан на рис.
1)?
Рис. 1
Нет ничего проще! Но прежде чем
рассказывать о том, как это сделать, надо немного
поговорить о так называемых функциях двух
переменных. Такая функция имеет вид z = f(x, y),
где x и y — координаты точки на плоскости1
,
а z — значение функции. Например, функция,
изображенная на рис. 1, записывается так: f(x,
y) = x2 + y2.
Определим интервалы, в которых будут
изменяться значения аргументов x и y.
Пусть это будет симметричный интервал (–5, 5) для x
и другой симметричный интервал (–9, 9) для y.
Шаг, с которым будут изменяться значения x и y,
установим равным 0,2. Вообще говоря, выбор
величины шага определяется исходя из требуемой
“подробности” построения графика. Теперь на
рабочем листе Excel зададим значения этих
координат в виде строки B1:AZ1 для x и столбца
A2:A92 для y (см. рис. 2, на котором показано
начало этой таблицы).
Рис. 2
Теперь введем в ячейку B2 формулу.
Необходимо предварительно продумать адресацию
ячеек, ведь этой формулой мы потом заполним весь
диапазон B2:AZ92. Кстати, если у вас компьютер не
слишком мощный, то диапазон следовало бы
уменьшить, так как в нем помещается ни много ни
мало 4641 ячейка. При небольшой производительности
и памяти машины этот объем данных может для нее
составить значительную сложность.
Итак, формула. При заполнении
интервала по горизонтали (оси x) формулы во
всех ячейках должны ссылаться на
соответствующую ячейку верхнего ряда,
следовательно, она должна иметь абсолютную
адресацию по номеру строки, а по номеру столбца —
относительную адресацию. Напомню, что абсолютная
адресация обозначается знаком “$”
перед
соответствующей координатой адреса ячейки. В
нашем случае адресация выглядит так: B$1. Что
касается y, то здесь наоборот: абсолютным
должен быть номер столбца, а номер строки —
относительным, т.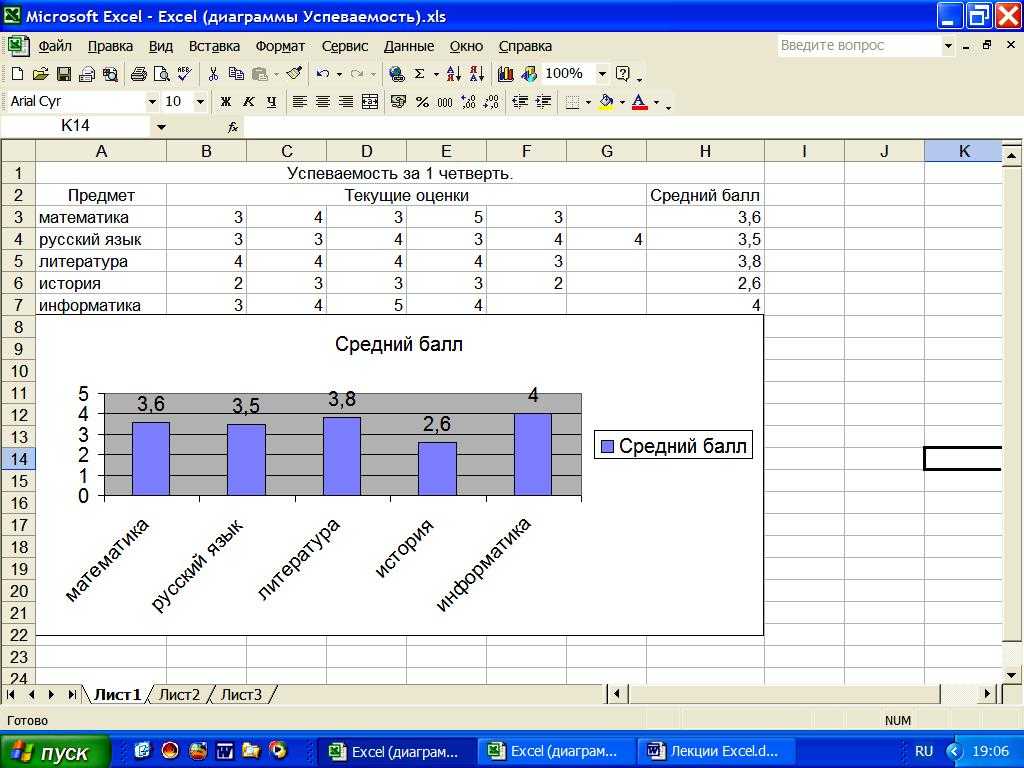
соберем всю формулу. Чтобы не использовать
дополнительных функций, в квадрат будем
возводить просто умножением: =B$1*B$1+$A2*$A2. Этой
формулой можно теперь заполнить весь
прямоугольник от B2 до AZ92. Исходный массив данных
готов. На рис. 3 — начало получившейся
таблицы.
Рис. 3
Теперь можно строить диаграмму.
Вызываем Мастер диаграмм. Для построения
трехмерных картинок надо выбрать тип диаграммы
— Поверхность, а вид — тот, который программа
предлагает по умолчанию — . Если у вас Excel
последних версий, то все уже готово (Мастер
диаграмм
сам выберет участок таблицы, из
которого надо брать данные, и построит
диаграмму), а если более старый — то надо указать
интервал данных (весь интервал A1:AZ92). Остается
только усовершенствовать оформление диаграммы,
в частности, если хотите получить более тонкие
полосы, то надо выбрать вертикальную ось (по
терминологии Excel — ось значений) и задать цену
основных делений.
4–5. Видно, что проработка улучшилась.
Рис.4
Рис. 5
В качестве упражнения попробуйте
построить “седло” (z = x2 – y2)
или такую поверхность, как на рис. 5 (z = sin(x
+ y) / (x + y)).
Желаю успехов!
1 В случае построения трехмерных
изображений. В общем случае это могут быть любые
параметры. — Ред.
3D-движок, написанный на формулах MS Excel / Хабр
Скриншот экрана игры
Эта статья посвящена тому, как я смог написать 3D-движок только на формулах Excel. Я реализовал следующий функционал:
- бесконечная процедурно генерируемая карта лабиринта
- рендеринг трассировкой лучей в реальном времени
- вычисление окклюзии
- рендеринг простейшего освещения
- шейдер освещения и вычислений
- движок естественного движения
- в 3D-движке не используются макросы
* чтобы управлять игрой нажатием клавиш, нужны макросы, управляющие движением с помощью одной простой инструкции копирования.
Можете скачать файл и протестировать его самостоятельно!
Файлы
- Файл без vba: http://public.cbel.free.fr/?file=Doom.xlsx
- Файл с vba для перехвата нажатий клавиш: http://public.cbel.free.fr/?file=Doom.xls-v1.1.xlsm
- Файл с vba и высоким разрешением: http://public.cbel.free.fr/?file=Doom-HD.xls-v1.1.xlsm
- Файл с vba и кнопками вместо горячих клавиш: http://public.cbel.free.fr/downloads/?file=Doom.xls-Buttons-v1.1.xlsm
Учитель информатики однажды сказал нам: «любые вычисления можно выполнить в любом языке программирования, даже через формулы электронной таблицы».
Поначалу, какой бы мудрой ни казалась эта фраза, упоминание в этом списке Excel выглядело глупо…
Затем, после изучения машины Тьюринга, фраза стала для нас полностью верной, хотя и не вполне реализуемой.
Получив многолетний опыт работы с Excel, мы уже поняли, что единственное ограничение формулы Excel — недостаток способов ввода-вывода.
Но множество задач, решаемых исключительно формулами, по-прежнему выглядит впечатляюще.
Как бы то ни было, эта работа — не просто какое-то хвастовство… У меня были для неё серьёзные причины.
Электронные таблицы — это мощный инструмент, которому должен научиться каждый, ведь его можно использовать почти в любых деловых задачах.
Однако когда большинство людей доходят до решения более сложных задач, они стремятся использовать язык VBA, даже не понимая толком, зачем.
А начав изучать его, они пытаются использовать его для решения любых видов задач, даже для простого поиска или визуализации.
Сегодня я преподаю Excel, поэтому постараюсь объяснить людям, почему написание макроса на VBA для решения любой задачи без хорошего знания программирования — это не только пустая трата времени, но и серьёзный риск снижения качества электронной таблицы.
При использовании в бизнесе формулы обладают следующими преимуществами перед макросами:
- Их быстрее писать для любого человека, если он не профессиональный программист-аналитик
- Их проще поддерживать любому человеку, а не только профессиональному программисту.
(Чаще всего макросы становятся бесполезны после ухода их разработчика.)
- Гарантированное качество благодаря постоянной проверке значений. (Принудительное применение техники «разработка через тестирование»)
- Они более эффективны в долговременной перспективе благодаря процессу создания формул в стиле «думай, прежде чем писать».
- И они совершенно точно гораздо лучше интегрированы в сам инструмент создания электронных таблиц и следуют изначальному паттерну разработки электронных таблиц, в то время как макросы часто оказываются специфическими конструкциями, требующими в дальнейшем активной поддержки.
Примечание: эти пункты в основном относятся к процедурам, используемым как макросы; дополнительная функция, написанная на VBA, может увеличить эффективность, не снижая качества.
Вот так я пришёл к написанию своей игры: она стала наглядной демонстрацией того, что макросы обычно не нужны даже для решения самых сложных задач.
Если конкретнее, то я нашёл всего два случая, когда потребовался VBA:
- Добавление специфического ввода или вывода (как я сделал здесь для получения событий клавиш), потому что формула всегда ограничена изменениями в самой ячейке
- Некоторые сложные задачи (например, оптимизация), в которых вычисления занимают слишком много времени и/или пространства. Но такие задачи довольно редки в реальной жизни.
В оставшейся части этой статьи я расскажу как работают электронные таблицы в различных аспектах игры.
Моя электронная таблица должна была стать игрой в стиле Doom в лабиринте.
Можно было создать для неё постоянную, построенную вручную карту, возможно, зацикленную по краям, но она бы потребовала дополнительного места, поисков и изначальной разработки дизайна.
В то же время, гораздо более интересной целью мне казалась идея процедурно генерируемой бесконечной карты.
Для создания случайно генерируемой карты нам нужно быть последовательными, поэтому функцию rand() использовать нельзя, ведь мы не можем контролировать начальное состояние (seed) генератора случайных чисел.
Начальные состояния генератора случайных чисел должны быть позициями (x;y) на карте, чтобы мы могли получать разные значения для каждой позиции, и мы не можем получить результат предыдущего случайного числа как начальное состояние для следующего, или нам придётся хранить всю карту с самого начала.
Обычные хэш-функции, несмотря на обеспечение высокого качества случайных чисел, оказались слишком затратными, поэтому мне нужно было найти другое решение.
Эксперименты с фрактальным генератором тоже оказались довольно затратными и давали интересные результаты только для небольшой части карты.
Тогда я обнаружил метод средних квадратов (middle-square method), который на самом деле не очень «случаен», потому что в нём используются последовательные начальные состояния.
Я выяснил, что если брать десятичные части sin(x)+cos(y), то наконец-то получаются красивые числа без какого-либо прослеживаемого паттерна, а время вычислений при этом на удивление малО.
Для получения десятичных частей математические функции mod() и floor() гораздо более эффективны по сравнению с текстовой функцией подстроки mid().
Я стремился сделать карту похожей на крысиный лабиринт, поэтому создавал блоки не сплошными, чтобы они походили не на пещеры (в стиле Minecraft), а на лабиринт.
То есть нам нужны тонкие стены с двумя возможными стенами для каждого квадрата. Тогда мы сможем брать два блока чисел вместе с тем же случайным значением.
Плотностью размещения стен управляют два параметра.
С учётом этих правил мы можем или отображать лабиринт, или тестировать любую стену с заданной позицией с помощью трассировки лучей.
Стоит заметить, что карта «плоская», без подъёмов и спусков.
Так, похоже, мы в аду
Трассировщик лучей должен определять для каждого пикселя экрана, какой первой поверхности касается луч, и получать от неё информацию (расстояние, угол падения света, цвет и т.д.).
Кроме того, трассировщику лучей требуется дополнительный луч, распространяющийся из этой точки (отражения, прозрачность), что напрямую увеличивает вычислительные затраты.
Окклюзия
Первым сложным моментом будет нахождение первого объекта на пути каждого луча.
Поскольку лабиринт на самом деле плоский с горизонтальными стенами, то ближайшая найденная стена будет одинаковой для всех пикселей одного столбца.
То есть процесс можно упростить до горизонтального «радара» в одном измерении.
Тогда у нас нет иного выбора, кроме как проверять луч на первой вероятной стене, потом на второй вероятной, и так далее, пока мы не найдём нужную.
Определение того, какую стену нужно проверять — это всего лишь тригонометрическая задача.
И поскольку у нас всего два типа стен, мы можем тестировать оба типа, а потом сохранять только ближайшую.
Одно из ограничений Excel заключается в отсутствии условного цикла и для экономии времени можно только пропускать тело цикла. Поэтому нам нужно ограничить максимальное расстояние проверки, считая, что если на этом расстоянии стена не найдена, то её нет.
Пол и потолок
Чтобы определить потолок и пол, нам достаточно определить, где заканчивается стена.
Отдельный лист изменяет расстояние до пола или потолка в зависимости от вертикального угла.
Затем для каждого пикселя мы определяем, дальше ли стена, чем потолок или пол, и соответствующим образом задаём цвет пикселя.
Эффективное сравнение реализовано использованием только проекции расстояния до стены и до пола/потолка по оси камеры. Конечное расстояние затем получается с помощью предварительно вычисленного коэффициента расстояния в шейдере расстояний. Постоянные предварительно вычисленные значения нужны для экономии ресурсов.
Освещение
Конечное освещение берётся из шейдера освещения, представляющего собой свет факела, в направлении камеры (и оружия).
Когда поверхность точно горизонтальна к лучу света, также добавляется отражение.
Стена может быть только горизонтальной (если добавить наклон, то он просто смещает окно экрана вверх и вниз, не поворачивая камеру)
Для каждого угла радара мы получаем угол между лучом и ближайшей найденной стеной.
Коэффициент отражения — это просто функция угла.
В конце концов освещение становится результатом функции коэффициента расстояния, потолка/пола или разрешения стен, коэффициента отражения и коэффициента шейдера освещения.
Экран дисплея
Эффективный дисплей реализуется с помощью условного форматирования — градиент цвета зависит от значения ячейки.
Сокрытие значения выполняется форматированием ячейки.
Игрок не должен проходить сквозь стены, иначе это разрушит весь смысл лабиринта.
Кроме того, игрок не должен прилипать к стене при контакте с ней. Он должен двигаться, скользя вдоль стены, пока не попадёт в угол.
Также необходимо соблюдать минимальное расстояние между стеной и игроком, чтобы избежать графических проблем и придать стенам толщину.
Оказалось, что довольно сложно обработать все возможные варианты стены и позиций игрока относительно этой стены.
Изучено 25 вариантов и к ним привязано три возможных исхода (для каждой оси смещения), чтобы получать результаты за как можно меньшее количество проверок.
Несмотря на то, что это казалось самой короткой частью игры, таблица смещений стала самой сложной в реализации.
Привет, красное привидение!
Графический рендеринг
Сложность с врагами заключалась в том, чтобы получить форму, которую легко можно располагать перед стеной, легко рендерить на любом расстоянии, и которая будет интереснее, чем простой куб.
Целый отдельный лист посвящён вычислению формы сфер с учётом горизонтального радиуса и вертикальной высоты овоида. Для анимирования существа используется соотношение высоты/ширины.
В рендеринге стен и потолка используется градиент только по одному цвету, однако Excel позволяет использовать два последовательных (не сливающихся) градиента. Поэтому врагов можно отображать другим цветом. Для этого градиента можно использовать диапазон значений ниже 0, при том, что значение 0 — это чёрный цвет.
Меняющуюся прозрачность реализовать оказалось не сложнее, чем плавный рендеринг поверхности сферы.
На границе сферы низкая толщина сохраняет только значение цвета по умолчанию стены за ней с отрицательным коэффициентом для превращения его в цвет монстра. Фильтр цвета освещения обеспечивает прозрачность на границе сферы.
Здесь вычисления тоже производятся в горизонтальной плоскости, а максимальный объём вычислений подготавливается перед завершением 3D-вычислений для каждого пикселя.
Поведение врагов
Чтобы избежать реализации сложного и некачественного процедурного поведения, враги не будут реагировать на действия игрока. Их позиция определяется только временем, они движутся по сложной траектории, чтобы паттерн был не таким заметным.
Чтобы позиция, скорость и ускорение были непрерывными (для плавного движения), я сделал траекторию своего рода конечным фракталом большого круга с добавленными к нему небольшими круговыми вариациями. Коэффициент соотношения между кругами (и даже соотношение x/y) случаен и ненатурален, поэтому траектория никогда не самозацикливается.
Так как траектории не могут учитывать стены, я был вынужден оставить монстрам возможность проходить сквозь них.
В каждый момент времени вычисляется несколько траекторий. Весь лабиринт населён одними и теми же десятью врагами, расположенными в сетке на значительном расстоянии, чтобы игрок не мог увидеть двух одинаковых монстров одновременно.
Можно уменьшать/увеличивать сетку повторов, чтобы повышать/снижать плотность расположения врагов. При этом следует внимательно следить за конечным смещением монстра, чтобы оно не было чрезмерным, и за скоростью, изменяющейся при масштабировании.
Создав ограниченное количество управляемых врагов, можно скопировать их по всему лабиринту.
Атаки врагов
Анимация врагов сделана с помощью соотношений их радиуса/высоты. Так как атака врага должна быть чётко заметна, но в то же время достаточно медленной, чтобы игрок смог отреагировать, враги просто увеличиваются в радиусе, когда замечают игрока.
Область видимости каждого монстра вычисляется на вкладке радара с учётом расположения стен.
Игрок получает урон, когда он оказывается внутри радиуса врага. Если игрок специально забирается внутрь врага, происходит то же самое.
Это создаёт эффект наносимого игроку урона — простой эффект негативного цвета во весь экран.
Добавлен также ещё один эффект — отмена рендеринга всех остальных врагов при нанесении урона игроку.
Жизнь игрока указана как один из элементов его статуса, который обрабатывается поэтапно, как и его положение.
Атаки игрока
Каждый враг получает значение статуса, определяющее его оставшуюся жизнь и фазу атаки. При некоторых значения враги просто не отображаются, при некоторых других враги медленно регенерируют, а последнее заставляет врага взорваться.
Эта упрощённая модель позволяет игроку предотвратить атаку врага, снизив его жизнь до нуля.
Чтобы увеличить сложность, добавлена сложность прицеливания в маленьких врагов, которые остаются на дальнем расстоянии, а боеприпас через какое-то время требует перезарядки.
При убийстве враг просто переходит в состояние бездействия и медленной регенерации. Так как по всей карте повторяется несколько врагов, ни одного из них нельзя уничтожать полностью.
Смерть и перезапуск
Когда жизнь игрока снижается до нуля, бОльшая часть его действий приостанавливается и появляется экран конца игры.
Этот экран рендерится с помощью ещё одного шейдера освещения. К цвету применён эффект негатива, чтобы подчеркнуть нанесение урона.
Постепенное отображение сообщения «game over» реализовано с помощью небольшого коэффициента, увеличивающегося как степенная функция. Это позволяет будущим пикселям оставаться скрытыми до их появления, когда степень становится достаточно большой.
Сдвигание вниз — это простое смещение шейдера освещения, в который добавлены другие сообщения, например, рекорды (high score) и перезапуск игры.
Очки должны отрисовываться с помощью пикселей шрифтом очень низкого разрешения.
При перезапуске генерируется новый начальный параметр, а сам игрок отправляется в другую точку, чтобы не встретиться с теми же врагами.
Диаграммы
— Как построить трехмерный (XYZ) график в Excel
Задавать вопрос
спросил
2 года 10 месяцев назад
Изменено
3 месяца назад
Просмотрено
5к раз
У меня есть таблица данных, но она в 2D (XY):
Х 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Д 4 4 4 4 10 15 20 25 25 25 25 25 25 20 15 10 4 4 4 4
И полученный график будет выглядеть так:
Итак, вот моя проблема. На самом деле, я хочу построить трехмерный график, который будет выглядеть точно так же, как изображение, прикрепленное выше, когда мы видим его в 2D, но для построения трехмерного графика у меня нет никаких идей о данных Z или уравнении Z, которые мне нужно учитывать.
Ниже приведен пример трехмерного графика, который мне нужен:
Мне очень жаль, если мой вопрос сбивает с толку. Я очень надеюсь, что кто-то может мне помочь. Мне нужна помощь в определении уравнения Z, чтобы я мог создать трехмерный график.
После того, как трехмерный график получен, мне нужно приступить к вычислению его наклона. Вот почему мне действительно нужно знать, как построить трехмерный график на основе прикрепленного изображения.
- Microsoft-Excel
- диаграммы
- 3D
2
Это видео содержит учебник по созданию 3D-графиков в Excel.
Как только ваши данные X и Y будут правильно подготовлены (в столбце и строке соответственно), вы можете ввести данные Z в ячейки, соответствующие каждому значению X и Y. На видео это делается по формуле.
Чтобы создать график Surface , как показано в видео, нажмите Insert , Other Charts , затем один из значков под Surface .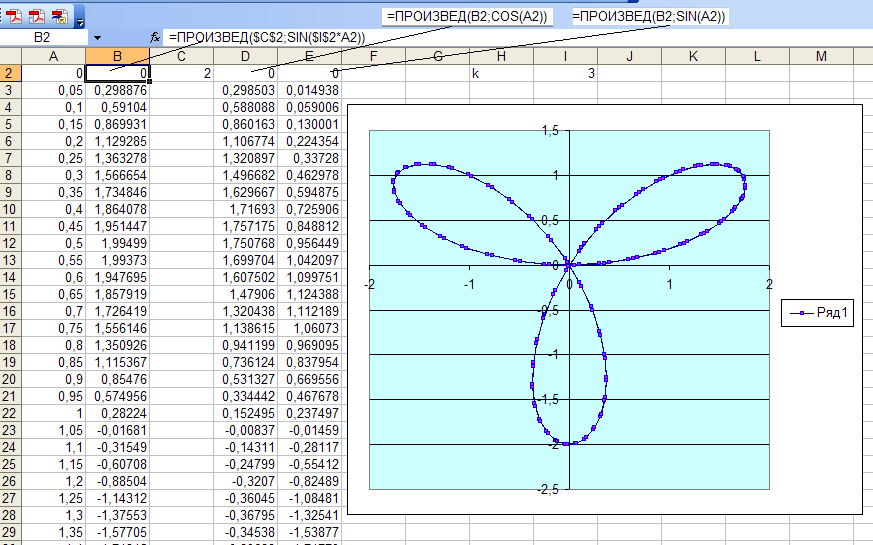
Другие методы построения 3D-данных можно найти здесь и здесь.
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
спросил
8 лет, 8 месяцев назад
Изменено
8 лет, 7 месяцев назад
Просмотрено
2к раз
Мне нужно сравнить два метода, называемых «Основная проблема» и «Наша итерация», нарисовав график. Для этого у меня есть следующие данные.
var number Ограничение Число итераций в основной проблеме Итерации в нашем предложении 1000 100 36 32 1000 200 40 32 1000 300 56 35 1000 400 66 37 1000 500 70 47 2000 100 76 52 2000 200 87 57 2000 300 91 67 2000 400 95 72 2000 500 110 83
Как я могу построить график из этого?
Я хочу иметь следующий график.
- Microsoft-Excel
- Microsoft-Excel-2010
6
Трехмерные гистограммы — очень плохая визуализация данных.

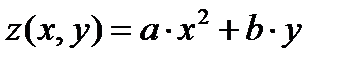


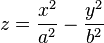
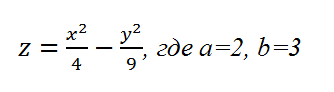


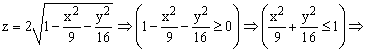
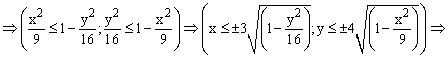




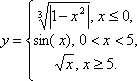




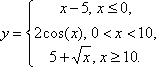







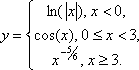






 <
<













































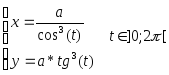












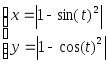
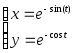






























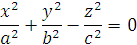





 (Чаще всего макросы становятся бесполезны после ухода их разработчика.)
(Чаще всего макросы становятся бесполезны после ухода их разработчика.)