Задание на построение графика функции в excel

Цель работы:

• научиться строить графики в Excel;
• развить самостоятельность;
• развить навыки мыслительной деятельности, включая каждого учащегося в учебно – познавательный процесс и создавая условия для работы каждого в индивидуальном темпе;

Оборудование:

• ПЭВМ, сеть, проектор;
• опорный конспект, план практической работы, варианты для самостоятельной работы учащихся.

Этапы	План урока + опорный конспект	Средства обучения
I	Подготовительный. Постановка учебных задач. Устное разъяснение порядка работы на уроке, тема урока.	—
II	Повторение. Фронтальный опрос изученного материала. Вопросы: предназначение Excel: Расчеты по формулам Графики и диаграммы путь к папке, где сохранить работу.	проектор
III	Объяснение нового материала и подготовка к практической работе: объяснение построения графиков в Excel; работа с проектором. Показать, как и что должно получиться; Раздача вариантов работы.	Проектор, раздаточный материал
IV	Выполнение проектной практической работы: сохранение работы в папку «ГРАФИКИ» под своими идентификаторами; помощь ученикам.	Компьютер
V	Итоги: демонстрация работ учащимися на проекторе и оценка за работы; определение лучшей работы; подведение итогов.	Проектор, раздаточный материал, компьютер

Опорный конспект

Построение совмещенных графиков в Microsoft Office Excel -2007.

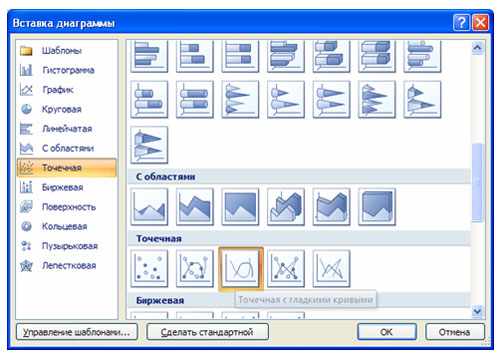
Для построения графиков функций Y(X) в Microsoft Office Excel используется тип диаграммы Точечная:

Для этого требуется два ряда значений: Х и Y значения, которые должны быть соответственно расположены в левом и правом столбцах.
Можно совместить построение нескольких графиков. Такая возможность используется для графического решения систем уравнений с двумя перемен­ными, при проведении сравнения анализа значений y при одних и тех же значениях x.

ПРИМЕР.
(Используется при объяснении материала через проектор.)
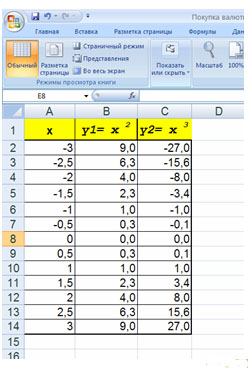
Построить графики функций y1= x ² и y2= x ³ на интервале [- 3 ; 3] с шагом 0,5.
Алгоритм выполнения задания:
1. Заполнить таблицу значений:

2. Выделить таблицу и указать тип диаграммы Точечная.
3. Выбрать формат точечной диаграммы с гладкими кривыми.
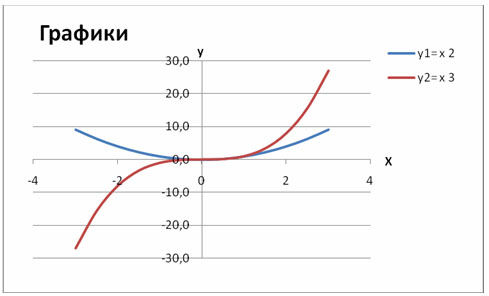
4. В Макете указать название диаграммы «Графики», дать название осей: X и Y

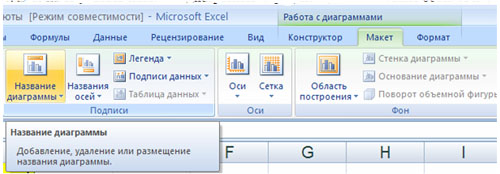
5. Должен получиться график:

P.S. В версии 97-2003 для получения графика, представленного на рисунке надо провести редактирование.

Раздаточный материал

Варианты

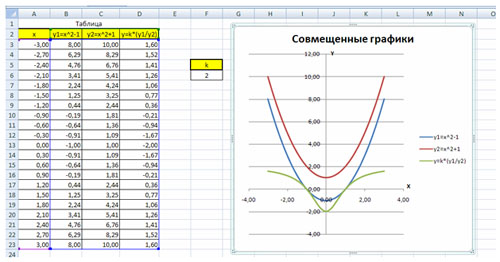
ВАРИАНТ 1
Построить графики функций y1= x ² -1, y2= x ²+1 иy=К·(y1/ y2)на интервале [- 3 ; 3] с шагом 0,3.

ВАРИАНТ 2
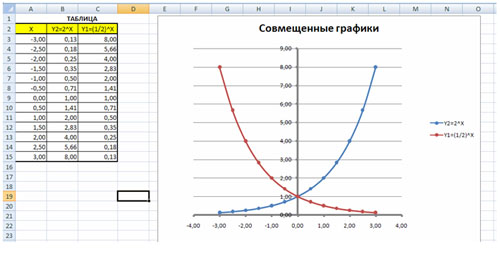
 Построить графики функций y1= и y2= 2^х на интервале [- 3 ; 3] с шагом 0,5.

ВАРИАНТ 3
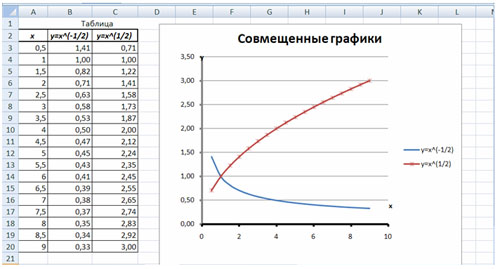
 Построить графики функций y1= , y2=на интервале [- 0,5 ; 9] с шагом 0,5.

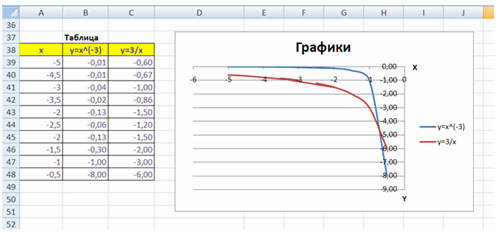
ВАРИАНТ 4
 Построить графики функций y1=, y2= на интервале [- 5 ; -0,5] с шагом 0,5.

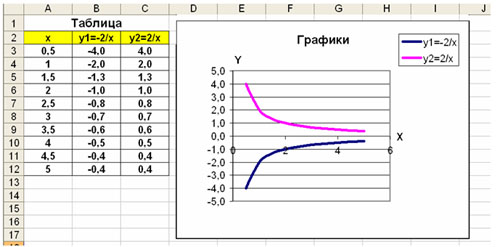
ВАРИАНТ 5
 Построить графики функций y1= , y2=на интервале [0,5 ; 5] с шагом 0,5.

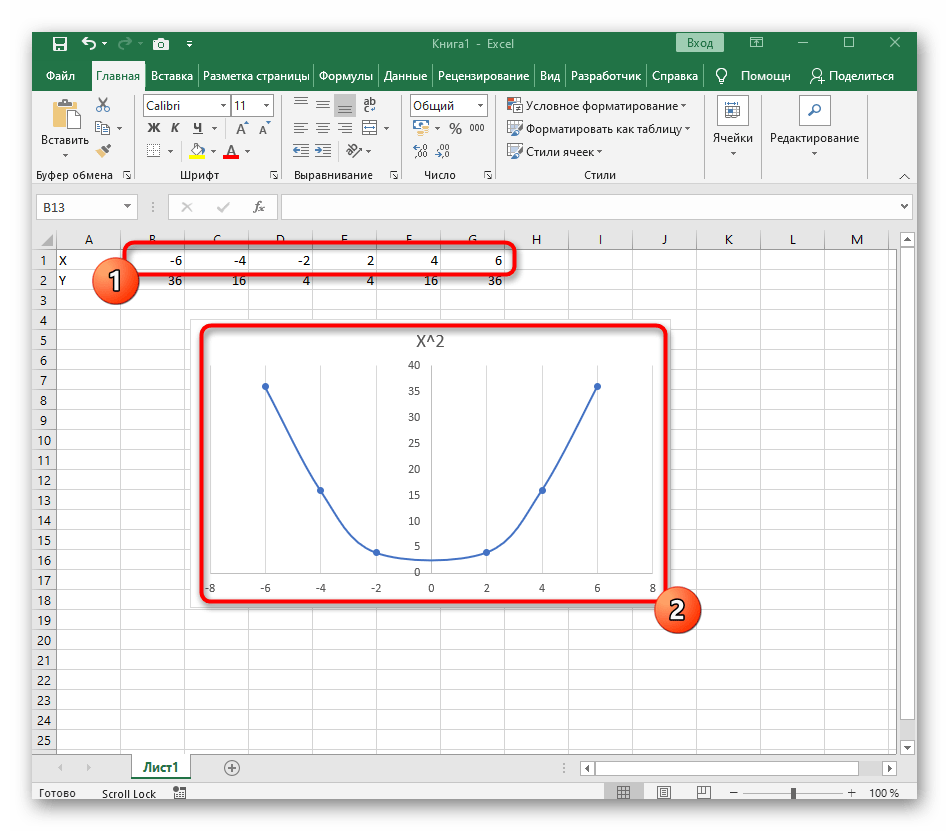
Вариант 1: График функции X^2

В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.

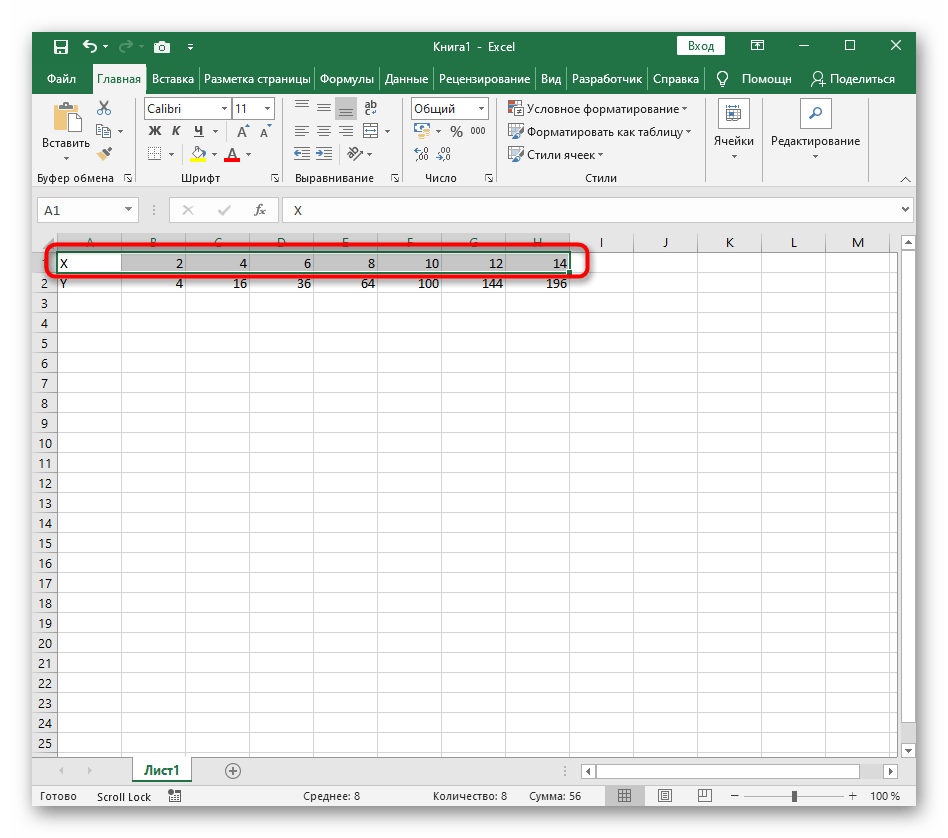
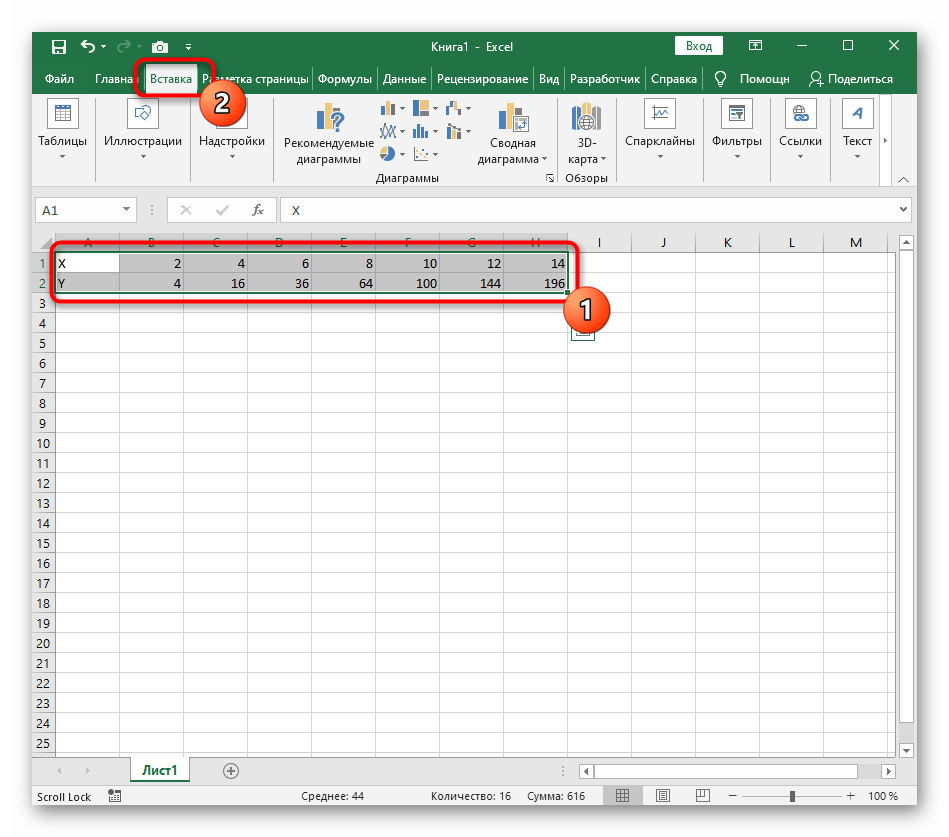
1. Создайте строку X, где укажите необходимый диапазон чисел для графика функции.



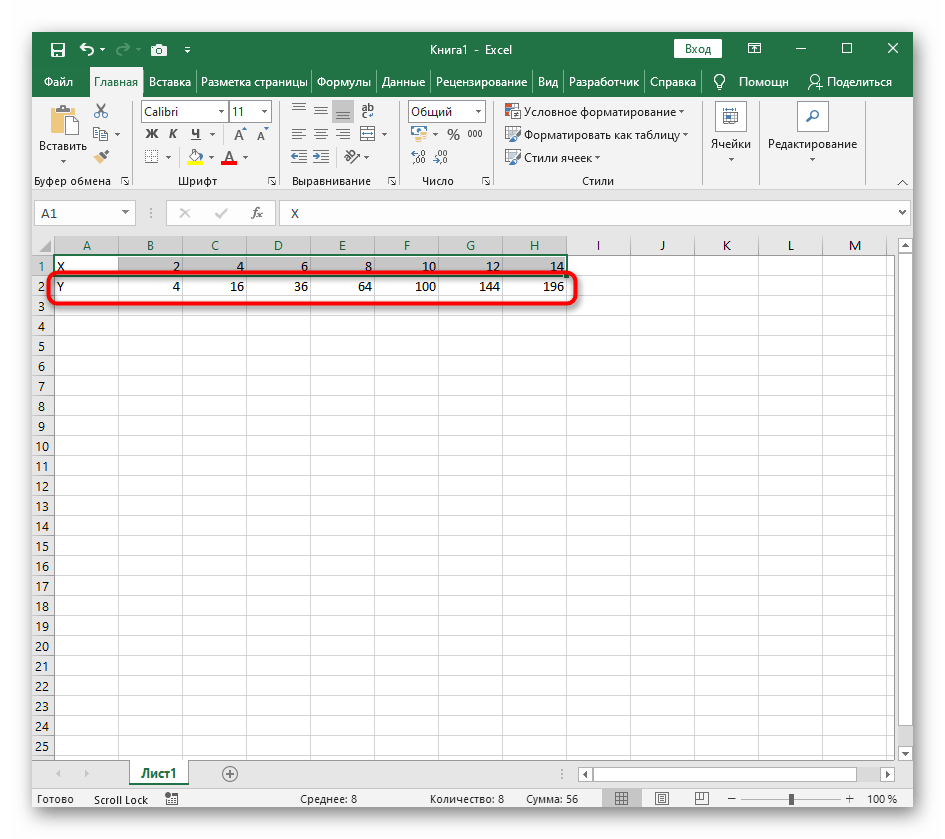
2. Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.



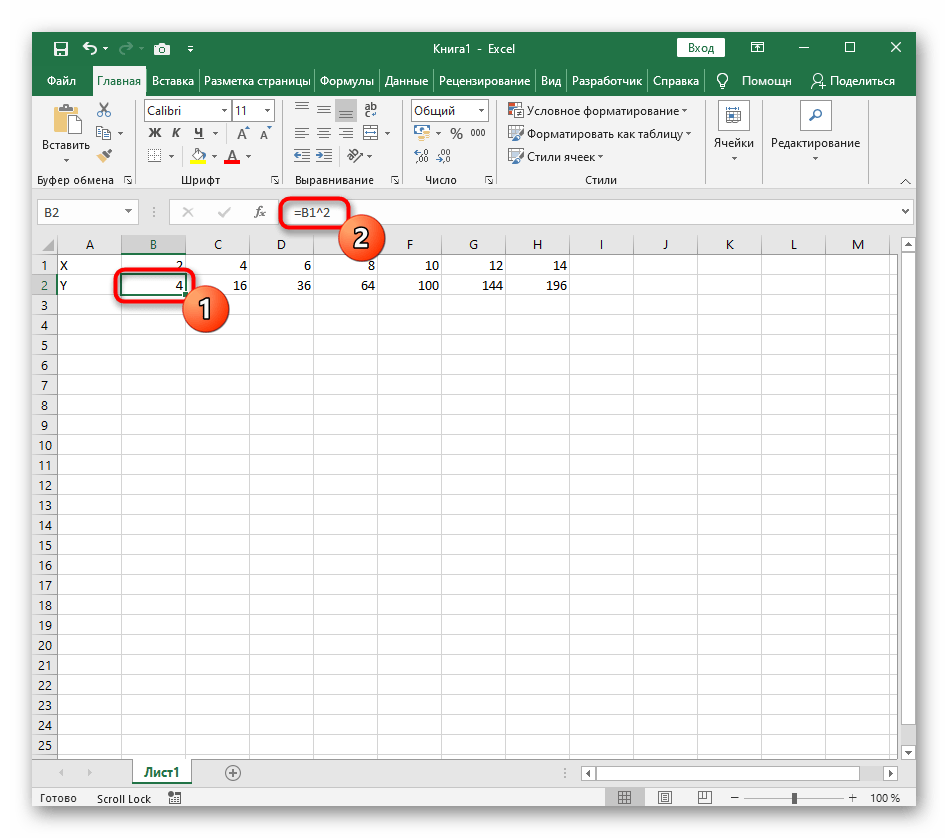
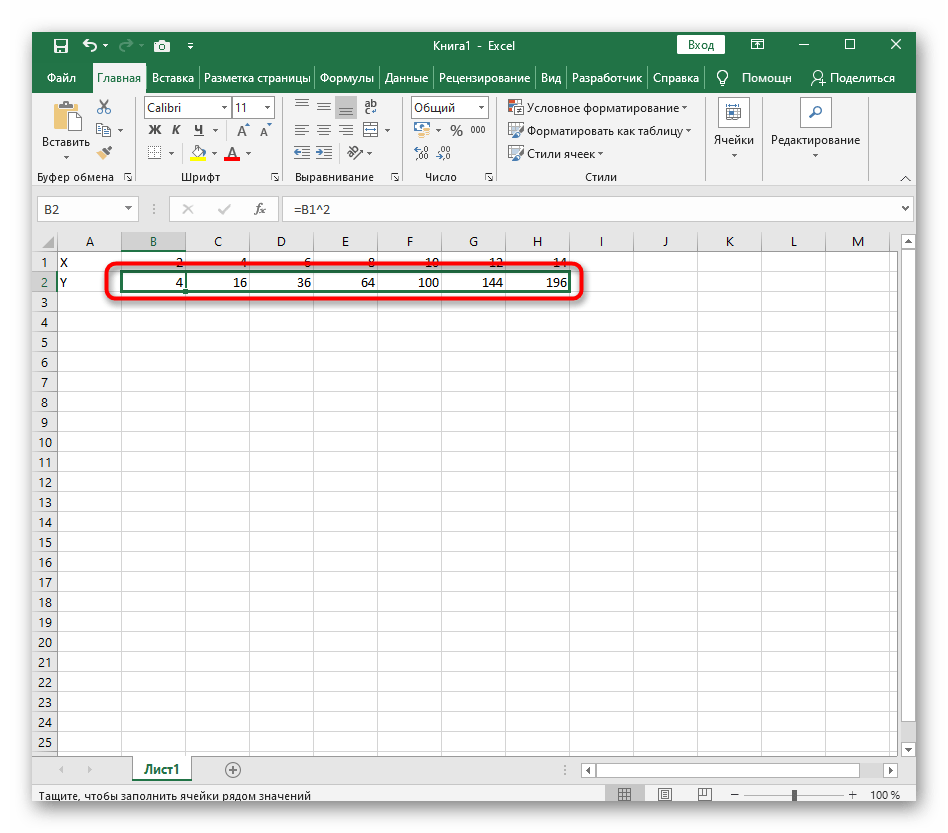
3. Нажмите по первой ячейке и впишите =B1^2, что значит автоматическое возведение указанной ячейки в квадрат.



4. Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.



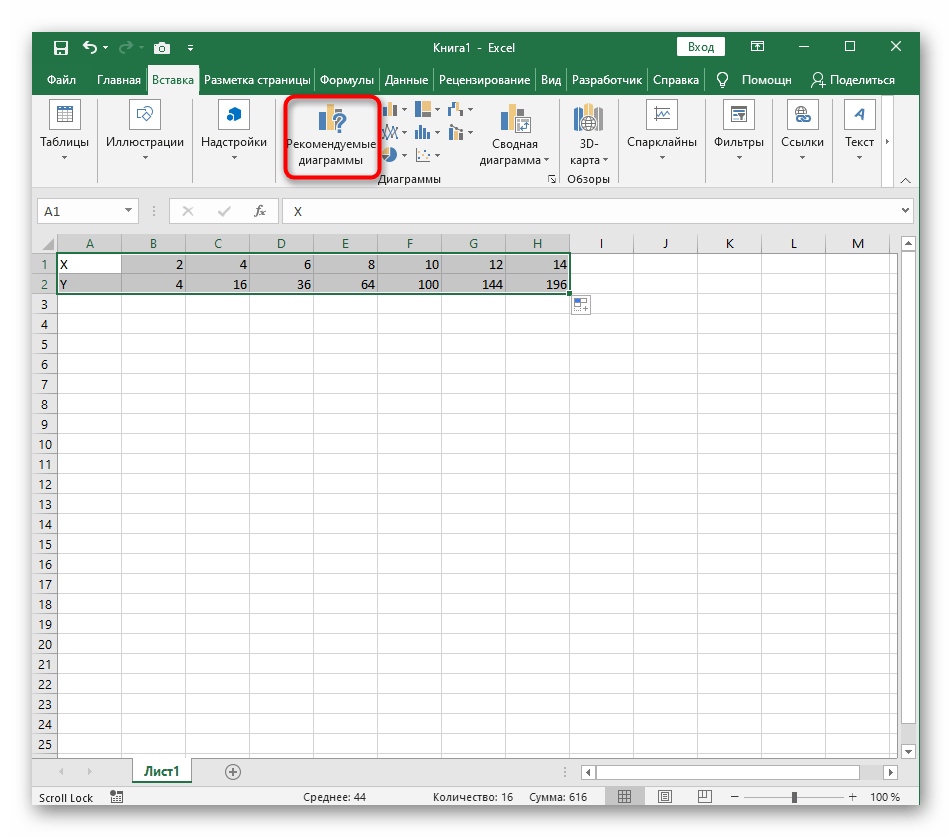
5. Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».



6. На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».



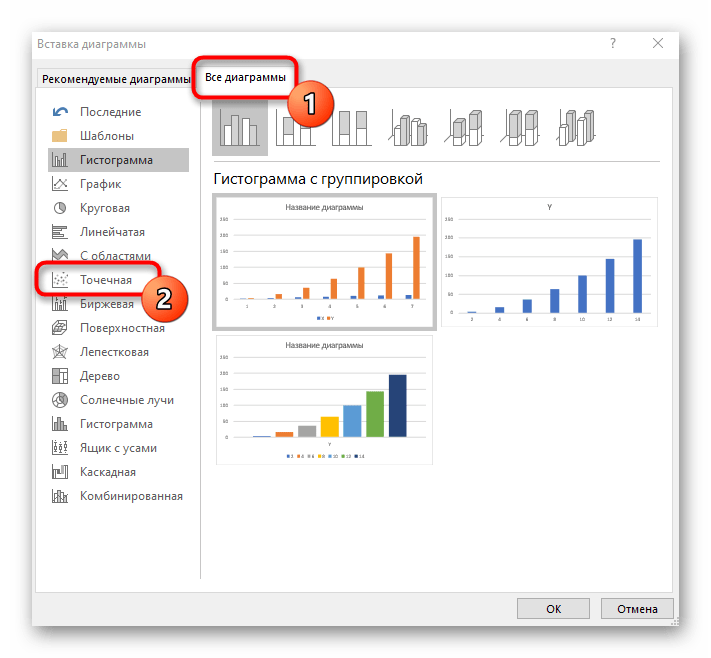
7. В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».



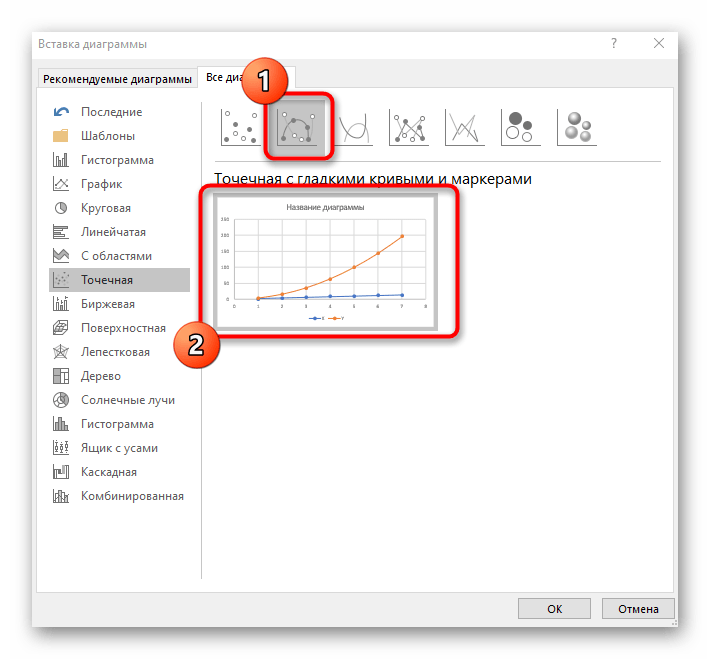
8. Подойдет вариант «Точечная с гладкими кривыми и маркерами».



9. После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.



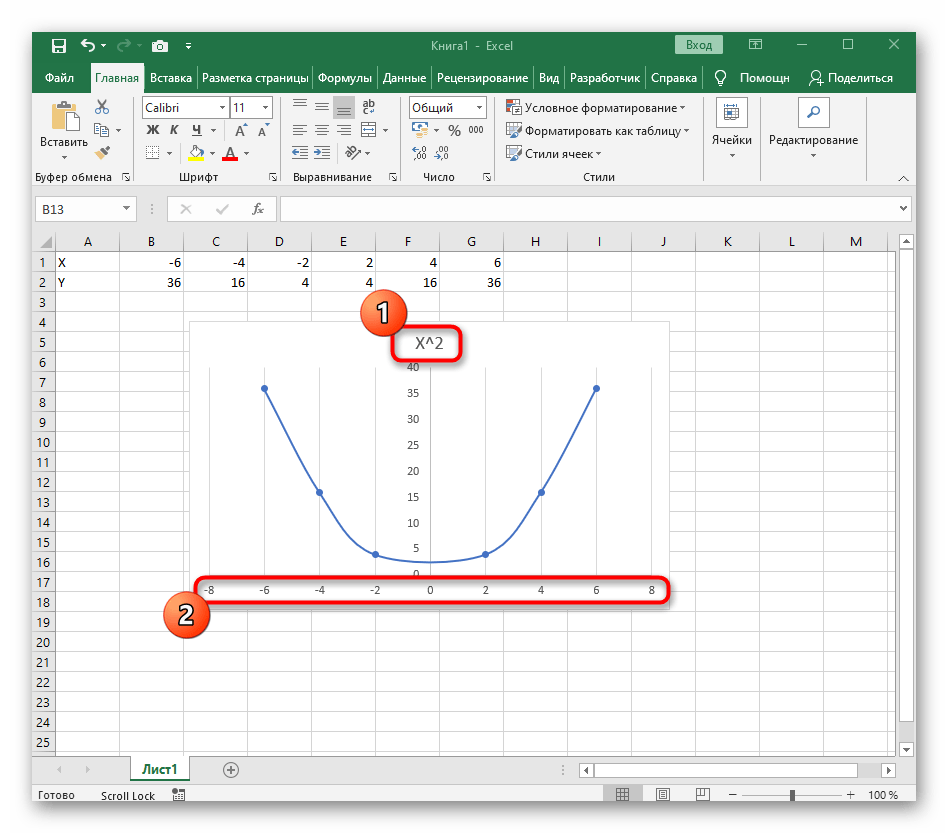
10. Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.



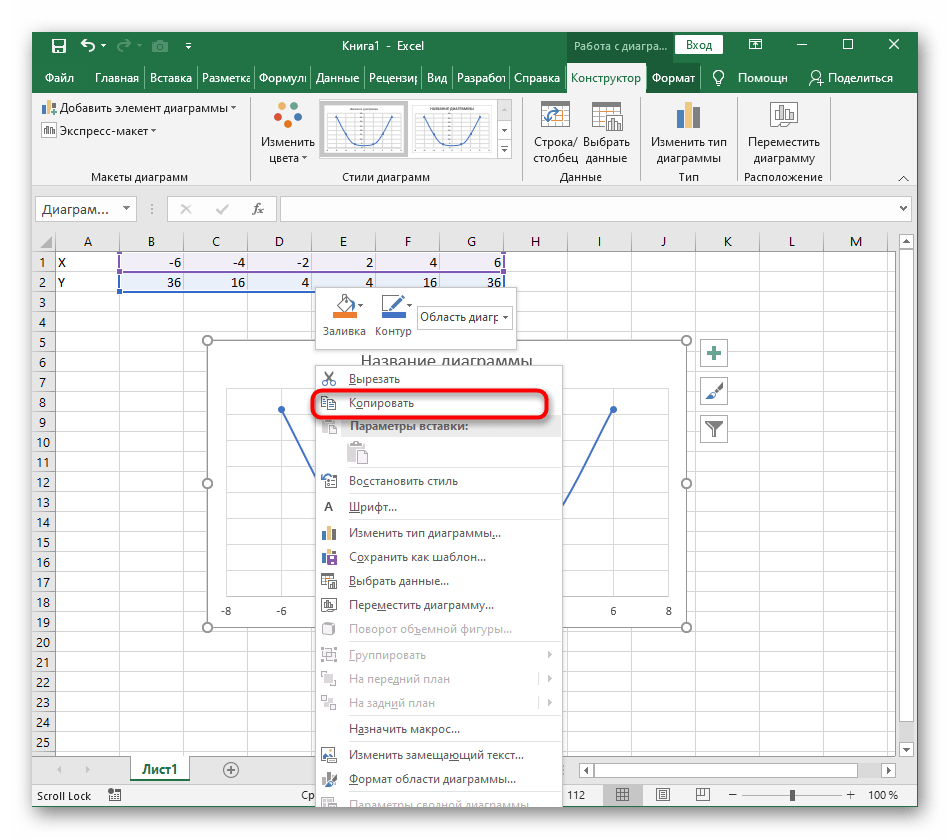
11. Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».



12. Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.

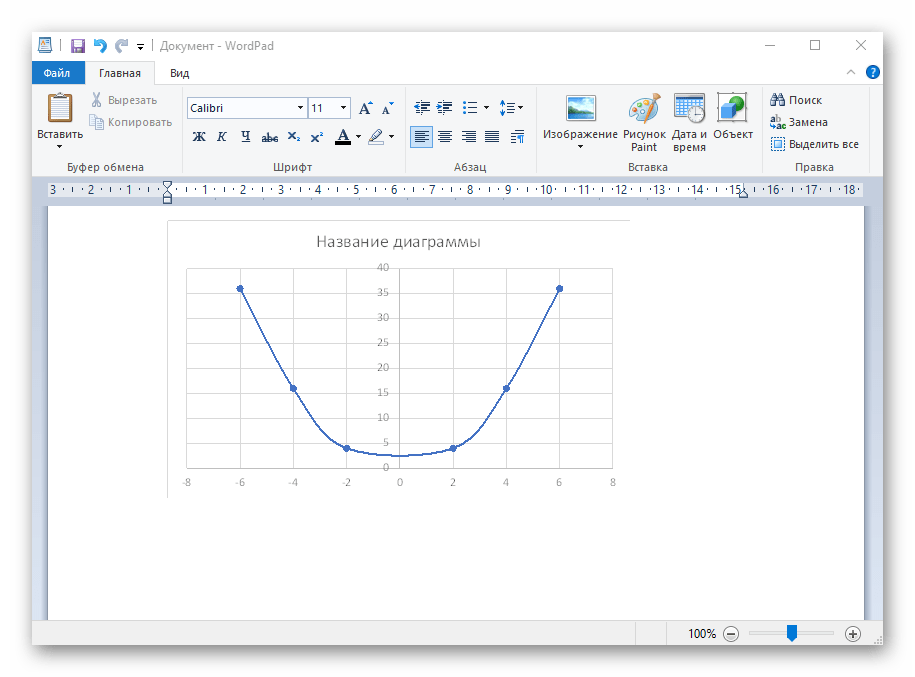
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.

Вариант 2: График функции y=sin(x)

Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.

1. Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.



2. Создайте сразу два столбца — X и Y, куда будете записывать данные.



3. Запишите самостоятельно первые два или три значения с указанным шагом.



4. Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.



5. Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.



6. Сама функция автоматически высчитает синус заданного числа.



7. Растяните столбец точно так же, как это было показано ранее.



8. Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.



9. Выделите столбец с Y и перейдите на вкладку «Вставка».



10. Создайте стандартный график, развернув выпадающее меню.



11. График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.

Еще статьи по данной теме:

Помогла ли Вам статья?

По теме: методические разработки, презентации и конспекты

Цель
работы:
Приобретение навыков построения графиков
функций на плоскости и в трехмерном
пространстве. Изучение графических
возможностей пакета MS Excel.

Задание
1.
Построить графики функций f(x) и g(x) для
x∈[-5;5]
с шагом 0,5. Задание выполняется на первом
листе рабочей книги MS Excel. Лист переименовать
в «Задание 1».

Варианты
задания 1

Порядок
работы:

Построить
график функции f(x)=
3 x2
⋅(x+3).
Определим функцию f(x).
Для этого в ячейки А2:А22 необходимо
ввести значение аргумента при помощи
автозаполнения.

Маркер
автозаполнения

В
ячейку В2 вводится значение функции,
вычисляемое по формуле =(A2^2*(A2+3))^(1/3).
Ячейки В3:В22 заполняются также при помощи
автозаполнения. Далее выделим диапазон
А2:В22 и воспользуемся «Мастером диаграмм».
Для построения графика функции лучше
выбрать точечную диаграмму, со значениями,
соединенными сглаживающими линиями
без маркера.

Рис.
3.2. Построение графика функции с помощью
мастера диаграмм

Чтобы
график получился выразительным,
необходимо определить промежуток
изменения аргумента, увеличить толщину
линий, выделить оси координат, нанести
на них соответствующие деления, сделать
подписи на осях и вывести заголовок.

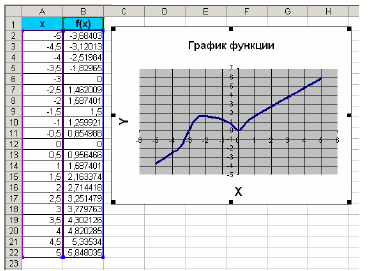
График
функции f(x)

При
построении графика функции
следует
обратить внимание на область определения
функции. В данном случае функция не
существует при обращении знаменателя
в ноль.

Решим
уравнение

Следовательно,
при определении значений аргумента
следует помнить, что при (-2) функция не
определена.

График
функции g(x)

Задание
2.
Построить график функций q(x) для x∈[-2;2]
с шагом 0,1. Задание выполняется на втором
листе рабочей книги MS Excel. Лист переименовать
в «Задание 2».

Варианты
задания 2

Порядок
работы:

Построить
график функции q(x) для x∈[-2;2]
с шагом 0,2:

При
построении этого графика используется
встроенная функция ЕСЛИ. Например, в
ячейке А2 (см. рис. 3.5) находится начальное
значение аргумента, тогда в ячейку В2
необходимо ввести формулу:
=ЕСЛИ(A2<0;1+A2+A2^2;ЕСЛИ(A2>=1;2*ABS(0,5+SIN(A2));КОРЕНЬ(1+2*A2))).

График
функции q(x)

В
том случае если при задании формулы не
требуется использовать функцию Если
дважды, удобнее вводить формулу в
диалоговом окне «Мастера функций».
Эта функция находится в категории
логические. Для вызова мастера
воспользуемся пунктом меню Вставка

Пункт
меню «Вставка» и Диалоговое окно Мастера
функций

Задание
3.
Построить поверхность Z(x,y) при x, y∈[-1;1]
с шагом 0.1. Задание выполняется на третьем
листе рабочей книги MS Excel. Лист переименовать
в «Задание 3».

Варианты
задания 3

Построить
поверхность
.

Приступим
к построению поверхности. В диапазон
C2:W2 введем последовательность значений
переменной x: -1, -0,9 … 1, а в диапазон ячеек
B3:B23 последовательность значений
переменой y: -1, -0,9 … 1. В ячейку C3 введем
формулу =2*EXP(C$2)-$B3*EXP($B3)

При
вводе формулы обратите внимание на то,
что необходимо сослаться на строку с
номером 2 и столбец с именем В. Для этого
при написании формулы следует использовать
абсолютные ссылки. Знак $, стоящий перед
буквой в имени ячейки, дает абсолютную
ссылку на столбец с данным именем, а
знак $, стоящий перед цифрой – абсолютную
ссылку на строку с этим именем. Поэтому
при копировании формулы из ячейки С3 в
ячейки диапазона С3:W23 в

них
будет найдено значение z при соответствующих
значениях x, y. Т.о. создается таблица
значений z(x,y).

Фрагмент
таблицы значений Z

Перейдем
к построению поверхности. Выделим
диапазон ячеек С3:W23, содержащий таблицу
значений функции и ее аргументов, вызовем
Мастер диаграмм и выберем тип диаграммы
Поверхность, далее заполним диалоговые
окна.

Построение
поверхности с помощью мастера диаграмм

После
нажатия кнопки Готово получим изображение
заданной поверхности.

Поверхность

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

СТРУКТУРИРОВАНИЕ ИНФОРМАЦИИ С ИСПОЛЬЗОВАНИЕМ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

Цели: сформировать понятие структурирование информации, осмыслить этапы структурирования при создании математической модели табличного вида; продемонстрировать умения структурировать информацию, используя математические модели табличного вида, строить графики функциональных зависимостей; усовершенствовать навыки работы с формулами и построения графиков функций в Excel.

Задание 1. Построение графиков степенных функций

1. Постановка задачи

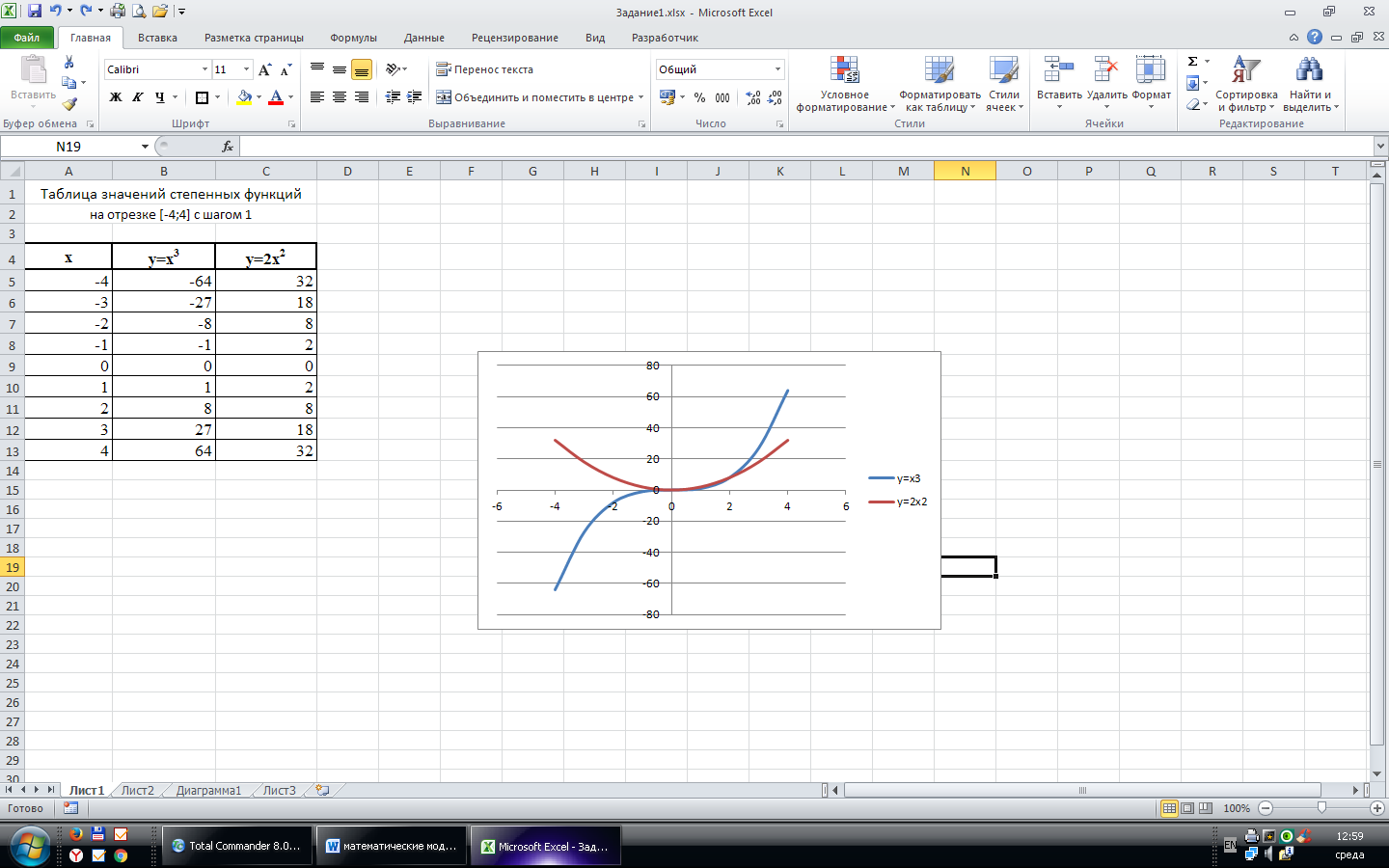
В электронных таблицах построить графики степенной функции у=х³ и квадратичной функции у=2х² на отрезке [-4;4].

2. Схема размещения данных в таблице:

3. Разработка модели

• В ячейки A1:С4 внести исходные данные

• В ячейки диапазона А5:А13 ввести последовательность значений независимой переменной х

• В ячейку В5 внести формулу =А5^3

• Скопировать формулу на диапазон В6:В13

• В ячейку С5 ввести расчетную формулу и скопировать её на диапазон С6:С13

• Оформить таблицу границами. Выполнить шрифтовое оформление.

• Сохранить работу в файле Задание1 в свою папку.

Дальше по данным в ячейках таблицы построить графики функций:

• Выделить диапазон ячеек A4:С13

• ВставкаДиаграммаТочечная Точечная с гладкими кривыми

• Поместить графики на отдельный лист (КонструкторПереместить диаграммуна отдельном листеОК)

• Добавить название Графики степенных функций

• Сохранить изменения в файле (ФайлСохранить).

В результате получим следующие графики

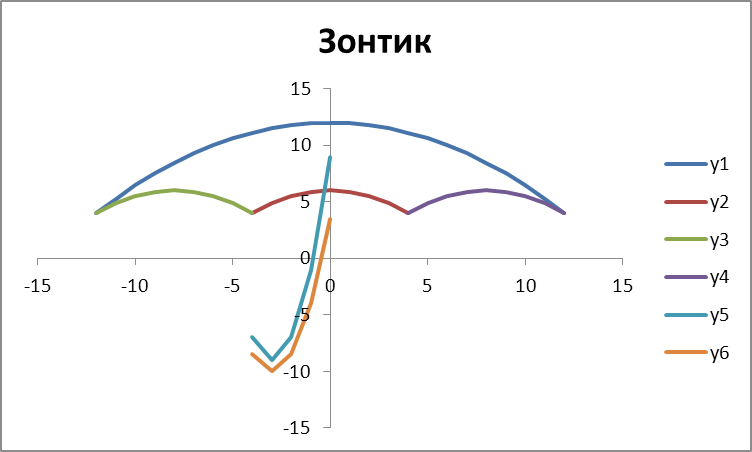
Задание 2. Построение рисунка «ЗОНТИК» с помощью графиков степенных функций.

1. Постановка задачи

С помощью электронных таблиц построить графики функций, которые участвуют в изображении зонтика:

у₁= -1/18х² + 12, х[-12;12]

y₂= -1/8х² +6, х[-4;4]

y₃= -1/8(x+8)² + 6, х[-12; -4]

y₄= -1/8(x-8)² + 6, х[4; 12]

y₅= 2(x+3)² – 9, х[-4;0]

y₆=1,5(x+3)² – 10, х[-4;0]

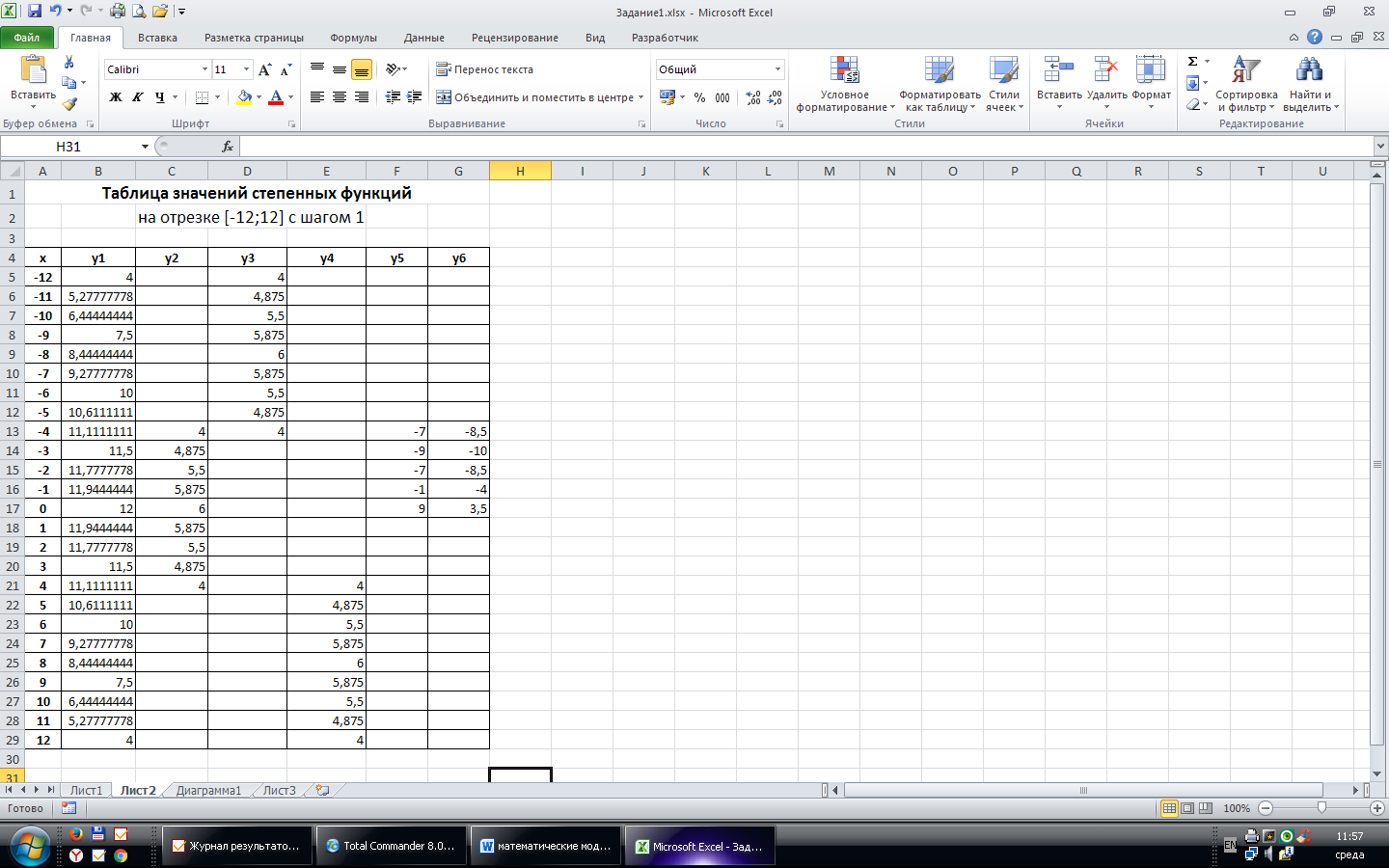
1. Схема размещения данных в таблице:

3. Разработка модели

1. Запустить MS EXCEL

2. Ввести информацию в 1, 2 и 4 строки.

3. Заполнить диапазон ячеек А5:А29 числами от -12 до 12 с шагом 1.

4. Вычислить значения каждой функции на заданном отрезке.

5. В ячейку В5 вводим формулу =-1/18*А5^2+12

6. Скопировать формулу на диапазон В5:В29

7. Аналогично ввести формулы для функций y2, y3, y4, y5 и y6 и скопировать их на заданный диапазон.

8. Оформить таблицу границами. Выполнить шрифтовое оформление. Включить режим отображения формул (ФормулаПоказать)

9. Сохранить таблицу в файле Задание 2 в свою папку.

10. Построить графики по значениям расчетных функций на отдельном листе. Оформите диаграмму в соответствии с образцом:

Задание 3. Построение графиков тригонометрических функций

1. Постановка задачи

П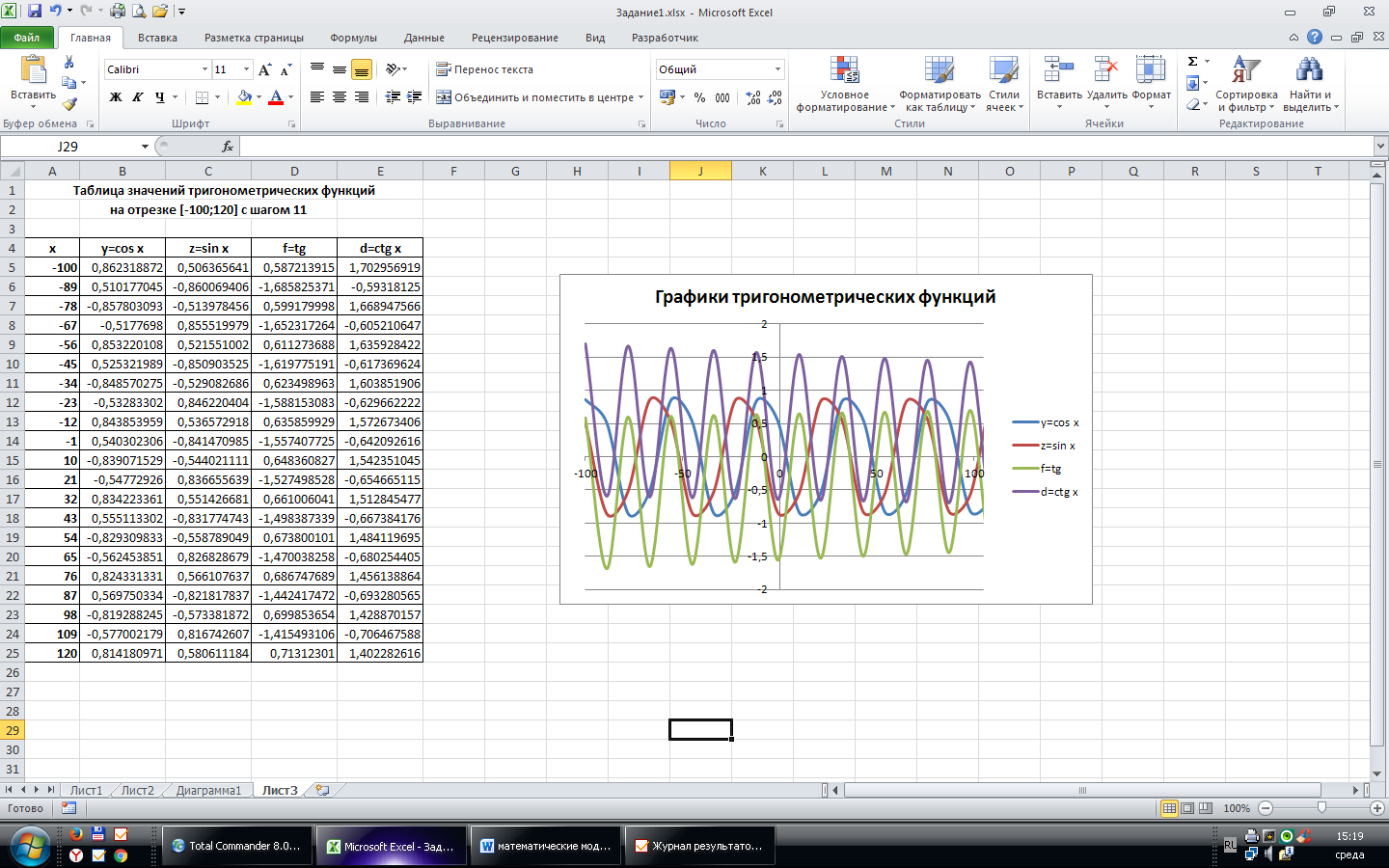остроить графики следующих тригономерических функций:

у = cos x; z = sin x; f = tg x; g =ctg x, где х  [–100;120] с шагом 11

2. Схема размещения данных в таблице показана на рисунке

3. Разработка модели

Шаг 1. В первой и второй строках ввести заголовок таблицы. Ввести данные в ячейки 4-й строки.

Шаг 2. Рассчитать значение переменной х в первом столбце.

Шаг 3. Во втором столбце рассчитать значения функции у = cos x.

Шаг 4. В третьем столбце рассчитать значения функции z = sin x.

Шаг 5. В четвертом столбце рассчитать значения функции f = tg x.

Шаг 6. В пятом столбце рассчитать значения функции d = ctg x.

Шаг 7. Нарисовать границы таблицы и отформатировать по образцу.

Шаг 8. На отдельном листе построить графики тригонометрических функций.

Шаг 9. Сохранить таблицу с именем Задание 3 в свою папку.

Критерии оценки

1. Правильный расчет по формулам

2. Оформление элементов таблицы (шрифты, границы, числовые данные)

3. Построение графиков и оформление элементов диаграммы

4. Степень самостоятельности в работе

Вспомните цели занятия и ответьте на вопросы:

1. Что такое структурирование информации?

2. Назовите этапы разработки табличной математической модели.

3. Какой тип диаграмм используется для построения графиков функциональных зависимостей?

4. Достигнуты ли вами цели занятия?

5. Какие умения вы сформировали в процессе выполнения заданий?

6. Какие навыки были усовершенствованы?

7. Какие трудности вы испывали? В чем причины трудностей?

8. Над чем нужно еще поработать?

9. Оцените свою работу на занятии в соответствии с критериями оценки. Для этого откройте из своей папки информационно-оценочный лист, заполните его и сохраните изменения.

10. Какую отметку в баллах вы получили и почему?

11. Как можно было проявить творчество?

12. Оцените психологический климат на занятии.