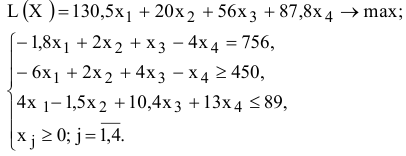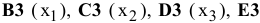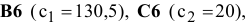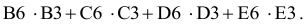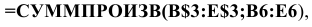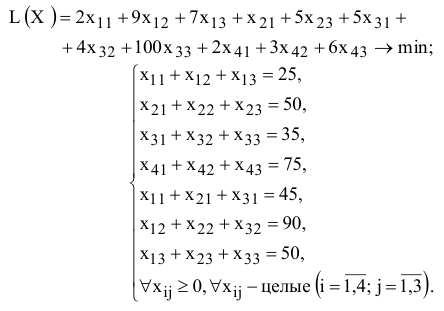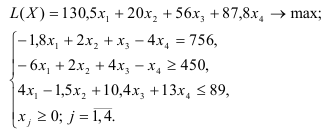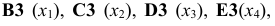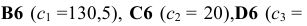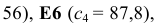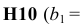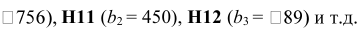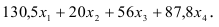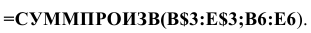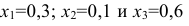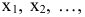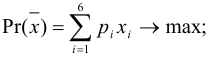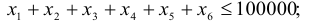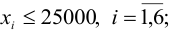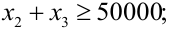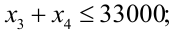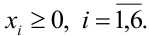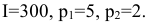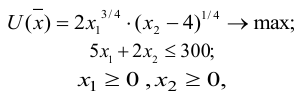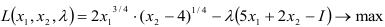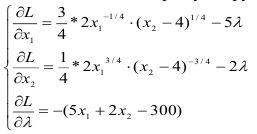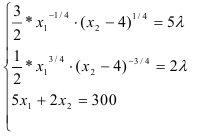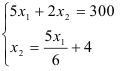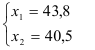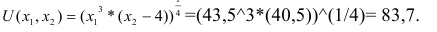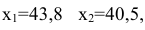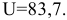Задание исходных данных excel

Лабораторная работа № 6 Microsoft Excel. Вычислительные процедуры. Ввод исходных данных и формул. Построение диаграмм

Цель работы: Уметь владеть основными правилами и приемами работы в среде Windows. Уметь работать в программной среде Microsoft Excel 2000, вводить исходные данные, формулы, выполнять расчеты в среде электронных таблиц.

Начало работы: Запустите программу Microsoft Excel.

Перед вводом информации сохраните будущий документ.

меню Файл è Сохранить как. В открывшемся диалоговом окне убедитесь, что вы находитесь в папке Мои документы, затем зайдите в вашу папку èукажите название вашего документа: Издатель. Нажмите кнопку Сохранить.

Ход работы: Создайте таблицу расходов за полгода для компании «Издатель» (Таблица 5).

Выполните следующие операции:

1. Выделите мышкой ячейку А1. Введите в нее текст Расходы. Нажмите .

В ячейке А1 появилась запись Расходы.

2. Заполнить ячейки А3:А10. (Перейти сразу к следующей ячейке можно клавишей Tab или клавишей со стрелкой или мышкой).

3. Заполните ячейки B3:G3, используя автозаполнение ячеек.

для ячейки H3 – введите текст Всего

Внимание: Чтобы целиком видеть текст, введенный вами в ячейки – нужно будет отрегулировать ширину столбцов. Лучше это сделать ПОСЛЕ ввода всей информации.

4. Заполните столбцы B4:G9

5. Заполните ячейки B10:H10, вводя формулу в строку формул:

=СУММ(B4:B9) и т.д. до ячейки с адресом H10.

6. Заполните ячейки H4:H10, вводя формулу в строку формул:

=СУММ(B4:G4) и т.д. до ячейки с адресом H10.

7. Выделите диапазон ячеек B4 : B10, затем в меню Формат Š Ячейки Š вкладка «Число», а в ней «Числовые форматы» – укажите формат Денежный. Нажмите OK.

Теперь тот же путь проделайте для диапазона ячеек C4 : C10;D4:G10.

8.Оформите таблицу 5. Выделите всю таблицу, и найдите вверху на Панели инструментов значок рамки – инструмент называется Границы. Раскройте эту панель и найдите значок Все границы .

9. Присвойте имя листу 1 «Расходы», щелкнув дважды на ярлычке.

Построение диаграммы на основе таблицы.

Диаграмма- это графическое представление числовых данных.

Выделите в вашей таблице диапазон В3:G9.

Зайдите меню Вставка → Диаграмма (или кнопка Мастер диаграмм в панели инструментов).

Слева выберите вариант Круговая, а справа среди картинок выберите «Объемный вариант разрезанной круговой диаграммы», нажмите на кнопку Далее.

Вы увидите макет будущей диаграммы. Нажмите кнопку Далее

На закладке Подписи Данных выберите Доля

На закладке Заголовки введите название диаграммы Расходы

На закладке Легенда выберите ее размещение Справа. Нажмите кнопку Далее.

Выберите пункт Поместить диаграмму на имеющемся листе. Нажмите ОК (см. Рис. 7).

Источник

Вкладка «Исходные данные»

«Исходные данные» — это вкладка, на которой указываются действия по обработке данных, предшествующие выводу на лист.

Можно образно сказать, что здесь загружаются, формируются или обрабатываются данные перед тем, как парсинг переходит к выводу на лист или к скачиванию файлов.

Вкладка состоит из двух блоков: верхний (Источник данных) и нижний (Список действий). Верхний блок также имеет несколько вариантов отображения в зависимости от выбранного через выпадающий список режима.

В программе реализованы 5 режимов для исходных данных

Задачей блока «Источник данных» является формирование массива исходных значений, которые по одному будут передаваться на первый уровень списка действий и подставляться в поле «Исходное значение» редактора списка действий (на скриншоте ниже выделено красным).

Реальной подстановки в поле значений не происходит. В данном контексте слово «подставляется» используется лишь для объяснения механизмов работы парсера.

То есть, если мы выбрали режим «Брать данные с листа Excel из заданного столбца» и указали столбец 1 «A» в качестве источника данных, то из этого столбца значения ячеек по одному будут подставляться в поле исходное значение (на скриншоте). И если в 1 столбце, например, было 10 ссылок, то парсер будет обрабатывать данные ссылки по одной.

Точно так же парсер будет работать для всех других режимов блока «Источник данных». Значения передаются по одному.

Список действий представляет из себя набор уровней (подуровней), каждый из которых является для последующего источником исходных значений. Взаимосвязь каждого уровня с последующим такая же, как между блоками «Источник данных» и «Список действий» — значения переходят с уровня на подуровень по одному.

Например, на первом уровне мы получили массив из 10 значений. Каждое из этих значений переходит по одному на 2 подуровень, где в результате преобразований мы получаем массив из 5 значений. Каждое из этих значений переходит по одному либо на следующий подуровень, либо если его нет — на вывод на лист или на загрузку файлов (в этом случае мы получим 10 * 5 = 50 строк).

Если в результате обработки данных списком действий мы получаем на самом «нижнем» подуровне пустое значение, то дальнейшего перехода к выводу на лист или к скачиванию файлов не происходит (с оговоркой, написанной в информационной сноске ниже). Поэтому если вам нужно, чтобы любое исходное значение было отражено на выходе (например, в новом формируемом файле), нужно быть уверенным в том, что значение «на выходе» вкладки «Исходные данные» будет не пустым. Для этого можно использовать, например, действие из раздела «Текстовые» — «Значение по умолчанию».

Данное правило не работает в случае перехода между уровнями. Если на выходе 1 уровня будет пустое значение, то действия второго подуровня все равно будут запущены. Это нужно учитывать при создании сложных настроек.

Если быть точным, то определение — перейдет ли парсер к действиям столбцов вывода на лист или нет — происходит на подвкладке «Дополнительно» вкладки «Вывод на лист». То же самое касается подвкладки «Дополнительно» вкладки «Загрузка файлов». Однако ввиду того, что данные подвкладки используется крайне редко и чаще всего остаются пустыми, в контексте данной статьи можно пренебречь ими.

Кнопка «Run ParserStart» отображается только при включенном в общих настройках программы «Режиме разработчика». Её функция — запуск специального набора действий «ParserStart». Используется, например, в тех случаях, когда нужно протестировать работу парсера и быстро пройти авторизацию (без перехода на вкладку «Дополнительно», подвкладку «Наборы действий» и т.д.)

Кнопка «Редактировать список действий» открывает второе окно программы — окно редактора списка действий. Редактируемый уровень выбирается переключателем «Текущий уровень». Также возможно перемещаться на нижележащий уровень при помощи кнопки «Перейти на подуровень . «. Если ниже нет никакого уровня, то кнопка меняется на «Добавить подуровень . «.

Справа от переключателя «Текущий уровень» находится кнопка удаления подуровня и всех его действий. Данное действие нельзя отменить.

Справа от кнопки «Редактировать список действий» находится кнопка вставки разрыва подуровней (она появляется только при условии, что в списке действий слева выбрано какое-либо действие). На скриншоте отмечена красным.

Данная кнопка сдвигает все нижележащие подуровни (если они существуют) на один уровень ниже, а действия из текущего подуровня ниже выделенной строки переносятся на следующий уровень (на скриншоте это действия ниже выделенного второго действия). После нажатия на кнопку список действий будет выглядеть следующим образом.

Выделенное действие и всё, что «выше», осталось на месте. 3 и 4 действие перешли на 2 подуровень. Если бы в настройке до нажатия кнопки был подуровень №2, он бы стал подуровнем №3.

Кстати, обратите внимание, что сейчас на скриншоте не выделено ни одно действие, как следствие кнопка вставки разрыва не видна.

Источник

Линейное программирование в Excel

Задачи линейного программирования относятся к широко распространённому классу задач, встречающихся в различных сферах деятельности: в бизнесе, на производстве, в быту. Как оптимально распорядиться бюджетом или за минимальное время добраться до нужного места в городе, как наилучшим образом спланировать деловые встречи, минимизировать риски капитальных вложений, определить оптимальные запасы сырья на складе – это те задачи, в которых нужно найти наилучшее из всех возможных решений.

Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Линейное программирование

Линейное программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово «программирование» заимствовано из зарубежной литературы, где оно используется в смысле «планирование».

Решение задач линейного программирования с использованием microsoft excel

Цель работы

Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel.

Порядок выполнения работы

Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.

Инструкция по использованию microsoft excel для решения задач линейного программирования

Для того чтобы решить задачу линейного программирования в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия.

Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

• переменных,
• целевой функции (ЦФ),
• ограничений,
• граничных условий;

b) ввести исходные данные в экранную форму:

• коэффициенты ЦФ,
• коэффициенты при переменных в ограничениях,
• правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

• формулу для расчета ЦФ,
• формулы для расчета значений левых частей ограничений;

d) задать ЦФ (в окне «Поиск решения»):

• целевую ячейку,
• направление оптимизации ЦФ;

e) ввести ограничения и граничные условия (в окне «Поиск решения»):

• ячейки со значениями переменных,
• граничные условия для допустимых значений переменных,
• соотношения между правыми и левыми частями ограничений.

a) установить параметры решения задачи (в окне «Поиск решения»);

b) запустить задачу на решение (в окне «Поиск решения»);

с) выбрать формат вывода решения (в окне «Результаты поиска решения»).

Возможно эта страница вам будет полезна:

Одноиндексные задачи линейного программирования

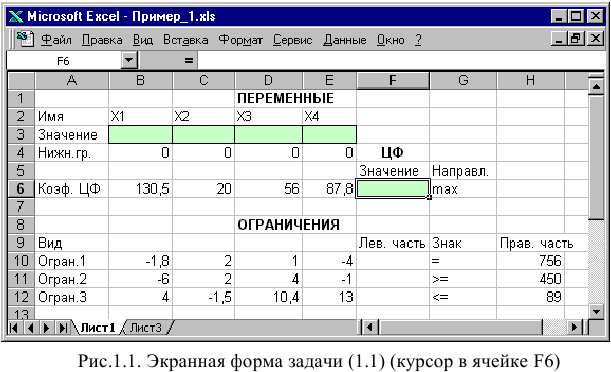
Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:

Ввод исходных данных

Создание экранной формы и ввод в нее условия задачи

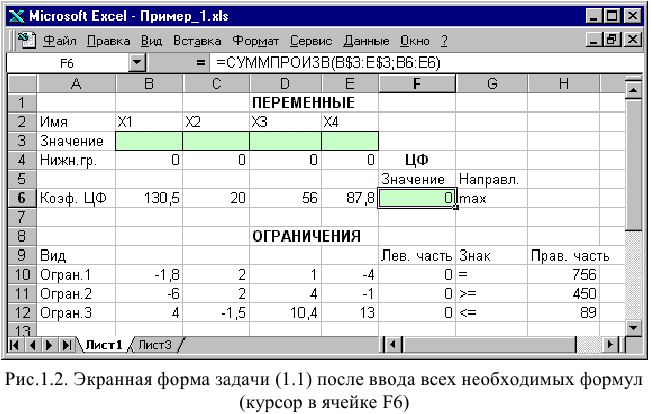
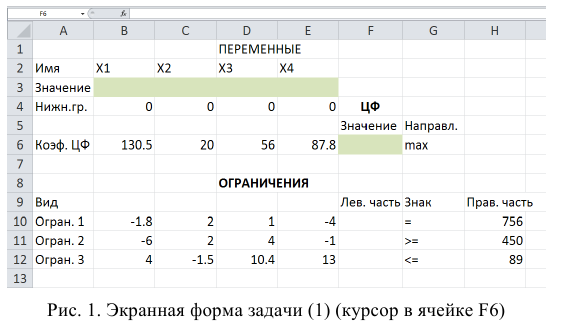
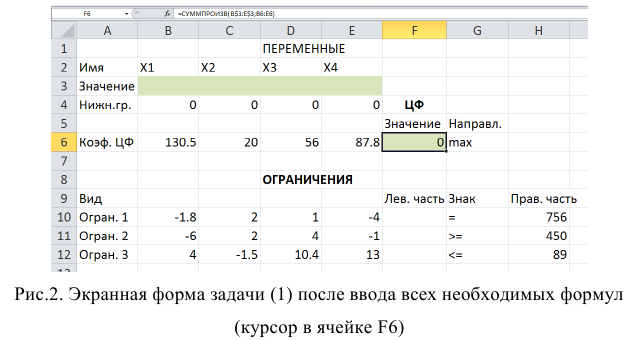
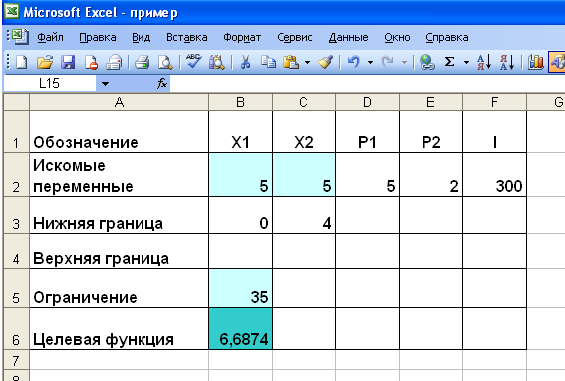
Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис. 1.1.

В экранной форме на рис. 1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи линейного программирования. Так, например, переменным задачи (1.1) соответствуют ячейки , коэффициентам ЦФ соответствуют ячейки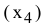

правым частям ограничений соответствуют ячейки

Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ

В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением

Используя обозначения соответствующих ячеек в Excel (см. рис. 1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6, Е6), то есть

Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу «Enter»

где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится;

символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись В6:Е6 указывает на ячейки В6, С6, D6 и Е6). После этого в целевой ячейке появится 0 (нулевое значение) (рис. 1.2).

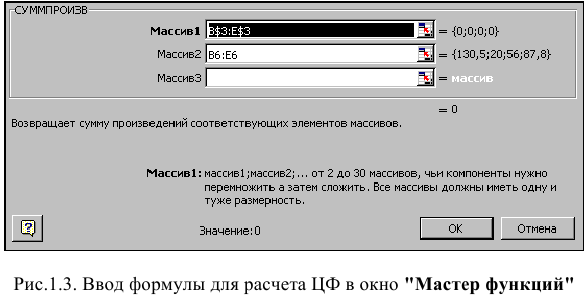
Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима «Вставка функций», который можно вызвать из меню «Вставка» или при нажатии кнопки «» на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:

• курсор в поле F6;

• нажав кнопку «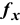«, вызовите окно «Мастер функций — шаг 1 из 2»;

• выберите в окне «Категория» категорию «Математические»;

• в окне «Функция» выберите функцию СУММПРОИЗВ;

• в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение В$3:Е$3, а в строку «Массив 2» — выражение В6:Е6 (рис. 1.3);

• после ввода ячеек в строки «Массив 1» и «Массив 2» в окне «СУММПРОИЗВ» появятся числовые значения введенных массивов (см. рис. 1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

Зависимости для левых частей ограничений

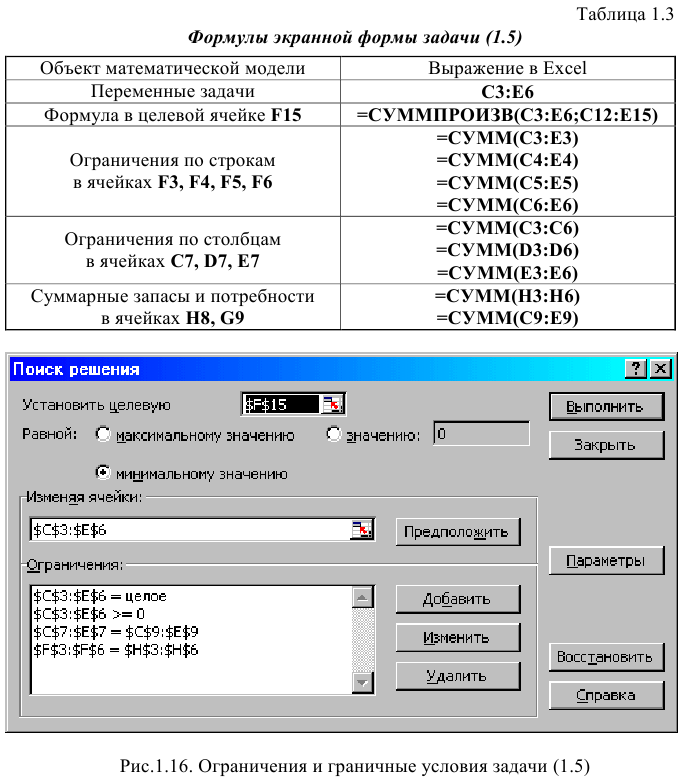
Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (В 10, СЮ, D10, ЕЮ — 1-е ограничение; В11, С11, D11, El 1 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл. 1.1.

Как видно из табл. 1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо:

• поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами «Ctrl-Insert»);

• помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11 и F12, и вставлять в эти поля содержимое буфера (клавишами «Shift-Insert») (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера);

• на экране в полях F10, F11 и F12 появится 0 (нулевое значение) (см. рис. 1.2).

Проверка правильности введения формул

Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле (рис. 1.4 и 1.5).

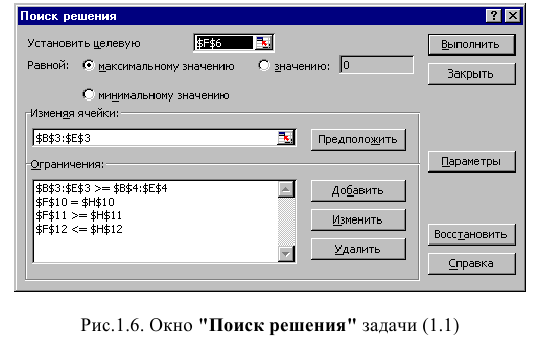
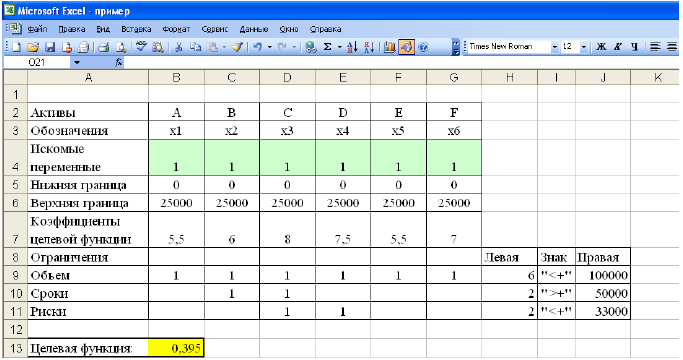
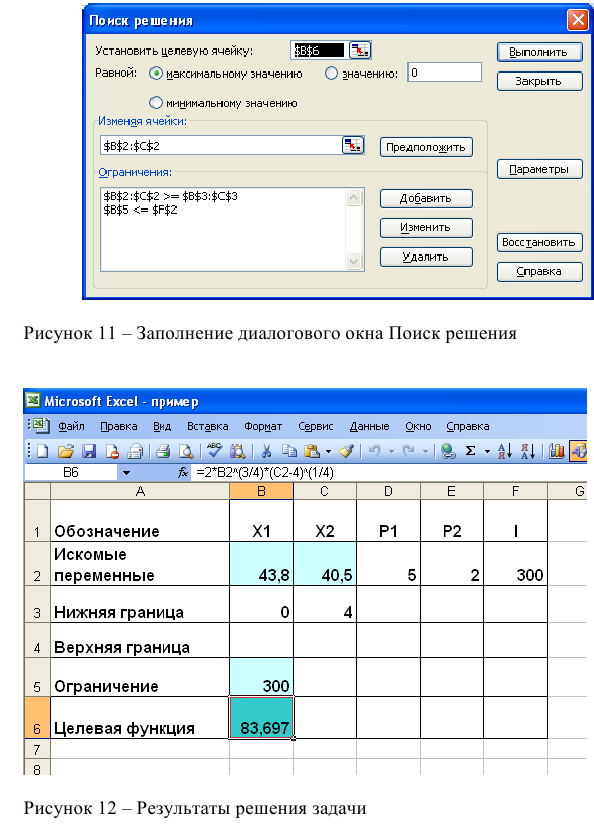
Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис» (рис. 1.6):

• поставьте курсор в поле «Установить целевую ячейку»;

• введите адрес целевой ячейки $F$6 или сделайте одно нажатие левой клавиши мыши на целевую ячейку в экранной форме — это будет равносильно вводу адреса с клавиатуры;

• введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по селекторной кнопке «максимальному значению».

Ввод ограничений и граничных условий

Задание ячеек переменных

В окно «Поиск решения» в поле «Изменяя ячейки» впишите адреса $BS3:$E$3. Необходимые адреса можно вносить в поле «Изменяя ячейки» и автоматически путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.

Задание граничных условий для допустимых значений переменных

В нашем случае на значения переменных накладывается только граничное условие неотрицательности, то есть их нижняя граница должна быть равна нулю (см. рис. 1.1).

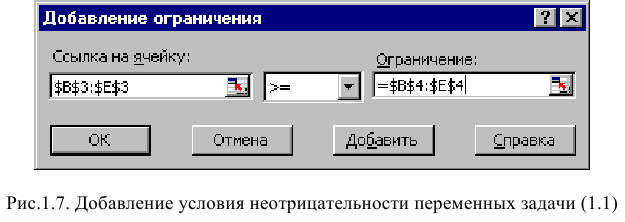
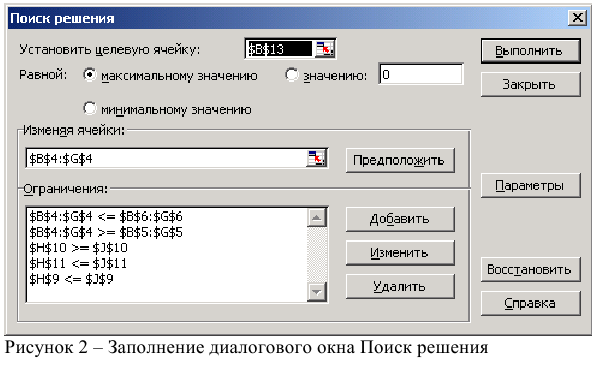
• Нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения» (рис. 1.7).

• В поле «Ссылка на ячейку» введите адреса ячеек переменных $BS3:$E$3. Это можно сделать как с клавиатуры, так и путем выделения мышью всех ячеек переменных непосредственно в экранной форме.

• В поле знака откройте список предлагаемых знаков и выберите >.

• В поле «Ограничение» введите адреса ячеек нижней границы значений переменных, то есть $В$4:$Е$4. Их также можно ввести путем выделения мышью непосредственно в экранной форме.

Задание знаков ограничений , =

• Нажмите кнопку «Добавить» в окне «Добавление ограничения».

• В поле «Ссылка на ячейку» введите адрес ячейки левой части конкретного ограничения, например $F$10. Это можно сделать как с клавиатуры, так и путем выделения мышью нужной ячейки непосредственно в экранной форме.

• В соответствии с условием задачи (1.1) выбрать в поле знака необходимый знак, например =.

• В поле «Ограничение» введите адрес ячейки правой части рассматриваемого ограничения, например $Н$10.

• Аналогично введите ограничения: $F$11>=$Н$11, $F$12 Решение задачи

Установка параметров решения задачи

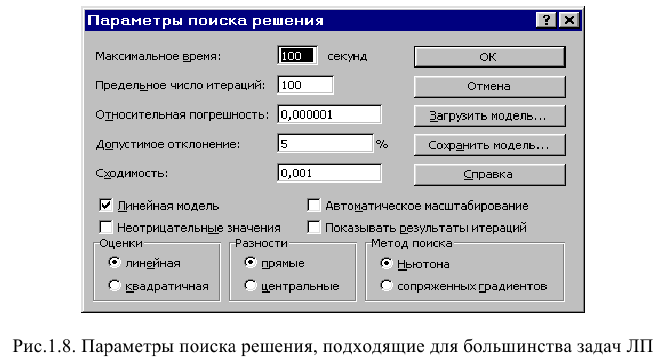
Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения» (рис. 1.8).

Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).

Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.

Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.

Параметр «Сходимость» применяется только при решении нелинейных задач.

Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.

Подтвердите установленные параметры нажатием кнопки «ОК».

Запуск задачи на решение

Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».

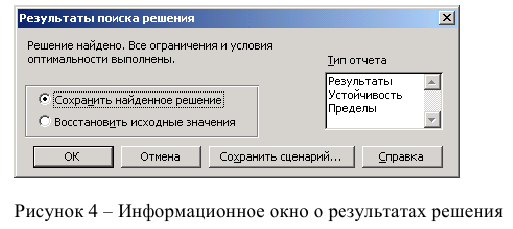
После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений, представленных на рис. 1.9, 1.10 и 1.11.

Иногда сообщения, представленные на рис. 1.10 и 1.11, свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условий задачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует (см. ниже подразд.1.3.5).

Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра «Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.

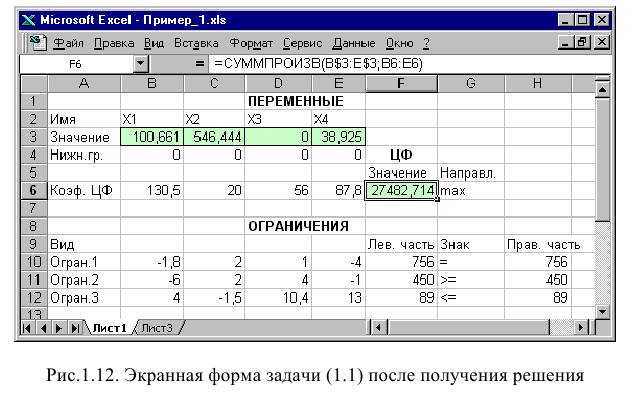
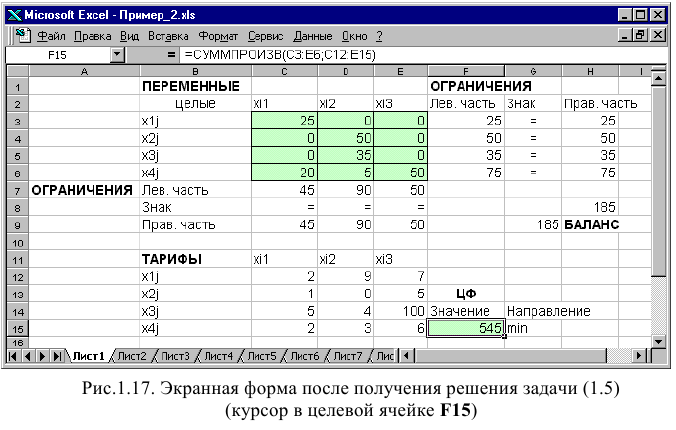
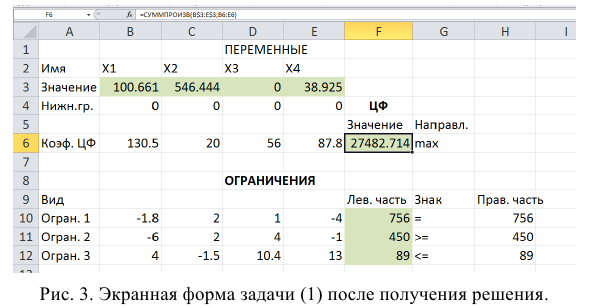
В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (см. ниже подразд.3.3). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис. 1.12).

Целочисленное программирование

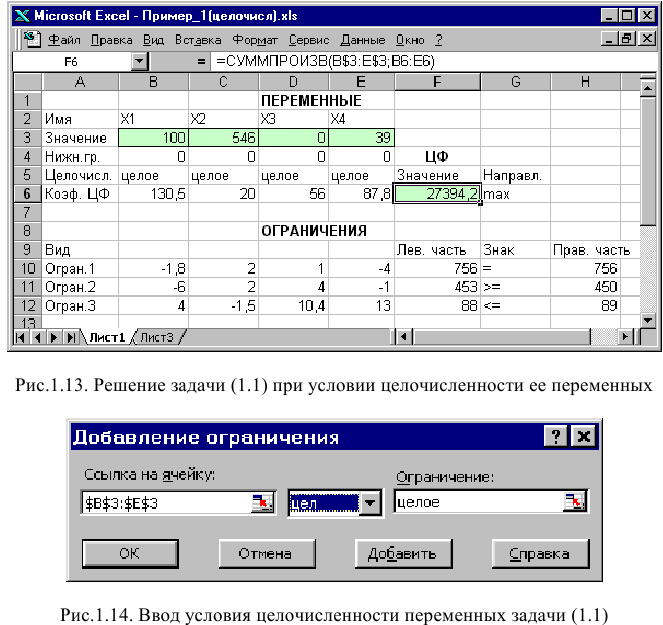
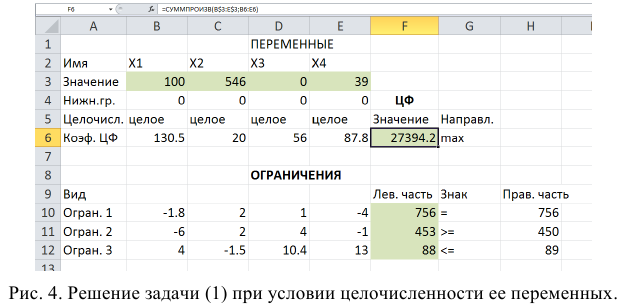
Допустим, что к условию задачи (1.1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.

• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 1.13).

• В окне «Поиск решения» (меню «Сервис»—>»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения следующим образом (рис.1.14):

• в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $В$3:$Е$3;
• в поле ввода знака ограничения установите «целое»;
• подтвердите ввод ограничения нажатием кнопки «ОК».

На рис. 1.13 представлено решение задачи (1.1), к ограничениям которой добавлено условие целочисленности значений ее переменных.

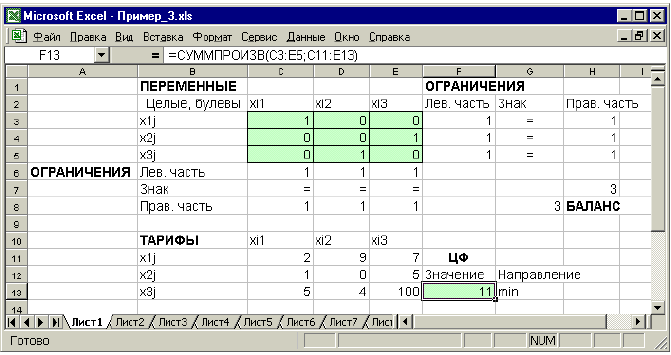
Двухиндексные задачи линейного программирования

Двухиндексные задачи линейного программирования вводятся и решаются в Excel аналогично одноиндексным задачам. Специфика ввода условия двухиндексной задачи ЛП состоит лишь в удобстве матричного задания переменных задачи и коэффициентов ЦФ.

Рассмотрим решение двухиндексной задачи, суть которой заключается в оптимальной организации транспортных перевозок штучного товара со складов в магазины (табл. 1.2).

Целевая функция и ограничения данной задачи имеют вид

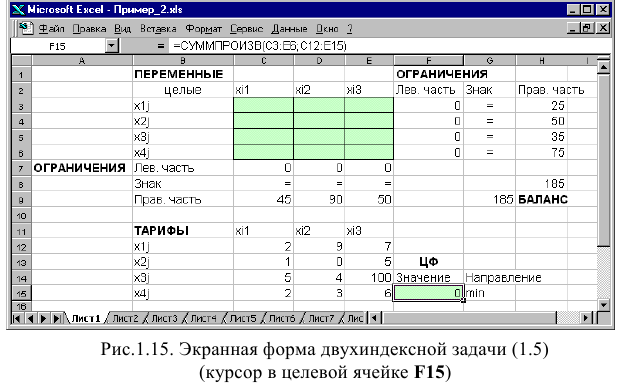
Экранные формы, задание переменных, целевой функции, ограничений и граничных условий двухиндексной задачи (1.5) и ее решение представлены на рис. 1.15, 1.16, 1.17 и в табл. 1.3.

Задачи с булевыми переменными

Частным случаем задач с целочисленными переменными являются задачи, в результате решения которых искомые переменные 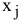могут принимать только одно из двух значений: 0 или 1. Такие переменные в честь предложившего их английского математика Джорджа Буля называют булевыми. На рис. 1.18 представлена экранная форма с решением некоторой двухиндексной задачи с булевыми переменными.

Рис. 1.18. Решение двухиндексной задачи с булевыми переменными

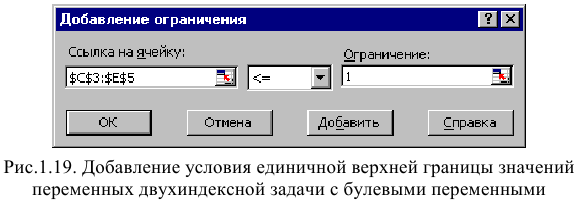
Помимо задания требования целочисленности (см. подразд.1.3.2) при вводе условия задач с булевыми переменными необходимо:

• для наглядности восприятия ввести в экранную форму слово «булевы» в качестве характеристики переменных (см. рис. 1.18);

• в окне «Поиск решения» добавить граничные условия, имеющие смысл ограничения значений переменных по их единичной верхней границе (рис. 1.19).

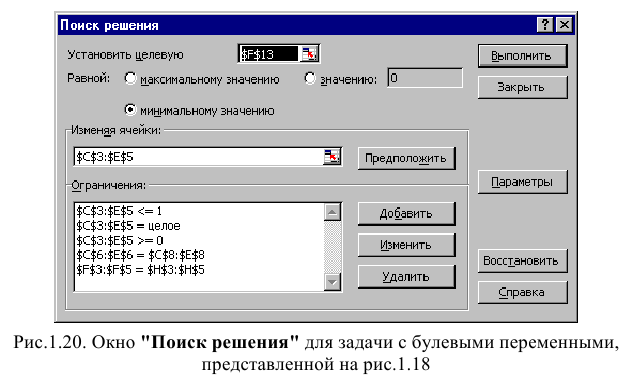
Вид окна «Поиск решения» для задачи с булевыми переменными, представленной на рис. 1.18, приведен на рис. 1.20.

Возможные ошибки при вводе условий задач линейного программирования

Если при решении задачи линейного программирования выдается сообщение о невозможности нахождения решения, то возможно, что причина заключается в ошибках ввода условия задачи в Excel.

Как решить задачу линейного программирования в excel

Цель работы

Приобретение навыков решения задач линейного программирования (ЗЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Для модели линейного программирования, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю.

Инструкция по использованию microsoft excel для решения задач линейного программирования

Для того чтобы решить ЗЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи:

a) создать экранную форму для ввода условия задачи:

• • переменных,
• • целевой функции (ЦФ),
• • ограничений,
• • граничных условий;

b) ввести исходные данные в экранную форму:

• • коэффициенты ЦФ,
• • коэффициенты при переменных в ограничениях,
• • правые части ограничений;

c) ввести зависимости из математической модели в экранную форму:

• • формулу для расчета ЦФ,
• • формулы для расчета значений левых частей ограничений; с!) задать ЦФ (в окне «Поиск решения»):
• • целевую ячейку,
• • направление оптимизации ЦФ;

е) ввести ограничения и граничные условия (в окне «Поиск решения»):

• • ячейки со значениями переменных,
• • граничные условия для допустимых значений переменных,
• • соотношения между правыми и левыми частями ограничений. 2. Решить задачу:

a)установить параметры решения задачи (в окне «Поиск решения»,);

b) запустить задачу на решение (в окне «Поиск решения»,);

c) выбрать формат вывода решения (в окне «Результаты поиска решения»).

Рассмотрим пример нахождения решения для следующей одноиндексной ЗЛП:

Создание экранной формы и ввод в нее условия задачи

Экранная форма для ввода условий задачи (1) вместе с введенными в нее исходными данными представлена на рис.1.

В экранной форме на рис. 1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Так, например, переменным задачи (1) соответствуют ячейки

коэффициентам ЦФ соответствуют ячейки

правым частям ограничений соответствуют ячейки

• Ввод зависимостей из математической модели в экранную форму

Зависимость для ЦФ.

В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1 (значение ЦФ определяется выражением

Используя обозначения соответствующих ячеек в Excel (см. рис. 1), формулу для расчета ЦФ (2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов ЦФ (В6, С6, D6,E6):

После этого в целевой ячейке появится 0 (нулевое значение) (рис. 2).

Зависимости для левых частей ограничений

Левые части ограничений задачи (1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи(ВЗ, СЗ, D3, ЕЗ), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, С10, D10, Е10 — 1-е ограничение; В11, C11,D11, Е11 — 2-е ограничение и В12, С12, D12, Е12 — 3-е ограничение). Формулы, соответствующие левым частям ограничений, записать самостоятельно. Проверка правильности введения формул

Для проверки правильности введенных формул производите поочередно двойное нажатие левой клавиши мыши на ячейки с формулами. При этом на экране рамкой будут выделяться ячейки, используемые в формуле. Дальнейшие действия производятся в окне «Поиск решения», которое вызывается из меню «Сервис». Решение задачи

Установка параметров решения задачи

Задача запускается на решение в окне «Поиск решения». Но предварительно для установления конкретных параметров решения задач оптимизации определенного класса необходимо нажать кнопку «Параметры»и заполнить некоторые поля окна «Параметры поиска решения».

Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).

Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее32 767. Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.

Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее. Параметр «Сходимость» применяется только при решении нелинейных задач. Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода. Подтвердите установленные параметры нажатием кнопки «ОК». Запуск задачи на решение

Запуск задачи на решение производится из окна «Поиск решения» путем нажатия кнопки «Выполнить».

После запуска на решение задачи линейного программирования на экране появляется окно «Результаты поиска решения» с одним из сообщений:

• Сообщение об успешном решении задачи

• Сообщение при несовместной системе ограничений задачи

• Сообщение при неограниченности ЦФ в требуемом направлении Иногда второе и третье сообщения свидетельствуют не о характере оптимального решения задачи, а о том, что при вводе условийзадачи в Excel были допущены ошибки, не позволяющие Excel найти оптимальное решение, которое в действительности существует.

Если при заполнении полей окна «Поиск решения» были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено. Иногда слишком малое значение параметра»Относительная погрешность» не позволяет найти оптимальное решение. Для исправления этой ситуации увеличивайте погрешность поразрядно, например от 0,000001 до 0,00001 и т.д.

В окне «Результаты поиска решения» представлены названия трех типов отчетов: «Результаты», «Устойчивость», «Пределы». Они необходимы при анализе полученного решения на чувствительность (будет рассмотрено позже). Для получения же ответа (значений переменных, ЦФ и левых частей ограничений) прямо в экранной форме просто нажмите кнопку «ОК». После этого в экранной форме появляется оптимальное решение задачи (рис.3).

Допустим, что к условию задачи (1) добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.

• В экранной форме укажите, на какие переменные накладывается требование целочисленности (этот шаг делается для наглядности восприятия условия задачи) (рис. 4).

• В окне «Поиск решения» (меню «Сервис»—►»Поиск решения»), нажмите кнопку «Добавить» и в появившемся окне «Добавление ограничений» введите ограничения целочисленности. Сравните результаты.

Получите у преподавателя индивидуальные задания.

Примеры решения экономических задач Задача 1.

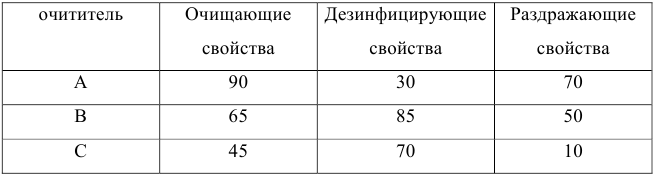
Средства очистки пола оценивают по следующим трем показателям:

• • очищающие свойства;
• • дезинфицирующие свойства;
• • раздражающее воздействие на кожу.

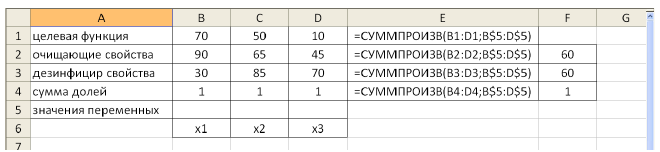
Каждый из этих показателей измеряется по линейной шкале от 0 до 100. Продукт на рынке должен иметь по крайней мере 60 ед. очищающих свойств и по крайней мере 60 ед. дезинфицирующих свойств по соответствующей шкале. При этом раздражающее воздействие на кожу должно быть минимальным. Конечный продукт должен быть смесью трех основных очистителей, характеристики которых приведены в таблице.

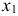
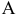
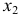
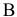
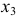
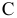
Составим математическую модель задачи. Пусть — доля очистителя в конечном продукте, — доля очистителя в конечном продукте, — доля очистителя в конечном продукте.

Целевая функция: 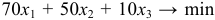(т.е. минимизируем раздражающее воздействие на кожу конечного продукта).

Решение задачи с помощью MS Excel.

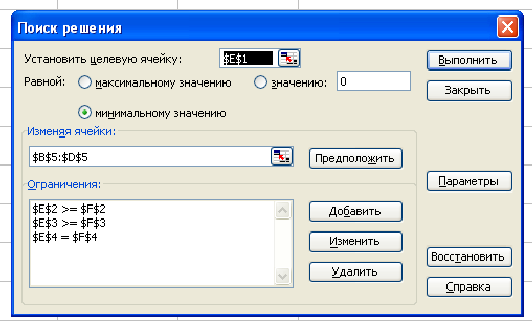
Заполним таблицу, содержащую исходные данные. Заполним диалоговое окно

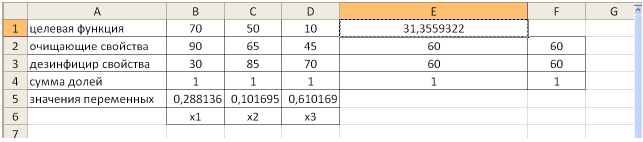
Щелкнув по кнопке ОК, мы получаем на месте исходной таблицы — таблицу с найденными оптимальными значениями. В результате в таблице получим значение целевой функции — 31,4 ед. раздражающего воздействия на кожу при

(т.е. очистители нужно брать в долях 30%, 10% и 60% соответственно).

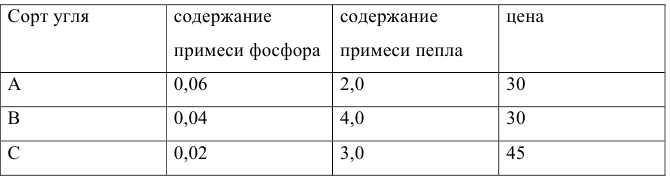
Фирме требуется уголь с содержанием фосфора не более 0,03% и с примесью пепла не более 3,25%. Доступны 3 сорта угля по следующим ценам (за тонну):

Как следует их смешать, чтобы удовлетворить ограничениям на примеси и минимизировать цену?

Решение задач математического программирования с помощью надстройки «Поиск решения» ЭТ Excel

Задачи линейного программирования, целочисленного программирования и ряд задач нелинейного программирования могут быть решены с помощью стандартного прикладного программного обеспечения. Например, в ЭТ MS Excel для этого имеется модуль «Поиск решения», вызываемый командой меню «Сервис/Поиск решения». Для активизации данного модуля необходимо выполнить команду «Сервис/Надстройки» и установить флажок напротив строки меню «Поиск решения».

Рассмотрим пример применения «Поиска решения» на основе решения задачи оптимизации портфеля ценных бумаг — одной из классических задач управления финансовыми средствами.

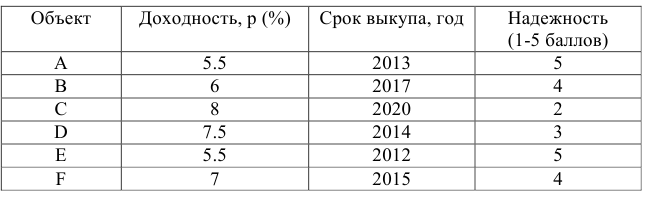
Постановка задачи. Перед инвестором стоит задача на основе информации, представленной в таблице 1, разместить имеющиеся средства так, чтобы получить максимальную прибыль за 1 период планирования (1 год), при этом должны быть выполнены следующие условия:

1. Суммарный объем капитала составляет 100 000 $;
2. доля средств, вложенная в один из объектов, не может превышать 25%;
3. более 40% всех средств должны быть вложены в долгосрочные активы;
4. доля высокорисковых активов не может превышать трети от суммарного объема.

Таблица 1 — Информация об объектах инвестирования

Построим экономико-математическую модель задачи.

Искомые переменные — объемы средств, вложенные в активы: .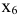

Прибыль, которую получит инвестор, задается целевой функцией:

Ограничения на суммарный объем активов —

Ограничение на размер доли каждого актива

Необходимость долгосрочного инвестирования (например, более 3 лет)

Учет необходимости снижения риска —

Естественное экономическое ограничение — неотрицательность искомых переменных —

Для решения задачи выполним следующие шаги.

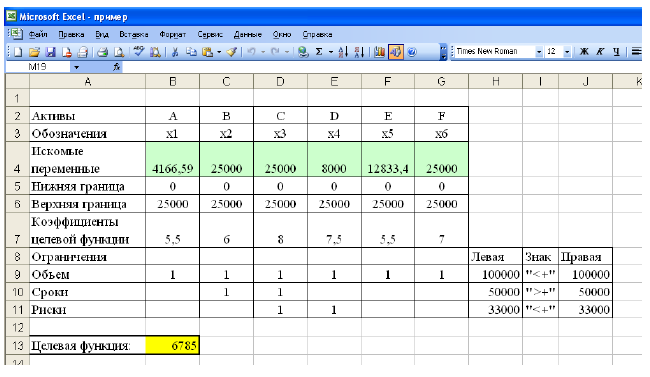
• На рабочем листе представим необходимую для решения информацию, согласно рисунку 1.

Ячейки В13, Н9-Н11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Суммпроизв(…), аргументами которой являются диапазоны B4-G4 и диапазоны соответствующих параметров.

Рисунок 1 — Исходные данные для решения ЗЛП

• Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Указать адрес ячейки (В 13), содержащей целевую функцию, указать тип целевой функции,

В поле «изменяя ячейки» указать адреса всех искомых переменных (от В4 до G4).

Затем последовательно заполнить все ограничения (Пример на рисунке 2.)

Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить».

Далее, если это необходимо, устанавливаются особые значения параметров (кнопка «Параметры»).

Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 5.

Рисунок 5 — Результаты решения задачи

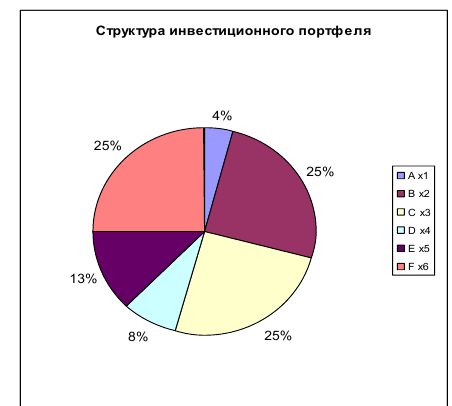
На рисунке 6 представлена структура инвестиционного портфеля.

На основе решения проводится анализ, и принимаются соответствующие управленческие решения.

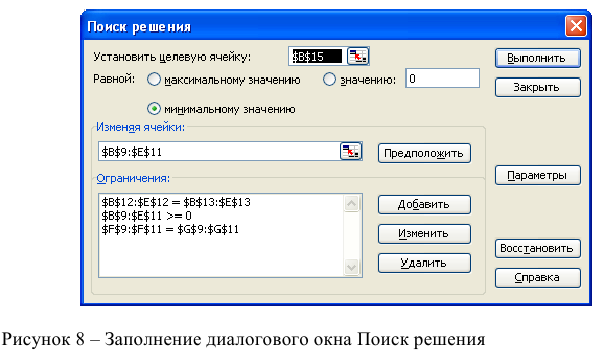
Технология решения транспортной задачи

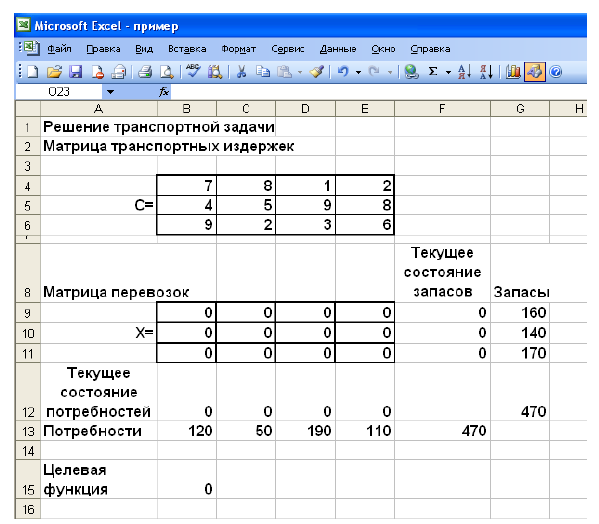
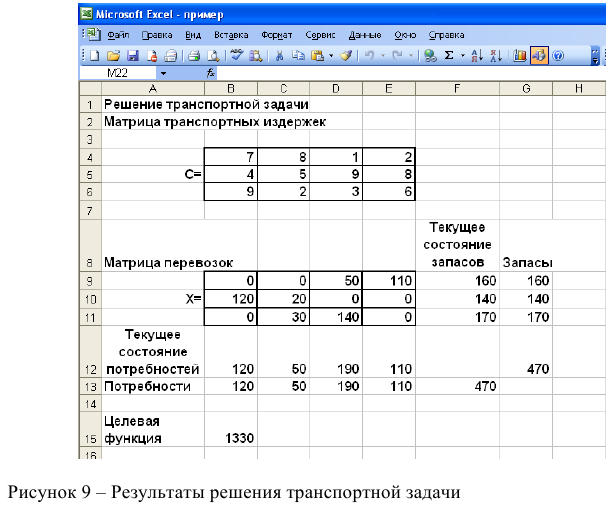
1. На рабочем листе представим необходимую для решения информацию, согласно рисунку 7.

Ячейки В15 содержит формулу Суммпроизв(…), аргументами которой являются диапазоны В4-Е6 и В9-Е11. Ячейки F9-F11 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае целесообразно использовать функцию Сумм(…), аргументами которой являются диапазоны В9-Е9, В10-Е 10 и В11 -Е11. Аналогично определяются формулы в В12-Е 12.

Рисунок 7 — Исходные данные для решения ЗЛП

• Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Указать адрес ячейки (В 15), содержащей целевую функцию, указать тип целевой функции (минимум),

В поле «изменяя ячейки» указать адреса всех искомых переменных (от В9 до Е11).

Затем последовательно заполнить все ограничения (Пример на рисунке 8.)

Если возникли ошибки ввода, то изменить или добавить ограничение можно с помощью командных кнопок «Добавить, изменить, удалить». Результаты отражаются на рабочем листе. Результаты решения представлены на рисунке 9.

Технология решения задачи нелинейного программирования

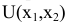
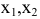
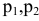
Построить математическую модель и решить задачу потребительского выбора для заданной функции полезности на товары , ценах и

доходе I. Найти максимальное значение функции полезности.

Построим математическую модель задачи потребительского выбора:

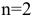
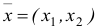
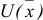
где — число потребляемых товаров или благ, — потребительский набор, — функция полезности потребителя.

Набор, который является решением задачи потребительского выбора, называется оптимальным потребительским набором, или точкой локального рыночного равновесия потребителя. Поставленная задача — задача потребительского выбора — является задачей нелинейного программирования.

• На рабочем листе представим необходимую для решения информацию, согласно рисунку 10.

Ячейки В5, В6 должны содержать формулы, отражающие зависимость между искомыми переменными и условиями задачи. В данном случае ячейка В5 содержит формулу «=D2B2+E2C2», а ячейка В6 содержит формулу «=2В2Л(3/4)(С2-4)А(1/4)».

Рисунок 10 — Исходные данные для решения ЗНП

• Выполнить команду Сервис/Поиск решения и заполнить все поля диалогового окна:

Аналитическое решение задачи нелинейного программирования.

В рассматриваемом случае ограничение можно записать в виде строгого равенства, так как оптимальное решение достигается при полном использовании имеющихся средств.

Для решения классической задачи нелинейного программирования применим метод множителей Лагранжа, для этого составим функцию Лагранжа:

Найдем точки экстремума функции Лагранжа.

Приравняем каждое уравнение к 0:

С помощью преобразований — разделим первое уравнение системы на второе, перейдем к системе:

Подставим второе уравнение в первое и построим аналитические функции спроса:

Максимальное значение функции полезности-

Решением задачи потребительского выбора будет набор

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Решение задачи коммивояжера при помощи надстройки MS Excel «Поиск решения»

Метод полного перебора

Мощным средством анализа данных MS Excel является надстройка «Поиск решения». С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки, данные которых, определяют значение целевой ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.

Программа Поиск решений – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации, используется с 1991 года.

Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями: количество неизвестных (decision variable) – 200; количество формульных ограничений (explicit constraint) на неизвестные – 100; количество предельных условий (simple constraint) на неизвестные – 400.

Постановка задачи коммивояжера, которую необходимо решить посредством надстройки «Поиск решения» методом полного перебора следующая:

«Сотруднику компании ООО «Новые технологии» Петрову Н.И. необходимо обновить программный продукт автоматизированного учета в пяти организациях: А, Б, В, Г и Д. Он решил начать свой обход с организации «А», так как она находится на первом этаже дома, в котором проживает Петров. Сотруднику необходимо, спланировать свой маршрут таким образом, чтобы к концу рабочего дня обойти все организации в определенном порядке и выполнив свою работу, вернутся домой (в пункт «А»). В каком порядке Петрову следует обходить организации, чтобы его замкнутый тур был кратчайшим? Если расстояния между каждой парой организаций заданы следующей квадратной матрицей (5×5):

Решение: Разместим исходные данные на рабочем листе (рис 2.1). Заменим знак 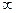числом 10000 (на результат решения исключение пути не оказывает влияния).

Рисунок 2.1 Исходные данные задачи

Ячейка	Формула	Примечание
B9	= СУММ(B4:B8)	Распространяем на диапазон B9:F9
G4	= СУММ(B4:F4)	Распространяем на диапазон G4:G8
C19	=СУММПРОИЗВ(B4:F8;B13:F17)	Целевая функция
E19	=B4+C5+D6+E7+F8	Исключение пути
B23	=$C$10-C10+4*C5	Распространяем на диапазон B23:E23
B24	=$D$10-C10+4*C6	Распространяем на диапазон B24:E24
B25	=$E$10-C10+4*C7	Распространяем на диапазон B25:E25
B26	=$F$10-C10+4*C8	Распространяем на диапазон B26:E26

1. Запускаем надстройку MS Excel «Поиск решения» командой Сервис/ Поиск решения. И заполняем (рис. 2.2).

2. Для того чтобы выполнялись условия однократного посещения сотрудником организаций и в то же время запланированный Петровым маршрут был пройден полностью, введем ограничения: в строки B9, G4 заводим формулы из таблицы 1 и распространяем их на соответствующие диапазоны B9:F9 и G4:G8. Задаем следующие данные $B$9:$F$9=1 и $G$4:$G$8=1 в Ограничения окна «Поиск решения». Таким образом, мы можем отследить порядок обхода организаций сотрудником, оценить правильность выбора и оптимальность его маршрута.

3. Выбираем ячейку B19 и устанавливаем ее адрес в Целевую ячейку окна «Поиск решения», чтобы определить длину наикратчайшего маршрута. Для этого в ячейку B19 предварительно заносим соответствующую формулу из таблицы 1. Когда программа «Поиск решения» вычислит оптимальный маршрут Петрова и станет известен порядок обхода организаций (из Матрицы переменных) будут известны и расстояния между конкретными парами организаций. Затем при помощи простых математических подсчетов программа рассчитает протяженность оптимального маршрута.

4. Устанавливаем еще одно ограничение в окно «Поиск решения»: $E$19=0. В указанную ячейку вводим формулу из таблицы 1 и исключаем таким образом, заведомо ложный порядок движения Петрова в порядке обхода организаций.

5. В связи с тем, что ячейки диапазона B4:F8 – изменяемые, в Ограничение окна «Поиск решения» необходимо добавить строку B$4$:F$8$=двоичное.

6. Заводим в ячейки B23; B24; B25; B26 соответствующие формулы из таблицы 1 и распространяем их на следующие диапазоны: B23:E23 B24:E24; B25:E25; B26:E26 для учета всех возможных вариантов обхода организаций сотрудником и выбора из них оптимального. Формулы задаем таким образом, чтобы обеспечить исключение ложного пути, соблюдая условие задачи об обходе всех организаций по одному разу.

7. Добавляем в Ограничения окна «Поиск решения» $B$23:$E$26 ≤ 3.

Рисунок 2.2 Окно «Поиск решения»

Так как это линейная модель, то необходимо фиксировать в окне Параметры поиска решений на позицию Линейная модель и Неотрицательные значения (рис. 2.3). После того, как все поля и ячейки заполнены нажимаем кнопку «Выполнить» и появляется окно диалога с описанием результатов процесса оптимизации. Чтобы отобразить найденное решение в ячейках листа, устанавливаем переключатель «Сохранить найденное решение» и нажимаем кнопку ОК. Найденная минимальная величина помещается в целевую ячейку, а переменные ячейки заполняются оптимальными значениями переменных, которые удовлетворяют установленным ограничениям.

Рисунок 2.3 Окно «Параметры поиска решения»

Таким образом, получаем следующий результат. Если Петров переходит из организации в организацию, то на рис. 2.4 в диапазоне B4:F8 мы будем наблюдать порядок его перемещений. Если видим, что в ячейке, которая отнесена к организации «В» стоит единица, значит сотрудник посетил эту организацию следующей за пунктом «А». Если в ячейке ноль – сотрудник организацию не посещал.

Рисунок 2.4 Результаты решения задачи коммивояжера

В ходе анализа полученных результатов, приходим к выводу: наиболее оптимальным маршрут Петрова будет в том случае, если он начал свой путь с организации «А», посетит другие организации в следующем порядке «В», затем «Д», далее «Б» и «Г», из которой вернется к началу своего пути (в организацию «А»). представим путь схематически:

Длина кратчайшего маршрута (значение целевой ячейки) в результате составит – 21.

Задача решена. Кратчайший маршрут Петрова найден.

ЗАКЛЮЧЕНИЕ

Задача коммивояжера была поставлена в 1934 году. Ее сущность заключается в поиске оптимального маршрута движения при необходимости посетить все запланированные объекты с наименьшими финансовыми и временными издержками. Как правило, речь идет о простом перемещении по заданным точкам, либо с перевозкой груза небольшого формата на транспортном средстве.

Задача коммивояжера является одной из знаменитых задач теории комбинаторики и пользуется популярностью благодаря тому, что к ней сводится большое количество практических задач.

Среди современных практических приложений задачи можно выделить: доставку продуктов в магазин со склада, работу почтальона по разноске корреспонденции, мониторинг объектов (нефтяные вышки, базовые станции сотовых операторов), изготовление отверстий на специализированном станке.

Для решения задачи коммивояжера используют различные группы простейших методов: полный и случайный перебор, жадный и деревянный алгоритмы, метод имитации отжига. Широкое применение получили различные модификации более эффективных методов, таких как метод ветвей и границ, генетических алгоритмов, а также алгоритм муравьиных колоний.

В работе была поставлена задача, сводимая к задаче коммивояжера, и составлена схема оптимального маршрута, подробно рассмотрен порядок выбора кратчайшего пути при помощи использования надстройки MS Excel «Поиск решения» методом полного перебора. Результаты решения были выведены на отдельный рабочий лист Excel.

Изучение особенностей задачи коммивояжера позволило сделать следующий вывод: актуальным в настоящее время остается поиск точных и приближенных способов решения этой задачи как с теоретической, так и с практической точек зрения. Более того, темпы современной жизни меняют отношение человека ко времени, сегодня пользователь не любит ждать, изыскивает возможности сократить время ожидания, найти оптимальное решение в кратчайшие сроки. Все это свидетельствует о росте в будущем потребности в эффективном решении задач коммивояжера и иных родственных им оптимизационных задач, которые позволили бы существенно сэкономить ограниченные ресурсы организаций.

Министерство образования и науки РФ

ГБОУ СПО «Шадринский политехнический колледж»

Заведующая учебной частью

____________ Блинова Н.А.

Курсовая работа

по дисциплине «Математические методы»

на тему «Задача о коммивояжере. Метод полного перебора»

Урок по теме «Решение уравнений в среде MS Excel»

Одна из наиболее актуальных проблем компьютерного обучения – проблема отбора и использования педагогически целесообразных обучающих программ.

При изучении отдельных тем и решении некоторых задач на уроках математики в старших классах громоздкие вычисления как, например, при решении уравнений методом деления отрезка пополам или методом последовательных приближений, затмевают существо математической задачи, не дают увидеть красоту, рациональность применяемого метода решения.

В данной статье я представила те задачи, решение которых с помощью MS EXCEL позволяет получить наглядное, доступное для понимания учащимися решение, показать его логику, рациональность. Попутно учащиеся получают устойчивые навыки работы с программой.

Нахождение корней уравнения с помощью подбора параметра

Пример 1.

Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 1000 000 условных единиц. Необходимо определить, какими должны быть оклады сотрудников больницы.

Решение такой задачи можно искать методом перебора. Однако в лучшем случае на это уходит много времени. Можно предложить другой способ решения. В EXCEL он реализован как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.

Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: A_i*С+В_i, где С – оклад санитарки; А_i и В_i – коэффициенты, которые для каждой должности определяют следующим образом:

• медсестра получает в 1,5 раза больше санитарки (А₂=1,5; В₂=0);
• врач – в 3 раза больше санитарки (А₃=3; В₃=0);
• заведующий отделением – на 30 y.e. больше, чем врач (А₄=3; B₄=30);
• заведующий аптекой – в 2 раза больше санитарки (А₅=2; В₅=0);
• заведующий хозяйством – на 40 y.e. больше медсестры (А₆=1,5; В₆=40);
• заведующий больницей – на 20 y.e. больше главного врача (А₈=4; В₈=20);
• главный врач – в 4 раза больше санитарки (А₇=4; В₇=0);

Зная количество человек на каждой должности, нашу модель можно записать как уравнение: N₁*(A₁*C+B₁)+N₂*(A₂*C+B₂)+. +N₈*(A₈*C+B₈) = 1000000, где N₁ – число санитарок, N₂ – число медсестер и т.д.

В этом уравнении нам известны A₁. A₈, B₁. B₈ и N₁. N₈, а С неизвестно. Анализ уравнения показывает, что задача вычисления заработной платы свелась к решению линейного уравнения относительно С. Предположим, что зарплата у санитарки 150,00 y.e.

Введите исходные данные в рабочий лист электронной таблицы, как показано ниже.

A

B

C

D

E

F

Оклад мед. Работников

Общий фонд равен

В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D4 формула расчета имеет вид =B4*$D$3+C4.

В столбце F вычислите заработную плату всех работников данной должности. Например, для ячейки F3 формула расчета имеет вид =D3*E3.

В ячейке F11вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже.

A

B

C

D

E

F

Оклад мед. Работников

Общий фонд равен

Чтобы определите оклад санитарки так, чтобы расчетный фонд был равен заданному надо:

• Активизировать команду Подбор параметра во вкладке Данные / Работа с данными /Анализ «Что, если»;
• В поле «Установить в ячейке» появившегося окна ввести ссылку на ячейку F11, содержащую формулу;
• В поле «Значение» набрать искомый результат 1000000;
• В поле «Изменяя значение ячейки» ввести ссылку на изменяемую ячейку D3 и щелкните на кнопке ОК.

Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако, благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, – это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.

Задание для учащихся:

Составить несколько вариантов штатного расписания с использованием функции Подбор параметра и оформить их в виде таблицы:

• Изменить количество сотрудников на различных должностях;
• Подобрать зарплату санитарки в новых условиях;
• Составить таблицу нескольких вариантов штатного расписания.

Рассмотрим еще один пример нахождения корней уравнения с помощью подбора параметра. При решении этого уравнения используется также метод последовательных приближений. Учащиеся в классах с углубленным изучением математики знакомы с этим методом. Поэтому, чтобы этот пример был доступен для других учащихся, предлагаю краткую теорию этого метода.

Пусть дано уравнение, записанное в виде x=F(x). Выбирают некоторое начальное приближение x₁ и подставляют его вместо x в F(x). Полученное значение x₂=F(x₁) этой функции считают вторым приближением. Далее находят третье приближение по формуле x₃=F(x₂) и так далее. Таким образом, получаем последовательность x₁, x₂, x₃,…, x_n,… чисел, имеющая предел α. Тогда если функция F(x) непрерывна, из равенства x_n+1=F(x_n) получаем α=F(α). Это означает, что α является решением уравнения x=F(x).

Пример 2.

Пусть нам дан многочлен третьей степени:

x 3 -0,01x 2 -0,7044x+0,139104=0.

Так как мы ищем корни полинома третьей степени, то имеются не более трех вещественных корней. Для нахождения корней их первоначально надо локализовать, то есть найти интервалы, на которых они существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположный знак. С целью нахождения интервалов, на концах которых функция изменяет знак, необходимо построить ее график или протабулировать ее. Составим таблицу значений функции на интервале [-1;1] с шагом 0,2. Для этого необходимо:

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

Функция ВПР в Экселе – быстрый перенос данных

Самое простое применение функция ВПР это быстрый перенос данных из одной таблицы в другую.

Например, у вас есть большой прайс на 500 позиций и запрос от покупателя, скажем на 50 позиций (в реальности и прайс и запрос могут быть гораздо больше, но принцип от этого не меняется).

Вам нужно быстро найти цены на эти 50 позиций. Разумеется, можно отдельно искать каждую позицию в большом прайсе и потратить на это 30 – 60 минут, а можно сделать это менее чем за минуту при помощи функции ВПР.

Итак, у нас в прайсе 500 позиций. Позиции обозначаются следующим образом, буквами обозначается вид позиции, а цифрами модификация.

Например, «Стул_1» и «Стул_21» это два совершенно разных стула.

Цены в прайсе указаны для примера и вряд ли имеют отношение к реальным ценам.

Обозначим задачу.

В ООО «ЫкэА» пришел запрос от «Петровича».

Петрович человек простой, любит всё делать быстро, но не очень чётко. Поэтому его запросы отличаются особым сумбуром в позициях.

Однако это нас не страшит, во-первых, у нас есть ВПР, во-вторых мы и не такое видали.

Петрович требует, чтобы мы очень быстро проставили цены в его запросе. Ждать он намерен максимум 5 минут. Ведь другие поставщики уже завалили его предложениями.

Нам не хочется терять такого клиента и мы практически мгновенно открываем прайс:

Получается у нас должно быть открыто два файла (две книги в Эксель). Запрос от Петровича и Прайс.

Это как раз то что необходимо, осталось только перенести цены из прайса в запрос.

Для этого перейдем в таблицу запроса и в первой ячейке столбца «Цены» (D4) введем «=впр» и два раза кликнем на значок функции:

Сразу же после этого, в строке формулы нужно поставить курсор внутри надписи ВПР и нажать Fx, перед вами появится окно с аргументами функции ВПР:

В аргументах функции вы говорите Экселю что и где нужно искать:

Искомое значение — это значение (в данном случае наименование), цену которого вы хотите найти в прайсе. Соответственно кликайте на первую ячейку столбца «Наименование».

Далее, сразу переходите в «Прайс»:

Теперь в аргументах функции заполните следующие поля:

Таблица — выделяете столбцы, которые содержат искомые наименования и цены, таким образом, чтобы наименования были крайним левым столбцом.

Так работает функция ВПР — ищет искомые значения в крайнем левом столбце (для ВПР это столбец №1). Когда ВПР находит искомое значение он начинает смотреть правее, в тот столбец, который вы указали в «Номере столбца».

Там вы должны указать столбец, содержащий необходимые для переноса данные. В нашем случае это цены и в нашем случае это столбец под номером два, относительно той таблицы, которую вы указали в аргументах.

Интервальный просмотр — ставьте 0. Ноль обозначает точное соответствие.

После заполнения аргументов функции нажимайте «Ок» и если всё сделано верно, то в столбце «Цена» (файл «Запрос от Петровича»), появится цена.

Вам нужно протянуть цены на оставшиеся ячейки:

Коллеги, вот и всё, вы овладели функцией ВПР.

Очень важное замечание!

Обратите внимание на то, что сейчас мы работали в двух разных файлах (книгах).

Когда работа идёт в двух разных книгах, Эксель автоматически закрепляет таблицу в функции ВПР:

Делает это он при помощи значка $, который проставляет перед столбцами и строками таблицы.

Это позволяет не съезжать формуле когда вы протягиваете её вниз. Это очень актуально когда вы работаете в рамках одного листа или одной книги (в этом случае Эксель автоматически Не закрепляет ячейки).

Давайте посмотрим что получиться если протянуть формулу «без закрепления»:

Обратите внимание, что для первой ячейки всё в порядке и диапазон B3:C502 точно соответствует той таблице, которую мы выделили для поиска данных, однако (без закрепления) так будет не всегда, по мере «протягивания» формулы ВПР вниз, будет смещаться и таблица, пока однажды, мы не увидим вот такую странную надпись #Н/Д:

#Н/Д значит что функция ВПР не смогла найти цену Стул_13 в прайсе и это не мудрено, ведь диапазон таблицы в формуле ВПР уехал ниже этого значения:

Посему, если не хотите чтобы от вас уезжали, закрепляйте диапазон.

Очень важное замечание №2

Как вы заметили, формулы ссылаются на определённые ячейки, другими словами между формулами и исходными данными есть связь. Стоит изменить исходные данные и значения в формулах сразу изменятся.

Особенно остро это чувствуется в ВПР. Если вы вдруг забудетесь и в исходной табличке добавите лишний столбец в «неположенном месте», то в формула ВПР выдаст совсем неожиданные значения.

Поэтому, если вам не нужна связь между таблицами, рекомендую формулы превратить в данные.

Для этого нужно выделить столбец с формулами, нажать Ctrl+C и в левом верхнем углу выбрать «Вставить» — «Вставить значения».

Для тех кто не любит изучать картинки, я записал небольшое видео в котором показываю всё то, что мы проговорили выше (кроме вставки значений):

Видео — «Быстрый перенос данных с помощью функции ВПР в Экселе»

Перенос данных при помощи ВПР, можно использовать не только для того, чтобы быстро получать данные из одной таблицы в другой, но и для того, чтобы сравнивать две таблицы.

Это очень актуально для тех кто работает в закупках и отправляет заказы поставщику.

Обычно происходит следующая ситуация. Вы отправляете заказ поставщику, через некоторое время получаете ответ в виде счёта и сверяете заказ с счётом.

Всё ли есть в счёте, в нужном ли количестве, по правильным ли ценам и т.д.

Функция ВПР в Экселе: пошаговая инструкция

Представим, что перед нами стоит задача определить стоимость проданных товаров. Стоимость рассчитывается, как произведение количества и цены. Сделать это очень легко, если количество и цены находятся в соседних колонках. Однако данные могут быть представлены не в столь удобном виде. Исходная информация может находиться в совершенно разных таблицах и в другом порядке. В первой таблице указаны количества проданных товаров:

Во второй – цены:

Если перечень товаров в обеих таблицах совпадает, то, зная магическое сочетание Ctrl+C и Ctrl+V, данные о ценах можно легко подставить к данным о количестве. Однако очередность позиций в обеих таблицах не совпадает. Тупо скопировать цены и подставить к количеству не получится.

Поэтому мы не можем прописать формулу умножения и «протянуть» вниз на все позиции.

Что делать? Надо как-то цены из второй таблицы подставить к соответствующему количеству в первой, т.е. цену товара А к количеству товара А, цену Б к количеству Б и т.д.

Вот так.

Функция ВПР в Эксель легко справится с задачей.

Добавим вначале в первую таблицу новый столбец, куда будут подставляться цены из второй таблицы.

Для вызова функции с помощью Мастера нужно активировать ячейку, где будет прописана формула и нажать кнопку f(x) в самом начале строки формул. Появится диалоговое окно Мастера, где из списка всех функций нужно выбрать ВПР.

Кликаем по надписи «ВПР». Открывается следующее диалоговое окно.

Теперь нужно заполнить предлагаемые поля. В первом окошке «Искомое_значение» нужно указать критерий для ячейки, в которую мы вписываем формулу. В нашем случае это ячейка с наименованием товара «А».

Следующее поле «Таблица». В нем нужно указать диапазон данных, где будет осуществляться поиск нужных значений. В нашем случае это вторая таблица с ценой. При этом крайний левый столбец выделяемого диапазона должен содержать те самые критерии, по которым осуществляется поиск (столбец с наименованиями товаров). Затем таблица выделяется вправо минимум до того столбца, где находятся искомые значения (цены). Можно и дальше вправо выделить, но это уже ни на что не влияет. Главное, чтобы выделенная таблица начиналась со столбца с критериями и захватывала нужный столбец с данными. Также следует обратить внимание на тип ссылок, они должны быть абсолютными, т.к. формула будет копироваться в другие ячейки.

Следующее поле «Номер_столбца» — это число, на которое столбец с искомыми данными (ценами) отстоит от столбца с критерием (наименованием товара) включительно. То есть отсчет идет, начиная с самого столбца с критерием. Если у нас во второй таблице оба столбца находятся рядом, то нужно указать число 2 (первый – критерий, второй — цены). Часто бывает, что данные отстоят от критерия на 10 или 20 столбцов. Это не важно, Excel все сосчитает.

Последнее поле «Интервальный_просмотр», где указывается тип поиска: точное (0) или приблизительное (1) совпадение критерия. Пока ставим 0 (или ЛОЖЬ). Второй вариант рассмотрен ниже.

Нажимаем ОК. Если все правильно и значение критерия есть в обеих таблицах, то на месте только что введенной формулы появится некоторое значение. Остается только протянуть (или просто скопировать) формулу вниз до последней строки таблицы.

Теперь легко рассчитать стоимость простым умножением количества на цену.

Формулу ВПР можно прописать вручную, набирая аргументы по порядку, и разделяя точкой с запятой (см. видеоурок ниже).

Функция ВПР имеет свои особенности, о которых следует знать.

1. Первую особенность можно считать общей для функций, которые используются для многих ячеек путем прописывания формулы в одной из них и дальнейшим копированием в остальные. Здесь нужно обращать внимание на относительность и абсолютность ссылок. Конкретно в ВПР критерий (первое поле) должно иметь относительную ссылку (без знаков $), так как у каждой ячейки свой собственный критерий. А вот поле «Таблица» должно иметь абсолютную ссылку (адрес диапазона прописывается через $). Если этого не сделать, то при копировании формулы диапазон «поедет» вниз и многие значения просто не найдутся, так как искать будет негде.

2. Номер столбца, указываемый в третьем поле «Номер_столбца» при использовании Мастера функций, должен отсчитываться, начиная с самого критерия.

3. Функция ВПР из диапазона с искомыми данными выдает первое сверху значение. Это значит, что, если во второй таблице, откуда мы пытаемся «подтянуть» некоторые данные, присутствуют несколько ячеек с одинаковым критерием, то в рамках выделенного диапазона ВПР захватит первое сверху значение. Об этом следует помнить. К примеру, если мы хотим к цене товара подтянуть количество из другой таблицы, а там этот товар встречается несколько раз (в нескольких строках), то к цене подтянется первое сверху количество.

4. Последний параметр формулы, который 0 (нуль), ставить нужно обязательно. Иначе формула может криво работать.

5. После использования ВПР саму формулу лучше сразу удалить, оставив только полученные значения. Делается это очень просто. Выделяем диапазон с полученными значениями, нажимаем «копировать» и на это же место с помощью специальной вставки вставляем значения. Если таблицы находятся в разных книгах Excel, то очень удобно разорвать внешние связи (оставив вместо них только значения) с помощью специальной команды, которая находится по пути Данные → Изменить связи.

После вызова функции разрывания внешних связей появится диалоговое окно, где нужно нажать кнопку «Разорвать связь» и затем «Закрыть».

Это позволит удалить сразу все внешние ссылки.

Интервальный просмотр в функции ВПР

Наступило время обсудить последний аргумент функции ВПР. Как правило, указываю 0, чтобы функция искала точное совпадение критерия. Но есть вариант приблизительного поиска, это называется интервальный просмотр.

Рассмотрим алгоритм работы ВПР при выборе интервального просмотра. Прежде всего (это обязательно), столбец с критериями в таблице поиска должен быть отсортированы по возрастанию (если числа) или по алфавиту (если текст). ВПР просматривает список критериев сверху и ищет равный, а если его нет, то ближайший меньший к указанному критерию, т.е. на одну ячейку выше (поэтому и нужна предварительная сортировка. После нахождения подходящего критерия ВПР отсчитывает указанное количество столбцов вправо и забирает оттуда содержимое ячейки, что и является результатом работы формулы.

Проще понять на примере. По результатам выполнения плана продаж каждому торговому агенту нужно выдать заслуженную премию (в процентах от оклада). Если план выполнен менее, чем на 100%, премия не положена, если план выполнен от 100% до 110% (110% не входит) – премия 20%, от 110% до 120% (120% не входит) – 40%, 120% и более – премия 60%. Данные находятся в следующем виде.

Требуется подставить премию на основании выполнения планов продаж. Для решения задачи в первой ячейке пропишем следующую формулу:

=ВПР(B2;$E$2:$F$5;2;1)

и скопируем вниз.

На рисунке ниже изображена схема, как работает интервальный просмотр функции ВПР.

Джеки Чан выполнил план на 124%. Значит ВПР в качестве критерия ищет во второй таблице ближайшее меньшее значение. Это 120%. Затем отсчитывает 2 столбца и возвращает премию 60%. Брюс Ли план не выполнил, поэтому его ближайший меньший критерий – 0%.

Синтаксис и описание функции ВПР в Excel

Итак, так как второе название этой статьи «Функция ВПР в Excel для чайников», начнем с того что узнаем, что же такое функция ВПР и что она делает? Функция ВПР на английском VLOOKUP, ищет указанное значение и возвращает соответствующее значение из другого столбца.

Как работает функция ВПР? Функция ВПР в Excel выполняет поиск по вашим спискам данных на основе уникального идентификатора и предоставляет вам часть информации, связанную с этим уникальным идентификатором.

Буква «В» в ВПР означает «вертикальный». Она используется для дифференциации функции ВПР и ГПР, которая ищет значение в верхней строке массива («Г» обозначает «горизонтальный»).

Функция ВПР доступна во всех версиях Excel 2016, Excel 2013, Excel 2010, Excel 2007, Excel 2003.

Синтаксис функции ВПР выглядит следующим образом:

ВПР(искомое_значение;таблица;номер_столбца;[интервальный_просмотр])

Как видите, функция ВПР имеет 4 параметра или аргумента. Первые три параметра обязательные, последний – необязательный.

1. искомое_значение – это значение для поиска.

Это может быть либо значение (число, дата или текст), либо ссылка на ячейку (ссылка на ячейку, содержащую значение поиска), или значение, возвращаемое некоторой другой функцией Excel. Например:

• Поиск числа: =ВПР(40; A2:B15; 2) – формула будет искать число 40.
• Поиск текста: =ВПР(«яблоки»; A2:B15; 2) – формула будет искать текст «яблоки». Обратите внимание, что вы всегда включаете текстовые значения в «двойные кавычки».
• Поиск значения из другой ячейки: =ВПР(C2; A2:B15; 2) – формула будет искать значение в ячейке C2.

1. таблица – это два или более столбца данных.

Помните, что функция ВПР всегда ищет искомое значение в первом столбце таблицы. Ваш таблица может содержать различные значения, такие как текст, дата, числа или логические значения. Значения нечувствительны к регистру, что означает, что прописные и строчные буквы считаются идентичными.

Итак, наша формула =ВПР(40; A2:B15; 2) будет искать «40» в ячейках от A2 до A15, потому что A – это первый столбец таблицы A2: B15.

1. номер_столбца – номер столбца в таблице, из которой должно быть возвращено значение в соответствующей строке.

Самый левый столбец в указанной таблице равен 1, второй столбец – 2, третий – 3 и т. д.

Итак, теперь вы можете прочитать всю формулу =ВПР(40; A2:B15; 2). Формула ищет «40» в ячейках от A2 до A15 и возвращает соответствующее значение из столбца B (потому что B является вторым столбцом в указанной таблице A2:B15).

4. интервальный_просмотр определяет, ищете ли вы точное соответствие (ЛОЖЬ) или приблизительное соответствие (ИСТИНА или опущено). Этот последний параметр является необязательным, но очень важным.

Как использовать именованный диапазон или таблицу в формулах ВПР

Если вы собираетесь использовать один и тот же диапазон поиска в нескольких формулах ВПР, вы можете создать именованный диапазон для него и ввести имя непосредственно в аргументе таблица вашей формулы ВПР.

Чтобы создать именованный диапазон, просто выберите ячейки и введите любое имя в поле «Имя», слева от панели «Формула».

Функция ВПР в Excel – Присвоение имени диапазону

Теперь вы можете написать следующую формулу ВПР, чтобы получить цену Продукта 1:

=ВПР(«Продукт 1»;Продукты;2)

Функция ВПР в Excel – Пример функции ВПР с именем диапазона

Большинство имен диапазонов в Excel применяются ко всей книге, поэтому вам не нужно указывать имя рабочего листа, даже если ваш диапазон поиска находится на другом листе. Такие формулы гораздо более понятны. Кроме того, использование именованных диапазонов может быть хорошей альтернативой абсолютным ссылкам на ячейки. Поскольку именованный диапазон не изменяется, когда формула копируется в другие ячейки, и вы можете быть уверены, что ваш диапазон поиска всегда останется верным.

Если вы преобразовали диапазон ячеек в полнофункциональную таблицу Excel (вкладка «Вставка» –> «Таблица»), вы можете выбрать диапазон поиска с помощью мыши, а Microsoft Excel автоматически добавит имена колонок или имя таблицы в формулу:

Функция ВПР в Excel – Пример функции ВПР с именем таблицы

Полная формула может выглядеть примерно так:

=ВПР(“Продукт 1”;Таблица6[[Продукт]:[Цена]];2)

или даже =ВПР(“Продукт 1”;Таблица6;2).

Как и именованные диапазоны, имена столбцов являются постоянными, а ссылки на ячейки не изменятся независимо от того, где копируется формула ВПР.

Постановка задачи

Итак, имеем две таблицы – таблицу заказов и прайс-лист:

Задача – подставить цены из прайс-листа в таблицу заказов автоматически, ориентируясь на название товара с тем, чтобы потом можно было посчитать стоимость.

Ошибки #Н/Д и их подавление

Функция ВПР (VLOOKUP) возвращает ошибку #Н/Д (#N/A) если:

• Включен точный поиск (аргумент Интервальный просмотр=0) и искомого наименования нет в Таблице.
• Включен приблизительный поиск (Интервальный просмотр=1), но Таблица, в которой происходит поиск не отсортирована по возрастанию наименований.
• Формат ячейки, откуда берется искомое значение наименования (например B3 в нашем случае) и формат ячеек первого столбца (F3:F19) таблицы отличаются (например, числовой и текстовый). Этот случай особенно характерен при использовании вместо текстовых наименований числовых кодов (номера счетов, идентификаторы, даты и т.п.) В этом случае можно использовать функции Ч и ТЕКСТ для преобразования форматов данных. Выглядеть это будет примерно так:
  =ВПР(ТЕКСТ(B3);прайс;0)
• Функция не может найти нужного значения, потому что в коде присутствуют пробелы или невидимые непечатаемые знаки (перенос строки и т.п.). В этом случае можно использовать текстовые функции СЖПРОБЕЛЫ (TRIM) и ПЕЧСИМВ (CLEAN) для их удаления:
  =ВПР(СЖПРОБЕЛЫ(ПЕЧСИМВ(B3));прайс;0)
  =VLOOKUP(TRIM(CLEAN(B3));прайс;0)

Для подавления сообщения об ошибке #Н/Д (#N/A) в тех случаях, когда функция не может найти точно соответствия, можно воспользоваться функцией ЕСЛИОШИБКА (IFERROR). Так, например, вот такая конструкция перехватывает любые ошибки создаваемые ВПР и заменяет их нулями:

=ЕСЛИОШИБКА(ВПР(B3;прайс;2;0);0)

=IFERROR(VLOOKUP(B3;прайс;2;0);0)

Аргументы функции

• lookup_value (искомое_значение) – это величина для поиска, из крайнего левого столбца таблицы. Это может быть значение, ссылка на ячейку или текстовая строка. В примере со студентами это их фамилии;
• table_array (таблица) – это диапазон данных, в котором будет осуществлен поиск. Это может быть ссылка на диапазон ячеек или именованный диапазон. В примере с таблицей со студентами, это будет вся таблица, которая содержит оценку и фамилии студентов;
• col_index (номер_столбца) – это порядковый номер столбца в диапазоне с данными, из которого будет получена искомая величина;
• [range lookup] ([интервальный_просмотр]) – этот аргумент указывает на точность совпадения данных при поиске. Укажите “0” – если точное, “1” – если приблизительное совпадение.

Как пользоваться функцией ВПР в Excel

Допустим, на склад предприятия по производству тары и упаковки поступили материалы в определенном количестве.

Стоимость материалов – в прайс-листе. Это отдельная таблица.

Необходимо узнать стоимость материалов, поступивших на склад. Для этого нужно подставит цену из второй таблицы в первую. И посредством обычного умножения мы найдем искомое.

Алгоритм действий:

1. Приведем первую таблицу в нужный нам вид. Добавим столбцы «Цена» и «Стоимость/Сумма». Установим денежный формат для новых ячеек.
2. Выделяем первую ячейку в столбце «Цена». В нашем примере – D2. Вызываем «Мастер функций» с помощью кнопки «fx» (в начале строки формул) или нажав комбинацию горячих клавиш SHIFT+F3. В категории «Ссылки и массивы» находим функцию ВПР и жмем ОК. Данную функцию можно вызвать перейдя по закладке «Формулы» и выбрать из выпадающего списка «Ссылки и массивы».



3. Откроется окно с аргументами функции. В поле «Искомое значение» – диапазон данных первого столбца из таблицы с количеством поступивших материалов. Это те значения, которые Excel должен найти во второй таблице.



4. Следующий аргумент – «Таблица». Это наш прайс-лист. Ставим курсор в поле аргумента. Переходим на лист с ценами. Выделяем диапазон с наименованием материалов и ценами. Показываем, какие значения функция должна сопоставить.



5. Чтобы Excel ссылался непосредственно на эти данные, ссылку нужно зафиксировать. Выделяем значение поля «Таблица» и нажимаем F4. Появляется значок $.



6. В поле аргумента «Номер столбца» ставим цифру «2». Здесь находятся данные, которые нужно «подтянуть» в первую таблицу. «Интервальный просмотр» – ЛОЖЬ. Т.к. нам нужны точные, а не приблизительные значения.

Нажимаем ОК. А затем «размножаем» функцию по всему столбцу: цепляем мышью правый нижний угол и тянем вниз. Получаем необходимый результат.

Теперь найти стоимость материалов не составит труда: количество * цену.

Функция ВПР связала две таблицы. Если поменяется прайс, то и изменится стоимость поступивших на склад материалов (сегодня поступивших). Чтобы этого избежать, воспользуйтесь «Специальной вставкой».

1. Выделяем столбец со вставленными ценами.
2. Правая кнопка мыши – «Копировать».
3. Не снимая выделения, правая кнопка мыши – «Специальная вставка».
4. Поставить галочку напротив «Значения». ОК.

Формула в ячейках исчезнет. Останутся только значения.

Быстрое сравнение двух таблиц с помощью ВПР

Функция помогает сопоставить значения в огромных таблицах. Допустим, поменялся прайс. Нам нужно сравнить старые цены с новыми ценами.

1. В старом прайсе делаем столбец «Новая цена».



2. Выделяем первую ячейку и выбираем функцию ВПР. Задаем аргументы (см. выше). Для нашего примера: . Это значит, что нужно взять наименование материала из диапазона А2:А15, посмотреть его в «Новом прайсе» в столбце А. Затем взять данные из второго столбца нового прайса (новую цену) и подставить их в ячейку С2.

Данные, представленные таким образом, можно сопоставлять. Находить численную и процентную разницу.

Как работает функция ВПР в Excel: несколько примеров для «чайников».

Предположим, нам необходимо из списка сотрудников выбрать данные определенного человека. Посмотрим, какие здесь есть тонкости.

Во-первых, нужно сразу определиться: точный либо приблизительный поиск нам нужен. Ведь они предъявляют разные требования к подготовке исходных данных.

Использование точного и приблизительного поиска.

Посмотрите, какие результаты выборки цен мы получаем с использованием приблизительного поиска на неупорядоченном массиве данных.

Обратите внимание, что четвертый параметр равен 1.

Кое-что из результатов определено верно, но в большинстве случаев – ошибки. Функция продолжает просматривать данные столбца D с наименованиями товаров до тех пор, пока не встретит значение больше, чем заданное ей в качестве критерия поиска. Тогда она останавливается и возвращает цену.

Поиск цены на египетские бананы закончился на первой же позиции, так как во второй записаны сливы. А это слово по правилам алфавита стоит ниже, чем «Бананы Египет». Значит, дальше искать не нужно. Получили 145. И не важно, что это цена абрикосов. Поиск цены на сливы происходил до тех пор, пока в D15 не встретилось слово, которое по алфавиту стоит ниже: яблоки. Остановились и взяли цену из предыдущей строки.

А теперь взгляните, как должно было все происходить, если все делать верно. Всего лишь делаем сортировку, как указано стрелкой.

Вы спросите: «А зачем тогда этот неточный просмотр, если с ним столько проблем?»

Он отлично подходит для выбора значений из определенных интервалов.

Допустим, у нас установлена скидка для покупателей в зависимости от количества приобретенного товара. Нужно быстро рассчитать, сколько процентов положено на совершенную покупку.

Если у нас количество товара 11 единиц, то мы просматриваем столбец D до тех пор, пока не встретим число, большее 11. Это 20 и находится оно в 4-й строке. Останавливаемся здесь. Значит, наша скидка расположена в 3-й строке и равна 3%.

Использование нескольких условий.

Еще один простой пример для «чайников» – как использовать при выборе нужного значения несколько условий?

Предположим, у нас есть список имен и фамилий. Нам нужно найти нужного человека и вывести сумму его дохода.

В F2 используем следующую формулу:

=ВПР(D2&” “&E2;$A$2:$B$21;2;0)

Разберем пошагово, как в этом случае работает ВПР.

В начале мы формируем условие. Для этого при помощи оператора & «склеиваем» вместе имя и фамилию, а между ними вставляем пробел.

Не забываем при этом пробел заключить в кавычки, иначе Excel не воспримет его как текст.

Затем в таблице с доходами ищем ячейку с именем и фамилией, разделенными пробелом.

Дальше все происходит по уже отработанной схеме.

Можно попробовать подстраховаться на тот случай, если между именем и фамилией введено несколько пробелов. Знак пробела в формуле заменяем на знак подстановки «*».

Приметно так – D2&”*”&E2

Заключение

Таким образом, функция ВПР – один из самых полезных инструментов при работе в Excel, когда нужно сопоставить данные двух таблиц и перенести значения из одной в другую при совпадении заданных значений. Правильное использование данной функции позволит сэкономить немало времени и сил, позволив автоматизировать процесс заполнения данных и исключив возможные ошибки из-за опечаток и т.д.