Для построения графика функции одной переменной, прежде всего, необходимо задать множество (диапазон) значений независимой переменной и соответствующее множество значений зависимой (функциональной) переменной. После этого следует воспользоваться мастером построения диаграмм программы MS Excel для изображения графика заданной функциональной зависимости. При этом задание значений независимой переменной удобно выполнить с помощью рассмотренной ранее операции автозаполнения. Ниже приводится описание последовательности практических действий для примера построения графика функции: f(x) = 2x2 - Зx - 5 в интервале изменения независимой переменной: х∈[-5, 5].
Для начала рекомендуется создать новую книгу с именем Графики Функций. На отдельном листе в ячейку А1 введем текст «Значения переменной:», а в ячейку В1 введем текст «Значения функции:». Хотя исходная независимая переменная принимает значения из непрерывного интервала действительных чисел [-5, 5], для построения графика необходимо для этой независимой переменной задать дискретные значения. Для наших целей вполне достаточно рассмотреть последовательный диапазон значений от -5 до 5 с интервалом их изменения, равным 0,1.
Для задания этого диапазона значений в ячейку А2 введем наименьшее значение интервала изменения независимой переменной: число -5, а в ячейку А3 — число -4,9. После чего вторым способом автозаполнения запишем диапазон значений независимой переменной в ячейки А2:А102. Далее в ячейку В2 введем формулу: =2*A2^2-3*A2-5, которую с помощью первого способа автозаполнения запишем в ячейки В2:В102. Результат выполнения данной последовательности операций по подготовке исходных данных будет иметь следующий вид (рис. 1).
Рис. 1. Исходные данные для построения графика функции одной переменной
Для построения графика необходимо воспользоваться мастером диаграмм, который может быть вызван с помощью кнопки стандартной панели инструментов или операции главного меню: Вставка → Диаграмма (рис. 2). Мастер диаграмм представляет собой самостоятельное диалоговое окно с набором вкладок, обеспечивающих задание отдельных свойств элементам графического изображения.
Рис. 2. Внешний вид диалогового окна мастера диаграмм (шаг 1 из 4)
На первой из вкладок содержится список стандартных диаграмм, которые могут быть использованы дня графического представления рядов данных. На второй вкладке пользователю предлагается выбор диаграммы из списка нестандартных, часть которых появилась в последних версиях программы MS Excel.
На первом шаге построения диаграммы необходимо выбрать тип диаграммы и ее вид. С этой целью следует выделить на вкладке Все диаграммы в левом списке тип диаграммы График, а в правом списке с графическими миниатюрами — первый вид графика, который отражает развитие процесса во времени или по категориям. После выбора типа и разновидности диаграммы следует нажать кнопку Далее и перейти ко второму шагу построения диаграммы с помощью мастера диаграмм (рис. 3).
Рис. 3. Спецификация источника данных для построения графика с помощью мастера диаграмм (шаг 2 из 4)
Первая из вкладок (рис. 3, а) служит для задания диапазона значений рядов данных, которые будут отображены на диаграмме. С этой целью на втором шаге построения диаграммы необходимо выбрать ячейки с данными, которые должны быть отображены на соответствующем графике. Применительно к рассматриваемому примеру это значения функции, которые содержатся в диапазоне ячеек В2:В102. Для указания этих значений следует установить переключатель Строка / столбец так, чтобы в левом окне были Элементы легенды (ряды). После этого выполнить щелчок на строке «Значения функции:», и затем на расположенной выше кнопке Изменить или Добавить.
В результате будет открыто дополнительное небольшое окно, в строке Значения необходимо указать источник данных диаграммы. Для указания источника данных следует на рабочем листе «Квадратный трехчлен» с помощью мыши или клавиатуры выделить диапазон значений функции В2:В102. Он будет иметь специальную рамку в форме мерцающей пунктирной линии, а в соответствующей строке появится надпись с указанием имени рабочего листа и абсолютных адресов ячеек этого диапазона (рис. 3, б). Далее на этом же шаге работы мастера диаграмм следует задать подписи по горизонтальной оси. С этой целью необходимо перейти на строку «Значения функции:» и выполнить щелчок на кнопке с именем Изменить и выбрать строку Имя ряда. Оба шага можно выполнить одновременно.
Рис. 4. Спецификация подписи горизонтальной оси X для построения графика с помощью мастера диаграмм (шаг 2 из 4)
В результате будет открыто дополнительное небольшое окно, в единственной строке которого необходимо указать источник данных для независимой переменной графика. Для указания соответствующего источника данных следует на рабочем листе «Квадратный трехчлен» с помощью мыши или клавиатуры выделить диапазон значений функции А2:А102. Выделенный диапазон также приобретет специальную рамку в форме мерцающей пунктирной линии, а в соответствующей строке появится надпись с указанием имени рабочего листа и абсолютных адресов ячеек этого диапазона (рис. 4, б). После выбора спецификации рядов данных и подписей оси X для графика следует перейти к третьему шагу построения диаграммы с помощью мастера диаграмм (рис. 5).
Рис. 5. Спецификация названия диаграммы и выбор варианта ее размещения с помощью мастера диаграмм (шаги 3 и 4 из 4)
На третьем шаге на вкладке Работа с диаграммами можно задать заголовки и названия диаграммы и осей, подписи данных и линии сетки. Применительно к рассматриваемому примеру можно указать название графика в соответствующем поле ввода. После спецификации параметров диаграммы следует сохранить изменения и перейти к последнему четвертому шагу построения диаграммы с помощью мастера диаграмм (рис. 5).
На этом шаге следует выбрать один из двух вариантов размещения диаграммы: на отдельном рабочем листе или на текущем рабочем листе, где содержатся ячейки с данными диаграммы. При необходимости можно изменить имя диаграммы, предлагаемой мастером по умолчанию. После этого следует нажать кнопку Готово. В результате будет построена диаграмма в форме графика кривой квадратного трехчлена (рис. 6).
Рис. 6. Результат построения графика функции: f(x) = 2x² — Зx — 5 в интервале изменения независимой переменной: х∈[-5, 5]
После построения диаграммы в случае необходимости можно редактировать отдельные ее свойства. Доступ к редактированию свойств построенной диаграммы можно получить либо с помощью контекстного меню диаграммы, либо с помощью операций меню Работа с диаграммами. Удобным оказывается способ получения доступа к выделенным элементам диаграммы с помощью комбинации клавиш: Ctrl+1 или двойного щелчка левой кнопкой мыши.
Так, например, для изменения цвета фона построенного графика квадратного трехчлена можно выполнить двойной щелчок левой кнопкой мыши на фоне соответствующего рисунка. В появившемся диалоговом окне выбрать желаемый цвет фона графика из предлагаемой палитры цветов. Аналогично можно изменить цвет линии кривой графика и интервал отображения промежуточных значений независимой и зависимой переменных. Изображенный на рис. 6 график функции получен после редактирования его свойств в результате изменения цвета фона диаграммы, линии кривой графика и интервала отображения промежуточных значений независимой переменной.
Пример 1
Дана функция:
Нужно построить ее график на промежутке [-5;5] с шагом равным 1.
Создание таблицы
Создадим таблицу, первый столбец назовем переменная x (ячейка А1), второй — переменная y (ячейка В1). Для удобства в ячейку В1 запишем саму функцию, чтобы было понятно, какой график будем строить. Введем значения -5, -4 в ячейки А2 и А3 соответственно, выделим обе ячейки и скопируем вниз. Получим последовательность от -5 до 5 с шагом 1.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак ^, который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
Построение графика
Выделим диапазон значений переменной x и функции y. Перейдем на вкладку Вставка и в группе Диаграммы выберем Точечная (можно выбрать любую из точечных диаграмм, но лучше использовать вид с гладкими кривыми).
Мы получили график данной функции. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графика.
Пример 2
Даны функции:
и y=50x+2. Нужно построить графики этих функций в одной системе координат.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Построение графиков
Для построения графиков выделяем значения трёх столбцов, на вкладке Вставка в группе Диаграммы выбираем Точечная.
Мы получили графики функций в одной системе координат. Используя вкладки Конструктор, Макет, Формат, можно изменить параметры графиков.
Последний пример удобно использовать, если нужно найти точки пересечения функций с помощью графиков. При этом можно изменить значения переменной x, выбрать другой промежуток или взять другой шаг (меньше или больше, чем 1). При этом столбцы В и С менять не нужно, диаграмму тоже. Все изменения произойдут сразу же после ввода других значений переменной x. Такая таблица является динамической.
Кратко об авторе:

Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.
Лабораторная работа
№2
Тема:
«Вычисление
функций одной переменной в Excel»
Цель
занятия:
получить практические навыки вычисления
функций одной переменной у=f(x)
и построения их графиков в Excel
Отрабатываемые
вопросы:
1.Создание
формул для вычисления функций одной
переменной.
2.Построение
графиков функций.
Организационно
– методические указания
В Excel
удобно осуществлять построение различных
функций на плоскости и поверхностей в
пространстве.
1.Построение
прямой.
Рассмотрим построение данной функции
в Excel
на примере уравнения у=2х+1
в диапазоне
: х[0; 3]
с шагом х=0,25. Решение
задачи
включает следующие этапы.
1.1. Ввод данных.
Для этого
значения аргумента Х
и функции У
следует
представить в таблице, первый
столбец
которой будет заполнен значениями Х ,
а второй
– функцией У.
Для этого в
ячейку А1 вводим заголовок Аргумент,
а в ячейку В1
– заголовок Прямая.
В ячейку А2 вводится
первое значение аргумента 0,
а в ячейку A3
вводится второе значение аргумента с
учетом шага построения (0,25).
Затем, выделив
блок ячеек А2:АЗ, автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее вводим
уравнение прямой: в ячейку В2 вводим
формулу: =2*A2+1,
затем копируем
эту формулу в ячейки В2:В14. В результате
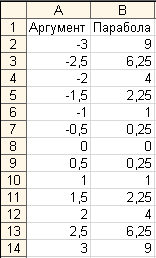
должна быть получена следующая таблица
исходных данных и результатов (рис.1.) .
Рис.1.Построение
прямой
1.2. Построение
графика функции. Выделите диаграмму и,
используя вкладку Вставка
График, постройте
график
функции у=2х+1
(рис.2.).
Рис.2. График прямой
1.3.
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
2.Решение
уравнения второго порядка.
Примерами уравнений второго порядка
являются: парабола,
гипербола, окружность,
эллипс и другие.
В качестве
примера рассмотрим построение параболы
вида: у =х2
в диапазоне
х[–3;
+3] с шагом х=0,5.
2.1. Ввод данных.
В ячейку А2
вводится первое значение аргумента
(-3), в
ячейку A3 вводится второе значение
аргумента (–2,5),
а затем, выделив
блок ячеек А2:АЗ,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки А14).
Далее в ячейку В2
вводим уравнение =А2*А2,
а затем копируем
эту формулу в диапазон В2:В14. В результате
должна быть получена следующая таблица
исходных данных.
2.2.Построение
графика функции. Используя вкладку
Вставка
ДИАГРАММА, постройте
график
функции у=х^2
(РИС.4).
Используя
вкладку
Макет, выполните
самостоятельно оформление полученного
графика (название графика и осей,
размещение легенды и т.п.).
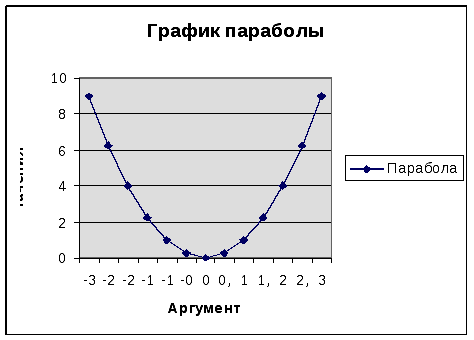
Рис.3. Построение
параболы
Рис.4.График параболы
Рис.5. График
гиперболы
3.Построение
гиперболы.
В простейшем
случае уравнение гиперболы имеет вид
y=k/x.
Задача построения гиперболы аналогична
построению параболы.
Рассмотрим
построение гиперболы y=1/x
в диапазоне х[0,1:
10,1] с шагом х=0,5. Выполните
все вышеуказанные действия самостоятельно
(рис.5).
Задания для
самостоятельного выполнения
-
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции Зх–5у+15=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции У=е2х в диапазоне х[0.1;
2] с шагом =0,2. -
Построить график
функции У=2х в диапазоне х[–2;
2] с шагом =0,5. -
Построить график
функции У=lnx в диапазоне х[0.5;
10] с шагом =0,5. -
Построить график
функции Зх+2у–4=0 в диапазоне х[–1;
3] с шагом =0,25. -
Построить график
функции y=2cos3x в диапазоне х[0.1;
1.8] с шагом =0,1. -
Построить график
функции y=x2 в диапазоне х[–3;
3] с шагом =0,25. -
Построить график
функции y=1/2x в диапазоне х[0.1;
10] с шагом =0,25. -
Построить верхнюю
часть параболы у2=х в диапазоне x[0;
4] с шагом =0,25. -
Построить гиперболу
y =1/2х в диапазоне х
[0,1; 5,1] с шагом =0,25 -
Построить верхнюю
полуокружность эллипса x4/4+у2=1 в диапазоне
х
[–2,25; 2,25] с шагом =0,25. -
Постройте параболу:
у2=6х в диапазоне х
[0; 4] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы. -
Постройте параболу:
х2=8у в диапазоне x
[–2,25; 2,25] с шагом =0,25.
Найдите координаты фокуса и уравнение
директрисы.
ЛАБОРАТОРНАЯ
РАБОТА №3
Тема:
Вычисление сложных функций в Excel
Цель
занятия:
получить практические навыки вычисления
сложных функций от двух переменных z
= f(x,у)
и построения их графиков в Excel.
Отрабатываемые
вопросы.
1.Создание
формул для вычисления функций от двух
переменных.
2.Построение
графиков типа поверхностей в трехмерном
пространстве.
Организационно
– методические указания
В качестве примера
рассмотрим построение поверхностей
второго порядка таких как: эллипсоид,
гиперболоид, параболоид и т.п.
1.
Рассмотрим
построение эллипсоида в Excel
в соответствии с уравнением:
Пусть необходимо
построить верхнюю часть эллипсоида,
лежащую в диапазонах: х[–3;
3], у[–2;
2] с шагом =0,5
для обеих переменных.
Решение данной
задачи включает следующие этапы.
1.1.Вначале необходимо
разрешить уравнение относительно
переменной z:
1.2.Ввести значения
переменных х
(по вертикали)
, начиная с
ячейки А2
и у (по
горизонтали) , начиная с ячейки B1:
-
в ячейку А2
вводится первое значение аргумента (х
= –3),
затем в ячейку A3
вводится второе значение аргумента (х
= –2,5)
и,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента х
(за правый нижний угол блока протягиваем
до ячейки А14). -
значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
(у = –2),
в ячейку С1
вводится второе значение переменной
( у = –1,5)
, а затем,
выделив блок ячеек В1:С1,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки J1).
1.3.Вычисление
значений функции z.
Для этого
курсор необходимо поместить в ячейку
В2
и вызвать Мастер
функций. В
появившемся диалоговом окне Мастер
функций — шаг 1 из 2
слева в поле Категория
выбираем Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В диалоговом окне Корень
в рабочем
поле вводим подкоренное выражение: 1
— $А2^2/9 — В$1^2/4.
Обратите
внимание, что символы $
предназначены для фиксации адреса
столбца А
— переменной х
и
строки 1
— переменной у.
Нажимаем
кнопку ОК
и в ячейке В2
появляется « #ЧИСЛО!»,
так как при значениях х
= –3 и у
= –2 точек
рассматриваемого эллипсоида не существует
(рис 1.).
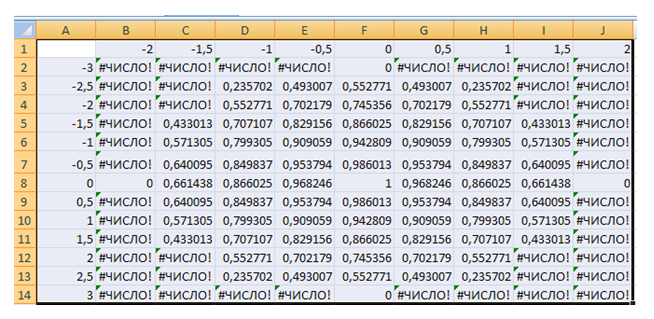
Рис.1. Построение
эллипсоида
1.4.Копирование
значений функции из ячейки В2,
для чего автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
а затем протягиванием вниз копируем в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица всех точек
эллипсоида (рис.1).
1.5.Построение
диаграммы. Выделяем полученную таблицу
(A1:
J14),
вызываем вкладку Вставка
и в группе
Диаграммы
выбираем
График
Все типы диаграмм
окно
Вставка диаграмм. В
данном окне выбираем Поверхность
тип
Проволочная поверхность и
нажимаем ОК,
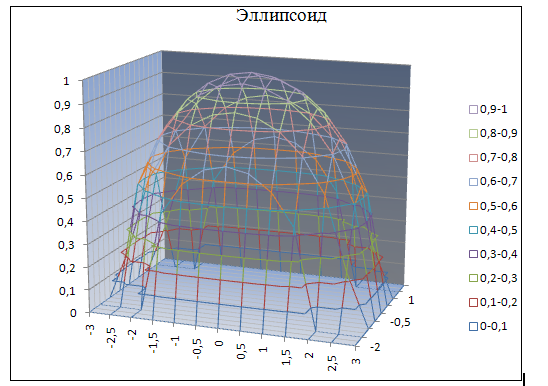
в результате
получаем поверхность эллипсоида (рис.2).
Далее,
используя
средства
Работа с диаграммами , оформляем
полученную поверхность. Например,
вкладки Стенка
и Основание диаграммы
позволяют определить их цвета. Для этого
выберите опцию Дополнительные параметры
стенок и вид заливки, название диаграммы
и т.п. Выполните данные действия
самостоятельно.
2.
Рассмотрим
построение гиперболоида следующего
вида:
Пусть необходимо
построить верхнюю часть гиперболоида,
лежащую в диапазонах:
х[–3;
3], у[–2;
2] с шагом
=0,5
для обеих переменных.
2.1.Вначале необходимо
преобразовать уравнение относительно
переменной Z:
Рис.2. Поверхность
эллипсоида
2.2.Введем значения
переменной х
в столбец
А.
Для этого в ячейку А1
вводим символ x,
в ячейку А2
вводится первое значение аргумента х
= –3, а в
ячейку A3
— второе значение аргумента х = –2,5
. Затем,
выделив блок ячеек А2:АЗ,
автозаполнением получаем все значения
аргумента (за правый нижний угол блока
протягиваем до ячейки А14).
Значения переменной
у
вводим в
строку 1.
Для этого в ячейку В1
вводится первое значение переменной
у= –2,
в ячейку С1
— второе значение переменной у
= –1,5,
а затем, выделив
блок ячеек В1:С1,
автозаполнением
получаем все значения аргумента (за
правый нижний угол блока протягиваем
до ячейки J1).
2.3.Вычисление
значения переменной Z.
Для этого
табличный курсор необходимо поместить
в ячейку В2
, вызвать Мастер
функций, в
поле Категория
выбрать Математические,
в поле Функция
выбираем функцию Корень
и нажимаем
кнопку ОК.
В рабочее поле вводим подкоренное
выражение: 1
+ $А2^2/9 + В$1^2/4 и
нажимаем
кнопку ОК.
В ячейке В2
появляется
1,732051.
Теперь необходимо
скопировать функцию из ячейки В2.
Для этого автозаполнением (протягиванием
вправо) копируем эту формулу вначале в
диапазон B2:J2,
после чего протягиванием вниз — в
диапазоне ВЗ:J14.
В результате должна
быть получена таблица точек гиперболоида
(рис.3.):
Рис.3. Построение
гиперболоида
Построение диаграммы
гиперболоида выполните самостоятельно
по аналогии с эллипсоидом. Ниже на рис.4
приведен вариант диаграммы гиперболоида
, построенного на основании данной
таблицы.
Рис.4.
Диаграмма гиперболоида
Задания для
самостоятельного выполнения
1.Построить верхнюю
часть эллипсоида:
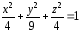
Диапазоны изменения
переменных х
и у: х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
2.Построить верхнюю
часть однополостного гиперболоида:
Диапазоны изменения
переменных х
и у:
х[–3;
3] с шагом =0,5,
у[–4;
4] с шагом =1.
3.Построить
эллиптический параболоид:

Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у[–3;
3] с шагом =1.
4.Построить верхнюю
часть конуса
Диапазоны изменения
переменных х
и у:
х[–2;
2] с шагом =0,5,
у [–3;
3] с шагом =1.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Microsoft Excel
- Построение в Excel графиков математических и тригонометрических функций
- Построение графиков математических функций с одной переменной
- Построение графиков математических функций с двумя переменными
- Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
Microsoft Excel
трюки • приёмы • решения
Построение в Excel графиков математических и тригонометрических функций
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x) .
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон А1:В22 .
- Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон A1:V22 .
- Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Источник
Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться график.
- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку

8. На третьем шаге заполним вкладку Заголовки.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем пункт Формат оси…. Во вкладке Шкала установим: цена основного деления: 1. Во вкладке Шрифт установим размер шрифта 8пт.
- Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х 3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево ячейки строки 3, до тех пор, пока не будет получено значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения функции: = С4^3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х 3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (ВидКолонтитулы…):
14. Верхний колонтитул слева: график функции у = x 3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (ВидКолонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого варианта проверяется с помощью проектора.
Источник
Анастасия Николаевна Королева
Эксперт по предмету «Информатика»
Задать вопрос автору статьи
Определение 1
Табулирование функции одной переменной средствами MS Excel — это определение значения функции для каждой соответствующей величины аргумента, который задан с некоторым шагом, в назначенных пределах.
Введение
Табулированием функции является процесс вычисления значений функции для всех аргументов, заданных с некоторым шагом, при назначенных пределах их изменения. Данная операция используется в качестве инструмента при решении задач определённого класса. Она позволяет осуществить локализацию корней уравнения, определять минимумы и максимумы, выполнять решение других задач. При помощи программы Excel осуществлять процесс табулирования значительно проще, чем просто на калькуляторе с записью результатов на бумаге.
Табулирование функции одной переменной средствами MS Excel
Табулирование осуществляется за счёт формирования таблицы, где в одной из колонок записывается значение аргумента с требуемым шагом, а в другой колонке будет располагаться определяемое данным аргументом значение функции. Далее на базе этих расчётов может быть построен график. Приведём конкретный пример. Прежде всего необходимо сформировать шапку таблицы, где есть колонка x, с указанием значений аргумента, и колонка f(x), в которой будет отображаться соответствующее аргументу значение функции.
В качестве примера используем следующую функцию:
f(x)=x^2+2x
Следует отметить, что в операции табулирования в принципе могут использоваться функции любого типа.
Выбираем шаг табулирования h равный двум. Диапазон допустимого изменения аргумента назначим от минус десяти до плюс десяти. Далее следует выполнить заполнение столбца аргументов, с соблюдением заданного шага два при заданных граничных значениях. То есть, необходимо сначала в первую ячейку столбца «х» записать величину минус десять. Непосредственно за этим действием следует нажать клавишу Enter. Это важное замечание, поскольку если попытаться манипулировать мышью, то значение в ячейке преобразуется в формулу, а для рассматриваемого примера это не требуется. Эта процедура показана на рисунке ниже.
«Табулирование функции одной переменной средствами MS Excel» 👇
Рисунок 1. Окно программы. Автор24 — интернет-биржа студенческих работ
Можно и дальше заполнять в ручном режиме этот столбец, выдерживая шаг два, однако более удобно эту операцию осуществить при помощи процедуры автоматического заполнения. Использование этого варианта особенно актуально, когда диапазон изменения аргумента значительный, а величина шага незначительная.
Для автоматического заполнения столбца следует выделить ячейку, содержащую величину первого аргумента. Далее на вкладке «Главная, нужно сделать клик по клавише «Заполнить», размещённой на ленте в группе настроек «Редактирование». Затем в представленном списке операций необходимо сделать выбор пункта «Прогрессия…». Появится окно настройки прогрессии. Надо выбрать параметр «Расположение» и там установить режим выбора «По столбцам», поскольку в рассматриваемом примере значения аргумента размещаются не в строчках, а в столбцах. В поле «Шаг», необходимо установить величину два. В поле «Предельное значение» нужно занести верхнюю границу диапазона изменения аргумента, то есть число десять. Для реализации прогрессии нужно нажать клавишу «ОК».
А затем требуется осуществить заполнение столбца функции f(x)=x^2+2x. Чтобы это выполнить, нужно в первую ячейку колонки с функцией записать выражение, используя следующий шаблон.
Рисунок 2. Окно программы. Автор24 — интернет-биржа студенческих работ
Следует вместо значения x в формуле подставить значение первой ячейки из столбца, где располагаются аргументы. После этого надо нажать клавишу Enter для вывода итога вычислений на дисплей. Для осуществления вычислений значения функции для других строк, можно также использовать технологию автоматического заполнения, но в этом варианте нужно применять маркер заполнения. Для этого нужно установить курсор в нижний правый угол ячейки, уже содержащей формулу. При этом должен появиться маркер заполнения, который будет представлен как небольшой по размерам крестик. Далее надо нажать левую клавишу мышки и протянуть курсор по всему заполняемому столбцу. Образец выполнения табуляции представлен на рисунке ниже.
Рисунок 3. Окно программы. Автор24 — интернет-биржа студенческих работ
На её базе возможно увидеть, к примеру, что минимальное значение функции, а именно нуль, получается, когда величина аргумента равняется минус два. Максимальное значение функции в заданном диапазоне изменения аргумента, то есть, от минус десяти до десяти, получается в точке с аргументом десять, и равняется ста двадцати.
Используя итоговые результаты выполненной табуляции в таблице, можно представить эту функцию в виде графика. Нужно выделить все значения в таблице при помощи курсора, зажав левую клавишу мышки. Далее надо перейти на вкладку «Вставка», в группе инструментов «Диаграммы» на ленте нужно нажать клавишу «Графики». Должен открыться перечень возможных версий формирования графика. Следует выбрать такой вид, который покажется пользователю самым подходящим. Можно сделать выбор, к примеру, простого типа графика. Далее программа на листе исполнит процедуру формирования графика на базе заданного табличного диапазона. Образец сформированного графика показан на рисунке ниже.
Рисунок 4. Окно программы. Автор24 — интернет-биржа студенческих работ
Если у пользователя появится желание, то он может осуществить редактирование этого графика таким образом, как ему будет необходимо, применяя для этого инструментальный набор программы Excel. Имеется возможность добавления наименований осей координат и всего графика, а также можно удалить легенду или присвоить ей новое имя, убрать линию аргументов и так далее.
Как видно из приведённого выше примера табулирование функции является достаточно простым процессом. Но следует отметить, что вычислительный процесс может занимать достаточно много времени, в частности, когда диапазон изменения аргументов имеет широкие пределы, а шаг табуляции, при этом, очень небольшой. Существенную экономию времени могут дать инструменты автоматического заполнения Excel. И, как показано выше, эта же программа на базе сформированных результатов позволяет сформировать график функции, дающий более наглядное представление.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме






![Рис. 6. Результат построения графика функции: f(x) = 2x² - Зx - 5 в интервале изменения независимой переменной: х∈[-5, 5] Рис. 6. Результат построения графика функции: f(x) = 2x² - Зx - 5 в интервале изменения независимой переменной: х∈[-5, 5]](https://img-fotki.yandex.ru/get/194778/40446132.f7/0_cd323_a555bcec_orig.jpg)















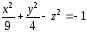
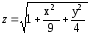


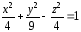







 Колонтитулы…):
Колонтитулы…): 


