Сегодняшняя статья посвящена таблицам, с которыми большинству приходилось работать при работе за компьютером (извиняюсь за тавтологию).
Многие начинающие пользователи часто задают один и тот же вопрос: «… а как создать в Excel таблицу с точными размерами до сантиметра. Вот в Word все намного проще, «взял» линейку, увидел рамку листа и начертил…».
На самом деле в Excel все намного проще, и так же можно нарисовать таблицу, ну а о том, какие возможности дает таблица в Excel я и говорить не буду (для начинающих будет интересно)…
И так, более подробно о каждом шаге…
Создание таблицы
Шаг 1: включение рамок страницы + режим разметки
Будем считать что вы только что открыли Excel 2013 (все действия практически аналогичны в версиях 2010 и 2007).
Первое, что многих пугает, это отсутствие видимости рамок страницы: т.е. не видно, где границы листа у страницы (в Word сразу отображается альбомный лист).
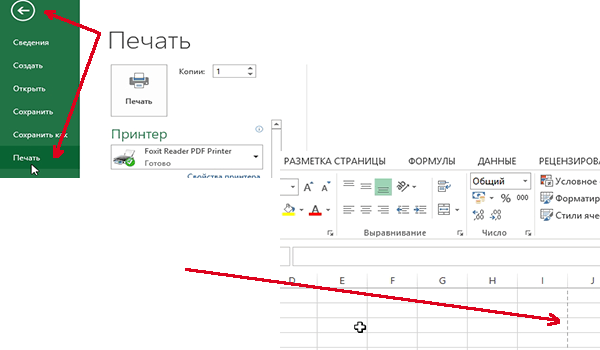
Чтобы увидеть границы листа, лучше всего отправить документ на печать (на просмотр), но не печатать его. Когда вы выйдите из режима печати, вы увидите в документе тонкую пунктирную линию — это и есть граница листа.
Режим печати в Excel: для включения зайти в меню «файл/печать». После выхода из него — в документе будут границы листа.
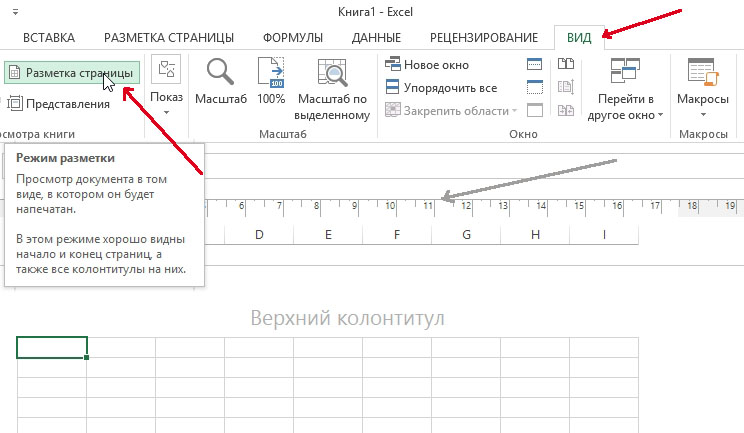
Для еще более точной разметки, зайдите в меню «вид» и включите режим «разметка страницы«. Перед вами должна появиться «линейка» (см. серую стрелку на скриншоте ниже) + альбомный лист предстанет с границами как в Word.
Разметка страницы в Excel 2013.
Шаг 2: выбор формата листа (А4, А3…), расположение (альбомный, книжный).
Перед тем, как начать создавать таблицу, нужно выбрать формат листа и его расположение. Лучше всего это проиллюстрирует 2 скриншота ниже.
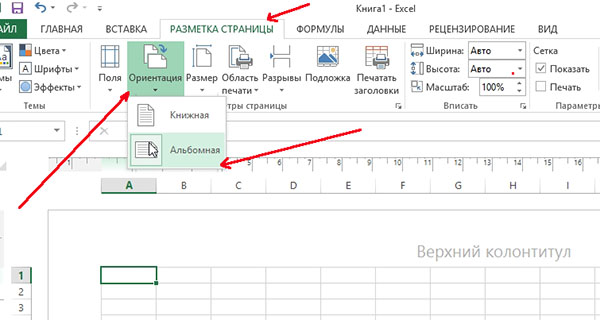
Ориентация листа: зайти в меню «разметка страницы», выбрать пункт «ориентация».
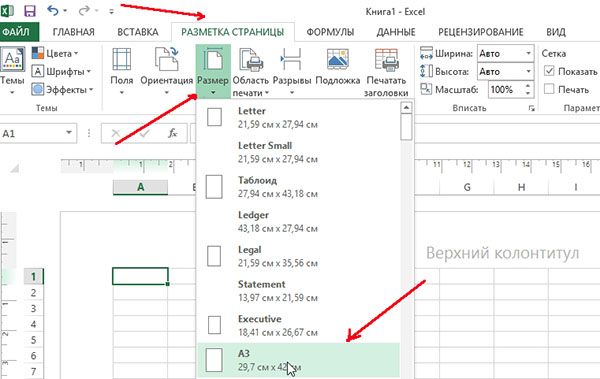
Размер страницы: для замены формата листа с А4 на А3 (или другой), необходимо зайти в меню «разметка страницы», далее выбрать пункт «размер» и во всплывающем контекстном меню выбрать требуемый формат.
Шаг 3: создание таблицы (рисование)
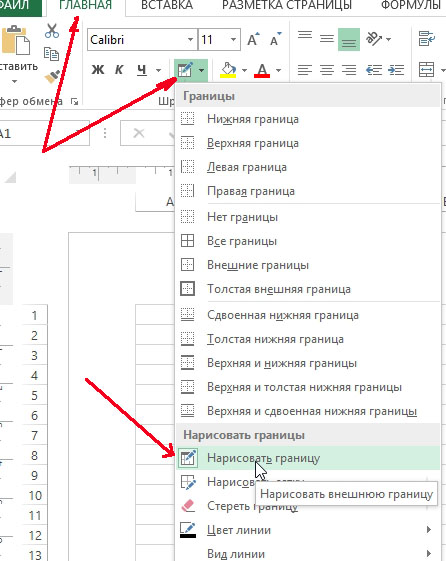
После всех приготовлений можно приступить к рисованию таблицы. Удобнее всего это делать с помощью функции «границы». Чуть ниже скриншот с пояснениями.
Для того, чтобы нарисовать таблицу: 1) перейти в раздел «главная»; 2) открыть меню «границы»; 3) в контекстном меню выбрать пункт «нарисовать границу».
Размер колонок
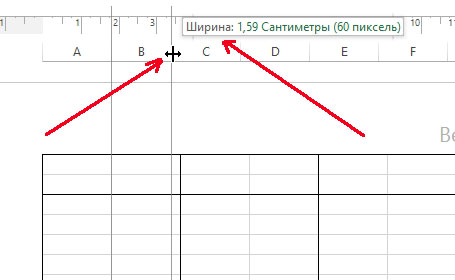
Размеры колонок удобно регулировать по линейке, которая покажет точный размер в сантиметрах (см.).
Если потянуть за ползунок, изменяя ширину колонок — то линейка будет показывать ее ширину в см.
Размер строк
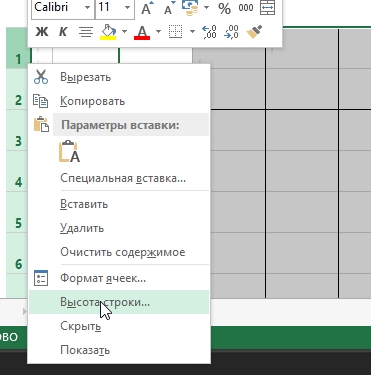
Размеры строк можно править аналогичным образом. См. скриншот ниже.
Для изменения высоты строк: 1) выделить нужные строки; 2) нажать по ним правой кнопкой мышки; 3) В контекстном меню выбрать «высота строки»; 4) Задать требуемую высоту.
На этом все. Кстати, более простой вариант создания таблицы был разобран в одной небольшой заметке: https://pcpro100.info/kak-sozdat-tablitsu-v-excel/.
Всем удачной работы!
- Распечатать
Оцените статью:
- 5
- 4
- 3
- 2
- 1
(10 голосов, среднее: 4.2 из 5)
Поделитесь с друзьями!
|
Формула по заданию в зависимости от размеров |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
Тихомирова
А.А. MS
Excel.
Практикум
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №1
Построение таблицы
Для выполнения
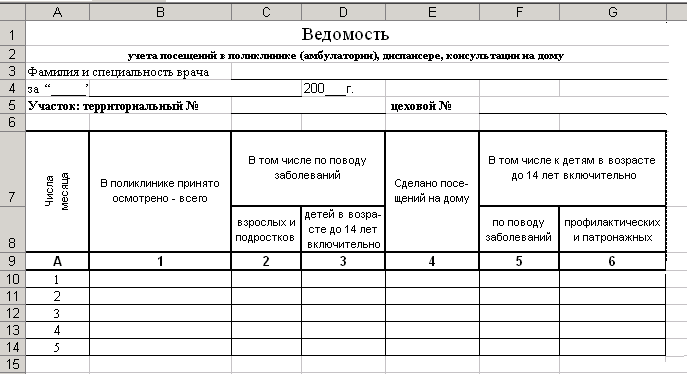
задания используйте в качестве образца
таблицу (рис. 1).
Рисунок 1- Бланк
ведомости учета посещений
-
Ввести в ячейку
А1 текст «Ведомость» -
Ввести в ячейку
А2 текст «учета посещений в поликлинике
(амбулатории), диспансере, консультации
на дому» -
Ввести в ячейку
А3 текст «Фамилия и специальность врача» -
Ввести в ячейку
А4 текст «за» -
Ввести в ячейку
А5 текст «Участок: территориальный №» -
Ввести в ячейку
Е5 текст «цеховой №» -
Создать шапку
таблицы:
-
ввести в ячейку
А7 текст «Числа месяца» -
ввести в ячейку
В7 текст «В поликлинике принято осмотрено-
всего» -
ввести в ячейку
С7 текст «В том числе по поводу заболеваний» -
ввести в ячейку
Е7 текст «Сделано посещений на дому» -
ввести в ячейку
F7
текст «В том числе к детям в возрасте
до 14 лет включительно» -
ввести в ячейку
C8
текст «взрослых и подростков» -
ввести в ячейку
D8
текст «детей в возрасте до 14 лет
включительно» -
ввести в ячейку
F8
текст «по поводу заболеваний» -
ввести в ячейку
G8
текст «профилактических и патронажных» -
ввести в ячейку
А9 текст «А» -
пронумеровать
остальные столбцы таблицы
-
Отформатировать
шапку таблицы по образцу
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №2
Вычисления в
таблицах. Автосумма.
-
В таблице,
построенной в предыдущем задании,
заполнить произвольными данными столбцы -
В строке 15
сформировать строку ИТОГО:
(в ячейках
В15, С15, D15,
Е15, F15
и G15)
использовать Автосумму .
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №3
Вычисления в
таблицах. Формулы
-
Выполните построение
и форматирование таблицы по образцу,
представленному на рис. 2, оставив
пустыми ячейки I6:J9
в столбцах 9 и 10 таблицы.
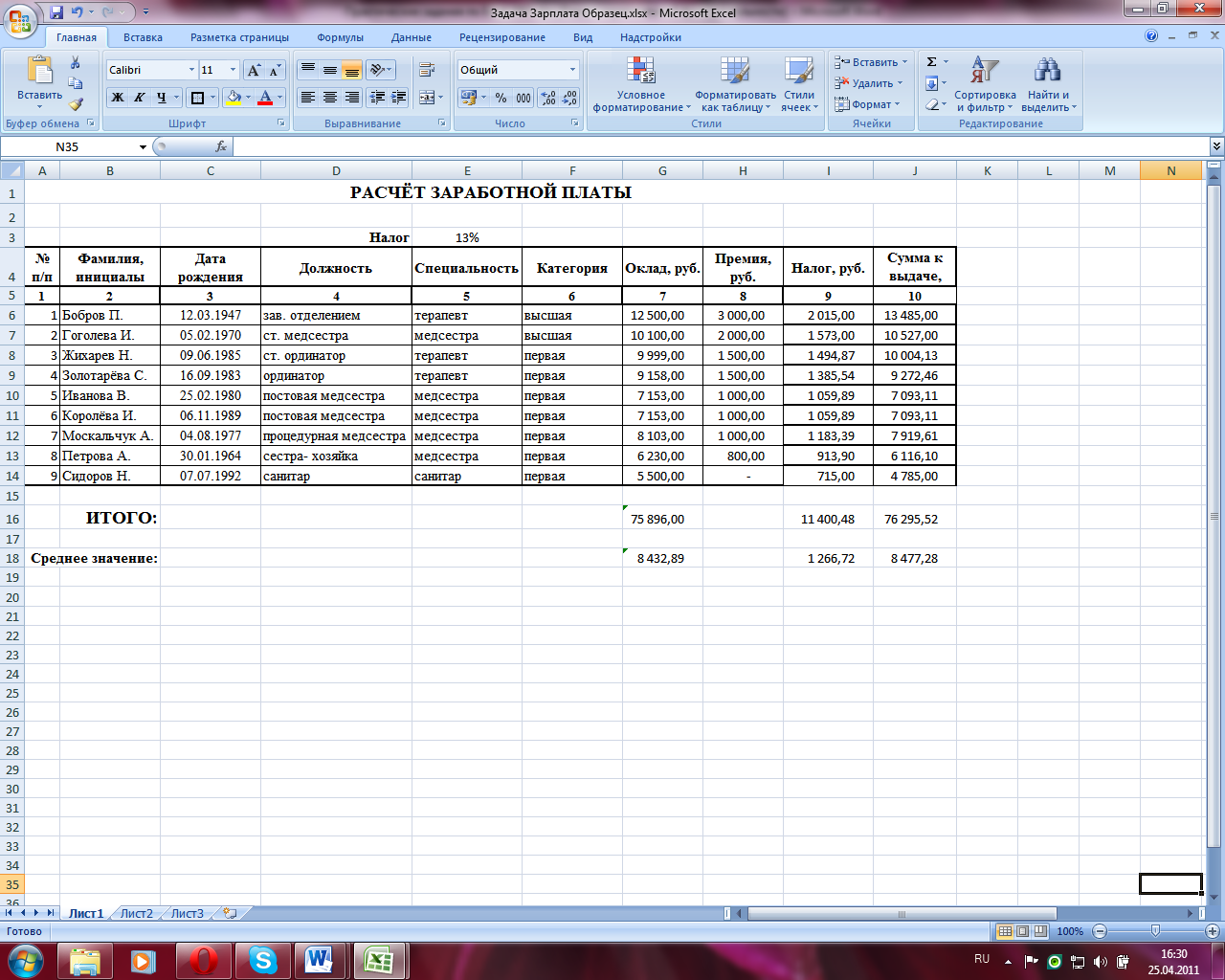
Рисунок 2- Расчет
заработной платы с использованием
формул
-
Введите в ячейку
J6
формулу для подсчета Суммы
к выдаче без учета налога:
=G6+H6 -
Скопируйте формулу
в ячейки диапазона J7:J14,
обратите внимание на автоматические
изменения в формулах, происходящие при
копировании -
Введите формулу
для расчета Налога
(столбец 9) : =$E$3*(G6+H6) -
Скопируйте формулу
в ячейки диапазона I7:I14,
обратите внимание на автоматические
изменения в формулах, происходящие при
копировании -
Измените формулу
в ячейке J6:
= G6+H6-I6 -
Скопируйте формулу
в ячейки диапазона J7:J14,
обратите внимание на автоматические
изменения в формулах, происходящие при
копировании -
Подсчитайте
итоговые значения в ячейках G16,
I16,
J16,
используя Автосумму -
Подсчитайте
среднее значение по столбцу Оклад в
ячейке G18,
используя Мастер
функций и
функцию СРЗНАЧ (категория Статистические).
Формула: = СРЗНАЧ (G6:G14) -
Скопируйте формулу
в ячейки I18
и J18,
обратите внимание на автоматические
изменения в формулах, происходящие при
копировании
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №4
Построение
диаграмм
-
Выполните построение
и форматирование таблицы по образцу,
представленному на рис. 3.
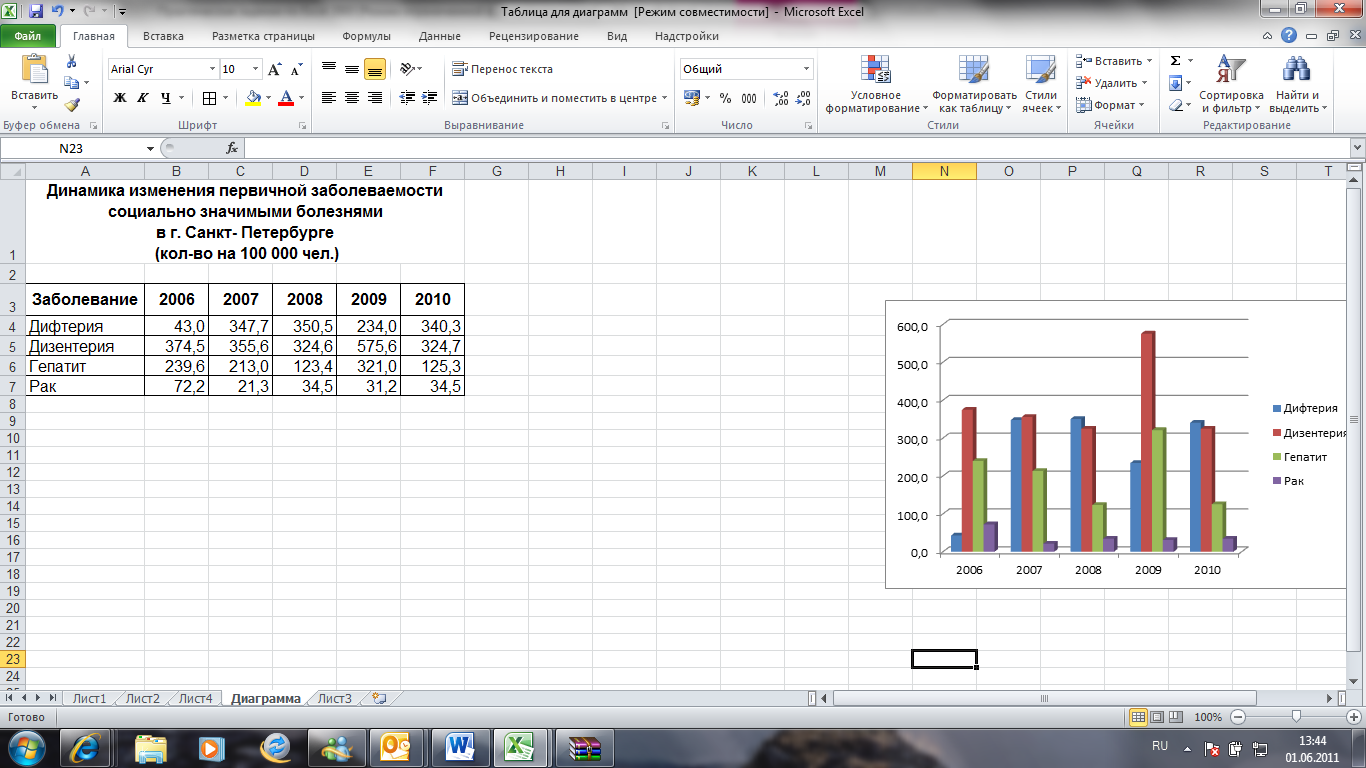
Рисунок 3- Таблица
для построения диаграмм
-
По данным таблицы
постройте диаграммы:
-
круговую диаграмму
первичной заболеваемости социально
значимыми болезнями в г. Санкт- Петербурге
в 2010 году; -
гистограмму
динамики изменения первичной
заболеваемости населения социально
значимыми болезнями в г. Санкт- Петербурге
в период 2006- 2010 гг. -
график динамики
изменения первичной заболеваемости
населения дизентерией в г. Санкт-
Петербурге в период 2006- 2010 гг.
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №5
Вычисления в
таблицах. Формулы.
Логическая
функция ЕСЛИ
-
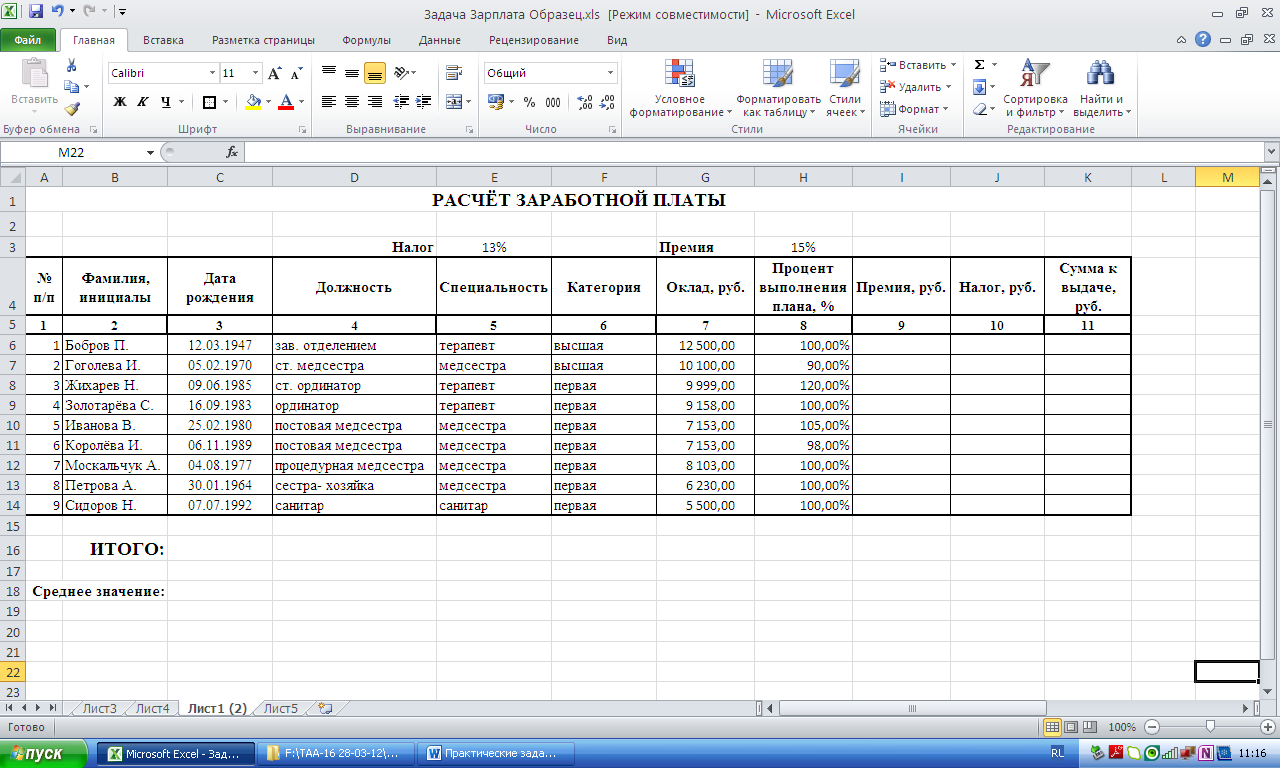
Преобразуйте
таблицу из задания №3 к виду на рис.4,
создав и заполнив столбец «Процент
выполнения плана», а также задайте
размер премии 15% в ячейке Н3. -
Выполните расчет
значений в столбце «Премия», используя
встроенную логическую функцию ЕСЛИ,
исходя из следующего условия:
«премию в размере
15% от оклада получают сотрудники,
перевыполнившие план».
Перед выполнением
расчетов составьте алгоритм решения
задачи в графической форме.
-
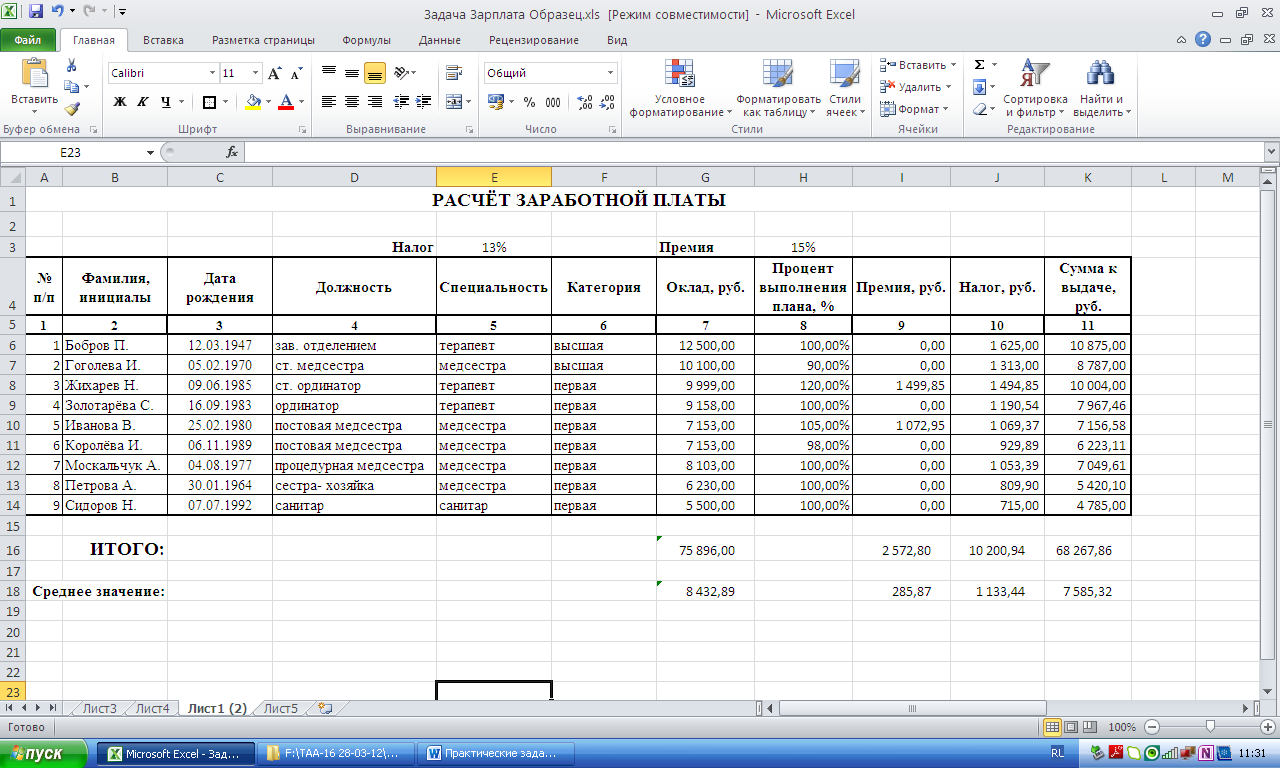
Пересчитайте в
соответствии с изменениями в таблице
столбцы «Налог», «Сумма к выдаче»,
итоговые и средние значения. -
Сравните полученные
результаты с таблицей на рис. 5.
Рисунок 4- Изменения
таблицы задания №3
Рисунок 5- Результат
выполнения задания 5
ПРАКТИЧЕСКОЕ
ЗАДАНИЕ №6
Вычисления в
таблицах. Формулы.
Использование
формул, содержащих вложенные функции
-
Выполните построение
и форматирование таблицы по образцу,
представленному на рис. 6.
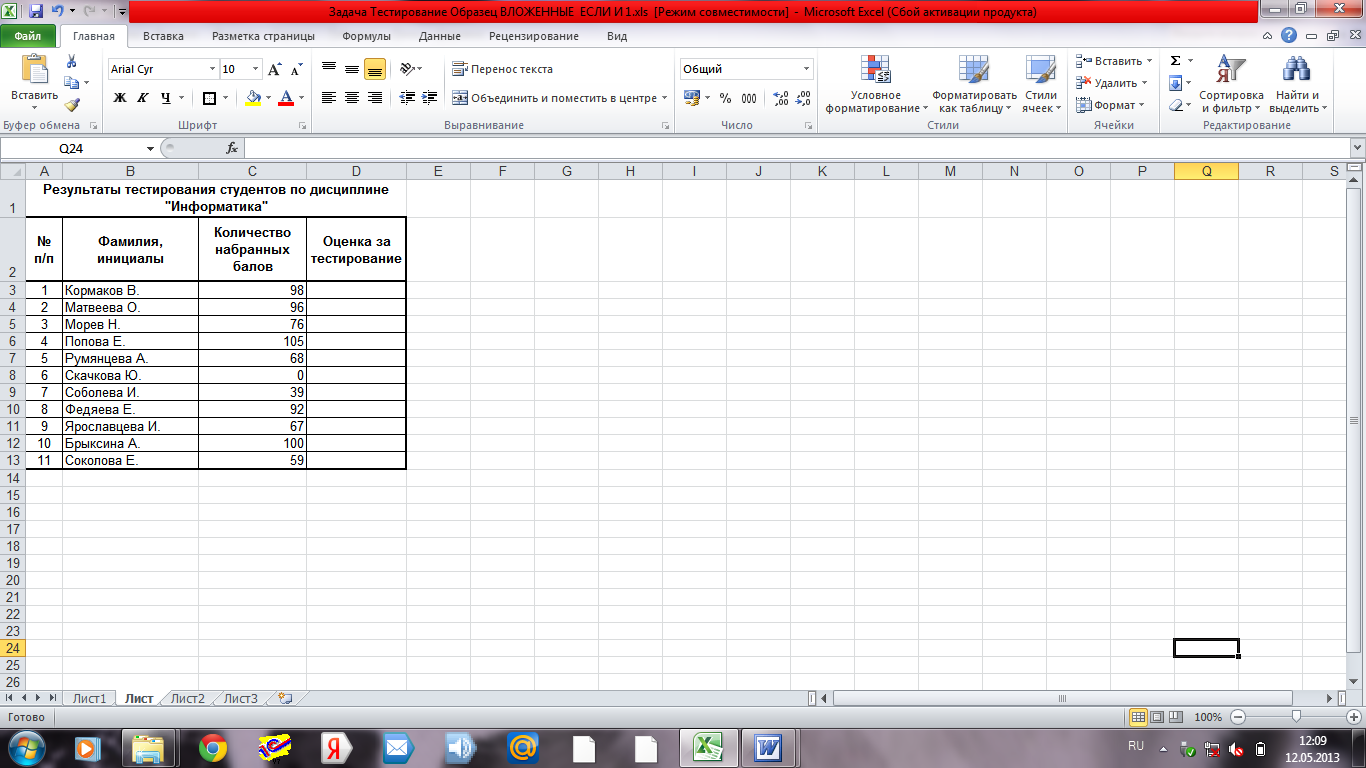
Рисунок 6 – Таблица
для определения результатов тестирования
студентов
-
Используя
логические функции, составьте формулу
для автоматизированного определения
оценок студентов в соответствии с
набранными баллами, исходя из следующих
условий:
—
Каждому студенту предложено ответить
на 100 вопросов. За каждый ответ начисляется
один балл.
—
По итогам тестирования выставляются
оценки по следующему критерию: от 90
до 100
баллов- оценка «отлично»,
от 75
до 89—
«хорошо»,
от 60
до 74
– «удовл.»,
от 50
до 59—
«неудовл.»
, до 49—
«единица»,
менее 35—
«ноль».
В остальных случаях должно выводиться
сообщение «ошибка».
Перед выполнением
расчетов составьте алгоритм решения
задачи в графической форме.
3.
Рассчитайте средний балл, установив
вывод его значения в виде целого числа.
4.
Упорядочьте данные, содержащиеся в
таблице, по убыванию набранных баллов.
5. Сравните полученные
результаты с таблицей на рис. 7.
Рисунок 7- Результат
выполнения задания 6
8
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Excel задания с решениями. Скачать примеры
- Задание 1
- Решение задания
- Задание 2
- Задачи по Excel
- Решение задач по Excel. Выпуск 4
- Решение задач по Excel. Выпуск 3
- Решение задач по Excel. Выпуск 2
- Решение задач по Excel. Выпуск 1
- Решение простых задач с помощью Excel
Excel задания с решениями. Скачать примеры
В этом уроке мы постараемся закрепить то, что прошли на предыдущих. Рассмотрим несколько заданий с примерами решения.
Задание 1
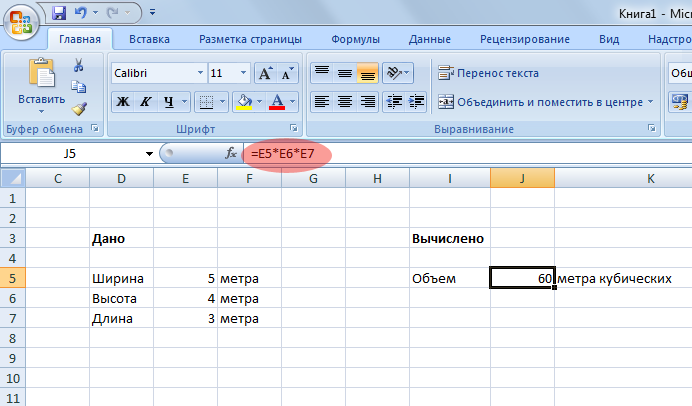
Ниже на рисунке изображена таблица автоматически вычисляющая объем прямоугольной канистры. Даны ее размеры. Это самое простое задание, с которого мы начнем. Для начала постарайтесь добиться решения самостоятельно.
Решение задания
Первое, что необходимо сделать это заполнить ячейки словами «дано», «ширина», «высота» и так далее. Обратите внимание на то, что слово «метра» я вписал один раз, а потом автозаполнением заполнил оставшиеся 2 ячейки. Для того, чтобы отформатировать текст (сделать жирным слова «дано» и «Вычислено» выберите ячейку и воспользуйтесь инструментом Ж (полужирный) на панели вверху в закладке Главная.
После того как вы создали внешний вид таблицы (т.е. вписали в ячейки все кроме цифр) переходим к решению самой задачи. У меня в примере ячейка J5 содержит формулу для вычисления объема. Сама по себе формула просто, чтобы вычислить объем прямоугольного параллелипипеда надо перемножить длины всех его 3 сторон.
В нашем примере значение ширины, высоты и длины содержится в ячейках E5, E6, E7. Как раз их нам надо и перемножить и результат записать в ячейку J5, для этого в ячейке J5 пишем формулу =E5*E6*E7. и жмем Enter.
Внимание! если вы не вписали значение ширины, высоты и длины, то там где будет ответ высветиться предупреждение об ошибки, чтобы оно исчезло просто введите значение сторон, чтобы компьютеру было, что ему перемножать.
Задание 2
Это задание не чуть не сложнее, просто больше надо заполнять и больше ввести формул, если Вы все верно поняли в первом задании и разобрались, то решение этого задание в не составит особого труда
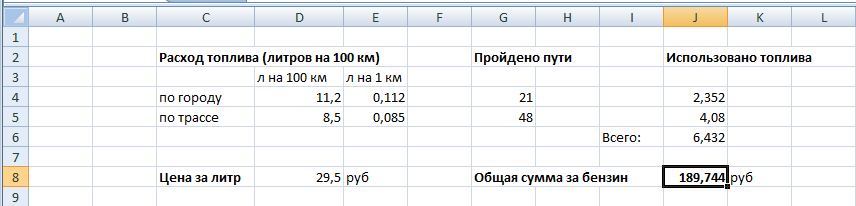
В этом задании все, что нам дано это количество расхода бензина на 100 км, пройденный путь и цена на топливо. Все остальное значения в ячейках программа Excel считает автоматически после того как будут введены формулы.
Скачать файл Еxcel с примером решения этой задачи.
Для тех кому понравился стиль объяснения и подробного описания рекомендую статью про выпадающие списки в экселе все так же подробно и понятно
Жми Привет! Если статья полезна, поддержи меня и сайт, поделись ей
Источник
Задачи по Excel
Решение задач по Excel. Выпуск 4
Задание 1.
- Ввести исходные данные, оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы, шапку таблицы оформить заливкой. Для форматирования текста используйте Формат Ячейки/ Выравнивание.
- Добавить в таблицу дополнительные ячейки для внесения формул и получения результата.
- Функции, используемые при выполнении работы:
Математические:
- СУММ — сумма аргументов;
- ПРОИЗВЕД — произведение аргументов;
- СУММПРОИЗВ — сумма произведений соответствующих массивов.
Статистические:
- СРЗНАЧ — среднее арифметическое аргументов;
- МАКС — максимальное значение из списка аргументов;
- МИН — минимальное значение из списка аргументов;
- СЧЕТЕСЛИ — подсчитывает количество непустых ячеек в диапазоне, удовлетворяющих заданному условию.
- Заполнить таблицу (5-7 строк). Имеющиеся в шапке таблицы данные (года, месяцы, дни недели) заносить с помощью автозаполнения.
- Оформить таблицу с помощью обрамления, добавить заголовок, расположив его по центру таблицы. Шапку таблицы выполнить в цвете (шрифт и фон), полужирным шрифтом.
- Переименовать лист книги по смыслу введенной информации.
- Добавить в начало таблицы столбец «№ пп» и заполнить его автоматически.
- Выполнить соответствующие вычисления.
Решение задач по Excel. Выпуск 3
1. Спланируйте расходы на бензин для ежедневных поездок из п. Половинка в г. Урай на автомобиле. Если известно:
- расстояние м/д населёнными пунктами в км. (30 км. в одну сторону)
- расход бензина (8 литров на 100 км.)
- количество поездок в месяц разное (т.к. разное количество рабочих дней.)
- цена 1 литра бензина ( n рублей за литр.)
- ежемесячный прогнозируемый рост цены на бензин — k% в месяц
Рассчитайте ежемесячный и годовой расход на бензин. Постройте график изменения цены бензина и график ежемесячных расходов.
2. Представьте, что вы директор ресторана. Общий месячный фонд заработной платы — 10000$. На совете акционеров было установлено, что:
- официант получает в 1,5 раза больше мойщика посуды;
- повар — в 3 раза больше мойщика посуды;
- шеф-повар — на 30$ больше.
Решение задач по Excel. Выпуск 2
1. Рассчитайте еженедельную выручку зоопарка, если известно:
- количество проданных билетов каждый день,
- цена взрослого билета — 15 руб,
- цена детского на 30% дешевле чем взрослого.
Постройте диаграмму (график) ежедневной выручки зоопарка.
2. Подготовьте бланк заказа для магазина, если известно:
- продукты (хлеб, мука, макаронные изделия и т.д., не менее 10 наименований)
- цена каждого продукта
- количество заказанного каждого продукта
Рассчитайте на какую сумму заказано продуктов. Усовершенствуйте бланк заказа, добавив скидку (например 10%), если стоимость купленных продуктов будет более 5000 руб. Постройте диаграмму (гистограмму) стоимости.
Решение задач по Excel. Выпуск 1
1. Найти решение уравнения вида kx + b = 0, где k, b — произвольные постоянные.
2. Сахарный тростник содержит 9% сахара. Сколько сахара будет получено из 20 тонн сахарного тростника?
3. Школьники должны были посадить 200 деревьев. Они перевыполнили план посадки на 23%. Сколько деревьев они посадили?
4. Из 50 кг. семян, собранных учениками, 17% составили семена клена, 15% — семена липы, 25% — семена акации, а стальное — семена дуба. Сколько килограмм.
Источник
Решение простых задач с помощью Excel
Классы: 6 , 7
Ключевые слова: Excel , функции в Excel , ячейка , адрес ячейки , таблица
Цель урока: продолжить формирование навыков работы с электронными таблицами.
Задачи:
- обучающие: формировать умения создания, редактирования, форматирования и выполнения простейших вычислений в электронных таблицах.
- развивающие: расширить представления учащихся о возможных сферах применения электронных таблиц; развивать навыки аналитического мышления, речи и внимания.
- воспитательные: формировать и воспитывать познавательный интерес; прививать навыки самостоятельности в работе.
План урока.
- Организационный момент.
- Актуализация знаний учащихся.
- Проверка домашнего задания.
- Решение задач.
- Самостоятельное решение задачи.
- Подведение итогов. Оценки.
- Домашнее задание.
1. Организационный момент.
Сообщить тему урока, сформулировать цели и задачи урока.
Сегодня мы вновь окажемся в гостях у маленького великана Васи в Сказочной стране. Ему, как всегда, требуется ваша помощь, ребята.
Сможете ли вы помочь Васе? Сейчас проверим!
2. Актуализация знаний учащихся.
1) Устно ответить на вопросы.
| A | B | C | D | |
| 1 | 2 | 1 | =A1+3*B1 | =A1^2+B1 |
| 2 | 4 | 6 | =A2+3*B2 | =A2^2+B2 |
- Что такое электронная таблица?
- Какие основные элементы электронной таблицы вам известны?
- Как задается имя ячейки (строки, столбца) в электронной таблице?
- Что может быть содержимым ячейки?
- Число 1 находится в столбце . в строке . в ячейке с адресом .
- Число 4 находится в ячейке с адресом .
- Каковы правила записи формул в ячейках?
- Чему равно значение, вычисляемое по формуле, в ячейке С1?
- Чему равно значение, вычисляемое по формуле, в ячейке D2?
2) Какой результат будет получен в ячейках с формулами?
| A | B | C | D |
| 1 | 5 | 2 | 1 |
| 2 | 6 | 8 | 3 |
| 3 | 8 | 3 | 4 |
| 4 | =СУММ(B1:D3) |
- Что означает запись =СУММ(В1:D3)?
- Сколько элементов содержит блок В1:D3? Ответ: 9.
- Содержимое ячейки D3? Ответ: 5+2+1+6+8+3+8+3+4= 40
3) Проверка домашнего задания
Результаты соревнований по плаванию
Один ученик рассказывает, как он выполнил домашнее задание (через проектор).
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3.23 | 3.44 | 3.30 | |||
| 2 | Моржов | 3.21 | 3.22 | 3.24 | |||
| 3 | Акулов | 3.17 | 3.16 | 3.18 | |||
| 4 | Рыбин | 3.24 | 3.20 | 3.18 | |||
| 5 | Черепахин | 3.56 | 3.44 | 3.52 | |||
| Лучший результат соревнований | |||||||
| Среднее время участников соревнований | |||||||
| Максимальное отклонение |
- Среднее время для каждого спортсмена находится как среднее арифметическое трех его заплывов.
- В ячейку «Лучшее время» записывается минимальный результат из 3 заплывов.
- В ячейку «Лучший результат соревнований» записывается минимальное время из столбца.
- В столбец «Отклонение» записывается разность между лучшим временем спортсмена и лучшим результатом соревнований.
- В ячейку «Максимальное отклонение» записывается максимальное значение столбца.
| Результаты соревнований по плаванию | |||||||
| № | Ф.И.О. | 1 | 2 | 3 | Лучшее время | Среднее время | Отклонение |
| 1 | Лягушкин | 3,23 | 3,44 | 3,30 | 3,23 | 3,32 | 0,07 |
| 2 | Моржов | 3,21 | 3,22 | 3,24 | 3,21 | 3,22 | 0,05 |
| 3 | Акулов | 3,17 | 3,16 | 3,18 | 3,16 | 3,17 | 0,00 |
| 4 | Рыбин | 3,24 | 3,20 | 3,18 | 3,18 | 3,21 | 0,02 |
| 5 | Черепахин | 3,56 | 3,44 | 3,52 | 3,44 | 3,51 | 0,28 |
| Лучший результат соревнований | 3,16 | ||||||
| Среднее время участников соревнований | 3,29 | ||||||
| Максимальное отклонение | 0,28 |
4) Решение простых задач.
Маленький великан Вася решил отремонтировать забор вокруг своего огорода и вскопать его под посадку овощей (наступила очередная весна), разметить грядки прямоугольной формы. Для работы ему потребовалось найти длину забора и площадь участка. Но ведь в школе он никогда не учился. Поможем Васе.
№ 1. Вычислить периметр и площадь прямоугольника со сторонами:
а) 3 и 5; б) 6 и 8; в) 10 и 7.
Эту задачу обсуждаем совместно с детьми:
- Как оформить таблицу?
- Какие формулы использовать?
- Как использовать уже записанные формулы для следующего прямоугольника?
Оформление таблицы – на доске и в тетрадях.
В то же время другой ученик самостоятельно решает следующую задачу и представляет свое решение учащимся (через проектор).
№ 2. Маленький великан Вася решил подсчитать, через сколько дней в его копилке будет 100 руб., если ежедневно он стал класть туда на 5 руб. больше, чем в предыдущий день. Помогите Васе. Сейчас в его копилке 2,02 руб.
Обсудив решение задачи № 2, переходим к решению следующей.
Один ученик показывает, как работать с формулами, другой – как использовать функцию суммирования, числовой формат (общий, денежный) и т.д. (Таблица уже готова, ученикам предстоит ввести формулы, использовать суммирование и получить ответ).
№ 3. Посчитайте, используя ЭТ, хватит ли Васе 150 рублей, чтобы купить все продукты, которые ему заказала мама, и хватит ли на чипсы за 10 рублей? Сдачу мама разрешила положить в копилку. Сколько рублей попадет в копилку?
Итого:
| № | Наименование | Цена в рублях | Количество | Стоимость |
| 1 | Хлеб | 9,6 | 2 | =C2*D2 |
| 2 | Кофе | 2,5 | 5 | =C3*D3 |
| 3 | Молоко | 13,8 | 2 | =C4*D4 |
| 4 | Пельмени | 51,3 | 1 | =C5*D5 |
| =СУММ(E2:E5) | ||||
| После покупок останется | =150-E6 | |||
| После покупки чипсов останется | =D7-10 |
5) Самостоятельное решение задачи.
Маленький великан Вася часто бывал в гостях у жителей Цветочного города.
Собираясь на пляж, веселые человечки решили запастись прохладительными напитками. Незнайка взял с собой 2 литра кваса, 1 литр газировки и 1 литр малинового сиропа, Пончик – 3 литра газировки и 2 литра малинового сиропа, Торопыжка – 2 литра газировки, доктор Пилюлькин – 1 литр кваса и 1 литр касторки.
- Сколько литров напитков каждого вида взяли все человечки вместе?
- Сколько всего литров напитков взял с собой каждый из человечков?
- Сколько всего литров напитков взяли все человечки вместе?
Оформите таблицу произвольно и сохраните в своей личной папке.
| Веселые человечки. Напитки. | |||||
| Напиток | Незнайка | Пончик | Торопыжка | Пилюлькин | Всего |
| Квас, л | 2 | 0 | 0 | 1 | 3 |
| Газировка, л | 1 | 3 | 2 | 0 | 6 |
| Сироп, л | 1 | 2 | 0 | 0 | 9 |
| Касторка, л | 0 | 0 | 0 | 1 | 1 |
| ИТОГО: | 4 | 5 | 2 | 2 | 13 |
7) Подведение итогов. Оценки.

Подумайте и решите эту задачу, если известны еще следующие величины.
Как изменится таблица? Какие формулы появятся?
Известно, что 1 литр кваса в Цветочном городе стоит 1 монету, 1 литр газировки – 3 монеты, 1 литр малинового сиропа – 6 монет, 1 литр касторки – 2 монеты.
- Сколько монет истратил на покупку напитков каждый человечек?
- Сколько монет затрачено на покупку напитков каждого вида?
- Сколько потрачено денег всеми человечками вместе?
Источник
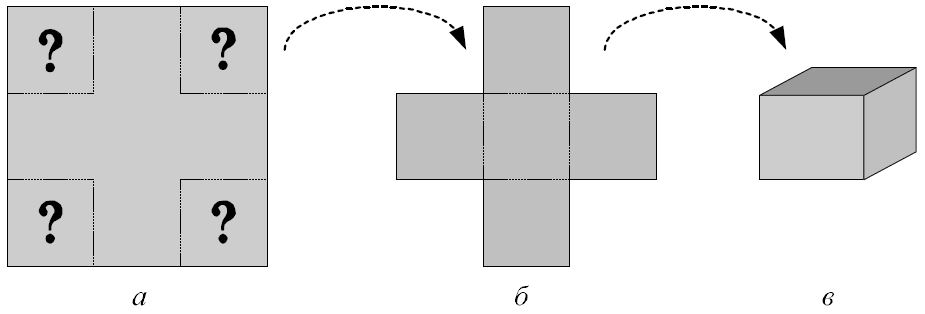
Данная задача формулируется следующим образом. Имеется квадратная заготовка из некоторого гибкого материала, например, картона или жести, причем размеры этой заготовки фиксированы для конкретной ситуации (Рис. 1. а). Из этой заготовки следует вырезать четыре равных квадрата по её углам, а полученную фигуру (Рис. 1. б) согнуть так, чтобы получилась коробка без верхней крышки (Рис. 1. в). При этом необходимо так выбрать размер вырезаемых квадратов, чтобы получилась коробка максимального объема.
Рис. 1. Схема изготовления коробки из прямоугольной заготовки фиксированного размера
На примере данной задачи можно проиллюстрировать все элементы постановки задач оптимизации. Оценочной функцией в данной задаче служит объем изготовленной коробки. Проблема выбора заключается в выборе размера вырезаемых квадратов. Действительно, если размер вырезаемых квадратов будет слишком мал, то будет получена широкая коробка малой высоты, а значит, и ее объем окажется невелик. С другой стороны, если размер вырезаемых квадратов будет слишком большой, то будет получена узкая коробка большой высоты, а значит, и ее объем также окажется невелик.
В то же время на выбор размера вырезаемых квадратов оказывает влияние ограничение размера исходной заготовки. Действительно, если вырезать квадраты со стороной, равной половине стороны исходной заготовки, то задача теряет смысл. Сторона вырезаемых квадратов также не может превышать половину стороны исходной заготовки, поскольку это невозможно из практических соображений. Из этого следует, что в постановке данной задачи должны присутствовать некоторые ограничения.
Задача о коробке максимального объема имеет не только наглядную интерпретацию, но и достаточно простое аналитическое решение. Она относится к классу задач нелинейной оптимизации, методы решения которых подробно рассматриваются ниже.
Математическая постановка задачи о коробке максимального объема
Для математической постановки данной задачи необходимо ввести в рассмотрение некоторые параметры, характеризующие геометрические размеры коробки. С этой целью дополним содержательную постановку задачи соответствующими параметрами. С этой целью будем рассматривать квадратную заготовку из некоторого гибкого материала, которая имеет длину стороны L (Рис. 2). Из этой заготовки следует вырезать четыре равных квадрата со стороной r по ее углам, а полученную фигуру согнуть, так чтобы получилась коробка без верхней крышки. Задача состоит в таком выборе размера вырезаемых квадратов, чтобы в результате получилась коробка максимального объема.
Рис. 2. Схема изготовления коробки из прямоугольной заготовки с указанием ее размеров
Для математической постановки данной задачи необходимо определить переменные соответствующей задачи оптимизации, задать целевую функцию и специфицировать ограничения. В качестве переменной следует взять длину стороны вырезаемого квадрата r, которая в общем случае, исходя из содержательной постановки задачи, принимает непрерывные действительные значения.
Целевой функцией является объем полученной коробки. Поскольку длина стороны основания коробки равна: L — 2r, а высота коробки равна r, то ее объем находится по формуле: V(r) = (L — 2r)² * r. Исходя из физических соображений, значения переменной r не могут быть отрицательными и превышать величину половины размера исходной заготовки Z, т. е. 0,5 * L.
С целью унификации, обозначим переменную через х = r, что не оказывает влияния на характер решаемой задачи оптимизации. Тогда математическая постановка задачи о коробке максимального объема может быть записана в следующем виде: f(x) = x * (L - 2x)² → max, где Δβ = {X ∈ R¹ | 0 ≤ x ≤ 0,5 * L}.
Целевая функция данной задачи является нелинейной, поэтому задача о коробке максимального размера относится к классу задач нелинейного программирования или нелинейной оптимизации.
Решение задачи о коробке максимального объема с помощью программы MS Excel
Не уменьшая общности математической постановки задачи, предположим: L = 1. Для решения данной задачи с помощью программы MS Excel создадим новую книгу с именем Нелинейная Оптимизация и изменим имя ее первого листа на Задача о коробке. Сделаем необходимые надписи в ячейках А1:В2. После этого введем в ячейку С2 формулу: =C1*(1-2*C1)^2, которая представляет целевую функцию. Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи о коробке максимального объема имеет следующий вид (Рис. 3).
Рис. 3. Исходные данные для решения задачи о коробке максимального объема
При изображении исходных данных для решения задачи о коробке максимального объема (Рис. 3.) выбран режим отображения формул в ячейках рабочего листа, что оказывается весьма удобным для визуального контроля правильности задания выражений для соответствующих формул. Этот режим может быть установлен с помощью выполнения операции главного меню: Формулы → Показать формулы. С помощью удаления этой отметки можно вернуться к обычному режиму изображения ячеек рабочего листа.
Для дальнейшего решения задачи следует воспользоваться инструментом поиска решения программы MS Office Excel. С этой целью необходимо выполнить операцию меню: Данные → Поиск решения.
После вызова инструмента поиска решения появится диалоговое окно мастера задания параметров для нахождения решения (Рис. 4). Ввиду важности этого инструмента следует более подробно остановиться па элементах его диалоговых окон.
Рис. 4. Диалоговое окно Поиск решения
Первое диалоговое окно Поиск решения (Рис. 4) имеет следующие элементы:
- поле Оптимизировать целевую функцию — используется для задания ссылки на ячейку, в которой задана формула с выражением целевой функции решаемой задачи оптимизации;
- переключатели в группе До: — определяют характер решаемой задачи оптимизации. Для нахождения решения с максимальным значением целевой функции этот переключатель ставится в положение максимальному значению, для нахождения решения с минимальным значением — в положение минимальному значению. Наконец, для нахождения решения, при котором целевая функция принимает некоторое фиксированное значение, переключатель ставится в положение Значению, справа от которого можно ввести требуемое фиксированное значение;
- поле Изменяя ячейки переменных — служит для указания ячеек, которые должны изменяться в процессе поиска решения задачи. Именно в этих ячейках должны находиться переменные решаемой задачи оптимизации;
- в многострочном поле В соответствии с ограничениями отображаются ограничения решаемой задачи оптимизации;
- кнопка Добавить — служит для вызова дополнительного окна Добавление ограничения (Рис. 5);
- кнопка Изменить — служит для вызова дополнительного окна Добавление ограничения, в котором будет отображено ограничение, выбранное в многострочном поле Ограничения;
- кнопка Удалить — служит для удаления ограничения, выбранного в многострочном поле Ограничения;
- кнопка Выполнить — служит для запуска процесса нахождения оптимального решения после спецификации всех параметров поиска решения;
- кнопка Сбросить — служит для сброса всех параметров поиска решения;
- кнопка Загрузить / сохранить — служит для загрузки сохраненных условий ограничений или сохранения условий ограничения;
- кнопка Выполнить — служит для запуска процесса нахождения оптимального решения после спецификации всех параметров поиска решения;
- кнопка Параметры — служит для вызова дополнительного окна Параметры поиска решения (Рис. 3.5) для спецификации дополнительных параметров поиска решения, часть которых уже задана по умолчанию.
Рис. 5. Диалоговое окно Добавление ограничения
Диалоговое окно Добавление ограничения (Рис. 5) предназначено для задания одного ограничения и имеет следующие элементы:
- поле Ссылки на ячейки — служит для указания ячейки или диапазона ячеек, в которых содержится левая часть задаваемого ограничения;
- выпадающий список в центре окна — содержит перечень знаков неравенств ограничений, а также возможность спецификации требования целочисленности или двоичных значений переменных. Мастер поиска решений допускает спецификацию ограничений в виде равенств и неравенств;
- поле Ограничение — служит для указания ячейки, диапазона ячеек или конкретного числа, которое специфицирует правую часть задаваемого ограничения;
- кнопка ОК — служит для добавления ограничения к параметрам поиска решения и закрытия окна Добавление ограничения;
- кнопка Отмена — для закрытия окна Добавление ограничения без добавления ограничения к параметрам поиска решения;
- кнопка Добавить — для добавления ограничения к параметрам поиска решения без закрытия окна Добавление ограничения;
- кнопка Справка — служит для получения справочной информации об элементах диалогового окна Добавление ограничения.
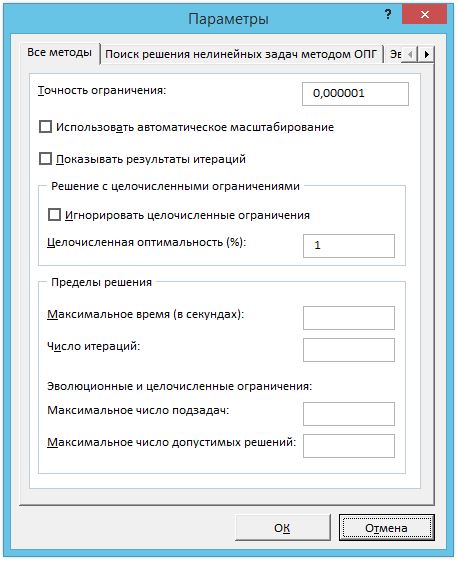
Рис. 6. Диалоговое окно Параметры поиска решения
Диалоговое окно Параметры поиска решения (Рис. 3.5) предназначено для спецификации дополнительных параметров нахождения решения или изменения уже заданных параметров. Следует заметить, что значения большинства этих параметров, используемых по умолчанию, подходят для решения типовых задач оптимизации. Диалоговое окно Параметры поиска решения имеет следующие элементы.
- Поле Максимальное время служит для ограничения времени, отпускаемого на поиск решения задачи. В это поле можно ввести время (в секундах), не превышающее 32 767. Установленное по умолчанию значение 100 подходит для решения рассматриваемых типовых задач.
- Поле Число итераций служит для ограничения времени решения задачи посредством задания некоторого предельного числа промежуточных вычислений. Установленное по умолчанию значение 100 подходит для решения рассматриваемых типовых задач.
- Флажок Показывать результаты итераций служит для приостановки поиска решения для просмотра результатов отдельных итераций.
- Флажок Автоматическое масштабирование служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, — например, максимизация прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей.
Продолжим решение задачи о коробке максимального объема. В первом окне мастера поиска решения следует в поле с именем Установить целевую ячейку указать ячейку $С$2, в которой содержится формула для расчета целевой функции задачи, а в поле е именем Изменяя ячейки ввести абсолютный адрес ячейки $C$1, в которую будет записано искомое решение задачи.
После этого следует добавить два ограничения на допустимые значения переменной. Для этого следует нажать кнопку Добавить, в результате чего появится дополнительное окно задания ограничений (Рис. 7). Для ввода адресов ячеек в левую часть ограничения предназначено поле е именем Ссылка на ячейку. Форма неравенства ограничения выбирается из вложенного списка в средней части окна.
Наконец, для задания правой части ограничений в поле ввода с именем Ограничение следует ввести с клавиатуры следующие числа: 0,5 — для первого ограничения и 0 — для второго. После спецификации каждого из ограничений их необходимо включить в модель расчета, для чего следует нажать кнопку Добавить или ОК. Для того чтобы закрыть дополнительное окно задания ограничений и вернуться в исходное окно мастера поиска решения, следует нажать кнопку Отмена или ОК.
Остальные параметры мастера поиска решения, для редактирования которых предназначено дополнительное второе окно этого мастера, можно оставить без изменения. Окончательный внешний вид диалогового окна мастера поиска решения после задания необходимой информации изображен на Рис. 7.
Рис. 7. Параметры мастера поиска решения для задачи о коробке
Для редактирования некоторого ограничения его следует выделить в многострочном поле с именем Ограничения и нажать кнопку с именем Изменить. В этом случае появится дополнительное окно, аналогичное изображенным на Рис. 7, в котором можно выполнить необходимые действия по редактированию выбранного ограничения.
После задания необходимых параметров поиска решения можно приступить к выполнению численных расчетов, для чего следует нажать кнопку Выполнить. После выполнения численных расчетов программой MS Excel практически мгновенно будет получено количественное решение, которое имеет следующий вид (Рис. 8).
Рис. 8. Результат количественного решения задачи о коробке максимального объема
Интерпретируя полученные количественные значения, можно прийти к следующему заключению. Результатом решения является оптимальное значение стороны вырезаемого квадрата: ropt = 0,166666693977061, при котором изготовленная коробка будет иметь максимальный объем: Vmax = 0,0740740740740726. Напомним, что это решение соответствует длине стороны исходной заготовки, равной 1.
Полученное решение имеет общий характер, поскольку в любом конкретном случае для получения решения рассматриваемой задачи оптимизации значение L следует умножить на найденное значение ropt. Например, если L = 2, то для получения коробки максимального объема следует вырезать по углам исходной заготовки квадраты со стороной 0,166666693977061 * 2 = = 0,333333387954122 м.
Таким образом, задача о коробке максимального объема в каждом конкретном случае может быть решена простой подстановкой в расчетную формулу ropt = 0,166666693977061 * L конкретного значения величины L. Допустимая точность решения задается в каждом конкретном случае, исходя из специфики задачи и соответствующей проблемной области.
Для анализа найденного решения можно построить график целевой функции и визуально оценить его корректность. С этой целью на отдельном рабочем листе е помощью операции автозаполнения ячеек зададим последовательный ряд чисел исходной переменной r в диапазоне от 0 до 1 с интервалом 0.01, которые запишем в ячейки с адресами А2:А52. Рядом в ячейки В2:В52 запишем соответствующие значения целевой функции. Для этого можно записать формулу: =A2*(1-2*A2)^2 в ячейку В2 и с помощью операции автозаполнения «протащить» содержание этой ячейки на диапазон В3:В52.
После этого для построения графика целевой функции для задачи о коробке следует воспользоваться мастером диаграмм. Построенный график целевой функции будет иметь следующий вид как на Рис. 9. Визуальный анализ этого графика показывает, что максимум целевой функции находится между значениями х = 0,16 и х = 0,17. Этот факт можно также проверить, сравнив значения в ячейках В18 и В19. Тем самым, можно сделать вывод о корректности полученного результата решения данной задачи оптимизации.
Рис. 9. График целевой функции в задаче о коробке максимального объема
Аналитическое решение задачи о коробке максимального объема
Поскольку задача о коробке максимального объема имеет достаточно простое аналитическое решение, оно приводится для дополнительной проверки правильности численных расчетов программы MS Excel.
Прежде всего, следует заметить, что целевая функция является непрерывной и дифференцируемой на всем интервале ее задания, включая множество допустимых альтернатив Δβ, которое, в свою очередь, является замкнутым. Как следует из курса математического анализа, непрерывная функция на замкнутом множестве достигает своих экстремальных значений, из которых нас интересуют точки максимума данной функции. Для нахождения экстремума аналитическим способом следует определить первую производную целевой функции и отыскать ее корни.
Первая производная функции: f(x) = x*(1-2x)² равна df(x)/dx = 12x²-8x+1. Соответствующее уравнение: 12x²-8x+1=0 является квадратным, которое имеет два корня: Х = 1/6 и х2 = 1/2. Анализ графика целевой функции (см. Рис. 3.5) показывает, что максимальному значению этой функции соответствует первый корень. Данное значение является допустимым и служит точным аналитическим решением задачи оптимизации о коробке максимального размера.
Таким образом, ropt = 1/6. Поскольку число 1/6 является иррациональным и представляет собой периодическую дробь 0.16(6), при желании можно получить его любое приближение произвольной точности. Сравнивая найденное ранее значение 0,166666693977061 с соответствующим округлением точного значения, можно получить относительную погрешность программы MS Excel. Это значение равно: 0.000016382137877% и свидетельствует о том, что решение задач оптимизации программой MS Excel с гладкой целевой функцией выполняется весьма эффективно.