В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Поможем с Excel, финансами и математикой 
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Помогаем с решением задач по финансовой математике
Может быть интересно:
|
|
Финансовые задачи в Excel
Экономический
факультет
Кафедра
Информационных технологий
Информационные
системы в экономике
Финансовые
задачи в Excel
Содержание
Раздел 1 Технология работы с
финансовыми Функциями Еxcel. Основные понятия финансовых методов расчета 4
.1 Операции наращения.
Функция бс(). 11
.2 Операции дисконтирования 16
.3 Определение срока
финансовой операции 17
.4 Определение процентной
ставки 18
.5 Расчет эффективной и
номинальной ставки процентов 19
.6 Начисление процентов по
плавающей ставке 20
Раздел 2. Потоки платежей и
финансовые ренты 22
.1 Определение будущей
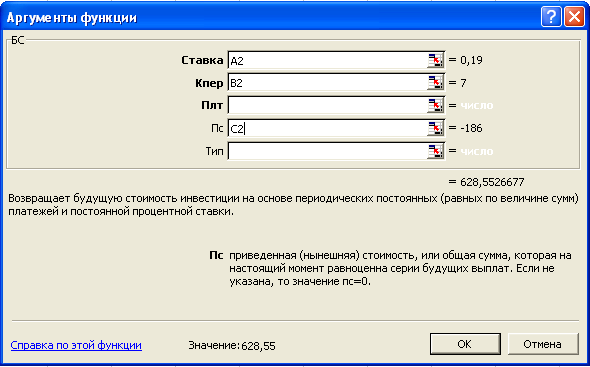
(наращенной) стоимости потока платежей. Функция бс() 23
.2 Современная (текущая)
величина аннуитета. Функция пс() 25
.3 Расчет периодических
платежей 27
Раздел 3. Оценка
инвестиционных процессов 36
.1.Чистый приведенный доход.
Функция чпс 37
.2 Срок окупаемости 41
.3 Индекс рентабельности 43
.4 Внутренняя норма
доходности.Функция чиствндох 45
.5 Модифицированная
внутренняя норма доходности.Функция мсвд 46
.6 Денежный поток
инвестиционного проекта с произвольными периодами поступления платежей 49
Раздел 4. Функции excel для
расчета амортизации 51
Аргументы функций excel для
расчета амортизации 51
Контрольные работы 55
Раздел 1. Технология работы с финансовыми функциями Еxcel. Основные понятия финансовых методов расчета
финансовый программа функция
Рассмотрим процесс наращения (accumulation), т.е. определения денежной сумм
будущем, исходя из заданной суммы сейчас.
Экономический смысл операции наращения состоит в
определении величины той суммы, которой будет или желает располагать инвестор
по окончании этой операции. Здесь идет движение денежного потока от настоящего
к будущему.
Существуют различные способы начисления процентов и
соответствующие процентных ставок
Величина FV показывает будущую стоимость «сегодняшней» величины инвестиции PV при заданном уровне интенсивности
начисления процентов r
Простая процентная ставка — применяется к одной и той же первоначальной сумме
долга на протяжении всего срока ссуд исходная база (денежная сумма) всегда одна
же.
Сложная процентная ставка — применяется к наращенной сумме долга, т.е сумме,
увеличенной на величину начисленных предыдущий период процентов, — таким
образом исходная база постоянно увеличивается.
Фиксированная процентная ставка — ставка, зафиксированная в виде
определенного числа (сумы) в финансовых контрактах.
Плавающая процентная ставка — привязанная к определенной величине, изменяющейся
во времени, включая надбавку к ней (маржу), которая определяется целым рядом
условий (сроком операции и т.п.).
Постоянная процентная ставка — неизменная на протяжении всего
периода ссуды.
Переменная процентная ставка — дискретно изменяющаяся во времени,
но имеющая конкретную числовую характеристику.
В любой простейшей финансовой операции всегда
присутствуют четыре величины:
время (n)
современная величина (PV),
— наращенная или будущая величина (FV),
— процентная ставка (r)
n — Срок погашения долга (англ. number of periods) — интервал времени, по истечении которого сумму
долга и проценты нужно вернуть. Срок измеряется числом расчетных периодов —
обычно равных по длине подинтервалов времени, в конце (или начале) которых
начисляются проценты.
Если начисление процентов будет производиться m раз в год, а срок погашения
долга — n лет, то общее количество периодов начисления за весь
срок финансовой операции составит
PV—
текущая стоимость (англ. present value) — исходная сумма или
оценка современной величины денежной суммы, поступление которой ожидается в
будущем, в пересчете на более ранний момент времени;
FV—
будущая стоимость (англ. future value) — наращенная сумма или
будущая стоимость, т.е. первоначальная сумма долга с начисленными на нее
процентами к концу срока ссуды;
I— Процентные деньги (англ. interest
money), называемые часто коротко «проценты», представляют
собой абсолютный доход от предоставления долга.
I=FV—PV
Оценка
эффективности финансовых операций по величине процентных денег на практике
используется достаточно редко, так сама их величина, не учитывающая фактор
времени, мало что может сказать о реальной доходности операции. Необходимо
иметь возможность сопоставить ее с темпом обесценивания денег (инфляции) или
результатами другой финансовой операции. Поэтому в финансово-экономических
расчетах наиболее широко пользуются относительные показатели:
г
— процентная ставка (rate of interest), характеризующая
интенсивность начисления процентов за единицу времени,- отношение суммы
процентных денег, выплачивающихся за определенный период времени, к величине
ссуды. Этот показатель выражается либо в долях единицы, либо в процентах.
На
рабочем листе в отдельных ячейках осуществляется подготовка значений основных
аргументов функции.
Для
расчета результата финансовой функции Excel курсор устанавливается в
новую ячейку для ввода формулы, использующей встроенную финансовую функцию.
Осуществляется
вызов «Мастера функций»
На
основной панели инструментов имеются кнопки «Мастер функций», с
помощью которой открывается диалоговое окно Диспетчера функций.
Диалоговое
окно «Диспетчер функций» организовано по тематическому принципу.
После выбора в левом списке «Категории» тематической группы «Финансовые»,
на экран будет выведено диалоговое окно с полным перечнем списка имен
функций, содержащихся в данной группе.
Поиск
необходимой финансовой функции осуществляется путем последовательного просмотра
списка.
Для
выбора функции курсор устанавливается на имя функции.
Рис.1-3.
Последовательность действий при выборе необходимой финансовой функции
В
результате выполненных действий на экране откроется диалоговое окно выбранной
функции.
В
поля диалогового окна функции:
можно
вводить как сами значения аргументов, так и ссылки на адреса ячеек, содержащие
необходимые значения;
все
расходы денежных средств (платежи) представляются отрицательными числами, а все
поступления денежных средств — положительными числами;
процентная
ставка вводится в виде десятичной дроби, либо с использованием знаке %;
Для
исчисления характеристик финансовых операций с наращением и дисконтированием
вложенных сумм удобно использовать функции БС, IIC, KIIEP,
СТАВКА, БЗРАСПИС, НОМИНАЛ, ЭФФЕКТ. ПРПЛТ, ОБЩПЛАТ, ОСППЛАТ, ОБЩДОХОД.
Таблица
1.
Функции
рабочего листа Excel для оценки разовых и периодических (потоков)
|
Наименование функции |
Формат функции |
Назначение функции |
|
БС |
БС(ставка ;кпер;плт;пс;тип) |
рассчитывает будущую |
|
ПС |
ПС(ставка ;кпер;плт;бс;тип) |
предназначена для расчета |
|
КПЕР |
КПЕР(ставка ;плт;пс;бс;тип) |
вычисляет количество |
|
СТАВКА |
СТАВКА(кпер;плт;пс;бс;тип) |
вычисляет процентную |
|
БЗРАСПИС |
БЗРАСПИС (сумма; массив |
удобно использовать для |
|
НОМИНАЛ |
НОМИНАЛ (эф_ставка;кол_пер) |
Возвращает номинальную |
|
ЭФФЕКТ |
ЭФФЕКТ (ном_ставка; |
Возвращает фактическую |
|
ПРПЛТ |
ПРПЛТ(ставка;период;кпер;пс |
Возвращает сумму платежей |
|
ОСПЛТ |
ОСПЛТ(ставка |
Возвращает величину платежа |
|
ОБЩДОХОД |
ОБДОХОД |
Вычисляет сумму основных |
|
ПЛТ |
ПЛТ(ставка;кпер;нз;бс; тип) |
позволяет рассчитать сумму |
|
ЧПС |
ЧПС (ставка;значение 1; |
Возвращает величину чистой |
|
ЧИСТВНДОХ |
ЧИСТВНДОХ |
Возвращает внутреннюю сумму |
|
ЧИСТНЗ |
ЧИСТНЗ |
Возвращает чистую текущую |
|
МСВД |
МСВД |
Возвращает модифицированную |
|
ВСД |
ВСД(значения;предположение) |
Возвращает внутреннюю |
|
АПЛ |
АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации) |
Возвращает величину |
|
АСЧ |
АСЧ(нач_стоимость;ост_стоимость; |
Возвращает величину |
|
ДДОБ |
ДДОБ(нач_стоимость;ост_стоимость;время_эксплуатации;период; |
Возвращает значение |
|
ФУО |
ФУО(нач_стоимость;ост_стоимость; |
Возвращает величину |
Как видно из приведенной таблицы, большинство
финансовых функций имеет одинаковый набор базовых аргументов:
ставка — процентная ставка за период (норма
доходности или цена заемных средств — r)
Например, если получена ссуда на автомобиль под 10
процентов годовых и делаются ежемесячные выплаты, то процентная ставка за месяц
составит 10%/12 или 0,83%. В качестве значения аргумента ставка нужно ввести в
формулу 10%/12 или 0,83% или 0,0083
кпер — срок (число периодов N) проведения операции. Например, если получена ссуда на
4 года под приобретение автомобиля и делаются ежемесячные платежи, то ссуда
имеет 4* 12 (или 48) периодов. В качестве значения аргумента кпер в
формулу нужно ввести число 48.
Плт — выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов. Например,
ежемесячная выплата по четырехгодичному займу в 10 000 руб. под 12 процентов
годовых составит 263,33 руб. В качестве значения аргумента выплата нужно ввести
в формулу число -263,33.
Пс — это приведенная к текущему моменту стоимость
(величина PV) или общая сумма, которая на текущий момент равноценна
ряду будущих платежей. Если аргумент ПС опущен, то он полагается равным
0. В этом случае должно быть указано значение аргумента Плт.;
Бс — требуемое значение будущей стоимости (FV) или остатка средств после последней выплаты. Если
аргумент опущен, он полагается равным 0 (будущая стоимость займа, например,
равна 0). Например, если предполагается накопить 50000 руб. для оплаты
специального проекта в течение 18 лет, то 50 000 руб. это и есть будущая
стоимость
[тип] — число 0 или 1, обозначающее, когда
должна производиться выплата, 1 — начало периода (обычная рента или
пренумерандо), 0 — конец периода (постнумерандо).
1.1
Операции наращения. Функция БС().
Функции, обслуживающие расчеты по операциям наращения
позволяют рассчитать будущую стоимость разовой суммы по простым и сложным
процентам, а также будущее значение потока платежей, как на основе постоянной
процентной ставки, так и на основе переменной процентной ставки.
Функция БС() — будущее значение — рассчитывает
наращенную величину разовой денежной суммы или периодических постоянных
платежей на основе постоянной процентной ставки.
Простые проценты. Для решения задач наращения по схеме
простых процентов функция БС() в качестве аргументов использует только
аргументы: норма; число периодов; ПС.
Остальные аргументы не используются.
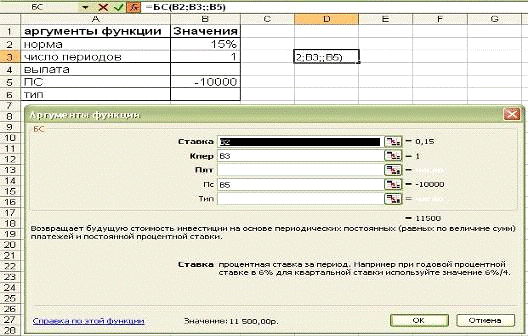
Пример 1-1
Определить наращенную сумму для
вклада в размере 10000 руб., размещенного под 15% годовых на один год.
Рис. 1-4 Решение примера 1-1.
Таким образом, через год наращенная
сумма составит 11500 руб.
В приведенном примере, в качестве аргумента функции Кпер
было указано целое число (1 год).
Если продолжительность финансовой операции
представлена в днях, то необходимо ввести корректировку в процентную ставку,
т.е. аргумент норма должен быть представлен как t/ T *r%.
Если время финансовой операции выражено в днях, то
расчет простых процентов может быть произведен одним из трех возможных
способов:
Обыкновенные проценты с приближенным числом дней
ссуды, или, как часто называют «германская практика расчета», когда
продолжительность года условно принимается за 360 дней, а целого месяца — 30
дней.
1.
Обыкновенные
проценты с точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года условно принимается за 360 дней, а продолжительность
суды рассчитывается точно по календарю.
2.
Точные проценты с
точным числом дней ссуды, или «английская практика расчета», когда
продолжительность года и продолжительность ссуды берутся точно по календарю
Пример 1-2
Вклад размером в 2000 руб. положен с
06.06 по 17.09 невисокосного года под 30% годовых. Найти величину капитала на
17.09 по различной практике начисления процентов.
Решение
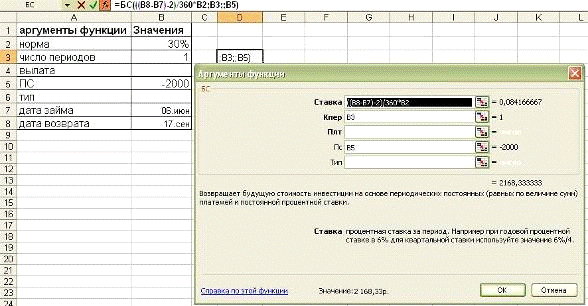
Германская практика расчета
В соответствии с германской практикой
расчета период накопления составляет 101 день.
БС(((В8-В7)-2)/360*В2;ВЗ;;В5) =2168,3
руб.
Рис. 1-5 Решение примера 1-2
(Германская практика расчета).
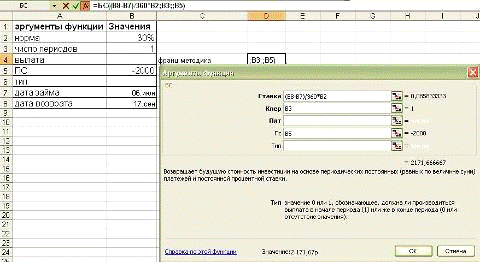
Французская система расчета
В соответствии с германской практикой
расчета период накопления составляет 103 дня.
БС(((В8-В7))/360*В2;ВЗ;;В5) = 2171,7
руб.
Рис. 1-6 Решение примера 1-2
(Французская система расчета).
Таким образом, начисление процентов
по германской практике приведет к получению суммы в размере 2168,33 руб., по
французской практике — 2171,7 руб.
Сложные проценты
При использовании сложных процентов используются те же
аргументы, что и в простых процентах, с использованием годовой процентной
ставки и целого числа лет.
Пример 1-3
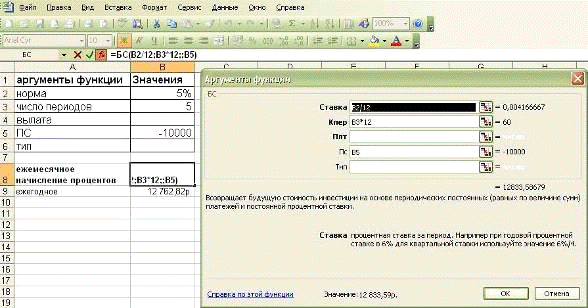
Определить будущую величину вклада в
10000 руб. помещенного в банк на 5 лет под 5% годовых, если начисление
процентов осуществляется:
а) раз в году;
б) раз в месяц.
Решение
Рис. 1-7 Решение примера 1-3 при
ежемесячном начислении процентов
а) 12762,83 руб.
б) 12833,59 руб.
Обратите внимание, что если же период начисления
процентов будет меньше года, то необходимо модифицировать аргументы ставка
и число периодов:
ставка — берется ставка процентов за период
начисления, т.е. используется номинальная годовая ставка процентов,
скорректированная на число раз (т) начисления процентов в течение года r% / т;
число периодов — указывается общее число раз
начисления процентов за весь срок финансовой операции п • т.
1.2
Операции дисконтирования
Для расчета приведенной к конкретному моменту времени
наращенной суммы Excel предлагает
использование встроенной финансовой функции ПС().
Расчет с использованием функции ПС() является
обратным к определению наращенной суммы при помощи функции БС, поэтому
сущность используемых аргументов в этих функциях аналогична. Вместе с тем,
аргумент ПС заменяется на аргумент БС — будущая стоимость или
будущее значение денежной суммы (FV).
Функция ПС() быть использована для расчета по простым
и сложным процентам.
Пример 1-4
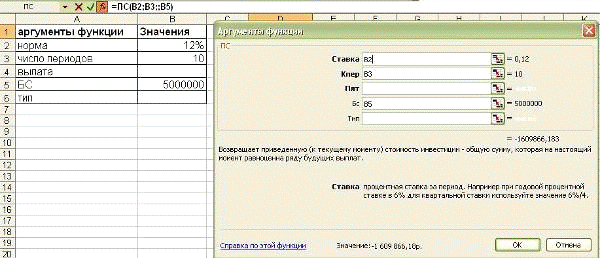
Фирме потребуется 5000 тыс. руб.
через 10 лет. В настоящее время располагает деньгами и готова положить их на
депозит единым вкладом с тем, чтобы через 10 лет получить необходимую сумму.
Определить необходимую сумму текущего вклада
если ставка процента по нему составляет 12% в год.
Решение.
ПС(В2;ВЗ;;В5) = -1609866,18 руб.
Рис. 1-8 Решение примера 1-4
Обратите внимание, что результат получился
отрицательным, так как это сумма, которую фирма должна положить на депозит, с
тем, чтобы через 10 лет получить необходимую сумму.
1.3
Определение срока финансовой операции
Для определения срока финансовой операции используется
функция КПЕР0, которая вычисляет общее число периодов начисления
процентов на основе постоянной процентной ставки. Данная функция используется
как для единого платежа, так и для платежей, распределенных во времени.
Синтаксис КПЕР (норма, выплата, нз, бс, тип).
Пример 1-5
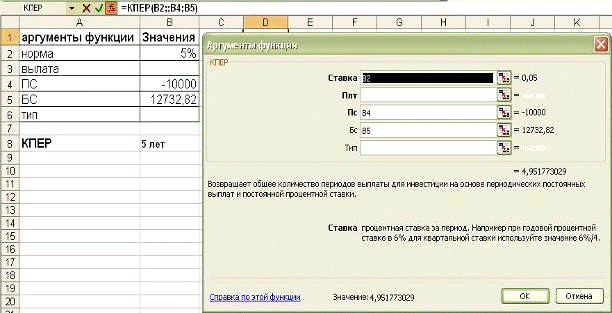
По вкладу в 10000,00, помещенному в
банк под 5% годовых, начисляемых ежегодно, была выплачена сумма 12762,82.
Определить срок проведения операции (количество периодов начисления).
Решение.
КПЕР(В2;;В5;В6) = 5 лет
Следует обратить особое внимание на то, что
результатом применения функции является число периодов (а не число лет),
необходимое для проведения операции.
Если платежи производятся несколько раз в год, то
значение функции означает общее число периодов начисления процентов.
Если необходимо срок платежа выразить в годах, то
полученное значение необходимо разделить на число начислений процентов в году
Рис. 1-9 Решение примера 1-5
Пример 1-6
Через сколько лет вклад размером 500
руб. достигнет величины 1000 руб. при ставке процентов 10% с ежемесячным
начислением процентов?
Решение. КПЕР(10%/12;;-500;1000)
=83,5 мес. =83,5 мес./12мес. = 7 лет.
1.4
Определение процентной ставки
Для определения величины процентной ставки при
известных величинах вложенных и наращенных сумм и количестве периодов
начисления процентов Excel
предлагает использование финансовой функции «Ставка».
Аргументы функции:
ПС — вложенная сумм
БС — наращенная сумма;
Кпер — количество периодов начисления
процентов.
Пример 1-7
Фирме через 2 года потребуется 100000
руб. Для достижения этой цели фирма готова положить на депозит 25000 руб. Каким
должен быть процент на инвестированные средства с тем, чтобы к концу второго
года была получена необходимая сумма?
Решение
СТАВКА(2*12;;-25000;100000)=6%
1.5 Расчет
эффективной и номинальной ставки процентов
Для расчета эффективной и номинальной ставки процентов
Excel предлагает использование функций ЭФФЕКТ()
и НОМИНАЛ().
Функция ЭФФЕКТ()
Функция вычисляет действующие (эффективные) ежегодные
процентные ставки, если задана номинальная годовая процентная ставка и
количество периодов начисления в году.
Синтаксис ЭФФЕКТ (номинальная ставка, кол_пер).
Пример 1-8
Номинальная ставка составляет 11%. Рассчитайте
эффективную процентную ставку при следующих вариантах начисления процентов:
полугодовом; квартальном; ежемесячном.
Решение
ЭФФЕКТ =
11,3% — при полугодовом начислении
процентов
,46% — при квартальном начислении
процентов
,57% — при ежемесячном начислении
процентов
Функция НОМИНАЛ()
Функция вычисляет номинальную годовую процентную
ставку, если известны эффективная ставка и число периодов начисления в год.
Синтаксис НОМИНАЛ (эффект_ставка, кол_пер).
Пример 1-9
Эффективная ставка составляет 28%, а
начисление процентов производится ежемесячно. Необходимо рассчитать номинальную
ставку
Решение: Номинальная ежемесячная процентная
ставка будет равна:
НОМИНАЛ (28%,12) = 0,2494 или 29,14%
1.6
Начисление процентов по плавающей ставке
Для расчета будущей величины разовой инвестиции в
случае, если начисление процентов осуществляется по плавающей ставке используется
функция БЗРАСПИС(). Подобные операции широко распространены в
отечественной финансовой и банковской практике. В частности, доходы по
облигациям государственного сберегательного займа (ОГСЗ), начисляются раз в
квартал по плавающей купонной ставке
Пример 1-10
Ставка банка по срочным валютным
депозитам на начало года составляет 20% годовых, начисляемых раз в квартал.
Первоначальная сумма вклада — $1000. В течении года ожидается снижение ставок
раз в квартал на 2, 3 и 5 процентов соответственно. Определить величину
депозита к концу года
Решение
Введем ожидаемые значения процентных
ставок в блок ячеек электронной таблицы, например: 20%/4 в ячейку В2, 18%/4 в
ячейку ВЗ, 17%/4 в ячейку В4 и 15%/4 в ячейку В5. Тогда функция будет иметь
следующий вид: =БЗРАСПИС(1000; С2:С5) = 1166,86$
Раздел
2. Потоки платежей и финансовые ренты
Проведение практически любой финансовой операции порождает движение
денежных средств. Такое движение может характеризоваться возникновением
отдельных платежей, или множеством выплат и поступлений, распределенных во
времени. В финансовой практике широко распространены контракты, предусматривающие
не разовое, а систематическое движение средств — выплаты/поступления по
заданному графику происходят регулярно.
В процессе количественного анализа финансовых операций, удобно
абстрагироваться от их конкретного экономического содержания и рассматривать
порождаемые ими движения денежных средств как численный ряд, состоящий из
последовательности распределенных во времени платежей CF1, CF2, …, CFn. Для
обозначения подобного ряда в мировой практике широко используется термин
«поток платежей» или «денежный поток» {cashflow — CF).
Каждый отдельный элемент такого численного ряда CF представляет собой разность между
всеми поступлениями (притоками) денежных средств и их расходованием (оттоками)
на конкретном временном отрезке проведения финансовой операции. Таким образом,
величина CFt может иметь как положительный, так и
отрицательный знак.
Количественный анализ денежных потоков, генерируемых
за определенный период времени в результате реализации финансовой операции, или
функционирования каких-либо активов, в общем случае сводится к исчислению
следующих характеристик:
— будущей стоимости потока за п периодов;
— современной стоимости потока за я периодов.
Часто возникает необходимость определения и ряда
других параметров финансовых операций, важнейшими из которых являются:
— величина потока платежей в периоде t;
r
— процентная ставка;
п
— срок (количество периодов)
проведения операции.
Поток платежей, все члены которого имеют одинаковое
направление (знак), а временные интервалы между последовательными платежами
постоянны, называется финансовой рентой или аннуитетом (англ.
annuity).
При рассмотрении финансовой ренты используются
основные категории:
член ренты (CFt) — величина каждого отдельного платежа;
период ренты (t) — временной интервал между членами ренты;
срок ренты (n) — время от начала финансовой ренты до конца последнего
ее периода;
процентная ставка (r) — ставка, используемая при наращении платежей, из которых
состоит рента.
В отличие от разовых платежей, рассмотренных
нами в предыдущем разделе, для количественного анализа аннуитетов нам
понадобятся все выделенные ранее характеристики денежных потоков: FV, PV, CF, r и n
( и соответственно, все аргументы рассмотренных ранее финансовых функций Excel, (функции: БС(); IIC(); КПЕР(); СТАВКА(); ПЛТ();
БЗРАСПИС(); НОМИНАЛ(); ЭФФЕКТ()) и др.)
2.1 Определение будущей (наращенной стоимости
потока платежей. Функция БС()
Наращенная сумма — сумма всех платежей с начисленными
на них процентами к концу срока ренты. Это может быть обобщенная сумма
задолженности, итоговый объем инвестиций и т.п.
Пример 2-1
На счет в банке в течении пяти лет в
конце каждого года будут вноситься суммы в размере 500 руб., на которые будут
начисляться проценты по ставке 30%. Определить сумму, которую банк выплатит
владельцу счета.
Решение:
БС(30%;5;-500;;0)=4521,55
сумма всех взносов с начисленными
процентами будет равна 4521,55 руб.
Пример 2-2
Предположим, что каждый год ежемесячно
в банк помещается сумма в 1000. Ставка равна 12% годовых, начисляемых в конце
каждого месяца. Какова будет величина вклада к концу 4-го года?
Общее количество платежей за 4 года
равно: 4* 12 = 48. Ежемесячная процентная ставка составит: 12% /12 = 1%.
Решение:
БС(12%/12;4*12;-1000)= 61222,61
2.2 Современная (текущая) величина
аннуитета. Функция ПС()
Современная (текущая) величина потока
платежей (капитализированная
или приведенная величина) — это сумма платежей, дисконтированных на момент
начала ренты по ставке начисляемых сложных процентов.
Пример 2-3
Предположим, что мы хотим получать
доход, равный $1000 в год, на протяжении 4-х лет. Какая сумма обеспечит
получение такого дохода, если ставка по срочным депозитам равна 10% годовых?
Решение.
PV = 1000*(1-(1+10%)-4)/10%= 3169,87.
При использовании финансовой функции Excel
=ПС(10%;4;-1000)=3169,87
Таким образом, для получения в течение четырех лет
ежегодного дохода в $1000 необходимо сегодня положить в банк $3169,87.
Пример 2-4
Рассматриваются два варианта
приобретения дома стоимостью 100 мл. руб.:
А) единовременный платеж.
Б) ежемесячно в течение 15 лет
вносить в банк по 1 млн., руб.
Определить какой из вариантов
приобретения дома предпочтительнее, если ставка процента — 8% годовых, а
проценты начисляются ежемесячно?
Решение.
Для ответа на поставленный вопрос нам
необходимо сравнить, что выгоднее: заплатить сегодня всю суммы полностью или
растянуть платежи на 15 лет.
Для сравнения необходимо привести эти
денежные потоки к одному периоду времени, т.е. рассчитать текущую стоимость
будущих фиксированных периодических выплат.
Таким образом, текущая стоимость
будущих периодических платежей больше запрашиваемой стоимости дома (104,64 млн.
руб. > 100 млн. руб.), следовательно, выгоднее покупать дом сразу.
2.3 Расчет периодических платежей
Функции Excel
помимо расчета наращенной и приведенной стоимости позволяют выполнить основные
расчеты, связанные с оценкой периодических платежей:
) периодические постоянные по величине платежи,
осуществляемые на основе постоянной процентной ставки (функция ПЛТ);
2) платежи по процентам за конкретный период (функция ПРПЛТ);
3) сумму платежей по процентам за несколько периодов,
идущих подряд друг за другом (функция ОБЩПЛАТ);
4) основные платежи по займу (за вычетом процентов) за
конкретный период (функция ОСПЛТ);
) сумму основных платежей за несколько периодов,
идущих подряд (функция ОБЩДОХОД).
Наиболее часто все эти величины используются при
составлении плана (схемы) равномерного погашения займа. Если заем погашается
равными платежами в конце (начале) каждого периода, то будущая стоимость этих
платежей ( при его полном погашении) будет равна сумме займа с начисленными
процентами к концу последнего расчетного периода. В тоже время текущая
стоимость выплат по займу должна быть равна настоящей сумме займа.
Если известна величина займа, срок на который он был
выдан и процентная ставка, то можно легко, используя функцию ПЛТ, определить
величину периодических платежей, необходимых для равномерного погашения займа.
Вычисленные платежи включают в себя сумму процентов по
непогашенной части займа и основную выплату по нему. Эти величины зависят от
номера периода и могут быть рассчитаны с помощью функций ПРПЛТ, ОСПЛАТ. Накопленные
суммы могут быть определены с помощью функций ОБЩПЛАТ и ОБЩДОХОД.
2.3.1
Определение величины периодического платежа. Функция ПЛТ().
Функция вычисляет величину выплаты за один период на
основе фиксированных периодических выплат и постоянной процентной ставки.
Выплаты, рассчитанные функцией ПЛТ, включают основные платежи и платежи по
процентам.
Синтаксис ПЛТ (норма, кпер, нз, бс, тип).
Функция ПЛТ применяется в следующих расчетах.
1.
Допустим,
известна будущая стоимость фиксированных периодических выплат, производимых в
начале или в конце каждого расчетного периода. Требуется рассчитать размер этих
выплат.
Соответствующая запись в EXCEL имеет вид:
ПЛТ (норма, кпер,, бс, тип).
2.
Предположим,
рассчитываются равные периодические платежи по займу величиной нз, необходимые
для полного погашения этого займа через кпер число периодов. Текущая
стоимость этих выплат должна равняться текущей сумме займе.
Соответствующий расчет в EXCEL выполняется по формуле:
ПЛТ (норма, кпер, нз, ,тип).
Пример 2-6
Предположим, что необходимо накопить
4000 руб. за 3 года, откладывая постоянную сумму в конце каждого месяца. Какой
должна быть эта сумма, если норма процента по вкладу составляет 12% годовых.
Решение.
Определим общее число периодов
начисления процентов и ставку процента за период по таблице 2. Эти величины
составят соответственно 3*12 (аргумент кпер) и 12%/12 (аргумент норма).
Аргумент тип = 0, т.к. по условию это вклады постнумерандо. Рассчитаем величину
ежемесячных выплат: ПЛТ(12%/12,12-3„4000) = -92,86 руб.
Пример 2-7
Допустим, банк выдал ссуду 200 тыс.
руб. на 4 года под 18% годовых. Ссуда выдана в начале года, а погашение
начинается в конце года одинаковыми платежами. Определите размер ежегодного
погашения ссуды.
Решение
Ежегодные платежи составят
ПЛТ (18%,4,200000,,) = -74,3 тыс.
руб.
2.3.2
Расчет платежей по процентам. Функция ПРПЛТ
Функция
позволят определить сумму платежей процентов по инвестиции за данный период на
основе постоянства сумм периодических платежей и постоянства процентной ставки.
Синтаксис
ПРПЛТ (норма, период, кпер, пс,
бс, тип).
Функция
предназначена для следующих расчетов.
1.
При равномерном
погашении займа постоянная периодическая выплата включает в себя платежи по
процентам по непогашенной части займа и выплату задолженности. Так как
непогашенная часть займа уменьшается по мерс его погашения, то уменьшается и
доля платежей по процентам в общей сумме выплаты, и увеличивается доля выплаты
задолженности. Чтобы найти размер платежа по процентам на конкретный период,
следует использовать формулу:
ПРПЛТ (норма, период, кпер, пс), если погашение займа производится равными
платежами в конце каждого расчетного периода.
2.
Допустим,
необходимо вычислить доход, который приносят постоянные периодические выплаты
за конкретный период. Этот доход представляет собой сумму процентов,
начисленных на накопленную (с процентами) к данному моменту совокупную величину
вложений. Расчет ведется по формуле:
ПРПЛТ (норма, период, кпер,, бс, тип).
Пример 2-8
Необходимо определить величину
платежей по процентам за первый месяц трехгодичного займа в 800тыс.руб. Ставка
банка 10%.
Решение.
ПРПЛТ(10%/12;1;3*12;-800) = 6666,67
руб.
·
В поле «Ставка»
диалогового окна заносится величина месячной процентной ставки;
·
в поле «Период»
заносится номер периода для которого мы хотим определить величину платежей
по процентам;
·
в поле
«Кпер»заносится количество периодов начисления процентов ( в нашем примере
3*12);
·
в поле «Пс»
заносится величина займа.
После нажатия кнопки «ОК» мы получим, что платежи по
процентам за первый месяц составили -6666,67 руб.
За счет ежегодных отчислений в течении
6 лет был создан фонд в 5 млн. руб. Необходимо определить какой доход принесли
вложения за последний год, если ставка банка составляла 12%
Решение
Доход за последний год (6 период)
составил:
ПРПЛТ(12%;6;6;;5) =0,469 млн. руб.
.3.3 Расчет суммы платежей по
процентам по займу
Функция
ОБШПЛАТ
Функция
позволяет вычислить накопленный доход (сумму платежей по процентам) по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами выплат.
Синтаксис
функции: ОБЩПЛАТ
(ставка;
Кол_пер; Нз ; нач_период; кон_период;тип)
Пример
2-10
Для
приобретения недвижимости была взята ссуда 12000 тыс. руб. Условия ссуды:
Процентная
ставка — 9%;
Срок
— 25 лет
Проценты
начисляются ежемесячно
Необходимо
найти сумму выплат за 2-й год и за 1 -й месяц займа
Решение
В диалоговом окне функции ОБЩПЛАТ() :
·
В строке «Ставка» заносится
величина процентной ставки, начислямой за период (9%/12);
·
в строке «Кол_пер»
записывается количество периодов начисления платежей (25*12);
·
в строке «Нз»
записывается величина займа;
·
в строках «Нач_период»
и «Кон_период» записываются начальный и конечный периоды, для
которых вычисляется сумма выплат по процентам (13 и 24), соответственно;
После щелчка на кнопке «ОК» будет
рассчитана сумма платежей по процентам за второй год:
=ОБЩПЛАТ(9%/12;25*12;12000;13;24;0)
=-1062 тыс. руб.
Аналогичным образом может быть
вычислена сумма выплат по
процентам за первый месяц займа:
=ОБЩПЛАТ(9%/12;25*1;12000;1;1;0)= -90
тыс. руб.
2.3.4
Расчет величины основных платежей по займу. Функция ОСПЛT
Функция позволяет вычислить величину основного платежа
(выплаты) по займу, который погашается равными платежами в конце или начале
расчетного периода, на расчетный период.
Пример 2-11
Была взята ссуда в размере 70000тыс. руб. сроком на 3
года под 17% годовых. Необходимо рассчитать величины основных платежей для
каждого года займа.
Решение
Напомним, что сумма основного платежа по займу
получается как разность между фиксированной периодической выплатой и процентами
по непогашенной части долга.
Размер основных выплат по займу, определяемый с
помощью функции ОСПЛТ может быть определен как:
|
Период |
Формула |
Основной платеж |
|
1-й год |
=ОСПЛТ(17%;1;3;70000) |
-19 780.16р. |
|
2-й год |
=ОСПЛТ(17%;2;3;70000) |
-23 142.78р. |
|
3-й год |
ОСПЛТ(17%;3;3;70000) |
-27 077.06р. |
|
ИТОГО |
-70 000.00р. |
2.3.5 Расчет суммы основных платежей
по займу. Функция ОБЩДОХОД
Функция позволяет вычислить сумму основных платежей по
займу, который погашается равными платежами в конце или начале каждого
расчетного периода, между двумя периодами.
Пример 2-12
Выдана ссуда в размере 1000 тыс. руб.
сроком на 6 лет под 15% годовых, начисляемых ежеквартально. Определить величину
основных выплат за 5-й год.
Решение
Периоды платежей за 5-й год будут
иметь номера 17 и 20, соответственно. Так как ссуда погашается равными
платежами в конце каждого периода (квартала), то размер выплаты за пятый год
составит:
=ОБЩДОХОД(15%/4;6*4;1000;17;20;0)=201,43
тыс. руб.
Раздел
3. Оценка инвестиционных процессов
Инвестиции — это долгосрочные финансовые
вложения экономических ресурсов с целью создания и получения выгоды в будущем,
которая должна быть выше начальной величины вложений.
Инвестиционный процесс — это последовательность связанных
инвестиций, растянутых во времени, отдача от которых также распределена во
времени. Этот процесс характеризуется двусторонним потоком платежей, где
отрицательные члены потока являются вложениями денежных средств в
инвестиционный проект, а положительные члены потока — доходы от инвестированных
средств.
Методы измерения доходности инвестиционных проектов
основаны на анализе равномерного денежного потока. Ожидаемые значения
элементов денежного потока, соответствующие будущим периодам, являются
результатом сальдирования всех статей доходов и расходов, связанных с
осуществлением проекта.
Для приведения значений элементов денежного потока к
сопоставимому во времени виду по выбранной норме дисконтирования оценивается
суммарная текущая стоимость на момент принятия решения о вложении капитала,
предшествующий началу движения средств. Уровень процентной ставки, применяемой
в качестве нормы дисконтирования, должен соответствовать длине периода,
разделяющего элементы денежного потока.
В качестве показателей эффективности инвестиционных
проектов обычно используются:
·
чистый
приведенный доход —
текущая стоимость всех доходов и расходов по проекту;
·
срок
окупаемости —
характеризует срок окупаемости средств, вложенных (инвестированных) в проект;
·
внутренняя
норма доходности —
это ставка дисконтирования, приравнивающая сумму приведенных доходов от
инвестиционного проекта к величине инвестиций, т.е. вложения окупаются, но не
приносят прибыль.
3.1 Чистый приведенный доход. Функция
ЧПС
При оценке инвестиционных проектов используется метод
расчета чистого приведенного дохода, который предусматривает
дисконтирование денежных потоков: все доходы и затраты приводятся к одному
моменту времени.
Центральным показателем в рассматриваемом методе
является показатель NPV (net present value) — текущая стоимость денежных потоков за вычетом
текущей стоимости денежных оттоков. Это обобщенный конечный результат
инвестиционной деятельности в абсолютном измерении.
Показатель NPV характеризует абсолютный прирост, поскольку оценивает,
на сколько приведенный доход перекрывает приведенные затраты:
·
при NPV > 0 проект может быть принят;
·
при NPV < 0 проект не принимается,
·
при NPV= 0 проект не имеет ни прибыли, ни убытков
Пример 3-1
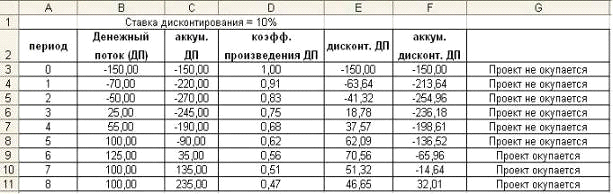
Найти чистый дисконтированный доход
проекта, требующего стартовых инвестиций в объеме 150 тыс. руб., денежный поток
которого задан рис.6-1, по ставке дисконтирования 10% годовых.
Решение
На листе Excel создадим таблицу, подобную
приведенной на Рис. 3-1.
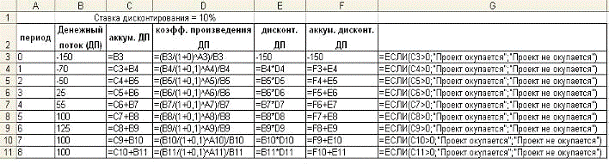
Рис. 3-1. Фрагмент рабочего листа MS Excel с вычислением величины чистого
дисконтированного потока
Рис. 3-2 Фрагмент рабочего листа MS Excel в режиме отображения формул с
вычислением величины чистого дисконтированного потока
В ячейках столбца:
·
«А»
размещены периоды поступления (оттока) денежных средств;
·
«В»
размещаются величины денежных потоков в соответствующие периоды;
·
«С»
размещены аккумулированные значения денежных потоков в данном периоде.
Например, в ячейке «С4» может быть записано: =СЗ+В4;
·
«D» размещаются формулы расчета величины
коэффициента дисконтирования денежных потоков. Например, в ячейке «D3» записывается: =(ВЗ/(1+0,1)^А3)/ВЗ;
в ячейке «D4» записывается: =(В4/(1+0,1)^А4)/В4 и т.д.;
^ — обозначение возведения в степень
·
«Е»
значения дисконтированных денежных потоков. Например, в ячейке «Е4»
записывается: =B4*D4
·
«F» записываются формулы расчеты
аккумулированных дисконтированных денежных потоков в соответствующий период
времени. Например, в ячейке «F3» записывается величина
денежного потока в начальный период (начальные инвестиции): =D3; в ячейке «F4» записывается: =F3+E4 и т.д.
·
«G» записывается логическая функция
анализа окупаемости проекта. Например, в ячейке «G3» записывается формула: =ЕСЛИ(СЗ>0;
«Проект окупается»;»Проект не окупается»), которая
копируется в ячейки G4:G11 таблицы.
Таким образом, в результате
выполненных вычислений получаем:
Чистый дисконтированный доход = 32,01
Дисконтированный доход =
-(-150)+32,01 = 182,01
Готовый результат 182,01 в
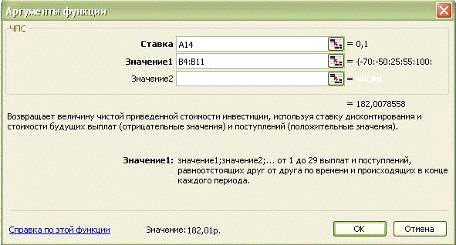
одной клетке дает табличная формула =NPV(10%;B4:B11), вызывающая специальную финансовую
функцию со ссылкой на норму дисконтирования («Ставка») и табличные
координаты блока значений («Значения1».,..)элементов денежного
потока, расположенных в хронологическом порядке.
В русских версиях MS Excel функция NPV имеет название ЧПС.
Рис. 3-4. Диалоговое окно функции ЧПС
Пояснения.
Функция ЧПС() возвращает величину чистой приведенной
стоимости инвестиции, используя ставку дисконтирования, а также стоимости
будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис функции: ЧПС(ставка;значение1;значение2;…)
Ставка — ставка дисконтирования за один период.
Значение1, значение2,… — от 1 до 29 аргументов,
представляющих расходы и доходы.
Значение1, значение2,… должны быть равномерно
распределены во времени, выплаты должны осуществляться в конце каждого периода.
Значение1, значение2,… могут вводится либо в
отдельные окна либо списком (при этом, порядок ввода значений (либо значений в
списке) определяется порядком поступлений и платежей)
Для вычисления чистого дисконтированного дохода к
выражению =NPV(10%;C4:C11) необходимо добавить отрицательную величину инвестиционных
затрат нулевого периода, записанное в таблице в ячейке ВЗ=ЧПС(10%;В4:В11)+В3 =
32,01
Метод определения чистой текущей
стоимости часто используется при оценке эффективности инвестиций. Он позволяет
определить нижнюю границу прибыльности и использовать ее в качестве критерия
при выборе наиболее эффективного проекта.
Положительное значение NPV является показателем того, что
проект приносит чистую прибыль, после покрытия всех связанных с ним расходов
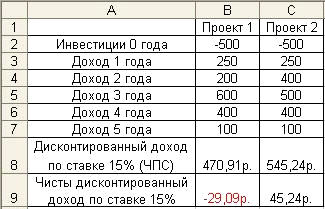
Пример 3-2
Сравним два проекта, денежные потоки
которых представлены на рис. 3-5 , при значениях ставки дисконтирования 15%
Рис. 3-5 Исходные данные и решение
Примера 3-2
В ячейках «В9» и «С9» вычисляется
значения чистого дисконтированного дохода для Проектов 1 и 2.
Выполненные расчеты показывают целесообразность
принятия Проекта 2, не смотря на то, что величины денежных потоков обоих
проектов различаются несущественно
3.2
Срок окупаемости
Для анализа эффективности инвестиций часто
используется такой показатель, как срок окупаемости — продолжительность
времени, в течение которого дисконтированные на момент завершения инвестиций
прогнозируемые денежные поступления равны сумме инвестиций. Иными словами — это
количество лет, необходимых для компенсации стартовых инвестиций.
Пример 3-3
Рассчитать срок окупаемости проекта,
для которого размер инвестиций составляет 1 млн. руб., а денежные поступления в
течение 5 лет будут составлять: 250; 400; 800; 900; 900 тыс. руб.
соответственно. Ставка дисконтирования 15%.
Решение.
На листе Excel создадим таблицу, подобную
приведенной на рис.3-7
Рис. 3-7. Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-3
Рис. 3-8. Фрагмент рабочего листа Excel в режиме отображения формул
исходными данными и решением примера 3-3
В ячейках:
·
CI :G1 размещены номера периодов
поступления денежных средств;
·
C2:G2 размещены величины поступления
денежных средств;
·
C3:G3 размещены формулы дисконтирования
поступающих денежных средств. Например, в ячейке СЗ записана формула
=С2/((1+15%)^С1),
соответствующая левой части формулы 6-3;
·
C4:G4 записаны формулы вычисления
накопленного в данный период дисконтированного денежного потока. Например, в
ячейке С4 записана формула =В4+С3 (сумма величины инвестиции и
поступивших в этот период (1) денежных средств), а в ячейке D4 записывается формула =C4+D3 (сумма величины накопленного
дисконтированного потока и поступивших в этот период (2) денежных средств) и
т.д.
Анализируя построенную таблицу легко
видеть, что инвестиции полностью окупаются в интервале между 2 и 3 периодами.
Следовательно, период окупаемости может быть найден как:
=Dl+(-D4/E3) =2+480,15/526,01 =2,91 года
Таким образом, период, реально
необходимый для возмещения инвестированной сумы, составит 2,91 года или 2 года
и 332 дня.
Период окупаемости может быть также
определен, если в ячейку С5 записать формулу: =ЕСЛИ(С4>0;С1-(В4+С3)/С3;0)
и скопировать ее в остальные ячейки строки.
3.3
Индекс рентабельности
Индекс рентабельности (PI) показывает, сколько единиц современной величины
денежного потока приходится на единицу предполагаемых первоначальных затрат.
Если величина критерия РI> 1, то современная стоимость денежного
потока проекта превышает первоначальные инвестиции, обеспечивая тем самым
наличие положительной величины NPV. При
этом норма рентабельности превышает заданную и проект следует принять.
При РI=1 величина NPV= 0 и инвестиции не приносят дохода.
В случае, если PI < 1, проект не обеспечивает заданного
уровня рентабельности и его следует отклонить
Пример 3-4
Фирма рассматривает возможность
участия в финансировании шести проектов, предполагаемые условия реализации
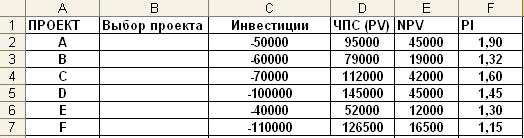
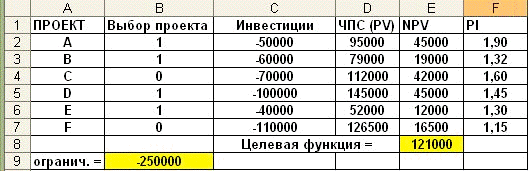
которых приведены в таблице рис. 3-8. Инвестиционный бюджет фирмы равен 250000.
Рис. 3-9 Фрагмент рабочего листа Excel с исходными данными и решением
примера 3-4
Как следует из таблицы (столбец
«Е»), чистая приведенная стоимость всех проектов (NPV) больше нуля, а индекс
рентабельность (PI) больше 1. И, если бы инвестиционный бюджет фирмы не был ограничен
суммой в 250000 то все проекты следовало бы принять. Однако из-за
ограниченности бюджета может быть реализован только тот набор (портфель)
проектов, при котором суммарные инвестиции не превышают 250000.
Для выбора наиболее привлекательных
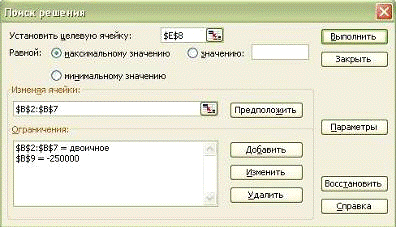
проектов воспользуемся операцией «Поиск решения».
В ячейке «Е8″запишем целевую
функцию: =СУММПРОИЗВ(В2:В7;Е2:Е7);
Примечание: в ячейках столбца «В»
размещаются результаты выбора проекта: «1» -проект выбран;
«0» — проект отклонен.
в ячейке «В9» запишем
формулу ограничений:
=СУММПРОИЗВ(В2:В7;С2:С7);
в диалоговом окне «Поиск
решения» выполним необходимые установки:
Рис. 3-10 Диалоговое окно «Поиск
решения»
В результате выполнения процедуры «Поиск
решения» оказывается оптимальным инвестирование четырех
проектов:»А», «И», «D» и «Е», при этом
суммарная величина NPV составит 121000 (см. рис. 3-11)
Рис. 3-11 Выбор проектов для инвестирования
3.4
Внутренняя норма доходности. Функция ЧИСТВНДОХ
Под внутренней нормой доходности понимают процентную
ставку, при которой чистая современная стоимость инвестиционного проекта равна
нулю.
Функция ЧИСТВНДОХ возвращает внутреннюю сумму дохода
для расписания денежных поступлений
Пример 3-5
Фирма намерена 1 января 2005 г.
инвестировать 200 млн. руб. в проект, ожидаемые доходы по которому в
последующие 5 лет составят 40, 60, 80, 90 и 100 млн. руб.
Определите внутреннюю норму дохода по проекту,
если поступление доходов будет производится 1 января каждого года
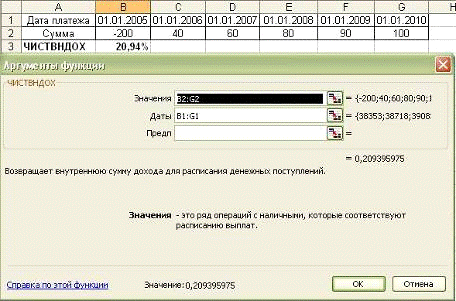
Решение
Рис.3-12 Решение примера 3-5
Таким образом, при рыночной ставке дисконта менее 20,94%
инвестирование проекта — целесообразно.
3.5 Модифицированная внутренняя норма доходности.
Функция МСВД
Функция возвращает модифицированную внутреннюю
скорость оборота средств для ряда периодических поступлений и выплат переменной
величины.
При этом учитывается как стоимость инвестиции, так и
доход, получаемый от реинвестирования.
Синтаксис МВСД (значения, финансовая норма,
реинвест_норма).
Значения — это массив или ссылка на ячейки,
содержащие числовые величины. Эти числа представляют ряд денежных выплат
(отрицательные значения) и поступлений (положительные значения), происходящие в
регулярные периоды времени.
Аргумент значения должен содержать по крайней мере
одно положительное и одно отрицательное значение для того, чтобы можно было
вычислить модифицированную внутреннюю скорость оборота. В противном случае
функция МВСД возвращает значение ошибки #ДЕЛУ0!.
Если аргумент, который является массивом или ссылкой,
содержит тексты, логические значения или пустые ячейки, то такие значения
игнорируются; однако, ячейки, которые содержат нулевые значения, учитываются.
Финансовая норма — это норма прибыли, выплачиваемой за
деньги, находящиеся в наличном обороте.
Реинвест_норма — это норма прибыли, получаемой за
деньги, находящиеся в наличном обороте при реинвестировании.
Замечания
МВСД использует порядок расположения чисел в аргументе
значения для определения порядка выплат и поступлений. Убедитесь, что значения
выплат и поступлений введены в нужной последовательности и с правильными
знаками (положительные зна чения для получаемых денег и отрицательные значения
для выплачиваемых).
Пример 3-6
Предположим, что Вы занимаетесь
рыболовным промыслом и только что завершили пятый год работы. Пять лет назад вы
взяли 120 000 руб. под 10 процентов годовых для покупки лодки.
Ваши годовые уловы принесли прибыль в
39 000 руб., 30 000 руб., 21 000 руб., 37 000 руб. и 46 000 руб.
соответственно. За эти годы Вы реинвестировали получаемую прибыль под 12%
процентов годовых. Пусть на рабочем листе Ваш заем введен как -120 000 в ячейку
В1 и в ячейки В2:В6 введены значения Вашей прибыли за каждый год.
Решение
Тогда модифицированная внутренняя
скорость оборота за пять лет вычисляется следующим образом:
МВСД(В1:В6; 10%; 12%) равняется 12,61
процентам
Модифицированная внутренняя скорость
оборота за три года вычисляется следующим образом:
МВСД(В1 :В4; 10%; 12%) равняется
-4,80 процентам
Модифицированная внутренняя скорость
оборота за пять лет, если значение аргумента реинвест_норма равно 14%,
вычисляется следующим образом:
МВСД(В1:В6; 10%; 14%) равняется 13,48
процентам
Примеры 3-7
Предположим, пять лет назад была взята ссуда в размере 1 млн.
руб. под 10% годовых для финансирования проекта, прибыль по которому за эти
годы составила: 100, 270, 450, 340 и 300 тыс. руб. Эти деньги были
реинвестированы под 12% годовых. Найти модифицированную внутреннюю скорость
оборота инвестиции.
Решение
Пусть на рабочем листе заем введен
как -1000 в ячейку В1, и в ячейки В2.В6 введены значения прибыли за каждый год.
Тогда модифицированная внутренняя скорость оборота за пять лет вычисляется
следующим образом:
МВСД(В1:В6,10%,12%)= 12.25%.
Модифицированная внутренняя скорость
оборота за пять лет, если бы ставка реинвестирования составляла 14%,
вычисляется следующим образом:
МВСД(В1:В6,10%14%)= 12.99%.
3.6 Денежный поток инвестиционного проекта с произвольными периодами
поступления платежей
Функции ЧИСТНЗ
В том случае, если поступления (оттоки) денежных
средств происходят в произвольные периоды времени), то для расчета величины
чистого дисконтированного дохода может быть использована функция Excel ЧИСТНЗ
|
Ставка |
это ставка |
|
Значения |
это ряд денежных потоков, |
|
Даты |
это расписание дат |
Пример 3-7
июля 2003 года была сделана инвестиция в проект
в размере 10000 тыс. рублей
В результате реализации проекта
ожидается получение прибыли: 15 сентября 200: — 2750 тыс. руб.; 1 ноября 2003г.
-4250 тыс. руб. и 1 января 2004г. — 5250 тыс. руб.
Норма дисконтирования 9%
Необходимо определить чистую текущую
стоимость инвестиции на 1 июля 2003 на 1 июля 2002г
Решение.
На листе Excel создайте таблицу, подобную
приведенной на рисунке.
Рис. 3-13 Исходные данные примера
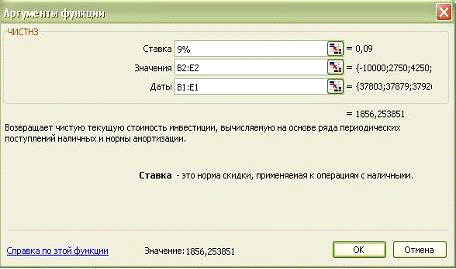
Вызовите функцию ЧИСТНЗ, расположенную
в категории функций «Финансовые» и введите в диалоговое окно этой функции
необходимые аргументы:
Рис. 3-13 Диалоговое окно Функции ЧИСТНЗ
Чистая текущая стоимость инвестиции
на 1 июля 2003 составит = 1856,25 тыс. руб.
на 1 июля 2002 = 1702,98 тыс. руб.,
при этом формула будет иметь вид: =ЧИСТНЗ(9%;А2:Е2;А1:Е1).
Раздел 4. Функции Excel для расчета
амортизации
Группа функций для расчета амортизации основных фондов позволяет
рассчитать амортизационные отчисления следующими методами:
) равномерным, функция АПЛ;
) суммы чисел (лет), функция АСЧ;
) фиксированного уменьшения остатка с использ. функции ФУО;
) уменьшающегося остатка или двойного процента, функция ДДОБ.
Аргументы функций Excel для расчета амортизации
|
Аргумент |
Значение аргумента |
|
без_переключения |
Логическое значение, |
|
время_ амортизации |
Срок эксплуатации имущества |
|
время_полн_аморт |
|
|
время_эксплуатации |
|
|
кон_период |
Конечный период для |
|
коэффициент |
Коэффициент ускоренной |
|
месяц |
Число месяцев в первом году |
|
нач_период |
Начальный период для |
|
остаточная_ стоимость |
Остаточная стоимость |
|
ост_стоим |
|
|
ликвидная_стоимость |
|
|
период |
Период, для которого |
|
стоимость |
Первоначальная стоимость |
|
ликв_стоимость |
Пример 3-1.
Определить величину ежегодной амортизации оборудования
начальной стоимостью 400 тыс. руб., если срок эксплуатации оборудования 10 лет,
остаточная стоимость 250 тыс. руб., используя различные методы расчета и
функции Excel. Результаты представить в виде табл. 2.
Таблица 5. Расчет амортизации различными методами.
|
год |
АПЛ |
АСЧ |
ФУО |
ДДОБ |
|
1 |
375,00 |
681,82 |
968,00 |
800,00 |
|
2 |
375,00 |
613,64 |
733,74 |
640,00 |
|
3 |
375,00 |
545,45 |
556,18 |
512,00 |
|
4 |
375,00 |
477,27 |
421,58 |
409,60 |
|
5 |
375,00 |
409,09 |
319,56 |
327,68 |
|
6 |
375,00 |
340,91 |
242,23 |
262,14 |
|
7 |
375,00 |
272,73 |
183,61 |
209,72 |
|
8 |
375,00 |
204,55 |
139,17 |
167,77 |
|
9 |
375,00 |
136,36 |
105,49 |
134,22 |
|
10 |
375,00 |
68,18 |
79,96 |
107,37 |
|
итого |
3750,0 |
3750,0 |
3749,5 |
3570,5 |
Функция AПЛ
Функция АПЛ вычисляет амортизацию имущества за один
период равномерным методом. При использовании равномерного метода для каждого
периода величина амортизационных отчислений одинакова, а совокупная величина
отчислений к концу последнего периода равна стоимости амортизируемого
имущества.
Синтаксис AПЛ (нач_стоимость, остат_стоимость,
время_эксплуатации).
При равномерном методе расчета за
каждый год амортизация составит:
АПЛ(4000,250,10) = 375 тыс. руб.
Функция АСЧ
Функция АМГД позволяет рассчитать амортизационные
отчисления за заданный период методом суммы чисел. Этот метод характеризуется
постоянным понижением амортизационных отчислений и обеспечивает полное
возмещение амортизируемой стоимости имущества.
Синтаксис АСЧ (нач_стоимость, ост_стоимость,
время_эксплуатации, период).
Определим величину амортизации за
первый и третий годы эксплуатации методом суммы чисел. За первый год
амортизация составит:
АСЧ(8000,500,10,1) = 681,82 тыс.
руб.,
за третий год величина
амортизационных отчислений составит:
АСЧ (8000,500,10,3)= 545,45 тыс.руб.
Функция ФУО
Функция ФУО вычисляет величину амортизации имущества
для заданного периода с использованием метода постоянного учета амортизации.
Данный метод использует фиксированную норму амортизации.
Синтаксис ФУО (нач_стоимость, ост_стоимость,
время_эксплуатации, период, месяцы).
Рассчитаем величину амортизации за
первый, третий и последний годы эксплуатации этим методом. За первый год
амортизация
составит:
ФУО(4000,250,10,1) = 968 тыс. руб.,
за третий год амортизация составит:
ФУО (4000,250,10,3) = 566,18 тыс.
руб.,
а в последнем году амортизационные
отчисления составят: ФУО (4000,250,10,10)= 79,96 тыс. руб.
Функция ДДОБ
Функция ДДОБ позволяет рассчитать сумму амортизации
для заданного периода методом уменьшающегося остатка. При этом можно задать
коэффициент ускоренной амортизации, по умолчанию равный двум.
Синтаксис ДДОБ (нач_стоимость, ост_стоимость,
время эксплуатации, период, коэффициент).
Амортизационные отчисления при использовании метода
двукратного учета амортизации (аргумент коэффициент = 2) постоянно
уменьшаются на протяжении срока эксплуатации, но их суммарная величина в итоге
полностью не возмещает амортизируемую стоимость имущества.
Рассчитаем величину амортизации за
первый и третий годы эксплуатации методом двукратного учета амортизации. За
первый год амортизация составит:
ДДОБ(4000,250,10,1) = 800 тыс. руб.,
за третий год:
ДДОБ(4000,250,10,3) = 512 тыс. руб.
Вариант 1
|
1. Рассчитать какая сумма |
БС |
|
2. Срок ссуды — 5 лет, |
БЗРАСПИС |
|
3. Компании X потребуется 100000 |
СТАВКА |
|
4. Определить эффективную |
(ЭФФЕКТ) |
|
5. Банк выдал ссуду 150 |
(ПЛТ) |
|
6. Определите эффективность |
(ЧПС) |
|
7. Определить величину |
(АПЛ) |
Вариант 2
|
1. У Вас есть возможность ежегодно в течение 4 лет |
(БС) |
|
2. По вкладу в 10000 |
(КПЕР) |
|
3. Определить величину |
(ДДОБ) |
|
4. Пять лет назад была |
(МСВД) |
|
5. Определите сумму |
(ОБЩДОХОД) |
|
6. Определите номинальную |
(НОМИНАЛ) |
|
7. Рассмотрим инвестиции, |
(ЧПС) |
Вариант 3
|
1. Вы решили приобрести |
(ПС) |
|
2. Для обеспечения будущих |
(КПЕР) |
|
3. Ставка банка по срочным |
(ЭФФЕКТ) |
|
4. Вычислить 10 годичную |
(ПЛТ) |
|
5. Определите чистую |
(ЧИСТНЗ) |
|
6. Определить величину |
(АСЧ) |
|
7. Пусть в долг на полтора |
(СТАВКА) |
Вариант 4
|
1. Предположим, что |
(ПС) |
|
2. Рассчитайте внутреннюю |
(ЧИСТВНДОХ) |
|
3. Определить величину |
(ДДОБ) |
|
4. Какую сумму |
(ПЛТ) |
|
5. Чему равна эффективная |
(ЭФФЕКТ) |
|
6. Рассчитайте процентную |
(СТАВКА) |
|
7. Ссуда 63200 руб., |
(КПЕР) |
Вариант 5
|
1. Вы хотите |
(БС) |
|
2. Ставка банка по срочным |
(БЗРАСПИС) |
|
3. Определить величину |
(ФУО) |
|
4. За какой срок в годах |
(КПЕР) |
|
5. Выдан кредит 200 000 |
(СТАВКА) |
|
6. Эффективная ставка |
(НОМИНАЛ) |
|
7. Определите платежи по |
(ПРПЛТ) |
Вариант 6
|
1. Рассматриваются два |
(ПС) |
|
2. Была выдана ссуда в |
(ОБЩДОХОД) |
|
3. Заем в 144 тыс. руб. |
(СТАВКА) |
|
4. Чему равна эффективная |
(ЭФФЕКТ) |
|
5. Найдите сумму выплат за |
(ОБЩПЛАТ) |
|
6. Определите |
(ВСД) |
|
7. Определить величину |
(ФУО) |
Вариант 7
|
1. Фирма создает фонд для |
(БС) |
|
2. Рассчитайте, через |
(КПЕР) |
|
3. В долг на 2 года дана |
(СТАВКА) |
|
4. Чему равна номинальная |
(НОМНАЛ) |
|
5. Определите основные |
(ОСПЛТ) |
|
6. Для приобретения |
(МСВД) |
|
7. Определить величину |
(АПЛ) |
Вариант 8
|
1. Ссуда в 20 000 руб. дана |
(БС) |
|
2. Ссуда 87000 руб., |
(КПЕР) |
|
3. Какой должна быть |
(СТАВКА) |
|
4. Чему равна эффективная |
(ЭФФЕКТ) |
|
5. Определите ежемесячные |
(ПЛТ) |
|
6. Затраты по проекту в |
(ЧПС) |
|
7. Определить величину |
(ДДОБ) |
Вариант 9
|
1. Вексель на 3 000 000 |
(ПС) |
|
2. Ссуда размером 61000 |
(КПЕР) |
|
3. Рассчитайте годовую |
(СТАВКА) |
|
4. Ставка банка по срочным |
(ЭФФЕКТ) |
|
5. Для приобретения |
(ОБЩПЛАТ) |
|
6. Определите чистую |
(ЧИСТНЗ) |
|
7. Определить величину |
(АПЛ) |
Вариант 10
|
1. Рассматриваются две |
(БС) |
|
2. Физическому лицу выдан |
(СТАВКА) |
|
3. Определите величину |
(ПРПЛТ) |
|
4. Сравните два проекта, |
(ЧПС) |
|
5. Определите чистую |
(ЧИСТНЗ) |
|
6. Определить величину |
(АСЧ) |
|
7. Ожидается, что ежегодные |
(КПЕР) |
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ
Государственное бюджетное образовательное учреждение
среднего профессионального образования города Москвы
КОММЕРЧЕСКО-БАНКОВСКИЙ КОЛЛЕДЖ №6
(ГБОУ СПО КБК № 6)
Методическое пособие
Решение финансово-экономических задач средствами Ms Excel для практических работ студентов
по дисциплине «ИТ в ПД», «АБС»
(3 и 4 курсов обучения, специальность 080110
уровень спо базовый/повышенный)
Автор:
Преподаватель спецдисциплин Руднева А. В.
Москва, 2014
УТВЕРЖДАЮ
Зам.директора по УМР
ГБОУ СПО КБК №6
_______________ Н. Е. Василенкова
____ ______________ 2014 г.
Автор: преподаватель спец.дисциплин Руднева А. В.
Рецензент: преподаватель спец.дисциплин Зайцева Е. Г.
СОГЛАСОВАНО
Протокол заседания кафедры
___________________________
от ____ ____________200___ №____
Оглавление:
Пояснительная записка
Практическая работа №1. Расчет распределения прибыли по итогам
работы за год
Практическая работа № 2. Остатки денежных средств на валютных счетах
Практическая работа № 3. Обменный пункт валюты
Практическая работа № 4. Налоговые отчисления предприятия по Единому социальному налогу
Практическая работа № 5. Налоговые отчисления сельскохозяйственных товаропроизводителей по Единому социальному налогу
Практическая работа № 6. Налоговые отчисления в пенсионный фонд
Практическая работа № 7. Налогообложение имущества
Практическая работа № 8. Динамика налоговых поступлений в бюджет
Литература
Средства обучения
Пояснительная записка
Данное методическое пособие представляет собой практические работы для дисциплин «Информационные технологии в профессиональной деятельности» и «Автоматизированные банковские системы».
В данном практикуме закрепляются возможности табличного процессора Microsoft Excel (Office 2007).
Табличный процессор Excel, имеет широчайшие возможности по обработке данных, в том числе финансово-экономического характера. В данном пособии многие из этих возможностей заложены в решение различных задач финансового характера.
Каждое практическое задание несет в себе закрепление предыдущего материала по финансовым, текстовым, даты, логическим, статистическим, математическим функциям.
Во время выполнения заданий студенты учатся самостоятельно анализировать полученные результаты – представлять их в виде диаграмм, а также работать в поисковых системах с сайтами и справочно — правовой системой ГАРАНТ.
Преподавателю рекомендуется данное методическое пособие для изучения тем, связанных с функциями Excel, а задачи сами по себе могут быть использованы как итоговые занятия по этим темам (см. раздел 2 УМК ИТ в ПД).
В дальнейшем, на знания, полученные в этой теме, студенты могут опираться при курсовом и дипломном проектировании.
При этом навыки, полученные студентами, сформируют у студентов системный и аналитический подход к решению любых профессиональных задач.
Практическая работа №1. Расчет распределения прибыли по итогам
работы за год
- Постановка задачи.
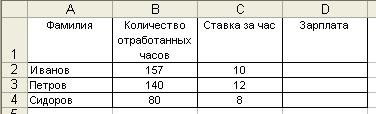
В конце отчетного года организация имеет некоторую величину денежных средств N, которую необходимо распределить между сотрудниками в качестве премии. Распределение производится на основе оклада сотрудника и в соответствии со стажем его работы в данной организации.
- Пояснения.
Требуется создать таблицу, состоящую из граф: «№ п/п» (1), «ФИО сотрудника» (2), «Дата приема на работу» (3), «Стаж работы» (4), «Оклад сотрудника» (5), «Модифицированный оклад» (6), «Премия сотрудника» (7).
Данные граф 1, 2, 3 и 5 задайте самостоятельно.
Значение графы 4 рассчитайте различными способами – с помощью функций даты и времени (ДНЕЙ360, ДОЛЯГОДА, РАЗНДАТ, ГОД и СЕГОДНЯ).
Для приведения сотрудников к одному знаменателю рассчитывается промежуточный показатель – модифицированный оклад, зависящий от стажа работы сотрудника (если стаж работы не менее 5 лет, то размер модифицированного оклада равен двойному окладу, в противном случае модифицированный оклад равен окладу). При расчете графы 6 используйте функцию ЕСЛИ.
Отдельно рассчитайте коэффициент распределения (К), как отношение всей суммы премиальных средств N к сумме всех модифицированных окладов. Данный коэффициент показывает, сколько рублей премии приходится на рубль модифицированного оклада.
Премия каждого сотрудника определяется путем умножения величины модифицированного оклада на коэффициент распределения. Полученную премию следует округлить до целого. При расчете графы 7 используйте функцию ОКРУГЛ и абсолютную ссылку.
Постройте круговую диаграмму процентного распределения премии между сотрудниками и точечный график зависимости премии от оклада.
Решение
|
№п/п |
ФИО |
Дата приема на работу |
Стаж работы |
Применяемые функции |
Оклад сотрудника |
Модифицированный оклад |
Премия сотрудника |
Функция (ОКРУГЛ) |
|
1 |
Иванов |
05.03.1995 |
17,22 |
ДНЕЙ360() |
40000 |
80000 |
29739,77695 |
29740 |
|
2 |
Петров |
16.04.2000 |
17,219444 |
ДОЛЯГОДА() |
25000 |
50000 |
18587,36059 |
18587 |
|
3 |
Корсакова |
23.12.2005 |
7,00 |
ГОД() |
20000 |
40000 |
14869,88848 |
14870 |
|
4 |
Жучкина |
07.09.1990 |
21 |
СЕГОДНЯ() |
42000 |
84000 |
31226,7658 |
31227 |
|
5 |
Северов |
10.05.2010 |
2 |
ГОД() |
15000 |
15000 |
5576,208178 |
5576 |
|
∑ |
269000 |
|||||||
|
24.05.12 |
||||||||
|
Установить в ячейках D5, D6 формат ГГ |
||||||||
|
коэффициент распределения |
0,3717472 |
|||||||
|
N |
100000 |
|||||||
Практическая работа № 2. Остатки денежных средств на валютных счетах
1. Постановка задачи.
Филиал банка работает с частными вкладчиками, имеющими валютные счета в четырех валютах. Необходимо получить на конец месяца остатки по всем валютным счетам в рублевом эквиваленте.
2. Пояснения.
Требуется создать таблицу, состоящую из граф: «№ п/п» (1), «ФИО вкладчика» (2), «Расчетный счет» (3), «Сумма в валюте» (4), «Код валюты» (5), «Остаток в рублях» (6). Данные граф 1, 2,3 и 4 задайте самостоятельно.
Вкладчики банка могут иметь от одного до четырех валютных счетов. Состояние счета оценивается и в валюте, и в рублях. Код валюты определяется исходя из расчетного счета клиента, состоящего из 20 символов. При этом код валюты занимает место с 6 по 8 символ в счете клиента.
Для извлечения кода валюты из счета клиента используйте несколько способов.
Первый способ – с помощью функции ПСТР.
Второй – с применением функции ПРАВСИМВ.
Третий – с помощью функции ЛЕВСИМВ.
Четвертый – с использованием функции ЗНАЧЕН.
Для расчета графы 6 (расчет рублевого эквивалента по каждой валюте) используются функции ЕСЛИ() и ПРОСМОТР в форме массива и «Информационный справочник Банка России». Выдержка из данного документа приведена в Таблице 1.[1]
|
Что означают цифры счета: |
||||
|
ААА-ББ-ВВВ-Г-ДДДД-ЕЕЕЕЕЕЕ (для удобства разделён дефисами): |
||||
|
ААА (1—3 цифры) — номер балансового счёта первого порядка; |
||||
|
ББ (4—5 цифры) — номер балансового счёта второго порядка; |
||||
|
ВВВ (6—8 цифры) — код валюты, проставляемый в соответствии с Общероссийским классификатором валют ОКВ, за исключением кода 810 который был заменён в ОКВ на код 643, но в структуре внутрироссийских счетов был оставлен; |
||||
|
Г (9 цифра) — контрольная цифра; |
||||
|
ДДДД (10—13 цифры) — четырехзначный код подразделения банка; |
||||
|
ЕЕЕЕЕЕЕ (14—20 цифры) — семизначный внутренний номер (лицевого) счёта в банке. |
Решение
|
№п/п |
ФИО |
Расчетный счет |
Сумма в валюте |
Код валюты ПСТР |
Код валюты ПРАВСИМВ |
Код валюты ЛЕВСИМВ |
Перевод текстового значения в числовое ЗНАЧЕН() |
Остаток на счете в рублях |
|
1 |
Иванов |
10501810700010000000 |
500 000,00р. |
810 |
810700010000000 |
810 |
810 |
500000 |
|
2 |
Петров |
10502840600010000000 |
$7 000,00 |
840 |
840600010000000 |
840 |
840 |
205435,3 |
|
3 |
Корсакова |
20202978000010000000 |
€ 3 600,00 |
978 |
978000010000000 |
978 |
978 |
141003,72 |
|
4 |
Жжучкина |
10501208000010000000 |
kr 82 350,00 |
208 |
208000010000000 |
208 |
208 |
4336155,72 |
- Выдержка из «Информационного справочника Банка России»
Центральный банк Российской Федерации установил с 03.04.2012 следующие курсы иностранных валют к рублю Российской Федерации без обязательств Банка России покупать или продавать указанные валюты по данному курсу
Таблица 1
|
Цифр. код |
Букв. код |
Единиц |
Валюта |
Курс |
|
036 |
AUD |
1 |
Австралийский доллар |
30,5629 |
|
944 |
AZN |
1 |
Азербайджанский манат |
37,3621 |
|
051 |
AMD |
1000 |
Армянских драмов |
75,0106 |
|
974 |
BYR |
10000 |
Белорусских рублей |
36,5934 |
|
975 |
BGN |
1 |
Болгарский лев |
20,0341 |
|
986 |
BRL |
1 |
Бразильский реал |
16,0678 |
|
348 |
HUF |
100 |
Венгерских форинтов |
13,3521 |
|
410 |
KRW |
1000 |
Вон Республики Корея |
26,0315 |
|
208 |
DKK |
10 |
Датских крон |
52,6552 |
|
840 |
USD |
1 |
Доллар США |
29,3479 |
|
978 |
EUR |
1 |
Евро |
39,1677 |
|
356 |
INR |
100 |
Индийских рупий |
57,7487 |
Практическая работа № 3. Обменный пункт валюты
1. Постановка задачи.
Для операциониста обменного пункта валют(операционной кассы) требуется разработать таблицу купли — продажи валют и рассчитать прибыль обменного пункта.
2. Пояснения.
Создайте таблицу, состоящую из граф: «Код валюты» (1), «Наименование валюты» (2), «Количество валюты купленной» (3), «Количество валюты проданной» (4), «Курс валюты ЦБ» (5), «Курс покупки» (6), «Курс продажи» (7), «Прибыль от покупки» (8), «Прибыль от продажи» (9), «Общая прибыль» (10), «Налог на прибыль» (11), «Прибыль обменного пункта» (12).
Данные для граф 1, 3 и 4 задайте самостоятельно.
Значение граф 2 и 5 определите с использованием дополнительной таблицы «Информационный справочник Банка России» (см. Таблицу 1) и функции ВПР (графа 2) и функции ВПР (графа 5).
Графы 6 и 7 рассчитайте в соответствии с инструкцией (маржа составляет не более 10%).
Подсчитайте общую сумму по графам 10, 11 и 12.
Решение
|
Код валюты |
Наименование валюты ВПР() |
Кол-во валюты купленной |
Кол-во валюты проданной |
Курс валюты ЦБ ВПР() |
Курс покупки |
Курс продажи |
Прибыль от покупки |
Прибыль от продажи |
Общая прибыль |
Налог на прибыль |
Прибыль обменного пункта |
|
840 |
USD |
1000 |
3000 |
29,3479 |
30,815295 |
31,69573 |
1467,395 |
7043,496 |
8510,891 |
1702,178 |
6808,713 |
|
978 |
EUR |
500 |
1000 |
39,1677 |
41,126085 |
42,30112 |
979,1925 |
3133,416 |
4112,609 |
822,5217 |
3290,087 |
|
208 |
DKK |
200 |
500 |
52,6552 |
55,28796 |
56,86762 |
526,552 |
2106,208 |
2632,76 |
526,552 |
2106,208 |
|
974 |
BYR |
400 |
1000 |
36,5934 |
38,42307 |
39,52087 |
731,868 |
2927,472 |
3659,34 |
731,868 |
2927,472 |
|
Дано, что маржа не более 10%, но маржа покупки чуть меньше, чем маржа продажи (чтобы получить прибыль с продажи), например, 5% и 8%) |
5,00% |
8,00% |
20% |
Налог на прибыль – 20% от общей прибыли – см. статья 284, Налоговые ставки (Поисковая система Гарант Налоговый кодекс)
Практическая работа № 4. Налоговые отчисления предприятия по Единому социальному налогу
1. Постановка задачи.
Рассчитать Единый социальный налог за 1-й квартал текущего года для каждого сотрудника и по предприятию в целом.
2. Пояснения.
Создайте таблицу, состоящую из граф: «№ п/п» (1), «ФИО сотрудника» (2), «Оклад» (3); «Иждивенцы» (4); «Налогооблагаемая база за квартал» (5); «Налог на доходы физических лиц (НДФЛ)» (6); Отчисления в: «Федеральный бюджет» (7); «Фонд социального страхования (ФСС РФ)» (8); «Федеральный фонд обязательного медицинского страхования» (9); «Территориальные фонды обязательного медицинского страхования» (10); «Итого Единый социальный1» (11); «Итого Единый социальный2» (12).
Данные граф 1, 2, 3 и 4 задаются самостоятельно.
Значение графы 5 вычисляется как утроенное значение графы 3.
Значение графы 6 вычисляется по ставке 13%.
Графы 7, 8, 9, 10 и 11 вычисляются с помощью функции ЕСЛИ(И))), ставки налогов содержатся в Таблице 2[2]
Значение графы 12 рассчитывается как сумма граф 7-10.
В соответствии со статьей 218 Налогового кодекса РФ налоговые вычеты предоставляются за каждый месяц налогового периода, то право на стандартные налоговые вычеты сохраняется у работника и в тех месяцах, когда он находится в отпуске без сохранения заработной платы.
Стандартные налоговые вычеты можно разделить на две группы:
1. Необлагаемый минимум дохода;
2. Расходы на содержание детей
Необлагаемый минимум дохода состоит из трех видов налоговых вычетов:
1. Налоговый вычет в размере 3000 руб. — предоставляется ежемесячно в течение налогового периода (календарного года) — на вычет в размере 3000 руб. имеют право категории налогоплательщиков, перечисленные в подпункте 1 пункта 1 статьи 218 Налогового кодекса РФ;
2. Налоговый вычет в размере 500 руб. — предоставляется ежемесячно в течение налогового периода (календарного года) — на вычет в размере 500 руб. могут претендовать налогоплательщики, указанные в подпункте 2 пункта 1 статьи 218 Налогового кодекса РФ;
3. Налоговый вычет в размере 400 руб.
Этот стандартный вычет применяется до того месяца, в котором доход налогоплательщика, облагаемый по ставке 13 процентов и исчисленный нарастающим итогом с начала налогового периода работодателем, предоставляющим налоговые вычеты, не превысит 40 000 руб. (Федеральный закон от 22 июля 2008 г. № 121-ФЗ «О внесении изменений в статью 218 части второй Налогового кодекса Российской Федерации»).
В соответствии с подпунктом 4 пункта 1 статьи 218 Налогового кодекса РФ налогоплательщики имеют право на стандартный налоговый вычет на каждого ребенка в возрасте до 18 лет, а также на учащегося очной формы обучения, студента, аспиранта, курсанта и ординатора в возрасте до 24 лет. Вычет предоставляется за весь период обучения детей в образовательном учреждении и (или) учебном заведении (включая академический отпуск, оформленный в установленном порядке в период обучения).
Сумма вычета 1000 руб. за каждый месяц налогового периода — распространяется:
1. На каждого ребенка у налогоплательщиков, на обеспечении которых находится ребенок и которые являются его родителями (при этом в соответствующих случаях вычет предоставляется и супругу родителя ребенка);
2. На каждого ребенка у налогоплательщиков, которые являются его опекунами, попечителями или приемными родителями.
Если же индивидуальный предприниматель является вдовой (вдовцом), одиноким родителем, опекуном или попечителем, то налоговый вычет производится в двойном размере. То же происходит в случае, если ребенок в возрасте до 18 лет — инвалид, а также в случае, если учащийся очной формы обучения, аспирант, ординатор, студент в возрасте до 24 лет является инвалидом I или II группы (подп. 4 п. 1 ст. 218 Налогового кодекса РФ).
Ставки ЕСН для основной категории плательщиков (организаций, индивидуальных предпринимателей, физических лиц, не признаваемые индивидуальными предпринимателями, за исключением выступающих в качестве работодателей налогоплательщиков — организаций и индивидуальных предпринимателей, имеющих статус резидента технико-внедренческой особой экономической зоны и производящих выплаты физическим лицам, работающим на территории технико-внедренческой особой экономической зоны, сельскохозяйственных товаропроизводителей, организаций народных художественных промыслов и родовых, семейных общин коренных малочисленных народов Севера, занимающихсятрадиционными отраслями хозяйствования, а также налогоплательщиков — организаций, осуществляющих деятельность в области информационных технологий):
Таблица 2
|
Налоговая база на каждое физическое лицо нарастающим итогом с начала года |
Федеральный бюджет |
Фонд социального страхования Российской Федерации |
Фонды обязательного медицинского страхования |
Итого |
|||||||
|
Федеральный фонд обязательного медицинского страхования |
Территориальные фонды обязательного медицинского страхования |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||||||
|
До 280 000 руб. |
20,00% |
2,90% |
1,10% |
2,00% |
26,00% |
||||||
|
От 280 001 руб. до 600 000 руб. |
56 000 руб. + 7,9 % с суммы, превышающей 280 000 руб. |
8 120 руб. +1,0 % с суммы, превышающей 280 000 руб. |
3 080 руб. + 0,6 % с суммы, превышающей 280 000 руб. |
5 600 руб. + 0,5 % с суммы, превышающей 280 000 руб. |
72 800 руб. + 10,0 % с суммы, превышающей 100 000 руб. |
||||||
|
Свыше 600 000 руб. |
81 280 руб. + 2,0 % с суммы, превышающей 600 000 руб. |
11 320 руб. |
5000 руб. |
7 200 руб. |
104 800 руб. + 2,0 % с суммы, превышающей 600 000 руб. |
||||||
|
№ п/п |
ФИО |
Оклад |
Иждивенцы |
Налогооблагаемая база за квартал |
Налог на доходы физических лиц (НДФЛ) ЕСЛИ(И()) |
Отчисления в «Федеральный бюджет» ЕСЛИ(И()) |
Фонд социального страхования ЕСЛИ(И()) |
Федеральный фонд обязательного медицинского страхования ЕСЛИ(И()) |
Территориальные фонды обязательного медицинского страхования ЕСЛИ(И()) |
Итого Единый социальный 1 ЕСЛИ(И()) |
Итого Единый социальный 2 СУММ() |
|
1 |
Иванов |
220000 |
0 |
660000 |
85800 |
94480 |
11320 |
5000 |
7200 |
118000 |
118000 |
|
2 |
Петров |
25000 |
2 |
75000 |
9438 |
15000 |
2175 |
825 |
1500 |
19500 |
19500 |
|
3 |
Корсакова |
150000 |
2 |
450000 |
58188 |
91550 |
12620 |
5780 |
7850 |
117800 |
117800 |
|
4 |
Жучкина |
42000 |
3 |
126000 |
15938 |
25200 |
3654 |
1386 |
2520 |
32760 |
32760 |
|
5 |
Северов |
15000 |
1 |
45000 |
5668 |
9000 |
1305 |
495 |
900 |
11700 |
11700 |
|
∑ |
299760 |
Решение
Практическая работа № 5. Налоговые отчисления сельскохозяйственных товаропроизводителей по Единому социальному налогу
1. Постановка задачи.
Рассчитать Единый социальный налог за 1-й квартал текущего года для каждого сотрудника и по сельскохозяйственной организации в целом.
2. Пояснения.
Разработать таблицу в соответствие с требованиями предыдущей практической работы.
Использовать ставки налогов, представленные в Таблице 3.(см. сноску 2).
Ставки ЕСН для налогоплательщиков — сельскохозяйственных товаропроизводителей, организаций народных художественных промыслов и родовых, семейных общин коренных малочисленных народов Севера, занимающихся традиционными отраслями хозяйствования:
Таблица 3
|
Налоговая база на каждое физическое лицо нарастающим итогом с начала года |
Федеральный бюджет |
Фонд социального страхования Российской Федерации |
Фонды обязательного медицинского страхования |
Итого |
|
|
Федеральный фонд обязательного медицинского страхования |
Территориальные фонды обязательного медицинского страхования |
||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
До 280 000 руб. |
15,8 % |
1,9 % |
1,1 % |
1,2 % |
20,0 % |
|
От 280 001 руб. до 600 000 руб. |
44 240 руб. + 7,9 % с суммы, превышающей 280 000 руб. |
5 320 руб. +0,9 % с суммы, превышающей 280 000 руб. |
3 080 руб. + 0,6 % с суммы, превышающей 280 000 руб. |
3 360 руб. + 0,6 % с суммы, превышающей 280 000 руб. |
56 000 руб. + 10,0 % с суммы, превышающей 280 000 руб. |
|
Свыше 600 000 руб. |
69 520 руб. + 2,0 % с суммы, превышающей 600 000 руб. |
8 200 руб. |
5000 руб. |
5 200 руб. |
88 000 руб. + 2,0 % с суммы, превышающей 600 000 руб. |
Решение
|
1 |
Иванов |
220000 |
0 |
660000 |
85800 |
82720 |
8200 |
5000 |
5200 |
101200 |
101120 |
|
2 |
Петров |
25000 |
2 |
75000 |
9438 |
11850 |
1425 |
825 |
900 |
15000 |
15000 |
|
3 |
Корсакова |
150000 |
2 |
450000 |
58188 |
79790 |
9370 |
5780 |
7850 |
101000 |
102790 |
|
4 |
Жучкина |
42000 |
3 |
126000 |
15938 |
19908 |
2394 |
1386 |
1512 |
25200 |
25200 |
|
5 |
Северов |
15000 |
1 |
45000 |
5668 |
7110 |
855 |
495 |
540 |
9000 |
9000 |
|
253110 |
Практическая работа № 6. Налоговые отчисления в пенсионный фонд
1. Постановка задачи.
Рассчитать обязательные взносы в пенсионный фонд за 1-й квартал текущего года по каждому сотруднику и по предприятию в целом.
2. Пояснения.
Создайте таблицу, состоящую из граф: «№ п/п» (1), «ФИО сотрудника» (2), «Дата рождения» (3); «Оклад» (4); «База для начисления страховых взносов за квартал» (5); Отчисления: «Для лиц 1966 г.р. и старше» (6); «Для лиц 1967 г.р. и моложе – страховая часть трудовой пенсии» (7); «Для лиц 1967 г.р. и моложе – накопительная часть трудовой пенсии» (8); «Итого отчислений» (9).
Данные граф 1, 2, 3 и 4 задаются самостоятельно.
Значение графы 5 вычисляется как утроенное значение графы 4.
Графы 6, 7 и 8 вычисляются с помощью функции ЕСЛИ(И()), ставки налогов содержатся в следующей Таблице 4.[3]
Ежегодно ПФР рассылает уведомления о результатах начисления взносов в системе персонифицированного учета пенсионных взносов (так называемые «письма счастья»).
Результаты отчисления в накопительную часть пенсии непосредственно будут влиять на размер трудовой пенсии. Если зарплата выплачивается в конверте, то необходимо учитывать потерю указанных отчислений. Их придется осуществлять самостоятельно в рамках добровольного пенсионного обеспечения.
Ставки налоговых отчислений в Пенсионный фонд. Ставки страховых взносов
|
База для начисления страховых взносов на каждое физическое лицо нарастающим итогом с начала года |
Для лиц 1966 г.р. и старше |
Для лиц 1967 г.р. и моложе |
|
|
на финансирование страховой части трудовой пенсии |
на финансирование страховой части трудовой пенсии |
на финансирование накопительной части трудовой пенсии |
|
|
1 |
2 |
3 |
4 |
|
До 280000 руб. |
14% |
10% |
4% |
|
От 280001 до 600000р. |
39200р.+5,5% с суммы, превышающей 280000 р. |
28000р.+3,9% с суммы, превышающей 280000 р. |
11200р+1,6% с суммы, превышающей 280000 р. |
|
Свыше 600000 р. |
56800 рублей |
40480 рублей |
16320 рублей |
Таблица 4
Решение
|
№ п/п |
ФИО |
Дата рождения |
Оклад |
База для начисления страховых взносов за квартал |
Отчисления: для лиц 1966 г и старше |
Для лиц 1967 г и моложе — страховая часть трудовой пенсии |
Для лиц 1967 г и моложе — накопительная часть трудовой пенсии |
Итого отчислений |
|
1 |
Иванов |
1957 |
40000 руб. |
120000 руб. |
16800 руб. |
для лиц 1966 г.р. и старше |
для лиц 1966 г.р. и старше |
16800 руб. |
|
2 |
Петров |
1961 |
35000 руб. |
105000 руб. |
14700 руб. |
для лиц 1966 г.р. и старше |
для лиц 1966 г.р. и старше |
14700 руб. |
|
3 |
Корсакова |
1985 |
25000 руб. |
75000 руб. |
моложе 1967 г. р |
7500 руб. |
3000 руб. |
10500 руб. |
|
4 |
Жучкина |
1990 |
14000 руб. |
42000 руб. |
моложе 1967 г. р |
4200 руб. |
1680 руб. |
5880 руб. |
|
5 |
Северов |
1994 |
10000 руб. |
30000 руб. |
моложе 1967 г. р |
3000 руб. |
1200 руб. |
4200 руб. |
Практическая работа № 7. Налогообложение имущества
1. Постановка задачи.
Имеется несколько различных видов имущества, которые можно подарить или передать по наследству. Используя данные налоговых шкал на наследование (табл. 5) и дарение (табл. 6), определите налог на имущество.
Сравните суммы полученных налогов.
2. Пояснения.
Создайте таблицу, состоящую из граф: «№ п/п» (1), «Вид имущества» (2), «Стоимость имущества» (3), «Налог на имущество, передаваемое по наследству: для наследников 1-й очереди и наследников 2-й очереди» (4, 5), «Налог на имущество, передаваемое в виде дара: для наследников 1-й очереди и наследников 2-й очереди» (6, 7).
Данные для граф 1, 2 и 3 задайте самостоятельно.
Значение граф 4, 5, 6 и 7 рассчитайте с помощью функции ЕСЛИ(И()).
Сравнение налогов осуществите путем построения графиков.
Примечания.
- Налог с имущества, переходящего в порядке наследования или дарения — федеральный налог, установленный Законом РФ от 12 декабря 1991 г. № 2020-1 (в ред. Федерального закона от 30 декабря 2001 г. № 196-ФЗ). Относится к группе налогов на переход права собственности безвозмездным способом.
Налогоплательщики — физические лица, которые принимают имущество, переходящее в их собственность в порядке наследования или дарения (ст. 1 Закона).
Объектами налогообложения признаются:
- жилые дома, квартиры, дачи, садовые домики в садоводческих товариществах (недвижимое имущество);
- автомобили, мотоциклы, моторные лодки, катера, яхты, другие транспортные средства;
- предметы антиквариата и искусства (культурные ценности);
- ювелирные изделия;
- бытовые изделия из драгоценных металлов и драгоценных камней и лом таких изделий;
- паенакопления в жилищно-строительных, гаражно-строительных и дачно-строительных кооперативах;
- суммы, находящиеся во вкладах в учреждениях банков и других кредитных учреждениях, средства на именных приватизационных счетах физических лиц;
- стоимость имущественных и земельных долей (паев);
- валютные ценности и ценные бумаги в их стоимостном выражении (ст. 2 Закона).
В таблицах 5 и 6 указан процент, который взимается со стоимости, превышающей нижнюю границу данной ступени налоговой шкалы.
Числами указан коэффициент, который, будучи умноженным на величину МРОТ – 11700 руб. на 2012 год (см. поисковую систему ГАРАНТ), определяет фиксированную сумму налога.
Налог с имущества, переходящего физическим лицам в порядке наследования, исчисляется по следующим налоговым ставкам, приведенным в табл.5
Размеры ставок налога с имущества, переходящего в порядке наследования
Таблица 5
|
СТОИМОСТЬ имущества |
850-1700 МРОТ |
1701-2550 МРОТ |
Свыше 2550 МРОТ |
|
Наследники 1-й очереди |
5% от стоимости имущества, превышающей 850 МРОТ |
42,5 МРОТ + 10% от стоимости имущества, превышающей 1700 МРОТ |
127,5 МРОТ + 15% от стоимости имущества, превышающей 2550 МРОТ |
|
Наследники 2-й очереди |
10% от стоимости имущества, превышающей 850 МРОТ |
85 МРОТ + 20% от стоимости имущества, превышающей 1700 МРОТ |
255 МРОТ + 30% от стоимости имущества, превышающей 2550 МРОТ |
|
Другие наследники |
20% от стоимости имущества, превышающей 850 МРОТ |
170 МРОТ + 30% от стоимости имущества, превышающей 1700 МРОТ |
425 МРОТ + 40% от стоимости имущества, превышающей 2550 МРОТ |
- До внесения изменений в соответствующие федеральные законы, определяющие порядок исчисления налогов, сборов, штрафов и иных платежей, исчисление налогов, сборов, штрафов и иных платежей, осуществляемое в соответствии с законодательством РФ в зависимости от минимального размера оплаты труда, производится: а) с 1 июля 2000 г. по 31 декабря 2000 г. исходя из базовой суммы, равной 83 р. 49 к.; б) с 1 января 2001 г. исходя из базовой суммы, равной 100 р. (ст. 5 Федерального закона о минимальном размере оплаты труда от 19 июня 2000 г. № 82-ФЗ). Источник: п. 1 ст. 3 Закона.
Налог с имущества, переходящего физическим лицам в порядке дарения, исчисляется по ставкам, приведенным в табл. 6.
Размеры ставок налога с имущества, переходящего в порядке дарения
Таблица 6
|
Стоимость имущества, МРОТ |
Дарение: детям, родителям (налог с получателя дарения) |
Другим физическим лицам |
|
80-850 МРОТ |
3% от стоимости имущества, превышающей 80 МРОТ |
10% от стоимости имущества, превышающей 80 МРОТ |
|
851-1700 МРОТ |
23,1 МРОТ + 7% от стоимости имущества, превышающей 850 МРОТ |
77 МРОТ + 20% от стоимости имущества, превышающей 850 МРОТ |
|
1701-2550 МРОТ |
82,6 МРОТ + 11% от стоимости имущества, превышающей 1700 МРОТ |
247 МРОТ + 30% от стоимости имущества, превышающей 1700 МРОТ |
|
Свыше 2550 МРОТ |
176,1 МРОТ + 15% от стоимости имущества, превышающей 2550 МРОТ |
502 МРОТ + 40% от стоимости имущества, превышающей 2550 МРОТ |
Решение
|
№ п/п |
Вид имущества |
Стоимость имущества |
Налог на имущество, передаваемое по наследству: для наследников 1 очереди |
Налог на имущество, передаваемое по наследству: для наследников 2 очереди |
Налог на имущество, передаваемое в виде дара: для наследников 1 очереди |
Налог на имущество, передаваемое в виде дара: для наследников 2 очереди |
|
1 |
10 700 000,00р. |
535000 |
1070000 |
1019270 |
3040900 |
|
|
2 |
1 550 000,00р. |
ЛОЖЬ |
ЛОЖЬ |
46500 |
155000 |
|
|
3 |
33 000 000,00р. |
6441750 |
12883500 |
7010370 |
19073400 |
|
|
4 |
24 570 000,00р. |
2954250 |
5908500 |
3669120 |
10260900 |
|
|
5 |
4 950 000,00р. |
ЛОЖЬ |
ЛОЖЬ |
148500 |
495000 |
|
|
МРОТ 2012 г |
11 700,00р. |
|||||
|
850 МРОТ |
9 945 000,00р. |
1701МРОТ |
19 901 700,00р. |
Свыше 2550 МРОТ |
29 846 700,00р. |
|
|
1700МРОТ |
19 890 000,00р. |
2550МРОТ |
29 835 000,00р. |
|||
|
80 МРОТ |
936 000,00р. |
851МРОТ |
9 956 700,00р. |
Практическая работа № 8. Динамика налоговых поступлений в бюджет
1. Постановка задачи.
Требуется получить прогноз поступлений налогов в бюджет на ближайшие три года, используя известные значения предыдущих лет. Сумма поступаемых в бюджет налогов зависит от количества налогоплательщиков данного региона. Количество налогоплательщиков зависит от количества зарегистрированных фирм.
2. Пояснения.
Создайте таблицу, состоящую из граф: «№ п/п» (1), «Год» (2), «Количество зарегистрированных фирм» (3), «Количество плательщиков» (4), «Поступления налогов в бюджет» (5).
Все графы таблицы заполните данными за предыдущие пять лет.
Используя статистические функции ТЕНДЕНЦИЯ и РОСТ, спрогнозируйте количество зарегистрированных фирм на следующие три года, определите количество налогоплательщиков в этих фирмах и рассчитайте количество поступлений налогов в бюджет от налогоплательщиков.
Проанализируйте результат, построив различные графики.
Решение
|
№ п/п |
Год |
Количество зарегистрированных фирм |
Количество плательщиков |
Поступления налогов в бюджет |
|
1 |
2007 |
5 |
100 |
15000 |
|
2 |
2008 |
7 |
60 |
7000 |
|
3 |
2009 |
4 |
80 |
5000 |
|
4 |
2010 |
3 |
120 |
3000 |
|
5 |
2011 |
6 |
150 |
17000 |
|
6 |
2012 |
4,4 |
150 |
9400 |
|
7 |
2013 |
4,2 |
166 |
9400 |
|
8 |
2014 |
4 |
182 |
9400 |
|
ТЕНДЕНЦИЯ() |
Литература
- Безручко В. Т. Практикум по курсу «Информатика». Работа в Widows, Word, Excel. М.: Финансы и статистика, 2003.
- Коцюбинский А.Ю., Грошев С.В. Excel для менеджера и экономиста в примерах. –М.: Гросс-Медиа, 2004. -300с.
- Лавренов С. М. Excel. Сборник примеров и задач. М.: Финансы и статистика, 2003.
- Михеева Е. В. Практикум по информационным технологиям в профессиональной деятельности. М.: Издательский центр «Академия», 2007.
- Пикуза В., Геращенко А. Экономические и финансовые расчеты в Excel. –СПб.: Питер, 2004. -396 с.
- Попов А. А. Excel. Практическое руководство. М.: ДессКом, 2005.
- Сингаевская Г.И. Функции в Excel. Решение практических задач. –М.: Вильямс, 2005. -879 с.
Средства обучения
Компьютерный класс, оснащенный персональными компьютерами Pentium 1V – 13 шт., объединенными в локальную сеть. Программное обеспечение – ОС Windows XP, Office 2007.
[1] Полные текущие сведения о курсе валют можно найти на странице официального сайта ЦБ РФ www.cbr.ru/currency_base/daily.asp, раскрыв гиперссылку «Официальные курсы валют на заданную дату, устанавливаемые ежедневно». Таблицу с курсами валют можно выделить и скопировать, вставив ее в последующем в документ Excel.
[2] Полные сведения о ставках единого социального налога(ЕСН) можно найти на сайте http://www.audit-it.ru/inform/account/19740.html#k1
[3] Полные сведения о взносах в пенсионный фонд России можно найти на сайте http://www.3-ndfl.net/nalog/pfr.html
Задание №2.
Тема: Решение финансовых задач в EXCEL
План занятия:
-
Применение финансовых функции
Цель занятия: С применением финансовых функции
решение задач в EXCEL
Рассмотрим пример.
Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 сом. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.
Оформим исходные данные в виде таблицы:
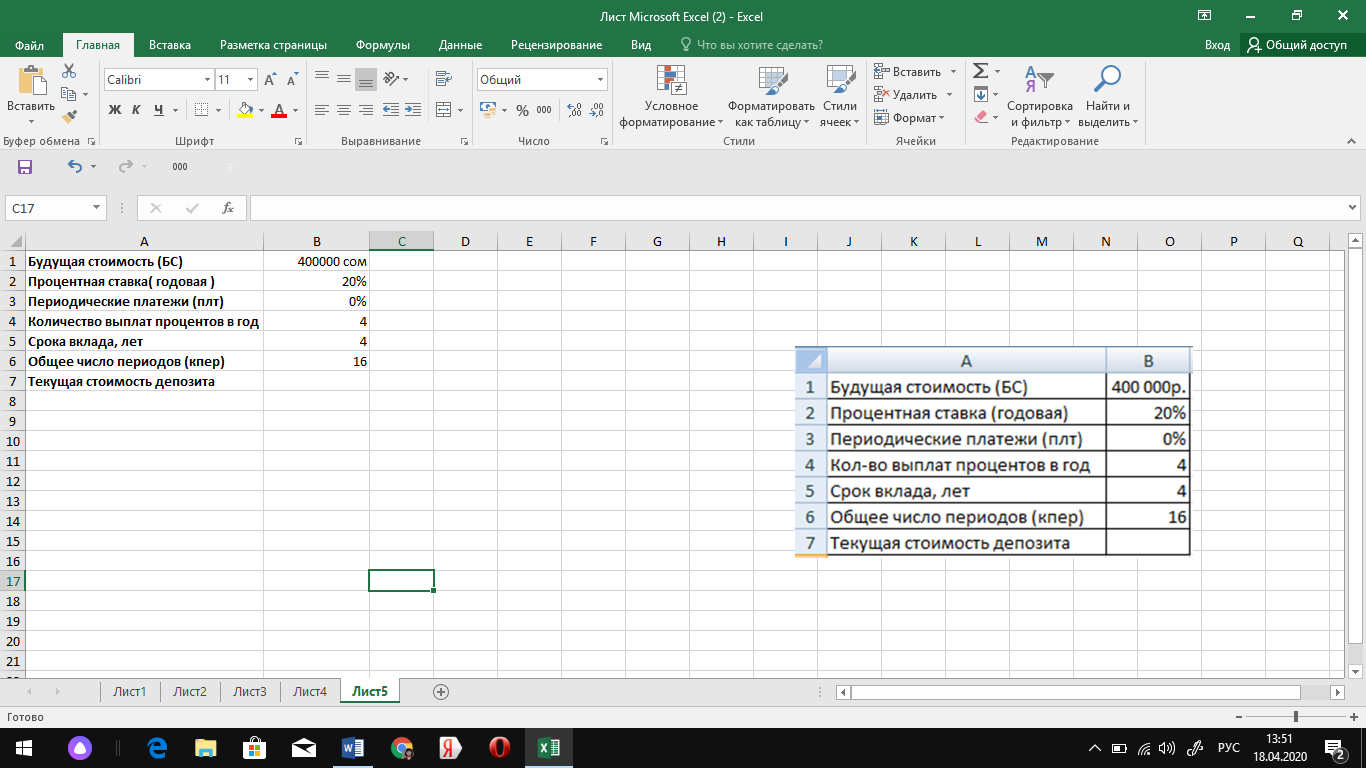
Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).
Заполнение аргументов:
-
Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
-
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
-
Плт – 0. Ничего не пишем, т.к. депозит
-
пополняться не будет.
-
Тип – 0.
-
БС – сумма, которую мы хотим получить в конце срока вклада.
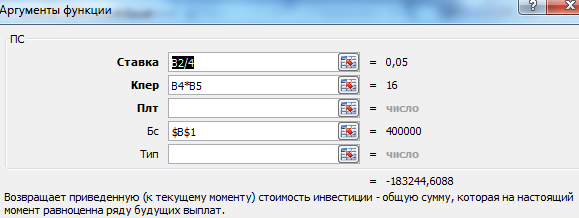
Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.
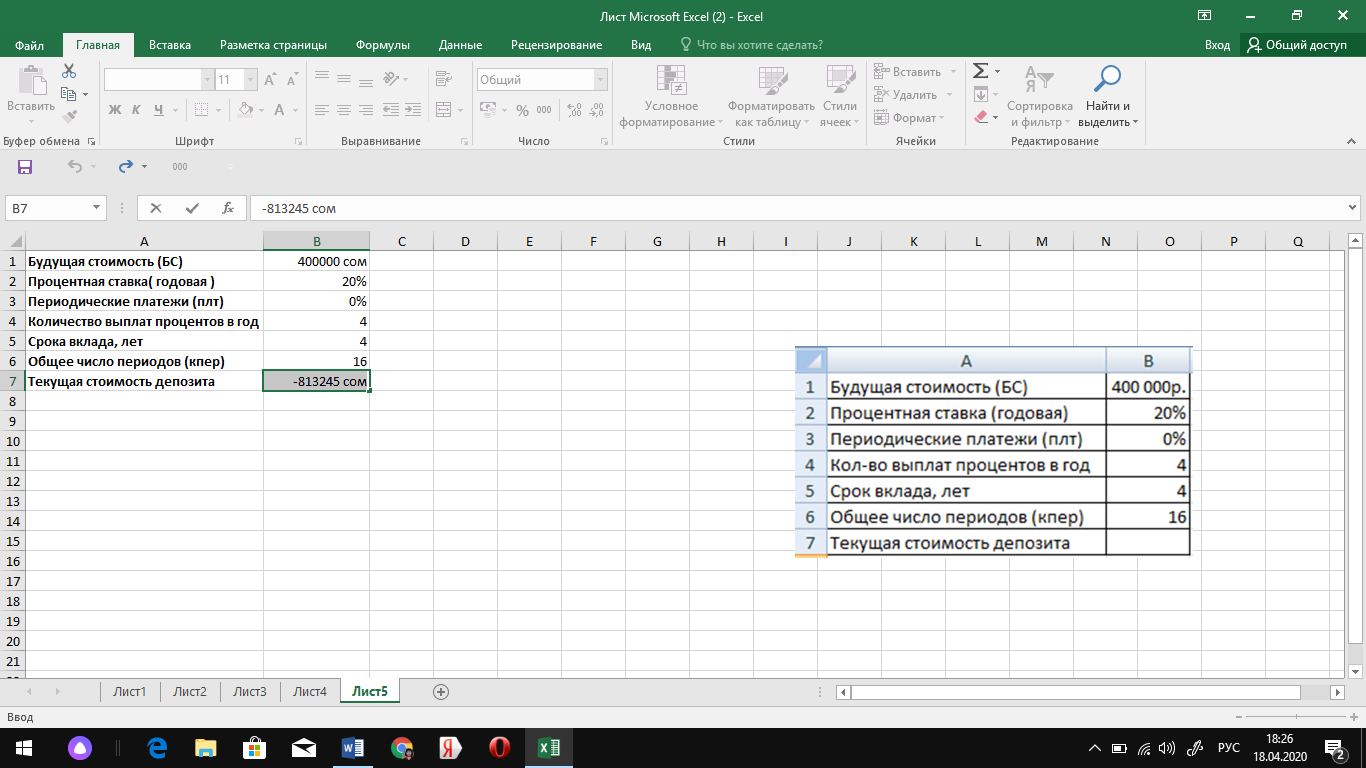
Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)16 = 183245 сом.
21
1. Цель работы
Ознакомление с финансовыми функциями.
2.Основные теоретические положения
ВExcel имеется около 50 функций, специально предназначенных для финансовых расчетов. В данной работе рассмотрим вычисления, связанные с начислением процентов.
Пусть на срок t предоставлена в кредит некоторая сумма Р. За использование кредита надо платить. Возврат кредита составит S=P+I. Плата I носит название “процент”. Чем больше время, на которое выдается кредит, тем больше процент. В простейшем случае полагают
I = P r t,
где r – процентная ставка.
Величина наращенной суммы для схемы простых процентов (когда проценты начисляются каждый период на начальную сумму кредита)
|
определяется по формуле |
|
|
S = P + I = P + P r t = P ( 1 + r t ). |
(1) |
Для схем сложных процентов (когда процент начисляется на наращенную
|
сумму, полученную за предыдущий период) используется формула |
|
|
S=P(1+r)t . |
(2) |
Большинство финансовых функций Excel используют эти формулы.
3. Порядок выполнения работы
Задание 1. Вычислить размер возвращаемой ссуды, используя формулу (1). Задание 2. Вычислить размер возвращаемой ссуды, используя финансовую
функцию БЗ (будущее значение).
Задание 3. Вычислить размер возвращаемой ссуды по схеме сложных процентов.
Задание 4. Рассчитать постоянную ренту, используя функцию БС (будущая сумма).
Задание 5. Используя функцию ПС (приведенная или современная Сумма), рассчитать сумму денег, которую можно получить под вексель.
Задание 6. Рассчитать срок вклада, необходимый для наращения нужной суммы.
Задание 7. Рассчитать процентную ставку кредита.
3.1. Выполнение задания 1
Рассмотрим порядок вычисления размера возвращаемой ссуды на следующем примере. В примере 1 и далее приведены фрагменты табл. 11.
ПРИМЕР 1 Ссуда в размере 1 млн долларов выдана 5 января 2005 г. по 20 сентября 2005 г.
включительно. Годовая процентная ставка – 15 %. Какую сумму придется заплатить должнику в конце срока?
22
РЕШЕНИЕ Процентная ставка дана годовая, но срок ссуды меньше, значит, следует
пересчитать ставку (или период), на который выдана ссуда. Произведем расчеты в Excel.
3.1.1.Ввод исходных данных в таблицу В ячейки А1:В8 введите текст и исходные данные задачи.
3.1.2. Расчет доли года. Ввод комментариев Для пересчета процентной ставки нужно знать, какую долю года составит
срок кредита. В ячейку В10 введите формулу =В7-В6. Установите для ячейки В10 числовой формат.
В ячейке В10 появится результат – 258 (период вклада в днях). Произведем пересчет в долях года, для этого в ячейку В11 введите формулу =В10/365. Итог расчета дает 0,71 года.
Для наглядности в столбец С введите комментарии – те же формулы из смежных ячеек столбца В, но перед знаком = вводите знак апостроф. Например: ‘= В7 – В6. В столбце С вычисления производиться не будут.
3.1.3. Расчет процентной ставки В ячейку В12 введите формулу для пересчета процентной ставки =В5*В11.
Ставка за период составила 11, а не 15 %. Теперь при подстановке значений в формулу (1) нужно брать либо рассчитанную долю года, либо 11 % вместо 15.
3.1.4. Расчет суммы возврата По формуле (1) наращенная сумма равна
|
255 |
|||||||||
|
S=P(1+rt)=1000000 1 |
+ 15% |
1 |
=1 104 795. |
||||||
|
365 |
|||||||||
|
255 |
|||||||||
|
Здесь r =15 % |
; t = 1. |
||||||||
|
365 |
|||||||||
Введите в ячейку В13 формулу =В8*(1+B5*В11) для расчета возвращаемой суммы, используя формулу (1).
|
Таблица 11 |
|||
|
А |
В |
С |
|
|
1 |
ФИНАНСОВЫЕ ВЫЧИСЛЕНИЯ В Excel |
||
|
2 |
Задание 1. Расчет возвращаемой суммы при получении кредита |
||
|
3 |
Исходные данные |
||
|
4 |
Переменные |
Вычисления |
Формулы и комментарии |
|
5 |
Годовая ставка |
15% |
|
|
6 |
Дата выдачи кредита |
05.01.05 |
|
|
7 |
Дата возврата кредита |
20.09.05 |
|
|
8 |
Сумма кредита |
$1 000 000 |
|
|
9 |
Расчеты |
||
|
10 |
Срок кредита в днях |
258 |
‘=В7-В6 |
|
11 |
Срок кредита в годах |
0,71 |
‘=В10/365 |
|
12 |
Ставка для периода |
11% |
‘=В5*В11 |
|
13 |
Сумма возврата |
$1 106 027,4 |
‘=В8*(1+В5*В11) |

23
3.2. Выполнение задания 2
3.2.1. Описание функции БС (будущая сумма)
Вычисления для примера 1 можно осуществить гораздо проще, если использовать финансовую функцию БС (будущая сумма). Ее синтаксис имеет вид:
=БС(ставка; количество периодов; выплаты; начальное значение; тип),
где
ставка – процентная ставка за период; выплаты – вводится, если имеются промежуточные выплаты;
начальное значение – ссуда;
тип – вводится равным единице, если промежуточные выплаты производят в начале периода, и равным нулю (или вообще не вводится), если выплаты производят в конце периода.
Примечание 1! При работе с операционной системой Windows 98 следует иметь в виду, что эта функция будет иметь название БЗ (Будущее Значение).
Примечание 2! Следует иметь в виду, что функцию БС можно использовать для расчета по схеме простых процентов только в том случае, если начисление процентов проводится только за один период.
3.2.2. Вызов функции БС Активизируйте ячейку В16, затем щелкните по пиктограмме Мастер
функций. В окне Категория выберите Финансовые, а в окне Функция
выберите БЗ и щелкните ОК. 3.2.3. Ввод аргументов
•в поле Ставка введите В12;
•в поле Количество периодов – введите 1;
•поле Выплаты пропустите;
•в поле НЗ (начальное значение) – введите В8.
В результате в ячейке В16 появится такая же сумма, что и в ячейке В13, но со знаком минус.
Обратите внимание! В финансовых функциях Excel, если сумму отдают, то она отображается со знаком минус, а если получают то со знаком плюс.
|
А |
В |
С |
|
|
15 |
Задание 2. Расчет возврата |
ссуды с использованием функции БС |
|
|
16 |
— $1 106 027,4 |
‘=БС(В12;1;;В8) |
3.3. Выполнение задания 3
ПРИМЕР 2 В банк на 5 лет помещен вклад в размере 50 000 руб. под 12 % годовых с
ежеквартальным начислением. Какую сумму получит вкладчик через 5 лет? РЕШЕНИЕ
В условии приведена годовая ставка, но начисление процентов ведется каждый квартал. Значит, процентная ставка за период равна
rпериод=rгод4 =124%=3%.
24
Значит, по формуле (2) получим
|
S = P(1+ r) |
t |
12 % |
5 |
|||
|
= 50 000 1 |
+ |
=57 963,7 руб. |
||||
|
4 |
3.3.1. Ввести в строку 17 комментарий к примеру
|
A |
B |
C |
|
|
17 |
Задание 3. Расчет по схеме сложных процентов |
||
|
18 |
57 693,70р. |
‘=БС(12%/4;5;;-50000) |
3.3.2. В ячейку В18 ввести формулу для вычисления наращенной суммы
(аналогично пп. 3.2.2): =БС(12%/4;5;;-50000).
3.3.3. В ячейку С18 ввести ту же формулу с апострофом (комментарий).
3.4. Выполнение задания 4
Финансовые схемы с многократными взносами или выплатами называются
Постоянными рентами.
ПРИМЕР 3 На счет в банке вносят сумму $ 20 000 в течение 10 лет равными долями в
конце каждого года. Годовая ставка равна 22 %. Какая сумма будет на счете по истечении 10 лет?
РЕШЕНИЕ 3.4.1. Ввод исходных данных в таблицу
Введите в ячейки А20:В25 текст и исходные данные из табл. 11. 3.4.2. Использование функции БС и ввод аргументов
Вячейку В27 введите формулу для расчета накопленной суммы при взносах
вконце периода. Для этого:
•активизируйте ячейку В27;
•щелкните по пиктограмме Мастер функций;
•выберите в списке категорий функций Финансовые;
•выберите в списке финансовых функций – функцию БС;
•в поле Ставка введите В25;
•в поле Количество периодов введите 1;
•в поле Выплаты введите –2000 (знак минус означает, что деньги отдают);
•остальные поля в данном случае пропускаются;
•щелкните ОК.
3.4.3. Расчет накопленной суммы при взносах в начале периода
•активизируйте ячейку В28;
•щелкните по пиктограмме Мастер функций;
•выберите в списке категорий функций Финансовые;
•выберите в списке финансовых функций – функцию БС;
•щелкните ОК;
•в поле Ставка введите В25;
•в поле Количество периодов введите 10;
•в поле Выплаты введите –2000 (знак минус означает, что деньги отдают);
25
•поле НЗ пропустите;
•в поле Тип введите 1, так как выплаты производят в начале периода;
•щелкните ОК.
По результатам расчетов видно, что накопленная сумма в последнем случае
выше.
|
А |
B |
C |
|
|
20 |
Задание 4. Расчет постоянной ренты с использованием функции БЗ |
||
|
21 |
Исходные данные |
||
|
22 |
Переменные |
Вычисления |
Формулы и комментарии |
|
23 |
Срок |
10 |
|
|
24 |
Сумма |
$20 000 |
|
|
25 |
Годовая ставка |
22% |
|
|
26 |
Расчеты |
||
|
27 |
Плата в конце периода |
$57 314,83 |
‘=БС(В25;10;-2000) |
|
28 |
Плата в начале периода |
$69 924,09 |
‘=БС(В25;10;-2000;;1) |
3.5. Выполнение задания 5
В финансовых вычислениях часто решают задачу, обратную описанной в примере 1. Рассмотрим следующий пример.
ПРИМЕР 4 Вексель на 4 млн долларов с процентной ставкой 18 % и начислением
процентов дважды в год выдан на три года. Найти исходную сумму, выданную под этот вексель.
РЕШЕНИЕ Для решения этой задачи используют функцию ПС (приведенная или
современная сумма). Синтаксис этой функции =ПС(ставка; количество периодов; выплаты; будущее значение; тип).
Все аргументы этой функции те же, что и у функции БС, только четвертым аргументом стоит не начальное, а будущее значение.
Примечание! При работе с ОС Windows 98 данная функция называется ПЗ (Приведенное Значение).
3.5.1. Ввод исходных данных Введите в ячейки А30:В36 текст и исходные данные из табл. 11.
3.5.2. Вычисление процентной ставки за период В задании приводится годовая учетная ставка, а начисление процентов
ведется дважды в год. Поэтому в ячейку В38 введите формулу, вычисляющую процентную ставку за полгода =В33/В34.
3.5.3. Вычисление исходной суммы, выданной по векселю
•активизируйте ячейку В39;
•щелкните по пиктограмме Мастер функций;
•выберите в списке категорий функций Финансовые;
•выберите в списке финансовых функций функцию ПЗ;
•щелкните ОК;
•в поле Ставка введите В38;
26
•в поле Количество периодов введите В34*В36;
•поле Выплаты пропустите (промежуточных выплат нет);
•в поле БС введите В35;
•поле Тип пропустите;
•щелкните ОК.
Врезультате в ячейке В39 появилось значение 2 385 069,32. Итак, под вексель 4 млн долларов можно получить сумму $2 385 069.
|
А |
В |
С |
|
|
30 |
Задание 5. Расчет платы за вексель с использованием функции ПЗ |
||
|
31 |
Исходные данные |
||
|
32 |
Переменные |
Вычисления |
Формулы и комментарии |
|
33 |
Процентная ставка |
18% |
|
|
34 |
Периодичность выплат |
2 |
|
|
35 |
Будущее значение |
-$4 000 000 |
|
|
36 |
Количество лет |
3 |
|
|
37 |
Расчеты |
||
|
38 |
Процент за период |
9% |
‘=В33/В34 |
|
39 |
Современное значение |
$2 385 069,31 |
‘=ПС(В38;В34*В36;;В35) |
3.6. Выполнение задания 6
Обратимся к задаче определения продолжительности срока ссуды при заданных современном, будущем значениях и процентной ставки.
ПРИМЕР 5 За какой срок сумма, равная 80 рублям, достигает 300 000 рублей при
начислении процентов по ставке 15 % раз в году и поквартально? РЕШЕНИЕ
Воспользуемся функцией КПЕР (количество периодов). Ее синтаксис: =КПЕР(ставка; выплаты; начальное значение; будущее значение; тип). Все аргументы этой функции известны из предыдущих заданий.
3.6.1. Ввод заголовка примера 5 (см. табл. 12).
3.6.2. Определениечислапериодоввгодахприначислениипроцентовразвгоду
•активизировать ячейку В42;
•щелкните по пиктограмме Мастер функций;
•выберите в списке категорий функций Финансовые;
•выберите в списке финансовых функций функцию КПЕР;
•щелкните ОК;
•в поле Ставка введите 15 %;
•в поле Выплаты введите 0 (или пропустите);
•в поле Начальное значение введите –80 (знак минус – отдаем);
•в поле БС введите 300000;
•поле Тип пропустите;
•щелкните ОК.
Врезультатевычисленийпериоднакоплениязаданнойсуммысоставит59 лет.
|
27 |
|||
|
А |
В |
С |
|
|
41 |
Задание 6. Расчет срока вклада с использованием функции КПЕР |
||
|
42 |
Начисление раз в год |
59 |
‘=КПЕР(15%;0;-80;300000) |
|
43 |
По кварталам |
56 |
‘=КПЕР(15%/4;0;-80;300000)/4 |
3.6.3. Определение числа периодов в годах при начислении процентов поквартально
•активизируйте ячейку В43;
•щелкните по пиктограмме Мастер функций;
•выберите в списке категорий функций Финансовые;
•выберите в списке финансовых функций функцию КПЕР;
•щелкните ОК;
•в поле Ставка введите 15%/4 (начисление процентов производят четыре раза в год и за каждый квартал ставка в четыре раза меньше);
•в поле Выплаты введите 0 (или пропустите);
•в поле Начальное значение введите –80 (знак минус – отдаем);
•в поле БС введите 300000;
•поле Тип пропустите;
•щелкните ОК.
Вячейке В43 введена формула =КПЕР(15%/4;0;-80;300000), которая рассчитывает интересующее нас число в кварталах, а нас интересует срок накоплений в годах.
3.6.4. Редактирование формулы КПЕР
•активизируйте ячейку В43;
•установите курсор в строке формул в конец выражения и после скобки наберите с клавиатуры /4 (см. табл. 12);
•нажмите Enter.
Врезультате вычисляется, что период накопления заданной суммы составит
56 лет.
Вывод: при начислении процентов по кварталам срок накопления заданной суммы меньше, чем при ежегодном начислении.
3.7. Выполнение задания 7
ПРИМЕР 6 В долг на 4 года предоставлена ссуда $ 4000 с условием возврата $ 6000.
Определить процентную ставку ссуды. РЕШЕНИЕ
Для расчета процентной ставки используется функция =СТАВКА (количество_периодов;выплаты;начальное_значение;будущая_
сумма;тип;начальное_приближение).
Здесь аргумент Начальное приближение вводится, если можно сделать предположение о значении процентной ставки. В противном случае этот аргумент опускается.
ВWindows 98 эта функция называется Норма.
3.7.1.В строку 45 ввести заголовок примера.
28
3.7.2.В ячейку В46 ввести формулу для расчета процентной ставки:
• Вставка – Функция – Финансовые – Ставка – Ок;
• ввести аргументы согласно табл. 12.
3.7.3.В ячейку С46 ввести ту же формулу с апострофом для комментария.
|
Таблица 12 |
||||
|
А |
В |
С |
||
|
1 |
ФИНАНСОВЫЕ |
ВЫЧИСЛЕНИЯ В Excel |
||
|
2 |
Задание 1. Расчет возвращаемой суммы при получении кредита |
|||
|
3 |
Исходные данные |
|||
|
4 |
Переменные |
Вычисления |
Формулы и комментарии |
|
|
5 |
Годовая ставка |
15% |
||
|
6 |
Дата выдачи кредита |
05.01.02 |
||
|
7 |
Дата кредита |
20.09.02 |
||
|
8 |
Сумма возврата |
$1 000 000 |
||
|
9 |
Расчеты |
|||
|
10 |
Срок кредита в днях |
258 |
‘=В7-В6 |
|
|
11 |
Срок кредита в годах |
0,71 |
‘=В10/365 |
|
|
12 |
Ставка для периода |
11% |
‘=В5*В11 |
|
|
13 |
Сумма возврата |
$1 106 024.4 |
‘=В8*(1+В5*В11) |
|
|
14 |
||||
|
15 |
Задание 2. Расчет возврата ссуды с использование функции БС |
|||
|
16 |
$1 106 024.4 |
‘=БС(В12;1;;В8) |
||
|
17 |
Задание 3. Расчет по схеме сложных процентов |
|||
|
18 |
57 693,70р. |
‘=БС(12%/4;5;;-50000) |
||
|
19 |
||||
|
20 |
Задание 4. Расчет постоянной ренты с использованием функции БС |
|||
|
21 |
Исходные данные |
|||
|
22 |
Переменные |
Вычисления |
Формулы и комментарии |
|
|
23 |
Срок |
10 |
||
|
24 |
Сумма |
$20 000 |
||
|
25 |
Годовая ставка |
22% |
||
|
26 |
Расчеты |
|||
|
27 |
Плата в конце периода |
$57 314,83 |
‘=БС(В25;10;-2000) |
|
|
28 |
Плата в начале периода |
$69 924,09 |
‘=БС(В25;10;-2000;;1) |
|
|
29 |
||||
|
30 |
Задание 5. Расчет платы |
за вексель с |
использованием функции ПЗ |
|
|
31 |
Исходные данные |
|||
|
32 |
Переменные |
Вычисления |
Формулы и комментарии |
|
|
33 |
Процентная ставка |
18% |
||
|
34 |
Периодичность выплат |
2 |
||
|
35 |
Будущее значение |
-$4 000 000 |
||
|
36 |
Количество лет |
3 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Практическая работа №9
ФИНАНСОВЫЕ ФУНКЦИИ MS EXCEL В
ЭКОНОМИЧЕСКИХ РАСЧЕТАХ
Цель:
научиться использовать финансовые функции для экономических расчётов.
Задания:
|
1. |
Функции даты и времени для финансовых |
Время – один из важнейших факторов в
финансовых операциях и сделках. Для проведения финансовых расчетов необходимо
находить срок между начальной и конечной датами операции, обычно заданный в
днях или годах.
Если рассчитывается точное число дней, то
надо просто вычесть из конечной даты (даты завершения операции) начальную
дату.
Однако в финансовой практике есть правило,
согласно которому в месяце считается 30 дней, а в году 360. В этом случае
используется функция ДНЕЙ360. Ее назначение – расчет количества дней между
двумя датами на основе 360-дневного года (12 30-дневных месяцев), аргументы:
нач_дата – начальная дата сделки; кон_дата – конечная дата сделки; метод –
логическое значение, если отсутствует, есть «ЛОЖЬ».
Аргументы «нач_дата» и «кон_дата» могут
быть введены как текстовые строки в двойных кавычках или в числовом формате,
могут также использоваться ссылки на ячейки, в которых заданы даты в формате
дата. Если аргумент «метод» принимает значение «ЛОЖЬ» или опущен, то
используется американский метод определения приближенного числа дней между
двумя датами, а если «ИСТИНА» – то европейский (эти два метода различаются,
только если конечная дата – 31-е число месяца).
Для определения срока между датами в годах
надо использовать функцию ДОЛЯГОДА с аргументами (нач_дата, кон_дата,
базис).
Первые два аргумента имеют то же значение,
что и у функции ДНЕЙ360. Аргумент «базис» может принимать пять различных
значений в зависимости от правила, установленного для расчета срока в годах:
0
или опущен – правило 30/360 (приближенный срок между
датами в днях
(американский метод расчета), приближенное
число дней в году);
1
– АСТ/АСТ (точный срок между датами в днях, точное
число дней в году);
2
– АСТ/360 (точный срок между датами в днях,
приближенное число дней в году);
3
– АСТ/365 (точный срок между датами в днях, но в любом
году 365 дней);
4
– 30/360 европейский (приближенный срок между датами в
днях (европейский метод
расчета), приближенное число дней в году).
Пример.
Дата
получения кредита – 15 января 2008 г., дата погашения – 15 марта того же года.
Найти срок кредита в днях и годах.
Решение выполнить на Листе 1.
Откройте Лист 1 и переименуйте его в
Задание 1.
Точное число дней = «15/03/2008» –
«15/01/2008» = 59.
Приближенное число дней =
ДНЕЙ360(«15/01/2008», «15/03/2008») = 60. Срок кредита в годах по правилу
АСТ/АСТ = ДОЛЯГОДА(«15/01/2008»,
«15/03/2008») = 0,161644.
Расчет
ипотечной ссуды осуществляются с использованием финансовой функции ПЛТ
Функция ПЛТ вычисляет величину постоянной
периодической выплаты ренты (например, регулярных платежей по займу) при
постоянной процентной ставке.
Синтаксис: ПЛТ(Ставка;Кпер;Пс;Бс;Тип).
Аргументы:
§ Ставка
– процентная ставка по ссуде,
§ Кпер
– общее число выплат по ссуде,
§ Пс
– приведенная к текущему моменту стоимость, или общая сумма, которая на текущий
момент равноценна ряду будущих платежей, называемая также основной суммой,
§ Бс
– требуемое значение будущей стоимости, или остатка средств после последней
выплаты.
Если
аргумент Бс опущен, то он полагается равным 0 (нулю), т.е. для займа, например,
значение Бс равно 0, Тип – число 0 (нуль) или 1, обозначающее, когда должна
производиться выплата.
Отметим, что очень важно быть
последовательным в выборе единиц измерения для задания аргументов Ставка и
Кпер.
Например,
если вы делаете ежемесячные выплаты по четырехгодичному займу из расчета 12
%
годовых, то для задания аргумента Ставка используйте 12 %/12, а для задания
аргумента Кпер – 4*12. Если вы делаете ежегодные платежи по тому же займу, то
для задания аргумента Ставка используйте 12 %, а для задания аргумента Кпер –
4.
Для нахождения общей суммы, выплачиваемой
на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на
величину Кпер. Интервал выплат – это последовательность постоянных денежных
платежей, осуществляемых за непрерывный период.
Например, заем под автомобиль или заклад
являются интервалами выплат. В функциях, связанных с интервалами выплат,
выплачиваемые вами деньги, такие как депозит на накопление, представляются
отрицательным числом, а деньги, которые вы получаете, такие как чеки на
дивиденды, представляются положительным числом.
Например,
депозит в банк на сумму 1000 руб. представляется аргументом – 1000, если вы
вкладчик,
и аргументом -1000, если вы – пpeдставитель банка.
Пример
1. Вычислить 30-летнюю ипотечную ссуду покупки квартиры за 201900 руб. с
годовой ставкой 8% и начальным взносом 20%. Сделать расчет для ежемесячных и
ежегодных выплат (табл. 1).
Решение:
1.
Откройте Лист 2 и переименуйте его в
Задание 2.
2.
Введите в ячейки A1:B6 данные,
представленные на рис. 1.
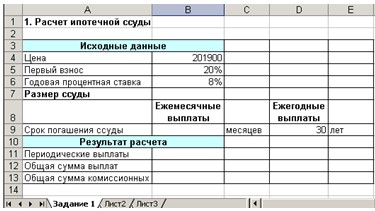
Рис.
1. Форма для расчета ипотечной ссуды
3.
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.
2.
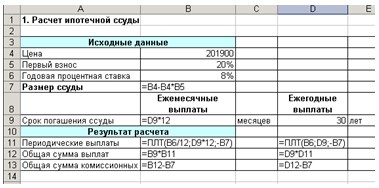
Рис.
2. Формулы для расчета ипотечной ссуды
4.
Результаты расчеты должны быть следующими
(рис. 3):
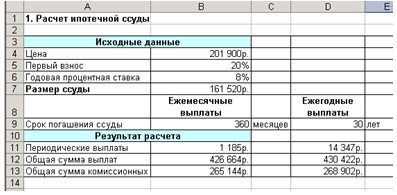
Рис.
3. Расчет ипотечной ссуды
3.
Функции для расчета годовой процентной ставки
Функция ЧПС возвращает чистый текущий
объем вклада, вычисляемый на основе ряда последовательных поступлений наличных
денег и нормы амортизации.
Чистый текущий объем вклада – это
сегодняшний объем будущих платежей (отрицательные значения) и поступлений
(положительные значения).
Например, вам предлагают следующую сделку.
У вас берут в долг некоторую сумму денег и предлагают через k1 лет вернуть
сумму, равную Рk1, через k2 лет – Рk2 и т. д. и, наконец, через kn лет – Рkn.
Кроме данной сделки, у вас есть альтернативный способ использования ваших
денег, например, положить их в банк под i процентов годовых. Тогда чистым
текущим объемом вклада является та сумма денег, которой вам нужно располагать
начальный год, чтобы, положив их в банк под i % годовых, получили предлагаемую
прибыль.
Синтаксис:
ЧПС(Ставка;Значение1;Значение2;…..) Аргументы:
§ ставка
– ставка дисконтирования за один период;
§ значение
1, значение 2, – от 1 до 29 аргументов, представляющих расходы и доходы:
• значение 1,
значение 2, … должны быть равномерно распределены во времени, выплаты должны
осуществляться в конце каждого периода.
ЧПС использует порядок аргументов значение
1, значение 2, … для определения порядка поступлений и платежей. Убедитесь в
том, что ваши платежи и поступления введены в правильном порядке.
Считается, что инвестиция, значение
которой вычисляет функция ЧПС, начинается за один период до даты денежного
взноса 1-го значения и заканчивается с последним денежным взносом в списке.
Вычисления функции ЧПС базируются на
будущих денежных взносах. Если первый денежный взнос приходится на начало
первого периода, то первое значение следует добавить к результату функции ЧПС,
но не включать в список аргументов.
Функция ЧПС
связана с функцией ВСД (внутренняя скорость оборота). ВСД – это скорость
оборота, для которой ЧПС равняется нулю:
ЧПС(ВСД(…);…)=0.
Функция ВСД возвращает внутреннюю скорость
оборота для ряда последовательных операций с наличными деньгами,
представленными числовыми значениями. Объемы операций не обязаны быть
регулярными, как в случае ренты.
Внутренняя скорость оборота – это
процентная ставка дохода, полученного от инвестиций, состоящих из выплат
(отрицательные значения) и поступлений (положительные значения), которые
происходят в регулярные периоды времени.
Синтаксис: ВСД (Значения;Предположение).
Аргументы:
§
значения – массив или ссылка на ячейки, содержащие
числовые величины, для которых вычисляется внутренняя ставка доходности.
Значения должны включать, по крайней мере, одно положительное значение и одно
отрицательное значение, для того чтобы можно было вычислить внутреннюю скорость
оборота.
Функция ВСД
использует порядок значений для интерпретации порядка денежных выплат или
поступлений, поэтому нужно следить, чтобы значения выплат и поступлений
вводились в правильном порядке.
§
предположение – величина, о которой предполагается,
что она близка к результату ВСД.
Для вычисления ВСД Excel использует метод
итераций. Начиная со значения прогноз, функция ВСД выполняет циклические
вычисления, пока не получит результат с точностью 0,00001. Если функция ВСД не
может получить результат после 20 попыток, то возвращается значение ошибки
#ЧИСЛО!
В большинстве случаев нет необходимости
задавать прогноз для вычислений с помощью функции ВСД. Если прогноз опущен, то
он полагается равным 0,1 (10 %).
Если
ВСД выдает значение ошибки #ЧИСЛО! Или результат далек от ожидаемого, можно
попытаться
выполнить вычисления еще раз, но уже с другим значением аргумента прогноз.
Пример
3. Вас просят в долг 10000 руб. и обещают вернуть через год 2000 руб., через
два года – 4000 руб., через три года – 7000 руб. При какой годовой процентной
ставке эта сделка выгодна?
Решение.
1. Откройте Лист 3 и
переименуйте его в Задание 3. 2. Введите в ячейки A1:B7 данные, представленные
на рис. 4.
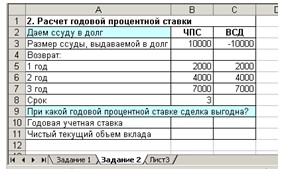
Рис. 4. Форма для расчета годовой
процентной ставки
3.
Для выполнения расчетов в ячейки должны
быть введены формулы, показанные на рис.
5.
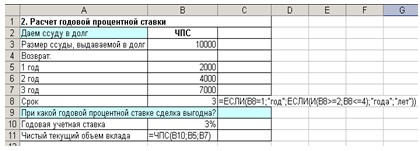
Рис. 5. Формулы для расчета годовой
процентной ставки
4.
Первоначально в ячейку В10 введите
произвольный процент, например 3 %.
В ячейку В11 введите формулу
=ЧПС(В10;В5:В7) (см. рис. 5).
5.
В ячейку С8 введите формулу:
=ЕСЛИ(В8=1;»год»;ЕСЛИ(И(В8>=2;B8<=4)
;»года»;»лет»)) В результате должно получиться (см. рис. 6):
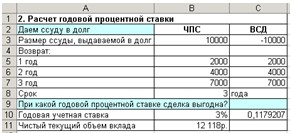
Рис. 6. Расчет чистого текущего объема
вклада
6.
Затем выбираем команду Сервис / Подбор
параметра и заполняем открывшееся
диалоговое окно Подбор параметра, как
показано на рис. 7.
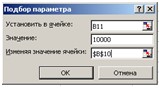
Рис. 7. Диалоговое окно Подбор параметра
при расчете годовой процентной ставки
7.
В поле Установить в ячейке: укажите ссылку
на ячейку В11, в которой вычисляется чистый текущий объем вклада по формуле:
=ЧПС(B10;B5:B7).
В поле Значение установить 10000 – размер
ссуды.
В
поле Изменения значения ячейки укажите ссылку на ячейку В10, в которой
вычисляется годовая процентная ставка.
После
нажатия кнопки ОК средство подбора параметров определит, при какой годовой
процентной ставке чистый текущий объем вклада равен 10000 руб. Результат
вычисления выводится в ячейку В10.
8.
В нашем случае годовая учетная ставка
равна 11,79 %.
Вывод:
если банки предлагают большую годовую процентную ставку, то предлагаемая сделка
не выгодна. 9. Результаты расчеты должны быть следующими:
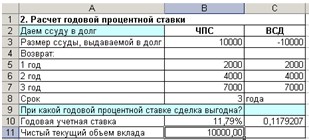
Рис. 8. Расчет годовой процентной ставки
4.  Функции для расчета
Функции для расчета
эффективности капиталовложений
Расчет
эффективности капиталовложений осуществляется с помощью функции ПС.
Функция ПС возвращает текущий объем вклада
на основе постоянных периодических платежей.
Функция ПС аналогична функции ЧПС.
Основное различие между ними заключается в том, что функция ПС допускает, чтобы
денежные взносы происходили либо в конце, либо в начале периода. Кроме того, в
отличие от функции ЧПС, денежные взносы в функции ПС должны быть постоянными на
весь период инвестиции.
Синтаксис:
ПС(Ставка;Кпер;Плт;Бс;Тип) Аргументы:
§
Ставка – процентная ставка за период,
§
Кпер – общее число периодов платежей по аннуитету,
§
Плт – выплата, производимая в каждый период и не
меняющаяся за все время выплаты ренты. Обычно выплаты включают основные платежи
и платежи по процентам, но не включают других сборов или налогов,
§
Бс – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент опущен, он полагается равным 0
(будущая стоимость займа, например, равна 0),
§
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.
Пример
4. У вас просят в долг 10000 руб. и обещают возвращать по 2000 руб. в течение 7
лет. Будет ли выгодна эта сделка при годовой ставке 7 %?
Решение:
1.
Откройте Лист 4 и переименуйте его в
Задание 4.
2.
Введите в ячейки A1:B6 данные,
представленные на рис. 9.
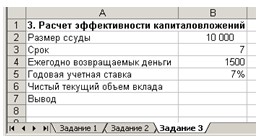
Рис. 9. Форма расчета эффективности
капиталовложений
3.
В ячейку В6 введите формулу:
=ПС(В5;В3;-В4)
4.
В ячейку С3 введите формулу:
=ЕСЛИ(В3=1;
«год»;ЕСЛИ(И(В3>=2;В3<=4); «года»;»лет»))
5. В ячейку В7:
=ЕСЛИ (В2<В6; «Выгодно дать деньги
в долг»; ЕСЛИ(В6=В2; «Варианты равносильны»;
«Выгоднее деньги положить под
проценты»))
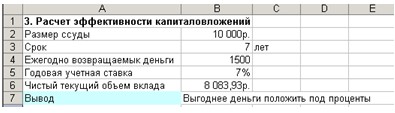
Рис. 10. Расчет эффективности
капиталовложений
5.  Функции для расчета основных
Функции для расчета основных
платежей и платы по процентам
Основные платежи и платы по процентам
вычисляются с помощью формул или финансовых функций ОСПЛТ и ПРПЛТ.
Функция ПРПЛТ возвращает платежи по
процентам за данный период на основе периодических постоянных выплат и
постоянной процентной ставки.
Синтаксис: ПРПЛТ (Ставка; Период; Кпер;
Пс; Бс; Тип).
Функция ОСПЛТ возвращает величину выплаты
за данный период на основе периодических постоянных платежей и постоянной
процентной ставки.
Синтаксис: ОСПЛТ(Ставка; Период; Кпер; Пс;
Бс; Тип).
Аргументы функций ПРПЛТ: и ОСПЛТ:
§
Ставка – процентная ставка за период,
§
Период – задает период, значение должно быть в
интервале от 1 до «Кпер»,
§
Кпер – общее число периодов выплат годовой ренты,
§
Пс – приведенная стоимость, то есть общая сумма,
которая равноценна ряду будущих платежей,
§
Бс – требуемое значение будущей стоимости, или остатка
средств после последней выплаты.
Если аргумент Бс
опущен, то он полагается равным 0 (нулю), то есть для займа, например, значение
Бс равно 0.
§
Тип – число 0 или 1, обозначающее, когда должна
производиться выплата.
Функции
ПРПЛТ и ОСПЛТ тесно связаны между собой, а именно ПЛПj= i Bj-1, ОСНПj = А —
ПЛПj,
Bj = Вj-1 — ОСНПj при j ∈[0,
n], где j – номер периода, п – КПЕР,
ПЛПj,
ОСНПj и Bj – это ПРПЛТ, ОСПЛТ и остаток долга, соответственно, за j-й период,
ПЛПо
= 0, ОСНПо = 0, Bо – Пс,
А – величина выплаты за один период
годовой ренты на основе постоянных выплат и постоянной процентной ставки,
вычисляемая с помощью функции ПЛТ.
Пример
5. Вычислить основные платежи, платы по процентам, общей ежегодной платы и
остатка долга на примере ссуды 100000 руб. на срок 5 лет при годовой ставке 2
%.
Решение:
1.
Откройте Лист 5 и переименуйте его в
Задание 5.
2.
Введите данные, представленные на рис. 13.
3.
Ежегодная плата вычисляется в ячейке В4 по
формуле: =ПЛТ(процент; срок; -размер_ссуды), где ячейки В2, В3 и В5 имеют
имена: процент, срок и размер_ссуды, соответственно.
4.
За первый год плата по процентам в ячейке
В8 вычисляется по формуле:
=D7*процент.
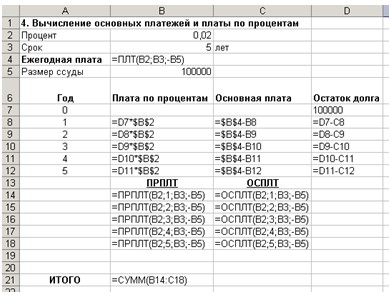
Рис. 13. Функции для вычисления основных
платежей и платы по процентам.
5.
Основная плата в ячейке С8 вычисляется по
формуле: =ежегодная_плата-В8, где ежегодная_плата – имя ячейки В4.
Остаток долга в ячейке D8
вычисляется по формуле: =D7-C8.
6.
В оставшиеся годы эти платы определяются с
помощью протаскивания маркера заполнения выделенного диапазона B8:D8 вниз по
столбцам.
7.
Данные результаты расчетов должны быть
следующими (рис. 14.):
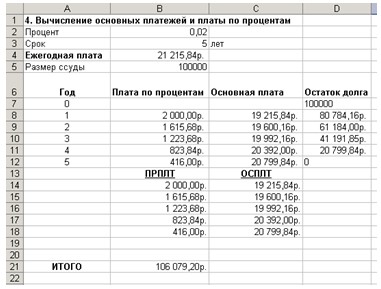
Рис. 14. Вычисление основных платежей и
платы по процентам
6. Функции для расчета
будущего значения вклада, процентной ставки и количества периодов выплаты долга
Функция БС вычисляет будущее значение
вклада на основе периодических постоянных платежей и постоянной процентной
ставки.
Функция
БС подходит для расчета итогов накоплений при ежемесячных банковских взносах. Синтаксис:
БС (Ставка; Кпер; Плт; Пс; Тип).
Аргументы:
§
Ставка – процентная ставка за период,
§
Кпер – общее число периодов выплат,
§
Плт – величина постоянных периодических платежей,
§
Пс – текущее значение, то есть общая сумма, которую
составят будущие платежи, § Тип – число 0 или 1,
обозначающее, когда должна производиться выплата.
Если
тип равен 0 или опущен, то оплата производится в конце периода, если 1 – в
начале
периода.
Если тип = 0 и БС = 0, то функция БС вычисляется по формуле (6):
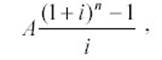
где
А – Плт; i – Ставка; n – Кпер.
Функция КПЕР вычисляет общее количество
периодов выплаты для данного вклада на основе периодических постоянных выплат и
постоянной процентной ставки.
Синтаксис: КПЕР(Ставка; Плт; Пс; БС; Тип).
Аргументы:
§
Ставка – процентная ставка за период,
§
Плт – величина постоянных периодических платежей,
§
Пс – текущее значение, т.е. общая сумма, которую
составят будущие платежи,
§
БС – будущая стоимость или баланс наличности, который
нужно достичь после последней выплаты.
Если аргумент БС опущен, он полагается
равным 0 (например, будущая стоимость займа равна 0), тип – число 0 или 1,
обозначающее, когда должна производиться выплата. Если тип равен 0 или опущен,
то оплата производится в конце периода, если 1 – то в начале периода. Если тип
= 0 и БС = 0 функция КПЕР вычисляется по формуле (7):
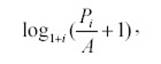
где
Р – ПС; i – Ставка; А – Плт.
Пример
6. Вы хотите зарезервировать деньги для специального проекта, который будет
осуществлен через год. Предположим, вы собираетесь вложить 1000 руб. при
годовой ставке 6 %. Вы собираетесь вкладывать по 100 руб. в начале каждого
месяца в течение года. Сколько денег будет на счете в конце 12 месяцев?
Решение:
1.
Откройте Лист 6 и переименуйте его в
Задание 6.
2.
Ведите данные в ячейки А1:С6 (см. рис.
15).
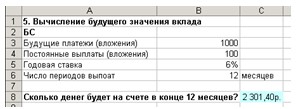
Рис. 15. Расчет будущего значения вклада
3.
В ячейку С8 введите формулу:
=БС(6 %/12; 12; -100;
-1000; 1) получаем ответ: 2 301,40 руб (см. рис. 16).
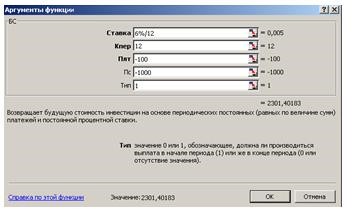
Рис. 16. Диалоговое окно Аргументы функции
БС
Пример
7. Вы берете в долг 1000 руб. при годовой ставке 1% и собираетесь выплачивать
по 100 руб. в год, Какое будет число выплат долга?
Решение:
1.
Откройте Лист 7 и переименуйте его в
Задание 7.
2.
Ведите данные в ячейки А1:В6 (см. рис.
17).
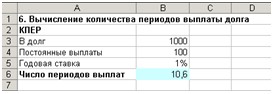
Рис. 17. Расчет количества периодов выплат
3.
В ячейку В6 введите формулу: =КПЕР(B5;
-B4; B3) В результате получаем ответ: ≈11. (см. рис. 18).
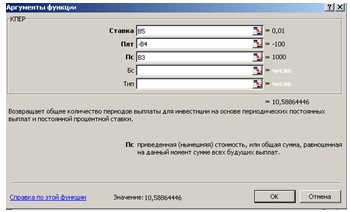
Рис. 18. Диалоговое окно Аргументы функции
КПЕР
Вычисление
процентной ставки
Функция СТАВКА вычисляет процентную
ставку, необходимую для получения определенной суммы в течение заданного срока
путем постоянных взносов, за один период.
Следует отметить, что функция СТАВКА
вычисляет процентную ставку методом итераций, поэтому решение может быть и не
найдено. Если после 20 итераций погрешность определения ставки превышает
0,0000001, то функция СТАВКА возвращает значение ошибки #ЧИСЛО!
Синтаксис: СТАВКА(КПЕР; Плт; Пс; БС; Тип;
Предположение).
Аргументы:
§
КПЕР – общее число периодов платежей по аннуитету;
§
Плт – регулярный платеж (один раз в период), величина
которого остается постоянной в течение всего срока аннуитета. Обычно Плт состоит
из платежа основной суммы и платежа процентов, но не включает других сборов или
налогов. Если аргумент опущен, должно быть указано значение аргумента БС;
§
Пс – приведенная к текущему моменту стоимость или
общая сумма, которая на текущий момент равноценна ряду будущих платежей;
§
БС – требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент БС опущен, то он полагается
равным 0 (например, БС для займа равно 0); тип – число 0 или 1, обозначающее,
когда должна производиться выплата; предположение – предполагаемая величина
ставки.
Если
БС = 0 и тип = 0, функция СТАВКА является корнем уравнения (8):
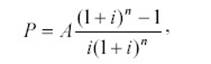
Пример
8. Определить процентную ставку для четырехлетнего займа размером в 8000 руб. с
ежемесячной выплатой 200 руб.
Решение:
1.
Откройте Лист 8 и переименуйте его в
Задание 8.
2.
Ведите данные в ячейки А1:В7 (см. рис.
19).
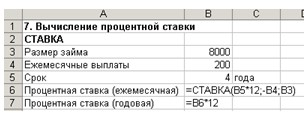
Рис. 19. Расчет процентной ставки
3.
В ячейку В6 введите формулу:
=СТАВКА(B5*12;-B4;B3).
4.
В ячейку В7 введите формулу: = В6*12.
В
результате получаем: месячная (так как период равен месяцу) процентная ставка
равна 0,77 %. Процентная ставка годовая равна 9 % см. рис 20).
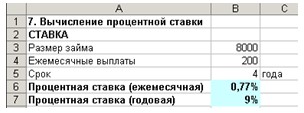
Рис.20. Результаты вычисления процентной
ставки
Контрольные вопросы:
1.
Как
рассчитать дату и временя с использованием финансовых функций?
2.
Каким
образом можно рассчитать ипотечную ссуду, годовую процентную ставку в Excel?
3.
Назовите
функции расчета постоянных рент.
Министерство образования и науки Республики Казахстан
Гуманитарно-технический колледж
Сборник экономических задач
для среды Microsoft Excel
Кокшетау – 2010 год
Сборник экономических задач для среды Microsoft Excel
Автор: Кучукова Тлеш Толегеновна,
преподаватель первой категории,
магистр экономики
Пособие для учащихся специальности «Информационные системы (в экономике)»,
а также для учащихся экономических специальностей, очной и заочной формы обучения, Кокшетау, 2010, 16 с.
В сборнике помещены задачи по основным темам изучения табличного процессора Microsoft Excel, содержащие экономическую направленность, в последовательном порядке, по степени сложности (от простого к сложному). Сборник полезен при организации практических занятий и индивидуальной работы с учащимися.
Тема работы: Ввод данных и формул в ячейки. Форматирование таблицы.
Задание 1. Создайте таблицу по образцу; заполните пустые ячейки (в формулах использовать относительные ссылки на ячейки); оформите таблицу (Автоформат – Классический 2); содержимое ячеек с числами выровнять по правому краю, с текстом – по левому краю.
|
Расчет повременной заработной платы |
|||||
|
Фамилия |
Ставка за час, в тенге |
Кол-во отработанных часов |
Итого начислено |
ИПН |
К выдаче |
|
Абилов А.О. |
569 |
157 |
|||
|
Петров К.Д. |
412 |
134 |
|||
|
Ахметова Б.Т. |
231 |
162 |
|||
|
Хамитов Т.К. |
455 |
278 |
|||
|
Михайлова В.И. |
378 |
115 |
|||
|
Дубинин А.П. |
267 |
54 |
|||
|
Всего: |
Задание 2. Подготовить таблицу для начисления пени в соответствии с образцом.
|
Оплата коммунальных услуг задержана на |
дней |
||
|
Вид оплаты |
Начисленная сумма |
Пени |
Всего к оплате |
|
Квартплата |
|||
|
Газ |
|||
|
Электричество |
|||
|
Телефон |
|||
|
Итого: |
Всего к оплате считается как Сумма начисления + Пени.
Наберите формулу в ячейке Всего к оплате за Квартплату (использовать абсолютную ссылку на количество дней) и распространите ее (примените автозаполнение) для остальных видов платежей.
Тема работы: Копирование формул. Фильтры. Сортировка данных.
Задание 1. Создайте таблицы по образцу; заполните пустые ячейки таблицы 2 (в формулах свяжите ячейки обеих таблиц); оформите таблицы; отсортируйте данные таблицы 2 по фамилиям в порядке возрастания; выберите из таблицы 2 тех, чья доля составляет больше 40 %; результат работы сохраните в файле.
|
Номинал акций |
Состав учредителей акционерного общества (таб. 2) |
|||||||
|
Вид акции |
Номинал акций, тг. |
Фамилия акционера |
Кол-во акций 1-го выпуска |
Кол-во акций 2-го выпуска |
Кол-во привиле-гирован-ных акций |
Итого акций на сумму, в тг. |
Доля акционера, в % |
|
|
Простые 1-го выпуска |
20 |
Борисов А.Т. |
160 |
80 |
50 |
|||
|
Простые 2-го выпуска |
50 |
Васильев П.П. |
135 |
95 |
0 |
|||
|
Привилегиро-ванные |
150 |
Дудкина А.В. |
270 |
125 |
125 |
|||
|
Костин Ф.С. |
315 |
0 |
85 |
|||||
|
Савина О.Д. |
120 |
120 |
90 |
|||||
|
Семенов Я.С. |
500 |
350 |
380 |
|||||
|
Итого: |
178000 |
100% |
Задание 2. Сравнить доходную часть городского бюджета в 2005 и 2006 году.
|
Статья |
2005 г. (отчет), в тыс.тг. |
Удельный вес, в % |
2006 г. (отчет) тыс.тг. |
Удельный вес, в % |
Изменение (+,-) |
В %% к 2005 г. |
|
Налоговые доходы |
||||||
|
1. Налоги на прибыль (доход), прирост капитала |
347660 |
666562 |
||||
|
2. Налоги на товары и услуги, лицензионные сборы |
396110 |
142887 |
||||
|
3. Налоги на совокупный доход |
53810 |
35696 |
||||
|
4. Налоги на имущество |
266900 |
107253 |
||||
|
5. Платежи за пользование природными ресурсами |
102600 |
382380 |
||||
|
6. Прочие налоги, пошлины и сборы |
236580 |
274296 |
||||
|
Неналоговые доходы |
||||||
|
1. Доходы на имущества, находящегося в гос. собственности |
10690 |
37366 |
||||
|
2. Административные платежи и сборы |
9500 |
4500 |
||||
|
3. Штрафные санкции |
3500 |
3600 |
||||
|
Итого доходов |
=100% |
=100% |
Задание 3. Рассчитать поступление и расходование денежных средств избирательных фондов зарегистрированных кандидатов в депутаты на должность главы администрации.
|
Показатели |
ФИО зарегистрированного кандидата |
|||||
|
Полесов В.М. |
Чарушников М.П. |
Кислярский М.Б. |
||||
|
Сумма, тыс.тг |
% к всего |
Сумма, тыс.тг |
% к всего |
Сумма, тыс.тг |
% к всего |
|
|
Поступило средств всего, |
||||||
|
в том числе: от избирательной комиссии |
2000 |
2000 |
2000 |
|||
|
собственные средства кандидата |
800 |
800 |
2000 |
|||
|
пожертвования юридических лиц |
125000 |
1057300 |
4193410 |
|||
|
пожертвования физических лиц |
0 |
0 |
10590 |
|||
|
Израсходовано средств всего, |
||||||
|
в том числе: радио и телевидение |
0 |
334112 |
752600 |
|||
|
печатные издания |
114418 |
604582 |
1332990 |
|||
|
публичные мероприятия |
0 |
7780 |
200330 |
|||
|
канцелярские расходы |
0 |
4169 |
106040 |
|||
|
аренда помещений и автотранспорта |
8800 |
14392 |
95170 |
|||
|
прочие расходы |
4940 |
30231 |
1172180 |
|||
|
Остаток неизрасходованных средств |
Задание 4. Рассчитать доход от реализации колбасных изделий.
|
Наименование изделий |
Объем производства, в тг. |
Цена за кг, в тг. |
Торгово-сбытовая скидка, в % |
Цена со скидкой, в тг. |
Сумма, в тг. |
|
Колбаса пермская, п/к, 1с. |
5 |
50 |
8 |
||
|
Колбаса одесская, п/к, 1с. |
12 |
60 |
8 |
||
|
Колбаски охотничьи, п/к, вс. |
2 |
79 |
8,5 |
||
|
Колбаса польская, п/к, 2с. |
14 |
46 |
7,8 |
||
|
Колбаса таллинская, п/к, вс. |
3 |
66 |
8,5 |
||
|
Всего: |
Задание 5. Сформировать и заполнить накопительную ведомость по переоценке основных средств производства.
|
Наименование объекта |
Балансовая стоимость |
Износ |
Остаточная стоимость |
Восстановительная полная стоимость |
Восстановительная остаточная стоимость |
|
Заводоуправление |
12556,4 |
589,3 |
|||
|
Диспечерская |
184,0 |
51,2 |
|||
|
Цех №1 |
954,4 |
235,1 |
|||
|
Цех №2 |
821,9 |
218,9 |
|||
|
Цех №3 |
529,6 |
124,7 |
|||
|
Цех №4 |
758,4 |
171,1 |
|||
|
Склад №1 |
580,2 |
223,3 |
|||
|
Склад №2 |
443,9 |
98,6 |
|||
|
Склад №3 |
579,0 |
123,4 |
|||
|
Склад №4 |
322,8 |
69,8 |
|||
|
Итого: |
Примечание 1. Восстановительная полная стоимость объекта (ВП) и восстановительная остаточная стоимость объекта (ВО) вычисляются по балансовой стоимости (БС) и износу объекта (ИО):
ВП = БС * К ; ВО = ОС * К,
где К=3,0 , если БС500; К=2,0, если БС
Примечание 2. Для заполнения столбцов использовать функцию ЕСЛИ.
Задание 6. Рассчитать структуру розничной цены продукции исходя из следующих данных:
|
№ |
Составляющие |
Виды продукции |
|||
|
A |
B |
C |
D |
||
|
1 |
Себестоимость |
50 |
71 |
36 |
12 |
|
2 |
Оптовая цена предприятия |
||||
|
3 |
Акциз (70% от оптовой цены) |
||||
|
4 |
Наценка посредника |
10 |
10 |
8 |
8 |
|
5 |
НДС (14% от оптовой цены предприятия) |
||||
|
6 |
Торговая наценка |
12 |
12 |
10 |
10 |
|
7 |
Розничная цена |
Задание 7. Рассчитать оклад в тенге, премию в %, премию в тенге, итог, налог, и к выдаче по следующим формулам:
-
Оклад (тг) рассчитывается исходя из оклада в долларах и курса доллара.
-
Процент премии рассчитывается так: если работник отработал все рабочие дни, то получает 100 % премии, если больше 14, но не 22, то 50%, во всех остальных случаях 25%.
-
Премия в тенге рассчитывается как оклад в тенге, умноженный на % премии.
-
Итого в тенге получается по формуле: (отработка * оклад / количество рабочих дней) + сумма премии.
-
Налог: если итог получается меньше 200 000 тенге, то 13% от итога, иначе 25%.
-
К выдаче: Итог-ИПН.
|
Расчет зарплаты за октябрь 2006 |
|||
|
рабочих дней |
22 |
||
|
курс доллара |
130 |
|
№ № |
ФИО |
таб. номер |
от-дел |
должность |
отра-ботка |
оклад, в $ |
оклад, в тг. |
премия, в % |
премия, в тг. |
итого , в тг. |
ИПН, в тг. |
к выдаче, в тг. |
|
1 |
Ахметов А.А. |
001 |
1 |
инженер |
15 |
300 |
||||||
|
2 |
Иванов И.И. |
002 |
1 |
инженер |
18 |
300 |
||||||
|
3 |
Ким Р.А. |
004 |
2 |
ст.инженер |
22 |
500 |
||||||
|
4 |
Петров Н.Б. |
120 |
1 |
техник |
10 |
250 |
||||||
|
5 |
Смирнов Е.П. |
451 |
3 |
инженер |
1 |
400 |
||||||
|
6 |
Исин Т.Б. |
340 |
3 |
инженер |
22 |
320 |
||||||
|
7 |
Туяков Р.В. |
005 |
2 |
ст.инженер |
21 |
350 |
||||||
|
8 |
Кузьмин В.И. |
006 |
2 |
ст.инженер |
18 |
550 |
||||||
|
9 |
Абишева Г.С. |
180 |
2 |
нач.лаб. |
22 |
600 |
||||||
|
10 |
Федоров С.Б. |
450 |
1 |
инженер |
13 |
400 |
Задание 8. Завод изготавливает три вида продукции: соки, йогурты, мороженое. Затраты на изготовление этих продуктов составляют 70, 30, 20 тенге соответственно. Прибыль от реализации одного вида изделий составляет 20, 10, 5 тенге. Было изготовлено соков – 12546 л., йогуртов – 65234 кг., мороженого – 52623 кг.
При помощи таблицы рассчитать:
-
Доход от реализации каждого вида изделий;
-
Общую прибыль;
-
Долю в процентах каждого вида изделий от общей прибыли;
-
Какое изделие приносит больший доход предприятию. Использовать функцию MAX;
-
Построить диаграмму по доходу от реализации одного вида изделия. Подписать диаграмму и значения;
-
Отформатировать таблицу: задать границы, цвет, размер столбцов и строк.
Задание 9. Рассчитать:
-
Дивиденды, объявленные на год составляют Номинал акций * 450%.
-
Доходность по дивидендам составляет Дивиденды, объявленные на год / Цена продажи.
|
Эмитет |
Номинал акций, |
Цена продажи, |
Дивиденды объявленные в расчете на год |
Доходность по дивидендам |
|
КазКоммерцБанк |
100000 |
125622 |
||
|
Народный Банк |
200000 |
230000 |
||
|
Банк Центркредит |
158000 |
160000 |
||
|
НаурызБанк |
125000 |
128000 |
||
|
ТемирБанк |
202000 |
220000 |
-
Среднюю цену продажи акций;
-
Максимальную цену продажи акций;
-
Минимальную цену продажи акций;
-
Максимальную доходность по дивидендам.
Построить диаграмму по доходности каждого из банков. Подписать диаграмму и значения.
Задание 10. На предприятии работники имеют следующие оклады начальник отдела – 1000 руб. инженер 1 кат. – 860 руб. инженер – 687 руб. техник – 315 руб. лаборант – 224 руб. Предприятие имеет два филиала в средней полосе и в условиях крайнего севера. Все работники получают надбавку 10 от оклада за вредный характер работы 25 от оклада ежемесячной премии. Со всех работников удерживают 20 подоходный налог профсоюзный взнос и 1% в пенсионный фонд. Работники филиала расположенного в средней полосе получают 15% районного коэффициента работники филиала расположенного в районе крайнего севера имеют 70% районный коэффициент и 50% северной надбавки от начислений.
Расчет заработной платы должен быть произведен для каждого филиала в отдельности. Результатом должны быть две таблицы.
Требуется
-
при помощи электронной таблицы рассчитать суммы к получению каждой категории работников
-
построить две диаграммы отражающие отношение районного коэффициента (районной и северной надбавки) и зарплаты для всех сотрудников обоих филиалов.
Задание 11. На книжную базу поступили 3 наименования книг словари книги по кулинарии и пособия по вязанию. Они были распределены по трем магазинам «Книжный мир» «Дом книги» и «Глобус».
В «Книжный магазин» поступило словарей – 10400 экземпляров кулинарных книг – 23650 экземпляров пособий по вязанию – 1500 экземпляров в «Дом книги» — 10300 словарей 22950 кулинарных книг и 1990 пособий по вязанию в «Глобус» соответственно 9100 23320 и 2500 экземпляров.
В первом магазине было продано словарей – 8945 экземпляров кулинарных книг – 19865 экземпляров пособий по вязанию – 873 экземпляра во втором магазине было продано словарей – 9300 экземпляров кулинарных книг – 21900 экземпляров пособий по вязанию – 1020 экземпляра в третьем магазине соответственно было продано 8530 18100 и 2010 экземпляров.
Требуется
-
при помощи электронной таблицы рассчитать
-
общее количество книг каждого наименования поступивших на книжную базу
-
процент продажи каждого наименования книг в каждом магазине
-
количество книг оставшихся после реализации
-
построить диаграмму по распределению книг в магазинах.
Задание 12. Рассчитать ежедневный предполагаемый доход от деятельности киносети.
|
Кинотеатры |
Вместимость зрительного зала, мест |
Средний % посещаемости |
Средняя цена билета, в тг. |
Количество сеансов в день |
Доход, в тг. |
|
Cinema – сити |
700 |
45 |
40 |
4 |
|
|
Юность |
150 |
40 |
30 |
5 |
|
|
ФОК «Мир» |
300 |
60 |
25 |
3 |
|
|
Час пик |
500 |
30 |
40 |
5 |
|
|
Ср. Значение |
|||||
|
Итого |
Задание 13. Рассчитать среднюю стоимость 1 кв. м. общей площади жилых помещений в городах Казахстана.
|
Рынок жилья, в тыс.тг. |
Кокшетау |
Караганда |
Кустанай |
Павлодар |
|
Первичный рынок |
||||
|
— улуч. планировки |
2640,4 |
3354,6 |
3132,0 |
2886,5 |
|
— элитные |
2576,0 |
3000,0 |
4127,3 |
3523,2 |
|
Средняя цена |
||||
|
Ср. цена по отношению к кокшетауской (в %) |
||||
|
Вторичный рынок: |
||||
|
— низкого качества |
2206,1 |
1394,7 |
1900,0 |
2486,7 |
|
— типовые |
2268,7 |
1847,5 |
1989,2 |
2999,0 |
|
— улуч. планировки |
2505,8 |
2176,4 |
2126,4 |
3150,3 |
|
— элитные |
3805,6 |
3891,1 |
3605,3 |
4500,2 |
|
Средняя цена |
||||
|
Ср. цена по отношению к кокшетауской (в %) |
Задание 14. Рассчитать и показать на графике структуру кредитных вложений коммерческого банка в зависимости от их обеспечения.
Для решения задачи используется следующая входная информация:
-
ссуды под залог ценных бумаг
-
ссуды под залог товарно-материальных ценностей
-
ссуды под залог валютных ценностей
-
ссуды под залог нематериальных активов
-
ссуды под залог долговых требований
-
гарантированные ссуды
-
застрахованные ссуды
-
ссуды без обеспечения
В результате решения задачи необходимо сформировать следующий входной документ:
Структура кредитных вложений коммерческого банка
|
Кредитные вложения коммерческого банка |
Сумма (млн. тенге) |
Уд.вес (%) |
|
Ссуды под залог ценных бумаг |
5000 |
U(1) |
|
Ссуды под залог товарно-материальных ценностей |
6500 |
U(2) |
|
Ссуды под залог валютных ценностей |
2000 |
U(3) |
|
Ссуды под залог нематериальных активов |
1000 |
U(4) |
|
Ссуды под залог долговых требований |
5000 |
U(5) |
|
Гарантированные ссуды |
10000 |
U(6) |
|
Ссуды без обеспечения |
4000 |
U(7) |
|
Застрахованные ссуды |
7000 |
U(8) |
|
ИТОГО: |
SS |
=100% |
-
Формулы для расчета выходных показателей имеют следующий вид:
SS = SUM(S(I)), где S(I) – сумма i-ой ссуды;
U(I) = S(I) / SS, U(I) – удельный вес i-ой ссуды;
I = [1,N], где N – количество видов предоставляемых ссуд.
-
Выполнить сортировку документа по возрастанию объектов вложения коммерческого банка.
-
Построить на отдельном рабочем листе круговую диаграмму, отражающую структуру сумм каждого вида ссуды в виде соответствующего сектора, вывести значения объемов вложений по каждому виду, а также легенду и название графика «Структура кредитных вложений банка».
-
Построить на отдельном листе смешанную диаграмму, в которой суммы объемов каждого вида ссуды были бы представлены в виде гистограмм, а их удельные веса в виде линейного графика на той же диаграмме. Вывести легенду и название графика «Анализ кредитных вложений банка».
-
Сформировать новый выходной документ, содержащий только те кредитные вложения банка, объем ссуд которых больше среднего значения этого показателя по всей таблице (использовать функцию СРЗНАЧ, выполнить фильтрацию, результаты скопировать). Выходной документ должен иметь следующий вид:
Кредитные вложения коммерческого банка
Сумма (млн. тенге)
-
На основании исходного документа Структура кредитных вложений коммерческого банка сформировать следующий документ:
Расчетная величина
Значения
Максимальная сумма под залог (по всем видам ссуд под залог)
Минимальная сумма под залог (по всем видам ссуд под залог)
Количество видов ссуды под залог
Максимальная сумма ссуды (по всем видам ссуд)
Минимальная сумма ссуды (по всем видам ссуд)
-
Подготовить результаты расчетов и диаграммы к выводу на печать.
Тема работы: Использование финансовых функций БС, ПС, ЧПС.
Функция БС
-
БС(ставка; кпер; плт; пс; тип) – выдает будущее значение вклада с периодическими постоянными платежами и постоянной процентной ставки ;
Пример решения задачи.
Условие задачи: Банк выдает долгосрочный кредит в размере 186 тыс. тг. по сложной ставке 19 % годовых. Определить сумму долга через 7 лет.
|
Проценты годовых |
Срок долга |
Размер кредита |
Сумма долга |
|
0,19 |
7,00 |
-186,00 |
Для того, чтобы получить ответ вызываем мастер функций:
f x – категория — Финансовые – Функция БС.
Рассчитать задачи, соблюдая порядок выполнения:
-
Составить таблицу, в которой будут отражаться все задачи:
-
Коммерческий банк выдает долгосрочный кредит в размере 200 тыс. тг. по сложной ставке 20 % годовых. Определить сумму долга через 10 лет.
-
КазКомерц Банк выдает долгосрочный кредит в размере 900 тыс. тг. по сложной ставке 13 % годовых. Определить сумму долга через 18 лет.
-
Народный Банк выдает долгосрочный кредит в размере 520 тыс. тг. по сложной ставке 15 % годовых. Определить сумму долга через 12 лет.
-
Национальный Банк выдает долгосрочный кредит в размере 129 тыс. тг. по сложной ставке 12 % годовых. Определить сумму долга через 20 лет.
-
После того, как были найдены все суммы долга, при помощи фильтра найти наиболее выгодное вложение денег, сравнивая (Срок долга, Сумму долга) при помощи сортировки в порядке возрастания.
Функция ПС
-
ПС(ставка; кпер;бс) – расчет текущей стоимости для единой суммы вклада;
-
ПС(ставка; кпер;плт;тип) – расчет текущей стоимости фиксированных периодических выплат;
Пример 1. Какую сумму необходимо положить в банк, выплачивающий 13,7 % годовых, чтобы через 3 года получить 250 тыс.тг.
Для решения следует использовать функцию =ПС(ставка:0,137; кпер:3;бс:-250)
Пример 2. Платежи в фонд будут вноситься ежегодно по 200 тыс.тг. в течение 4 лет с начислением на них сложных процентов по ставке 8 % годовых. Определить современную сумму всех платежей с начисленными процентами.
Для решения следует использовать функцию =ПС(ставка:0,08; кпер:4; плт:-200;тип:0)
Функция ЧПС
-
ЧПС(ставка;значение1;значение2;…) – расчет текущей стоимости периодических поступлений переменной величины.
Пример. Инвестиции в проект составляют 800 тыс.тг. В последующие 5 лет ожидаются следующие долговые доходы по проекту: 250,320,210,400,150 тыс.тг. Издержки привлечения капитала 7 %. Рассчитать чистую текущую стоимость проекта.
|
Год |
Инвестиции |
Издержки привлеченного капитала |
Ответ |
|
Год 0 |
-800 |
0,07 |
296,67 |
|
Год 1 |
250 |
||
|
Год 2 |
320 |
||
|
Год 3 |
210 |
||
|
Год 4 |
400 |
||
|
Год 5 |
150 |
Для решения следует использовать функцию =ЧПС(ставка: 0,07; значения: 250;320;210;400;150). Для нахождения непосредственного значения NPV необходимо вычесть начальную инвестицию.
Задача. Инвестиции в проект составляют 1000 тыс.тг. В последующие 6 лет ожидаются следующие долговые доходы по проекту: 182, 456, 210, 163, 245, 259 тыс.тг. Издержки привлечения капитала 15 %. Рассчитать чистую текущую стоимость проекта.
Тема работы: Использование поиска решения
Пример 1. Оптимизация плана доставки товаров.
Рассмотрим задачу нахождения такого плана перевозок продукции с M складов к N потребителям, который требовал бы минимальных затрат.
Обозначим Xij – количество продукции, поставляемое со склада i потребителю j. Предполагается, что транспортные расходы пропорциональны количеству перевозимой продукции, т.е. Q = P * X.
Обозначим
где: Ci – количество продукции, находящееся на складе i;
Bj — количество продукции, необходимой потребителю j.
Для решения задачи необходимо соблюдение равенства:
Таким образом, потребность в продукции должна быть обеспечена.
Целевая функция определяется равенством:
Исходными данными при решении данной задачи являются:
-
Издержки транспортировки либо прибыль от реализации товара;
-
Количество товара на каждом складе;
-
Количество товара, нужного каждому потребителю.
Решение задачи рассмотрим на примере доставки товара с 4 складов для 5 потребителей.
З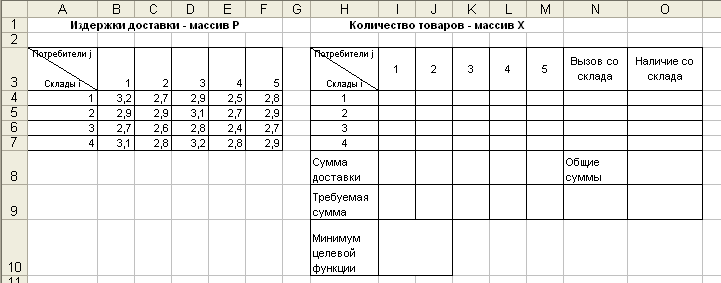
Выделите диапазон ячеек B4:F7 выполните команду меню Вставка, Имя, Присвоить. В диал.окне Присвоение имени введите имя массива P и нажмите Ok. В области имя строки формул появилось имя P выделенного диапазона ячеек B4:F7.
Определим массив X – доставка товара со склада i потребителю j, т.е. присвоим имя X диапазону ячеек I4:M7.
В строке «Сумма доставки» необходимо ввести формулу расчета товара фактически доставленного каждому потребителю. Для этого в ячейку I8 введите формулу =СУММ(I8:I7). Скопируйте формулу в диапазон J8:M8.
В строке «Требуемая сумма» введите числа, соответствующие количеству товара, необходимого каждому потребителю 190,210,220,230,150. Для получения общей суммы выделите диапазон I9:M9 и нажмите кнопку Автосумма.
В колонке «Вывоз со склада» введите формулу расчета фактического вывоза товара с каждого склада: в ячейку N4 введите формулу =СУММ(I4:M4). Скопируйте формулу в N5:N7.
В колонку «Наличие на складе» введите числа, соответствующие количеству товара, находящегося на складах 250,220,280,250. Для получения общей суммы выделите диапазон O4:O7 и нажмите кнопку Автосумма.
В ячейку O9 введите формулу контроля общих сумм =ЕСЛИ(N9=O8; «совпадают»; «не совпадают»).
Создайте имена для диапазонов данных по вывозу и доставке товаров: выделите диапазон N3:O9 и выполните Вставка, Имя, Создать, Ok. Выполните аналогичные действия для диапазона H8:M9.
В ячейку H10 введите «Минимум целевой функции», а в ячейку I10 – формулу =СУММПРОИЗ(P;X).
Итак, данные для решения задачи подготовлены.
В приложении MS Excel задачи оптимизации решаются программой Поиск решения (Solver).
Выполните Сервис, Поиск решения. В диал.окне Поиск решения укажите адрес целевой ячейки, выделив I10.
Д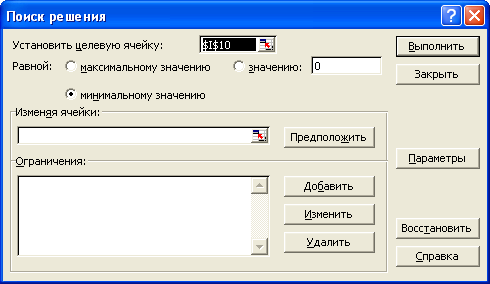
Д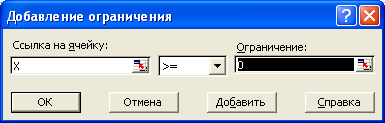
Добавьте ограничения:
-
X=0
-
X=целое
-
I8:M8=I9:M9
-
N4:N7=O4:O7
Нажмите кнопку Выполнить. В строке сообщения будет отображаться процесс поиска решения.
В окне Результаты поиска решения нажмите Сохранить сценарий. Введите название сценария «Трансп.задача№1».
Появился новый рабочий лист Отчет по результатам 1, в котором будут отображены исходные данные и результаты решения. Просмотрите его и вернитесь на Лист 1.
Поскольку сценарий был сохранен, вы всегда можете вывести результаты решения задачи. Выделите диапазон I4:M7 и удалите данные, нажав Del. Выполните команду Сервис, Сценарии. В окне Диспетчер сценариев нажмите Изменить, Ok. В окне Значение ячеек сценария округлите все данные до целых чисел, Ok, затем Вывести.
Массив X таблицы вновь заполниться данными, полученными при решении оптимизации.
Вы также можете создать отчет по сохраненному сценарию. В окне Диспетчер сценариев нажмите Отчет. В окне Отчет по сценарию введите адрес I10 (ячейки результата) и Ok.
Получите диаграмму доставки товара.
Задание 1.
-
Постройте диаграмму по расчетным данным.
-
Используя прежние исходные данные и полагая, что массив P – прибыль от реализации продукции, определите максимум целевой функции. (Ответ 2899).
-
Сохраните сценарий под именем «Трансп.задача№2» и создайте отчет.
Пример 2. Оптимизация плана распределения транспортных средств.
Рассмотрим задачу нахождения оптимального плана перевозок пассажиров самолетами M типов по N направлениям, при котором затраты минимальны.
Обозначим Xij – количество самолетов типа i, обслуживающих направление j. Транспортные расходы пропорциональны количеству самолетов, т.е. Q = P * X.
Обозначим
где: Ci – количество самолетов типа i;
Bj — количество пассажиров, перевозимых в направлении j;
Gi – грузоподъемность самолета типа i.
Таким образом, суммарное количество пассажиров, перевозимых всеми самолетами, должно находиться в заданных пределах.
Целевая функция определяется равенством:
Исходными данными при решении данной задачи являются:
-
себестоимость либо прибыль от перевозок пассажиров;
-
количество самолетов каждого типа;
-
грузоподъемность самолетов каждого типа;
-
количество пассажиров, перевозимых в каждом направлении (диапазон: наибольшая и наименьшая потребности).
Решение задачи рассмотрим на примере перевозки пассажиров самолетами 3 типов по 4 направлениям.
Заполним таблицы: Себестоимость перевозок и Перевозки пассажиров.
Колонка «Грузоподъемность» содержит данные о количестве пассажиров, перевозимых самолетом типа i.
Для C3:E5 присвойте имя P_2.
Для F3:F5 – Вставка, Имя, Создать, в строке выше, Ok.
Для I3:L5 присвойте имя X_2. Массив X_2 – количество самолетов типа i , обслуживающих направление j.
В строке «Перевозка пассажиров» введите формулу расчета перевозки пассажиров в каждом направлении: для I6 ввести =СУММПРОИЗВ(I3:I5;Грузоподъемность). Для остальных скопировать.
Создайте имена для диапазонов данных по перевозке пассажиров: для I6:L8.
Для получения общей суммы: выделить I6:M8, Автосумма.
«Всего самолетов» — введите формулу расчета фактического количества самолетов каждого типа на всех направлениях: для M3 – Автосумма, скопировать в M4:M5.
Создайте имена для диапазонов данных по количеству самолетов M2:N5.
В ячейку N6 введите формулу расчета количества пассажиров, перевозимых всеми самолетами: =СУММПРОИЗВ(N3:N5;F3:F5). Вы получите формулу =СУММПРОИЗВ(Наличие_самолетов; Грузоподъемность).
В N7 введите формулу контроля общей суммы =ЕСЛИ(И(N6= M7;N6M7); «потребность в заданных пределах»; «потребность вне заданных пределов»). Таким образом производиться контроль в перевозках.
В ячейку I9 введите формулу.
Итак, данные для решения задачи оптимизации подготовлены.
Задание 2.
-
Найдите решение.
-
Назовите сценарий «Трансп.зад.№3».
-
Предоставьте результаты поиска решения, отчет, диаграмму.
Пример 3. Организация плана загрузки контейнера товарами.
Задача нахождения плана загрузки контейнера товарами M типов, при котором прибыль от реализации товаров будет максимальна. Решение задачи рассмотрим на примере загрузки контейнера товарами 4 типов.
Создайте имена для B4:F9 (в столбце слева), G4:I6 (в строке выше).
Найти максимальное значение целевой ячейки.
Ограничения:
Суммарные значения
X_3 Xmax
X_3 = целое
X_3 = Xmin
Получить Результаты, Отчет по результатам, Диаграмму загрузки товаров.
Задание 3.
-
Постройте диаграмму по расчетным данным.
-
Добавьте в таблицу колонку с наибольшими суммарными значениями по объему и весу товара: =СУММПРОИЗВ(O;Xmax), =СУММПРОИЗВ(B;Xmax). Остальные исходные данные оставьте неизменными. Решите задачу загрузки товара в случае предельных значений, близких к максимальным: объем контейнера 15000, загрузка по весу 5000. В этом случае все товары загружаются по максимальному количеству. (Ответ 27527).
-
Сохраните сценарий.
Задание 4.
Задание 5. Завод производит электронные приборы трех видов (прибор А, прибор В и прибор С), используя при сборке микросхемы трех видов (тип 1, тип 2 и тип 3). Расход микросхем задается следующей таблицей:
|
Прибор А |
Прибор В |
Прибор С |
|
|
Тип 1 |
2 |
5 |
1 |
|
Тип 2 |
2 |
0 |
4 |
|
Тип 3 |
2 |
1 |
1 |
Стоимость изготовленных приборов одинакова.
Ежедневно на склад завода поступает 500 микросхем типа 1 и по 400 микросхем типов 2 и 3. Каково оптимальное соотношение дневного производства приборов различного типа, если производственные мощности завода позволяют использовать запас поступивших микросхем полностью?
Тема работы: Запись и использование макросов
Макрос – это последовательность некоторых операций и действий с данными, записанная на языке программирования (Visual Basic).
П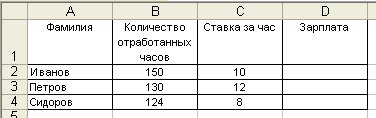
Лист 1 Лист 2
На обоих листах требуется рассчитать данные в последнем столбце и построить диаграмму
-
Информационные системы/ В.Н. Петров/учебник/ПИТЕРСпб 2002г.
-
Информационные технологии в экономике и управлении. Учебник/ Козырев А.А./ Спб.: Питер, 2001.
-
Информационные системы в экономике/ Патрушина С.М./ М.: ИКЦ «МарТ», 2004.
-
Проектирование баз данных СУБД MS Access/ Гринченко н.Н. и др./ М.: Горячая линия-Телеком, 2004.
-
Экономическая информатика/ П.В. Конюховский, Д.Н. Колесова/Спб.: Питер, 2001.
-
Информационные системы в экономике/ С.М. Патрушина/Издательский центр «МарТ» 2004 г.
-
Информатика для юристов и экономистов/ Симонович С.В./ Спб.: Питер, 2003.
-
Электронные таблицы MS Excel/ Ульрих Л.А./ М.: Издательство Эком, 2002.