Задачи с подбором параметра в excel примеры - Word и Excel

Часто нам нужно предварительно спрогнозировать, какие будут результаты вычислений при определенных входящих параметрах. Например, если получить кредит на закупку товара в банке с более низкой процентной ставкой, а цену товара немного повысить – существенно ли возрастет прибыль при таких условиях?

При разных поставленных подобных задачах, результаты вычислений могут завесить от одного или нескольких изменяемых условий. В зависимости от типа прогноза в Excel следует использовать соответствующий инструмент для анализа данных.

Подбор параметра и решение уравнений в Excel

Данный инструмент следует применять для анализа данных с одним неизвестным (или изменяемым) условием. Например:

2x+1=7

y=7 является функцией x;
нам известно значение y, следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

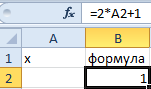
Заполните ячейки листа, так как показано на рисунке:

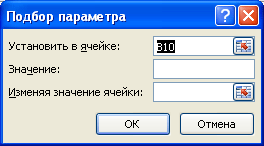
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
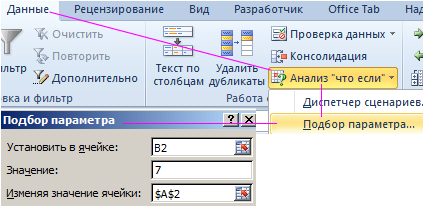
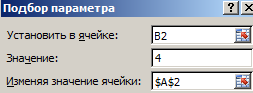
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

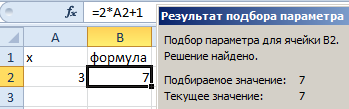
В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

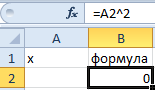
x²=4

Решение:

Заполните ячейку B2 формулой как показано на рисунке:

Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):

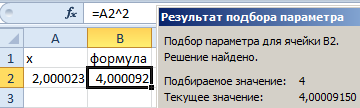
Сравните 2 результата вычисления:

Обратите внимание! В первом примере мы получили максимально точный результат, а во втором – максимально приближенный.

Это простые примеры быстрого поиска решений формул с помощью Excel. Сегодня каждый школьник знает, как найти значение x. Например:

x=(7-1)/2

Excel в своих алгоритмах инструментов анализа данных использует более простой метод – подстановки. Он подставляет вместо x разные значения и анализирует, насколько результат вычислений отклоняется от условий указанных в параметрах инструмента. Как только будет, достигнут результат вычисления с максимальной точностью, процесс подстановки прекращается.

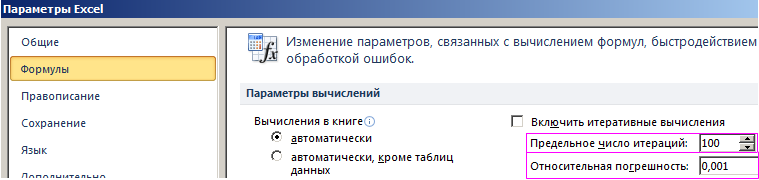
По умолчанию инструмент выполняет 100 повторений (итераций) с точностью 0.001. Если нужно увеличить количество повторений или повысить точность вычисления измените настройки: «Файл»-«Параметры»-«Формулы»-«Параметры вычислений»:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

Используя эти способы настроек можно существенно облегчить и ускорить процесс поиска максимально точного решения.

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

Источник

Функция Excel: подбор параметра

Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.

Зачем нужна функция

Как было уже выше упомянуто, задача функции Подбор параметра состоит в нахождении начального значения, из которого можно получить заданный конечный результат. В целом, эта функция похожа на Поиск решения (подробно вы можете с ней ознакомиться в нашей статье – “Поиск решения в Excel: пример использования функции”), однако, при этом является более простой.

Применять функцию можно исключительно в одиночных формулах, и если потребуется выполнить вычисления в других ячейках, в них придется все действия выполнить заново. Также функционал ограничен количеством обрабатываемых данных – только одно начальное и конечное значения.

Использование функции

Давайте перейдем к практическому примеру, который позволит наилучшим образом понять, как работает функция.

Итак, у нас есть таблица с перечнем спортивных товаров. Мы знаем только сумму скидки (560 руб. для первой позиции) и ее размер, который для всех наименований одинаковый. Предстоит выяснить полную стоимость товара. При этом важно, чтобы в ячейке, в которой в дальнейшем отразится сумма скидки, была записана формула ее расчета (в нашем случае – умножение полной суммы на размер скидки).

Итак, алгоритм действий следующий:

Переходим во вкладку “Данные”, в которой нажимаем на кнопку “Анализ “что если” в группе инструментов “Прогноз”. В раскрывшемся списке выбираем “Подбор параметра” (в ранних версиях кнопка может находиться в группе “Работа с данными”).
На экране появится окно для подбора параметра, которе нужно заполнить:
- в значении поля “Установить в ячейке” пишем адрес с финальными данными, которые нам известны, т.е. это ячейка с суммой скидки. Вместо ручного ввода координат можно просто щелкнуть по нужной ячейке в самой таблице. При этом курсор должен быть в соответствующем поле для ввода информации.

Решение уравнений с помощью подбора параметра

Несмотря на то, что это не основное направление использования функции, в некоторых случаях, когда речь идет про одну неизвестную, она может помочь в решении уравнений.

Например, нам нужно решить уравнение: 7x+17x-9x=75 .

Пишем выражение в свободной ячейке, заменив символ x на адрес ячейки, значение которой нужно найти. В итоге формула выглядит так: =7*D2+17*D2-9*D2 .
Щелкаем Enter и получаем результат в виде числа 0, что вполне логично, так как нам только предстоит вычислить значение ячейки D2, которе и является “иксом” в нашем уравнении.

Заключение

Подбор параметра – функция, которая может помочь в поиске неизвестного числа в таблице или, даже решении уравнения с одной неизвестной. Главное – овладеть навыками использования данного инструмента, и тогда он станет незаменимым помощников во время выполнения различных задач.

Уравнения и задачи на подбор параметра в Excel

Подбор параметра и решение уравнений в Excel

y =7 является функцией x ;
нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

Заполните ячейки листа, так как показано на рисунке:
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

Заполните ячейку B2 формулой как показано на рисунке:
Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
Сравните 2 результата вычисления:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.

Первый метод

Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».

1. Зададимся простым квадратичным уравнением и найдем решение при х=0.

2. Переходите к инструменту и заполняете все необходимые поля

3. После проведения вычислений программа выдаст результат в ячейке с иксом.

4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.

Второй метод

Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.

1. Создаете два диапазона.

На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.

2. Переходите во вкладку Вставка и выбираете обычный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Важно! В настройках оси поставьте положение по делениям.

4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.

Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.

Третий метод

Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.

1. Записываете произвольную систему уравнений.

2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.

3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.

4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.

Четвертый метод

Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.

Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.

1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строку.

4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.

5. Повторяете операцию для третьей строки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.

6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78

7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.

Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.

Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.

Жми «Нравится» и получай только лучшие посты в Facebook ↓

источники:

http://exceltable.com/vozmojnosti-excel/uravnenie-i-podbor-parametra

http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/

Источник

Практическое
занятие по теме: «Подбор параметра и оптимизация (поиск решений) в Excel»

Цель
практического занятия: Изучение технологии «Подбора параметра и оптимизация
(поиск решений) » для решения задач, имеющих точное целевое значение, зависящее
от одного неизвестного параметра

Задачи:

1)
Познакомится
с основными ключевыми понятиями «Подбора параметра»

2)
рассматривается
процесс нахождения исходных данных, которые при подстановке в формулы, дают
необходимое значение в ячейке результата

3)
Решение
задач по теме «Подбор параметра» по образцу и по алгоритму.

4)
Решение
задач по указанной теме самостоятельно

План занятия:

1)
Ознакомление
студентов с ключевыми понятиями.

2)
Рассмотрение
процесса нахождения
исходных данных

3)
Знакомство
с понятием Подбор параметра и Поиск решения

4)
Решение
задач по теме «Подбор параметра» по образцу и по алгоритму

5)
Решение
задач по указанной теме самостоятельно

Ход занятия

Для
эффективного использования формул необходимо ознакомиться с тремя ключевыми
понятиями.

Вычисление
— это процесс расчета по формулам и последующего отображения значений
результатов в ячейках, содержащих формулы. Во избежание ненужных вычислений
Microsoft Office Excel автоматически пересчитывает формулы только при изменении
влияющих на формулу ячеек. Это является стандартной процедурой при первом
открытии книги и ее редактировании. Однако тем, как и когда Excel будет
пересчитывать формулы, можно управлять.

Итерация
— это многократный пересчет листа до удовлетворения определенного числового
условия. Excel не может автоматически рассчитать значение по формуле, которая
ссылается (прямо или косвенно) на ячейку, содержащую формулу (это называется
циклической ссылкой). Если формула содержит обратную ссылку на одну из своих
собственных ячеек, необходимо определить, сколько раз следует пересчитывать
формулу. Циклические ссылки могут пересчитываться до бесконечности. Однако
существует возможность управления максимальным числом итераций и количеством
допустимых изменений.

Точность
— это показатель степени сходимости вычислений. Excel хранит и выполняет
вычисления с точностью 15 значащих цифр. Однако существует возможность изменить
точность вычислений, так что Excel при пересчете формул будет использовать для
вычислений не хранимое, а отображаемое значение.

Процесс
изменения значений ячеек и анализа влияния этих изменений на результат
вычисления формул в Excel
называется анализом «что-если».

Рассмотрим
процесс нахождения исходных данных, которые при подстановке в формулы, дают
необходимое значение в ячейке результата. Если вы знаете, каким должен быть
результат вычисления по формуле, то Excel подскажет вам
значения одного или нескольких входных параметров, которые позволяют получить
нужный результат.

Другими
словами, вы можете задать вопрос типа: Какой рост продаж необходим для получения
дохода в $1 200 000? В Excel для этого
предусмотрены два подходящих средства.

·
Подбор
параметра
– определяет значение одной входной ячейки, которое требуется для получения
желаемого результата в зависимой ячейке (ячейке результата).

·
Поиск
решения
— определяет значения в нескольких входных ячейках, которые требуются для
получения желаемого результата. Более того, можно накладывать ограничения на
входные данные, поэтому здесь можно получить решение (если оно существует)
многих практических задач.

Подбор
параметра
является удобным средством для решения задач, которые имеют точное целевое
значение, зависящее от одного неизвестного параметра. С помощью Подбора
параметра можно определить значение, которое будет давать желаемый
результат.

Решим
следующую задачу:

Вы хотите
положить деньги в банк под 4,5% и получить ровно 1000 руб. по истечении года.
Необходимо определить сумму вклада. Для решения данной задачи используем
средство Подбор параметра.

Задание:

1.
Создайте
новый файл под именем Лаб.раб. Лист 1 переименуйте в Подбор.

2.
Оформите
таблицу (рис. 1). Введите указанную формулу.

Рис.1

3.
Активизируйте
ячейку В3. Выполните команду Данные — -Анализ «что- если» ÞПодбор
параметра.

4.
В
открывшемся диалоговом окне укажите значение необходимой конечной суммы и
ссылку на ячейку с искомым значением вклада (рис.2).

Рис.2

5.
Нажмите
кнопку ОК. Средство подбор параметра найдет решение и сообщит об этом
(рис. 3). Нажмите кнопку ОК и убедитесь, что искомое значение помещено в
ячейке В2.

Рис.3

Задание для самостоятельной работы:

1.
Решите
задачу:
Для покупки автомобиля Вам необходима сумма 200 000 руб. У Вас есть
возможность взять ипотечную ссуду, при этом нужно сделать первый взнос 20%.
Определите, какую сумму нужно взять в банке, чтобы на руки вы получили
требуемую сумму.

2.
Для
решения задачи оформите таблицу (рис.4). Введите формулы.

Рис.4

3.
С
помощью средства Подбор параметра определите размер ссуды.

Задачи оптимизации
(поиск решения)

Цель: Изучение
технологии поиска решения для задач оптимизации (минимизации, максимизации).

Задание 1. Составление плана
выгодного производства.

Фирма производит несколько видов продукции
из одного и того же сырья – А, В, С. Реализация продукции А дает прибыль 10р.,
В – 15р., С-20р. На единицу изделия. Продукцию можно производить в любых
количествах, поскольку известно, что сбыт обеспечен, но ограничены запасы
сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы
общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство
продукции каждого вида приведены в таблице.

Сырье	Нормы расхода сырья	Запас сырья
А	В	С
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20

Решение:

1. Создать
расчетную таблицу

А
В              С           D
E                                   F

План выгодного производства

Сырье	Норма расхода сырья	Запас сырья	Расход сырья
	А	В	С
Сырье 1	18	15	12	350	=$B$9B5+$C$9C5+$D$9*D5
Сырье 2	6	4	8	200	=$B$9B6+$C$9C6+$D$9*D6
Сырье 3	5	3	3	100	=$B$9B7+$C$9C7+$D$9*D7
Прибыль на ед. изделия	10	15	20
Количество
Общая прибыль	=B8*B9	=C8*C9	=D8*D9	=СУММ(B10:D10)

2. В
меню Сервис активизируйте
команду Поиск решения и введите параметры поиска

Сервис — настройки
– поиск решения

Параметры:

В результате должно получиться следующее:

Сырье	Норма расхода сырья	Запас сырья	Расход сырья
	А	В	С
Сырье 1	18	15	12	350	350
Сырье 2	6	4	8	200	200
Сырье 3	5	3	3	100	83,33333333
Прибыль на ед. изделия	10	15	20
Количество	0	5,5555556	22,222
Общая прибыль	0	83,333333	444,44	527,77778

Сохранить под именем «План
производства» и сделать выводы.

Задание№2. Выполнить
аналогичные расчеты

Вариант 1

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	25	17	11	350
Сырье 2	9	7	10	400
Сырье 3	15	8	5	300
Прибыль на ед. изделия	5	10	12
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 2

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	12	11	8	3500
Сырье 2	14	15	2	280
Сырье 3	8	9	10	711
Прибыль на ед. изделия	10	9	8
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 3

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	10	20	15	2700
Сырье 2	16	25	13	3800
Сырье 3	8	9	10	1200
Прибыль на ед. изделия	7	8	6
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 4

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	14	15	19	460
Сырье 2	7	8	12	820
Сырье 3	17	24	6	214
Прибыль на ед. изделия	15	10	25
Количество	?	?	?
Общая прибыль	?	?	?	?

Источник

Обычно при создании формулы пользователь задает значения параметров и формула (уравнение) возвращает результат. Например, имеется уравнение 2*a+3*b=x, заданы параметры а=1, b=2, требуется найти x (2*1+3*2=8). Инструмент Подбор параметра позволяет решить обратную задачу: подобрать такое значение параметра, при котором уравнение возвращает желаемый целевой результат X. Например, при a=3, требуется найти такое значение параметра b, при котором X равен 21 (ответ b=5). Подбирать параметр вручную — скучное занятие, поэтому в MS EXCEL имеется инструмент Подбор параметра

.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке

Данные,

группа

Работа с данным

.

Простейший пример

Найдем значение параметра

b

в уравнении

2*а+3*b=x

, при котором

x=21

, параметр

а=

3

.

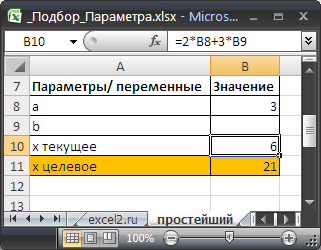
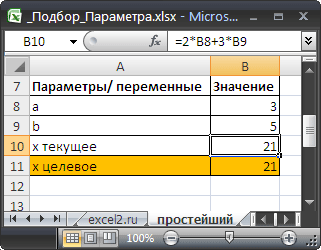
Подготовим исходные данные.

Значения параметров

а

и

b

введены в ячейках

B8

и

B9

. В ячейке

B10

введена формула

=2*B8+3*B9

(т.е. уравнение

2*а+3*b=x

).

Целевое значение x

в ячейке

B11

введено

для информации.

Выделите ячейку с формулой

B10

и вызовите

Подбор параметра (на вкладке

Данные

в группе

Работа с данными

выберите команду

Анализ «что-если?»

, а затем выберите в списке пункт

Подбор параметра

…)

.

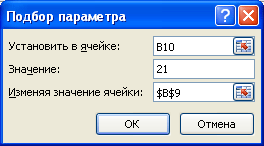
В качестве целевого значения для ячейки

B10

укажите 21, изменять будем ячейку

B9

(параметр

b

).

Нажмите ОК.

Инструмент

Подбор параметра

подобрал значение параметра

b

равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку

B9

последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без

Подбора параметра

параметр будет подобрать сложно

.

Примечание

: Уравнение

2*а+3*b=x

является линейным, т.е. при заданных

a

и

х

существует только одно значение

b

, которое ему удовлетворяет. Поэтому инструмент

Подбор параметра

работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то

Подбор параметра

найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в

файле примера

на листе

Простейший

.

Еще один путь нахождения неизвестного параметра b в уравнении 2*a+3*b=X — аналитический. Решение b=(X-2*a)/3) очевидно. Понятно, что не всегда удобно искать решение уравнения аналитическим способом, поэтому часто используют метод последовательных итераций, когда неизвестный параметр подбирают, задавая ему конкретные значения так, чтобы полученное значение х стало равно целевому X (или примерно равно с заданной точностью).

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

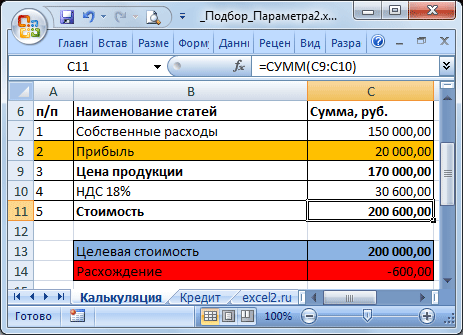
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка

С13

). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (

С8

), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (

С14

) равно 0.

В структуре цены в ячейке

С9

(Цена продукции) введена формула Собственные расходы + Прибыль (

=С7+С8

). Стоимость договора (ячейка

С11

) вычисляется как Цена продукции + НДС (=

СУММ(С9:C10)

).

Конечно, можно подобрать значение вручную, для чего необходимо уменьшить значение прибыли на величину расхождения без НДС. Однако, как говорилось ранее, зависимости в формулах могут быть достаточно сложны. В этом случае поможет инструмент

Подбор параметра

.

Выделите ячейку

С14

, вызовите

Подбор параметра

(на вкладке

Данные

в группе

Работа с данными

выберите команду

Анализ «что-если?»

, а затем выберите в списке пункт

Подбор параметра

…). В качестве целевого значения для ячейки

С14

укажите 0, изменять будем ячейку

С8

(Прибыль).

Нажмите ОК.

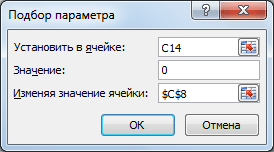
Теперь, о том когда этот инструмент работает. 1. Изменяемая ячейка не должна содержать формулу, только значение.2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание

: В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

Предположим, что нам необходимо

определить максимальную сумму кредита

, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция

ПЛТ()

для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см.

статьи про аннуитет

). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции

ПЛТ()

) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента

Подбор параметра

сумму займа пришлось бы подбирать в ручную с помощью функции

ПЛТ()

или использовать соответствующую формулу.

Введем в ячейку

B

6

ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку

B

7

, % ставку по кредиту введем в ячейку

B8,

а формулу

=ПЛТ(B8/12;B7;B6)

для расчета суммы ежемесячного платежа в ячейку

B9

(см.

файл примера

).

Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

на вкладке

Данные

в группе

Работа с данными

выберите команду

Анализ «что-если?»

, а затем выберите в списке пункт

Подбор параметра

…;
в поле

Установить

введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка

B9

;
введите искомый результат в поле

Значение

. В данном примере он равен

-1800

;
В поле

Изменяя значение ячейки

введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка

B6

;
Нажмите ОК

Что же сделал

Подбор параметра

? Инструмент

Подбор параметра

изменял по своему внутреннему алгоритму сумму в ячейке

B6

до тех пор, пока размер платежа в ячейке

B9

не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра

подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте

инструмент

Поиск решения

. Точность подбора параметра можно задать через меню

.

Вопросом об единственности найденного решения

Подбор параметра

не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент

Подбор параметра

позволяет сэкономить несколько минут по сравнению с ручным перебором.

Источник

Главная > Решение

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

Решение задач – Подбор параметра

Задачи оптимизации с одним неизвестным

Задача оптимизации затрат

Подбор параметра и таблицы подстановки

РЕШЕНИЕ ЗАДАЧ – Подбор параметра

Решение задач – одно из важных применений Excel. Самый простой инструмент предназначен для подбора значений и называется «что-если» анализ: задается некоторая целевая функция и ее числовое значение, Excel автоматически подбирает параметры целевой функции до получения целевого значения. Формула в целевой функции должна логически зависеть от подбираемого параметра.

В Excel встроены инструменты для решения задач статистического и инженерного анализа, сложных задач со многими неизвестными и ограничениями, в частности, решения уравнений и задач оптимизации. Эти инструменты поставляются в виде надстроек Поиск решения и Пакет анализа ; устанавливаются через пункт меню Сервис  Надстройки…, далее пометить пункты Поиск решения и Пакет анализа . Смотрите справку – клавиша F1.

Эти инструменты Excel (будут рассмотрены в следующих разделах) полезны экономистам, администраторам, менеджерам, которым для решения деловых проблем и принятия решений в сферах финансов, бухгалтерского учета, маркетинга, управления операциями, экономики, менеджмента необходимо применять количественные методы анализа и прогнозирования.

В качестве примера разберем расчет прибыли от продаж, показанный на рис. 1.20. В ячейках А3, А4 и А7 записаны формулы – формулы для наглядности продублированы в скобках. Поскольку Другие затраты и Количество здесь постоянны, то нужную прибыль можно получить подбором Цены единицы или Себестоимости единицы товара. Попробуем получить прибыль 20000, изменяя Цену единицы . Проделайте следующие действия:

Встаньте на целевую ячейку А7. Выберите пункт меню С е рвис  П одбор параметра… . Введите значение ожидаемой прибыли. Для ввода адреса изменяемой ячейки, перейдите в нижнее поле и встаньте на ячейку А9 в таблице – адрес будет записан автоматически в поле. Нажмите ОК.

В следующем окне можно либо принять, либо отменить результат подбора параметра. Результат:

Самостоятельно попробуйте подобрать Себестоимость единицы , чтобы получить прибыль 20000 при Цене единицы =200.

Далее приводятся другие применения инструмента Подбор параметра .

Задачи оптимизации с одним неизвестным

Часто уравнения не имеют точного аналитического решения. Тогда их решают методом последовательных приближений (итераций) неизвестных параметров так, чтобы они давали минимум ошибки целевой функции.

Для численного решения уравнений с одним неизвестным в Excel имеется эффективный инструмент Подбор параметра . Целевая функция может быть линейной, квадратичной, третьей и выше степени.

Инструмент Подбор параметра был рассмотрен в предыдущем разделе для расчета прибыли от продаж. Здесь рассмотрим его применение для решения некоторого уравнения, например 2х 3 -3х 2 +х-5=0.

Решение задачи состоит из двух этапов. На первом этапе следует ввести уравнение в ячейку (В2), а в другую ячейку (А2) ввести некоторое ориентировочное значение, здесь 1:

На втором этапе следует воспользоваться инструментом Подбор параметра :

Встаньте на ячейку В2 и вызовите его – С е рвис  П одбор параметра… .

В открывшемся окне введите искомое значение функции и адрес изменяемой ячейки:

После нажатия кнопки ОК Вы получите следующее решение:

Найденное решение приближенное, поэтому можно считать, что при х=1,918578609 значение уравнения 2х 3 -3х 2 +х-5 стремится к нулю, т.е. к 0,000107348. Смело установите для ячеек А2 и В2 числовой формат отображения данных и получите следующее:

Следует отметить, что уравнение может иметь более одного решения. Поэтому рекомендуется выполнить подбор параметра для разных начальных значений Х, указывая положительные, отрицательные, большие и малые значения. В нашем примере установите начальное значение А2=–1 и повторите подбор. Решение будет таким же.

Задача оптимизации затрат

С помощью подбора параметров можно решать задачи оптимального распределения ресурсов следующего плана. Требуется закупить составляющие (конфета карамельная, конфета шоколадная, упаковка печенья и мармелада) для комплектования подарочных наборов так, чтобы цена набора не превышала 100 руб. При этом известны соотношения цен относительно одной из компонент (здесь карамели): цена шоколадной конфеты в 2.5 раза выше цены карамели, цена печенья на 10 руб. больше карамели и цена мармелада в 8.5 раза выше цены карамели. В наборе должно быть 5-10 конфет карамель, 4-6 шоколадных конфет, 1-2 упаковки печенья и 1 упаковка мармелада. Рассчитать закупочные цены для разных комплектов.

Ниже показаны расчеты закупочных цен для максимального и минимального комплектов:

В ячейки В4:В6 запишите формулы: =B3*2.5, =B3+10 и =B3*8.5. В колонки D3:D6 поставьте формулы вычисления сумм по строкам, а в D7 вычислите общую сумму: =СУММ(D3:D6). В итоге целевая функция – стоимость набора D7 есть C3* x +C4*2.5* x +C5*( x +10)+C6*8.5* x , где x =B3 цена одной компоненты – конфеты карамель. Параметры инструмента Подбор параметра заполните так:

Подбор параметра и таблицы подстановки

В паре с инструментом Подбор параметра обычно применяют инструмент Таблица подстановки , который позволяет расширить количество одновременно рассчитываемых вариантов решений. Таблицы подстановки создаются на основе одной или двух изменяемых параметров.

Рассмотрим пример. Фирма производит изделия и продает их по цене 90руб. Ежемесячные постоянные затраты составляют 5000руб., переменные затраты на единицу изделия – 30руб. Необходимо определить точку безубыточности, т.е. вычислить количество изделий, при котором прибыль равна 0. Кроме того, требуется определить изменение прибыли для 10 следующих значений количества с шагом 5, а также прибыль при этих значениях количества для цен 80, 85, 95 и 100руб.

Решение. Введите в Excel исходные данные, приведенные ниже:

В точке безубыточности валовая прибыль равна валовым затратам, т.е. (В3*В4)-(В1+В2*В4)=0. Вызовите Подбор параметра , заполните параметры и нажмите ОК – в ячейке В4 будет вычислено значение 83.33 (рис. 17).

На следующем шаге рассчитаем 10 значений прибыли для следующих значений количества с шагом 5. Используем для этого таблицу подстановки с одним изменяемым параметром. Подготовьте исходные данные (рис. 2.35) : в ячейки C4:C13 запишите значения количества с шагом 5, а в колонке справа в строке выше (ячейка D3) — формулу из ячейки В7.

Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон C3:D13 (рис. 2.36), вызовите пункт Д анные  Т аблица подстановки… , укажите изменяемую ячейку ($B$4) и порядок расположения исходных данных (в строках) в окне запроса – рис. 2.36. После нажатия ОК в ячейках D4:D13 будут рассчитаны значения прибыли.

На последнем шаге рассчитаем значения прибыли для тех же значений количества при ценах 80, 85, 95 и 100руб. Используем для этого таблицу подстановки с двумя изменяемыми параметрами. Результат показан на рис. 2.37.

Для его получения подготовьте исходные данные : в ячейки F4:F13 запишите значения количества, в строке G3:J3 запишите значения цен, на пересечении строки и столбца с данными в ячейке F3 запишите формулу из ячейки В7. Примените инструмент Таблица подстановки к подготовленным данным: выделите диапазон F3:F13 (рис. 2.37), вызовите пункт Д анные  Т аблица подстановки… , укажите изменяемую ячейку по строкам ($B$4) и по столбцам ($B$3) в окне запроса – рис. 2.38. После нажатия ОК в ячейках G4:J13 будут рассчитаны значения прибыли.

Задания для самостоятельного выполнения:

Найдите решение уравнения х 3 +5х 2 -х+1=0

Найдите два решения уравнения х 2 -3х+2=0.

Найдите решение уравнения е х =20000.

Примените инструмент Таблица подстановки при решении предыдущей задачи комплектования подарочных наборов.

Подбор параметра и решение уравнений в Excel

y =7 является функцией x ;
нам известно значение y , следует узнать при каком значении x мы получим y вычисляемый формулой.

Решим данную задачу встроенными вычислительными инструментами Excel для анализа данных:

Заполните ячейки листа, так как показано на рисунке:
Перейдите в ячейку B2 и выберите инструмент, где находится подбор параметра в Excel: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».
В появившемся окне заполните поля значениями как показано на рисунке, и нажмите ОК:

В результате мы получили правильное значение 3.

Получили максимально точный результат: 2*3+1=7

Второй пример использования подбора параметра для уравнений

Немного усложним задачу. На этот раз формула выглядит следующим образом:

Заполните ячейку B2 формулой как показано на рисунке:
Выберите встроенный инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра» и снова заполните его параметрами как на рисунке (в этот раз значение 4):
Сравните 2 результата вычисления:

Таким образом, если нас не устраивает результат вычислений, можно:

Увеличить в настройках параметр предельного числа итераций.
Изменить относительную погрешность.
В ячейке переменной (как во втором примере, A3) ввести приблизительное значение для быстрого поиска решения. Если же ячейка будет пуста, то Excel начнет с любого числа (рандомно).

О подборе нескольких параметров в Excel узнаем из примеров следующего урока.

В MS EXCEL 2007-2010 Подбор параметра находится на вкладке Данные, группа Работа с данным.

Простейший пример

Найдем значение параметра b в уравнении 2*а+3*b=x, при котором x=21, параметр а=3.

Подготовим исходные данные.

Значения параметров а и b введены в ячейках B8 и B9. В ячейке B10 введена формула =2*B8+3*B9 (т.е. уравнение 2*а+3*b=x). Целевое значение x в ячейке B11 введено для информации.

Выделите ячейку с формулой B10 и вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…).

В качестве целевого значения для ячейки B10 укажите 21, изменять будем ячейку B9 (параметр b).

Инструмент Подбор параметра подобрал значение параметра b равное 5.

Конечно, можно подобрать значение вручную. В данном случае необходимо в ячейку B9 последовательно вводить значения и смотреть, чтобы х текущее совпало с Х целевым. Однако, часто зависимости в формулах достаточно сложны и без Подбора параметра параметр будет подобрать сложно.

Примечание: Уравнение 2*а+3*b=x является линейным, т.е. при заданных a и х существует только одно значение b, которое ему удовлетворяет. Поэтому инструмент Подбор параметра работает (именно для решения таких линейных уравнений он и создан). Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (имеет 2 решения), то инструмент решение найдет, но только одно. Причем, он найдет, то которое ближе к начальному значению (т.е. задавая разные начальные значения, можно найти оба корня уравнения). Решим квадратное уравнение x^2+2*x-3=0 (уравнение имеет 2 решения: x1=1 и x2=-3). Если в изменяемой ячейке введем -5 (начальное значение), то Подбор параметра найдет корень = -3 (т.к. -5 ближе к -3, чем к 1). Если в изменяемой ячейке введем 0 (или оставим ее пустой), то Подбор параметра найдет корень = 1 (т.к. 0 ближе к 1, чем к -3). Подробности в файле примера на листе Простейший.

Калькуляция, подбираем значение прибыли

Еще пример. Пусть дана структура цены договора: Собственные расходы, Прибыль, НДС.

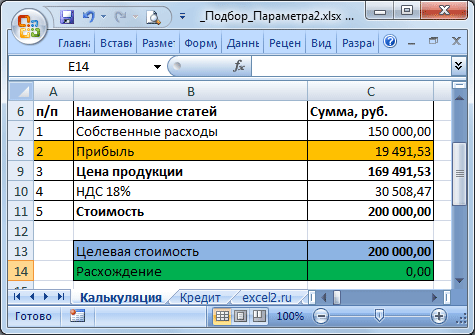
Известно, что Собственные расходы составляют 150 000 руб., НДС 18%, а Целевая стоимость договора 200 000 руб. (ячейка С13). Единственный параметр, который можно менять, это Прибыль. Подберем такое значение Прибыли (С8), при котором Стоимость договора равна Целевой, т.е. значение ячейки Расхождение (С14) равно 0.

В структуре цены в ячейке С9 (Цена продукции) введена формула Собственные расходы + Прибыль ( =С7+С8 ). Стоимость договора (ячейка С11) вычисляется как Цена продукции + НДС (= СУММ(С9:C10) ).

Выделите ячейку С14, вызовите Подбор параметра (на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…). В качестве целевого значения для ячейки С14 укажите 0, изменять будем ячейку С8 (Прибыль).

Теперь, о том когда этот инструмент работает.
1. Изменяемая ячейка не должна содержать формулу, только значение.
2. Необходимо найти только 1 значение, изменяя 1 ячейку. Если требуется найти 1 конкретное значение (или оптимальное значение), изменяя значения в НЕСКОЛЬКИХ ячейках, то используйте Поиск решения.
3. Уравнение должно иметь решение, в нашем случае уравнением является зависимость стоимости от прибыли. Если целевая стоимость была бы равна 1000, то положительной прибыли бы у нас найти не удалось, т.к. расходы больше 150 тыс. Или например, если решать уравнение x2+4=0, то очевидно, что не удастся подобрать такое х, чтобы x2+4=0

Примечание : В файле примера приведен алгоритм решения Квадратного уравнения с использованием Подбора параметра.

Подбор суммы кредита

Предположим, что нам необходимо определить максимальную сумму кредита, которую мы можем себе позволить взять в банке. Пусть нам известна сумма ежемесячного платежа в рублях (1800 руб./мес.), а также процентная ставка по кредиту (7,02%) и срок на который мы хотим взять кредит (180 мес).

В EXCEL существует функция ПЛТ() для расчета ежемесячного платежа в зависимости от суммы кредита, срока и процентной ставки (см. статьи про аннуитет). Но эта функция нам не подходит, т.к. сумму ежемесячного платежа мы итак знаем, а вот сумму кредита (параметр функции ПЛТ() ) мы как раз и хотим найти. Но, тем не менее, мы будем использовать эту функцию для решения нашей задачи. Без применения инструмента Подбор параметра сумму займа пришлось бы подбирать в ручную с помощью функции ПЛТ() или использовать соответствующую формулу.

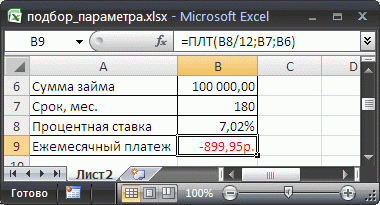
Введем в ячейку B6 ориентировочную сумму займа, например 100 000 руб., срок на который мы хотим взять кредит введем в ячейку B7, % ставку по кредиту введем в ячейку B8, а формулу =ПЛТ(B8/12;B7;B6) для расчета суммы ежемесячного платежа в ячейку B9 (см. файл примера ).

Чтобы найти сумму займа соответствующую заданным выплатам 1800 руб./мес., делаем следующее:

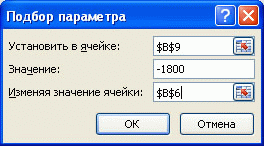
на вкладке Данные в группе Работа с данными выберите команду Анализ «что-если?», а затем выберите в списке пункт Подбор параметра…;
в поле Установить введите ссылку на ячейку, содержащую формулу. В данном примере — это ячейка B9;
введите искомый результат в поле Значение. В данном примере он равен -1800;
В поле Изменяя значение ячейки введите ссылку на ячейку, значение которой нужно подобрать. В данном примере — это ячейка B6;
Нажмите ОК

Что же сделал Подбор параметра? Инструмент Подбор параметра изменял по своему внутреннему алгоритму сумму в ячейке B6 до тех пор, пока размер платежа в ячейке B9 не стал равен 1800,00 руб. Был получен результат — 200 011,83 руб. В принципе, этого результата можно было добиться, меняя сумму займа самостоятельно в ручную.

Подбор параметра подбирает значения только для 1 параметра. Если Вам нужно найти решение от нескольких параметров, то используйте инструмент Поиск решения. Точность подбора параметра можно задать через меню Кнопка офис/ Параметры Excel/ Формулы/ Параметры вычислений . Вопросом об единственности найденного решения Подбор параметра не занимается, вероятно выводится первое подходящее решение.

Иными словами, инструмент Подбор параметра позволяет сэкономить несколько минут по сравнению с ручным перебором.

Источник