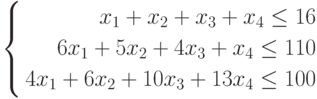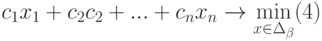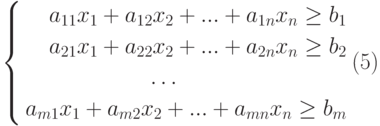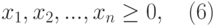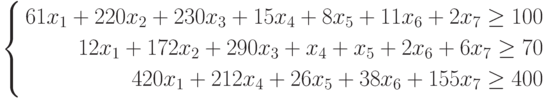Задачи решаемые с помощью табличного процессора excel - Word и Excel

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

Источник

Тема:
Решение задач с помощью уравнений средствами табличного процессора Microsoft Excel

Эпиграф
урока:

«Сосредотачивая
на задаче свое внимание, вы подготавливаете свою память к тому, чтобы извлечь
из нее все, что может принести вам пользу»

Пойа
Д.

Оборудование: цветные карточки
«Светофор», карточки с заданиями (уравнения, задачи), компьютер с проектором,
ноутбуки для учащихся 4-5 шт.

Ход урока.

1. Этап.
Организационный момент.

Приветствие.

2. Этап. Актуализация знаний.

Повторение. Решение уравнений.

1. Устный счет (Работа в парах). Диктант: /учащиеся записывают + или — /

а) Корни
уравнения изменяются, если обе части уравнения умножить на число (-10) (Нет)

б) Может
ли разность двух отрицательных чисел быть целым положительным числом? (Да)

в) Корни
уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части
уравнения в другую, изменив при этом его знак (Да)

г) Если
перед скобками стоит знак «–», то нужно раскрыть скобки, сохранив знаки
слагаемых (Нет)

д) На
ноль делить можно (Нет)

е) Чтобы
сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить
на общую буквенную часть (Да)

ж) Если
перед скобками стоит знак «+», то можно опустить скобки, сохранив знаки
слагаемых (Да)

з) Чтобы
перемножить два числа с разными знаками, надо перемножить модули этих чисел «–»
(Нет)

и) Произведение
может быть равно нулю, когда хотя бы один из множителей равен нулю (Да)

к) Может
ли сумма двух целых положительных чисел быть равной 0?(Нет)

Учащиеся обмениваются тетрадями. Проверка:
– + + – – + + – + –

Оценивание работы на полях: “5” – 10-9
верных знаков, “4” – 7-8 знаков, “3” – 6-5 знака.

2.
Решение уравнений.

При решении
уравнений были допущены ошибки. Найдите и исправьте их.

а) х+2,7=3 (х+2,7=3
х=3-2,7 х=0,3)

х=3+2,7

х=5,7

б) 3х-1=2(х-2) (3х-1=2х-4
3х-2х=1-4 х=-3)

3х-1=2х-4

3х+2х=1+4

5х=5

х=1

в) 25-4х=12-5х (5х-4х=12-25
х=-13)

5х-4х=12+25

х=37

г) 2х+7=х+5,5 (2х-х=5,5-7
х=-1,5)

2х-х=5,5-7

х=4,8

д) 7х+3=7х+5 (0х=2,
уравнение не имеет корней)

7х-7х=5-3

х=2

е) 3х+х-7=4х-7 (0х=0,
х — любое число)

4х-4х=7-7

х=0

3.
Упрощение выражений.

Докажите, что
значение выражения 5(а+1)-(5а-4) не зависит от значения переменной.

Доказательство:

5(а+1)-(5а-4)=5а+5-5а+4=9

Следовательно,
значение выражения 5(а+1)-(5а-4) не зависит от значения переменной.

3.
Этап. Закрепление.

Решение задач с помощью табличного
процессора Microsoft Excel.
(Учащиеся работают на компьютерах)

Задача№1

Сейчас отцу 34 года, а сыну 11 лет. Через
сколько лет возраст отца будет в 2 раза больше возраста сына?

На экранах компьютеров учащиеся видят
таблицу:

Необходимо
составить уравнение к задаче по данной таблице и решить его:

Составим
уравнение: 34+х=2(11+х)

Решаем уравнение:

34+х=22+2х;

2х-х=34-22;

х=12.

Ответ: через 12 лет возраст отца будет в 2
раза больше возраста сына.

Проверка:

Учащиеся вводят в таблицу полученный
результат и формулы:

При условии, что в ячейке D2
получается значение 2, задача решена верно.

Задача№2

2.Расстояние от
пристани А до пристани В катер проплыл за 6 ч., а от пристани В до пристани А –
за 7 ч. Скорость течения реки 2км/ч. Найти собственную скорость катера.

На экранах компьютеров учащиеся видят
таблицу:

х км/ч.- собственная скорость катера

Необходимо
составить уравнение к задаче по данной таблице и решить его:

Составим
уравнение: 6(х+2)= 7(х-2)

Решаем уравнение:

6х+12=7х-14;

6х-7х=-14-12;

-х=-26;

х=26.

Ответ: собственная скорость катера 26
км/ч.

Проверка:

Учащиеся вводят в таблицу полученный
результат и формулы:

При условии, что в ячейках E2
и E3 получаются равные
значения, задача решена верно.

Физминутка для глаз.

4. Этап. Самостоятельная работа

1.На первой стоянке в 4 раза меньше
автомашин, чем на второй. После того как на первую приехали 35 автомашин, а со
второй уехали 25 автомашин, автомашин на стоянках стало поровну. Сколько
автомашин было на каждой стоянке первоначально.

На экранах компьютеров учащиеся видят
таблицу:

Необходимо
составить уравнение к задаче по данной таблице, решить его и выполнить проверку
средствами табличного процессора Microsoft Excel:

Составим
уравнение: х+35=4х-25

Решаем
уравнение:

х-4х=-25-35

-3х=-60

х=20 (машин)

4*20=80 (машин)

Ответ: на каждой стоянке
первоначально было 20 машин и 80 машин соответственно.

5. Этап. Домашнее задание

Уровень “3” —
№606 из учебника

Уровень “4” —
№611 из учебника

Уровень “5” –
составить 3 задачи, одну из них решить

6. Этап. Рефлексия.

Учащиеся оценивают
свою деятельность на уроке с помощью «Светофора»: Зелёная карточка – мне все
понятно

Желтая
карточка – у меня возникли затруднения

Красная
карточка – много непонятного

Источник

во втором поле выбрать оператор ограничения (>, Поиск решения).

Найденные решения (значения изменяемых ячеек) можно сохранить в качестве сценария. Для этого нужно:

В диалоговом окне Результаты поиска решения выбрать Сохранить сценарий.
В поле Название сценария ввести имя сценария. Просмотреть сценарии можно с помощью команды Данные > Работа с данными > Анализ что-если > Диспетчер сценариев > Сценарии.

С помощью программы Поиск решения можно создать три типа отчетов по результатам, полученным при успешном завершении процедуры решения.

Каждый отчет создается на отдельном листе текущей рабочей книги.

Для создания отчета надо в диалоговом окне Результаты поиска решения выбрать нужный тип отчета в поле Тип отчета. Можно выбрать сразу несколько типов (при выделении нескольких строк используется клавиша ).

Результаты – отчет содержит целевую ячейку, список изменяемых ячеек, их исходные и конечные значения, ограничения и сведения о них.
Устойчивость – отчет содержит сведения о степени зависимости модели от изменений величин, входящих в формулы, применяемые в задаче (формулы модели и формулы ограничений).
Пределы – выводится целевая ячейка и ее значение, а также список изменяемых ячеек, их значений, нижних и верхних пределов и целевых результатов.

Рассмотрим применение процессора Excel для решения ЗЛП на примерах.

Задача 1. Планирование производства

Модель линейного программирования дает возможность определить наиболее выгодную производственную программу выпуска нескольких видов продукции при заданных ограничениях на ресурсы.

МП выпускает товары х₁,х₂,х₃,х₄, получая от реализации каждого прибыль в 60,70,120,130 руб. соответственно. Затраты на производство приведены в таблице.

Затраты	х₁	х₂	x₃	х₄	Всего
Трудовые	1	1	1	1	16
Сырьевые	6	5	4	1	110
Финансы	4	6	10	13	100

Максимум прибыли в зависимости от оптимального распределения затрат.
Минимум ресурсов, необходимых для получения максимальной прибыли.

Решение задачи средствами Excel состоит из 4 этапов:

Создание математической модели задачи ЛП.
Создание формы для ввода условий задачи, ввод в неё исходных данных и зависимостей из математической модели.
Ввод данных из формы в окно Excel Поиск решения из меню Данные.
Задание параметров поиска и решение задачи.

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

— целевая функция прибыли.

— граничные условия модели, так как количество производимых товаров не может быть отрицательной величиной.

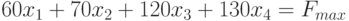
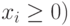
Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее первого рабочего листа на Задача о производстве.

Создание формы

Составление формы в виде:

A	B	C	D	E	F	G	H
1	Переменная	х₇	х₂	x₃	х₄	Формула	Знак	Св.член
2	Значение
3	Коэф. ЦФ	60	70	120	130	=СУММПРОИЗВ(В$2:Е$2;В3:Е3)	Max
4	Трудовые	1	1	1	1	=СУММПРОИЗВ(В$2:Е$2;В4:Е4)		16
5	Сырьевые	6	5	4	1	=СУММПРОИЗВ(В$2:Е$2;В5:Е5)		110
6	Финансы	4	6	10	13	=СУММПРОИЗВ(В$2:Е$2;В6:Е6)		100

Запись в ячейки В3:Е3 коэффициентов целевой функции F (1), в В4:Е6 коэффициентов из системы ограничений (2) и в ячейки Н4:Н6 – свободных членов из системы (2).
Ввод формул с помощью f_x – Мастера функций.

Для ввода формулы в целевую ячейку (целевой функции): щелкнуть левой клавишей мыши по ячейке F3 , затем по значку Мастера функций f_x на панели инструментов, в появившемся окне «Мастер функций, Шаг 1» выбрать категорию «Математические», далее выбрать функцию СУММПРОИЗВ, нажать клавишу ОК, в окне «Мастер функций Шаг 2» в поле Массив 1 ввести с клавиатуры В2:Е2 (ячейки, в которых будут варьироваться х₁..х₄), в поле Массив 2 ввести В3:Е3 (коэффициенты целевой функции ЦФ).

Примечание. Можно вводить В2:Е2 не с клавиатуры, а поставить курсор в окно Массив 1, а затем протащить курсор при нажатой левой клавише мыши по ячейкам В2:Е2, имена ячеек сами запишутся в окно. Аналогично поступить с полем Массив 2.

Нажать клавишу ОК, в ячейку F3 запишется формула 60х₁+70х₂+120х₃+ 130х₄ в виде СУММПРОИЗВ(В2:Е2;В3:Е3).

Чтобы не вводить формулы в другие ячейки, необходимо изменить тип адресации для ячеек В2:Е2 с относительной на абсолютную $B$2:$E$2 , установив курсор перед нужным адресом B2 и нажав функциональную клавишу F4 , затем повторить эти действия для адреса E2 . Формула примет следующий вид:

После внесенных изменений необходимо скопировать формулу в ячейки F4:F6 c помощью маркера заполнения. Для этого необходимо выделить ячейку F3 , содержащую нужную формулу, установить указатель мыши на черный квадратик в правом нижнем углу ячейки (он примет форму черного крестика) и протащить с помощью левой кнопки мыши на весь требуемый диапазон.

В результате копирования мы увидим следующие формулы:

в ячейке F4 – СУММПРОИЗВ($В$2:$Е$2;В4:Е4),
в ячейке F5 – СУММПРОИЗВ($В$2:$Е$2;В5:Е5),
в ячейке F6 – СУММПРОИЗВ($В$2:$Е$2;В6:Е6).

Заполнение окна Поиск решения

Выбрать в пункте меню Данные команду Поиск решения, поставить курсор в поле целевой функции, выделить ячейку F3 в форме (или ввести F3 с клавиатуры), поставить переключатель в положение «Максимальному значению» (см. рис. 12.1 рис. 12.1). В поле «Изменяя ячейки» ввести $В$2:$Е$2(с клавиатуры или протащив мышью).

Нажать клавишу «Добавить», в окне «Добавление ограничения» в поле «Ссылка на ячейку» ввести F4 , выбрать через «стрелка вниз» знак ««, в поле справа ввести Н4 (рис. 12. рис. 12.2).

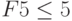
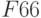
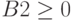
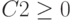
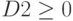
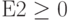
Аналогично через «Добавить» ввести , для системы ограничений (2), а также , , и .

Также необходимо добавить ограничения для получения целочисленных величин по количеству товаров: B2=цел, C2=цел, D2=цел и Е2=цел.

После ввода последнего граничного условия вместо «Добавить» нажать клавишу ОК, появится окно «Поиск решения».

Для изменения или удаления ограничений и граничных условий используются клавиши Изменить, Удалить.

Параметры поиска

В окне «Поиск решения» нажать клавишу «Параметры», выбрать по умолчанию Максимальное время – 100 с, число итераций – 100 (для большинства задач это количество просчётов подходит с большим запасом), установить флажок в строке «Линейная модель», нажать ОК, в появившемся окне Поиск Решения нажать Выполнить (рис. 12. рис. 12.3).

Результаты поиска решения с таблицей результатов:

A	B	C	D	E	F	G	H
1	Переменная	X1	X₂	X₃	X₄	Формула	Знак	Св.член
2	Значение	10	0	6	0
3	Коэф. ЦФ	60	70	120	130	1320	Max
4	Трудовые	1	1	1	1	16		16
5	Сырьевые	6	5	4	1	84		110
6	Финансы	4	6	10	13	100		100

Таким образом оптимальный план Х(Х₁,Х₂,Х₃,Х₄)=(10,0,6,0) при минимальном использовании ресурсов

Трудовые – 16 (У₁)
Сырьевые – 84 (У₂)
Финансы – 100 (У₃)

даёт максимум прибыли F в 1320 руб.

_Вывод: Максимальная прибыль F в 1320 руб. получается при выпуске только товаров Х₁ и Х₃ в количестве 10 и 6 штук соответственно, товары Х₃ и Х₄ выпускать не нужно (это приведёт к снижению прибыли). Трудовые (У₁) и финансовые (У₃) ресурсы используются полностью, по сырьевым ресурсам (У₂) есть запас в 110-84=26 ед.

Кроме того, это означает, что изменение трудовых ( y₁ ) и финансовых ( y₃ ) ресурсов приведёт к изменению прибыли F , а изменение сырьевых ресурсов ( y₂ ) – нет.

Разности между плановыми ресурсами и использованными являются двойственными переменными y₁, y₂ и y₃ сопряжённой задачи линейного программирования. В данном случае y₁=y₃=0 , а y₂=26 ед. Таким образом, ресурс y₂ можно уменьшить на 26 ед., тогда план по сырью тоже будет оптимальным.

Задача 2. Задача об оптимальной диете

Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Ведем в рассмотрение следующие переменные: х – весовое количество продукта питания i-го типа в суточном рационе.

Тогда в общем случае математическая постановка задачи об оптимальной диете может быть сформулирована следующим образом:

где множество допустимых альтернатив 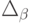формируется следующей системой ограничений типа неравенств:

Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи.

Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3).

Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы.

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂= 70, в углеводах b3 = 400.

Для решения данной задачи c помощью программы MS Excel создадим новую книгу с именем Линейное программирование и изменим имя ее второго рабочего листа на Задача о диете.

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	61	220	230	15	8	11	6
Жиры	12	172	290	1	1	2	2
Углеводы	420	0	0	212	26	38	155

Создание математической модели задачи

Составим математическую модель процесса по описанию задачи:

– целевая функция (суммарная калорийность продуктов).

– граничные условия

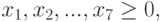
Создание формы

Для решения поставленной задачи выполним следующие подготовительные действия:

Внесем необходимые надписи в ячейки A1:I1, A2:A7, B4, I4, J4 .
В ячейки ВЗ:НЗ введем значения коэффициентов целевой функции: с₁ = 2060, с₂ = 2430, с₃ = 3600, с₄ = 890, с₅ = 140, с₆ = 230, с₇ = 650.
В ячейку I2 введем формулу: =СУММПРОИЗВ( b ₂:Н2;B3:H3), которая представляет целевую функцию (4).
В ячейки В5:Н7 введем значения коэффициентов ограничений, взятых из таблицы.

В ячейки J5 :J7 введем значения правых частей ограничений, соответствующих минимальной суточной потребности в питательных веществах: в белках b ₁=100 , жирах b ₂= 70 и углеводах b3 = 400.
В ячейку I5 введем формулу: =СУММПРОИЗВ($B$2:$H$2;В5:Н5), которая представляет левую часть первого ограничения (5).
Скопируем формулу, введенную в ячейку I5 , в ячейки I6 и I7 .
Внешний вид рабочего листа MS Office Excel с исходными данными для решения задачи об оптимальном рационе питания имеет следующий вид (pиc. 12.4).

Для отображения формул в ячейках рабочего листа необходимо выполнить команду меню: Формулы и на панели инструментов в группе Зависимости формул выбрать Показать формулы.

Заполнение окна Поиск решения

Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные > Поиск решения.

После появления диалогового окна Поиск решения следует выполнить следующие действия:

В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2 .
Для группы Равной: выбрать вариант поиска решения – минимальному значению.
В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2 .
Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
- для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 12.5 рис. 12.5, а);
- в появившемся дополнительном окне выбрать ячейку $I$5 , которая должна отобразиться в поле с именем Ссылка на ячейку;
- в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство » «;
- в качестве значения правой части ограничения выбрать ячейку $J$5 ;
- для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
- аналогичным образом задать оставшиеся два ограничения (рис. 12.5 рис. 12.5, б).

Параметры

В окне «Поиск решения» нажать клавишу «Параметры», выбрать «Поиск решения Линейных задач симплекс-методом», нажать ОК, затем нажать Найти Решение (рис. 12.6 рис. 12.6, б).

После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 12. рис. 12.7.

Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: х₁ = 0, х₂ = 0,211, 3 = 0,109, х₄= 1,887, х₅ = 0, х₆ = 0, х₇ = 0, которым соответствует значение целевой функции: f_опт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.

Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будет приближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

ЗАДАНИЕ

Составить математическую модель задачи линейного программирования.
Решить задачу линейного программирования в Excel с помощью Поиска решения.
Сохранить в виде модели установочные параметры.

Предприятие легкой промышленности выпускает две модели машин, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 80 изделий, второй линии – 85 изделий. На машину первой модели расходуются 12 однотипных элементов электронных схем, на машину второй модели – 6 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одной машины первой и второй моделей равна $30 и $40 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех приборах. Время использования этих приборов для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма имеет возможность рекламировать свою продукции, используя местные радио- и телевизионную сеть. Затраты на рекламу в бюджете фирмы ограничены $1000 в месяц. Каждая минута радиорекламы обходится в $5, а минута телерекламы – в $100. Фирма хотела бы использовать радиосеть, по крайней мере, в два раза чаще, чем сеть телевидения. Опыт прошлых лет показал, что объем сбыта, который обеспечивает каждая минута телерекламы, в 25 раз больше сбыта, обеспечиваемого одной минутой радиорекламы. Определить оптимальное распределение ежемесячно отпускаемых средств между радио- и телерекламой.

Фирма производит два вида продукции – А и B . Объем сбыта продукции вида A составляет не менее 70% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 120 кг. Расход сырья на единицу продукции A составляет 3 кг, а на единицу продукции В – 5 кг. Цены продукции А и В равны $20 и $60 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает женские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $6, а фасона 2 – $7. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Изделия четырех типов проходят последовательную обработку на двух станках. Время обработки одного изделия каждого типа на каждом из станков:

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства, максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ) Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 5000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Трудоемкость изготовления модели I вдвое больше, чем изделия модели II , и втрое больше, чем изделие модели III . Численность рабочих завода позволяет выпускать 1500 изделий I . Анализ условий сбыта показывает, что минимальный спрос на продукцию завода составляет 200, 200 и 150 изделий моделей I,II и III соответственно. Однако соотношение выпуска изделий моделей I,II и III должно быть равно 3:2:5. Удельная прибыль от реализации изделий моделей I,II и III составляет $30, $20 и $50 соответственно. Определить выпуск изделий, максимизирующий прибыль.

Требуется распределить имеющиеся денежные средства по четырем альтернативным вариантам. Игра имеет три исхода. Ниже приведены размеры выигрыша (или проигрыша) на каждый доллар, вложенный в соответствующий альтернативный вариант, для любого из трех исходов. У игрока имеется $500, причем, использовать в игре их можно только один раз. Точный исход игры заранее неизвестен, и, учитывая эту неопределенность, игрок решил распределить деньги так, чтобы максимизировать максимальную отдачу от этой суммы.

Бройлерное хозяйство птицеводческой фермы насчитывает 80000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Для того чтобы цыплята достигли к восьмой неделе необходимых весовых кондиций, кормовой рацион должен удовлетворять определенным требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов или ингредиентов. Ограничим наше рассмотрение только тремя ингредиентами: известняком, зерном и соевыми бобами. Ниже приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента.

Смесь должна содержать:

не менее 0.8%, но не более 1.2% кальция;
не менее 22% белка;
не более 5% клетчатки.

Необходимо определить количество каждого из трех ингредиентов, образующих смесь минимальной стоимости при соблюдении требований к общему расходу кормовой смеси и ее питательности.

Имеется n видов продуктов питания, в которых содержится m типов питательных веществ (белки, жиры, углеводы). В одной весовой единице продукта i-го типа содержится а_i единиц питательного вещества j-го вида . Известна минимальная суточная потребность b _j человека в каждом из видов питательных веществ. Задана калорийность сi одной весовой единицы i-го продукта ( i принадлежит <1, 2, . n >). Требуется определить оптимальный состав рациона продуктов, такой, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

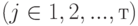
Для решения задачи об оптимальной диете с помощью программы MS Excel необходимо задать конкретные значения параметрам исходной задачи. Для определенности предположим, что в качестве исходных типов продуктов рассматриваются: хлеб, мясо, сыр, бананы, огурцы, помидоры, виноград ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность одной весовой единицы каждого из продуктов следующая:с₁ = 2060,с₂= 2430,с₃= 3600,с₄= 890,с₅= 140,с₆= 230, с₇ = 650. Содержание питательных веществ в каждом из продуктов может быть задано в форме следующей таблицы (см. табл.).

Таблица 1. Содержание питательных веществ в продуктах питания

Продукты/питательные вещества	Хлеб ржаной	Мясо баранина	Сыр «Российский»	Банан	Огурцы	Помидоры	Виноград
Белки	66	225	235	20	13	16	11
Жиры	17	177	295	1	1	7	7
Углеводы	425	0	0	217	31	43	200

Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 105, в жирах b ₂ = 75, в углеводах b ₃ = 405.

Определить суточную потребности в питательных веществах (белки, жиры, углеводы) и общую калорийность оптимальной диеты.

Предприятие электронной промышленности выпускает две модели радиоприемников, причем каждая модель производится на отдельной технологической линии. Суточный объем производства первой линии – 60 изделий, второй линии – 75 изделий. На радиоприемник первой модели расходуются 10 однотипных элементов электронных схем, на радиоприемник второй модели – 8 таких же элементов. Максимальный суточный запас используемых элементов равен 800 единицам. Прибыль от реализации одного радиоприемника первой и второй моделей равна $30 и $20 соответственно. Определить оптимальный суточный объем производства первой и второй моделей.

Процесс изготовления двух видов промышленных изделий состоит в последовательной обработке каждого из них на трех станках. Время использования этих станков для производства данных изделий ограничено 10 ч. в сутки. Найти оптимальный объем производства изделий каждого вида.

Фирма производит два вида продукции – A и B . Объем сбыта продукции вида A составляет не менее 60% общего объема реализации продукции обоих видов. Для изготовления продукции А и В используется одно и то же сырье, суточный запас которого ограничен величиной 100 кг. Расход сырья на единицу продукции A составляет 2 кг, а на единицу продукции В – 4 кг. Цены продукции А и В равны $20 и $40 соответственно. Определить оптимальное распределение сырья для изготовления продукции А и В.

Фирма выпускает ковбойские шляпы двух фасонов. Трудоемкость изготовления шляпы фасона 1 вдвое выше трудоемкости изготовления шляпы фасона 2. Если бы фирма выпускала только шляпы фасона 1, суточный объем производства мог бы составить 60 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 50 до 100 штук. Прибыль от продажи шляпы фасона 1 равна $8, а фасона 2 – $5. Определить какое количество шляп каждого фасона следует изготавливать, чтобы максимизировать прибыль.

Затраты на производство одного изделия каждого типа определяются как величины, прямо пропорциональные времени использования станков (в машино-часах). Стоимость машино-часа составляет $10 и $15 для станка 1 и 2 соответственно. Допустимое время для использования станков для обработки изделий всех типов ограничено следующими значениями: 500 машино-часов – для станка 1 и 380 машино-часов для станка 2. Цены изделий типов 1,2,3 и 4 равны $65, $70, $55 и $45 соответственно. Составить план производства максимизирующий чистую прибыль.

Завод выпускает изделия трех моделей ( I, II III ). Для их изготовления используется два вида ресурсов (А и В), запасы которых составляют – 4000 и 6000 единиц. Расходы ресурсов на одно изделие каждой модели:

Некоторое производственное предприятие выпускает три вида клея. Для производства клея используется 4 типа химических веществ: крахмал, желатин, квасцы и мел. Расход этих веществ в кг для получения 1 кг каждого вида клея и их запас на складе предприятия представлены в таблице.

Таблица 1. Расход химических веществ на изготовления клея, их запас на складе

Вид клея /Химические вещества	Клей № 1	Клей № 2	Клей № 3	Запас на складе
Крахмал	0,4	0,3	0,2	20
Желатин	0,2	0,3	0,4	35
Квасцы	0,05	0,07	0,1	7
Мел	0,01	0,05	0,15	10

Стоимость каждого вида клея для оптовых покупателей следующая:с₁ = 380 руб/кг,с₂ =430 руб/кг,с₃ = 460 руб/кг. Требуется определить оптимальный объем выпуска клея каждого вида, обеспечивающий максимум общей стоимости готовой продукции.

Бройлерное хозяйство птицеводческой фермы насчитывает 20000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Хотя недельный рацион цыплят зависит от их возраста, в дальнейшем будем считать, что в среднем (за 8 недель) он составляет 1 фунт.

Смесь должна содержать:

не менее 0.8%, но не более 1.2% кальция;
не менее 22% белка;
не более 5% клетчатки.

Имеется конечное число видов продуктов питания: ананас, арбуз, грейпфрут, язык говяжий, сардельки говяжьи, хлеб «Бородинский», картофель ( n = 7), а в качестве питательных веществ рассматриваются белки, жиры, углеводы ( m = 3). Калорийность 1 кг каждого из продуктов следующая:с₁ = 470,с₂= 380,с₃ = 350,с₄ = 1460,с₅ = 2150,с₆ = 2070, с₇ = 800. Минимальная суточная потребность в питательных веществах следующая: в белках b ₁ = 100, в жирах b ₂ = 70, в углеводах b3 = 400. Содержание питательных веществ в каждом из продуктов может быть задано в форме нижеприведенной таблицы (табл.).

Требуется определить такой рацион питания, чтобы каждое питательное вещество содержалось в нем в необходимом количестве, обеспечивающем суточную потребность человека, и при этом суммарная калорийность рациона была минимальной.

Поиск решения задач в Excel с примерами

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Решение задач оптимизации в Excel

В Excel для решения задач оптимизации используются следующие команды:

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

Количество изделий нам пока неизвестно. Это переменные.
В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.

Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Оформим исходные данные в виде таблицы:

Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
Тип – 0.
БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер . Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Дано 2 диапазона значений:

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =, Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

Делаем таблицу со значениями матрицы А.
Выделяем на этом же листе область для обратной матрицы.
Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
В поле аргумента «Массив» вписываем диапазон матрицы А.
Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

источники:

http://intuit.ru/studies/courses/3659/901/lecture/32717

http://exceltable.com/vozmojnosti-excel/poisk-resheniya-v-excel

Источник

Муниципальное образовательное учреждение

Октябрьская средняя общеобразовательная школа

Радищевского района Ульяновской области

Реферат на тему:

«Решение прикладных (экономических) задач

в Excel»

Работу выполнил:

Учащийся 11 класса

Чахоян Каруш

Руководитель:

Учитель информатики

Юдахина Т. М.

П. Октябрьский. 2007 г

Оглавление:

1. Введение. Обоснование выбора темы реферата…………………………….3

2. Решение прикладных задач в Excel………….…………………………………3

3. Задачи оптимизации …………………………………………………………..6

4. Прогнозирование ……………………………………………………………..11

5. Заключение. Актуальность выбранной темы……………………………….13

6. Используемая литература………………………………….…………………14

7. ПРИЛОЖЕНИЕ (файлы таблицы Excel) ……………………………………..…… 15

ВВЕДЕНИЕ

Обоснование выбора темы реферата.

Целью данной работы является использование функций Excel для решения экономических задач. Данные задачи будут решаться с помощью программ табличного процессора Excel. Microsoft Excel средство для работы с электронными таблицами, намного превышающее по своим возможностям существующие редакторы таблиц, первая версия данного продукта была разработана фирмой Microsoft в 1985 году. Табличные процессоры — удобный инструмент для экономистов, бухгалтеров, инженеров, научных работников — всех тех, кому приходится работать с большими массивами числовой информации. Эти программы позволяют создавать таблицы, которые являются динамическими, т. е. содержат так называемые вычисляемые поля, значения которых автоматически пересчитываются по заданным формулам при изменении значений исходных данных, содержащихся в других полях. В дальнейшем ее можно просматривать, изменять, записывать на магнитный диск для хранения, печатать на принтере. Microsoft Excel – это программа управления электронных таблицами общего назначения, которая используется для вычислений, организации и анализа деловых данных. Многие фирмы разработчики программного обеспечения для ПК создали свои версии табличных процессоров. Из них наибольшую известность приобрели Lotus 1-2-3 фирмы Lotus Development, Supercalc фирмы Computer Associates.

Excel — очень мощный инструмент для решения задач, имеющих дело с массивами разнообразных данных, поэтому область его применения обширна, начиная от бухгалтерских и складских задач и заканчивая расчетами энергетики спутниковых линий. В Excel удобно решать задачи линейной алгебры, такие как работа с матрицами и др. Также есть все возможности по полноценной работе (сортировка, выборка, сводные таблицы, анализ) с базами данных. Благодаря наличию языка программирования в Excel возможно создание различных пользовательских программ, которые автоматизируют специфические стандартные задачи.

Мне интересна данная тема именно в использовании электронной таблицы в ведении бухгалтерии. Я собираюсь связать свою профессию с экономикой. Наша семья имеет частный магазин. Поэтому я взялся за данную тему. Я уже сейчас занимаюсь экономическими и бухгалтерскими расчетами, помогая отцу в содержании магазина и организации его эффективной работы. Использование компьютера очень помогает мне быстро и правильно производить расчеты и строить перспективы на дальнейшую работу.

2. Решение прикладных задач в Excel

В данном разделе вы убедитесь, что Excel позволяет не только производить расчеты, но и решать сложные задачи в различных сферах деятельности, такие как решение уравнений, задачи оптимизации, прогнозирования. Решение этих задач может быть существенно облегчено с помощью инструмента Поиск решения (Solver в английских версиях Excel).

Формулировка таких задач может представлять собой систему уравнений с несколькими неизвестными и набор ограничений на решения. Поэтому решение задачи необходимо начинать с построения соответствующей модели.

Если надстройка Поиск решения (Solver) не была установлена при первоначальной установке Excel, то следует запустить процесс установки повторно и выбрать только эту настройку.

Для того чтобы надстройка Поиск решения (Solver) загружалось сразу при запуске Excel:

-выберите команду Сервис, Надстройки;

-в диалоговом окне Надстройки в списке надстроек установите флажок напротив надстройки Поиск решения. Если в списке нет элемента Поиск решения, то нажмите кнопку Обзор, чтобы самостоятельно найти файл Solver.XLA.

Виды математических моделей.

При решении оптимизационных задач с помощью надстройки Поиск решения необходимо различать линейные и нелинейные модели. Под линейными понимаются модели, в которых связь между входными значениями переменных и результирующими значениями описывается линейными функциями. Например:

Y=A*X1+B*X2+C*X3+…

В этом выражении А,В,С — константы, Х1,Х2,Х3-переменные, Y-результат.

Если выражение для целевой величины и выражение для ограничений являются линейными, то можно применять быстрые и надежные методы поиска решения. Для использования именно линейных методов следует установить параметр Линейная модель в окне Параметры поиска решения. Если этот параметр не установить, то даже для линейной задачи будут использоваться общие, более медленные методы.

Ограничения в задачах.

Под ограничениями понимаются соотношения типа A1>=B1, A2=B2, A3>0.

По крайней мере, одна из ячеек в соотношении, определяющем ограничение, должна зависеть от переменных задачи, в противном случае это ограничение не может влиять на процесс решения. Часто ограничения записываются сразу для групп ячеек, например:

A1:A10<=B1:B10 или A1:E1>=0.

Правильная формулировка ограничений является наиболее ответственной частью при формировании модели для поиска решения.

В одних случаях ограничения просты и очевидны, например ограничения на количество сырья. Другие ограничения менее очевидны и могут быть указаны неверно или , хуже того, оказаться пропущенными.

Решение уравнений.

Часто при решении практических задач возникают ситуации, когда необходимо достичь какой-то конкретной цели. Например, необходимо, чтобы себестоимость продукции составляло 20 у. е.

Специфика таких задач состоит в том, что в вашем распоряжении есть математическая модель исследуемого процесса, например закон ценообразования, но вы не знаете, при каком значении входящего в нее параметра можно достичь поставленной цели.

Решение таких задач можно искать методом перебора, однако на это уходит много времени (в лучшем случае).

Можно предложить другие способы решения. В Excel они реализованы как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.

Эта процедуру используют для поиска такого значения ячейки, при котором значение другой ячейки, вычисляемая по формуле, заранее задано. В формуле должна быть ссылка на ячейку, значение которой ищут. Ограничения на искомое значение ячейки не налагают.

Познакомимся с этой процедурой на примере составления штатного расписания.

Задача 1. Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 10 000 у. е. Необходимо определить, какими должны быть оклады сотрудников больницы.

Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальное оклады будем вычислять, исходя из него: во сколько-то раз или на сколько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*C+Bi, где С- оклад санитарки; Ai и Bi-коэффициенты, которые для каждой должности определяются следующим образом:

-медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);

-врач в 3раза больше санитарки (А3=3;В3=0);

-заведующий отделением –на 30у.е. больше, чем врач (А4=3;В4=30);

-заведующий аптекой- в 2 раза больше санитарки (А5=2;В5=0);

-заведующий хозяйством – на 40 у. е. больше медсестры (А6=1,5; В6=40);

-главный врач — в 4 раза больше санитарки (А7=4; В7=0);

-заведующий больницей — на 20 у.е больше главного врача (А8=4;В8=20).

Зная количество человек на каждой должности, нашу модель можно записать как уравнение:

N1*A1*C+N2(A2*C+B2)+…+N8*(A8*C+B8)=10000, где N1-число санитарок, N2-число медсестер и т. д.

В этом уравнений нам известны А1…А8, В1…В8 и N1…N8, а С неизвестно.

Анализ уравнения показывает, что задача составления расписания свелась к решению линейного уравнения относительно С.

Решим его.

Технология работы:

-Запустите табличный процессор Excel.

-Заполните таблицу в соответствии с образцом в таблице (файл hospital.xls) cм Приложения

В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D2 формула расчета имеет вид =B2*$G$2+C2.Затем заполните вниз.

В столбце F вычислите заработную плату всех работающих на данной должности. Например, для ячейки F2 формула расчета имеет вид =D2*Е2. Затем заполните вниз.

В ячейке F10 вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже: (файл hospital 1.xls) cм Приложения

Как видите, взяв оклад санитарки за 150, мы превысили месячный фонд зарплаты. Определите оклад санитарки так, чтобы расчетный фонд был равен заданному. Для этого:

-активизируйте команду Подбор параметра из меню Сервис;

-в поле «Установить в ячейке» появившегося окна введите ссылку на ячейку F10, содержащую формулу;

-в поле «Значение» наберите искомый результат 10000.

В поле «Изменяя значение ячейки» введите ссылку на изменяемую ячейку G2 и щелкните кнопкой ОК. Таблица будет выглядеть следующим образом: (Таблица сохранена в каталоге Приложения под именем hospital2.xls.)

Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако благодаря этому простому примеру стало очевидно, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, — это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решить любые уравнения с одной переменной.

3.Задачи оптимизации

Иногда интересует не конкретный результат, а минимально или максимально возможный. Например, как минимизировать затраты на содержание персонала или максимизировать прибыли от реализации продукции?

Такие задачи в Excel также решаются с помощью Поиска решения.

Если математическая модель исследуемого процесса и ограничения на значения ее параметров линейны, то задача достижения цели является задачей линейного программирования.

Познакомимся с решением этих задач на следующем примере.

Задача 2. Составление штатного расписания.

Усложним рассмотренную ранее задачу. Пусть известно, что для нормальной работы больницы необходимо 5-7 санитарок, 8-10 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующий хозяйством и заведующий больницей. Общий месячный фонд зарплаты должен быть минимален, Необходимо определить, какими должны быть оклады сотрудников больницы, при условии, что оклад санитарки не должен быть меньше прожиточного минимума — 80у.е.

В качестве модели решения этой задачи возьмем, как и раньше, линейную. Запишем ее так:

N1*A1*C+N2*(A2*C+B2)+…+N8*(A8*C+B8)=Минимум.

В этом уравнений нам не известно число санитарок (N1), медсестер (N2), врачей (N3) и оклад санитарки (C).

Используя Поиск решения, найдем их.

Откройте созданный в предыдущей задаче (файл hospital 1.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения.

В окне установить целевую ячейку укажите ячейку F10, содержащую модель.

Поскольку необходимо минимизировать общий месячный фонд зарплаты, то активизируйте радиокнопку Минимальному значению.

Используя кнопку Добавить, опишите ограничения задачи.

$E$2<=7

$E$2>=5

$E$3<=10

$E$3>=8

$G$2>=80

Щелкните кнопкой ОК, затем — Выполнить.

Решение приведено ниже: (файл hospital3.xls) см Приложения

Оно тривиально: чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд заработной платы.

Задача 3. План выгодного производства

Предположим, что мы решили производить несколько видов конфет. Назовем их условно «А», «В», «С». Известно, что реализация 10 килограммов конфет «А» дает прибыль 9 у. е., «В»-10 у. е., «С»-16 у.е.

Конфеты можно производить в любых количествах (сбыт обеспечен), но запасы сырья ограничены. Необходимо определить, каких конфет и сколько десятков килограммов необходимо произвести, чтобы общая прибыль от реализаций была максимальной.

Нормы расхода сырья на производство 10 кг конфет каждого вида приведены ниже.

Сырье	Нормы расхода	Запас
А	B	C
Какао	18	15	12	360
сахар	6	4	8	192
наполнитель	5	3	3	180
прибыль	9	10	16

Решение.

Технология работы:

-Запустите табличный процессор Excel.

-Заполните таблицу в соответствии с данными задачи (таблица файл konfetki.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:

$A$10<=360

$B$10<=192

$B$3>=0

$B$4>=0

$B$5>=0

$C$10<=180.

Не забудьте указать, что изменяются ячейки $B$3:$B$5 и в Параметрах на Линейность модели.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл konfetki 1.xls) см. Приложения

Из решения видно, что оптимальный план выпуска предусматривает изготовление 80 кг конфет «В» и 20 кг конфет «С». Конфеты «А» производить не стоит. Полученная вами прибыль составит 400 у. е.

Задача 4. Ваше предприятие выпускает изделия 1, изделия 2, изделия 3, используя общий склад комплектующих. Каждое изделие состоит из деталей, имеющихся на складе. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Прибыль, получаемая от каждого изделия, равна соответственно 47,32; 31,55; 22,08. Число деталей, идущих на каждое изделие, указано в таблице.

	Наличие на складе	Изделие1	Изделие 2	Изделие 3
Деталь 1	450	1	1	0
Деталь 2	250	1	0	0
Деталь 3	800	2	2	1
Деталь 4	450	1	1	0
Деталь 5	600	2	1	1

Решение.

Технология работы:

-Запустите табличный процессор Excel.

-Заполните таблицу в соответствий с образцом: (файл detali.xls) см Приложения

В ячейках D4:F8 указывается, из какого числа деталей состоит каждое изделие.

В ячейках D2:F2 указываем примером количество изделий, которые собирается выпускать.

В ячейках В4:В8 указывается число деталей на складе.

В ячейках С4:С8 подсчитываем число деталей, взятых со склада для изготовления изделий.

В ячейках D11:G11 подсчитываем прибыль, полученную от изготовления каждого изделия, и общую прибыль.

В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:

$B$4:$B$8>=$C$4:$C$8

$D$2:$F$2>=0.

Самостоятельно укажите изменяемые ячейки.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано в таблице (файл detali1.xls) cм. Приложения

Задача 5. Найти оптимальный объём перевозок товаров с 3 заводов на 5 региональных складов. То есть минимизировать затраты на перевозку грузов от заводов – производителей на торговые склады.

Производительность каждого завода и затраты на перевозку от завода на каждый склад приведены в таблице:

Заводы	Поставки	затраты
Склад 1	Склад 2	Склад3	Склад4	Склад5
Завод1	310	10	8	6	5	4
Завод2	260	6	5	4	3	6
6Завод3	280	3	4	5	5	9

Решение

Технология работы:

-Запустите табличный процессор Excel.

Заполните таблицу в соответствии с образцом: (файл sklad.xls) см Приложения

Допускаем, что от каждого завода на каждый склад перевозиться единица продукций. Ячейки $C$6:$G$6.

В меню Сервис активизируйте команду Поиск решения и опешите его ограничения, как указано ниже:

$B$2:$B$4>=$B$10:$B$12 Количество перевезенных грузов не может превышать производственных возможностей заводов.

$C$6:$G$6>=$C$8:$G$8 Количество доставляемых грузов не должно быть меньше потребностей складов. То есть производство должно быть не меньше потребностей.

$C$2:$G$4>=0 Число перевозок не может быть отрицательным.

Целевая ячейка $B$14. Изменяемые ячейки $C$2:$G$4.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sklad1.xls) см Приложения

Обратите внимание, что с первого завода вывезена не вся изготовленная продукция, а склады заполнены полностью. Измените потребности складов, затраты на перевозку от заводов к складу, и вы получите другое решение.

Задача 6. Парк отдыха обслуживается семью группами сотрудников. (Группы обозначены А, Б, В, Г, Д, Е, Ж..) Каждая группа имеет разные выходные дни. Выходных дней для каждой группы должно быть не менее двух, выходные следуют подряд. Один сотрудник входит только в одну группу. Известна потребность в сотрудниках в каждый из дней. Все сотрудники имеют одинаковый размер недельной оплаты, который не зависит от графика работы. Необходимо подобрать такую численность сотрудников в каждой группе, чтобы добиться минимизации затрат на оплату труда при выполнении требования по числу сотрудников на каждый день. Дневная зарплата сотрудников 40 у. е.

Решение

Технология работы:

-Запустите табличный процессор Excel.

-Заполните таблицу в соответствии с образцом (файл sоtrudniki.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:

$C$2:$C$8>=0 Количество сотрудников в группе не может быть отрицательным.

$C$2:$C$8= целое. Число сотрудников должно быть целым.

$D$10:$J$10>=$D$12:$J$12. Число ежедневно занятых сотрудников не должно быть меньше ежедневной потребности.

Целевая ячейка $C$15. Изменяемые ячейки $C$2:$C$8.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл sоtrudniki1.xls) см Приложения

Вот тут-то и начинается самое интересное!

Важной особенностью этой задачи является наличие нескольких оптимальных решений, каждое из которых обеспечивает достижение целевой функций при выполнений всех ограничений.

Вызовите диалоговое окно Поиск решения и вновь выполните расчет. Вы получите новое оптимальное решение. Но общее число сотрудников в любом из решении равно 25. Таким образом, можно найти все оптимальные решения и выбрать наиболее подходящее с точки зрения дополнительных критериев.

Задача7. В нескольких пунктах (пункты отправки) скопились транспортные средства (ТС). Эти ТС необходимо перегнать в другие пункты (пункты приемки). Необходимо составить такой план перегона, чтобы общая стоимость перегона была минимальной.

В этой задаче мы имеем следующие значимые факторы:

-число ТС, имеющихся на каждом из трех пунктов отправки:

Пункты	Скопилось ТС
А1	120
А2	110
А3	130

-необходимые количества ТС для каждого из пяти пунктов приема:

Пункты приема	В1	В2	В3	В4	В5
Требуется ТС	80	60	70	100	50

-стоимость перегона одного ТС по каждому из пятнадцати маршрутов:

Пункты отправки	В1	В2	В3	В4	В5
А1	2	4	1	6	7
А2	3	10	5	4	2
А3	8	9	8	3	4

Решение.

Технология работы:

-Запустите табличный процессор Excel.

-Заполните таблицу в соответствий с образцом: (файл transport.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:

$B$6:$F$6=$B$11:$F$11 Исходные данные – требуемое число ТС по каждому маршруту и число принятых ТС должно быть одинаковым.

$B$8:$F$10>=0 и $B$8:$F$10=целое. Изменяемые данные должны быть целыми и положительными.

$G#3:$G$5=$G$8:$G$10 Исходные данные – количество ТС, скопившихся в каждом из пунктов отравления и отправляемых из этого пункта.

Целевая ячейка $G$16. Изменяемые ячейки $B$8:$F$10.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл transport1.xls) см Приложения

В заключение отметим, что при некоторых исходных данных задача может иметь несколько оптимальных решений.

Задача 8. Для некоторого технологического процесса требуется использование угля с определенным содержанием фосфора и пепла. Доступны три сорта угля – А, В, С. Как их следует смешать, чтобы удовлетворить ограничения на примеси и минимизировать цену? Характеристики каждого угля приведены в таблице:

Сорт угля	Содержание примеси фосфора, %	Содержание примеси пепла, %	Цена
А	0,06	2,00	30,00
В	0,04	4,00	30,00
С	0,02	3,00	45,00

Смесь угля должна иметь следующие характеристики:

Содержание примеси фосфора в смеси не более, %	0,03
Содержание примеси пепла в смеси не более, %	3,25

Технология работы:

Запустите табличный процессор Excel.

Заполните таблицу в соответствии с образцом: (файл ugol.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:

Целевая ячейка $E$11. Изменяемые ячейки: $B$8:$B$10.

Ограничения:

$B$11=1 Сумма долей угля от разных поставщиков равна единице.

$C$11<=$E$1 Суммарные доли примесей фосфора не должны быть больше предельно допустимых.

$D$11<=$E2 Суммарные доли примесей пепла не должны быть больше предельно допустимых.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл ugol1.xls) см Приложения

Попробуйте выяснить, несколько дешевым должен стать уголь сорта «А», чтобы стало целесообразным его покупать.

Задача 9. Задача о рюкзаке.

Имеется 4 предмета, каждый из которых характеризуется весом и ценой. Нужно выбрать из них такие и столько, чтобы их общий вес не превышал 83, а суммарная цена была максимальной.

Решение.

Введите исходные данные и формулы в электронную таблицу, как указано ниже (в режиме просмотра формул): (файл rukzak.xls) см Приложения

В меню Сервис активизируйте команду Поиск решения и опишите его ограничения, как указано ниже:

Целевая ячейка $G$7. Находим максимальное значение.

Изменяемые ячейки: $E$3:$E$6.

Ограничения:

$E$3:$E$6>=0 Количество предметов не может быть отрицательным.

$E$3:$E$6= целое Предметы не разделяются.

$F$7<=B$1 общий вес не должен превышать предельно допустимый.

Запустите Поиск решения. Если вы сделали все верно, то решение будет таким, как указано ниже: (файл rukzak1.xls) см Приложения

4. Прогнозирование

Иногда нам хочется знать, «что будет», заранее. Это облегчает принятие предстоящих решений в свою пользу. Как принято говорить, мы хотим «подстелить соломку».

В науке предвидения называют прогнозированием. Основой прогнозирования являются наблюдения. Точнее, не сами наблюдения, а числовые значения неких состояний наблюдаемого явления. Например, курс ценных бумаг. Фиксируя значения курса во времени, мы получим табличное описание процесса изменения курса. Понятно, что если описать аналитический этот процесс, то есть поставить ему в соответствие некую функциональную зависимость:

ПРОГНОЗ=f(x), где х – некий момент времени, то ПРОГНОЗ будет не чем иным, как значением f(x) в некоторой наперед заданный момент времени х.

Аппроксимация позволяет описать наблюдаемые результаты аналитической функцией.

Продемонстрируем возможность прогнозирования на примере определения зависимости высоты от времени свободного падения тела.

Заполните данными рабочий лист электронной таблицы, как показано ниже:

	A	B	C	D	E	F	G	H	I	J	K
1	Время	1	2	3	4	5	6	7	8	9	10
2	Высота	5.1	19.4	45.2	78.4	122.8	176.3	238.6	312.9	396.9	499.6

Постройте диаграмму зависимости высоты от времени свободного падения.

Аппроксимируйте полученную кривую с помощью степенной зависимости. Для этого:

-выделите данные диаграммы, установив курсор на графике и щелкнув правой кнопкой мыши;

-выберите из меню команду Формат линий тренда. На экране появится окно выбора линий тренда.

Сделайте настройку линий тренда:

-выберите на вкладе «Тип» степенную аппроксимацию;

-выберите на вкладе «Параметры» «Показать уравнение на диаграмме»;

-щелкните кнопкой ОК.

Результат аппроксимации показан на рисунке (файл prognoz.xls) см Приложения

Как видно, получена следующая аппроксимирующая функция: y=5,0118x 1,9895

Если бы мы не знали из школьного курса физики, что точная зависимость y=gx2/2, то по полученной с помощью Excel зависимости можно было бы предсказать, например, что за время х=20с тело пролетит 1962 м.

Это же можно проверить и с помощью Excel, выбрав на вкладе «Параметры» «Прогноз вперед на … периодов».

Таким образом, как показывает рассмотренный пример, Excel позволяет не только определить аналитические выражение зависимости таблично представляемых данных, но и предсказать тенденцию их изменения.

Заключение.

Актуальность выбранной темы:

Данная тема актуальна потому, что табличные редакторы на сегодняшний день — одни из самых распространенных программных продуктов, используемых во всем мире. Они без специальных навыков позволяют создавать достаточно сложные приложения, которые удовлетворяют до 90% запросов средних пользователей.

Я выбрал эту тему из-за того, что мне нравится использовать сложные формулы в Excel и решать экономические задачи, не прилагая больших усилий и не требуя обширных знаний в области экономики.

Надеюсь, что данная работа заинтересует, поможет разобраться в решении достаточно сложных задач. А главное — даст возможность убедиться, что Excel – одна из самых интересных и полезных программ, используемых пользователями разного уровня!

Список литературы

1. Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов.-М.: Высш. шк., 1986.

2. Microsoft Excel. Руководство пользователя. — Корпорация Microsoft, 1993.

3. Гусева О.Л., Миронова Н. Н. Excel для Windows. Практические работы //Информатика и образование. 1996 №3.

4. Электронные учебники по Excel.

Источник