Решение задачи о дневном рационе: нахождение решения задачи о дневном рационе средствами Microsoft Excel
Задание 1. Запустите приложение Microsoft Excel
Задание 2. Найдите оптимальное решение задачи о дневном рационе:
Для этого выполните следующую последовательность действий:
1. Откройте из папки МАТ_МОД файл _1(а), содержащий экранную форму для ввода условия задачи (Рис. 1).
Рис. 1. Экранная форма для ввода условия задачи
2. Введите исходные данные в экранную форму:
- коэффициенты ЦФ;
- направление целевой функции (min);
- коэффициенты при переменных в ограничениях;
- знаки в ограничениях ( >= );
- правые части ограничений.

После заполнения форма должна выглядеть следующим образом (Рис. 2).
Рис. 2. Ввод исходных данных
1. Введите формулы, описывающие математическую модель задачи, в экранную форму:
- формулу для расчета ЦФ в ячейку;
согласно условию задачи значение ЦФ определяется выражением
поэтому в ячейку B9 необходимо внести формулу

- установите курсор в ячейку B9;
- нажав кнопку «
», вызовите окно «Мастер функций – шаг 1 из 2»;
- выберите в окне «Категория» категорию «Математические»;
- в окне «Функция» выберите функцию СУММПРОИЗВ;
- в появившемся окне «СУММПРОИЗВ» в строку «Массив 1» введите выражение B3:D3, а в строку «Массив 2» – выражение B7:D7;
- нажмите OK.

- аналогичным образом введите формулы для расчета значений левых частей ограничений (это потребляемое количество в сутки) в ячейки E13, E14, E15, E16, E17 соответственно.
Формулы, описывающие ограничения модели можно увидеть ниже (Таблица 2).
Таблица 2. Формулы, описывающие ограничения модели


Рис. 3. Окно после ввода зависимостей в математической модели
1. Установите целевую ячейку и укажите направление поиска, для этого:
- зайдите в меню Сервис / Поиск решения;
- в поле «Установить целевую ячейку» укажите целевую ячейку $B$9;
- введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по кнопке «минимальному значению»;
2.Укажите диапазон изменения ячеек, для этого в окне «Поиск решения» в поле «Изменяя ячейки» впишите адреса $B$3:$D$3.

3. Внесите условие неотрицательности для переменных (в окне «Поиск решения») (Рис. 4), для этого:
- нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения»;
- в поле «Ссылка на ячейку» введите адреса ячеек переменных $B$3:$D$3;
- в поле знака откройте список предлагаемых знаков и выберите
;
- в поле «Ограничение» введите число 0.
Рис. 4. Добавление условия неотрицательности переменных
Аналогичным образом введите оставшиеся ограничения (Рис. 5).
Рис. 5. Ввод ограничений




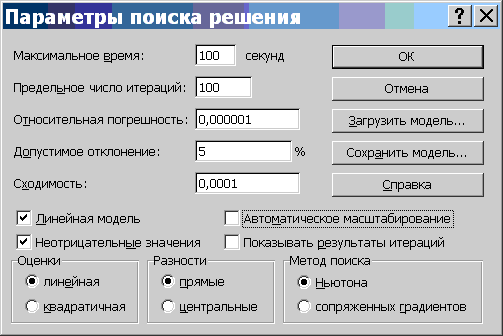
8. Установите параметры решения задачи (Рис. 6) и подтвердите установленные параметры нажатием кнопки «OK».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Рис. 6. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применения симплекс-метода.
9. Запустите задачу на решение путем нажатия кнопки «Выполнить».
После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения» (Рис. 7).
Рис. 7. Сообщение об успешном решении задачи
10. В появившемся окне нажмите кнопку ОК и посмотрите на экране оптимальное решение задачи (Рис. 8).

Рис. 8. Экранная форма задачи после получения решения
Рис. 9. Сообщение при несовместной системе ограничений задачи
Рис. 10. Сообщение при неограниченности ЦФ в требуемом направлении

Задание 3. Сохраните файл в своей папке с именем lab_1(a).

Допустим, что к условию задачи добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
Задание 4. Найдите целочисленное оптимальное решение задачи о дневном рационе, для этого:
- в окне «Поиск решения» (меню «Сервис»/«Поиск решения»), нажмите кнопку «Добавить»;
- в появившемся окне «Добавление ограничений» введите ограничения следующим образом: в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $B$3:$D$3;
- в поле ввода знака ограничения установите «целое» (Рис. 11);
Рис. 11. Ввод условия целочисленности переменных задачи
- подтвердите ввод ограничения нажатием кнопки OK и проанализируйте полученный результат (Рис. 12).
Рис. 12. Решение задачи при условии целочисленности ее переменных
Задание 5. Сохраните файл в своей папке с именем lab_1(b).
Решение задачи о дневном рационе: построение модели
Решение задачи о выпуске продукции: постановка задачи
Поиск
решения
Excel
имеет несколько программ-надстроек,
выполняющих решение различных задач.
Одной из надстроек является «Поиск
решения», позволяющая решать
оптимизационные задачи в Excel. Чаще всего
это задачи линейного программирования
(ЛП).
Общая
формулировка задачи ЛП: найти
неотрицательное решение X системы
линейных уравнений AX=B, при котором
целевая функция f=CX принимает максимальное
(минимальное) значение, где A — матрица
коэффициентов; B — объемы ресурсов.
Экономический
смысл системы AX=B заключается в задании
ограничений на расходуемые ресурсы.
Экономический
смысл целевой функции f=CX заключается
в максимальной прибыли или минимальной
себестоимости, получаемой от оптимального
решения X. Например, если X — вектор
объемов выпуска продукции, а С — вектор
прибыли, получаемой от единицы каждого
вида продукции, то f — суммарная прибыль
от выпуска всей продукции.
Рассмотрим
работу надстройки «Поиск решения»
на примере задачи о рационе кормления
животных. Требуется составить такой
рацион кормления животных тремя видами
корма, при котором они получат необходимое
количество питательных веществ A и B и
себестоимость кормов будет минимальна.
Цены кормов, требуемое количество
питательных веществ и их содержание в
каждом корме показаны в таблице.
|
Питательные |
Корм |
Корм |
Корм |
Требуемое |
|
А |
10 |
6 |
12 |
50 |
|
Б |
7 |
10 |
11 |
45 |
|
Цена |
2,20 |
1,95 |
2,87 |
Если
обозначить X=(x1,
x2,
x3)
— искомое количество кормов, то задача
ЛП формулируется так:
Найти
решение X системы
при
котором целевая функция
принимает
минимальное значение.
Математическую
формулировку задачи необходимо оформить
в виде таблицы, отражающей основные
зависимости.
Ячейки
таблицы имеют следующий смысл:
-
диапазон
A1:C2 — содержит матрицу A; -
диапазон
D1:D2 — содержит вектор ресурсов В; -
диапазон
A6:C6 — содержит вектор цен С; -
диапазон
A4:C4 — содержит вектор решений X, начальные
значения которого заданы нулю и который
будет оптимизирован программой; -
диапазон
E1:E2 — содержит выражения, вычисляющие
произведение AX; -
ячейка
E6 — содержит выражение, вычисляющее
f=CX.
Вызов
программы поиска решения выполняется
через меню «СервисПоиск
решения…».
В открывшемся окне «Поиск
решения»
необходимо установить следующие
параметры:
-
«Установить
целевую ячейку» — E6; -
установить
переключатель «Равной минимальному
значению»; -
в
поле «изменяя ячейки» указать
диапазон A4:C4; -
в
области «Ограничения» нажать
кнопку «Добавить» и в окне «Добавление
ограничений» ввести ограничения:
E1>=D1 и E2>=D2;
-
нажать
кнопку «Параметры…» и в открывшемся
окне установить флажки «Линейная
модель», «Неотрицательные значения»
и выбрать переключатель «Оценка»
— «Линейная».
Для
запуска программы необходимо в окне
«Поиск
решения»
нажать кнопку «Выполнить«.
Результаты вычислений будут записаны
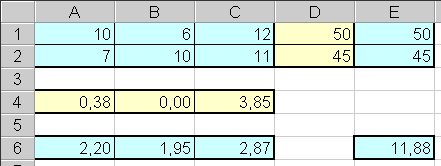
в изменяемые ячейки таблицы. В итоге
таблица должна иметь следующий вид.
Таким
образом, животных следует кормить первым
кормом в количестве 0,38 кг, третьим —
3,85 кг и не использовать второй корм
вообще. При таком рационе затраты на
кормление одного животного составят
11,88 руб.
 Контрольные
Контрольные
вопросы
-
Каково
назначение программы-надстройки «Поиск
решения»? -
Какова
общая формулировка задачи линейного
программирования? -
В
чем заключается экономический смысл
задачи линейного программирования? -
Как
будет сформулирована задача линейного
программирования для рассматриваемого
примера задачи о рациональном кормлении
животных? -
Как
оформить в виде таблицы, отражающей
основные зависимости, математическую
формулировку задачи линейного
программирования? -
Каков
смысл ячеек таблицы, подготовленной
для поиска решения? -
Как
загрузить программу поиска решения
задачи линейного программирования? -
Какие
параметры следует установить в окне
«Поиск решения»? -
Как
интерпретировать полученные результаты
решения задачи линейного программирования?
Соседние файлы в папке Alg i metodi vichisl
- #
- #
- #
Наряду со множеством других возможностей, в Microsoft Excel есть одна малоизвестная, но очень полезная функция под названием “Поиск решения”. Несмотря на то, что найти и освоить ее, может быть, непросто, ее изучение и применение может помочь в решении огромного количества задач. Функция берет данные, перебирает их и выдает самое оптимальное решение из возможных. Итак, давайте разберемся, как именно работает поиск решения и попробуем применить данную функцию на практике
Содержание
- Как включить функцию “Поиск решения”
- Подготовительный этап
- Применение функции и ее настройка
- Заключение
Как включить функцию “Поиск решения”
Несмотря на свою эффективность, функция “Поиск решения” не находится в первых рядах панели инструментов или контекстного меню. Многие пользователи, работающие в Excel годами, даже не подозревают о ее существовании. Дело в том, что по умолчанию она вообще отключена и для ее добавления на ленту нужно проделать следующие шаги:
- Открываем меню “Файл”, кликнув по соответствующему названию.
- Кликаем по разделу “Параметры”, который находится внизу вертикального перечня с левой стороны.
- Далее щелкаем по подразделу “Надстройки”. Здесь отображаются все надстройки программы, а внизу будет надпись “Управление”. Справа от нее представлено выпадающее меню, в котором должны быть выбраны “Надстройки Excel”, обычно уже установленные по умолчанию. Нажимаем кнопку “Перейти”.
- На экране появится новое вспомогательное окно “Надстройки”. Устанавливаем флажок напротив опции “Поиск решения” и нажимаем ОК.
- Все готово. Требуемая функция появится на ленте в правой части вкладки “Данные”.
Подготовительный этап
Добавить функцию на ленту программы – половина дела. Нужно еще понять принцип ее работы.
Итак, у нас есть данные про продаже товаров, представленные в табличном виде.
И перед нами стоит задача – назначить каждому товару скидку таким образом, чтобы сумма по всем скидкам составила 4,5 млн. рублей. Она должна отобразиться в отдельной ячейке, которая называется целевой. Ориентируясь на нее мы должны рассчитать остальные значения.
Наша задача – вычислить скидку, на которую будут умножены все суммы по продажам всех наименований. Она и будет найдена с помощью функции “Поиск решения”, а ячейка с этой скидкой будет называется искомой.
Данные ячейки (искомая и целевая) связываем вместе формулой, которую пишем в целевой ячейке следующим образом: =D13*$G$2, где ячейка D13 содержит итоговую сумму по продажам всех товаров, а ячейка $G$2 – абсолютные (неизменные) координаты искомой ячейки.
Применение функции и ее настройка
Формула готова. Теперь нужно применить саму функцию.
- Переключаемся во вкладку “Данные” и нажимаем кнопку “Поиск решения”.
- Откроются “Параметры”, где необходимо задать нужные настройки. В поле “Оптимизировать целевую функцию:” указываем адрес целевой ячейки, где планируется вывести сумму по всем скидкам. Можно прописать координаты вручную, либо выбрать из таблицы, для чего сначала кликаем по области ввода, затем – по нужной ячейке.
- Переходим к настройке других параметров. В пункте “До:” можно задать максимальную границу, минимальную границу или же точное число. Исходя из поставленной задачи ставим отметку рядом с опцией “Значение” и набираем “4500000” – сумма скидок по всем наименованиям.
- Следующее для заполнения поле – “Изменяя значения переменных:”. В него нужно внести координаты искомой ячейки, содержащей определенное значение. Это значение и есть та самая скидка, которую мы пытаемся вычислить. Также, как и с выбором целевой ячейки, координаты можно написать вручную, либо кликнуть по нужной ячейке в самой таблице.
- Теперь нужно отредактировать раздел “В соответствии с ограничениями:”, в котором задаем ограничения используемых данных. Например, можно исключить десятичные дроби или, скажем, отрицательные числа. Это делается через кнопку “Добавить”.
- Откроется вспомогательно окно, позволяющее добавить ограничения во время вычислений. В первом поле указываем координаты определенной ячейки или области ячеек, для которых это условие должно действовать. Согласно нашей задаче, указываем координаты искомой ячейки, в которой будет выводиться значение скидки. Следующий шаг – определить знак сравнения. Устанавливаем “больше или равно”, чтобы итоговое число не могло быть отрицательным. “Ограничение”, которое устанавливается в третьем поле, в этом случае будет равно цифре 0, поскольку именно относительно этого значения задается условие.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
- После выполнения описанных выше действий в самом большом поле окна появится установленное только что ограничение. Список может быть довольно большим и зависит от сложности предполагаемых расчетов, но в данном случае будет достаточно и одного условия.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
- Также можно задать немалое количество дополнительных настроек. Чуть ниже справа есть кнопка “Параметры”, позволяющая это сделать. Нажимаем на нее и открываем новое окно.
- В этих настройках у нас есть возможность установить “Точность ограничения” и “Пределы решения”. В нашем случае задавать данные параметры нет необходимости, поэтому после ознакомления с представленным окном, его можно закрыть, нажав OK.
- Итак, все настройки выполнены и параметры установлены. Пора запускать функцию – для этого нажимаем кнопку “Найти решение”.
- После этого программа сделает все необходимые расчеты и выдаст результаты в нужных ячейках. При этом сразу же откроется окно “Результаты поиска решения”, где можно сохранить/отменить результаты или настроить параметры поиска заново. Если результаты нас устраивают, оставляем отметку напротив опции “Сохранить найденное решение” и нажимаем ОК. При этом, если мы предварительно установим галочку слева от надписи “Вернуться в диалоговое окно параметров поиска решения”, после того, как мы щелкнем OK, мы обратно переключимся к настройке функции поиска решения.
- Вполне вероятно, что расчеты могут показаться неправильными, либо возникнет желание немного изменить исходные данные и получить другой результат. В этом случае нужно снова открыть окно с параметрами поиска решения и внимательно посмотреть поля с введенными данными.
- Если с данными все нормально, можно попробовать задействовать другой метод решения. Для этого щелкаем по текущему варианту и из раскрывшегося перечня выбираем способ, который нам кажется наиболее подходящим:
- Первый – ищет решение методом обобщенного приведенного градиента (ОПГ) для нелинейных задач. Стандартно выбран именно этот вариант, но можно попробовать и другие.
- Второй – пытается отыскать решение для линейных задач, используя симплекс-метод.
- Третий – для выполнения поставленной задачи использует эволюционный поиск.
- В том случае, если ни один из методов не принес удовлетворительных результатов, стоит проверить данные в таблице и параметрах еще раз, поскольку именно это является самой частой ошибкой в подобного рода задачах.
- Теперь, когда мы получили требуемую скидку, осталось ее применить, чтобы рассчитать суммы скидок по всем наименованиям. Для этого отмечаем первую ячейку столбца “Сумма скидки”, пишем в ней формулу “=D2*$G$2” и нажимаем Enter. Знаки доллара ставятся для того, чтобы при растягивании/копировании формулы на другие строки, ячейка G2 со скидкой оставалась неизменной в расчетах.
- Мы получили сумму скидки для первого наименования. Теперь наводим курсор на нижний правый угол ячейки с результатом, как только он поменяет форму на крестик, зажав левую кнопку мыши растягиваем формулу на все строки, по которым хотим посчитать аналогичную сумму.
- Теперь наша таблица полностью готова в соответствии с поставленной задачей.
Заключение
Таким образом, функция “Поиск решения” в Эксель может помочь в решении определенных задач, которые достаточно сложно или невозможно решить простыми методами. Однако, проблема в использовании данного способа заключается в том, что по умолчанию данная функция скрыта в программе, из-за чего многие пользователи не догадываются о ее существовании. Также функция довольно трудна в освоении и использовании, но при ее должном изучении, она может принести значительную пользу и облегчить работу.
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Большаков А.А. 1
1МОУ «Канашевская СОШ»
Воротилкина Т.П. 1
1МОУ «Канашевская СОШ»
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Проблема лишнего веса в наше время стоит очень остро. Один из мудрецов сказал: «Мы — это то, что едим и пьем…». У людей с лишним весом страдает, прежде всего, энергетика: от любой работы быстро наступает усталость, которая со временем переходит в безразличие к жизни. Кроме того, страдают от повышенной нагрузки все внутренние органы. Увеличение веса тела наблюдается при неумеренном питании, малоподвижном образе жизни [3].
Один из древних лекарей отметил, что необходимо есть еду как лекарство, чтобы не принимать лекарства как еду. Пища — источник белков, жиров, углеводов, витаминов, микроэлементов и других полезных веществ, также пища является своеобразным топливом для человека. Калории, содержащиеся в продуктах питания — эквивалент энергии, которую человек получает, употребляя тот или иной продукт. Если питание правильное, сбалансированное, то человек получает полный объем необходимых ему веществ и энергии, и чувствует при этом себя здоровым, бодрым. А если режим питания нарушен, нет баланса между употребляемыми продуктами, то это чревато не только плохим самочувствием, а и серьезными заболеваниями, лишним весом, нарушением обмена веществ [3].
Рассчитанные нами данные по калорийности продуктов питания в пересчете на среднесуточные показатели для одного человека соответствуют опубликованным в литературе нормам среднесуточного потребления для людей умственного труда: 2550-2800 ккал для мужчин и 2200-2400 ккал для женщин [4,5,6].
Различные аспекты оптимизации занимают очень важное место в деятельности по организации здорового питания. Решение задач оптимизации состоит в поиске оптимального плана с использованием математических моделей и вычислительных методов, которые реализуются с помощью компьютеров и специальных программ.
Применение компьютеров позволяет заниматься исследовательской работой при решении задач из различных областей, при этом учащиеся учатся четко формулировать задачу, решать ее и оценивать полученный результат.
Использование информационных технологий позволяет решать задачи нетрадиционными способами, а также решать прикладные задачи, которые ранее не могли рассматриваться в силу сложности математического аппарата. Причем, это становится доступным учащимся, владеющим программированием недостаточно хорошо. Главным этапом становится не разработка программы, а постановка задачи (запись ограничений, задание точности решения) и исследование полученных результатов.
Тема моей исследовательской работы «Решение задачи по организации диетического питания средством анализа данных Поиск решения MS Excel».
Выбранная тема была актуальна во все времена. Но в настоящее время актуальность диетического питания особенно возросла. Изменения в сложившемся рационе питания молодых людей, характере нагрузок на организм провоцируют негативные сдвиги в состоянии их здоровья. И мое исследование направлено на создание условий для улучшения состояния здоровья современного молодого поколения.
Задачи исследования можно сформулировать следующим образом:
1) выявить возможности использования информационных технологий, в частности, прикладных программ MS Excel для расчета оптимального рациона питания;
2) разработать модель и алгоритм расчета оптимального рациона;
3) использовать результаты исследования в просветительской работе по пропаганде здорового и рационального питания.
Все расчёты выполнены при помощи средства анализа данныхПоиск решения, встроенного в программу MS Excel.
1 Средства Анализа данных
Особенностью электронных таблиц является то, что в них структурирование информации начинается непосредственно на этапе ввода данных: с самого начала своего существования в машинной форме они привязываются к структурным подразделениям таблиц — ячейкам. Статистическая обработка данных и прогнозирование, функции, реализующие статистические методы обработки и анализа данных, в Excel реализованы в виде специального программного расширения — надстройки Пакет анализа.
В рамках Excel с помощью команд, доступных из окна Анализ данных, можно провести:
— описательный статистический анализ (Описательная статистика);
— ранжирование данных (Ранг и персентиль);
— графический анализ данных (Гистограмма);
— прогнозирование данных (Скользящее среднее, Экспоненциальное сглаживание);
— регрессионный анализ (Регрессия) и др.
Широкое применение на практике находят функции и режимы Excel, предназначенные для поиска решения уравнений и оптимизационных задач.
В Excel имеются два мощных средства для анализа данных:
1. ПОДБОР ПАРАМЕТРА – служит для определения входной величины, обеспечивающей определенное значение функции. Подбор параметра — удобный и простой для понимания инструментом решения уравнений. Он реализует алгоритм численного решения уравнения, зависящего от одной или нескольких переменных. Процесс решения с помощью данного метода распадается на два этапа: 1. Задание на рабочем листе ячеек, содержащих переменные решаемого уравнения (так называемых влияющих ячеек), и ячейки, содержащей формулу уравнения (зависимой или целевой ячейки). 2. Ввод адресов влияющих и целевой ячеек в диалоговое окно Подбор параметра и получение ответа (или сообщения о его отсутствии/невозможности найти).
ПОИСК РЕШЕНИЯ – позволяет определить величину или группу величин, обеспечивающих оптимальное в некотором смысле значение функции при заданных ограничениях [2].
Для средства «Поиск решения»ячеек-параметров может быть несколько.
Иными словами, если значение в целевой ячейке зависит от содержимого нескольких ячеек-параметров, или на входные параметры накладываются ограничения, потребуется использование средств Поиск решения.
Вызов Поиска решения: кнопка «Office» — параметры Excel – надстройки – перейти… — Поиск решения [1].
Так в моей работе необходимо определить группу величин, то я использую средство анализа Поиск решения.
1.1 Поиск решения
ПОИСК РЕШЕНИЯ – позволяет определить величину или группу величин, обеспечивающих оптимальное в некотором смысле значение функции при заданных ограничениях [1].
Обычными задачами, решаемыми с помощью средства Поиск решения, являются задачи оптимизации. Задачи, которые решаются с помощью средства «Поиск решения», имеют три свойства:
имеется КРИТЕРИЙ, показывающий в каком смысле принимаемое решение должно быть оптимальным (максимальное значение, минимальное значение или заданное какому-то конкретному значению);
имеются ОГРАНИЧЕНИЯ, выражающиеся в виде неравенств. Под ограничениями понимаются соотношения типа А1<=B1, А1=B1, А1> = 0;
имеется НАБОР ВХОДНЫХ ЗНАЧЕНИЙ — переменных, непосредственно или косвенно влияющих на ограничения и на оптимизирующие величины [1].
1.2 Этапы решения задач оптимизации
При решении задач оптимизации следует придерживаться следующего алгоритма действий:
постановка задачи, построение математической модели;
создание формы для ввода условий задачи;
ввод исходных данных в созданную форму;
ввод зависимостей из математической модели (для целевой функции, для ограничений);
РАБОТА в диалоговом окне «Поиск решения» (м. Сервис – Поиск решения): заполнение соответствующих полей
В диалоговом окне Поиск решения необходимо выполнить следующие действия:
5.1. задание адреса целевой ячейки в поле
5.2. задание критерия оптимизации в поле Равной: (установить переключатель в зависимости от требуемого критерия:
Например: )
5.3. задание адресов поисковых переменных (ячеек — параметров) в поле
5.4. задание ограничений. Чтобы определить набор ограничений кнопку Добавить в поле Ограничения.
В появившемся диалоговом окне Добавление ограничения необходимо задать ограничения.
При задании ограничений необходимо ввести а) адрес ячейки ограничения, б) оператор > = или <= и т.д., в) ограничивающее значение или адрес ячейки этого значения
Решение задачи оптимизации ↓ Выполнить в окне Поиск решения (в диалоговом окне Поиск решения – кнопка Параметры служит для уточнения параметров).
Сохранение найденного решения (в диалоговом окне Результаты поиска решения установить переключатель Сохранить найденное решение — ↓ ОК).
Примечание: в случае необходимости в диалоговом окне Результаты поиска решения возможны другие варианты при работе с полученными результатами (отмена, сохранение как сценария), а также создание отчета
Компьютер является единственно возможным средством решения сложных задач оптимизации. Для решения задач оптимизации пользуются математическим аппаратом электронных таблиц Excel [2].
2 Решение задачи по организации диетического питания с помощью электронных таблиц
2.1 Цель моделирования
В ходе выполнения работы происходит практическое знакомство с электронными таблицами Microsoft Excel, приобретение навыков работы с данными различных типов, различными видами ссылок на ячейки электронной таблицы, формулами, математическими функциями рабочего листа Microsoft Excel, приемами заполнения таблиц; умений пользоваться средством анализа данных Поиск решения; решается задача по организации диетического питания.
2.2 Формализация задачи
Задача формулируется следующим образом: решить задачу по организации диетического питания средством анализа данных Поиск решения MSExcel. Найти количество каждого продукта, при котором общая калорийность продуктов питания в пересчете на среднесуточные показатели для одного человека не превышает 2400 ккал, в среднем соотношение количества употребляемых белков, жиров и углеводов должно составлять 1:1:4 (набор продуктов может варьироваться) [8].
Для решения задачи необходимо составить формулы. Формулы представляют собой выражения, по которым выполняются вычисления на странице. Формула начинается со знака равенства (=). В формулах используются операции: арифметические, сравнения, логические.
Порядок выполнения арифметических действий и определенных операций представлен в таблице (рис. 1).
Рис.1 Порядок выполнения арифметических действий и операций.
Для изменения порядка выполнения операций используются круглые скобки.
Пример: =(А2+В2)/(1-3,5*В2^2).
2.2.1 Виды адресации в электронных таблицах
При обращении к ячейкам используется относительная, абсолютная и смешанная адресация [1, 2].
Адрес ячейки образуется на пересечении столбца и строки.
1) Относительная адресация (примеры: А6, В3:Н5): при использовании относительной адресации в формулах приложение MS Excel запоминает расположение относительно текущей ячейки.
Относительный адрес – это адрес, который ссылается на ячейку, основываясь на ее текущее местоположение.
Например: при вводе в ячейку В4 формулу = В1+В2. Excel понимает формулу, как «прибавить» содержимое ячейки, расположенное тремя рядами выше, к содержимому ячейки двумя рядами выше.
Если скопировать формулу = В1+В2 из ячейки В4 в С4, Excel также понимает формулу как «прибавить» содержимое ячейки, расположенное тремя рядами выше, к содержимому ячейки двумя рядами выше. Таким образом, формула в ячейке С4 примет вид = С1+С2
2) Абсолютная адресация (примеры: $A$6, $В$3:$Н$5): если при копировании формул необходимо сохранить ссылку на «конкретную» ячейку или область, то нужно воспользоваться абсолютной адресацией.
Абсолютный адрес — это адрес, который ссылается на ячейку, используя ее точный адрес, и не изменяется при копировании ячейки с формулой.
Для задания абсолютного адреса перед именем столбца и перед номером строки необходимо ввести знак $. Например: $В$4, $В$3:$Н$5
3) СМЕШАННАЯ АДРЕСАЦИЯ (примеры: В$4, $Н5)
Символ $ ставится только перед неизменяемой частью адреса, при копировании один параметр адреса изменяется, а другой – нет:
В$4 – адрес столбца при копировании меняется, а номер строки всегда четвертый;
$Н5 – адрес столбца не меняется при копировании, а адресация строк меняется.
Примечание: Для замены вида ссылки на адрес ячейки в строки формул выделить нужный адрес, нажать F4, пока ссылка не отобразится в нужном виде.
2.3 Разработка модели
Постановка задачи: найти массу продуктов: мяса, рыбы, молока, масла, сыра, крупы, картофеля, чтобы общая калорийность продуктов питания в пересчете на среднесуточные показатели для одного человека не превышала 2400 ккал, соотношение количества употребляемых белков, жиров и углеводов составляло приблизительно 1:1:4.
Алгоритм работы:
1 этап. Заполнение в электронной таблице диапазона ячеек данными (числовыми, формульными) для нахождения оптимального значения.
СОЗДАТЬ файл в приложении MSExcel с произвольным именем и расширением *.xls.
СОЗДАТЬ таблицу на листе 1 книги (файла), начало которой начало которой представлено на рис. 2.
Рис.2 Рацион питания
ЗАПОЛНИТЬ диапазон В3:В5, В7 и D3:J5 числами, указанными на рис. 3;
Рис.3 Рацион питания
ЗАПОЛНИТЬ диапазон D7:J7, значениями калорийности заявленных продуктов
Примечание: данные взяты из диетологических таблиц [4, 8].
ЗАНЕСТИ в ячейку С3 формулу расчета значений функции массы белков в заявленных продуктах, употребляемых за день.
Формула и результат для ячейки С3 представлен в таблице:
Таблица 1. Формула в Excel
|
Формула |
Результат |
|
=СУММПРОИЗВ(D3:J3;$D$6:$J$6) |
85 |
Примечание: при записи функции использовали соответствующую адресацию ячеек.
СКОПИРОВАТЬ формулу из ячейки С3 для остальных ячеек диапазона С3:С5, используя маркер заполнения.
СРАВНИТЬ результат с фрагментом (на рисунке 4 представлено окончание таблицы):
Рис.4 Фрагмент таблицы
2 этап. Нахождение оптимального решения: массы потребляемых продуктов (мяса, рыбы, молока, масла, сыра, крупы, картофеля).
ЗАПОЛНИТЬ диапазон D7:J7 нулями (0) — Ячейки параметр
РАЗМЕСТИТЬ курсор в ячейке С7 – целевая ячейка
Запустить средство Поиск решения (MSExcel 2007) (кнопка Office – параметры – надстройки – перейти… — Поиск решения)
ЗАПОЛНИТЬ диалоговое окно Поиск решения согласно рисунку 5.
Рис.5 Окно средства анализа данных Поиск решения
НАЖАТЬ на кнопку Выполнить.
НАЖАТЬ на кнопку ОК.
Результат представлен на рисунке 6.
Рис.6 Результат расчета
Результат решения задачи: масса продуктов: мяса (0,07 кг), рыбы (0,06 кг), молока (0,04 кг), масла (0,08 кг), сыра (0,10 кг), крупы (0,38 кг), картофеля (0,11 кг), общая калорийность продуктов питания в пересчете на среднесуточные показатели для одного человека не превышает 2400 ккал, соотношение количества употребляемых белков, жиров и углеводов составляет приблизительно 1:1:4.
Результаты исследования
Перед проведением исследования были сформулированы его задачи, в ходе выполнения исследовательской работы задачи были решены и реализованы на практике:
1) выявлены возможности использования информационных технологий, в частности, прикладной программы MS Excel для решения задачи по организации диетического питания средством анализа данных Поиск решения MS Excel;
2) разработана модель и алгоритмы решения задачи в среде прикладной программы MS Excel;
3) результаты исследования рекомендованы к использованию в просветительской работе по пропаганде здорового и рационального питания. В таблицу для расчетов можно добавить потребляемые продукты, можно удалить. И произвести индивидуальный подбор количества потребляемых продуктов.
Полученные результаты были предложены одноклассникам для ознакомления (18 человек — 10 девушек и 8 юношей). Оказалось: 5 (28%) впервые слышат о существовании баланса в потребляемых продуктах ; 9 человек(50%) знают о сбалансированном питании, но не придают этому значение; 4 человека (девушки) (22%) стараются придерживаться сбалансированного питания.
Все участники опроса отметили, что будут пользоваться предложенной таблицей для расчета необходимого количества продуктов.
Использование информационных технологий позволяет решать задачи нетрадиционными способами, а также решать прикладные задачи, которые ранее не могли рассматриваться в силу сложности математического аппарата.
Заключение
Использование информационных технологий позволяет решать задачи нетрадиционными способами, а также решать прикладные задачи, которые ранее не могли рассматриваться в силу сложности математического аппарата. Причем, это становится доступным учащимся владеющим программированием недостаточно хорошо. Главным этапом становится не разработка программы, а постановка задачи (запись ограничений, задание точности решения) и исследование полученных результатов.
В данной работе показана возможность применения информационных технологий для решения повседневных задач, в частности применения MSExcel для расчета калорийности диетического питания. В современном обществе эта тема является актуальной: изменения в сложившемся рационе питания молодых людей, характере нагрузок на организм провоцируют негативные сдвиги в состоянии их здоровья. С молодыми людьми необходимо вести просветительскую работу по правильному питанию, сбалансированности потребляемых продуктов, о их пользе и вреде. Научить молодежь самим следит за качеством потребляемых продуктов и их количеством. Помощником в этом вопросе могут быть информационные технологии, в частности результат исследований данной работы.
Ход проведения исследования показал, что использование прикладной программы MS Excel при решении задач оптимизации способствует:
Повышению интереса к информационным технологиям;
Решению повседневных задач нетрадиционными способами.
Список используемой литературы
Киселев С.В. Оператор ЭВМ: учебник для нач. проф. образования / С.В. Киселев. – М.: Издательский центр «Академия», 2006. – 352 с.
Угринович Н.Д. Информатика и информационные технологии. Учебник для 10-11 классов / Н.Д. Угринович. – 2-е изд. – М.: БИНОМ. Лаборатория знаний, 2010. – 511 с.: ил.
Гущо Юрий. 12 ключей от сейфа долголетия. Редакция журнала «Партнер. Dortmund, 2013.
http://www.poedim.ru/pp/
http://www.babyeda.ru/colory.html
http://www.poedim.ru/pp_energy/
http://exsolver.narod.ru/LM/LM_eat.html
http://tele-conf.ru/teoreticheskaya-i-prikladnaya-biologiya-i-meditsina/individualnyiy-raschet-pischevogo-ratsiona.html
Приложение
Глоссарий
ЦЕЛЕВАЯ ЯЧЕЙКА содержит целевую функцию (формулу), для которой отыскивается оптимальное значение (максимальное, минимальное или заданное какому-то конкретному значению).
ЦЕЛЕВАЯ ФУНКЦИЯ показывает, в каком смысле решение должно быть оптимальным, т.е. наилучшим.
ЯЧЕЙКА-ПАРАМЕТР – та ячейка, для которой средствами Excel, подбирается нужный параметр. ЯЧЕЙКА-ПАРАМЕТРвлияет на целевую ячейку, но сама не содержит формулы.
ФОРМУЛА – выражение, состоящее из констант, ссылок, функций, соединенных знаками арифметических и/или логических операций.
КОНСТАНТА представляет собой готовое (невычисляемое) значение.
ССЫЛКА – адрес объекта (ячейки, строки, столбца, диапазона), используемый при записи формулы.
ФУНКЦИЯ — это переменная величина, значение которой зависит от значений аргументов.
Просмотров работы: 392
Содержание
- Задача составления кормовой смеси или задача о диете
- Задача о составлении рациона (задача о диете, задача о смесях)
- Задача о смесях
- Решение задачи о дневном рационе
- Постановка задачи
- Сводная таблица условий задачи о дневном рационе
- Построение модели
- 1 Этап. Определение переменных, для которых будет составляться математическая модель.
- 2 Этап. Формирование целевой функции.
- 3 Этап. Формирование системы ограничений.
- Нахождение решения задачи о дневном рационе средствами Microsoft Excel
Задача составления кормовой смеси или задача о диете
Содержание
- Задача о составлении рациона (задача о диете)
- Задача о смесях (смешивания этих ингредиентов в пропорциях)
- Задача об оптимальном составе бетонной смеси
Пример №1 . Бройлерное хозяйство птицеводческой фермы насчитывает 20 000 цыплят, которые выращиваются до 8-недельного возраста и после соответствующей обработки поступают в продажу. Недельный расход корма в среднем (за 8 недель) составляет 500г = 0.5 кг .
Для того, чтобы цыплята достигли к 8-й неделе необходимого веса, кормовой рацион должен удовлетворять определённым требованиям по питательности. Этим требованиям могут соответствовать смеси различных видов кормов, или ингредиентов.
В таблице приведены данные, характеризующие содержание (по весу) питательных веществ в каждом из ингредиентов и удельную стоимость каждого ингредиента. Смесь должна содержать:
- не менее 0.8% кальция (от общего веса смеси)
- не менее 22% белка (от общего веса смеси)
- не более 5% клетчатки (от общего веса смеси )
Требуется определить количество (в кг) каждого из трёх ингредиентов, образующих смесь минимальной стоимости, при соблюдении требований к общему расходу кормовой смеси и её питательности.
| Ингредиент | Содержание питательных веществ (кг/ингредиента) | Стоимость (руб./кг) | ||
| Кальций | Белок | Клетчатка | ||
| Известняк Зерно Соевые бобы |
0.38 0.001 0.002 |
— 0.09 0.5 |
— 0.02 0.08 |
0.04 0.15 0.40 |
Математическая формулировка задачи. Введём следующие обозначения:
X 1 — содержание известняка в смеси (кг);
Х2 — содержание зерна в смеси (кг);
Х3 — содержание соевых бобов в смеси (кг);
Общий вес смеси, еженедельно расходуемый на кормление цыплят: 20 000 х 0.5 = 10 000 кг.
Ограничения, связанные с содержанием кальция, белка и клетчатки в кормовом рационе, имеют вид:
0.38X1 + 0.001Х2 + 0.002Х3 ≥ 0.008 х 10 000,
0.09Х2 + 0.50Х3 ≥ 0.22 х 10 000,
0.02Х2+ 0.08Х3 ≤ 0.05 х 10 000.
Окончательный вид математической формулировки задачи:
min f(X) = 0.04 x1 + 0.15Х2 +0,40Х3
при ограничениях
Х1+Х2+Х3= 10 000
0.38Х1 + 0.001Х2 + 0.002Х3 ≥ 80
0.09Х2+ 0.50Х3 ≥ 2200
0.02Х2+ 0.08Х3 ≤ 500
Xj > 0, j = 1, 2, 3.
Задача о составлении рациона (задача о диете, задача о смесях)
Таблица 2
Питательные вещества
Число единиц питательных веществ в единице продукции
Необходимый минимум питательных веществ
| П1 | П2 | ||
| S1 | 1 | 2 | 10 |
| S2 | 3 | 2 | 8 |
| S3 | 2 | 1 | 9 |
| S4 | 2 | 2 | 11 |
Стоимость единицы продукции П1 и П2 соответственно равна 3 и 4 д.е.
Решение. Обозначим через х1 и х2 – количество продукции П1 и П2, входящей в дневной рацион. Тогда общая стоимость рациона составит (д.е.)
F = 3x1 + 4x2. (5)
С учетом необходимого минимума питательных веществ составим систему ограничений. Рацион включает (x1 + 2x2) единиц питательного вещества S1, (3x1 + 2x2) единиц питательного вещества S2, (2x1 + x2) единиц питательного вещества S3 и (2x1 + 2x2) единиц питательного вещества S4. Так как содержание питательных веществ S1, S2, S3, S4 в рационе должно быть не менее 10, 8, 9, 11 единиц, соответственно, то получим систему ограничений неравенств:
x1+2x2 ≥ 10 (6)
3x1+2x2 ≥ 8
2x1+x2 ≥ 9
2x1+2x2 ≥ 11
x1 ≥ 0, x2 ≥ 0
Итак, экономико-математическая модель задачи: составить дневной рацион , удовлетворяющий системе ограничений (6), при котором функция (5) принимает минимальное значение.
Сформулируем данную задачу в общей постановке.
Обозначим через xj (j = 1, 2,…, n) – количество единиц j-го продукта в дневном рационе. В рационе используется n видов продуктов. Каждый продукт содержит m питательных веществ в количестве не менее bi (i = 1,2,…,m) единиц, aij – число единиц питательного вещества si в единице продукта j-го вида. Известна стоимость cj единицы j-го продукта. Необходимо составить рацион нужной питательности при минимальных затратах на него.
Экономико-математическая модель примет вид:

Замечание 1. Целевую функцию (7) и систему ограничений неравенств можно записать, используя знак ∑ (суммы).


Замечание 2. В задаче составления рациона (диеты, кормовой смеси) могут использоваться ограничения не только по необходимому минимуму питательных веществ, но и по минимальному общему весу смеси.
Например. Некоторая фирма имеет возможность купить n различных видов сырья и приготавливать различные виды смесей (продуктов). Каждый вид сырья содержит разное количество питательных веществ. Установлено, что продукция должна удовлетворять некоторым минимальным требованиям с точки зрения питательности (полезности). Необходимо определить количество каждого j-го вида сырья, образующего смесь минимальной стоимости при соблюдении требований к общему расходу смеси и её питательность.
Экономико-математическая модель задачи будет иметь вид:

при ограничениях: на общий расход смеси
на питательность смеси
на не отрицательность переменных
xj≥0, j=1,2,…n,
где xj – количество j-го сырья в смеси;
n – количество видов сырья;
m – количество питательных веществ;
aij – количество i-го питательного вещества, содержащегося в единице j-го вида сырья;
b1 – минимальное количество i-го питательного вещества, содержащегося в единице смеси;
cj – стоимость единицы сырья j;
q – минимальный общий вид смеси.
Пример №3 . В заводской лаборатории создается антифрикционный сплав (оловянистый баббит), который должен содержать: олова — не меньше 15%, сурьмы — не меньше 15%, свинца — около 70%. Есть четыре сплава, процентный состав и цены на которые приведенные в таблице:
| Элементы | Сплав | |||
| 1 | 2 | 3 | 4 | |
| Олово | 12 | 20 | 12 | 20 |
| Сурьма | 12 | 18 | 18 | 14 |
| Свинец | 76 | 62 | 70 | 66 |
| Цена на 1 кг | 3,5 | 5,2 | 4,0 | 4,6 |
Рассчитать количество элементов для сплава каждого вида, необходимое для 1 кг смеси, которая бы обеспечила минимальные затраты.
Решение
Составим экономико-математическую модель задачи.
Обозначим через
x1 – количество сплава 1, кг
x2 – количество сплава 2, кг
x3 – количество сплава 3, кг
x4 – количество сплава 4, кг
Пример №4 . Для сохранения здоровья и работоспособности человек должен в сутки потреблять не менее 63 усл.ед. белков, не менее 147 усл.ед. жиров и не менее 126 усл.ед. углеводов. Для простоты допустим, что имеется всего два вида продуктов и ; стоимость единицы каждого из них равна соответственно 12 и 9 ден.ед. Содержание названных питательных веществ в различных продуктах неодинаково. Предположим, что в единице продукта содержится 9 усл.ед. белков, 7 усл.ед. жиров 9 усл.ед. углеводов; а в единице продукта содержится соответственно 3, 21, 10 усл.ед. тех же питательных веществ. Требуется:
- составить экономико-математическую модель задачи, позволяющую сформировать из продуктов и суточную диету, которая с одной стороны содержала бы белков, жиров и углеводов не менее минимально научно обоснованных норм и вместе с тем требовала бы минимальных затрат;
- решить задачу графическим способом.
Решение.
Задача о смесях
Постановка задачи: N ингредиентов — y1, y2, y3, y4. В результате смешивания этих ингредиентов в пропорциях g11:g12:g13:g14, g21:g22:g23:g24, g31:g32:g33:g34 и g41:g42:g43:g44 получают смесь n сортов x1, x2, x3, x4. Цена его реализации соответственно s1, s2, s3, s4.
Экономико-математическая модель задачи
| Компоненты | Сорта | Объем ресурсов | |||
| x1 | x2 | x3 | x4 | ||
| N1 | g11/Σg1i | g21/Σg2i | g31/Σg3i | g41/Σg4i | y1 |
| N2 | g12/Σg1i | g22/Σg2i | g32/Σg3i | g42/Σg4i | y2 |
| N3 | g13/Σg1i | g23/Σg2i | g33/Σg3i | g43/Σg4i | y3 |
| N4 | g14/Σg1i | g24/Σg2i | g34/Σg3i | g44/Σg4i | y4 |
| Цена | s1 | s2 | s3 | s4 |
Назначение сервиса . С помощью данного сервиса можно в онлайн режиме составить математическую модель задачи о смесях и решить ее симплекс-методом или средствами MS Excel .
- Ввод данных
- Решение
- Видеоинструкция
Пример . Завод выпускает 4 вида полуфабрикатов Bi в количествах: В1 – 400 т, В2 – 250 т, В3 – 350 т и В4 – 100 т.
В результате смешения этих компонентов получают 3 вида продукции Aj. Пропорции смешиваемых полуфабрикатов следующие: для А1 – 2:3:5:2, для А2 – 3:1:2:1, для A3 – 2:2:1:3. Стоимость 1 т продукции Aj составляет: А1 – 12 руб., А2 – 10 руб., А3 – 15 руб.
Составить оптимальный план выпуска продукции по критерию:
а) максимальной стоимости выпущенной продукции;
б) максимального использования полуфабрикатов
Источник
Решение задачи о дневном рационе
Постановка задачи
Для сохранения здоровья и работоспособности человек должен потреблять в сутки определенное количество белков, жиров, углеводов, воды и витаминов (Таблица 25). Предположим (для простоты решения задачи), что дневной рацион человека составляется из трех продуктов — П1, П2, П3. Стоимость этих продуктов задана в табл. 25. Запасы ингредиентов в различных продуктах различны (Таблица 25). Следует таким образом определить дневной рацион, чтобы стоимость рациона была наименьшей, но при этом в рационе содержалось необходимое количество питательных веществ.
Сводная таблица условий задачи о дневном рационе
Количество питательных веществ в единице продукта
Минимально необходимое кол-во питательных веществ
Стоимость единицы продукта (руб.)
Построение модели
Построение математической модели осуществляется в три этапа:
1 Этап. Определение переменных, для которых будет составляться математическая модель.
Так как требуется определить дневной рацион, то есть необходимое количество продуктов П1, П2, П3, то переменными модели будут:
x1 — количество продукта П1, в ед.;
x2— количество продукта П2, в ед.;
x3 — количество продукта П3, в ед.
2 Этап. Формирование целевой функции.
Так как стоимость единицы продукции П1, П2, П3известна, то стоимость всего рациона будет выражаться функцией 40x1+20x2+30x3 (руб.). Обозначив общий расход через F, можно дать следующую математическую формулировку целевой функции: определить допустимые значения переменных x1, x2, x3, минимизирующих целевую функциюL=40x1+.20x2+30x3.
3 Этап. Формирование системы ограничений.
Величины х1 , х2 , х3 следует выбрать так, чтобы стоимость рациона была наименьшей, но при этом в рационе содержалось необходимое количество питательных веществ, т.е. должны выполняться неравенства:
Так как количество продуктов не может быть отрицательным значением, то появляется условие неотрицательности:
Таким образом, математическая модель задачи представлена в виде: определить рацион x1, x2 , x3, обеспечивающий минимальное значение функции:L=40x1+20x2+30x3 при наличии ограничений:
Нахождение решения задачи о дневном рационе средствами Microsoft Excel
Запустите приложение Microsoft Excel (ПускПрограммы Microsoft Excel).
Найдите оптимальное решение задачи о дневном рационе:
Для этого выполните следующую последовательность действий:
Создайте экранную форму для ввода условия задачи (Рис. 1).
Введите исходные данные в экранную форму:
направление целевой функции (min);
коэффициенты при переменных в ограничениях;
знаки в ограничениях ( >= );
правые части ограничений.
Напоминаем, для того, чтобы ввести знаки =, >=,

поэтому в ячейку B9 необходимо внести формулу
=
Напоминаем, что данную формулу можно ввести, воспользовавшись функцией =СУММПРОИЗВ(B3:D3;B7:D7), для этого:
установите курсор в ячейку B9;
нажав кнопку «
выберите в окне «Категория»категорию«Математические»;
в окне «Функция»выберите функциюСУММПРОИЗВ;
в появившемся окне «СУММПРОИЗВ»в строку«Массив 1»введите выражениеB3:D3, а в строку«Массив 2»– выражениеB7:D7;
В экранной форме (Рис. 3) в ячейке B9 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
аналогичным образом введите формулы для расчета значений левых частей ограничений (это потребляемое количество в сутки) в ячейки E13,E14, E15, E16, E17соответственно.
Формулы, описывающие ограничения модели можно увидеть ниже (Таблица 26).
Источник











 », вызовите окно «Мастер функций – шаг 1 из 2»;
», вызовите окно «Мастер функций – шаг 1 из 2»;

 ;
;










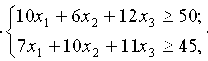















 Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK.
Можно установить еще одно ограничение с помощью кнопки “Добавить”. Дальнейшие действия по его настройке будут аналогичными. По готовности щелкаем OK. Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.
Под этим полем также есть опция, позволяющая делать все остальные переменные, не затрагиваемые ограничениями, неотрицательными. Однако, будьте внимательны и проследите за тем, чтобы между этим параметром и поставленными ограничениями не было противоречия, иначе при расчете в программе может возникнуть конфликт.










