Задачи по теме поиск решения в excel

Применение команды «Поиск решений»

в работе с профессионально-ориентированными задачами

Постановка задачи

В ресторане установлены 7 графиков работы официантов:

График	Выходные
1	Суббота. Воскресение
2	Воскресение, Понедельник
3	Понедельник, Вторник
4	Вторник, Среда
5	Среда, Четверг
6	Четверг, Пятница
7	Пятница, Суббота

Количество работающих по ним соответственно – №1, №2, №3, №4, №5, №6, №7. Опытным путём было определено требуемое  количество официантов на каждый день недели:

День недели	Пн	Вт	Ср	ЧТ	Пт	Сб	Вс
Требуется, чел.	11	10	9	10	12	12	13

Необходимо распределить работающих официантов по каждому графику таким образом, чтобы затраты на еженедельную зарплату всем официантам были минимальными (найти N1, N2, N3, N4, N5, N6, N7). При этом нужно учитывать следующие факторы:

1. Ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности.
2. Число работников, работающих по каждому графику, не может быть отрицательным.
3. Число работников, работающих по каждому графику, должно быть целочисленным.

Рассмотреть ситуацию, когда по графику 1 обязательно должно работать 3 человека.

Создание таблицы для анализа данных

Исходя из условий постановки задачи, создадим в табличном процессоре Excel таблицу, где будем потом рассматривать и анализировать ситуации.

1. Открываем программу Excel, например, щёлкнув два раза её ярлык на рабочем столе или через Пуск – Программы – Microsoft Excel.
2. Устанавливаем поля документа через Файл — Параметры страницы:
3. Сохраняем книгу (файл в Excel) через Файл – Сохранить как под именем Анализ графиков работы.xls.
4. Начиная с ячейки A1, оформляем таблицу (см. следующий лист). В те дни недели, где предусмотрен по графику рабочий день, ставим 1, а где  выходной – 0. при этом формат данных в этих  ячейках оставляем по умолчанию – Общий.
5. После заполнения таблицы данными, отформатируем ячейки так, чтобы текст и числа в них располагались по горизонтали и вертикали По центру. Для этого выделим мышкой всю таблицу и используем меню Формат – Ячейки – вкладка Выравнивание (или по правой клавише мыши).
6. Оформим  внешние и внутренние границы ячеек.
7. Получим таблицу следующего вида:

Здесь A2…G2 – количество официантов, работающих в соответствующий день недели, A1..G1 – требуемое (определённое опытным путём, меньше нельзя).

Всего работников – N.

K – дневная заработная плата одного официанта, она составляет, к примеру, 200 рублей.

1. Поскольку файл в программе Excel называется книга, а каждая книга состоит из листов, переименуем ярлычок первого листа книги, где создана таблица, и назовём его Заготовка. Переименовать можно щелчком правой клавишей по ярлычку листа, выбрать пункт Переименовать или просто два раза щёлкнуть по ярлычку листа, название Лист1 выделиться, можно вводить новое название.
2. Мышкой выделим всю таблицу и скопируем её в Буфер обмена.
3. Перейдём на Лист2 книги, щёлкнув ярлычок этого листа.
4. Вставим из буфера скопированную таблицу: щёлкнем значок  на панели Стандартная.
5. В ячейках C2:C8 удалим набранный текст. В этих ячейках будут вычисляться значения при применении команды Поиск решения.
6. В ячейки D10:J10 введём определённое опытном путём минимальное количество официантов по дням недели.

Требуется (определено опыт. путём)

11

10

9

10

12

12

13

Цвет шрифта этих ячеек для лучшей наглядности сделаем синим.    

1. В ячейках D9:J9 также удалим текст. Сюда необходимо вписать формулы.
2. В ячейку C12 запишем 200, изменим формат данных в ячейке на Денежный в рублях, получим 200р.
3. Переименуем Лист2 в Ситуация 1.

Таблица для проведения анализа готова.

Ввод формул для получения решения

Чтобы в дальнейшем проанализировать ситуации, необходимо в ячейки D9:J9 ввести формулы. рассчитывающие фактическое количество официантов по дням недели и по графикам работы.

Формулы для вычислений могут быть простыми, такими как сложение содержимого двух ячеек, а могут быть сложными, такими как определение отклонения какой-либо величины от других значений последовательности.

Ввод формулы в Excel начинается со знака =. За ним записывается функция, потом в скобках () аргументы. Некоторые функции, например, многие статистические, финансовые используют несколько аргументов. Тогда аргументы отделяются друг от друга запятыми.

Простейшие формулы, такие как сложение, вычитание, умножение, деление состоят из двух частей: арифметического оператора и хотя бы одного адреса ячейки.

При составлении формул для вычислений или преобразований данных необходимо указать содержимое каких именно ячеек используется в формулах.

Введём в ячейку D9 формулу =D2*C2+D5*C5+D6*C6+D7*C7+C8.

 Она рассчитывает сколько официантов должно работать в понедельник с учётом графиков их работы. Там, где в таблице 0, т.е. выходной, ячейки не обсчитываем.

Для подсчёта работников во вторник в ячейку E9 запишем формулу

=C2*E2+E3*C3+E6*C6+E7*C7+E8*C8.

Для ячейки F9 – =F2*C2+F3*C3+F4*C4+F7*C7+F8*C8. Среда.

Для ячейки G9 – =G2*C2+G3*C3+G4*C4+G5*C5+G8*C8. Четверг.

Для ячейки H9 – =H2*C2+H3*C3+H4*C4+H5*C5+H6*C6. Пятница.

Для ячейки I9 – =I3*C3+I4*C4+I5*C5+I6*C6+I7*C7. Суббота.

Для ячейки J9 – =J4*C4+J5*C5+J6*C6+J7*C7+J8*C8. Воскресенье.

В ячейку C11 нужно записать формулу подсчёта общего количества официантов с учётом всех семи графиков работы: =СУММ(C2:C8), т.е. просуммировать всех официантов, работающих по графикам 1…7.

В ячейку C13 введём формулу подсчёта недельной зарплаты всех официантов:

=(C11*C12).

 Все необходимые формулы  и данные введены в таблицу. Теперь можно приступать к поиску решения поставленной задачи.

Поиск решения

Команда Поиск решения из меню Сервис анализирует ситуацию с учётом ограничений, накладываемых на отдельные ячейки, рассчитывает значение целевой ячейки, изменяя значения указанных нами ячеек.

При поиски решения  целевая ячейка должна содержать формулу, но ячейки, которые будут изменяться, должны содержать значения, а не формулу.

Для решения нашей задачи выполним следующие действия:

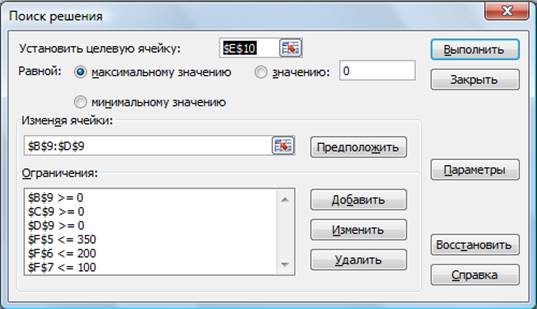
1. Выделим ячейку C13. (Еженедельная зарплата, она должна быть минимальной.)
2. Сервис — Поиск решения.
3. Установим целевую ячейку $C$13 равной минимальному значению.

1. Укажем, что будут меняться значения ячеек $C$2:$C$8. Это можно сделать, щёлкнув по красной стрелке в правом углу окошечка, перейдя в таблицу и выделив нужные ячейки.
2. Введём ограничения на значения отдельных ячеек: в ячейках C2…C8 должно быть целое число; ячейка D9>=11, E9>=10, F9>=9, G9>=10, H9>=12, I9>=12, J9>=13. Ввод ограничений проводим через кнопку.
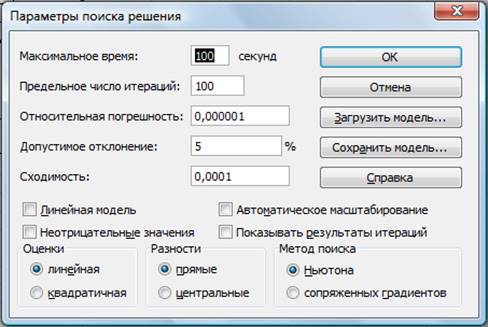
3. Через кнопку Параметры установим, что значения в изменяемых ячейках должны быть неотрицательными. Другие параметры в открывшемся окне Параметры поиска решения оставляем внесёнными по умолчанию.

1. Нажимаем кнопку Выполнить. Получаем решение задачи для первой ситуации, когда определяем минимальное количество официантов с учётом всех графиков их работы при условии, что ежедневно фактическое количество работающих официантов должно быть не менее ежедневной потребности. Решение представлено в Приложении.
2. В ситуации 2 официантов, работающих по графику №1, должно быть обязательно 3. Для учёта этого обстоятельства при новом поиске решения введём ещё одно ограничение: $C$2 =3.  Тогда после нажатия кнопки Выполнить получим решение для этой ситуации. Это решение представлено также в Приложении.
3. Проанализировав обе ситуации видим, что общее количество официантов одинаково (16). Это минимальное количество при заданных условиях. Соответственно подсчитана и еженедельная зарплата всех официантов. Но в ситуации 2 распределение официантов по графикам работы другое. Фактическое количество работающих по дням недели  также изменилось.

Заключение

Табличный процессор Excel обладает удобными возможностями для анализа и обработки данных. Такие команды или средства программы как Подбор параметров и Поиск решения можно использовать для решения задач прогнозирования различных ситуаций в работе менеджера, финансиста и других специалистов, гибкого подбора новых параметров при изменении ситуации, поиска более гибкого и многовариантного решения задачи с учётом различных обстоятельств и ограничений.

Приложение

Решение задачи, найденное с помощью программы MS Excel

Ситуация 1

Ситуация 2

Практическая работа №11

Тема: Задачи оптимизации (поиск решения) в MS Excel.

Цель: — изучение технологии поиска решения для задач
оптимизации (минимизации, максимизации).

Вид
работы: фронтальный

Время
выполнения: 2 часа

Задания к практической работе

Задание
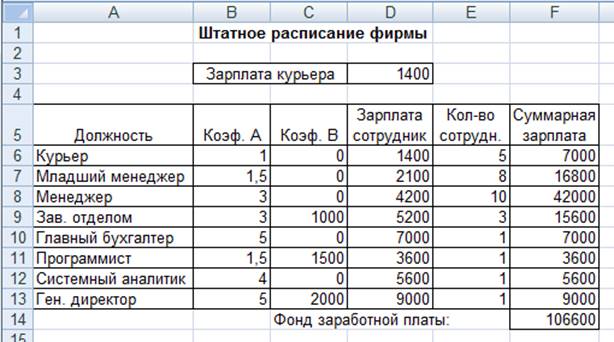
1. Минимизация фонда заработной платы
фирмы.

Пусть известно, что для нормальной работы фирмы
требуется 5…7 курьеров, 8…10 младших менеджеров, 10 менеджеров, 3 заведующих
отделами, главный бухгалтер, программист, системный аналитик, генеральный
директор фирмы.

Общий месячный фонд зарплаты должен быть минимален.
Необходимо определить, какими должны быть оклады сотрудников фирмы, при
условии, что оклад курьера не должен быть меньше 1400 р.

В качестве модели решения этой задачи возьмем линейную
модель. Тогда условие задачи имеет вид N₁*A₁*x+N₂*(A₂*x+B₂)+…+N₈*(A₈*x+B₈)
= Минимум, где N_i – количество работников данной специальности; x
– зарплата курьера; A_i и B_i – коэффициенты заработной
платы сотрудников фирмы.

Ход работы

1.  
Запустите редактор электронных
таблиц Microsoft Excel и откройте созданный в Практической работе 4 файл
«Штатное расписание».

Скопируйте содержимое листа «Штатное расписание 1» на
новый лист и присвойте копии листа имя «Штатное расписание 2».

2.  
В меню Данные – Анализ «что –
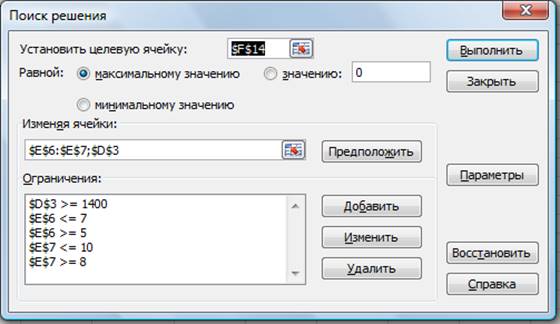
если» активизируйте команду Поиск решения (рис. 1).

3.  
В окне Установить целевую
ячейку укажите ячейку F14, содержащую модель – суммарный фонд заработной
платы.

Рисунок 1 — Задание условий для минимизации фонда заработной
платы

Поскольку необходимо минимизировать общий месячный
фонд зарплаты, активизируйте кнопку равный – Минимальному значению.

В окне Изменяя ячейки укажите адреса ячеек, в
которых будет отражено количество курьеров и младших менеджеров, а также
зарплата курьера — $E$6:$E$7:$D$3 (при задании ячеек E6, E7 и D3 держите
нажатой клавишу [Ctrl]).

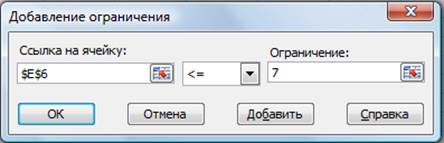
Используя кнопку Добавить в окнах Поиск
решения и Добавление ограничений, опишите все ограничения задачи:
количество курьеров изменяется от 5 до 7, младших менеджеров од 8 до 10, а
зарплата курьера >1400 (рис.2).

Рисунок
2 — Добавление ограничений для минимизации фонда заработной платы

Ограничения наберите в виде

$D$3>=1400

$E$6>5

$E$6<7

$E$7>=8

$E$7 <=10.

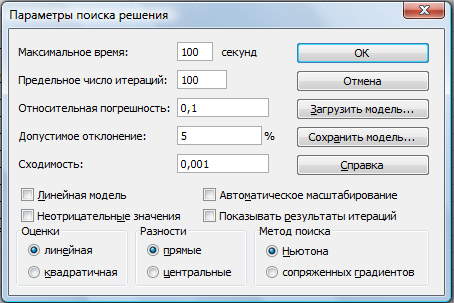
Активизируйте кнопку Параметры, введите
параметры поиска, как показано на рис. 3.

Рисунок
3 — Задание параметров поиска решения по минимизации фонда заработной платы.

Окончательный вид окна Поиск решения приведен
на рис. 1.

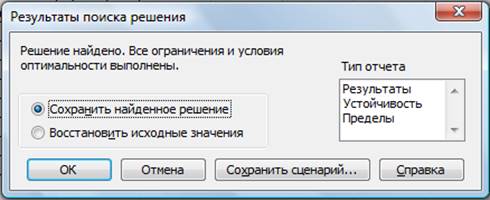
Запустите процесс поиска решения нажатием кнопки Выполнить.
В открывшемся диалоговом окне Результаты поиска решения задайте
опцию Сохранить найденное решение (рис. 4).

Рисунок
4 — Сохранение найденного при поиске решения

Решение задачи приведено на рис. 5. Оно тривиально:
чем меньше сотрудников и чем меньше их оклад, тем меньше месячный фонд
заработной платы.

Рисунок
5 — Минимизация фонда заработной платы

Задание
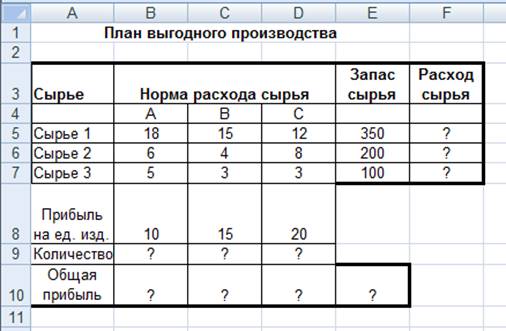
2. Составление плана выгодного
производства.

Фирма производит несколько видов продукции из одного и
того же сырья – А, В и С. Реализация продукции А дает прибыль 10 р., В – 15 р.
и С – 20 р. на единицу изделия.

Продукцию можно производить в любых количествах,
поскольку известно, что сбыт обеспечен, но ограничены запасы сырья. Необходимо
определить, какой продукции и сколько надо произвести, чтобы общая прибыль от
реализации была максимальной.

Нормы расхода сырья на производство продукции каждого
вида приведены в табл. 1.

Таблица 1

Сырье	Нормы расхода сырья	Запас сырья
А	В	С
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20

Ход работы

1.  
Запустите редактор электронных таблиц
Microsoft Excel и создайте новую электронную книгу.

2.  
Создайте расчетную таблицу как на
рис. 6. Введите исходные данные и формулы в электронную таблицу. Расчетные
формулы имеют такой вид:

Расход сырья 1=(количество сырья 1) * (норма расхода
сырья А) + (количество сырья 1) * (норма расхода сырья В) + (количество сырья
1) * (норма расхода сырья С).

Значит, в ячейку F5 нужно ввести формулу =
B5*$B$9+C5*$C$9+D5*$D$9.

Обратите внимание, что значения количества сырья
каждого вида пока не известны и будут подобраны в процессе решения задания
(ячейки В9:D9 пока пустые).

(Общая прибыль по А) = (прибыль на ед.
изделий А) * (количество А),

Следовательно в ячейку В10 следует
ввести формулу = В8 * В9.

Итоговая общая прибыль = (Общая прибыль
по А) + (Общая прибыль по В) + (Общая прибыль по С),

значит в ячейку Е10 следует ввести
формулу = СУММ(В10:D10).

Рисунок 6 — Исходные
данные для Задания 2

3.  
В меню Данные активизируйте
команду Поиск решения и введите параметры поиска, как указано на рис 7.

Рисунок 7 — Задание
условий и ограничений для поиска решений

В качестве целевой ячейки укажите ячейку «Итоговая
общая прибыль» (Е10), в качестве изменяемых ячеек – ячейки количества сырья –
(В9:D9).

Не забудьте задать максимальное значение суммарной
прибыли и указать ограничения на запас сырья:

расход сырья 1<=350; расход сырья 2<=200; расход
сырья 3<=100, а также положительные значения количества сырья А,  В, С
>=0.

Установите параметры поиска решения (рис. 8). Для
этого кнопкой Параметры откройте диалоговое окно Параметры поиска
решения, установите параметры по образцу, задайте линейную модель расчета (Линейность
модели).

Рисунок 8 — Задание
параметров поиска решения

4.  
Кнопкой Выполнить запустите
Поиск решения. Если вы сделали все верно, то решение будет как на рис.
9.

Рисунок 9 — Найденное
решение максимизации прибыли при заданных ограничениях

5.  
Сохраните созданный документ под
именем «План производства».

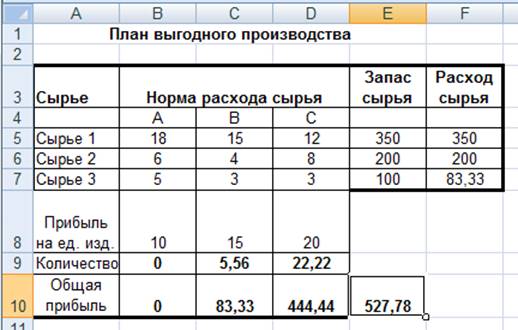
Вывод. Из решения видно, что оптимальный план выпуска предусматривает
изготовление 5,56 кг продукции В и 22,22
кг продукции С. Продукцию А производить не стоит. Полученная прибыль при этом
состоит 527,78 р.

Задание
3. Используя файл «План производства»
(см.задание 2), определить план выгодного производства, т. е. какой продукции и
сколько необходимо произвести, чтобы общая прибыль от реализации была
максимальной.

Выберите нормы расхода сырья на производство продукции
каждого вида и ограничения по запасам сырья из таблицы соответствующего
варианта (5 вариантов):

Вариант 1

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	25	17	11	500
Сырье 2	9	7	10	400
Сырье 3	15	8	5	300
Прибыль на ед. изделия	5	10	12
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 2

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	11	8	3500
Сырье 2	14	15	2	280
Сырье 3	8	9	10	711
Прибыль на ед. изделия	10	9	8
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 3

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	10	20	15	2700
Сырье 2	16	25	13	3800
Сырье 3	8	9	10	1200
Прибыль на ед. изделия	7	8	6
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 4

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	14	15	19	460
Сырье 2	7	8	12	820
Сырье 3	17	24	6	214
Прибыль на ед. изделия	15	10	25
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Вариант 5

Сырье	Норма расхода сырья	Запас сырья
А	В	С
Сырье 1	12	18	3	625
Сырье 2	16	25	13	227
Сырье 3	8	9	10	176
Прибыль на ед. изделия	18	15	9
Количество продукции	?	?	?
Общая прибыль	?	?	?	?

Рекомендуемая
литература: 1, 2, 3, 4

Практическое
занятие по теме: «Подбор параметра и оптимизация (поиск решений)  в Excel»

Цель
практического занятия: Изучение технологии «Подбора параметра и оптимизация
(поиск решений) » для решения задач, имеющих точное целевое значение, зависящее
от одного неизвестного параметра

Задачи:

1)               
Познакомится
с основными ключевыми понятиями «Подбора параметра»

2)               
 рассматривается
процесс нахождения исходных данных, которые при подстановке в формулы, дают
необходимое значение в ячейке результата

3)               
Решение
задач по теме «Подбор параметра» по образцу и по алгоритму.

4)               
Решение
задач по указанной теме самостоятельно

План занятия:

1)               
Ознакомление
студентов с ключевыми понятиями.

2)               
Рассмотрение
процесса нахождения
исходных данных

3)               
Знакомство
с понятием Подбор параметра и Поиск решения

4)               
Решение
задач по теме «Подбор параметра» по образцу и по алгоритму

5)               
Решение
задач по указанной теме самостоятельно

Ход занятия

Для
эффективного использования  формул необходимо ознакомиться с тремя ключевыми
понятиями.

Вычисление  
— это процесс расчета по формулам и последующего отображения значений
результатов в ячейках, содержащих формулы. Во избежание ненужных вычислений
Microsoft Office Excel автоматически пересчитывает формулы только при изменении
влияющих на формулу ячеек. Это является стандартной процедурой при первом
открытии книги и ее редактировании. Однако тем, как и когда Excel будет
пересчитывать формулы, можно управлять.

Итерация  
— это многократный пересчет листа до удовлетворения определенного числового
условия. Excel не может автоматически рассчитать значение по формуле, которая
ссылается (прямо или косвенно) на ячейку, содержащую формулу (это называется
циклической ссылкой). Если формула содержит обратную ссылку на одну из своих
собственных ячеек, необходимо определить, сколько раз следует пересчитывать
формулу. Циклические ссылки могут пересчитываться до бесконечности. Однако
существует возможность управления максимальным числом итераций и количеством
допустимых изменений.

Точность  
— это показатель степени сходимости вычислений. Excel хранит и выполняет
вычисления с точностью 15 значащих цифр. Однако существует возможность изменить
точность вычислений, так что Excel при пересчете формул будет использовать для
вычислений не хранимое, а отображаемое значение.

Процесс
изменения значений ячеек и анализа влияния этих изменений на результат
вычисления формул в Excel
называется анализом «что-если».

Рассмотрим 
процесс нахождения исходных данных, которые при подстановке в формулы, дают
необходимое значение в ячейке результата. Если вы знаете, каким должен быть
результат вычисления по формуле, то Excel подскажет вам
значения одного или нескольких входных параметров, которые позволяют получить
нужный результат.

Другими
словами, вы можете задать вопрос типа: Какой рост продаж необходим для получения
дохода в $1 200 000? В Excel для этого
предусмотрены два подходящих средства.

·
Подбор
параметра
– определяет значение одной входной ячейки, которое требуется для получения
желаемого результата в зависимой ячейке (ячейке результата).

·
Поиск
решения
— определяет значения в нескольких входных ячейках, которые требуются для
получения желаемого результата. Более того, можно накладывать ограничения на
входные данные, поэтому здесь можно получить решение  (если оно существует)
многих практических задач.

Подбор
параметра
является удобным средством для решения задач, которые имеют точное целевое
значение, зависящее от одного неизвестного параметра. С помощью Подбора
параметра можно определить значение, которое будет давать желаемый
результат.

Решим
следующую задачу:

Вы хотите
положить деньги в банк под 4,5% и получить ровно 1000 руб. по истечении года.
Необходимо определить сумму вклада. Для решения данной задачи используем
средство Подбор параметра.

Задание:

1.                
Создайте
новый файл под именем Лаб.раб. Лист 1 переименуйте в  Подбор.

2.                
Оформите
таблицу (рис. 1). Введите указанную формулу.

Рис.1

3.                
 Активизируйте
ячейку В3. Выполните команду Данные — -Анализ «что- если» ÞПодбор
параметра.

4.                
В
открывшемся диалоговом окне укажите значение необходимой конечной суммы и
ссылку на ячейку с искомым значением вклада (рис.2).

Рис.2

5.                
Нажмите
кнопку ОК. Средство подбор параметра найдет решение и сообщит об этом
(рис. 3). Нажмите кнопку ОК и убедитесь, что искомое значение помещено в
ячейке В2.

Рис.3

Задание для самостоятельной работы:

1.                
Решите
задачу:
Для покупки автомобиля Вам необходима сумма 200 000 руб. У Вас есть
возможность взять ипотечную ссуду, при этом нужно сделать первый взнос 20%.
Определите, какую сумму нужно взять в банке, чтобы на руки вы получили
требуемую сумму.

2.                
Для
решения задачи оформите таблицу (рис.4). Введите формулы.

Рис.4

3.                
С
помощью средства Подбор параметра определите размер ссуды.

Задачи оптимизации
(поиск решения)

Цель: Изучение
технологии поиска решения для задач оптимизации (минимизации, максимизации).

Задание 1.  Составление плана
выгодного производства.

Фирма производит несколько видов продукции
из одного и того же сырья – А, В, С. Реализация продукции А дает прибыль 10р.,
В – 15р., С-20р. На единицу изделия. Продукцию можно производить в любых
количествах, поскольку известно, что сбыт обеспечен, но ограничены запасы
сырья. Необходимо определить, какой продукции и сколько надо произвести, чтобы
общая прибыль от реализации была максимальной.

Нормы расхода сырья на производство
продукции  каждого вида приведены в таблице.

Сырье	Нормы расхода сырья	Запас сырья
А	В	С
Сырье 1	18	15	12	350
Сырье 2	6	4	8	200
Сырье 3	5	3	3	100
Прибыль	10	15	20

Решение:

1.     Создать
расчетную таблицу

А                    
В              С           D                   
E                                   F

План выгодного производства
Сырье	Норма расхода сырья	Запас сырья	Расход сырья
	А	В	С
Сырье 1	18	15	12	350	=$B$9*B5+$C$9*C5+$D$9*D5
Сырье 2	6	4	8	200	=$B$9*B6+$C$9*C6+$D$9*D6
Сырье 3	5	3	3	100	=$B$9*B7+$C$9*C7+$D$9*D7
Прибыль на ед. изделия	10	15	20
Количество
Общая прибыль	=B8*B9	=C8*C9	=D8*D9	=СУММ(B10:D10)

2.     В
меню Сервис активизируйте
команду Поиск решения и введите параметры поиска

Сервис — настройки
– поиск решения

Параметры:

В результате должно получиться следующее:

Сырье	Норма расхода сырья	Запас сырья	Расход сырья
	А	В	С
Сырье 1	18	15	12	350	350
Сырье 2	6	4	8	200	200
Сырье 3	5	3	3	100	83,33333333
Прибыль на ед. изделия	10	15	20
Количество	0	5,5555556	22,222
Общая прибыль	0	83,333333	444,44	527,77778

Сохранить под именем «План
производства» и сделать выводы.

Задание№2. Выполнить
аналогичные расчеты

Вариант 1

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	25	17	11	350
Сырье 2	9	7	10	400
Сырье 3	15	8	5	300
Прибыль на ед. изделия	5	10	12
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 2

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	12	11	8	3500
Сырье 2	14	15	2	280
Сырье 3	8	9	10	711
Прибыль на ед. изделия	10	9	8
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 3

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	10	20	15	2700
Сырье 2	16	25	13	3800
Сырье 3	8	9	10	1200
Прибыль на ед. изделия	7	8	6
Количество	?	?	?
Общая прибыль	?	?	?	?

Вариант 4

Сырье	Норма расхода сырья	Запас сырья
	А	В	С
Сырье 1	14	15	19	460
Сырье 2	7	8	12	820
Сырье 3	17	24	6	214
Прибыль на ед. изделия	15	10	25
Количество	?	?	?
Общая прибыль	?	?	?	?

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» — 250 рублей. «3» — 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Условие. Рассчитать, какую сумму положить на вклад, чтобы через четыре года образовалось 400 000 рублей. Процентная ставка – 20% годовых. Проценты начисляются ежеквартально.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка)^кпер. Подставим значения: ПС = 400 000 / (1 + 0,05)¹⁶ = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, <, >=, <=). Результат логического выражения – логическое значение ИСТИНА или логическое значение ЛОЖЬ.

Пример задачи. Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter — это обязательное условие для ввода массивов.

Скачать примеры

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

На этой странице вы найдете примеры решений различных оптимизационных задач с использованием пакета электронных таблиц MS Excel (используется как надстройка Поиск решения, так и ручные вычисления).

Задачи оптимизации и Excel

Задачи оптимизации имеют огромное прикладное значение и возникают в самых разных разделах экономики, техники, военного дела и т.п. В таких задачах нас интересуют поиск некоторого оптимального решения (минимизующего или максимизирующего целевую функцию: прибыль, затраты, калорийность и т.п.) в условиях ограничений (наличия ресурсов, дорог, времени, продуктов и т.п.).

Вот некоторые примеры экономических задач: минимизация расходов при формировании состава сырья (например, на текстильных предприятиях), оптимизация раскроя (например, на швейных производствах), минимизация расходов при формировании штатного расписания, оптимизация калорийности и стоимости рациона (как для людей, так и для животных), минимизация расходов на перевозку грузов по маршрутам, оптимизация расходов на изготовление при выборе ассортимента продукции, максимизация прибыли при формировании инвестиционной программы и др.

Часто эти задачи (даже учебные, даже в случае линейности) содержат более десяти переменных(а в случае, например, транспортных задач, и вовсе десятки), что делает ручные расчеты нерациональными. В то же время привычная для всех программа Excel прекрасно подходит для поиска решения.

Алгоритм решения с помощью надстройки «Поиск решения» следующий:

• составить математическую модель задачи: выделить и обозначить переменные, ограничения на них в виде равенств и неравенств (естественные, например, неотрицательность количества, и дополнительные, например, «запасов железной руды не более 10 т»), целевую функцию (то, что нужно оптимизировать) выразить через переменные.
• выделить место под переменные задачи; внести ограничения (левые части — в виде формул от переменных, правые — в виде констант) в файл электронной таблицы Excel,
• внести в ячейку формулу для целевой функции,
• запустить надстройку Поиск решения,
• установить нужные параметры решения (ограничения в листе, ограничения неотрицательности, условие линейности при необходимости и т.п.) и запустить выполнение.

Excel вычислит оптимальные значения переменных и покажет их в ячейках, а также значение целевой функции. Дополнительно можно построить отчеты для анализа решения задачи.

Некоторые задачи оптимизации решаются не с помощью надстройки Поиск решения, а путем подбора параметра или ручных расчетов. Ниже вы найдете примеры разных задач, а также ссылки на другие разделы со сходными заданиями.

Задачи оптимизации: примеры в Excel

Задача 1. Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля $R_j$. Определена экономическая эффективность $К$ — каждого проекта в зависимости от рентабельности производства. По истечении трех сроков $S_i$ рассматриваются как некоторые состояния среды (природы). Значения экономической эффективности для различных проектов и состояний природы приведены в следующей таблице (д. е.):


Выберите оптимальное решение в соответствии с критериями Лапласа, Вальда, Сэвиджа и Гурвица (при $а = 0,5$).

Задача 2. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода каждого вида сырья на изготовление единицы продукции данного вида в таблице 6. В ней же указаны прибыль от реализации единицы изделия каждого вида и общее количество сырья данного, которое может быть использовано предприятием.
Требуется такой составить такой план производства изделий А и В, при котором прибыль от реализации будет максимальной?

Задача 3. Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов $b_{ki}$, приведены в табл.1.
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО (j =1-7). Выход готового продукта из 1 тонны сырья $a_{ij}$ показан в табл.2.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, $С_{kj}$ , показана в табл.3.
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, ($x_j$), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.

Задача 4. Для изготовления одного пирожка требуется 0,8 ед. начинки и 4 ед. теста, одного пирожного 4 ед. начинки и 0,5 ед. теста, одного рулета 2 ед. начинки и 2,5 ед. теста. Сколько пирожков, пирожных и рулетов нужно сделать кондитерской, если в наличии имеется 120 ед. теста и 300 ед. начинки?
Определите доход от реализации кондитерских изделий, если доход от продажи одного пирожка составляет 3 рубля, одного пирожного 2 рубля, одного рулета 1,5.
Для решения задачи используется ППП Excel.

Задача 5. Менеджер проекта по строительству нового торгового гипермаркета компании Наше дело надеется завершить проект за пару недель до Рождества.
После обзора оценок времени выполнения отдельных стадий выяснилось, что потребуются дополнительные инвестиции, чтобы сократить длительность проекта так, чтобы он действительно завершился вовремя. В таблице приведены оценки длительностей стадий и стоимость их сокращения на 1 и на 2 недели.
a. Нарисуйте сетевую диаграмму проекта и найдите критический путь.
b. Определите минимальную стоимость сокращения проекта на 5 недель.

Полезные ссылки

Методички

• Решение оптимизационных задач в среде MS Excel 2013 Методические указания небольшого объема. Разобраны стандартные задачи: ЛП, транспортная, нелинейная, приведены скриншоты решения и пояснения.
• Решение задач оптимизации в Microsoft Excel 2010 Учебное пособие ТОГУ, 101 страница, более увесистый и подробный документ. Разбирается надстройка Поиск решения, решение задач линейного и нелинейного программирования и СЛАУ.