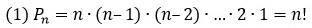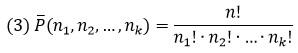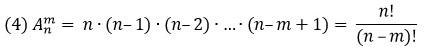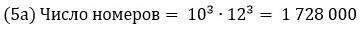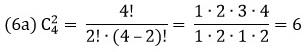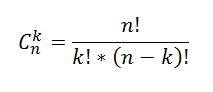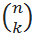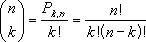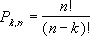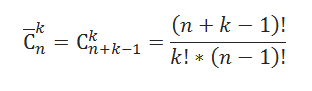Задачи по комбинаторике в excel

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

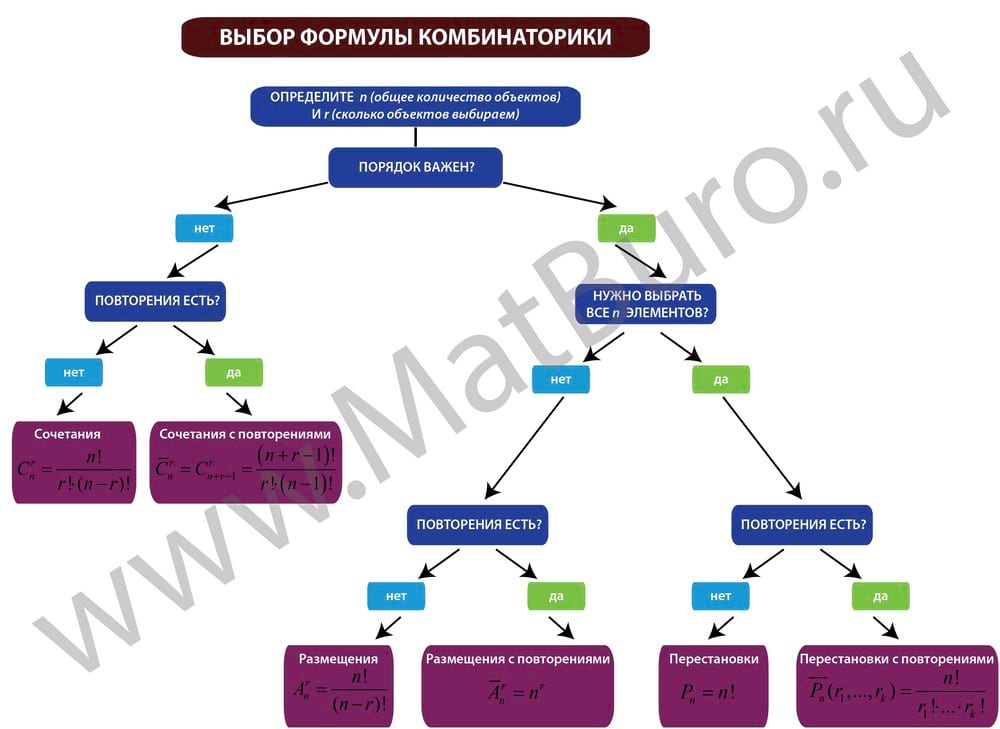
Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

• Сколько у нас есть объектов (число $n$)?
• Важен ли их порядок в комбинации?
• Могут ли встречаться повторяющиеся элементы?
• Нужно выбрать все элементы или только $klt n$?

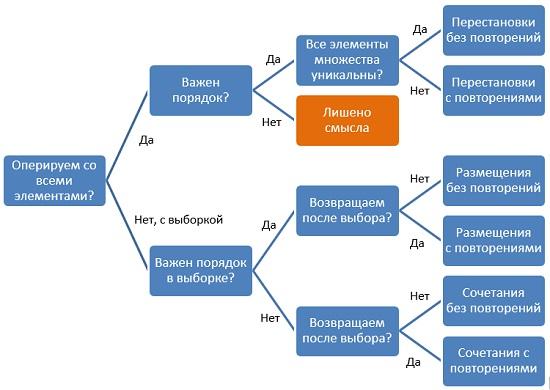
Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Схема выбора формул с примерами задач

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Подробнее: факториал в эксель.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.

Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$

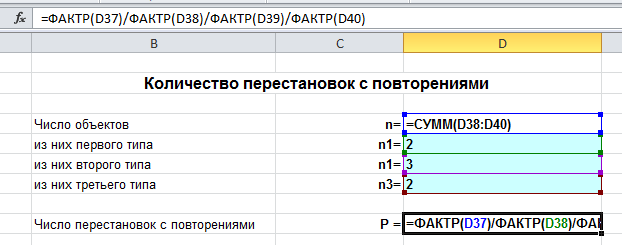
Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).

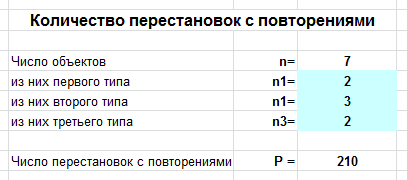
Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок c повторениями.

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

$$C_n^k=frac{n!}{(n-k)!cdot k!} $$

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).

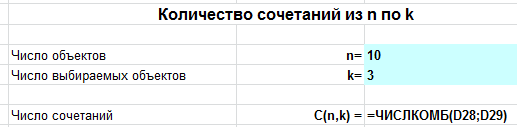
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний.

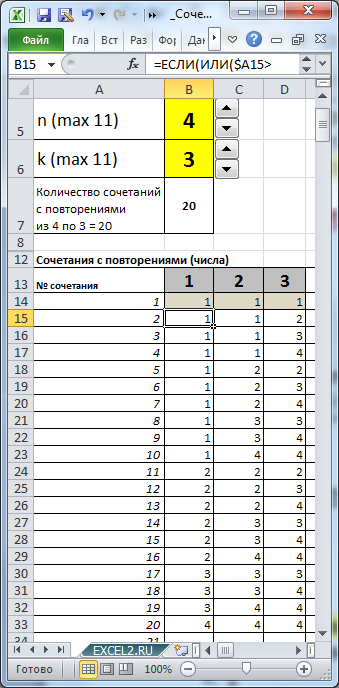
Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Онлайн калькуляторы Онлайн учебник: Элементы комбинаторики Примеры решений

Как решать задачи по комбинаторике? Видеоуроки по комбинаторике Решение на заказ

Решебник задач по комбинаторике

Комбинаторика в Excel

Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:

1. Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
2. Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
3. Важен ли порядок элементов в выборке?
4. После выбора элемента мы его возвращаем назад?

Рис. 1. Дерево решений, какую формулу комбинаторики использовать

Скачать заметку в формате Word или pdf, примеры в формате Excel

Перестановки без повторений

Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.

Рис. 2. Перестановки (картинка взята здесь)

Если все n элементы разные, то число перестановок обозначается Pn от perturbation.

С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!

Например

По определению: 1! = 1; 0! = 1.

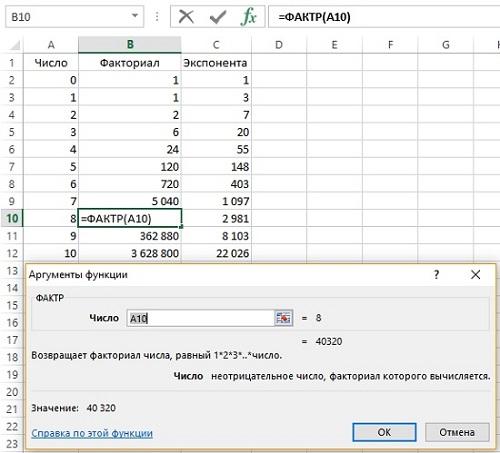
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).

Рис. 3. Расчет числа перестановок без повторений с помощью факториала

Перестановки с повторениями

Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)

В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.

Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?

Решение. Буквы а и н повторяются 2 раза, а буква м один раз.

Размещение без повторений

Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается  от arrangement.

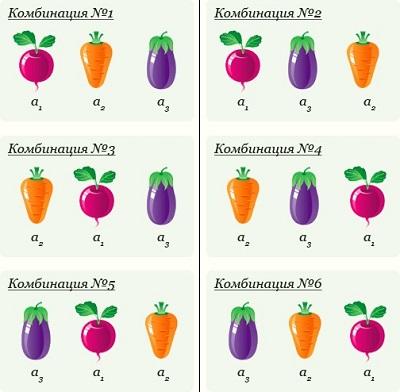
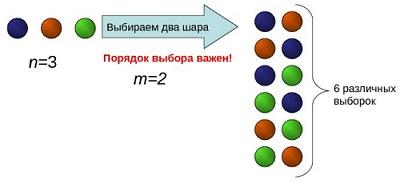
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

Рис. 5. Размещение без повторений (картинка из презентации)

Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).

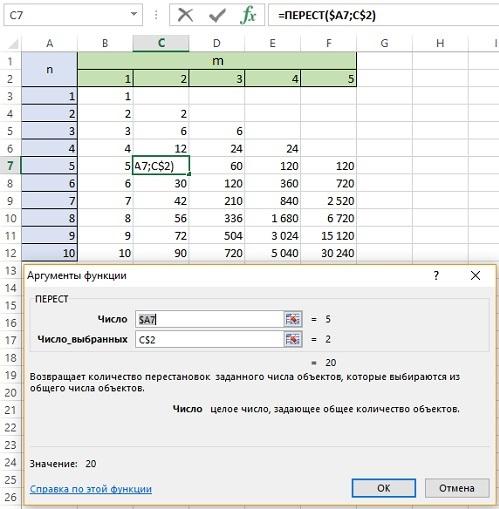
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)

Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу

Размещение с повторениями

Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.

Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями

В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:

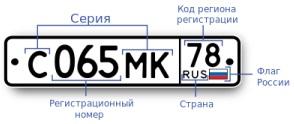
Задача. Сколько различных номеров можно составить в одном коде региона?

Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).

Рис. 8. Номер автомобиля

Решение. Можно воспользоваться формулой для размещения с повторениями:

Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.

Сочетания без повторений

Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).

Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

Рис. 9. Сочетания без повторений из 4 по 2

Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке

В Excel используется функция =ЧИСЛКОМБ(n;m).

Сочетания с повторениями

Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.

Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

Рис. 11. Сочетания с повторениями

В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами

В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.

Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.

Описание алгоритма генерации под калькулятором.

Алгоритм

Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания

1 2 3 Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.

1 2 4 Снова проверяется последний элемент, и опять он инкрементируется.

1 2 5 Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.

Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.

1 3 5 Затем — проверка для i = 2.

1 4 5 Потом наступает очередь i = 1.

(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,

2 3 52 4 53 4 5 — последнее сочетание, так как все его элементы равны n — m + i.

Did you find apk for android? You can find new Free Android Games and apps.

Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание

: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.

Отличие Сочетаний от Размещений

В отличие от

Размещений

следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор

Сочетаний

включается только одна из этих комбинаций. Очевидно, что для тех же n и k число

Сочетаний

всегда меньше чем число

Размещений

(так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.

Подсчет количества Сочетаний

Число всех

Сочетаний

из n элементов по k можно вычислить по формуле:

Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6}  равно 15=6!/(4!(6-4)!)

Примечание

:  Для

Сочетаний

из n элементов по k также используется и другая запись:

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .

Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.

Примечание

: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье

Сочетания с повторениями: Комбинаторика в MS EXCEL

Вывод всех комбинаций Сочетаний

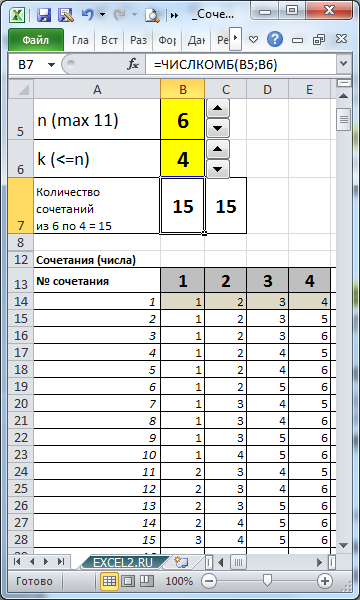
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью

элементов управления Счетчик

количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.

Задача

Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число

Сочетаний

7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.

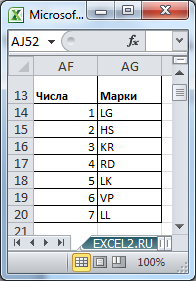
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках

В5

и

В6

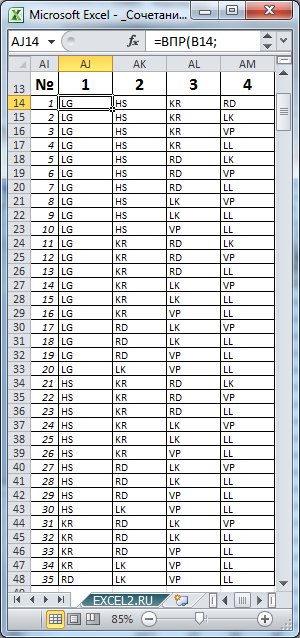
значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).

Примечание

: О Перестановках можно прочитать в статье

Перестановки без повторений: Комбинаторика в MS EXCEL

, а о Размещениях в статье

Размещения без повторений: Комбинаторика в MS EXCEL

.

Сочетания без повторений: Комбинаторика в EXCEL

history 2 февраля 2016 г.

Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).

Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов <1; 2; 3; 4; 5>:

(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)

Примечание : Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье — плохая идея.

Отличие Сочетаний от Размещений

В отличие от Размещений следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор Сочетаний включается только одна из этих комбинаций. Очевидно, что для тех же n и k число Сочетаний всегда меньше чем число Размещений (так как при размещениях порядок важен, а для сочетаний — нет), причем в k! раз.

Подсчет количества Сочетаний

Число всех Сочетаний из n элементов по k можно вычислить по формуле:

Например, количество 4-х элементных комбинаций из 6 чисел <1; 2; 3; 4; 5; 6>равно 15=6!/(4!(6-4)!)

Примечание : Для Сочетаний из n элементов по k также используется и другая запись:

В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции — COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .

Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.

Примечание : О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье Сочетания с повторениями: Комбинаторика в MS EXCEL

Вывод всех комбинаций Сочетаний

В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.

В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.

Задача

Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.

Нам нужно определить число Сочетаний 7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.

Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.

Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …

Выставив в ячейках В5 и В6 значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).

Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL .

Источник

Комбинаторика в Excel

Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.

Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!

Как выбрать формулу комбинаторики?

Нужно последовательно (см. схему выше) ответить на несколько вопросов:

• Сколько у нас есть объектов (число $n$)?
• Важен ли их порядок в комбинации?
• Могут ли встречаться повторяющиеся элементы?
• Нужно выбрать все элементы или только $klt n$?

Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:

Перестановки в Excel

Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

$$P_n=n!=1cdot 2cdot 3 cdot . cdot (n-1) cdot n$$

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.

Для нахождения числа перестановок в Excel можно использовать одну из двух функций:

=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$) , где $n$ — число переставляемых объектов.

Задача. Сколькими способами можно расставить 10 различных книг на одной полке?

Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Перестановки с повторениями в Excel

Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа. $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?

Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть

Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР() , которая находит факториал чисел и обычные действия ( умножение, деление ).

Задача. Сколько различных слов можно составить из букв слова «колокол»?

Вводим число букв $n=7$, а также $n_1=2$ (2 буквы «к»), $n_2=3$ (3 буквы «о»), $n_3=2$ (2 буквы «л»), и получаем ответ: 210 слов.

В режиме формул это выглядит так:

Размещения в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно

Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$) .

Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Размещения с повторениями в Excel

Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле

Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$) .

Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?

Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Сочетания в Excel

Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно

Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$) .

Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?

Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:

Сочетания с повторениями в Excel

Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле

Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$) .

Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?

Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Полезные ссылки

Для собственных расчетов скачайте файл: Комбинаторика в Excel.

Источник

Функция ЧИСЛКОМБ

В этой статье описаны синтаксис формулы и использование функции ЧИСЛКОМБ в Microsoft Excel.

Описание

Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.

Синтаксис

Аргументы функции ЧИСЛКОМБ описаны ниже.

Число — обязательный аргумент. Количество элементов.

Число_выбранных — обязательный аргумент. Количество элементов в каждой комбинации.

Замечания

Числовые аргументы усекаются до целых чисел.

Если хотя бы один из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.

Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.

Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы видеть все данные.

Возможные команды по два человека, которые могут быть сформированы из восьми кандидатов.

Источник

Сочетания с повторениями: Комбинаторика в EXCEL

history 2 февраля 2016 г.

Подсчитаем в MS EXCEL количество Сочетаний с повторениями из n по k (выборка с возвращением). Также с помощью формул выведем на лист соответствующие варианты Сочетаний (английский перевод термина: combinations with repetition).

Сочетания с повторениями (выборка с возвращением) — это Сочетание n объектов по k в предположении, что каждый объект может участвовать в сочетании несколько раз .

Примечание : О Сочетаниях без повторений (без возвращения элементов) можно прочитать в статье Сочетания без повторений: Комбинаторика в MS EXCEL

Например, из множества содержащего 3 (n) различных элемента ( a, b, c ) можно сформировать 6 =ФАКТР(3+2-1) / (ФАКТР (3-1) * ФАКТР (2)) упорядоченных наборов по 2 (k) элемента: аа, ab, ac, bb, bc, сс . В отличие от Сочетаний без повторений наборы аа, bb и сс допустимы. В отличие от Размещений наборы ac и ca считаются одинаковыми (порядок не важен).

В отличие от Сочетаний без повторений , k может быть меньше или больше n. Например, из множества содержащего 2 (n) различных элемента ( a, b ) можно сформировать 4 =ФАКТР(2+3-1) / (ФАКТР (2-1) * ФАКТР (3)) упорядоченных наборов по 3 (k) элемента (т.е. 4 сочетания с повторениями из 2 по 3): ааa, аab, abb, bbb.

В файле примера MS EXCEL приведен подсчет количества Сочетаний с повторениями и созданы формулы для вывода всех Сочетаний для заданных n и k.

Задавая с помощью элементов управления Счетчик количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания с повторениями.

Задача

В магазине платки 4-х цветов продаются вперемешку в огромной корзине. Женщина не может определиться с выбором, и поэтому решается довериться случаю – выбрать не глядя 3 платка. Определить число различных вариантов покупки 3-х платков.

Так как не важно, в какой последовательности женщина будет выбирать платки, то нам нужно определить число Сочетаний с повторениями покупки 3-х платков 4-х возможных цветов. Т.е. n=4, а k=3. Оказывается, что таких вариантов =(4+3-1)!/(4-1)!/3! равно 20.

Воспользуемся файлом примера , чтобы убедиться, что мы решили задачу правильно.

По аналогии с решением задачи в статье Размещения без повторений сопоставим произвольным образом 4-м различным цветам числовые значения: 1; 2; 3; 4.

Выставив в ячейках В5 и В6 значения 4 и 3 соответственно, определим все варианты размещений.

Примечание : О Перестановках можно прочитать в статье Перестановки без повторений: Комбинаторика в MS EXCEL , а о Размещениях в статье Размещения без повторений: Комбинаторика в MS EXCEL .

Источник

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---

---