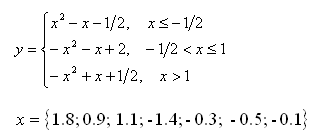Содержание
- Лабораторная работа № 4 «Работа с массивами»
- Сохранить документ.
- Работа с массивами функций в Excel
- Виды массивов функций Excel
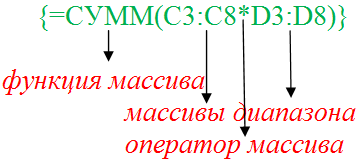
- Синтаксис формулы массива
- Функции работы с массивами Excel
Лабораторная работа № 4 «Работа с массивами»
Цель работы: Научиться работать с массивами. Вычислять определители матриц, произведения матриц и матрицы на вектор. Находить скалярное произведение векторов.
Вычислить скалярное произведения найденных векторов.
Вычислить определители матриц M и S.
Вычислить произведение матрицы S на обратную к ней S – 1 .
Выполнить проверку для найденных решений.
Сохранить документ.
A=(2, -1, 0); B=(-1, 4, -6); C=(1, -3, -5); D=(-2, -1, 0);

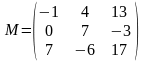
Для того чтобы найти координаты векторов, заданных координатами точек начала и конца вектора, занесем координаты этих точек в Excel.
Для этого создадим новый лист и назовем его «массивы». В ячейку А2 запишем «А», в ячейки В1:В3 заполним значения координат точки А. В ячейку D2 запишем «В», в ячейки Е1:Е3 заполним значения координат точки В. Аналогично для точки С заполняем ячейки: А6 и В5:В7, для точки D – D6, E5:E7. Получаем:
Примечание. Напомним, что для вычисления координат вектора, заданного координатами начала и конца, необходимо из координат конца вектора вычесть координаты его начала.
В ячейку А10 запишем «а», теперь выделим ячейки В9:В11 и в строку формул запишем:
Примечание. Напомним, что при таких комбинациях клавиш следует нажать и удерживать клавиши Ctrl+Shift одной рукой, а второй рукой нажать клавишу Enter. Настоятельно рекомендуем производить данную комбинацию двумя руками, а не одной. Если не получилось, установите текстовой курсор в строку формул и попробуйте нажать вышеуказанную комбинацию клавиш еще раз.
Если вы правильно нажали клавиши, то получите результат, а в строке формул увидите следующую запись:
Примечание. Отметим, что исправлять, удалять и переносить такие формулы можно только всем блоком. Для этого выделяем все (в нашем случае три) ячейки и удаляем. Если нужно формулу исправить, опять выделяем все ячейки и исправляем в строке формул, после чего нажимаем Ctrl+Sift+Enter.
Для вычисления вектора b в ячейку D10 набираем «b», далее выделяем ячейки Е9:Е11 и в строке формул набираем:
Для этого в ячейку А15 наберем «a*b=», а в ячейку В15 наберем формулу:
и нажмем Ctrl+Sift+Enter.
Отметим, что все массивы в Excel умножаются при помощи функции МУМНОЖ(), по принципу умножения матриц, т.е. строка на столбец. Поэтому если вы умножаете два вектора, то для правильного результата, необходимо умножать вектор-строку на вектор-столбец. Преобразовать же вектор-столбец в вектор-строку позволяет функция ТРАНСП().
Для получения скалярного произведения b*a в ячейку D15 наберем «b*a=», а в ячейку Е15:
Научимся вычислять произведение вектора на матрицу.
Для этого заполним заданные матрицы. В ячейку G2 запишем «М», а в ячейки H1:J3 заполним значения матрицы. Аналогично заполним значения матрицы S в ячейки G6 и H5:J7. Получим:
Теперь в ячейку L2 заполним «a*M=», выделим ячейки M2:O2 и в строке формул запишем:
Заметим, что для того чтобы умножить матрицу на вектор слева, необходимо, чтобы вектор был записан в виде вектора-строки, для этого мы и применяем функцию транспонирования. Отметим, что из алгебры вам должно быть известно, что результат представляет собой вектор-строку, что мы и получили.
Для умножения матрицы на вектор справа вектор должен иметь вид вектора-столбца; результат также имеет вид вектора-столбца.
В ячейку L6 запишем «M*b=», выделим ячейки M5:M7 и в строку формул наберем:
В результате получим:
Вычислим определители заданных матриц.
Для этого в ячейку L10 наберем «|M|=», а в ячейку М10 формулу:
Теперь в ячейку L14 наберем «|S|=», а в ячейку M14 формулу:
Так как определители наших матриц не равны нулю, то мы можем найти обратные матрицы M – 1 и S – 1 .
Для этого в ячейку G10 запишем «1/М», выделим ячейки H9:J11 и в строку формул поместим:
В ячейку G14 заполним «1/S», выделим ячейки H13:J15, в строку формул запишем:
и нажмем Ctrl+Sift+Enter.
Мы получим две обратные матрицы вида:
Для проверки правильности вычисления обратной матрицы найдем произведение матрицы М на ей обратную – если вычисления были произведены правильно, то мы получим единичную матрицу.
Для этого в ячейку G18 заполним «М*1/М=», выделим ячейки H17:J19 и в строке формул наберем:
Аналогично для матрицы S заполним ячейки G22 и H21:J23, получим:
Мы видим, что в некоторых ячейках, где ожидали получить нули, мы получили некие значения с записью Е-16 и Е-17. Такая запись означает, что число умножается на 10 – 16 или 10 – 17 , что можно считать числом близким к нулю. Как правило, в прикладных задачах значимыми являются лишь 2–3 знака после запятой, поэтому с точностью до двух знаков мы получили нули. Чтобы запись приобрела нормальный вид, зададим для данных ячеек числовой формат с двумя позициями после запятой. Для чего выделим ячейки H8:J14 и нажмем в меню ГлавнаяЧисло кнопку 
На закладке «Число» в поле выбора «Числовые форматы» выберем «Числовой», в поле «Число десятичных знаков» установим «2» и нажмем «ОК». В результате получим:
Как мы убедились, обратные матрицы вычислены верно, теперь можно их использовать для дальнейших вычислений.
Сначала решим первую систему, для этого в ячейку А21 заполним «х1=», выделим ячейки В20:В22 и в строку формул запишем:
Решение второй системы получим в ячейки Е20:Е22, в результате имеем:
Выполним проверку полученных решений.
Аналогично, для проверки решения второй системы выделим ячейки Е25:Е27 и в строку формул запишем:
В результате получим:
Как видим, здесь тоже необходимо задать формат ячеек. Зададим такой же формат, как и для произведений матриц, и получим:
Источник
Работа с массивами функций в Excel
Массив функций Excel позволяет решать сложные задачи в автоматическом режиме одновременно. Те, которые выполнить посредством обычных функций невозможно.
Фактически это группа функций, которые одновременно обрабатывают группу данных и сразу выдают результат. Рассмотрим подробно работу с массивами функций в Excel.
Виды массивов функций Excel
Массив – данные, объединенные в группу. В данном случае группой является массив функций в Excel. Любую таблицу, которую мы составим и заполним в Excel, можно назвать массивом. Пример:
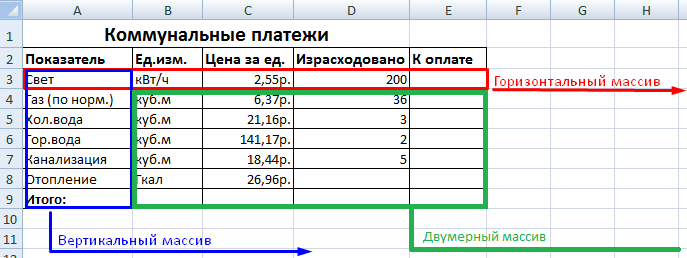
В зависимости от расположения элементов различают массивы:
- одномерные (данные находятся в ОДНОЙ строке или в ОДНОМ столбце);
- двумерные (НЕСКОЛЬКО строк и столбцов, матрица).
Одномерные массивы бывают:
- горизонтальными (данные – в строке);
- вертикальными (данные – в столбце).
Примечание. Двумерные массивы Excel могут занимать сразу несколько листов (это сотни и тысячи данных).
Формула массива – позволяет обработать данные из этого массива. Она может возвращать одно значение либо давать в результате массив (набор) значений.
С помощью формул массива реально:
- подсчитать количество знаков в определенном диапазоне;
- суммировать только те числа, которые соответствуют заданному условию;
- суммировать все n-ные значения в определенном диапазоне.
Когда мы используем формулы массива, Excel видит диапазон значений не как отдельные ячейки, а как единый блок данных.
Синтаксис формулы массива
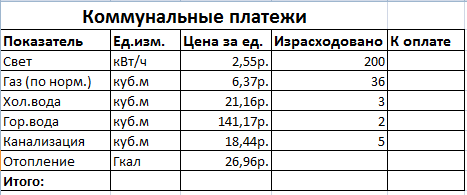
Используем формулу массива с диапазоном ячеек и с отдельной ячейкой. В первом случае найдем промежуточные итоги для столбца «К оплате». Во втором – итоговую сумму коммунальных платежей.
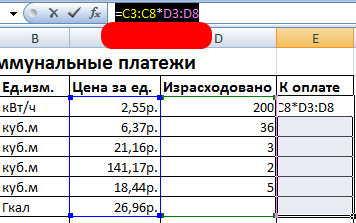
- Выделяем диапазон Е3:Е8.
- В строку формул вводим следующую формулу: =C3:C8*D3:D8.
- Нажимаем одновременно клавиши: Ctrl + Shift + Enter. Промежуточные итоги посчитаны:
Формула после нажатия Ctrl + Shift + Enter оказалась в фигурных скобках. Она подставилась автоматически в каждую ячейку выделенного диапазона.
Если попытаться изменить данные в какой-либо ячейке столбца «К оплате» — ничего не выйдет. Формула в массиве защищает значения диапазона от изменений. На экране появляется соответствующая запись:
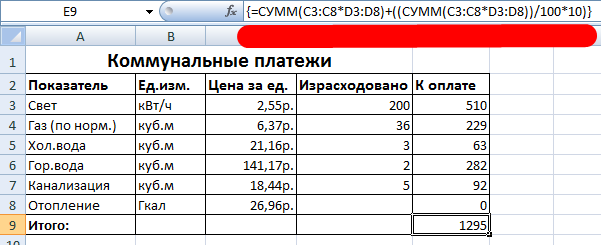
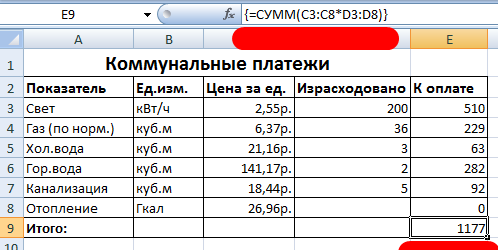
Рассмотрим другие примеры использования функций массива Excel – рассчитаем итоговую сумму коммунальных платежей с помощью одной формулы.
- Выделяем ячейку Е9 (напротив «Итого»).
- Вводим формулу вида: =СУММ(C3:C8*D3:D8).
- Нажимаем сочетание клавиш: Ctrl + Shift + Enter. Результат:
Формула массива в данном случае заменила две простые формулы. Это сокращенный вариант, вместивший всю необходимую информацию для решения сложной задачи.
Аргументы для функции – одномерные массивы. Формула просматривает каждый из них по отдельности, совершает заданные пользователем операции и генерирует единый результат.
Рассмотрим ее синтаксис:
Функции работы с массивами Excel
Предположим, в следующем месяце планируется увеличение коммунальных платежей на 10%. Если мы введем обычную формулу для итога =СУММ((C3:C8*D3:D8)+10%), то вряд ли получим ожидаемый результат. Нам нужно, чтобы каждый аргумент увеличился на 10%. Чтобы программа поняла это, мы используем функцию как массив.
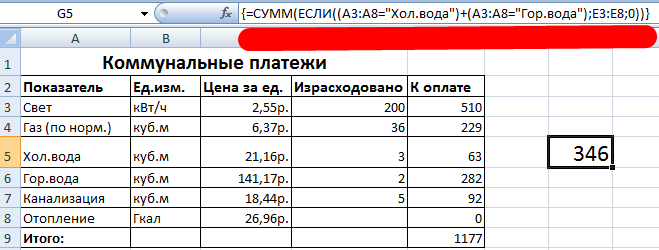
- Посмотрим, как работает оператор «И» в функции массива . Нам нужно узнать, сколько мы платим за воду, горячую и холодную. Функция: . Итого – 346 руб.
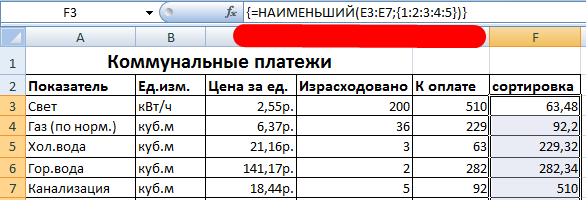
- Функция «Сортировки» в формуле массива. Отсортируем суммы к оплате в порядке возрастания. Для списка отсортированных данных создадим диапазон. Выделим его. В строке формул вводим . Жмем сочетание Ctrl + Shift + Enter.
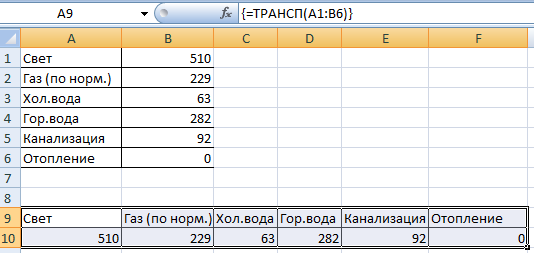
- Транспонированная матрица. Специальная функция Excel для работы с двумерными массивами. Функция «ТРАНСП» возвращает сразу несколько значений. Преобразует горизонтальную матрицу в вертикальную и наоборот. Выделяем диапазон ячеек, где количество строк = числу столбцов в таблице с исходными данными. А количество столбцов = числу строк в исходном массиве. Вводим формулу: . Получается «перевернутый» массив данных.
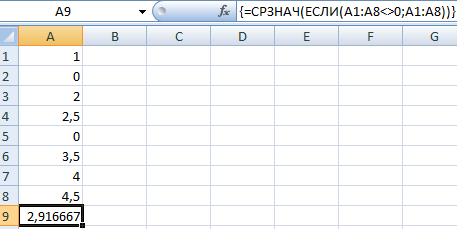
- Поиск среднего значения без учета нулей. Если мы воспользуемся стандартной функцией «СРЗНАЧ», то получим в результате «0». И это будет правильно. Поэтому вставляем в формулу дополнительное условие: 0;A1:A8))’ >. Получаем:
Распространенная ошибка при работе с массивами функций – НЕ нажатие кодового сочетания «Ctrl + Shift + Enter» (никогда не забывайте эту комбинацию клавиш). Это самое главное, что нужно запомнить при обработке больших объемов информации. Правильно введенная функция выполняет сложнейшие задачи.
Источник
В этой статье приводится контрольное задание по теме Одномерный массив MS EXCEL. За основу взято реальное Контрольное задание, которое предлагается решить по информатике студентам обучающимся на инженера-строителя. Желающие могут самостоятельно потренироваться и воспользоваться решением приведенном в
файле примера
.
Задание выложено «как есть», т.е. как оно было сформулировано преподавателем.
Комментарии по поводу решений — приветствуются.
Желающих поделиться собственными коллекциями заданий (в том числе и не решенных) ждут по адресу
creator@excel2.ru
(задачи, аналогичные рассмотренным здесь, с просьбой их решить, прошу не направлять — повторно их решать не интересно). При направлении задания сообщайте свою специальность.
Задание
Тема
: Одномерные массивы.
Цель работы
: приобретение навыков по созданию и преобразованию одномерных массивов в рабочей книге приложения
MS
Excel
.
Задача
:
Получить массив значений функции
y
на заданном массиве значений аргумента
x
. Оформить массивы
x
и
y
в виде таблиц.
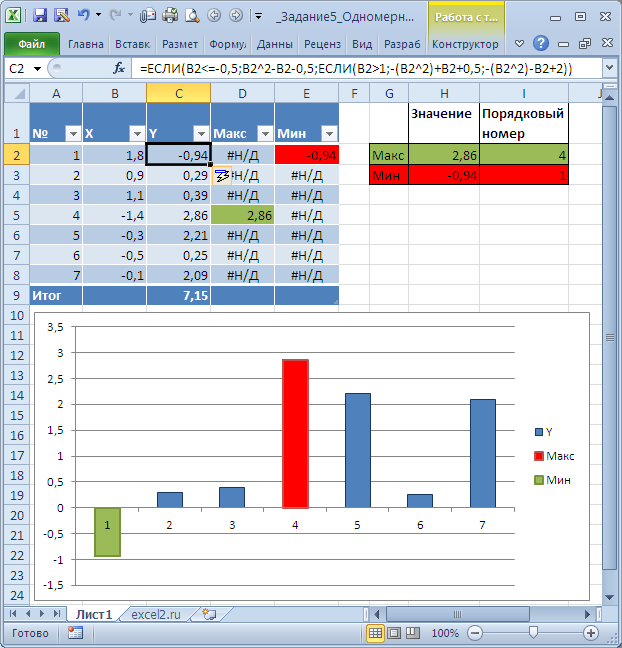
В массиве
y
найти сумму всех его элементов, а с помощью построения диаграммы наибольший и наименьший элементы массива и их порядковые номера.
Решение
Решение приведено в
файле примера
.
Цель работы: Научиться
работать с массивами. Вычислять
определители матриц, произведения
матриц и матрицы на вектор. Находить
скалярное произведение векторов.
Рекомендуемая литература:
[1–9].
Задание:
-
По заданным координатам точек A,
B, C,
D найти координаты
векторов a=AB
и b=CD. -
Вычислить скалярное произведения
найденных векторов. -
Найти следующие произведения векторов
на заданную матрицу M:
a*M
и M*b. -
Вычислить определители матриц M
и S. -
Найти обратные матрицы S–1
и М–1. -
Вычислить произведение матрицы S
на обратную к ней S–1. -
Найти решение системы линейных уравнений
Sх=b
и Мх=а. -
Выполнить проверку для найденных
решений. -
Сохранить документ.
Пример выполнения задания:
Задание:
A=(2, -1, 0); B=(-1, 4, -6); C=(1, -3, -5);
D=(-2, -1, 0);
;
.
-
Для того чтобы найти координаты векторов,
заданных координатами точек начала и
конца вектора, занесем координаты этих
точек в Excel.
Для этого создадим новый лист и назовем
его «массивы». В ячейку А2
запишем «А», в ячейки В1:В3 заполним
значения координат точки А. В ячейку
D2 запишем «В», в
ячейки Е1:Е3 заполним значения
координат точки В. Аналогично для
точки С заполняем ячейки: А6 и
В5:В7, для точки D
– D6, E5:E7.
Получаем:
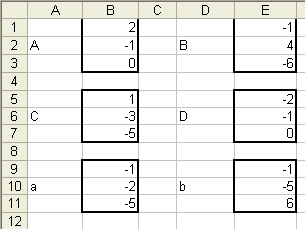
Примечание. Напомним, что для
вычисления координат вектора, заданного
координатами начала и конца, необходимо
из координат конца вектора вычесть
координаты его начала.
В ячейку А10 запишем «а», теперь
выделим ячейки В9:В11 и в строку формул
запишем:
=Е1:Е3-В1:В3
после чего нажмем Ctrl+Shift+Enter.
Примечание. Напомним, что при
таких комбинациях клавиш следует нажать
и удерживать клавиши Ctrl+Shift
одной рукой, а второй рукой нажать
клавишу Enter.
Настоятельно рекомендуем
производить данную комбинацию двумя
руками, а не одной. Если не
получилось, установите текстовой курсор
в строку формул и попробуйте нажать
вышеуказанную комбинацию клавиш еще
раз.
Если вы правильно нажали клавиши, то
получите результат, а в строке формул
увидите следующую запись:
{=E1:E3-B1:B3}
Примечание. Отметим, что
исправлять, удалять и переносить такие
формулы можно только всем блоком. Для
этого выделяем все (в нашем случае три)
ячейки и удаляем. Если нужно формулу
исправить, опять выделяем все ячейки и
исправляем в строке формул, после чего
нажимаем Ctrl+Sift+Enter.
Для вычисления вектора b
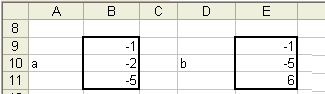
в ячейку D10 набираем
«b», далее выделяем ячейки
Е9:Е11 и в строке формул набираем:
=E5:E7-B5:B5
нажимаем Ctrl+Shift+Enter
и получаем:
-
Вычислим скалярное произведение a*b
и b*a.
Для этого в ячейку А15 наберем «a*b=»,
а в ячейку В15 наберем формулу:
=МУМНОЖ(ТРАНСП(В9:В11);Е9:Е11)
и нажмем
Ctrl+Sift+Enter.
Отметим, что все массивы в Excel
умножаются при помощи функции МУМНОЖ(),
по принципу умножения матриц, т.е. строка
на столбец. Поэтому если вы умножаете
два вектора, то для правильного результата,
необходимо умножать вектор-строку на
вектор-столбец. Преобразовать же
вектор-столбец в вектор-строку позволяет
функция ТРАНСП().
Для получения скалярного произведения
b*a
в ячейку D15 наберем
«b*a=», а в
ячейку Е15:
=МУМНОЖ(ТРАНСП(Е9:Е11);В9:В11)
нажмем Ctrl+Sift+Enter.
Получим результат:

-
Научимся вычислять произведение вектора
на матрицу.
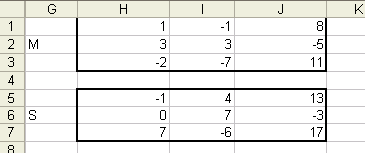
Для этого заполним заданные матрицы. В
ячейку G2 запишем
«М», а в ячейки H1:J3
заполним значения матрицы. Аналогично
заполним значения матрицы S
в ячейки G6 и H5:J7.
Получим:
Теперь в ячейку L2
заполним «a*M=»,
выделим ячейки M2:O2
и в строке формул запишем:
=МУМНОЖ(ТРАНСП(В9:В11);H1:J3)
нажмем Ctrl+Sift+Enter.
Заметим, что для того чтобы умножить
матрицу на вектор слева, необходимо,
чтобы вектор был записан в виде
вектора-строки, для этого мы и применяем
функцию транспонирования. Отметим, что
из алгебры вам должно быть известно,
что результат представляет собой
вектор-строку, что мы и получили.
Для умножения матрицы на вектор справа
вектор должен иметь вид вектора-столбца;
результат также имеет вид вектора-столбца.
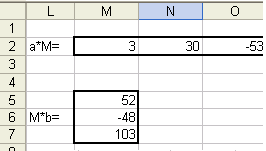
В ячейку L6 запишем
«M*b=», выделим
ячейки M5:M7
и в строку формул наберем:
=МУМНОЖ(H1:J3;Е9:Е11)
нажмем Ctrl+Sift+Enter.
В результате получим:
-
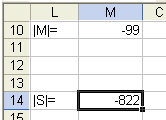
Вычислим определители заданных матриц.
Для этого в ячейку L10
наберем «|M|=», а в ячейку
М10 формулу:
=МОПРЕД(H1:J3)
и нажмем Ctrl+Sift+Enter.
Теперь в ячейку L14
наберем «|S|=», а в ячейку
M14 формулу:
=МОПРЕД(H5:J7)
и нажмем Ctrl+Sift+Enter.
Получим:
-
Так как определители наших матриц не
равны нулю, то мы можем найти обратные
матрицы M–1
и S–1.
Для этого в ячейку G10
запишем «1/М», выделим ячейки H9:J11
и в строку формул поместим:
=МОБР(H1:J3)
нажмем Ctrl+Sift+Enter.
В ячейку G14 заполним
«1/S», выделим ячейки
H13:J15,
в строку формул запишем:
=МОБР(H5:J7)
и нажмем
Ctrl+Sift+Enter.
Мы получим две обратные матрицы вида:
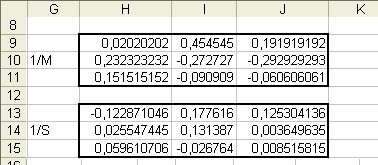
-
Для проверки
правильности вычисления обратной
матрицы найдем произведение матрицы
М
на ей обратную
– если вычисления были произведены
правильно, то мы получим единичную
матрицу.
Для этого в ячейку G18
заполним «М*1/М=», выделим ячейки H17:J19
и в строке формул наберем:
=МУМНОЖ(H1:J3;H9:J11)
нажмем Ctrl+Sift+Enter.
Аналогично для матрицы S
заполним ячейки G22
и H21:J23,
получим:
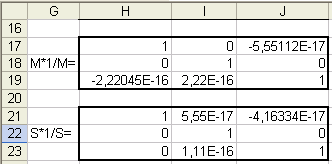
Мы видим, что в некоторых ячейках, где
ожидали получить нули, мы получили некие
значения с записью Е-16 и Е-17. Такая запись
означает, что число умножается на
10–16
или 10–17, что
можно считать числом близким к нулю.
Как правило, в прикладных задачах
значимыми являются лишь 2–3 знака после
запятой, поэтому с точностью до двух
знаков мы получили нули. Чтобы запись
приобрела нормальный вид, зададим для
данных ячеек числовой формат с двумя
позициями после запятой. Для чего выделим
ячейки H8:J14
и нажмем в меню ГлавнаяЧисло
кнопку
,
получим окно:
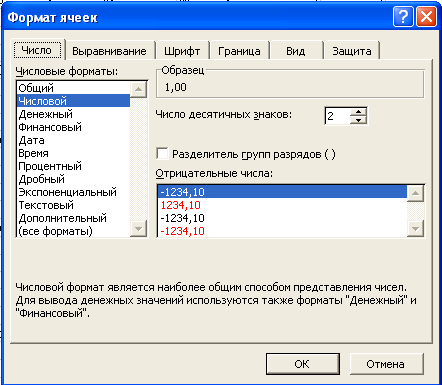
На закладке «Число» в поле выбора
«Числовые форматы» выберем «Числовой»,
в поле «Число десятичных знаков»
установим «2» и нажмем «ОК».
В результате получим:
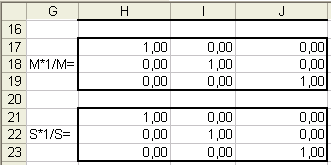
Как мы убедились, обратные матрицы
вычислены верно, теперь можно их
использовать для дальнейших вычислений.
-
Найдем решение систем линейных уравнений
М*х1=а и S*x2=b.
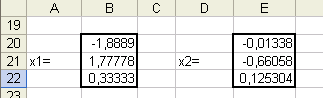
Сначала решим первую систему, для этого
в ячейку А21 заполним «х1=», выделим
ячейки В20:В22 и в строку формул
запишем:
=МУМНОЖ(H9:J11;B9:B11)
нажмем Ctrl+Sift+Enter.
Решение второй системы получим в ячейки
Е20:Е22, в результате имеем:
-
Выполним проверку полученных решений.
Для этого вычислим следующие значения:
|M*x1-a|
и |S*x2-b|.
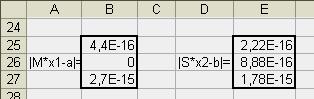
В ячейку А26 заполним «|M*x1-a|=»,
выделим ячейки В25:В27 и в строку
формул запишем:
=ABS(МУМНОЖ(H1:J3;B20:B22)-B9:B11)
нажмем Ctrl+Sift+Enter.
Аналогично, для проверки решения второй
системы выделим ячейки Е25:Е27 и в
строку формул запишем:
=ABS(МУМНОЖ(H5:J7;Е20:Е22)-Е9:Е11)
нажмем Ctrl+Sift+Enter.
В результате получим:
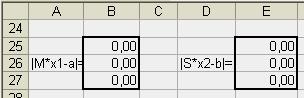
Как видим, здесь тоже необходимо задать
формат ячеек. Зададим такой же формат,
как и для произведений матриц, и получим:
-
Остается только сохранить файл.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Массив функций Excel позволяет решать сложные задачи в автоматическом режиме одновременно. Те, которые выполнить посредством обычных функций невозможно.
Фактически это группа функций, которые одновременно обрабатывают группу данных и сразу выдают результат. Рассмотрим подробно работу с массивами функций в Excel.
Виды массивов функций Excel
Массив – данные, объединенные в группу. В данном случае группой является массив функций в Excel. Любую таблицу, которую мы составим и заполним в Excel, можно назвать массивом. Пример:
В зависимости от расположения элементов различают массивы:
- одномерные (данные находятся в ОДНОЙ строке или в ОДНОМ столбце);
- двумерные (НЕСКОЛЬКО строк и столбцов, матрица).
Одномерные массивы бывают:
- горизонтальными (данные – в строке);
- вертикальными (данные – в столбце).
Примечание. Двумерные массивы Excel могут занимать сразу несколько листов (это сотни и тысячи данных).
Формула массива – позволяет обработать данные из этого массива. Она может возвращать одно значение либо давать в результате массив (набор) значений.
С помощью формул массива реально:
- подсчитать количество знаков в определенном диапазоне;
- суммировать только те числа, которые соответствуют заданному условию;
- суммировать все n-ные значения в определенном диапазоне.
Когда мы используем формулы массива, Excel видит диапазон значений не как отдельные ячейки, а как единый блок данных.
Синтаксис формулы массива
Используем формулу массива с диапазоном ячеек и с отдельной ячейкой. В первом случае найдем промежуточные итоги для столбца «К оплате». Во втором – итоговую сумму коммунальных платежей.
- Выделяем диапазон Е3:Е8.
- В строку формул вводим следующую формулу: =C3:C8*D3:D8.
- Нажимаем одновременно клавиши: Ctrl + Shift + Enter. Промежуточные итоги посчитаны:
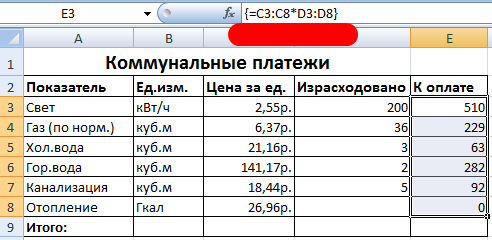
Формула после нажатия Ctrl + Shift + Enter оказалась в фигурных скобках. Она подставилась автоматически в каждую ячейку выделенного диапазона.
Если попытаться изменить данные в какой-либо ячейке столбца «К оплате» — ничего не выйдет. Формула в массиве защищает значения диапазона от изменений. На экране появляется соответствующая запись:
Рассмотрим другие примеры использования функций массива Excel – рассчитаем итоговую сумму коммунальных платежей с помощью одной формулы.
- Выделяем ячейку Е9 (напротив «Итого»).
- Вводим формулу вида: =СУММ(C3:C8*D3:D8).
- Нажимаем сочетание клавиш: Ctrl + Shift + Enter. Результат:
Формула массива в данном случае заменила две простые формулы. Это сокращенный вариант, вместивший всю необходимую информацию для решения сложной задачи.
Аргументы для функции – одномерные массивы. Формула просматривает каждый из них по отдельности, совершает заданные пользователем операции и генерирует единый результат.
Рассмотрим ее синтаксис:
Функции работы с массивами Excel
Предположим, в следующем месяце планируется увеличение коммунальных платежей на 10%. Если мы введем обычную формулу для итога =СУММ((C3:C8*D3:D8)+10%), то вряд ли получим ожидаемый результат. Нам нужно, чтобы каждый аргумент увеличился на 10%. Чтобы программа поняла это, мы используем функцию как массив.
- Посмотрим, как работает оператор «И» в функции массива. Нам нужно узнать, сколько мы платим за воду, горячую и холодную. Функция: . Итого – 346 руб.
- Функция «Сортировки» в формуле массива. Отсортируем суммы к оплате в порядке возрастания. Для списка отсортированных данных создадим диапазон. Выделим его. В строке формул вводим . Жмем сочетание Ctrl + Shift + Enter.
- Транспонированная матрица. Специальная функция Excel для работы с двумерными массивами. Функция «ТРАНСП» возвращает сразу несколько значений. Преобразует горизонтальную матрицу в вертикальную и наоборот. Выделяем диапазон ячеек, где количество строк = числу столбцов в таблице с исходными данными. А количество столбцов = числу строк в исходном массиве. Вводим формулу: . Получается «перевернутый» массив данных.
- Поиск среднего значения без учета нулей. Если мы воспользуемся стандартной функцией «СРЗНАЧ», то получим в результате «0». И это будет правильно. Поэтому вставляем в формулу дополнительное условие: . Получаем:
Скачать примеры массива функций
Распространенная ошибка при работе с массивами функций – НЕ нажатие кодового сочетания «Ctrl + Shift + Enter» (никогда не забывайте эту комбинацию клавиш). Это самое главное, что нужно запомнить при обработке больших объемов информации. Правильно введенная функция выполняет сложнейшие задачи.
Время на прочтение
16 мин
Количество просмотров 236K
Добрый день, уважаемые хаброжители!
Время от времени некоторым (а может и более, чем некоторым) из нас приходится сталкиваться с задачами по обработке небольших массивов данных, начиная от составления и анализа домашнего бюджета и заканчивая какими-либо расчетами по работе, учебе и т.д. Пожалуй, наиболее подходящим инструментом для этого является Microsoft Excel (или возможно иные его аналоги, но они менее распространены).
Поиск выдал мне всего одну статью на Хабре по схожей тематике — «Талмуд по формулам в Google SpreadSheet». В ней дано хорошее описание базовых вещей для работы в excel (хотя он и не 100% про сам excel).
Таким образом, накопив определенный пул запросов/задач, появилась идея их типизировать и предложить возможные решения (пусть не все возможные, но быстро дающие результат).
Речь пойдет о решении наиболее распространенных задач, с которыми сталкиваются пользователи.
Описание решений построено следующим образом – дается кейс, содержащий исходное задание, которое постепенно усложняется, к каждому шагу дано развернутое решение с пояснениями. Наименования функций будут даваться на русском языке, но в скобках при первом упоминании будет приводиться оригинальное наименование на английском языке (т.к. по опыту у подавляющего большинства пользователей установлена русскоязычная версия).
Кейс_1: Логические функции и функции поиска совпадений
«У меня есть набор значений в табличке и необходимо что бы при выполнении определенного условия/набора условий выводилось определенное значение» (с) Пользователь
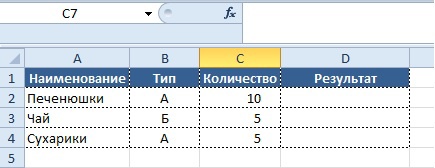
Данные, как правило, представлены в табличной форме:
Условие:
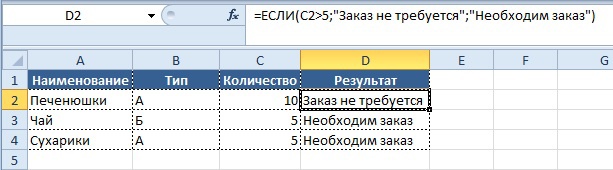
- если значение в столбце «Количество» больше 5,
- то нужно вывести в колонке «Результат» значение «Заказ не требуется»,
В этом нам поможет формула «ЕСЛИ» (IF), которая относится к логическим формулам и может выдавать в решении любые значения, которые мы заранее записываем в формуле. Обращаю внимание, что любые текстовые значения записываются, используя кавычки.
Синтаксис формулы следующий:
ЕСЛИ(лог_выражение, [значение_если_истина], [значение_если_ложь])
- Лог_выражение — выражение, дающее в результате значение ИСТИНА или ЛОЖЬ.
- Значение_если_истина — значение, которое выводится, если логическое выражение истинно
- Значение_если_ложь — значение, которое выводится, если логическое выражение ложно
Синтаксис формулы для решения:
Вывод результата в ячейку D2:
=ЕСЛИ(C5>5;«Заказ не требуется»;«Необходим заказ»)
На выходе получаем результат:
Бывает, что условие носит более сложный характер, например выполнение 2-х и более условий:
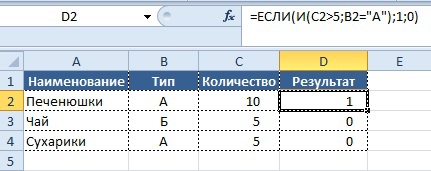
- если значение в столбце «Количество» больше 5, а значение в колонке «Тип» равно «А»
- то нужно вывести в колонке «Результат» значение «1», в обратном случае «0».
В данном случае мы уже не можем ограничиться использованием одной только формулы «ЕСЛИ», необходимо добавить в ее синтаксис другую формулу. И это будет еще одна логическая формула «И» (AND).
Синтаксис формулы следующий:
И(логическое_значение1, [логическое_значение2], …)
- Логическое_значение1-2 и т.д. — проверяемое условие, вычисление которого дает значение ИСТИНА или ЛОЖЬ
Синтаксис решения будет следующим:
Вывод результата в ячейку D2:
=ЕСЛИ(И(C2>5;B2=«А»);1;0)
Таким образом, используя сочетание 2-х формул, мы находим решение нашей задачи и получаем результат:
Попробуем усложнить задачу – новое условие:
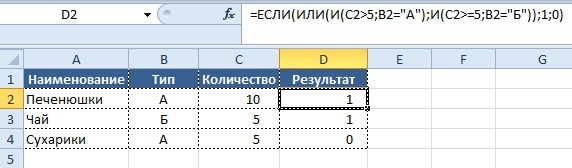
- если значение в столбце «Количество» равно 10, а значение в колонке «Тип» равно «А»
- или же значение в столбце «Количество» больше или равно 5, а значение «Тип» равен «Б»
- то нужно вывести в колонке «Результат» значение «1», в обратном случае «0».
Синтаксис решения будет следующим:
Вывод результата в ячейку D2:
=ЕСЛИ(ИЛИ(И(C2=10;B2=«А»); И(C2>=5;B2=«Б»));1;0)
Как видно из записи, в формулу «ЕСЛИ» включено одно условие «ИЛИ» (OR) и два условия с использованием формулы «И», включенных в него. Если хотя бы одно из условий 2-го уровня имеет значение «ИСТИНА», то в колонку «Результат» будет выведен результат «1», в противном случае будет «0».
Результат:
Теперь перейдем к следующей ситуации:
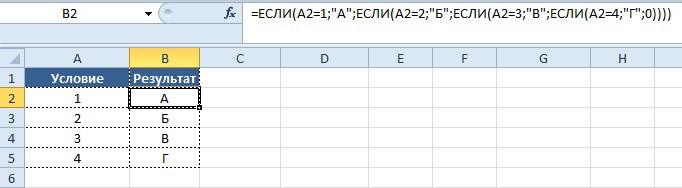
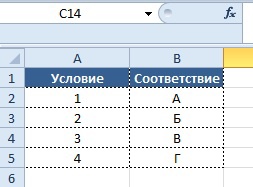
Представим, что в зависимости от значения в столбце «Условие» должно выводиться определенное условие в столбце «Результат», ниже приведено соответствие значений и результата.
Условие:
- 1 = А
- 2 = Б
- 3 = В
- 4 = Г
При решении задачи с помощью функции «ЕСЛИ», синтаксис будет следующим:
Вывод результата в ячейку B2:
=ЕСЛИ(A2=1;«А»; ЕСЛИ(A2=2;«Б»; ЕСЛИ(A2=3;«В»; ЕСЛИ(A2=4;«Г»;0))))
Результат:
Как видно, написание подобной формулы не только не очень удобно и громоздко, но и может занять некоторое время на ее редактирование у неопытного пользователя в случае ошибки.
Минус подобного подхода в том, что он применим для небольшого количества условий, ведь, все их придется набирать вручную и «раздувать» нашу формулу до больших размеров, однако подход отличает полная «всеядность» к значениям и универсальность использования.
Альтернативное решение_1:
Использование формулы «ВЫБОР» (CHOOSE),
Синтаксис функции:
ВЫБОР(номер_индекса, значение1, [значение2], …)
- Номер_индекса — номер выбираемого аргумента-значения. Номер индекса должен быть числом от 1 до 254, формулой или ссылкой на ячейку, содержащую число в диапазоне от 1 до 254.
- Значение1, значение2,… — значение от 1 до 254 аргументов-значений, из которых функция «ВЫБОР», используя номер индекса, выбирает значение или выполняемое действие. Аргументы могут быть числами, ссылками на ячейки, определенными именами, формулами, функциями или текстом.
При ее использовании, мы сразу заносим результаты условий в зависимости от указанных значений.
Условие:
- 1 = А
- 2 = Б
- 3 = В
- 4 = Г
Синтаксис формулы:
=ВЫБОР(A2;«А»;«Б»;«В»;«Г»)
Результат аналогичен решению с цепочкой функций «ЕСЛИ» выше.
При применении этой формулы существуют следующие ограничения:
В ячейку «А2» (номер индекса) могут быть указаны только цифры, а значения результата будут выводиться в порядке возрастания от 1 до 254 значений.
Иными словами, функция будет работать только если в ячейке «А2» указаны цифры от 1 до 254 в порядке возрастания и это накладывает определенные ограничения при использовании этой формулы.
Т.е. если мы захотим, что бы значение «Г» выводилось при указании числа 5,
- 1 = А
- 2 = Б
- 3 = В
- 5 = Г
то формула будет иметь следующий синтаксис:
Вывод результата в ячейку B2:
=ВЫБОР(A31;«А»;«Б»;«В»;;«Г»)
Как видно, значение «4» в формуле нам приходится оставить пустым и перенести результат «Г» на порядковый номер «5».
Альтернативное решение_2:
Вот мы и подошли к одной из самых популярных функций Excel, овладение которой автоматически превращает любого офисного работника в «опытного пользователя excel» /sarcasm/.
Синтаксис формулы:
ВПР(искомое_значение, таблица, номер_столбца, [интервальный_просмотр])
- Искомое_значение – значение, поиск которого осуществляется функцией.
- Таблица – диапазон ячеек, содержащий данные. Именно в этих ячейках будет происходить поиск. Значения могут быть текстовыми, числовыми или логическими.
- Номер_столбца — номер столбца в аргументе «Таблица», из которого будет выводиться значение в случае совпадения. Важно понимать, что отсчет столбцов происходит не по общей сетке листа (A.B,C,D и т.д.), а внутри массива, указанного в аргументе «Таблица».
- Интервальный_просмотр — определяет, какое совпадение должна найти функция — точное или приблизительное.
Важно: функция «ВПР» ищет совпадение только по первой уникальной записи, если искомое_значение присутствует в аргументе «Таблица» несколько раз и имеет разные значения, то функция «ВПР» найдет только самое ПЕРВОЕ совпадение, результаты по всем остальным совпадениям показаны не будутИспользование формулы «ВПР» (VLOOKUP) связано с еще одним подходом в работе с данными, а именно с формированием «справочников».
Суть подхода в создании «справочника» соответствия аргумента «Искомое_значение» определенному результату, отдельно от основного массива, в котором прописываются условия и соответствующие им значения:
Затем в рабочей части таблицы уже прописывается формула со ссылкой на справочник, заполненный ранее. Т.е. в справочнике в столбце «D» происходит поиск значения из столбца «А» и при нахождении соответствия выводится значение из столбца «Е» в столбец «В».
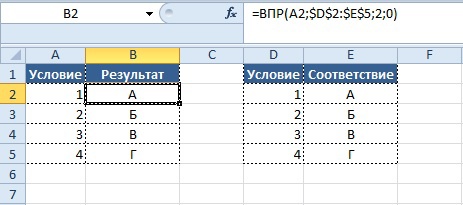
Синтаксис формулы:
Вывод результата в ячейку B2:
=ВПР(A2;$D$2:$E$5;2;0)
Результат:
Теперь представим ситуацию, когда необходимо подтянуть данные в одну таблицу из другой, при этом таблицы не идентичны. См. пример ниже
Видно, что строки в столбцах «Продукт» обеих таблиц не совпадают, однако, это не является препятствием для использования функции «ВПР».
Вывод результата в ячейку B2:
=ВПР($A3;$H$3:$M$6;2;0)
Но при решении сталкиваемся с новой проблемой – при «протягивании» написанной нами формулы вправо от столбца «В» до столбца «Е», нам придется вручную заменять аргумент «номер_столбца». Дело это трудоемкое и неблагодарное, потому, на помощь нам приходит другая функция — «СТОЛБЕЦ» (COLUMN).
Синтаксис функции:
СТОЛБЕЦ([ссылка])
- Ссылка — ячейка или диапазон ячеек, для которых требуется возвратить номер столбца.
Если использовать запись типа:
=СТОЛБЕЦ()
то функция выведет номер текущего столбца (в ячейке которого написана формула).
В результате получается число, которое можно использовать в функции «ВПР», чем мы и воспользуемся и получаем следующую запись формулы:
Вывод результата в ячейку B2:
=ВПР($A3;$H$3:$M$6; СТОЛБЕЦ();0)
Функция «СТОЛБЕЦ» определит номер текущего столбца, который будет использоваться аргументом «Номер_столбца» для определения номера столбца поиска в справочнике.
Кроме того, можно использовать конструкцию:
=СТОЛБЕЦ()-1
Вместо числа «1» можно использовать любое число (а также не только вычитать его, но и прибавлять к полученному значению), для получения желаемого результата, если нет желания ссылаться на определенную ячейку в столбце с нужным нам номером.
Получившийся результат:
Продолжаем развивать тему и усложняем условие: представим, что у нас есть два справочника с разными данными по продуктам и необходимо вывести в таблицу с результатом значения в зависимости от того, какой тип справочника указан в колонке «Справочник»
Условие:
- Если в столбце «Справочник» указано число 1, данные должны тянуться из таблицы «Справочник_1», если число 2, то из таблицы «Справочник_2» в соответствии с указанным месяцем
Вариант решения, который сразу приходит на ум, следующий:
Вывод результата в ячейку C3:
=ЕСЛИ($B3=1; ВПР($A3;$G$3:$I$6; СТОЛБЕЦ()-1;0); ВПР($A3;$K$3:$M$6; СТОЛБЕЦ()-1;0))
Плюсы: наименование справочника может быть любым (текст, цифры и их сочетание), минусы – плохо подходит, если вариантов более 3-х.
Если же номера справочников всегда представляют собой числа, имеет смысл использовать следующее решение:
Вывод результата в ячейку C3:
=ВПР($A3; ВЫБОР($B3;$G$3:$I$6;$K$3:$M$6); СТОЛБЕЦ()-1;0)
Плюсы: формула может включать до 254 наименований справочников, минусы – их наименование должно быть строго числовым.
Результат для формулы с использованием функции «ВЫБОР»:
Бонус: ВПР по двум и более признакам в аргументе «искомое_значение».
Условие:
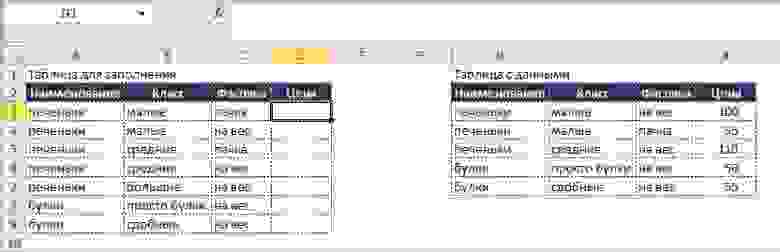
- Представим, что у нас как всегда есть массив данных в табличной форме (если нет, то мы к нему приводим данные), из массива по определенным признакам необходимо получить значения и поместить их в другую табличную форму.
Обе таблицы приведены ниже:
Как видно из табличных форм, каждая позиция имеет не только наименование (которое не является уникальным), но также и относится к определенному классу и имеет свой вариант фасовки.
Используя сочетание имени и класса и фасовки, мы можем создать новый признак, для этого в таблице с данными создаем дополнительный столбец «Доп.признак», который заполняем при помощи следующей формулы:
=H3&»_»&I3&»_»&J3
Используя символ «&», объединяем три признака в один (разделитель между словами может быть любым, как и не быть вовсе, главное использовать аналогичное правило и для поиска)
Аналогом формулы может быть функция «СЦЕПИТЬ» (CONCATENATE), в этом случае она будет выглядеть следующим образом:
=СЦЕПИТЬ(H3;»_»;I3;»_»;J3)
После того, как дополнительный признак создан для каждой записи в таблице с данными, приступаем к написанию функции поиска по этому признаку, которая будет иметь вид:
Вывод результата в ячейку D3:
=ЕСЛИОШИБКА(ВПР(A2&»_»&B2&»_»&C2;$G$2:$K$6;5;0);0)
В функции «ВПР» в качестве аргумента «искомое_значение» используем все ту же связку трех признаков (наименование_класс_фасовка), но берем ее уже в таблице для заполнения и заносим непосредственно в аргумент (как вариант, можно было бы выделить значение для аргумента в дополнительный столбец в таблице для заполнения, но это действие будет излишним).
Напоминаю, что использование функции «ЕСЛИОШИБКА» (IFERROR) необходимо, если искомое значение так и не будет найдено, и функция «ВПР» выведет нам значение «#Н/Д» (об этом ниже).
Результат на картинке ниже:
Данный прием можно использовать и для большего количества признаков, единственное условие – уникальность получаемых комбинаций, если она не соблюдается, то результат будет некорректным.
Кейс_3 Поиск значения в массиве, или когда ВПР не в силах нам помочь
Рассмотрим ситуацию, когда необходимо понять, есть ли в массиве ячеек нужные нам значения.
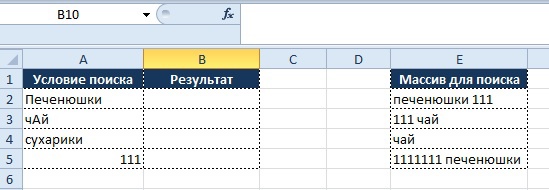
Задача:
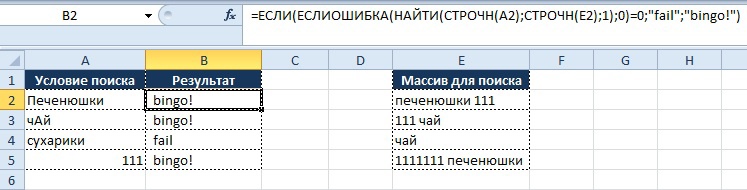
- в столбце «Условие поиска» указано значение и необходимо определить, присутствует ли оно в столбце «Массив для поиска»
Визуально все выглядит в следующем виде:
Как мы видим, функция «ВПР» тут бессильна, т.к. мы ищем не точное совпадение, а именно наличие в ячейке нужного нам значения.
Для решения задачи необходимо использовать комбинацию нескольких функций, а именно:
«ЕСЛИ»
«ЕСЛИОШИБКА»
«СТРОЧН»
«НАЙТИ»
По порядку обо всех, «ЕСЛИ» мы уже разобрали ранее, потому перейдем к функции «ЕСЛИОШИБКА» (IFERROR)
ЕСЛИОШИБКА(значение, значение_при_ошибке)
- Значение — аргумент, проверяемый на возникновение ошибок.
- Значение_при_ошибке — значение, возвращаемое при ошибке при вычислении по формуле. Возможны следующие типы ошибок: #Н/Д, #ЗНАЧ!, #ССЫЛКА!, #ДЕЛ/0!, #ЧИСЛО!, #ИМЯ? и #ПУСТО!.
Важно: данная формула практически всегда обязательна при работе с массивами информации и справочниками, т.к. зачастую бывает, что искомое значение не находится в справочнике и в этом случае функция возвращает ошибку. Если же в ячейке выводится ошибка и ячейка участвует, например, в вычислении, то оно так же произойдет с ошибкой. Плюс ко всему, ячейкам, где формула возвратила ошибку можно присваивать различные значения, которые облегчают их статистическую обработку. Также, в случае ошибки можно выполнять другие функции, что очень удобно при работе с массивами и позволяет строить формулы с учетом довольно разветвленных условий.
«СТРОЧН» (LOWER)
СТРОЧН(текст)
- Текст — текст, преобразуемый в нижний регистр.
Важно: функция «СТРОЧН» не заменяет знаки, не являющиеся буквами.
Роль в формуле: поскольку функция «НАЙТИ» (FIND) осуществляет поиск и учетом регистра текста, то необходимо привести весь текст к одному регистру, в противном случае «чАй» будет не равно «чай» и т.д. Это актуально, если значение регистра не является условием поиска и отбора значений, в противном случае формулу «СТРОЧН» можно не использовать, так поиск будет более точным.
Теперь подробнее о синтаксисе функции «НАЙТИ» (FIND).
НАЙТИ(искомый_текст, просматриваемый_текст, [нач_позиция])
- Искомый_текст — текст, который необходимо найти.
- Просматриваемый_текст — текст, в котором нужно найти искомый текст.
- Нач_позиция — знак, с которого нужно начать поиск. Первый знак в тексте «просматриваемый_текст» имеет номер 1. Если номер не указан, он по умолчанию считается равным 1.
Синтаксис формулы-решения будет иметь вид:
Вывод результата в ячейку B2:
=ЕСЛИ(ЕСЛИОШИБКА(НАЙТИ(СТРОЧН(A2); СТРОЧН(E2);1);0)=0;«fail»;«bingo!»)
Разберем логику формулы по действиям:
- СТРОЧН(A2) – преобразует аргумент «Искомый_текст» в ячейке в А2 в текст с нижним регистром
- Функция «НАЙТИ» начинает поиск преобразованного аргумента «Искомый_текст» в массиве «Просматриваемый_текст», который преобразовывается функцией «СТРОЧН(E2)», также в текст с нижним регистром.
- В случае если, функция находит совпадение, т.е. возвращает порядковый номер первого символа совпадающего слова/значения, срабатывает условие ИСТИНА в формуле «ЕСЛИ», т.к. полученное значение не равно нулю. Как результат, в столбце «Результат» будет выведено значение «Bingo!»
- Если же, функция не находит совпадение т.е. порядковый номер первого символа совпадающего слова/значения не указывается и вместо значения возвращается ошибка, срабатывает условие, заложенное в формулу «ЕСЛИОШИБКА» и возвращается значение равное «0», что соответствует условию ЛОЖЬ в формуле «ЕСЛИ», т.к. полученное значение равно «0». Как результат, в столбце «Результат» будет выведено значение «fail».
Как видно из рисунка выше, благодаря функциям «СТРОЧН» и «НАЙТИ» мы находим искомые значения вне зависимости от регистра символов, и места нахождения в ячейке, но необходимо обратить внимание на строку 5.
Условие поиска задано как «111», но в массиве поиска указано значение «1111111 печенюшки», однако формула выдает результат «Bingo!». Это происходит потому, что значение «111» входит в ряд значений «1111111», как следствие находится совпадение. В обратном случае данное условие не сработает.
Кейс_4 Поиск значения в массиве по нескольким условиям, или когда ВПР тем более не в силах нам помочь
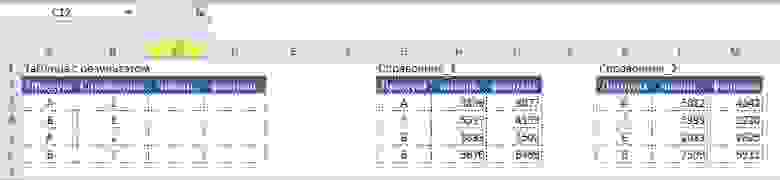
Представим ситуацию, когда необходимо найти значение из «Таблица с результатом» в двумерном массиве «Справочник» по нескольким условиям, а именно по значению «Наименование» и «Месяц».
Табличная форма задания будет иметь следующий вид:
Условие:
- В таблицу с результатом необходимо подтянуть данные в соответствии с совпадением условий «Наименование» и «Месяц».
Для решения подобной задачи подойдет комбинация функций «ИНДЕКС» и «ПОИСКПОЗ»
Синтаксис функции «ИНДЕКС» (INDEX)
ИНДЕКС(массив, номер_строки, [номер_столбца])
- Массив — диапазон ячеек, из которого будут показываться значения в случае совпадения условий их поиска.
- Если массив содержит только одну строку или один столбец, аргумент «номер_строки» или «номер_столбца» соответственно не является обязательным.
- Если массив занимает больше одной строки и одного столбца, а из аргументов «номер_строки» и «номер_столбца» задан только один, то функция «ИНДЕКС» возвращает массив, состоящий из целой строки или целого столбца аргумента «массив».
- Номер_строки — номер строки в массиве, из которой требуется возвратить значение.
- Номер_столбца — номер столбца в массиве, из которого требуется возвратить значение.
Иными словами функция возвращает из указанного массива в аргументе «Массив» значение, которое находится на пересечении координат, указанных в аргументах «Номер_строки» и «Номер_столбца».
Синтаксис функции «ПОИСКПОЗ» (MATCH)
ПОИСКПОЗ(искомое_значение, просматриваемый_массив, [тип_сопоставления])
- Искомое_значение — значение, которое сопоставляется со значениями в аргументе просматриваемый_массив. Аргумент искомое_значение может быть значением (числом, текстом или логическим значением) или ссылкой на ячейку, содержащую такое значение.
- Просматриваемый_массив — диапазон ячеек, в которых производится поиск.
- Тип_сопоставления — необязательный аргумент. Число -1, 0 или 1.
Функция ПОИСКПОЗ выполняет поиск указанного элемента в диапазоне ячеек и возвращает относительную позицию этого элемента в диапазоне.
Суть использования комбинации функций «ИНДЕКС» и «ПОИСКПОЗ» в том, то мы производим поиск координат значений по их наименованию по «осям координат».
Осью Y будет столбец «Наименование», а осью X – строка «Месяцы».
часть формулы:
ПОИСКПОЗ($A4;$I$4:$I$7;0)
возвращает число по оси Y, в данном случае оно будет равно 1, т.к. значение «А» присутствует в искомом диапазоне и имеет относительную позицию «1» в этом диапазоне.
часть формулы:
ПОИСКПОЗ(B$3;$J$3:$L$3;0)
возвращает значение #Н/Д, т.к. значение «1» отсутствует в просматриваемом диапазоне.
Таким образом, мы получили координаты точки (1; #Н/Д) которые функция «ИНДЕКС» использует для поиска в аргументе «Массив».
Полностью написанная функция для ячейки B4 будет иметь следующий вид:
=ИНДЕКС($J$4:$L$7; ПОИСКПОЗ($A4;$I$4:$I$7;0); ПОИСКПОЗ(B$3;$J$3:$L$3;0))
По сути, если бы мы знали координаты нужного нам значения, функция выглядела бы следующим образом:
=ИНДЕКС($J$4:$L$7;1;#Н/Д))
Поскольку, аргумент «Номер_столбца» имеет значение «#Н/Д», то результат для ячейки «B4» будет соответствующий.
Как видно из получившегося результата не все значения в таблице с результатом находят совпадение со справочником и в итоге мы видим, что часть значений в таблице выводится в виде «#Н/Д», что затрудняет использование данных для дальнейших расчетов.
Результат:
Что бы нейтрализовать этот негативный эффект используем функцию «ЕСЛИОШИБКА», о которой мы читали ранее, и заменяем значение, возвращающееся при ошибке на «0», тогда формула будет иметь вид:
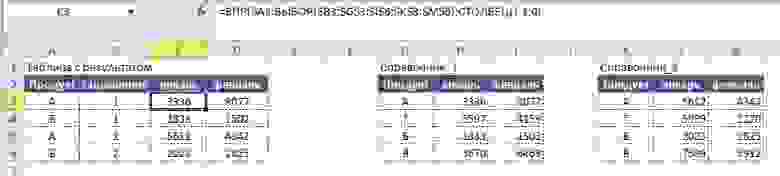
Вывод результата в ячейку B4:
=ЕСЛИОШИБКА(ИНДЕКС($J$4:$L$7; ПОИСКПОЗ($A4;$I$4:$I$7;0); ПОИСКПОЗ(B$3;$J$3:$L$3;0));0)
Демонстрация результата:
Как видно на картинке, значения «#Н/Д» более не мешают нам в последующих вычислениях с использованием значений в таблице с результатом.
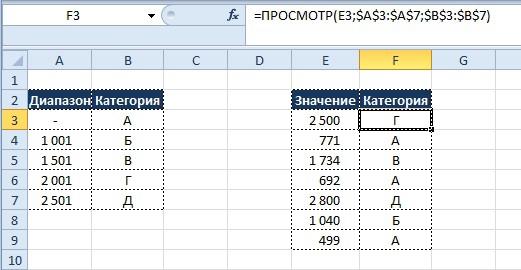
Кейс_5 Поиск значения в диапазоне чисел
Представим, что нам необходимо дать определенный признак числам, входящим в определенный диапазон.
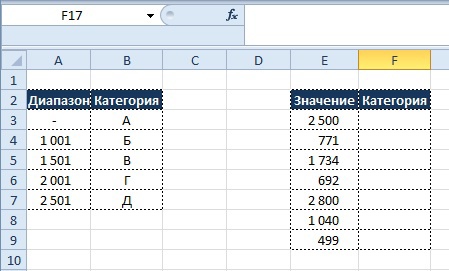
Условие:
В зависимости от стоимости продукта ему должна присваиваться определенная категория
Если значение находится в диапазоне
- От 0 до 1000 = А
- От 1001 до 1500 = Б
- От 1501 до 2000 = В
- От 2001 до 2500 = Г
- Более 2501 = Д
Функция ПРОСМОТР (LOOKUP) возвращает значение из строки, столбца или массива. Функция имеет две синтаксических формы: векторную и форму массива.
ПРОСМОТР(искомое_значение; просматриваемый_вектор; [вектор_результатов])
- Искомое_значение — значение, которое функция ПРОСМОТР ищет в первом векторе. Искомое_значение может быть числом, текстом, логическим значением, именем или ссылкой на значение.
- Просматриваемый_вектор — диапазон, состоящий из одной строки или одного столбца. Значения в аргументе просматриваемый_вектор могут быть текстом, числами или логическими значениями.
- Значения в аргументе просматриваемый_вектор должны быть расположены в порядке возрастания: …, -2, -1, 0, 1, 2, …, A-Z, ЛОЖЬ, ИСТИНА; в противном случае функция ПРОСМОТР может возвратить неправильный результат. Текст в нижнем и верхнем регистрах считается эквивалентным.
- Вектор_результатов — диапазон, состоящий из одной строки или столбца. Вектор_результатов должен иметь тот же размер, что и просматриваемый_вектор.
Вывод результата в ячейку B3:
=ПРОСМОТР(E3;$A$3:$A$7;$B$3:$B$7)
Аргументы «Просматриваемый_вектор» и «Вектор_результата» можно записать в форме массива – в этом случае не придется выводить их в отдельную таблицу на листе Excel.
В этом случае функция будет выглядеть следующим образом:
Вывод результата в ячейку B3:
=ПРОСМОТР(E3;{0;1001;1501;2001;2501};{«А»;«Б»;«В»;«Г»;«Д»})
Кейс_6 Суммирование чисел по признакам
Для суммирования чисел по определенным признакам можно использовать три разных функции:
СУММЕСЛИ (SUMIF) – суммирует только по одному признаку
СУММЕСЛИМН (SUMIFS) – суммирует по множеству признаков
СУММПРОИЗВ (SUMPRODUCT) – суммирует по множеству признаков
Существует также вариант с использованием «СУММ» (SUM) и функции формулы массивов, когда формула «СУММ» возводится в массив:
({=СУММ(()*())}
но такой подход довольно неудобен и полностью перекрывается по функционалу формулой «СУММПРОИЗВ»
Теперь подробнее по синтаксису «СУММПРОИЗВ»:
СУММПРОИЗВ(массив1, [массив2], [массив3],…)
- Массив1 — первый массив, компоненты которого нужно перемножить, а затем сложить результаты.
- Массив2, массив3… — от 2 до 255 массивов, компоненты которых нужно перемножить, а затем сложить результаты.
Условие:
- Найти общую сумму по стоимости отгрузок по каждому из продуктов за определенный период:
Как видно из таблицы с данными, что бы посчитать стоимость необходимо цену умножить на количество, а полученное значение, применив условия отбора переносить в таблица с результатом.
Однако, формула «СУММПРОИЗ» позволяет проводить такие расчеты внутри формулы.
Вывод результата в ячейку B4:
=СУММПРОИЗВ(($A4=$H$3:$H$11)*($K$3:$K$11>=B$3)*($K$3:$K$11<C$3);($M$3:$M$11)*($L$3:$L$11))
Разберем формулу по частям:
($A4=$H$3:$H$11)
– задаем условие по отбору в столбце «Наименование» таблицы с данными по столбцу «Наименование» в таблице с результатом
($K$3:$K$11>=B$3)*($K$3:$K$11<C$3)
– задаем условие по временным рамкам, дата больше или равна первого числа текущего месяца, но меньше первого числа месяца следующего. Аналогично – условие в таблице с результатом, массив – в таблице с данными.
($M$3:$M$11)*($L$3:$L$11)
– перемножаем столбцы «Количество» и «Цена» в таблице с данными.
Несомненным плюсом данной функции является свободный порядок записи условий, их можно записывать в любом порядке, на результат это не повлияет.
Результат:
Теперь усложним условие и добавим требование, что бы отбор по наименованию «печеньки» происходил только по классам «малые» и «большие», а по наименованию «булки» все, кроме по классу «с джемом»:
Вывод результата в ячейку B4:
=СУММПРОИЗВ(($A4=$H$3:$H$11)*($J$3:$J$11>=B$3)*($J$3:$J$11<C$3)*(($I$3:$I$11=«малые»)+($I$3:$I$11=«большие»));($L$3:$L$11*$K$3:$K$11))
В формуле для отбора по печенькам добавилось новое условие:
(($I$3:$I$11=«малые»)+($I$3:$I$11=«большие»))
– как видно, два или более условия по одному столбцу выделяются в отдельную группу при помощи символа «+» и заключения условий в дополнительные скобки.
В формуле для отбора по булкам также добавилось новое условие:
=СУММПРОИЗВ(($A5=$H$3:$H$11)*($J$3:$J$11>=B$3)*($J$3:$J$11<C$3)*($I$3:$I$11<>«с джемом»);($L$3:$L$11)*($K$3:$K$11))
это:
($I$3:$I$11<>«с джемом»)
– на самом деле, в данной формуле можно было написать условие отбора также как и при отборе по печенькам, но тогда, пришлось бы перечислять три условия в формуле, в данном случае, проще написать исключение – не равно «с джемом» для этого используем значение «<>».
Вообще, если группы признаков/классов заранее известны, то лучше объединять их в эти группы, создавая справочники, чем записывать все условия в функцию, раздувая ее.
Результат:
Что ж, вот мы и подошли к концу нашего краткого мануала, который на самом деле мог бы быть намного больше, но целью было все-таки дать решение наиболее встречающихся ситуаций, а не описывать решение частных (но гораздо более интересных случаев).
Надеюсь, что мануал поможет кому-нибудь в решении задач при помощи Excel, ведь это будет значить, что мой труд не пропал зря!
Спасибо за уделенное время!