Рассмотрим простые проценты — метод начисления, при котором сумма начисленных процентов определяется исходя только из первоначальной величины вклада (или долга). Процент на начисленные проценты не начисляется (проценты не капитализируются).
Немного теории
Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.
Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по простым процентам и по
сложным процентам
.
Сущность метода начисления по простым процентам сводится к тому, что проценты начисляются в течение всего срока кредита на одну и ту же величину капитала, предоставленного в кредит (или на одну и ту же величину вклада).
В случае известной годовой процентной ставки (i), суммы капитала, предоставленного в кредит (P) и срока ссуды (n, лет), можно рассчитать так называемую
Наращенную сумму S
– сумму первоначального капитала (Р) и начисленных на него процентов (I).
Примечание
.
В случае вклада на определенный срок, S представляет собой
Будущую стоимость
вклада, вычисленную по методу простых процентов.
Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) записывается в следующем виде: S= P+I= P+P*n*i= P*(1+n*i)
Выражение (1+n*i) называется множителем наращения процентов. В формуле предполагается, что процентная ставка (i) не изменяется в течение всего срока предоставления кредита. В
файле примера
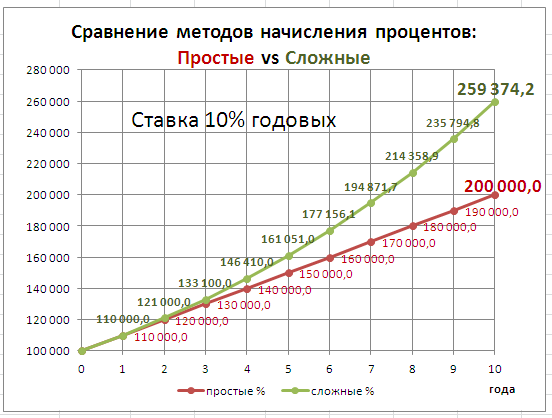
приведен расчет наращенной суммы для заданного количества лет, годовой % ставке и заданной величине первоначальной суммы. Также приведен график для сравнения наращенной суммы с использованием простых и
сложных процентов
.
Вычисление наращенной суммы при постоянной процентной ставке
Вышеуказанная формула простых процентов настолько проста, что не понятно, в чем вообще состоит проблема вычислений? Вычислить
Наращенную сумму
S
при известных Р, n, i или вычислить i при известных Р, n, S можно и на калькуляторе. Однако, все несколько усложняется в случае, когда срок финансовой сделки не равен целому числу лет.
Если срок предоставления кредита определен в месяцах, то формулу для определения наращенной суммы необходимо изменить, разделив годовую ставку i на 12 (12 месяцев в году). Под n теперь будем понимать количество месяцев. S=P*(1+n*i/12) i/12 – это ставка за период (за месяц).
Если срок финансовой сделки определен в кварталах, то под n будем понимать количество кварталов, на который был выдан кредит (или заключен договор срочного вклада). Годовую ставку i нужно разделить на 4 (4 квартала в году). Формула выглядит так: S=P*(1+n*i/4)
По аналогии, можно предположить, что если срок финансовой сделки определен в днях, то под n разумно понимать количество дней, на который был выдан кредит. Однако со ставкой за период не все так просто. Действительно, i нужно делить на 365 (365 дней в году) или на 366 в случае
високосного года
? Поэтому, если срок финансовой сделки определен в днях, то формулу определения наращённой суммы записывают несколько в ином виде:
где t — число дней функционирования сделки (число дней, на которое предоставили кредит); К — временная база (число дней в году).
Временную базу года можно брать число дней в году (365 или 366), или даже 360. Откуда 360? Дело в том, что в ряде стран для удобства вычислений год делится на 12 месяцев, по 30 дней в каждом, т.е. продолжительность года
К
принимается равной 360 дням (12*30).
В этой связи различают три метода процентных расчетов, зависимых от выбранного периода начисления.
- Точные проценты с точным числом дней ссуды (английский (британский) метод). При этом методе продолжительность года К принимается равной 365 (или 366) дням и определяется фактическое число дней t между двумя датами (датой получения и погашения кредита), т.е. временная база – календарный год.
Примечание
.
Вычисление по формуле S=P*(1+n*i/365) является лишь приблизительным по английскому методу в случае високосного года (см. ниже).
- Обыкновенные (обычные) проценты с точным числом дней ссуды (французский метод, банковское правило, гибридный метод). При этом методе величина t рассчитывается, как и в предыдущем методе, а продолжительность года принимается равной К = 360 дням (коммерческий год, обыкновенный год). Это позволяет французским банкирам зарабатывать в 1,01388 раза больше денег, чем английским (365/360= 1,01388) за тот же период.
Примечание
.
Вычисление по французскому методу можно производить по формуле S=P*(1+n*i/360), где i – годовая ставка, n – число дней ссуды.
-
Обыкновенные проценты с приближенным числом дней ссуды (германский метод). При этом методе величина t определяется так:
количество полных месяцев
ссуды *умноженное на 30 дней в каждом + точное число дней ссуды в неполных месяцах; продолжительность года К = 360 дней.
В
файле примера
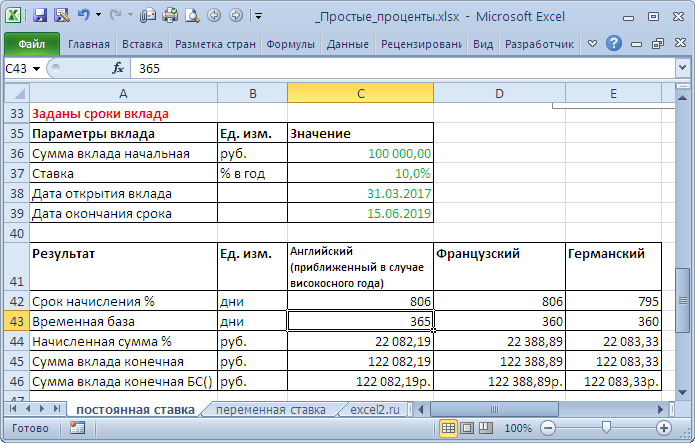
приведен расчет начисления процентов по 3-м методам.
Примечание
.
При точном и приближенном методах начисления процентов день выдачи и день погашения ссуды принимаются за 1 день.
Понятно, что вычисления по английской и германской системе могут быть сделаны, только если заданы конкретная дата выдачи кредита и дата окончания его срока. Т.к. чтобы вычислить по английской системе – требуется знать продолжительность конкретного года (високосный или нет), а по немецкой – требуется знать количество полных месяцев и число дней ссуды в неполных месяцах. По французскому методу количество дней ссуды берется фактическое, а временная база всегда =360, поэтому вычисления производить можно и без знания конкретных дат (достаточно знать количество дней ссуды). Еще одно замечание о вычислении наращенной суммы при использовании английского метода. Напомним, что продолжительность года в этом методе принимается равной 365 (или 366) дней, правда, не всегда понятно как проводить вычисления, если срок кредита приходится и на високосный и обычный год (например, кредит выдан 31.10.2016, а должен быть погашен в 15.06.2017, високосный 2016). Т.к. в РФ используется английский метод, то ЦЕНТРАЛЬНЫЙ БАНК РОССИЙСКОЙ ФЕДЕРАЦИИ опубликовал письмо от 27 декабря 1999 г. N 361-Т для разъяснения этой ситуации:
В случае, если дни периода начисления процентов по привлеченным (размещенным) банками денежным средствам приходятся на календарные годы с разным количеством дней (365 и 366 дней соответственно), то начисление процентов за дни, приходящиеся на календарный год с количеством дней 365, производится из расчета 365 календарных дней в году, а за дни, приходящиеся на календарный год с количеством дней 366, производится из расчета 366 календарных дней в году.
В
файле примера
в ячейке
В50
приведена
формула массива
, которая позволяет вычислить наращенную сумму в случае кредита, когда года даты выдачи и даты погашения ссуды не совпадают (например, кредит выдан 31.03.2015, а должен быть погашен в 15.06.2017).
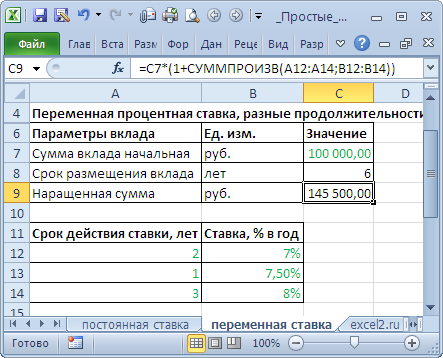
Вычисление наращенной суммы при переменной процентной ставке
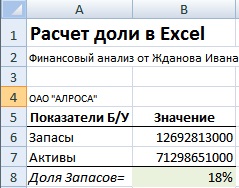
При установлении переменной процентной ставки, т.е. дискретно изменяющейся во времени ставки, наращенная ставка определяется по формуле:
В
файле примера
на листе
Переменная ставка
сделаны расчеты по этой формуле: =
C7*(1+СУММПРОИЗВ(A12:A14;B12:B14))
В случае, если процентная ставка изменяется через равные периоды, то вышеуказанную формулу можно несколько упростить.
n – период действия ставки без изменения.
На чтение 5 мин Просмотров 71.5к.
Разберем различные формулы расчета процентов в Excel, для этого рассмотрим реальные практические примеры, формулы и типовые финансовые задачи.
Содержание
- Формула расчета процентов. Как посчитать проценты в Экселе?
- Формула расчета доли
- Формула расчета размера процента от капитала
- Формула расчета размера капитала с процентами
- Формула уменьшения размера капитала на процент
- Формула расчета очищенной стоимости капитала (продукции)
- Формула расчета простых процентов по банковскому вкладу
- Формула расчета сложных процентов по банковскому вкладу
- Видео-урок: «Примеры расчета простых и сложных процентов»
Формула расчета процентов. Как посчитать проценты в Экселе?
Проценты (латин. pro centum) – являются неотъемлемой частью финансовой математики и используются в банковском секторе, финансах, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность предприятия, ставку по банковским кредитам и займам, налоговые ставки и т.д. Можно привести в подтверждение важности процентов в финансовом мире высказывание А. Энштейна: «Сложные проценты – самая мощная сила в природе». Перед тем как рассмотреть формулы расчета процентов введем основные термины и понятия.
- Капитал (англ. Capital, Principal) – является базой относительно которого вычисляют процент.
- Частота начисления процентов – период выплат процентов на капитал.
- Процентная ставка (англ. Rate) – размер процента или доля капитала, который будет выплачен.
- Период вложения (англ. Period) – временной интервал передачи капитала банку или другому финансовому институту.
Итак, рассмотрим различные эконометрические задачи с процентами.
Формула расчета доли
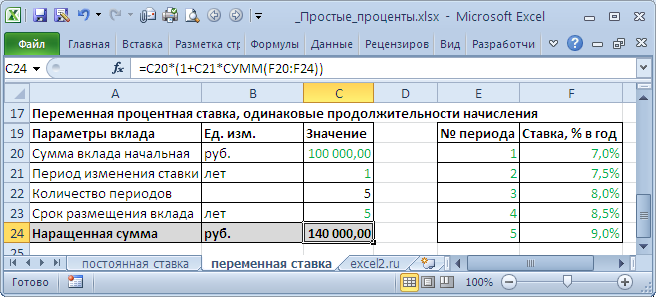
Расчет доли часто необходим в бухгалтерском и финансовом учете, где необходимо определить долю тех или иных видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО «АЛРОСА».
Пример задачи. Необходимо рассчитать долю «Запасов» в структуре «Активов» предприятия. Для этого воспользуемся формулой:
Доля запасов в Активах =B6/B7
Для того чтобы в ячейке полученные доли имею процентный вид можно воспользоваться сочетанием клавиш «Ctrl» + «Shift» + «%».
Формула расчета размера процента от капитала
Рассмотрим вторую постоянно встречающуюся экономическую задачу: расчет абсолютного значения процента по капиталу.
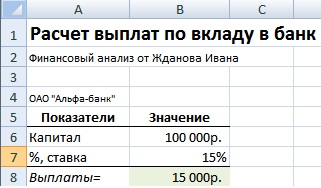
Пример задачи. Необходимо определить размер выплаты банка ОАО «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь следующий вид:
Выплаты по вкладу в банке =B6*B7
Формула расчета размера капитала с процентами
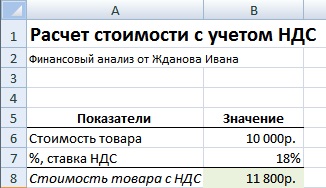
Пример задачи. Требуется рассчитать итоговую стоимость товара с НДС (налог на добавленную стоимость), тогда как стоимость товара без НДС составляет 10000 руб., процентная ставка налога равна 18%. Формула расчета стоимости товара с учетом НДС рассчитывается по формуле:
Стоимость товара с учетом НДС =B6*(1+B7)
Формула уменьшения размера капитала на процент
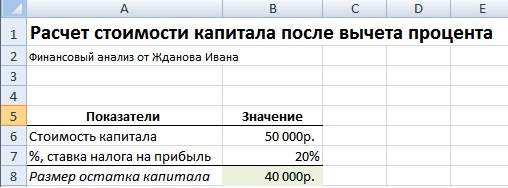
Пример задачи. Необходимо рассчитать размер капитала после вычета налога на прибыль, процентная ставка налога равна 24%, текущее значение капитала равно 50000 руб. Формула расчета остатка капитала после вычета налога следующая:
Остаток капитала =B6-B6*B7
Формула расчета очищенной стоимости капитала (продукции)
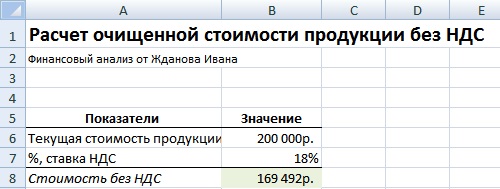
Пример задачи. Необходимо рассчитать начальную стоимость продукции без НДС (налог на добавленную стоимость), текущая стоимость продукции составляет 200000 руб., процентная ставка налога 18%. Формула расчета процентов следующая:
Стоимость продукции без НДС=B6/(1+B7)
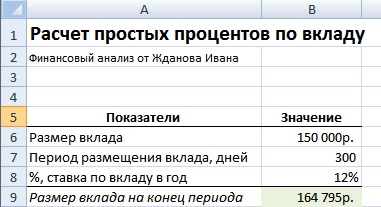
Формула расчета простых процентов по банковскому вкладу
При использовании простых процентов выплаты по вкладу осуществляются только в конце срока (периода) размещения.
Пример задачи. Требуется рассчитать размер выплат по банковскому вкладу, на который начисляется простые проценты. Размер вклада составляет 150000 руб., годовая процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel следующая:
Размер банковского вклада на конец периода размещения =(1+B8*300/365)*B6
Формула расчета сложных процентов по банковскому вкладу
Сложные проценты отличаются от простых тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.
Пример задачи. Необходимо рассчитать размер банковского вклада, который был размещен по сложный процент. Первоначальный размер депозита составляет 100000 руб., годовая процентная ставка равна 14%, период начисления процентов – каждые 4 месяца, срок размещения вклада 1 год.
Формула расчета сложных процентов:
Размер вклада со сложными процентами на конец года =B6*(1+B8*B9/B7)^4
Метод сложных процентов имеет широкое использование в финансовом анализе и применяется для дисконтирования денежных потоков. Более подробно о методе дисконтирования читайте в статье: «Дисконтирование денежных потоков (DCF). Формула. Расчет в Excel«.
Видео-урок: «Примеры расчета простых и сложных процентов»
Резюме
Расчет процентов является неотъемлемой частью финансовой математики и всей экономики в целом. Навык быстрого расчета процентов в Excel позволяет экономить время при оценке будущей стоимости капитала.
Автор: к.э.н. Жданов Иван Юрьевич
-
Основные понятия
Термин «процент»
происходит от латинского pro centum, что
переводится как «на сотню, или за
сто». При такой трактовке процент
выступает в качестве так называемого
процентного числа, указывающего на
часть целой величины или доли, и широко
используется в социально-экономической
статистике и законодательной практике
регулирования предпринимательской
деятельности (например, при начислении
налогов). В процентных вычислениях важно
понимать, какая величина принята за
100%, т.е. что используется в качестве базы
[2].
В финансово-кредитной
сфере важную роль играет временной
фактор денег, поскольку разумно вложенные
денежные средства должны приносить их
владельцу определенный доход (процент),
зависящий от длительности их использования.
В данном случае
процент — это абсолютная величина дохода
от предоставления денег в долг (кредит)
в любой его форме. Процентная ставка —
относительная величина дохода за
фиксированный интервал времени (период
начисления), измеряемая в процентах
(сотая часть числа) или в виде дроби.
Проценты
различаются по базе начисления, которая
может быть либо постоянной, либо
последовательно изменяющейся
(наращиваемой). В первом случае
рассчитываются простые проценты, к
которым прибегают при выдаче краткосрочных
(до одного года) ссуд или при периодических
выплатах процентов кредитору (когда
проценты не присоединяются к сумме
долга).
Во втором случае
рассчитываются сложные проценты, к
которым обычно прибегают в среднесрочных
и долгосрочных кредитно-финансовых
отношениях, когда проценты не выплачиваются
немедленно после их начисления, а
присоединяются к сумме долга (капитализация
процентов). База для начисления сложных
процентов увеличивается (наращивается)
с каждым периодом начисления процентов.
-
Наращение по простой процентной ставке
Ниже рассмотрены
основные типы моделей финансовых
расчетов на основе простых процентов.
Следует отметить, что в Excel отсутствуют
встроенные финансовые функции для
вычисления простых процентов, но они
могут быть сравнительно легко реализованы
на основе следующих формул [3]:
I = P • n
• i, (1.1)
S = P +1 =
P+ P • n • i = P • (1 + n • i) (1.2),
где I
— проценты за весь срок, на который
предоставлена ссуда;
P — первоначальная
сумма ссуды (долга);
S — наращенная сумма
в конце срока погашения ссуды;
i — величина
процентной ставки (десятичная дробь);
n — срок погашения
ссуды (обычно в годах).
При сроке ссуды,
не кратном периоду начисления, n
рассчитывается по следующей формуле:
n = t/k
(1.3)
где t — количество
дней, составляющих срок ссуды;
k — количество
дней в периоде начисления (при расчете
обыкновенных или коммерческих процентов
принимается: год — 360 дней, месяц — 30 дней;
при расчете точных процентов берутся
фактические значения).
Задача №1.
Вкладчик поместил
вклад в размере 3000 рублей в банк под 7%
годовых (простых). Какая сумма будет на
счете вкладчика:
а) через 3 месяца;
б) через 1 год;
в) через 3 года
5 месяцев?
Решение.
Для расчета
суммы вклада в каждом из трех случаев
используем формулу (1.2) согласно которой
а) S = 3000 * (1 + 0,07
* 90 / 360) = 3000 * (1 + 0,0175) = 3000 * 1,0175 = 3052,5 р.
б) S = 3000 * (1 + 0,07)
= 3000 * 1,07 = 3210 р.
в) S = 3000 * (1 + 0,07
* ( 3 + 5 * 30 / 360)) =3000 * (1 + 0,239) = 3000 * 1,293 = 3717,5 р.
Задача №2.
Реализовать
приведенные выше расчеты наращенной
суммы в зависимости от первоначального
вклада, процентной ставки и периода
начисления в Excel. Использовать при этом
возможность присвоения содержательных
имен ячейкам таблицы.
Из базовой
формулы (1.2) можно получить ряд соотношений,
часто используемых в финансовой практике.
Например, зная наращенную сумму S,
количество периодов начисления простых
процентов n и величину процентной ставки
i, можно рассчитать вложенную сумму
P
=
(1.4)
Эта операция,
обратная наращению, называется
дисконтированием; она позволяет по
известной будущей стоимости (S) получить
текущую стоимость (P), называемую также
современной капитализированной
стоимостью.
Дисконтный
множитель, равный 1/(1+n*i), показывает,
какую долю составляет первоначальная
величина вклада (займа) в его окончательной
сумме. При этом говорят, что сумма S
дисконтируется или учитывается, а сам
процесс начисления процентов и их
удержания называется учетом; величина
удержанных процентов называется
дисконтом (D) и рассчитывается как
D = S — P.
(1.5)
Задача №3.
Банк выплачивает
7% простых в год. Гражданин Иванов хочет
получить через 2 года и 6 месяцев 10000
рублей. Какую сумму он должен положить
в банк в настоящий момент?
Решение.
Подставляя
данные, приведенные в условии задачи,
в формулу (1.4), получаем ответ
P = 10000 / (1 + 0,07 *
2,5) = 10000 / 1,175 = 8510,64 р.
Задача №4.
Реализовать
приведенный выше расчет первоначального
вклада в зависимости от суммы приращения,
простой процентной ставки и периода
начисления в Excel.
Зная вложенную
сумму P, наращенную сумму S и количество
периодов начисления простых процентов
n, можно рассчитать величину процентной
ставки
i =
(1.6)
Задача №5.
В банке был
размещен вклад в размере 1500 р. Через 1
год и 3 месяца на счете было 1631,25 р. Сколько
простых процентов в год выплачивает
банк? Реализовать расчет простой
процентной ставки в Excel.
Задача №6.
Гражданин Петров
взял в долг у своего приятеля Сидорова
9800 р., выдав последнему вексель (долговую
расписку), по которому обязался выплатить
10000 р. через 3 месяца. Под какой годовой
процент выдан данный вексель? Реализовать
расчет простой процентной ставки в
Excel.
Соседние файлы в папке практическе работы
- #
- #
- #

Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента! Воистину, это один из главных секретов, как с помощью инвестирования увеличить количество нулей в сумме на вашем банковском счёте.
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Приглашаю подписываться на мой Telegram-канал Блог Вебинвестора! Там вы найдёте еженедельные отчёты по инвестициям, аналитические материалы, комментарии по важным новостям и многое другое. Также прошу делиться ссылкой на блог в социальных сетях и мессенджерах:
Что такое простой и сложный процент
и чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:

Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:

В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:

Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:

без капитализации депозит растёт линейно,
а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
⬆️ К СОДЕРЖАНИЮ ⬆️
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
- К0 — начальная сумма вклада;
- К — конечная сумма вклада;
- R — ставка доходности, переводится из процентов в число (10% = 0.1);
- N — количество периодов (лет).
Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 
⬆️ К СОДЕРЖАНИЮ ⬆️
Примеры решения задач
по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Вычисляем прибыль:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:

Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:

Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:

Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
⬆️ К СОДЕРЖАНИЮ ⬆️
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
- расчёт конечной суммы вклада;
- расчёт начальной суммы вклада;
- расчёт необходимой процентной ставки;
- расчёт срока инвестирования;
- расчёт конечной суммы вклада с учётом регулярных пополнений и капитализацией;
- ожидаемый пассивный доход в каждом из случаев.
В будущем я планирую добавить много калькуляторов по самым разным темам, оставляйте свои пожелания в комментариях!
Пример одного из калькуляторов для расчёта сложных процентов в Excel:

Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:

А также уже знакомые вам таблицы:

Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
⬆️ К СОДЕРЖАНИЮ ⬆️
Как использовать сложные проценты
в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Статья в тему: Как деньги делают еще больше денег или Что такое реинвестирование
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:

Источники: statbureau.org
Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:

Источник: ru.investing.com
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
- Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
- Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
- Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.
Оптимальный портфель инвестора предполагает использование всех этих инструментов, поскольку генерируемый ими денежный поток позволяет гибко управлять вложениями: делать ребалансировку, выводить прибыль или реинвестировать. Использовать правило сложных процентов можно в любых инвестициях, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
⬆️ К СОДЕРЖАНИЮ ⬆️
Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.
Удачных инвестиций и не болейте!
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Skip to content
В этом руководстве вы познакомитесь с быстрым способом расчета процентов в Excel, найдете базовую формулу процента и еще несколько формул для расчета процентного изменения, процента от общей суммы и т.д.
Расчет процента нужен во многих ситуациях, будь то комиссия продавца, ваш подоходный налог или процентная ставка по кредиту. Допустим, вам посчастливилось получить скидку 25% на новый телевизор. Это хорошая сделка? И сколько в итоге придется заплатить?
Сейчас мы рассмотрим несколько методов, которые помогут вам эффективно вычислять процент в Excel, а также освоим основные формулы процента, которые избавят вас от догадок при расчетах.
- Базовая формула подсчета процента от числа.
- Как посчитать процент между числами по колонкам.
- Как рассчитать процент по строкам.
- Доля в процентах.
- Считаем процент скидки
- Отклонение в процентах для отрицательных чисел
- Вычитание процентов
- Как избежать ошибки деления на ноль
Что такое процент?
Как вы, наверное, помните из школьного урока математики, процент — это доля от 100, которая вычисляется путем деления двух чисел и умножения результата на 100.
Основная процентная формула выглядит следующим образом:
(Часть / Целое) * 100% = Процент
Например, если у вас было 20 яблок и вы подарили 5 своим друзьям, сколько вы дали в процентном отношении? Проведя несложный подсчет =5/20*100% , вы получите ответ — 25%.
Так обычно рассчитывают проценты в школе и в повседневной жизни. Вычислить процентное соотношение в Microsoft Excel еще проще, поскольку он выполняет некоторые операции за вас автоматически.
К сожалению, универсальной формулы расчета процентов в Excel, которая охватывала бы все возможные случаи, не существует. Если вы спросите кого-нибудь: «Какую формулу процентов вы используете, чтобы получить желаемый результат?», Скорее всего, вы получите ответ типа: «Это зависит от того, какой именно результат вы хотите получить».
Итак, позвольте мне показать вам несколько простых формул для расчета процентов в Excel.
Расчет процентов в Excel.
Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:
Часть / Целое = Процент
Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.
И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.
То есть, чтобы, к примеру, посчитать 10% в Экселе, то вместо =A1*0,1 или =A1*10/100, просто запишите формулу процентов =A1*10%.
Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.
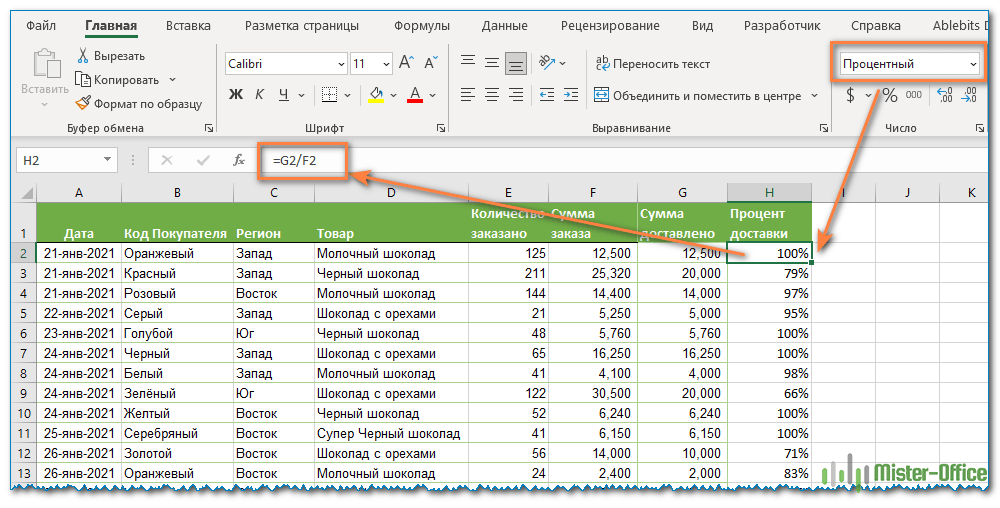
А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:
- Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
- Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
- Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
- Готово!
Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.
На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.
Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.
Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.
Как найти процент между числами из двух колонок?
Предположим, у нас имеются данные о продажах шоколада за 2 месяца. Необходимо определить, какие произошли изменения в реализации. Проще и нагляднее всего отклонения в продажах выразить в процентах.
Чтобы вычислить разницу в процентах между значениями A и B, используйте следующую формулу:
Процентное изменение = (B — A) / A
При применении этой формулы к реальным данным важно правильно определить, какое значение равно A, а какое — B. Например, вчера у вас было 80 яблок, а сейчас — 100. Это означает, что теперь у вас на 20 яблок больше, чем раньше, что произошло увеличение на 25%. Если у вас было 100 яблок, а теперь – 90, то количество яблок у вас уменьшилось на 10, то есть на 10%.
Учитывая вышеизложенное, наша формула Excel для процентного изменения принимает следующую форму:
=(новое_значение – старое_значение)/старое_значение
А теперь давайте посмотрим, как вы можете использовать эту формулу процентного изменения в своих таблицах.
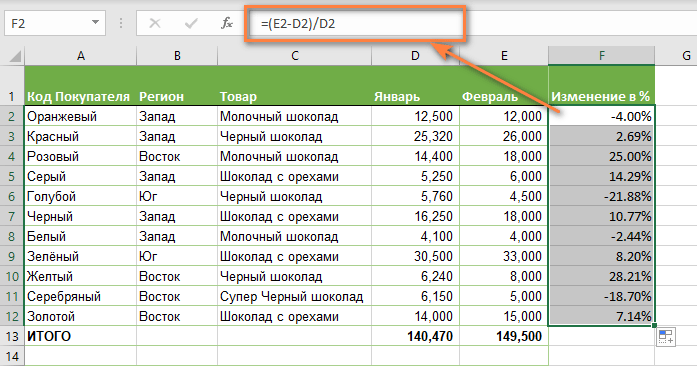
В нашем случае —
=(E2-D2)/D2
Эта формула процентного изменения вычисляет процентное увеличение (либо уменьшение) в феврале (столбец E) по сравнению с январём (столбец В).
И затем при помощи маркера заполнения копируем ее вниз по столбцу. Не забудьте применить процентный формат.
Отрицательные проценты, естественно, означают снижение продаж, а положительные — их рост.
Аналогичным образом можно подсчитать и процент изменения цен за какой-то период времени.
Как найти процент между числами из двух строк?
Такой расчет применяется? Если у нас есть много данных об изменении какого-то показателя. И мы хотим проследить, как с течением времени изменялась его величина. Поясним на примере.
Предположим, у нас есть данные о продажах шоколада за 12 месяцев. Нужно проследить, как изменялась реализация от месяца к месяцу. Цифры в столбце С показывают, на сколько процентов в большую или меньшую сторону изменялись продажи в текущем месяце по сравнению с предшествующим.
Обратите внимание, что первую ячейку С2 оставляем пустой, поскольку январь просто не с чем сравнивать.
В С3 записываем формулу:
=(B3-B2)/B2
Можно также использовать и другой вариант:
=B3/B2 — 1
Копируем содержимое этой ячейки вниз по столбцу до конца таблицы.
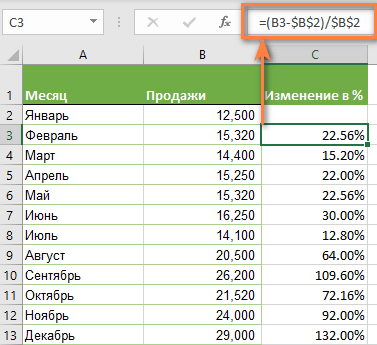
Если нам нужно сравнивать продажи каждого месяца не с предшествующим, а с каким-то базисным периодом (например, с январём текущего года), то немного изменим нашу формулу, использовав абсолютную ссылку на цифру продаж января:
Абсолютная ссылка на $B$2 останется неизменной при копировании формулы в C4 и ниже:
=(B3-$B$2)/$B$2
А ссылка на B3 будет изменяться на B4, B5 и т.д.
Напомню, что по умолчанию результаты отображаются в виде десятичных чисел. Чтобы отобразить проценты , примените к столбцу процентный формат. Для этого нажмите соответствующую кнопку на ленте меню или используйте комбинацию клавиш Ctrl + Shift + %.
Десятичное число автоматически отображается в процентах, поэтому вам не нужно умножать его на 100.
Расчет доли в процентах (удельного веса).
Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.
Пример 1. Сумма находится в конце таблицы в определенной ячейке.
Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.
Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы:
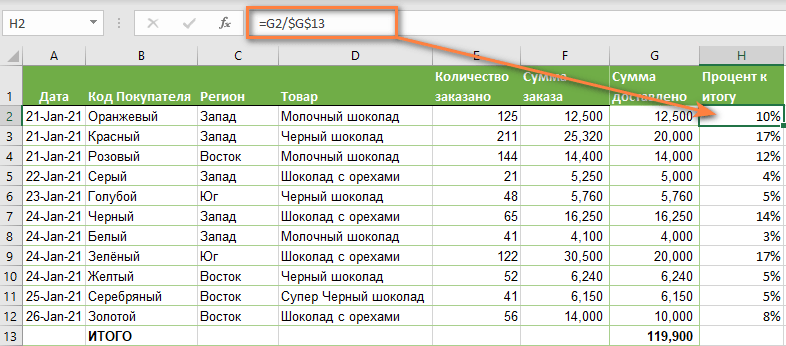
=G2/$G$13
Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.
Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.
На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.
Пример 2. Часть итоговой суммы находится в нескольких строках.
В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.
В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:
=СУММЕСЛИ( диапазон; критерий; диапазон_суммирования ) / Итог
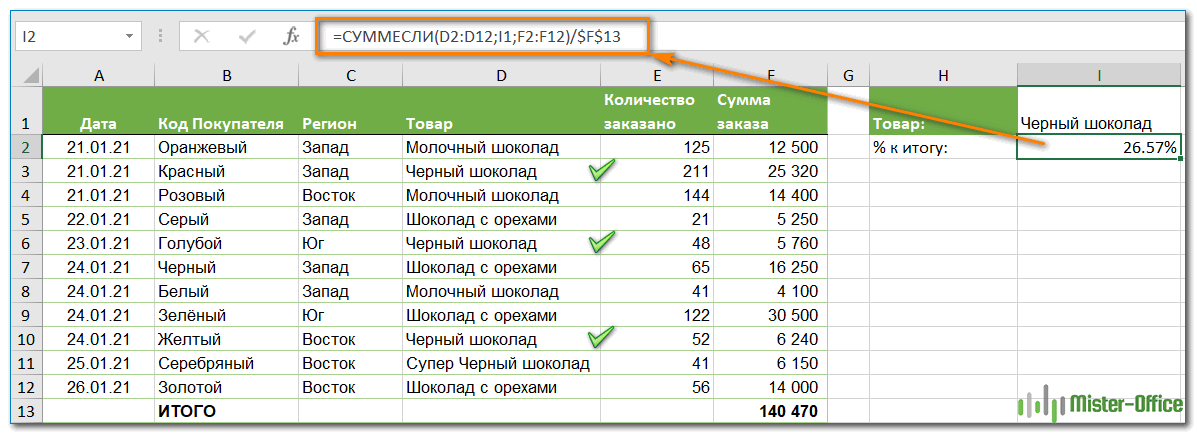
Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:
=СУММЕСЛИ(D2:D12;I1;F2:F12)/$F$13
Естественно, вы можете указать название товара прямо в формуле, например:
=СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13
Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.
Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:
=(СУММЕСЛИ(D2:D12;”Черный шоколад”;F2:F12)/$F$13 + =СУММЕСЛИ(D2:D12;”Супер черный шоколад”;F2:F12)) / $F$13
Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.
Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:
- Как использовать функцию СУММЕСЛИ в Excel
- СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями
Процент скидки
Формулы процентов пригодятся для расчета уровня скидки. Итак, отправляясь за покупками, помните следующее:
Скидка в % = (цена со скидкой – обычная цена) / обычная цена
Скидка в % = цена со скидкой / обычная цена — 1
В результатах вычисления процент скидки отображается как отрицательное значение, поскольку новая цена со скидкой меньше старой обычной цены. Чтобы вывести результат в виде положительного числа , оберните формулы в функцию ABS. Например:
=ABS((C2-B2)/B2)
или
=ABS((C2/B2 — 1)
Так будет гораздо привычнее.
Как рассчитать отклонение в процентах для отрицательных чисел
Если некоторые из исходных значений представлены отрицательными числами, приведенные выше формулы не будут работать.
Обычный обходной путь — сделать знаменатель в формуле положительным числом. Для этого воспользуйтесь функцией ABS:
( Новое_значение – старое_значение ) / ABS( старое_значение )
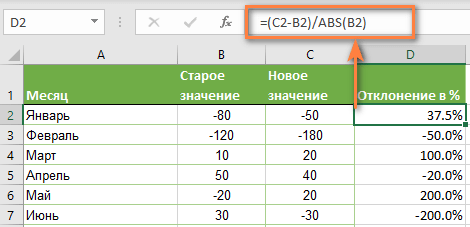
Со старым значением в B2 и новым значением в C2 формула выглядит следующим образом:
=(C2-B2)/ABS(B2)
Как видите, достаточно корректно работает с самыми разными комбинациями положительных и отрицательных чисел.
Положительный процент означает рост, отрицательный — снижение величины показателя.
Вычитание процентов.
Часто случается, что вам известен процент скидки на товар. И вам нужно высчитать, какой процент от первоначальной стоимости придётся заплатить. Как мы уже говорили, процент в Экселе — это обычное число. Поэтому и правила вычисления здесь – как с обычными числами.
Формула расчета в Excel будет выглядеть так:
=1 – процент_скидки
Как обычно, не забываем про процентный формат ячеек.
Предотвратить ошибки деления на ноль #ДЕЛ/0
Если вы хотите посчитать процент от числа в таблице, и ваш набор данных содержит несколько нулевых значений, заключите формулы в функцию ЕСЛИОШИБКА, чтобы предотвратить появление ошибок деления на ноль (#ДЕЛ/0! или #DIV/0!).
=IFERROR(=ЕСЛИОШИБКА((C2-B2)/B2;0)
=IFERROR(=ЕСЛИОШИБКА(C2/B2-1;0)
Вот как можно вычислить процент от числа в Excel. И даже если работа с процентами никогда не была вашим любимым видом математики, с помощью этих основных процентных формул вы можете заставить Excel делать работу за вас.
На сегодня все, спасибо, что прочитали!
Интегрированый урок.
Тема: Простой и сложный процентный рост. Решение задач на проценты с помощью табличного процессора MS Excel
обучение решению задач на проценты с помощью формул «простых и сложных процентов», обобщение методов решения задач проценты; научить переводить реальные предметные ситуации в различные математические модели; формирование умений решать задачи повышенной сложности;
развитие логического мышления, умений работать в группе, навыков решения экономических задач на проценты;
воспитание у учащихся потребности в новых знаниях и творческой деятельности, привитие любви к процессу обучения.
Тип урока: урок комплексного применения новых и прежних знаний, умений.
Оборудование: проектор, презентация к теме «Простой и сложный процентный рост», компьютеры, калькулятор.
|
I этап. Организационный момент (1 мин.) Цель: ознакомить учащихся с темой и задачей урока, актуальность изучаемого материала, формирование учебной мотивации. |
||||||||||||||||||||||
|
II этап. Повторение (5 мин) Цель: повторение знаний и навыков по теме «Проценты». |
1)Устный опрос (слайд 3) Что называется процентом? (одна сотая часть какого-либо числа) Как называется 1% от центнера? (кг) Метра? (см) Гектара? (ар или сотка) Как найти 1% от данного числа а? (0,01∙а) Как определить р% от данного числа а? (число а умножить на 0,01∙р ) Как перевести десятичную дробь в проценты? (умножить на 100). Как перевести проценты в десятичную дробь? (разделить на сто, т.е. умножить на 0,01) Как найти какую часть одно число составляет от другого в процентах? (отношение этих чисел умножить на 100) Как находится число а по его проценту? (данную часть числа разделить на 0,01р) 2) Устный счет (слайд 4) Представьте данные десятичные дроби в процентах: 1; 0,5; 0,763; 1,7; 256. Представьте проценты десятичными дробями: 2%; 12%; 12,5%; 0,1%; 200%. Найдите % от числа: 0,1% от числа 1200? (1,2) 15% от числа 2? (0,3) Найдите число по его проценту: Сколько центнеров весит мешок сахарного песка, если 13% составляет 6,5 кг? (50 кг.= 0,5 ц.) Сколько процентов от 10 составляет 9? (90%) |
|||||||||||||||||||||
|
III этап: Формирование новых знан ий и навыков. (15 мин) Цель: ознакомление с формулами « простых и сложных процентов» и формирование навыков применения формул при решении задач. |
Тема. Простые и сложные проценты. (Лекция + Презентация) Эти термины чаще всего встречаются в банковских делах, в финансовых задачах. Банки привлекают средства (вклады) за определенные процентные ставки. В зависимости от процентной ставки вычисляется доход. На практике применяются два подхода к оценке процентного дохода – простые и сложные проценты. При применении простых процентов доход рассчитывается от первоначальной суммы вложенных средств не зависимо от срока вложения. В финансовых операциях простые проценты используются преимущественно при краткосрочных финансовых сделках. (слайд 5) Пусть некоторая величина подвержена поэтапному изменению. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на начальном этапе. Так вычисляются простые проценты. При применении сложных процентов накопленная сумма процентов добавляется во вклад по окончании очередного периода начислений. При этом каждый раз ее изменение составляет определенное число процентов от значения, которое эта величина имела на предыдущем этапе. В этом случае имеем дело со «сложными процентами» (т.е. используются начисления “процентов на проценты”) Первоначальная сумма и полученные проценты в совокупности называются накопленной (наращенной) суммой. (слайд 6) Так, если банковская ставка равна 10%, а первоначальная сумма 100 руб., то накопленная сумма за пять лет при применении простых и сложных процентов будет иметь вид: Накопленная сумма с использованием простых и сложных процентов.
Формулы простых и сложных процентов. ( слайд 7) Пусть некоторая величина A увеличивается n раз (n год) и каждый раз на р%. Вводим обозначения: A0 – первоначальное значение величины A; р – постоянное количество процентов; процентная ставка; р/100 = ·р An – накопленная сумма за n раз (к концу n-го года) — по формуле простых процентов; Sn — накопленная сумма за n раз (к концу n-го года) — по формуле сложных процентов. Тогда ее значение A1 для простых процентов после первого увеличения (к концу первого года) вычисляется по формуле: A1 = A0 + A0 · (0,01р) = A0 (1 + (0,01р) = A0 (1 + ) В конце второго этапа A2= A1 + A0 · (0,01р) = A0 (1 + ) + A0 · = A0 (1 + 2 ). В конце третьего этапа A3= A2 + A0 · (0,01р) = A0 (1 + 2) + A0 · = A0 (1 + 3 ). Тогда для простых процентов сумма по годам равна:
Для сложных процентов это выглядит иначе: (слайд Тогда ее значение S1 для сложных процентов после первого увеличения (к концу первого года) вычисляется по формуле: S1 = S0 + S0 (0,01р) = S0 · (1 + 0,01р) = S0 · (1 + ). В конце второго этапа S2= S1 + S1 (0,01р) = S1 · (1 + 0,01р) = S0 (1 + р)2 = S0 (1 + )2. В конце третьего этапа S3= S2 + S2 (0,01р) = S2 · (1 +0,01р) = S0(1 +0,01р)2·(1 +0,01р)=S0(1 +0,01р)3 = S0 (1 + )3. Тогда для сложных процентов сумма по годам равна: Sn = S0 (1 + )n Sn = S0 ( 1 + 0,01р )n
или (2) Пример 1. (слайд 9) В банке открыт срочный депозит на сумму 50 тыс. руб. по 12% на 3 года. Рассчитать накопленную сумму если проценты: а) простые; б) сложные. По формуле простых процентов Sn=(1+3*0.12)*50 000 = 68000 руб. По формуле сложных процентов Sn=(1+0.12)3*50 000 = 70246 руб. (слайд 10) Формула сложных процентов связывает четыре величины: начальный вклад, накопленную сумму (будущую стоимость вклада), годовую процентную ставку и время в годах. Поэтому, зная три величины, всегда можно найти четвертую: Sn = S0 · (1+0,01р)n Для определения количество процентов р необходимо:
Операция нахождения первоначального вклада S0, если известно что через n лет он должен составить сумму Sn, называется дисконтированием:
Сколько лет вклад S0 должен пролежать в банке под р % годовых, чтобы достигнуть величины Sn.
В банковской практике проценты могут начисляться чаще, чем 1 раз в год. При этом банковская ставка обычно устанавливается в пересчете на год. Формула сложных процентов будет иметь вид: Sn = (1 + /t )n∙t S0 (3) где t – число реинвестиций процентов в году. (слайд 11) Реинвестиции — это средства в виде доходов и благ, полученных инвестором от осуществленной успешной инвестиции в какой-либо объект и направленных повторно в тот же объект. Также реинвестиции связаны с дополнительным или повторным вложением капитала независимого от того осуществляется ли это вложение в тот же объект или уже в совершено иной. Например, реинвестиция государственного долга. Реинвестиции представляет собой максимально быстрое увеличение доходов, путем планомерного повторного вложения средств в объект инвестиций. Минусом реинвестиций является то, что инвестор получает всю прибыль только по окончанию инвестиционного периода. Пример 2. (слайд 12) В банке открыт срочный депозит на сумму 50 тыс. руб. по 12% на 3 года. Рассчитать начисленную сумму, если проценты начисляются ежеквартально. n = 3 t = 4 (в году – 4 квартала) По формуле сложных процентов S3 = (1+0.12/4)3*4*50000 = 1.0312*50000 = 71288 руб. Как следует из примеров 1 и 2, накопленная сумма будет возрастать тем быстрее, чем чаще начисляются проценты. Приведем обобщение формулы (2), когда прирост величины S на каждом этапе свой. (слайд 14) Пусть Sо, первоначальное значение величины S, в конце первого этапа испытывает изменение на р1%, в конце второго на р2%, а в конце третьего этапа на р3% и т.д. В конце n—го этапа значение величины S определяется формулой
Пример 3. (слайд 14) Торговая база закупила партию товара у изготовителя и поставила ее в магазин по оптовой цене, которая на 30% больше цены изготовителя. Магазин установил розничную цену на товар 20% выше оптовой. При распродаже магазин снизил эту цену на 10%. На сколько рублей больше заплатил покупатель по сравнению с ценой изготовителя, если на распродаже он приобрел товар за 140 руб. 40 коп. Пусть первоначальная цена составляет S руб., тогда по формуле (4) имеем: S0 (1 + 0,01·30)( 1 + 0,01·20)···( 1 – 0,01·10) = 140,4 S0·1,3·1,2·0,9 = S0·1,404 = 140,4 S0 = 140,4: 1,404 = 100 (руб.) Находим разность последней и первоначальной цены 140,4 – 100 = 40,4 |
|||||||||||||||||||||
|
Физкультминутка- 2 мин. |
||||||||||||||||||||||
|
IV этап: Актуализация знаний по теме вычисление по формулам в программе Microsoft Office Exsel (10 мин) Цель: повторение прежних знаний и навыков по теме «вычисление по формулам в программе Microsoft Office Exsel» |
Тема сегодняшнего урока хорошо вписывается в тему уроков информатики «Работа с электронной таблицей MS Excel. Решение расчетных задач». Вспомним что, на лекционном занятии мы с вами рассмотрели структуру, возможности, функции табличного процессора MS Excel, форматы представления данных в электронных таблицах программы, основные стандартные функции. Напомню, что электронные таблицы предназначены для хранения и обработки информации, представленной в табличной форме. Программа MS Excel относится к наиболее практически значимым и востребованным. Знания, полученные при изучении электронных таблиц, могут пригодиться вам при планировании на самых различных уровнях: от государственного до домашнего. Электронные таблицы позволяют производить быстрые, точные расчеты и автоматические перерасчеты при изменении исходных данных, представлять графически содержимое таблиц. С помощью электронных таблиц можно выполнять различные экономические, бухгалтерские и инженерные расчеты, а также строить диаграммы, моделировать и оптимизировать решение различных хозяйственных ситуаций и др. К преимуществам программы MS Excel относят также возможность автозаполнения электронных таблиц, что позволяет экономить время работы. Сегодня на уроке мы закрепим полученные теоретические знания по работе с программой MS Excel, а также научимся создавать, редактировать и форматировать электронные таблицы, использовать формулы и стандартные функции при решении практических задач. Устный опрос: — Сейчас мы с вами вспомним основные понятия, которые нам пригодятся сегодня на уроке. Для этого надо ответить на поставленные вопросы. Тот, кто знает ответ на вопрос, поднимает руку и отвечает по разрешению преподавателя Что называется ячейкой электронной таблицы? (Ячейка – место пересечения столбца и строки таблицы.) Как обозначаются заголовки столбцов электронной таблицы? (Заголовки столбцов обозначаются латинскими буквами или сочетаниями букв (например, А, С, АВ)) Как определяется адрес ячейки? (Адрес ячейки образуется из заголовка соответствующего столбца и номера соответствующей строки (например, В120)). Что называют диапазоном ячеек? Как задается адрес диапазона? (Группа смежных ячеек называется диапазоном. Диапазон задается адресами первой и последней входящих в него ячеек.) Что представляет собой файл, созданный в программе MS Excel? ( Каждый файл MS Excel является рабочей книгой, которая состоит из рабочих листов. Каждый рабочий лист представляет собой таблицу и имеет название. Количество, порядок расположения и названия рабочих листов можно изменять.) Как выделить несмежные ячейки, диапазоны ячеек, столбцы или строки? (При выделении надо удерживать клавишу CTRL на клавиатуре. Чтобы выделить целиком всю строку или весь столбец, надо щелкнуть мышкой по их заголовкам). Какие типы данных можно использовать в электронной таблице? (В работе с электронными таблицами можно выделить три основных типа данных: текст, число, формула.) Как выравниваются по умолчанию числовые данные в ячейках? Почему? (По умолчанию числа в ячейках выравниваются по правому краю, так как числа удобно выравнивать по разрядам (единицы под единицами, десятки под десятками и т.д.) Как выравнивается по умолчанию текст в ячейках таблицы? (Текст по умолчанию выравнивается в ячейке по левому краю.) С какого знака начинается ввод формулы в ячейку таблицы? (Ввод формулы в ячейку начинается со знака «=». Также можно использовать кнопку «Вставка функции» на Панели инструментов или команду Вставка Функция.) Какие типы данных можно использовать в формуле? (Формула может содержать числа, адреса ячеек, функции, знаки арифметических операций, знаки операций отношения.) Какую команду нужно выполнить для форматирования ячеек? (Чтобы отформатировать ячейки, надо выделить нужный диапазон и дать команду Формат Ячейки.) Какие форматы чисел можно использовать в электронной таблице? (Основные форматы чисел: Общий (без использования специальных средств, применяется для отображения числовых и текстовых данных), Числовой (выравниваются разряды), Денежный (выровнены разряды, используются символы валют), Финансовый (разряды выровнены по десятичному разделителю), Дата, Время, Процентный, Дробный, Экспоненциальный (в научной нотации Е+, например, 1,33Е+11), Текстовый, Дополнительный (почтовый индекс, телефонный номер и др.). Как изменить числовой формат данных? (Необходимо выполнить команду ФорматЯчейки, вкладка Число) Какие вкладки содержит диалоговое окно форматирования ячеек? («Число» — позволяет выбрать формат для отображения чисел, «Выравнивание» — задает метод выравнивания ячейки по горизонтали и вертикали, а также угол наклона надписи, «Шрифт» — определяет начертание шрифта, «Граница» — позволяет задать внешние и внутренние рамки таблицы,«Вид» — для управления цветовым оформлением, «Защита». |
|||||||||||||||||||||
|
V этап: Работа в парах за компьютером. Решение практических задач (10-15 мин.) Цель: Выработка практических навыков по теме. |
Сейчас мы закрепим полученные теоретические знания по математике и работе с программой MS Excel с помощью компьютера, а также продолжим учиться создавать, редактировать и форматировать электронные таблицы, использовать формулы и стандартные функции при решении практических задач. Предлагаю сесть за компьютеры парами и реализовать одну из разобранных задач с помощью табличного процессора MS Excel. Для этого вам нужно открыть документ Задачи к уроку.xls и выполнить все 3 примера с сегодняшнего урока выбрать которые расположены на листах под именами: Задача1, Задача2, Задача3. На работу у вам отводиться 15 минут. |
|||||||||||||||||||||
|
VI этап: Домашнее задание. (1 мин) |
№1. Сберегательный банк начисляет по вкладам ежегодно 5,5% годовых. Вкладчик внес в банк 150 тысяч рублей. Какой станет сумма вклада через 2 года? (Ответ: 166953,75 руб.) №2. Банк предлагает два варианта депозита (депози́т (банковский вклад) — это сумма денег, помещённая вкладчиком в банк на определённый или неопределённый срок. Банк пускает эти деньги в оборот, а в обмен выплачивает вкладчику проценты. Депозит является долгом банка перед вкладчиком, то есть, подлежит возврату.) 1) под 120% с начислением процентов в конце года; 2) под 100% с начислением процентов в конце каждого квартала. Определить более выгодный вариант размещения депозитов на один год. Решение. Более выгодным считается тот вариант, при котором наращенная за год сумма будет больше. Для оценки вариантов начальную сумму примем равную 100 руб. По первому варианту накопленная сумма будет равна (1+1,2)*100 руб. = 220 руб. По второму варианту проценты начисляются ежеквартально. По окончании первого квартала накопленная сумма равна (1+1,0/4)*100 руб. = 125 руб. По окончании 2-го квартала (1+1,0/4)2*100 руб. = 156 руб. За год накопленная сумма равна (1+1,0/4)4*100 руб. = 244 руб. Как следует из расчетов второй вариант значительно выгоднее (244>220). Правда, только при условии применения сложных процентов. |
|||||||||||||||||||||
|
VII этап: Подведение итогов. (3 мин) |
Рефлексия: • — С какими новыми понятиями мы познакомились на уроке? • — Что такое «сложный процент»? Чем он отличается от «простого процента»? • — Как найти «сложный процент»? • — Где используется эти проценты? • — Какие трудности вы испытывали при решении задач? • — Чему научились? • — Оцените свою работу на уроке. Итоги по решению задач (на компьютере). Выставление оценок. |
Галицкий М.Л.,. Гольдман А.М., Звавич Л.И. Сборник задач по алгебре 8-9 класс.- Москва «Просвещение», 1995г.
Кузнецова Л.В., Бунимович Е.А., Пигарев Б.П., Суворова С.Б. Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы.- Москва «Дрофа», 2001г.
Артеменко А.Р. Задачи на концентрацию и процентное содержание //Математика в школе» 1994 г, № 4.
Барабанов О.О. Задачи на проценты как проблема нормы словоупотребления // Математика в школе, 2003 , №5.
Водинчар М.И., Лайкова Т.А., Рябова Ю.К. Решение задач на смеси, растворы и сплавы методом уравнений //Математика в школе, 2001, №4.
Гончарова Л.В. Предметные недели в школе. Математика. Волгоград: издательство «Учитель», 2003г.
Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. Изучение процентов в основной школе //Математика в школе, 2002, №1.
Дорофеев Г.В., Седова Е.А. Процентные вычисления. – Москва: Дрофа, 2003г.
Симонов А.С. Некоторые применения геометрической прогрессии в экономике // Математика в школе, 1998, №3
Симонов А.С. Проценты и банковские расчеты //Математика в школе, 1998, № 4.
Симонов А.С. Сложные проценты //Математика в школе, 1998, № 5.
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Чтобы рассчитывать доходность банковских вкладов, нужно разобраться с простыми и сложными процентами.
- Простые проценты (P — principal) начисляют на первоначальный вклад в конце отчетного периода.
- Частота начисления процентов — период времени, в конце которого банк пересчитывает сумму на вкладе.
- Период вложения — время, на которое сделан вклад. При этом за период вложения проценты могут начисляться несколько раз.
- Процентная ставка (r — rate) — собственно величина, на которую умножается сумма на вкладе с определённой частотой.
Например, при начислении процентов раз в год по вкладу в 10 тыс. рублей под 12% годовых в конце мы получим прибыль 10 000 х 0,12 = 1200 рублей.
Сложные проценты — это когда проценты начисляются не только на основной капитал, но и на полученную в предыдущих периодах прибыль. То есть, с определённой периодичностью сумма вклада пересчитывается и начисляются, в том числе, проценты на проценты. Сумма растёт по экспоненте.
Сложные проценты могут называть по-разному:
- эффективные проценты;
- проценты на проценты;
- композиционный процент;
- норма доходности с учетом капитализации;
- норма доходности с учетом реинвестирования.
Расчёт сложных и простых процентов на реальном примере
Предположим, есть два брата, и у обоих на руках есть первоначальный капитал в размере 10 000 рублей. Они решают сделать вклад на 20 лет.
Первый брат делает вклад на депозитный счет с простой процентной ставкой 9%, а второй делает вклад на счет со сложной процентной ставкой 8%.
Начисление процентов происходит в конце каждого года.
Итак имеем:
- P0 = 10 000 руб.,
- r1 = 9%,
- r2 = 8%,
- t = 20 лет.
Формула расчета простых процентов:


Формула расчета сложных процентов:

t — число реинвестиций (капитализаций) в течение одного года. В нашем примере t = 1, поскольку начисление процентов происходит только раз в год.
В Excel рост капитала двух братьев будет выглядеть следующим образом.
- Период — год от момента открытия вклада.
- Капитал — сумма, на которую начисляются проценты в конце года.
- Процент — проценты по вкладу за этот год. В первом случае процент считаем от первоначального капитала, каждый год прибыль одинаковая. Во втором случае процент начисляется на весь капитал, то есть на первоначальную сумму плюс проценты за все прошлые годы — прибыль постоянно реинвестируется.
- Баланс — итого на счёте в конце года.
Если хотите узнать больше о работе в Excel, то рекомендуем записаться на наш обширный онлайн-курс «Академия Excel».

Можно заметить, что первые несколько лет вклад с простыми процентами выгоднее за счёт более высокой процентной ставки. Но затем ситуация меняется, и даже при меньшей ставке второй брат получил через 20 лет 466% от первоначальной суммы, а первый брат — 280%.
На рисунке ниже показан рост капитала при различных видах процента.

Корректировки на ситуацию вокруг
Чтобы получить высокую доходность при сложном проценте, необходимо ждать длительное время. С этим могут быть сложности в реальных условиях российской экономики (например: кризисы 1998 г., 2008 г., 2014 г. и т.д.).
Кроме того, уровень инфляции постепенно растёт, и прибыль по вкладам, особенно с более низкой ставкой при сложных процентах, может свестись к нулю.
Читайте также: О курсе «Excel Academy»
По норме доходность акции значительно превосходят доходность по банковским вкладам, но это более рискованный инструмент. С другой стороны, многие российские банки получают прибыль как раз за счёт активной деятельности на фондовом рынке — то есть несут те же риски, но прибыль вы получаете меньше.
Таким образом, банковские вклады могут выступать в роли сохранения первоначальной ценности капитала (с небольшим риском), и никак не являются механизмом получения прибыли. Чтобы капитал рос в имеющихся условиях, целесообразнее самостоятельно заниматься инвестированием в развивающиеся отрасли.
Это тоже интересно:
Правда и вымысел о финансовой безграмотности россиян
Как работать с дублями в Excel?
Что должен уметь финансист будущего: технические навыки и инструменты
КУРС
EXCEL ACADEMY
Научитесь использовать все прикладные инструменты из функционала MS Excel.
Блог SF Education
MS Office
Мультипликаторы для оценки бизнеса
Содержание статьи Основные методы сравнительного подхода к оценке бизнеса — метод рынка капитала и метод сделок, применение которых предполагают обязательный этап — расчет оценочных мультипликаторов…
Разбор структуры капитала «Райффайзенбанк»
Содержание статьи Капитал банка является обязательным условием образования и функционирования любого коммерческого банка. Капитал формируется из собственных средств акционеров или участников банка. Основной функцией…

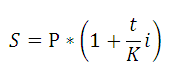
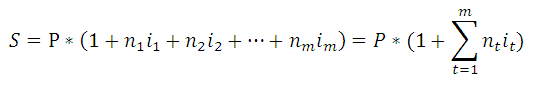
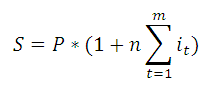






 (2.2) (выводят формулу учащиеся 2 ряда)
(2.2) (выводят формулу учащиеся 2 ряда)