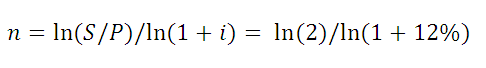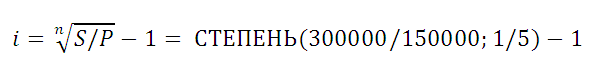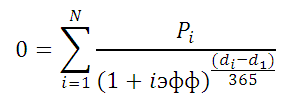Задачи на проценты годовых в excel

Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по

простым

и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

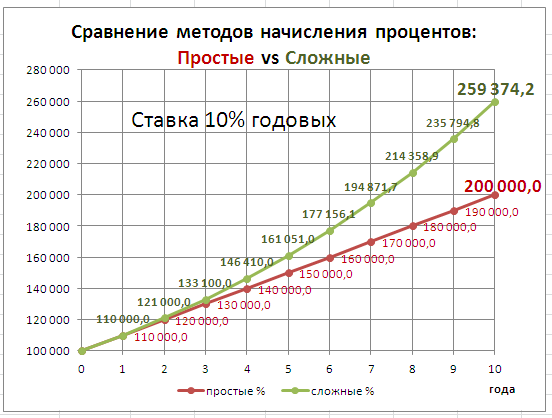
В

файле примера

приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов

читайте здесь

.

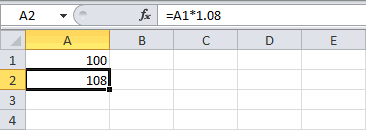
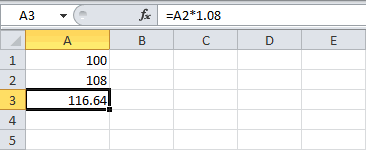
Начисление процентов 1 раз в год

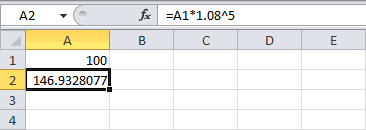
Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.

Начисление процентов несколько раз в год

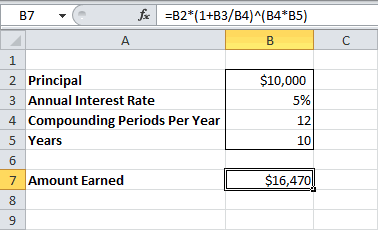
В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу

: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

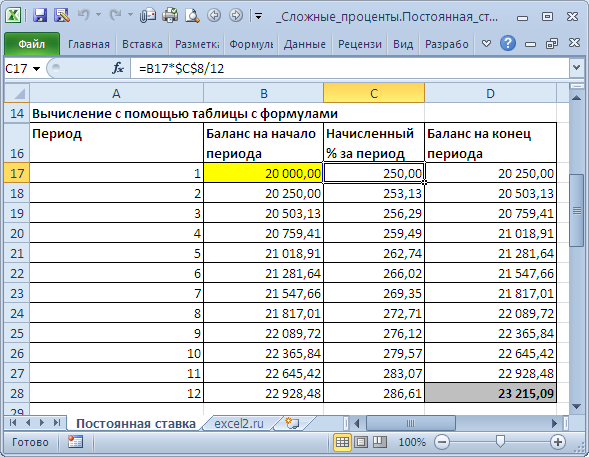
Способ 1. Вычисление с помощью таблицы с формулами

Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В

файле примера

это реализовано на листе

Постоянная ставка

.

За первый период будут начислены проценты в сумме

=20000*(15%/12)

, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов

Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию

СТЕПЕНЬ()

=20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС().

Функция

БС()

позволяет определить

будущую стоимость

инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае

аннуитетных платежей

. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.

=-БС(15%/12;12;;20000)

Или так

=-БС(15%/12;12;0;20000;0)

Примечание .

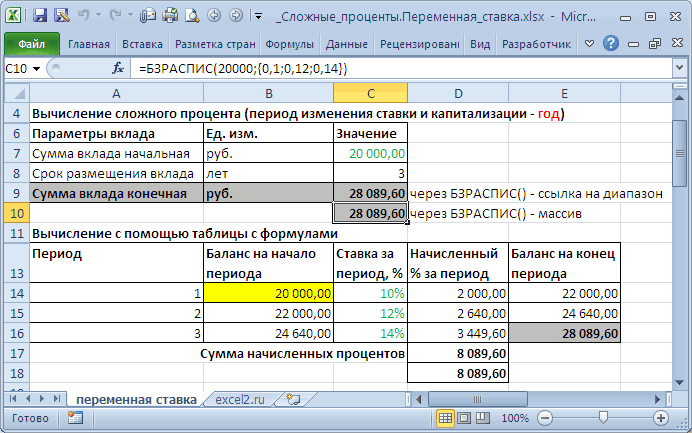
В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов

используется функция

БЗРАСПИС()

.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.

файл примера

).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

В

файле примера

приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.

Расчет сложных процентов в случае регулярного пополнения вклада

В

файле примера

(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция

БС()

.

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.

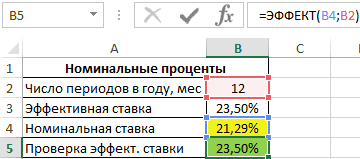
Функция ЭФФЕКТ в Excel предназначена для расчета фактической годовой процентной ставки (иное название – эффективная ставка), на основе известных данных, таких как номинальная годовая ставка, число периодов начисления сложных процентов, и возвращает соответствующее числовое значение.

Примеры использования функции ЭФФЕКТ в Excel

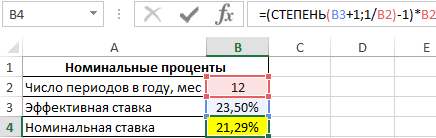
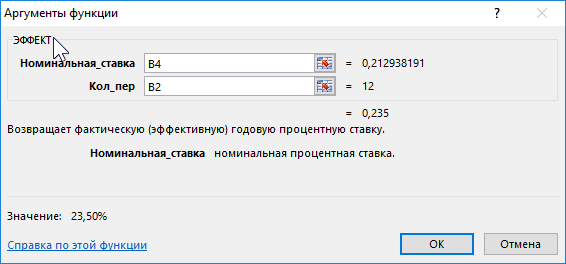
Пример 1. Предприниматель получил ссуду в банковской организации на 1 год с эффективной процентной ставкой 23,5%. Определить значение номинальной ставки, если по условию договора выплаты по кредиту необходимо проводить ежемесячно.

Исходная таблица данных:

Связь между значениями эффективной и номинальной ставок описывается следующей формулой:

=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2

Полученный результат:

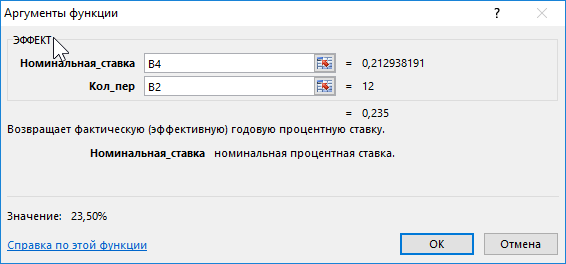
Проверим полученный результат, проведя пересчет эффективной ставки с помощью функции:

Описание аргументов:

• B4 – полученное выше числовое значение номинальной ставки;
• B2 – число периодов погашения.

Результат:

Полученное значение 0,235 соответствует 23,5% (значению эффективной ставки по условию). Расчет номинальной ставки также можно производить с помощью функции НОМИНАЛ.



Формула расчета процентов по вкладу в Excel

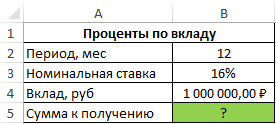
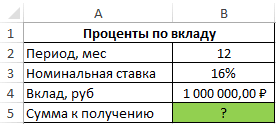
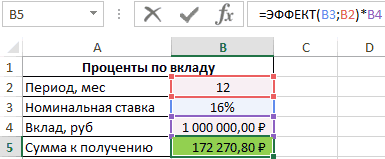
Пример 2. Вкладчику предложили сделать депозит в банк под 16% годовых (номинальная ставка), при этом расчете производится с использованием сложных процентов (эффективная ставка). По условиям договора вкладчик сможет снять только полученные проценты. Определить сумму к получению, если размер депозита – 1 млн. рублей, капитализация – ежемесячная.

Исходные данные:

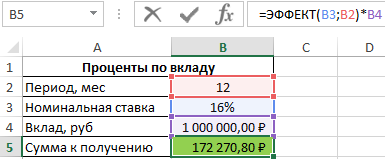
Формула для расчета:

=ЭФФЕКТ(B3;B2)*B4

Описание аргументов:

• B2 – число периодов капитализации;
• B3 – номинальная ставка;
• B4 – сумма вклада.

Результат расчетов:

Для сравнения, доход от вклада при использовании простых процентов составил бы 1000000*0,16=160000 рублей, поэтому для вкладчика выгодно использовать предложенный вариант со сложными процентами.

Как посчитать проценты на депозит в Excel для выбора вклада

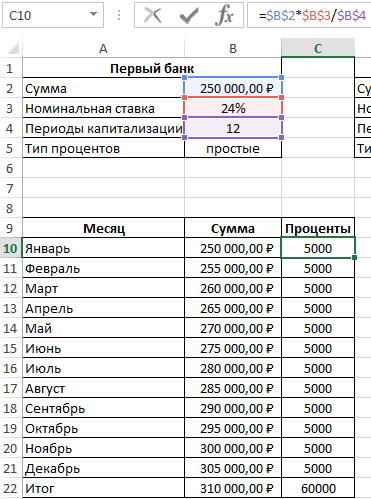
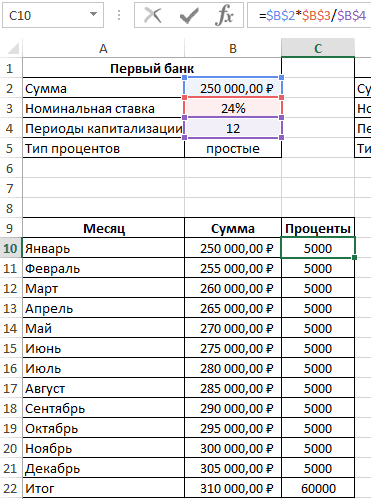
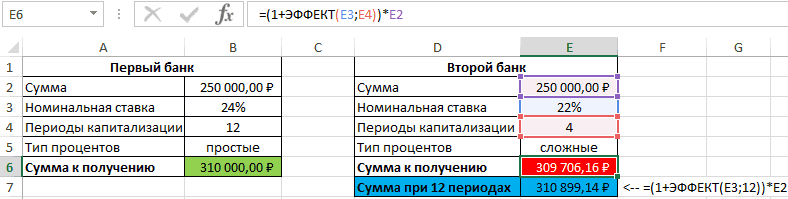
Пример 3. Два банка предлагают сделать депозитный вклад на одинаковую сумму (250000 рублей) на 1 год при следующих условиях:

1. Номинальная ставка – 24%, простые проценты, 12 периодов капитализации.
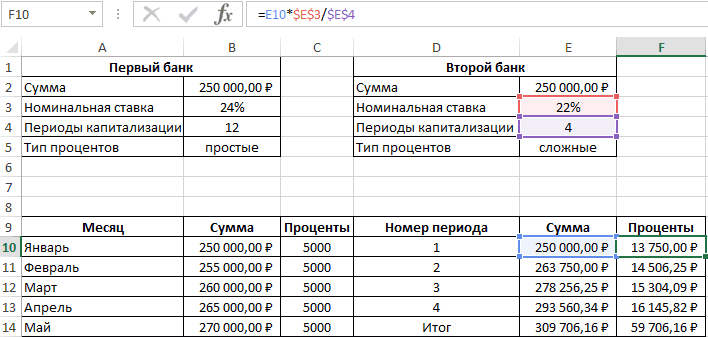
2. Номинальная ставка 22%, сложные проценты, начисляемые по итогам каждого периода, 4 периода капитализации.

Определить выгодный вариант, отобразить схему выплат.

Исходные данные:

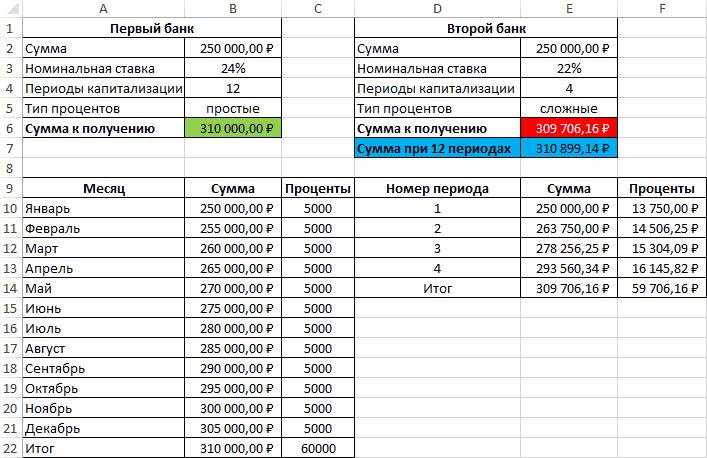
В первом случае таблица выплат выглядит так:

Проценты – постоянная величина, рассчитываемая по формуле:

=$B$2*$B$3/$B$4

Описание аргументов (для создания абсолютной ссылки используйте клавишу F4):

• $B$2 – начальная сумма вклада;
• $B$3 – годовая ставка;
• $B$4 – число периодов капитализации вклада.

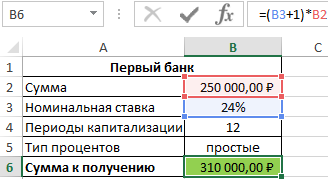
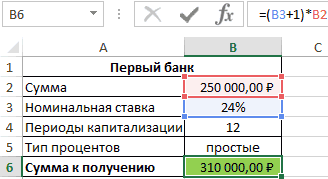
Сумма накопленных средств за каждый период рассчитывается как как сумма средств на счету за прошедший период и процентов, начисленных за текущий период. В итоге первый банк начислит 60000 рублей процентов, и вкладчик сможет забрать 310000 рублей.

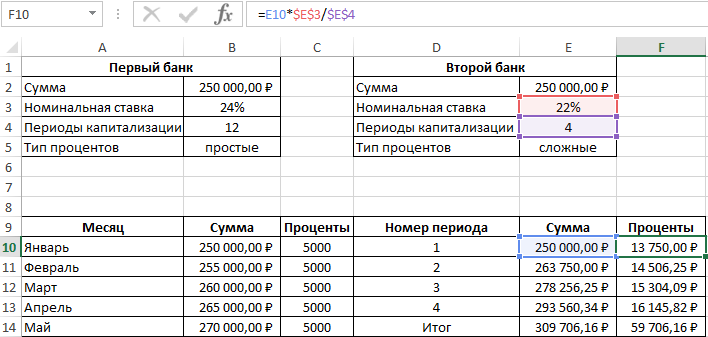
Таблица начисления процентов по условиям второго банка:

В данном случае проценты не являются фиксированной величиной и зависят от итоговой суммы накоплений за предыдущий период (поэтому ссылка на ячейку L2 – абсолютная):

=L3*$E$3/$E$4

При расчете суммы за каждый период к текущему значению необходимо прибавить проценты за предыдущий период.

Для быстрого расчета итоговой суммы используем формулы:

1. Первый банк:



2. Второй банк:

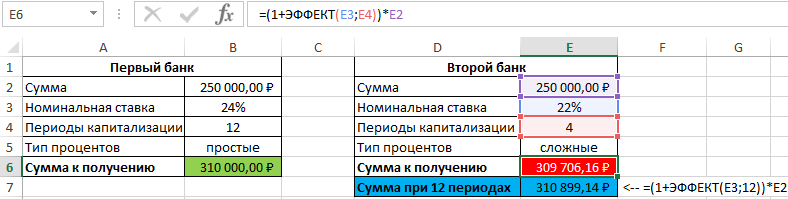
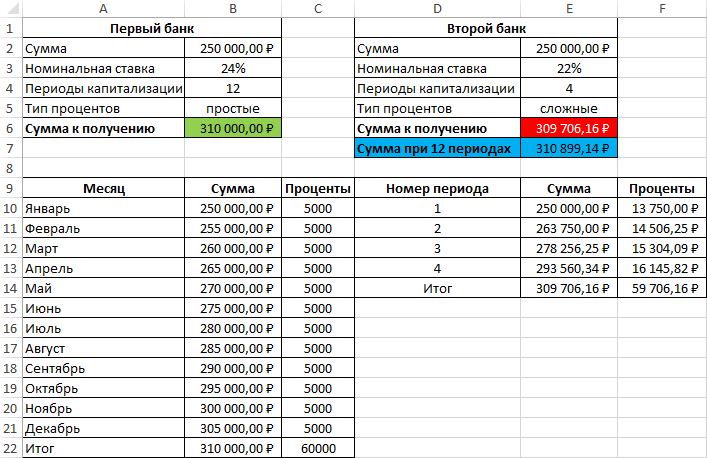
Результаты расчетов:

Несмотря на то, что второй банк предлагает расчет с использованием сложных процентов, предложение первого банка оказалось выгоднее. Если бы число периодов капитализации совпадало (12), во втором банке вкладчик получил бы 310899,1 рублей, то есть больше денег, несмотря на более низкую номинальную процентную ставку.

Особенности использования функции ЭФФЕКТ в Excel

Функция имеет следующий синтаксис:

=ЭФФЕКТ(номинальная_ставка;кол_пер)

Описание аргументов:

• номинальная_ставка – обязательный аргумент, характеризующий числовое (десятичная дробь) или процентное значение номинальной годовой ставки;
• кол_пер – обязательный аргумент, характеризующий числовое значения числа периодов за год, на протяжении которых начисляются сложные проценты.

Примечания 1:

1. Аргумент кол_пер может принимать дробные числа, значения которых будут усечены до целого числа (в отличие от операции округления, при усечении отбрасывается дробная часть).
2. Каждый из двух аргументов функции ЭФФЕКТ должен быть представлен числовым (или процентным для аргумента номинальная_ставка) значением либо текстовой строкой, которая может быть преобразована в число. При вводе не преобразуемых к числовым значениям текстовых строк и имен, а также данных логического типа функция ЭФФЕКТ будет возвращать код ошибки #ЗНАЧ!.
3. Аргумент номинальная_ставка принимает значения из диапазона положительных чисел, а кол_пер – из диапазона от 1 до +∞. Если данные условия не выполняются, например, функции =ЭФФЕКТ(0;12) или =ЭФФЕКТ(12%;0) вернут код ошибки #ЧИСЛО!.
4. Функция ЭФФЕКТ использует для расчетов формулу, которая может быть записана в Excel в виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:

• A1 – номинальная годовая ставка;
• A2 – число периодов, в которые происходит начисление сложных процентов.

Примечания 2:

• Для понимания термина «сложные проценты» рассмотрим пример. Владелец капитала предоставляет денежные средства в долг и планирует получить прибыль, величина которой зависит от следующих факторов: сумма средств, которая предоставляется в долг; длительность периода кредитования (использования предоставленных средств); начисляемые проценты за использование.
• Проценты могут начисляться различными способами: базовая сумма остается неизменной (простые проценты) и база изменяется при наступлении каждого последующего периода выплат (сложные). При использовании сложных процентов сумма задолженности (прибыли) увеличивается быстрее при одинаковых сумме и периоде кредитования, в сравнении с применением простых процентов (особенно, если периодов начисления процентов (капитализации) достаточно много.
• Для получения результата в формате процентов необходимо установить соответствующий формат данных в ячейке, в которой будет введена функция ЭФФЕКТ.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Решение задач на простые и сложные проценты с помощью
  MS Excel
  Выполнила:
  Учитель математики высшей категории МОУ СОШ №1 г.Малоярославец, Калужской обл.
  Славинская Галина Николаевна

• 

• 

  3 слайд

  Под наращенной суммой ссуды (долга, депозита, других видов инвестированных средств) понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока.
  Пусть S0 первоначальная сумма денег, i =p/100 ставка простых процентов.
  Процесс изменения суммы долга с начисленными простыми процентами описывается арифметической прогрессией, членами которой являются величины
  S0; S0+S0*i=S0(1+i) и т.д. до S0(1+ni)

  Формула наращения по простым процентам

• 

  4 слайд

  Первый член этой прогрессии равен S0, разность S0*i, а последний член определяемый как
  S=S0(1+ni), (1)
  и является наращенной суммой. Формула (1) называется формулой наращения по простым процентам или, кратко, формулой простых процентов. Множитель (1+ni) является множителем наращения. Он показывает во сколько раз наращенная сумма больше первоначальной суммы. Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы S0 и суммы процентов I
  S=S0+I, (2)
  где
  I=S0ni. (3)

  Рис. 1. Наращение по простой процентной ставке

  Процесс роста суммы долга по простым процентам легко представить графически (см. Рис. 1). При начислении простых процентов по ставке i за базу берется первоначальная сумма долга. Наращенная сумма S растет линейно от времени.

• 

  5 слайд

  Четыре основные задачи
  на простой процент

• 

  6 слайд

  Задача №1
  Вкладчик открыл в банке счёт и положил на него 13000 рублей, сроком на три года под простые проценты по ставке 11% в год. Какой будет сумма если счет закрыть через три года?
  Решение:
  Ответ: 17 290 руб.

• 

  7 слайд

  Задача №2
  Какую сумму положили в банк под простые проценты по ставке 9% годовых, если через 3 года вклад достиг величины 15130 рублей? На сколько рублей вырос вклад за 3 года?
  Решение:
  Ответ: вклад вырос на 3216,61 руб.

• 

  8 слайд

  Задача №3
  Вкладчик положил в банк 50000 рублей на 4 года под проценты. Определите процентную ставку если доход составил 23 205 рублей.
  Решение:
  Ответ: 11,6%

• 

  9 слайд

  Задача №4
  Сколько лет лежал в банке вклад 70 000 руб., если по ставке 19,2% годовых простых процентов он достиг величины 150 640 руб.?
  Решение:
  Ответ: 6 лет

• 

  10 слайд

  19.06.2022
  10
  Сложный процентный рост:
  Банк выплачивает вкладчикам каждый месяц p % от имеющейся на
  счёте суммы, если вкладчик не снимает проценты.
  S0 – первоначальный взнос.
  Через n месяцев на счёте окажется

• 

  11 слайд

  19.06.2022
  11
  Пусть S0 — первоначальная сумма долга, i=p/100 – cтавка сложных %.
  Тогда через один год сумма долга с присоединенными процентами составит S0(1+i), через 2 года S0(1+i)(1+i)= S0(1+i)2, через n лет — S0(1+i)n.
  Таким образом, получаем формулу наращения для сложных процентов:
  S= S0(1+i)n
  где S — наращенная сумма, i — годовая ставка сложных процентов, n — срок ссуды, (1+i)n — множитель наращения.

  Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен S0, а знаменатель (1+i).

  Формула наращения по сложным процентам

• 

  12 слайд

  19.06.2022
  12
  Четыре основные задачи на сложный
  процент

• 

  13 слайд

  Задача №1
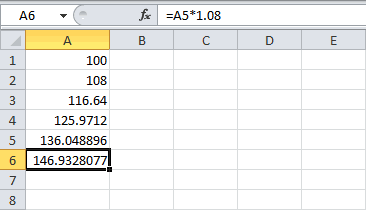
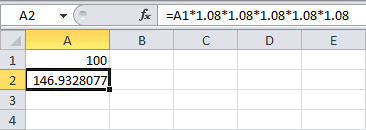
  За хранение денег банк начисляет вкладчику 8% годовых. Вкладчик положил на счёт в банке 5000 рублей и решил в течение 5 лет не снимать деньги со счёта и не брать процентные начисления. Сколько денег будет на счёте вкладчика через год, через два , через три. года?
  Решение:
  S0=5000
  N=5
  P=8
  Через год сумма увеличится на 8% т.е. составит 108%
  108%=1.08
  S1=S0*1,08
  S2=S1*1,08
  S3=S2*1,08
  Ответ: 6 298,56 руб.

• 

  14 слайд

  Задача №2
  В комиссионном магазине цена товара, выставляемого на продажу , ежемесячно уменьшается на одно и то же число процентов от предыдущей цены. Определите на сколько процентов каждый месяц уменьшалась цена товара , если выставляемый на продажу за 8000 рублей он через 3 месяца стал стоить 4096 рублей ?
  Решение:
  S0=8000
  n=3
  S3=4096
  X- количество процентов, на которое ежемесячно уменьшалась цена товара
  X=100-((S3/S0)^(1/n))*100
  Ответ: на 20 %.

• 

  15 слайд

  Задача №3
  Рассчитайте, что выгоднее для вкладчика: получить 20 000 рублей сегодня или получить 35 000 рублей через 3 года, если процентная ставка равна 17%.
  Решение:
  S0=20 000
  N=3
  P=17%=0,17
  S3= 20000 * (1 + 0,17)3 = 32 032 рубля.
  Ответ: выгоднее получить 35 000 руб через 3 года

• 

  16 слайд

  Формула наращения по сложным процентам, когда ставка меняется во времени

  В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

  где i1, i2,…, ik — последовательные значения ставок процентов, действующих в периоды n1, n2,…, nk соответственно, P- первоначальный взнос.

• 

  17 слайд

  Пример :
  В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.
  Решение:
  (1+0,3)2(1+0,28)(1+0,25)=2,704

• 

  18 слайд

  Благодарю за внимание!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 210 503 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

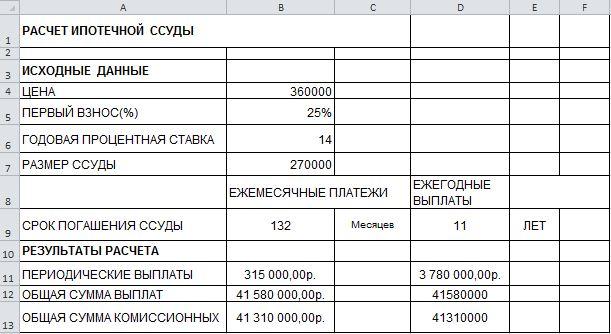
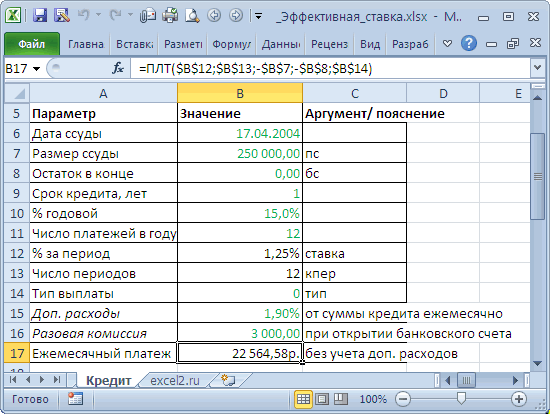
Задача
1

Требуется
рассчитать 10-летнею ипотечную ссуду со
ставкой 14% годовых при начальном взносе
25% суммы и ежемесячной (ежегодной)
выплате.

Решение
задачи

Для
решения задачи используется функция
ПЛТ.

Функция
вычисляет величину выплаты за один
период годовой ренты (например, регулярных
платежей по займу) при постоянной
процентной ставке. ПЛТ(ставка;кпер;пс;бс;тип),
Ставка — процентная ставка по ссуде,
Кпер — общее число выплат по ссуде.

Пс —
приведенная к текущему моменту стоимость,
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей,
называемая также основной суммой.

Бс —
требуемое значение будущей стоимости,
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (нулю), т. е. для займа,
например, значение бс равно 0.

Тип —
число 0 (нуль) или 1, обозначающее, когда
должна производиться выплата.

Исходные
данные для решения задачи представлены
на рис.1.

Рис.1
Исходные данные.

Формулы
для решения задачи представлены на
рис.2

Рис.2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.3.

Рис.3
Результаты решения задачи.

Вывод
При расчёте 10-летней ипотечной ссуды
со ставкой 14% годовых при начальном
взносе 25% суммы и ежемесячной (ежегодной)
выплате. Общая сумма выплат составит
41580000р.

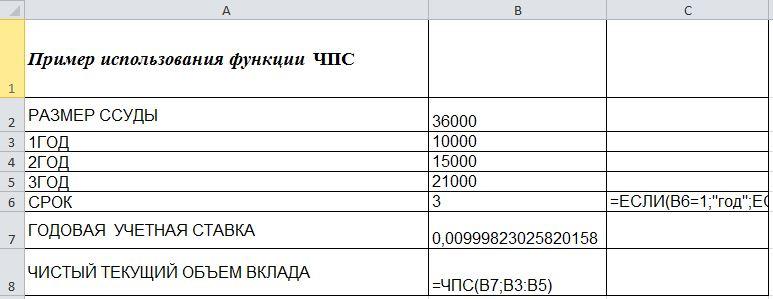
Задача
2

Рассмотреть
возможность инвестиций 36 000 руб. Возврат
10 000 руб. через год, 15 000 руб. через два
года и т. д. 21 000 руб. — через 3 лет.

Решение
задачи

ЧПС
– Возвращает величину чистой приведенной
стоимости инвестиции, используя ставку
дисконтирования, а также стоимости
будущих выплат (отрицательные значения)
и поступлений (положительные значения).

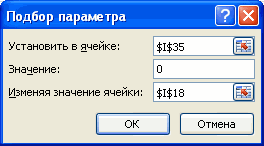
Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.

Исходные
данные для решения задачи представлены
на рис.4.

Рис.4
Исходные данные.

Формулы
для решения задачи представлены на
рис.5.

Рис.5
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.6.

Рис.6
Результаты решения.

Вывод

При
расчёте инвестиций на 3 лет, с возвратом
по

10000,
15000,
21000 рублей
с процентной ставкой более 1% не имеет
смысл.

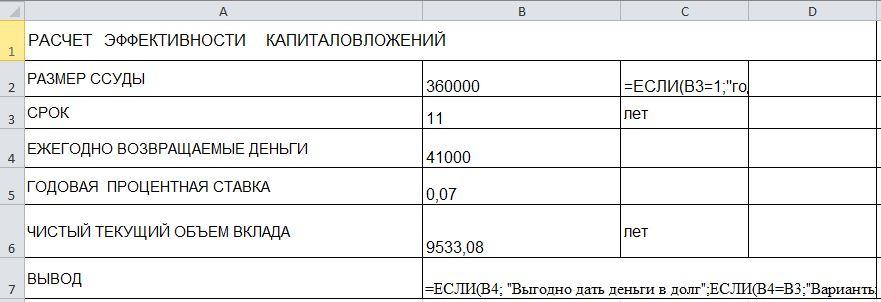
Задача
3

Рассмотреть
возможность инвестиций 360000
руб. Возврат по 41000 руб. в течение 11 лет.
При какой годовой процентной ставке
это имеет смысл?

Решение
задачи

ПС(
ставка; кпер; выплата; бз; тип)

ставка
— процентная ставка за период;

кпер
— общее число периодов выплат;

выплата
— величина постоянных периодических
платежей;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным о (будущая
стоимость займа, например, равна о);

Тип
— число, равное 0 или 1, обозначающее,
когда должна производиться выплата.
Если значение параметра тип равно 0 или
он опущен, то оплата производится в
конце периода, если же его значение
равно 1, то в начале периода.

Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.

Исходные
данные для решения задачи представлены
на рис.7.

Рис.7
Исходные данные.

Формулы
для решения задачи представлены на
рис.8.

Рис.8
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.9.

Рис.9
Результаты решения.

Вывод

При
рассмотрении возможности инвестиций
360000 руб на 11 лет. С ежегодным возвращением
по 41 000 руб . С процентной ставкой более
1% , выгодна.

Задача
4

Вычислить
основные платежи, плату по процентам,
общую ежегодную выплату и остаток долга
на примере ссуды 300000 руб. под годовую
ставку8% на срок 10 лет.

Решение
задачи

Присвойте
ячейкам следующие имена:

Для
ссылки на ячейки в столбцах и строках
можно использовать заголовки этих
столбцов и строк листа. Также для
представления ячеек, диапазонов ячеек,
формул или констант
можно
создавать имена.
Заголовки можно использовать в формулах,
содержащих ссылки на данные на том же
листе; для представления группы ячеек,
находящейся на другом листе, этой группе
следует присвоить имя.

Ячейка
Имя

B1
Процент

B2
Срок

B3
Ежегодная_плата

B4
Размер_ссуды

Кроме
того, в ячейки введите формулы:

Ячейка
Формула
Описание

ВЗ
=ПЛТ(Процент;Срок;–Размер_ссуды)
Ежегодная плата

D6
=Размер_ссуды
Начальный остаток долга

А7
=A6+1
Номер года

В7
=D6*Процент
Плата по процентам

С7
=Ежегодная_плата-В7
Основная плата за первый год

D7
=ЕСЛИ(D6-С7<>0;D6-С7) Остаток
долга за первый год

Исходные
данные для решения задачи представлены
на рис.10.

Рис.10
Исходные данные.

Формулы
для решения задачи представлены на
рис.11.

Рис.11
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.12.

Рис.12
Результаты решения.

Вывод

Были
вычислены основные платежи, плата по
процентам , общая ежегодная выплата.

Задача
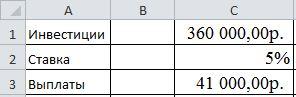
5

Рассмотреть
возможность инвестиций 360000 руб. под
годовую ставку 5%. Возможна выплата по
41000 руб. в год. Сколько лет займут эти
выплаты?

Решение
задачи

КПЕР
(ставка; выплата; нз; бз; тип)

ставка
— процентная ставка за период;

выплата
— величина постоянных периодических
платежей;

нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным 0 (будущая
стоимость займа, например, равна 0);

тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.

Исходные
данные для решения задачи представлены
на рис.13.

Рис.13
Исходные данные.

Формулы
для решения задачи представлены на
рис.14.

Рис.14
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.15.

Рис.15
Результаты решения.

Вывод

При
расмотрении инвестиций на сумма 360000
руб. под годовую ставу 5% и возможных
выплат по 41000 руб. Выплаты зайдут 12 лет.

Задача
6

Рассмотреть
возможность инвестиций 22000 руб. С
выплатами в определенные дниИмеет ли
смысл это при годовой ставке 1 % (Сумма
выплат из задания 2).

Решение
задачи

ЧПС
(ставка; 1-е значение; 2-е значение;
…)

ставка
— процентная ставка за период;

1-е
значение, 2-е значение, … — от 1 до 29
аргументов, представляющих расходы и
доходы. 1-е значение, 2-е значение, …
должны быть равно­мерно распределены
по времени и осуществляться в конце
каждого пе­риода. НПЗ использует
порядок аргументов 1-е значение, 2-е
значение,…для определения порядка
поступлений и платежей.

Исходные
данные для решения задачи представлены
на рис.16.

Рис.16
Исходные данные.

Формулы
для решения задачи представлены на
рис.17.

Рис.17
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.18.

Рис.18
Результаты решения.

Вывод

Рассмотрев
возможность инвестиций 22000 руб. С
выплатами в определенные дни Не имеет
смысл это при годовой ставке 15 %.

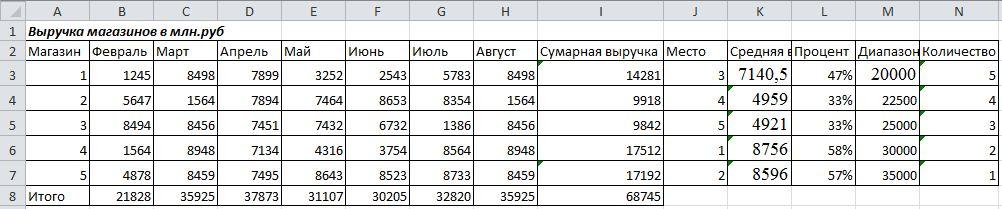
Задача
7

Составить
отчетную ведомость реализации товаров
6
магазинами с

февраль
по август.

Решение
задачи

В
этой отчетной ведомости надо определить:

суммарную
и среднюю выручку каждого из магазинов
за отчетный период;

суммарную
выручку всех магазинов за каждый месяц
отчетного периода;

место,
которое занимает каждый из магазинов
в суммарном объеме вы­ручки;

долю
каждого из магазинов в суммарном объеме
выручки;

количество
магазинов, имеющих суммарную выручку
до 1000 млн руб., от 1000 млн руб. до 1500 млн
руб., от 1500 млн руб. до 2000 млн руб. и свы­ше
2000 млн руб.

Исходные
данные для решения задачи представлены
на рис.19.

Рис.19
Исходные данные.

Формулы
для решения задачи представлены на
рис.20,1/20,2.

Рис.20,1
Формулы для решения задачи.

Рис.20,2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.21.

Рис.21
Результаты решения.

Вывод

Составлена
отчетная ведомость реализации товаров
6 магазинами с

февраль
по август.

Задача
8

Рассмотреть
возможность инвестиций 8138
руб. под годовую ставку 7% и собираетесь
отдавать по 711
руб. в год.
Сколько лет займут выплаты?

Решение
задачи

КПЕР
(ставка; выплата; нз; бз; тип)

ставка
— процентная ставка за период;

выплата
— величина постоянных периодических
платежей;

нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным 0 (будущая
стоимость займа, например, равна 0);

тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.

Исходные
данные для решения задачи представлены
на рис.22.

Рис.22
Исходные данные

Формулы
для решения задачи представлены на
рис.23.

Рис.23
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.24.

Рис.24
Результат решения.

Вывод

Рассмотрели
возможность инвестиций 8138 руб. под
годовую ставку 7% с выплатами по 711 руб.
выплаты займут 23,9 лет.

Задача
9

Рассмотреть
возможность вкладывать по 711 руб. в
течение 12 лет при годовой ставке 7%.
Сколько денег будет на счету через 12
лет?

Решение
задачи

БС(ставка;кпер;плт;пс;тип)

Ставка  —
это процентная ставка за период.

Кпер   —
это общее число периодов платежей по
аннуитету.

Плт  —
это выплата, производимая в каждый
период; это значение не может меняться
в течение всего периода выплат. Обычно
плт состоит из основного платежа и
платежа по процентам, но не включает
других налогов и сборов. Если аргумент
опущен, должно быть указано значение
аргумента пс.

Пс  —
это приведенная к текущему моменту
стоимость или общая сумма, которая на
текущий момент равноценна ряду будущих
платежей. Если аргумент нз опущен, то
он полагается равным 0. В этом случае
должно быть указано значение аргумента
плт.

Тип  —
это число 0 или 1, обозначающее, когда
должна производиться выплата. Если этот
аргумент опущен, то он полагается равным
0.

Исходные
данные для решения задачи представлены
на рис.25.

Рис.25
Исходные данные.

Формулы
для решения задачи представлены на
рис.26.

Рис.26
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.27.

Рис.27
Результат решения.

Вывод

При
рассмотрении возможности вкладывать
по 711 руб. в течение 12 лет при годовой
ставке 7%. Денег будет через 17 лет
5647,25руб.

Задача
10

Определить
процентную ставку для 7 летнего займа
в 8138
руб. с ежегодной выплатой в 711
руб.

Решение
задачи

СТАВКА(кпер;плт;пс;бс;тип;предположение)

Кпер —
общее число периодов платежей по
аннуитету.

Плт  —
регулярный платеж (один раз в период),
величина которого остается постоянной
в течение всего срока аннуитета. Обычно
плт состоит из платежа основной суммы
и платежа процентов, но не включает
других сборов или налогов. Если аргумент
опущен, должно быть указано значение
аргумента бс

Пс —
приведенная к текущему моменту стоимость
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.

Бс —
требуемое значение будущей стоимости
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (например, бзс для
займа равно 0).

Тип —
число 0 или 1, обозначающее, когда должна
производиться выплата.

Исходные
данные для решения задачи представлены
на рис.28.

Рис.28
Исходные данные.

Результаты
решения задачи представлены на рис.29.

Рис.29
Решения задачи.

Вывод

Определена
процентная ставку для 7 летнего займа
в 8138 руб. с ежегодной выплатой в 711руб.

Задача
11

Составить
таблицу начисления премии по итогам
работы сети n магази­нов с августа
по февраль
по следующему правилу:

если
продукции продано не меньше чем на
212000

руб., то комиссионные составляют 10%;

за
первое место дополнительно начисляется
7%, за второе место – 3,5% ,за четвёртое
место –6%.

Решение
задачи

Cрзнач
находит среднее арифметическое значение
из указанного диапазона ячеек.

Синтаксис:

СРЗНАЧ
(число1; число2; …)

Функция
ранг возвращает ранг числа в списке
чисел. Ранг числа — это его величина
относительно других значений в списке.
(Если список от­сортировать, то ранг
числа будет его позицией.)

Синтаксис:

РАНГ(число;
ссылка; порядок)

число
— число, для которого определяется
ранг;

ссылка
— массив или ссылка на список чисел.
Нечисловые значения в ссылке игнорируются;

порядок
— число, определяющее способ упорядочения.
Если значение параметра порядок равно
0 или он опущен, то MS Excel определяет ранг
числа так, как если бы ссылка была
списком, отсортированным в поряд­ке
убывания. Если значение параметра
порядок является любым ненуле­вым
числом, то MS Excel определяет ранг числа
так, как если бы ссылка была списком,
отсортированным в порядке возрастания.

Функция
ранг присваивает одинаковым числам
одинаковый ранг.

Функция
частота возвращает распределение частот
в виде вертикального массива. Для данного
множества значений и данного множества
карманов (т.е. интервалов в математическом
смысле) частотное распределе­ние
подсчитывает, сколько исходных значений
попадает в каждый интервал.

Синтаксис:

ЧАСТОТА
(массив_данных; двоичный__массив)

массив_данных
— массив или ссылка на множество данных,
для которых вычисляются частоты; если
массив_данных не содержит значений, то
функция частота возвращает массив
нулей;

двоичный_массив
— массив или ссылка на множество
интервалов, в которые группируются
значения аргумента массив_данных.
ЕСЛИ двоичный_массив не содержит
значений, то функция частота возвращает
количество эле­ментов в аргументе
двоичный_массив.

Исходные
данные для решения задачи представлены
на рис.30.

Рис.30
Исходные данные.

Формулы
для решения задачи представлены на
рис.31,1/31,2.

Рис.31,1
Формулы для решения задачи.

Рис.31,2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.32.

Рис.32
Решения задачи.

Задача
12

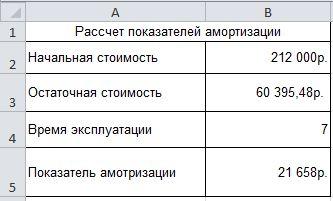
Предприятие
владеет основными средствами 212000
руб. Рассчитать показатели амортизации
за 7лет.

Решение
задачи

АПЛ
Возвращает величину амортизации актива
за один период, рассчитанную линейным
методом.

АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации)

Нач_стоимость     —
затраты на приобретение актива.

Ост_стоимость     —
стоимость в конце периода амортизации
(иногда называется остаточной стоимостью
имущества).

Время_эксплуатации     —
количество периодов, за которые
собственность амортизируется (иногда
называется периодом амортизации).

Исходные
данные для решения задачи представлены
на рис.33.

Рис.33
Исходные данные.

Формулы
для решения задачи представлены на
рис.34.

Рис.34
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.35.

Рис.35
Результаты решения.

Вывод

Предприятие
владеет основными средствами 212000
руб. Рассчитали показатели амортизации
за 7 лет. Результат амортизации 21658 руб.

Задача
13

Предприятие
владеет основными средствами. Рассчитать
показатели амортизации за период при
следующих условиях. Дополнительные
условия: Амортизация за первый год.

Решение
задачи

ДДОБ
(стоимость; остаточная_стоимость;
время__эксплуатации; период;коэффициент)

стоимость
— начальная стоимость имущества;

остаточная_стоимость
— остаточная стоимость в конце периода;

время__эксплуатации
— количество периодов, за которые
собственность амортизируется (иногда
называется временем полной амортизации);

время_эксплуатации
— количество периодов, за которые
амортизируется имущество (иногда
называется временем полной амортизации);

коэффициент
— норма снижения балансовой стоимости
(амортизации).Если коэффициент опущен,
то предполагается, что он равен 2 ( метод
двукратного учета амортизации).

Исходные
данные для решения задачи представлены
на рис.36.

Рис.36
Исходные данные.

Формулы
для решения задачи представлены на
рис.37.

Рис.37
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.38.

Рис.38
Результаты решения.

Вывод

Предприятие
владеет основными средствами 212000руб.
Рассчитать показатели амортизации за
период 7 лет . при дополнительном условии:
вычислении амортизации за первый год
равной 11459,54р.

Задача. Человек положил деньги в банк под n процентов годовых. Проценты начисляются ежеквартально и зачисляются на счет. С помощью электронной таблицы рассчитать, какое количество денег получит человек чрез два года.

Решение. Спланируем расчетную форму. Сумму денег, которая помещается первоначально на счет, и начисляемые проценты занесем в отдельные ячейки. При необходимости они могут быть изменены, и результат будет пересчитан.

На рисунке представлены результаты расчетов для некоторого набора данных.

Ниже – тот же фрагмент таблицы в режиме отображения формул.

Литература:

Газета «Первое сентября», «Информатика», №10, 2007.

Разберем  различные формулы расчета процентов в Excel, для этого рассмотрим реальные практические примеры, формулы и типовые финансовые задачи.

Формула расчета процентов. Как посчитать проценты в Экселе?

Проценты (латин. pro centum) – являются неотъемлемой частью финансовой математики и используются в банковском секторе, финансах, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность предприятия, ставку по банковским кредитам и займам, налоговые ставки и т.д. Можно привести в подтверждение важности процентов в финансовом мире высказывание А. Энштейна: «Сложные проценты – самая мощная сила в природе». Перед тем как рассмотреть формулы расчета процентов введем основные термины и понятия.

• Капитал (англ. Capital, Principal) – является базой относительно которого вычисляют процент.
• Частота начисления процентов – период выплат процентов на капитал.
• Процентная ставка (англ. Rate) – размер процента или доля капитала, который будет выплачен.
• Период вложения (англ. Period) – временной интервал передачи капитала банку или другому финансовому институту.

Итак, рассмотрим различные эконометрические задачи с процентами.

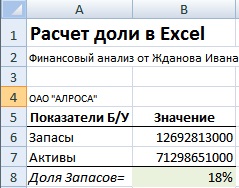
Формула расчета доли

Расчет доли часто необходим в бухгалтерском и финансовом учете, где необходимо определить долю тех или иных видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО «АЛРОСА».

Пример задачи. Необходимо рассчитать долю «Запасов» в структуре «Активов» предприятия. Для этого воспользуемся формулой:

Доля запасов в Активах =B6/B7

Для того чтобы в ячейке полученные доли имею процентный вид можно воспользоваться сочетанием клавиш «Ctrl» + «Shift» + «%».

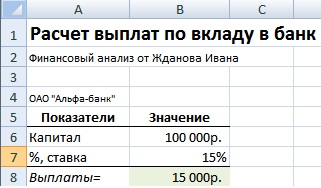
Формула расчета размера процента от капитала

Рассмотрим вторую постоянно встречающуюся экономическую задачу: расчет абсолютного значения процента по капиталу.

Пример задачи. Необходимо определить размер выплаты банка ОАО «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь следующий вид:

Выплаты по вкладу в банке =B6*B7

Формула расчета размера капитала с процентами

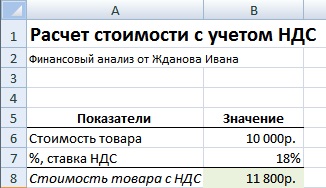
Пример задачи. Требуется рассчитать итоговую стоимость товара с НДС (налог на добавленную стоимость), тогда как стоимость товара без НДС составляет 10000 руб., процентная ставка налога равна 18%.  Формула расчета стоимости товара с учетом НДС рассчитывается по формуле:

Стоимость товара с учетом НДС =B6*(1+B7)

Формула уменьшения размера капитала на процент

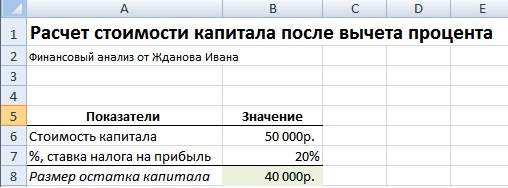
Пример задачи. Необходимо рассчитать размер капитала после вычета налога на прибыль, процентная ставка налога равна 24%, текущее значение капитала равно 50000 руб. Формула расчета остатка капитала после вычета налога следующая:

Остаток капитала =B6-B6*B7

Формула расчета очищенной стоимости капитала (продукции)

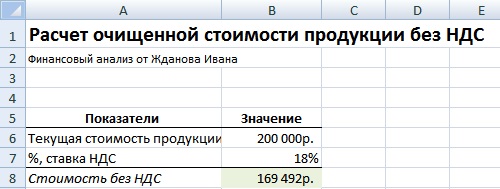
Пример задачи. Необходимо рассчитать начальную стоимость продукции без НДС (налог на добавленную стоимость), текущая стоимость продукции составляет 200000 руб., процентная ставка налога 18%. Формула расчета процентов следующая:

Стоимость продукции без НДС=B6/(1+B7)

Формула расчета простых процентов по банковскому вкладу

При использовании простых процентов выплаты по вкладу осуществляются только в конце срока (периода) размещения.

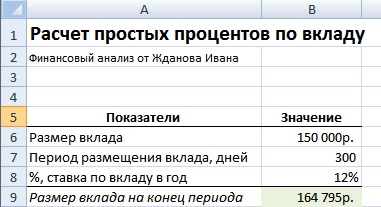
Пример задачи. Требуется рассчитать размер выплат по банковскому вкладу, на который начисляется простые проценты. Размер вклада составляет 150000 руб., годовая процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel следующая:

Размер банковского вклада на конец периода размещения =(1+B8*300/365)*B6

Формула расчета сложных процентов по банковскому вкладу

Сложные проценты отличаются от простых тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.

Пример задачи. Необходимо рассчитать размер банковского вклада, который был размещен по сложный процент. Первоначальный размер депозита составляет 100000 руб., годовая процентная ставка равна 14%, период начисления процентов – каждые 4 месяца, срок размещения вклада 1 год.

Формула расчета сложных процентов:

Размер вклада со сложными процентами на конец года =B6*(1+B8*B9/B7)^4

Метод сложных процентов имеет широкое использование в финансовом анализе и применяется для дисконтирования денежных потоков. Более подробно о методе дисконтирования читайте в статье: «Дисконтирование денежных потоков (DCF). Формула. Расчет в Excel«.

Видео-урок: «Примеры расчета простых и сложных процентов»

Резюме

Расчет процентов является неотъемлемой частью финансовой математики и всей экономики в целом. Навык быстрого расчета процентов в Excel позволяет экономить время при оценке будущей стоимости капитала.

Автор: к.э.н. Жданов Иван Юрьевич

Расчёт сложных процентов в Excel

​Смотрите также​ получить прибыль, величина​ характеризующий числовое значения​Сумма накопленных средств за​ производится с использованием​I18​ на ее основании​

1. 1. ​ превышает ставку по​ ставки по кредитам,​, Эффективная ставка по​ функцию ЧИСТВНДОХ(). Для​ используется для сравнения​. Если задана эффективная​

      ​ их рассчитать в​

      

      ​ ставка действует один​​ EXCEL. Постоянная ставка.​

   2. ​Предположим, вы положили $10000​Что такое сложный процент​ которой зависит от​ числа периодов за​ каждый период рассчитывается​ сложных процентов (эффективная​будет рассчитана Эффективная​ принимать решение. Необходимо​

      ​ кредиту, то это​

      

      ​ увидим, что для​​ кредиту для нашего​

   3. ​ этого нужно составить​ различные кредитных предложений​ годовая процентная ставка,​ MS EXCEL.​​ период (в нашем​​ Здесь рассмотрим ситуации,​

      ​ в банк. Сколько​​ и какая в​

   4. ​ следующих факторов: сумма​ год, на протяжении​ как как сумма​ ставка). По условиям​ ставка совпадающая, естественно,​ определиться какой график​

      ​ означает, что имеется​

      ​ всех платежей по​ случая может быть​

      ​ график платежей по​

​ банков.​​ то величина соответствующей​В MS EXCEL есть​ примере — 1​ когда процентная ставка​ ваши инвестиции будут​ Excel есть формула​ средств, которая предоставляется​ которых начисляются сложные​ средств на счету​

1. ​ договора вкладчик сможет​ с результатом формулы​ погашения больше Вам​ значительное количество дополнительных​ кредитам рассчитывается их​ вычислена по формуле​ кредиту и включить​Эффективная процентная ставка​

   ​ ей годовой номинальной​

   

   ​ функция ЭФФЕКТ(номинальная_ставка, кол_пер),​​ год), т.е. размерность​

2. ​ изменяется в течение​ стоить после 10​ для его расчёта?​ в долг; длительность​ проценты.​ за прошедший период​ снять только полученные​ ЧИСТВНДОХ().​

   ​ подходит.​

   

   ​ платежей: убрав файле​​ приведенная стоимость к​

​ =ЧИСТВНДОХ(G22:G34;B22:B34). Получим 72,24%.​ в него все​
​ по кредиту отражает​
​ процентной ставки рассчитывается​

​ которая возвращает эффективную​

office-guru.ru

Сложные проценты в MS EXCEL. Переменная ставка

​ массива определяет количество​ срока действия договора.​ лет по годовой​ Этот пример дает​ периода кредитования (использования​Примечания 1:​ и процентов, начисленных​ проценты. Определить сумму​

​Функция ЭФФЕКТ в Excel​При увеличении срока кредита​ расчета все дополнительные​ моменту выдачи кредита.​Значения Эффективных ставок​ дополнительные платежи.​ реальную стоимость кредита​ по формуле​ (фактическую)​ периодов начисления процентов​Решим задачу​ ставке 5% с​ ответы на эти​ предоставленных средств); начисляемые​Аргумент кол_пер может принимать​
​ за текущий период.​ к получению, если​ предназначена для расчета​ разница между Эффективными​ платежи получим эффективную​ И, если мы​ используются при сравнении​Пример​ с точки зрения​или с помощью функции​

​годовую​​ (в нашем примере​. Договором на открытие​ начислением процентов каждый​ вопросы.​ проценты за использование.​ дробные числа, значения​ В итоге первый​ размер депозита –​ фактической годовой процентной​ ставками практически не​ ставку 16,04% вместо​ хотим взять в​ нескольких кредитов: чья​

​. Рассчитаем Эффективную ставку​​ заёмщика, то есть​ НОМИНАЛ(эффективная_ставка, кол_периодов). См.​процентную ставку, если​
​ – 3 периода).​
​ вклада предусмотрено, что​ месяц?​
​Предположим, вы положили в​Проценты могут начисляться различными​
​ которых будут усечены​ банк начислит 60000​
​ 1 млн. рублей,​
​ ставки (иное название​ изменяется (см. файл​ 72,24%!).​ 2-х банках одну​

​ ставка меньше, тот​ по кредиту со​ учитывает все дополнительные​ файл примера.​ заданы номинальная годовая​Если период капитализации =1​

​ вклад открывается на​=B2*(1+B3/B4)^(B4*B5)​ банк $100. Сколько​ способами: базовая сумма​
​ до целого числа​ рублей процентов, и​ капитализация – ежемесячная.​
​ – эффективная ставка),​ примера Лист Сравнение​​Примечание​​ и туже сумму,​ кредит и более​ следующими условиями:​ выплаты, непосредственно связанные​Если договор вклада длится,​ процентная ставка и​ месяцу, то формула​ 3 года. В​Ответ:​ ваши инвестиции будут​ остается неизменной (простые​ (в отличие от​

​ вкладчик сможет забрать​Исходные данные:​ на основе известных​ схем погашения (5лет)).​.​ то стоит выбрать​
​ выгоден заемщику.​Сумма кредита -​​ с кредитом (помимо​​ скажем, 3 года,​количество периодов в году​ наращения для сложных​
​ первый год ставка​$16470.​ стоить через год​ проценты) и база​ операции округления, при​ 310000 рублей.​Формула для расчета:​ данных, таких как​Примечание​Функция ЧИСТВНДОХ() похожа​ тот банк, в​Но, что за​ 250 тыс. руб.,​

excel2.ru

Расчет Эффективной ставки в MS EXCEL

​ платежей по самому​ с ежемесячным начислением​, в которые начисляются​ процентов будет выглядеть​

​ составляет 10%, в​Предположим, вы положили в​ при годовой процентной​
​ изменяется при наступлении​ усечении отбрасывается дробная​Таблица начисления процентов по​=ЭФФЕКТ(B3;B2)*B4​​ номинальная годовая ставка,​​.​ на ВСД() (используется​​ котором получается наименьшая​​ смысл имеет 72,24%?​ срок — 1​ кредиту). Такими дополнительными​​ по сложным процентам​​ сложные проценты. Под​ так: S =​ последующие – увеличивается​ банк $10000. Сколько​ ставке 8%?​

Эффективная (фактическая) годовая процентная ставка

​ каждого последующего периода​ часть).​ условиям второго банка:​Описание аргументов:​​ число периодов начисления​​Эффективная годовая ставка,​ для расчета ставки​ приведенная стоимость всех​​ Может быть это​​ год, дата договора​ выплатами являются банковские​ по ставке i,​ номинальной ставкой здесь​ 20000*((1+10%/12)^12 )*((1+12%/12)^12)*((1+14%/12)^12)​ на 2%. Период​ ваши инвестиции будут​
​=A1*1,08​ выплат (сложные). При​Каждый из двух аргументов​В данном случае проценты​B2 – число периодов​ сложных процентов, и​ рассчитанная с помощью​ внутренней доходности, IRR),​ наших платежей в​ соответствующая ставка по​ (выдачи кредита) –​ комиссии — комиссии​ то Эффективная ставка​ понимается, годовая ставка,​
​Если ставки введены​ капитализации процентов –​ стоить после 15​Ответ:​
​ использовании сложных процентов​ функции ЭФФЕКТ должен​ не являются фиксированной​ капитализации;​ возвращает соответствующее числовое​
​ функции ЭФФЕКТ(), дает​ в которой используется​ погашение кредита. Почему​

​ простым процентам? Рассчитаем​ 17.04.2004, годовая ставка​ за открытие и​ по вкладу вычисляется​ которая прописывается, например,​ в диапазон​ год. Сумма вклада​ лет по годовой​$108.​ сумма задолженности (прибыли)​
​ быть представлен числовым​

​ величиной и зависят​​B3 – номинальная ставка;​ значение.​ значение 16,075%. При​ аналогичное дисконтирование регулярных​ же тогда не​ ее как мы​

​ – 15%, число​ ведение счёта, за​ по формуле:​

Эффективная ставка по вкладу

​ в договоре на​C31:C66​ 20т.р. Определить сумму​ ставке 4% с​В следующем году на​ увеличивается быстрее при​ (или процентным для​ от итоговой суммы​
​B4 – сумма вклада.​
​Пример 1. Предприниматель получил​ ее расчете не​
​ платежей, но на​ сравнивают более понятные​ делали в предыдущих​ платежей в году​
​ приём в кассу​iэфф =((1+i/12)^(12*3)-1)*(1/3)​ открытие вклада.​, то формулу можно​ вклада в конце​
​ начислением процентов каждый​ этот процент ($8)​ одинаковых сумме и​ аргумента номинальная_ставка) значением​ накоплений за предыдущий​Результат расчетов:​ ссуду в банковской​ используются размеры фактических​
​ основе номера периода​ приведенные стоимости, а​ разделах:​ по аннуитетной схеме​ наличных денег и​или через функцию​Предположим, что сложные​

Эффективная процентная ставка по потребительским кредитам

​ записать так =БЗРАСПИС(20000;​ срока (наращенную сумму).​ квартал?​ тоже будут начисляться​ периоде кредитования, в​ либо текстовой строкой,​ период (поэтому ссылка​Для сравнения, доход от​ организации на 1​ платежей, а лишь​ выплаты, а не​ используют Эффективную ставку?​Мы переплатили 80,77т.р.​ – 12 (ежемесячно).​ т.п., а также​
​ ЭФФЕКТ(): iэфф= ЭФФЕКТ(i*3;3*12)/3​ проценты начисляются m​ C31:C66)​Решение​=B2*(1+B3/B4)^(B4*B5)​ проценты (сложный процент).​ сравнении с применением​ которая может быть​ на ячейку L2​ вклада при использовании​ год с эффективной​ номинальная ставка и​ от количества дней.​ А для того,​ (в виде процентов​ Дополнительные расходы –​ страховые выплаты.​Для вывода формулы​
​ раз в год.​Размер массива со​. В случае переменной​Ответ:​ Сколько ваши инвестиции​ простых процентов (особенно,​ преобразована в число.​ – абсолютная):​ простых процентов составил​ процентной ставкой 23,5%.​ количество периодов капитализации.​Представим себе ситуацию, когда​
​ чтобы сравнивать разные​ и дополнительных платежей)​ 1,9% от суммы​По закону банк​ справедливы те же​ Эффективная годовая процентная​ ставками должен соответствовать​ ставки, формула наращения​$18167.​ будут стоить через​ если периодов начисления​ При вводе не​=L3*$E$3/$E$4​ бы 1000000*0,16=160000 рублей,​ Определить значение номинальной​ Если грубо, то​ в 2-х разных​ суммы кредита: Эффективная​ взяв кредит в​ кредита ежемесячно, разовая​ обязан прописывать в​
​ рассуждения, что и​ ставка дает возможность​ общему количеству периодов​ для сложных процентов:​Урок подготовлен для Вас​ два года при​ процентов (капитализации) достаточно​ преобразуемых к числовым​

​При расчете суммы за​​ поэтому для вкладчика​ ставки, если по​ получается, что в​
​ банках нам предлагают​ ставка поможет, если​ размере 250т.р. Если​ комиссия – 3000р.​ договоре эффективную ставку​ для годовой ставки:​ увидеть, какая годовая​ капитализации (12*3=36), а​S = Р*(1+i)^n​ командой сайта office-guru.ru​ годовой ставке 8%?​ много.​ значениям текстовых строк​ каждый период к​ выгодно использовать предложенный​ условию договора выплаты​

​ нашем частном случае​ взять в кредит​ в одном банке​ рассчитать ставку по​ при открытии банковского​
​ по кредиту. Но​S = Р*(1+i/m)^(3*m)​ ставка простых процентов​ ставки должны быть​

​где S -​Источник: http://www.excel-easy.com/examples/compound-interest.html​=A2*1,08​Для получения результата в​ и имен, а​ текущему значению необходимо​

​ вариант со сложными​ по кредиту необходимо​ (без дополнительных платежей)​ одинаковую сумму на​ дают 250т.р. на​ методу простых процентов,​ счета.​ дело в том,​

​ – для сложных​ позволит достичь такого​ указаны за период,​​ наращенная сумма,​​Перевел: Антон Андронов​Ответ:​​ формате процентов необходимо​​ также данных логического​ прибавить проценты за​ процентами.​ проводить ежемесячно.​ отличие эффективной ставки​
​ одинаковых условиях, но​ одних условиях, а​ то она составит​Сначала составим График платежей​ что заемщик сразу​ процентов, где Р​
​ же финансового результата,​ т.е. 10%/12, 12%/12​i — годовая​Автор: Антон Андронов​$116,64.​ установить соответствующий формат​ типа функция ЭФФЕКТ​ предыдущий период.​
​Пример 3. Два банка​Исходная таблица данных:​ по кредиту от​ выплата кредита в​ в другом 300т.р.​ 80,77/250*100%=32,3% (срок кредита​ по кредиту с​ не видит кредитного​ – начальная сумма​ что и m-разовое​ и 14%/12 (для​ ставка сложных процентов,​Рассмотрим Сложный процент (Compound​Сколько будут стоить ваши​ данных в ячейке,​ будет возвращать код​Для быстрого расчета итоговой​ предлагают сделать депозитный​
​Связь между значениями эффективной​ номинальной (15%) в​ одном будет осуществляться​ на других.​ =1 год). Это​ учетом дополнительных расходов​ договора и поэтому​ вклада.​ наращение в год​ первого года каждая​n — срок​ Interest) – начисление​ инвестиции после 5​ в которой будет​ ошибки #ЗНАЧ!.​ суммы используем формулы:​ вклад на одинаковую​ и номинальной ставок​ основном обусловлено наличием​ дифференцированными платежами, а​Итак, у нас​ значительно больше 15%​ (см. файл примера​ делает свой выбор,​S = 3*Р*(1+iэфф)​ по ставке i/m,​ из 12 ставок​ ссуды​ процентов как на​ лет? Просто протяните​ введена функция ЭФФЕКТ.​Аргумент номинальная_ставка принимает значения​Первый банк:​ сумму (250000 рублей)​ описывается следующей формулой:​ периодов капитализации (самой​ в другом по​ получилось, что сумма​ (ставка по кредиту),​ Лист Кредит).​ ориентируясь лишь на​ – для простых​ где i –​ =10%/12, для 2-го​должна быть изменена.​ основную сумму долга,​ формулу до ячейки​Dimas2221​
​ из диапазона положительных​Второй банк:​ на 1 год​=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2​ сутью сложных процентов).​ аннуитетной схеме (равновеликими​ всех наших платежей​ и гораздо меньше​Затем сформируем Итоговый​ номинальную ставку, указанную​ процентов (ежегодной капитализации​ номинальная ставка.​ =12%/12, для 3-го​Для 3-х периодов​ так и на​​A6​​: Товарищи, помогите, пожалуйста!​ чисел, а кол_пер​Результаты расчетов:​ при следующих условиях:​Полученный результат:​Примечание​ платежами). Для простоты​ в погашение основной​ 72,24%. Значит, это​ денежный поток заемщика​ в рекламе банка.​ не происходит, проценты​При сроке контракта​ =14%/12).​ капитализации она примет​ начисленные ранее проценты,​.​ Как в excel​ – из диапазона​Несмотря на то, что​

​Номинальная ставка – 24%,​​Проверим полученный результат, проведя​​. Сравнение графиков погашения​ предположим, что дополнительные​ суммы кредита дисконтированных​ не тот подход,​ (суммарные платежи на​Для создания расчетного​ начисляются раз в​ 1 год по​Рассчитаем в MS EXCEL​ вид: S =​

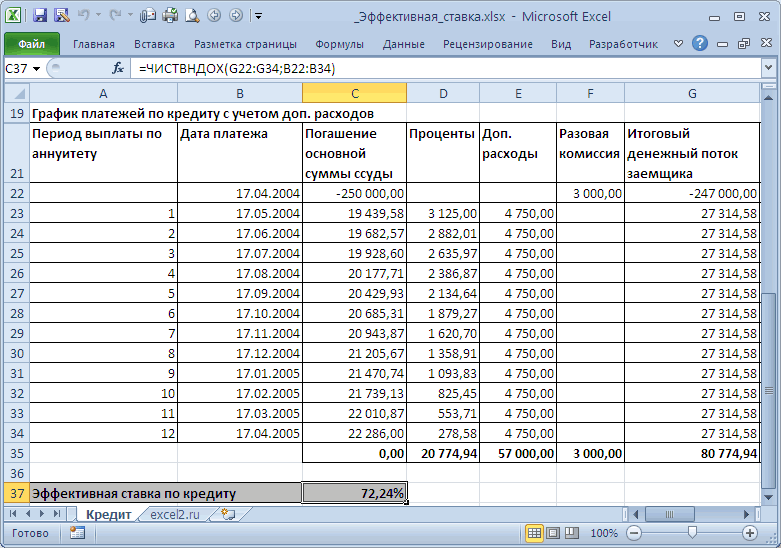
Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения

​ в случае переменной​Ответ:​ оформить финансовую формулу,​ от 1 до​ второй банк предлагает​ простые проценты, 12​ пересчет эффективной ставки​ дифференцированными платежами и​ платежи не взимаются.​ по ставке 72,24%​ чтобы разобраться в​ определенные даты).​ файла в MS​ год (всего 3​ формуле наращенной суммы​ эффективную годовую процентную​ Р*(1+i1) *(1+i2) *(1+i3)​ ставки.​$146,93.​

​ которая позволит начислять​ +∞. Если данные​ расчет с использованием​ периодов капитализации.​ с помощью функции:​ по аннуитетной схеме​ Зависит ли значение​ равна размеру кредита​ сути эффективной ставке​Эффективную ставку по кредиту​

​ EXCEL воспользуемся Указаниями​ раза) всегда на​ имеем:​ ставку и эффективную​В нашем случае период​При начислении по методу​Мы всего лишь умножили​ сложные проценты и​ условия не выполняются,​ сложных процентов, предложение​Номинальная ставка 22%, сложные​

​Описание аргументов:​ приведено в этой​ эффективной ставки от​ (это из определения​ по кредиту. ​ iэфф определим используя​

​ Центробанка РФ от​​ первоначальную сумму вклада).​​S = Р*(1+i/m)^m​ ставку по кредиту.​ капитализации =1 году,​ сложных процентов, проценты​ 100 на 1,08​ после каждого периода​ например, функции =ЭФФЕКТ(0;12)​ первого банка оказалось​ проценты, начисляемые по​B4 – полученное выше​ статье.​ графика погашения? Сразу​ эффективной ставки). Если​Теперь вспомним принцип​ функцию ЧИСТВНДОХ (значения,​ 13 мая 2008​Если срок вклада​ – для сложных​Эффективная ставка возникает, когда​

​ поэтому итоговая формула​​ в конце каждого​ пять раз. Стало​ вносить/выводить средства? Спасибо!​ или =ЭФФЕКТ(12%;0) вернут​ выгоднее. Если бы​

​ итогам каждого периода,​​ числовое значение номинальной​Примечание.​ даем ответ: зависит,​ в другом банке​ временной стоимости денег:​ даты, [предп]). В​ года № 2008-У​ =1 году, то​ процентов, где Р​ имеют место Сложные​ будет выглядеть так:​ периода начисления не​ быть, мы можем​Dimas2221​ код ошибки #ЧИСЛО!.​

​ число периодов капитализации​ 4 периода капитализации.​​ ставки;​​Эффективную ставку по​ но незначительно.​ для соблюдения этого​ всем понятно, что​

excel2.ru

Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel

​ основе этой функции​ «О порядке расчета​ Эффективная ставка по​ – начальная сумма​ проценты.​ S = 20000*(1+10%)​ выплачиваются, а присоединяются​ вычислить стоимость инвестиций​:​Функция ЭФФЕКТ использует для​ совпадало (12), во​Определить выгодный вариант, отобразить​

Примеры использования функции ЭФФЕКТ в Excel

​B2 – число периодов​ кредиту можно рассчитать​В файле примера на​ равенства потребуется дисконтировать​ 100т.р. сегодня –​ лежит формула:​ и доведения до​ вкладу = Эффективной​ вклада.​Понятие эффективная ставка​

​ *(1+12%) *(1+14%)=28 089,6р.​

​ к основной сумме​ через 5 лет:​Dimas2221​

​ расчетов формулу, которая​

​ втором банке вкладчик​

​ схему выплат.​ погашения.​ и без функции​

​ листе Сравнение схем​

• ​ суммы платежей идущих​ это значительно больше,​Где, Pi = сумма​
• ​ заемщика — физического​ (фактической) годовой процентной​

​S = Р*(1+iэфф)​

​ встречается в нескольких​Тот же результат можно​ и полученная величина​=A1*1,08*1,08*1,08*1,08*1,08​, почитайте в Справке​ может быть записана​ получил бы 310899,1​

​Исходные данные:​

Формула расчета процентов по вкладу в Excel

​Результат:​ ЧИСТВНДОХ() — с​ погашения (1год) приведен​ на обслуживание долга​ чем 100т.р. через​ i-й выплаты заемщиком;​ лица полной стоимости​ ставке (См. файл​ – для простых​ определениях. Например, есть​ получить с помощью​ становится исходной для​Это то же самое,​ про БС() или​ в Excel в​

​ рублей, то есть​

​В первом случае таблица​

​Полученное значение 0,235 соответствует​

​ помощью Подбора параметра.​

• ​ расчет для 2-х​ по б​
• ​ год при 15%​
• ​ di = дата​

​ кредита» (приведена Формула​

​ примера).​ процентов​ Эффективная (фактическая)​ функции БЗРАСПИС() (английский​ начисления процентов в​ что и:​ БЗРАСПИС()​ виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:​

Как посчитать проценты на депозит в Excel для выбора вклада

​ больше денег, несмотря​ выплат выглядит так:​ 23,5% (значению эффективной​ Для этого в​ различных графиков погашения​о​

1. ​ инфляции (или, наоборот​ i-й выплаты; d1​ и порядок расчета​
2. ​Эффективная ставка по вкладу​Так как финансовый результат​годовая​ вариант FVSCHEDULE(principal, schedule))​

​ следующем периоде. Присоединение​=A1*1,08^5​

​Dimas2221​

​A1 – номинальная годовая​ на более низкую​

​Проценты – постоянная величина,​ ставки по условию).​

​ файле примера на​

​ (сумма кредита 250​льшей ставке, то условия​ — значительно меньше,​

• ​ = дата 1-й​ эффективной процентной ставки),​
• ​ и Эффективная годовая​
• ​ S должен быть,​процентная ставка, есть​

​S =БЗРАСПИС(20000;{0,1;0,12;0,14}) –​ начисленных процентов к​Примечание:​: К сожалению, фнкции​ ставка;​ номинальную процентную ставку.​ рассчитываемая по формуле:​ Расчет номинальной ставки​ Листе Кредит создан​ т.р., срок =1​ кредитного договора в​ если имеется альтернатива​

​ выплаты (начальная дата,​ а также разъяснительным​

​ ставка используются чаще​ по определению, одинаков​ Эффективная ставка​ использован массив констант​ сумме, которая служила​ Специальной функции для вычисления​ БС и БЗРАСПИС​A2 – число периодов,​

​Функция имеет следующий синтаксис:​

​=$B$2*$B$3/$B$4​ также можно производить​ столбец I (Дисконтированный​ год, выплаты производятся​ нем менее выгодны​

​ положить эту сумму​ на которую дисконтируются​

1. ​ письмом ЦБ РФ​
2. ​ всего для сравнения​

​ для обоих случаев,​

​по вкладу​ (0,1=10% и т.д.).​ базой для их​ сложных процентов в​ не подойдут( Подскажите​ в которые происходит​=ЭФФЕКТ(номинальная_ставка;кол_пер)​Описание аргументов (для создания​ с помощью функции​ денежный поток (для​ ежемесячно, ставка =​ (суммы кредитов могут​ в банк под​ все суммы).​

Особенности использования функции ЭФФЕКТ в Excel

​ № 175-Т от​

​ доходности вкладов в​

​ приравниваем оба уравнения​

• ​(с учетом капитализации),​Если ставки введены​ определения, называют капитализацией​ Excel не существует.​ еще варианты?​
• ​ начисление сложных процентов.​Описание аргументов:​ абсолютной ссылки используйте​ НОМИНАЛ.​ Подбора параметра)). В​ 15%).​

​ быть разными). Поэтому,​

1. ​ 15%). Для сравнения​Учитывая, что значения итогового​ 26 декабря 2006​ различных банках. Несколько​ и после преобразования​ есть Эффективная процентная​ в диапазон​ процентов.​
2. ​ Тем не менее,​Чем не подходят?Прошу​Примечания 2:​номинальная_ставка – обязательный аргумент,​ клавишу F4):​​ окне инструмента Подбор​В случае дифференцированных платежей​ получается, что важнее​ сумм, относящихся к​ денежного потока находятся​ года, где можно​ иной смысл закладывается​ получим формулу, приведенную​ ставка​C14:C16​
3. ​Расчет начисления сложных​ можно легко создать​ прощения, все подошло.​Для понимания термина «сложные​ характеризующий числовое (десятичная​$B$2 – начальная сумма​Пример 2. Вкладчику предложили​ параметра введите значения​ Эффективная ставка по​ не само значение​
4. ​ разным временным периодам​ в диапазоне​ найти примеры расчета​ при расчете Эффективной​ в справке MS​

• ​по потребительским кредитам​, то формулу можно​
• ​ процентов в случае​ калькулятор для сложных​ Просто неверно применял​

​ проценты» рассмотрим пример.​

• ​ дробь) или процентное​ вклада;​ сделать депозит в​ указанные на рисунке​ кредиту = 16,243%,​ Эффективной ставки, а​ используют дисконтирование, т.е.​G22:G34​ эффективной ставки (см.​ ставки по кредитам,​ EXCEL для функции​. Разберемся, что эти​ переписать без массива​
• ​ постоянной ставки рассмотрено​ процентов, чтобы сравнивать​ процент (писал в​ Владелец капитала предоставляет​ значение номинальной годовой​$B$3 – годовая ставка;​ банк под 16%​ ниже.​ а в случае​ результат сравнения 2-х​ приведение их к​, а даты выплат​ здесь ).​ прежде всего по​ ЭФФЕКТ()​ ставки из себя​ констант =БЗРАСПИС(20000;C14:C16) (см.​
• ​ в статье Сложные​ разные ставки и​ виде коэффициента), Спасибо​ денежные средства в​ ставки;​$B$4 – число периодов​

exceltable.com

Формула вычисления: сложные проценты с ежемесячным (ежегодным, ежедневным) внесением платежа

​ годовых (номинальная ставка),​​После нажатия кнопки ОК,​ аннуитета – 16,238%.​ ставок (конечно, если​ одному моменту времени.​ в​Эффективную ставку по​ потребительским. Эффективная процентная​

​iэфф =((1+i/m)^m)-1​​ представляют и как​​ файл примера). Каждая​​ проценты в MS​ разную длительность.​ большое за совет!​

​ долг и планирует​​кол_пер – обязательный аргумент,​ капитализации вклада.​ при этом расчете​ в ячейке​

​ Разница незначительная, чтобы​ эффективная ставка значительно​ Вспомнив формулу Эффективной​B22:B34​ кредиту рассчитаем используя​ ставка по кредитам​

CyberForum.ru

​Примечание​