Задачи на процентную ставку в excel

Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа.

Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.

Для расчета процентной ставки в аннуитетной схеме используется функция

СТАВКА()

.

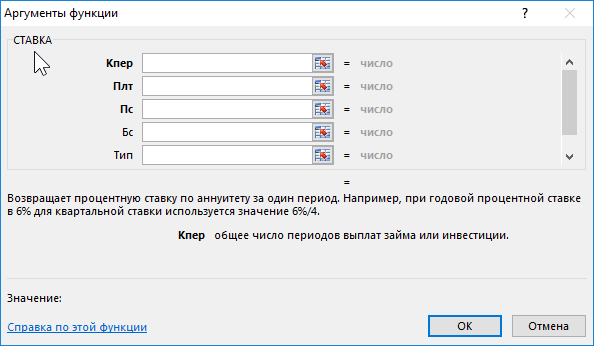
Функция СТАВКА(кпер; плт; пс; [бс]; [тип]; [предположение])

возвращает процентную ставку по аннуитету.

Примечание

.

Английский вариант функции: RATE(nper, pmt, pv, [fv], [type], [guess]), т.е. Number of Periods – число периодов.

Вот что написано на сайте MS

: Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см.

обзорную статью о функциях аннуитета

).

Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути,

метод подбора

). Чтобы облегчить поиск Ставки методом итераций, используется аргумент

Предположение. Предположение

— это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение

Предположение

также полезно в случае

,

если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к

Предположению

.

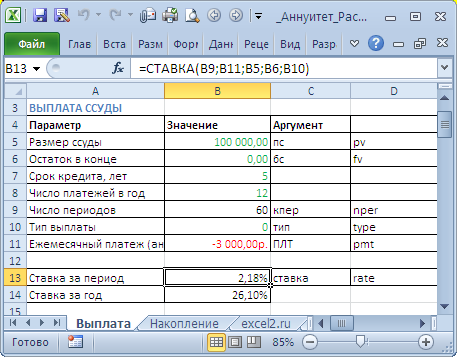
Задача1 – Выплата кредита

Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.

Примечание

. Аннуитетная схема погашения кредита подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа)

.

В условии задачи содержится следующая информация:

• Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
• Проценты начисляются
  
  в конце
  
  каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0;
• В конце срока задолженность должна быть равна 0 (БС=0).

В результате формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-3000;100000;0;0)

или

=12*СТАВКА(12*5;-3000;100000)

Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые

банк

дал

нам, -3000 – это деньги, которые мы

возвращаем банку

. Результат вычисления = 26,10%

Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в

файле примера на Листе Выплата

установить платеж =-1000).

Если задать платеж = 0 или того же знака, что и сумма кредита, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.

Примечание

. С помощью

Подбора параметра

можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция

ПЛТ()

.

Задача2 – Накопление суммы вклада

Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см.

файл примера на Лист Накопление

)

Примечание

. Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье

Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад

.

Формула для вычисления годовой ставки будет выглядеть так

=12*СТАВКА(12*5;-10000;0;1000000)

=19,38%

Здесь ПС=0, т.е. начальная сумма вклада =0 (

Приведенная Стоимость

). Целевой вклад = 1000000 (БС –

Будущая Стоимость

).

Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.

Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция

СТАВКА()

вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.

Функция СТАВКА используется для определения процентной ставки по инвестиции либо денежному займу с аннуитетной структурой графика погашения для одного периода выплат (при условии, что будущая стоимость ценных бумаг, обеспечивающих инвестицию либо кредит является известной величиной) и возвращает полученное значение.

Если при заключении сделки процентная ставка не была установлена жестко, функция СТАВКА позволяет определить размер неявной ставки (то есть такой ставки, которая обеспечила бы получение эквивалентного дохода).

Примеры финансовых расчетов по функции СТАВКА в Excel

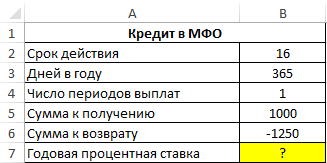
Пример 1. В МФО был взят кредит сроком на 16 дней, сумма которого составляет 1000 долларов. Сумма возврата составляет 1250 долларов. Определить годовую процентную ставку по указанным условиям займа.

Таблица данных:

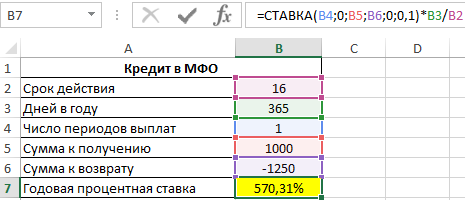
Для расчета в ячейку B7 введем следующую формулу:

=СТАВКА(B4;0;B5;B6;0;0,1)*B3/B2

Описание аргументов:

• B4 – число периодов выплат (в данном случае – 1);
• 0 – размер фиксированной выплаты (поскольку в данном примере только один период выплат, указано значение 0);
• B5 – тело кредита;
• B6 – сумма на момент погашения долга;
• 0 – характеризует тип выплат, при котором выплата производится в конце периода;
• 0,1 – предполагаемое значение процентной ставки (любое число из диапазона от 0 до 1);
• B3/2 – коэффициент для пересчета полученного значения ставки к годовой процентной ставке.

Результат вычислений:

Пи данных условиях микрокредитования сроком займа на 16 дней процентная ставка составляет 570,31% годовых! Несмотря на это, услуги по микрокредитованию сегодня продолжают набирать популярность.



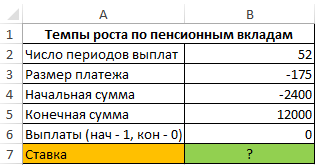
Анализ пенсионных отчислений с использованием функции СТАВКА в Excel

Пример 2. Определить темпы роста пенсионных отчислений (процентную ставку), если баланс средств на конец года составляет 12000 долларов, а в начале года – 2400 долларов. Еженедельные платежи на протяжении года составляли 150 долларов (то есть, количество периодов – 52).

Исходные данные:

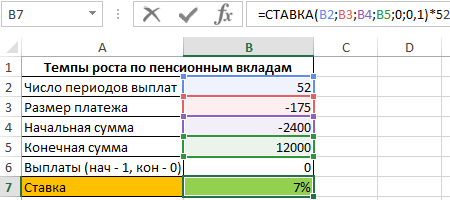
Формула для расчета:

=СТАВКА(B2;B3;B4;B5;0;0,1)*52

Описание аргументов:

• B2 – количество периодов выплат;
• B3 – сумма платежа (расходная операция, поэтому отрицательное значение);
• B4 – сумма средств до наступления первого периода выплат;
• B5 – сумма по окончанию последнего периода выплат;
• 0 – выплаты в конце периода;
• 0,1 – произвольное значение из интервала от 0 до 1;
• 52 – количество периода выплат для пересчета размера ставки в годовых.

Результат вычислений:

То есть, пенсионные отчисления выполняются под 7% годовых.

Определение реальной процентной ставки по кредиту

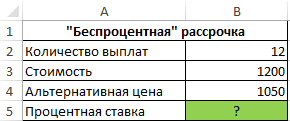
Пример 3. Ноутбук одной и той же модели можно приобрести за 1200 долларов в рассрочку (беспроцентную, судя по рекламе в первом магазине) или за 1050 долларов в другом магазине. Рассрочка выдается на 1 год с 12 периодами выплат. Определить реальный процент «беспроцентной» рассрочки платежей по кредиту.

Исходные данные:

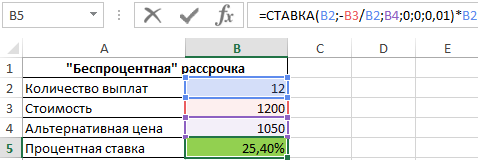
Формула для расчета:

=СТАВКА(B2;-B3/B2;B4;0;0;0,01)*B2

Описание аргументов:

• B2 – число периодов выплат;
• -B3/B2 – выражение для расчета размера ежемесячного платежа;
• B4 – реальная стоимость ноутбука (используется как начальная стоимость финансового инструмента, цена которого повысится до 1200 к окончанию последнего периода выплат);
• 0 – остаток по окончанию последнего периода выплат;
• 0 — выплаты в конце периода;
• 0,01 — произвольное значение предполагаемой ставки.

Результат расчетов:

То есть, фактически в первом магазине клиенту предложили кредит на ноутбук под 25,4% годовых.

Функция СТАВКА в Excel и особенности ее использования

Функция СТАВКА имеет следующий синтаксис:

= СТАВКА(кпер; плт; пс; [бс]; [тип]; [прогноз])

Описание аргументов:

• кпер – обязательный аргумент, характеризующий число периодов выплат по аннуитетной схеме.
• плт – обязательный аргумент, характеризующий фиксированное значение выплаты, производимой в каждый из периодов выплат. Сумма выплаты за каждый период включает две составляющие: тело и проценты без учета прочих комиссий и сборов. Если данный аргумент опущен, следующий аргумент должен быть указан явно.
• пс – обязательный аргумент, характеризующий текущую стоимость задолженности (либо вознаграждения), эквивалентную общей сумме последующих платежей на данный момент. Если значение неизвестно, необходимо явно указать значение 0 (нуль).
• [бс] – необязательный аргумент, характеризующий размер желаемого остатка средств после выполнения последней выплаты согласно графика платежей. Если явно не указан, по умолчанию используется значение 0 (нуль), а аргумент пс становится обязательным для заполнения.
• [прогноз] – необязательный аргумент, характеризующий предполагаемый размер процентной ставки. Если аргумент явно не указан, по умолчанию принимается значение 10%. Если полученное в результате вычислений значение не сходится с указанной прогнозной величиной, величину данного аргумента следует изменить. Рекомендуется выбирать значение для аргумента [прогноз] из диапазона от 0 до 1.
• [тип] – необязательный аргумент, принимающий значения 0 или 1:

1. Если введен 0, считается, что выплата производится в конце периода;
2. Если введен 1, считается, что выплата производится в начале периода.

Примечания:

1. Единицы измерения величин, указанных в качестве аргументов кпер и [прогноз], должны соответствовать друг другу. Например, при расчете ставки по займу, выданному на два года под 16% с ежемесячными выплатами необходимо, в качестве аргумента [прогноз] необходимо использовать значение 16%/12, а кпер – 2*12.
2. Если хотя бы в качестве одного из аргументов функции было передано текстовое значение, результатом выполнения функции будет являться код ошибки #ЗНАЧ!.
3. Аннуитетная схема выплаты вознаграждения либо погашения задолженности предполагает выплаты фиксированной суммы, включающей вознаграждение или тело кредита и дополнительных процентов (в зависимости от установленной процентной ставки) на протяжении установленного количества периодов выплат. В отличие от классической схемы, при которой проценты начисляются на остаток вознаграждения или задолженности, в аннуитетной схеме соотношение тело кредита/проценты является изменяющейся величиной.
4. При выполнении расчетов функция СТАВКА использует итерационный метод. Если после 20 итераций последующие результаты вычислений отличаются друг от друга более, чем на 10-7, результатом вычислений будет являться код ошибки #ЗНАЧ!.

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Решение задач на простые и сложные проценты с помощью
  MS Excel
  Выполнила:
  Учитель математики высшей категории МОУ СОШ №1 г.Малоярославец, Калужской обл.
  Славинская Галина Николаевна

• 

• 

  3 слайд

  Под наращенной суммой ссуды (долга, депозита, других видов инвестированных средств) понимается первоначальная ее сумма вместе с начисленными на нее процентами к концу срока.
  Пусть S0 первоначальная сумма денег, i =p/100 ставка простых процентов.
  Процесс изменения суммы долга с начисленными простыми процентами описывается арифметической прогрессией, членами которой являются величины
  S0; S0+S0*i=S0(1+i) и т.д. до S0(1+ni)

  Формула наращения по простым процентам

• 

  4 слайд

  Первый член этой прогрессии равен S0, разность S0*i, а последний член определяемый как
  S=S0(1+ni), (1)
  и является наращенной суммой. Формула (1) называется формулой наращения по простым процентам или, кратко, формулой простых процентов. Множитель (1+ni) является множителем наращения. Он показывает во сколько раз наращенная сумма больше первоначальной суммы. Наращенную сумму можно представить в виде двух слагаемых: первоначальной суммы S0 и суммы процентов I
  S=S0+I, (2)
  где
  I=S0ni. (3)

  Рис. 1. Наращение по простой процентной ставке

  Процесс роста суммы долга по простым процентам легко представить графически (см. Рис. 1). При начислении простых процентов по ставке i за базу берется первоначальная сумма долга. Наращенная сумма S растет линейно от времени.

• 

  5 слайд

  Четыре основные задачи
  на простой процент

• 

  6 слайд

  Задача №1
  Вкладчик открыл в банке счёт и положил на него 13000 рублей, сроком на три года под простые проценты по ставке 11% в год. Какой будет сумма если счет закрыть через три года?
  Решение:
  Ответ: 17 290 руб.

• 

  7 слайд

  Задача №2
  Какую сумму положили в банк под простые проценты по ставке 9% годовых, если через 3 года вклад достиг величины 15130 рублей? На сколько рублей вырос вклад за 3 года?
  Решение:
  Ответ: вклад вырос на 3216,61 руб.

• 

  8 слайд

  Задача №3
  Вкладчик положил в банк 50000 рублей на 4 года под проценты. Определите процентную ставку если доход составил 23 205 рублей.
  Решение:
  Ответ: 11,6%

• 

  9 слайд

  Задача №4
  Сколько лет лежал в банке вклад 70 000 руб., если по ставке 19,2% годовых простых процентов он достиг величины 150 640 руб.?
  Решение:
  Ответ: 6 лет

• 

  10 слайд

  19.06.2022
  10
  Сложный процентный рост:
  Банк выплачивает вкладчикам каждый месяц p % от имеющейся на
  счёте суммы, если вкладчик не снимает проценты.
  S0 – первоначальный взнос.
  Через n месяцев на счёте окажется

• 

  11 слайд

  19.06.2022
  11
  Пусть S0 — первоначальная сумма долга, i=p/100 – cтавка сложных %.
  Тогда через один год сумма долга с присоединенными процентами составит S0(1+i), через 2 года S0(1+i)(1+i)= S0(1+i)2, через n лет — S0(1+i)n.
  Таким образом, получаем формулу наращения для сложных процентов:
  S= S0(1+i)n
  где S — наращенная сумма, i — годовая ставка сложных процентов, n — срок ссуды, (1+i)n — множитель наращения.

  Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен S0, а знаменатель (1+i).

  Формула наращения по сложным процентам

• 

  12 слайд

  19.06.2022
  12
  Четыре основные задачи на сложный
  процент

• 

  13 слайд

  Задача №1
  За хранение денег банк начисляет вкладчику 8% годовых. Вкладчик положил на счёт в банке 5000 рублей и решил в течение 5 лет не снимать деньги со счёта и не брать процентные начисления. Сколько денег будет на счёте вкладчика через год, через два , через три. года?
  Решение:
  S0=5000
  N=5
  P=8
  Через год сумма увеличится на 8% т.е. составит 108%
  108%=1.08
  S1=S0*1,08
  S2=S1*1,08
  S3=S2*1,08
  Ответ: 6 298,56 руб.

• 

  14 слайд

  Задача №2
  В комиссионном магазине цена товара, выставляемого на продажу , ежемесячно уменьшается на одно и то же число процентов от предыдущей цены. Определите на сколько процентов каждый месяц уменьшалась цена товара , если выставляемый на продажу за 8000 рублей он через 3 месяца стал стоить 4096 рублей ?
  Решение:
  S0=8000
  n=3
  S3=4096
  X- количество процентов, на которое ежемесячно уменьшалась цена товара
  X=100-((S3/S0)^(1/n))*100
  Ответ: на 20 %.

• 

  15 слайд

  Задача №3
  Рассчитайте, что выгоднее для вкладчика: получить 20 000 рублей сегодня или получить 35 000 рублей через 3 года, если процентная ставка равна 17%.
  Решение:
  S0=20 000
  N=3
  P=17%=0,17
  S3= 20000 * (1 + 0,17)3 = 32 032 рубля.
  Ответ: выгоднее получить 35 000 руб через 3 года

• 

  16 слайд

  Формула наращения по сложным процентам, когда ставка меняется во времени

  В том случае, когда ставка сложных процентов меняется во времени, формула наращения имеет следующий вид

  где i1, i2,…, ik — последовательные значения ставок процентов, действующих в периоды n1, n2,…, nk соответственно, P- первоначальный взнос.

• 

  17 слайд

  Пример :
  В договоре зафиксирована переменная ставка сложных процентов, определяемая как 20% годовых плюс маржа 10% в первые два года, 8% в третий год, 5% в четвертый год. Определить величину множителя наращения за 4 года.
  Решение:
  (1+0,3)2(1+0,28)(1+0,25)=2,704

• 

  18 слайд

  Благодарю за внимание!

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 210 503 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»

• Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»

• Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Приведенные в этой статье примеры и упражнения покажут, как применять средство Подбор параметра для решения задач, связанных с кредитом на покупку квартиры, автомобиля и банковскими депозитами.

Кредит на покупку квартиры

Прежде чем рассматривать задачи, связанные с кредитом на покупку квартиры, создайте рабочий лист, показанный на рис. 1.9. Если вы не в курсе, то Excel доступен и в онлайн-режиме, для этого вам потребуется Mozilla Firefox скачать бесплатно.

На этом рабочем листе сумма кредита, срок погашения кредита (в месяцах) и годовая процентная ставка представлены в виде чисел, а ежемесячный платеж рассчитывается с помощью функции =ПЛТ(Ставка;Кпер;Пс). В этой функции аргумент Ставка задает ежемесячную процентную ставку по кредиту (поэтому в нашей формуле этот аргумент равен В5/12), аргумент Кпер — количество периодов погашения кредита (ячейка В4), аргумент Пс — сумма кредита (ячейка В3).

Подбор параметра для вычисления суммы кредита

Задача: кредит берется на 15 лет с процентной ставкой 5,75% при условии, что сумма ежемесячных платежей не должна превышать 11 000 руб. Какова максимальная сумма кредита?

1. В ячейку В4 введите число 180 (15 лет, умноженных на 12 месяцев). В ячейку В5 введите 5,75%.
2. Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра
3. В поле ввода Установить в ячейке введите В6 или щелкните на ячейке В6.
4. В поле ввода Значение введите число — 11000.

[stextbox id=»info»]В поле Значение вводится отрицательное число, что указывает на то, что ежемесячные платежи заемщик отдает, а не получает (как при банковских вкладах).[/stextbox]

5. В поле ввода Изменяя значение ячейки введите В3 или щелкните на ячейке В3.
6. Щелкните на кнопке ОК.
7. В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.

Ответ: если кредит берется на 15 лет с процентной ставкой 5,75% при условии, что сумма ежемесячных платежей не должна превышать 11 000 руб., то максимальная сумма кредита составит 1 324 647 руб.

Подбор параметра для вычисления срока погашения кредита

Задача: каков срок погашения кредита, если сумма кредита равна 2 250 000 руб., процентная ставка составляет 7% годовых, а ежемесячные платежи равны 14 230 руб.?

1. В ячейку В3 введите число 2250000, в ячейку В5 введите 7%.
2. Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра
3. В поле ввода Установить в ячейке введите В6 или щелкните на ячейке В6.
4. В поле ввода Значение введите число — 14230.
5. В поле ввода Изменяя значение ячейки введите В4 или щелкните на ячейке В4.
6. Щелкните на кнопке ОК.
7. В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.

Ответ: кредит в сумме 2 250 000 руб. с процентной ставкой 7% годовых и ежемесячными платежами в размере 14 230 руб. берется на 439 месяцев (примерно 36,6 года).

Подбор параметра для вычисления процентной ставки

Задача: кредит в размере 8 500 000 руб. берется на 30 лет с максимальными ежемесячными платежами 52 250 руб. На какую максимальную процентную ставку можно согласиться при таких условиях?

1. В ячейку В3 введите число 8500000, в ячейку В4 введите 360.
2. Выберите команду Подбор параметра, выполните команду Данные → Работа с данными → Подбор параметра. Откроется диалоговое окно Подбор параметра
3. В поле ввода Установить в ячейке введите В6 или щелкните на ячейке В6.
4. В поле ввода Значение введите число — 52250.
5. В поле ввода Изменяя значение ячейки введите В4 или щелкните на ячейке В4.
6. Щелкните на кнопке ОК.
7. В открывшемся окне Результат подбора параметра щелкните на кнопке ОК.

Ответ: если кредит в размере 8 500 000 руб. берется на 30 лет с максимальными ежемесячными платежами 52 250 руб., то можно согласиться на процентную ставку в размере 6,23%.

Разберем  различные формулы расчета процентов в Excel, для этого рассмотрим реальные практические примеры, формулы и типовые финансовые задачи.

Формула расчета процентов. Как посчитать проценты в Экселе?

Проценты (латин. pro centum) – являются неотъемлемой частью финансовой математики и используются в банковском секторе, финансах, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность предприятия, ставку по банковским кредитам и займам, налоговые ставки и т.д. Можно привести в подтверждение важности процентов в финансовом мире высказывание А. Энштейна: «Сложные проценты – самая мощная сила в природе». Перед тем как рассмотреть формулы расчета процентов введем основные термины и понятия.

• Капитал (англ. Capital, Principal) – является базой относительно которого вычисляют процент.
• Частота начисления процентов – период выплат процентов на капитал.
• Процентная ставка (англ. Rate) – размер процента или доля капитала, который будет выплачен.
• Период вложения (англ. Period) – временной интервал передачи капитала банку или другому финансовому институту.

Итак, рассмотрим различные эконометрические задачи с процентами.

Формула расчета доли

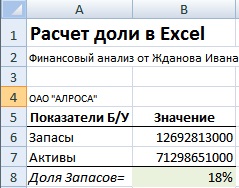
Расчет доли часто необходим в бухгалтерском и финансовом учете, где необходимо определить долю тех или иных видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО «АЛРОСА».

Пример задачи. Необходимо рассчитать долю «Запасов» в структуре «Активов» предприятия. Для этого воспользуемся формулой:

Доля запасов в Активах =B6/B7

Для того чтобы в ячейке полученные доли имею процентный вид можно воспользоваться сочетанием клавиш «Ctrl» + «Shift» + «%».

Формула расчета размера процента от капитала

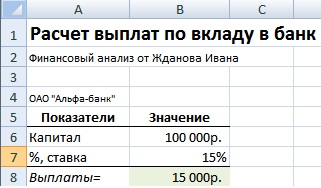
Рассмотрим вторую постоянно встречающуюся экономическую задачу: расчет абсолютного значения процента по капиталу.

Пример задачи. Необходимо определить размер выплаты банка ОАО «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь следующий вид:

Выплаты по вкладу в банке =B6*B7

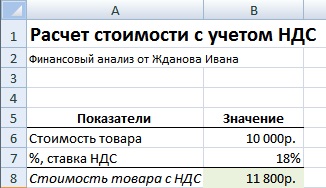
Формула расчета размера капитала с процентами

Пример задачи. Требуется рассчитать итоговую стоимость товара с НДС (налог на добавленную стоимость), тогда как стоимость товара без НДС составляет 10000 руб., процентная ставка налога равна 18%.  Формула расчета стоимости товара с учетом НДС рассчитывается по формуле:

Стоимость товара с учетом НДС =B6*(1+B7)

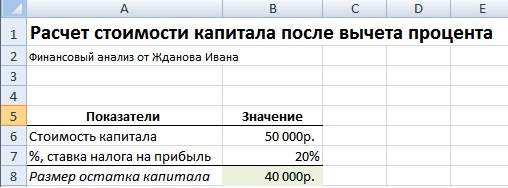
Формула уменьшения размера капитала на процент

Пример задачи. Необходимо рассчитать размер капитала после вычета налога на прибыль, процентная ставка налога равна 24%, текущее значение капитала равно 50000 руб. Формула расчета остатка капитала после вычета налога следующая:

Остаток капитала =B6-B6*B7

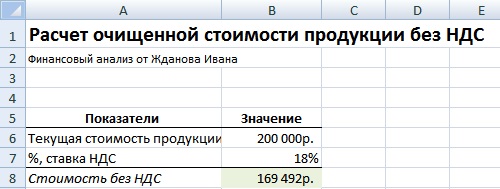
Формула расчета очищенной стоимости капитала (продукции)

Пример задачи. Необходимо рассчитать начальную стоимость продукции без НДС (налог на добавленную стоимость), текущая стоимость продукции составляет 200000 руб., процентная ставка налога 18%. Формула расчета процентов следующая:

Стоимость продукции без НДС=B6/(1+B7)

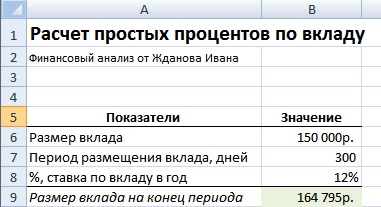
Формула расчета простых процентов по банковскому вкладу

При использовании простых процентов выплаты по вкладу осуществляются только в конце срока (периода) размещения.

Пример задачи. Требуется рассчитать размер выплат по банковскому вкладу, на который начисляется простые проценты. Размер вклада составляет 150000 руб., годовая процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel следующая:

Размер банковского вклада на конец периода размещения =(1+B8*300/365)*B6

Формула расчета сложных процентов по банковскому вкладу

Сложные проценты отличаются от простых тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.

Пример задачи. Необходимо рассчитать размер банковского вклада, который был размещен по сложный процент. Первоначальный размер депозита составляет 100000 руб., годовая процентная ставка равна 14%, период начисления процентов – каждые 4 месяца, срок размещения вклада 1 год.

Формула расчета сложных процентов:

Размер вклада со сложными процентами на конец года =B6*(1+B8*B9/B7)^4

Метод сложных процентов имеет широкое использование в финансовом анализе и применяется для дисконтирования денежных потоков. Более подробно о методе дисконтирования читайте в статье: «Дисконтирование денежных потоков (DCF). Формула. Расчет в Excel«.

Видео-урок: «Примеры расчета простых и сложных процентов»

Резюме

Расчет процентов является неотъемлемой частью финансовой математики и всей экономики в целом. Навык быстрого расчета процентов в Excel позволяет экономить время при оценке будущей стоимости капитала.

Автор: к.э.н. Жданов Иван Юрьевич

В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.

Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.

Решение финансовой математики в Excel

Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.

Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.

Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.

Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?

Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?

Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.

Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.

Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?

Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?

Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.

Может быть интересно:

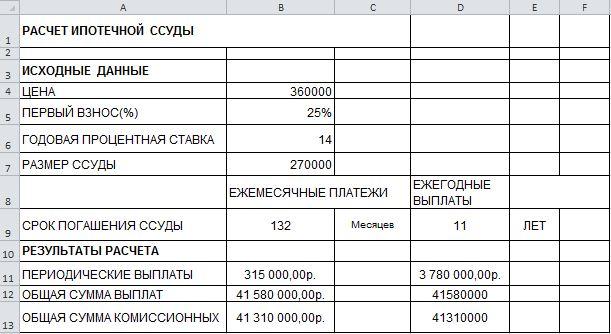
Задача
1

Требуется
рассчитать 10-летнею ипотечную ссуду со
ставкой 14% годовых при начальном взносе
25% суммы и ежемесячной (ежегодной)
выплате.

Решение
задачи

Для
решения задачи используется функция
ПЛТ.

Функция
вычисляет величину выплаты за один
период годовой ренты (например, регулярных
платежей по займу) при постоянной
процентной ставке. ПЛТ(ставка;кпер;пс;бс;тип),
Ставка — процентная ставка по ссуде,
Кпер — общее число выплат по ссуде.

Пс —
приведенная к текущему моменту стоимость,
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей,
называемая также основной суммой.

Бс —
требуемое значение будущей стоимости,
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (нулю), т. е. для займа,
например, значение бс равно 0.

Тип —
число 0 (нуль) или 1, обозначающее, когда
должна производиться выплата.

Исходные
данные для решения задачи представлены
на рис.1.

Рис.1
Исходные данные.

Формулы
для решения задачи представлены на
рис.2

Рис.2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.3.

Рис.3
Результаты решения задачи.

Вывод
При расчёте 10-летней ипотечной ссуды
со ставкой 14% годовых при начальном
взносе 25% суммы и ежемесячной (ежегодной)
выплате. Общая сумма выплат составит
41580000р.

Задача
2

Рассмотреть
возможность инвестиций 36 000 руб. Возврат
10 000 руб. через год, 15 000 руб. через два
года и т. д. 21 000 руб. — через 3 лет.

Решение
задачи

ЧПС
– Возвращает величину чистой приведенной
стоимости инвестиции, используя ставку
дисконтирования, а также стоимости
будущих выплат (отрицательные значения)
и поступлений (положительные значения).

Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.

Исходные
данные для решения задачи представлены
на рис.4.

Рис.4
Исходные данные.

Формулы
для решения задачи представлены на
рис.5.

Рис.5
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.6.

Рис.6
Результаты решения.

Вывод

При
расчёте инвестиций на 3 лет, с возвратом
по

10000,
15000,
21000 рублей
с процентной ставкой более 1% не имеет
смысл.

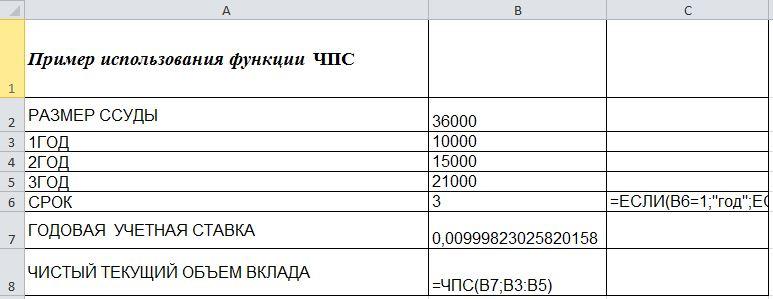
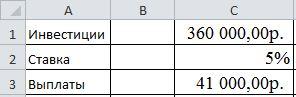
Задача
3

Рассмотреть
возможность инвестиций 360000
руб. Возврат по 41000 руб. в течение 11 лет.
При какой годовой процентной ставке
это имеет смысл?

Решение
задачи

ПС(
ставка; кпер; выплата; бз; тип)

ставка
— процентная ставка за период;

кпер
— общее число периодов выплат;

выплата
— величина постоянных периодических
платежей;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным о (будущая
стоимость займа, например, равна о);

Тип
— число, равное 0 или 1, обозначающее,
когда должна производиться выплата.
Если значение параметра тип равно 0 или
он опущен, то оплата производится в
конце периода, если же его значение
равно 1, то в начале периода.

Подбор
параметров,
выбрав
команду Подбор
параметров в
меню Сервис.
При подборе параметра Excel изменяет
значение в одной конкретной ячейке до
тех пор, пока вычисления по формуле,
ссылающейся на эту ячейку, не дадут
нужного результата.

Исходные
данные для решения задачи представлены
на рис.7.

Рис.7
Исходные данные.

Формулы
для решения задачи представлены на
рис.8.

Рис.8
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.9.

Рис.9
Результаты решения.

Вывод

При
рассмотрении возможности инвестиций
360000 руб на 11 лет. С ежегодным возвращением
по 41 000 руб . С процентной ставкой более
1% , выгодна.

Задача
4

Вычислить
основные платежи, плату по процентам,
общую ежегодную выплату и остаток долга
на примере ссуды 300000 руб. под годовую
ставку8% на срок 10 лет.

Решение
задачи

Присвойте
ячейкам следующие имена:

Для
ссылки на ячейки в столбцах и строках
можно использовать заголовки этих
столбцов и строк листа. Также для
представления ячеек, диапазонов ячеек,
формул или констант
можно
создавать имена.
Заголовки можно использовать в формулах,
содержащих ссылки на данные на том же
листе; для представления группы ячеек,
находящейся на другом листе, этой группе
следует присвоить имя.

Ячейка
Имя

B1
Процент

B2
Срок

B3
Ежегодная_плата

B4
Размер_ссуды

Кроме
того, в ячейки введите формулы:

Ячейка
Формула
Описание

ВЗ
=ПЛТ(Процент;Срок;–Размер_ссуды)
Ежегодная плата

D6
=Размер_ссуды
Начальный остаток долга

А7
=A6+1
Номер года

В7
=D6*Процент
Плата по процентам

С7
=Ежегодная_плата-В7
Основная плата за первый год

D7
=ЕСЛИ(D6-С7<>0;D6-С7) Остаток
долга за первый год

Исходные
данные для решения задачи представлены
на рис.10.

Рис.10
Исходные данные.

Формулы
для решения задачи представлены на
рис.11.

Рис.11
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.12.

Рис.12
Результаты решения.

Вывод

Были
вычислены основные платежи, плата по
процентам , общая ежегодная выплата.

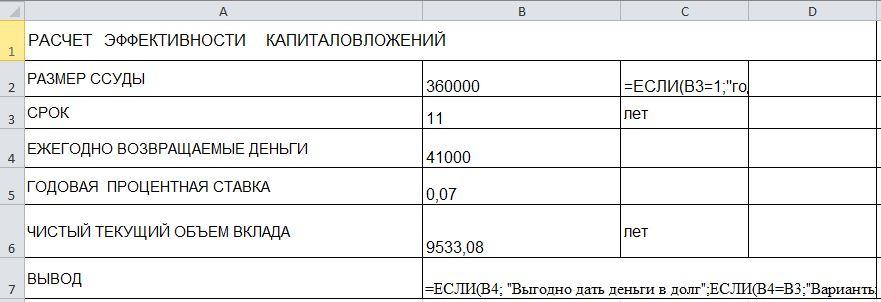
Задача
5

Рассмотреть
возможность инвестиций 360000 руб. под
годовую ставку 5%. Возможна выплата по
41000 руб. в год. Сколько лет займут эти
выплаты?

Решение
задачи

КПЕР
(ставка; выплата; нз; бз; тип)

ставка
— процентная ставка за период;

выплата
— величина постоянных периодических
платежей;

нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным 0 (будущая
стоимость займа, например, равна 0);

тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.

Исходные
данные для решения задачи представлены
на рис.13.

Рис.13
Исходные данные.

Формулы
для решения задачи представлены на
рис.14.

Рис.14
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.15.

Рис.15
Результаты решения.

Вывод

При
расмотрении инвестиций на сумма 360000
руб. под годовую ставу 5% и возможных
выплат по 41000 руб. Выплаты зайдут 12 лет.

Задача
6

Рассмотреть
возможность инвестиций 22000 руб. С
выплатами в определенные дниИмеет ли
смысл это при годовой ставке 1 % (Сумма
выплат из задания 2).

Решение
задачи

ЧПС
(ставка; 1-е значение; 2-е значение;
…)

ставка
— процентная ставка за период;

1-е
значение, 2-е значение, … — от 1 до 29
аргументов, представляющих расходы и
доходы. 1-е значение, 2-е значение, …
должны быть равно­мерно распределены
по времени и осуществляться в конце
каждого пе­риода. НПЗ использует
порядок аргументов 1-е значение, 2-е
значение,…для определения порядка
поступлений и платежей.

Исходные
данные для решения задачи представлены
на рис.16.

Рис.16
Исходные данные.

Формулы
для решения задачи представлены на
рис.17.

Рис.17
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.18.

Рис.18
Результаты решения.

Вывод

Рассмотрев
возможность инвестиций 22000 руб. С
выплатами в определенные дни Не имеет
смысл это при годовой ставке 15 %.

Задача
7

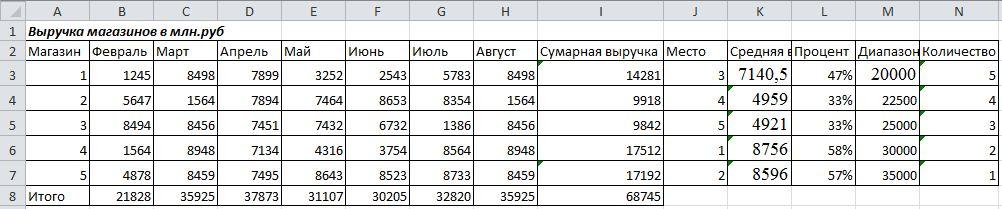
Составить
отчетную ведомость реализации товаров
6
магазинами с

февраль
по август.

Решение
задачи

В
этой отчетной ведомости надо определить:

суммарную
и среднюю выручку каждого из магазинов
за отчетный период;

суммарную
выручку всех магазинов за каждый месяц
отчетного периода;

место,
которое занимает каждый из магазинов
в суммарном объеме вы­ручки;

долю
каждого из магазинов в суммарном объеме
выручки;

количество
магазинов, имеющих суммарную выручку
до 1000 млн руб., от 1000 млн руб. до 1500 млн
руб., от 1500 млн руб. до 2000 млн руб. и свы­ше
2000 млн руб.

Исходные
данные для решения задачи представлены
на рис.19.

Рис.19
Исходные данные.

Формулы
для решения задачи представлены на
рис.20,1/20,2.

Рис.20,1
Формулы для решения задачи.

Рис.20,2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.21.

Рис.21
Результаты решения.

Вывод

Составлена
отчетная ведомость реализации товаров
6 магазинами с

февраль
по август.

Задача
8

Рассмотреть
возможность инвестиций 8138
руб. под годовую ставку 7% и собираетесь
отдавать по 711
руб. в год.
Сколько лет займут выплаты?

Решение
задачи

КПЕР
(ставка; выплата; нз; бз; тип)

ставка
— процентная ставка за период;

выплата
— величина постоянных периодических
платежей;

нз
— текущее значение, т. е. общая сумма,
которую составят будущие платежи;

бз
— будущая стоимость или баланс наличности,
который нужно достичь после последней
выплаты. Если параметр бз опущен, то его
значение по­лагается равным 0 (будущая
стоимость займа, например, равна 0);

тип—
число, равное 0 или 1, обозначающее, когда
должна производиться выплата. Если
значение параметра тип равно 0 или он
опущен, то оплата производится в конце
периода, если его значение равно 1, то в
начале периода.

Исходные
данные для решения задачи представлены
на рис.22.

Рис.22
Исходные данные

Формулы
для решения задачи представлены на
рис.23.

Рис.23
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.24.

Рис.24
Результат решения.

Вывод

Рассмотрели
возможность инвестиций 8138 руб. под
годовую ставку 7% с выплатами по 711 руб.
выплаты займут 23,9 лет.

Задача
9

Рассмотреть
возможность вкладывать по 711 руб. в
течение 12 лет при годовой ставке 7%.
Сколько денег будет на счету через 12
лет?

Решение
задачи

БС(ставка;кпер;плт;пс;тип)

Ставка  —
это процентная ставка за период.

Кпер   —
это общее число периодов платежей по
аннуитету.

Плт  —
это выплата, производимая в каждый
период; это значение не может меняться
в течение всего периода выплат. Обычно
плт состоит из основного платежа и
платежа по процентам, но не включает
других налогов и сборов. Если аргумент
опущен, должно быть указано значение
аргумента пс.

Пс  —
это приведенная к текущему моменту
стоимость или общая сумма, которая на
текущий момент равноценна ряду будущих
платежей. Если аргумент нз опущен, то
он полагается равным 0. В этом случае
должно быть указано значение аргумента
плт.

Тип  —
это число 0 или 1, обозначающее, когда
должна производиться выплата. Если этот
аргумент опущен, то он полагается равным
0.

Исходные
данные для решения задачи представлены
на рис.25.

Рис.25
Исходные данные.

Формулы
для решения задачи представлены на
рис.26.

Рис.26
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.27.

Рис.27
Результат решения.

Вывод

При
рассмотрении возможности вкладывать
по 711 руб. в течение 12 лет при годовой
ставке 7%. Денег будет через 17 лет
5647,25руб.

Задача
10

Определить
процентную ставку для 7 летнего займа
в 8138
руб. с ежегодной выплатой в 711
руб.

Решение
задачи

СТАВКА(кпер;плт;пс;бс;тип;предположение)

Кпер —
общее число периодов платежей по
аннуитету.

Плт  —
регулярный платеж (один раз в период),
величина которого остается постоянной
в течение всего срока аннуитета. Обычно
плт состоит из платежа основной суммы
и платежа процентов, но не включает
других сборов или налогов. Если аргумент
опущен, должно быть указано значение
аргумента бс

Пс —
приведенная к текущему моменту стоимость
или общая сумма, которая на текущий
момент равноценна ряду будущих платежей.

Бс —
требуемое значение будущей стоимости
или остатка средств после последней
выплаты. Если аргумент бс опущен, то он
полагается равным 0 (например, бзс для
займа равно 0).

Тип —
число 0 или 1, обозначающее, когда должна
производиться выплата.

Исходные
данные для решения задачи представлены
на рис.28.

Рис.28
Исходные данные.

Результаты
решения задачи представлены на рис.29.

Рис.29
Решения задачи.

Вывод

Определена
процентная ставку для 7 летнего займа
в 8138 руб. с ежегодной выплатой в 711руб.

Задача
11

Составить
таблицу начисления премии по итогам
работы сети n магази­нов с августа
по февраль
по следующему правилу:

если
продукции продано не меньше чем на
212000

руб., то комиссионные составляют 10%;

за
первое место дополнительно начисляется
7%, за второе место – 3,5% ,за четвёртое
место –6%.

Решение
задачи

Cрзнач
находит среднее арифметическое значение
из указанного диапазона ячеек.

Синтаксис:

СРЗНАЧ
(число1; число2; …)

Функция
ранг возвращает ранг числа в списке
чисел. Ранг числа — это его величина
относительно других значений в списке.
(Если список от­сортировать, то ранг
числа будет его позицией.)

Синтаксис:

РАНГ(число;
ссылка; порядок)

число
— число, для которого определяется
ранг;

ссылка
— массив или ссылка на список чисел.
Нечисловые значения в ссылке игнорируются;

порядок
— число, определяющее способ упорядочения.
Если значение параметра порядок равно
0 или он опущен, то MS Excel определяет ранг
числа так, как если бы ссылка была
списком, отсортированным в поряд­ке
убывания. Если значение параметра
порядок является любым ненуле­вым
числом, то MS Excel определяет ранг числа
так, как если бы ссылка была списком,
отсортированным в порядке возрастания.

Функция
ранг присваивает одинаковым числам
одинаковый ранг.

Функция
частота возвращает распределение частот
в виде вертикального массива. Для данного
множества значений и данного множества
карманов (т.е. интервалов в математическом
смысле) частотное распределе­ние
подсчитывает, сколько исходных значений
попадает в каждый интервал.

Синтаксис:

ЧАСТОТА
(массив_данных; двоичный__массив)

массив_данных
— массив или ссылка на множество данных,
для которых вычисляются частоты; если
массив_данных не содержит значений, то
функция частота возвращает массив
нулей;

двоичный_массив
— массив или ссылка на множество
интервалов, в которые группируются
значения аргумента массив_данных.
ЕСЛИ двоичный_массив не содержит
значений, то функция частота возвращает
количество эле­ментов в аргументе
двоичный_массив.

Исходные
данные для решения задачи представлены
на рис.30.

Рис.30
Исходные данные.

Формулы
для решения задачи представлены на
рис.31,1/31,2.

Рис.31,1
Формулы для решения задачи.

Рис.31,2
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.32.

Рис.32
Решения задачи.

Задача
12

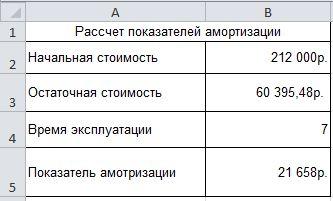
Предприятие
владеет основными средствами 212000
руб. Рассчитать показатели амортизации
за 7лет.

Решение
задачи

АПЛ
Возвращает величину амортизации актива
за один период, рассчитанную линейным
методом.

АПЛ(нач_стоимость;ост_стоимость;время_эксплуатации)

Нач_стоимость     —
затраты на приобретение актива.

Ост_стоимость     —
стоимость в конце периода амортизации
(иногда называется остаточной стоимостью
имущества).

Время_эксплуатации     —
количество периодов, за которые
собственность амортизируется (иногда
называется периодом амортизации).

Исходные
данные для решения задачи представлены
на рис.33.

Рис.33
Исходные данные.

Формулы
для решения задачи представлены на
рис.34.

Рис.34
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.35.

Рис.35
Результаты решения.

Вывод

Предприятие
владеет основными средствами 212000
руб. Рассчитали показатели амортизации
за 7 лет. Результат амортизации 21658 руб.

Задача
13

Предприятие
владеет основными средствами. Рассчитать
показатели амортизации за период при
следующих условиях. Дополнительные
условия: Амортизация за первый год.

Решение
задачи

ДДОБ
(стоимость; остаточная_стоимость;
время__эксплуатации; период;коэффициент)

стоимость
— начальная стоимость имущества;

остаточная_стоимость
— остаточная стоимость в конце периода;

время__эксплуатации
— количество периодов, за которые
собственность амортизируется (иногда
называется временем полной амортизации);

время_эксплуатации
— количество периодов, за которые
амортизируется имущество (иногда
называется временем полной амортизации);

коэффициент
— норма снижения балансовой стоимости
(амортизации).Если коэффициент опущен,
то предполагается, что он равен 2 ( метод
двукратного учета амортизации).

Исходные
данные для решения задачи представлены
на рис.36.

Рис.36
Исходные данные.

Формулы
для решения задачи представлены на
рис.37.

Рис.37
Формулы для решения задачи.

Результаты
решения задачи представлены на рис.38.

Рис.38
Результаты решения.

Вывод

Предприятие
владеет основными средствами 212000руб.
Рассчитать показатели амортизации за
период 7 лет . при дополнительном условии:
вычислении амортизации за первый год
равной 11459,54р.