Содержание
- Решение транспортной задачи в Excel с примером и описанием
- Виды транспортных задач
- Пример решения транспортной задачи в Excel
- Решение открытой транспортной задачи в Excel
- Транспортная задача в Microsoft Excel
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
- Решение транспортных задач ЛП в Excel
- Как решить транспортную задачу в Excel
- Алгоритм решения ТЗ в Эксель
- Транспортные задачи: примеры в Excel
Решение транспортной задачи в Excel с примером и описанием
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
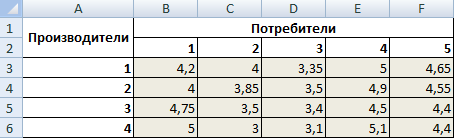
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
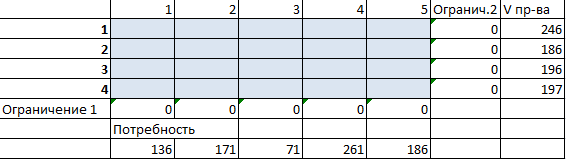
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
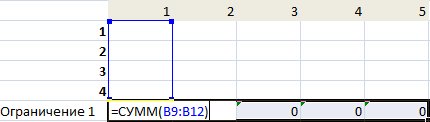
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
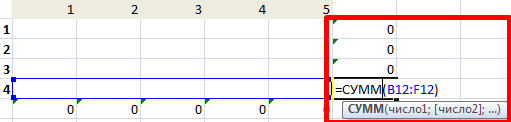
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
- Вносим известные значения потребности в товаре и объема производства.
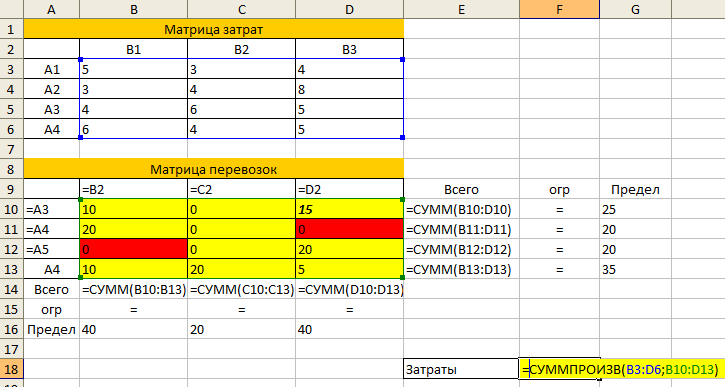
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
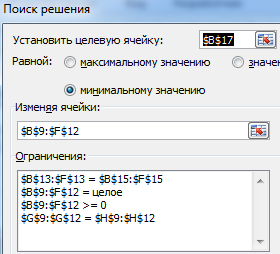
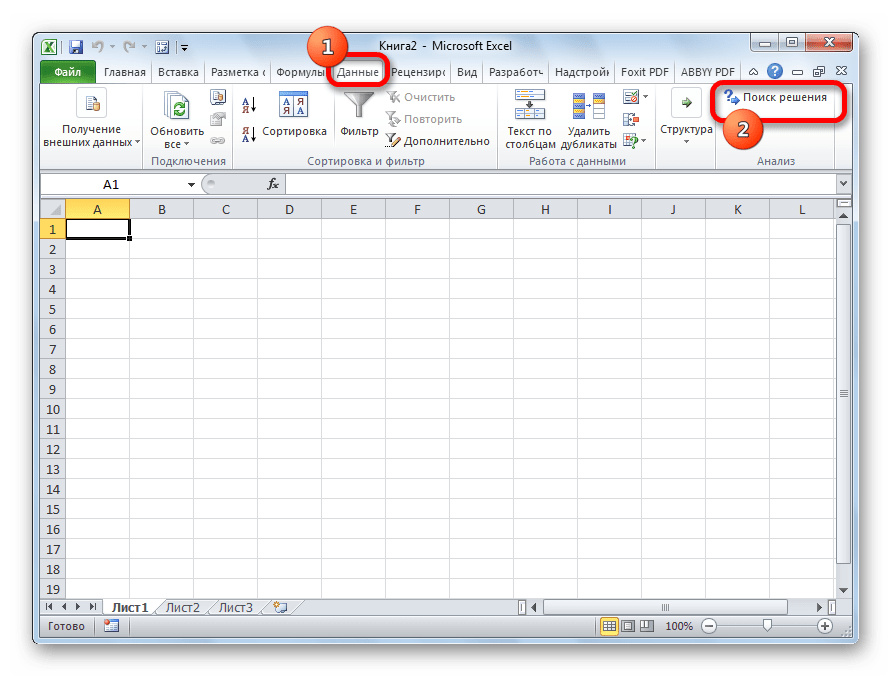
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
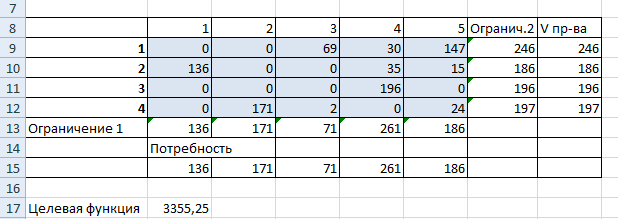
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Источник
Транспортная задача в Microsoft Excel
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
Пример решения транспортной задачи в Excel
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
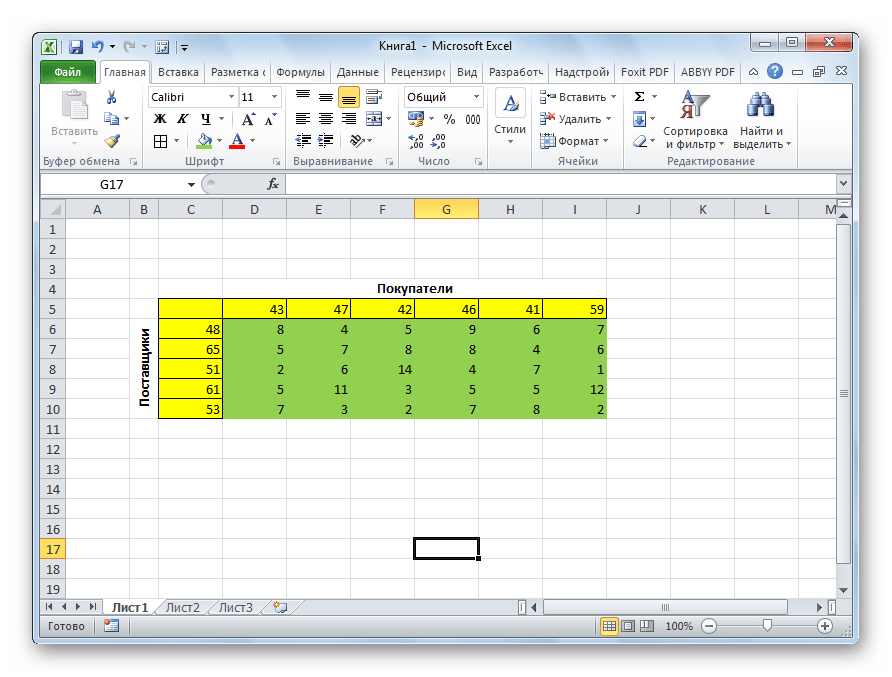
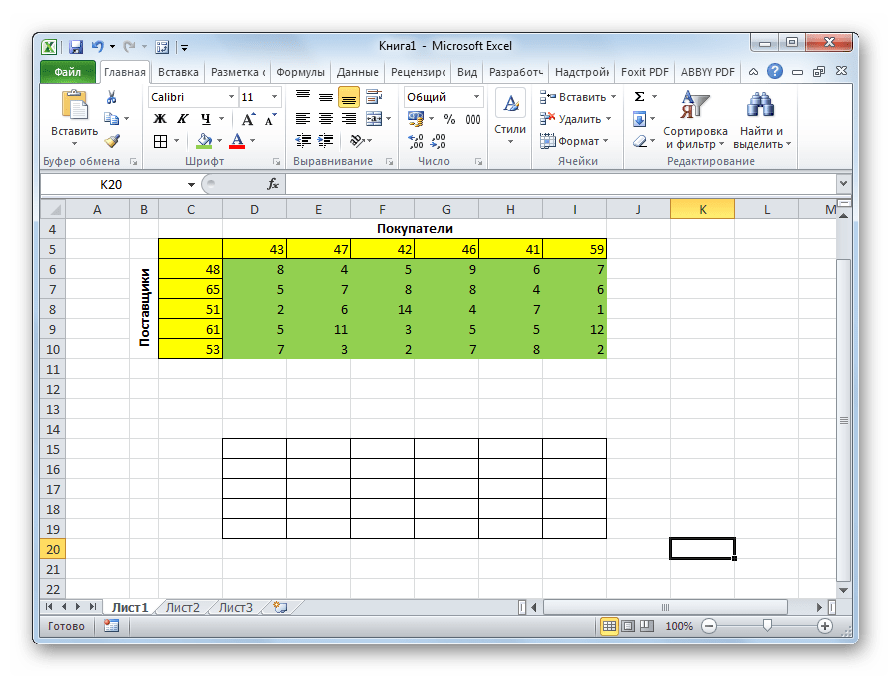
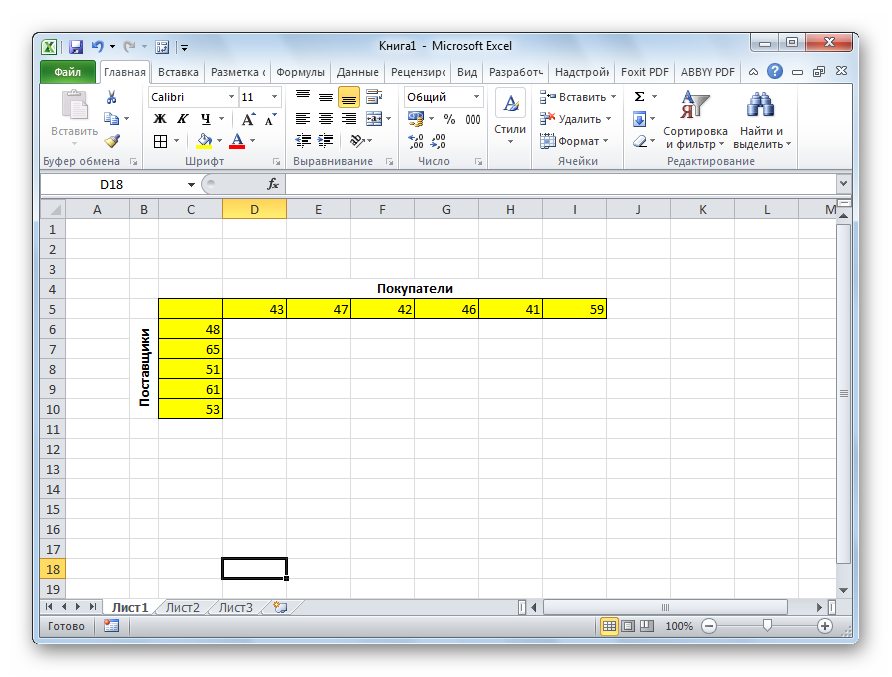
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
- Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
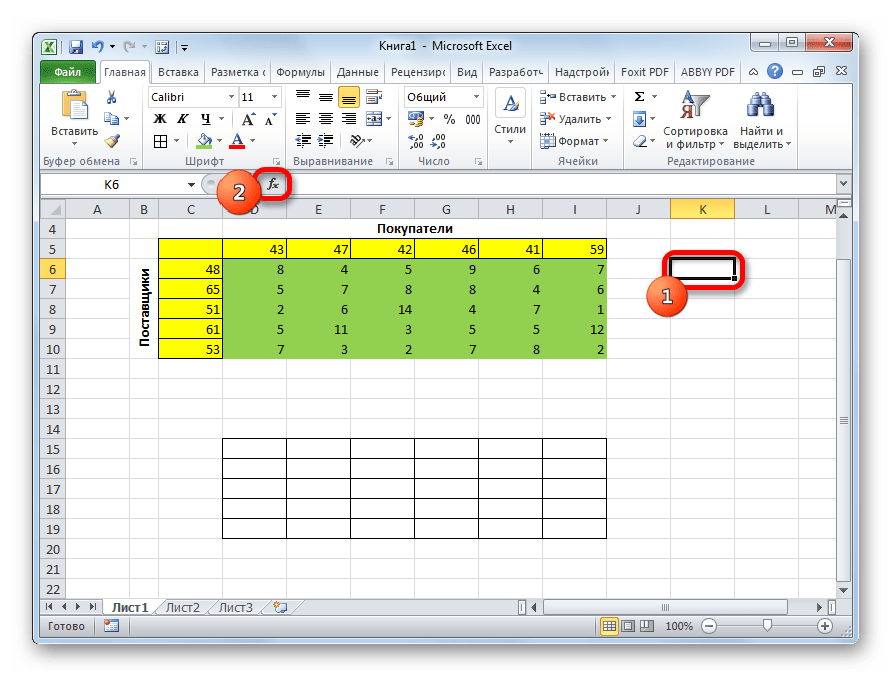
- Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
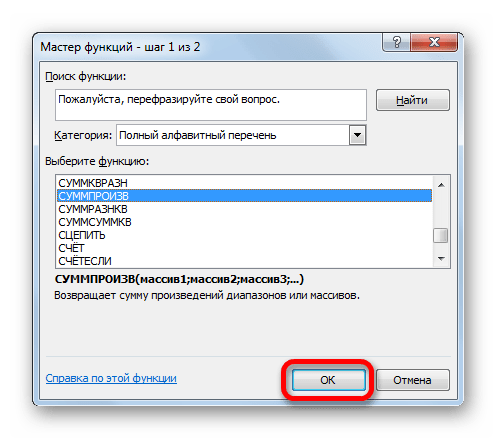
- Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
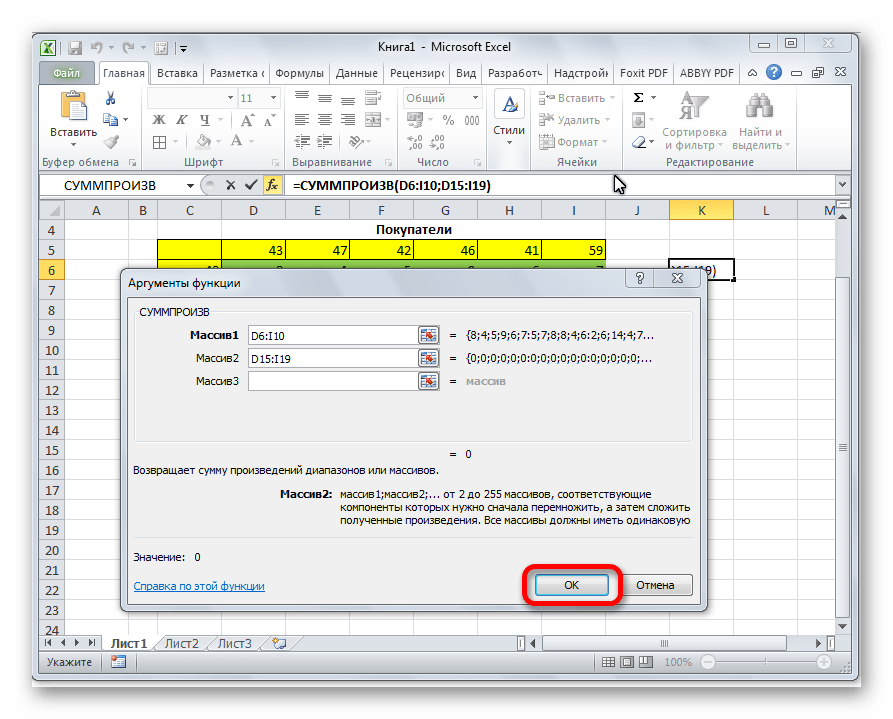
- Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
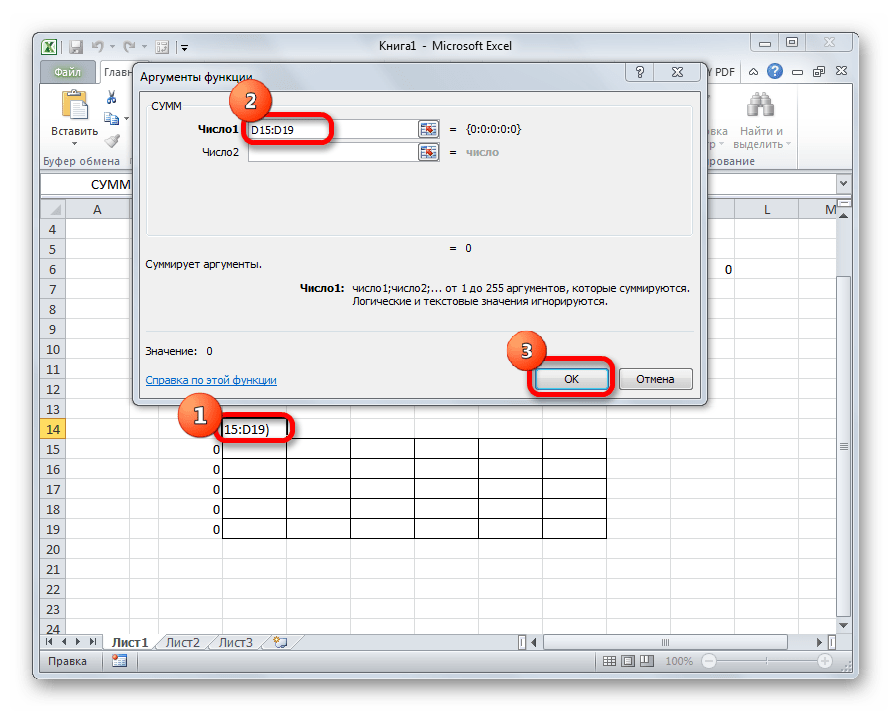
- Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
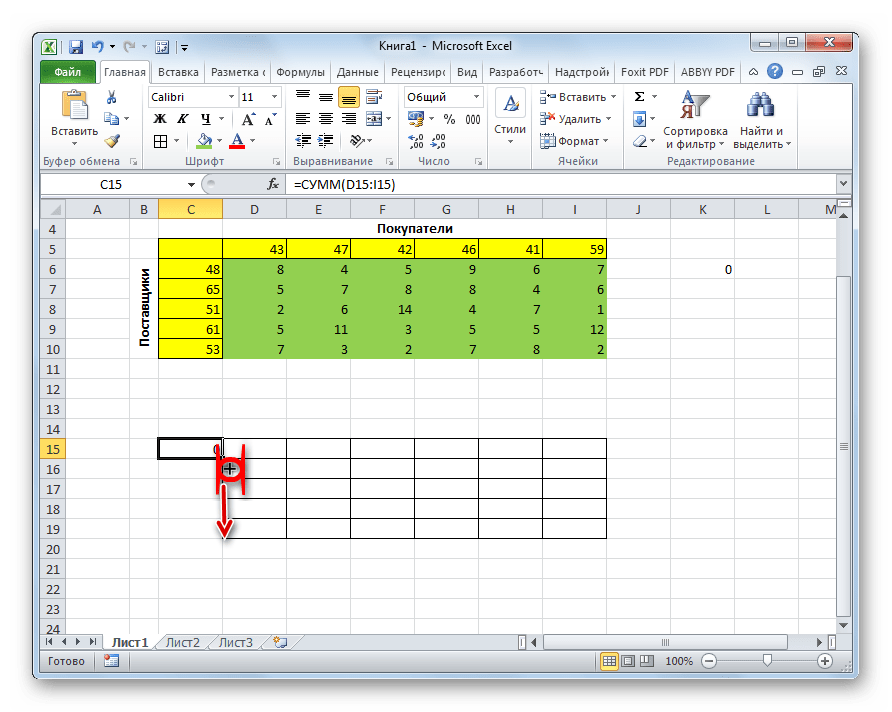
- Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
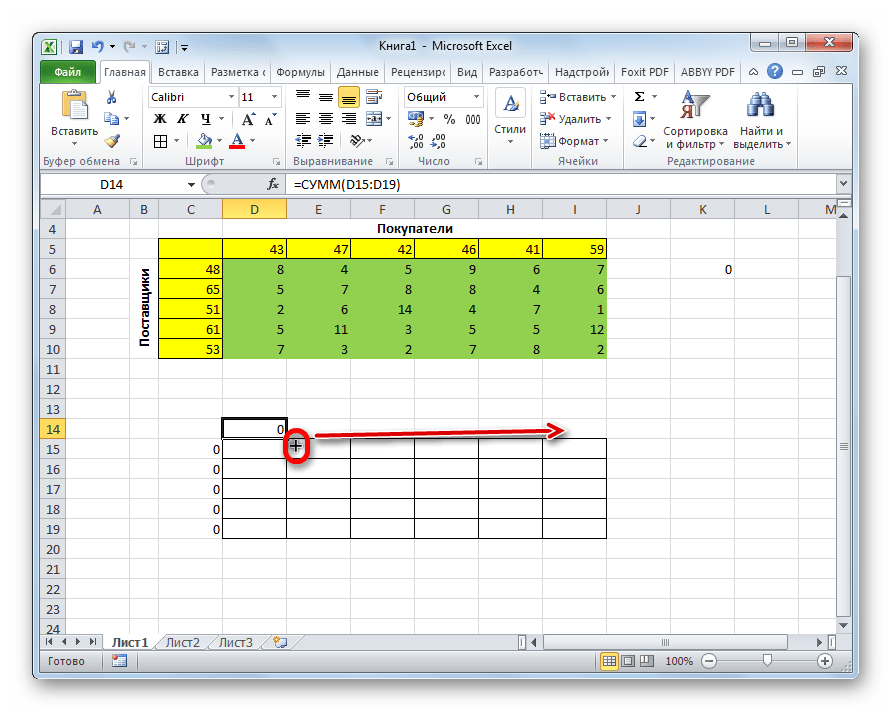
- Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
- Копируем маркером заполнения формулу на всю строку.
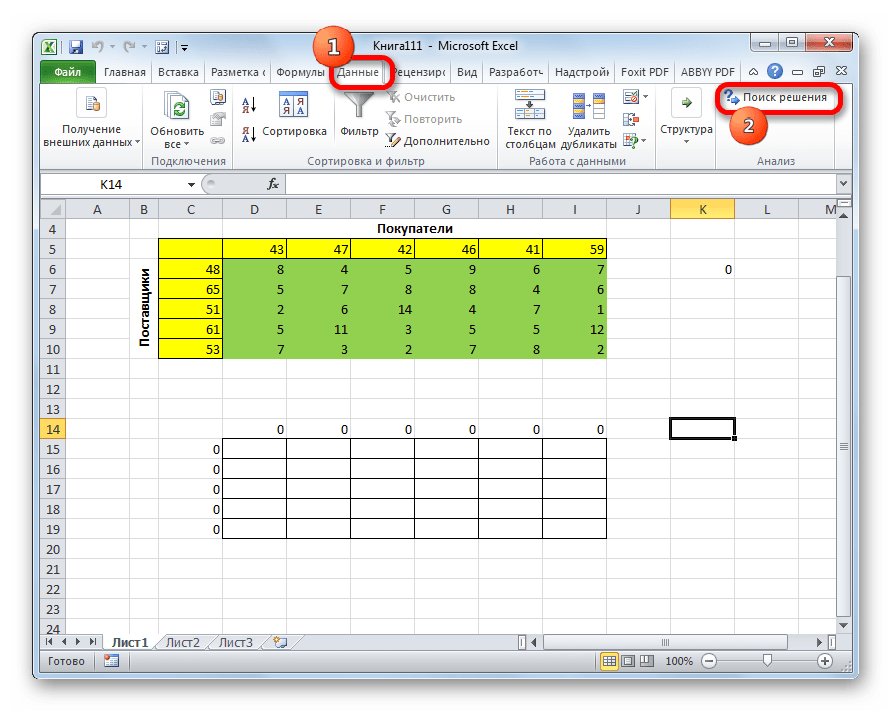
- Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
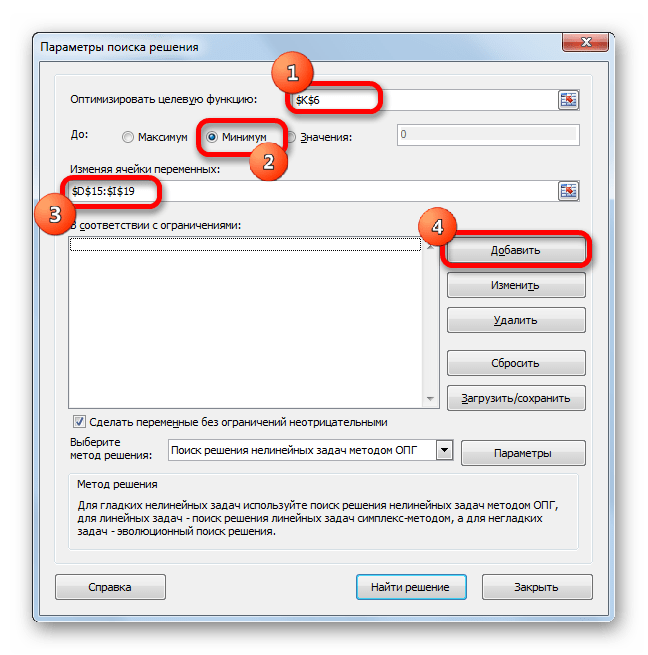
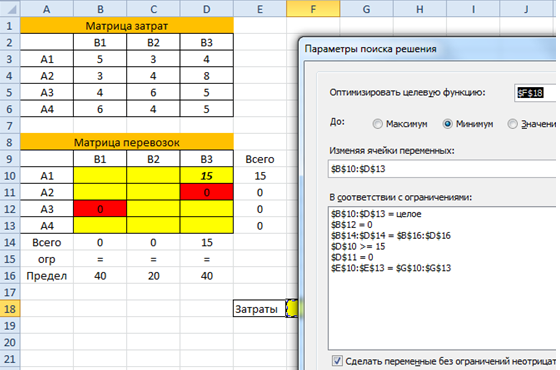
- Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
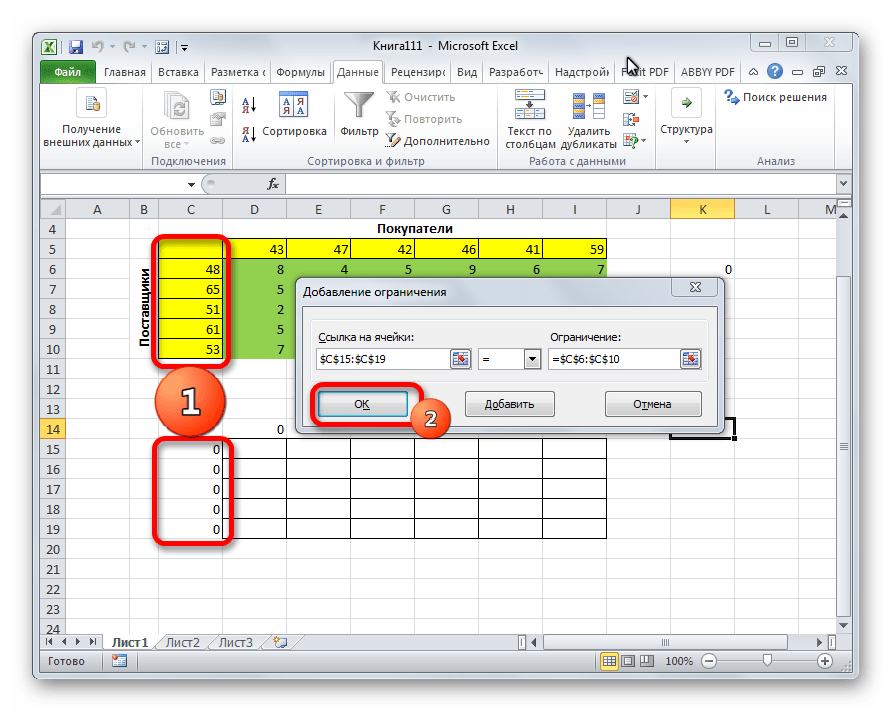
- Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
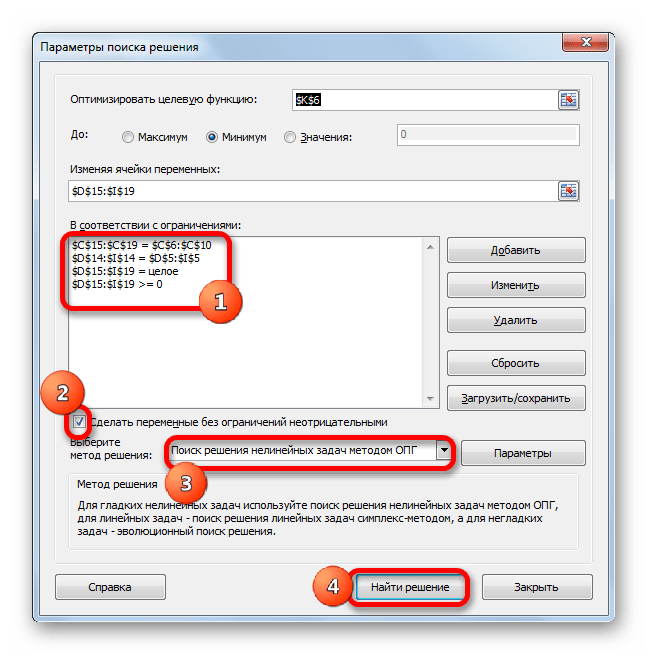
- Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
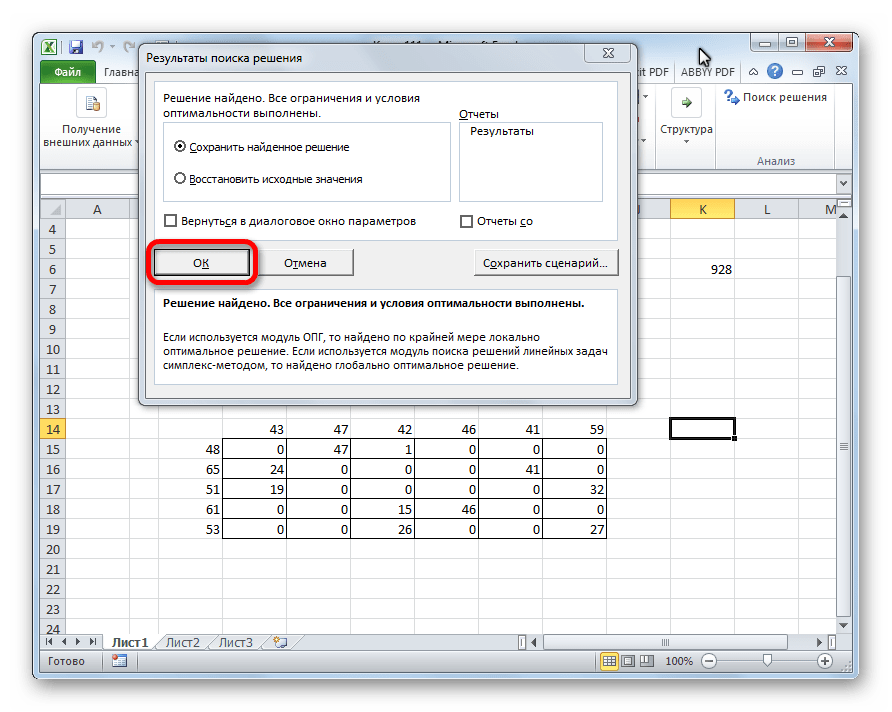
- После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.
Источник
Решение транспортных задач ЛП в Excel
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
В режиме формул таблица будет выглядеть так: - Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
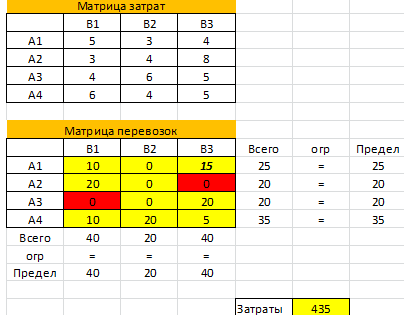
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Источник
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Содержание
- Транспортная задача: описание
- Подготовительный этап: включение функции “Поиск решения”
- Пример задачи и ее решение
- Условия
- Алгоритм решения
- Заключение
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
- Открываем меню “Файл”.
- В перечне слева выбираем пункт “Параметры”.
- В параметрах кликаем по подразделу “Надстройки”. Затем в правой части окна в самом низу, выбрав значение “Надстройки Excel” для параметра “Управление”, щелкаем по кнопке “Перейти”.
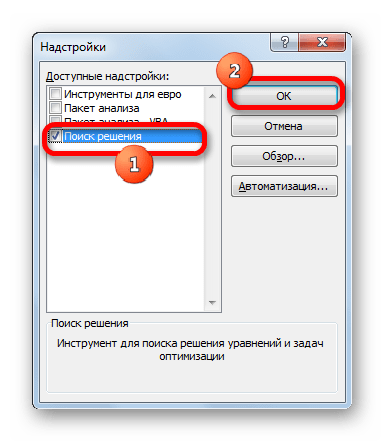
- В открывшемся окне ставим галочку напротив надстройки “Поиск решения” и жмем OK.
- В результате, если мы перейдем во вкладу “Данные”, то увидим здесь кнопку “Поиск решения” в группе инструментов “Анализ”.
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.
Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).
Алгоритм решения
Итак, приступи к решению нашей задачи:
- Для начала строим таблицу, количество строк и столбцов в которой соответствует числу продавцов и покупателей, соответственно.
- Перейдя в любую свободную ячейку щелкаем по кнопке “Вставить функцию” (fx).
- В открывшемся окне выбираем категорию “Математические”, в списке операторов отмечаем “СУММПРОИЗВ”, после чего щелкаем OK.
- На экране отобразится окно, в котором нужно заполнить аргументы:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
- по готовности жмем OK.
- Щелкаем по ячейке, расположенной слева от самого верхнего левого элемента новой таблицы, после чего снова жмем кнопку “Вставить функцию”.
- На этот раз нам нужна функция “СУММ”, которая также, находится в категории “Математические”.
- Теперь нужно заполнить аргументы. В качестве значения аргумента “Число1” указываем верхнюю строку созданной для расчетов таблицы (целиком) – вручную или методом выделения на листе. Жмем кнопку OK, когда все готово.
- В ячейке с функцией появится результат, равный нулю. Наводим указатель мыши на ее правый нижний угол, и когда появится Маркер заполнения в виде черного плюсика, зажав левую кнопку мыши тянем его до конца таблицы.
- Это позволит скопировать формулу и получить аналогичные результаты для остальных строк.
- Выбираем ячейку, которая находится сверху от самого верхнего левого элемента созданной таблицы. Аналогично описанным выше действиям вставляем в нее функцию “СУММ”.
- В значении аргумента “Число1” теперь указываем (вручную или с помощью выделения на листе) все ячейки первого столбца, после чего кликаем OK.
- С помощью Маркера заполнения выполняем копирование формулы на оставшиеся ячейки строки.
- Переключаемся во вкладку “Данные”, где жмем по кнопке функции “Поиск решения” (группа инструментов “Анализ”).
- Перед нами появится окно с параметрами функции:
- в качестве значения параметра “Оптимизировать целевую функцию” указываем координаты ячейки, в которую ранее была вставлена функция “СУММПРОИЗВ”.
- для параметра “До” выбираем вариант – “Минимум”.
- в области для ввода значений напротив параметра “Изменяя ячейки переменных” указываем диапазон ячеек новой таблицы (без суммирующей строки и столбца).
- нажимаем кнопку “Добавить” в блоке “В соответствии с ограничениями”.
- Откроется небольшое окошко, в котором мы можем добавить ограничение – сумма значений первых столбцов исходной и созданной таблицы должны быть равны.
- становимся в поле “Ссылка на ячейки”, после чего указываем нужный диапазон данных в таблице для расчетов.
- затем выбираем знак “равно”.
- в качестве значения для параметра “Ограничение” указываем координаты аналогичного столбца в исходной таблице.
- щелкаем OK по готовности.
- Таким же способом добавляем условие по равенству сумм верхних строк таблиц.
- Также добавляем следующие условия касательно суммы ячеек в таблице для расчетов (диапазон совпадает с тем, который мы указали для параметра “Изменяя ячейки переменных”):
- больше или равно нулю;
- целое число.
- В итоге получаем следующий список условий в поле “В соответствии с ограничениями”. Проверяем, чтобы обязательно была поставлена галочка напротив опции “Сделать переменные без ограничений неотрицательными”, а также, чтобы в качестве метода решения стояло значение “Поиск решения нелинейных задач методов ОПГ”. Когда все готово, нажимаем “Найти решение”.
- В результате будет выполнен расчет и отобразится окно с результатами поиска решения. Оцениваем их, и в случае, когда они нас устраивают, нажимаем OK.
- Все готово, мы получили таблицу с заполненными данными и транспортную задачу можно считать успешно решенной.
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Практически все транспортные задачи имеют единую математическую модель. Классический вариант решения иллюстрирует самый экономный план перевозок одинаковых или схожих продуктов от производственного объекта в пункт потребления.
Планирование перевозок с помощью математических и вычислительных методов дает хороший экономический эффект.
Виды транспортных задач
Условия и ограничения транспортной задачи достаточно обширны и разнообразны. Поэтому для ее решения разработаны специальные методы. С помощью любого из них можно найти опорное решение. А впоследствии улучшить его и получить оптимальный вариант.
Условия транспортной задачи можно представить двумя способами:
- в виде схемы;
- в виде матрицы.
В процессе решения могут быть ограничения (либо задача решается без них).
По характеру условий различают следующие типы транспортных задач:
- открытые открытые транспортные задачи (запас товара у поставщика не совпадает с потребностью в товаре у потребителя);
- закрытые (суммарные запасы продукции у поставщиков и потребителей совпадают).
Закрытая транспортная задача может решаться методом потенциалов. Она всегда разрешима. Открытый тип сводят к закрытому с помощью прибавления к суммарному запасу или потребности в товаре недостающих единиц, чтобы добиться равенства.
Пример решения транспортной задачи в Excel
Предприятия А1, А2, А3 и А4 производят однородную продукцию а1, а2, а3 и а4, соответственно. В условных единицах – 246, 186, 196 и 197. Затем товар поступает в пять пунктов назначения: В1, В2, В3, В4 и В5. Это потребители продукции. Они готовы ежедневно принимать 136, 171, 71, 261 и 186 единиц товара.
Стоимость перевозки единицы продукции с учетом удаленности от пункта назначения:
| Производители | Потребители | Объем производства | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | 4,2 | 4 | 3,35 | 5 | 4,65 | 246 |
| А2 | 4 | 3,85 | 3,5 | 4,9 | 4,55 | 186 |
| А3 | 4,75 | 3,5 | 3,4 | 4,5 | 4,4 | 196 |
| А4 | 5 | 3 | 3,1 | 5,1 | 4,4 | 197 |
| Объем потребления | 136 | 171 | 71 | 261 | 186 |
Задача: минимизировать транспортные расходы по перевозке продукции.
- Проверим, является ли модель транспортной задачи сбалансированной. Для этого все количество производимого товара сравним с суммарным объемом потребности в продукции: 246 + 186 + 196 + 197 = 136 + 171 + 71 + 261 + 186. Вывод – модель сбалансированная.
- Сформулируем ограничения: объем перевозимой продукции не может быть отрицательным и весь товар должен быть доставлен к пунктам назначения (т.к. модель сбалансированная).
- Введем стоимость перевозки единицы продукции в рабочие ячейки Excel.
- Введем формулы для расчета суммарной потребности в товаре. Это будет первое ограничение.
- Введем формулы для расчета суммарного объема производства. Это будет второе ограничение.
- Вносим известные значения потребности в товаре и объема производства.
- Вводим формулу целевой функции СУММПРОИЗВ(B3:F6; B9:F12), где первый массив (B3:F6) – стоимость единицы перевозки товаров. Второй (B9:F12) – искомые значения транспортных расходов.
- Вызываем команду «Поиск решения» на закладке «Данные» (если там нет данного инструмента, то его нужно подключить в настройках Excel, а как это сделать описано в статье: расширенные возможности финансового анализа). Заполняем диалоговое окно. В графе «Установить целевую ячейку» — ссылка на целевую функцию. Ставим галочку «Равной минимальному значению». В поле «Изменяя ячейки» — массив искомых критериев. В поле «Ограничения»: искомый массив >=0, целые числа; «ограничение 1» = объему потребностей; «ограничение 2» = объему производства.
- Нажимаем «Выполнить». Команда подберет оптимальные переменные при заданных ограничениях.
Так выглядит «сырой» вариант работы инструмента. Экспериментируя с полученными данными, находим подходящие значения.
Решение открытой транспортной задачи в Excel
При таком типе возможны два варианта развития событий:
- суммарный объем производства превышает суммарную потребность в товаре;
- суммарная потребность больше суммы запасов.
Открытую транспортную задачу приводят к закрытому типу. В первом случае вводят фиктивного потребителя. Его потребности равны разнице всего объема производства и суммы существующих потребностей.
Во втором случае вводят фиктивного поставщика. Объем его производства равен разнице суммарной потребности и суммарных запасов.
Единица перевозки груза для фиктивного участника равняется 0.
Когда все преобразования выполнены, транспортная задача становится закрытой и решается обычным способом.
Читайте также по теме: решение транспортной задачи методом потенциалов в Excel.
Содержание
- Общее описание транспортной задачи
- Инструменты для решения транспортной задачи в Эксель
- Пример решения транспортной задачи в Excel
- Условия задачи
- Решение задачи
- Вопросы и ответы
Транспортная задача представляет собой задачу поиска наиболее оптимального варианта перевозок однотипного товара от поставщика к потребителю. Её основой является модель, широко применяемая в различных сферах математики и экономики. В Microsoft Excel имеются инструменты, которые значительно облегчают решение транспортной задачи. Выясним, как их использовать на практике.
Общее описание транспортной задачи
Главной целью транспортной задачи является поиск оптимального плана перевозок от поставщика к потребителю при минимальных затратах. Условия такой задачи записываются в виде схемы или матрицы. Для программы Excel используется матричный тип.
Если общий объем товара на складах поставщика равен величине спроса, транспортная задача именуется закрытой. Если эти показатели не равны, то такую транспортную задачу называют открытой. Для её решения условия следует привести к закрытому типу. Для этого добавляют фиктивного продавца или фиктивного покупателя с запасами или потребностями равными разнице между спросом и предложением в реальной ситуации. При этом в таблице издержек добавляется дополнительный столбец или строка с нулевыми значениями.
Инструменты для решения транспортной задачи в Эксель
Для решения транспортной задачи в Excel используется функция «Поиск решения». Проблема в том, что по умолчанию она отключена. Для того, чтобы включить данный инструмент, нужно выполнить определенные действия.
- Делаем перемещение во вкладку «Файл».
- Кликаем по подразделу «Параметры».
- В новом окне переходим по надписи «Надстройки».
- В блоке «Управление», который находится внизу открывшегося окна, в выпадающем списке останавливаем выбор на пункте «Надстройки Excel». Делаем клик по кнопке «Перейти…».
- Запускается окно активации надстроек. Устанавливаем флажок возле пункта «Поиск решения». Кликаем по кнопке «OK».
- Вследствие этих действий во вкладке «Данные» в блоке настроек «Анализ» на ленте появится кнопка «Поиск решения». Она нам и понадобится при поиске решения транспортной задачи.
Урок: функция «Поиск решения» в Экселе
Теперь давайте разберем конкретный пример решения транспортной задачи.
Условия задачи
Имеем 5 поставщиков и 6 покупателей. Объёмы производства этих поставщиков составляют 48, 65, 51, 61, 53 единиц. Потребность покупателей: 43, 47, 42, 46, 41, 59 единиц. Таким образом, общий объем предложения равен величине спроса, то есть, мы имеем дело с закрытой транспортной задачей.
Кроме того, по условию дана матрица затрат перевозок из одного пункта в другой, которая отображена на иллюстрации ниже зеленым цветом.
Решение задачи
Перед нами стоит задача при условиях, о которых было сказано выше, свести транспортные расходы к минимуму.
- Для того, чтобы решить задачу, строим таблицу с точно таким же количеством ячеек, как и у вышеописанной матрицы затрат.
- Выделяем любую пустую ячейку на листе. Кликаем по значку «Вставить функцию», размещенному слева от строки формул.
- Открывается «Мастер функций». В списке, который предлагает он, нам следует отыскать функцию СУММПРОИЗВ. Выделяем её и жмем на кнопку «OK».
- Открывается окно ввода аргументов функции СУММПРОИЗВ. В качестве первого аргумента внесем диапазон ячеек матрицы затрат. Для этого достаточно выделить курсором данные ячейки. Вторым аргументом выступит диапазон ячеек таблицы, которая была приготовлена для расчетов. Затем, жмем на кнопку «OK».
- Кликаем по ячейке, которая расположена слева от верхней левой ячейки таблицы для расчетов. Как и в прошлый раз вызываем Мастер функций, открываем в нём аргументы функции СУММ. Кликнув по полю первого аргумента, выделяем весь верхний ряд ячеек таблицы для расчетов. После того, как их координаты занесены в соответствующее поле, кликаем по кнопке «OK».
- Становимся в нижний правый угол ячейки с функцией СУММ. Появляется маркер заполнения. Жмем на левую кнопку мыши и тянем маркер заполнения вниз до конца таблицы для расчета. Таким образом мы скопировали формулу.
- Кликаем по ячейке размещенной сверху от верхней левой ячейки таблицы для расчетов. Как и в предыдущий раз вызываем функцию СУММ, но на этот раз в качестве аргумента используем первый столбец таблицы для расчетов. Жмем на кнопку «OK».
- Копируем маркером заполнения формулу на всю строку.
- Переходим во вкладку «Данные». Там в блоке инструментов «Анализ» кликаем по кнопке «Поиск решения».
- Открываются параметры поиска решения. В поле «Оптимизировать целевую функцию» указываем ячейку, содержащую функцию СУММПРОИЗВ. В блоке «До» устанавливаем значение «Минимум». В поле «Изменяя ячейки переменных» указываем весь диапазон таблицы для расчета. В блоке настроек «В соответствии с ограничениями» жмем на кнопку «Добавить», чтобы добавить несколько важных ограничений.
- Запускается окно добавления ограничения. Прежде всего, нам нужно добавить условие того, что сумма данных в строках таблицы для расчетов должна быть равна сумме данных в строках таблицы с условием. В поле «Ссылка на ячейки» указываем диапазон суммы в строках таблицы расчетов. Затем выставляем знак равно (=). В поле «Ограничение» указываем диапазон сумм в строках таблицы с условием. После этого, жмем на кнопку «OK».
- Аналогичным образом добавляем условие, что столбцы двух таблиц должны быть равны между собой. Добавляем ограничение, что сумма диапазона всех ячеек в таблице для расчета должна быть большей или равной 0, а также условие, что она должна быть целым числом. Общий вид ограничений должен быть таким, как представлен на изображении ниже. Обязательно проследите, чтобы около пункта «Сделать переменные без ограничений неотрицательными» стояла галочка, а методом решения был выбран «Поиск решения нелинейных задач методом ОПГ». После того, как все настройки указаны, жмем на кнопку «Найти решение».
- После этого происходит расчет. Данные выводятся в ячейки таблицы для расчета. Открывается окно результатов поиска решения. Если результаты вас удовлетворяют, жмите на кнопку «OK».
Как видим, решение транспортной задачи в Excel сводится к правильному формированию вводных данных. Сами расчеты выполняет вместо пользователя программа.
Еще статьи по данной теме:
Помогла ли Вам статья?
На этой странице разберем подробные решения транспортной задачи (алгоритм и примеры разных типов) с использованием пакета электронных таблиц MS Excel (надстройка Поиск решения).
Как решить транспортную задачу в Excel
Ручное решение транспортной задачи занимает очень много времени и сил (скажем, даже для учебной задачи типа 3*5 решение может составлять от 4 до 10 страниц расчетов!). Тогда как решение в Эксель для задачи размерности как 3*3, так и 5*7 потребует буквально 10-15 минут и немного опыта (правда, если уже составлена математическая модель).
Использовать можно любую версию программы — 2003, 2007, 2010 и так далее, главное, включить использование надстройки Поиск решения (интерфейс может немного отличаться в разных версиях).
Алгоритм решения ТЗ в Эксель
- Составить математическую модель транспортной задачи — то есть получить таблицу со стоимостью перевозок, запасами груза у поставщиков и потребностями потребителей (и, возможно, дополнительными ограничениями).
- Если задача открытая (несбалансированная), то добавить потребителя или поставщика с нулевыми тарифами перевозки.
- Внести на лист таблицы Excel данную модель в виде матрицы тарифов (затрат).
- Создать рядом на листе еще одну таблицу, где будут выводиться искомые перевозки (такой же размерности, что и таблица тарифов). Просуммировать перевозки по строкам и столбцам (чтобы сравнивать с аналогичными ячейками — предельными ограничениями задачи — запасами поставщиков и потребностями потребителей).
- Ввести в ячейку формулу, подсчитывающую суммарную стоимость перевозок (это число мы должны минимизировать по смыслу транспортной задачи)
В режиме формул таблица будет выглядеть так:
- Запустить надстройку Поиск решения и указать а) ячейку, которую мы минимизируем, б) все ограничения на запасы поставщиков и потребности потребителей, в) дополнительные ограничения (иногда бывают запреты перевозок или требования по минимальному объему груза между определенными пунктами, как в данном случае).
- Получить решение транспортной задачи: в целевой ячейке вы увидите минимальную стоимость перевозок (в примере 435), а в таблице перевозок — искомые значения объема перевозимого груза (см. желтые ячейки).
- Проанализировать решение, если требуется и записать более подробно, например
Минимальные затраты на перевозку составят 435. План перевозок:
Из 1 карьера 10 тонн везем на 1-й участок, 15 тонн на 3-й.
Из 2 карьера 20 тонн везем на 1-й участок.
Из 3 карьера 20 тонн везем на 3-й.
Из 4 карьера 10 тонн везем на 1-й участок, 20 тонн на 2-й, 5 тонн на 3-й.
Полезная страница? Сохрани или расскажи друзьям
Транспортные задачи: примеры в Excel
Задача 1. Решить транспортную задачу вручную (методом потенциалов) и в программе Эксель.
Задача 2. Исходные данные задачи приведены схематически: внутри прямоугольника заданы удельные транспортные затраты на перевозку единицы груза, слева указаны мощности поставщиков, а сверху — мощности потребителей.
Сформулировать экономико-математическую модель исходной транспортной задачи, найти оптимальный план закрепления поставщиков за потребителями, установить единственность или не единственность оптимального плана, используя Поиск решений.
Задача 3. Имеется 3 нефтеперерабатывающих завода, 4 спиртовых завода, 3 завода по производству синтетического каучука.
Схема кооперационных связей (см. файл).
Далее приведены производственные показатели предприятий.
Также заданы расстояния между предприятиями.
Необходимо найти решение транспортной задачи с ориентацией на спрос СК и минимизацией транспортных суммарных затрат.
Задача 4. Используя метод потенциалов, решить транспортную задачу. Выполнить проверку, используя табличный редактор Microsoft Excel Компания владеет тремя заводами А1, А2, А3. Соответствующие объемы производства равны 600, 300 и 330 единиц продукции. Компания обязалась поставить в города В1, В2, В3 и В4 соответственно 350, 350, 230 и 300 единиц. При заданных в таблице стоимостях перевозок единицы продукции составьте план ее распределения, чтобы общая стоимость перевозок была наименьшей.
Задача 5. Свести задачу к виду ТЗ и решить с помощью надстройки «Поиск решения»
Четыре ремонтные мастерские могут за год отремонтировать соответственно 400, 500, 450 и 550 машин при себестоимости ремонта одной машины в 500, 700, 650 и 600 рублей. Планируется годовая потребность в ремонте пяти автобаз: 550, 350, 300, 375 и 400 машин.
Ремонт машин с 1 автобазы должен осуществляться в 100% случаев силами ремонтных мастерских.
На 4 АБ возможно самостоятельное проведение ремонтных работ (бесплатное) в объеме, не превышающем 8% от планируемой годовой потребности этой мастерской. Платное (на стороне) — совсем не возможно.
Вторая, третья и пятая АБ могут «ремонтироваться» на стороне, стоимость ремонта +трансп.расходы каждой машины в таком случае составит 695 руб.
Дана матрица, характеризующая транспортные расходы на доставку машины с j-й автобазы в i-ю ремонтную мастерскую. Определить минимальную годовую потребность в кредитах на выполнение указанного объема работ по всем автобазам
Решаем транспортные задачи любой сложности
Полезные ссылки
|
|
Недостаточно только получить знания;
надо найти им приложение.
Недостаточно только желать – надо делать.
(И.-В. Гёте)
В условиях жесткой конкуренции между средне
специальными учебными заведениями, в поиске
новых способов привлечения абитуриентов,
решающим фактором является качество
обучения.
В государственных образовательных стандартах
предыдущего поколения для профессионального
образования подразумевали формирование у
студентов знаний, умений и навыков (ЗУН). В
стандартах третьего поколения эти понятия
практически исключены, теперь говорится о
формировании компетенций.
Таким образом, возникает противоречие между
требованиями стратегии модернизации
образования в компетентностном подходе к
процессу и результатам образования и не
разработанностью его методологии, теории и
практики в образовательном процессе, в
частности, в обучении математике. Данное
противоречие говорит об актуальности.
Каменский политехнический техникум выпускает
высококвалифицированных специалистов. Но сейчас
это осуществляется все с большими трудностями.
Одной из причин, на мой взгляд, является плохая
школьная подготовка, особенно по математике,
которая обнаруживается, когда студент подходит к
специальным дисциплинам, где уже из объекта
изучения, математика становится инструментом
изучения другого предмета. И получается, что
пользоваться этим инструментом студент
затрудняется.
В данной разработке рассмотрена возможность
реализации компетентностного подхода на
занятиях по математике, в частности с
применением персонального компьютера при
решении реальных производственных задач.
Приведенное практическое занятие по своей
структуре почти традиционно, но отличается
формой организации учебно-поисковой,
исследовательской деятельности.
Цели занятия:
- Образовательная: совершенствование
навыков и умений решения простейших
транспортных задач с помощью табличного
процессора MS Excel; приобщение студентов к
самостоятельному, оперативному решению
учебно-производственных задач, используя
взаимосвязь предметов математики и информатики. - Развивающая: выработать умения и навыки
применять полученные знания при решении
транспортных задач различной направленности,
развитие умения пользоваться предложенными
инструментами; развивать навыки индивидуальной
и групповой практической работы. - Воспитательная: формирование творческой
самостоятельности студентов; профессиональная
ориентация и подготовка к дальнейшему
самообразованию, к будущей трудовой
деятельности.
Тип занятия: совершенствование
навыков и умений.
Вид и форма занятия: Практическая
работа. Общественный смотр знаний.
Методы обучения: практический;
частично-поисковый, проблемный,
исследовательский, Case-Study.
Комплексно-методическое обеспечение: ПК,
проектор; табличный процессор MS Excel; MS Power Point, Paint.
Авторская монография «Технология решения
линейных алгебраических уравнений (ЛАУ), задач
линейного программирования (ЛП) с использованием
персонального компьютера и их практическое
применение»; раздаточный материал, специальная
карта, таблица для отражения результатов.
Выставка творческих самостоятельных работ
студентов к изучаемой теме. Слайды Power Point:
«Историческая справка о задачах линейного
программирования», «Модели транспортных задач
(ТЗ) и этапы их решения менеджером», «Общая
постановка ТЗ»; «Учебно-исследовательская
работа студентов 2010 г.».
Междисциплинарные связи: Математика:
действительные числа и действия над ними;
решение системы ЛАУ. Информатика: экономические
расчеты в MS Excel. Организация, обслуживание на
предприятиях сферы сервиса: организация,
обслуживание производства.
ХОД ЗАНЯТИЯ
I. Организационный момент.
Проверка готовности студентов; рабочих мест.
Инструктаж по ТБ.
Группа предварительно разделилась на две
команды, каждая избрала капитана. Жюри – в
составе двух человек (из присутствующих
преподавателей).
II. Определение и мотивация учебной
деятельности
Преподаватель. Пройденная нами тема
“Электронные таблицы” – одна из наиболее
практически значимых, востребованных, после
текстового редактора MS Word и его возможностей.
Знания, полученные при изучении электронных
таблиц пригодятся вам при планировании на самых
различных уровнях: от государственного до
домашнего.
Приведите пример?
Правительство в конце каждого года
составляет бюджет на будущий год, вам и вашим
родителям приходится планировать как личный, так
и семейный бюджеты.
– Освоенный табличный процессор MS Excel
поможет нам переложить решение задач на плечи
компьютера и окажет незаменимую помощь в
освоении следующей темы «Решение транспортных
задач». Перечислите, что вы научились делать,
изучая табличный процессор MS EXCEL? (Мы научились
выполнять вычислительные операции при помощи
формул, решили массу задач различного
содержания, составляли много различных таблиц и
диаграмм.)
На плакатах демонстрируются примеры
различных таблиц, графиков, диаграмм, изученных и
построенных на предыдущих уроках.
– Давайте, перечислим области деятельности
человека, к которым можно отнести использование
возможностей табличного процессора MS EXCEL? (Это
– наука, производство, бухгалтерия, торговля,
статистика, экология. Вывод: области применения
электронных таблиц очень разнообразны, без них
не может обойтись практически ни один
современный специалист.)
III. Актуализация опорных знаний
3.1. Конкурс капитанов
Связь изученного материала по математике с
изучаемым материалом на занятии: конкурс
мультимедийных презентаций «Историческая
справка о задачах линейного программирования»,
«Модели транспортных задач, этапы их решения
менеджером», разработанных капитанами
предварительно.
Максимальное количество баллов за конкурс
– 5 баллов.
3.2. Конкурс математиков-экономистов –
«Наука – всему голова»
Дидактическая игра «Математическое лото».
Максимальное количество баллов, присуждаемых
командам – 5 баллов.
Каждой команде предлагается набор карточек из 10
вопросов. Отвечаем на вопрос и накрываем
клеточку с правильным ответом в специальной
карте. Если карта заполнена верно – получим
рисунок, на оборотных сторонах карточек.
1. Что такое целевая функция задачи линейного
программирования?
2. Оптимальной базисное решение следует искать …
выпуклого многогранника, описывающего область
допустимых решений задачи линейного
программирования.
3. При решении транспортной задачи (ТЗ) в EXCEL Вы
получили ответ: «Поиск решения не может найти
подходящего решения». Ваши действия …
4. Как изменяется значение целевой функции при
решении ТЗ?
5. Каких типов бывают транспортные задачи?
6. Какое максимальное количество поставщиков
может быть задано в транспортной задаче?
7. Что оптимизируется в транспортной задаче?
8. Ограничения на входящие переменные
указываются в параметре … .
9.Средство «Поиск решения» можно установить
с помощью команд:
10. С помощью средства «Поиск
решения» решаются:
| Функция, наибольшее или наименьшее значение которой отыскивается |
В одной из вершин | Проверить правильность ограничений и повторить «Поиск решения» |
Минимизируется | И открытые, и закрытые |
| Не ограничено, связано с возможностями программы |
Стоимость всех перевозок | Изменяя ячейки | Сервис, Надстройки, Поиск решения |
Задачи оптимизации |
3.3. Конкурс «Промышленный шпионаж»
Программированный контроль с использованием
ПК состоит из 8 заданий и нескольких вариантов.
Максимальное количество баллов – 5. Примерное
содержание одного варианта:
1. Выражение 5(A2+C3)2:3(2B2–3D3) в MS Excel имеет вид:
1. 5(A2+C3)/3(2B2–3D3) ;
2. 5*(A2+C3)/3*(2*B2–3*D3);
3. 5*((A2+C3)^2)/(3*(2*B2–3*D3));
4. 5(A2+C3)/(3(2B2–3D3)).
2. Выберите верную запись формулы для
электронной таблицы:
1. C3+4*D4;
2. =C1+2*C2;
3. A5B5+23;
4. R3=A2*A3–A4
3. При перемещении или копировании в
электронной таблице относительные ссылки:
1. Не изменяются;
2. Преобразуются вне зависимости от нового
положения формулы;
3. Преобразуются в зависимости от нового
положения формулы;
4. Преобразуются в зависимости от длины формулы.
4. Диапазон – это:
1. Совокупность клеток, образующих в таблице
область прямоугольной формы;
2. Все ячейки одной строки;
3. Все ячейки одного столбца;
4. Множество допустимых значений.
5. Как активировать Поиск решения?
1. Поиск решения;
2. Сервис;
3. Сервис-Настройки-Поиск решения;
4. Сервис-Надстройки-Поиск решения.
6. Какая формула будет получена при копировании
в ячейку С3, формулы =$A$1*A1+B1 из ячейки С1:
1. =A1*A2+B2;
2. =$A$1*$A$2+$B$2;
3. =$A$1*A3+B3;
4. =$A$2*A3+B3;
5. =$B$2*A3+B4?
7. Чему будет равно значение ячейки С1, если в нее
ввести формулу =А1+B1, если А1 = 24; В1 = 26:
1. 20;
2.15;
3.10;
4.50?
8. Чему будет равно значение ячейки С1, если в нее
ввести формулу =СУММ(A1:В1)*2, если А1 = 14; В1 =16:
1. 280;
2.60;
3.40;
4.35?
IV. Изучениевводногоматериала
Объяснение студентам приемов выполнения
работы; работа с материалом презентации,
разработанной преподавателем «Общая постановка
транспортной задачи, методы решения,
экономико-математический анализ решения».
V.Формирование, закрепление первичных
умений и применение их в стандартных ситуациях
5.1. Решите закрытую транспортную
задачу, проверьте полученный результат. Команда
может заработать до 12 баллов.
Задача 1. С двух полей хозяйства
нужно перевести картофель в три хранилища. На
первом поле собрано 1800 т картофеля, на втором –
2600 т. Вместимости хранилищ, т: первого 1000, второго
–1200, третьего – 2200. Средние расстояния по
существующим дорогам от каждого поля до
хранилища указаны в таблице:
| Расстояние до хранилища, км | |||
| первого | второго | третьего | |
| 1 2 |
20 30 |
20 40 |
30 20 |
Требуется составить такой план перевозок, при
котором весь картофель будет доставлен в
указанных количествах в каждое хранилище с
минимальным общим пробегом транспорта,
исчисляемым в тонно-километрах.
Решение: Составим математическую
модель задачи.
1) Обозначим через хij количество груза, которое
нужно перевезти с i-го поля в j-е хранилище (i = 1,2; j =
1,2,3). Тогда критерий оптимальности плана
перевозок (целевая функция) примет вид:
F = 20х11 + 20х12 + 30х13 +30 х21
+ 40х22 + 20х23 ––>
min.
(1)
2)Предложение (1800+2600=4400 тонн продукции) равно
спросу (вместимость хранилищ: 1000+1200+2200=4400). Имеем
закрытую транспортную задачу.
Система уравнений баланса перевозок картофеля
примет вид:
| х11 + х12 + х13 = 1800; х21 + х22 + х23 = 2600; х11 + х21 = 1000; х12 + х22 = 1200; х13 + х23 = 2200. |
(2) |
3)Добавим ограничения на исключение обратных
перевозок:
хij> 0; i = 1,2; j = 1,2,3.
(3)
Итак, полученные выражения (1) – (3) есть
математическая модель искомого плана перевозок.
Решим задачу с использованием процессора MS Excel.
1) Войдем в MS Excel.
2) Переведем исходные данные в электронную
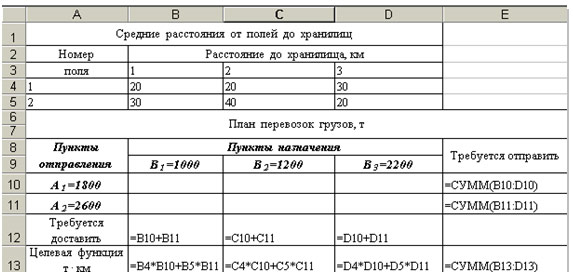
таблицу:
- средние расстояния от полей до хранилищ запишем
в ячейки B4:D5 (табл. 1). Отведем диапазон ячеек B10:D11 (6
ячеек) под искомые объемы перевозок х11, х12,
… , х23;
Таблица 1
-
в ячейки В12:D12 и Е10:Е11 запишем левые
части уравнений-ограничений: в ячейку В12 вводим
=В10+В11 и заполняем этой формулой С12 и D12, в
ячейку Е10 вводим =СУММ(В10:D10) и далее
заполняем ячейку Е11. -
в ячейку В13 введем для вычисления
целевой функции выражение =В4*В10+В5*В11 и
заполним им С13 и D13, -
а в ячейку Е13 — их сумму =СУММ(В13:D13).
3) Приступим к решению задачи.
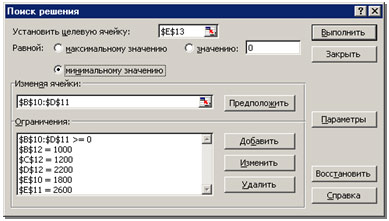
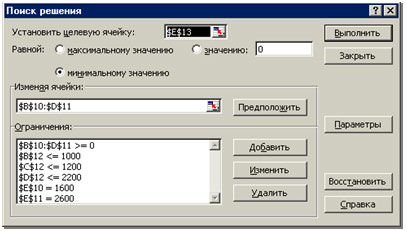
- Открываем окно Поиск решения:
[Сервис–Поиск решения].
Таблица 2
- Зададим необходимые параметры.
В поле Установить целевую функцию указать
ячейку $Е$13
и выбрать кнопку Минимальное значение.
-
В поле Изменяя ячейки отметить
диапазон ячеек B10:D11, отведенные под искомые
корни: х11, х12, …, х23. -
В поле Ограничения (таблица 2)
указать:
ячейку В12, выбрать тип ограничения = и ввести
число 1000;
затем — ячейку С12, выбрать тип ограничения = и
ввести 1200;
затем — ячейку D12, выбрать тип ограничения = и
ввести 2200;
затем — ячейку Е10, выбрать тип ограничения = и
ввести 1800;
затем — ячейку Е11, выбрать тип ограничения = и
ввести 2600;
ввести условие не отрицательности переменных:
В10:D11> 0.
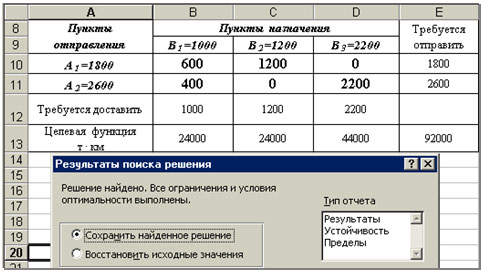
4) И, наконец, для получения результата нужно
щелкнуть на кнопке Выполнить и получить
оптимальный план перевозок (ячейки B10:D11) —
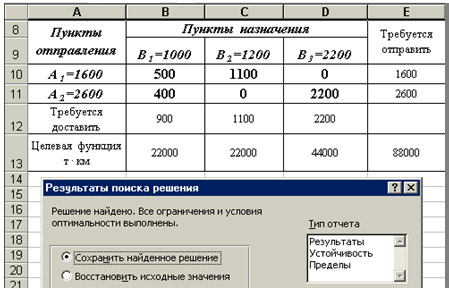
таблица 3.
Таблица 3
5) Проверяем выполнение ограничений – системы
(2) и (3): все найденные переменные положительны и
удовлетворяют ограничениям-равенствам: Е10=1800 –
1-е уравнение; Е11=2600 – 2-е уравнение; В12 = 1000 – 3-е
уравнение; В13=1200 и В14=2200, т.е. все ограничения
выполнены.
Ответ: Минимальный объем
перевозок составит 92 000 т • км.
Оптимальный план перевозок: х11 = 600 т; х12
= 1200 т; х13 = 0 т; х21 = 400 т; х22
= 0 т; х23 = 2200 т; т.е. перевозки с 1-го поля
в 3-е хранилище и со 2-го поля во 2-е хранилище не
нужно производить.
Пауза психологической разгрузки
5.2. Закрепите навыки решения закрытой
транспортной задачи профессиональной
направленности, дайте экономико-математический
анализ решения.
Команда может заработать до 18 баллов.
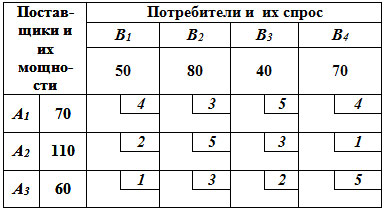
Задача 2. В задачах, оформленных в
виде таблиц, приведены данные о мощностях
поставщиков и ёмкостях потребителей. Мощности и
ёмкости заданы в тысячах кубометров, показатели
критерия оптимальности в рублях. Найти
оптимальный план перевозок и вычислить значение
целевой функции. Дать экономико-математический
анализ.
Примерное содержание одного варианта.
Вариант I.
Вариант II.
VI. Творческое применение знаний и умений в
нестандартных условиях – решение открытой
транспортной задачи
6.1.Решите открытую ТЗ, объясните ответ
Команда может заработать до 24 баллов.
Задача 3. В условиях задачи
1 найти оптимальную схему перевозок с
учётом, что на первом поле хозяйства собрано 1600 т
картофеля. Остальные условия задачи 1
оставим без изменения.
Решение: Таким образом, предложение
(1600+2600=4200 тонн продукции) меньше спроса
(вместимость хранилищ: 1000+1200+2200=4400). Имеем
открытую транспортную задачу с дефицитом
предложения.
Для таких задач ограничения для пунктов
отправления (полей) записываются в виде равенств,
а ограничения для пунктов назначения (хранилищ)
– в виде неравенств. Изменится лишь система
уравнений баланса перевозок картофеля:
| х11 + х12 + х13 = 1600; х21 + х22 + х23 = 2600; х11 + х21 < 1000; х12 + х22 < 1200; х13 + х23 < 2200. |
(2) |
Дальше решаем, как и задачу 1, изменения
коснутся лишь на третьем шаге – в окне Поиск
решения (табл. 4):
Таблица 4
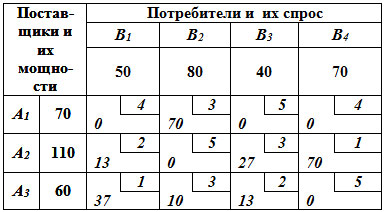
Для получения результата нужно щелкнуть на
кнопке Выполнить и получить оптимальный план
перевозок (ячейки B10:D11) – таблица 5.
Полученное решение почти в точности повторяет
решение закрытой задачи за исключением того, что
теперь хранилища 1 и 2 недополучат по 100 т
продукции. Минимальный объем перевозок составит
88000 т•км (значение целевой функции в ячейке Е13).
Таблица 5
6.2. Просмотр мультимедийный
презентации «Учебно-исследовательская работа
студентов 2013 г.» на тему «Решение транспортных
задач и их практическое применение в современном
производственном процессе».
VII. Подведение итогов:
7.1. Подсчет баллов членами жюри и
сообщение результатов.
7.2. Выставление оценок и их
комментарий.
VIII. Сообщение и комментирование домашнего
задания.
1 уровень. Компания «Витамин» хранит
свою готовую продукцию на трёх складах (первом,
втором и третьем), расположенных в разных частях
города. На этих складах хранится продукция в
количествах 1000, 3000 и 2500 штук соответственно.
Продукцию необходимо доставить четырем оптовым
покупателям П1, П2, П3 и П4, заявки которых
составляют 1300, 800, 2700 и 1700 штук соответственно.
Склады оптовых покупателей также расположены в
разных частях города. Стоимости (в рублях)
доставки одной штуки продукции со складов
компании на склады покупателей показаны в
следующей таблице. Найти оптимальную схему
перевозок.
| Склады компании | Оптовые покупатели | |||
| П1 | П2 | П3 | П4 | |
| №1 | 50 | 150 | 60 | 75 |
| №2 | 100 | 30 | 100 | 40 |
| №3 | 70 | 180 | 210 | 120 |
2 уровень. В условиях предыдущей
задачи найти оптимальную схему перевозок с
учётом, что в связи с ремонтными дорогами в
городе перекрыт маршрут со склада №1 до склада
покупателя П3.
3 уровень. Составить самостоятельно
транспортную задачу профессиональной
направленности, дать экономический анализ
решения.
Исследуя результат данного занятия,
проведенного в нашем техникуме со студентами
второго курса специальности 100102 «Организация
обслуживания в сфере сервиса», можно сделать
вывод, что с заданием I-го уровня сложности
(задача 1) справились 100% студентов, II-го уровня
(задача 2) – 88 % и с заданием III-го уровня (задача 3)
– 56 % студентов; процент качества знаний составил
67 % – это почти вдвое больше обычного у данной
группы (38 %) показателя.
Таким образом, предмет «Математика» также
формирует профессиональные компетенции
специалиста СПО. Главное, чтобы студенты
постоянно ощущали, что, изучая математику, они
приближаются к более глубокому пониманию
предмета и к своей специальности. Явления и
процессы, называемые во время учебных занятий
новыми для студентов терминами, становятся
конкретными, когда находят применение на
практике.
Данная работа может быть продолжена в
следующих направлениях:
- сравнить эффективность формирования
профессиональных компетенций на уроках
математики у студентов разных профилей; - разработать приемы формирования
профессиональных компетенций на уроках
математики у слабоуспевающих студентов.
Литература:
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая
математика в упражнениях и задачах. Ч.1. – М.:
Высшая школа, 1986. – 304 стр.
2. Сергованцев В.Т., Воронин Е.А., Воловник Т.И.,
Катасонова Н.Л. Компьютеризация
сельскохозяйственного производства.– М.: Колос,
2001. – 272 стр.
Приложение 1
Приложение 2
Визуализация движения по маршруту
Предположим, что перед нами стоит классическая задача транспортной логистики: визуализировать движение некоего объекта по заданному маршруту из нескольких промежуточных точек. Для конкретики, давайте возьмем скорый фирменный поезд «Жигули», движущийся по маршруту Москва — Самара по следующему графику (взято из Яндекс.Расписаний):
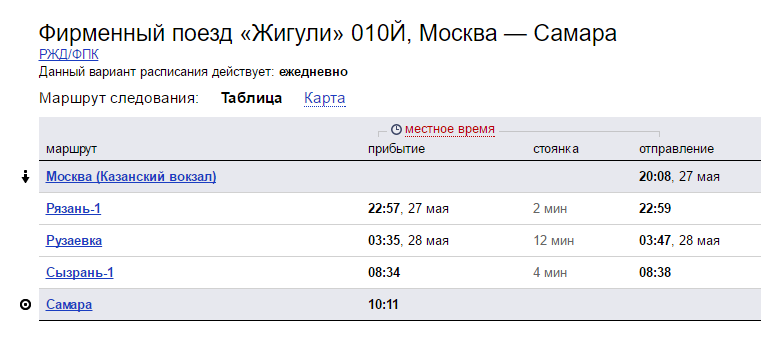
Для решения задачи нам потребуется Excel 2013-2016 с установленной надстройкой Power Map. В Excel 2016 она установлена по умолчанию, для Excel 2013 можно скачать ее бесплатную превью-версию.
Этап 1. Находим координаты
Для однозначной привязки к промежуточным пунктам маршрута лучше использовать не названия населенных пунктов (они могут повторяться либо отсутствовать в принципе в нужном месте), а нормальные географические координаты. Достаточно щелкнуть по нужному месту в Яндекс-картах или Google Maps и вы увидите широту и долготу этой точки:
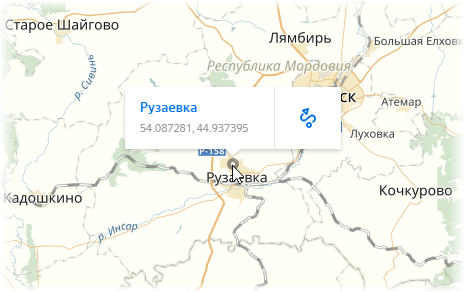
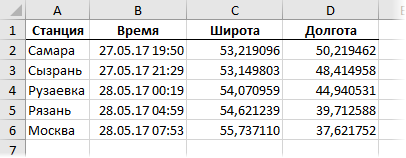
Добавим найденные координаты к нашей исходной таблице расписания движения поезда:
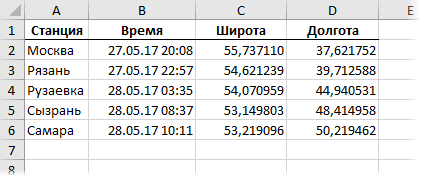
Этап 2. Дробим перегоны
Для плавного отображения движения поезда на карте нам необходимо разделить каждый перегон на несколько участков (чем их больше, тем плавнее будет анимация). Таким образом, перед нами встает задача получить примерные координаты и время для каждой промежуточной точки. Решить проблему можно формулой либо макросом.
Например, если хотим разбить каждый перегон на шесть интервалов (т.е. пять точек), то можно реализовать все одной формулой:
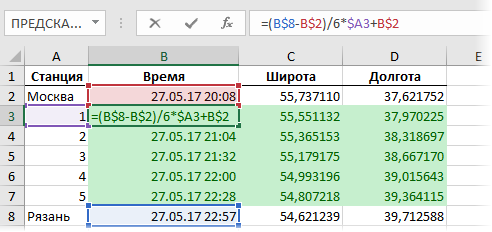
Но вставлять промежуточные строки, вводить и копировать формулу на все зеленые ячейки для каждого перегона придется вручную.
Другой вариант — макрос, что гораздо удобнее при большом количестве перегонов и промежуточных точек маршрута. Откройте редактор Visual Basic на вкладке Разработчик (Developer) или нажмите сочетание клавиш Alt+F11. Вставьте в вашу книгу новый пустой модуль через меню Insert — Module и скопируйте туда этот код:
Sub MakeRouteTable()
Dim DeltaT#, DeltaS#, DeltaD#, NumSteps%, FirstRow%, LastRow%
Const MINS_IN_ONE_STEP = 1
Application.ScreenUpdating = False
FirstRow = ActiveCell.CurrentRegion.Rows(3).Row
LastRow = ActiveCell.CurrentRegion.Rows.Count + FirstRow - 3
For i = 6 To 3 Step -1
'определяем число шагов на перегоне
NumSteps = Int((Cells(i, 2) - Cells(i - 1, 2)) * 24 * 60 / MINS_IN_ONE_STEP)
'вычисляем изменение координат и времени на каждом шаге
DeltaT = (Cells(i, 2) - Cells(i - 1, 2)) / (NumSteps + 1)
DeltaS = (Cells(i, 3) - Cells(i - 1, 3)) / (NumSteps + 1)
DeltaD = (Cells(i, 4) - Cells(i - 1, 4)) / (NumSteps + 1)
'заполняем строки интервалов по каждому перегону
For j = 1 To NumSteps
Rows(i).Insert
Cells(i, 2) = Cells(i + 1, 2) - DeltaT
Cells(i, 3) = Cells(i + 1, 3) - DeltaS
Cells(i, 4) = Cells(i + 1, 4) - DeltaD
Next j
Next i
Как легко сообразить, константа MINS_IN_ONE_STEP задает количество минут в каждом шаге — можете менять ее значение по своему усмотрению. Теперь если выделить таблицу с данными или установить в нее активную ячейку, а потом запустить наш макрос сочетанием клавиш Alt+F8 или кнопкой Макросы на вкладке Разработчик (Developer — Macros), то наша таблица будет преобразована в следующий вид:
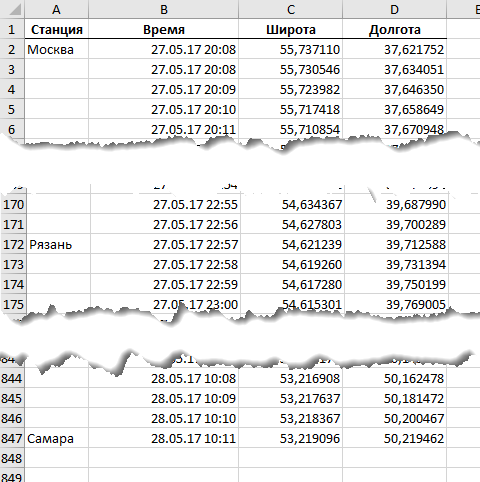
Как видите, каждый перегон теперь делится на несколько интервалов — по 1 минуте каждый.
Этап 3. Переходим к карте
Осталось совсем чуть-чуть. Выделите полученную таблицу и на вкладке Вставка нажмите кнопку 3D-карта (Insert — 3D-map):
Не перепутайте ее с кнопкой Карты (которая с глобусом) или Карты Bing (желтого цвета). После нажатия должно открыться окно надстройки Power Map.
В правой части окна на панели добавьте в группе Расположение (Location) поля широты и долготы и выберите напротив каждого название соответствующего столбца из нашей таблицы. Если все сделаете правильно, то на карте тут же должен отобразиться наш маршрут:
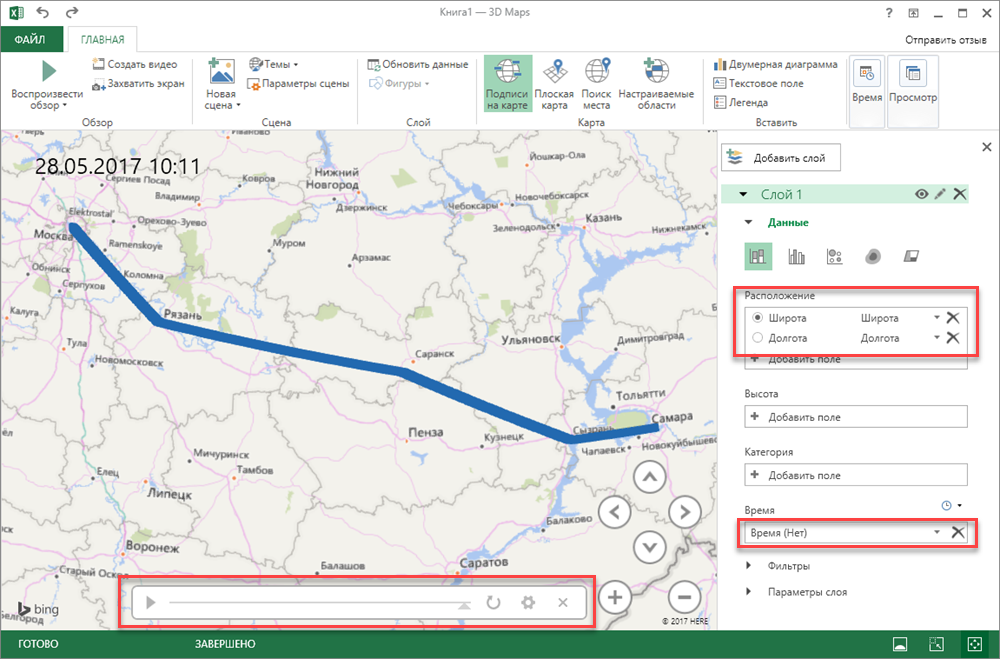
Теперь осталось выбрать в выпадающем списке Время (Time) столбец со значениями даты-времени из нашей таблицы и можно запускать анимацию с помощью кнопки воспроизведения в нижней части окна:

Дополнительно можно поиграться настройками слоя — кнопка Параметры слоя (Layer Options) в правом нижнем углу — и установить цвет, размер, прозрачность и т.д. отображаемых точек.
Если нажать на неприметную иконку с часами рядом с выпадающим списком Время, то можно поменять режим отображения и рисовать не маршрут, а сам поезд.
При щелчке левой кнопкой мыши по любой интересующей точке маршрута мы увидим ее подробные данные — координаты и время прохождения:
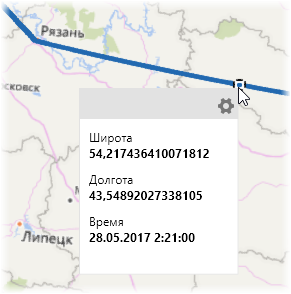
Этап 4. Несколько поездов сразу
Не секрет, что на самом деле по маршруту Москва-Самара курсируют два состава — в противофазе: когда один стартует из Москвы, другой примерно в то же время начинает движение ему навстречу из Самары. Утром один из них приходит в Самару, а другой, соответственно, в Москву и вечером процесс запускается заново. Расписание второго примерно отзеркаливает первый:
Что сделать, чтобы отобразить их на карте оба сразу?
Если по маршруту одновременно движется больше одного объекта, то данные по ним можно обработать аналогичным образом (Этапы 1 и 2) и просто добавить в продолжение нашей маршутной таблицы. А чтобы отличать поезда друг от друга, добавить еще один столбец с названием объекта:
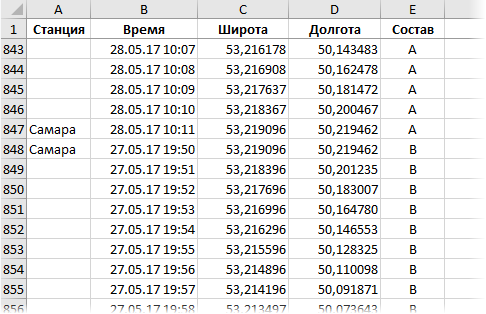
Теперь, если построить по такой таблице еще одну визуализацию, мы будем видеть движение двух составов одновременно:
Красота 
Ссылки по теме
- Все способы визуализация геоданных на картах в Excel
- Анимированная пузырьковая диаграмма
Тема: Решение задач по теме «Механическое движение» графическим методом с использованием построения графиков (диаграмм) в MS Excel.
Цели:
-
закрепить ранее изученный материал
-
научить применять знания и умения, полученные на уроках информатики к решению физических задач, а именно задач по механике
-
продолжить работу по формированию навыков учащихся анализировать уравнение движения тела, описывать движение;
-
повторить этапы построения графиков (диаграмм) в MS Excel;
-
показать практическое применение знаний полученных на уроках информатики и ИКТ к решению физических задач
-
показать связь между предметами
План урока.
-
Орг. момент 1 мин
-
Опрос д/з. (проверка знаний и умений)
-
Решение задач
-
Закрепление материала (с/р)
-
Д/з.
|
УФ: |
Сегодня мы проводим интегрированный урок физики и информатики, для того, что бы вы убедились во взаимосвязи этих предметов и научились применять знания и умения, полученные на уроках информатики к решению физических задач, а именно задач по механике Вспомним для начала основные моменты, изучаемые в теме «Механическое движение»:
Таким образом, исходя из целей нашего урока, (А какова цель?/решение физических задач, применяя знания по ИВТ/) Какова будет тема нашего урока?/ Решение задач по теме «Механическое движение» В тетради записываем тему урока: «Решение задач по теме «Механическое движение»» Осуществлять нашу цель мы будем решая следующую задачу. (записана на доске). Задача: движение двух автомобилей по шоссе заданы уравнениями: x1=2t+0.2t2 x2=80-4t
Записываем условие в тетрадь и описываем картину движения. (вид движения, x0, V0, ax
|
||||||||||||||||
|
УИ |
Так как находить место и время встречи мы будем графическим методом, то наша задача построить график и его проанализировать.
Итак наша задача:
Мы имеем два уравнения x1=2t+0.2t2 и x2=80-4t
|
||||||||||||||||
|
УФ |
То есть, с точки зрения физики, тела движутся в разные стороны и в этом случае достаточно выбрать диапазон значений по оси t от 0с – момента начала движения тел и до того момента, когда координата второго тела будет равна нулю. Давайте определим этот момент времени (устно): 0=80-4t => t=20c. |
||||||||||||||||
|
УИ |
Проходим к компьютерам вместе с тетрадями. Открываем программу. Строим таблицу значений для обоих уравнений движения, диапазон значений по оси времени выбираем [0;20] Строим диаграмму (график по точкам), переносим ось координат, строим точки пересечения, отмечаем их значения. /Ученики строят графики движения, выделяют необходимые точки под руководством учителя информатики./ |
||||||||||||||||
|
УФ |
Определим:
Таким образом, имея графики движения тел, мы можем извлечь из них любую интересующую нас информацию.
Далее продолжим решать самостоятельно в тетради и строя графики на компьютере. |
||||||||||||||||
|
При решении и построении графиков в самостоятельной работе измените цвет линий следующим образом:
|
|||||||||||||||||
|
ИТОГ УРОКА |
Судя по цвету ваших графиков, у некоторых возникли затруднения при применении нового метода. Давайте их обсудим.
Вывод делают ученики оценивая эффективность применения информационных технологий при решении задач по механике. |
||||||||||||||||
|
ДОМАШНЕЕ ЗАДАНИЕ |
|
.
|
|
|
|
.
|
Вариант 1 При решении и построении графиков в самостоятельной работе измените цвет линий следующим образом:
Движение материальных точек заданы уравнениями x1=10t+0,4t2 ; x2=300-10,2t. Описать движение каждой точки, найти время и место встречи графическим и математическим методами |
|
Вариант 4 При решении и построении графиков в самостоятельной работе измените цвет линий следующим образом:
Движение материальных точек заданы уравнениями x1=1050-t-6t2 ; x2=-150+10t. Описать движение каждой точки, найти время и место встречи графическим и математическим методами. |
|
Вариант 3 При решении и построении графиков в самостоятельной работе измените цвет линий следующим образом:
Движение материальных точек заданы уравнениями x1=-136-4t+2t2 ; x2=480-20t. Описать движение каждой точки, найти время и место встречи графическим и математическим методами |
|
Вариант 2 При решении и построении графиков в самостоятельной работе измените цвет линий следующим образом:
Движение материальных точек заданы уравнениями x1=2t-t2 ; x2=-198+15t. Описать движение каждой точки, найти время и место встречи графическим и математическим методами Решение задач по теме «Механическое движение» графическим методом с использованием построения графиков (диаграмм) в MS Excel |