Мощным средством
анализа данных MS
Excel
является надстройка «Поиск
решения».
С ее помощью можно определить, при каких
значениях указанных влияющих ячеек
формула в целевой ячейке принимает
нужное значение (минимальное, максимальное
или равное какой-либо величине). Для
процедуры поиска решения можно задать
ограничения, причем не обязательно,
чтобы при этом использовались те же
влияющие ячейки, данные которых,
определяют значение целевой ячейки.
Для расчета заданного значения применяются
различные математические методы поиска.
Вы можете установить режим, в котором
полученные значения переменных
автоматически заносятся в таблицу.
Кроме того, результаты работы программы
могут быть оформлены в виде отчета.
Программа Поиск
решений – дополнительная надстройка
табличного процессора MS Excel, которая
предназначена для решения определенных
систем уравнений, линейных и нелинейных
задач оптимизации, используется с 1991
года.
Размер задачи,
которую можно решить с помощью базовой
версии этой программы, ограничивается
такими предельными показателями:
количество неизвестных (decision variable) –
200; количество формульных ограничений
(explicit constraint) на неизвестные – 100; количество
предельных условий (simple constraint) на
неизвестные – 400.
Постановка задачи
коммивояжера, которую необходимо решить
посредством надстройки «Поиск решения»
методом полного перебора следующая:
«Сотруднику
компании ООО «Новые технологии» Петрову
Н.И. необходимо обновить программный
продукт автоматизированного учета в
пяти организациях: А, Б, В, Г и Д. Он решил
начать свой обход с организации «А»,
так как она находится на первом этаже
дома, в котором проживает Петров.
Сотруднику необходимо, спланировать
свой маршрут таким образом, чтобы к
концу рабочего дня обойти все организации
в определенном порядке и выполнив свою
работу, вернутся домой (в пункт «А»). В
каком порядке Петрову следует обходить
организации, чтобы его замкнутый тур
был кратчайшим? Если расстояния между
каждой парой организаций заданы следующей
квадратной матрицей (5×5):
Решение: Разместим
исходные данные на рабочем листе (рис
2.1). Заменим знак
числом 10000 (на результат решения
исключение пути не оказывает влияния).
Рисунок 2.1 Исходные
данные задачи
Вводим формулы:
Таблица 1
|
Ячейка |
Формула |
Примечание |
|
B9 |
= |
Распространяем |
|
G4 |
= |
Распространяем |
|
C19 |
=СУММПРОИЗВ(B4:F8;B13:F17) |
Целевая функция |
|
E19 |
=B4+C5+D6+E7+F8 |
Исключение пути |
|
B23 |
=$C$10-C10+4*C5 |
Распространяем |
|
B24 |
=$D$10-C10+4*C6 |
Распространяем |
|
B25 |
=$E$10-C10+4*C7 |
Распространяем |
|
B26 |
=$F$10-C10+4*C8 |
Распространяем |
Сценарий решения.
1. Запускаем
надстройку MS
Excel
«Поиск решения» командой Сервис/ Поиск
решения. И заполняем (рис. 2.2).
2. Для того чтобы
выполнялись условия однократного
посещения сотрудником организаций и в
то же время запланированный Петровым
маршрут был пройден полностью, введем
ограничения: в строки B9,
G4
заводим формулы из таблицы 1 и распространяем
их на соответствующие диапазоны B9:F9
и G4:G8.
Задаем следующие данные $B$9:$F$9=1
и $G$4:$G$8=1
в Ограничения окна «Поиск решения».
Таким образом, мы можем отследить порядок
обхода организаций сотрудником, оценить
правильность выбора и оптимальность
его маршрута.
3. Выбираем ячейку
B19
и устанавливаем ее адрес в Целевую
ячейку окна «Поиск решения», чтобы
определить длину наикратчайшего
маршрута. Для этого в ячейку B19
предварительно заносим соответствующую
формулу из таблицы 1. Когда программа
«Поиск решения» вычислит оптимальный
маршрут Петрова и станет известен
порядок обхода организаций (из Матрицы
переменных) будут известны и расстояния
между конкретными парами организаций.
Затем при помощи простых математических
подсчетов программа рассчитает
протяженность оптимального маршрута.
4. Устанавливаем
еще одно ограничение в окно «Поиск
решения»: $E$19=0.
В указанную ячейку вводим формулу из
таблицы 1 и исключаем таким образом,
заведомо ложный порядок движения Петрова
в порядке обхода организаций.
5.
В связи с тем, что ячейки диапазона
B4:F8
– изменяемые, в Ограничение окна «Поиск
решения» необходимо добавить строку
B$4$:F$8$=двоичное.
6. Заводим в ячейки
B23;
B24;
B25;
B26
соответствующие формулы из таблицы 1 и
распространяем их на следующие диапазоны:
B23:E23
B24:E24;
B25:E25;
B26:E26
для учета всех возможных вариантов
обхода организаций сотрудником и выбора
из них оптимального. Формулы задаем
таким образом, чтобы обеспечить исключение
ложного пути, соблюдая условие задачи
об обходе всех организаций по одному
разу.
7. Добавляем в
Ограничения окна «Поиск решения»
$B$23:$E$26
≤ 3.
Рисунок 2.2 Окно
«Поиск решения»
Так как это линейная
модель, то необходимо фиксировать в
окне Параметры поиска решений на позицию
Линейная модель и Неотрицательные
значения (рис. 2.3). После того, как все
поля и ячейки заполнены нажимаем кнопку
«Выполнить» и появляется окно диалога
с описанием результатов процесса
оптимизации. Чтобы отобразить найденное
решение в ячейках листа, устанавливаем
переключатель «Сохранить найденное
решение» и нажимаем кнопку ОК. Найденная
минимальная величина помещается в
целевую ячейку, а переменные ячейки
заполняются оптимальными значениями
переменных, которые удовлетворяют
установленным ограничениям.
Рисунок 2.3 Окно
«Параметры поиска решения»
Таким
образом, получаем следующий результат.
Если Петров переходит из организации
в организацию, то на рис. 2.4 в диапазоне
B4:F8
мы будем наблюдать порядок его перемещений.
Если видим, что в ячейке, которая отнесена
к организации «В» стоит единица, значит
сотрудник посетил эту организацию
следующей за пунктом «А». Если в ячейке
ноль – сотрудник организацию не посещал.
Рисунок 2.4 Результаты
решения задачи коммивояжера
Вывод
к главе 2:
В ходе анализа
полученных результатов, приходим к
выводу: наиболее оптимальным маршрут
Петрова будет в том случае, если он начал
свой путь с организации «А», посетит
другие организации в следующем порядке
«В», затем «Г», далее «Б» и «Д», из которой
вернется к началу своего пути (в
организацию «А»). представим путь
схематически:
АВГБДА
Если оставишь
этот, то сотри желтое выделение!!!
В ходе анализа
полученных результатов, приходим к
выводу: наиболее оптимальным маршрут
Петрова будет в том случае, если он начал
свой путь с организации «А», посетит
другие организации в следующем порядке
«В», затем «Д», далее «Б» и «Г», из которой
вернется к началу своего пути (в
организацию «А»). представим путь
схематически:
АВДБГА
Длина кратчайшего
маршрута (значение целевой ячейки) в
результате составит – 21.
Задача решена.
Кратчайший маршрут Петрова найден.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Skip to content
Постановка задачи коммивояжера
Целевая функция:
Ограничения на посещение только одного города:
Решим данную задачу коммивояжера в Excel
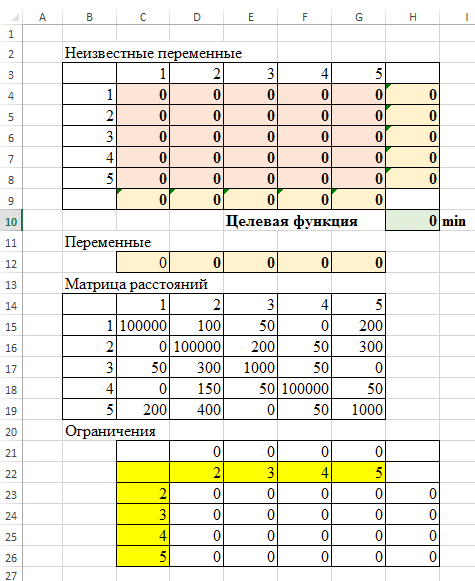
Для начала запишем условие задачи в виде таблицы неизвестных переменных, матрицы расстояний, целевой функции и ограничений
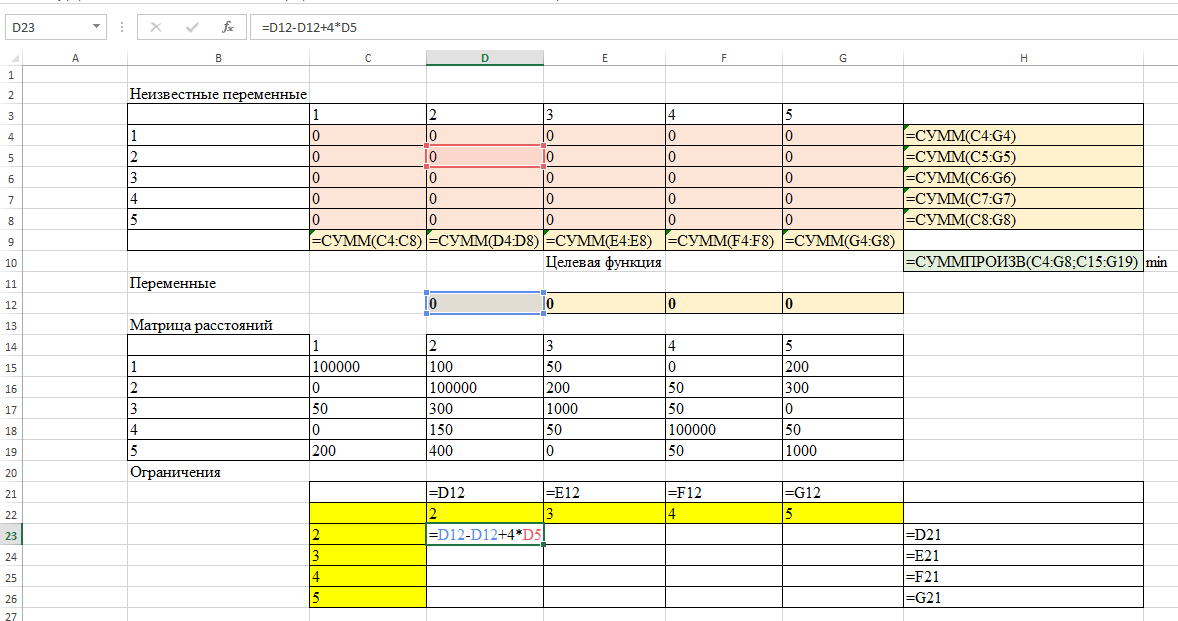
Формулы приведены ниже
Формула целевой функции
=СУММПРОИЗВ(C4:G8;C15:G19)
Затем переходим на вкладку Данные -> Поиск решения, вводим целевую функцию, вводим диапазон изменяемых ячеек переменных, ограничения, ставим галочку сделать переменные без ограничений неотрицательными, метод решения — поиск решения линейной задачи симплекс-методом и жмём Найти решение
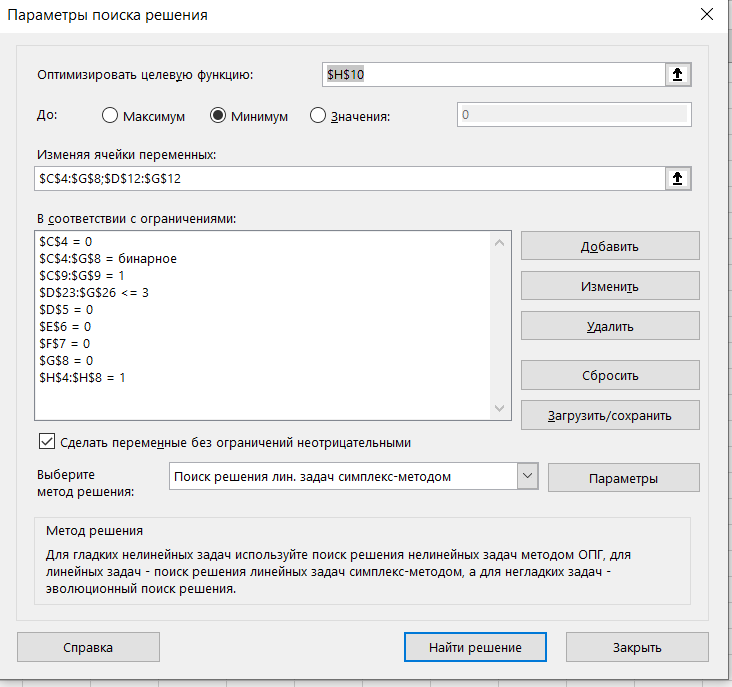
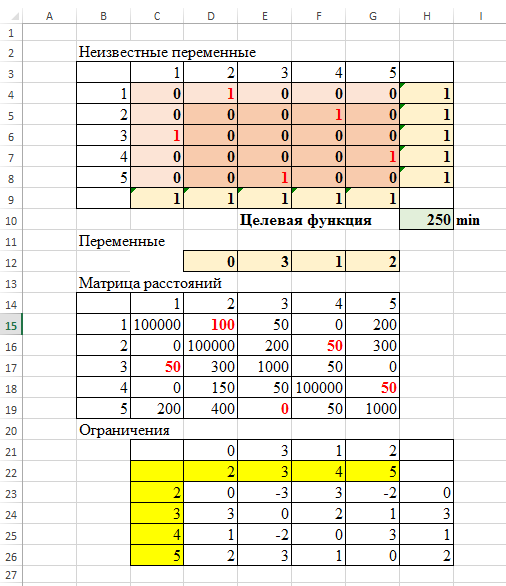
В результате получаем решение, то есть целевая функция равна 250
3318
Решим один из вариантов задачи коммивояжера для небольшого количества городов (5-10) с помощью надстройки Поиск решения. Построим нелинейную модель.
Рассмотрим задачу коммивояжера (англ. Travelling Salesman Problem, TSP) заключающуюся в отыскании самого короткого маршрута, проходящего через заданные города по одному разу с последующим возвратом в исходный город (также рассмотрим вариант без возврата).
Задача
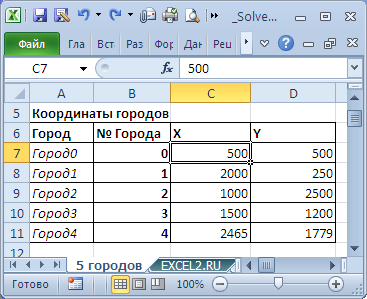
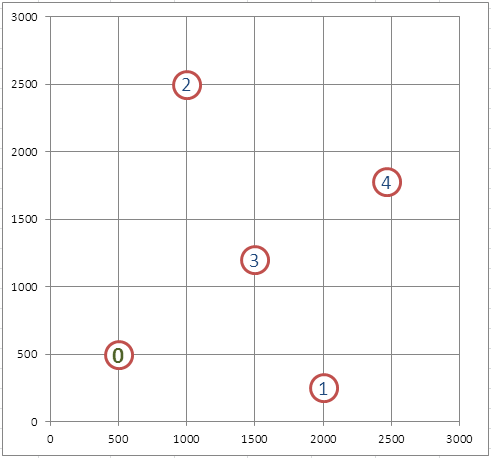
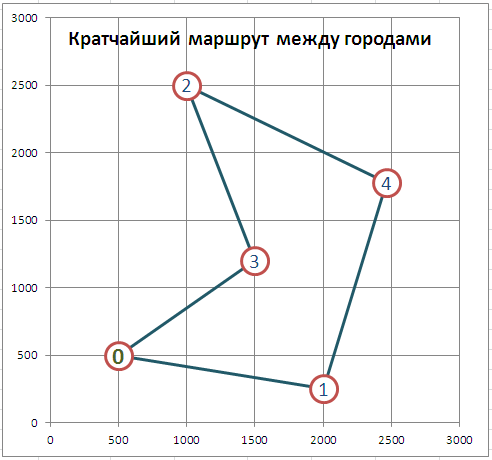
Найдем кратчайший путь между 5 городами, координаты которых известны. Рассмотрим замкнутый вариант задачи: коммивояжёру требуется посетить все города, после чего вернуться в исходный город.
Решение
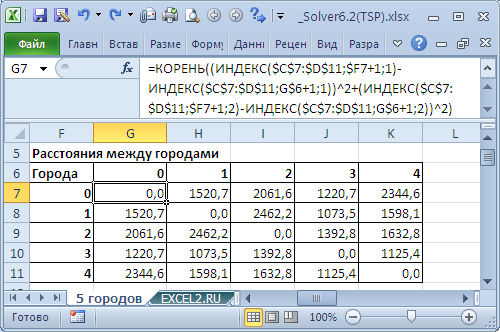
Так как даны координаты городов, то сначала найдем расстояния между ними (см.
файл примера, лист
5 городов
).
Расстояния рассчитаем с помощью формулы: =
КОРЕНЬ((ИНДЕКС($C$7:$D$11;$F7+1;1)-ИНДЕКС($C$7:$D$11;G$6+1;1))^2 +(ИНДЕКС($C$7:$D$11;$F7+1;2)-ИНДЕКС($C$7:$D$11;G$6+1;2))^2)
Теперь создадим модель для
Поиска решения
.
Совет
: Вводная статья про
Поиск решения
в MS EXCEL 2010
находится здесь
.
Переменные (выделено зеленым)
. В качестве переменных модели следует взять номера городов. Так как начальная и конечная точка известны (Город0), то переменных будет 4.
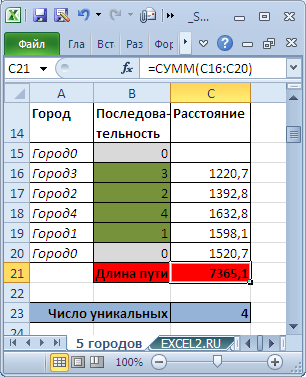
Ограничения (выделено синим)
. Необходимо, чтобы номера городов не повторялись. Это означает, что количество уникальных (неповторяющихся) номеров городов должно быть равно 4. Для этого используется формула для
подсчета уникальных значений
: =
СУММПРОИЗВ(1/СЧЁТЕСЛИ(B16:B19;B16:B19))
Целевая функция (выделено красным)
.
Длина маршрута должна быть минимальной.
Примечание
: для удобства настройки
Поиска решения
используются
именованные диапазоны
.
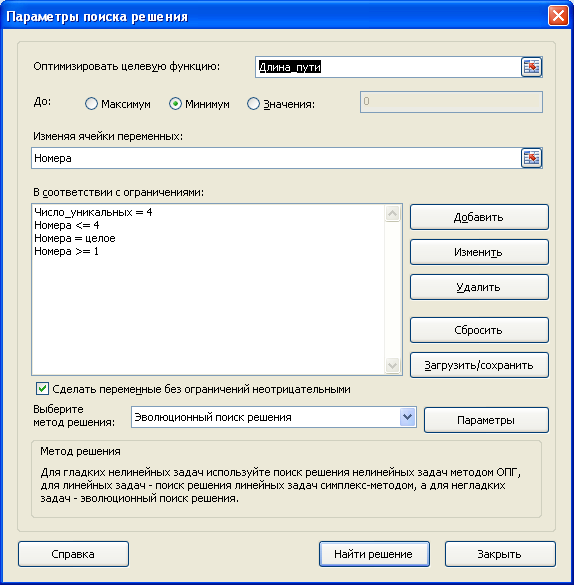
Выберите Эволюционный метод поиска решения, т.к. созданная модель не является линейной из-за наложенного на переменные ограничения.
Найденное
Решение
Поиск решения
найдет (должен найти) самый короткий маршрут, т.е. последовательность 0-1-4-2-3-0 (или обратную).
В этой простейшей задаче можно проверить, действительно ли этот маршрут имеет минимальную длину, путем перебора всех вариантов маршрутов. Это реализовано в
файле примера
.
Совет
. Таблицы перебора перестановок от 1 до 5, от 1 до 6, … от 1 до 9 можно найти в этой статье
Перебор всех возможных Перестановок в MS EXCEL
.
Результаты Эволюционного метода сильно зависят от начальных условий и параметров его настройки (скорость изменения, размер совокупности). Повторный поиск, с теми же начальными условиями и параметрами, может привести к различным результатам. Убедиться в этом можно с помощью модели, созданной в
файле примера
на листе
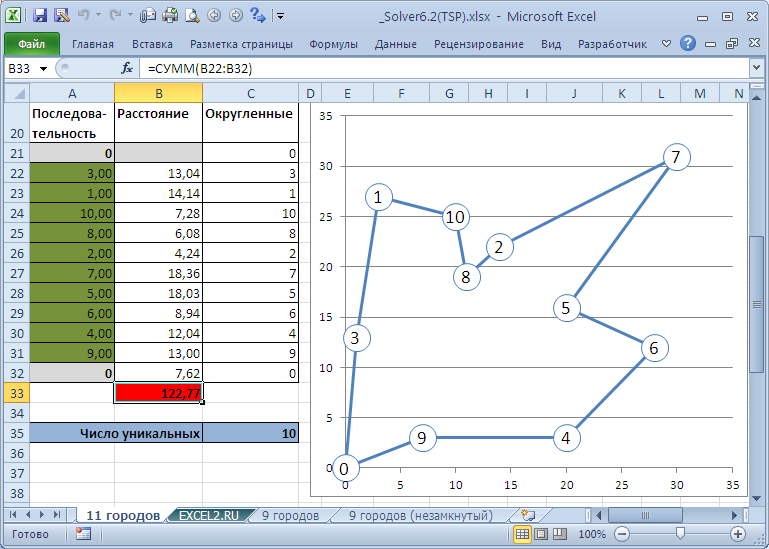
11 городов.
Обнулите значения переменных модели на Листе
11 городов,
запустите
Поиск решения.
После окончания поиска (может занять несколько минут) опять обнулите значения переменных и перезапустите
Поиск решения:
найденные решения могут серьезно отличаться.
Совет
. Иногда, для того чтобы улучшить найденное решение, помогает следующий прием: запустите
Поиск решения
, сохраните найденное решение, измените параметры поиска (например, размер совокупности), повторно запустите
Поиск решения.
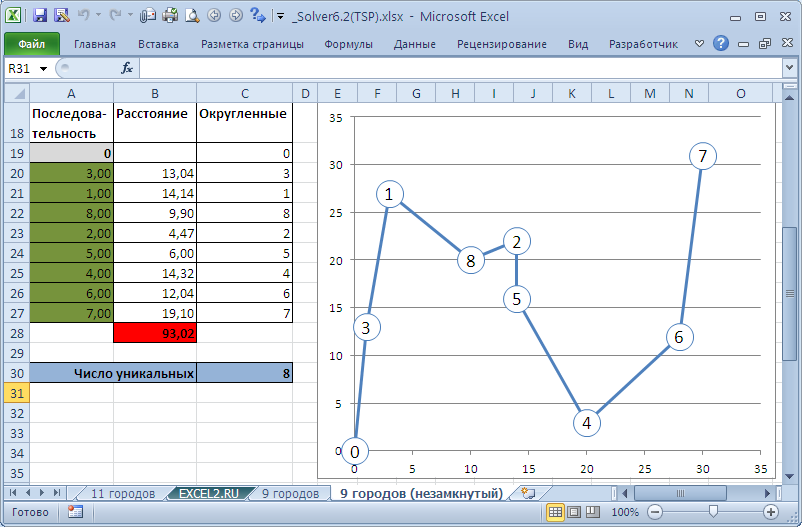
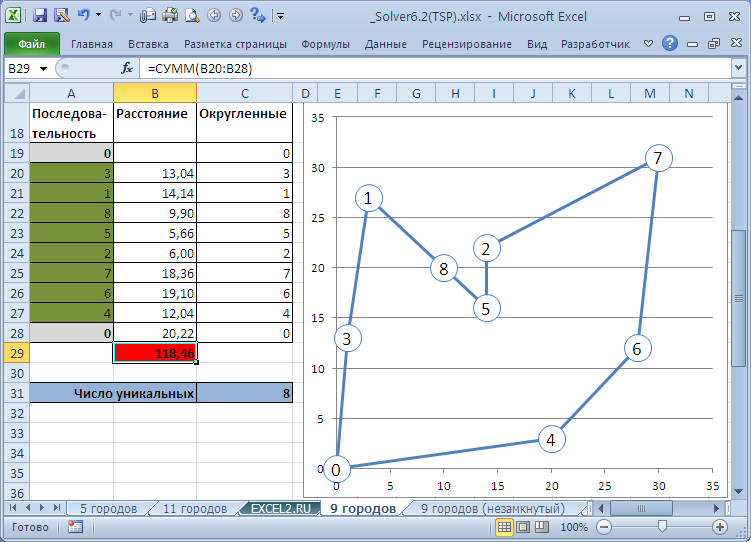
В
файле примера
также приведено решение задачи для замкнутого и незамкнутого маршрута посещения 9 городов. Решения найдены с помощью Эволюционного метода со следующими параметрами: Целочисленная оптимальность 0%, Использовать автоматическое масштабирование, Скорость изменения варьировалась 0,25-0,5; Размер совокупности варьировался 10-50. Оба решения проверены с помощью таблиц перебора всех маршрутов (см.
таблицы перебора перестановок
). Если при первом прогоне
Поиска решения
не удавалось найти оптимальное решение, то он запускался повторно, при этом 1 или 2 параметра изменялись. После второго прогона оптимальное решение, как правило, было найдено.
Вывод
: задачу коммивояжера (граф полностью связный, гамильтоновый цикл) можно решить стандартным
Поиском решения
с помощью построения нелинейных моделей. При количестве вершин графа (городов) <10 найденное решение можно проверить с помощью таблиц перебора перестановок, т.к. Эволюционный метод не гарантирует, что найденный путь является кратчайшим. Поиск решения может продолжаться значительное время. Однако, более лучшей альтернативой решения этой задачи в MS EXCEL является построение линейной модели (см. статью
Поиск решения MS EXCEL (6.3). Задача коммивояжера (полный граф, линейная модель)
) или написание программы на VBA.
Совет
: Решение задачи о поиске кратчайшего пути между 2-мя заданными городами можно найти в статье
Поиск решения MS EXCEL (6.4). Кратчайший путь (неполный граф, линейная модель)
.
Решение задачи коммивояжера при помощи надстройки MS Excel «Поиск решения»
Метод полного перебора
Мощным средством анализа данных MS Excel является надстройка «Поиск решения». С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки, данные которых, определяют значение целевой ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.
Программа Поиск решений – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных и нелинейных задач оптимизации, используется с 1991 года.
Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями: количество неизвестных (decision variable) – 200; количество формульных ограничений (explicit constraint) на неизвестные – 100; количество предельных условий (simple constraint) на неизвестные – 400.
Постановка задачи коммивояжера, которую необходимо решить посредством надстройки «Поиск решения» методом полного перебора следующая:
«Сотруднику компании ООО «Новые технологии» Петрову Н.И. необходимо обновить программный продукт автоматизированного учета в пяти организациях: А, Б, В, Г и Д. Он решил начать свой обход с организации «А», так как она находится на первом этаже дома, в котором проживает Петров. Сотруднику необходимо, спланировать свой маршрут таким образом, чтобы к концу рабочего дня обойти все организации в определенном порядке и выполнив свою работу, вернутся домой (в пункт «А»). В каком порядке Петрову следует обходить организации, чтобы его замкнутый тур был кратчайшим? Если расстояния между каждой парой организаций заданы следующей квадратной матрицей (5×5):
Решение: Разместим исходные данные на рабочем листе (рис 2.1). Заменим знак 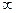
Рисунок 2.1 Исходные данные задачи
| Ячейка | Формула | Примечание |
| B9 | = СУММ(B4:B8) | Распространяем на диапазон B9:F9 |
| G4 | = СУММ(B4:F4) | Распространяем на диапазон G4:G8 |
| C19 | =СУММПРОИЗВ(B4:F8;B13:F17) | Целевая функция |
| E19 | =B4+C5+D6+E7+F8 | Исключение пути |
| B23 | =$C$10-C10+4*C5 | Распространяем на диапазон B23:E23 |
| B24 | =$D$10-C10+4*C6 | Распространяем на диапазон B24:E24 |
| B25 | =$E$10-C10+4*C7 | Распространяем на диапазон B25:E25 |
| B26 | =$F$10-C10+4*C8 | Распространяем на диапазон B26:E26 |
1. Запускаем надстройку MS Excel «Поиск решения» командой Сервис/ Поиск решения. И заполняем (рис. 2.2).
2. Для того чтобы выполнялись условия однократного посещения сотрудником организаций и в то же время запланированный Петровым маршрут был пройден полностью, введем ограничения: в строки B9, G4 заводим формулы из таблицы 1 и распространяем их на соответствующие диапазоны B9:F9 и G4:G8. Задаем следующие данные $B$9:$F$9=1 и $G$4:$G$8=1 в Ограничения окна «Поиск решения». Таким образом, мы можем отследить порядок обхода организаций сотрудником, оценить правильность выбора и оптимальность его маршрута.
3. Выбираем ячейку B19 и устанавливаем ее адрес в Целевую ячейку окна «Поиск решения», чтобы определить длину наикратчайшего маршрута. Для этого в ячейку B19 предварительно заносим соответствующую формулу из таблицы 1. Когда программа «Поиск решения» вычислит оптимальный маршрут Петрова и станет известен порядок обхода организаций (из Матрицы переменных) будут известны и расстояния между конкретными парами организаций. Затем при помощи простых математических подсчетов программа рассчитает протяженность оптимального маршрута.
4. Устанавливаем еще одно ограничение в окно «Поиск решения»: $E$19=0. В указанную ячейку вводим формулу из таблицы 1 и исключаем таким образом, заведомо ложный порядок движения Петрова в порядке обхода организаций.
5. В связи с тем, что ячейки диапазона B4:F8 – изменяемые, в Ограничение окна «Поиск решения» необходимо добавить строку B$4$:F$8$=двоичное.
6. Заводим в ячейки B23; B24; B25; B26 соответствующие формулы из таблицы 1 и распространяем их на следующие диапазоны: B23:E23 B24:E24; B25:E25; B26:E26 для учета всех возможных вариантов обхода организаций сотрудником и выбора из них оптимального. Формулы задаем таким образом, чтобы обеспечить исключение ложного пути, соблюдая условие задачи об обходе всех организаций по одному разу.
7. Добавляем в Ограничения окна «Поиск решения» $B$23:$E$26 ≤ 3.
Рисунок 2.2 Окно «Поиск решения»
Так как это линейная модель, то необходимо фиксировать в окне Параметры поиска решений на позицию Линейная модель и Неотрицательные значения (рис. 2.3). После того, как все поля и ячейки заполнены нажимаем кнопку «Выполнить» и появляется окно диалога с описанием результатов процесса оптимизации. Чтобы отобразить найденное решение в ячейках листа, устанавливаем переключатель «Сохранить найденное решение» и нажимаем кнопку ОК. Найденная минимальная величина помещается в целевую ячейку, а переменные ячейки заполняются оптимальными значениями переменных, которые удовлетворяют установленным ограничениям.
Рисунок 2.3 Окно «Параметры поиска решения»
Таким образом, получаем следующий результат. Если Петров переходит из организации в организацию, то на рис. 2.4 в диапазоне B4:F8 мы будем наблюдать порядок его перемещений. Если видим, что в ячейке, которая отнесена к организации «В» стоит единица, значит сотрудник посетил эту организацию следующей за пунктом «А». Если в ячейке ноль – сотрудник организацию не посещал.
Рисунок 2.4 Результаты решения задачи коммивояжера
В ходе анализа полученных результатов, приходим к выводу: наиболее оптимальным маршрут Петрова будет в том случае, если он начал свой путь с организации «А», посетит другие организации в следующем порядке «В», затем «Д», далее «Б» и «Г», из которой вернется к началу своего пути (в организацию «А»). представим путь схематически:
Длина кратчайшего маршрута (значение целевой ячейки) в результате составит – 21.
Задача решена. Кратчайший маршрут Петрова найден.
ЗАКЛЮЧЕНИЕ
Задача коммивояжера была поставлена в 1934 году. Ее сущность заключается в поиске оптимального маршрута движения при необходимости посетить все запланированные объекты с наименьшими финансовыми и временными издержками. Как правило, речь идет о простом перемещении по заданным точкам, либо с перевозкой груза небольшого формата на транспортном средстве.
Задача коммивояжера является одной из знаменитых задач теории комбинаторики и пользуется популярностью благодаря тому, что к ней сводится большое количество практических задач.
Среди современных практических приложений задачи можно выделить: доставку продуктов в магазин со склада, работу почтальона по разноске корреспонденции, мониторинг объектов (нефтяные вышки, базовые станции сотовых операторов), изготовление отверстий на специализированном станке.
Для решения задачи коммивояжера используют различные группы простейших методов: полный и случайный перебор, жадный и деревянный алгоритмы, метод имитации отжига. Широкое применение получили различные модификации более эффективных методов, таких как метод ветвей и границ, генетических алгоритмов, а также алгоритм муравьиных колоний.
В работе была поставлена задача, сводимая к задаче коммивояжера, и составлена схема оптимального маршрута, подробно рассмотрен порядок выбора кратчайшего пути при помощи использования надстройки MS Excel «Поиск решения» методом полного перебора. Результаты решения были выведены на отдельный рабочий лист Excel.
Изучение особенностей задачи коммивояжера позволило сделать следующий вывод: актуальным в настоящее время остается поиск точных и приближенных способов решения этой задачи как с теоретической, так и с практической точек зрения. Более того, темпы современной жизни меняют отношение человека ко времени, сегодня пользователь не любит ждать, изыскивает возможности сократить время ожидания, найти оптимальное решение в кратчайшие сроки. Все это свидетельствует о росте в будущем потребности в эффективном решении задач коммивояжера и иных родственных им оптимизационных задач, которые позволили бы существенно сэкономить ограниченные ресурсы организаций.
Министерство образования и науки РФ
ГБОУ СПО «Шадринский политехнический колледж»
Заведующая учебной частью
____________ Блинова Н.А.
Курсовая работа
по дисциплине «Математические методы»
на тему «Задача о коммивояжере. Метод полного перебора»
Урок по теме «Решение уравнений в среде MS Excel»
Одна из наиболее актуальных проблем компьютерного обучения – проблема отбора и использования педагогически целесообразных обучающих программ.
При изучении отдельных тем и решении некоторых задач на уроках математики в старших классах громоздкие вычисления как, например, при решении уравнений методом деления отрезка пополам или методом последовательных приближений, затмевают существо математической задачи, не дают увидеть красоту, рациональность применяемого метода решения.
В данной статье я представила те задачи, решение которых с помощью MS EXCEL позволяет получить наглядное, доступное для понимания учащимися решение, показать его логику, рациональность. Попутно учащиеся получают устойчивые навыки работы с программой.
Нахождение корней уравнения с помощью подбора параметра
Пример 1.
Пусть известно, что в штате больницы состоит 6 санитарок, 8 медсестер, 10 врачей, 3 заведующих отделениями, главный врач, заведующий аптекой, заведующая хозяйством и заведующий больницей. Общий месячный фонд зарплаты составляет 1000 000 условных единиц. Необходимо определить, какими должны быть оклады сотрудников больницы.
Решение такой задачи можно искать методом перебора. Однако в лучшем случае на это уходит много времени. Можно предложить другой способ решения. В EXCEL он реализован как поиск значения параметра формулы, удовлетворяющего ее конкретному значению.
Построим модель решения этой задачи. За основу возьмем оклад санитарки, а остальные оклады будем вычислять, исходя из него: во столько-то раз или на столько-то больше. Говоря математическим языком, каждый оклад является линейной функцией от оклада санитарки: Ai*С+Вi, где С – оклад санитарки; Аi и Вi – коэффициенты, которые для каждой должности определяют следующим образом:
- медсестра получает в 1,5 раза больше санитарки (А2=1,5; В2=0);
- врач – в 3 раза больше санитарки (А3=3; В3=0);
- заведующий отделением – на 30 y.e. больше, чем врач (А4=3; B4=30);
- заведующий аптекой – в 2 раза больше санитарки (А5=2; В5=0);
- заведующий хозяйством – на 40 y.e. больше медсестры (А6=1,5; В6=40);
- заведующий больницей – на 20 y.e. больше главного врача (А8=4; В8=20);
- главный врач – в 4 раза больше санитарки (А7=4; В7=0);
Зная количество человек на каждой должности, нашу модель можно записать как уравнение: N1*(A1*C+B1)+N2*(A2*C+B2)+. +N8*(A8*C+B8) = 1000000, где N1 – число санитарок, N2 – число медсестер и т.д.
В этом уравнении нам известны A1. A8, B1. B8 и N1. N8, а С неизвестно. Анализ уравнения показывает, что задача вычисления заработной платы свелась к решению линейного уравнения относительно С. Предположим, что зарплата у санитарки 150,00 y.e.
Введите исходные данные в рабочий лист электронной таблицы, как показано ниже.
A
B
C
D
E
F
Оклад мед. Работников
Общий фонд равен
В столбце D вычислите заработную плату для каждой должности. Например, для ячейки D4 формула расчета имеет вид =B4*$D$3+C4.
В столбце F вычислите заработную плату всех работников данной должности. Например, для ячейки F3 формула расчета имеет вид =D3*E3.
В ячейке F11вычислите суммарный фонд заработной платы больницы. Рабочий лист электронной таблицы будет выглядеть, как показано ниже.
A
B
C
D
E
F
Оклад мед. Работников
Общий фонд равен
Чтобы определите оклад санитарки так, чтобы расчетный фонд был равен заданному надо:
- Активизировать команду Подбор параметра во вкладке Данные / Работа с данными /Анализ «Что, если»;
- В поле «Установить в ячейке» появившегося окна ввести ссылку на ячейку F11, содержащую формулу;
- В поле «Значение» набрать искомый результат 1000000;
- В поле «Изменяя значение ячейки» ввести ссылку на изменяемую ячейку D3 и щелкните на кнопке ОК.
Анализ задачи показывает, что с помощью Excel можно решать линейные уравнения. Конечно, такое уравнение может решить любой школьник. Однако, благодаря этому простому примеру стало, очевидным, что поиск значения параметра формулы, удовлетворяющего ее конкретному значению, – это не что иное, как численное решение уравнений. Другими словами, используя Excel, можно решать любые уравнения с одной переменной.
Задание для учащихся:
Составить несколько вариантов штатного расписания с использованием функции Подбор параметра и оформить их в виде таблицы:
- Изменить количество сотрудников на различных должностях;
- Подобрать зарплату санитарки в новых условиях;
- Составить таблицу нескольких вариантов штатного расписания.
Рассмотрим еще один пример нахождения корней уравнения с помощью подбора параметра. При решении этого уравнения используется также метод последовательных приближений. Учащиеся в классах с углубленным изучением математики знакомы с этим методом. Поэтому, чтобы этот пример был доступен для других учащихся, предлагаю краткую теорию этого метода.
Пусть дано уравнение, записанное в виде x=F(x). Выбирают некоторое начальное приближение x1 и подставляют его вместо x в F(x). Полученное значение x2=F(x1) этой функции считают вторым приближением. Далее находят третье приближение по формуле x3=F(x2) и так далее. Таким образом, получаем последовательность x1, x2, x3,…, xn,… чисел, имеющая предел α. Тогда если функция F(x) непрерывна, из равенства xn+1=F(xn) получаем α=F(α). Это означает, что α является решением уравнения x=F(x).
Пример 2.
Пусть нам дан многочлен третьей степени:
x 3 -0,01x 2 -0,7044x+0,139104=0.
Так как мы ищем корни полинома третьей степени, то имеются не более трех вещественных корней. Для нахождения корней их первоначально надо локализовать, то есть найти интервалы, на которых они существуют. Такими интервалами локализации корней могут служить промежутки, на концах которых функция имеет противоположный знак. С целью нахождения интервалов, на концах которых функция изменяет знак, необходимо построить ее график или протабулировать ее. Составим таблицу значений функции на интервале [-1;1] с шагом 0,2. Для этого необходимо:
Решение уравнений в excel — примеры решений
Microsoft Office Excel может здорово помогать студентам и магистрантам в решении различных задач из высшей математики. Не многие пользователи знают, что базовые математические методы поиска неизвестных значений в системе уравнений реализованы в редакторе. Сегодня рассмотрим, как происходит решение уравнений в excel.
Первый метод
Суть этого способа заключается в использовании специального инструмента программы – подбор параметра. Найти его можно во вкладке Данные на Панели управления в выпадающем списке кнопки Анализ «что-если».
1. Зададимся простым квадратичным уравнением и найдем решение при х=0.
2. Переходите к инструменту и заполняете все необходимые поля
3. После проведения вычислений программа выдаст результат в ячейке с иксом.
4. Подставив полученное значение в исходное уравнение можно проверить правильность решения.
Второй метод
Используем графическое решение этого же уравнения. Суть заключается в том, что создается массив переменных и массив значений, полученных при решении выражения. Основываясь на этих данных, строится график. Место пересечения кривой с горизонтальной осью и будет неизвестной переменной.
1. Создаете два диапазона.
На заметку! Смена знака результата говорит о том, что решение находится в промежутке между этими двумя переменными.
2. Переходите во вкладку Вставка и выбираете обычный график.
3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.
Важно! В настройках оси поставьте положение по делениям.
4. Теперь на графике четко видно, что решение находится между семеркой и восьмеркой ближе к семи. Чтобы узнать более точное значение, необходимо изменять масштаб оси и уточнять цифры в исходных массивах.
Такая исследовательская методика в первом приближении является достаточно грубой, однако позволяет увидеть поведение кривой при изменении неизвестных.
Третий метод
Решение систем уравнений можно проводить матричным методом. Для этого в редакторе есть отдельная функция МОБР. Суть заключается в том, что создаются два диапазона: в один выписываются аргументы при неизвестных, а во второй – значения в правой стороне выражения. Массив аргументов трансформируется в обратную матрицу, которая потом умножается на цифры после знака равно. Рассмотрим подробнее.
1. Записываете произвольную систему уравнений.
2. Отдельно выписываете аргументы при неизвестных в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами после знака равно.
3. Выделяете в свободной зоне диапазон ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтобы функция сработала корректно нажимаете одновременно Ctrl+Shift+Enter.
4. Теперь находите решение при помощи функции МУМНОЖ. Также предварительно выделяете диапазон размером с матрицу результатов и нажимаете уже известное сочетание клавиш.
Четвертый метод
Методом Гаусса можно решить практически любую систему уравнений. Суть в том, чтобы пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это прямая последовательность. Для полного решения необходимо еще провести обратное вычисление до тех пор, пока диагональ матрицы не станет единичной, а остальные элементы – нулевыми. Полученные значения в последнем столбце и являются искомыми неизвестными. Рассмотрим на примере.
Важно! Если первый аргумент является нулевым, то необходимо поменять строки местами.
1. Зададимся произвольной системой уравнений и выпишем все коэффициенты в отдельный массив.
2. Копируете первую строку в другое место, а ниже записываете формулу следующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).
Поскольку работа идет с массивами, нажимайте Ctrl+Shift+Enter, вместо Enter.
3. Маркером автозаполнения копируете формулу в нижнюю строку.
4. Выделяете две первые строчки нового массива и копируете их в другое место, вставив только значения.
5. Повторяете операцию для третьей строки, используя формулу
=C73:F73-$C$72:$F$72*(D73/$D$72). На этом прямая последовательность решения закончена.
6. Теперь необходимо пройти систему в обратном порядке. Используйте формулу для третьей строчки следующего вида =(C78:F78)/E78
7. Для следующей строки используйте формулу =(C77:F77-C84:F84*E77)/D77
8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76
9. При получении матрицы с единичной диагональю, правая часть дает искомые неизвестные. После подстановки полученных цифр в любое из уравнений значения по обе стороны от знака равно являются идентичными, что говорит о правильном решении.
Метод Гаусса является одним из самых трудоемких среди прочих вариантов, однако позволяет пошагово просмотреть процесс поиска неизвестных.
Как видите, существует несколько методов решения уравнений в редакторе. Однако каждый из них требует определенных знаний в математике и четкого понимания последовательности действий. Однако для упрощения можно воспользоваться онлайн калькулятором, в который заложен определенный метод решения системы уравнений. Более продвинутые сайты предоставляют несколько способов поиска неизвестных.
Жми «Нравится» и получай только лучшие посты в Facebook ↓
источники:
http://urok.1sept.ru/articles/606276
http://mir-tehnologiy.ru/reshenie-uravnenij-v-excel-primery-reshenij/
|
Задача коммивояжера |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |






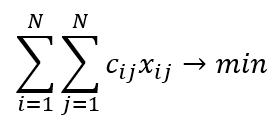
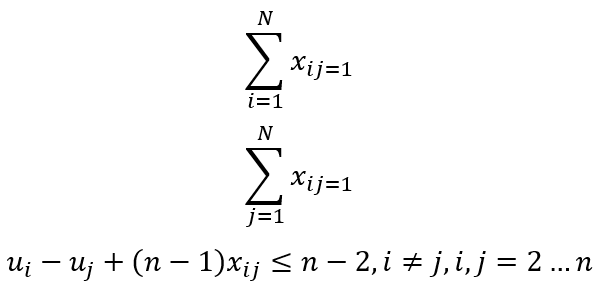





























 :
: