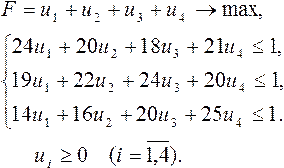Решение задач теории игр в MS
Exsel на примере задания ЕГЭ по информатики 19, 20, 21
Задача Два игрока
Петя и Ваня играют в следующую игру- перед ними лежит 2 кучи камней, игроки
ходят по очереди, первым ходит Петя, вторым Ваня. За один ход игрок может
добавить в любую кучу 1 камень или увеличить кол-во камней в 2 р . Игра
заканчивается, когда камней в обеих кучах становится не менее 53. Победителем
считается тот кто последним сделал ход. На начальном этапе игры в одной куче 9
камней, а во второй куче S камней
1 ≤ S≤43
Задача 19
Известно, что Ваня выиграл своим первым ходом
после неудачного ход Пети
Укажите минимальное кол-во камней S при такой ситуации
1.В ячейку в3 ввести 1 куча. В ячейку с3
ввести 2 куча В ячейку с4 ввести S. В ячейку в5 ввести 9. В
ячейку с5 ввести 5.
2. Построить таблицу от ячнйки d4 до g8
3. Ячейки d4 e4 объединить в них напечатать Петя, а в ячейки f4
Ваня, в ячейки g4 итог
ТО общий вид таблицы будет иметь вид
|
D |
E |
F |
G |
||
|
3 |
|||||
|
4 |
ПЕТЯ |
ВАНЯ |
ИТОГ |
||
|
5 |
|||||
|
6 |
|||||
|
7 |
|||||
|
8 |
|||||
4. Необходимо разобрать все возможные ходя
Пети для этого в ячейку D5 ввести B5+1,
первый возможный слабый ход, в ячейку E5 *с5
5. В ячейку D6 ввести в5,
те кол-во камней без изменения. В ячейку Е6 ввести с5+1, те кол-во камней без
изменения.
6. В ячейку D7 ввести
в5*2, в ячейку е7 ввести с5, в ячейку D8 ввести в5, в
ячейку е8 ввести с5*2,
ТО 1 чсть таблицы заполняется всевозможными
ходами Пети выделить их цветом.
Самая важная часть в таблице в комбинации D8 и е8 – это сильные ходы Пети.
7. В ячейку F5 ввести
МАКС (D5:Е5)*2+МИН(D5:Е5) растягиваем
значение формулы на все область ячеек F.
8. В ячейках столбца итог необходимо выяснить
какой из вариантов даст победу , для этого в ячейку g5
ввести фор-лу ЕСЛИ (F5>=53; ‘’+’’; ‘’-’’) растягиваем знач-е фор-лы на все ячейки от g5 до g8
Если в таблице не появится плюс, то меняется
значение С5.
Задача 20
Найдите 2 значения S при
которых у Пети есть выигрышная стратегия , но должны выполняться два условия
— Петя может выиграть за один ход
— Петя может выиграть за 2-м ходом независимо
отходов Вани.
Найденные значения записать в порядке
возрастания.
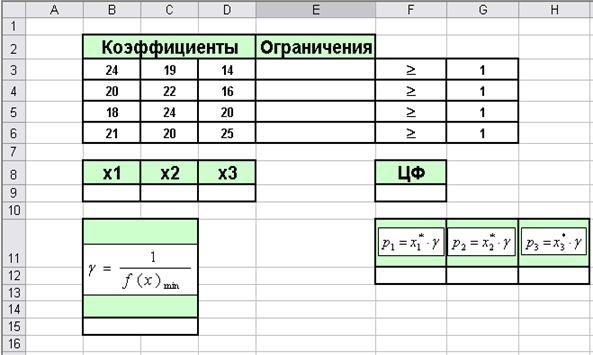
1. Таблицу из первой части копируем в область ячеек I3
—N8
2. Добавим в таблицу допол. поля
Там где столбец Ваня , чтоб
их стало два
,
верхнюю строку объединить , а также столбец Безопасность перед столбцом Итог.
ТО общий вид таблицы будет иметь вид:
|
K |
L |
M |
N |
O |
P |
Q |
|
|
3 |
|||||||
|
4 |
ПЕТЯ |
ВАНЯ |
Петя |
Безоп-ть |
Итог |
||
|
5 |
|||||||
|
6 |
|||||||
|
7 |
|||||||
|
8 |
|||||||
3. В ячейку I3 ввести 1 куча, в ячейку J3 ввести 2
куча,в ячейку J4 — S , I5 ввести 9,
J5 -11 .
4.
Удалить значения из столбцов ходов Пети. В ячейку
к5 ввести I5+1, L5 ввести J5, тогда
в ячейках ходов Вани вводятся формулы всех возможных его ходов В ячейку М5
ввести к5+1 , N5 ввести J5, М6
ввести к5, N6 ввести L5+1, , М7
ввести к5*2, N7 ввести L5, , М8
ввести к5, N8 ввести L5*2
ТО
будут перебраны все возможные варианты ходов Вани, тогда ходы Пети должны быть
все сильные.
Для
этого в столбец О5 вводится фор-ла МАКС (м5: N 5)*2+МИН(м5:
N 5), растягиваем знач-е этой фор-лы на область всех ячеек
в низ.
5. Т.к надо оценить игру Пети в столбце Итог вводят фор-лу ЕСЛИ (О5>=53; ‘’+’’; ‘’-’’) растягиваем знач-е этой
фор-лы на область всех ячеек в низ.
6. Т.к надо , чтоб выиграл Петя проконтролировать чтобы не выиграл Ваня
первым ходом именно для этой цели нужен столбец безопасность. В ячейку Р5
ввести фор-лу
ЕСЛИ
(м5+ N 5 >=53;
‘’+’’; ‘’-’’) растягиваем знач-е этой фор-лы на область всех ячеек в низ.
7.
Построенная таблица — это только один вариант
поведения Пети при игре, поэтому копируем таблицу ниже 4 раза не пропуская ни
одной строки, те вплотную. По следующему принципу:
ё
8. Внесем следующие изменения в скопированную часть
В К10 ввести I5, L 10 ввести J5 +1 (это будет второй возможный
выигрышный ход); в К15 ввести I5*2, L 15 ввести J5(это будет 3 возможный выигрышный ход);в К20- I5, в L 20 — J5*2(это будет 4 возможный выигрышный ход);.
Остальные
столбцы заполнятся автоматически благодаря относительной адресации.
9.Теперь необходимо просмотреть и проанализировать значения ячейки J5. Изменяя в ней значения по возрастанию до тех пор пока плюсы не
появятся в столбце Итога причем плюсы должны быть во всех четырех строках каждого
из 4 вариантов ходов а столбец безопасность должен быть отрицательным во всех 4
строках.
Задача 21
Сколько существует значений S которых одновременно выполняются два условия
— у Вани есть выигрышная стратегия при которой он выиграет 1 или 2 ходом
при любой игре Пети. —
у Вани нет стратегии, которая позволит ему гарантированно выиграть 1
ходом. С учетом полученного в задачи 20
можно уверенно утверждать, что выигрышные ходы Вани (9;16) и (9; 21) это
возможно при ходах Пети (9;15) и (9; 20). Решение этой задачи электронным
способом возможно только посте решения 19 и 20 зад на одной предметной
области. 1. Для решения
этой задачи скопируем таблицу из задания задачи 20 в область ячеек от U до AA в соответствии изображения
Внести изменения в значение столбцов S И T.
2.Очищаем значение столбцов игры Пети U И V.
Добавляем дополнительные столбцы в таблицу у
Пети будет два варианта ходов , поскольку в задании выигрыш может наступит и
на 1 и на 2 ходе.
ТО общий вид таблицы будет иметь вид:
Причем протяженность таблицы будет от столбцов
от U до АС, и от строк от 4 до 23 .
3. В ячейку U 5 ввести S5+1, а в ячейку V5 ввести Т5.
Ваня на подобный ход может ответить 4 разными
вариантами. Для х реализации очищаем все значения столбцов w и x.
В ячейки вводим фор-лы: w5=
U5+1; х2= V5; w10=
U5;х10= V5+1; w15=U5*2;х15=V5; w20= U5;х20= V5*2.
4. Для оценки возможных вариантов ходов Пети
скопировать данные из ячеек М5- N8 в ячейки y5-z8 из таблицы предыдущего задания. Формулы при
копировании изменятся в виду относительной адресации, хотя при копировании это
должно быть проконтролировано. Копируем эти значения и во все остальные ячейки y, z.
5. Второй ход Вани должен быть обязательно сильным, поэтому в ячейку
АА5 вводится фор-ла МАКС (y5: z5)*2+МИН(y5:
z5) ), растягиваем знач-е этой фор-лы на область всех
ячеек в низ.
Далее необходимо внести изменения в столбец Безопасность В ячейку АВ5
ввести фор-лу:
ЕСЛИ (y5+ z5>=53; ‘’+’’; ‘’-’’) , растягиваем знач-е этой
фор-лы на область всех ячеек в низ.
6. Для изменения столбца ИТОГ в ячейку АС5 вводится фор-ла: ЕСЛИ (АА5>=53; ‘’+’’; ‘’-’’) , растягиваем знач-е этой
фор-лы на область всех ячеек в низ.
7. Нельзя не учесть вариант при котором Ваня выигрывает первым ходом
для этого в ячейку х7 вводится фор-ла: ЕСЛИ (w5+ x5>=53; ‘’+’’; ‘’-’’) копировать
эту фор-лу в ячейки х12, х17, х22.
На основе предыдущего задания был сделан вывод что оптимальные s
либо 20, либо 15, поэтому рекомендуется проверку начать именно с
этих значений.
В ячейку s9 ввести 15, а в s10
ввести 20.
8.Полученная таблица отражает только 1 ход, а
их более, поэтому копируем эту таблицу ниже 4 раза в сплошную, тогда таблица
получится протяженностью до 64 строки. Внесем изменения в скопированную
таблицу: U25= s5+1; V25=Т5+1; U45= s5*2; V45=Т5; U65= s5; V65=Т5*2.
Для анализа заполненной таблицы введем в т5
значение 15 . Первым делом просматриваются ячейки х7, х12, х17, х22, если там
появится + , что Ваня выигрывает первым ходом и второй уже не нужен. Затем там
где в ячейках х плюсы не найдены просматривается столбец ИТОГ, там должны
встретится плюсы в 4-х подряд идущих строках , а безопасность должна идти с -.
Проделывается тоже самое для значения т5=20.
Библиографическое описание:
Захарова, Т. Н. Решение игровых задач с нулевой суммой с помощью Microsoft Excel / Т. Н. Захарова. — Текст : непосредственный // Актуальные задачи педагогики : материалы I Междунар. науч. конф. (г. Чита, декабрь 2011 г.). — Чита : Издательство Молодой ученый, 2011. — С. 176-181. — URL: https://moluch.ru/conf/ped/archive/20/1343/ (дата обращения: 15.04.2023).
Рассмотрим
общий случай игровой задачи m
x
n
с нулевой суммой, когда модель задачи не имеет седловой точки. Такую
модель можно представить в виде матрицы (табл.1):
Таблица 1. Общая таблица стратегий
|
Стратегии |
В1 |
В2 |
… |
Вn |
|
A1 |
a11 |
a12 |
a1n |
|
|
A2 |
a21 |
a22 |
a2n |
|
|
…. |
||||
|
Am |
am1 |
am2 |
amn |
Оптимальное
решение необходимо искать в области смешанных стратегий. Обозначим
вероятности применения стратегий первого игрока (игрока А) через
,
а цену игры — через v.
Оптимальная смешанная стратегия игрока А определяется из условия
Пусть
Поскольку при
оптимальной стратегии средний выигрыш не меньше v
при любой стратегии противника, то справедлива система n
неравенств:
Или
(1)
Тогда задача отыскания
оптимальной смешанной стратегии игрока А может быть сформулирована в
виде задачи линейного программирования.
Для этого
необходимо максимизировать целевую функцию F
=v
при ограничениях
(2)
Введем новые
неизвестные:
Поскольку
Разделим левую и
правую части неравенств (1) и (2) на v, получим:
(3)
В силу того что
max
v
= min
1/v
= min{x1+x2+…+xm}.
задача принимает вид
F=
x1+x2+…+xm
→
min
(4)
при ограничениях
(5)
Для
второго игрока (игрока В) оптимальная стратегия определяется из
условия:
при условии
q1+q2+…+qn
= 1
Эта задача
записывается как симметричная двойственная задача линейного
программирования к задаче игрока A
(4), (5):
L=
y1
+y2+…
+yn
→
max
(6)
при ограничениях
(7)
Задачи игроков A
и В решают симплекс-методом.
Использование
возможностей Microsoft
Excel
позволяет существенно облегчить и ускорить решение этой задачи.
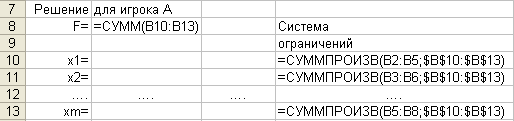
Сначала нужно создать исходную таблицу:
Затем, на основе этой таблицы записать
формулы для нахождения решения:
Для нахождения
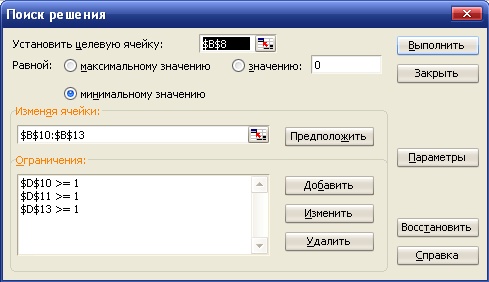
решения используется надстройка Поиск решения. Нужно выделить ячейку,
в которой вычисляется значение функции F
и вызвать надстройку Поиск решения. Заполнить окно поиска решения:
В поле Ограничения
нужно задать формулы для всех ограничений. Затем нажать кнопку
Параметры и отметить поля Линейная модель и Неотрицательные значения.
Нажать кнопку ОК, затем Выполнить.
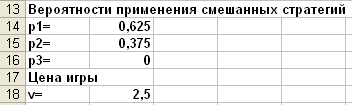
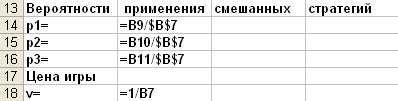
Чтобы найти значения вероятностей и цену
игры нужно записать формулы:
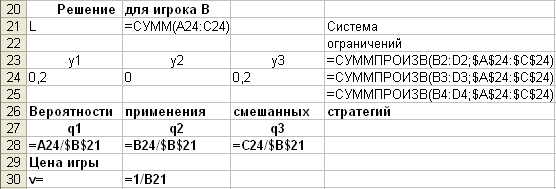
Решение задачи для
игрока В выполняется по аналогичной схеме согласно формулам (6), (7).
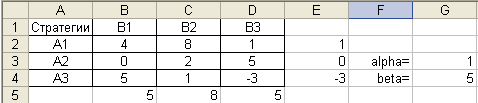
Рассмотрим пример
решения задачи. Найдем
решение игры, заданной матрицей
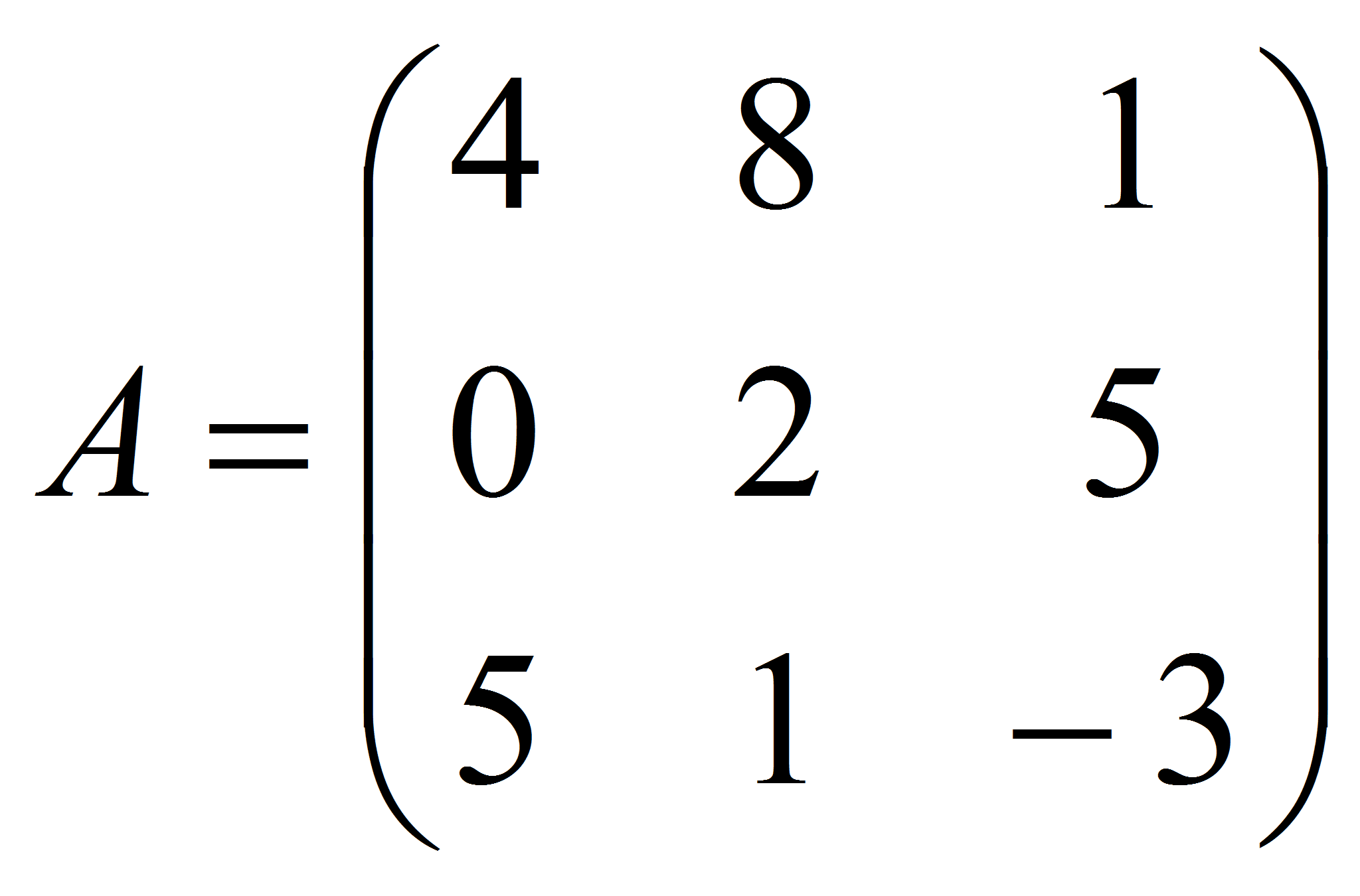
Проверим наличие седловой точки.
В режиме отображения
формул эта запись имеет вид:
Поскольку нижняя цена
игры (минимальный выигрыш игрока А) и верхняя цена игры (максимальный
проигрыш игрока В) не равны, то модель данной задачи не имеет
седловой точки. Поэтому решение следует искать в смешанных
стратегиях. Составим задачи линейного программирования для нахождения
решений игроков А (согласно формулам (4), (5)) и В(согласно формулам
(6), (7)):
для игрока А и
для игрока В.
Для решения этих систем используем
надстройку «Поиск решения». Сначала оформим задачу для
поиска решения игрока А:
В режиме отображения формул:
Затем нужно активировать ячейку В7 и
запустить надстройку Поиск решения. Далее заполнить окно Поиска
решения:
Затем нажать кнопку Параметры и отметить
поля Линейная модель и Неотрицательные значения. Нажать кнопку ОК,
затем Выполнить.
Получим результат:
Вероятности применения смешанных
стратегий и цену игры найдем по формулам: pi=xi/F,
v=1/F.
В режиме отображения формул:
Аналогично найдем решение для игрока В:
В режиме отображения формул:
Литература:
1. Акулич И.Л. Математическое
программирование в примерах и задачах. М. «Высшая школа»,
1993г.
2. Агальцов В.П., Волдайская И.В.
Математические методы в программировании М. ИД «Форум» —
ИНФРА-М, 2006г.
3. Бережная Е.В., Бережной В.И.
Математические методы моделирования экономических систем М. «Финансы
и статистика», 2003г.
4. Партыка Т.Л., Попов И.И.
Математические методы М. ИД «Форум» — ИНФРА-М, 2007г.
Основные термины (генерируются автоматически): игрок А, Поиск решения, режим отображения формул, игрок В, линейное программирование, цена игры, кнопка ОК, Линейная модель, оптимальная смешанная стратегия, оптимальная стратегия.
Похожие статьи
Создание и использование программы для статистического…
стратегия, игра, игрок, матричная игра, цена игры, решение игры, нулевая сумма, участник, верхняя цена игры, платежная матрица. Поиск решения как средство решения задач оптимизации…
Теория игр: основные понятия, типы игр, примеры
Для второго игрока самой оптимальной смешанной стратегией является стратегия . Запишем цену игры
Алгоритм. Иначе цена игры находится в промежутке и решение игры находится в смешанных стратегиях.
Поиск решения как средство решения задач оптимизации…
Получится запись как на рис.1. В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок Линейная модель и задать условия неотрицательности переменных, установив флажок
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
Математическое моделирование оптимальных стратегий…
‒ аспект оптимальных решений — теория математических моделей принятия оптимальных решений вусловиях конфликтов.
игрок, функция распределения, стратегия, конфликтная ситуация, функция, математическая модель, непрерывная игра, обычный риманов интеграл…
Интеграл Стильтьеса в теории игр | Статья в журнале…
Аналогичным образом с помощью интеграла Стильтьеса находится цена непрерывной игры и оптимальная смешанная стратегия для обоих игроков-стратегов. Предположим, что есть платежная функция (или функция выигрыша)…
Целочисленное решение задач линейного программирования…
Оптимальное решение в примере, в принципе, не может быть получено каким-либо округлением решения соответствующей задачи линейного программирования.
Решение многокритериальных задач линейного…
Рис. 1. Оптимальное решение задачи.
Основные термины (генерируются автоматически): критерий, задача, учет уступок, полученное решение, поиск решения, матрица коэффициентов, важность критерия, допустимая уступка, линейное программирование.
Применение метода линейного программирования для решения…
Метод линейного программирования при решении текстовых задач графически имеет следующий алгоритм
Литература: 1. Шикин Е. В., Чхартишвили А. Г. Математические методы и модели.
Линейное программирование | Статья в журнале «Молодой…»
Модель линейного программирования имела бы множество переменных решений
Решение задач оптимального раскроя средствами MS Excel. Симплекс-метод, основанный на идеях Л. В. Канторовича, был описан и детально разработан рядом ученых из США в середине 20 века.
Как
уже отмечалось, любая парная игра с
нулевой суммой может быть сведена к
решению задачи линейной оптимизации.
Используя значение функции и неизвестных
взаимно двойственных задач линейной
оптимизации, легко найти цену игры и
вероятности применения стратегий каждым
из игроков.[5.c.89]
Пример
1
В
качестве примера применения информационных
технологий Excel найдем решение парной
игры с платежной матрицей
|
|
||||
Решение
Для
данной задачи (седловая
точка отсутствует). Запишем пару
двойственных задач линейной оптимизации
для решения игры.
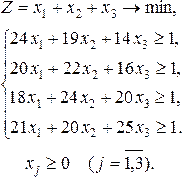
Решим
исходную и двойственную задачи с помощью
Excel.
Внесем
данные на рабочий лист в соответствии
с Ри.1.
матричный
игра решение линейный
Рис.1.14лист
в соответствии с
Рис.
Данные для решения исходной задачи
примера 1
В
ячейки E3:E6 введем формулы для расчета
функций – ограничений, ячейки B9:D9 отведем
для переменных ,
ячейку B15 – для расчетного значения
цены игры,
диапазон ячеек F12:H12 – для расчетных
значений вероятностей применения
стратегий игроком I, и, наконец, ячейку
F9 – для расчета целевой функции. Введем
все необходимые формулы в соответствующие
ячейки. Установим все необходимые
ограничения исходной задачи перед
запуском Поиска решения. С помощью
Поиска решения получим следующий ответ
|
Таким
образом, оптимальная смешанная стратегия
игрока I:
Решим
двойственную задачу. Во избежание
возможных ошибок расположим данные для
ее решения на отдельном рабочем листе
Excel (Рис.2.).
Рис
2 Данные для решения двойственной задачи
примера 1
Ввод
данных и формул производится аналогично
предыдущему случаю. Поиск решения дает
ответ:
|
U |
0,0026 |
Q1=U1* |
0,0541 |
ЦФ |
|
|
U |
0,0195 |
Q2=U2* |
0,4054 |
0,048177 |
|
|
U |
0,0000 |
Q3=U3* |
0,0000 |
|
|
|
U |
0,0260 |
Q4=U4* |
0,5405 |
20,75676 |
Таким
образом, оптимальная смешанная стратегия
игрока II есть
.
[7]
Заключение
В
условиях альтернативы (выбора) очень
часто нелегко принять решение и выбрать
ту или иную стратегию. Исследование
операций позволяет с помощью использования
соответствующих математических методов
принять обоснованное решение о
целесообразности той или иной стратегии.
Таким образом, теория игр, имеющая в
запасе арсенал методов решения матричных
игр, позволяет эффективно решать
указанные задачи несколькими методами
и из их множества выбрать наиболее
эффективные, а также упрощать исходные
матрицы игр.
В
теории игр страте́гия игрока в игре или
деловой ситуации — это полный план
действий при всевозможных ситуациях,
способных возникнуть. Стратегия
определяет действие игрока в любой
момент игры и для каждого возможного
течения игры, способного привести к
каждой ситуации .Вданной работе были
изучены понятия стратегий ,и выявлены
их решения,т.ж было проведенно ознакомление
решений стратегий с помощью программы
Excel.
К
тому же с помощью теории игр можно
выработать такую оптимальную стратегию,
при которой система не будет существенно
изменяться под управлением каких-то
внешних воздействий, да и потери будут
не столь существенными.
Список
используемой литературы
|
Следующая |
||
-
Вентцель
Е. С. «Элементы теории игр» 2-ое изд. М.:
Физматгиз,2001. — 68 с. -
Дуплякин
В.М. Теория игр: учеб. пособие / В.М.Дуплякин
— Самара : Изд-во Самар. гос. аэрокосм.
ун-та, 2011. – 191 с. -
Олейник
А.Н.. Институциональная экономика:
Учебное пособие. — М.: ИНФРА-М,2002. — 416 с.
— (Серия «Высшее образование»)., 2002. -
Писарук,
Н. Н.Введение в теорию игр .Учебник .М.:—
Минск : БГУ, 2015. —256 c. -
Холявин
И.И. Математическое программирование
и экономико-математические методы.
Учебное пособие для студентов
экономических вузов Часть 2. Гатчина
2009. -
Экономико-
математический энциклопедический
словарь(под ред. В.И.Данилова-Данильяца),М.:Изд.Дом
«ИНФРА-М»,2003. -
Электронный
ресурс [Режим доступа]:
http://studopedia.org/5-41115.htm
22
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #




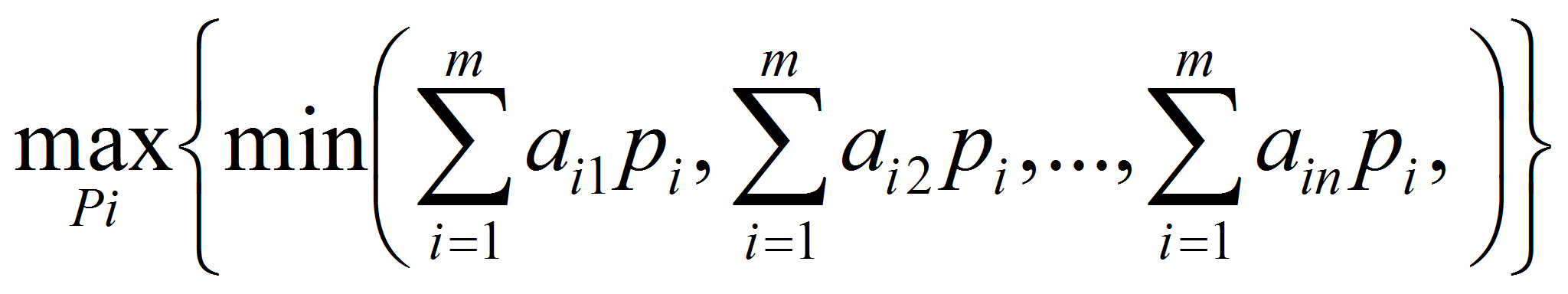
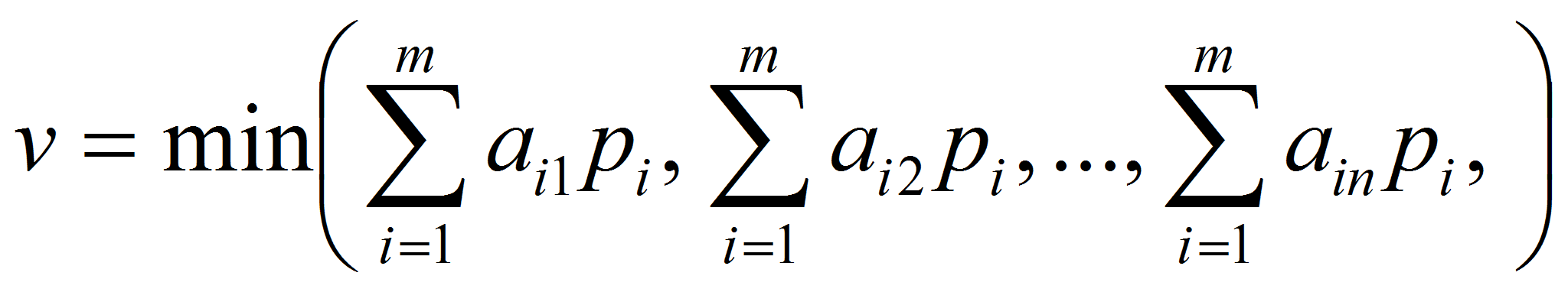
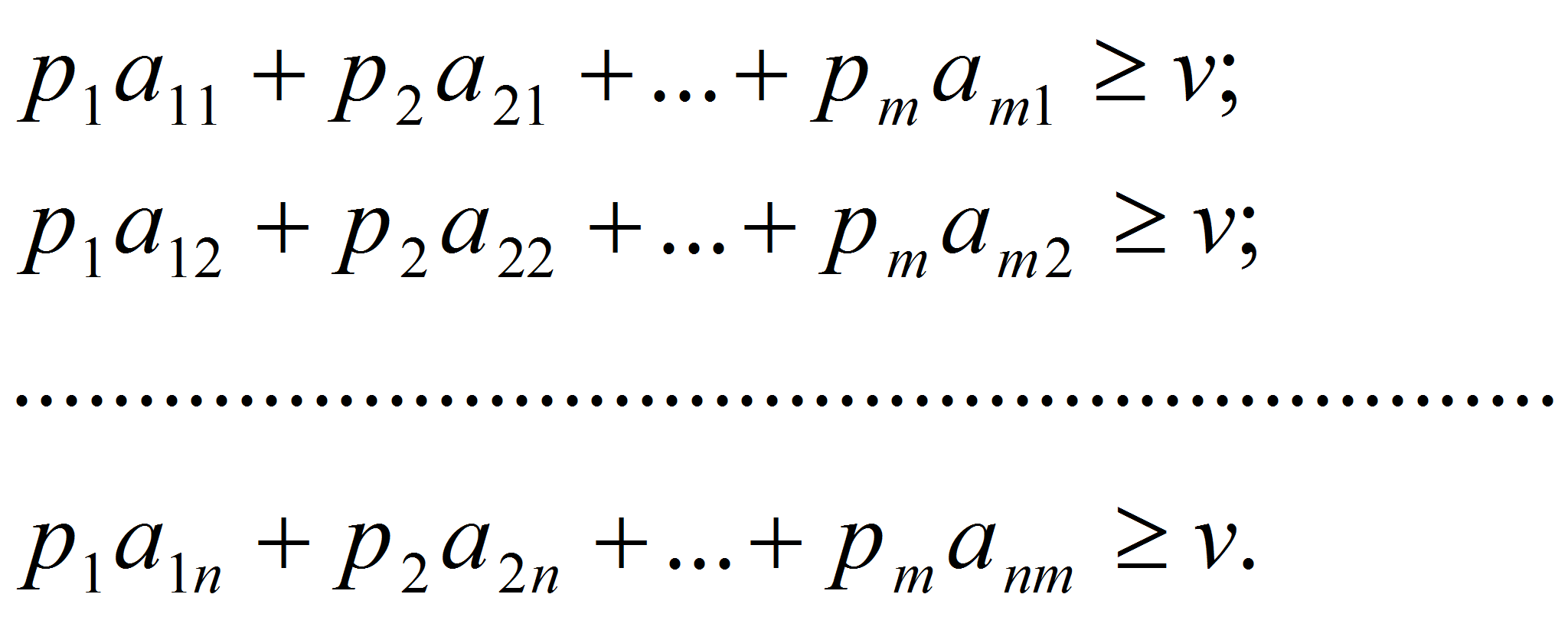
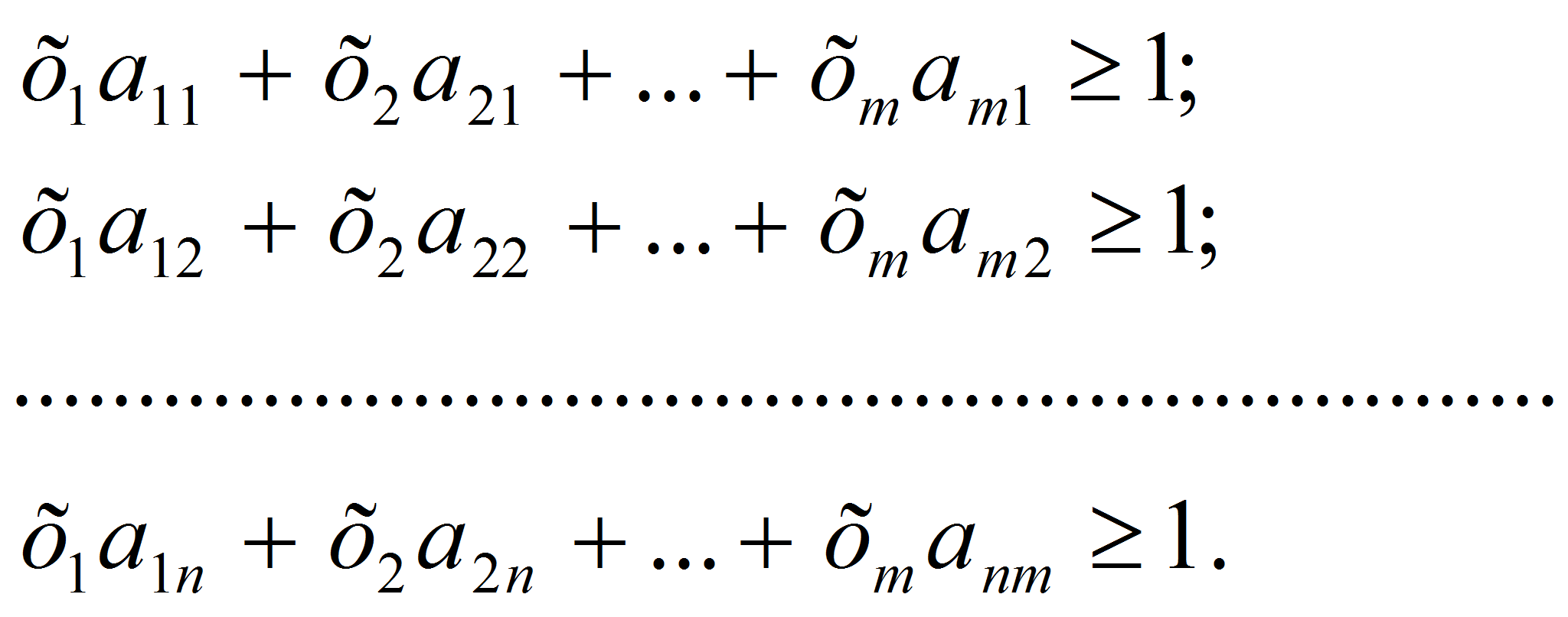
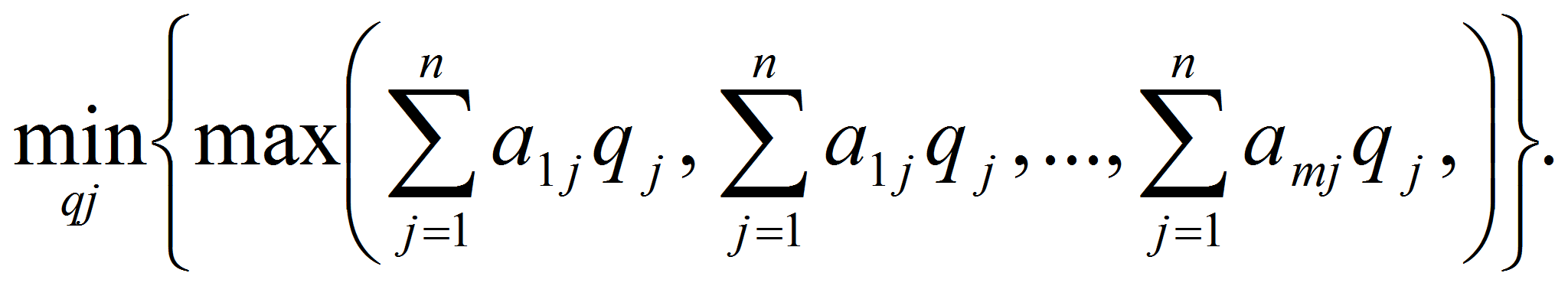
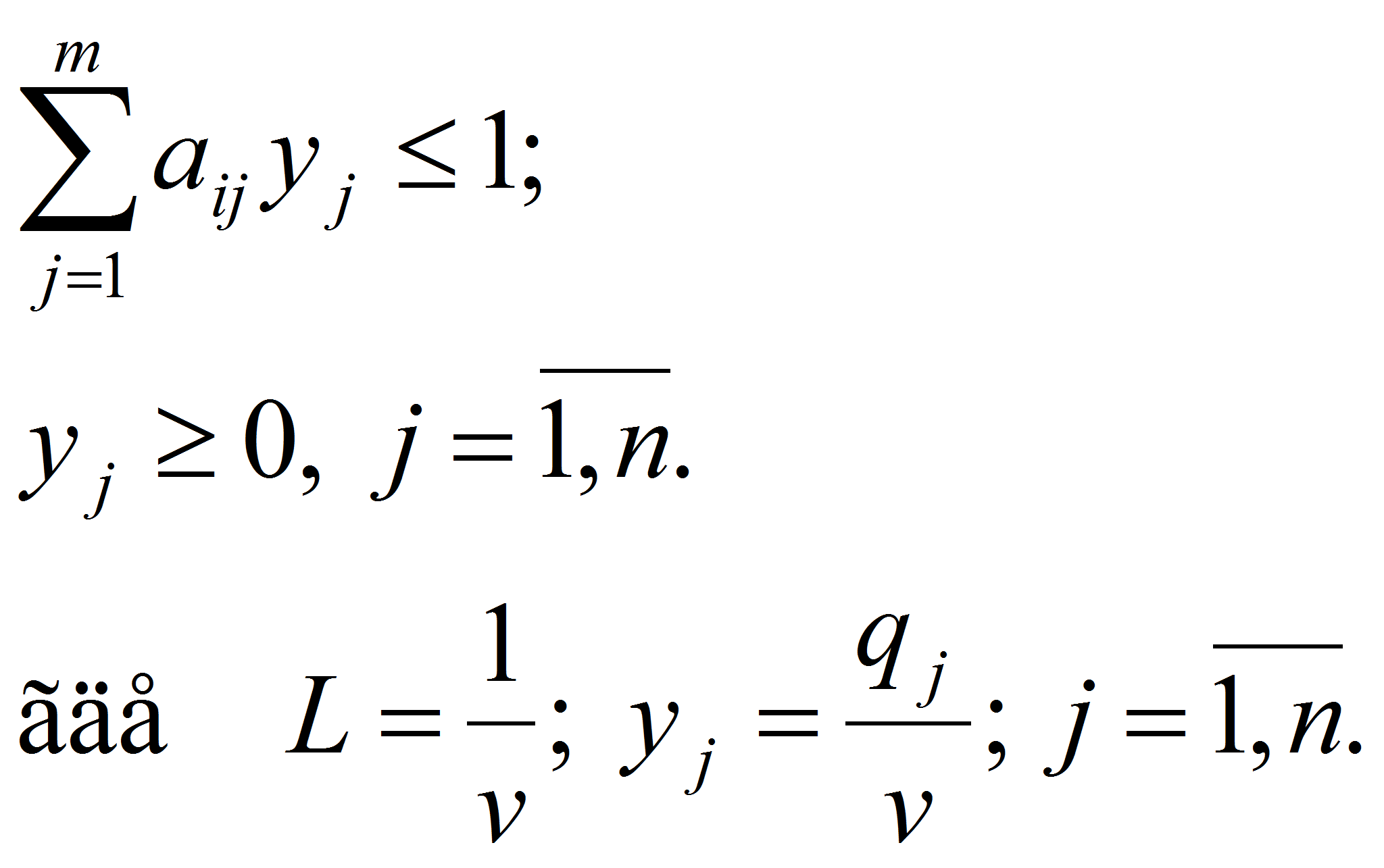



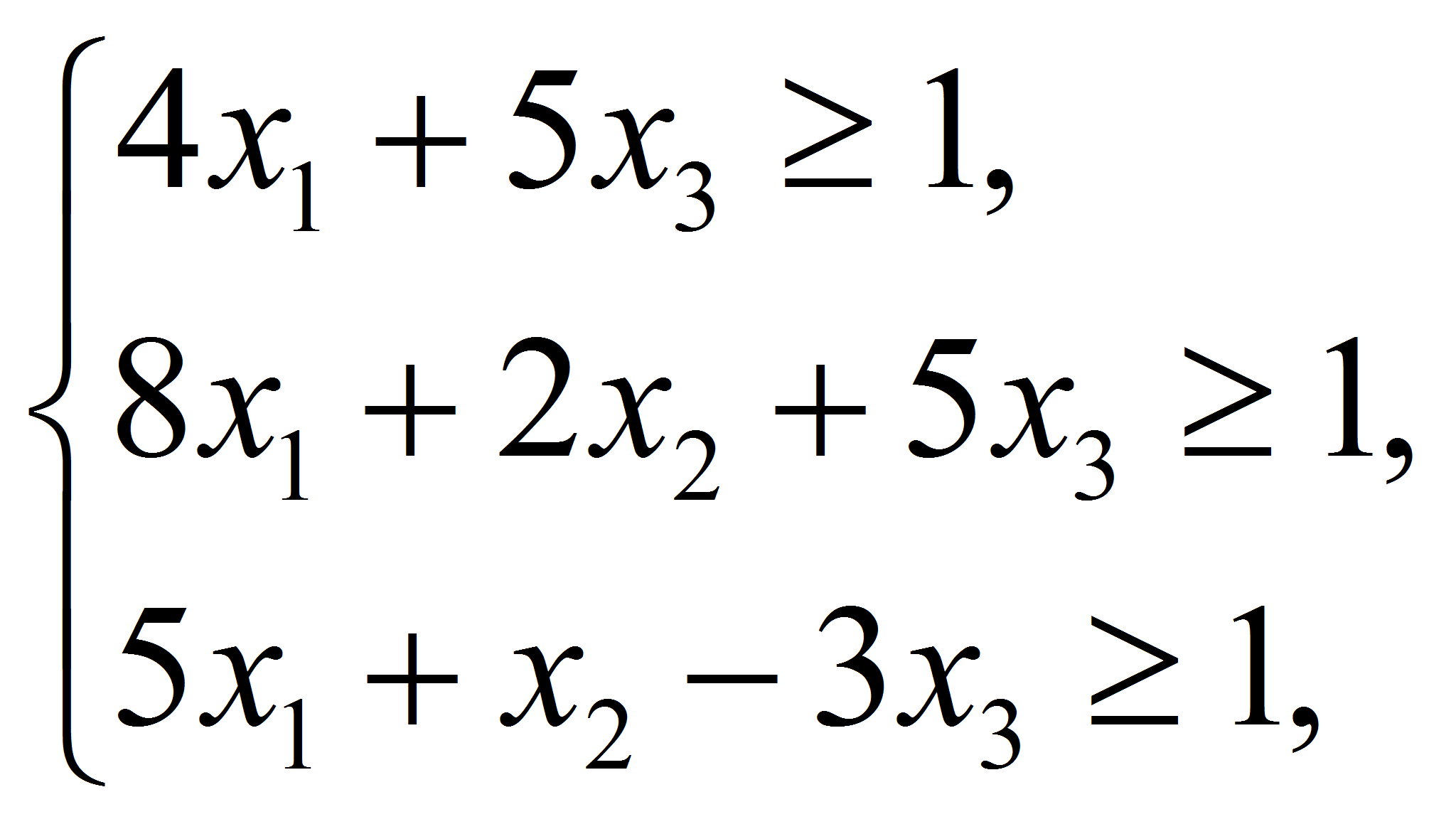
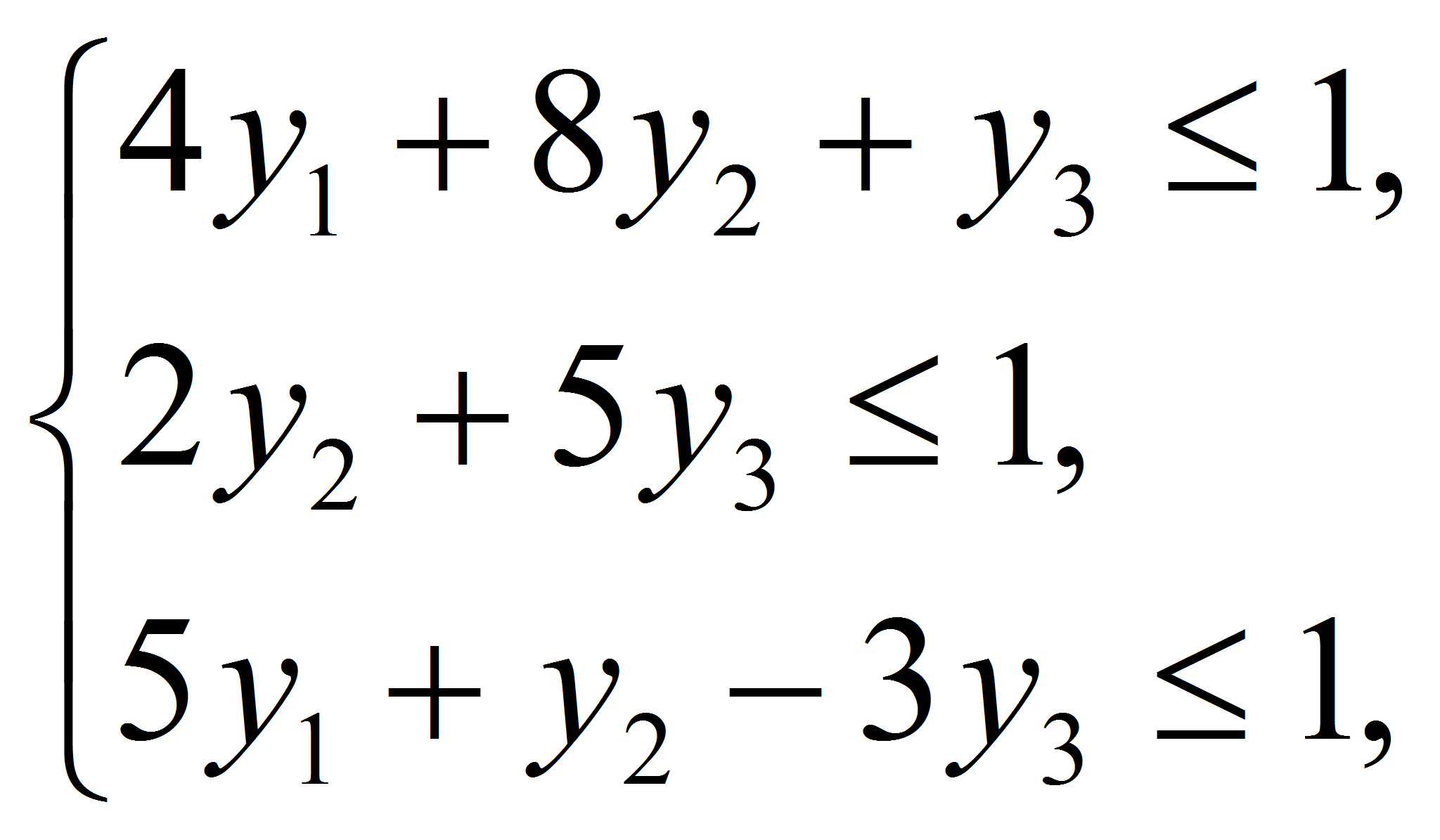





 II
II