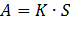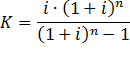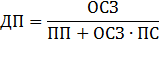Содержание
- Примеры по финансовой математике в Excel
- Решение финансовой математики в Excel
- ПРАКТИЧЕСКАЯ РАБОТА «РАСЧЁТ ПЛАТЕЖЕЙ ПО КРЕДИТУ В EXCEL»
- «РАСЧЕТ ПЛАТЕЖЕЙ ПО КРЕДИТУ В EXCEL»
- Математика и информатика: теория и методика преподавания в профессиональном образовании
- Методы и инструменты современного моделирования
- Теоретические и методологические основы преподавания информатики с учётом требований ФГОС ООО
- Основы работы с программой PowerPoint
- Опытные онлайн-репетиторы
- Разговоры о важном
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Онлайн-занятия с репетиторами
- Подарочные сертификаты
Примеры по финансовой математике в Excel
В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена. 9500 13000
Генерируемый годовой доход. 2100 2250
Срок эксплуатации. 8 лет 12 лет
Ликвидационная стоимость. 500 800
Требуемая норма прибыли. 11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Источник
ПРАКТИЧЕСКАЯ РАБОТА «РАСЧЁТ ПЛАТЕЖЕЙ ПО КРЕДИТУ В EXCEL»
«РАСЧёт ПЛАТЕЖей ПО КРЕДИТУ В EXCEL»
Допустим, что нам нужно взять кредит в 2 млн. рублей на покупку квартиры под 10,2% годовых на 10 лет. Банк предлагает два вида платежей аннуитетный платеж или дифференцированный платеж. Какой вид платежа выгоден клиенту и почему?
1. Рассчитать платежи по аннуитетной схеме погашения.
2. Рассчитать платежи по дифференцированной схеме погашения.
3. Сравнить переплату при аннуитетной и дифференцированной схеме погашения кредита.
4. Сделать вывод (какой вид платежа выгоден клиенту, а какой банку).
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
1. Рассчитать платежи по аннуитетной схеме погашения.
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
· А – сумма платежа по кредиту;
· К – коэффициент аннуитетного платежа;
· S – величина займа.
Формула коэффициента аннуитета:
· где i – процентная ставка за месяц, результат деления годовой ставки на 12;
· n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это = ПЛТ:
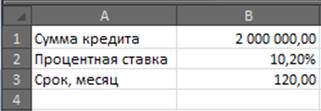
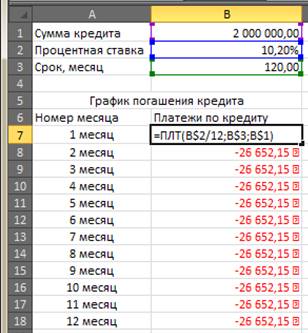
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
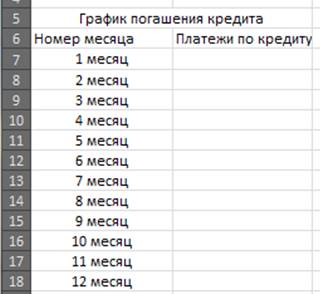
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводится формула расчета кредита аннуитетными платежами: =ПЛТ($B$2/12; $B$3; $B$1). Чтобы закрепить ячейки, используем абсолютные ссылки.
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
4. Подсчитаем сумму выплат.
В ячейку столбца «Выплачено» вводится формула суммирования выплат по кредиту: =СУММ(B7:B126)*(-1). Чтобы закрепить ячейки, используем абсолютные ссылки.
Сумму переплат подсчитайте самостоятельно.
2. Рассчитать платежи по дифференцированной схеме погашения.
Дифференцированный способ оплаты предполагает, что:
· сумма основного долга распределена по периодам выплат равными долями;
· проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
· ДП – ежемесячный платеж по кредиту;
· ОСЗ – остаток займа;
· ПП – число оставшихся до конца срока погашения периодов;
· ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения кредита по дифференцированной схеме.
Составим график погашения займа:
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =K2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(K9>$K$4;0;L8-N8). Где K9 – номер текущего периода, K4 – срок кредита; L8 – остаток по кредиту в предыдущем периоде; N8 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =L8*($K$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: = ЕСЛИ(K8
Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =M8+N8
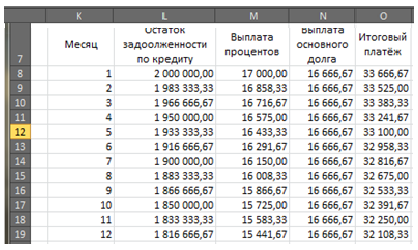
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сумму выплат и переплат посчитайте самостоятельно.
3. Сравнить переплату при аннуитетной и дифференцированной схеме погашения кредита.
Источник
«РАСЧЕТ ПЛАТЕЖЕЙ ПО КРЕДИТУ В EXCEL»
«РАСЧёт ПЛАТЕЖей ПО КРЕДИТУ В EXCEL»
Допустим, что нам нужно взять кредит в 2 млн. рублей на покупку квартиры под 10,2% годовых на 10 лет. Банк предлагает два вида платежей аннуитетный платеж или дифференцированный платеж. Какой вид платежа выгоден клиенту и почему?
1. Рассчитать платежи по аннуитетной схеме погашения.
2. Рассчитать платежи по дифференцированной схеме погашения.
3. Сравнить переплату при аннуитетной и дифференцированной схеме погашения кредита.
4. Сделать вывод (какой вид платежа выгоден клиенту, а какой банку).
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
1. Рассчитать платежи по аннуитетной схеме погашения.
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
· А – сумма платежа по кредиту;
· К – коэффициент аннуитетного платежа;
· S – величина займа.
Формула коэффициента аннуитета:
· где i – процентная ставка за месяц, результат деления годовой ставки на 12;
· n – срок кредита в месяцах.
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это = ПЛТ:
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводится формула расчета кредита аннуитетными платежами: =ПЛТ($B$2/12; $B$3; $B$1). Чтобы закрепить ячейки, используем абсолютные ссылки.

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
4. Подсчитаем сумму выплат.
В ячейку столбца «Выплачено» вводится формула суммирования выплат по кредиту: =СУММ(B7:B126)*(-1). Чтобы закрепить ячейки, используем абсолютные ссылки.
Сумму переплат подсчитайте самостоятельно.
2. Рассчитать платежи по дифференцированной схеме погашения.
Дифференцированный способ оплаты предполагает, что:
· сумма основного долга распределена по периодам выплат равными долями;
· проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного платежа:
· ДП – ежемесячный платеж по кредиту;
· ОСЗ – остаток займа;
· ПП – число оставшихся до конца срока погашения периодов;
· ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения кредита по дифференцированной схеме.
Составим график погашения займа:
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =K2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(K9>$K$4;0;L8-N8). Где K9 – номер текущего периода, K4 – срок кредита; L8 – остаток по кредиту в предыдущем периоде; N8 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =L8*($K$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: = ЕСЛИ(K8
Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =M8+N8
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сумму выплат и переплат посчитайте самостоятельно.
3. Сравнить переплату при аннуитетной и дифференцированной схеме погашения кредита.

Курс профессиональной переподготовки
Математика и информатика: теория и методика преподавания в профессиональном образовании
- Сейчас обучается 30 человек из 22 регионов

Курс повышения квалификации
Методы и инструменты современного моделирования

Курс повышения квалификации
Теоретические и методологические основы преподавания информатики с учётом требований ФГОС ООО
- Сейчас обучается 134 человека из 50 регионов

Основы работы с программой PowerPoint

Лучшее для учеников, педагогов и родителей
Опытные
онлайн-репетиторы
- По любым предметам 1-11 классов
- Подготовка к ЕГЭ и ОГЭ
Рабочие листы и материалы для учителей и воспитателей
Более 7 500 дидактических материалов для школьного и домашнего обучения
Разговоры о важном
Рекомендуем всем учителям 1-11 классов
Подача заявок до 22 марта
Ценности гуманной педагогики
Открытая сессия для учителей и руководителей образовательных организаций
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 168 714 материалов в базе
Материал подходит для УМК
«Информатика», Босова Л.Л., Босова А.Ю.
§ 3.2. Организация вычислений в электронных таблицах
Другие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 05.11.2020 4267
- DOCX 862 кбайт
- 101 скачивание
- Оцените материал:
Настоящий материал опубликован пользователем Осипчук Анастасия Николаена. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 5 месяцев
- Подписчики: 0
- Всего просмотров: 4371
- Всего материалов: 1
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 490 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Онлайн-занятия с репетиторами
для весеннего интерьера
Основы хлебопечения дома: база
Детско-родительские отношения и формирование образа партнера
Целеполагание. Техники достижения цели
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
В этом разделе вы найдете примеры задач c решением по финансовой математике, выполненные с помощью пакета Excel. Другие примеры с решениями вручную вы найдете здесь.
Для решения финансовых задач в Эксель используются как встроенные финанансовые функции (например, ПЛТ, СТАВКА, КПЕР, ПС, БС, ПОЛУЧЕНО и т.д), так и формулы, вводимые вручную, чтобы получить ответ согласно некоторой сложной формуле (для которой нет встроенной функции). Иногда используются также функции подбора параметра и поиска решения.
Поможем с Excel, финансами и математикой 
Решение финансовой математики в Excel
Задача 1. Вас просят дать в долг 03.03.2012 г. 20000 р. и обещают вернуть 18.08.2012 г. 4800 р., 13.11. 2012 г. – 5400 р., 07.03.2013 г. – 5700 р. и 31.05.2013 г. – 6200 р. Оценить выгодность предложения, если существует возможность положить деньги в банк под 13% годовых.
Задача 2. Вы заняли на 4 года 10000 руб. под 14% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Определить величину годового платежа.
Задача 3. Предприятие рассматривает целесообразность принятия новой технологической линии. На рынке имеются две модели со следующими параметрами:
П1 П2
Цена……………………………………….. 9500 13000
Генерируемый годовой доход…….2100 2250
Срок эксплуатации……………………. 8 лет 12 лет
Ликвидационная стоимость………..500 800
Требуемая норма прибыли…………..11% 11%
Обоснуйте целесообразность приобретения той или иной технологической линии.
Задача 4. Вы открываете счёт и собираетесь вкладывать по 1400 р. в начале каждого года в течении 8 лет при годовой ставке 3,5%. Сколько денег будет на счете через 8 лет?
Задача 5. Контракт между фирмой и банком предусматривает в течение 3 лет фирме ежегодными платежами в размере 24 тыс. руб. в начале каждого года под ставку 14% годовых. Фирма возвращает долг, выплачивая последовательно в конце 3,4,5 годов. Какова чистая современная величина NPV для банка?
Задача 6. Годовая процентная ставка составляет 9% и остается неизменной в течение всего периода, а годовая купонная ставка по облигации с номиналом 1400 руб. со сроком обращения 10 лет установлена в размере 14%. Сколько стоит эта облигация при эмиссии? Сколько будет стоить эта облигация через 5 лет. Какова доходность облигации за 10 лет.
Задача 7. Кредит в размере 500 млн. руб. выдан на 5 лет под 17 % годовых с начислением процентов и выплатой в конце каждого года. Выплаты основного долга должны уменьшаться ежегодно на 8 млн. руб. Составить план погашения кредита.
Задача 8. На вклад начисляются сложные проценты: а) каждые полгода; б) ежеквартально; в) ежемесячно. Вычислить годовую номинальную процентную ставку, при которой происходит реальное наращение капитала, если ежеквартальный темп инфляции составляет 2%. Известно:
h = 2%; m1 = 2; m2 = 4; m3 = 12.
Найти: i1 — ? i2 — ? i3 — ?
Задача 9. Предприниматель получил ссуду в банке в размере 20 млн. руб. сроком на 5 лет на следующих условиях: для первых двух лет процентная ставка равна 25% годовых, на оставшиеся 3 года ставка равна 23% годовых. Найдите доход банка за 5 лет, если сложные ссудные проценты начисляются ежеквартально.
Известно: Р = 20 000 000 руб.; i1 = 0,25 или 25% n1 = 2 года i2 = 0,23 или 23% n2 = 3 года m = 4
Найти: I — ?
Задача 10. Определить годовую процентную ставку банка, если вкладчик внес 3297 д.е. на 6 лет, сумма на счете в конце срока составила 12934 д.е. В первую треть срока начислялись простые проценты, а в оставшийся – сложные, 5 раз в год.
Помогаем с решением задач по финансовой математике
Может быть интересно:
|
|
Задача. Человек положил деньги в банк под n процентов годовых. Проценты начисляются ежеквартально и зачисляются на счет. С помощью электронной таблицы рассчитать, какое количество денег получит человек чрез два года.
Решение. Спланируем расчетную форму. Сумму денег, которая помещается первоначально на счет, и начисляемые проценты занесем в отдельные ячейки. При необходимости они могут быть изменены, и результат будет пересчитан.
На рисунке представлены результаты расчетов для некоторого набора данных.
Ниже – тот же фрагмент таблицы в режиме отображения формул.
Литература:
Газета «Первое сентября», «Информатика», №10, 2007.
Практическая
работа
«РАСЧёт
ПЛАТЕЖей ПО КРЕДИТУ В EXCEL»
Задача.
Допустим, что нам
нужно взять кредит в 2 млн. рублей на покупку квартиры под 10,2% годовых на 10
лет. Банк предлагает два вида платежей аннуитетный
платеж или дифференцированный платеж. Какой вид платежа выгоден клиенту и почему?
План работы:
1. Рассчитать
платежи по аннуитетной схеме погашения.
2. Рассчитать
платежи по дифференцированной схеме погашения.
3. Сравнить
переплату при аннуитетной и дифференцированной схеме погашения кредита.
4. Сделать
вывод (какой вид платежа выгоден клиенту, а какой банку).
Ежемесячные
выплаты зависят от схемы погашения кредита. Различают аннуитетные и
дифференцированные платежи:
1. Аннуитет
предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При
дифференцированной схеме погашения долга перед финансовой организацией проценты
начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут
уменьшаться.
1. Рассчитать
платежи по аннуитетной схеме погашения.
Ежемесячная сумма
аннуитетного платежа рассчитывается по формуле:
где:
·
А – сумма платежа по кредиту;
·
К – коэффициент аннуитетного платежа;
·
S – величина займа.
Формула коэффициента
аннуитета:
·
где i – процентная ставка за месяц, результат деления годовой
ставки на 12;
·
n – срок кредита в месяцах.
В программе Excel существует
специальная функция, которая считает аннуитетные платежи. Это =ПЛТ:
1. Заполним
входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа,
проценты и срок.
2. Составим
график погашения кредита. Пока пустой.
3. В первую
ячейку столбца «Платежи по кредиту» вводится формула расчета кредита аннуитетными
платежами: =ПЛТ($B$2/12; $B$3; $B$1). Чтобы закрепить ячейки, используем
абсолютные ссылки.
Ячейки окрасились в красный
цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать
банку, терять.
4. Подсчитаем
сумму выплат.
В ячейку столбца «Выплачено» вводится
формула суммирования выплат по кредиту: =СУММ(B7:B126)*(-1). Чтобы закрепить
ячейки, используем абсолютные ссылки.
Сумму переплат подсчитайте
самостоятельно.
2. Рассчитать
платежи по дифференцированной схеме погашения.
Дифференцированный способ
оплаты предполагает, что:
·
сумма основного долга распределена по периодам выплат равными
долями;
·
проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного
платежа:
где:
·
ДП – ежемесячный платеж по кредиту;
·
ОСЗ – остаток займа;
·
ПП – число оставшихся до конца срока погашения периодов;
·
ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения
кредита по дифференцированной схеме.
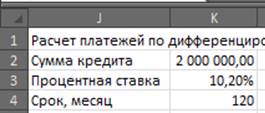
Входные данные:
Составим график погашения
займа:
Остаток
задолженности по кредиту: в первый месяц равняется всей
сумме: =K2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(K9>$K$4;0;L8-N8).
Где K9 – номер текущего периода, K4 – срок кредита; L8 – остаток по кредиту в
предыдущем периоде; N8 – сумма основного долга в предыдущем периоде.
Выплата
процентов: остаток по кредиту в текущем периоде умножить
на месячную процентную ставку, которая разделена на 12 месяцев: =L8*($K$3/12).
Выплата
основного долга: сумму всего кредита разделить на
срок: = ЕСЛИ(K8<=$K$4;$K$2/$K$4;0).
Итоговый
платеж: сумма «процентов» и «основного долга» в
текущем периоде: =M8+N8
Внесем формулы в
соответствующие столбцы. Скопируем их на всю таблицу.
Сумму выплат и переплат
посчитайте самостоятельно.
3. Сравнить
переплату при аннуитетной и дифференцированной схеме погашения кредита.
Аннуитетный платёж:
___________________________
Дифференцированный платёж:
____________________________
4. Вывод
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Практическая
работа
«РАСЧёт
ПЛАТЕЖей ПО КРЕДИТУ В EXCEL»
Задача.
Допустим, что нам нужно взять
кредит в 2 млн. рублей на покупку квартиры под 10,2% годовых на 10 лет. Банк
предлагает два вида платежей аннуитетный платеж или дифференцированный платеж. Какой вид
платежа выгоден клиенту и почему?
План работы:
1.
Рассчитать платежи по аннуитетной схеме погашения.
2.
Рассчитать платежи по дифференцированной схеме погашения.
3.
Сравнить переплату при аннуитетной и дифференцированной схеме
погашения кредита.
4.
Сделать вывод (какой вид платежа выгоден клиенту, а какой банку).
Ежемесячные
выплаты зависят от схемы погашения кредита. Различают аннуитетные и
дифференцированные платежи:
1. Аннуитет
предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной
схеме погашения долга перед финансовой организацией проценты начисляются на
остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.
1.
Рассчитать платежи по аннуитетной схеме погашения.
Ежемесячная сумма аннуитетного
платежа рассчитывается по формуле:
где:
·
А – сумма платежа по кредиту;
·
К – коэффициент аннуитетного платежа;
·
S – величина займа.
Формула коэффициента аннуитета:
·
где i – процентная ставка за месяц, результат деления годовой
ставки на 12;
·
n – срок кредита в месяцах.
В программе Excel существует
специальная функция, которая считает аннуитетные платежи. Это =ПЛТ:
1. Заполним
входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа,
проценты и срок.
2. Составим
график погашения кредита. Пока пустой.
3. В первую
ячейку столбца «Платежи по кредиту» вводится формула расчета кредита аннуитетными
платежами: =ПЛТ($B$2/12; $B$3; $B$1). Чтобы закрепить ячейки, используем
абсолютные ссылки.
Ячейки окрасились в красный цвет,
перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку,
терять.
4. Подсчитаем
сумму выплат.
В ячейку столбца «Выплачено» вводится формула суммирования
выплат по кредиту: =СУММ(B7:B126)*(-1). Чтобы закрепить ячейки, используем
абсолютные ссылки.
Сумму переплат подсчитайте самостоятельно.
2.
Рассчитать платежи по дифференцированной схеме погашения.
Дифференцированный способ оплаты
предполагает, что:
·
сумма основного долга распределена по периодам выплат равными
долями;
·
проценты по кредиту начисляются на остаток.
Формула расчета дифференцированного
платежа:
где:
·
ДП – ежемесячный платеж по кредиту;
·
ОСЗ – остаток займа;
·
ПП – число оставшихся до конца срока погашения периодов;
·
ПС – процентная ставка за месяц (годовую ставку делим на 12).
Составим график погашения кредита
по дифференцированной схеме.
Входные данные:
Составим график погашения займа:
Остаток
задолженности по кредиту: в первый месяц равняется всей
сумме: =K2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(K9>$K$4;0;L8-N8).
Где K9 – номер текущего периода, K4 – срок кредита; L8 – остаток по кредиту в
предыдущем периоде; N8 – сумма основного долга в предыдущем периоде.
Выплата
процентов: остаток по кредиту в текущем периоде умножить на месячную
процентную ставку, которая разделена на 12 месяцев: =L8*($K$3/12).
Выплата
основного долга: сумму всего кредита разделить на срок: =
ЕСЛИ(K8<=$K$4;$K$2/$K$4;0).
Итоговый
платеж: сумма «процентов» и «основного долга» в текущем периоде: =M8+N8
Внесем формулы в соответствующие
столбцы. Скопируем их на всю таблицу.
Сумму выплат и переплат посчитайте
самостоятельно.
3.
Сравнить переплату при аннуитетной и дифференцированной схеме
погашения кредита.
Аннуитетный платёж:
___________________________
Дифференцированный платёж:
____________________________
4. Вывод
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________