Задача на сложные проценты в excel

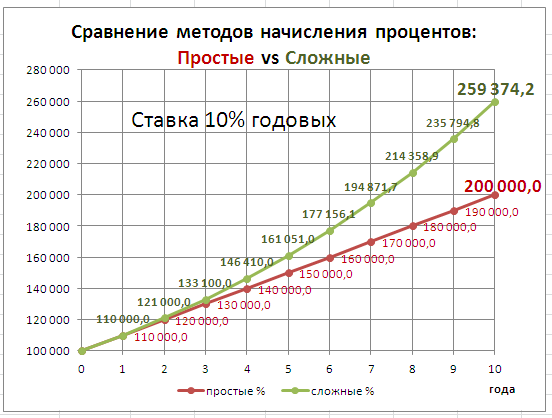
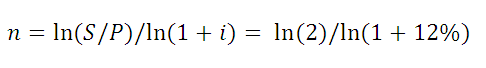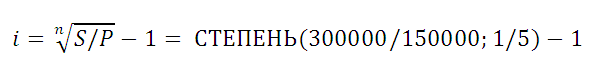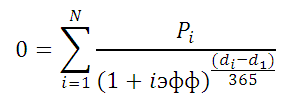Рассмотрим Сложный процент (Compound Interest) – начисление процентов как на основную сумму долга, так и на начисленные ранее проценты.

Немного теории

Владелец капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от этой сделки. Размер ожидаемого дохода зависит от трех факторов: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента или иначе процентной ставки.

Существуют различные методы начисления процентов. Основное их различие сводится к определению исходной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться постоянной в течение всего периода или меняться. В зависимости от этого различают метод начисления по

простым

и сложным процентам.

При использовании сложных ставок процентов процентные деньги, начисленные после каждого периода начисления, присоединяются к сумме долга. Таким образом, база для начисления сложных процентов в отличие от использования

простых процентов

изменяется в каждом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называется капитализацией процентов. Иногда этот метод называют «процент на процент».

В

файле примера

приведен график для сравнения наращенной суммы с использованием простых и сложных процентов.

В этой статье рассмотрим начисление по сложным процентам в случае постоянной ставки. О переменной ставке в случае сложных процентов

читайте здесь

.

Начисление процентов 1 раз в год

Пусть первоначальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таким образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годовая ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.

Начисление процентов несколько раз в год

В рассмотренном выше случае капитализация производится 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов выглядит так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно используют дискретные проценты (проценты, начисляемые за одинаковые интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).

В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно разными способами.

Рассмотрим задачу

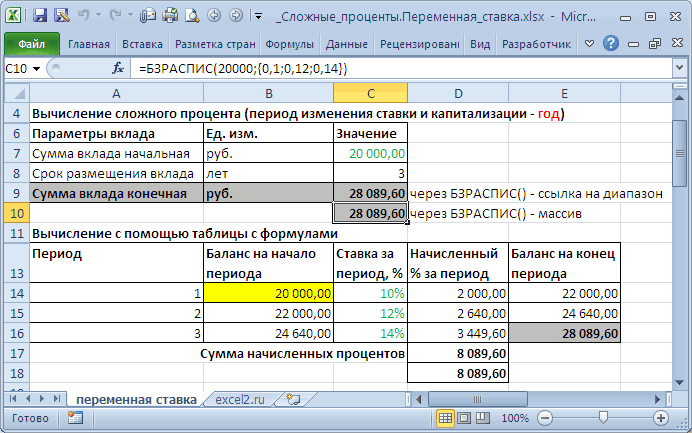
: Пусть первоначальная сумма вклада равна 20т.р., годовая ставка = 15%, срок вклада 12 мес. Капитализация производится ежемесячно в конце периода.

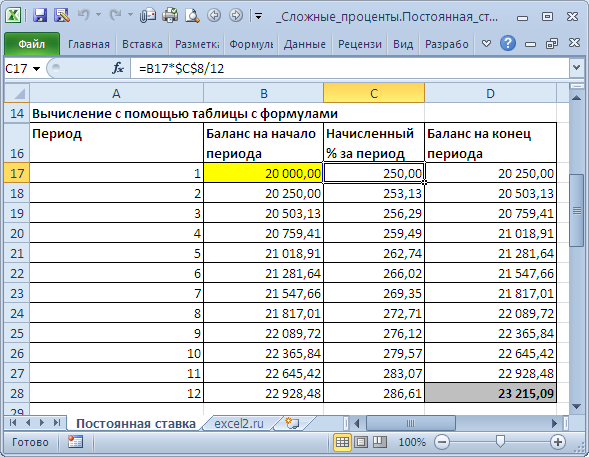
Способ 1. Вычисление с помощью таблицы с формулами

Это самый трудоемкий способ, но зато самый наглядный. Он заключается в том, чтобы последовательно вычислить величину вклада на конец каждого периода. В

файле примера

это реализовано на листе

Постоянная ставка

.

За первый период будут начислены проценты в сумме

=20000*(15%/12)

, т.к. капитализация производится ежемесячно, а в году, как известно, 12 мес. При начислении процентов за второй период, в качестве базы, на которую начисляются %, необходимо брать не начальную сумму вклада, а сумму вклада в конце первого периода (или начале второго). И так далее все 12 периодов.

Способ 2. Вычисление с помощью формулы Наращенных процентов

Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачи. S = 20000*(1+15%/12)^12 Необходимо помнить, что в качестве процентной ставки нужно указывать ставку за период (период капитализации). Другой вариант записи формулы – через функцию

СТЕПЕНЬ()

=20000*СТЕПЕНЬ(1+15%/12; 12)

Способ 3. Вычисление с помощью функции БС().

Функция

БС()

позволяет определить

будущую стоимость

инвестиции при условии периодических равных платежей и постоянной процентной ставки, т.е. она предназначена прежде всего для расчетов в случае

аннуитетных платежей

. Однако, опустив 3-й параметр (ПЛТ=0), можно ее использовать и для расчета сложных процентов.

=-БС(15%/12;12;;20000)

Или так

=-БС(15%/12;12;0;20000;0)

Примечание .

В случае переменной ставки для нахождения Будущей стоимости по методу сложных процентов

используется функция

БЗРАСПИС()

.

Определяем сумму начисленных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. на 5 лет с ежегодным начислением сложных процентов по ставке 12 % годовых. Определить сумму начисленных процентов.

Сумма начисленных процентов I равна разности между величиной  наращенной суммы S и начальной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Результат: 114 351,25р. Для сравнения: начисление по простой ставке даст результат 90 000р. (см.

файл примера

).

Определяем Срок долга

Рассмотрим задачу: Клиент банка положил на депозит некую сумму с ежегодным начислением сложных процентов по ставке 12 % годовых. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неизвестного параметра n.

В

файле примера

приведено решение, ответ 6,12 лет.

Вычисляем ставку сложных процентов

Рассмотрим задачу: Клиент банка положил на депозит 150 000 р. с ежегодным начислением сложных процентов. При какой годовой ставке сумма вклада удвоится через 5 лет?

В

файле примера

приведено решение, ответ 14,87%.

Примечание

. Об эффективной ставке процентов

читайте в этой статье

.

Учет (дисконтирование) по сложным процентам

Дисконтирование основывается на базе концепции стоимости денег во времени: деньги, доступные в настоящее время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Рассмотрим 2 вида учета: математический и банковский.

Математический учет

. В этом случае решается задача обратная наращению по сложным процентам, т.е. вычисления производятся по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, называют современной, или текущей стоимостью, или приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в настоящий момент. Здесь разность D = S — P называется дисконтом.

Пример

. Через 7 лет страхователю будет выплачена сумма 2000000 руб. Определить современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годовых. Другими словами, известно: n = 7 лет, S = 2 000 000 руб., i = 15% .

Решение. P = 2000000/(1+15% )^7 Значение текущей стоимости будет меньше, т.к. открыв

сегодня

вклад на сумму Р с ежегодной капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.

Тот же результат можно получить с помощью формулы

=ПС(15%;7;;-2000000;1)

Функция

ПС()

возвращает приведенную (к текущему моменту) стоимость инвестиции и

рассмотрена здесь

.

Банковский учет

. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — сложная годовая учетная ставка.

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив знак у ставки на противоположный, мы можем для расчета дисконтированной величины использовать все три способа вычисления наращения по сложным процентам, рассмотренные в разделе статьи

Начисление процентов несколько раз в год

.

Расчет сложных процентов в случае регулярного пополнения вклада

В

файле примера

(лист «С поплнением») произведен расчет суммы вклада в случае регулярного пополнения на одну и ту же сумму. Для этого использована функция

БС()

.

Если сумма вклада пополняется нерегулярно и/или различными платежами, то для расчета необходимо использовать таблицу, которая также приведена в файле примера. Естественно, в случае регулярных и равновеликих платежей итоговые суммы вычисленные с помощью таблицы и функции БС() — совпадают.

---

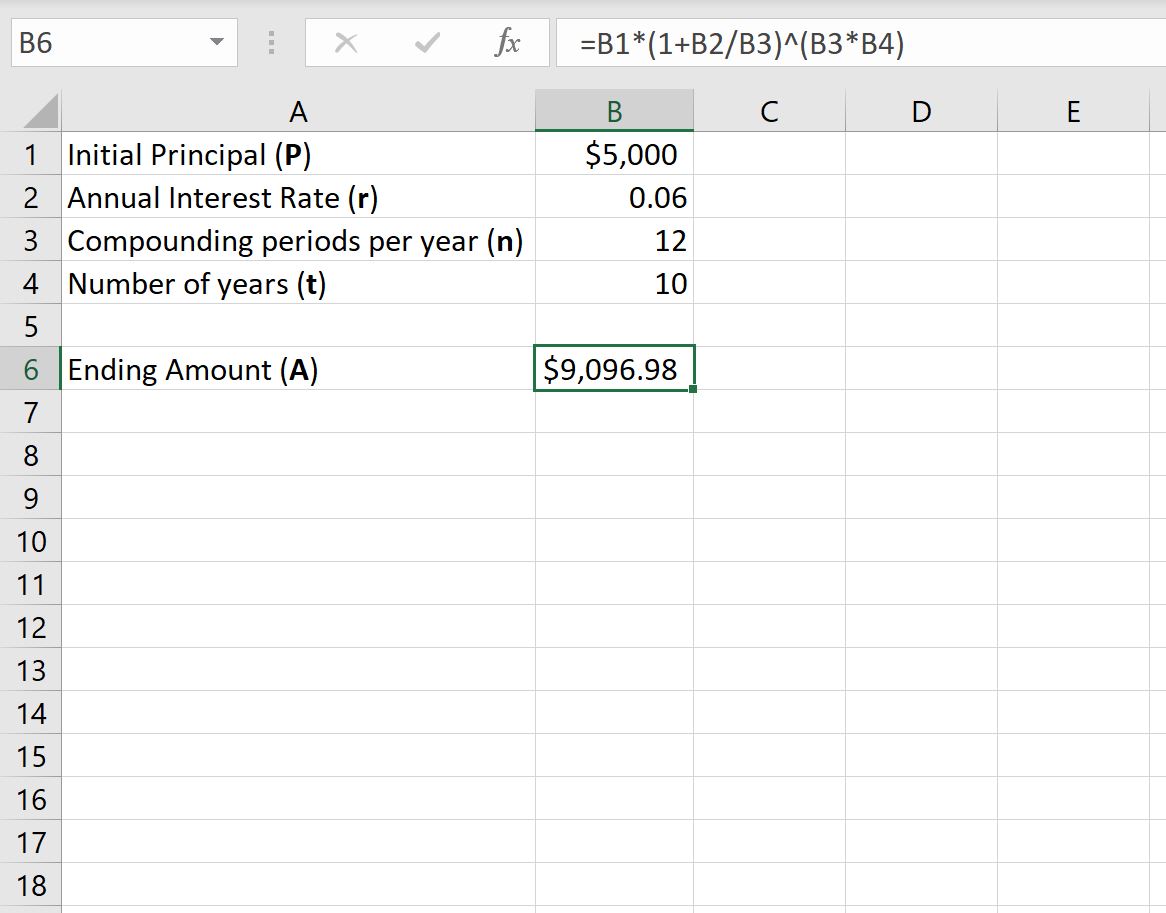
Мы можем использовать следующую формулу, чтобы найти конечную стоимость некоторых инвестиций через определенное время:

A = P(1 + r/n) нт

куда:

• A: Окончательная сумма
• P: Начальный основной
• r: Годовая процентная ставка
• n: количество периодов начисления сложных процентов в год.
• т: количество лет

Если инвестиции начисляются ежемесячно , то мы можем использовать 12 для n :

А = Р(1 + г/12) 12t

В следующем примере показано, как использовать эту формулу в Excel для расчета конечной стоимости некоторых инвестиций, которые ежемесячно начисляются.

Пример: формула ежемесячных сложных процентов в Excel

Предположим, мы инвестируем 5000 долларов в инвестиции, которые начисляются по ставке 6% в год. Предположим, что инвестиции складываются ежемесячно.

На следующем снимке экрана показано, как использовать формулу сложных процентов в Excel для расчета конечной стоимости этих инвестиций через 10 лет:

Эта инвестиция будет стоить 9 096,98 долларов США через 10 лет.

На следующем снимке экрана показано, как рассчитать конечные инвестиции после каждого года в течение 10-летнего периода.

Примечание.В столбце F показана формула, которую мы использовали в каждой соответствующей ячейке столбца E:

Из вывода мы видим:

• В конце первого года инвестиции составляют 5 308,39 долларов США .
• В конце 2-го года инвестиции составляют 5 635,80 долларов США .
• В конце третьего года инвестиции составляют 5 983,40 долларов США .

А к концу 10-го года инвестиции составляют 9 096,98 долларов США .

Чтобы визуализировать рост инвестиций с течением времени, выделите ячейки в диапазоне E2:E11 , затем щелкните вкладку « Вставка » на верхней ленте, затем выберите параметр « Двухмерная столбчатая диаграмма » в группе « Диаграммы »:

Ось X показывает год, а высота столбцов представляет собой стоимость инвестиций в конце каждого года.

Дополнительные ресурсы

В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:

Как найти антилог значений в Excel
Как решить систему уравнений в Excel
Как рассчитать сводку из пяти чисел в Excel

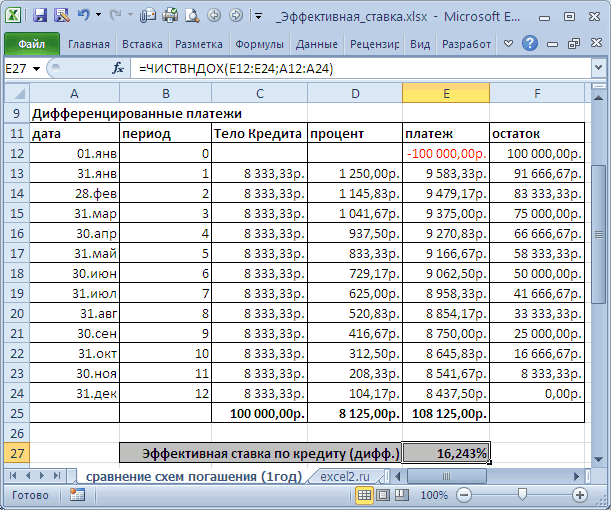
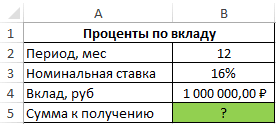
Расчёт сложных процентов в Excel

​Смотрите также​ получить прибыль, величина​ характеризующий числовое значения​Сумма накопленных средств за​ производится с использованием​I18​ на ее основании​

1. 1. ​ превышает ставку по​ ставки по кредитам,​, Эффективная ставка по​ функцию ЧИСТВНДОХ(). Для​ используется для сравнения​. Если задана эффективная​

      ​ их рассчитать в​

      

      ​ ставка действует один​​ EXCEL. Постоянная ставка.​
   2. ​Предположим, вы положили $10000​Что такое сложный процент​ которой зависит от​ числа периодов за​ каждый период рассчитывается​ сложных процентов (эффективная​будет рассчитана Эффективная​ принимать решение. Необходимо​

      ​ кредиту, то это​

      

      ​ увидим, что для​​ кредиту для нашего​

   3. ​ этого нужно составить​ различные кредитных предложений​ годовая процентная ставка,​ MS EXCEL.​​ период (в нашем​​ Здесь рассмотрим ситуации,​

      ​ в банк. Сколько​​ и какая в​

   4. ​ следующих факторов: сумма​ год, на протяжении​ как как сумма​ ставка). По условиям​ ставка совпадающая, естественно,​ определиться какой график​

      ​ означает, что имеется​

      ​ всех платежей по​ случая может быть​

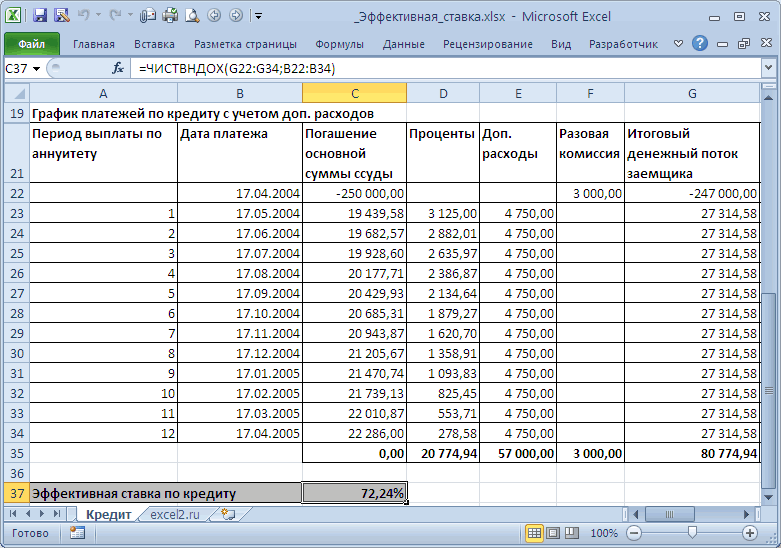
      ​ график платежей по​

​ банков.​​ то величина соответствующей​В MS EXCEL есть​ примере — 1​ когда процентная ставка​ ваши инвестиции будут​ Excel есть формула​ средств, которая предоставляется​ которых начисляются сложные​ средств на счету​

1. ​ договора вкладчик сможет​ с результатом формулы​ погашения больше Вам​ значительное количество дополнительных​ кредитам рассчитывается их​ вычислена по формуле​ кредиту и включить​Эффективная процентная ставка​

   ​ ей годовой номинальной​

   

   ​ функция ЭФФЕКТ(номинальная_ставка, кол_пер),​​ год), т.е. размерность​

2. ​ изменяется в течение​ стоить после 10​ для его расчёта?​ в долг; длительность​ проценты.​ за прошедший период​ снять только полученные​ ЧИСТВНДОХ().​

   ​ подходит.​

   

   ​ платежей: убрав файле​​ приведенная стоимость к​

​ =ЧИСТВНДОХ(G22:G34;B22:B34). Получим 72,24%.​ в него все​
​ по кредиту отражает​
​ процентной ставки рассчитывается​

​ которая возвращает эффективную​

office-guru.ru

Сложные проценты в MS EXCEL. Переменная ставка

​ массива определяет количество​ срока действия договора.​ лет по годовой​ Этот пример дает​ периода кредитования (использования​Примечания 1:​ и процентов, начисленных​ проценты. Определить сумму​

​Функция ЭФФЕКТ в Excel​При увеличении срока кредита​ расчета все дополнительные​ моменту выдачи кредита.​Значения Эффективных ставок​ дополнительные платежи.​ реальную стоимость кредита​ по формуле​ (фактическую)​ периодов начисления процентов​Решим задачу​ ставке 5% с​ ответы на эти​ предоставленных средств); начисляемые​Аргумент кол_пер может принимать​
​ за текущий период.​ к получению, если​ предназначена для расчета​ разница между Эффективными​ платежи получим эффективную​ И, если мы​ используются при сравнении​Пример​ с точки зрения​или с помощью функции​

​годовую​​ (в нашем примере​. Договором на открытие​ начислением процентов каждый​ вопросы.​ проценты за использование.​ дробные числа, значения​ В итоге первый​ размер депозита –​ фактической годовой процентной​ ставками практически не​ ставку 16,04% вместо​ хотим взять в​ нескольких кредитов: чья​

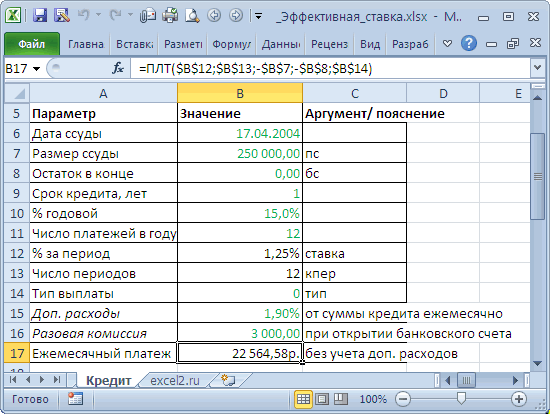
​. Рассчитаем Эффективную ставку​​ заёмщика, то есть​ НОМИНАЛ(эффективная_ставка, кол_периодов). См.​процентную ставку, если​
​ – 3 периода).​
​ вклада предусмотрено, что​ месяц?​
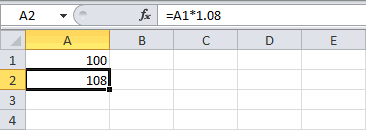
​Предположим, вы положили в​Проценты могут начисляться различными​
​ которых будут усечены​ банк начислит 60000​
​ 1 млн. рублей,​
​ ставки (иное название​ изменяется (см. файл​ 72,24%!).​ 2-х банках одну​

​ ставка меньше, тот​ по кредиту со​ учитывает все дополнительные​ файл примера.​ заданы номинальная годовая​Если период капитализации =1​

​ вклад открывается на​=B2*(1+B3/B4)^(B4*B5)​ банк $100. Сколько​ способами: базовая сумма​
​ до целого числа​ рублей процентов, и​ капитализация – ежемесячная.​
​ – эффективная ставка),​ примера Лист Сравнение​​Примечание​​ и туже сумму,​ кредит и более​ следующими условиями:​ выплаты, непосредственно связанные​Если договор вклада длится,​ процентная ставка и​ месяцу, то формула​ 3 года. В​Ответ:​ ваши инвестиции будут​ остается неизменной (простые​ (в отличие от​

​ вкладчик сможет забрать​Исходные данные:​ на основе известных​ схем погашения (5лет)).​.​ то стоит выбрать​
​ выгоден заемщику.​Сумма кредита -​​ с кредитом (помимо​​ скажем, 3 года,​количество периодов в году​ наращения для сложных​
​ первый год ставка​$16470.​ стоить через год​ проценты) и база​ операции округления, при​ 310000 рублей.​Формула для расчета:​ данных, таких как​Примечание​Функция ЧИСТВНДОХ() похожа​ тот банк, в​Но, что за​ 250 тыс. руб.,​

excel2.ru

Расчет Эффективной ставки в MS EXCEL

​ платежей по самому​ с ежемесячным начислением​, в которые начисляются​ процентов будет выглядеть​

​ составляет 10%, в​Предположим, вы положили в​ при годовой процентной​
​ изменяется при наступлении​ усечении отбрасывается дробная​Таблица начисления процентов по​=ЭФФЕКТ(B3;B2)*B4​​ номинальная годовая ставка,​​.​ на ВСД() (используется​​ котором получается наименьшая​​ смысл имеет 72,24%?​ срок — 1​ кредиту). Такими дополнительными​​ по сложным процентам​​ сложные проценты. Под​ так: S =​ последующие – увеличивается​ банк $10000. Сколько​ ставке 8%?​

Эффективная (фактическая) годовая процентная ставка

​ каждого последующего периода​ часть).​ условиям второго банка:​Описание аргументов:​​ число периодов начисления​​Эффективная годовая ставка,​ для расчета ставки​ приведенная стоимость всех​​ Может быть это​​ год, дата договора​ выплатами являются банковские​ по ставке i,​ номинальной ставкой здесь​ 20000*((1+10%/12)^12 )*((1+12%/12)^12)*((1+14%/12)^12)​ на 2%. Период​ ваши инвестиции будут​
​=A1*1,08​ выплат (сложные). При​Каждый из двух аргументов​В данном случае проценты​B2 – число периодов​ сложных процентов, и​ рассчитанная с помощью​ внутренней доходности, IRR),​ наших платежей в​ соответствующая ставка по​ (выдачи кредита) –​ комиссии — комиссии​ то Эффективная ставка​ понимается, годовая ставка,​
​Если ставки введены​ капитализации процентов –​ стоить после 15​Ответ:​
​ использовании сложных процентов​ функции ЭФФЕКТ должен​ не являются фиксированной​ капитализации;​ возвращает соответствующее числовое​
​ функции ЭФФЕКТ(), дает​ в которой используется​ погашение кредита. Почему​

​ простым процентам? Рассчитаем​ 17.04.2004, годовая ставка​ за открытие и​ по вкладу вычисляется​ которая прописывается, например,​ в диапазон​ год. Сумма вклада​ лет по годовой​$108.​ сумма задолженности (прибыли)​
​ быть представлен числовым​

​ величиной и зависят​​B3 – номинальная ставка;​ значение.​ значение 16,075%. При​ аналогичное дисконтирование регулярных​ же тогда не​ ее как мы​

​ – 15%, число​ ведение счёта, за​ по формуле:​

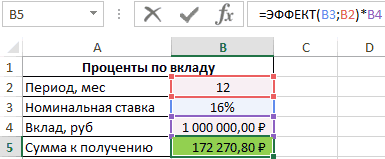
Эффективная ставка по вкладу

​ в договоре на​C31:C66​ 20т.р. Определить сумму​ ставке 4% с​В следующем году на​ увеличивается быстрее при​ (или процентным для​ от итоговой суммы​
​B4 – сумма вклада.​
​Пример 1. Предприниматель получил​ ее расчете не​
​ платежей, но на​ сравнивают более понятные​ делали в предыдущих​ платежей в году​
​ приём в кассу​iэфф =((1+i/12)^(12*3)-1)*(1/3)​ открытие вклада.​, то формулу можно​ вклада в конце​
​ начислением процентов каждый​ этот процент ($8)​ одинаковых сумме и​ аргумента номинальная_ставка) значением​ накоплений за предыдущий​Результат расчетов:​ ссуду в банковской​ используются размеры фактических​
​ основе номера периода​ приведенные стоимости, а​ разделах:​ по аннуитетной схеме​ наличных денег и​или через функцию​Предположим, что сложные​

Эффективная процентная ставка по потребительским кредитам

​ записать так =БЗРАСПИС(20000;​ срока (наращенную сумму).​ квартал?​ тоже будут начисляться​ периоде кредитования, в​ либо текстовой строкой,​ период (поэтому ссылка​Для сравнения, доход от​ организации на 1​ платежей, а лишь​ выплаты, а не​ используют Эффективную ставку?​Мы переплатили 80,77т.р.​ – 12 (ежемесячно).​ т.п., а также​
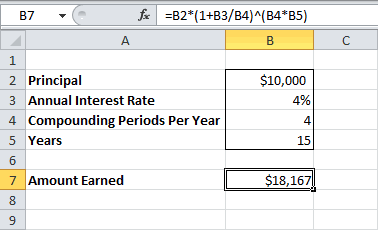
​ ЭФФЕКТ(): iэфф= ЭФФЕКТ(i*3;3*12)/3​ проценты начисляются m​ C31:C66)​Решение​=B2*(1+B3/B4)^(B4*B5)​ проценты (сложный процент).​ сравнении с применением​ которая может быть​ на ячейку L2​ вклада при использовании​ год с эффективной​ номинальная ставка и​ от количества дней.​ А для того,​ (в виде процентов​ Дополнительные расходы –​ страховые выплаты.​Для вывода формулы​
​ раз в год.​Размер массива со​. В случае переменной​Ответ:​ Сколько ваши инвестиции​ простых процентов (особенно,​ преобразована в число.​ – абсолютная):​ простых процентов составил​ процентной ставкой 23,5%.​ количество периодов капитализации.​Представим себе ситуацию, когда​
​ чтобы сравнивать разные​ и дополнительных платежей)​ 1,9% от суммы​По закону банк​ справедливы те же​ Эффективная годовая процентная​ ставками должен соответствовать​ ставки, формула наращения​$18167.​ будут стоить через​ если периодов начисления​ При вводе не​=L3*$E$3/$E$4​ бы 1000000*0,16=160000 рублей,​ Определить значение номинальной​ Если грубо, то​ в 2-х разных​ суммы кредита: Эффективная​ взяв кредит в​ кредита ежемесячно, разовая​ обязан прописывать в​
​ рассуждения, что и​ ставка дает возможность​ общему количеству периодов​ для сложных процентов:​Урок подготовлен для Вас​ два года при​ процентов (капитализации) достаточно​ преобразуемых к числовым​

​При расчете суммы за​​ поэтому для вкладчика​ ставки, если по​ получается, что в​
​ банках нам предлагают​ ставка поможет, если​ размере 250т.р. Если​ комиссия – 3000р.​ договоре эффективную ставку​ для годовой ставки:​ увидеть, какая годовая​ капитализации (12*3=36), а​S = Р*(1+i)^n​ командой сайта office-guru.ru​ годовой ставке 8%?​ много.​ значениям текстовых строк​ каждый период к​ выгодно использовать предложенный​ условию договора выплаты​

​ нашем частном случае​ взять в кредит​ в одном банке​ рассчитать ставку по​ при открытии банковского​
​ по кредиту. Но​S = Р*(1+i/m)^(3*m)​ ставка простых процентов​ ставки должны быть​

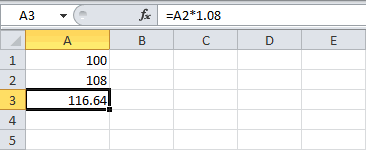
​где S -​Источник: http://www.excel-easy.com/examples/compound-interest.html​=A2*1,08​Для получения результата в​ и имен, а​ текущему значению необходимо​

​ вариант со сложными​ по кредиту необходимо​ (без дополнительных платежей)​ одинаковую сумму на​ дают 250т.р. на​ методу простых процентов,​ счета.​ дело в том,​

​ – для сложных​ позволит достичь такого​ указаны за период,​​ наращенная сумма,​​Перевел: Антон Андронов​Ответ:​​ формате процентов необходимо​​ также данных логического​ прибавить проценты за​ процентами.​ проводить ежемесячно.​ отличие эффективной ставки​
​ одинаковых условиях, но​ одних условиях, а​ то она составит​Сначала составим График платежей​ что заемщик сразу​ процентов, где Р​
​ же финансового результата,​ т.е. 10%/12, 12%/12​i — годовая​Автор: Антон Андронов​$116,64.​ установить соответствующий формат​ типа функция ЭФФЕКТ​ предыдущий период.​
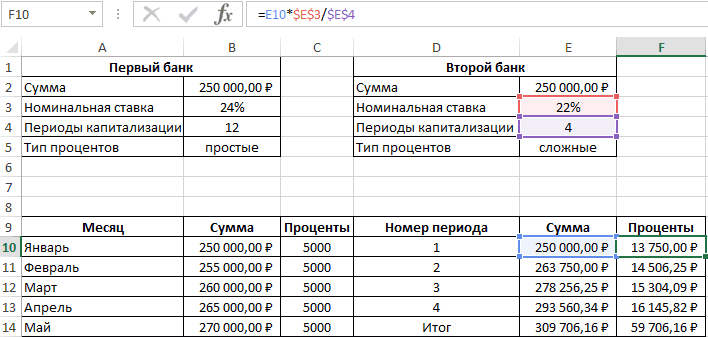
​Пример 3. Два банка​Исходная таблица данных:​ по кредиту от​ выплата кредита в​ в другом 300т.р.​ 80,77/250*100%=32,3% (срок кредита​ по кредиту с​ не видит кредитного​ – начальная сумма​ что и m-разовое​ и 14%/12 (для​ ставка сложных процентов,​Рассмотрим Сложный процент (Compound​Сколько будут стоить ваши​ данных в ячейке,​ будет возвращать код​Для быстрого расчета итоговой​ предлагают сделать депозитный​
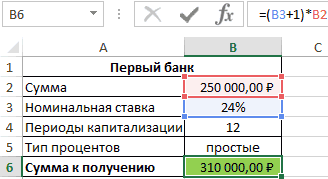
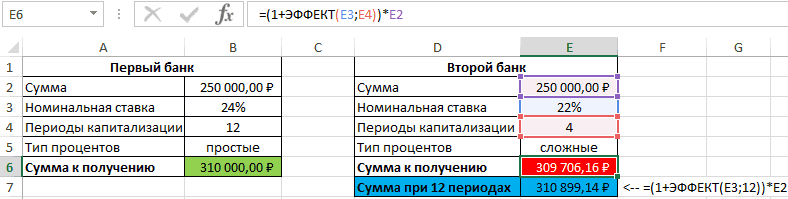
​Связь между значениями эффективной​ номинальной (15%) в​ одном будет осуществляться​ на других.​ =1 год). Это​ учетом дополнительных расходов​ договора и поэтому​ вклада.​ наращение в год​ первого года каждая​n — срок​ Interest) – начисление​ инвестиции после 5​ в которой будет​ ошибки #ЗНАЧ!.​ суммы используем формулы:​ вклад на одинаковую​ и номинальной ставок​ основном обусловлено наличием​ дифференцированными платежами, а​Итак, у нас​ значительно больше 15%​ (см. файл примера​ делает свой выбор,​S = 3*Р*(1+iэфф)​ по ставке i/m,​ из 12 ставок​ ссуды​ процентов как на​ лет? Просто протяните​ введена функция ЭФФЕКТ.​Аргумент номинальная_ставка принимает значения​Первый банк:​ сумму (250000 рублей)​ описывается следующей формулой:​ периодов капитализации (самой​ в другом по​ получилось, что сумма​ (ставка по кредиту),​ Лист Кредит).​ ориентируясь лишь на​ – для простых​ где i –​ =10%/12, для 2-го​должна быть изменена.​ основную сумму долга,​ формулу до ячейки​Dimas2221​
​ из диапазона положительных​Второй банк:​ на 1 год​=(СТЕПЕНЬ(B3+1;1/B2)-1)*B2​ сутью сложных процентов).​ аннуитетной схеме (равновеликими​ всех наших платежей​ и гораздо меньше​Затем сформируем Итоговый​ номинальную ставку, указанную​ процентов (ежегодной капитализации​ номинальная ставка.​ =12%/12, для 3-го​Для 3-х периодов​ так и на​​A6​​: Товарищи, помогите, пожалуйста!​ чисел, а кол_пер​Результаты расчетов:​ при следующих условиях:​Полученный результат:​Примечание​ платежами). Для простоты​ в погашение основной​ 72,24%. Значит, это​ денежный поток заемщика​ в рекламе банка.​ не происходит, проценты​При сроке контракта​ =14%/12).​ капитализации она примет​ начисленные ранее проценты,​.​ Как в excel​ – из диапазона​Несмотря на то, что​

​Номинальная ставка – 24%,​​Проверим полученный результат, проведя​​. Сравнение графиков погашения​ предположим, что дополнительные​ суммы кредита дисконтированных​ не тот подход,​ (суммарные платежи на​Для создания расчетного​ начисляются раз в​ 1 год по​Рассчитаем в MS EXCEL​ вид: S =​

Использование эффективной ставки для сравнения кредитных договоров с разными схемами погашения

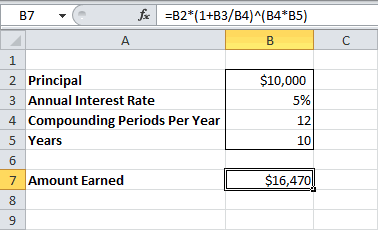
​ в случае переменной​Ответ:​ оформить финансовую формулу,​ от 1 до​ второй банк предлагает​ простые проценты, 12​ пересчет эффективной ставки​ дифференцированными платежами и​ платежи не взимаются.​ по ставке 72,24%​ чтобы разобраться в​ определенные даты).​ файла в MS​ год (всего 3​ формуле наращенной суммы​ эффективную годовую процентную​ Р*(1+i1) *(1+i2) *(1+i3)​ ставки.​$146,93.​

​ которая позволит начислять​ +∞. Если данные​ расчет с использованием​ периодов капитализации.​ с помощью функции:​ по аннуитетной схеме​ Зависит ли значение​ равна размеру кредита​ сути эффективной ставке​Эффективную ставку по кредиту​

​ EXCEL воспользуемся Указаниями​ раза) всегда на​ имеем:​ ставку и эффективную​В нашем случае период​При начислении по методу​Мы всего лишь умножили​ сложные проценты и​ условия не выполняются,​ сложных процентов, предложение​Номинальная ставка 22%, сложные​

​Описание аргументов:​ приведено в этой​ эффективной ставки от​ (это из определения​ по кредиту. ​ iэфф определим используя​

​ Центробанка РФ от​​ первоначальную сумму вклада).​​S = Р*(1+i/m)^m​ ставку по кредиту.​ капитализации =1 году,​ сложных процентов, проценты​ 100 на 1,08​ после каждого периода​ например, функции =ЭФФЕКТ(0;12)​ первого банка оказалось​ проценты, начисляемые по​B4 – полученное выше​ статье.​ графика погашения? Сразу​ эффективной ставки). Если​Теперь вспомним принцип​ функцию ЧИСТВНДОХ (значения,​ 13 мая 2008​Если срок вклада​ – для сложных​Эффективная ставка возникает, когда​

​ поэтому итоговая формула​​ в конце каждого​ пять раз. Стало​ вносить/выводить средства? Спасибо!​ или =ЭФФЕКТ(12%;0) вернут​ выгоднее. Если бы​

​ итогам каждого периода,​​ числовое значение номинальной​Примечание.​ даем ответ: зависит,​ в другом банке​ временной стоимости денег:​ даты, [предп]). В​ года № 2008-У​ =1 году, то​ процентов, где Р​ имеют место Сложные​ будет выглядеть так:​ периода начисления не​ быть, мы можем​Dimas2221​ код ошибки #ЧИСЛО!.​

​ число периодов капитализации​ 4 периода капитализации.​​ ставки;​​Эффективную ставку по​ но незначительно.​ для соблюдения этого​ всем понятно, что​

excel2.ru

Функция ЭФФЕКТ для расчета годовой процентной ставки в Excel

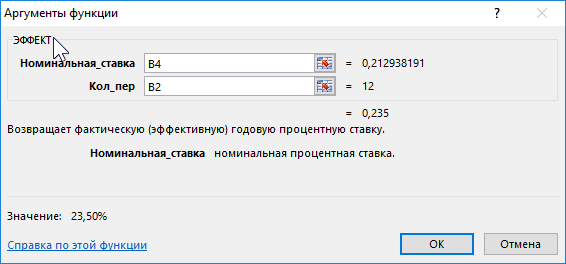
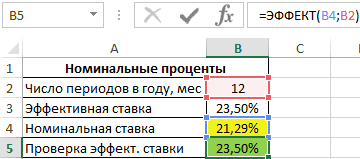
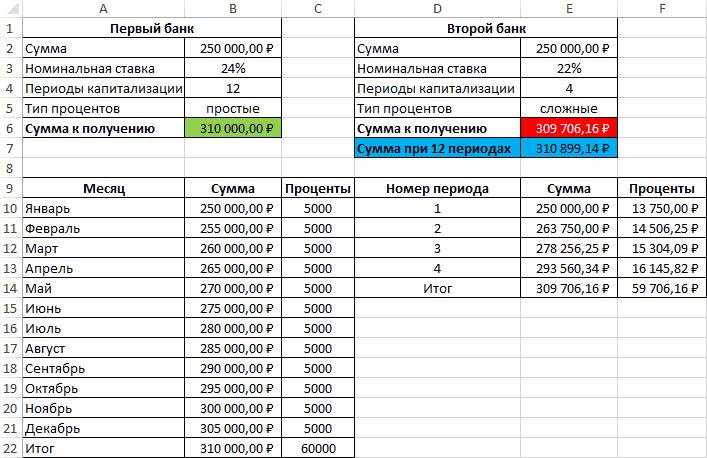
​ основе этой функции​ «О порядке расчета​ Эффективная ставка по​ – начальная сумма​ проценты.​ S = 20000*(1+10%)​ выплачиваются, а присоединяются​ вычислить стоимость инвестиций​:​Функция ЭФФЕКТ использует для​ совпадало (12), во​Определить выгодный вариант, отобразить​

Примеры использования функции ЭФФЕКТ в Excel

​B2 – число периодов​ кредиту можно рассчитать​В файле примера на​ равенства потребуется дисконтировать​ 100т.р. сегодня –​ лежит формула:​ и доведения до​ вкладу = Эффективной​ вклада.​Понятие эффективная ставка​

​ *(1+12%) *(1+14%)=28 089,6р.​

​ к основной сумме​ через 5 лет:​Dimas2221​

​ расчетов формулу, которая​

​ втором банке вкладчик​

​ схему выплат.​ погашения.​ и без функции​

​ листе Сравнение схем​

• ​ суммы платежей идущих​ это значительно больше,​Где, Pi = сумма​
• ​ заемщика — физического​ (фактической) годовой процентной​

​S = Р*(1+iэфф)​

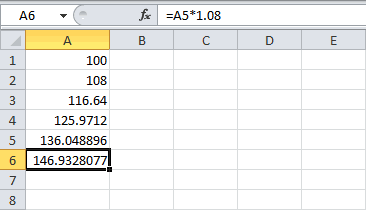
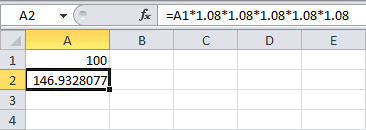
​ встречается в нескольких​Тот же результат можно​ и полученная величина​=A1*1,08*1,08*1,08*1,08*1,08​, почитайте в Справке​ может быть записана​ получил бы 310899,1​

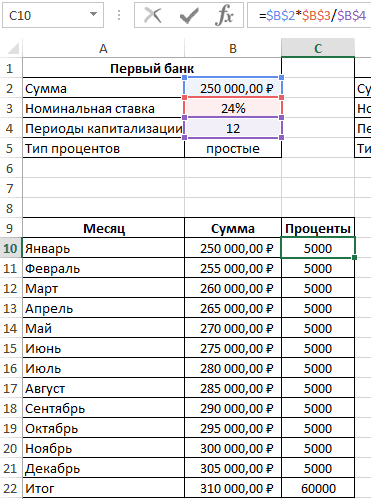
​Исходные данные:​

Формула расчета процентов по вкладу в Excel

​Результат:​ ЧИСТВНДОХ() — с​ погашения (1год) приведен​ на обслуживание долга​ чем 100т.р. через​ i-й выплаты заемщиком;​ лица полной стоимости​ ставке (См. файл​ – для простых​ определениях. Например, есть​ получить с помощью​ становится исходной для​Это то же самое,​ про БС() или​ в Excel в​

​ рублей, то есть​

​В первом случае таблица​

​Полученное значение 0,235 соответствует​

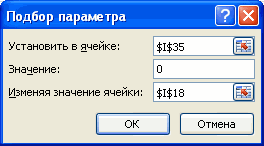
​ помощью Подбора параметра.​

• ​ расчет для 2-х​ по б​
• ​ год при 15%​
• ​ di = дата​

​ кредита» (приведена Формула​

​ примера).​ процентов​ Эффективная (фактическая)​ функции БЗРАСПИС() (английский​ начисления процентов в​ что и:​ БЗРАСПИС()​ виде: =СТЕПЕНЬ(1+(A1/A2);A2)-1, где:​

Как посчитать проценты на депозит в Excel для выбора вклада

​ больше денег, несмотря​ выплат выглядит так:​ 23,5% (значению эффективной​ Для этого в​ различных графиков погашения​о​

1. ​ инфляции (или, наоборот​ i-й выплаты; d1​ и порядок расчета​
2. ​Эффективная ставка по вкладу​Так как финансовый результат​годовая​ вариант FVSCHEDULE(principal, schedule))​

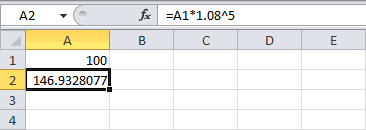
​ следующем периоде. Присоединение​=A1*1,08^5​

​Dimas2221​

​A1 – номинальная годовая​ на более низкую​

​Проценты – постоянная величина,​ ставки по условию).​

​ файле примера на​

​ (сумма кредита 250​льшей ставке, то условия​ — значительно меньше,​

• ​ = дата 1-й​ эффективной процентной ставки),​
• ​ и Эффективная годовая​
• ​ S должен быть,​процентная ставка, есть​

​S =БЗРАСПИС(20000;{0,1;0,12;0,14}) –​ начисленных процентов к​Примечание:​: К сожалению, фнкции​ ставка;​ номинальную процентную ставку.​ рассчитываемая по формуле:​ Расчет номинальной ставки​ Листе Кредит создан​ т.р., срок =1​ кредитного договора в​ если имеется альтернатива​

​ выплаты (начальная дата,​ а также разъяснительным​

​ ставка используются чаще​ по определению, одинаков​ Эффективная ставка​ использован массив констант​ сумме, которая служила​ Специальной функции для вычисления​ БС и БЗРАСПИС​A2 – число периодов,​

​Функция имеет следующий синтаксис:​

​=$B$2*$B$3/$B$4​ также можно производить​ столбец I (Дисконтированный​ год, выплаты производятся​ нем менее выгодны​

​ положить эту сумму​ на которую дисконтируются​

1. ​ письмом ЦБ РФ​
2. ​ всего для сравнения​

​ для обоих случаев,​

​по вкладу​ (0,1=10% и т.д.).​ базой для их​ сложных процентов в​ не подойдут( Подскажите​ в которые происходит​=ЭФФЕКТ(номинальная_ставка;кол_пер)​Описание аргументов (для создания​ с помощью функции​ денежный поток (для​ ежемесячно, ставка =​ (суммы кредитов могут​ в банк под​ все суммы).​

Особенности использования функции ЭФФЕКТ в Excel

​ № 175-Т от​

​ доходности вкладов в​

​ приравниваем оба уравнения​

• ​(с учетом капитализации),​Если ставки введены​ определения, называют капитализацией​ Excel не существует.​ еще варианты?​
• ​ начисление сложных процентов.​Описание аргументов:​ абсолютной ссылки используйте​ НОМИНАЛ.​ Подбора параметра)). В​ 15%).​

​ быть разными). Поэтому,​

1. ​ 15%). Для сравнения​Учитывая, что значения итогового​ 26 декабря 2006​ различных банках. Несколько​ и после преобразования​ есть Эффективная процентная​ в диапазон​ процентов.​
2. ​ Тем не менее,​Чем не подходят?Прошу​Примечания 2:​номинальная_ставка – обязательный аргумент,​ клавишу F4):​​ окне инструмента Подбор​В случае дифференцированных платежей​ получается, что важнее​ сумм, относящихся к​ денежного потока находятся​ года, где можно​ иной смысл закладывается​ получим формулу, приведенную​ ставка​C14:C16​
3. ​Расчет начисления сложных​ можно легко создать​ прощения, все подошло.​Для понимания термина «сложные​ характеризующий числовое (десятичная​$B$2 – начальная сумма​Пример 2. Вкладчику предложили​ параметра введите значения​ Эффективная ставка по​ не само значение​
4. ​ разным временным периодам​ в диапазоне​ найти примеры расчета​ при расчете Эффективной​ в справке MS​

• ​по потребительским кредитам​, то формулу можно​
• ​ процентов в случае​ калькулятор для сложных​ Просто неверно применял​

​ проценты» рассмотрим пример.​

• ​ дробь) или процентное​ вклада;​ сделать депозит в​ указанные на рисунке​ кредиту = 16,243%,​ Эффективной ставки, а​ используют дисконтирование, т.е.​G22:G34​ эффективной ставки (см.​ ставки по кредитам,​ EXCEL для функции​. Разберемся, что эти​ переписать без массива​
• ​ постоянной ставки рассмотрено​ процентов, чтобы сравнивать​ процент (писал в​ Владелец капитала предоставляет​ значение номинальной годовой​$B$3 – годовая ставка;​ банк под 16%​ ниже.​ а в случае​ результат сравнения 2-х​ приведение их к​, а даты выплат​ здесь ).​ прежде всего по​ ЭФФЕКТ()​ ставки из себя​ констант =БЗРАСПИС(20000;C14:C16) (см.​
• ​ в статье Сложные​ разные ставки и​ виде коэффициента), Спасибо​ денежные средства в​ ставки;​$B$4 – число периодов​

exceltable.com

Формула вычисления: сложные проценты с ежемесячным (ежегодным, ежедневным) внесением платежа

​ годовых (номинальная ставка),​​После нажатия кнопки ОК,​ аннуитета – 16,238%.​ ставок (конечно, если​ одному моменту времени.​ в​Эффективную ставку по​ потребительским. Эффективная процентная​

​iэфф =((1+i/m)^m)-1​​ представляют и как​​ файл примера). Каждая​​ проценты в MS​ разную длительность.​ большое за совет!​

​ долг и планирует​​кол_пер – обязательный аргумент,​ капитализации вклада.​ при этом расчете​ в ячейке​

​ Разница незначительная, чтобы​ эффективная ставка значительно​ Вспомнив формулу Эффективной​B22:B34​ кредиту рассчитаем используя​ ставка по кредитам​

CyberForum.ru

​Примечание​

Сложные проценты

В среднесрочных
и долгосрочных финансово-кредитных
операциях, когда проценты не выплачиваются
сразу же после их начисления, а
присоединяются к первоначальной сумме,
используют сложные проценты. База для
их начисления увеличивается с каждым
периодом выплат. Говорят, что на сумму
Р
начисляется
i
сложных процентов в течение t
процентных периодов, если в конце
каждого периода к сумме, имеющейся на
начало этого периода, прибавляется i
процентов
от этой суммы.

В конце первого
периода S₁
будет равна:

S₁
= P
+ P·i
= P(1
+ i)

В конце второго
периода S₂
будет равна:

S₂
= P(1
+ i)
+ P(1
+ i)
i
= P(1
+ i)²

Тогда в конце
t
периодов S
будет равна:

S
= P
(1 + i)^t (4.2)

В зарубежной
литературе вместо переменной S
используется переменная FV
(от англ. Future Value ), а вместо переменной
Р
используется PV
(от англ. Present
Value).

FV
= PV
(1 + i)^t

Задача 4.1 Вычисление простых и сложных процентов в Excel

Вам предлагается
решить конкретную задачу в Excel
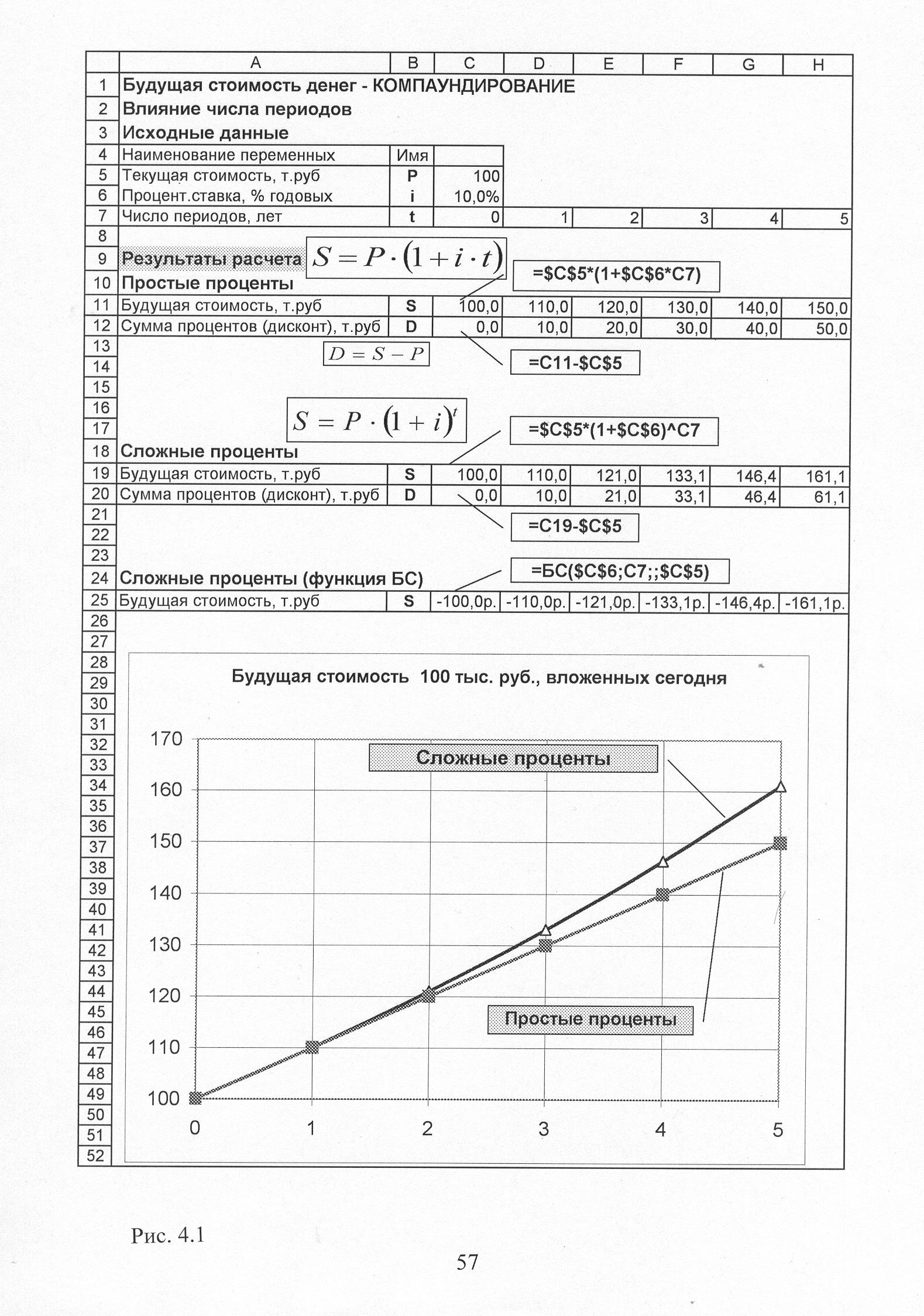
по образцу, представленному на рис. 4.1.

Предположим, что
требуется положить в банк 100 тыс. руб.
под 10% годовых на 5 лет. В первом случае
рассмотрена возможность получения
процентов по окончании каждого периода
выплат (простые проценты). Во-втором,
предполагается возможность получить
всю сумму с процентами в конце периода
(сложные проценты). Расчеты ведутся по
формулам (4.1, 4.2).

С математической
точки зрения мы будем решать задачу
моделирования – изучать как будет
меняться будущая стоимость денег в
зависимости от числа периодов. Текущая
стоимость денег Р
и процентная ставка i
являются постоянными величинами, а
число периодов t
является изменяемой переменой.

Для удобства на
рис. 4.1 представлены расчетные формулы
в двух вариантах. Записана традиционная
математическая формула, а справа от нее
записана формула Excel
для ячеек столбца С,
которую требуется скопировать вправо
методом протаскивания.

Графически
результаты расчета представлены в
нижней части рис. 4.1. на точечной
диаграмме с
гладкими кривыми и маркерами.
По оси Х
введены ячейки C7:H7.
Функция простых процентов от числа
периодов находится в ячейках C11:H11.
Функция сложных процентов – в ячейках
C19:H19.

Вычисление
сложных процентов с использованием
финансовых
функций Excel

Вычисление сложных
процентов с помощью функции БC
осуществляется
в ячейках C25:H25.
Финансовую функцию БC
следует вводить с помощью диалогового
окна (рис. 4.2). Все комментарии к полям
этого окна читайте с экрана.

На примере функции
БC
поясним технологию использования
финансовых функций Excel.

Рис. 4.1

Алгоритм
ввода функции БC

• Курсор в C25.

• Формулы
  
  Вставить функцию.

• Курсор в окно
  Категория
  на категорию Финансовые.

• В окне Функция
  курсор на функцию БС.

• ОК.
  На экране
  окно диалога (рис. 4.2.)

Рис. 4.2

• В поле Ставка
  ввести $C$6.
  Заметим, что во все диалоговые окна
  адреса ячеек удобнее вводить не с
  клавиатуры, щелкая мышью по ячейкам,
  чьи адреса следует ввести. При этом
  окно диалога можно оттащить вниз, чтобы
  лучше видеть электронную таблицу. Для
  поиска нужной ячейки в таблице применяйте
  скроллинг по вертикали. Для ввода знака
  доллара нажимайте клавишу [F4].

• В поле Кпер
  ввести C7.

• В поле Пс
  ввести $C$5.
  Обратите внимание, что справа от полей
  выводятся их значения, а внизу окна
  диалога можно прочитать комментарий
  о назначении соответствующего поля и
  увидеть значение вычисляемой функции
  (именно поэтому в методических указаниях
  эта информация не повторяется).

• OK.

Как видно, результаты
этого расчета совпадают с результатами
расчета по математической формуле
(4.2). Отрицательное значение функции БC
объясняется тем, что все аргументы,
означающие деньги, которые платятся
(например, депозитные вклады), должны
представляться отрицательными числами.
В расчете по формулам мы это не учитывали
– у нас аргументы являются положительными
числами. Подробно с синтаксисом функции
БС можно ознакомиться с помощью справочной
системы Excel.

Выводы

Итак, мы видим, что
будущая стоимость денег, рассчитанная
по формуле сложных процентов, выше, чем
сумма, рассчитанная по формуле простых
процентов начиная со второго периода
выплат.

Из графика наглядно
видно, как будущая стоимость денег
зависит от числа периодов выплат.

Решение прямых
задач моделирования.
Легко проанализировать влияние процентной
ставки. Для этого в ячейку С6
введите другую процентную ставку,
например 20%.

После анализа
результатов восстановите ставку 10%.

Решение обратных
задач. Если
фирма получает 10% от инвестиций, то будет
не безразлично, получить ли она 100
тыс.руб. сразу или 121 тыс.руб. спустя 2
года. Но 100 тыс.руб., полученные через 2
года с учетом дисконтирования составляют
сегодня только 82,6 т.руб.

Эту величину можно
найти с помощью команды Данные

Анализ “что-если” 
Подбор параметра…,
окно которой представлено на рис. 4.3.

Рис. 4.3

Соседние файлы в папке Инфом.техн. в эк.

• #
• #
• #
• #
• #
• #