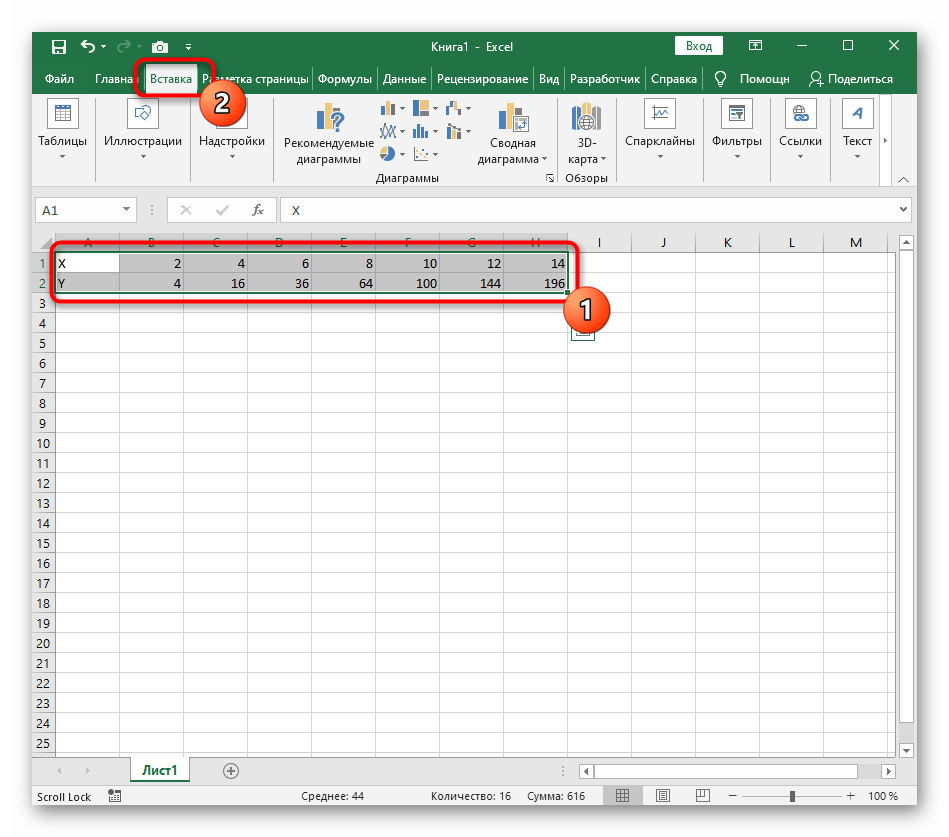
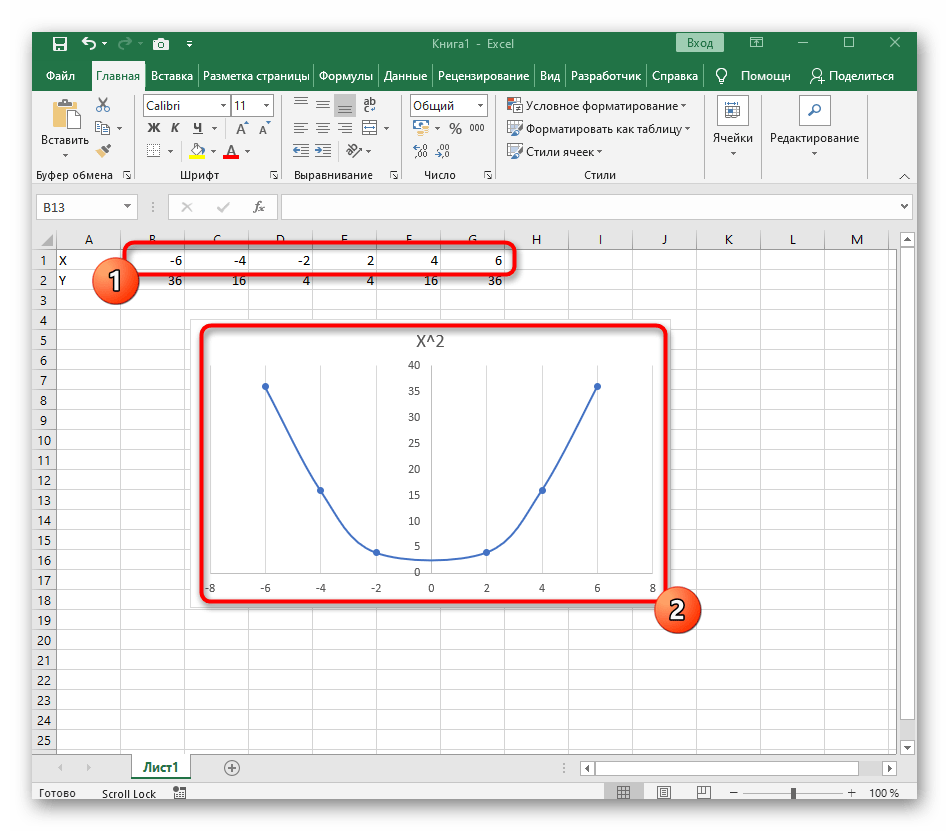
Вариант 1: График функции X^2
В качестве первого примера для Excel рассмотрим самую популярную функцию F(x)=X^2. График от этой функции в большинстве случаев должен содержать точки, что мы и реализуем при его составлении в будущем, а пока разберем основные составляющие.
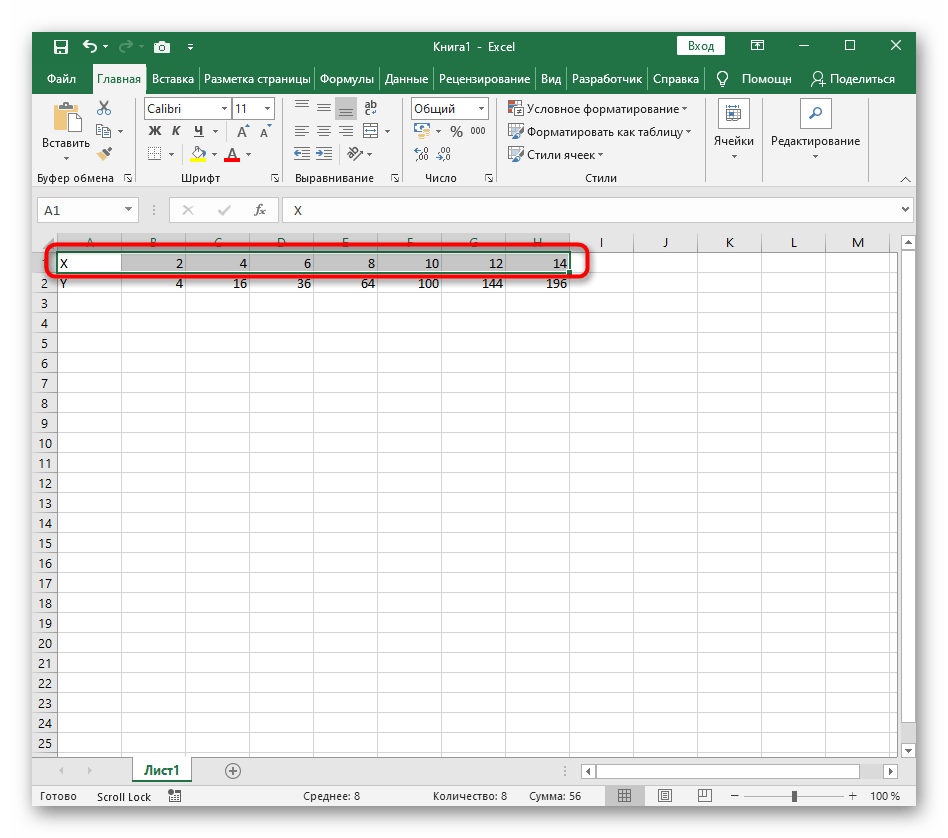
- Создайте строку X, где укажите необходимый диапазон чисел для графика функции.
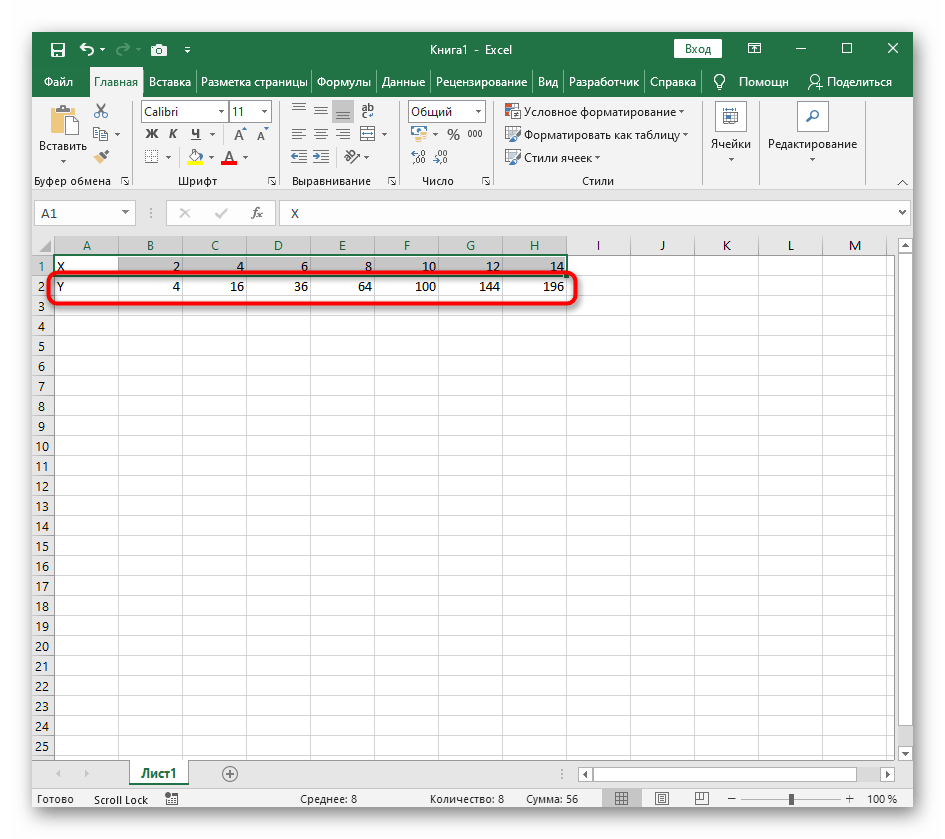
- Ниже сделайте то же самое с Y, но можно обойтись и без ручного вычисления всех значений, к тому же это будет удобно, если они изначально не заданы и их нужно рассчитать.
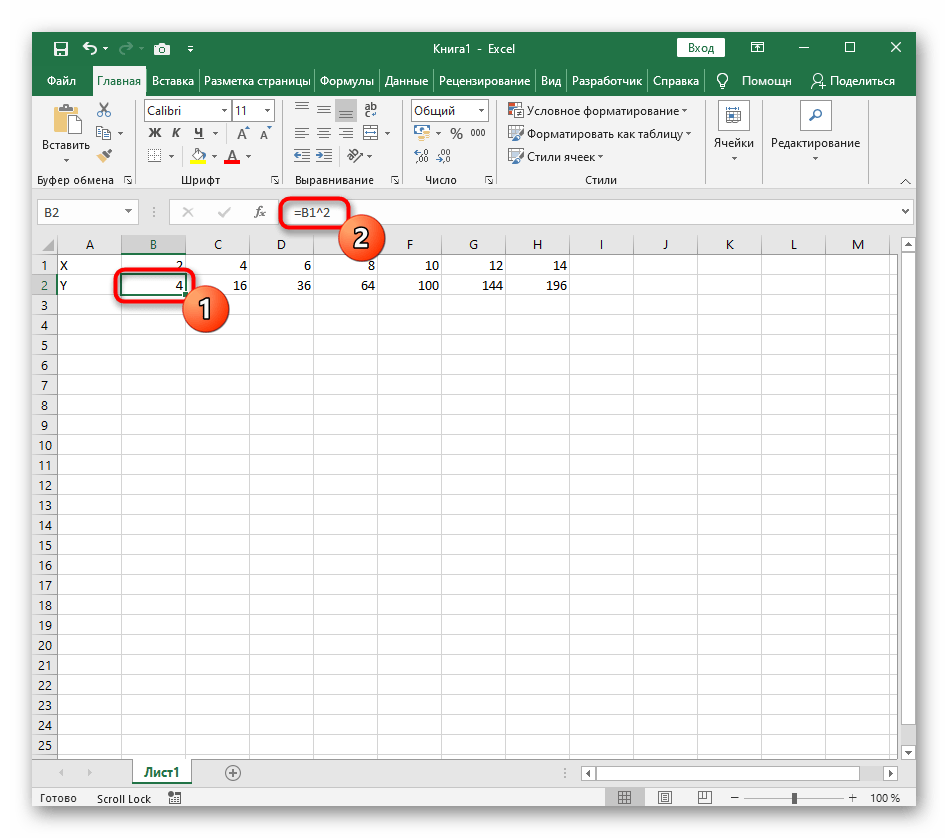
- Нажмите по первой ячейке и впишите
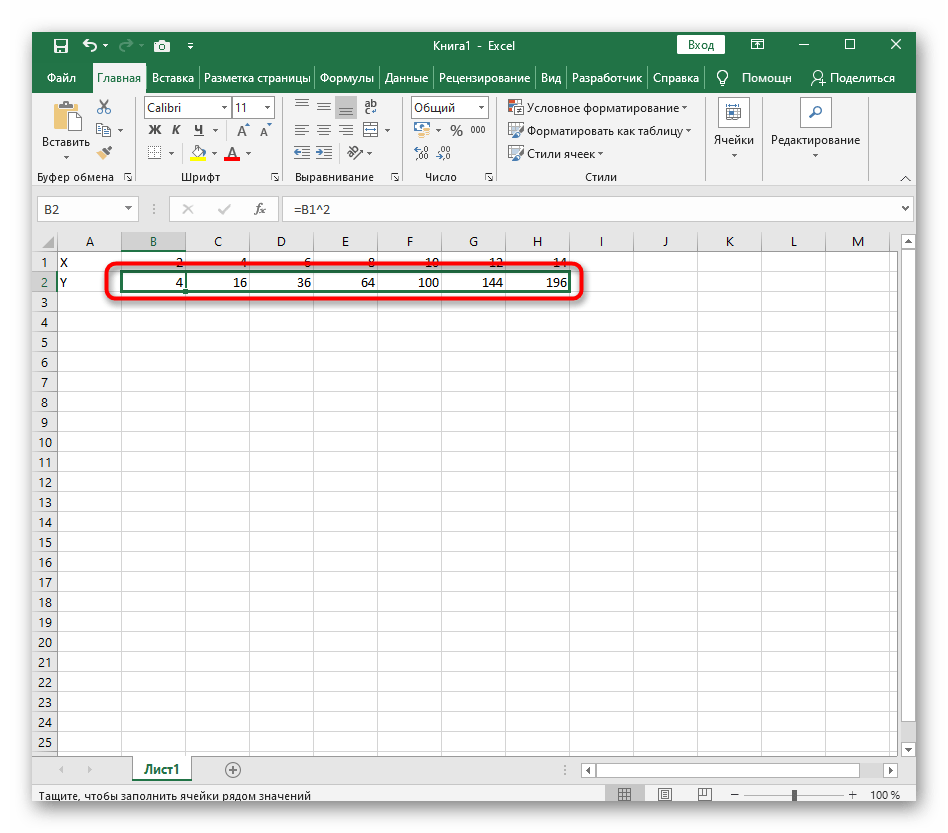
=B1^2, что значит автоматическое возведение указанной ячейки в квадрат. - Растяните функцию, зажав правый нижний угол ячейки, и приведя таблицу в тот вид, который продемонстрирован на следующем скриншоте.
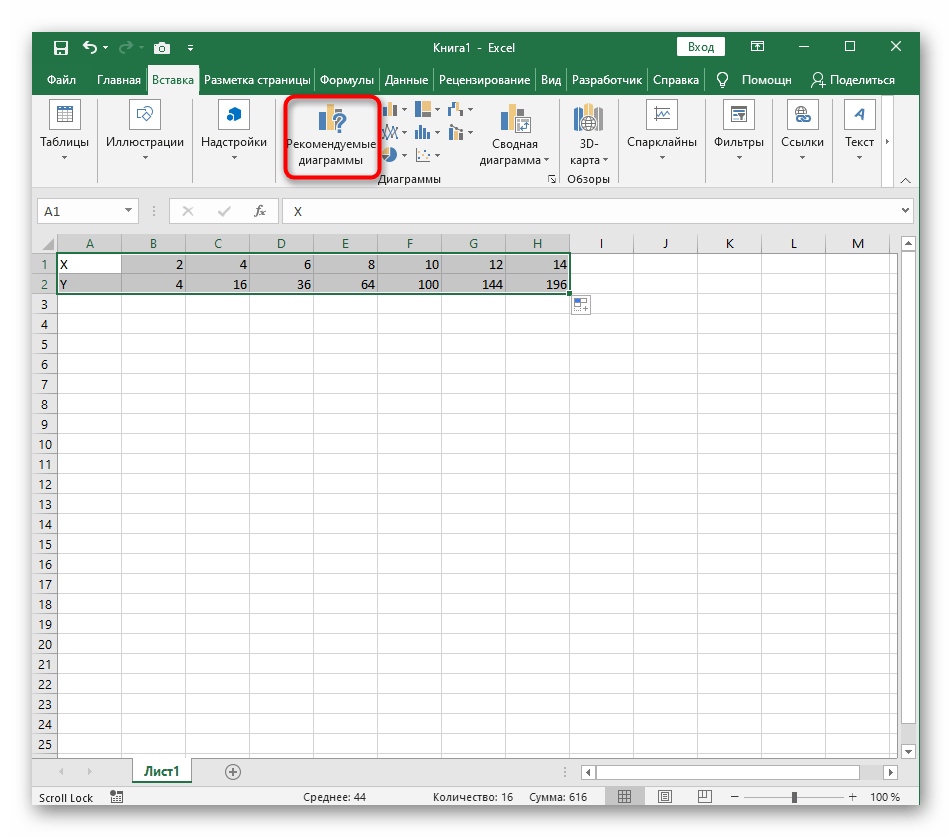
- Диапазон данных для построения графика функции указан, а это означает, что можно выделять его и переходить на вкладку «Вставка».
- На ней сразу же щелкайте по кнопке «Рекомендуемые диаграммы».
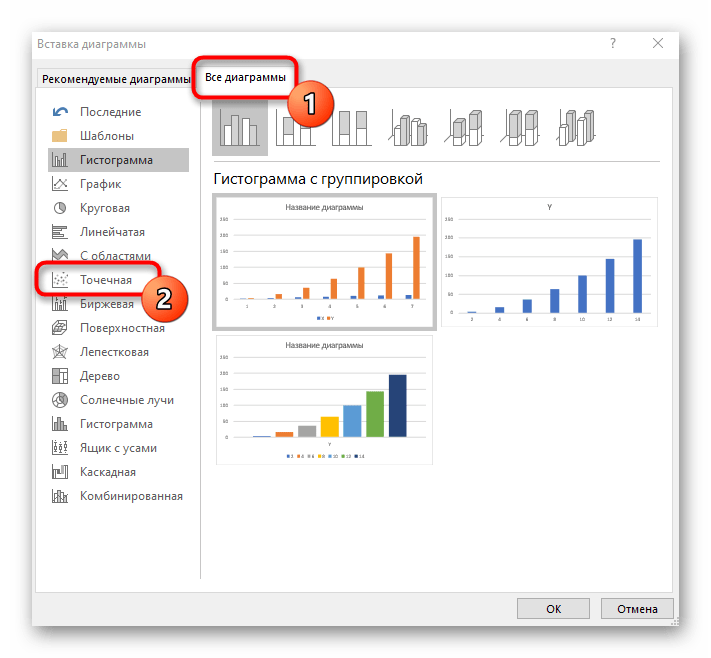
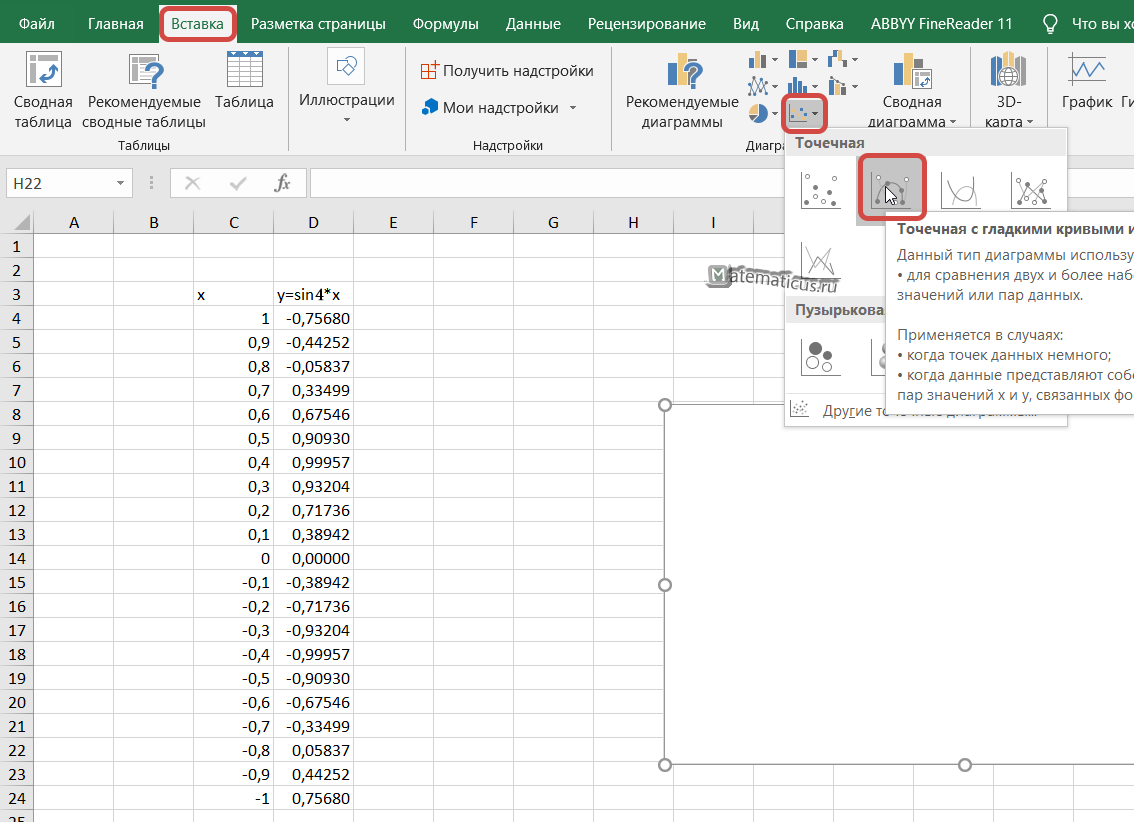
- В новом окне перейдите на вкладку «Все диаграммы» и в списке найдите «Точечная».
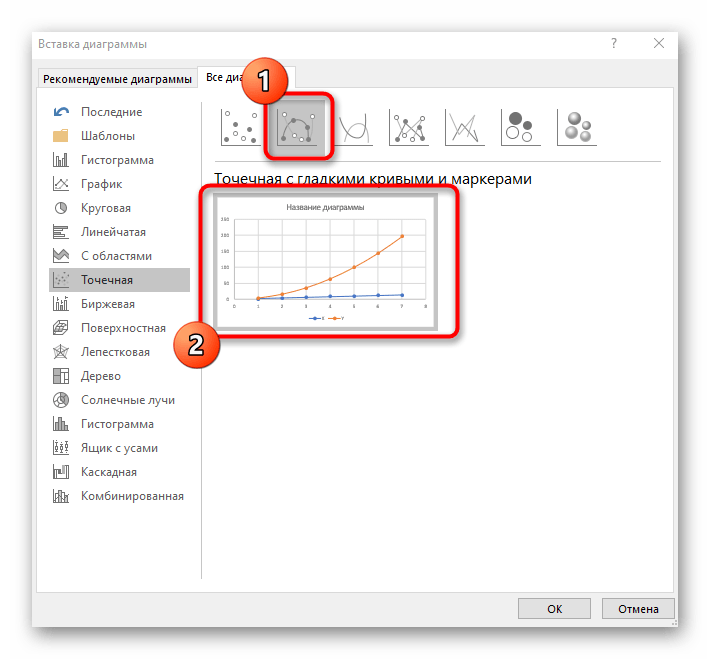
- Подойдет вариант «Точечная с гладкими кривыми и маркерами».
- После ее вставки в таблицу обратите внимание, что мы добавили равнозначный диапазон отрицательных и плюсовых значений, чтобы получить примерно стандартное представление параболы.
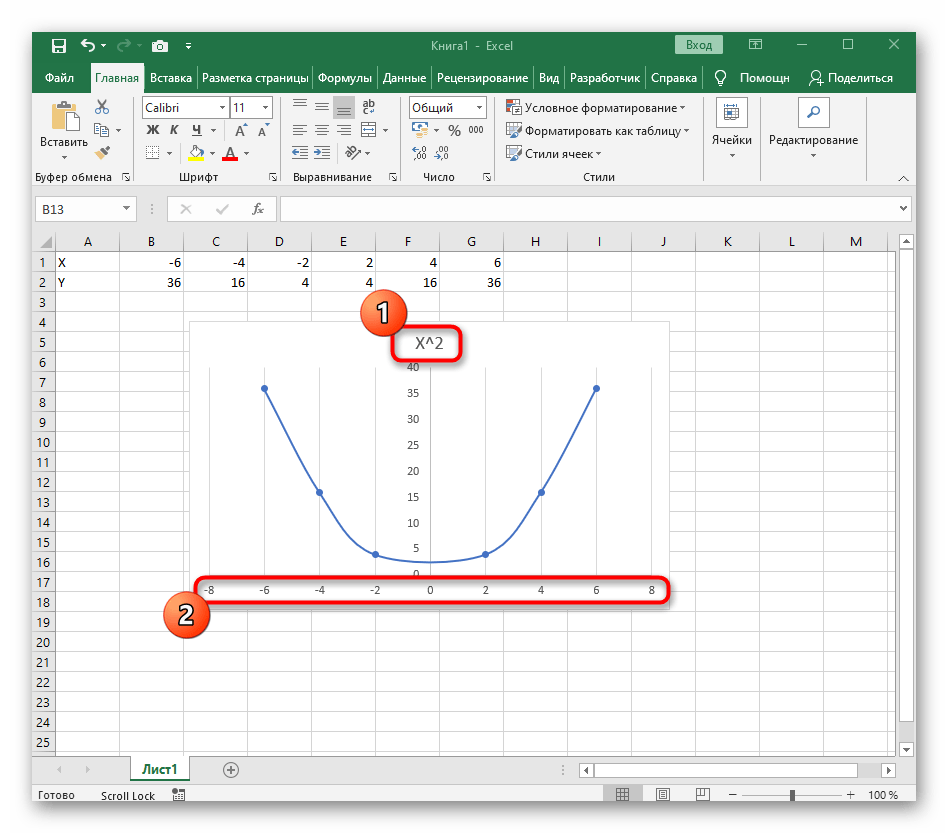
- Сейчас вы можете поменять название диаграммы и убедиться в том, что маркеры значений выставлены так, как это нужно для дальнейшего взаимодействия с этим графиком.
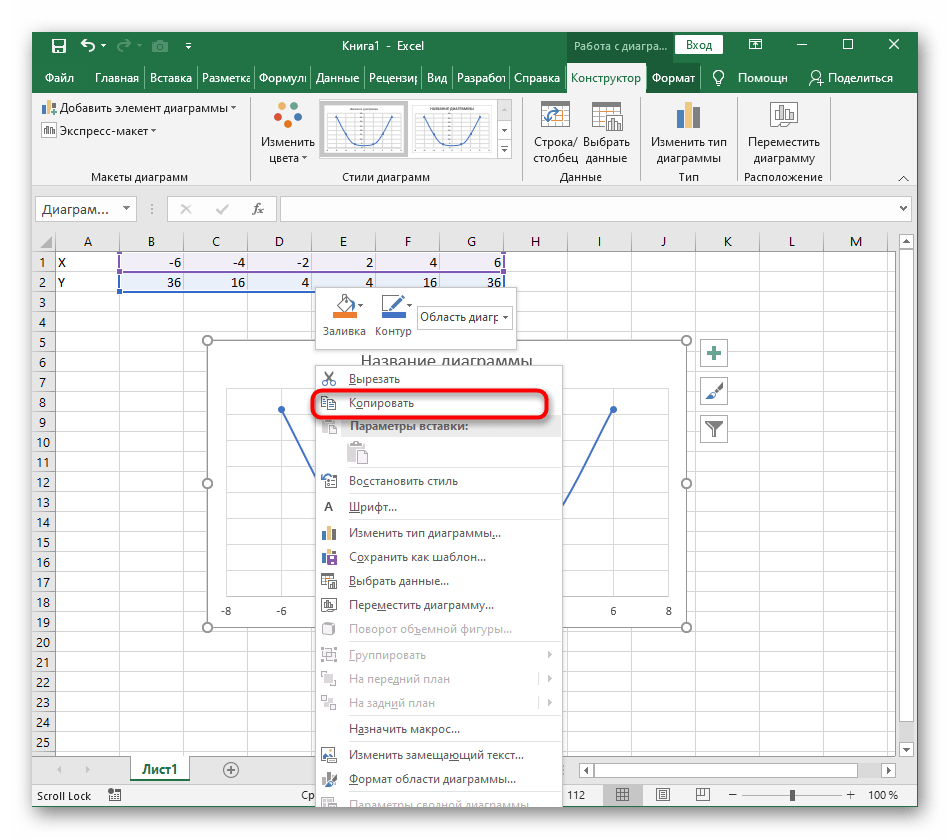
- Из дополнительных возможностей отметим копирование и перенос графика в любой текстовый редактор. Для этого щелкните в нем по пустому месту ПКМ и из контекстного меню выберите «Копировать».
- Откройте лист в используемом текстовом редакторе и через это же контекстное меню вставьте график или используйте горячую клавишу Ctrl + V.
Если график должен быть точечным, но функция не соответствует указанной, составляйте его точно в таком же порядке, формируя требуемые вычисления в таблице, чтобы оптимизировать их и упростить весь процесс работы с данными.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию
=SIN(, а в качестве числа укажите первое значение X. - Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.


Еще статьи по данной теме:
Помогла ли Вам статья?
Как построить график синусоиды в Excel.
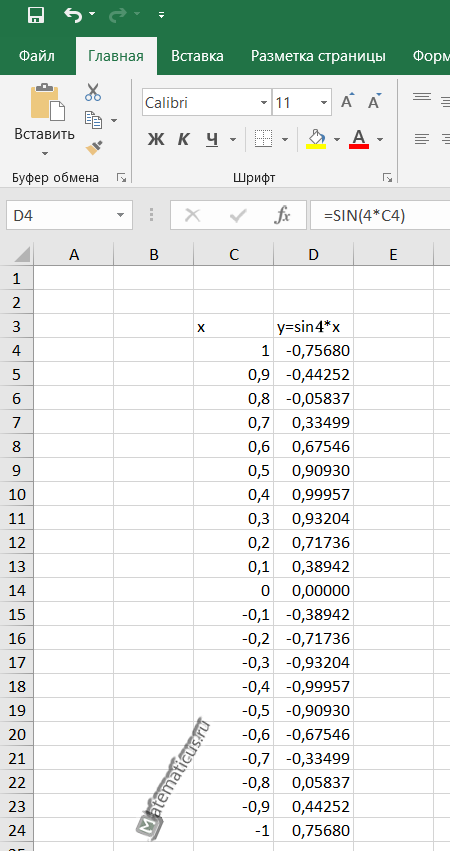
Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:
=SIN(4*C4)
Требуется построить график функции.
Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.
В итоги у нас должна получится таблица вида:
| x | y=sin4*x |
| 1 | -0,75680 |
| 0,9 | -0,44252 |
| 0,8 | -0,05837 |
| 0,7 | 0,33499 |
| 0,6 | 0,67546 |
| 0,5 | 0,90930 |
| 0,4 | 0,99957 |
| 0,3 | 0,93204 |
| 0,2 | 0,71736 |
| 0,1 | 0,38942 |
| 0 | 0,00000 |
| -0,1 | -0,38942 |
| -0,2 | -0,71736 |
| -0,3 | -0,93204 |
| -0,4 | -0,99957 |
| -0,5 | -0,90930 |
| -0,6 | -0,67546 |
| -0,7 | -0,33499 |
| -0,8 | 0,05837 |
| -0,9 | 0,44252 |
| -1 | 0,75680 |
Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.
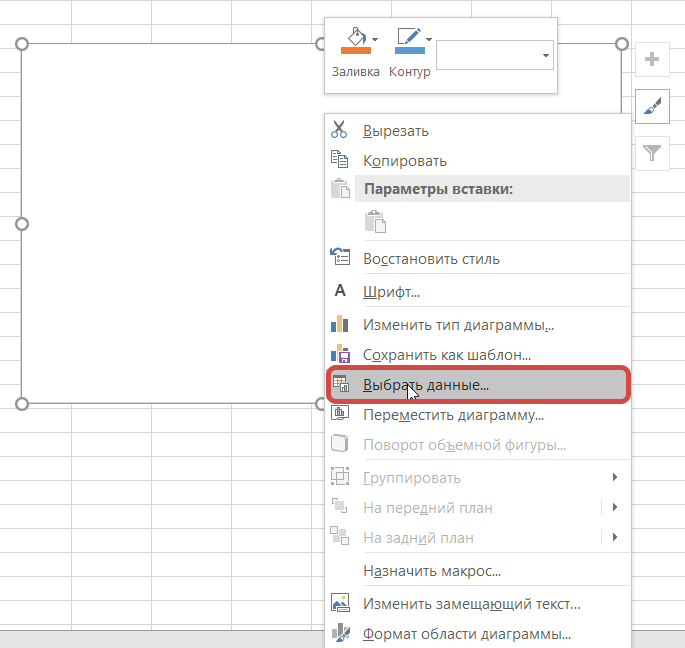
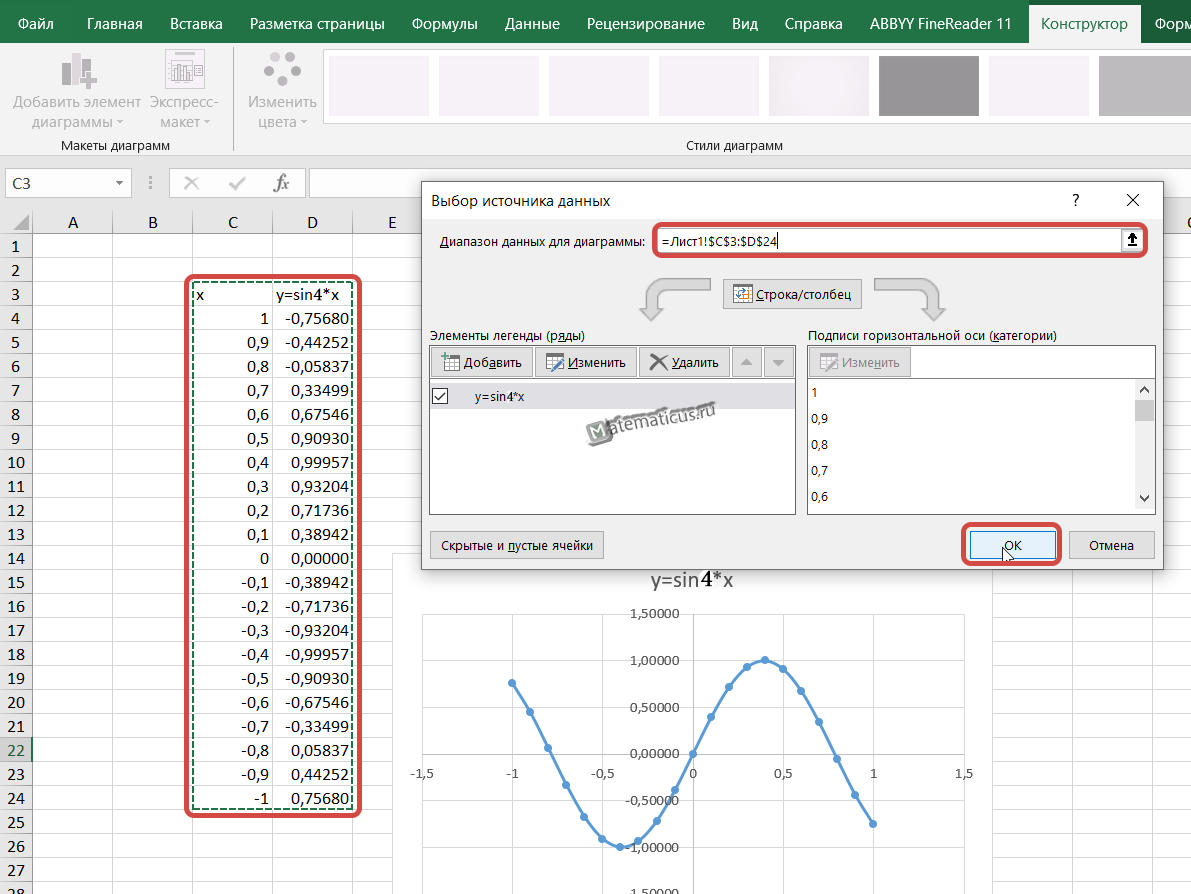
Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.
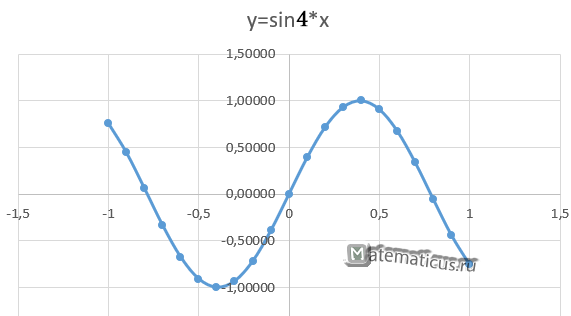
В итоги у нас получается график вида.
Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.
12778
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x).
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2).
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон
А1:В22. - Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22, а значения у — в диапазоне B1:V1.
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1).
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон
A1:V22. - Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
В статье «Excel 29. Оформление диаграммы» я рассказала о правилах оформления диаграмм. И один пунктов этих правил гласил: «Удаляйте лишние линии сетки и заливку». Но сейчас мы рассмотрим случай, когда сетка просто необходима. В качестве примера рассмотрим диаграмму «Синусоида».
С моего любимого ресурса https://dic.academic.ru/
СИНУСОИДА – плоская кривая – график функции y=sin x.
По окончании этого урока вы сможете:
- Построить диаграмму «Синусоида»
- Отформатировать оси и сетку диаграммы
1. Диаграмма «Синусоида»
Шаг 1. Открываем таблицу Excel и вводим в ячейку А1 «1»
Шаг 2. Распространяем список до ячейки А20 (статья «Excel 2. Нумерация ячеек»):
Шаг 3. В ячейку В1 вводим функцию «y=sin x» (статья «Excel 9. Формулы»):
Шаг 4. Распространяем формулу на диапазон В2:В20 (статья «Excel 10. Диапазон и вычисления в нем»):
Шаг 5. Строим график (не снимая выделения → лента Вставка → группа команд Диаграммы → команда График):
Получилось не очень красиво. График составлен из ломанных линий. Непривычная синусоида.
Шаг 6. Двойным щелчком по графику открываем рабочее окно «Формат ряда данных»
Шаг 7. Делаем график гладким (рабочее окно Формат ряда данных → вкладка Заливка → выпадающее меню Линия → галочка «сглаженная линия»):
Для закрепления сделаем еще один график. Повторяем шаги 2÷4 в диапазоне С1:С20, но формула будет y=cos(A1).
Шаг 8. Выделяем любой элемент диаграммы, кроме области диаграммы, → ПМ → команда Выбрать данные из контекстного меню (статья «Excel 27. Данные диаграммы»):
Контекстное меню «Области диаграммы» не под запретом, просто в этом меню 18 команд и команда «Выбрать данные» находится на 8 месте (статья «Excel 37. Шаблон диаграммы».
Шаг 9. Диалоговое окно Выбор источника данных:
- Команда Добавить
- Поле Значения
- Выделение диапазона С1:С20
И два раза ОК в диалоговых окнах.
Шаг 10. Делаем график гладким (рабочее окно Формат ряда данных → вкладка Заливка → выпадающее меню Линия → галочка «сглаженная линия»):
2. Форматирование оси и сетки диаграммы
Шаг 1. Выделяем вертикальную ось → рабочее окно Формат оси → вкладка Заливка → выпадающая палитра Цвет → выпадающее меню Тип конечной стрелки:
Шаг 2. Выделяем горизонтальную ось → рабочее окно Формат оси → вкладка Заливка → выпадающая палитра Цвет → выпадающее меню Тип конечной стрелки:
Шаг 3. Выделяем диаграмму → кнопка Элементы диаграммы → галочка Сетка → отмечаем галочками все линии сетки:
- Кнопка Элементы диаграммы
- Галочка Сетка → боковое меню
- Галочкой отмечены все виды сетки
Шаг 4. Выделяем главные линии оси → рабочее окно Формат основных линий сетки → увеличиваем ширину линий:
Теперь сможете:
- Построить диаграмму «Синусоида»
- Отформатировать оси и сетку диаграммы
Содержание
- Microsoft Excel
- Построение в Excel графиков математических и тригонометрических функций
- Построение графиков математических функций с одной переменной
- Построение графиков математических функций с двумя переменными
- Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
Microsoft Excel
трюки • приёмы • решения
Построение в Excel графиков математических и тригонометрических функций
Использование диаграмм Excel — хороший способ отображения графиков математических и тригонометрических функций. В этой статье описываются два метода построения графика функции: с одной переменной с помощью точечной диаграммы и с двумя переменными с помощью 3D-диаграммы.
Построение графиков математических функций с одной переменной
Точечная диаграмма (известная как диаграмма XY в предыдущих версиях Excel) отображает точку (маркер) для каждой пары значений. Например, на рис. 140.1 показан график функции SIN. На диаграмму наносятся рассчитанные значения у для значений х (в радианах) от -5 до 5 с инкрементом (приращением) 0,5. Каждая пара значений х и у выступает в качестве точки данных в диаграмме, и эти точки связаны линиями.
Рис. 140.1. Диаграмма представляет собой график функции SIN(x)
Функция выражается в таком виде: у = SIN(x) .
Соответствующая формула в ячейке В2 (которая копируется в ячейки, расположенные ниже) будет следующей: =SIN(A2) .
Чтобы создать эту диаграмму, выполните следующие действия.
- Выделите диапазон А1:В22 .
- Выберите Вставка ► Диаграммы ► Точечная ► Точечная с прямыми отрезками и маркерами.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Измените значения в столбце А для построения графика функции при различных значениях х. И, конечно, вы можете использовать любую формулу с одной переменной в столбце В. Вот несколько примеров, которые приводят к построению интересных графиков:
=SIN(ПИ()*A2)*(ПИ()*A2)
=SIN(A2)/A2
=SIN(A2^3)*COS(A2^2)
=НОРМ.РАСП(A2;0;1;ЛОЖЬ)
Чтобы получить более точную диаграмму, увеличьте количество значений для построения графика и сделайте приращение в столбце А меньше.
Вы можете использовать онлайн наш файл примера графиков математических функций с одной переменной, расположенной в Excel Web Apps при помощи Skydrive, и внести свои данные (изменения не будут сохраняться) или скачать себе на компьютер, для чего необходимо кликнуть по иконке Excel в правом нижнем углу. Это бесплатно 🙂
Построение графиков математических функций с двумя переменными
Вы также можете строить графики функций, которые используют две переменные. Например, следующая функция рассчитывает z для различных значений двух переменных (х и у): =SIN($A2)*COS($B1)
На рис. 140.2 приведена поверхностная диаграмма, которая рассчитывает значение z для 21 значения х в диапазоне от -3 до 0 и для 21 значения у в диапазоне от 2 до 5. Для х и у используется приращение 0,15.
Рис. 140.2. Использование трехмерной поверхностной диаграммы для построения графика функции с двумя переменными
Значения х находятся в диапазоне А2:А22 , а значения у — в диапазоне B1:V1 .
Формула в ячейке В2 копируется в другие ячейки таблицы и имеет следующий вид: =SIN($A2)*C0S(B$1) .
Чтобы создать диаграмму, выполните приведенные ниже действия.
- Выделите диапазон A1:V22 .
- Выберите Вставка ► Диаграммы ► Другие ► Поверхность.
- Выберите макет диаграммы, который вам нравится, а затем настройте его.
Пока значения х и у имеют равные приращения, вы можете задавать любую формулу с двумя переменными. Вам, возможно, потребуется настроить начальные значения и значение приращения для х и у. Для увеличения сглаживания используйте больше значений х и у при меньшем приращении. Вот другие формулы, которые вы можете попробовать:
=SIN(КОРЕНЬ($A2^2+B$1^2))
=SIN($A2)*COS($A2*B$1)
=COS($A2*B$1)
Источник
Урок информатики по теме: «Excel: Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться график.
- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
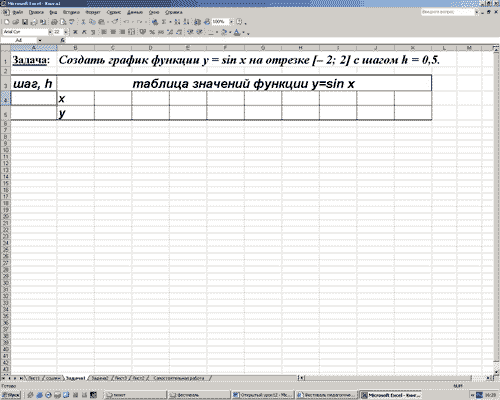
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
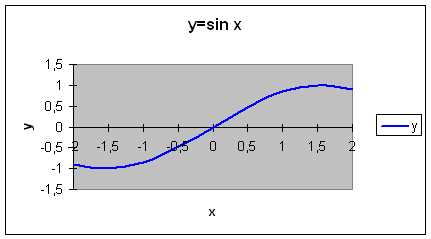
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку

8. На третьем шаге заполним вкладку Заголовки.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем пункт Формат оси…. Во вкладке Шкала установим: цена основного деления: 1. Во вкладке Шрифт установим размер шрифта 8пт.
- Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
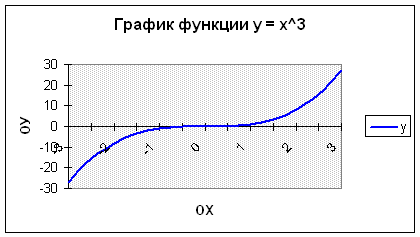
Задача 2. Построить график функции у = х 3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево ячейки строки 3, до тех пор, пока не будет получено значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения функции: = С4^3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х 3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (ВидКолонтитулы…):
14. Верхний колонтитул слева: график функции у = x 3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (ВидКолонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого варианта проверяется с помощью проектора.
Источник
Содержание статьи (кликните для открытия/закрытия)
- Построение графика линейной функции в Excel
- Подготовка расчетной таблицы
- Построение графика функции
- Построение графиков других функций
- Квадратичная функция y=ax2+bx+c
- Кубическая парабола y=ax3
- Гипербола y=k/x
- Построение тригонометрических функций sin(x) и cos(x)
Построение графика зависимости функции является характерной математической задачей. Все, кто хотя бы на уровне школы знаком с математикой, выполняли построение таких зависимостей на бумаге. В графике отображается изменение функции в зависимости от значения аргумента. Современные электронные приложения позволяют осуществить эту процедуру за несколько кликов мышью. Microsoft Excel поможет вам в построении точного графика для любой математической функции. Давайте разберем по шагам, как построить график функции в excel по её формуле
Построение графиков в Excel 2016 значительно улучшилось и стало еще проще чем в предыдущих версиях. Разберем пример построения графика линейной функции y=kx+b на небольшом интервале [-4;4].
Подготовка расчетной таблицы
В таблицу заносим имена постоянных k и b в нашей функции. Это необходимо для быстрого изменения графика без переделки расчетных формул.
Далее строим таблицу значений линейной функции:
- В ячейки A5 и A6 вводим соответственно обозначения аргумента и саму функцию. Запись в виде формулы будет использована в качестве названия диаграммы.
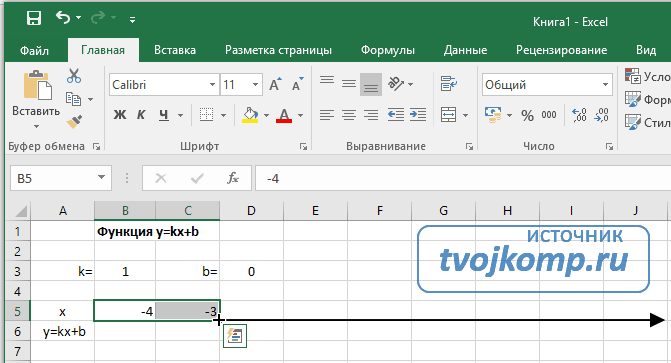
- Вводим в ячейки B5 и С5 два значения аргумента функции с заданным шагом (в нашем примере шаг равен единице).
- Выделяем эти ячейки.
- Наводим указатель мыши на нижний правый угол выделения. При появлении крестика (смотри рисунок выше), зажимаем левую кнопку мыши и протягиваем вправо до столбца J.
Ячейки автоматически будут заполнены числами, значения которых различаются заданным шагом.
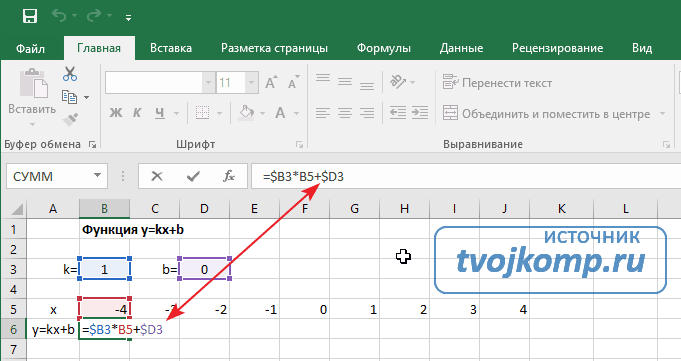
Далее в строку значений функции в ячейку B6 записываем формулу =$B3*B5+$D3
Внимание! Запись формулы начинается со знака равно(=). Адреса ячеек записываются на английской раскладке. Обратите внимание на абсолютные адреса со знаком доллара.
Чтобы завершить ввод формулы нажмите клавишу Enter или галочку слева от строки формул вверху над таблицей.
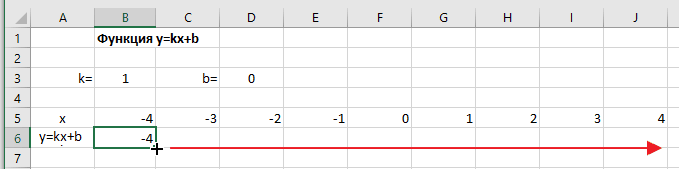
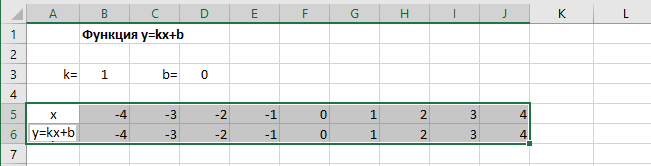
Копируем эту формулу для всех значений аргумента. Протягиваем вправо рамку от ячейки с формулой до столбца с конечными значениями аргумента функции.
Построение графика функции
Выделяем прямоугольный диапазон ячеек A5:J6.
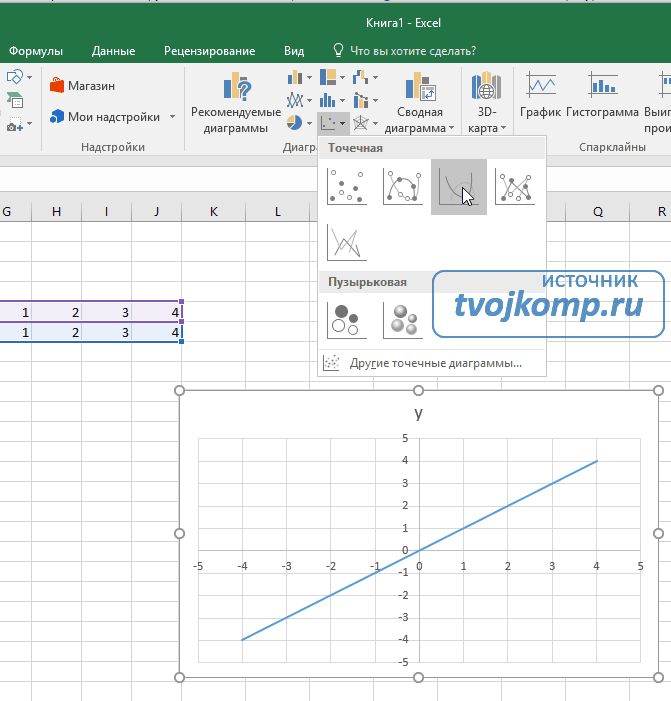
Переходим на вкладку Вставка в ленте инструментов. В разделе Диаграмма выбираем Точечная с гладкими кривыми (см. рисунок ниже).Получим диаграмму.
После построения координатная сетка имеет разные по длине единичные отрезки. Изменим ее перетягивая боковые маркеры до получения квадратных клеток.
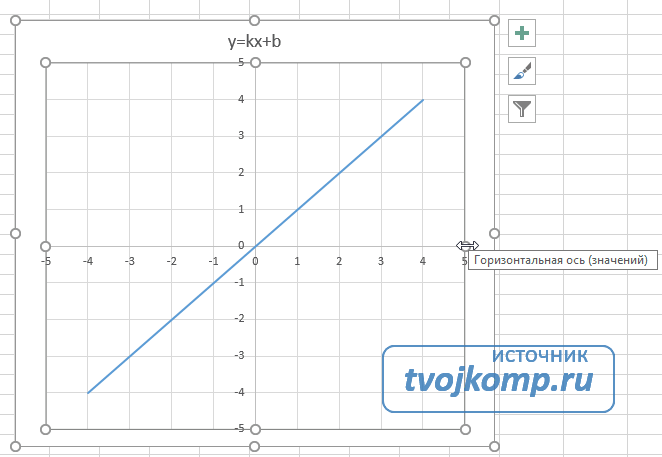
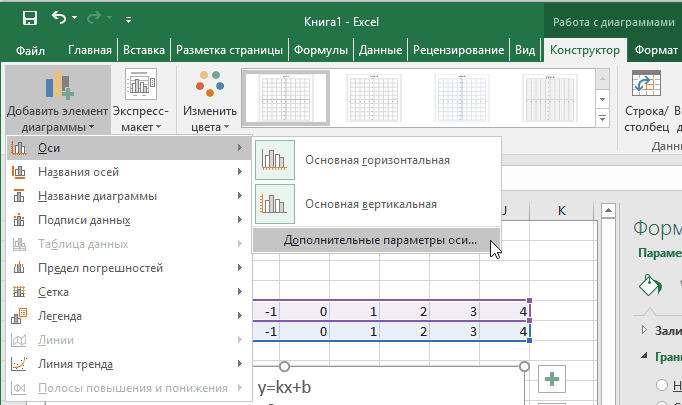
Теперь можно ввести новые значения постоянных k и b для изменения графика. И видим, что при попытке изменить коэффициент график остается неизменным, а меняются значения на оси. Исправляем. Кликните на диаграмме, чтобы ее активировать. Далее на ленте инструментов во вкладке Работа с диаграммами на вкладке Конструктор выбираем Добавить элемент диаграммы — Оси — Дополнительные параметры оси..
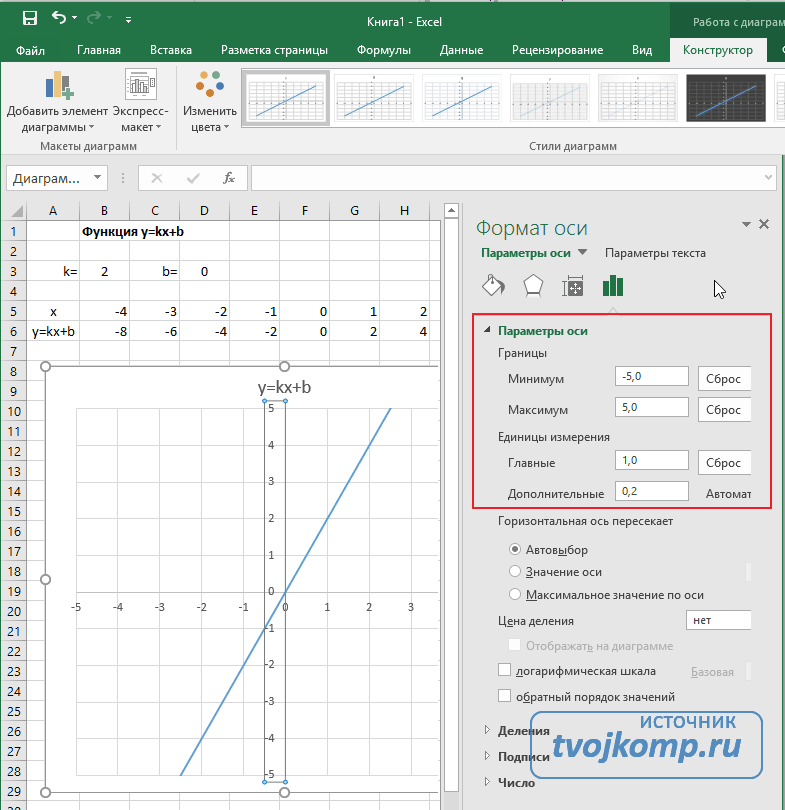
В правой части окна появиться боковая панель настроек Формат оси.
- Кликните на раскрывающийся список Параметры оси.
- Выберите Вертикальная ось (значений).
- Кликните зеленый значок диаграммы.
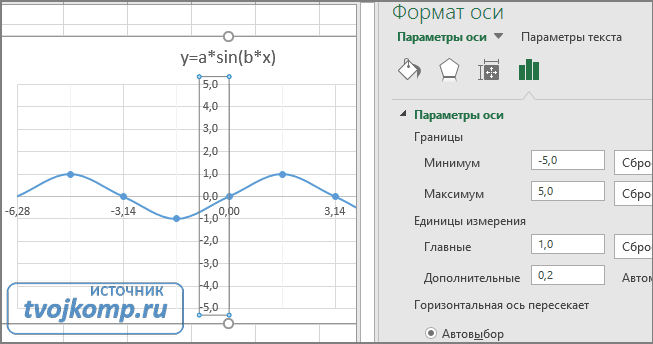
- Задайте интервал значений оси и единицы измерения (обведено красной рамкой). Ставим единицы измерения Максимум и минимум (Желательно симметричные) и одинаковые для вертикальной и горизонтальной осей. Таким образом, мы делаем мельче единичный отрезок и соответственно наблюдаем больший диапазон графика на диаграмме.И главную единицу измерения — значение 1.
- Повторите тоже для горизонтальной оси.
Теперь, если поменять значения K и b , то получим новый график с фиксированной сеткой координат.
Построение графиков других функций
Теперь, когда у нас есть основа в виде таблицы и диаграммы, можно строить графики других функций, внося небольшие корректировки в нашу таблицу.
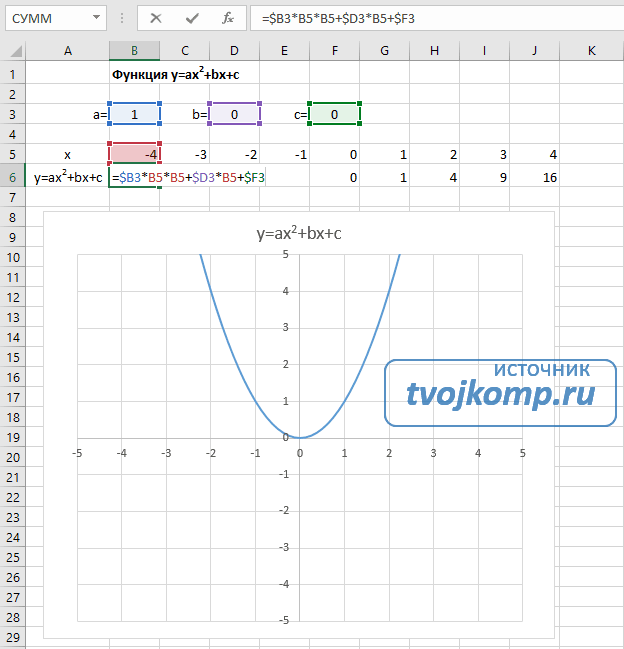
Квадратичная функция y=ax2+bx+c
Выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5+$D3*B5+$F3
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
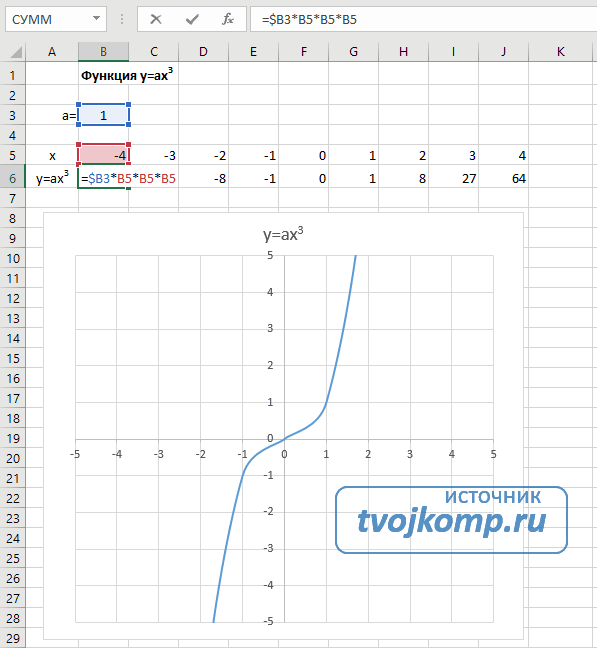
Кубическая парабола y=ax3
Для построения выполните следующие действия:
- В первой строке меняем заголовок
- В третьей строке указываем коэффициенты и их значения
- В ячейку A6 записываем обозначение функции
- В ячейку B6 вписываем формулу =$B3*B5*B5*B5
- Копируем её на весь диапазон значений аргумента вправо
Получаем результат
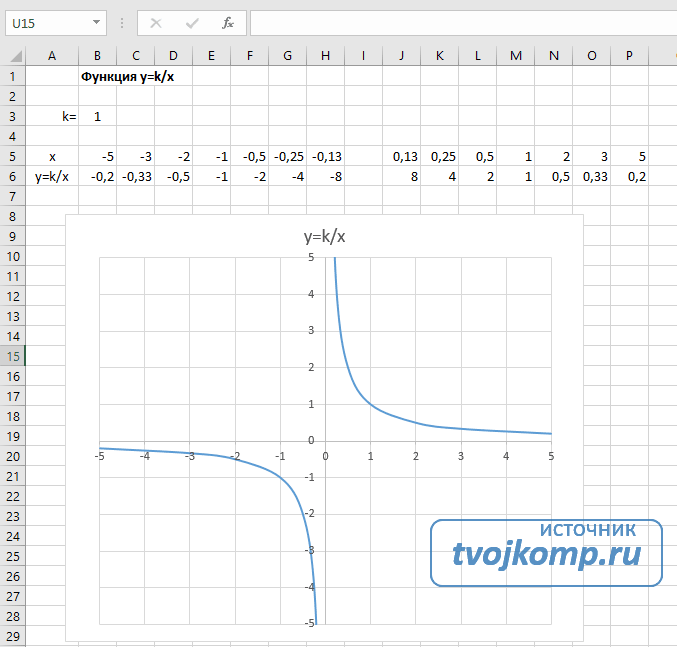
Гипербола y=k/x
Для построения гиперболы заполните таблицу вручную (смотри рисунок ниже). Там где раньше было нулевое значение аргумента оставляем пустую ячейку.
Далее выполните действия:
- В первой строке меняем заголовок.
- В третьей строке указываем коэффициенты и их значения.
- В ячейку A6 записываем обозначение функции.
- В ячейку B6 вписываем формулу =$B3/B5
- Копируем её на весь диапазон значений аргумента вправо.
- Удаляем формулу из ячейки I6.
Для корректного отображения графика нужно поменять для диаграммы диапазон исходных данных, так как в этом примере он больше чем в предыдущих.
- Кликните диаграмму
- На вкладке Работа с диаграммами перейдите в Конструктор и в разделе Данные нажмите Выбрать данные.
- Откроется окно мастера ввода данных
- Выделите мышкой прямоугольный диапазон ячеек A5:P6
- Нажмите ОК в окне мастера.
Получаем результат
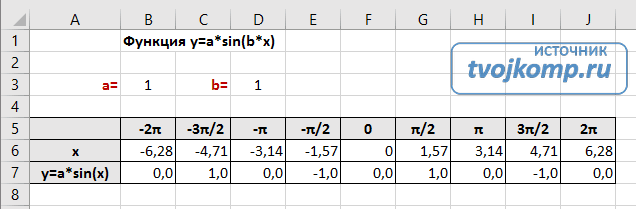
Построение тригонометрических функций sin(x) и cos(x)
Рассмотрим пример построения графика тригонометрической функции y=a*sin(b*x).
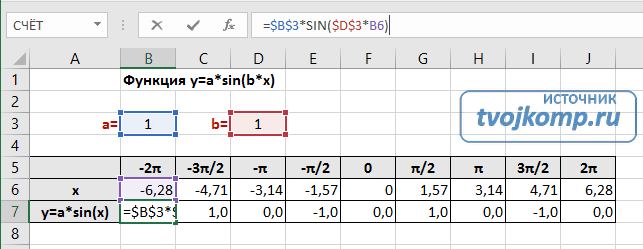
Сначала заполните таблицу как на рисунке ниже
В первой строке записано название тригонометрической функции.
В третьей строке прописаны коэффициенты и их значения. Обратите внимание на ячейки, в которые вписаны значения коэффициентов.
В пятой строке таблицы прописываются значения углов в радианах. Эти значения будут использоваться для подписей на графике.
В шестой строке записаны числовые значения углов в радианах. Их можно прописать вручную или используя формулы соответствующего вида =-2*ПИ(); =-3/2*ПИ(); =-ПИ(); =-ПИ()/2; …
В седьмой строке записываются расчетные формулы тригонометрической функции.
В нашем примере =$B$3*SIN($D$3*B6). Адреса B3 и D3 являются абсолютными. Их значения – коэффициенты a и b, которые по умолчанию устанавливаются равными единице.
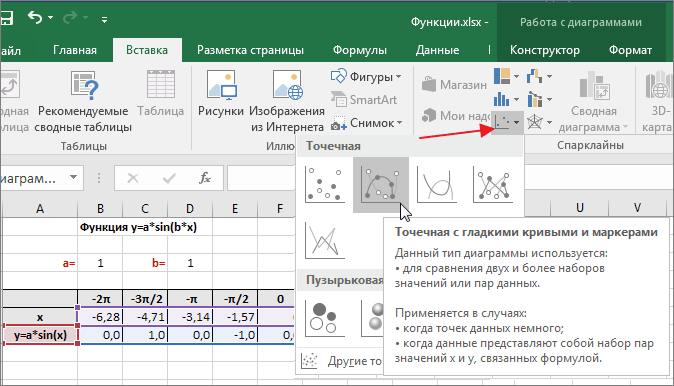
После заполнения таблицы приступаем к построению графика.
Выделяем диапазон ячеек А6:J7. В ленте выбираем вкладку Вставка в разделе Диаграммы указываем тип Точечная и вид Точечная с гладкими кривыми и маркерами.
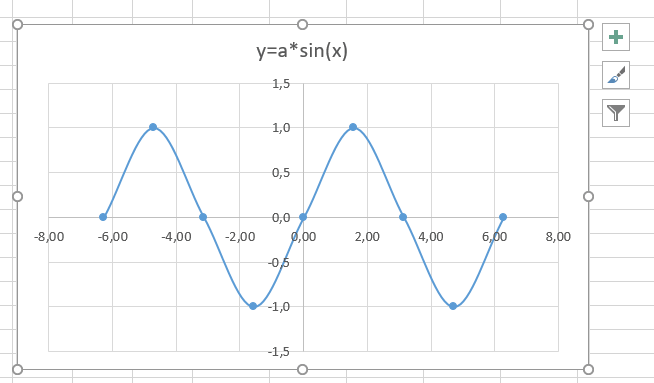
В итоге получим диаграмму.
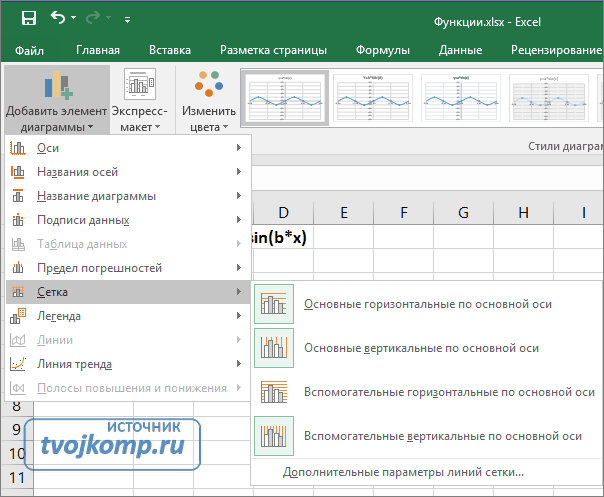
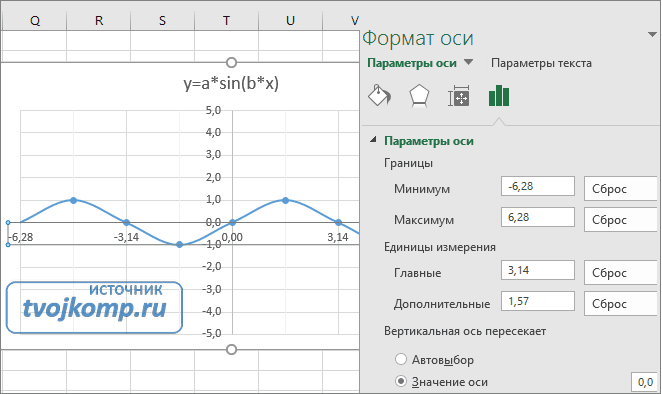
Теперь настроим правильное отображение сетки, так чтобы точки графика лежали на пересечении линий сетки. Выполните последовательность действий Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Сетка и включите три режима отображения линий как на рисунке.
Теперь зайдите в пункт Дополнительные параметры линий сетки. У вас появится боковая панель Формат области построения. Произведем настройки здесь.
Кликните в диаграмме на главную вертикальную ось Y (должна выделится рамкой). В боковой панели настройте формат оси как на рисунке.
Кликните главную горизонтальную ось Х (должна выделится) и также произведите настройки согласно рисунку.
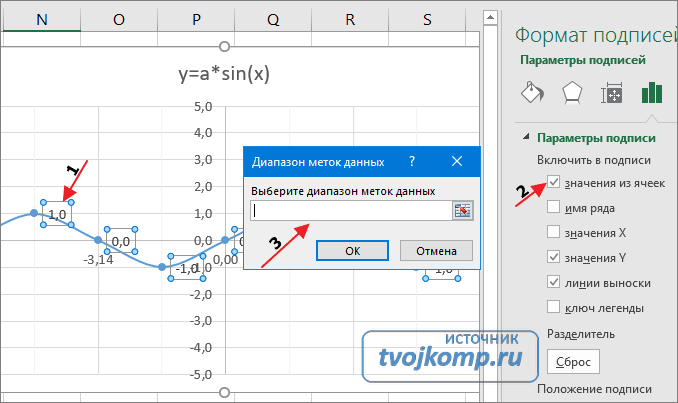
Теперь сделаем подписи данных над точками. Снова выполняем Работа с диаграммами –Конструктор – Добавить элемент диаграммы – Подписи данных – Сверху. У вас подставятся значения числами 1 и 0, но мы заменим их значениями из диапазона B5:J5.
Кликните на любом значении 1 или 0 (рисунок шаг 1) и в параметрах подписи поставьте галочку Значения из ячеек (рисунок шаг 2). Вам будет сразу же предложено указать диапазон с новыми значениями (рисунок шаг 3). Указываем B5:J5.
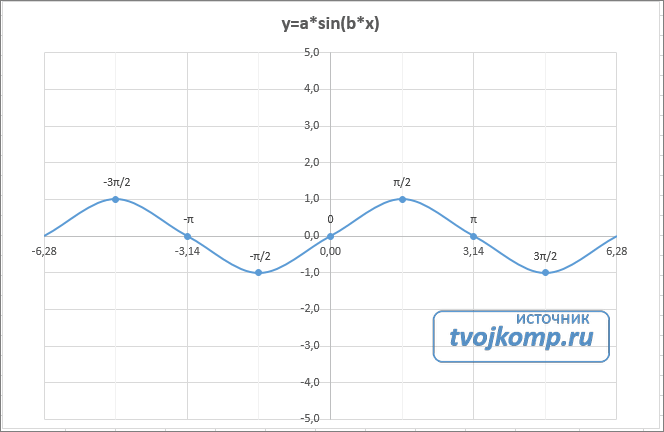
Вот и все. Если сделали правильно, то и график будет замечательным. Вот такой.
Чтобы получить график функции cos(x), замените в расчетной формуле и в названии sin(x) на cos(x).
Аналогичным способом можно строить графики других функций. Главное правильно записать вычислительные формулы и построить таблицу значений функции. Надеюсь, что вам была полезна данная информация.
Дополнительные статьи по теме:
- Знакомство с таблицами в Excel
- Изменение строк и столбцов в Excel
- Работа с ячейками: объединение, изменение, защита…
- Ошибки в формулах: почему excel не считает
- Использования условий в формулах Excel
- Функция CЧЕТЕСЛИМН
- Работа с текстовыми функциями Excel
- Все уроки по Microsoft Excel
Дорогой читатель! Вы посмотрели статью до конца.
Получили вы ответ на свой вопрос? Напишите в комментариях пару слов. Если ответа не нашли, укажите что искали или откройте содержание блога.
ОЧЕНЬ ВАЖНО! Оцени лайком или дизлайком статью!

График функции – графическое представление математического выражения, показывающее его решение. Для построения обычно используются линейные графики с точками, с чем прекрасно справляется Microsoft Excel. Кроме того, в нем еще можно выполнить автоматические расчеты, быстро подставив нужные значения.
Существует огромное количество функций, поэтому в качестве примера я разберу только две самые наглядные, чтобы вы поняли базовые правила составления подобных элементов в таблице.
Построение графиков в Excel по данным таблицы
В MS Excel есть возможность не только проводить вычисления, используя разные формулы, но и также строить на их основе различные диаграммы: гистограммы, круговые диаграммы, точечные и т.д. В этом уроке мы разберем, для чего применяют графики. И так, графики – это разновидность диаграммы, схожая с гистограммой. Они бывают трех видов: простой, график с накоплением и нормированный график с накоплением. Каждый из этих графиков бывает двух видов: с маркером и без. Так эти два вида строятся одинаково, рассмотрим только маркированные графики. Коротко опишем применение каждого графика, и далее на примерах разберем более подробно, как их построить. a) Простой график нужен для того, чтобы изобразить, как изменяется некое значение во времени (прибыль по месяцам; рождаемость по годам и т.д.). b) График с накоплением показывает, как изменяется составляющая целого значения с течением времени. (Лучше использовать диаграмму с накоплением) c) Нормированный график с накоплением показывает изменение доли каждого значения с течением времени. Есть еще объемный график, который схож с простым графиком. Поэтому мы покажем только его конечный вид.
Вариант 2: График функции y=sin(x)
Функций очень много и разобрать их в рамках этой статьи просто невозможно, поэтому в качестве альтернативы предыдущему варианту предлагаем остановиться на еще одном популярном, но сложном — y=sin(x). То есть изначально есть диапазон значений X, затем нужно посчитать синус, чему и будет равняться Y. В этом тоже поможет созданная таблица, из которой потом и построим график функции.
- Для удобства укажем всю необходимую информацию на листе в Excel. Это будет сама функция sin(x), интервал значений от -1 до 5 и их шаг весом в 0.25.
- Создайте сразу два столбца — X и Y, куда будете записывать данные.
- Запишите самостоятельно первые два или три значения с указанным шагом.
- Далее растяните столбец с X так же, как обычно растягиваете функции, чтобы автоматически не заполнять каждый шаг.
- Перейдите к столбцу Y и объявите функцию =SIN(, а в качестве числа укажите первое значение X.
- Сама функция автоматически высчитает синус заданного числа.
- Растяните столбец точно так же, как это было показано ранее.
- Если чисел после запятой слишком много, уменьшите разрядность, несколько раз нажав по соответствующей кнопке.
- Выделите столбец с Y и перейдите на вкладку «Вставка».
- Создайте стандартный график, развернув выпадающее меню.
- График функции от y=sin(x) успешно построен и отображается правильно. Редактируйте его название и отображаемые шаги для простоты понимания.
Мы рады, что смогли помочь Вам в решении проблемы. Помимо этой статьи, на сайте еще 12419 инструкций. Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам. Отблагодарите автора, поделитесь статьей в социальных сетях.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Простая диаграмма
Рассмотрим простой график на примере таком примере прибыли некоторой фирмы по 3 товарам за определенный период. Для этого выделим нужные нам ячейки, как на рисунке ниже.
Теперь строим простой маркированный график. Для этого выделяем диапазон В1:D6, на главное ленте выбираем Вставка–Диаграммы (нажимаем на стрелочку справа сверху). В появившемся окне выберем нужную нам диаграмму. В первом случае – простой график. Нажимаем ОК.
Выбираем график слева, т.к. он показывает изменение прибыли во времени. Если вы все сделали правильно, то должно получиться так, как на рисунке ниже:
Итак, диаграмма построена, но на ней не отображаются года. Изменить название диаграммы очень просто. Нужно нажать на заголовок и ввести подходящее название. Например, Прибыль по товарам в 2010-214 гг. Для того, чтобы года отображались на оси Х, необходимо нажать на ось правой кнопкой мыши для вызова контекстного меню и нажать Выбрать данные.
После этого появится такое окошко:
Изменяем подписи горизонтальной оси. Должно открыться такое окошко:
Нажимаем туда, где выделено красным и выбираем диапазон. В нашем случае это А2:А6. И нажимаем клавишу Enter и ОК. В результате этого должно открыться предыдущее окно, но выглядеть будет следующим образом:
Нажимаем ОК, меняем название диаграммы. Теперь она должна выглядеть так:
Осталось добавить подписи данных. В версии Excel 2013–2016 это делается очень просто. Нажимаем на плюсик справа, который вызывает различные команды и ставим галочку Название осей. Должно получиться так:
Как и в случае с названием, ставим курсор в область каждой из осей и подписываем их согласно условию. Например, ось Х – Год, ось Y – Прибыль. Должно получиться так, как на рисунке ниже:
В MS Excel версиях 2007-2010 форматировать оси, область диаграммы и т.д. с помощью дополнительной вкладки на ленте Работа с диаграммами.
Вычисление значений функции
Нужно вычислить значения функции в данных точках. Для этого в ячейке В2 создадим формулу, соответствующую заданной функции, только вместо x будем вводить значение переменной х, находящееся в ячейке слева (-5).
Важно: для возведения в степень используется знак , который можно получить с помощью комбинации клавиш Shift+6 на английской раскладке клавиатуры. Обязательно между коэффициентами и переменной нужно ставить знак умножения * (Shift+8).
Ввод формулы завершаем нажатием клавиши Enter. Мы получим значение функции в точке x=-5. Скопируем полученную формулу вниз.
Мы получили последовательность значений функции в точках на промежутке [-5;5] с шагом 1.
График с накоплением
Строим по этим же данным график с накоплением. Повторяем все те же самые действия, как и в п.1. Поэтому мы покажем начало, на котором видно, какой график выбираем, и конец, на котором виден результат работы.
Создание таблицы и вычисление значений функций
Таблицу для первой функции мы уже построили, добавим третий столбец — значения функции y=50x+2 на том же промежутке [-5;5]. Заполняем значения этой функции. Для этого в ячейку C2 вводим формулу, соответствующую функции, только вместо x берем значение -5, т.е. ячейку А2. Копируем формулу вниз.
Мы получили таблицу значений переменной х и обеих функций в этих точках.
Объемный график
Объемный график похож на первый с той лишь разницей, что выполнен в объеме.
В этой работе были рассмотрены различные варианты построения такой разновидности диаграмм, как графики. А также случаи их применения. Для изучения построения диаграмм в программе Эксель заходите читать статьи на Справочнике!
Решение (3 ряда данных)
Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График .
Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).
Добавление второй оси
Как добавить вторую (дополнительную) ось? Когда единицы измерения одинаковы, пользуемся предложенной выше инструкцией. Если же нужно показать данные разных типов, понадобится вспомогательная ось.
Сначала строим график так, будто у нас одинаковые единицы измерения.
Выделяем ось, для которой хотим добавить вспомогательную. Правая кнопка мыши – «Формат ряда данных» – «Параметры ряда» — «По вспомогательной оси».
Нажимаем «Закрыть» — на графике появилась вторая ось, которая «подстроилась» под данные кривой.
Это один из способов. Есть и другой – изменение типа диаграммы.
Щелкаем правой кнопкой мыши по линии, для которой нужна дополнительная ось. Выбираем «Изменить тип диаграммы для ряда».
Определяемся с видом для второго ряда данных. В примере – линейчатая диаграмма.
Всего несколько нажатий – дополнительная ось для другого типа измерений готова.
Как добавить название в график Эксель
На примерах выше мы строили графики курсов Доллара и Евро, без заголовка сложно понять про что он и к чему относится. Чтобы решить эту проблему нам нужно:
- Нажать на графике левой клавишей мыши;
- Нажать на “зеленый крестик” в правом верхнем углу графика;
- Во всплывающем окне поставить галочку напротив пункта “Название диаграммы”:
- Над графиком появится поле с названием графика. Кликните по нему левой клавишей мыши и внесите свое название:
( 1 оценка, среднее 5 из 5 )
Цели урока:
- научить строить графики элементарных
математических функций с помощью табличного
процессора Excel; - показать возможности использования программы
Excel для решения задач по математике; - закрепить навыки работы с Мастером диаграмм.
Задачи урока:
- образовательная – знакомство учащихся с
основными приемами построения графиков функций
в программе Excel; - развивающие – формирование у учащихся
логического и алгоритмического мышления;
развитие познавательного интереса к предмету;
развитие умения оперировать ранее полученными
знаниями; развитие умения планировать свою
деятельность; - воспитательные – воспитание умения
самостоятельно мыслить, ответственности за
выполняемую работу, аккуратности при выполнении
работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред.
С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.
- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на
построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7
мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка
отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный
опрос)
Вопросы для проверки
- Что представляет собой рабочая область
программы Excel? - Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она
задается? - Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как
изменить ориентацию бумаги? - Что такое функциональная зависимость у = f(х)?
Какая переменная является зависимой, а какая
независимой? - Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.
При объяснении нового материала может быть
использован файл Excel с шаблонами задач (Приложение 1), который
выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного
процессора Excel для графиков функций. На
предыдущих практических вы уже строили
диаграммы к различным задачам, используя Мастер
диаграмм. Графики функций, так же как и диаграммы
строятся с помощью Мастера диаграмм программы
Excel.
Рассмотрим построение графиков функций на
примере функции у = sin x.
Вид данного графика хорошо известен вам по
урокам математики, попробуем построить его
средствами Excel.
Программа будет строить график по точкам: точки
с известными значениями будут плавно
соединяться линией. Эти точки нужно указать
программе, поэтому, сначала создается таблица
значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график. - шаг переменной х, т.е. через какой промежуток
будут вычисляться значения функции.
Задача 1.Построить график функции у = sin
x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4
введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево
ячейки строки 4, до тех пор, пока получим значение
другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в
категории математические выберем функцию SIN, в
качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу
в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов
(х) и значений (у) функции у = sin x на отрезке [-2;2] с
шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6. Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на
кнопку “Удалить” (график изменений х нам не
нужен. График функции – это график изменения
значений у)
В поле Подписи оси Х нажать на кнопку.
Выделить в таблице ячейки со значениями х и
нажмите на кнопку . Подписи по горизонтальной оси
станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график
функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси…. Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт
Формат оси….
Во вкладке Шкала установим: пересечение с осью
ОУ установите номер категории 5 (чтобы ось ОУ
пересекала ось ОХ в категории с подписью 0, а это
пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт.
Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на
построение графика функций. Эту задачу
попробуйте решить самостоятельно, сверяясь с
экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и
сформулировать следующую задачу.
Задача 2. Построить график функции у = х3
на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица
значений функции у = f(х).
2. В ячейку С4 ввести первое значение отрезка: –3
3. В ячейку D4 ввести формулу, которая будет
добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
4. Маркером заполнения ячейки D3 заполнить влево
ячейки строки 3, до тех пор, пока не будет получено
значение другого конца отрезка: 3.
5. В ячейку С5 ввести формулу вычисления значения
функции: = С4^3
6. Маркером заполнения скопировать формулу в
ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица
аргументов (х) и значений (у) функции у = х3 на
отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7. Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
8. На втором шаге во вкладке Ряд выполнить:
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры
диаграмм таким образом, что бы все поместилось на
одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
14. Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем
График.
Самостоятельная работа.
Работа по карточкам с индивидуальными
заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде,
выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с
шагом h=c
2. Установить параметры страницы и размеры
графика таким образом, что бы все поместилось на
одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид
Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный
график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.





























 Колонтитулы…):
Колонтитулы…):