Work done word problems

What is a Work Word Problem?

Work word problems usually involve two or more entities working together to complete a task. Work problems have direct real-life applications. We often need to determine how many people are needed to complete a task within a given time. Alternatively, given a limited number of workers, we may need to determine how long it will take to finish a project. Here, we will deal with the basic math concepts of how to calculate work word problems.

How To Solve Work Word Problems For Two Persons?

This formula can be extended for more than two persons. It can also be used in problems
that involve pipes filling up a tank.

Example 1:
Peter can mow the lawn in 40 minutes and John can mow the lawn in 60 minutes. How long will it take for
them to mow the lawn together?

Solution:
Step 1: Assign variables:
Let x = time to mow lawn together.

Step 2: Use the formula:

Step 3: Solve the equation
The LCM of 40 and 60 is 120
Multiply both sides with 120

Answer: The time taken for both of them to mow the lawn together
is 24 minutes.

Example 2:
It takes Maria 10 hours to pick forty bushels of apples. Kayla can pick the same amount in 12 hours.
How long will it take if they work together? Round your answer to the nearest hundredths.

• Show Video Lesson

“Work” Problems: More Than Two Persons

Example 1:
Jane, Paul and Peter can finish painting the fence in 2 hours. If Jane does the job alone she can finish
it in 5 hours. If Paul does the job alone he can finish it in 6 hours. How long will it take for Peter
to finish the job alone?

Solution:
Step 1: Assign variables:
Let x = time taken by Peter

Step 2: Use the formula:

Step 3: Solve the equation
Multiply both sides with 30x

Example 2:
Jim can dig a hole by himself in 12 hours.
John can do it in 8 hours and Jack can do it in 6.
How long will it take if they work together?

• Show Video Lesson

“Work” Problems: Pipes Filling Up A Tank

Example 1:
A tank can be filled by pipe A in 3 hours and by pipe B in 5 hours. When the tank is full, it can be
drained by pipe C in 4 hours. if the tank is initially empty and all three pipes are open, how many
hours will it take to fill up the tank?

Solution:
Step 1: Assign variables:
Let x = time taken to fill up the tank

Step 2: Use the formula:
Since pipe C drains the water it is subtracted.

Step 3: Solve the equation

The LCM of 3, 4 and 5 is 60

Answer: The time taken to fill the tank is
hours.

Example 2:
Pipe 1 takes 5 days to drain a pool and pipe 2 takes 7 days to drain the pool.
How long will it take for the two pipes to drain the pool together?

• Show Video Lesson

Work Word Problems

It is possible to solve word problems when two people are doing a work job together by solving systems
of equations. To solve a work word problem, multiply the hourly rate of the two people working together
by the time spent working to get the total amount of time spent on the job. Knowledge of solving systems
of equations is necessary to solve these types of problems.

Example:
Latisha and Ricky work for a computer software company. Together they can write a particular computer
program in 19 hours. Latisha can write the program by herself in 32 hours. How long will it take Ricky
to write the program alone?

• Show Video Lesson

Example:
A swimming pool is being drained through the drain at the bottom of the pool, and filled by the hose
at the top. If the hose can fill the pool in 21 hours and the drain can empty the pool in 24 hours,
how many hours will it take to fill the pool if the drain is left open? Express the answer in hours
and round the answer to the nearest hour if needed.

• Show Video Lesson

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

This problem has to do with mowing lawns, someone who’s a contractor of a landscaping business works in a way where they’re ordering different people to do different jobs. In this situation Brooks and Jeremy are asked to mow a lawn together. Here’s what we’re going to do to solve it. Brooks can mow a lawn in 4 hours, Jeremy could mow the same lawn twice as fast. How long would it take them working together? Before we do that let’s figure out how fast Jeremy mows, he goes twice as fast as Brooks so if Brooks takes 4 hours then Jeremy is going to take 2 hours right? Does that make sense? Twice as fast means half as much time so Jeremy is going to be 2 hours to do the job by himself. 2 hours alone, okay so what I’m going to be doing is writing fractions for each of these guys and then adding those fractions together to see how quickly they could do this job working together.
Brooks could mow the lawn in 4 hours that means every hour he does 1 fourth of the job does that make sense think about it I’m going to say it again. Brooks could mow the lawn in 4 hours that means he does 1 fourth of the job in every hour. Similarly Jeremy could mow the lawn in 2 hours. So every hour he’s going to do half of the job. This represents 1 hour together one half plus one fourth when you find a common denominator instead of one half I’m going to write that as two fourths, one fourth plus 2 fourths equals 3 fourths. What that means is that in 1 hour working together they could do 3 fourths of the jobs. Does that make sense we say it again 1 hour working together, they could do 3 fourths of the job, they’re almost done not all the way done.
The way to figure out how long it would take them and to complete the job all the way would be to use the formula fraction they could do together times sum amount of time that they’re working equals 1 total job, 1 complete job. All we need to do here is solve for x. Well the way to undo multiplying by a fraction is to either divide by the fraction, or multiply by the reciprocal. I’m going to multiply both sides here by 4 thirds, 4 thirds these cancel out so I’m left with x equals 4 thirds. What that tells me is it would take them 4 thirds of an hour working together in order to mow this lawn.
Before you start doing your homework problems make sure you’re not doing the meatball answer, the meatball answer for this kind of a problem would be well if Brooks mows it in 4 hours, Jeremy mows it in 2 hours the meatball would say it takes them 6 hours working together what it does it you guys when they work together it goes faster, that’s why again the answer that’s faster than either guy working alone. Keep that straight in your head and don’t pick the silly multiple choice question. Answer.

General Rules

Problems on Time and Work :

1. Aaron alone can finish a piece of work in 12 days and Brandon alone can do it in 15 days. If both of them work at it together, how much time will they take to finish it?

2. A and B together can do a piece of work in 15 days, while B alone can finish it 20 days. In how many days can A alone finish the work?

3. A can do a piece of work in 25 days and B can finish it in 20 days. They work together for 5 days and then A leaves. In how many days will B finish the remaining work?

4. A and B can do a piece of work in 18 days; B and C can do it in 24 days while C and A can finish it in 36 days. If A, B, C works together, in how many days will they finish the work?

5. A and B can do a piece of work in 12 days; B and C can do it in 15 days while C and A can finish it in 20 days. If A, B, C works together, in how many days will they finish the work? In how many days will each one of them finish it, working alone?

● Time and Work

Time and Work

Pipes and Cistern

Practice Test on Time and Work

● Time and Work — Worksheets

Worksheet on Time and Work

Are you feeling confident about your Work Word Problem-Solving Skills? Practice using the worksheets below:

1. Work Word Problem Worksheet #1
2. Work Word Problem Worksheet #2
3. Work Word Problem Worksheet #3
4. Work Word Problem Worksheet #4
5. Work Word Problem Worksheet #5

Are you already part of Team Lyqa?

Join us on Facebook by liking this page:https://www.facebook.com/teamlyqa

and follow this WordPress site to get an update as soon as I publish a new post.

Keep praying. Keep learning. Keep believing.

Work word problems in physics

These work word problems will show how to calculate the work when the
force applied to the object and the displacement of the object
are known. You will therefore use the formula w = F × d

Problem #1:

How many joules of work are done against a cart when a force of 50 N pushes it 1 kilometer away?

Solution:

First convert 1 kilometer to meter. 1 kilometer  = 100 meters.

Then, use the formula w = F × d

w = 50 N × 100 meters

w = 5000 N.m

w = 5000 joules

Interesting work word problems

Problem #2:

Work of 2000 J is required to push an object.

1)  Give 2 examples of what F and d could be.

2)  How much work is required to lift the same object if the distance pushed is 3 times bigger?

3) How much work is required if the force is doubled?

Solution

1)  Examples of what F and d could be

F = 200  N and d  = 10 meters

F = 20 N and d  = 100 meters

F = 50 N and d  = 40 meters

2)  Pick F  = 50 N and d  = 40 meters.

If the distance is 3 times bigger, d = 3 times 40 = 120 meters

W = 50 N × 120 m = 6000 Joules

When the distance is tripled, the work is also tripled

3)  Pick F  = 200 N and d  = 10 meters

If F is 2 times bigger, F  = 2 times 200 = 400

W = 400 N × 10 m = 4000 Joules

When the force is doubled, the work is also doubled

Problem #3:

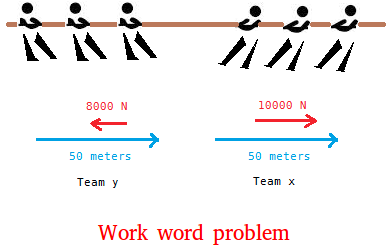
In
a tug of war, team x pulled team y with a force of 10000 N a distance
of 50 meters. Team y did not win because they were only able to exert of
force of 8000 N. Calculate the work of each team.

Since the direction may or may not be the same, we will use the formula w = F × d × cos(x)

The graph above shows the force and direction for both teams.

For team x, the angle between the force and the direction is 0 degrees.

w = 10000 × 50 × cos(0)

{ cos(0) = 1

w = 10000 × 50 × 1

w = 500000 joules

For team y, the angle between the force and the direction is 180 degrees.

w = 10000 × 50 × cos(180)

{ cos(180) = -1

w = 8000 × 50 × -1

w = -400000 joules

Notice that the work is negative for team y.

This is going to be the case when the direction of the force is opposite to the direction of movement. 

Twelve machines work twelve hours a day to complete a task .

1. How many machines will be required to finish double the task in the same time?
2. How many machines will be required to finish the task in same time if four of the machines broke down after 3^rd hour?

Solution:

Using Logic :

Let number of machines be y.

a) 12 machines complete the task in 12 hrs. Double the machines are required to finish double the task in the same time. Therefore, number of machines required to complete double the task = 24 .

b) 4 machines worked for 3 hrs = 12 machine hrs – work of one machine in 12 hrs

To finish the task 4 machines should have worked for 12 hrs = 12 X 4 = 48 machine hrs. Therefore, 12 machines + 3 extra machines = 15 machines.

Using Formula:

Let number of machines be Y.

a) Task = 12 machines x 12 hrs = 144 machine hrs

Double task = 2 x 144 hrs = 288  machine hrs

288 machine hrs = Y machines X 12hrs

Number of machines Y = 288 machine hrs/ 12 hrs = 24 machines

b) Task = 12 machines x 12 hrs = 144 machine-hrs

     144 = (4 machines x 3 hrs ) + (Y-4) machines  x 12 hrs

           = 12 machine hrs + 12 Y machine hrs  – 12 x 4 machine hrs

     144 = 12 y machine hrs – 36 machine hrs

     180 machine hrs = 12 Y machine hrs

     Y= 180 machine hrs/12 hrs  = 15 machines  

Example:

A road can be constructed by twelve employees working eight hours a day for thirty days. To speed completion of the project , a contractor deploys 30 employees to complete the project in sixteen days. How many hours a day must the employees work , in order to finish the construction work?

Solution:

Using logic:

Number of men in 1^st case= 12

Number of men in 2^nd case=30

Number of men in 2^nd case is 2.5 times more than that in 1^st case.

Therefore, number of hrs in 1^st case will be = 2.5 x number of hrs in 2^nd case

i.e. 30 days x 8 hrs = 2.5 (16days x h)

h = 30×8 / 2.5×16 hrs = 6hrs

Using Formula:

Construction is done by 12 men in 30 days working 8 hrs a day

Construction of road  is Work W = man x hrs = man x (days x hrs)

                                            = 12 men x 30 days x 8 hrs

                                            = 2880man hrs

Construction of same road by 30 men takes h hrs per day for 16 days

 W = 2880 man-hrs = 30 men x 16 days x h hrs

 h = 2800 man-hrs / (30 men x 16) = 6 hrs

‘Work’ Word Problems Made Easy

This post is a part of [GMAT MATH BOOK]

created by: sriharimurthy
edited by: bb, walker, Bunuel

———————————————————

NOTE: In case you are not familiar with translating word problems into equations please go through THIS POST FIRST.

What is a ‘Work’ Word Problem?

• It involves a number of people or machines working together to complete a task.
• We are usually given individual rates of completion.
• We are asked to find out how long it would take if they work together.

Sounds simple enough doesn’t it? Well it is!

There is just one simple concept you need to understand in order to solve any ‘work’ related word problem.

The ‘Work’ Problem Concept

STEP 1: Calculate how much work each person/machine does in one unit of time (could be days, hours, minutes, etc).

How do we do this? Simple. If we are given that A completes a certain amount of work in X hours, simply reciprocate the number of hours to get the per hour work. Thus in one hour, A would complete (frac{1}{X}) of the work. But what is the logic behind this? Let me explain with the help of an example.

Assume we are given that Jack paints a wall in 5 hours. This means that in every hour, he completes a fraction of the work so that at the end of 5 hours, the fraction of work he has completed will become 1 (that means he has completed the task).

Thus, if in 5 hours the fraction of work completed is 1, then in 1 hour, the fraction of work completed will be (1*1)/5

STEP 2: Add up the amount of work done by each person/machine in that one unit of time.

This would give us the total amount of work completed by both of them in one hour. For example, if A completes (frac{1}{X}) of the work in one hour and B completes (frac{1}{Y}) of the work in one hour, then TOGETHER, they can complete (frac{1}{X}+frac{1}{Y}) of the work in one hour.

STEP 3: Calculate total amount of time taken for work to be completed when all persons/machines are working together.

The logic is similar to one we used in STEP 1, the only difference being that we use it in reverse order. Suppose (frac{1}{X}+frac{1}{Y}=frac{1}{Z}). This means that in one hour, A and B working together will complete (frac{1}{Z}) of the work. Therefore, working together, they will complete the work in Z hours.

Advice here would be: DON’T go about these problems trying to remember some formula. Once you understand the logic underlying the above steps, you will have all the information you need to solve any ‘work’ related word problem. (You will see that the formula you might have come across can be very easily and logically deduced from this concept).

Now, lets go through a few problems so that the above-mentioned concept becomes crystal clear. Lets start off with a simple one :

Example 1.
Jack can paint a wall in 3 hours. John can do the same job in 5 hours. How long will it take if they work together?

Solution:
This is a simple straightforward question wherein we must just follow steps 1 to 3 in order to obtain the answer.

STEP 1: Calculate how much work each person does in one hour.
Jack → (1/3) of the work
John → (1/5) of the work

STEP 2: Add up the amount of work done by each person in one hour.
Work done in one hour when both are working together = (frac{1}{3}+frac{1}{5}=frac{8}{15})

STEP 3: Calculate total amount of time taken when both work together.
If they complete (frac{8}{15}) of the work in 1 hour, then they would complete 1 job in (frac{15}{8}) hours.

Example 2.
Working, independently X takes 12 hours to finish a certain work. He finishes 2/3 of the work. The rest of the work is finished by Y whose rate is 1/10 of X. In how much time does Y finish his work?

Solution:
Now the only reason this is trickier than the first problem is because the sequence of events are slightly more complicated. The concept however is the same. So if our understanding of the concept is clear, we should have no trouble at all dealing with this.

‘Working, independently X takes 12 hours to finish a certain work’ This statement tells us that in one hour, X will finish (frac{1}{12}) of the work.

‘He finishes 2/3 of the work’ This tells us that (frac{1}{3}) of the work still remains.

‘The rest of the work is finished by Y whose rate is (1/10) of X’ Y has to complete (frac{1}{3}) of the work.

‘Y’s rate is (1/10) that of X‘. We have already calculated rate at which X works to be (frac{1}{12}). Therefore, rate at which Y works is (frac{1}{10}*frac{1}{12}=frac{1}{120}).

‘In how much time does Y finish his work?’ If Y completes (frac{1}{120}) of the work in 1 hour, then he will complete (frac{1}{3}) of the work in 40 hours.

So as you can see, even though the question might have been a little difficult to follow at first reading, the solution was in fact quite simple. We didn’t use any new concepts. All we did was apply our knowledge of the concept we learnt earlier to the information in the question in order to answer what was being asked.

Example 3.
Working together, printer A and printer B would finish a task in 24 minutes. Printer A alone would finish the task in 60 minutes. How many pages does the task contain if printer B prints 5 pages a minute more than printer A?

Solution:
This problem is interesting because it tests not only our knowledge of the concept of word problems, but also our ability to ‘translate English to Math’

‘Working together, printer A and printer B would finish a task in 24 minutes’ This tells us that A and B combined would work at the rate of (frac{1}{24}) per minute.

‘Printer A alone would finish the task in 60 minutes’ This tells us that A works at a rate of (frac{1}{60}) per minute.

At this point, it should strike you that with just this much information, it is possible to calculate the rate at which B works: Rate at which B works = (frac{1}{24}-frac{1}{60}=frac{1}{40}).

‘B prints 5 pages a minute more than printer A’ This means that the difference between the amount of work B and A complete in one minute corresponds to 5 pages. So, let us calculate that difference. It will be (frac{1}{40}-frac{1}{60}=frac{1}{120})

‘How many pages does the task contain?’ If (frac{1}{120}) of the job consists of 5 pages, then the 1 job will consist of (frac{(5*1)}{frac{1}{120}} = 600) pages.

Example 4.
Machine A and Machine B are used to manufacture 660 sprockets. It takes machine A ten hours longer to produce 660 sprockets than machine B. Machine B produces 10% more sprockets per hour than machine A. How many sprockets per hour does machine A produce?

Solution:
The rate of A is (frac{660}{t+10}) sprockets per hour;
The rate of B is (frac{660}{t}) sprockets per hour.

We are told that B produces 10% more sprockets per hour than A, thus (frac{660}{t+10}*1.1=frac{660}{t}) —> (t=100) —> the rate of A is (frac{660}{t+10}=6) sprockets per hour.

As you can see, the main reason the ‘tough’ problems are ‘tough’ is because they test a number of other concepts apart from just the ‘work’ concept. However, once you manage to form the equations, they are really not all that tough.

And as far as the concept of ‘work’ word problems is concerned – it is always the same!

More on Work/Rate Problems Under the Spoiler

_________________

Sometimes you will encounter a word problem that asks you to determine how long it would take two people working together to finish a job.  Solving this type of problem requires a few steps of logic.  Let’s jump straight to an example.

Example:  Jennifer can mop a warehouse in 8.3 hours.  Heather can mop the same warehouse in 11.2 hours.  Find how long it would take them if they worked together.

Solution:  We set up an equation to model Jen’s work.  We know that Jen can mop a warehouse in 8.3 hours, which means

(Large frac{{1{text{Warehouse  Mopped}}}}{{8.3{text{  hours}}}} = 0.12{text{Warehouse  Mopped  in  }}1{text{  hour}})

That is, Jen can mop 12 percent of the warehouse in one hour.  We set up a similar equation for Heather.  We know that Heather can mop the same warehouse in 11.2 hours, which means

(Large frac{{1{text{Warehouse  Mopped}}}}{{11.2{text{  hours}}}} = 0.09{text{Warehouse  Mopped  in  }}1{text{  hour}})

That is, Heather can mop about 9 percent of the warehouse in one hour.  Now we can find out how much of the warehouse they can mop together in one hour.  We have

(0.12left( {for  Jen} right) + 0.09left( {for  Heather} right) = 0.21)

That is, together they can mop 21 percent of the warehouse in 1 hour.  Let’s set up our final equation to model this word problem.  We use a simple ratio:

(Large frac{{1{text{Warehouse  Mopped}}}}{{x{text{  hours}}}} = Large frac{{0.21{text{Warehouse  Mopped}}}}{{1{text{  hour}}}})

Cross multiplying gives

(x = Large frac{1}{{0.21}} = 4.76{text{   hours}})

Another Example:  Molly can clean an attic in 10.6 hours.  Jasmine can clean the same attic in 15 hours.  If they worked together how long would it take them?

(Large frac{{1  Attic}}{{10.6  hours}} = 0.09  in  one  hour)

For Jasmine, we have

(Large frac{{1  Attic}}{{15  hours}} = 0.07  in  one  hour)

Together, their labor yields

(0.09 + 0.07 = 0.16  together  in  one  hour)

Then we use another ratio to solve the problem

(Large frac{{1  Attic  Cleaned}}{{x  hours}} = Large frac{{0.16  Cleaned}}{{1  hour}})

Then, by cross multiplying,

(x = Large frac{1}{{0.16}} = 6.25  hours)

Below you can download some free math worksheets and practice.