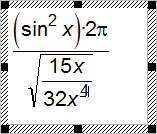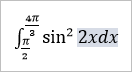Word все формулы по математике для

Оглавление:

• Формулы сокращенного умножения
• Квадратное уравнение и формула разложения квадратного трехчлена на множители
• Свойства степеней и корней
• Формулы с логарифмами
• Арифметическая прогрессия
• Геометрическая прогрессия
• Тригонометрия
• Тригонометрические уравнения
• Геометрия на плоскости (планиметрия)
• Геометрия в пространстве (стереометрия)
• Координаты
• Таблица умножения
• Таблица квадратов двухзначных чисел
• Расширенная PDF версия документа «Все главные формулы по школьной математике»

Формулы сокращенного умножения

К оглавлению…

Квадрат суммы:

Квадрат разности:

Разность квадратов:

Разность кубов:

Сумма кубов:

Куб суммы:

Куб разности:

Последние две формулы также часто удобно использовать в виде:

Квадратное уравнение и формула разложения квадратного трехчлена на множители

К оглавлению…

Пусть квадратное уравнение имеет вид:

Тогда дискриминант находят по формуле:

Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:

Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:

Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:

Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:

Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:

Произведение корней квадратного уравнения может быть вычислено по формуле:

Парабола

График параболы задается квадратичной функцией:

При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:

Игрек вершины параболы:

Свойства степеней и корней

К оглавлению…

Основные свойства степеней:

Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.

Основные свойства математических корней:

Для арифметических корней:

Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:

Для корня четной степени имеется следующее свойство:

Формулы с логарифмами

К оглавлению…

Определение логарифма:

Определение логарифма можно записать и другим способом:

Свойства логарифмов:

Логарифм произведения:

Логарифм дроби:

Вынесение степени за знак логарифма:

Другие полезные свойства логарифмов:

Арифметическая прогрессия

К оглавлению…

Формулы n-го члена арифметической прогрессии:

Соотношение между тремя соседними членами арифметической прогрессии:

Формула суммы арифметической прогрессии:

Свойство арифметической прогрессии:

Геометрическая прогрессия

К оглавлению…

Формулы n-го члена геометрической прогрессии:

Соотношение между тремя соседними членами геометрической прогрессии:

Формула суммы геометрической прогрессии:

Формула суммы бесконечно убывающей геометрической прогрессии:

Свойство геометрической прогрессии:

Тригонометрия

К оглавлению…

Пусть имеется прямоугольный треугольник:

Тогда, определение синуса:

Определение косинуса:

Определение тангенса:

Определение котангенса:

Основное тригонометрическое тождество:

Простейшие следствия из основного тригонометрического тождества:

Формулы двойного угла

Синус двойного угла:

Косинус двойного угла:

Тангенс двойного угла:

Котангенс двойного угла:

Тригонометрические формулы сложения

Синус суммы:

Синус разности:

Косинус суммы:

Косинус разности:

Тангенс суммы:

Тангенс разности:

Котангенс суммы:

Котангенс разности:

Тригонометрические формулы преобразования суммы в произведение

Сумма синусов:

Разность синусов:

Сумма косинусов:

Разность косинусов:

Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму

Произведение синусов:

Произведение синуса и косинуса:

Произведение косинусов:

Формулы понижения степени

Формула понижения степени для синуса:

Формула понижения степени для косинуса:

Формула понижения степени для тангенса:

Формула понижения степени для котангенса:

Формулы половинного угла

Формула половинного угла для тангенса:

Формула половинного угла для котангенса:

Тригонометрические формулы приведения

Формулы приведения задаются в виде таблицы:

Тригонометрическая окружность

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения

К оглавлению…

Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:

Для остальных тригонометрических функций запись однозначна. Для косинуса:

Для тангенса:

Для котангенса:

Решение тригонометрических уравнений в некоторых частных случаях:

Геометрия на плоскости (планиметрия)

К оглавлению…

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Геометрия в пространстве (стереометрия)

К оглавлению…

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Координаты

К оглавлению…

Длина отрезка на координатной оси:

Длина отрезка на координатной плоскости:

Длина отрезка в трёхмерной системе координат:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):

Таблица умножения

К оглавлению…

Таблица квадратов двухзначных чисел

К оглавлению…

Расширенная PDF версия документа «Все главные формулы по школьной математике»:

К оглавлению…

Как писать формулы в Ворд, на этот вопрос будет дан подробный ответ в статье. Многие новички, которые работают с этим редактором, пишут формулы в Ворде вручную, что не удобно. В Word есть редактор готовых формул в виде заготовок, которые мы можем использовать для написания различных документов.

Работа с формулами в Ворде, кому и зачем это надо

Здравствуйте друзья! Текстовый редактор Word имеет много полезных функций и инструментов, которые помогают сделать ту или иную работу достаточно быстро.

Например, Вам нужно написать контрольную (научную, дипломную) работу по алгебре, геометрии, химии, физике, работу по другим предметам. В этих работах часто пишут формулы. Вам придется писать формулы в программе Ворд, если Вы делаете курсовую или дипломную работу на заказ.

Работа с формулами в Ворде нужна в основном студентам, школьникам и тем, кто зарабатывает через Интернет с помощью Word. Иногда формулы встречаются в статьях на сайтах и блогах. Как писать формулы в Ворд быстро? На данный вопрос стоит ответить, поскольку это надо знать студентам, школьникам и тем, кто зарабатывает через Интернет с помощью Ворда. По инструкции, Вы сможете написать любую формулу, без особых затруднений.

к оглавлению ↑

Как писать формулы в Ворд (вставлять)

Есть несколько способов вставки формул в документ Ворда:

• через функцию «П»;
• с помощью функции «Объект».

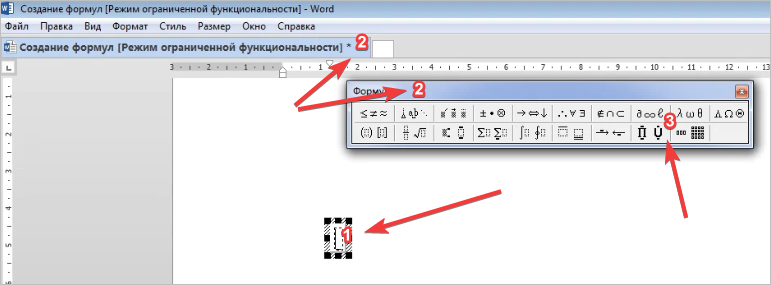
Рассмотрим оба варианта. Первое, что нам нужно сделать, это открыть документ Word на компьютере и кликнуть мышкой  на то место в документе где будет установлена формула. Далее, нажимаем вверху этого же документа раздел «Вставка» и кликаем мышкой по функции «П» «Формула» (Скрин 1).

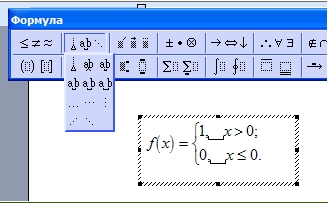
Отобразятся различного вида формулы. Нажимаем левой кнопкой мыши на любую из них.

После этого в документ вставиться готовый редактор формулы, которым Вы сможете полноценно управлять (Скрин 2).

В самом верху панели документа, можно увидеть объекты, которые вставляются в формулу:

• дроби;
• индексы;
• радикалы;
• интегралы и так далее.

После работы над формулой, её можно сохранить. Нажимаете с правой стороны редактора формулы – «Параметры формул» (Скрин 3).

Затем, выбираете из списка «Сохранить, как новую формулу».

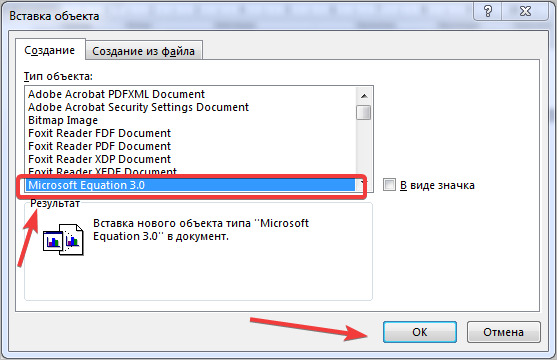
Итак, как писать формулы в Ворд вторым способом? Здесь, всё просто. Нажимаем, снова  на «Вставка» далее «Объект» из раздела выбираем «Microsoft Equation 3.0» и сохраняемся с помощью кнопки «ОК» (Скрин 4).

Появится панель управления с формулами, и сам редактор, в котором можно прописать любую формулу через эту панель (Скрин 5).

Просто выбирайте готовые значения формул левой кнопкой мыши и устанавливаете их в редакторе.

к оглавлению ↑

Как поменять шрифт в Ворде в формулах

В формулах можно поменять шрифт. Для этого мы нажимаем по вставленной формуле и правой кнопкой мыши из меню выбираем шрифт (Скрин 6).

Откроется панель со списком разных шрифтов. Выбираете любой из них, и сохраняете все изменения кнопкой «ОК». После этого, шрифт Вашей формулы должен изменится на другой.

к оглавлению ↑

Как в Ворде вставлять формулы с дробями

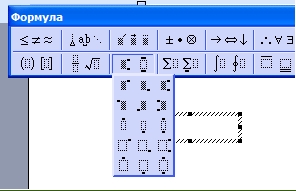
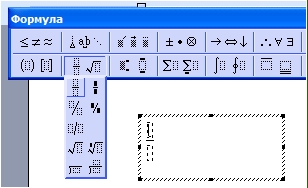
Теперь, мы попробуем вставить в Ворде формулы с дробями. Это делается очень легко. Выделяете формулу в редакторе, и наверху в панели управления формулами, нужно нажать кнопку «Дробь». Там можно выбрать формулы с дробями (Скрин 7).

И заменить основную формулу на другую.

к оглавлению ↑

Как перемещать формулу в Ворде

Перемещать формулу в Word Вам помогут обычные горячие клавиши. Для этого выделяем формулу с помощью таких клавиш, как CTRL+A, (нужно нажать их одновременно). Далее, нажимаем ещё клавиши CTRL+C копировать.

Затем, следует кликнуть на кнопку «Enter», чтобы выбрать расположение для формулы в Ворде и нажать на CTRL+V вставить. Таким образом, Ваша формула переместится в определённое место документа.

к оглавлению ↑

Заключение

Мы рассмотрели в этой статье, как писать формулы в Ворд. Вы можете вставлять формулы автоматически, через панель редактора формул, который предоставляет пользователям редактор Word. Важно отметить, что в таких операционных системах,  как Windows 8,10 есть панель математического ввода. С помощью которой, можно также легко создавать формулы. Удачи Вам и всего хорошего!

С уважением, Иван Кунпан.

Просмотров: 122457

Обычно в Word создаются таблицы, которые содержат числовую информацию, такую ​​как простые выписки или прайс-листы. Если бы потребовалось применить простые операции расчета, эти формулы можно решить в программе Word без необходимости использования электронной таблицы Excel. В этом разделе обсуждается использование основных математических операторов и функций для разработки простых операций вычисления в таблицах Word.

Возможно вы искали статью на тему Как написать математическую формулу в ворд

Сумма в ворде

Для настройки операции суммирования необходимо использовать поле формулы, действуя следующим образом:
1 — Поместите точку вставки в ячейку, где должен быть получен результат.
2 — На вкладке «Макет» группы кнопок «данные» нажмите кнопку Формула FX

После того, как вы нажали кнопку «Формула» на вкладке «Макет», откроется диалоговое окно «Формула», в котором в качестве параметра предлагается ввести функцию суммы = SUM (ВЫШЕ)

Word: диалоговое окно «Формула»

В окне Формула по умолчанию предлагается операция суммирования ( SUM ).
Названия функций расчета, применимых в Word, в последних версиях программы, больше не переводятся.

Предлагаемых операторов 18 и в их синтаксисе в скобках необходимо указывать направление расчета. Например, выше ( ABOVE ), ниже (BELOW) , слева ( LEFT ), справа RIGHT )
Функции AVERAGE (), COUNT (), MAX (), MIN (), PRODUCT () и SUM () также могут принимать ссылки на ячейки таблицы в качестве аргументов. ссылочные координаты в режиме Excel или в первом столбце таблицы будут называться A, затем B, C, D …. и первая строка 1, а затем 2,3,4 ….

Пример: чтобы добавить значения в столбец 2 вместо = SUM (ABOVE), можно написать = B2 + B3 + B4, учитывая, что подразумеваются альфа-заголовки (как если бы мы были в листе Excel) –числа столбцов и строк.

В этом режиме выражения формулы можно организовать еще более сложные расчеты, например, расчет НДС (см. Изображение ниже).
При построении этих формул следует учитывать, что они будут выполняться слева направо. Как и в математических уравнениях, операторы * (умножение) и / (деление) будут иметь приоритет при расчете сумм и вычитаний.
Если были суммы или вычитания, которые можно было выполнить перед умножением или делением, они будут заключены в скобки (). Пример = (А1 + А2) * А5

Обновить формулы в ворде

Формулы в Word автоматически обновляются при открытии документа. Вы можете вручную обновить результат формулы. Просто выделите результат и щелкните правой кнопкой мыши по нему и выберите опцию «Обновить поле».

Все функции, рассмотренные в Word, перечислены ниже.

ABS Возвращает положительное значение числа формулы, независимо от того, является ли его значение положительным или отрицательным.
AND Возвращает значение 1, если все выраженные логические выражения являются истинными, или значение 0 (ноль), если хотя бы одно из выражений является ложным.
AVERAGE Рассчитывает среднее значение ряда значений.
COUNT Подсчитывает количество элементов в списке.
DEFINED Возвращает значение 1 или 0 в зависимости от того, является ли выражение допустимым или не может быть вычислено.
FALSE Возвращает нулевое значение.
IF Вычисляет первый аргумент. Если первый аргумент является истинным, возвращает второй аргумент; если ложным — третий. Пример (=IF(SUM(ABOVE)>10;да;нет))
INT Возвращает только целочисленные значения, исключая десятичные дроби без аппроксимации.
MIN Возвращает наименьшее значение числового ряда.
MAX Возвращает наибольшее значение числового ряда.
MOD Возвращает остаток, полученный в результате деления значения x на значение y несколько раз.
NOT Возвращает значение 0 (false), если логическое выражение x истинно, или значение 1 (true), если выражение ложно. ИЛИ Возвращает значение 1 (истина), если одно или оба из логических выражений x и y являются истиной, или значение 0 (ложь), если оба выражения ложны.
OR Имеет два аргумента. Если хотя бы один из них является истинным, возвращает значение 1. Если оба аргумента являются ложными, возвращает значение 0. В основном используется в функции IF.
PRODUCT Рассчитать произведение элементов, указанных в скобках.
ROUND. Вернуть округленное значение для указанного числа десятичных знаков.
SIGN Возвращает значение 1, если ссылочная ячейка x имеет положительное значение, -1 и отрицательное.
SUM Рассчитать сумму заданного диапазона ячеек TRUE Возвращает значение 1.
TRUE Если аргумент является истинным, возвращает значение 1, если ложным — 0. В основном используется в функции IF.

В статье использовался Microsoft word 2016 купить который вы можете на сайта softtools.ru

Видео инструкция

Ниже представлены практические советы, как с помощью офисного пакета Word вставить в текст простые и сложные математические формулы.

Значок суммы на панели

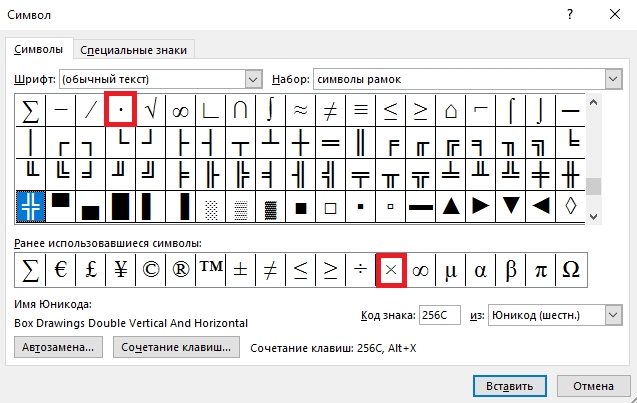
Символы стандартных математических операций можно найти на вкладке Вставка, панель инструментов Символы.

К примеру знак Суммы найдете в этом всплывающем окне.

Если его не найдете, то откройте Другие символы и поищите в перечне.

Вставляем сумму, вычитание, умножение и деление

Простую формулу суммы можно записать также с использованием этой панели.

Плюс

Минус

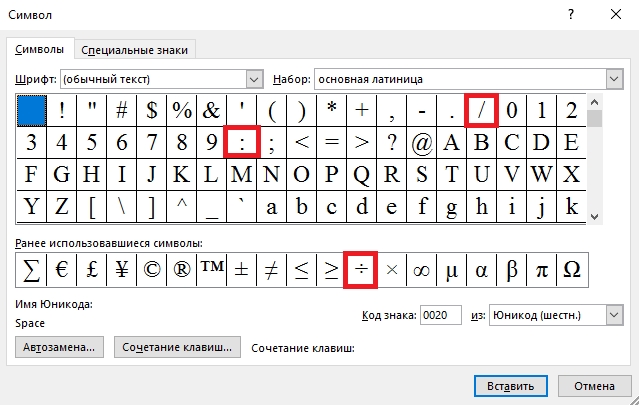
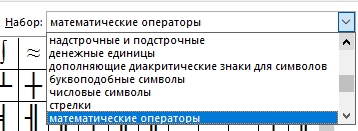
Деление сразу в трёх вариантахУмножить в двух вариациях

Найдете там также корень, интеграл, дифференциал и множество других полезных символов. Справа раскрывающийся список Набор открывает перечень групп символов для вставки.

При желании, можно настроить параметры автозамены и сочетание клавиш, для ускорения процесса ввода требуемых символов.

Составляем сложную формулу

Если же потребуется вставить сложную формулу, содержащую дроби, степени, индексы или что-то еще, то лучше прибегнуть к другому механизму.

В Microsoft Word специально для этого предусмотрен комплексный редактор. Этот инструмент, интегрированный в текстовый редактор, работает с уравнениями, как с текстом, а не как с изображениями, а затем, в случае необходимости любую функцию можно легко отредактировать, что довольно удобно.

Окно редактора выглядит следующим образом.

Как написать уравнение

Посмотрим, как вставить сложное уравнение в различных версиях офисного пакета Word.

Редактор формул в Word 2003

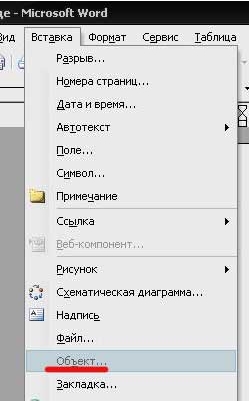
Устанавливаем курсор в требуемое, для вставки место документа и нажимаем вкладку Вставка – Объект.

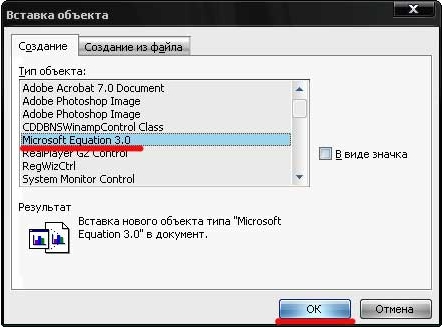
В выплывающем окне выбираем Microsoft equation 3.0 и жмем ОК.

В окне редактора можно выбрать любые требуемые знаки и символы для создания уравнения любой сложности, среди них: дроби, степени, корни, и так далее.

Для выхода из режима ввода кликните на любом пустом месте вне этого окна, затем набирайте дальше свой текст.

Вставляем формулы в Word 2007, 2010, 2013

Во всех этих версиях принцип нахождения редактора подобен. На панели вверху переходим на вкладку Вставка.

Там находим Формула или Уравнение.

Применяем нужные шаблоны и создаем Формулу.

Редактор может быть не установлен. Тогда потребуется дополнительно проинсталлировать этот компонент, запустив программу установки в категории Средства выбрать «Редактор формул».

Составляем формулы

Для удобства работы с большим количеством математических значений, рекомендуем эту панель прикрепить к основной, простым перетаскивание с помощью левой кнопки мыши (Word 2003). В более старших версиях, этот значок уже располагается на панели.

Вводим по нужному шаблону. Например, верхние и нижние индексы вводятся таким образом.

Для набора дробей используется эта панель.

Здесь, следует отметить, что заштрихованные прямоугольники значат, что текст в этой части уже содержится, а пустые служат для ввода нового текста.

Дроби могут быть в двух вариантах, исходя из задач можете выбрать как наклонные, так и прямые.

Окно для заключения выражения в скобки.

Таки же образом можно выделить и отдельные части выражения.

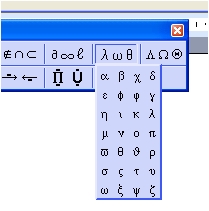
Панель ввода греческих символов.

Аналогичное окно с заглавными буквами располагается справа от этой.

Используя следующую панель можно поставить пробел, так как стандартный его ввод с клавиатуры в этом случае работать не будет.

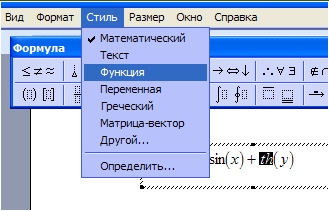
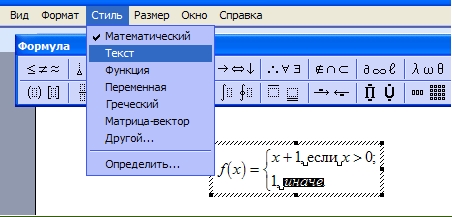
Можно настроить шрифт для названия функций, переменных, векторов, текста и всего остального. Для этого используем меню Стиль.

Для того чтобы текст был наклонным его следует помечать стилем «текст».

Формулы применяются во всех науках, где нужно выполнять вычисления. Они представляют собой численное выражение с известными или неизвестными переменными.

Начиная с версии 2007, в Word можно вставлять формулы не только через Вставка – Объект, но и Вставка – Уравнение. Между двумя вариантами есть некоторые отличия, которые мы рассмотрим ниже.

Первый вариант — Редактор формул

Первый способ создания формулы – вставка объекта. Для этого на главное ленте выбираем вкладку Вставка – Объект, как на рисунке 1:

Рисунок 1

После этого появится окно выбора объекта. В данном случае нам нужно выбрать Microsoft Equation 3.0, как указано на рисунке 2, и нажать ОК:

Рисунок 2

После этого появится рабочая область для набора формул, обозначенная на рисунке цифрой 1, панели редакторов, обозначенные цифрой 2 и элементы формулы под цифрой 3 (рисунок 3):

Рисунок 3

Теперь наберем любую простую формулу в этом редакторе, показанную на рисунке 4:

Рисунок 4

У этого способа создания формул есть один недостаток, который компенсируется во втором варианте: использование некоторых горячих клавиш для более быстрого набора различных математических действий и формул.

Рассмотрим подробнее.

Второй вариант — Использование вкладки Уравнения

Второй вариант ввода формул стал возможен в версиях Word, начиная с 2007.
Выбираем вкладку Вставка-Уравнение, как на рисунке 5:

Рисунок 5

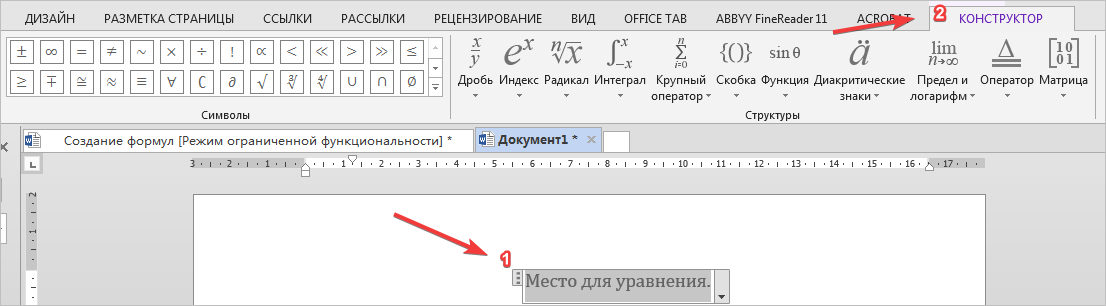
Также можно воспользоваться горячими клавишами «Alt + =». Появится окно для ввода формулы и на ленте откроется редактор формул (рис. 6):

Рисунок 6

Цифрой 1 на рисунке 6 обозначено место для уравнения, цифрой 2 – конструктор, в котором выбирать необходимые символы.

Данный вариант набора формул отличается от предыдущего компактностью, названием группы символов, что упрощает поиск нужного.

Набирать формулы с помощью вкладки *Уравнение тоже просто. Можно использовать горячие клавиши, как при наборе в LaTex. Вот некоторые для примера:

• «^» – ввод надстрочного индекса;
• «_» – ввод подстрочного индекса.

Греческие большие и малые буквы можно вводить, используя для этого обратный слеш и английскую раскладку:

• mu – μmu;
• gamma – γgamma и т.д.

В самом редакторе можно найти варианты быстрого набора символов или знаков. Для этого нужно зайти на вкладку Сервис на вкладке Конструктор (рисунок 7):

Рисунок 7

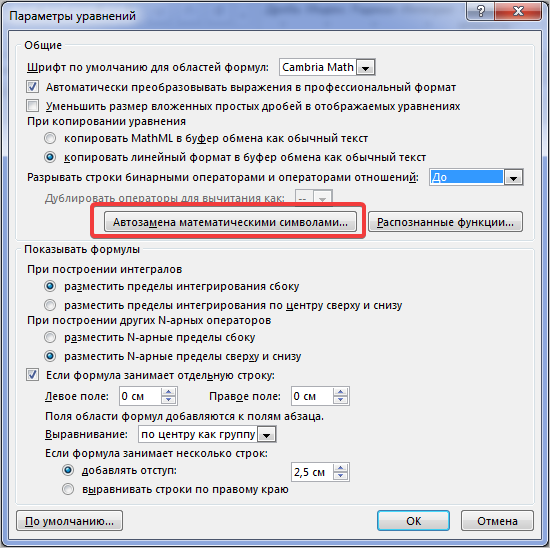
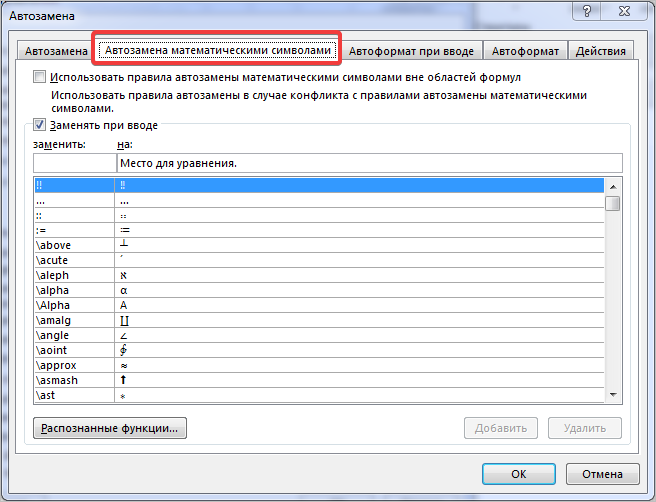
После этого выбираем Автозамена математическими символами (рисунок 8):

Рисунок 8

На рисунке 9 нам нужна вкладка Автозамена математическими символами:

Рисунок 9

На рисунке слева видим, как набрать те или иные символы в линейной формуле, справа – в профессиональной.

Если в первом пункте поставить галочку, то автозаменой можно воспользоваться вне редактора формул.

Для наглядного примера наберем в этом редакторе простую формулу (рисунок 10):

Рисунок 10

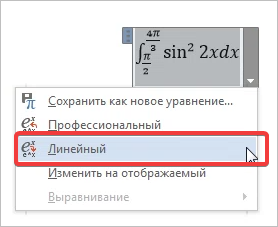
Чтобы посмотреть, как эта формула будет выглядеть в линейном виде, просто выберем функцию Линейный (рисунок 11):

Рисунок 11

Теперь формула примет вид, как на рисунке 12:

Рисунок 12

Мы рассмотрели два варианта создания формул, с помощью которых вид будет понятнее, чем использование линейного варианта.

Редактирование формул будет рассмотрено в другой статье (См. Редактирование формул).

Тест по теме «Формулы в Ворд»