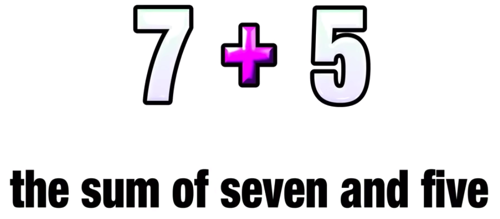Welcome to this complete guide to translating words into algebraic expressions (also known as algebraic translation), where you will learn how to identify and apply key information, in the form of words and phrases, to accurately translate a given set of words into an algebraic expression involving both numbers and variables.
Why is learning how to translate words into algebraic expressions a crucial skill that every math student must learn? Because it is often the case that math problems are expressed completely in words without any explicit use of numbers, expressions, or equations. In order to solve these types of math word problems, students have to be able to translate words into expressions or equations so they may model and solve such scenarios.
Are you ready to learn everything there is to know about algebraic translation?
The following free Translating Words into Algebraic Expressions lesson guide is a step-by-step tutorial that will teach you how to easily and accurately translate any given word phrase into a mat equation.
How can you translate written expressions into numerical form?
The key skill associated with algebraic translation is being able to rewrite mathematical situations expressed in words as a mathematical expression involving numbers, operations, and variables.
Before we get to actually translating words into algebraic expressions, let’s lay some important groundwork!
Tip #1: Expressing Variables
For example, what if we wanted to translate the phrase the sum of seven and five into an expression. It would be pretty easy to translate this phrase into 7 + 5 and your job would be done.
But what if we changed the phrase to the sum of a number and five? How would our numerical expression change? Since a number could represent any value, we have to use a variable (since a variable can represent any value).
In this case, you could translate the sum of a number and five into x + 5 where x represents a number.
When using letters as variables in a math expression or equation, x is the most commonly chosen letter, but you can actually choose any letter to represent an unknown value.
Example A: Translate the phrase ten plus a number into an algebraic expression.
To complete this translation, we can break the given phrase down into three parts:
I: ten ➔ 10
II: plus ➔ +
III: a number ➔ x
Now, you can translate ten into 10, plus into an addition sign, and a number into a variable leaving you with:
ten plus a number ➔ 10 + x
Tip #2: More Than/Less Than
Now, let’s slightly change the words given in Example A as follows:
Example B: Translate the phrase ten more than a number into an algebraic expression.
You probably already know that more than is associated with addition so the sign is not going to change. But what about the order of the terms?
Think about it this way: we have a number (some unknown value) and this phrase represents ten more than whatever that value is. So, in this case, you will start with the variable first and then add ten to it as follows:
ten more than a number ➔ x+ 10
You would be correct to wonder whether or not the order of the terms matters in this example. Technically, it does not because addition is commutative. But what about subtraction, which is not commutative?
See Also: The Commutative Property: Everything You Need to Know
Example C: Translate the phrase six less than a number into an algebraic expression.
Notice again that we are seeing the word than.
You probably already know that less than is associated with subtraction so you already know what sign you will be using.
This phrase represents a value that is six units smaller than whatever our unknown value is. So, to find that number, we would have to take our variable and subtract six from it as follows:
six less than a number ➔ n-6
In cases like Example B and Example C, the second term comes first and the first term comes second (you have to switch the order).
So, we can conclude that than is a switch word, which means that the operator in the middle stays the same, but the first term and the last term are switched. Look out for this relationship when you see the phrase more than or less than in words.
Tip #3: Groupings and Parenthesis
Lets move onto another example…
Example D: Translate the phrase the difference of three and a number into an algebraic expression.
Translating this phrase into an expression should be pretty straightforward.
Since difference means subtraction, we can easily perform the following algebraic translation:
the difference of three and a number ➔ 3 — p
Now, what if we changed this expression to the difference of three and twice a number plus one
Example D: Translate the phrase the difference of three and twice a number plus one into an algebraic expression.
So, now instead of 3 — p, we have to write the expression as 3 — the entire expression twice a number plus one, which we can call 2p + 1.
Note that you will have to use parenthesis to enclose the entire expression twice a number plus one as follows:
the difference of three and twice a number plus one ➔ 3 — (2p+1)
So, whenever you are performing algebraic translations, you can use parenthesis to separate independnt groupings.
Translate Algebraic Expressions Practice
Now that you understand some key elements of translating words into algebraic expressions, you are ready to practice on your own. Go ahead and translate the following words into algebraic expressions on your own and then check the answer key at the end of this post to see how you did!
Practice Problems: Translate each phrase into an algebraic expression.
1.) nine times a number
2.) the sum of a number and twelve
3.) twice a number decreased by eleven
4.) twenty less than a number
5.) half a number plus two
6.) the quotient of five and a number
7.) five times the difference of a number and one
8.) the sum of sixteen and three times a number minus four
Wait! Don’t scroll further until you’re ready to see the answer key.
Answer Key:
1.) nine times a number ➔ 9x
2.) the sum of a number and twelve ➔ n + 12
3.) twice a number decreased by eleven ➔ 2y — 11
4.) twenty less than a number ➔ m — 20
5.) half a number plus two ➔ (x/2) + 2
6.) the quotient of five and a number ➔ 5 ÷ p
7.) five times the difference of a number and one ➔ 5(x-1)
8.) the sum of sixteen and three times a number minus four ➔ 16 + (3y — 4)
How to Translate Algebraic Expressions Video
Are you looking for more help with translating algebraic expressions? Check out our free step-by-step video lesson below:
Keep Learning:
2 Comments
We use math every day, even if we realize it or not. In fact, math is hidden in the very phrases we say or in the books we read.
Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)
You may not express everything into a mathematical expression or equation, but whenever you have to figure out how much time is left to complete a task or how much money you need to buy an item you’re using math and you’re intuitively Translating Words into Algebraic Expressions!
For example, you’re in the middle of math class and you look up at the clock and notice that it is 9:12am. You quickly do some mental math and realize that if class started at 8:10am and gets out 9:20am, that means you only have 8 minutes left in class and that you’ve been happily learning for one hour and 2 minutes.
Mathematical Symbols
Do you realize we just created a mathematical expression?
Okay, so an expression contains variables, numbers and/or symbols, whereas an equation has an equal sign between two expressions. And without even realizing it, we created an expression that related the time on the clock to the amount of we had left in class.
In this lesson we are going to first come up with a list of some common vocabulary that is used in mathematics, like Palm Beach State College, and make sure we know what operation goes with each key word, so we are able to convert english words into mathematical symbols.
Common Key Words for Translating into Symbols
- Add: sum, addition, more than, increased by, greater, plus, total
- Subtract: decreased by, less, less than, subtract, difference, diminished by, reduced, minus
- Multiply: times, product of, percent of, twice, doubled
- Divide: quotient, divided by, per, quantity
- Equals: is, was, equals, will be, results in
This list is just the beginning, and we will explore other key terms together throughout the lesson. But just knowing these common words will undoubtedly help you in solving word problems, for you will have the tools necessary to take any word or phrase and determine what is being asked and how to go about finding the answer you seek.
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Get My Subscription Now
Still wondering if CalcWorkshop is right for you?
Take a Tour and find out how a membership can take the struggle out of learning math.

Related Pages
More Lessons for Algebra
Math Worksheets
Correctly translating words to equations is the key to solving math word problems. Recognizing some key words and phrases may help you in the translation.
Keywords that involve Addition
sum
total
altogether
more than
greater than
consecutive
increased by
plus
gained
added
grew by
older than
farther than
Example:
| The sum of the length and width is 30. | l + w = 30 |
| The length is 4 more than the width. | l = w + 4 |
| The length is greater than the width by 5. | l = w + 5 |
| The consecutive integer after the integer n is 20. | n + 1 = 20 |
| Jane is two years older than Alice. | j = a + 2 |
| Alice ran 5 kilometers farther than Jane. | a = j + 5 |
Keywords that involve Subtraction
difference
diminished by br>
fewer than
less than
decreased by
removed
taken away
lost
minus
subtracted from
younger than
Example:
| The difference between Jane’s age and Alice’s age is 10. | |J — A| = 10 |
| John has 10 fewer coins than Alice. | J = A — 10 |
Keywords that involve Multiplication
product
twice
doubled
tripled
times
multiplied by
of
Example:
| The product of the length and the width is 50. | lw = 50 |
| The length is twice the width. | l = 2w |
| John took half the number of marbles. |
Keywords that involve Division
quotient
divided by
divided into
quotient of
shared equally
in
per
Example:
The following video shows more keywords that can be used for algebra word problems
More examples and videos of algebra word problems.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Translating Words into Math
It’s no big surprise that variables act like pronouns, because (believe it or not) math is basically its own language, defined by numeric and logical rules. Therefore, one of the first skills you must master is how to translate regular English into this new (much geekier) math language. For now, I will help you translate English phrases into mathematical phrases, called expressions.
The expressions we’ll be translating are very straightforward. For example, the phrase «3 more than an unknown number» becomes the mathematical expression «x + 3.» Because the unknown number has no explicitly stated value, we label it with a variable x. To get a value three more than x, simply add 3 to it. If this is tricky to you, just think in terms of a real number example. Ask yourself «What is 3 more than the number 7?» Clearly the answer is 10, and you get that answer via the expression «7 + 3 = 10.» So, to get 3 more than an unknown number, replace the known number 7 with the unknown number x.
In this translation problem, the key words were «more than,» because they clued you in that addition will be necessary. Each operation has its own cue words, and I’ve listed them here, with an example for each:
Addition
Kelley’s Cautions
Since subtraction is not commutative, be careful to get the order of the numbers right. Notice that «5 less a number» and «5 less than a number» mean completely different things.
- More than/greater than: «11 greater than a number» means «x + 11″
- Sum: «The sum of a number and 6» means «x + 6″
Subtraction
Critical Point
If no symbol is written between two things, multiplication is implied. Thus, 5y means «5 times y» and 2(x + 1) means «2 times the whole expression (x + 1).» Also, from this point forward, I will usually use the symbol «·» to indicate multiplication, because it’s too easy to mix up the other multiplication symbol, , with the variable x.
- Fewer than/less than: «7 fewer than a number» means «x — 7″
- Less: «17 less a number» means «17 — x«
- Difference: «The difference of a number and 6» means «x — 6″
Multiplication
You’ve Got Problems
Problem 1: Translate into a mathematical expression: 5 less than one third of a number.
- Product: «The product of a number and 3» means «x · 3″, also written «3x» (since multiplication is commutative, the order in which you write the numbers doesn’t matter)
- Of: «Half of 20″ means » 12 · 20″
Division
- Quotient: «The quotient of 10 and a number» means «10 · x«
- Fractions: Don’t forget that any expression written as a fraction is technically a division problem in disguise.
Example 1: Translate into mathematical expressions.
- (a) The sum of 6 and twice a number
- Solution: The phrase «twice a number» translates into two times the number, or 2x. (Think about ittwice the number 8 would be 2 · 8 = 16.) The word «sum» indicates that you should add 6 and 2x together to get a final answer of 6 + 2x.
- (b) The product of 2 and 3 more than a number
- Solution: You may be tempted to give an answer of 2 · x + 3, but that equals 2x + 3, or «3 more than 2 times a number.» You need to use parentheses to keep the x + 3 together like so: 2(x + 3). Now, the 2 is multiplied by the entire x + 3, not just the x.
Excerpted from The Complete Idiot’s Guide to Algebra © 2004 by W. Michael Kelley. All rights reserved including the right of reproduction in whole or in part in any form. Used by arrangement with Alpha Books, a member of Penguin Group (USA) Inc.
You can purchase this book at Amazon.com and Barnes & Noble.
- Behold the Power of Exponents
In the 19th century, Felix Klein proposed a new perspective on geometry known as transformational geometry. Most of the proofs in geometry are based on the transformations of objects. There are four types of transformations possible for a graph of a function (and translation in math is one of them). They are:
- Rotations
- Translations
- Reflections
- Dilation
In this chapter, we will learn about translation in mathematics using translation math definition and translation math examples. Do try your hand at a few translation math problems on translation geometry at the end of the page.
| 1. | What is Translation in Math? |
| 2. | Preimages and Images of Translation |
| 3. | Translations on the Coordinate Plane |
| 4. | How to Graph Translations in Math? |
| 5. | Translations of Functions |
| 6. | Translation Represented by a Column Vector or Matrix |
| 7. | FAQs on Translations Math |
What is Translation in Math?
Translation Math Definition
A translation in math moves a shape left or right and/or up or down. The translated shapes look exactly the same size as the original shape, and hence the shapes are congruent to each other. They just have been shifted in one or more directions. Since it is just moving of the shape from one place to other, there is no change in the shape.
The direction or the path of this change in position of the object can vary i.e., initially the object can move left, then turn right, and so on. While translating, all the points on the shape will shift by the same number of units. For example, if one point shifts 2 units to the right, then all the points will also move 2 units to the right.
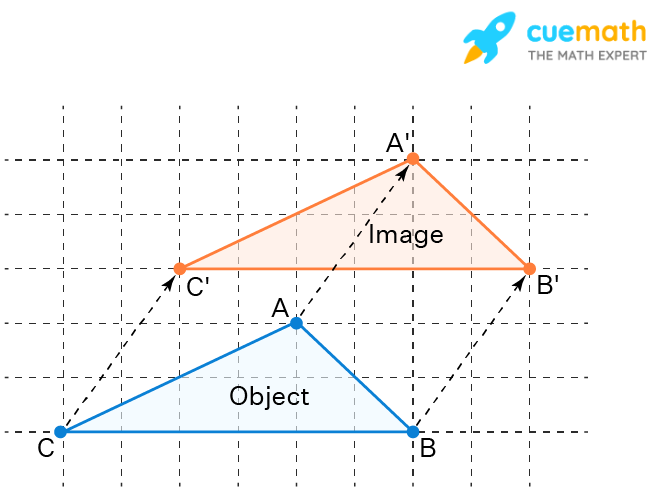
Translation is one of the transformations in math. When a shape has been transformed, the original shape is called the preimage and the vertices are usually labeled using uppercase letters (Example: ABCD). The translated shape is called the image and the vertices are labeled using uppercase letters with a “prime” next to each (Example: A′B′C′D′, and is pronounced “A-prime, B-prime, C-prime, D-prime”).
Translation in Geometry Example
In the below figure, the preimage is ABC and its image is A’B’C’. Here, ABC is translated in the following two ways (one after the other) to form A’B’C’.
- Moved up (vertically) by 3 units and then
- Moved right (horizontally) by 2 units
Note that while translating the triangle to the left/right/up/down, we moved all the points of the triangle by an equal number of units in the same direction.
Preimages and Images of Translation
As we have just seen, a shape before translations are applied is known as «preimage» and the shape that is obtained after the application of translations is known as «image. In simple words:
- «Preimage» is the shape before translation.
- «Image» is the shape after translation.
Look at the following figure where ABCD is the preimage and A’B’C’D’ is the image of ABC.
Translations on the Coordinate Plane
Any object represented in the coordinate plane can be translated horizontally (left/right) or vertically (up/down). Let us look at the last example to understand translations on the coordinate plane. A graph is represented in the coordinate plane as shown in the figure. While translating, the quadrilateral is shifted 5 units horizontally to the right and 1 unit vertically upward, which means the new translated function for the given figure would be
(x, y) → (x + 5, y + 1)
By this time, you might have got an understanding of the process of writing the translations. Left/right affect the x-coordinate and up/down affect the y-coordinate of a point. Here are the rules of translations.
Translation Rules
- When the shape is moved towards the left by k units, then replace x with x — k.
- When the shape is moved towards the right by k units, then replace x with x + k.
- When the shape is moved up by k units, then replace y with y + k.
- When the shape is moved down by k units, then replace y with y — k.
Example: What are the new coordinates when the translation (x, y) → (x — 2, y + 3) is applied to the point (2, 5).
Solution:
The coordinates of old point (preimage) are (x, y) = (2, 5). Now, applying the given transoformation to this point,
x — 2 = 2 — 2 = 0
y + 3 = 5 + 3 = 8
Thus, the coordinates of the translated point (image) are (0, 8).
How to Graph Translations in Math?
To graph the translation of a shape, we follow the steps below:
- Identify the vertices of the shape.
- Apply the given transformation on each of the vertices to find the new vertices (as shown in the above example).
- Then just plot the new points on the coordinate plane and join them as per the given shape.
Example: A shape is formed with vertices (1, 8), (−3, −5), (−4, 7), and (−6, −2). Plot the image of this shape with respect to the translation (x, y) → (x + 6, y + 1).
Solution:
Let us compute the new coordinates of each of the given vertices.
| Old Coordinates (Before the Translation) |
New Coordinates (After the Translation) |
|---|---|
A (1,  |
(1 + 6, 8 + 1) = (7, 9) = A’ |
| B (−3, −5) | (-3 + 6, -5 + 1) = (3, -4) = B’ |
| C (−4, 7) | (-4 + 6, 7 + 1) = (2,  = C’ = C’ |
| D (−6, −2) | (-6 + 6, -2 + 1) = (0, -1) = D’ |
Let us just plot the preimage and the image.
Translations of Functions
The horizontal translations of curves that represent functions work a little differently when compared to the horizontal translations of points on the coordinate plane. Let us observe the example below.
Here, the preimage is f(x) and the image is f(x + 2). Surprisingly, f(x) has moved left by 2 units (instead of right by 2 units) to give f(x + 2). Yes, this is the case with horizontal translations of functions. But this is not the case with vertical translations. Vertical translations work just like how they work with the translations of points on the coordinate plane.
Rules of Translation of Functions
By the above observation, the rules for writing the translated functions can be summarized as follows:
| Translation of Function | When k > 0 | When k < 0 |
|---|---|---|
|
Horizontal Translation |
Moves f(x) «k» units left. | Moves f(x) «k» units right. |
| Vertical Translation f(x) becomes f(x) + k |
Moves f(x) «k» units up | Moves f(x) «k» units down |
Here are some examples:
- f(x — 2) + 3 moves f(x) by 2 units right and 3 units up.
- g(x + 3) — 5 moves g(x) by 3 units left and 5 units down.
Translating Graphs of Functions
To graph the translated graphs, we can move the given graph left/right/up/down using the above rules. Instead of this, we can translate a graph using the coordinates of some points on it. To graph a function translation f(x + k) + C when the graph of the function f(x) is given, just take some important points of the graph (where the shape is changing or taking turns) and find the new x and y coordinates of each point as follows.
- To find the new x-coordinate, set «x + k = old x-coordinate» and solve this for x.
- To find the new y-coordinate, use «old y-coordinate + C».
After finding all the new points, just plot them and join them. This would give the translated graph. You can find an example of this process in the «Examples» section below.
Translation Represented by a Column Vector or Matrix
The translation of any object can be represented by a column vector or column matrix as: (left(begin{array}{l}
a \ \
b
end{array}right)),
where a is the number of units to move right or left along the x-axis and b is the number of units to move up or down along the y-axis.
- The number at the top represents the right or left movement. A positive number means moving to the right and a negative number means moving to the left.
- The number at the bottom represents up and down movement. A positive number means moving up and a negative number means moving down.
In the following figure, triangle ABC is being translated to triangle A’B’C’:
The translation from ABC to A’B’C’ is «2 units right and 3 units down» and the column vector that represents this translation is (left(begin{array}{c}
2 \ \
-3
end{array}right)).
Important Notes on Translations Math:
- While translating, all the points will shift by the same number of units.
- The shape or size of the object remains unaffected after translation.
- In the horizontal translation, the domain may be affected, whereas in the vertical translation, the range may be affected.
☛ Related Topics:
- Types of Functions
- Cartesian Plane
- Coordinate Geometry
FAQs on Translations Math
What are Translations Math?
A translation in math (also called an isometry) is a transformation of a shape in a plane that preserves length, which means that the object is transformed without getting its dimensions affected. i.e., it may just be shifted to left/right/up/down.
What is the Process of Graphing Translations?
To graph translations, take care of the following things:
- In the coordinate plane (x, y) → (x + k, y + C) means:
moving horizontally right if k > 0 and left if k < 0.
moving vertically up if C > 0 and down if C < 0. - In case of functions, f(x) → f(x + k) + C means:
moving horizontally left if k > 0 and right if k < 0.
moving vertically up if C > 0 and down if C < 0.
Just take care of the above things and move the shape accordingly while graphing translation.
How Do You Solve Translations?
Translation for any object can be solved in two sections, depending on whether the object is translated horizontally, vertically, or both. A function, f(x), after translation can be represented in the general form as f(x) = f(x + k) + C, where
- k is the number of units translated horizontally (right if k < 0 and left if k >0)
- C is the number of units translated vertically (up if C > 0 and down if C < 0)
What are Translations Rules in Math?
The basic rules to be followed while translating an object are as follows:
- Positive translation in the x-axis or horizontally would mean shifting to the left, while negative horizontal translation means shifting to the right.
- Positive translation in the y-axis or vertically would mean shifting the object upward while negative vertical translation means shifting downward.
- The shape or size of the object remains unaffected after translation.
- All the points in the object will shift by the same number of units and direction.
How to Graph Functions Translations?
To graph the translation f(x + k) + C of a function f(x) in math, follow the steps below.
- Note down some coordinates of the old graph (of f(x)). The process of finding x and y coordinates of a point differs and is explained below.
- Set each old x-coordinate to x + k and solve for x and that gives the new x-coordinate of that point.
- Just add C to the old y-coordinate to find the new y-coordinate.
- Just plot all new points and join them as per the shape of the given curve.
How Do You Translate a Shape in Math?
Translation of an object in the coordinate plane involves alteration in the position of the shape by a given number of units in the given direction. The size and shape remain unaffected after the translation. While translating, all the points will shift by the same number of units. If one point on the shape shifts by 4 units to the left, then all the points also will move 4 units to the left.