Содержание
- 1 Доступные наборы символов
- 1.1 Вставка символа
- 1.2 Вставка специального знака
- 2 Вставка символов Юникода
- 2.1 Выбор знака Юникода в окне “Символ”
- 2.2 Добавление знака Юникода с помощью кода
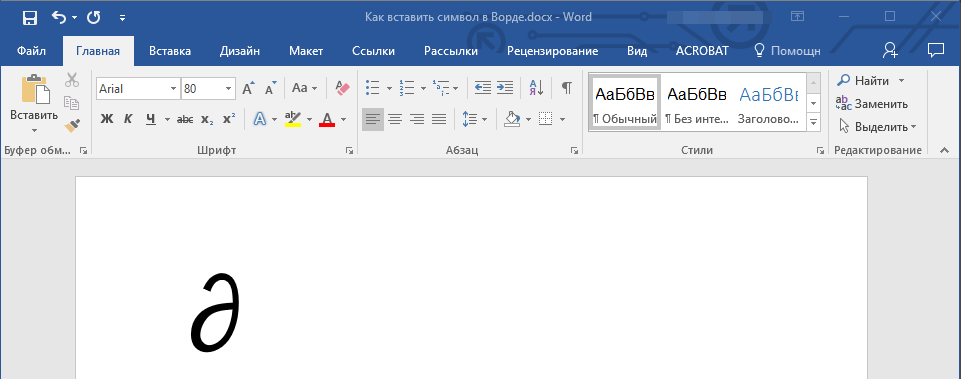
В Word можно вставлять математические символы в уравнения и текст.
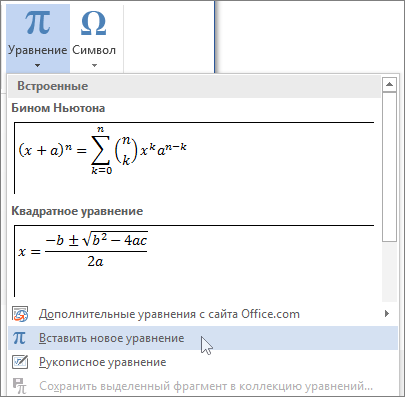
На вкладке Вставка в группе Символы щелкните стрелку рядом с надписью Формула и выберите Вставить новую формулу.
В области Работа с формулами в группе Символы на вкладке Конструктор щелкните стрелку Еще.
Щелкните стрелку рядом с названием набора символов и выберите набор символов, который вы хотите отобразить.
Щелкните нужный символ.
Доступные наборы символов
В группе Символы в Word доступны указанные ниже наборы математических символов. Щелкнув стрелку Еще, выберите меню в верхней части списка символов, чтобы просмотреть группы знаков.
Основные математические символы
Часто используемые математические символы, такие как > и
Вероятнее всего, вы хотя бы раз сталкивались с необходимостью вставить в MS Word знак или символ, которого нет на компьютерной клавиатуре. Это могло быть, к примеру, длинное тире, символ градуса или правильной дроби, а также много чего другого. И если в некоторых случаях (тире и дроби) на помощь приходит функция автозамены, то в других все оказывается намного сложнее.
Мы уже писали о вставке некоторых специальных символов и знаков, в этой статье мы расскажем о том, как быстро и удобно добавлять в документ MS Word любые из них.
Вставка символа
1. Кликните в том месте документа, куда необходимо вставить символ.
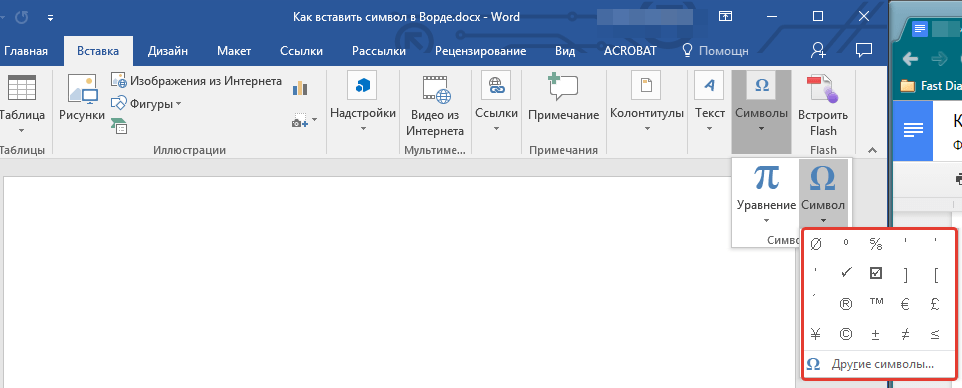
2. Перейдите во вкладку “Вставка” и нажмите там кнопку “Символ”, которая находится в группе “Символы”.
3. Выполните необходимое действие:
- Выберите в развернувшемся меню нужный символ, если он там есть.
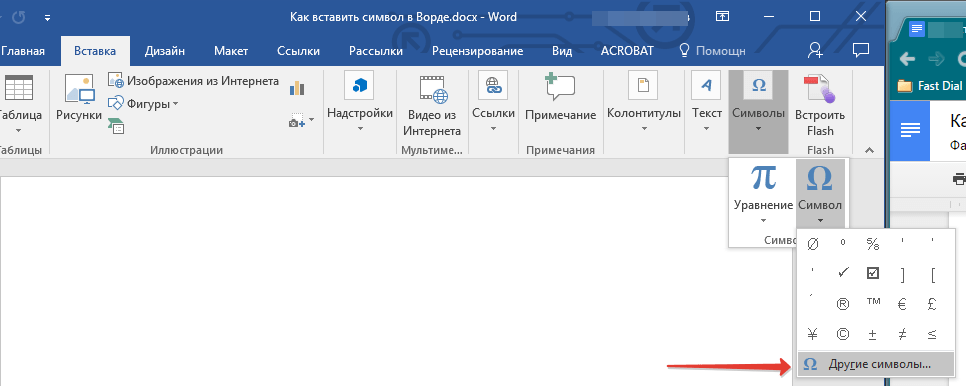
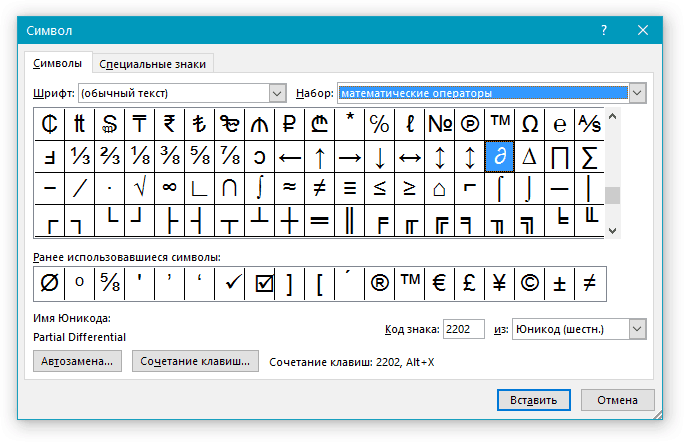
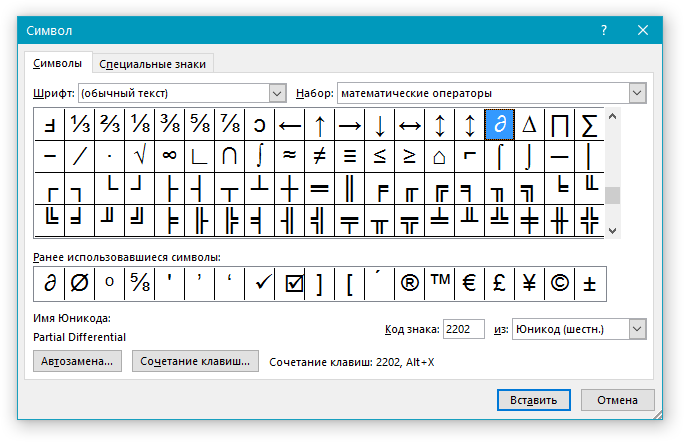
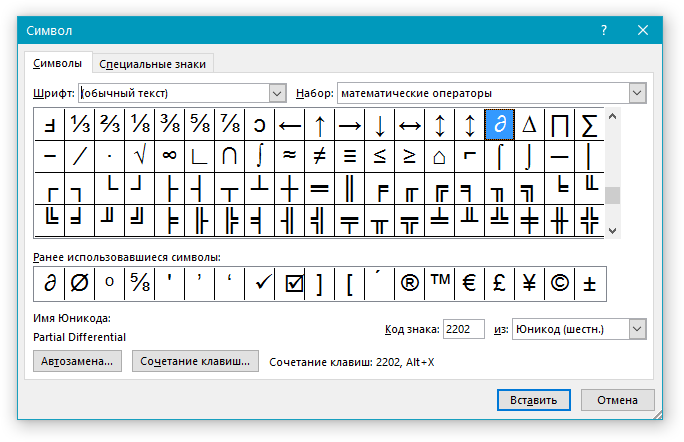
- Если же нужный символ в этом небольшом окошке будет отсутствовать, выберите пункт “Другие символы” и найдите его там. Кликните по необходимому символу, нажмите кнопку “Вставить” и закройте диалоговое окно.
Примечание: В диалоговом окне “Символ” содержится очень много различных символов, которые сгруппированы по тематикам и стилям. Для того, чтобы быстрее найти нужный символ, вы можете в разделе “Набор” выбрать характерный для этого символа, например, “Математические операторы” для того, чтобы найти и вставить математические символы. Также, можно изменять шрифты в соответствующем разделе, ведь во многих из них тоже есть различные символы, отличные от стандартного набора.
4. Символ будет добавлен в документ.
Вставка специального знака
1. Кликните в том месте документа, куда необходимо добавить специальный знак.
2. Во вкладке “Вставка” откройте меню кнопки “Символы” и выберите пункт “Другие символы”.
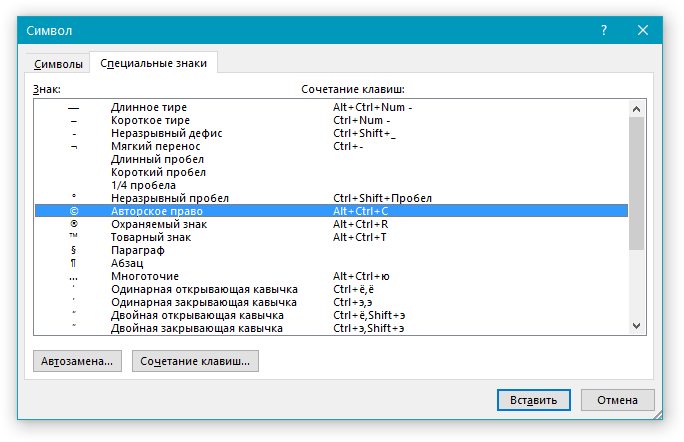
3. Перейдите во вкладку “Специальные знаки”.
4. Выберите необходимый знак, кликнув по нему. Нажмите кнопку “Вставить”, а затем “Закрыть”.
5. Специальный знак будет добавлен в документ.
Примечание: Обратите внимание, что в разделе “Специальные знаки” окна “Символ”, помимо самих специальных знаков вы также можете увидеть горячие комбинации клавиш, которые можно использовать для их добавления, а также настроить автозамену для конкретного символа.
Вставка символов Юникода
Вставка знаков Юникода мало чем отличается от вставки символов и специальных знаков, за исключением одного важного преимущества, заметно упрощающего рабочий процесс. Более подробная инструкция о том, как это сделать, изложена ниже.
Выбор знака Юникода в окне “Символ”
1. Кликните в том месте документа, куда нужно добавить знак Юникода.
2. В меню кнопки “Символ” (вкладка “Вставка”) выберите пункт “Другие символы”.
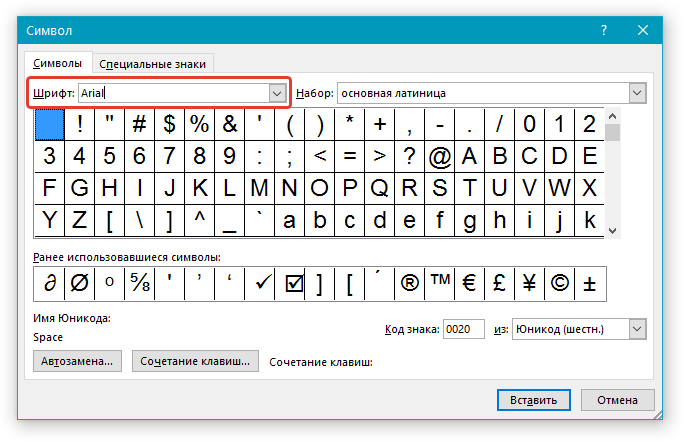
3. В разделе “Шрифт” выберите необходимый шрифт.
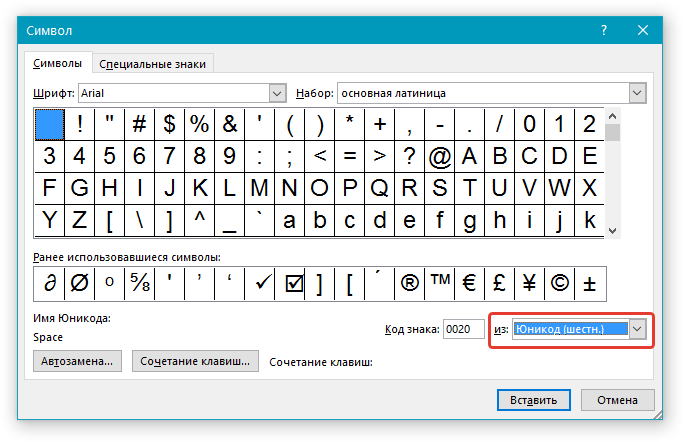
4. В разделе “Из” выберите пункт “Юникод (шестн)”.
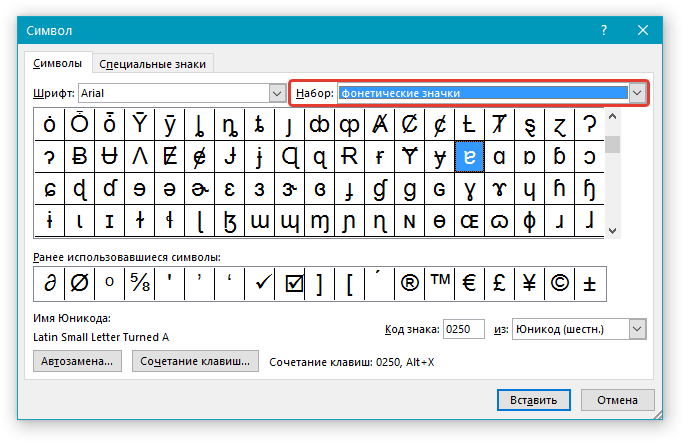
5. Если поле “Набор” будет активно, выберите необходимый набор символов.
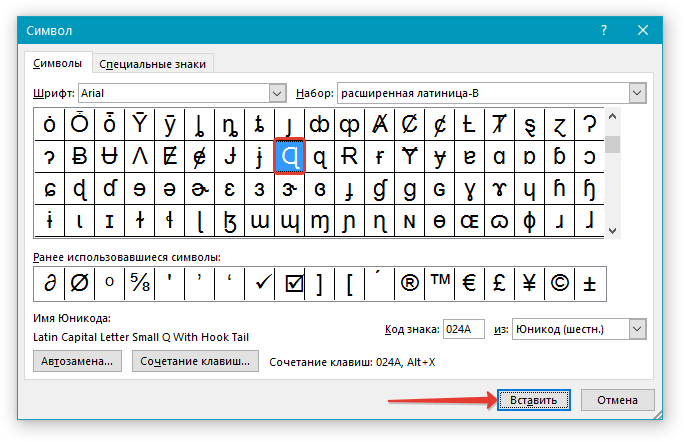
6. Выбрав нужный символ, кликните по нему и нажмите “Вставить”. Закройте диалоговое окно.
7. Знак Юникода будет добавлен в указанное вами место документа.
Урок: Как в Word поставить символ галочки
Добавление знака Юникода с помощью кода
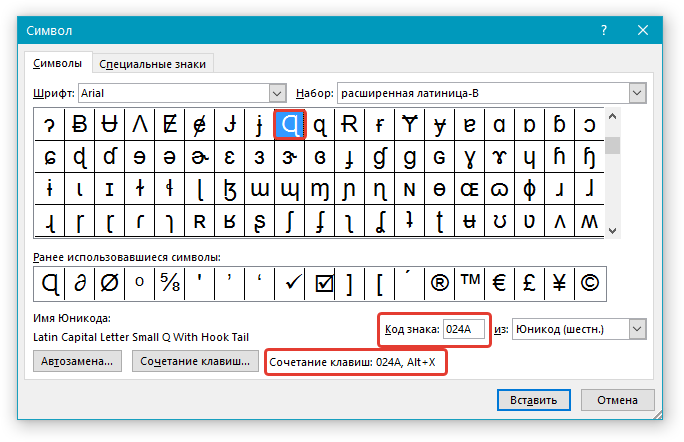
Как уже было сказано выше, у знаков Юникода есть одно важное преимущество. Заключается оно в возможности добавления знаков не только через окно “Символ”, но и с клавиатуры. Для этого необходимо ввести код знака Юникода (указан в окне “Символ” в разделе “Код”), а затем нажать комбинацию клавиш.
Очевидно, что запомнить все коды этих знаков невозможно, но самые необходимые, часто используемые выучить точно можно, ну, или хотя бы записать их где-нибудь и хранить под рукой.
1. Кликните левой кнопкой мышки там, где требуется добавить знак Юникода.
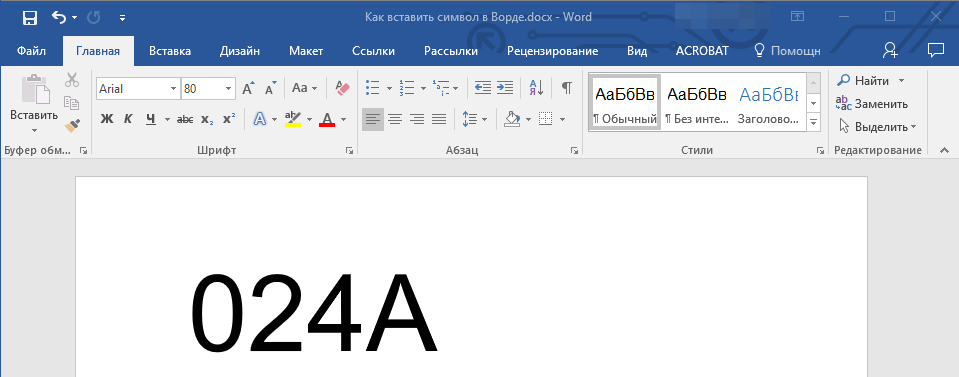
2. Введите код знака Юникода.
Примечание: Код знака Юникода в Word всегда содержит буквы, вводить их необходимо в английской раскладке заглавным регистром (большими).
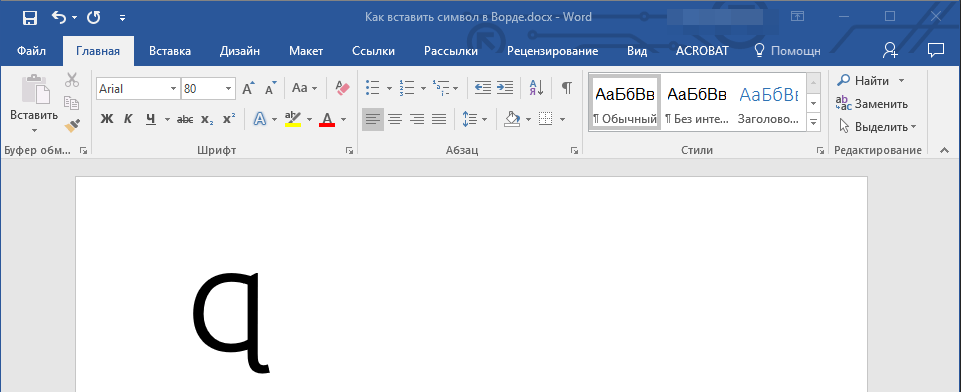
3. Не перемещая указатель курсора с этого места, нажмите клавиши “ALT+X”.
4. В указанном вами месте появится знак Юникода.
Вот и все, теперь вы знаете о том, как вставить в Майкрософт Ворд специальные знаки, символы или знаки Юникода. Желаем вам положительных результатов и высокой продуктивности в работе и обучении.
Отблагодарите автора, поделитесь статьей в социальных сетях.
| Состояние | отпатрулирована |
В математике повсеместно используются символы для упрощения и сокращения текста. Ниже приведён список наиболее часто встречающихся математических обозначений, соответствующие команды в TeX, объяснения и примеры использования. Список и смысл обозначений соответствует международным стандартам ISO 31-11 и ISO 80000-2.
Кроме указанных символов, иногда используются их зеркальные отражения, например, A ⊂ B <displaystyle Asubset B> 
Знаки операций, или математические символы — знаки, которые символизируют определённые математические действия со своими аргументами.
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
1 |
|
Знак принадлежит в математических формулах20.02.2017, 01:12. Показов 72512. Ответов 11
Где в формулах в ворде знак принадлежности одного множества другому?
0 |
|
8927 / 4839 / 1885 Регистрация: 11.02.2013 Сообщений: 10,246 |
|
|
20.02.2017, 08:04 |
2 |
|
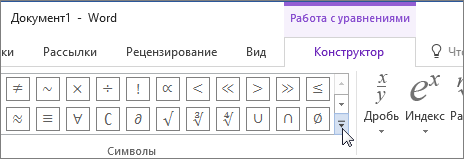
На вкладке работы с формулами Миниатюры
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
20.02.2017, 18:18 [ТС] |
3 |
|
ViterAlex, мне нужен знак принадлежности множества множеству, а не элемента множеству.
0 |
|
8927 / 4839 / 1885 Регистрация: 11.02.2013 Сообщений: 10,246 |
|
|
20.02.2017, 19:18 |
4 |
|
РешениеА они разные? Ну ладно, раскрой список, там море этих операторов. Неужели это так сложно? Миниатюры
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 13:15 [ТС] |
5 |
|
ViterAlex, в заскриненном вами списке нет знака принадлежности одного множества другому. Данный знак выглядит как тот, который Вы предложили изначально, лишь только без чёрточки посредине. В списке есть похожий на искомый мною знак, но этот из списка слишком высокий.
0 |
|
5942 / 3154 / 698 Регистрация: 23.11.2010 Сообщений: 10,524 |
|
|
21.02.2017, 14:45 |
6 |
|
Решениеoobarbazanoo, Вы об этом? Миниатюры
1 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 14:50 |
7 |
|
А разве не проще напечатать на клавиатуре, а не искать по спискам?
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 15:05 [ТС] |
8 |
|
А на форуме почему запись subset в символ не превращается? Тут отличный от ворда текстовый редактор?
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 15:28 |
9 |
|
oobarbazanoo, должно превратиться. У меня же превратилось. Наведите мышку на эти символы и дождитесь всплывающего окна. Там есть исходный код этой формулы.
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 22:44 [ТС] |
10 |
|
palva, не превращается ведь. Миниатюры
0 |
|
3944 / 2858 / 665 Регистрация: 08.06.2007 Сообщений: 9,666 Записей в блоге: 4 |
|
|
21.02.2017, 23:35 |
11 |
|
oobarbazanoo, Теперь я понял вопрос. Эта запись, как и любой текст LATEX работает только в тэгах LATEX. Можно поставить эти тэги с клавиатуры, а можно выделить текст, записанный на LATEX, и нажать метку LATEX, расположенную выше окна текстового редактора форума, так же как вы выделяете C++ или PHP.
1 |
|
7 / 30 / 9 Регистрация: 13.05.2015 Сообщений: 1,835 |
|
|
21.02.2017, 23:43 [ТС] |
12 |
|
palva,
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
21.02.2017, 23:43 |
|
Помогаю со студенческими работами здесь
Составить программу, которая определяет, принадлежит или не принадлежит круг полностью в квадрат Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 12 |
Таблица математических символов. Сокращённая запись математического текста, математические обозначения. Математический алфавит. Математическая скоропись. Негламурный эксклюзив от Проекта DPVA.info
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Знак (символ, сокращение) |
Пояснения (расшифровка, легенда) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
т.о. |
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
ЧТД QED |
Конец доказательства = «Что и требовалось доказать» = quod erat demonstrandum | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
|
Что и требовалось доказать = окончание доказательства | |||||||||||||||||||||||
|
= |
Равенство | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
По определению равно | |||||||||||||||||||||||
|
|
Записывается a |
|||||||||||||||||||||||
|
|
По определению логически эквивалентно | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Неравенство | |||||||||||||||||||||||
|
|
Меньше | |||||||||||||||||||||||
|
|
Больше | |||||||||||||||||||||||
|
|
Много меньше | |||||||||||||||||||||||
|
|
Много больше | |||||||||||||||||||||||
|
<= |
Меньше или равно | |||||||||||||||||||||||
|
>= |
Больше или равно | |||||||||||||||||||||||
|
|
Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Разделить | |||||||||||||||||||||||
|
|
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G
Если X — множество с заданным на нем отношением эквивалентности |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Минус плюс — имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
P(A|B) — вероятность события А, при условии, что событие B уже произошло
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f
A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. |
|||||||||||||||||||||||
|
|
a||b — параллельные прямые a и b
Если X — множество с отношением частичного порядка ≤, а a и b — его элементы, то a||b — a и b несравнимы, если про них невозможно сказать ни a≤b, ни b≤a
|
|||||||||||||||||||||||
|
|
n# — произведение простых чисел, не превышающих n |
|||||||||||||||||||||||
|
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
|||||||||||||||||||||||
|
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
|||||||||||||||||||||||
|
|
мощность континуума — теория множеств |
|||||||||||||||||||||||
|
: |
E:K значит, что E — это расширение поля K
|
|||||||||||||||||||||||
|
! |
n!=1*2*3…..*(n-1)*n читается n-факториал
!A=1, если А=0, !А=0, если А=1, читается не А. |
|||||||||||||||||||||||
|
|
сплетение групп в теории групп (Также обозначается как АwrВ) | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Антисоединение отношений (Antijoin) — операция реляционной алгебры, которая оставляет только те кортежи первого отношения, для которых не найдется кортежей второго отношения, совпадающих с ними по общему атрибуту. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Естественное соединение отношений (Natural Join)- операция реляционной алгебры, результатом которой является набор всех возможных комбинаций кортежей исходных отношений, то есть комбинаций тех кортежей, у которых совпадают общие атрибуты |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
импликация (материальная) логика |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Материальная эквивалентность, равносильность= «тогда и только тогда» |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
Логическое отрицание = не |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
исключающее ИЛИ (только в логике) |
|||||||||||||||||||||||
|
|
обозначение понятия — любой, читается как — «для любого», «для всех», «для каждого» |
|||||||||||||||||||||||
|
|
обозначение понятия — существует, читается как «найдется», «существует», «существуют»… |
|||||||||||||||||||||||
|
|
обозначение понятия — существует единственный, читается как «найдется ровно один «, «существует один и только один «, «существует единственный «… |
|||||||||||||||||||||||
|
|
внутри скобок записываются элементы множества |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок множества со значком определяющего признака элементов множеств. Читается, как элементы «икс», такие что «для всех икс верно….». |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок пустого множества |
|||||||||||||||||||||||
|
|
значок принадлежности к множеству — читается «принадлежит…» |
|||||||||||||||||||||||
|
|
значок не принадлежности к множеству — читается «не принадлежит…» |
|||||||||||||||||||||||
|
|
Знак подмножества. А |
|||||||||||||||||||||||
|
|
Знак собственного (строгого = истинного ) подмножества. А |
|||||||||||||||||||||||
|
|
Знак надмножества. А |
|||||||||||||||||||||||
|
|
Знак строгого = истинного надмножества. А |
|||||||||||||||||||||||
|
|
В теории множеств-объединение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — пересечение множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — симметрическая разность множеств. С= А |
|||||||||||||||||||||||
|
|
В теории множеств — разность множеств (или относительное дополнение одного множества до другого). С= А |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Стрелка, определяющая отображение (функцию) f. Запись f: a Наример, f: x |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Множество натуральных чисел. В зависимости от контекста и области применения этого обозначения за  обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. обозначают либо множество {1, 2, 3, 4, …}, либо множество {0, 1, 2, 3, 4…}. |
|||||||||||||||||||||||
|
|
Множество целых чисел.
Также можно написать |
|||||||||||||||||||||||
|
|
Множество положительных целых чисел. Т.е. множество {1, 2, 3, …} | |||||||||||||||||||||||
|
|
Множество неотрицательных целых чисел. Т.е. множество {0, 1, 2, …} | |||||||||||||||||||||||
|
Z/(n)Z Z/(n) |
Кольцо вычетов по модулю n. Стоит понимать, что вместо n может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Множество p-адических чисел вида Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||||||||||||||||||||||
|
|
Проективное пространство. В частности,  n n-мерное проективное пространство. n n-мерное проективное пространство. |
|||||||||||||||||||||||
|
P(X) Pr(X) P[X] Pr[X] |
В теории вероятности — вероятность. |
|||||||||||||||||||||||
|
|
Множество рациональных чисел.
|
|||||||||||||||||||||||
|
|
Множество действительных чисел | |||||||||||||||||||||||
|
|
Множество комплексных чисел.
|
|||||||||||||||||||||||
|
|
Множество кватернионов (кватернионов Гамильтона).
Другими словами, a — это рациональное число, а b i +c j +d k — это вектор трехмерного пространства с координатами {b, c, d}. |
|||||||||||||||||||||||
|
O |
O-большое в исследовании ассимптотического поведения функций. Описывает ассимптотическое поведение функции, когда ее аргумент стремится к числу или к бесконечности. Запись f(x)=O(g(x)) при x |
|||||||||||||||||||||||
|
|
Бесконечность. Элемент расширенной числовой прямой, который больше любого числа. Чаще всего употребляется, когда речь идет о пределах. | |||||||||||||||||||||||
|
|
Огругление числа до целого в меньшую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до целого в большую сторону.
Например, |
|||||||||||||||||||||||
|
|
Огругление числа до ближайшего целого к нему. Например, |
|||||||||||||||||||||||
|
|
[E:K] — это по определению размерность векторного пространства E над K. Например, [
|
|||||||||||||||||||||||
|
|
Например, [2=3]=0; [4<5]=1.
Иными словами, f[X]={f(x) | x∈X} |
|||||||||||||||||||||||
|
|
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы.
|
|||||||||||||||||||||||
|
|
Смешанное произведение векторов. | |||||||||||||||||||||||
|
|
f(x) — образ x при применении f.
Иными словами, f(X)={f(x) | x∈X}
|
|||||||||||||||||||||||
| (( )) |
Количество мультимножеств -число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
|||||||||||||||||||||||
|
|
(a, b)=НОД(a, b) — наибольший общий делитель чисел a и b.
(a,b)={x∈
|
|||||||||||||||||||||||
|
|
Интервал (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый слева) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
Полуинтервал (открытый справа) (a,b)={x∈ |
|||||||||||||||||||||||
|
|
<S> — среднее значение элементов множества S.
Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S, т.е. прересечение всех подпространств линейного пространства L, содержащих в себе множество S.
Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S, т.е. минимальная подгруппа G, содержащая S. |
|||||||||||||||||||||||
|
|
Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an.
Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an, т.е. минимальная подгруппа G, содержащая в себе элементы a1, a2…,an.
|
|||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
Скалярное произведение векторов в предгильбертовом пространстве. (Следует понимать, что скалярное произведение может быть определено множеством способов) | |||||||||||||||||||||||
|
|
В обозначениях Дирака — кет-вектор. |φ> — вектор φ некоторого гильбертого пространства | |||||||||||||||||||||||
|
|
В обозначениях Дирака — бра-вектор из пространства, сопряженного некоторому гильбертовому пространству. <φ| — бра вектор, соответствующий кет-вектору |φ> (говорят, даже, совпадающий с кет-фектором |φ>), задающий линейный функционал, ставящий в соответствие каждому кет-вектору |ψ> скалярное произведение <φ|ψ>. | |||||||||||||||||||||||
|
|
число советаний из r элементов, выбранных из n элементов | |||||||||||||||||||||||
|
|
Сумма, ряд.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
В теории категорий — копроизведение (категорная сумма) | |||||||||||||||||||||||
|
|
Производная. f'(x) — значение производной функции f в точке x (Тангенс угла наклона касательно к функции f в точке x). | |||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Интеграл по контуру (поверхности — знак интеграла удваивается, объему-знак интеграла утраивается). | |||||||||||||||||||||||
|
|
Если вектор
Если вектор где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то |
|||||||||||||||||||||||
|
|
Если M — некоторое множество, то
Если f — многочлен, то |
|||||||||||||||||||||||
|
|
Оператор Лапласа ставит функции от n переменных в соответствие ее дифференциал второго порядка.
|
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
Операция, которая из заданного отношения (таблицы) выбирает подмножество, которое получается выбором нескольких из имеющихся атрибутов и (если потребуется) вычеркиванием повторяющихся кортежей. Результатом перации Например: Если в изначальной таблице ЛЮДИ атрибутами являются рост, вес, пол, то результатом операции
Математическая константа, равная отношению длины окружности к ее диаметру. |
|||||||||||||||||||||||
|
|
В реляционной алгебре — выборка Операция |
|||||||||||||||||||||||
|
|
В теории порядка — покрытие (понятие, определяющее смежность вершин диаграммы Хассе некоторого частично-упорядоченного множества). Если X — множество с отношением частичного порядка ≤ , а отношение < на этом множестве задается следующим образом : a<b, если a≤b и а ≠ b, то элемент y покрывает элемент x и пишется x x<z<y. Если a |
|||||||||||||||||||||||
|
|
В теории типов — подтип (подкласс, дочерний тип(класс)). Часто используется в объектно-ориентированном программировании. S  T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. T значит, что S — подтип T, т.е. все элементы S являются элементами типа Т, и их объединяет какое-то общее свойство. Например, Круги  Фигуры. Фигуры.S  T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. T значит, что любой элемент типа S можно использовать в том месте, где ожидается использование элемента типа T, и при этом не возникнет ошибки. |
|||||||||||||||||||||||
|
|
Эрмитово-сопряженная (комплексно-сопряженная) матрица. A† — матрица, полученная из матрицы A транспонированием и заменой каждого элемента матрицы A комплексно-сопряженным ему. Чаще всего такая матрица обозначается A*, а также встречаются обозначения A*T, AT*, |
|||||||||||||||||||||||
|
|
Транспонирование матрицы. AT — матрица, в которой в качестве строк записаны столбцы матрицы А. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
x⊥y значит, что векторы (прямые) x и y перпендикулярны, или, в более общем случае, ортогональны.
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W, т.е. множество векторов пространства V, перпендикулярных каждому из векторов подпространства W.
a⊥b значит, что наибольший общий делитель чисел a и b равен единице. Часто записывается как (a, b)=1
A⊥B значит, что случайные события A и B независимы, т.е. наступление одного из них не влияет на вероятность наступления другого.
⊥ — наименьший (нижний) элемент решетки
⊥ — тип, у которого нет подтипов
x⊥y значит, что элементы x и y частично упорядоченного множества сравнимы, т.е. про них известно, что x≤y или y≤x |
|||||||||||||||||||||||
|
|
Импликация (логическое следование) — в теории моделей A |
|||||||||||||||||||||||
|
|
Вывод — в логике высказываний (предикатов). A |
|||||||||||||||||||||||
|
|
Тензорное произведение (модулей) — в линейной алгебре. Если A и B — линейные пространства, то Если а
a Если A и B — модули над коммутативным кольцом R, то A |
|||||||||||||||||||||||
|
|
a
где f, g — функции, определенные и интегрируемые относительно меры Лебега на пространстве Rd
z* — число, комплексно-сопряженное к z. Если z=a+bi, то z*=a-bi
R* — группа обратимых элементов кольца R
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. Вместо R можно использовать также другие множества, например, N*.
Линейный оператор из пространства p-векторов в пространства (n-p)-форм. Если вектор v — поливектор степени p, то *v — дифференциальная форма степени n-p. |
|||||||||||||||||||||||
|
|
Если S — некоторое подмножество топологического пространства, то |
- Сортировка знак / легенда
- Сортировка легенда / знак
|
Легенда (пояснение, расшифровка) |
Символ (знак, сокращение) |
|||
| Следовательно, таким образом, поэтому |
1. 2. т.о. 3. |
|||
| Потому что, из-за того что, вследствие того что, поскольку, в результате того, что |
|
|||
| Конец доказательства, что и требовалось доказать |
1. ЧТД, QED (Что и требовалось доказать, quod erat demonstrandum) 2. 3. 4. |
|||
| Таких что, так что, такие что |
1. A={x | |x|<1} читается: «А — множество x таких, что модуль x меньше 1» и значит, что множество А — множество элементов числовой прямой, лежащих между -1 и 1. 2. :
|
|||
| Материальная эквивалентность, равносильность, тогда и только тогда |
1. 2. |
|||
| Любой, для любого | ||||
| Существует, найдется | ||||
| Существует единственный | ||||
| Или | ||||
| Бесконечность |  |
|||
| Приращение, изменение |  |
|||
| Стремится |  |
|||
| Равно | = | |||
| По определению равно | 1. 2. 3. 4. 5. 6. |
|||
| По определению эквивалентно | ||||
| Равно по модулю |
Записывается a |
|||
| Не равно | ||||
| Приблизительно равно | ||||
| Сложение, ряд |
1. 2.
|
|||
| Вычитание | ||||
| Умножение, произведение |
1. 2. 3. * 4.
|
|||
| Деление, разделить |
1. : 2. 3. |
|||
| Квадратный корень (действительный, мнимый) | ||||
| Возведение в степень |
2^3 = 23 |
|||
| Факториал |
! n!=1*2*3…..*(n-1)*n читается n-факториал |
|||
| Модуль числа |
1. |a| — модуль а 2. Abs(a) |
|||
| Плюс-минус, минус-плюс |
1. 2. имеет смысл только при употреблении вместе со знаком плюс минус cos(x ± y) = cos(x) cos(y) |
|||
| Больше | ||||
| Больше или равно |
1. 2. >= |
|||
| Меньше | ||||
| Меньше или равно |
1. 2. <= |
|||
| Много больше | ||||
| Много меньше | ||||
| Числа одного порядка | ||||
| Приоритет операций | ( ) | |||
| Число сочетаний из n по r |
1. 2. |
|||
| Количество мультимножеств, число различных мультимножеств мощности k, состоящих из элементов, выбранных из множества мощности n |
(( )) |
|||
| Число Пи |  |
|||
| Кортеж , упорядоченный набор (список) некоторых величин, или горизонтальный вектор |
1. 2. |
|||
| Среднее значение, усреднение |
1. 2. |
|||
| Множество, знак множества |
1. 2. 3. |
|||
| Пустое множество |
1. 2. 3. |
|||
| Знак принадлежности множеству, принадлежит | ||||
| Знак «не принадлежит множеству» |  |
|||
| Множество натуральных чисел |
|
|||
| Множество целых чисел |
1. 2. 3. |
|||
| Множество рациональных чисел |
|
|||
| Множество действительных чисел |
|
|||
| Множество комплексных чисел |
|
|||
| Множество кватернионов |
|
|||
| Множество p-адических чисел |
Стоит понимать, что вместо p может стоять любая буква, а в частном случае цифра. |
|||
| Множество гипердействительных чисел |
R* — расширение множества R действительных чисел, в котором каждый элемент представляется в виде суммы действительного числа и бесконечно малой добавки, бесконечно малые величины в котором являются величинами постоянными. В R* входят также бесконечно большие числа. |
|||
| Мощность множества, кардинальное число, количество элементов |
1. 2. |
|||
|
Алеф — кардинальное число, характеризующее мощность бесконечного вполне упорядоченного множества |
||||
|
Бет — кардинальное число, характеризующее мощность бесконечного множества |
||||
|
Континуум, мощность континуума |
||||
| Знак подмножества |
1. А 2. А |
|||
| Знак надмножества |
1. А 2. А |
|||
| Объединение (множеств) |  |
|||
| Пересечение (множеств) |  |
|||
| Симметрическая разность (множеств) |
1. 2. |
|||
| Разность множеств |
1. 2. — (редко) |
|||
| Прямое (декартово) произведение множеств | 1. 
2. |
|||
| Прямая сумма | ||||
| Несвязное объединение, несвязная сумма, дизъюнктное объединение | ||||
| Логическое отрицание |
1. 2. 3. ! |
|||
| Логическая конъюнкция |
1. 2. & |
|||
| Логическая дизъюнкция | ||||
| Исключающее или | ||||
| Импликация (логическое следование) |
1. 2. 3. 4. |
|||
| Вывод в логике высказываний |  |
|||
| Нотация Айверсона, или скобка Айверсона. Сопоставляет некоторому утверждению 1 или 0, в зависимости от того, истинно или ложно данное утверждение. |  |
|||
| Сведение по Карпу (Karp reduction) — теория сложности, левое сводимо по Карпу к правому, левое «не сложнее правого», естественно возможно и использование знака острием вправо (но нам лень было рисовать) |
1. 2. |
|||
| Делитель, делит/ не делит нацело |
1. 2. |
|||
| Точный делитель (при разложении числа в произведение степеней простых чисел — простое число в максимальной степени, делящее исходное) | ||||
| Взаимно простые числа |  |
|||
| Примориал или праймориал | ||||
| Наибольший общий делитель |
1. 2. НОД |
|||
| Окргугление числа до целого |
1. 2. 3. 4. 5. 6. Round(x) — до ближайшего целого 7. Nint(x) — до ближайшего целого |
|||
| Сопряжение комплексных чисел |
1. z* — число, комплексно-сопряженное к z 2.
|
|||
| Пропорциональность | ||||
| Отрезок |  |
|||
| Интервал |
1. 2. |
|||
| Полуинтервал |
1. 2. 3. 4. |
|||
| Норма, длина вектора |
1. 2. |
|||
| Обозначения Дирака: кет-вектор |  |
|||
| Обозначения Дирака: бра-вектор |  |
|||
| Скалярное произведение |
1. 2. 3. 4. 5. |
|||
| Векторное произведение векторов |
1. 2. |
|||
| Смешанное произведение векоторов |  |
|||
| Ортогональность (перпендикулярность) |  |
|||
| Параллельность | ||||
| Эквивалентность матриц | ||||
| Скалярное произведение матриц | : | |||
| Определитель матрицы |
1. 2. det(A), где А — матрица 3. |
|||
| Транспонирование матрицы |
АТ — транспонированная матрица А |
|||
| Эрмитово-сопряженная (комплексно-сопряженная) матрица к матрице А |
1. A† 2.A* 3.А*T 4. AT* 5. 6. |
|||
| Произведение Адамара двух матриц одинакового размера | ||||
| Определение функции, область определения и область значений функции |
Запись f : X |
|||
| Определение функции (отображения) , задание функции |
Запись f: a |
|||
| Образ элемента/множества |
1. f(x) — образ элемента x; f(X) — образ множества X 2. f[X] — образ множества X |
|||
| Ограничение функции на множестве, сужение области определения функции |
Если функция f определена на R, то f|N определена только на N и принимает на N те же значения, что и f |
|||
| Композиция функций | ||||
| Производная |
1. 2.
3. |
|||
| Интеграл, первообразная |
1. 2. 3. 4. |
|||
| Свертка функция |
|
|||
| Градиент |
|
|||
| Дивергенция |
|
|||
| Ротор |
|
|||
| Эквивалентность функций при определенной базе | ||||
| О-большое | O | |||
| Степень многочлена |
1.
2. deg f |
|||
| Лапласиан, оператор Лапласа |  |
|||
| Кольцо вычетов по модулю n | 1. 
2. 3. Z/(n)Z 4. Z/(n) |
|||
| Проективное пространство |
1. 2. |
|||
| Изоморфизм |
1. 2. |
|||
| Конгруэнтность | ||||
| Коммутатор |
[g, h] = g-1h-1gh, если g, h∈G, где G — группа. [a,b]=ab-ba, если a, b∈R, где R — кольцо. [A, B]=AB-BA, если A и B — операторы |
|||
| Группа, порожденная подмножеством/элементом группы |
1. Если S — некоторое подмножество элементов группы G, то <S> — подгруппа G, порожденная S 2. Если a1, a2…,an— некоторые элементы группы G, то <a1, a2…,an> — подгруппа G, порожденная элементами a1, a2…,an |
|||
| Линейная оболочка подмножества/векторов линейного пространства |
1. Если S — подмножество линейного пространства L, <S> — линейная оболочка множества S 2. Если a1, a2…,an — векторы линейного пространства L, то <a1, a2…,an> — линейная оболочка векоторов a1, a2…,an т.е. пересечение всех подпространств пространства L, содержащих в себе векторы a1, a2…,an. |
|||
| Ортогональное дополнение подпространства |
Если W — подпространство предгильбертового пространства V, то W⊥ — ортогональное дополнение подпространства W |
|||
| Тензорное произведение |  |
|||
| Нормальная (инвариантная) подгруппа | ||||
| Идеал кольца | ||||
| Индекс подгруппы |
Если H — подгруппа группы G, то [G:H] — индекс подгруппы H |
|||
| Расширение поля |
: E:K значит, что E — это расширение поля K |
|||
| Степень расширения поля |
[E:K] — это степень расширения поля E:K, где E — это расширение поля K. |
|||
| Факторгруппа |
Если G -группа, а H- ее нормальная подгруппа, то G/H — факторгруппа G по H, т.е. группа классов смежности H в G |
|||
| Фактормножество |
Если X — множество с заданным на нем отношением эквивалентности |
|||
| Сплетение групп |
1. 2. АwrВ |
|||
| Граница множества |
Если M — некоторое множество, |
|||
| Группа единиц (обратимых элементов) кольца |
1. R* 2. Rx 3. U(R) |
|||
| Звезда Ходжа |  |
|||
| Замыкание (алгебраическое, топологическое) |  |
|||
| Полупрямое произведение групп | ||||
| Копроизведение (категорная сумма) |  |
|||
| Антисоединение отношений (Antijoin) — реляционная алгебра | ||||
| Полусоединение отношений (Semijoin) — реляционная алгебра | ||||
| Естественное соединение отношений (Natural Join) — реляционная алгебра | ||||
| Проекция — реляционная алгебра |
|
|||
| Выборка — реляционная алгебра |
|
|||
| Отношение эквивалентности, принадлежность одному классу эквивалентности | ||||
| Класс эквивалентности |
[a] — это множество элементов, эквивалентных a. Более точная запись — [a]R означает класс эквивалентности, порожденный элементом a относительно отношения эквивалентности R |
|||
| Вероятность события X |
1. 2. 3. P(X) 4. Pr(X) 5. P[X] 6. Pr[X] |
|||
| Условная вероятность |
P(A|B) — вероятность события А, при условии, что событие B уже произошло |
|||
| Независимость случайных событий |  |
|||
| Распределение вероятности случайной величины | ||||
| Несравнимость в теории порядка | ||||
| Сравнимость в теории порядка |  |
|||
| Покрытие в теории порядка |
x |
|||
| Наибольший (верхний )элемент решетки в теории порядка |  |
|||
| Наименьший (нижний) элемент решетки |  |
|||
| Подтип, подкласс, дочерний класс в теории типов |
S |
|||
| Высший (универсальный) тип в теории типов |  |
|||
| Нижайший тип (универсальный подтип) в теории типов |  |
|||
| Дельта-функция |
|
|||
| Символ Кронекера, индикатор равенства переменных |
|
- Сортировка знак / легенда
- Сортировка легенда / знак
The does not equal symbol, or ≠, is often not part of a standard keyboard setup – or it’s well hidden. So if you need to write it, how do you do it?
How to Write the Not Equal Sign on Desktop Devices
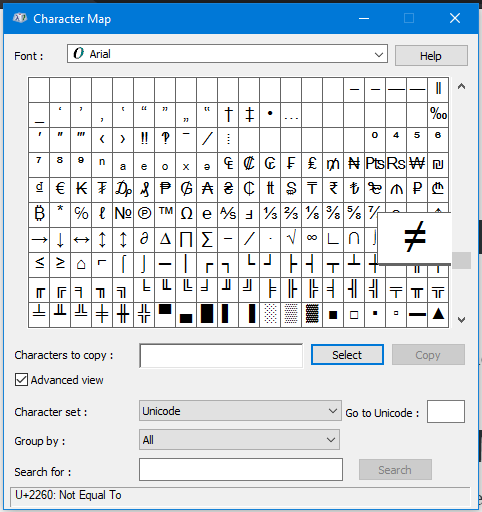
On Windows: Use the Character Map
The Character Map is a useful utility from which you can select all possible characters.
To get to the character map, click on Start, and then navigate to Programs -> Accessories -> System Tools, and then finally click on Character Map.
You can find the not equal sign in the mathematical symbols. Then you can just copy and paste the sign from that character map where you need it.
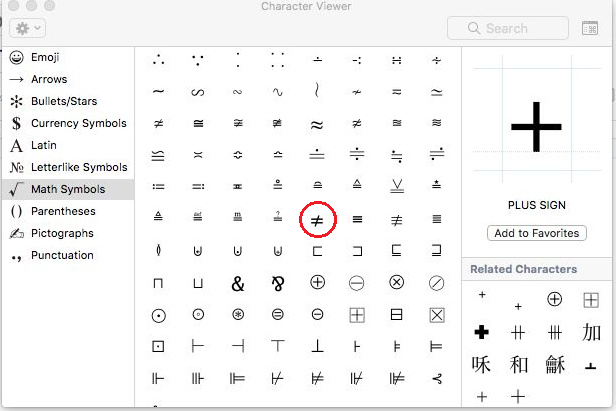
Not Equal Sign Keyboard Shortcut On Mac
If you are using a Mac, typing the does not equal sign is as easy as typing Option+= (This may vary between languages and locations).
Alternatively you can press Control+Command+Space bar to open the Character Viewer. Then you can scroll through the available emoji and symbols until you find the Math Symbols section. There, you’ll find the Does Not Equal symbol (or you can use the Search bar).
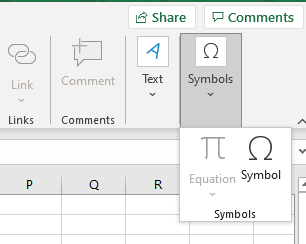
How to Write the Not Equal Sign in Microsoft Office Suite
In the Microsoft Office suite, you can add the not equal sign to your document using the Symbol tool in the Insert tab.
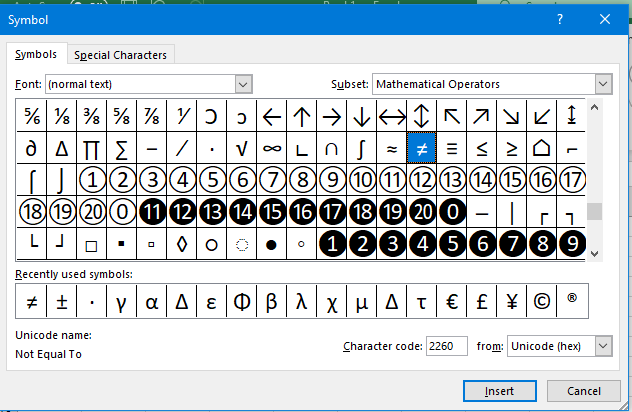
Clicking on Symbol (or More Symbols… for Word) opens a window from where you can select the symbols. You can find the not equal symbol toward the end, in the subset of Mathematical Operators.
You can reach it faster from the drop down menu that lets you select the subset. Once selected, the Insert button will Insert the symbol in your document.
Use a Keyboard Shortcut
You can also type Alt+8800, and this will type the does not equal sign in any of the Suite Office apps.
Microsoft Word Only Keyboard Shortcut
In Microsoft Word only there is an additional shortcut that will let you type the does not equal sign – just type 2260 and then press Alt+x and the ≠ sign will substitute for the numbers.
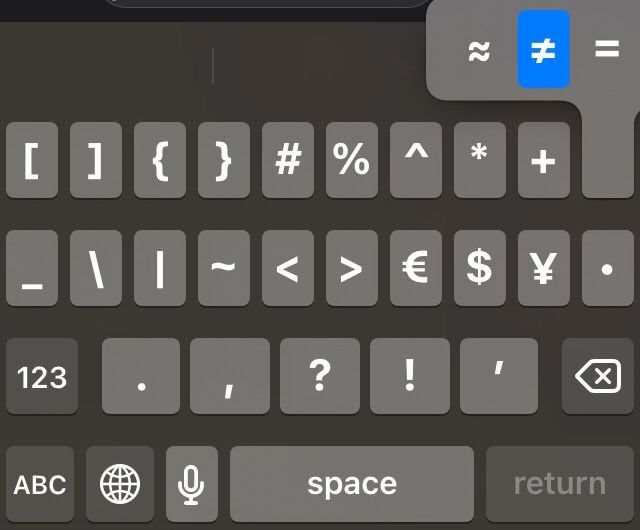
Most mobile keyboards have different panels, one for letters, and one or more additional symbol panels. The equal sign is often included in one of those non-letter panels. Try long-pressing on the equal sign, and the not equal sign may be included.
The screenshot above is for the iPhone keyboard. On it, you can find the equal sign in the second symbol panel.
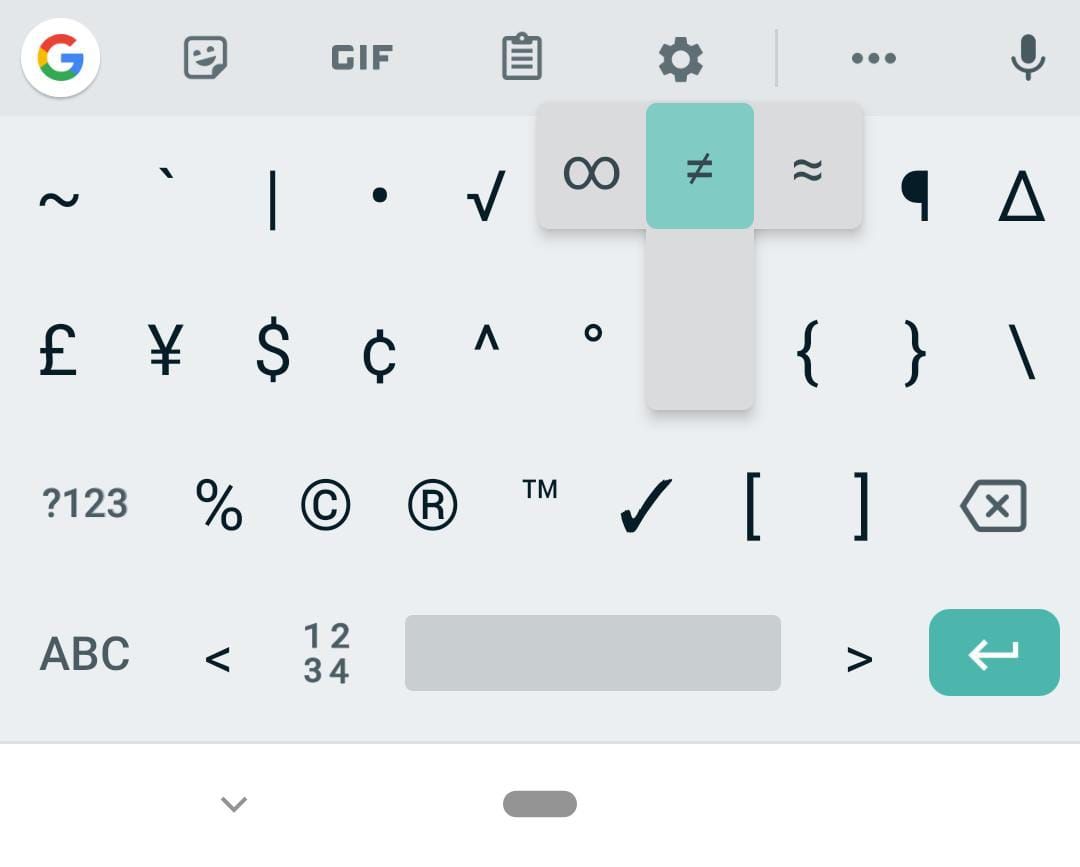
For Android keyboards, you’ll need to take a couple more steps to reach the symbol panel that includes the equal and not equal signs. You can usually navigate between the panels using the buttons that have multiple symbols in them, like ABC or 123.
How to Write the Not Equal Sign in HTML
In HTML, you can use one of the following codes to write the ≠ sign:
≠≠≠
Special characters are best included using the codes that render them instead of typing the symbol directly.
Conclusion
You probably won’t need to type the not equal symbol that often. But when you need it, it’s useful to know how to type it on your laptop or your smart phone using the keyboard or alternative methods.
Learn to code for free. freeCodeCamp’s open source curriculum has helped more than 40,000 people get jobs as developers. Get started
Word: специальные символы и подстановочные знаки
В окне «Найти и заменить» Microsoft Word есть два типа подстановок — специальные символы и подстановочные знаки.
Те и другие можно вводить в строки поиска и замены, включив используя список «Special» («Специальный») в полностью открытом окне «Найти и заменить» (нажать комбинацию клавиш Ctrl+H, потом кнопку «Больше>>«).
Специальные символы — это те, которых нет на клавиатуре или которые нельзя непосредственно вписать в строки поиска/замены,
например, разрыв строки.
Если в окне поиска/замены включен чекбокс Use wildcards (Подстановочные знаки), то можно задавать достаточно сложные условия поиска и замены, потому что подстановчные знаки — это офисная реализация всё тех же регулярных выражений.
Чекбокс «Подстановочные знаки» в работе — убираем лишние пробелы в тексте
Некоторые символы и знаки можно использовать только в строке поиска, а некоторые — только в строке замены.
При этом возможность применения
части символов зависит от того, включен ли чекбокс Use wildcards (Подстановочные знаки).
Полный список подстановок в самом Word отсутствует или я его не нашёл, поэтому ниже приводится более-менее адекватный список, актуальный для всех версий Word плюс немного примеров.
1. Строка поиска
| Спец. символы | Обозначение (англ.) | Обозначение (рус.) |
| ^p | Paragraph mark (¶) | Конец абзаца (¶) |
| ^? | Any character | Любой символ |
| ^# | Any digit | Любая цифра |
| ^$ | Any letter | Любая буква |
| ^e | Endnote mark | Концевая сноска |
| ^d | Field | Поле |
| ^f | Footnote mark | Нижняя сноска |
| ^b | Section break (===End of section===) | Разрыв секции |
| ^w | Whitespace | Любое количество и комбинация обыкновенных и неразрываемых пробелов, табуляций и концов абзаца |
| Спец. символы | Обозначение (англ.) | Обозначение (рус.) |
| ^t | Tab character | Символ табуляции |
| ^a | Comment mark | Комментарий |
| ^0nnn | ANSI or ASCII characters | Любой ANSI или ASCII символ с кодом nnn |
| ^^ | Caret character | Символ ^ |
| ^g | Graphic | Графика |
| ^n | Column break (···Column Break···) | Разрыв колонки |
| ^l | Manual line break | Принудительный разрыв строки |
| ^m | Manual page break (—Page Break—) | Принудительный разрыв страницы (—Page Break—). Если опция Use wildcards включена, то ищет принудительный разрыв и страницы, и секции |
| ^+ | Em dash (—) | Длинное тире (—). Символ с кодом 0151 |
| ^= | En dash (–) | Короткое тире (–). Символ с кодом 0150 |
| ^s | Nonbreaking space (°) | Неразрывный пробел (°) |
| ^~ | Nonbreaking hypen (-) | Неразрывный дефис (-) |
| ^- | Optional hypen (¬) | Мягкий перенос (¬) |
| Подстановочные знаки | Обозначение (рус.) | Пример строки поиска | Примеры результатов поиска (в кавычках) |
| ? | Один любой символ | б?к | «бак», «бок», «бук», «б5к», «б¶к» |
| * | Любое количество любых символов | б*к | «бык», «бардак», «белый¶ полковник» |
| [] | Один из указанных символов | б[аоу]к | «бак», «бок», «бук» |
| [-] | Один символ из диапазона. Диапазон должен быть указан в порядке возрастания кодов символов. |
[а-яё] | Любая строчная русская буква |
| [А-ЯЁ] | Любая прописная русская буква | ||
| [0-9] | Любая цифра | ||
| [!] | Один любой символ, не указанный после восклицательного знака | б[!ы]к | «бак», «бок», но не «бык» |
| [!x-z] | Один любой символ, не входящий в диапазон, указанный после восклицательного знака | [!а-яё]ок | «Бок», «Док», но не «бок», «док» |
| [!0-9] | Любой символ, кроме цифр | ||
| {n} | Строго n вхождений предыдущего символа или выражения. Выражением является все то, что заключено в круглые скобки. Выражение может состоять как из конкретных символов, так и содержать спец. символы. |
10{3} | «1000», но не «100», «10000» |
| 10(20){2} | «102020», но не «1020», «10202020» | ||
| {n;} | n и более вхождений предыдущего символа или выражения | 10{3;} | «1000», «10000», «100000», но не «100» |
| {n;m} | От n до m включительно вхождений предыдущего символа или выражения | 10{3;4} | «1000», «10000», но не «100», «100000» |
| @ | Ноль или более вхождений предыдущего символа или выражения | 10@ | «10», «100», «1000», «10000» |
| < | Начало слова | <бок | «боксёр», но не «колобок» |
| > | Конец слова | бок> | «колобок», но не «боксёр» |
2. Строка замены
| Спец. символы | Обозначение (англ.) | Обозначение (рус.) |
| ^p | Paragraph mark (¶) | Разрыв абзаца (¶) |
| ^t | Tab character | Символ табуляции |
| ^0nnn | ANSI or ASCII characters | Любой ANSI или ASCII символ с кодом nnn |
| ^^ | Caret character | Символ ^ |
| ^c | Clipboard contents | Содержимое буфера обмена |
| ^& | Contents of the Find what box | Содержимое строки поиска (или то, что найдено) |
| ^n | Column break (···Column Break···) |
Разрыв колонки |
| ^l | Manual line break (¿) | Принудительный разрыв строки |
| ^m | Manual page break (—Page Break—) | Принудительный разрыв страницы |
| ^+ | Em dash (-) | Длинное тире (-). Символ с кодом 0151 |
| ^= | En dash (–) | Короткое тире (–). Символ с кодом 0150 |
| ^s | Nonbreaking space (°) | Неразрывный пробел (°) |
| ^~ | Nonbreaking hypen (-) | Неразрывный дефис (-) |
| ^- | Optional hypen (¬) | Мягкий перенос (¬) |
| Спец. символы | Обозначение (англ.) | Обозначение (рус.) |
| n | Expression n | Выражение номер n из строки поиска |
Примечание 1. В операторах {n;} и {n;m} точка с запятой означает List separator (Разделитель элементов списка) из настроек операционной системы, зависящих от локали
(например, в США — запятая, в России — точка с запятой).
Примечание 2. Для поиска в документе символов, которые в строке поиска «заняты» как специальные перед ними ставится обратный слэш ().
Например, если включена опция Use wildcards (Подстановочные знаки), для поиска восклицательного знака в строке поиска вводится !
3. Примеры для поиска
| Строка поиска | Что ищет |
| [!^0013]^0013[!^0013] | Конец абзаца в окружении двух других символов |
| ^0032{2;} | Два и более пробелов |
| [.,:;!?] | Знак препинания |
| <[0-9]@,[0-9]@> | Вещественное число, набранное через запятую |
| <[А-яЁё]@> | Русское слово (зависит от кодировки) |
4. Примеры для замены
Подстановочные знаки включены!
| Строка поиска | Строка замены | Что заменяет |
| (^0013){2;} | 1 | Удаление пустых строк (если они создавались нажатием Enter) |
| ^0032([.,:;!?]) | 1 | Удаление пробелов перед знаками препинания |
| ([0-9])^0032([0-9]) | 1^s2 | Замена пробелов между цифрами на неразрывные пробелы |
| -([0-9]) | ^01501 | Замена дефисов перед цифрами на правильный символ «минус» |
| Ивано([а-я]@>) | Петро1 | Замена Ивановых на Петровых во всех падежах сразу (конечно, фамилии должны склоняться одинаково) |
| (<[0-9]@).([0-9]@>) | 1,2 | Замена десятичных точек между цифрами на запятые |
24.09.2020, 10:16 [28924 просмотра]



 Сообщение было отмечено oobarbazanoo как решение
Сообщение было отмечено oobarbazanoo как решение



 — матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц
— матрица того же размера, элементы которой равны произведению соответствующих элементов перемножаемых матриц 





 , где m≥0; ak — целые числа, а p — простое число.
, где m≥0; ak — целые числа, а p — простое число.









 x
x — это наибольшее целое число, меньшее или равное х.
— это наибольшее целое число, меньшее или равное х.
 x
x -это наименьшее целое число, большее или равное х.
-это наименьшее целое число, большее или равное х.

























 =vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то
=vx i +vy j +vz k , где vx, vy, vz — функции от трех переменных x, y, z, а i, j, k — стандартный базис в пространстве, то




 — граница множества M (другими словами, множество всех граничных точек множества M)
— граница множества M (другими словами, множество всех граничных точек множества M) — степень многочлена f. Чаще встречается обозначение deg f.
— степень многочлена f. Чаще встречается обозначение deg f.





 ,
,  .
.



 — топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
— топологическое замыкание подмножества S, т.е. пересечение всех замкнутых надмножеств подмножества S.
 — строгое, истинное подмножество
— строгое, истинное подмножество