Time Word Search is at the expanding stage of English where there is more focus on academic tasks and language functions. Can you find the words in the Time Word Search?
The more words you encounter and understand, the broader your day-to-day vocabulary will become. Our word games and puzzles, such as this Time Word Search, are an excellent way to help to reinforce spellings in your mind.
Especially helpful are exercises that are focussed on a theme or topic as these provide word retention practice so you can be confident to read, write, speak and listen successfully. We have many activities to get your English up to speed in no time.
Cambridge English Examinations:
Cambridge English exams are designed for learners at all levels from the Elementary level Cambridge English: Key (KET) to the very advanced level Cambridge English: Proficiency (CPE). These exams give candidates proof of their ability to use English in a wide variety of contexts, relevant to work, study and leisure activities.
A2 Key | B1 Preliminary | B2 First
10000+ результатов для ‘time words’
Time
Откройте поле
English
vocabulary
test
time
words
Time words A2
Викторина
12-13
English
A2
B1
Cambridge KET
Cambridge Preliminary
Writing a story
Time words
Случайное колесо
12-13
14-17
English
B1
B2
Cambridge First
Cambridge Preliminary
FCE
First Certificate
Prepare 5
Writing a story
Future Simple
Привести в порядок
Начальная школа / начальная
Future Simple
What time… ? Questions
Откройте поле
kids
teenagers
teens
collocations
English
english
grammar
nouns
Phrases
Speaking
verbs
Dialogue
drill
phrases
prepositions
Questions
study
test
time
words
work
Valentine’s Day Word Search
11,463 Views

A fun classroom Valentine’s Day activity where kids can find 22 words relating to Valentine’s Day in a heart shaped design that they can decorate.
Read More »
St. Patrick’s Day Word Search Printable
13,115 Views

Classroom activity St. Patrick’s Day Word Search Printable with 18 words to find in a shamrock shape.
Read More »
Mardi Gras Word Search
12,587 Views

Printable Mardi Gras Word Search
Read More »
Earth Day Word Search
9,693 Views

Printable Earth Day Word Search
Read More »
Winter Words Word Search
23,661 Views

A great winter classroom printout for the holidays. Free printable winter words search has 18 words to find relating to winter.
Read More »
New Year’s Word Search
21,082 Views

Printable New Year’s Eve Word Search for your classroom. Free printout with 21 terms and words for the New Year.
Read More »
Christmas Tree Word Search
15,807 Views

Elementary school age Christmas Tree Word Search printable has eleven words to find for the holiday season.
Read More »
Christmas Story Word Search
22,547 Views

The Nativity, a Christmas Story Word Search puzzle for kids. Printable word search contains with words that are associated with the Nativity Christmas Story.
Read More »
Time Word Search
12,336 Views
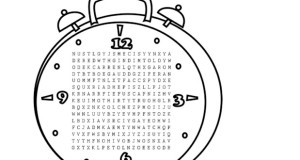
A clock shaped word search for telling time. Great Daylight Savings activity for kids.
Read More »
Color Word Search – Word Scramble
36,153 Views

Printable word search and word scramble using color names. Two printouts per page.
Read More »
The word-search puzzle is a string-search problem in which several words are to be located within an n ´ m array filled with letters. The following table shows a 30 ´ 30 array and some words that must be found in it.
Each word must occur entirely in a row, a column or a diagonal, that is, it cannot be bent from one direction into another. Words can be placed forward or backward, but not scrambled. Furthermore, words can share characters. A brute-force approach is extremely inefficient: if the puzzle has n rows and m columns, and if the average length of the words to search for is q, then the time complexity would be nmq. For typical values of n = 30, m = 30, and q = 5, the time complexity would be 4500, which is much higher than 110.
If the fingerprints are the same (pFP == tFP), the actual match of the pattern against the target is attempted. A mismatching character causes the matching loop to be aborted, while a complete match makes the function to return with the position of the pattern in the target string. If the fingerprints are not equal, the fingerprint substring of the target being matched (tFP) is updated by considering the effect of “sliding” the pattern under the target one character position to the right. The beauty of the fingerprint approach is that words have the same fingerprint whether they are forward or backward in any direction.
The following function KRsearch, implements a variation on the “fingerprinting” method of Karp-Rabin (Sedgewick, Robert, Algorithms, 1990, pp. 289-291). Function fp is used to compute the initial fingerprint of the pattern (pFP) and of the corresponding prefix of the target (tFP). The fingerprint is simply the sum of the ASCII codes of the characters.
int KRsearch( char p[], char t[] ) { int i, j, k, m = strlen( p ), n = strlen( t ), pFP, tFP; pFP = fp( p, 0, m ); tFP = fp( t, 0, m ); for ( i = 0; i <= n-m; ++i ) { if ( pFP == tFP ) { for ( j = 0, k = i; j < m; ++j, ++k ) if ( p[ j ] != t[ k ] ) break; if ( j == m ) return i; } else if ( i + m < n ) tFP += t[ i+m ] - t[ i ]; else break; } return -1; } int fp( char s[], int i, int m ) { int j, sum; sum = 0; for ( j = i; j < m; ++j ) sum += s[ j ]; return sum; }
Assume that the puzzle is given in the text file wpuzzle.txt. The first line contains two numbers (n and m) separated by a blank space. Those numbers are the rows and columns of the puzzle and are followed by n lines of m characters each. Assume that the words to be found are given in the text file words.txt, one word per line. No assumptions should be made as to whether or not the words appear in the puzzle. The program must fill (and print) a solution array with the words in the position and direction in which they were found, as shown below for the example puzzle.
The global variables to be used and the main function are as follows.
#define maxN 50 #define maxM 50 char puzzle[ maxN ][ maxM ], puzsol[ maxN ][ maxM ], line[ maxM + 1 ]; int n, m, maxOFnm, pFP; void main() { FILE *fp; int len; if ( LoadPuzzle() ) { ShowPuzzle(); if ( (fp = fopen( "words.txt", "r" )) != NULL ) { while ( fgets( line, maxM + 1, fp ) != NULL ) { len = removeNL( line ); FindWord( line, len ); } fclose( fp ); ShowSolution(); } } }
The trivial auxiliary functions are defined as follows.
int LoadPuzzle() { FILE *fp; int ok = 0, i, j; if ( (fp = fopen( "wpuzzle.txt", "r" )) != NULL ) { fscanf( fp, "%d %dn", &n, &m ); if ( 0 < n && n <= maxN && 0 < m && m <= maxM ) { maxOFnm = n < m ? m: n; for ( i = 0; i < n; ++i ) { fgets( line, maxM+1, fp ); removeNL( line ); strcpy( &(puzzle[ i ][ 0 ]), line ); } fclose( fp ); ok = 1; } } return ok; } int removeNL( char *str ) { int l = strlen( str ) - 1; str[ l ] = ''; return l; } void ShowPuzzle() { int i, j; printf( "Puzzle array: (%dx%d)n", n, m ); for ( i = 0; i < n; ++i ) { for ( j = 0; j < m; ++j ) { printf( "%c ", puzzle[ i ][ j ] ); puzsol[ i ][ j ] = ' '; } printf( "n" ); } } void ShowSolution() { int i, j; printf( "nWords found:n" ); for ( i = 0; i < n; ++i ) { for ( j = 0; j < m; ++j ) printf( "%c ", puzsol[ i ][ j ] ); printf( "n" ); } }
To find a word, conduct a search in the horizontal, vertical, and diagonal directions, stopping the search when the word is found in any direction. The diagonal directions involve a search either in the southeast (upper-left corner to lower-right corner) or in the southwest (upper-right corner to lower-left corner) directions.
void FindWord( char *w, int wLen ) { pFP = hvFP( w, 0, wLen, 1 ); printf( "searching for '%s', fp = %d", w, pFP ); if ( !( hKRsearch( w, wLen ) || vKRsearch( w, wLen ) || seKRsearch( w, wLen ) || swKRsearch( w, wLen ) ) ) printf( " not" ); printf( " foundn" ); }
The implementation of functions hKRsearch, vKRsearch, seKRsearch, and swKRsearch rely on adaptations of the basic KRsearch function to perform searches over a two-dimensional array. Function hvFP, to compute the fingerprint in the horizontal and vertical directions of the puzzle, is trivially used to obtain the fingerprint of a word as if it were in a horizontal direction.
Since the fingerprint of a word is the same whether the word occurs foward or backward in the puzzle, it is convenient to define a global structure in which the search functions can return the position of the array at which a word was found, and the word’s direction.
typedef enum { forw, back } FillDir; typedef struct { int pos; FillDir dir; } FIstr; FIstr finfo;
The following figure shows typical searches in the vertical (column 3) and horizontal (row 1) directions.
The computation of the initial fingerprint of the target and the actual search in these directions can be done in the same way. To reach the “next” character in the horizontal direction an increment of 1 is needed, while for the vertical direction we an increment of maxM is needed. This is the third argument to functions hvFP (horizontal/vertical fingerprint) and hvKRsearch (horizontal/ vertical Karp-Rabin search) defined below.
int hvFP( char s[], int i, int len, int d ) { int j, sum; sum = 0; for ( j = i; j < len; j += d ) sum += s[ j ]; return sum; } int hvKRsearch( char *p, char *t, int pLen, int tLen, int d ) { int i, j, k, tFP, pMaxIdx = pLen*d, tMaxIdx = (tLen-pLen)*d; tFP = hvFP( t, 0, pMaxIdx, d ); for ( i = 0; i <= tMaxIdx; i += d ) { if ( pFP == tFP ) { for ( j = 0, k = i; j < pLen; ++j, k += d ) if ( p[ j ] != t[ k ] ) break; if ( j == pLen ) { finfo.pos = i; finfo.dir = forw; return 1; } else { for ( j = pLen-1, k = i; j >= 0; --j, k +=d ) if ( p[ j ] != t[ k ] ) break; if ( j == -1 ) { finfo.pos = i; finfo.dir = back; return 1; } } } else tFP += t[ i + pMaxIdx ] - t[ i ]; } return 0; }
Filling a word in the solution depends on whether it was found forward or backward in the vertical or horizontal direction. This is taken care of by function hvFillWord.
void hvFillWord( char *psol, char *w, int wLen, int d ) { int i, j = finfo.pos; if ( finfo.dir == forw ) for ( i = 0; i < wLen; ++i ) { psol[ j ] = w[ i ]; j += d; } else for ( i = wLen-1; i >= 0; --i ) { psol[ j ] = w[ i ]; j += d; } }
Horizontal and vertical searches are implemented by the two functions below.
int hKRsearch( char *w, int wLen ) { int i; for ( i = 0; i < n; ++i ) if ( hvKRsearch( w, &(puzzle[ i ][ 0 ]), wLen, m, 1 ) ) { hvFillWord( &(puzsol[ i ][ 0 ]), w, wLen, 1 ); break; } return i < n; } int vKRsearch( char *w, int wLen ) { int j; for ( j = 0; j < m; ++j ) if ( hvKRsearch( w, &(puzzle[ 0 ][ j ]), wLen, n, maxM ) ) { hvFillWord( &(puzsol[ 0 ][ j ]), w, wLen, maxM ); break; } return j < m; }
Searches along the diagonals are performed in a similar way. The following figure shows typical searches.
In the southeast direction, the increment must be maxM + 1 to reach the “next” character, while in the southwest direction, the increment must be maxM – 1. Because all functions use upper bounds for the indices, it is not a good idea to conduct searches in the north-east direction.
The functions to compute the initial fingerprint, and to search in the diagonal directions are defined below.
int dgFP( char s[], int i, int len, int d ) { int j, sum; sum = 0; for ( j = i; j < len; j += d + 1 ) sum += s[ j ]; return sum; } int dKRsearch( char *p, char *t, int pLen, int tLen, int d ) { int i, j, k, tFP, pMaxIdx = pLen*(d+1), tMaxIdx = (tLen-pLen)*(d+1); tFP = dgFP( t, 0, pMaxIdx, d ); for ( i = 0; i <= tMaxIdx; i += d + 1 ) { if ( pFP == tFP ) { for ( j = 0, k = i; j < pLen; ++j, k += d + 1 ) if ( p[ j ] != t[ k ] ) break; if ( j == pLen ) { finfo.pos = i; finfo.dir = forw; return 1; } else { for ( j = pLen-1, k = i; j >= 0; --j, k +=d + 1 ) if ( p[ j ] != t[ k ] ) break; if ( j == -1 ) { finfo.pos = i; finfo.dir = back; return 1; } } } else tFP += t[ i + pMaxIdx ] - t[ i ]; } return 0; }
The function to fill words in the diagonal directions is similar to the one to fill words in the horizontal and vertical directions.
void dgFillWord( char *psol, char *w, int wLen, int d ) { int i, j = finfo.pos; if ( finfo.dir == forw ) for ( i = 0; i < wLen; ++i ) { psol[ j ] = w[ i ]; j += d + 1; } else for ( i = wLen-1; i >= 0; --i ) { psol[ j ] = w[ i ]; j += d + 1; } }
To find a word in the diagonals, start at the main diagonals, and search for as long as a diagonal contains at least as many characters as the word being sought.
int seKRsearch( char *w, int wLen ) { int i, tLen, found = 0; tLen = maxOFnm; for ( i = 0; wLen <= tLen; ++i ) { if ( dKRsearch( w, &(puzzle[ i ][ 0 ]), wLen, tLen, maxM ) ) { found = 1; dgFillWord( &(puzsol[ i ][ 0 ]), w, wLen, maxM ); break; } --tLen; } if ( tLen < wLen ) { tLen = maxOFnm - 1; for ( i = 1; wLen <= tLen; ++i ) { if ( dKRsearch( w, &(puzzle[ 0 ][ i ]), wLen, tLen, maxM ) ) { found = 1; dgFillWord( &(puzsol[ 0 ][ i ]), w, wLen, maxM ); break; } --tLen; } } return found; } int swKRsearch( char *w, int wLen ) { int i, tLen, found = 0; tLen = maxOFnm; for ( i = m-1; wLen <= tLen; --i ) { if ( dKRsearch( w, &(puzzle[ 0 ][ i ]), wLen, tLen, maxM-2 ) ) { found = 1; dgFillWord( &(puzsol[ 0 ][ i ]), w, wLen, maxM-2 ); break; } --tLen; } if ( tLen < wLen ) { tLen = maxOFnm - 1; for ( i = 1; wLen <= tLen; ++i ) { if ( dKRsearch( w, &(puzzle[ i ][ m-1 ]), wLen, tLen, maxM-2 ) ) { found = 1; dgFillWord( &(puzsol[ i ][ m-1 ]), w, wLen, maxM-2 ); break; } --tLen; } } return found; }
This member has not yet provided a Biography. Assume it’s interesting and varied, and probably something to do with programming.
Make your own word search puzzles with the Word Search Maker! This easy-to-use tool allows you to provide your own word list and create custom word searches in minutes. You can then download and print them instantly, or play online the pre-made puzzles right away. So get creative and have some fun!
How do you create custom Word Search Puzzles?
It’s easy! Just provide your word list and the Word Search Maker will create a puzzle for you.
- Enter your words into the text box provided. Make sure to add no more than 30 words.
- Select the theme or topics of your word search.
- Words should only include letters from a-z – uppercase or lowercase. You can use space and dash but these will be omitted while searching for your word search.
- Make sure not to use any personal information if you want your puzzles added to our database.
- When you are ready, click on “Regenerate” and the word search will be generated for you.
- If you want to download and print your word search puzzle, just click on “Download PDF.” The word search will be downloaded as a PDF file which you can then print.
NOTE: These are randomly generated words so be sure to proofread carefully before using. You can also regenerate the puzzle with new array of words.



