Solving word problems at KS1 and KS2 is an essential part of the new maths curriculum. Here you can find expert guidance on how to solve maths word problems as well as examples of the many different types of word problems primary school children will encounter with links to hundreds more.
What is a word problem?
A word problem in maths is a maths question written as one sentence or more that requires children to apply their maths knowledge to a ‘real-life’ scenario.
This means that children must be familiar with the vocabulary associated with the mathematical symbols they are used to, in order to make sense of the word problem.
For example:
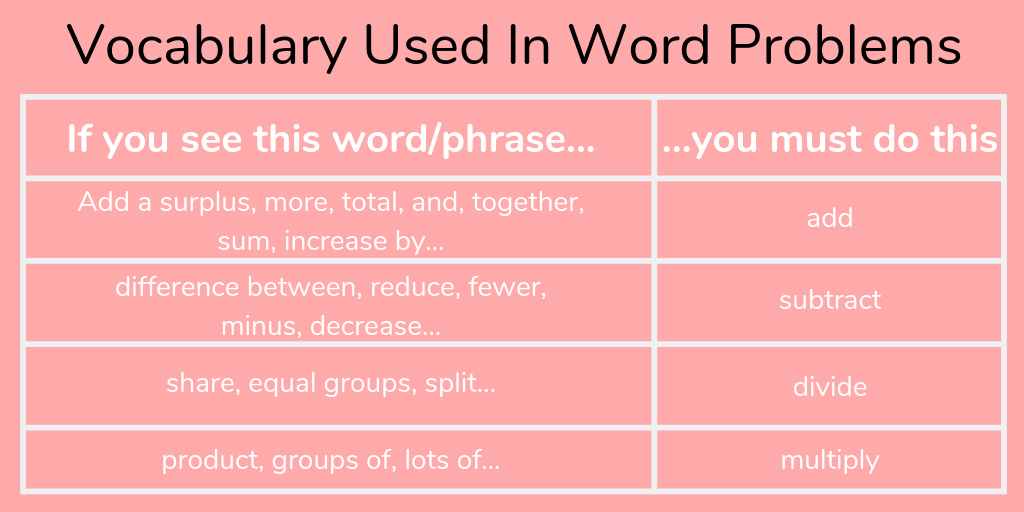
Importance of word problems within the national curriculum
The National Curriculum states that its mathematics curriculum “aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately;
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language;
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions.”
To support this schools are adopting a ‘mastery’ approach to maths
The National Centre for Excellence in the Teaching of Mathematics (NCETM) have defined “teaching for mastery”, with some aspects of this definition being:
- Maths teaching for mastery rejects the idea that a large proportion of people ‘just can’t do maths’.
- All pupils are encouraged by the belief that by working hard at maths they can succeed.
- Procedural fluency and conceptual understanding are developed in tandem because each supports the development of the other.
- Significant time is spent developing deep knowledge of the key ideas that are needed to underpin future learning. The structure and connections within the mathematics are emphasised, so that pupils develop deep learning that can be sustained.
(The Essence of Maths Teaching for Mastery, 2016)

Year 3 to 6 Rapid Reasoning Worksheet for Weeks 1-6
Download for FREE 6 weeks of Rapid Reasoning worksheets. That include six weeks of daily reasoning and problem-solving questions for years 3, 4, 5 and 6!
Mastery helps children to explore maths in greater depth
One of NCETM’s Five Big Ideas in Teaching for Mastery (2017) is “Mathematical Thinking: if taught ideas are to be understood deeply, they must not merely be passively received but must be worked on by the student: thought about, reasoned with and discussed with others”.
In other words – yes, fluency in arithmetic is important; however, with this often lies the common misconception that once a child has learnt the number skills appropriate to their level/age, they should be progressed to the next level/age of number skills.
The mastery approach encourages exploring the breadth and depth of these concepts (once fluency is secure) through reasoning and problem solving.
See the following example:
| Year 6 objective | Fluency | Reasoning | Problem solving |
|---|---|---|---|
| Solve addition and subtraction multi-step problems in contexts, deciding which operations and methods to use and why. | 7,208 females attended a concert as well as 8,963 males. There were originally 20,000 seats on sale. How many empty seats were there at the concert? | Abdul says, “If I add any two 4-digit numbers together, it will make a 5-digit number.” Do you agree? Explain why. | Three pandas are eating bamboo sticks. There are 51 altogether. They all eat an odd number of sticks. How many bamboo sticks did they each eat? How many different ways can you do it? |
What sort of word problems might my child encounter at school?
In Key Stage 2, there are nine ‘strands’ of maths – these are then further split into ‘sub-strands’. For example, ‘number and place value’ is the first strand: a Year 3 sub-strand of this is to “find 10 or 100 more or less than a given number”; a Year 6 sub-strand of this is to “determine the value of each digit in numbers up to 10 million”. The table below shows how the ‘sub-strands’ are distributed across each strand and year group in KS2.
| Strand | Year 3 | Year 4 | Year 5 | Year 6 | Total |
|---|---|---|---|---|---|
| Number and place value | 6 | 9 | 7 | 5 | 27 |
| Calculations | 7 | 8 | 15 | 9 | 39 |
| Fractions, decimals and percentages | 7 | 10 | 12 | 11 | 40 |
| Ratio and proportion | 0 | 0 | 0 | 4 | 4 |
| Algebra | 0 | 0 | 0 | 5 | 5 |
| Measurement | 17 | 9 | 10 | 8 | 44 |
| Geometry: properties of shape | 5 | 4 | 6 | 7 | 22 |
| Geometry: position and direction | 0 | 3 | 1 | 2 | 6 |
| Statistics | 2 | 2 | 2 | 2 | 8 |
How to teach children to solve word problems?
Here are two simple strategies that can be applied to many word problems before solving them.
- What do you already know?
- How can this problem be drawn/represented pictorially?
Let’s see how this can be applied to a word problem to help achieve the answer.
Solving a simple word problem
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
1. What do you already know?
- There are 1,000ml in 1 litre
- Pours = liquid leaving the bottle = subtraction
- For every = multiply
- Left over = requires subtraction at some point
2. How can this problem be drawn/represented pictorially?
The bar model is always a brilliant way of representing problems, but if you are not familiar with this, there are always other ways of drawing it out.
Read more: What is a bar model
For example, for this question, you could draw 28 pupils (or stick man x 28) with ‘225 ml’ above each one and then a half-empty bottle with ‘8 litres’ marked at the top.
Now to put the maths to work. This is a Year 6 multi-step problem, so we need to use what we already know and what we’ve drawn to break down the steps.
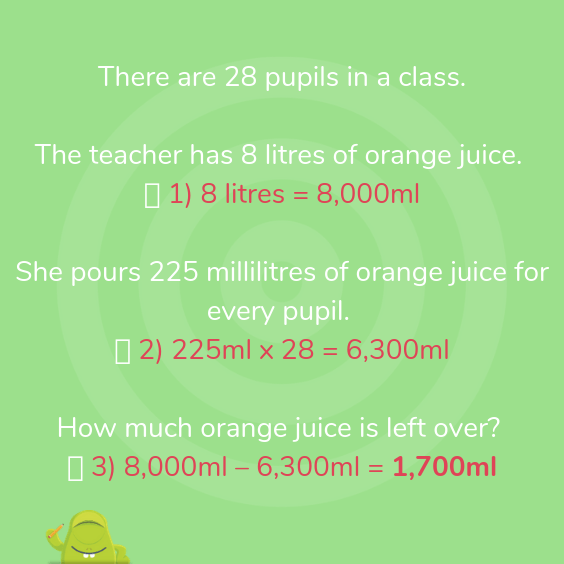
Solving a more complex word problem
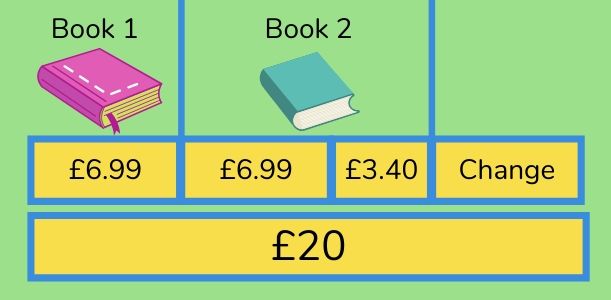
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book.
She pays using a £20 notes.
What change does Mara get?
1. What do you already know?
- More than = add
- Using decimals means I will have to line up the decimal points correctly in calculations
- Change from money = subtract
2. How can this problem be drawn/represented pictorially?
See this example of bar modelling for this question:
Now to put the maths to work using what we already know and what we’ve drawn to break down the steps.
Mara is in a bookshop.
She buys one book for £6.99 and another that costs £3.40 more than the first book. 1) £6.99 + (£6.99 + £3.40) = £17.38
She pays using a £20 note.
What change does Mara get? 2) £20 – £17.38 = £2.62
Maths word problems for years 1 to 6
The more children learn about maths as the go through primary school, the trickier the word problems they face will become.
Below you will find some information about the types of word problems your child will be coming up against on a year by year basis, and how word problems apply to each primary year group
Word problems in Year 1
Throughout Year 1 a child is likely to be introduced to word problems with the help of concrete resources (pieces of physical apparatus like coins, cards, counters or number lines) to help them understand the problem.
An example of a word problem for Year 1 would be:
Chris is going to buy a cake for his mum which costs 80p. How many 20p coins would he need to do this?
Word problems in Year 2
Year 2 is a continuation of Year 1 when it comes to word problems, with children still using concrete maths resources to help them understand and visualise the problems they are working on
An example of a word problem for Year 2 would be:
A class of 10 children each have 5 pencils in their pencil cases. How many pencils are there in total?
Word problems in Year 3
With word problems for year 3, children will move away from using concrete resources when solving word problems, and move towards using written methods. Teachers will begin to demonstrate the four operations such as addition and subtraction word problems, multiplication and division problems too.
This is also the year in which 2-step word problems will be introduced. This is a problem which requires two individual calculations to be completed.
Year 3 word problem: Geometry properties of shape
Shaun is making 3-D shapes out of plastic straws.
At the vertices where the straws meet, he uses blobs of modelling clay to fix them together
Here are some of the shapes he makes:
| Shape | Number of straws | Number of blobs of modelling clay |
|---|---|---|
| A | 8 | 5 |
| B | 12 | 8 |
| C | 6 | 4 |
One of Sean’s shapes is a cuboid. Which is it? Explain your answer.
Answer: shape B as a cuboid has 12 edges (straws) and 8 vertices (clay)
Year 3 word problem: Statistics
Year 3 are collecting pebbles. This pictogram shows the different numbers of pebbles each group finds.

Answer: a) 9 b) 3 pebbles drawn
Top tip
By the time children are in Year 3 many of the word problems, even one-step story problems tend to be a variation on a multiplication problem. For this reason learning times tables becomes increasingly essential at this stage. One of the best things you can do to help with Year 3 maths at home is support your child to do this.
Word problems in Year 4
At this stage of their primary school career, children should feel confident using the written method for each of the four operations.
Word problems for year 4 will include a variety of problems, including 2-step problems and be children will be expected to work out the appropriate method required to solve each one.
Year 4 word problem: Number and place value
My number has four digits and has a 7 in the hundreds place.
The digit which has the highest value in my number is 2.
The digit which has the lowest value in my number is 6.
My number has 3 fewer tens than hundreds.
What is my number?
Answer: 2,746
Word problems in Year 5
One and 2-step word problems continue with word problems for year 5, but this is also the year that children will be introduced to word problems containing decimals.
These are some examples of Year 5 maths word problems.
Year 5 word problem: Fractions, decimals and percentages
Stan, Frank and Norm are washing their cars outside their houses.
Stan has washed 0.5 of his car.
Frank has washed 1/5 of his car.
Norm has washed 5% of his car.
Who has washed the most?
Explain your answer.
Answer: Stan (he has washed 0.5 whereas Frank has only washed 0.2 and Norm 0.05)
Word problems in Year 6
Word problems for year 6 shift from 2-step word problems to multi-step word problems. These will include fractions, decimals, percentages and time word problems.
Here are some examples of the types of maths word problems Year 6 will have to solve.
Year 6 word problem – Ratio and proportion
This question is from the 2018 key stage 2 SATs paper. It is worth 1 mark.
The Angel of the North is a large statue in England. It is 20 metres tall and 54 metres wide.
Ally makes a scale model of the Angel of the North. Her model is 40 centimetres tall. How wide is her model?
Answer: 108cm
Year 6 word problem – Algebra
This question is from the 2018 KS2 SATs paper. It is worth 2 marks as there are 2 parts to the answer.
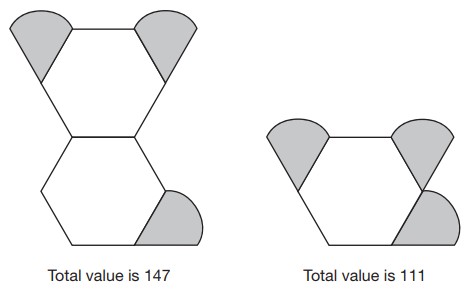
Amina is making designs with two different shapes.
She gives each shape a value.
Calculate the value of each shape.
Answer: 36 (hexagon) and 25.
Year 6 word problem: Measurement
This question is from the 2018 KS2 SATs paper. It is worth 3 marks as it is a multi-step problem.
There are 28 pupils in a class.
The teacher has 8 litres of orange juice.
She pours 225 millilitres of orange juice for every pupil.
How much orange juice is left over?
Answer: 1.7 litres or 1,700ml
Topic based word problems
The following examples give you an idea of the kinds of maths word problems your child will encounter for each of the 9 strands of maths in KS2.
Place value word problems
Place value word problem Year 5
This machine subtracts one hundredth each time the button is pressed. The starting number is 8.43. What number will the machine show if the button is pressed six times? Answer: 8.37
Download free number and place value word problems for Years 3, 4, 5 and 6
Addition and subtraction word problems
Addition and subtraction word problem Year 3
In Year 3 pupils will solve addition word problems and subtraction word problems with 2 and 3 digits.
Sam has 364 sweets. He gets given 142 more. He then gives 277 away. How many sweets is he left with? Answer: 229
Download free addition and subtraction word problems for Years 3, 4, 5 and 6
Addition word problem Year 3
Alfie thinks of a number. He subtracts 70. His new number is 12. What was the number Alfie thought of? Answer: 82
Subtraction word problem Year 6
The temperature at 7pm was 4oC. By midnight, it had dropped by 9 degrees. What was the temperature at midnight? Answer: -5oC
More here: 25 addition and subtraction word problems
Multiplication and division word problems
Multiplication and division word problem Year 3
A baker is baking chocolate cupcakes. She melts 16 chocolate buttons to make the icing for 9 cakes. How many chocolate buttons will she need to melt to make the icing for 18 cakes? Answer: 32
Multiplication word problem Year 4
Eggs are sold in boxes of 12. The egg boxes are delivered to stores in crates. Each crate holds 9 boxes. How many eggs are in a crate? Answer: 108
Download free multiplication word problems for Years 3, 4, 5 and 6
Division word problem Year 6
A factory produces 1,692 paintbrushes every day. They are packaged into boxes of 9. How many boxes does the factory produce every day? Answer: 188
Download our free division word problems worksheets for Years 3, 4, 5 and 6.
More here: 20 multiplication word problems
More here: 25 division word problems
Free resource: Use these four operations word problems to practise addition, subtraction, multiplication and division all together.
Fraction word problems
Fraction word problem Year 5
At the end of every day, a chocolate factory has 1 and 2/6 boxes of chocolates left over. How many boxes of chocolates are left over by the end of a week? Answer: 9 and 2/6 or 9 and 1/3
Download free fractions and decimals word problems worksheets for Years 3, 4, 5 and 6
More here: 28 fraction word problems
Decimals word problem Year 4 (crossover with subtraction)
Which two decimals that have a difference of 0.5? 0.2, 0.25, 0.4, 0.45, 0.6, 0.75. Answer: 0.25 and 0.75
Download free decimals and percentages word problems resources for Years 3, 4, 5 and 6
Percentage word problem Year 5
There are 350 children in a school. 50% are boys. How many boys are there? Answer: 175
Measurement word problem Year 3 (crossover with subtraction)
Lucy and Ffion both have bottles of strawberry smoothie. Each bottle contains 1 litre. Lucy drinks ½ of her bottle. Ffion drinks 300ml of her bottle. How much does each person have left in both bottles? Answer: Lucy = 500ml, Ffion = 300ml
More here: 25 percentage word problems
Money word problem Year 3
James and Lauren have different amounts of money. James has twelve 2p coins. Lauren has seven 5p coins. Who has the most money and by how much? Answer: Lauren by 11p.
More here: 25 money word problems
Area word problem Year 4
A rectangle measures 6cm by 5cm.
What is its area? Answer: 30cm2
Perimeter word problem Year 4
The swimming pool at the Sunshine Inn hotel is 20m long and 7m wide. Mary swims around the edge of the pool twice. How many metres has she swum? Answer: 108m
Ratio word problem Year 6 (crossover with measurement)
A local council has spent the day painting double yellow lines. They use 1 pot of yellow paint for every 100m of road they paint. How many pots of paint will they need to paint a 2km stretch of road? Answer: 20 pots
More here: 24 ratio word problems
Bodmas word problem Year 6
Draw a pair of brackets in one of these calculations so that they make two different answers. What are the answers?
50 – 10 × 5 =
50 – 10 × 5 =
Volume word problem Year 6
This large cuboid has been made by stacking shipping containers on a boat. Each individual shipping container has a length of 6m, a width of 4m and a height of 3m. What is the volume of the large cuboid? Answer: 864m3
How important are word problems when it comes to the SATs?
In the KS1 SATs, 58% (35/60 marks) of the test is comprised of maths ‘reasoning’ (word problems).
In KS2, this increases to 64% (70/110 marks) spread over two reasoning papers, each worth 35 marks. Considering children have, in the past, needed approximately 55-60% to reach the ‘expected standard’, it’s clear that children need regular exposure to and a solid understanding of how to solve a variety of word problems.
Children have the opportunity to practice SATs style word problems in Third Space Learning’s online one-to-one SATs revision programme. Personalised to meet the needs of each student, our programme helps to fill gaps and give students more confidence going in to the SATs exams.
Remember: The word problems can change but the maths won’t
It can be easy for children to get overwhelmed when they first come across word problems in KS2, but it is important that you remind them that whilst the context of the problem may be presented in a different way, the maths behind it remains the same.
Word problems are a good way to bring maths into the real world and make maths more relevant for your child, so help them practise, or even ask them to turn the tables and make up some word problems for you to solve.
This article while written by a teacher for teachers is also suitable for those at home supporting children with home learning. More free home learning resources are also available.
Do you have pupils who need extra support in maths?
Every week Third Space Learning’s maths specialist tutors support thousands of pupils across hundreds of schools with weekly online 1-to-1 lessons and maths interventions designed to plug gaps and boost progress.
Since 2013 we’ve helped over 145,000 primary and secondary school pupils become more confident, able mathematicians. Learn more or request a personalised quote for your school to speak to us about your school’s needs and how we can help.
Last updated
22 February 2018
Addition and Subtraction word problems for Year 1/2. Differentiated into 4 abilities.
Children can cut and stick each question into their books and work it out underneath!
NC Guidance:
«They discuss and solve problems in familiar practical contexts, including using
quantities. Problems should include the terms: put together, add, altogether, total, take
away, distance between, difference between, more than and less than, so that pupils
develop the concept of addition and subtraction and are enabled to use these operations
flexibly»
Creative Commons «Sharealike»
Something went wrong, please try again later.
Thank you, ideal for my little group in class
THANK YOU FOR SHARING THIS COLOURFUL AND VERY USEFUL RSOURCE
Perfect, just what I was looking for, thanks so much!
Thank you for these resources, great for my home learning lessons.
Report this resourceto let us know if it violates our terms and conditions.
Our customer service team will review your report and will be in touch.
Last updated
22 February 2018
Not the right resource?
See other similar resources
We explain what a word problem is and give examples of the types of word problems your child might be challenged with in each primary-school maths year group, from Year 1 to Year 6.
What is a word problem?
A word problem is a few sentences describing a ‘real-life’ scenario where a problem needs to be solved by way of a mathematical calculation.
Word problems are seen as a crucial part of learning in the primary curriculum, because they require children to apply their knowledge of various different concepts to ‘real-life’ scenarios.
Word problems also help children to familiarise themselves with mathematical language (vocabulary like fewer, altogether, difference, more, share, multiply, subtract, equal, reduced, etc.).
Teachers tend to try and include word problems in their maths lessons at least twice a week.
What is RUCSAC?
In the classroom children might be taught the acronym RUCSAC (Read, Understand, Choose, Solve, Answer, Check) to help them complete word problems.
By following the acronym step by step children learn to apply a structured, analytical strategy to their calculations. They will need to understand what the problem is asking them to find out by reading the question carefully, choosing the correct mathematical operation to help them solve the query and finally checking their answer by using the inverse operation.
Word problem examples for Years 1 to 6
The following are example word problems that apply to each primary year group.
Year 1
In Year 1 a child would usually been given apparatus to help them with a problem (counters, plastic coins, number cards, number lines or picture cards).
Sarah wants to buy a teddy bear costing 30p. How many 10p coins will she need?
Brian has 3 sweets. Tom has double this number of sweets. How many sweets does Tom have?
Year 2
In Year 2, children continue to use apparatus to help them with problem-solving.
Faye has 12 marbles. Her friend Louise has 9 marbles. How many marbles do they both have altogether?
Three children are each given 5 teddy bears. How many teddy bears do they have altogether?
Year 3
In Year 3, some children may use apparatus, but on the whole children will tend to work out word problems without physical aids. Teachers will usually demonstrate written methods for the four operations (addition, subtraction, multiplication and division) to support children in their working out of the problems.
A jumper costs £23. How much will 4 jumpers cost?
Sarah has 24 balloons. She gives a quarter of them away to her friend. How many balloons does she give away?
Children will also start to do two-step problems in Year 3. This is a problem where finding the answer requires two separate calculations, for example:
I have £34. I am given another £26. I divide this money equally into four different bank accounts. How much money do I put in each bank account?
- In this case, the first step would be to add £34 and £26 to make £60.
- The second step would be to divide £60 by 4 to make £15.
Year 4
Children should feel confident in an efficient written method for each operation at this stage. They will continue to be given a variety of problems and have to work out which operation and method is appropriate for each. They will also be given two-step problems.
I have 98 marbles. I share them equally between 6 friends. How many marbles does each friend get? How many marbles are left over?
Year 5
Children will continue to do one-step and two-step problems. They will start to carry out problem-solving involving decimals.
My chest of drawers is 80cm wide and my table is 1.3m wide. How much wall space do they take up when put side by side?
There are 24 floors of a car park. Each floor has room for 45 cars. How many cars can the car park fit altogether?
Year 6
In Year 6 children solve ‘multi-step problems’ and problems involving fractions, decimals and percentages.
Sarah sees the same jumper in two different sales:
In the first sale, the original price of the jumper is £36.15, but has been reduced by a third.
In the second sale, the jumper was priced at £45, but now has 40% off.
How much does each jumper cost and which one is the cheapest?
In the past, calculators were sometimes used for solving two-step problems like the one above, but the new curriculum does not include the use of calculators at any time during primary school.
Related Pages
More Lessons for Grade 1
Common Core for Grade 1
Solve word problems that call for addition of three whole numbers whose sum is less than or equal to 20, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem.
Common Core: 1.OA.1 and 1.OA.2
Suggested Learning Target
- I can model addition and subtraction word problems using objects, drawings, and equations with unknown numbers in different positions.
- I can solve addition and subtraction word problems using objects, drawings, and equations.
- I can solve word problems with unknown numbers in different positions (e.g., 6 + ? = 8, ? + 2 = 8, 6 + 2 = ?).
- I can represent a problem in multiple ways including drawings and or objects/manipulatives (e.g., counters, unifix cubes, Digi-Blocks, number lines)
- I can take apart and combine numbers in a wide variety of ways
- I can make sense of quantity and be able to compare numbers
- I can use flexible thinking strategies to develop the understanding of the traditional algorithms and their processes
- I can solve a variety of addition and subtraction word problems
- I can use _ or ? to represent an unknown in an equation
- I can model addition and subtraction word problems using objects, drawings, and equations with unknown numbers in different positions.
- I can add three whole numbers whose sum is less than or equal to 20.
- I can solve word problems with three whole numbers using objects, drawings, and equations.
- I can add numbers in any order and be able to identify the most efficient way to solve the problem
Addition Examples:
Result Unknown
Two bunnies sat on the grass. Three more bunnies hopped there.
How many bunnies are on the grass now?
2 + 3 = ?
Change Unknown
Two bunnies were sitting on the grass. Some more bunnies hopped there. Then there were five bunnies. How many bunnies hopped over to the first?
2 + ? = 5
Start Unknown
Some bunnies were sitting on the grass. Three more bunnies hopped there. Then there were five bunnies. How many bunnies were on the grass before?
? + 3 = 5
Subtraction Examples:
Result Unknown
Five apples were on the table. I ate two apples.
How many apples are on the table now?
5 – 2 = ?
Change Unknown
Five apples were on the table. I ate some apples. Then there were three apples.
How many apples did I eat?
5 – ? = 3
Start Unknown
Some apples were on the table. I ate two apples. Then there were three apples.
How many apples were on the table before?
? – 2 = 3
Word Problems. Addition with pictures (up to sum 20)
Example:
Lily had 5 apples and her aunt gave her 9 apples later. How many apples did Lily have finally?
- Show Video Lesson
Subtraction by counting back — word problems with pictures
Example:
There are 5 books on the desk. Betty took 2 away. How many books are left on the desk?
- Show Video Lesson
Word problems — subtraction with pictures — cross out — 1 digit
Example:
There are 9 cars in the shop and 8 of them are sold. How many cars are left?
- Show Video Lesson
Word problems — Subtraction with pictures — cross out (numbers to 20)
Example:
Mary had 11 toys and she gave 5 of them to Emma. How many toys did Mary have finally?
- Show Video Lesson
Word problems — adding multiple one-digit numbers
Example:
A furniture store sold 6 tables, 2 bookcases and 1 bed. How many pieces of furniture did the store sell in all?
-
Show Video Lesson
Addition word problems that add up multiple values to sums less than or equal to ten.
Example:
-
Laurem gave Troy two yellow pencils, three blue pencils and one green pencil. How many pencils did Lauren give him in all?
-
Ms. Ellis gave Lauren and Troy some cookies. Lauren ate two sugar and two chocolate chip cookies. Troy ate three oatmeal raisin and two sugar cookies. How many cookies did they eat in all?
- Show Video Lesson
Subtraction Strategies
This video gives suggestions for solving subtraction story problems using a math mountain, equation, and circle drawing.
Example:
I have 8 peanuts. Then I eat 5 of them. How many peanuts are left?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
This article is for parents who think about how to help with math and support their children. The math word problems below provide a gentle introduction to common math operations for schoolers of different grades.
What are math word problems?
During long-time education, kids face various hurdles that turn into real challenges. Parents shouldn’t leave their youngsters with their problems. They need an adult’s possible help, but what if the parents themselves aren’t good at mathematics? All’s not lost. You can provide your kid with different types of support. Not let a kid burn the midnight oil! Help him/ her to get over the challenges thanks to these captivating math word examples.
Math word problems are short math questions formulated into one or several sentences. They help schoolers to apply their knowledge to real-life scenarios. Besides, this kind of task helps kids to understand this subject better.
Addition for the first and second grades
These math examples are perfect for kids that just stepped into primary school. Here you find six easy math problems with answers:
1. Peter has eight apples. Dennis gives Peter three more. How many apples does Peter have in all?
Show answer
Answer: 8 apples + 3 apples = 11 apples.
2. Ann has seven candies. Lack gives her seven candies more. How many candies does Ann have in all?
Show answer
Answer: 7 candies + 7 candies = 14 candies.
3. Walter has two books. Matt has nine books. If Matt gives all his books to Walter, how many books will Walter have?
Show answer
Answer: 2 books + 9 books = 11 books.
4. There are three crayons on the table. Albert puts five more crayons on the table. How many crayons are on the table?
Show answer
Answer: 3 crayons + 5 crayons = 8 crayons.
5. Bill has nine oranges. His friend has one orange. If his friend gives his orange to Bill, how many oranges will Bill have?
Show answer
Answer: 9 oranges + 1 orange = 10 oranges.
6. Jassie has four leaves. Ben has two leaves. Ben gives her all his leaves. How many leaves does Jessie have in all?
Show answer
Answer: 4 leaves + 2 leaves = 6 leaves.
Subtraction for the first and second grades
1. There were three books in total at the book shop. A customer bought one book. How many books are left?
Show answer
Answer: 3 books – 1 book = 2 books.
2. There are five pizzas in total at the pizza shop. Andy bought one pizza. How many pizzas are left?
Show answer
Answer: 5 pizzas – 1 pizza = 4 pizzas.
3. Liza had eleven stickers. She gave one of her stickers to Sarah. How many stickers does Liza have?
Show answer
Answer: 11 stickers – 1 sticker = 10 stickers.
4. Adrianna had ten stones. But then she left two stones. How many stones does Adrianna have?
Show answer
Answer: 10 stones – 2 stones = 8 stones.
5. Mary bought a big bag of candy to share with her friends. There were 20 candies in the bag. Mary gave three candies to Marissa. She also gave three candies to Kayla. How many candies were left?
Show answer
Answer: 20 candies – 3 candies – 3 candies = 14 candies.
6. Betty had a pack of 25 pencil crayons. She gave five to her friend Theresa. She gave three to her friend Mary. How many pencil crayons does Betty have left?
Show answer
Answer: 25 crayons – 5 crayons – 3 crayons = 17 crayons.
Multiplication for the 2nd grade and 3rd grade
See the simple multiplication word problems. Make sure that the kid has a concrete understanding of the meaning of multiplication before.
Bill is having his friends over for the game night. He decided to prepare snacks and games.
1. He makes mini sandwiches. If he has five friends coming over and he made three sandwiches for each of them, how many sandwiches did he make?
Show answer
Answer: 5 x 3 = 15 sandwiches.
2. He also decided to get some juice from fresh oranges. If he used two oranges per glass of juice and made six glasses of juice, how many oranges did he use?
Show answer
Answer: 2 x 6 = 12 oranges.
3. Then Bill prepared the games for his five friends. If each game takes 7 minutes to prepare and he prepared a total of four games, how many minutes did it take for Bill to prepare all the games?
Show answer
Answer: 7 x 4 = 28 minutes.
4. Bill decided to have takeout food as well. If each friend and Bill eat three slices of pizza, how many slices of pizza do they have in total?
Show answer
Answer: 6 (5 friends and Bill) x 3 slices of pizza = 18 slices of pizza.
Mike is having a party at his house to celebrate his birthday. He invited some friends and family.
1. He and his mother prepared cupcakes for dessert. Each box had 8 cupcakes, and they prepared four boxes. How many cupcakes have they prepared in the total?
Show answer
Answer: 8 x 4 = 32 cupcakes.
2. They also baked some cookies. If they baked 6 pans of cookies, and there were 7 cookies per pan, how many cookies did they bake?
Show answer
Answer: 6 x 7 = 42 cookies.
3. Mike planned to serve some cold drinks as well. If they make 7 pitchers of drinks and each pitcher can fill 5 glasses, how many glasses of drinks are they preparing?
Show answer
Answer: 7 x 5 = 35 glasses.
4. At the end of the party, Mike wants to give away some souvenirs to his 6 closest friends. If he gives 2 souvenir items for each friend, how many souvenirs does Mike prepare?
Show answer
Answer: 6 x 2 = 12 souvenirs.
Division: best for 3rd and 4th grades
1. If you have 10 books split evenly into 2 bags, how many books are in each bag?
Show answer
Answer: 10 : 2 = 5 books.
2. You have 40 tickets for the fair. Each ride costs 2 tickets. How many rides can you go on?
3. The school has $20,000 to buy new equipment. If each piece of equipment costs $100, how many pieces can the school buy in total?
Show answer
Answer: $20,000 : $100= 200.
4. Melissa has 2 packs of tennis balls for $10 in total. How much does 1 pack of tennis balls cost?
5. Jack has 25 books. He has a bookshelf with 5 shelves on it. If Jack puts the same number of books on each shelf, how many books will be on each shelf?
6. Matt is having a picnic for his family. He has 36 cookies. There are 6 people in his family. If each person gets the same number of cookies, how many cookies will each person get?
Division with remainders for fourth and fifth grades
1. Sarah sold 35 boxes of cookies. How many cases of ten boxes, plus extra boxes does Sarah need to deliver?
Show answer
Answer: 35 boxes divided by 10 boxes per case = 3 cases and 5 boxes.
2. Candies come in packages of 16. Mat ate 46 candies. How many whole packages of candies did he eat, and how many candies did he leave? 46 candies divided by 16 candies = 2 packages and 2 candies left over.
3. Mary sold 24 boxes of chocolate biscuits. How many cases of ten boxes, plus extra boxes does she need to deliver?
Show answer
Answer: 24 boxes divided by 10 boxes per case = 2 cases and four boxes.
4. Gummy bears come in packages of 25. Suzie and Tom ate 30 gummy bears. How many whole packages did they eat? How many gummy bears did they leave?
Show answer
Answer: 30 divided by 25 = 1 package they have eaten and 20 gummy bears left over.
5. Darel sold 55 ice-creams. How many cases of ten boxes, plus extra boxes does he need to deliver?
Show answer
Answer: 55 boxes divided by 10 boxes per case = 5 cases and 5 boxes.
6. Crackers come in packages of 8. Mat ate 20 crackers. How many whole packages of crackers did he eat, and how many crackers did he leave?
Show answer
Answer: 20 divided by 8 = 2 packages eaten and 4 crackers are left.
Mixed operations for the fifth grade
These math word problems involve four basic operations: addition, multiplication, subtraction, and division. They suit best for the fifth-grade schoolers.
200 planes are taking off from the airport daily. During the Christmas holidays, the airport is busier — 240 planes are taking off every day from the airport.
1. During the Christmas holidays, how many planes take off from the airport in each hour if the airport opens 12 hours daily?
Show answer
Answer: 240÷12=20 planes take off from this airport each hour during the Christmas holidays.
2. Each plane takes 220 passengers. How many passengers depart from the airport every hour during the Christmas holidays? 20 x 220 = 4400.
Show answer
Answer: 4400 passengers depart from the airport every hour.
3. Compared with a normal day, how many more passengers are departing from the airport in a day during the Christmas holidays?
Show answer
Answer: (240-200) x 220 = 8800 more passengers departing from the airport in a day during the Christmas holidays.
4. During normal days on average 650 passengers are late for their plane daily. During the Christmas holidays, 1300 passengers are late for their plane. That’s why 14 planes couldn’t take off and are delayed. How many more passengers are late for their planes during Christmas week?
Show answer
Answer: 1300 – 650 = 650 more passengers are late for their planes each day during the Christmas holidays.
5. According to the administration’s study, an additional 5 minutes of delay in the overall operation of the airport is caused for every 27 passengers that are late for their flights. What is the delay in the overall operation if there are 732 passengers late for their flights?
Show answer
Answer: 732 ÷ 27 × 5 = 136. There will be a delay of 136 minutes in the overall operation of the airport.
Extra info math problems for the fifth grade
1. Ann has 7 pairs of red socks and 8 pairs of pink socks. Her sister has 12 pairs of white socks. How many pairs of socks does Ann have?
2. Kurt spent 17 minutes doing home tasks. He took a 3-minute snack break. Then he studied for 10 more minutes. How long did Kurt study altogether?
Show answer
Answer: 17 + 10 = 27 minutes.
3. There were 15 spelling words on the test. The first schooler spelled 9 words correctly. Miguel spelled 8 words correctly. How many words did Miguel spell incorrectly?
4. In the morning, Jack gave his friend 2 gummies. His friend ate 1 of them. Later Jack gave his friend 7 more gummies. How many gummies did Jack give his friend in all?
5. Peter wants to buy 2 candy bars. They cost 8 cents, and the gum costs 5 cents. How much will Peter pay?
Finding averages for 5th grade
We need to find averages in many situations in everyday life.
1. The dog slept 8 hours on Monday, 10 hours on Tuesday, and 900 minutes on Wednesday. What was the
average number of hours the dog slept per day?
Show answer
Answer: (8+10+(900:60)) : 3 = 11 hours.
2. Jakarta can get a lot of rain in the rainy season. The rainfall during 6 days was 90 mm, 74 mm, 112 mm, 30 mm, 100 mm, and 44 mm. What was the average daily rainfall during this period?
Show answer
Answer: (90+74+112+30+100+44) : 6 = 75 mm.
3. Mary bought 4 books. The prices of the first 3 books were $30, $15, and $18. The average price she paid for the 4 books was $25 per books. How much did she pay for the 4th books?


Math & logic courses for kids
Times more complex than school, extremely fun, interactive and rewarding to keep 7-13 years old kids engaged. We’re gonna make them love math!
learn more
Ordering and number sense for the 5th grade
1. There are 135 pencils, 200 pens, 167 crayons, and 555 books in the bookshop. How would you write these numbers in ascending order?
Show answer
Answer: 135, 167, 200, 555
2. There are five carrots, one cabbage, eleven eggs, and 15 apples in the fridge. How would you write these numbers in descending order?
3. Peter has completed exercises on pages 279, 256, 264, 259, and 192. How would you write these numbers in ascending order?
Show answer
Answer: 192, 256, 259, 264, 279.
4. Mary picked 32 pants, 15 dresses, 26 pairs of socks, 10 purses. Put all these numbers in order.
5. The family bought 12 cans of tuna, 23 potatoes, 11 onions, and 33 pears. Put all these numbers in order.
Fractions for the 6th-8th grades
1. Jannet cooked 12 lemon biscuits for her daughter, Jill. She ate up 4 biscuits. What fraction of lemon biscuits did Jill eat?
Show answer
Answer: 1/3 of the lemon biscuits.
2. Guinet travels a distance of 7 miles to reach her school. The bus covers only 5 miles. Then she has to walk 2 miles to reach the school. What fraction of the distance does Guinet travel by bus?
Show answer
Answer: 5/7 of the distance
3. Bob has 24 pencils in a box. Eighteen pencils have #2 marked on them, and the 6 are marked #3. What fraction of pencils are marked #3?
Show answer
Answer: 1/4 of the pencils.
4. My mother places 15 tulips in a glass vase. It holds 6 yellow tulips and 9 red tulips. What fraction of tulips are red?
Show answer
Answer: 3/5 of the tulips.
5. Bill owns 14 pairs of socks, of which 7 pairs are white, and the rest are brown. What fraction of pairs of socks are brown?
Show answer
Answer: 1/2 of the pairs of socks.
6. Bred spotted a total of 39 birds in an aviary at the Zoo. He counted 18 macaws and 21 cockatoos. What fraction of macaws did Bred spot at the aviary?
Show answer
Answer: 6/13 of the birds.
Decimals for the 6th grade
Write in words the following decimals:
- 0,004
- 0,07
- 2,1
- 0,725
- 46,36
- 2000,19
Show answer
Answer:
- 0,004 = four thousandths.
- 0,07 = seven hundredths.
- 2,1 = two and one tenth.
- 0,725 = seven hundred twenty five thousandths.
- 46,36 = foury six and thirty six hundredths.
- 2000,19 = two thousand and nineteen hundredths.
Comparing and sequencing for the 6th grade
1. The older brother picked 42 apples at the orchard. The younger brother picked only 22 apples. How many more apples did the older brother pick?
Show answer
Answer: 42 – 22 = 20 apples more.
2. There were 16 oranges in a basket and 66 oranges in a barrel. How many fewer oranges were in the basket than were in the barrel?
Show answer
Answer: 66 – 16 = 50 fewer oranges.
3. There were 40 parrots in the flock. Some of them flew away. Then there were 25 parrots in the flock. How many parrots flew away?
Show answer
Answer: 40 – 25 = 15 parrots flew away.
4. One hundred fifty is how much greater than fifty-three?
5. On Monday, the temperature was 13°C. The next day, the temperature dropped by 8 degrees. What was the temperature on Tuesday?
6. Zoie picked 15 dandelions. Her sister picked 22 ones. How many more dandelions did her sister pick than Zoie?
Show answer
Answer: 22-15 = 7 dandelions more.
Time for the 4th grade
1. The bus was scheduled to arrive at 7:10 p.m. However, it was delayed for 45 minutes. What time was it when the bus arrived?
2. My mother starts her 7-hour work at 9:15 a.m. What time does she get off from work?
3. Jack’s walk started at 6:45 p.m. and ended at 7:25 p.m. How long did his walk last?
4. The school closes at 9:00 p.m. Today, the school’s principal left 15 minutes after the office closed, and his secretary left the office 25 minutes after he left. When did the secretary leave work?
5. Suzie arrives at school at 8:20 a.m. How much time does she need to wait before the school opens? The school opens at 8:35 a.m.
6. The class starts at 9:15 a.m.. The first bell will ring 20 minutes before the class starts. When will the first bell ring?
Money word problems for the fourth grade
1. James had $20. He bought a chocolate bar for $2.30 and a coffee cup for $5.50. How much money did he have left?
Show answer
Answer: $20.00 – $2.30 – $5.50 = $12.20. James had $12.20 left.
2. Coffee mugs cost $1.50 each. How much do 7 coffee mugs cost?
Show answer
Answer: $1.5 x 7 = $10.5.
3. The father gives $32 to his four children to share equally. How much will each of his children get?
4. Each donut costs $1.20. How much do 6 donuts cost?
Show answer
Answer: $1.20 * 6 = $7,2.
5. Bill and Bob went out for takeout food. They bought 4 hamburgers for $10. Fries cost $2 each. How much does one hamburger with fries cost?
Show answer
Answer: $10 ÷ 4 = $2.50. One hamburger costs $2.50. $2.50 + $2.00 = $4.50. One hamburger with fries costs $4.50.
6. A bottle of juice costs $2.80, and a can is $1.50. What would it cost to buy two cans of soft drinks and a bottle of juice?
Show answer
Answer: $1.50 x 2 + $2.80 = $5.80.
Measurement word problems for the 6th grade
The task is to convert the given measures to new units. It best suits the sixth-grade schoolers.
- 55 yd = ____ in.
- 43 ft = ____ yd.
- 31 in = ____ ft.
- 29 ft = ____ in.
- 72 in = ____ ft.
- 13 ft = ____ yd.
- 54 lb = ____ t.
- 26 t = ____ lb.
- 77 t = ____ lb.
- 98 lb = ____ t.
- 25 lb = ____ t.
- 30 t = ____ lb.
Show answer
Answer:
- 55 yd = 1.980 in
- 43 ft = 14 yd 1 ft
- 31 in = 2 ft 7 in
- 29 ft = 348 in
- 72 in = 6 ft
- 13 ft = 4 yd 1 ft.
- 54 lb = 0,027 t
- 26 t = 52.000 lb
- 77 t = 154.000 lb
- 98 lb = 0,049 t
- 25 lb = 0?0125 t
- 30 t = 60.000 lb.
Ratios and percentages for the 6th-8th grades
It is another area that children can find quite difficult. Let’s look at simple examples of how to find percentages and ratios.
1. A chess club has 25 members, of which 13 are males, and the rest are females. What is the ratio of males to all club members?
2. A group has 8 boys and 24 girls. What is the ratio of girls to all children?
3. A pattern has 4 red triangles for every 12 yellow triangles. What is the ratio of red triangles to all triangles?
4. An English club has 21 members, of which 13 are males, and the rest are females. What is the ratio of females to all club members?
5. Dan drew 1 heart, 1 star, and 26 circles. What is the ratio of circles to hearts?
6. Percentages of whole numbers:
- 50% of 60 = …
- 100% of 70 = …
- 90% of 70 = …
- 20% of 30 = …
- 40% of 10 = …
- 70% of 60 = …
- 100% of 20 = …
- 80% of 90 = …
Show answer
Answer:
- 50% of 60 = 30
- 100% of 70 = 70
- 90% of 70 = 63
- 20% of 30 = 6
- 40% of 10 = 4
- 70% of 60 = 42
- 100% of 20 = 20
- 80% of 90 = 72.
Probability and data relationships for the 8th grade
1. John ‘s probability of winning the game is 60%. What is the probability of John not winning the game?
2. The probability that it will rain is 70%. What is the probability that it won’t rain?
3. There is a pack of 13 cards with numbers from 1 to 13. What is the probability of picking a number 9 from the pack?
4. A bag had 4 red toy cars, 6 white cars, and 7 blue cars. When a car is picked from this bag, what is the probability of it being red or blue?
5. In a class, 22 students like orange juice, and 18 students like milk. What is the probability that a schooler likes juice?
Geometry for the 7th grade
The following task is to write out equations and find the angles. Complementary angles are two angles that sum up to 90 degrees, and supplementary angles are two angles that sum up to 180 degrees.
1. The complement of a 32° angle = …
2. The supplement of a 10° angle = …
3. The complement of a 12° angle = …
4. The supplement of a 104° angle = …
Variables/ equation word problems for the 5th grades
1. The park is 𝑥 miles away from Jack’s home. Jack had to drive to and from the beach with a total distance of 36 miles. How many miles is Jack’s home away from the park?
Show answer
Answer: 2𝑥 = 36 → 𝑥 = 18 miles.
2. Larry bought some biscuits which cost $24. He paid $x and got back $6 of change. Find x.
Show answer
Answer: x = 24 + 6 = $30.
3. Mike played with his children on the beach for 90 minutes. After they played for x minutes, he had to remind them that they would be leaving in 15 minutes. Find x.
Show answer
Answer: x = 90 – 15 = 75 minutes.
4. At 8 a.m., there were x people at the orchard. Later at noon, 27 of the people left the orchard, and there were 30 people left in the orchard. Find x.
Show answer
Answer: x = 30 + 27 = 57 people
Travel time word problems for the 5th-7th grades
1. Tony sprinted 22 miles at 4 miles per hour. How long did Tony sprint?
Show answer
Answer: 22 miles divided by 4 miles per hour = 5.5 hours.
2. Danny walked 15 miles at 3 miles per hour. How long did Danny walk?
Show answer
Answer: 15 miles divided by 3 miles per hour = 5 hours.
3. Roy sprinted 30 miles at 6 miles per hour. How long did Roy sprint?
Show answer
Answer: 30 miles divided by 6 miles per hour = 5 hours.
4. Harry wandered 5 hours to get Pam’s house. It is 20 miles from his house to hers. How fast did Harry go?
Show answer
Answer: 20 miles divided by 5 hours = 4 miles per hour.
STEM subjects for kids
STEM courses for kids ages 7-13 in physics, chemistry, math and logic in interactive game format
learn more