Word problems with money

Word problems with money are first introduced in the Maths Curriculum in Year 2. At this stage, children learn to recognise the different coins and the symbols for pounds and pence; find different combinations of coins and begin to solve simple addition and subtraction word problems.

As pupils progress through primary, they continue to encounter money and word problems involving money, right through to upper Key Stage 2. By Year 6 money is no longer specifically identified in the curriculum. However, pupils continue to be exposed to money word problems, through a range of mathematical concepts and word problems including: addition and subtraction word problems, division word problems, multiplication word problems decimals, fractions, percentages, ratio and algebra.

When children are first introduced to money problems, it is important for them to physically have the money to hold and manipulate, to help solve the problems. As students progress through the school, there is less of a need to have the money physically in their hands. Once they have built confidence in using written calculation methods, they are able to solve more complex problems involving money.

Children benefit from regular exposure to word problems, alongside any fluency work they are doing. To help you with this, we have put together a collection of 25 money word problems, which can be used with pupils from Year 2 to Year 6.

Children are also exposed to money word problems in Third Space Learning’s online one-to-one tutoring programmes. Adapted to the needs of each individual students, our programmes help to build maths skills and grow confidence in our young mathematicians.

Money word problems in the national curriculum

Money word problems in Year 2

In Year 2, pupils are introduced to the different coins; learn the symbols for pounds and pence and combine amounts to make a particular value. They work on simple problems in a practical context involving addition word problems, and subtraction word problems of money of the same unit, including giving change.

Money word problems in Year 3

Pupils in Year 3 continue to build on their understanding of money and its use in a practical context. They progress from adding and subtracting money of the same unit, to working with both pounds and pence; adding and subtracting amounts and giving change. Pupils in Year 3 start to solve simple 2-step calculations, by finding totals and working out how much change would be given.

Money word problems in Year 4

In Year 4, the curriculum no longer mentions money under measures, but pupils continue to work with money through fractions and decimals. At this stage, pupils are expected to solve simple measures and money problems involving fractions and decimals to two decimal places.

Money word problems in Year 5

Pupils in Year 5 are becoming more confident with the formal written methods for the four operations and are exposed to money word problems involving all four. They also continue to build on the knowledge of fractions and decimals and are first introduced to percentages through a range of word problems.

Money word problems in Year 6

By Year 6, money is no longer explicitly mentioned in the curriculum, however pupils are exposed to word problems across a range of concepts, including: the four operations, fractions, decimals and percentage word problems, ratio word problems and algebra.

Why are word problems important for children’s understanding of money

Word problems are essential to children’s understanding of money, because they enable students to use money in a range of contexts they will be using in real-life. Confidence with money is a key life skill and it is important children have plenty of exposure to using it in a wide range of contexts. Money problems give children the opportunity to utilise the skills they have learnt in the maths lessons and put them into context, in a situation they understand and can relate to.

How to teach money word problem solving in primary school

Pupils need to be taught the skills needed to solve word problems. It is essential they understand the importance of reading questions carefully, making sure they fully understand what is being asked. They then need to identify which calculation is required and whether there are any concrete resources or pictorial representations they can use to help them, alongside the coins, such as place value counters and bar models.

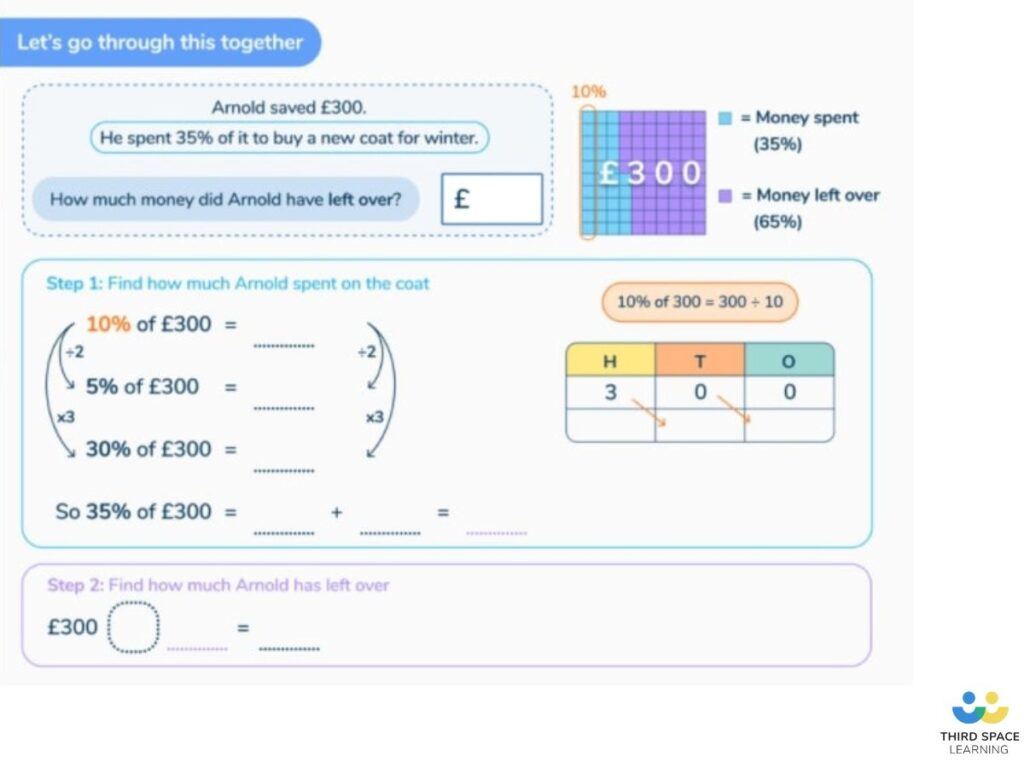
Here is an example:

An adult’s ticket to the water park costs £15.50, whilst a children’s ticket cost £9.50.

How much would it cost for 2 adults and 2 children to visit the water park and how much change would they get from £100?

How to solve:

What do you already know?

• We know that an adult ticket costs £15.50 and a child ticket costs £9.50.
• To calculate the cost of both adults, we are going to need to multiply the £15.50 by 2, or add £15.50 and £15.50.
• We will also need to do the same with the child’s ticket, costing £9.50.
• Once we have calculated the total cost of both adults and both children, we’ll need to add these answers together, to establish the total cost for the whole family.
• To calculate the amount of money from £100, we will need to subtract the total cost for the family from £100.

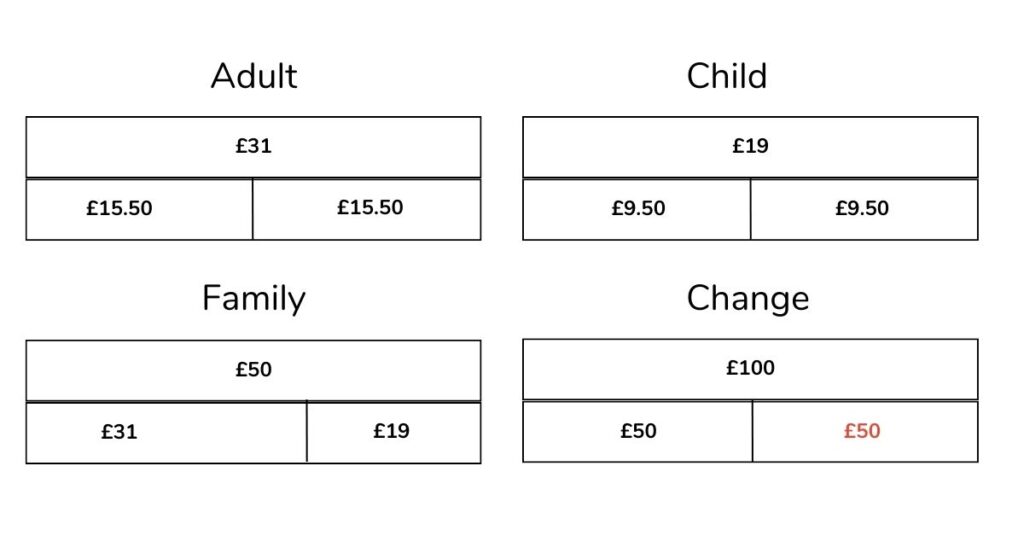
How can this be represented pictorially?

• We can draw bar models to represent the cost of the adult tickets, child tickets and the total for the family.
• We can then use the answer from the third bar model to represent finding how much change from £100.
• We can see from these bar models that there would be £50 left once the family had paid to enter the waterpark.

Money word problems for year 2

Money word problems in Year 2 require students to recognise coins and use the symbols for pounds and pence. Children solve real world problems –  finding totals and calculating change when working with the same unit (pounds or pence). 

Money word problems for year 3

Word problems for year 3 build upon the knowledge from year 2,  solving word problems involving both pounds and pence together and calculating change. At this stage, children should be using decimal notation for amounts of money and using both formal and informal methods to add and subtract money amounts in pounds and pence.

Money word problems for year 4

With word problems for year 4, pupils need to be able to order amounts of money, using rounding to estimate and calculate using the four operations. They also encounter money maths problems through other concepts, such as fractions.

Money word problems for year 5

Word problems for year 5 include the four operations, but with larger numbers than pupils were working with in Lower Key Stage 2. They are also presented to students through fraction word problems, decimal and percentages topics 

Money word problems for year 6

With word problems for year 6, pupils encounter multi-step word problems and those involving larger amounts of money and cover a range of concepts, including: the 4 operations, fractions, decimals, percentages, ratio and algebra. Money word problems are often included in the KS2 reasoning SATs papers.

More word problems resources

Looking for more word problems on a range of topics? Take a look at our collection of time word problems.

In this lesson, students will solve math word problems using money, decimals, and fractions. These problems will include all four operations (addition, subtraction, multiplication, and division). Students will solve problems involving multiple steps (for example, students may be asked to first add, then subtract). Lastly, students will solve money problems using simple fractions.

Learning Outcomes

On successful completion of this lesson your child will be able to:

• Solve money problems using all four operations (addition, subtraction, multiplication, and division)
• Solve multi-step problems (e.g. first multiply, then subtract)
• Solve money problems using simple fractions

Warm Up

Work through the warm up section below with your children and then try the worksheet before moving on to the main part of the lesson.

Operations and Key Words in Word Problems

The chart below shows common terms for the 4 operations found in many word problems.

Add	Subtract	Multiply	Divide
Total	Difference	Each	Each
In all	Less than	Row	Split
Together/ All together	How many more	Group	Row
And	Minus	Total	Half
Sum	Left over	Double	Fourth

Below are some examples of key words in word problems.

1. Jackson has 250 baseball cards and 175 football cards. How many baseball and football cards does he have in all? (Add 250 + 175 = 425 cards).
2. How many more baseball cards than football cards does Jackson have? (Subtract 250 – 175 = 75 cards).
3. Mrs. Silver has 5 rows of daisies in her garden. There are 6 daisies in each row. How many total daises are in Mrs. Silver’s garden? (Multiply 6 x 5 = 30 daisies).
4. Mrs. Silver also has lilies in her garden. She planted 18 daisies. She has 6 rows of daisies. How many daisies are in each row? (Divide 18 ÷ 6 = 3 daisies in each row)

Money, Decimals, Fraction Connections

The chart below shows you connections between money, decimals, and fractions

Money	Decimal	Fraction
Quarter	0.25	¼
Fifty cents/ half dollar	0.5 or 0.50	½
Seventy-five cents	0.75	¾
Dollar	1.0 or 1	1 whole

Pre-assessment worksheet

Have your children try the assessment worksheet below before starting the main lesson.

• Word Problems: Money – Pre-assessment

Main Lesson: Money Word Problems

Below are eight examples of money word problems. Work through these with your children and have them try the word problem worksheets as they go.

Example 1 of 8: Money Word Problem With Addition

Stephanie received {$15.25} for babysitting on Friday night and {$17.75} for babysitting on Saturday night. How much did she make in total?

Step 1:  Underline operation key terms and {bracket} important numbers.

Step 2:  Ask: What is this question asking me to do? (How much did she make in total).

Step 3: Write a number sentence (15.25 + 17.75)

Step 4:  Rewrite the problem vertically.  Line up decimal points. 15.25 +17.75 33.00

Step 5: Solve and write the answer in dollars.  Stephanie made $33 dollars in total.

Help your children add money using real dollars and coins. Encourage them to count dollars and coins left over from change, that is in your wallet, or spare change in the house. Remind them that when they count money, they are adding and that coins are decimals. Coins are parts of dollars just like decimals are parts of whole numbers.

Example 2 of 8: Money Word Problem With Subtraction

Jessica has {$25.00} to spend in the video game store. She buys a used game for {$15.83}. How much money does she have left over?

Step 1:  Underline operation key terms and {bracket} important numbers.

Step 2:  Ask: What is this question asking me to do? (How much did she have left over?).

Step 3: Write a number sentence (25.00 – 15.83)

Step 4:  Rewrite the problem vertically.  Line up decimal points.

25.00 – 15.83 9.17

Step 5: Solve and write the answer in dollars.  Jessica has $9.17 left over

Example 3 of 8: Money Word Problem With Multiplication

Sol wants to buy a candy bar for {$0.75}. If he buys {4} candy bars, how much total money will he spend?

• Step 1: Underline important information and {bracket} important numbers.
• Step 2: Ask: What is this question asking me to do? (Determine how much total money will Sol spend?).
• Step 3: Write a number sentence ($0.75 x 4)
• Step 4: Count the number of decimal places in 0.75. There are 2 decimal places. The 7 is in the tenths place and the 5 is in the hundredths place.
• Step 5: Multiply 75 x 4 = 300
• Step 6: Put the decimal point back into the product.  3.00
• Step 7: Write the answer.  Sol will have to spend $3.00

Encourage your children to use the partial product method to multiply 75 by 4. Partial product involves multiply the 75 in expanded form (70 x 4)+(5 x 4)=300

Example 4 of 8: Money Word Problem With Division

Rudy received {$24.75} for his birthday. He wants to split the money into groups to save for {three things}: movie tickets; art supplies; music downloads. If he wants the same amount for each activity, how much money will he put into each group?

• Step 1: Underline operation key terms and {bracket} important numbers.
• Step 2: Ask: What is this question asking me to do? (How much will Rudy put into each group?).
• Step 3: Write a number sentence ($24.75 ÷ 3)
• Step 4: Divide whole dollars first (24 ÷ 3 =
• Step 5: Divide cents next (0.75 ÷ 3 = 0.25)
• Step 6: Add dollars and cents. $8 + 0.25 = $8.25
• Step 7: Write the answer.  Rudy will put $8.25 in each group.

Try this Word Problems Worksheet to practice with money word problems that are similar to examples 1 to 4 above.

Remind your children that 0.75 is 3 quarters. Three quarters divided by 3 is one quarter or 0.25.

Example 5 of 8: Multi-step Money Word Problem

Talia is at the mall with her friends. She buys a DVD for {$10.99}. Then she buys a new pair of earrings for {$8.25}. Lastly, she gets her mother a bouquet of flowers for {$9.50}. If she starts with {$50}, how much does she have after she goes shopping?

• Step 1: Underline operation key terms and {bracket} important numbers.
• Step 2: Ask: What is this question asking me to do? (How much will Talia have after she goes shopping?).
• Step 3: First, add the total amount that she spent ($10.99 + $8.25 + $9.50 = $28.74)
• Step 4: Then, subtract the total amount Talia spent from the amount she started with ($50.00 – $28.74 = $21.26)
• Step 5: Write the answer. Talia spent $21.26

Remind your child that a multi-step problem means that there is more than one step in solving the problem. In this case, first you add, then you subtract.

Example 6 of 8: Multi-step Money Word Problem

Josiah is buying {5} packs of gum that cost {$1.50} each. He wants to share his gum with {two} friends. He asks his friends to pay him for their share. Including Josiah, how much does each person spend on gum?

Step 1:  Underline operation key terms and {bracket} important numbers.

Step 2:  Ask: What is this question asking me to do? (How much did each person spend on gum?).

Step 3: First, multiply the number of packs of gum (5) by the cost of each pack ($1.50)

5 x $1.50 = $7.50 (5 x $1) = $5.00 ($0.50 x 5) = $2.50 ($5.00 + $2.50) = $7.50

Step 4: Then, divide the total amount of the gum ($7.50) by the number of people (3). One way to do this is to convert $7.50 into cents. This gives 750 cents which we then divide by 3 750 cents ÷ 3 = 250 cents. We then convert the cents back into dollars: 250 cents = $2.50

Step 5: Write the answer.  Each friend spent $2.50.

Try this Multi-step word problems worksheet to practice with problems that are similar to examples 5 and 6 above.

Dividing decimals may present a challenge for your child. Also, in the above problem, encourage your child to make connections between the 7.50 and the 3 as “seventy-five cents” and “three.” If you divided 75 cents by 3, you would get 25 cents.
Note: Your children might not be shown how perform operations with decimals until 5th Grade.

Example 7 of 8: Money Word Problem With Fractions

Todd has {$100} saved from shoveling snow and raking leaves. If { ½ } his money came from shoveling snow, how much money did he make raking leaves?

• Step 1: Underline operation key terms and {bracket} important numbers.
• Step 2: Ask: What is this question asking me to do? (How much money did Todd make raking leaves?).
• Step 3: First find ½ of $100. $100 ÷ 2 = $50
• Step 4: Since half divides the $100 into two equal amounts, Todd made $50 from raking leaves and $50 from shoveling snow.
• Step 5: Write the answer. Todd made $50 shoveling snow.

Example 8 of 8: Money Word Problem With Fractions

Spencer received {$240} a month for tutoring 4th grade students. { ¼ } of his earnings came from tutoring students in math. How much money did he make tutoring students in math?

• Step 1: Underline operation key terms and {bracket} important numbers.
• Step 2: Ask: What is this question asking me to do? (How much money did Spencer make tutoring math?).
• Step 3: First find ¼ of $240. Since one-fourth (¼) means to divide by 4, you are now dividing by a whole number: $240 ÷ 4 = $60.
• Step 5: Write the answer. Spencer made $60 tutoring math.

Try this Money Word Problems Worksheet to practice with problems that are similar to examples 7 and 8 above.

Money Word Problems: Worksheets

Listed below are the 3 worksheets included in the above lesson

• Word Problems: Decimals Worksheet – with addition, subtraction, multiplication, & division
• Word Problems: Multi-step
• Word Problems: Money With Fractions

Test Questions

Have your children try the 8 questions in the Post-assessment worksheet below. Check their answers and review this lesson with them if necessary.

• Word Problems: Money – Post-assessment (8 questions)

Related Topics:
Compound Interest Word Problems
Other Algebra Word Problems

First, we will look at a money word problem involving calculating Simple Interest. Simple Interest word problems are based on the formula for Simple Interest and the formula for Amount. Then, we will look at a money word problem that involves coins and dollar bills.

The following diagram gives the Simple Interest Formula. Scroll down the page for more examples and solutions on how to use the Simple Interest Formula to solve simple interest word problems.

Simple Interest Word Problems

Formula for Simple Interest

i = prt

i represents the interest earned.
p represents the principal which is the number of dollars invested.
r represents the interest rate per year.
t represents the time the money is invested which is generally stated in years or fractions of a year.

Formula for Amount

A = p + i

A represents what your investment is worth if you consider the total amount of the original investment (p) and the interest earned (i)

Example:

James needs interest income of $5,000. How much money must he invest for one year at 7%? (Give your answer to the nearest dollar)

Solution:

5,000 = p(0.07)(1)

p = 71,428.57

Simple Interest Word Problems

Example:
Pam invested $5000. She earned 14% on part of her investment and 6% on the rest. If she earned a total of $396 in interest for the year, how much did she invest at each rate?
Note that this problem requires a chart to organize the information. The chart is based on the interest formula, which states that the amount invested times the rate of interest = interest earned. The chart is then used to set up the equation.

• Show Step-by-step Solutions

How to solve simple interest word problems?
Example:
Suppose $7,000 is divided into two bank accounts. One account pays 10% simple interest per year and the other pays 5%. After three years there is a total of $1451.25 in interest between the two accounts. How much was invested into each account (rounded to the nearest cent)?

• Show Step-by-step Solutions

Dollar and Coin Word Problems

Example:

Paul has $31.15 from paper route collections. He has 5 more nickels than quarters and 7 fewer dimes than quarters. How many of each coin does Paul have?

Solution:

Let x be the number of quarters
x + 5 be the number of nickels
x – 7 be the number of dimes

25x + 5(x + 5) + 10(x – 7) = 3,115
25x + 5x + 25 + 10x – 70 = 3,115
40x = 3,160
x = 79

Paul has 79 quarters, 84 nickels and 72 dimes.

Algebra Money Word Problems

Algebra Money Word Problems with two variables (x and y). How to solve equations with two variables?

Example:
David has only $5
bills and $10 bills in his wallet. If he has 5 bills totaling $35, how many of each does he have?

• Show Step-by-step Solutions

Coin Word Problem

Example:
Martin has a total of 19 nickels and dimes worth $1.65. How many of each type of coin does he have? Note that this problem requires a chart to organize the information. The chart is based on the total value formula, which states that the number of coins times the value of each coin = the total value. The chart is then used to set up the equation.

• Show Step-by-step Solutions

How to solve word problems involving coins and money?

Example:
You have three times as many quarters as dimes and the total amount of money is $6.80. How many quarters and dimes do you have?

• Show Step-by-step Solutions

How to solve algebra word problem involving money?
Example:
You have 6 times as many quarters as dimes and the total amount of money ia $8.00. How many quarters and dimes do you have?

• Show Step-by-step Solutions

How to solve a coin word problem involving pennies and nickels?
Example:
A pile of 16 coins consists of pennies and nickels. The total amount of money is 36 cents. How many nickels and pennies do you have?

• Show Step-by-step Solutions

How to solve a word problem involving stamps?
Example:
You bought 16 stamps consisting of 37-cent stamps and 23-cent stamps. If the total cost of the stamps is $4.10, find the number and types of stamps purchased.

• Show Step-by-step Solutions

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.