Related Pages
Rate Distance Time Word Problems
Distance Word Problems
Average Speed Problems
What Are Distance Word Problems Or Distance Rate Time Problems?
Distance problems are word problems that involve the distance
an object will travel at a certain average rate for a given
period of time.
The formula for distance problems is:
distance = rate × time or
d = r × t
Things to watch out for:
Make sure that you change the units when necessary. For example, if the rate is given in miles
per hour and the time is given in minutes then change the units appropriately.
It would be helpful to use a table to organize the information for distance problems. A table
helps you to think about one number at a time instead being confused by the question.
The following diagrams give the steps to solve Distance-Rate-Time Problems. Scroll down the page
for examples and solutions.
We will show you how to solve distance problems by the following examples:
- Traveling At Different Rates
- Traveling In Different Directions
- Given Total Time
- Wind and Current Problems
How To Solve Distance Problems: Traveling At Different Rates
Example:
A bus traveling at an average rate of 50 kilometers per hour made the trip to town in 6 hours.
If it had traveled at 45 kilometers per hour, how many more minutes would it have taken to make
the trip?
Solution:
Step 1: Set up a rtd table.
| r | t | d | |
| Case 1 | |||
| Case 2 |
Step 2: Fill in the table with information given in the question.
A bus traveling at an average rate of 50 kilometers per hour
made the trip to town in 6 hours. If it had traveled at
45 kilometers per hour, how many more minutes would it
have taken to make the trip?
Let t = time to make the trip in Case 2.
| r | t | d | |
| Case 1 | 50 | 6 | |
| Case 2 | 45 | t |
Step 3: Fill in the values for d using the formula d = rt
| r | t | d | |
| Case 1 | 50 | 6 | 50 × 6 = 300 |
| Case 2 | 45 | t | 45t |
Step 4: Since the distances traveled in both cases are the same,
we get the equation:
45t = 300
Isolate variable t
Step 5: Beware — the
question asked for “how many more minutes would it
have taken to make the trip”, so we need to deduct the original 6 hours taken.
Answer: The time taken would have been 40 minutes longer.
How To Solve Distance Problems: Two Objects Traveling In The Same Direction
Example:
This motion problem (or distance rate time problem or uniform rate problem) involves traveling
in the same direction, solving for “how long” one moving object traveling until it meets up with
the second moving object.
It uses d = rt (distance equals rate times time).
Car 1 starts from point A and heads for point B at 60 mph. Fifteen minutes later, car 2 leaves the
same point A and heads for point B at 75 mph. How long before car 2 overtakes car 1?
-
Show Video Lesson
How To Solve Distance Problems: Two Objects Traveling In The Opposite Directions
Example:
A bus and a car leave the same place and traveled in opposite directions. If the bus is traveling
at 50 mph and the car is traveling at 55 mph, in how many hours will they be 210 miles apart?
Solution:
Step 1: Set up a rtd table.
| r | t | d | |
| bus | |||
| car |
Step 2: Fill in the table with information given in the question.
If the bus is traveling at 50 mph and the car is traveling
at 55 mph, in how many hours will they be 210 miles apart?
Let t = time when they are 210 miles apart.
| r | t | d | |
| bus | 50 | t | |
| car | 55 | t |
Step 3: Fill in the values for d using the formula d = rt
| r | t | d | |
| bus | 50 | t | 50t |
| car | 55 | t | 55t |
Step 4: Since the total distance is 210, we get the equation:
50t + 55t = 210
105t = 210
Isolate variable t
Answer: They will be 210 miles apart in 2 hours.
Objects Traveling At Opposite Directions, Calculate How Long It Takes For Them To Be A Given Distance Apart
This motion problem (or distance rate time problem or uniform rate problem) involves one object
traveling in one direction and the other in the opposite direction, solving for “how long”
(or the amount of time) two moving objects traveling until they are certain distance apart.
Example:
Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at
450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart?
How far has each plane traveled?
- Show Video Lesson
How To Solve Distance Problems: Given The Total Time
Example:
John took a drive to town at an average rate of 40 mph. In the evening, he drove back at 30 mph.
If he spent a total of 7 hours traveling, what is the distance traveled by John?
Solution:
Step 1: Set up a rtd table.
| r | t | d | |
| Case 1 | |||
| Case 2 |
Step 2: Fill in the table with information given in the question.
John took a drive to town at an average rate of 40 mph. In the
evening, he drove back at 30 mph. If he spent a total of
7 hours traveling, what is the distance traveled by John?
Let t = time to travel to town.
7 – t = time to return from town.
| r | t | d | |
| Case 1 | 40 | t | |
| Case 2 | 30 | 7 – t |
Step 3: Fill in the values for d using the formula d = rt
| r | t | d | |
| Case 1 | 40 | t | 40t |
| Case 2 | 30 | 7 – t | 30(7 – t) |
Step 4: Since the distances traveled in both cases are the same,
we get the equation:
40t = 30(7 – t)
Use distributive property
40t = 210 – 30t
Isolate variable t
40t + 30t = 210
70t = 210
Step 5: The distance traveled by John to town is
40t = 120
The distance traveled by John to go back is also 120
So, the total distance traveled by John is 240
Answer: The distance traveled by John is 240 miles.
How To Find The Total Distance Given Total Time And Two Rates?
Example:
Roy took 5 hours to complete a journey. For the first 2 hours, he traveled at an average speed
of 65 km/h. For the rest of the journey, he traveled at an average speed of 78 km/h. What was
the total distance of the journey?
- Show Video Lesson
How To Solve Wind And Current Word Problems?
There is another group of distance-time problems that involves the speed of the water current or
the speed of wind affecting the speed of the vehicle. The following video shows an example of
such a problem.
How to solve Wind Word Problems?
Example:
Into the headwind, the plane flew 2000 miles in 5 hours. With a tailwind, the return trip took 4
hours. Find the speed of the plane in still air and the speed of the wind.
- Show Video Lesson
How to find the speed of the current of a stream?
Example:
The speed of a boat in still water is 10 mph. It travels 24 miles upstream and 24 miles downstream
in 5 hours. What is the speed of the current?
- Show Video Lesson
How to solve Current Word Problems?
Example:
Traveling downstream, Elmo can go 6 km in 45 minutes. On the return trip, it takes him 1.5 hours.
What is the boat’s speed in still water and what is the rate of the current?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Lesson 10: Distance Word Problems
/en/algebra-topics/introduction-to-word-problems/content/
What are distance word problems?
Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast, how far, or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.
In this lesson, you’ll learn how to solve train problems and a few other common types of distance problems. But first, let’s look at some basic principles that apply to any distance problem.
The basics of distance problems
There are three basic aspects to movement and travel: distance, rate, and time. To understand the difference among these, think about the last time you drove somewhere.
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.
The relationship among these things can be described by this formula:
distance = rate x time
d = rt
In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:
- You drove 25 miles—that’s the distance.
- You drove an average of 50 mph—that’s the rate.
- The drive took you 30 minutes, or 0.5 hours—that’s the time.
According to the formula, if we multiply the rate and time, the product should be our distance.
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25, which is our distance.
What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.
60 ⋅ 0.5 is 30, so our distance would be 30 miles.
Solving distance problems
When you solve any distance problem, you’ll have to do what we just did—use the formula to find distance, rate, or time. Let’s try another simple problem.
On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?
First, we should identify the information we know. Remember, we’re looking for any information about distance, rate, or time. According to the problem:
- The rate is 65 mph.
- The time is two-and-a-half hours, or 2.5 hours.
- The distance is unknown—it’s what we’re trying to find.
You could picture Lee’s trip with a diagram like this:
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance, rate, and time. To keep track of the information in the problem, we’ll set up a table. (This might seem excessive now, but it’s a good habit for even simple problems and can make solving complicated problems much easier.) Here’s what our table looks like:
| distance | rate | time |
|---|---|---|
| d | 65 | 2.5 |
We can put this information into our formula: distance = rate ⋅ time.
We can use the distance = rate ⋅ time formula to find the distance Lee traveled.
d = rt
The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d.
d = 65 ⋅ 2.5
To find d, all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5.
d = 162.5
We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.
Be careful to use the same units of measurement for rate and time. It’s possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour. However, what if the time had been written in a different unit, like in minutes? In that case, you’d have to convert the time into hours so it would use the same unit as the rate.
Solving for rate and time
In the problem we just solved we calculated for distance, but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:
After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?
We can picture Janae’s walk as something like this:
And we can set up the information from the problem we know like this:
| distance | rate | time |
|---|---|---|
| 1.5 | r | 0.5 |
The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.
As always, we start with our formula. Next, we’ll fill in the formula with the information from our table.
d = rt
The rate is represented by r because we don’t yet know how fast Janae was walking. Since we’re solving for r, we’ll have to get it alone on one side of the equation.
1.5 = r ⋅ 0.5
Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5:
1.5 / 0.5 = 3.
3 = r
r = 3, so 3 is the answer to our problem. Janae walked 3 miles per hour.
In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time. You can even use it to solve certain problems where you’re trying to figure out the distance, rate, or time of two or more moving objects. We’ll look at problems like this on the next few pages.
Two-part and round-trip problems
Do you know how to solve this problem?
Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?
This problem is a classic two-part trip problem because it’s asking you to find information about one part of a two-part trip. This problem might seem complicated, but don’t be intimidated!
You can solve it using the same tools we used to solve the simpler problems on the first page:
- The travel equation d = rt
- A table to keep track of important information
Let’s start with the table. Take another look at the problem. This time, the information relating to distance, rate, and time has been underlined.
Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?
If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There’s too much information. For instance, the problem contains two rates—30 mph and 70 mph. To include all of this information, let’s create a table with an extra row. The top row of numbers and variables will be labeled in town, and the bottom row will be labeled interstate.
| distance | rate | time | |
|---|---|---|---|
| in town | 30 | ||
| interstate | 70 |
We filled in the rates, but what about the distance and time? If you look back at the problem, you’ll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225. This means this is true:
Interstate distance + in-town distance = Total distance
Together, the interstate distance and in-town distance are equal to the total distance. See?
In any case, we’re trying to find out how far Bill drove on the interstate, so let’s represent this number with d. If the interstate distance is d, it means the in-town distance is a number that equals the total, 225, when added to d. In other words, it’s equal to 225 — d.
We can fill in our chart like this:
| distance | rate | time | |
|---|---|---|---|
| in town | 225 — d | 30 | |
| interstate | d | 70 |
We can use the same technique to fill in the time column. The total time is 3.5 hours. If we say the time on the interstate is t, then the remaining time in town is equal to 3.5 — t. We can fill in the rest of our chart.
| distance | rate | time | |
|---|---|---|---|
| in town | 225 — d | 30 | 3.5 — t |
| interstate | d | 70 | t |
Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here’s the one for in-town travel:
225 — d = 30 ⋅ (3.5 — t)
And here’s the one for interstate travel:
d = 70t
If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can’t be solved on their own. Try for yourself. If you work either equation on its own, you won’t be able to find a numerical value for d. In order to find the value of d, we’ll also have to know the value of t.
We can find the value of t in both problems by combining them. Let’s take another look at our travel equation for interstate travel.
While we don’t know the numerical value of d, this equation does tell us that d is equal to 70t.
d = 70t
Since 70t and d are equal, we can replace d with 70t. Substituting 70t for d in our equation for interstate travel won’t help us find the value of t—all it tells us is that 70t is equal to itself, which we already knew.
70t = 70t
But what about our other equation, the one for in-town travel?
225 — d = 30 ⋅ (3.5 — t)
When we replace the d in that equation with 70t, the equation suddenly gets much easier to solve.
225 — 70t = 30 ⋅ (3.5 — t)
Our new equation might look more complicated, but it’s actually something we can solve. This is because it only has one variable: t. Once we find t, we can use it to calculate the value of d—and find the answer to our problem.
To simplify this equation and find the value of t, we’ll have to get the t alone on one side of the equals sign. We’ll also have to simplify the right side as much as possible.
225 — 70t = 30 ⋅ (3.5 — t)
Let’s start with the right side: 30 times (3.5 — t) is 105 — 30t.
225 — 70t = 105 — 30t
Next, let’s cancel out the 225 next to 70t. To do this, we’ll subtract 225 from both sides. On the right side, it means subtracting 225 from 105. 105 — 225 is -120.
— 70t = -120 — 30t
Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right. We’ll cancel out the -30t on the right side by adding 30t to both sides. On the right side, we’ll add it to -70t. -70t + 30t is -40t.
— 40t = -120
Finally, to get t on its own, we’ll divide each side by its coefficient: -40. -120 / — 40 is 3.
t = 3
So t is equal to 3. In other words, the time Bill traveled on the interstate is equal to 3 hours. Remember, we’re ultimately trying to find the distance Bill traveled on the interstate. Let’s look at the interstate row of our chart again and see if we have enough information to find out.
| distance | rate | time | |
|---|---|---|---|
| interstate | d | 70 | 3 |
It looks like we do. Now that we’re only missing one variable, we should be able to find its value pretty quickly.
To find the distance, we’ll use the travel formula distance = rate ⋅ time.
d = rt
We now know that Bill traveled on the interstate for 3 hours at 70 mph, so we can fill in this information.
d = 3 ⋅ 70
Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210.
d = 210
So d = 210. We have the answer to our problem! The distance is 210. In other words, Bill drove 210 miles on the interstate.
Solving a round-trip problem
It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they’ll go. Let’s try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let’s take a look:
Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?
If you’re having trouble understanding this problem, you might want to visualize Eva’s commute like this:
As always, let’s start by filling in a table with the important information. We’ll make a row with information about her trip to work and from work.
1.75 — t to describe the trip from work. (Remember, the total travel time is 1.75 hours, so the time to work and from work should equal 1.75.)
From our table, we can write two equations:
- The trip to work can be represented as d = 36t.
- The trip from work can be represented as d = 27 (1.75 — t).
In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work.
Just like with the last problem we solved, we can solve this one by combining the two equations.
We’ll start with our equation for the trip from work.
d = 27 (1.75 — t)
Next, we’ll substitute in the value of d from our to work equation, d = 36t. Since the value of d is 36t, we can replace any occurrence of d with 36t.
36t = 27 (1.75 — t)
Now, let’s simplify the right side. 27 ⋅(1.75 — t) is 47.25.
36t = 47.25 — 27t
Next, we’ll cancel out -27t by adding 27t to both sides of the equation. 36t + 27t is 63t.
63t = 47.25
Finally, we can get t on its own by dividing both sides by its coefficient: 63. 47.25 / 63 is .75.
t = .75
t is equal to .75. In other words, the time it took Eva to drive to work is .75 hours. Now that we know the value of t, we’ll be able to can find the distance to Eva’s work.
If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.
d = rt
First, let’s fill in the values we know. We’ll work with the numbers for the trip to work. We already knew the rate: 36. And we just learned the time: .75.
d = 36 ⋅ .75
Now all we have to do is simplify the equation: 36 ⋅ .75 = 27.
d = 27
d is equal to 27. In other words, the distance to Eva’s work is 27 miles. Our problem is solved.
Intersecting distance problems
An intersecting distance problem is one where two things are moving toward each other. Here’s a typical problem:
Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?
This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it’s a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:
If you’re still confused, don’t worry! You can solve this problem the same way you solved the two-part problems on the last page. You’ll just need a chart and the travel formula.
Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?
Let’s start by filling in our chart. Here’s the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate. The problem gives us the speed of each train. We’ll label them fast train and slow train. The fast train goes 60 mph. The slow train goes only 45 mph.
We can also put this information into a table:
| distance | rate | time | |
|---|---|---|---|
| fast train | 60 | ||
| slow train | 45 |
We don’t know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.
This means that—just like last time—we’ll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d, and the distance for the slow train will be 420 — d.
| distance | rate | time | |
|---|---|---|---|
| fast train | d | 60 | |
| slow train | 420 — d | 45 |
Because we’re looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t.
| distance | rate | time | |
|---|---|---|---|
| fast train | d | 60 | t |
| slow train | 420 — d | 45 | t |
The table gives us two equations: d = 60t and 420 — d = 45t. Just like we did with the two-part problems, we can combine these two equations.
The equation for the fast train isn’t solvable on its own, but it does tell us that d is equal to 60t.
d = 60t
The other equation, which describes the slow train, can’t be solved alone either. However, we can replace the d with its value from the first equation.
420 — d = 45t
Because we know that d is equal to 60t, we can replace the d in this equation with 60t. Now we have an equation we can solve.
420 — 60t = 45t
To solve this equation, we’ll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60t on the left by adding 60t to both sides. 45t + 60t is 105t.
420 = 105t
Now we just need to get rid of the coefficient next to t. We can do this by dividing both sides by 105. 420 / 105 is 4.
4 = t
t = 4. In other words, the time it takes the trains to meet is 4 hours. Our problem is solved!
If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4. For our fast train, the equation would be d = 60 ⋅ 4. 60 ⋅ 4 is 240, so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4. 45 ⋅ 4 is 180, so the distance traveled by the slow train is 180 miles.
Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles, which is the total distance from our problem. Our answer is correct.
Practice problem 1
Here’s another intersecting distance problem. It’s similar to the one we just solved. See if you can solve it on your own. When you’re finished, scroll down to see the answer and an explanation.
Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?
Problem 1 answer
Here’s practice problem 1:
Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?
Answer: 2 hours.
Let’s solve this problem like we solved the others. First, try making the chart. It should look like this:
| distance | rate | time | |
|---|---|---|---|
| Jon | d | 65 | t |
| Dani | 270 — d | 70 | t |
Here’s how we filled in the chart:
- Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That’s 270. Jon’s distance is represented by d, so Dani’s distance is 270 — d.
- Rate: The problem tells us Dani and Jon’s speeds. Dani drives 65 mph, and Jon drives 70 mph.
- Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t.
Now we have two equations. The equation for Jon’s travel is d = 65t. The equation for Dani’s travel is 270 — d = 70t. To solve this problem, we’ll need to combine them.
The equation for Jon tells us that d is equal to 65t. This means we can combine the two equations by replacing the d in Dani’s equation with 65t.
270 — 65t = 70t
Let’s get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65t on the left side. We’ll cancel it out by adding 65t to both sides: 70t + 65t is 135t.
270 = 135t
All that’s left to do is to get rid of the 135 next to the t. We can do this by dividing both sides by 135: 270 / 135 is 2.
2 = t
That’s it. t is equal to 2. We have the answer to our problem: Dani and Jon drove 2 hours before they met up.
Overtaking distance problems
The final type of distance problem we’ll discuss in this lesson is a problem in which one moving object overtakes—or passes—another. Here’s a typical overtaking problem:
The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?
You can picture the moment the Platter family left for the road trip a little like this:
The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family’s rate. Like some of the other problems we’ve solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let’s start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.
| distance | rate | time | |
|---|---|---|---|
| the Hills | d | ||
| the Platters | d |
Filling in the rate and time will require a little more thought. We don’t know the rate for either family—remember, that’s what we’re trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family’s rate is r, the Platter family’s rate would be r + 15.
| distance | rate | time | |
|---|---|---|---|
| the Hills | d | r | |
| the Platters | d | r + 15 |
Now all that’s left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they’d been driving 3 hours more than the Platters. 13 + 3 is 16, so we know the Hills had been driving 16 hours by the time the Platters caught up with them.
| distance | rate | time | |
|---|---|---|---|
| the Hills | d | r | 16 |
| the Platters | d | r + 15 | 13 |
Our chart gives us two equations. The Hill family’s trip can be described by d = r ⋅ 16. The equation for the Platter family’s trip is d = (r + 15) ⋅ 13. Just like with our other problems, we can combine these equations by replacing a variable in one of them.
The Hill family equation already has the value of d equal to r ⋅ 16. So we’ll replace the d in the Platter equation with r ⋅ 16. This way, it will be an equation we can solve.
r ⋅ 16 = (r + 15) ⋅ 13
First, let’s simplify the right side: r ⋅ 16 is 16r.
16r = (r + 15) ⋅ 13
Next, we’ll simplify the right side and multiply (r + 15) by 13.
16r = 13r + 195
We can get both r and their coefficients on the left side by subtracting 13r from 16r : 16r — 13r is 3r.
3r = 195
Now all that’s left to do is get rid of the 3 next to the r. To do this, we’ll divide both sides by 3: 195 / 3 is 65.
r = 65
So there’s our answer: r = 65. The Hill family drove an average of 65 mph.
You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you’re setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.
Practice problem 2
Try solving this problem. It’s similar to the problem we just solved. When you’re finished, scroll down to see the answer and an explanation.
A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?
Problem 2 answer
Here’s practice problem 2:
A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?
Answer: 4 p.m.
To solve this problem, start by making a chart. Here’s how it should look:
| distance | rate | time | |
|---|---|---|---|
| fast train | d | 80 | t |
| slow train | d | 60 | t + 1 |
Here’s an explanation of the chart:
- Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d.
- Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph, and the slow train has a rate of 60 mph.
- Time: We’ll use t to represent the fast train’s travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It’s t + 1.
Now we have two equations. The equation for the fast train is d = 80t. The equation for the slow train is d = 60 (t + 1). To solve this problem, we’ll need to combine the equations.
The equation for the fast train says d is equal to 80t. This means we can combine the two equations by replacing the d in the slow train’s equation with 80t.
80t = 60 (t + 1)
First, let’s simplify the right side of the equation: 60 ⋅ (t + 1) is 60t + 60.
80t = 60t + 60
To solve the equation, we’ll have to get t on one side of the equals sign and a number on the other. We can get rid of 60t on the right side by subtracting 60t from both sides: 80t — 60t is 20t.
20t = 60
Finally, we can get rid of the 20 next to t by dividing both sides by 20. 60 divided by 20 is 3.
t = 3
So t is equal to 3. The fast train traveled for 3 hours. However, it’s not the answer to our problem. Let’s look at the original problem again. Pay attention to the last sentence, which is the question we’re trying to answer.
A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?
Our problem doesn’t ask how long either of the trains traveled. It asks what time the second train catches up with the first.
The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m. From our equations, we know the fast train traveled 3 hours. 1 + 3 is 4, so the fast train caught up with the slow one at 4 p.m. The answer to the problem is 4 p.m.
Solving geometry word problems is often a challenge. The biggest one is how to translate the description of the problem from words into a graphical representation. In other words, how to visualize the problem. Here is an example, sent to me by a reader who was having difficulty with this very issue of visualization.
Problem
A malfunction occurred in a nuclear power-plant. Following the malfunction, the area of the plant, measuring a square kilometer, was contaminated with radioactive waste. Because of the radiation, no one can live within one kilometer of any point within the contaminated area. Find the total area that has become uninhabitable, including the interior of the square.
Strategy
The first step in solving geometry word problems is to translate the description into a graphical representation of the problem. Sometime, we face a challenge in that the description itself is a bit ambiguous. In those cases, we need to make assumptions. Whenever we do so, we should note what assumptions we are making.
So for example, in the above problem, we are told that that the area of the plant measures a square kilometer — but we are not explicitly told its shape, until the last sentence that says «including the interior of the square». If we did not have that last sentence, we would not know the shape of the plant area- it could be a circle with an area of 1 square kilometer, or a square with a side measuring 1 km, or it could be just a random shape. So we would make an assumption » I assume the plant area was a square» or » assume the plant was a circle», and solve based on the assumption.
So here, we have a square shaped plant, with an area of 1 square kilometer. From the formula for an area of a square , Asquare=side2, we get 1=side2, so each side measures 1 Km:
Step 1
Now, let’s figure out what other areas are within one kilometer of any point within the this area.
The strategy here is to look at the square’s edges — because every point inside the square is going to be farther away from a point outside the square then the edge:
So the farthest point from each side of the square that is still within 1 km of it, is a point that is 1 km from the edge. Now, if we recall that Parallel lines are equidistant from each other, we can draw a parallel line measuring one kilometer in length, 1 Km away from the edge of the square, and all points between that parallel line and the edge of the square will be within 1 Km of the square, and thus also part of the uninhabitable area. It is easy to see that this forms another square, also measuring 1 square kilometer, constructed on the edge of the original square:
Step 2
But we have 4 such squares, one on each edge of the original plant site:
So , a total of 5 squares, each measuring 1 square kilometer.
Step 3
So we’ve made some progress solving this geometry word problem. But that’s not all. What about the space between the squares? There are points in that space that are also within 1 kilometer of the original square — any point that is less than 1 kilometer from the corner. We know that a circle is defined as the collection of all points that are the same distance from one point, which is the center of the circle. We can think of that corner of the square as the center of a circle with radius 1 Km.
Then, we have between each of the squares we constructed on the side of the original plant, a quarter of a circle. Within that quarter-circle, all the points are within 1 Km of the corner. They, too, are part of the uninhabitable area:
So now we have translated this geometry word problem into a simple graphical representation. All that remains are a few simple calculations.
There are four such quarter-circles, and they are identical. The total area of them is the area of one full circle with radius 1: Acircle=π*r2 , with r=1, so the area is just π.
So, the solution to this problem is now to sum it all up. The total uninhabitable area is: 1(original square)+ 4×1(squares on each edge) + π = 5+π square kilometers have become uninhabited.
Before you get into distance, time and speed word problems, take a few minutes to read this first and understand: How to build your credit score in USA as an international student.
Problems involving Time, Distance and Speed are solved based on one simple formula.
Distance = Speed * Time
Which implies →
Speed = Distance / Time and
Time = Distance / Speed
Let us take a look at some simple examples of distance, time and speed problems.
Example 1. A boy walks at a speed of 4 kmph. How much time does he take to walk a distance of 20 km?
Solution
Time = Distance / speed = 20/4 = 5 hours.
Example 2. A cyclist covers a distance of 15 miles in 2 hours. Calculate his speed.
Solution
Speed = Distance/time = 15/2 = 7.5 miles per hour.
Example 3. A car takes 4 hours to cover a distance, if it travels at a speed of 40 mph. What should be its speed to cover the same distance in 1.5 hours?
Solution
Distance covered = 4*40 = 160 miles
Speed required to cover the same distance in 1.5 hours = 160/1.5 = 106.66 mph
Now, take a look at the following example:
Example 4. If a person walks at 4 mph, he covers a certain distance. If he walks at 9 mph, he covers 7.5 miles more. How much distance did he actually cover?
Now we can see that the direct application of our usual formula Distance = Speed * Time or its variations cannot be done in this case and we need to put in extra effort to calculate the given parameters.
Let us see how this question can be solved.
Solution
For these kinds of questions, a table like this might make it easier to solve.
| Distance | Speed | Time |
| d | 4 | t |
| d+7.5 | 9 | t |
Let the distance covered by that person be ‘d’.
Walking at 4 mph and covering a distance ‘d’ is done in a time of ‘d/4’
IF he walks at 9 mph, he covers 7.5 miles more than the actual distance d, which is ‘d+7.5’.
He does this in a time of (d+7.5)/9.
Since the time is same in both the cases →
d/4 = (d+7.5)/9 → 9d = 4(d+7.5) → 9d=4d+30 → d = 6.
So, he covered a distance of 6 miles in 1.5 hours.
Example 5. A train is going at 1/3 of its usual speed and it takes an extra 30 minutes to reach its destination. Find its usual time to cover the same distance.
Solution
Here, we see that the distance is same.
Let us assume that its usual speed is ‘s’ and time is ‘t’, then
| Distance | Speed | Time |
| d | s | t min |
| d | S+1/3 | t+30 min |
s*t = (1/3)s*(t+30) → t = t/3 + 10 → t = 15.
So the actual time taken to cover the distance is 15 minutes.
Note: Note the time is expressed in terms of ‘minutes’. When we express distance in terms of miles or kilometers, time is expressed in terms of hours and has to be converted into appropriate units of measurement.
Solved Questions on Trains
Example 1. X and Y are two stations which are 320 miles apart. A train starts at a certain time from X and travels towards Y at 70 mph. After 2 hours, another train starts from Y and travels towards X at 20 mph. At what time do they meet?
Solution
Let the time after which they meet be ‘t’ hours.
Then the time travelled by second train becomes ‘t-2’.
Now,
Distance covered by first train+Distance covered by second train = 320 miles
70t+20(t-2) = 320
Solving this gives t = 4.
So the two trains meet after 4 hours.
Example 2. A train leaves from a station and moves at a certain speed. After 2 hours, another train leaves from the same station and moves in the same direction at a speed of 60 mph. If it catches up with the first train in 4 hours, what is the speed of the first train?
Solution
Let the speed of the first train be ‘s’.
Distance covered by the first train in (2+4) hours = Distance covered by second train in 4 hours
Therefore, 6s = 60*4
Solving which gives s=40.
So the slower train is moving at the rate of 40 mph.
Questions on Boats/Airplanes
For problems with boats and streams,
Speed of the boat upstream (against the current) = Speed of the boat in still water – speed of the stream
[As the stream obstructs the speed of the boat in still water, its speed has to be subtracted from the usual speed of the boat]
Speed of the boat downstream (along with the current) = Speed of the boat in still water + speed of the stream
[As the stream pushes the boat and makes it easier for the boat to reach the destination faster, speed of the stream has to be added]
Similarly, for airplanes travelling with/against the wind,
Speed of the plane with the wind = speed of the plane + speed of the wind
Speed of the plane against the wind = speed of the plane – speed of the wind
Let us look at some examples.
Example 1. A man travels at 3 mph in still water. If the current’s velocity is 1 mph, it takes 3 hours to row to a place and come back. How far is the place?
Solution
Let the distance be ‘d’ miles.
Time taken to cover the distance upstream + Time taken to cover the distance downstream = 3
Speed upstream = 3-1 = 2 mph
Speed downstream = 3+1 = 4 mph
So, our equation would be d/2 + d/4 = 3 → solving which, we get d = 4 miles.
Example 2. With the wind, an airplane covers a distance of 2400 kms in 4 hours and against the wind in 6 hours. What is the speed of the plane and that of the wind?
Solution
Let the speed of the plane be ‘a’ and that of the wind be ‘w’.
Our table looks like this:
| Distance | Speed | Time | |
| With the wind | 2400 | a+w | 4 |
| Against the wind | 2400 | a-w | 6 |
4(a+w) = 2400 and 6(a-w) = 2400
Expressing one unknown variable in terms of the other makes it easier to solve, which means
a+w = 600 → w=600-a
Substituting the value of w in the second equation,
a-w = 400
a-(600-a) = 400 → a = 500
The speed of the plane is 500 kmph and that of the wind is 100 kmph.
More solved examples on Speed, Distance and Time
Example 1. A boy travelled by train which moved at the speed of 30 mph. He then boarded a bus which moved at the speed of 40 mph and reached his destination. The entire distance covered was 100 miles and the entire duration of the journey was 3 hours. Find the distance he travelled by bus.
Solution
| Distance | Speed | Time | |
| Train | d | 30 | t |
| Bus | 100-d | 40 | 3-t |
Let the time taken by the train be ‘t’. Then that of bus is ‘3-t’.
The entire distance covered was 100 miles
So, 30t + 40(3-t) = 100
Solving which gives t=2.
Substituting the value of t in 40(3-t), we get the distance travelled by bus is 40 miles.
Alternatively, we can add the time and equate it to 3 hours, which directly gives the distance.
d/30 + (100-d)/40 = 3
Solving which gives d = 60, which is the distance travelled by train. 100-60 = 40 miles is the distance travelled by bus.
Example 2. A plane covered a distance of 630 miles in 6 hours. For the first part of the trip, the average speed was 100 mph and for the second part of the trip, the average speed was 110 mph. what is the time it flew at each speed?
Solution
Our table looks like this.
| Distance | Speed | Time | |
| 1st part of journey | d | 100 | t |
| 2nd part of journey | 630-d | 110 | 6-t |
Assuming the distance covered in the 1st part of journey to be ‘d’, the distance covered in the second half becomes ‘630-d’.
Assuming the time taken for the first part of the journey to be ‘t’, the time taken for the second half becomes ‘6-t’.
From the first equation, d=100t
The second equation is 630-d = 110(6-t).
Substituting the value of d from the first equation, we get
630-100t = 110(6-t)
Solving this gives t=3.
So the plane flew the first part of the journey in 3 hours and the second part in 3 hours.
Example 2. Two persons are walking towards each other on a walking path that is 20 miles long. One is walking at the rate of 3 mph and the other at 4 mph. After how much time will they meet each other?
Solution
| Distance | Speed | Time | |
| First person | d | 3 | t |
| Second person | 20-d | 4 | t |
Assuming the distance travelled by the first person to be ‘d’, the distance travelled by the second person is ’20-d’.
The time is ‘t’ for both of them because when they meet, they would have walked for the same time.
Since time is same, we can equate as
d/3 = (20-d)/4
Solving this gives d=60/7 miles (8.5 miles approximately)
Then t = 20/7 hours
So the two persons meet after 2 6/7 hours.
Practice Questions for you to solve
Problem 1: Click here
Answer 1: Click here
Problem 2: Click here
Answer 2: Click here
A 12 min read
GMAT Word problems on Time, and Speed, and Distance are based on the simple formula of D = S x T, where D is the distance, S is speed and T is time. These GMAT word problems might look easy at first but if your concepts are not clear you will end up cringing in front of the computer screen. You’ll end up wasting valuable time as well as your morale. Therefore, it’s essential you understand how to easily solve Distance Speed Time Problems. This article cites the importance of average speed and its different applications in solving questions on time, speed, and distance. We will learn these concepts through Illustrative Examples.
To get the best learning out of it, you should know some basics such as:
- You are expected to possess a conceptual understanding of the basics of Distance topic
- And the relationship between the three variables; time, speed, and distance – in the form of D = S x T formula
The highlights of this article on GMAT Word Problems on Time, Speed and Distance are as follows
- What will you learn from this article
- The concept of average speed explained with illustrative GMAT word problems
- Calculation of Average Speed when the journey is divided into more than two parts
- Takeaways
What will you learn from this article?
The concept of Average Speed is an important one in the context of GMAT. Hence, the basic objective of this article is to:
- Provide conceptual clarity of the topic, Average Speed
- Solving relevant examples explaining the concepts
- Looking into different learnings and important takeaways
Guillermo scored a Q50 on the GMAT and received an admit for The Wharton School. Take a look at his success story.
For any strategic advice about the GMAT or MBA Admissions, write to us at acethegmat@e-gmat.com. Sign up for a free trial and get unlimited access to concept files, live sessions, and practice questions.
The concept of Average Speed
In theoretical terms, average speed = (Total distance traveled/ Total time taken to travel that distance)
Let’s take an example to have a more detailed explanation of the definition.
Example 1
A bus covers a certain distance at an average speed of 40 mph, while returning the same distance it runs at an average speed of 60 mph. What is the average speed of the bus throughout the journey?
- 20 mph
- 36 mph
- 48 mph
- 50 mph
- 54 mph
Solution
The information in the question can be collated in the following DST table:
| Distance | Speed | Time | |
| Onward Journey | D | 40 mph | – |
| Return Journey | D | 60 mph | – |
A Common Mistake:
While apparently, it may look like the average speed is the arithmetic average of the two speeds given, i.e. (40+60)/2= 50 mph, this is not the correct approach.
If we assume the distance on the onward journey as D, return journey distance will also be D.
- Therefore, the total distance traveled = 2D
Now, the time taken for the onward journey = (D/40) hrs and time taken for the return journey = (D/60) hrs.
- Therefore, the average speed = (Total distance travelled/ total time taken) = 2D/ [(D/40) + (D/60)] = 48 mph
Key Takeaways
As you have observed, although we assumed the value of the unknown distance as D, the final answer doesn’t contain D.
It happens whenever you have the distance as constant and the journey is divided into two equal parts. This can be generalized as follows:
The generalized formula:
Let us assume that a journey has two equidistant part, D each, covered at an average speed of a and b.
Time taken to complete the first half of the journey = D/a
Time taken to complete the second half of the journey = D/b
Therefore, the overall average speed of the journey = 2D/ [(D/40) + (D/60)] = 2ab/a+b
The above specific case shows the example when the journey is divided into two equal parts.
Let’s take another example to understand the application of the above takeaway.
BTW, do you know how to identify a regular polygon? Read our article on Polygons to know more.
Example 2
Joey covered his journey of 15 miles in two parts. He covered the 1st part of his journey at x mph and the second part in y mph. What is Joey’s average speed throughout the whole journey?
Statement 1: x = 2.5, y = 5
Statement 2: Distance covered in both parts of the journey is the same
Solution
In this question it is given that:
- Joey covered a journey of total distance 15 miles in two parts
- Speed in the 1st part of the journey = x mph
- Speed in the 2nd part of the journey = y mph
| Distance covered (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | D1 | x | |
| 2nd part of the journey | D2 | y | |
| Total | D1 + D2 = 15 |
As we need to find out the average speed of Joey’s whole journey, we need to know two things:
- The total distance, which is already provided as 15 miles
- The total time taken to cover that distance, which is the sum of the individual times taken to cover the 1st and 2nd part separately
Analyzing Statement 1:
Now, analyzing Statement 1 independently, it says x = 2.5 mph and y = 5 mph.
| Distance covered (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | 2.5 | ||
| 2nd part of the journey | 5 | ||
| Total | 15 |
- Considering this statement only, we get the information about the individual speeds only
- But this does not provide any information about the distances covered in each individual part of the journey – so, we cannot calculate the time taken for the parts of the journey
Hence, Statement 1 is not sufficient to answer the question.
Analyzing Statement 2:
Analyzing Statement 2 independently, it says the distance covered in both parts of the journey is the same.
| Distance covered (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | 7.5 | x | |
| 2nd part of the journey | 7.5 | y | |
| Total | 15 |
- It means each of the individual parts of the journey is of 7.5 miles.
- But this does not provide any information about the speeds in each individual part of the journey – so, we cannot calculate the time taken for the parts of the journey
Hence, Statement 2 is not sufficient to answer the question.
Combining Both Statements:
Now, combining the information from both the statements, we have:
- Individual speeds in each part, x = 2.5 mph and y = 5 mph
- Distance in each part of the journey = 7.5 miles
| Distance covered (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | 7.5 | 2.5 | |
| 2nd part of the journey | 7.5 | 5 | |
| Total | 15 |
Considering both together, we can calculate the time taken for individual parts of the journey, and hence the total journey time. From that, we can calculate the average speed.
As we are getting the answer by combining both the statements, correct answer choice is option C.
Note:-
Although for the question you don’t need to calculate the final value, the average speed here will be as follows:
Average Speed = (Total distance traveled)/(Total time taken to travel that distance)
= 15/ [(7.5/2.5) + (7.5/5)] = 15/4.5 = 3.33 mph
Because the distance is divided into two equal parts, we can also calculate the average speeds as
= (2×2.5×5)/(2.5+5) = 3.33 mph [application of the 2ab/a+b formula]
The devil is in the details! Planning out the finer details of your study schedule takes you one step closer to your target GMAT score. Learn the other benefits of a well defined study plan in this article.
Save 60+ hours of GMAT preparation by crafting a well-defined study plan in just 3 steps:
Let us take another example to solidify our understanding and then move to the next topic.
Example 3
Mike started his road trip on his bike and moved at a constant speed of 50 mph. After completing p% of his total journey, his bike started malfunctioning, and therefore, he had to complete his journey at half of his normal speed. What is the average of Mike’s whole journey, in terms of p?
Solution
In this question, first, we can consolidate all the given information.
- Here Mike’s journey is getting divided into two parts –
- 1st part is p% of total journey distance, completed at 50 mph
- 2nd or the remaining part of the journey, completed at 25 mph
We need to find out the average speed of Mike throughout the whole journey.
| Distance | Speed | Time | |
| Before bike malfunction | p % of total journey distance | 50 mph | – |
| After bike malfunction | (100-p) % of the total journey distance | 25 mph | – |
Now you can see that the total distance is not mentioned here. If we assume the total distance to be D, then
1st part of the journey = p% of D = pD/100, and remaining part of the journey = (D-(pD/100))
As we have the individual distances and speeds for every segment of the journey, we can now calculate the time taken for each segment as follows:
Time taken to complete the 1st part of the journey = (pD/100)/50 hrs = pD/5000 hrs
And, time taken to complete the 2nd part of the journey = [(D-pD)/100]/25 hrs = (100D-pD) /2500 hrs
Now that we know the total distance and total time for the journey, we can calculate the average speed of the whole journey as follows:
Average Speed = D/ [(pD/5000) + (100D-pD)/2500] = 5000/ (200-p)
Key Takeaways
- Although we assumed the value of the total distance as D, the final answer is independent of D. This is happening because the distance remains constant and does not influence the average speed.
- Although the journey is taking place in two separate parts, the overall journey distance remains constant. In cases like this, one can assume any constant value as the total distance for the ease of calculation. For example, in this case, if the distance is assumed to be 100 in place of D, the overall simplification process becomes very easy. Check the following:
As the total distance is assumed to be 100, then
- 1st part of the journey = p% of 100 = p, and remaining part of the journey = (100 – p)
As we have the individual distances and speeds for every segment of the journey, we can now calculate the time taken for each segment as follows:
Time taken to complete the 1st part of the journey = p/50 hrs
And, time taken to complete the 2nd part of the journey = (100-p)/25 hrs
Now that we know the total distance and total time for the journey, we can calculate the average speed of the whole journey as follows:
Average speed = 100/(p/50) + (100-p)/25 = 5000/ (200-p)
Example 4
On a certain day, Rosita started driving towards Stevie’s place at a speed of 45 mph. After moving for 2 hours, she realized that she needed to reach Stevie’s place in another 2 hours only. Therefore, she increased her speed to 65 mph and reached Stevie’s place exactly on time. What is the average speed of her journey?
Solution
In this question, the journey has happened in two parts.
- In the 1st part, Rosita moved at 45 mph for 2 hrs. Therefore, the distance covered = (45 × 2) = 90 miles
- In the 2nd part, Rosita moved at 65 mph for 2 hrs. Therefore, the distance covered = (65 × 2) = 130 miles
| Distance (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | 45 x 2 = 90 | 45 | 2 |
| 2nd part of the journey | 65 x 2 = 130 | 65 | 2 |
Total distance travelled by Rosita = (90 + 130) miles = 220 miles
Total time taken to travel that distance = (2 + 2) hrs = 4 hrs
Hence, the average speed of the journey = Total distance travelled/ Total time taken = 220/4 mph = 55 mph
Key Takeaways
If looked closely, one can see that the average speed, in this case, is the arithmetic average of the two given speeds. Let us see the logic behind that:
Assume a scenario when a moving body travels at a speed of x mph for t hrs and at a speed of y mph for next ‘t’ hrs
- In the 1st t hours, the distance covered = xt miles
- In the next t hours, the distance covered = yt miles
- The total distance covered = (xt + yt) miles = t (x + y) miles
- Total time taken to cover the distance = (t + t) hrs = 2t hrs
Therefore, the average speed = Total distance travelled/ Total time taken to travel that distance = t(x+y)/2t = (x+y)/2 mph
- which is essentially the numerical average of two speeds given
Hence, we can say if the journey is divided into two parts, in which every part is traveled for the same amount of time, the average speed of the journey is the numerical average of the two individual speeds.
This logic can also be generalized for journeys which are divided into more than two parts, and the time taken to cover each part is same.
Let’s say we are considering a scenario where the journey is divided into 3 parts, with the speeds in the three parts are x, y, and z respectively and the time taken to cover each part of the journey is same.
- In such a scenario, we can say the average speed of the whole journey is nothing but the average or arithmetic mean of the three individual speeds, i.e. x+y+z/3
The same concept can also be generalized for journeys which are divided into multiple parts, with each part takes the same time to cover.
Want to boost your Quant score but no able to define the path to your Target Score? Attend our Quant Workshop and get personalised feedback from Subject Matter Experts which will help you hit your Target GMAT Scores.
Example 5
A bus covers a certain distance at an average speed of 100 mph without any stoppages. While returning the same journey the bus covers the distance at an average speed of 60 mph with stoppages. What is the average stoppage time per hour taken by the bus?
Solution
This question can be solved using multiple methods:
Method 1:
Let’s assume the total journey distance in either direction is D
Therefore, time taken for the onward journey = D/100 hrs
And time taken for the return journey = D/60 hrs
The difference in journey time indicates the stoppage time, which is (D/60)-(D/100) = D/150 hrs
In the journey of D/60 hrs, stoppage time is D/150 hrs
Therefore, the average stoppage time per hour = (D/150)/ (D/60) hrs = 60/150 hrs = 2/5 hrs = 24 minutes
Method 2:
Let’s assume the distance to be 300 miles (LCM of 100 and 60).
Therefore, time for the onward journey = 300/100 = 3 hrs
And time for the return journey = 300/60 = 5 hrs
The extra time indicates the stoppage time, which is (5-3) = 2 hrs
In the journey of 5 hrs, stoppage time is 2 hrs, therefore, average stoppage time per hour = 2/5 hrs = 24 minutes
Method 3:
As the decrease in speed is happening due to stoppages, that decrease would have been absent if there were no stoppages. Here the decrease in speed is (100 – 60) = 40 miles per hour.
Now, when the bus was running without any stoppages, the average speed was 100 mph. At this speed, the bus could have completed 40 miles distance in a time of 40/100 hrs or 24 minutes, which is effectively the stoppage time.
On a similar note, if the decrease in speed was 80 miles per hour, then the bus would have completed that 80 miles distance in a time of 80/100 hrs or 48 minutes.
Key Takeaway
Although the distance remains the same in both onward and return journey, the average speed decreases because of the increase in the total journey time due to stoppages.
Generic case: Calculation of Average Speed when the journey is divided into more than two parts
Till now we have mostly taken up those examples where the average speed is calculated in the journeys divided into two parts. However, the concept of average speed is applicable to cases where the journey is divided into more than 2 parts. Let’s consider the following example:
Example 6
A train covered first 150 miles of its journey at an average speed of 50 mph. After that, it met with a small accident and its speed decreases to ‘a’ mph. It continued its journey for 4 hrs and then its speed decreased further to 20 mph. Running at this speed, the train completed the journey in total 12 hrs. Find the value of ‘a’, if the average speed of the whole journey is 33.33 mph.
Solution
In this question, the journey is separated into 3 parts, with each of them having different speeds. We can consider the whole information in the following tabular form:
| Distance covered (in miles) | Speed (in mph) | Time Taken (in hrs) | |
| 1st part of the journey | 150 | 50 | 3 |
| 2nd part of the journey | a | 4 | |
| 3rd part of the journey | 100 | 20 | |
| Total | 12 |
As the total journey time is 12 hrs, the journey time for the 3rd part = 12 – (3 + 4) hrs = 5 hrs
Also, we know average speed = Total distance traveled/ Total time taken
Or, 33.33 = Total distance travelled/12
Or, Total Distance travelled = 33.33×12 = 400 miles
Therefore, the distance traveled in the 2nd part of the journey = 400 – (150 + 100) miles = 150 miles
So, the average speed in the 2nd part of the journey = 150/4 = 37.5 mph
Key Takeaways
In this question, we can see the application of average speed where the journey is completed in more than two parts. But the procedural approach of the concept remains same –
- Average speed is used as per the basic definition, i.e. the ratio of total distance traveled, and total time taken
- Whether the journey is divided into two or more than two parts, the procedure of calculating the average speed remains the same
Key Takeaways from the article | GMAT Word Problems | Time, Speed, and Distance
- By definition, the average speed of a journey = (total distance traveled)/(total time taken to travel that distance)
- If a journey is divided into two equal parts, with individual speeds a and b respectively, then the average speed of the whole journey is denoted by 2ab/(a+b). However, this formula cannot be generalized for a journey which is divided into more than 2 parts
- If a journey is divided into multiple parts, and the time taken to cover every part is same, then the average speed of the whole journey is denoted by the average or arithmetic mean of the individual speeds at which the individual parts are covered.
Questions on time, speed and distance are very commonly asked on the GMAT. Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. We are the most reviewed online GMAT Prep company with 2400+ reviews on GMATClub.
| Introduction to Systems | Distance Word Problem |
| Solving Systems by Graphing | Which Plumber Problem |
| Solving Systems with Substitution | Geometry Word Problem |
| Solving Systems with Linear Combination or Elimination | Work Problem |
| Types of Equations | Three Variable Word Problem |
| Systems with Three Equations | The “Candy” Problem |
| Algebra Word Problems with Systems: | Right Triangle Trigonometry Systems Problem |
| Investment Word Problem | Inequality Word Problem (in Linear Programming section) |
| Mixture Word Problems | More Practice |
Note that we solve Algebra Word Problems without Systems here, and we solve systems using matrices in the Matrices and Solving Systems with Matrices section here.
Introduction to Systems
“Systems of equations” just means that we are dealing with more than one equation and variable. So far, we’ve basically just played around with the equation for a line, which is (y=mx+b). Let’s say we have the following situation:
You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50. You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?
Now, you can always do “guess and check” to see what would work, but you might as well use algebra! It’s much better to learn the algebra way, because even though this problem is fairly simple to solve, the algebra way will let you solve any algebra problem – even the really complicated ones.
The first trick in problems like this is to figure out what we want to know. This will help us decide what variables (unknowns) to use. What we want to know is how many pairs of jeans we want to buy (let’s say “(j)”) and how many dresses we want to buy (let’s say “(d)”). Always write down what your variables will be:
Let (j=) the number of jeans you will buy
Let (d=) the number of dresses you’ll buy
Like we did before, let’s translate word-for-word from math to English:
|
English |
Math |
Explanation |
| “You really, really want to take home 6 items of clothing because you need that many.” |
(j+d=6) (Number of Items) |
If you add up the pairs of jeans and dresses, you want to come up with 6 items. |
| “… you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50.” |
(25j+50d=200) (Money) |
This one’s a little trickier. Use easier numbers if you need to: if you buy 2 pairs of jeans and 1 dress, you spend (left( {2times $25} right)+left( {1times $50} right)). Now you can put the variables in with their prices, and they have to add up to $200. |
Now we have the 2 equations as shown below. Notice that the (j) variable is just like the (x) variable and the (d) variable is just like the (y). It’s easier to put in (j) and (d) so we can remember what they stand for when we get the answers.
This is what we call a system, since we have to solve for more than one variable – we have to solve for 2 here. The cool thing is to solve for 2 variables, you typically need 2 equations, to solve for 3 variables, you need 3 equations, and so on. That’s easy to remember, right?
We need to get an answer that works in both equations; this is what we’re doing when we’re solving; this is called solving simultaneous systems, or solving system simultaneously. There are several ways to solve systems; we’ll talk about graphing first.
Solving Systems by Graphing
Remember that when you graph a line, you see all the different coordinates (or (x/y) combinations) that make the equation work. In systems, you have to make both equations work, so the intersection of the two lines shows the point that fits both equations (assuming the lines do in fact intersect; we’ll talk about that later). The points of intersections satisfy both equations simultaneously.
Put these equations into the (y=mx+b) ((d=mj+b)) format, by solving for the (d) (which is like the (y)):
(displaystyle j+d=6;text{ },text{ }text{solve for }d:text{ }d=-j+6text{ })
(displaystyle 25j+50d=200;text{ },,text{solve for }d:text{ }d=frac{{200-25j}}{{50}}=-frac{1}{2}j+4)
Now graph both lines:
|
Solving Systems using Graph |
Explanation |
 |
To graph, solve for the “(y)” value (“(d)” in our case) to use the slope-intercept method, or keep the equations as is and use the cover-up, or intercept method.
The easiest way to graph the second equation is the intercept method; when we put 0 in for “(d)”, we get 8 for the “(j)” intercept; when we put 0 in for “(j)”, we get 4 for the “(d)” intercept. We can do this for the first equation too, or just solve for “(d)” to see that the slope is (-1) and the (y)-intercept is (6). The two graphs intercept at the point ((4,2)). This means that the numbers that work for both equations are 4 pairs of jeans and 2 dresses! |
We can also use our graphing calculator to solve the systems of equations:
|
Graphing Calculator Instructions |
Screens |
|
(displaystyle begin{array}{c}j+d=6text{ }\25j+50d=200end{array}) Solve for (y,left( d right)) in both equations. Push (Y=) and enter the two equations in ({{Y}_{1}}=) and ({{Y}_{2}}=), respectively. Note that we don’t have to simplify the equations before we have to put them in the calculator. Push GRAPH. You may need to hit “ZOOM 6” (ZoomStandard) and/or “ZOOM 0” (ZoomFit) to make sure you see the lines crossing in the graph. (You can also use the WINDOW button to change the minimum and maximum values of your (x)- and (y)-values.) |
 |
| To get the point of intersection, push “2nd TRACE” (CALC), and then either push 5, or move cursor down to intersect. You should see “First curve?” at the bottom.
Then push ENTER. Now you should see “Second curve?” and then press ENTER again. Now you should see “Guess?”. Push ENTER one more time, and you will get the point of intersection on the bottom! Pretty cool! |
 |
Note that with non-linear equations, there will most likely be more than one intersection; an example of how to get more than one solution via the Graphing Calculator can be found in the Exponents and Radicals in Algebra section. Also, there are some examples of systems of inequality here in the Linear Inequalities section.
Solving Systems with Substitution
Substitution is the favorite way to solve for many students! It involves exactly what it says: substituting one variable in another equation so that you only have one variable in that equation. Here is the same problem:
You’re going to the mall with your friends and you have $200 to spend from your recent birthday money. You discover a store that has all jeans for $25 and all dresses for $50. You really, really want to take home 6 items of clothing because you “need” that many new things. How many pairs of jeans and how many dresses you can buy so you use the whole $200 (tax not included)?
Below are our two equations, and let’s solve for “(d)” in terms of “(j)” in the first equation. Then, let’s substitute what we got for “(d)” into the next equation. Even though it doesn’t matter which equation you start with, remember to always pick the “easiest” equation first (one that we can easily solve for a variable) to get a variable by itself.
|
Steps Using Substitution |
Notes |
| (displaystyle begin{array}{c}j+d=text{ }6;,,,,d=6-j\25j+50d=200end{array})
(displaystyle begin{array}{c}25j+50(6-j)=200\25j+300-50j=200\-25j=-100,,\j=4,\d=6-j=6-4=2end{array}) |
Solve for (d): (displaystyle d=6-j). Plug this in for (d) in the second equation and solve for (j).
When you get the answer for (j), plug this back in the easier equation to get (d): (displaystyle d=6-(4)=2). The solution is ((4,2)). |
We could buy 4 pairs of jeans and 2 dresses. Note that we could have also solved for “(j)” first; it really doesn’t matter. You’ll want to pick the variable that’s most easily solved for. Let’s try another substitution problem that’s a little bit different:
|
Steps Using Substitution |
Notes |
| (displaystyle begin{array}{c}color{#800000}{begin{array}{c}37x+4y=124,\x=4,end{array}}\\37(4)+4y=124\4y=124-148\4y=-24\y=-6end{array}) | This one is actually easier: we already know that (x=4).
Now plug in 4 for the second equation and solve for (y). The solution is ((4,-6)). |
Solving Systems with Linear Combination or Elimination
Probably the most useful way to solve systems is using linear combination, or linear elimination. The reason it’s most useful is that usually in real life we don’t have one variable in terms of another (in other words, a “(y=)” situation).
The main purpose of the linear combination method is to add or subtract the equations so that one variable is eliminated. We can add, subtract, or multiply both sides of equations by the same numbers – let’s use real numbers as shown below. We are using the Additive Property of Equality, Subtraction Property of Equality, Multiplicative Property of Equality, and/or Division Property of Equality that we saw here in the Types of Numbers and Algebraic Properties section:
| (displaystyle begin{array}{c},,,3,,=,,3\underline{{+4,,=,,4}}\,,,7,,=,,7end{array}) | (displaystyle begin{array}{l},,,12,=,12\,underline{{-8,,=,,,8}}\,,,,,4,,=,,4end{array}) | (displaystyle begin{array}{c}3,,=,,3\4times 3,,=,,4times 3\12,,=,,12end{array}) | (displaystyle begin{array}{c}12,,=,,12\frac{{12}}{3},,=,,frac{{12}}{3}\4,,=,,4end{array}) |
If we have a set of 2 equations with 2 unknowns, for example, we can manipulate them by adding, multiplying or subtracting (we usually prefer adding) so that we get one equation with one variable. Let’s use our previous problem:
| Linear Elimination Steps | Notes |
| (displaystyle begin{array}{c}color{#800000}{begin{array}{c}j+d=6text{ }\25j+50d=200end{array}}\\,left( {-25} right)left( {j+d} right)=left( {-25} right)6text{ }\,,,,-25j-25d,=-150,\,,,,,underline{{25j+50d,=,200}}text{ }\,,,0j+25d=,50\\25d,=,50\d=2\\d+j,,=,,6\,2+j=6\j=4end{array}) | Since we need to eliminate a variable, we can multiply the first equation by –25. Remember that we need to multiply every term (anything separated by a plus, minus, or (=) sign) by the –25.
Then we add the two equations to get “(0j)” and eliminate the “(j)” variable (thus, the name “linear elimination”). We then solve for “(d)”. Now that we get (d=2), we can plug in that value in the either original equation (use the easiest!) to get the other variable. The solution is ((4,2)): (j=4) and (d=2). |
We could buy 4 pairs of jeans and 2 dresses.
Here’s another example:
| Linear Elimination Steps | Notes |
|
(displaystyle begin{array}{l}color{#800000}{{2x+5y=-1}},,,,,,,text{multiply by –}3\color{#800000}{{7x+3y=11}}text{ },,,,,,,text{multiply by }5end{array}) (displaystyle begin{array}{l}-6x-15y=3,\,underline{{35x+15y=55}}text{ }\,29x,,,,,,,,,,,,,,,=58\,,,,,,,,,,,,,x=2\,,,,,,,,,,,,,,,\2(2)+5y=-1\,,,,,,4+5y=-1\,,,,,,,,,,,,,,,5y=-5\,,,,,,,,,,,,,,,,,y=-1end{array}) |
Since we need to eliminate a variable, we can multiply the first equation by –3 and the second one by 5. There are many ways to do this, but we want to make sure that either the (x) or (y) will be eliminated when adding the two equations. (We could have also picked multiplying the first by –7 and the second by 2).
We then get the second set of equations to add, and the (y)’s are eliminated. Solving for (x), we get (x=2). Now we can plug in that value in either original equation (use the easiest!) to get the other variable. The solution is ((2,-1)). |
Types of equations
In the example above, we found one unique solution to the set of equations. Sometimes, however, for a set of equations, there are no solutions (when lines are parallel) or an infinite number of solutions or infinitely many solutions (when the two lines are actually the same line, and one is just a “multiple” of the other).
When there is at least one solution, the equations are consistent equations, since they have a solution. When there is only one solution, the system is called independent, since they cross at only one point. When equations have infinite solutions, they are the same equation, are consistent, and are called dependent or coincident (think of one just sitting on top of the other).
When equations have no solutions, they are called inconsistent equations, since we can never get a solution.
Here are graphs of inconsistent and dependent equations that were created on a graphing calculator:
| Systems of Equations Calculator Screens | Notes |
 |
(displaystyle begin{array}{l}y=-x+4\y=-x-2end{array}) Notice that the slope of these two equations is the same, but the (y)-intercepts are different. In this situation, the lines are parallel, as we can see from the graph. These types of equations are called inconsistent, since there are no solutions. If we were to “solve” the two equations, we’d end up with “(4=-2)”; no matter what values we give to (x) or (y), (4) can never equal (-2). Thus, there are no solutions. The symbol (emptyset ) is sometimes used for no solutions; it is called the “empty set”. |
 |
(displaystyle x+y=6,,,,,,,text{or},,,,,,,y=-x+6) (displaystyle 2x+2y=12,,,,,,,text{or},,,,,,,y=frac{{-2x+12}}{2}=-x+6) Sometimes we have a situation where the system contains the same equations even though it may not be obvious. See how we may not know unless we actually graph, or simplify them? These types of equations are called dependent or coincident since they are one and the same equation and they have an infinite number of solutions, since one “sits on top of” the other. Since they have at least one solution, they are also consistent. If we were to “solve” the two equations, we’d end up with “(6=6)”, and no matter what values we give to (x) or (y), (6) always equals (6). Thus, there are an infinite number of solutions (infinitely many), but (y) always has to be equal to (-x+6). We can also write the solution as ((x,-x+6)). |
Systems with Three Equations
Let’s get a little more complicated with systems; in real life, we rarely just have two unknowns to solve for.
Let’s say at the same store, they also had pairs of shoes for $20 and we managed to get $60 more to spend! Now we have a new problem. To spend the even $260, how many pairs of jeans, dresses, and pairs of shoes should we get if want, for example, exactly 10 total items (Remember that jeans cost $25 each and dresses cost $50 each).
Let’s let (j=) the number of pair of jeans, (d=) the number of dresses, and (s=) the number of pairs of shoes we should buy. So far, we’ll have the following equations:
(displaystyle begin{array}{c}j+d+s=10text{ }\25j+text{ }50d+,20s=260end{array})
We’ll need another equation, since for three variables, we need three equations (otherwise, we theoretically might have infinite ways to solve the problem). In this type of problem, you would also need something like this: We want twice as many pairs of jeans as pairs of shoes. Now, since we have the same number of equations as variables, we can potentially get one solution for the system of equations. Here are the three equations:
| (displaystyle begin{array}{c}j+d+s=10text{ }\25j+50d+,20s=260\j=2send{array}) | Note that when we say “we have twice as many pairs of jeans as pair of shoes”, it doesn’t translate that well into math.
We can think in terms of real numbers, such as if we had 8 pairs of jeans, we’d have 4 pairs of shoes. Then it’s easier to put it in terms of the variables. |
We’ll learn later how to put these in our calculator to easily solve using matrices (see the Matrices and Solving Systems with Matrices section). For now, we can use two equations at a time to eliminate a variable (using substitution and/or elimination), and keep doing this until we’ve solved for all variables. These can get really difficult to solve, but remember that in “real life”, there are computers to do all this work!
Remember again, that if we ever get to a point where we end up with something like this, it means there are an infinite number of solutions: (4=4) (variables are gone and a number equals another number and they are the same). And if we up with something like this, it means there are no solutions: (5=2) (variables are gone and two numbers are left and they don’t equal each other).
And another note: equations with three variables are represented by planes, not lines (you’ll learn about this in Geometry). If all the planes crossed in only one point, there is one solution, and if, for example, any two were parallel, we’d have no solution, and if, for example, two or three of them crossed in a line, we’d have an infinite number of solutions.
Let’s solve our system: (displaystyle begin{array}{c}j+d+s=10text{ }\25j+text{ }50d+20s=260\j=2send{array}):
|
Solving Systems Steps |
Notes |
|
(displaystyle begin{array}{c}j+d+s=10text{ }\25j+50d+20s=260\j=2send{array}) (displaystyle begin{array}{c}2s+d+s=10,,,,,,,,,,Rightarrow ,,,,,,,,,,,,,,3s+d=10\25(2s)+50d+,20s=260,,,,,,Rightarrow ,,,,70s+50d=260end{array}) (displaystyle begin{array}{l}-150s-50d=-500\,,,,,underline{{,,70s+50d=,,,,260}}\,,-80s,,,,,,,,,,,,,,,,=-240\,,,,,,,,,,,,,,,,,,,s=3\\3(3)+d=10;,,,,,d=1,\j=2s=2(3);,,,,,,j=6end{array}) |
Use substitution since the last equation makes that easier. We’ll substitute (2s) for (j) in the other two equations and then we’ll have 2 equations and 2 unknowns.
We then multiply the first equation by –50 so we can add the two equations to get rid of the (d). We could have also used substitution again. First, we get that (s=3), so then we can substitute this in one of the 2 equations we’re working with. Now we know that (d=1), so we can plug in (d) and (s) in the original first equation to get (j=6). The solution is ((6,1,3)). |
We could buy 6 pairs of jeans, 1 dress, and 3 pairs of shoes.
Here’s one more example of a three-variable system of equations, where we’ll only use linear elimination:
(displaystyle begin{align}5x-6y-,7z,&=,7\6x-4y+10z&=,-34\2x+4y-,3z,&=,29end{align})
|
Solving Systems Steps |
Notes |
|
(displaystyle begin{array}{l}5x-6y-,7z,=,,7\6x-4y+10z=,-34\2x+4y-,3z,=,29,end{array}) (displaystyle begin{array}{l}6x-4y+10z=-34\underline{{2x+4y-,3z,=,29}}\8x,,,,,,,,,,,,,+7z=-5end{array}) (require{cancel} displaystyle begin{array}{l}cancel{{5x-6y-7z=7}},,,,,,,,,,,,,,20x-24y-28z,=,28,\cancel{{2x+4y-,3z,=29,,}},,,,,,,,underline{{12x+24y-18z=174}}\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,32x,,,,,,,,,,,,,,-46z=202end{array}) (displaystyle begin{array}{l},,,cancel{{8x,,,+7z=,-5}},,,,,-32x,-28z=,20\32x,-46z=202,,,,,,,,,,,,underline{{,,32x,-46z=202}}\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,-74z=222\,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,z=-3end{array}) (displaystyle begin{array}{l}32x-46(-3)=202,,,,,,,,,,,,,x=frac{{202-138}}{{32}}=frac{{64}}{{32}}=2\\5(2)-6y-7(-3)=7,,,,,,,,y=frac{{-10+-21+7}}{{-6}}=4end{array}) |
We first pick any 2 equations and eliminate a variable; we’ll use equations 2 and 3 since we can add them to eliminate the (y).
We then use 2 different equations (one will be the same!) to also eliminate the (y); we’ll use equations 1 and 3. To eliminate the (y), we can multiply the first by 4, and the second by 6. Now we use the 2 equations we’ve just created without the (y)’s and solve them just like a normal set of systems. We can multiply the first by –4 to eliminate the (x)’s to get the (z), which is –3. We can then get the (x) from either of the equations we just worked with. Since we have the (x) and the (z), we can use any of the original equations to get the (y). The solution is ((2,4,-3)). |
I know – this is really difficult stuff! But if you do it step-by-step and keep using the equations you need with the right variables, you can do it. Think of it like a puzzle – you may not know exactly where you’re going, but do what you can in baby steps, and you’ll get there (sort of like life sometimes, right?!). And we’ll learn much easier ways to do these types of problems.
Algebra Word Problems with Systems
Let’s do more word problems; you’ll notice that many of these are the same type that we did earlier in the Algebra Word Problems section, but now we can use more than one variable. This will actually make the problems easier! Again, when doing these word problems:
- If you’re wondering what the variables (or unknowns) should be when working on a word problem, look at what the problem is asking. These are usually (but not always) what your variables are!
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
Here are some problems:
Investment Word Problem
| Investment Word Problem | Solution |
| Suppose Lindsay’s mom invests $10,000, part at 3%, and the rest at 2.5%, in interest bearing accounts.
The totally yearly investment income (interest) is $283. How much did Lindsay’s mom invest at each rate? |
Define a variable, and look at what the problem is asking. Use two variables: let (x=) the amount of money invested at 3%, and (y=) the amount of money invested at 2.5%.
The yearly investment income or interest is the amount that we get from the yearly percentages. (This is the amount of money that the bank gives us for keeping our money there.) To get the interest, multiply each percentage by the amount invested at that rate. Add these amounts up to get the total interest. We have two equations and two unknowns. The total amount ((x+y)) must equal $10000, and the interest ((.03x+.025y)) must equal $283: (displaystyle begin{array}{c}x,+,y=10000\.03x+.025y=283end{array}) (displaystyle begin{array}{c}y=10000-x\.03x+.025(10000-x)=283\,,,.03x,+,250,-.025x=283\,.005x=33;,,,,x=6600,,\,,y=10000-6600=3400end{array}) Turn the percentages into decimals: move the decimal point two places to the left. Substitution is the easiest way to solve. Lindsay’s mom invested $6600 at 3% and $3400 at 2.5%. |
We also could have set up this problem with a table:
| Amount | Turn % to decimal | Total | ||
| Amount at 3% | (x) | (.03) | (.03x) | Multiply across |
| Amount at 2.5% | (y) | (.025) | (.025y) | Multiply across |
| Total | (10000) | (283) | Do Nothing Here | |
| Add Down:
(x+y=10000) |
Do Nothing Here | Add Down: (.03x+.025y = 283) and solve the system |
Mixture Word Problems
Here’s a mixture word problem. With mixture problems, remember if the problem calls for a pure solution or concentrate, use 100% (if the percentage is that solution) or 0% (if the percentage is another solution).
| Mixture Word Problem | Solution | ||||||||||||||||||||||||
| Two types of milk, one that has 1% butterfat, and the other that has 3.5% of butterfat, are mixed.
How many liters of these two different kinds of milk are to be mixed together to produce 10 liters of low-fat milk, which has 2% butterfat? |
(Note that we did a similar mixture problem using only one variable here in the Algebra Word Problems section.)
First define variables for the number of liters of each type of milk. Let (x=) the number of liters of the 1% milk, and (y=) the number of liters of the 3.5% milk. Use a table again:
We can also set up mixture problems with the type of figure below. We add up the terms inside the box, and then multiply the amounts in the boxes by the percentages above the boxes, and then add across. This will give us the two equations. Let’s do the math (use substitution)! (displaystyle begin{array}{c}x,,+,,y=10\.01x+.035y=10(.02)end{array}) (displaystyle begin{array}{c},y=10-x\.01x+.035(10-x)=.2\.01x,+,.35,,-,.035x=.2\,-.025x=-.15;,,,,,x=6\,y=10-6=4end{array}) We would need 6 liters of the 1% milk, and 4 liters of the 3.5% milk. |
Here’s another mixture problem:
| Mixture Word Problem with Money | Solution | ||||||||||||||||||||||||
| A store sells two different types of coffee beans; the more expensive one sells for $8 per pound, and the cheaper one sells for $4 per pound.
The beans are mixed to provide a mixture of 50 pounds that sells for $6.40 per pound. How much of each type of coffee bean should be used to create 50 pounds of the mixture? |
First define variables for the number of pounds of each type of coffee bean. Let (x=) the number of pounds of the $8 coffee, and (y=) the number of pounds of the $4 coffee.
Use a table again:
Let’s do the math (use substitution)! (displaystyle begin{array}{c}x+y=50\8x+4y=50left( {6.4} right)end{array}) (displaystyle begin{array}{c}y=50-x\8x+4left( {50-x} right)=320\8x+200-4x=320\4x=120,;,,,,x=30\y=50-30=20\8x+4y=50(6.4)end{array}) We would need 30 pounds of the $8 coffee bean, and 20 pounds of the $4 coffee bean. See how similar this problem is to the one where we use percentages? |
Distance Word Problem:
Here’s a distance word problem using systems; distance problems have to do with an object’s speed, time, and distance. Note that, as well as the distance word problem here in the Algebra Word Problems section, there’s an example of a Parametric Distance Problem here in the Parametric Equations section.
| Distance Word Problem | Solution |
| Lia walks to the mall from her house at 5 mph. 10 minutes later, Lia’s sister Megan starts riding her bike at 15 mph (from the same house) to the mall to meet Lia. They arrive at the mall the same time.
How far is the mall from the sisters’ house? How long did it take Megan to get there? |
Remember always that (text{distance}=text{rate}times text{time}). It’s difficult to know how to define the variables, but usually in these types of distance problems, we want to set the variables to time, since we have rates, and we’ll want to set distances equal to each other in this case (the house is always the same distance from the mall). (Sometimes we’ll need to add the distances together instead of setting them equal to each other.)
Let (L) equal the how long (in hours) it will take Lia to get to the mall, and (M) equal to how long (in hours) it will take Megan to get to the mall. The rates of the Lia and Megan are 5 mph and 15 mph respectively. (Usually a rate is “something per something”). Lia’s time is Megan’s time plus (displaystyle frac{{10}}{{60}}=frac{1}{6},,,,(L=M+frac{1}{6})), since Lia left 10 minutes earlier than Megan (convert minutes to hours by dividing by 60 – try real numbers to see this). Use the distance formula for each of them separately, and then set their distances equal, since they are both traveling the same distance (house to mall). Then use substitution to solve the system for Megan’s time: after dividing both sides by 5, multiply both sides by 6 to get rid of the fractions.
Megan’s time is (displaystyle frac{1}{{12}}) of any hour, which is 5 minutes. The distance to the mall is rate times time, which is 1.25 miles. |
Which Plumber Problem
Many word problems you’ll have to solve have to do with an initial charge or setup charge, and a charge or rate per time period. In these cases, the initial charge will be the (boldsymbol {y})-intercept, and the rate will be the slope. Here is an example:
| “Which Plumber” Systems Word Problem | Solution |
| Michaela’s mom is trying to decide between two plumber companies to fix her sink.
The first company charges $50 for a service call, plus an additional $36 per hour for labor. The second company charges $35 for a service call, plus an additional $39 per hour of labor. At how many hours will the two companies charge the same amount of money? |
The money spent depends on the plumber’s set up charge and number of hours, so let (y=) the total cost of the plumber, and (x=) the number of hours of labor. Again, set up charges are typical (boldsymbol {y})-intercepts, and rates per hour are slopes. The total price of the plumber’s house call will be the initial or setup charge, plus the number of hours ((x)) at the house times the price per hour for labor.
To get the number of hours when the two companies charge the same amount of money, we just put the two (y)’s together and solve for (x) (substitution, right?): First plumber’s total price: (displaystyle y=50+36x) Second plumber’s total price: (displaystyle y=35+39x) (displaystyle 50+36x=35+39x;,,,,,,x=5) Here’s what a graph would look like: At 5 hours, the two plumbers will charge the same. At this time, the (y)-value is 230, so the total cost is $230. Note that, in the graph, before 5 hours, the first plumber will be more expensive (because of the higher setup charge), but after the first 5 hours, the second plumber will be more expensive. Thus, the plumber would be chosen based on how many hours Michaela’s mom thinks the plumber will be there. |
Geometry Word Problem:
Many times, we’ll have a geometry problem as an algebra word problem; these might involve perimeter, area, or sometimes angle measurements (so don’t forget these things!). Let’s do one involving angle measurements.
| Geometry Systems Word Problem | Solution |
| Two angles are supplementary. The measure of one angle is 30 degrees smaller than twice the other.
Find the measure of each angle. |
From Geometry, we know that two angles are supplementary if their angle measurements add up to 180 degrees (and remember also that two angles are complementary if their angle measurements add up to 90 degrees).
Define the variables and turn English into Math. Let (x=) the first angle, and (y=) the second angle. We really don’t need to worry at this point about which angle is bigger; the math will take care of itself. (x) plus (y) must equal 180 degrees by definition, and also (x=2y-30) (Remember the English-to-Math chart?) Solve, using substitution: (displaystyle begin{array}{c}x+y=180\x=2y-30end{array}) (displaystyle begin{array}{c}2y-30+y=180\3y=210;,,,,,,,,y=70\x=2left( {70} right)-30=110end{array}) The larger angle is 110°, and the smaller is 70°. Let’s check our work: The two angles do in fact add up to 180°, and the larger angle (110°) is 30° less than twice the smaller (70°). |
See – these are getting easier! Here’s one that’s a little tricky though:
Work Problem:
Let’s do a “work problem” that is typically seen when studying Rational Equations (fraction with variables in them) and can be found here in the Rational Functions, Equations and Inequalities section.
Note that there’s also a simpler version of this problem here in the Direct, Inverse, Joint and Combined Variation section.
| Work Word Problem
(Systems) |
Solution |
| 8 women and 12 girls can paint a large mural in 10 hours.
6 women and 8 girls can paint it in 14 hours. Find the time to paint the mural, by 1 woman alone, and 1 girl alone. |
Let’s let (w=) the part of the job by 1 woman in 1 hour, and (g=) the part of the job by 1 girl in 1 hour. We have 10 hours with 8 women and 12 girls that paint the mural (do 1 job), and 14 hours with 6 women and 8 girls that paint the mural (do 1 job).
Since (w=) the part of the job that is completed by 1 woman in 1 hour, then (8w=) the amount of the job that is completed by 8 women in 1 hour. Also, if (8w=) the amount of the job that is completed by 8 women in 1 hour, (10times 8w) is the amount of the job that is completed by 8 women in 10 hours. Similarly, (10times 12g) is the amount of the job that is completed by 12 girls in 10 hours. Add these two amounts and we get (displaystyle 10left( {8w+12g} right)), which will be the whole job. Use the same logic for the 6 women and 8 girls to paint the mural in 14 hours. The whole job is 1 (this is typical in work problems), and we can set up two equations that equal 1 to solve the system. Use linear elimination to solve the equations; it gets a little messy with the fractions, but we can get it! (displaystyle begin{array}{c}10left( {8w+12g} right)=1,text{ or }8w+12g=frac{1}{{10}}\,14left( {6w+8g} right)=1,text{ or },6w+8g=frac{1}{{14}}end{array}) (displaystyle begin{array}{c}text{Use elimination:}\left( {-6} right)left( {8w+12g} right)=frac{1}{{10}}left( {-6} right)\left( 8 right)left( {6w+8g} right)=frac{1}{{14}}left( 8 right)\cancel{{-48w}}-72g=-frac{3}{5}\cancel{{48w}}+64g=frac{4}{7},\,-8g=-frac{1}{{35}};,,,,,g=frac{1}{{280}}end{array}) (begin{array}{c}text{Substitute in first equation to get }w:\,10left( {8w+12cdot frac{1}{{280}}} right)=1\,80w+frac{{120}}{{280}}=1;,,,,,,w=frac{1}{{140}}\g=frac{1}{{280}};,,,,,,,,,,,w=frac{1}{{140}}end{array}) The answers we get is the part of the job that is completed by 1 woman or girl in 1 hour, so to get how long it would take them to do a whole job, we have to take the reciprocal. (Think about it; if we could complete (displaystyle frac{1}{3}) of a job in an hour, we could complete the whole job in 3 hours). Thus, it would take one of the women 140 hours to paint the mural by herself, and one of the girls 280 hours to paint the mural by herself. |
Three Variable Word Problem:
Let’s do one more with three equations and three unknowns:
| Three Variable Word Problem | Solution |
| A florist is making 5 identical bridesmaid bouquets for a wedding.
She has $610 to spend (including tax) and wants 24 flowers for each bouquet. Roses cost $6 each, tulips cost $4 each, and lilies cost $3 each. She wants to have twice as many roses as the other 2 flowers combined in each bouquet. How many roses, tulips, and lilies are in each bouquet? The trick is to put real numbers in to make sure you’re doing the problem correctly, and also make sure you’re answering what the question is asking! |
Look at the question being asked to define our variables: Let (r=) the number of roses, (t=) the number of tulips, and (l=) the number of lilies in each bouquet. Put the money terms together, and also the counting terms together:
(begin{array}{l}5left( {6r+4t+3l} right)=610,,,text{(price of each flower times number of flowers x }5text{ bouquets= total price)}\,,,,,,,,,r=2(t+l)text{ },,,,,,,,,,text{ (two times the sum of the other two flowers = number of roses)}\,,,,,,r+t+l=24text{ },,,,,,,,,text{(total number of flowers in each bouquet is }24text{)}end{array}) Use substitution and put (r) from the middle equation in the other equations. Then, use linear elimination to put those two equations together: multiply the second by –5 to eliminate the (l). We typically have to use two separate pairs of equations to get the three variables down to two! (begin{array}{c}6r+4t+3l=122\r=2left( {t+l} right)\,r+t+l=24\\6left( {2t+2l} right)+4t+3l=122\,12t+12l+4t+3l=122\16t+15l=122\\left( {2t+2l} right)+t+l=24\3t+3l=24end{array}) (displaystyle begin{array}{c},16t+15l=122\,,,,,,,,,cancel{{3t+3l=24}}\,,,,underline{{-15t-15l=-120}}\,,,,,t,,,,,,,,,,,,,,,,,=2\16left( 2 right)+15l=122;,,,,l=6\\r=2left( {2+6} right)=16\,,,,,,,,,,r=16,,,,t=2,,,,l=6end{array}) We get (t=2). Solve for (l) in this same system, and (r) by using the value we got for (t) and (l) (most easily in the second equation at the top). Thus, for one bouquet, we’ll have 16 roses, 2 tulips, and 6 lilies. If we had solved for the total number of flowers, we would have had to divide each number by 5. |
The “Candy” Problem
Sometimes we get lucky and can solve a system of equations where we have more unknowns (variables) then equations. (Actually, I think it’s not so much luck, but having good problem writers!) Here’s one like that:
| More Unknowns Than Variables Problem | Solution |
| Sarah buys 2 pounds of jelly beans and 4 pounds of chocolates for $4.00.
She then buys 1 pound of jelly beans and 4 pounds of caramels for $3.00. She also buys 1 pound of jelly beans, 3 pounds of licorice and 1 pound of caramels for $1.50. How much will it cost to buy 1 pound of each of the four candies? |
Look at the question being asked to define our variables: Let (j=) the cost of 1 pound of jelly beans, (o=) the cost of 1 pound of chocolates, (c=) the cost of 1 pound of caramels, and (l=) the cost of 1 pound of licorice. Here is the system of equations:
(begin{array}{c}2j+4o=4\j+4c=3\j+3l+1c=1.5\text{Want: }j+o+c+lend{array}) Wait! Something’s not right since we have 4 variables and 3 equations. But note that they are not asking for the cost of each candy, but the cost to buy all 4! Maybe the problem will just “work out” so we can solve it; let’s try and see. From our three equations above (using substitution), we get values for (o), (c) and (l) in terms of (j). (displaystyle begin{align}o=frac{{4-2j}}{4}=frac{{2-j}}{2},,,,,,,,,c=frac{{3-j}}{4},\j+3l+1left( {frac{{3-j}}{4}} right)=1.5\4j+12l+3-j=6\,l=frac{{6-3-3j}}{{12}}=frac{{3-3j}}{{12}}=frac{{1-j}}{4}end{align}) (require{cancel} displaystyle begin{align}j+o+c+l&=j+frac{{2-j}}{2}+frac{{3-j}}{4}+frac{{1-j}}{4}\&=cancel{j}+1-cancel{{frac{1}{2}j}}+frac{3}{4}cancel{{-frac{j}{4}}}+frac{1}{4}cancel{{-frac{j}{4}}}=2end{align}) When we substitute back in the sum (text{ }j+o+c+l), all in terms of (j), our (j)’s actually cancel out, which is very unusual! We can’t really solve for all the variables, since we don’t know what (j) is. But we can see that the total cost to buy 1 pound of each of the candies is $2. Pretty cool! |
There are more Systems Word Problems in the Matrices and Solving Systems with Matrices section, Linear Programming section, and Right Triangle Trigonometry section.
Understand these problems, and practice, practice, practice!
For Practice: Use the Mathway widget below to try a Systems of Equations problem. Click on Submit (the blue arrow to the right of the problem) and click on Solve by Substitution or Solve by Addition/Elimination to see the answer.
You can also type in your own problem, or click on the three dots in the upper right hand corner and click on “Examples” to drill down by topic.
If you click on Tap to view steps, or Click Here, you can register at Mathway for a free trial, and then upgrade to a paid subscription at any time (to get any type of math problem solved!).
On to Algebraic Functions, including Domain and Range – you’re ready!
Problem 1 :
The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouses at M(−70, 10) and N(50, 10). How long does it take a truck that drives 40 miles per hour to travel from warehouse M to warehouse N ?
Solution :
Let us locate the points M(−70, 10) and N(50, 10) on the graph.
Step 1 :
Identify the important information.
One warehouse is located at M(−70, 10). The other is at N(50, 10).
A truck drives from M to N at a speed of 40 miles per hour.
Step 2 :
Find the distance between M and N by adding the absolute values of the x-coordinates of the points.
Find the time it takes the truck to drive this distance by using this relationship : distance = rate · time.
Step 3 :
Add the absolute values of the x-coordinates to find the distance between point M and point N on the grid.
|-70| + |50| = 70 + 50 = 120
The warehouses are 120 miles apart.
The truck drives 120 miles at 40 mi/h. Because 120 = 40(3), it takes the truck 3 hours to travel from M to N.
Justify and Evaluate :
We found the sum of the absolute values of the x-coordinates to find the horizontal distance on the grid.
Then, we used the formula
Distance = Rate · Time
to find the time it takes to drive that distance.
Problem 2 :
The coordinate plane represents a map. Each grid unit represents 20 miles. A retail company has warehouse at and N(50, 10) and a store is located at P(50, -30). How long will it take a truck driving at 50 miles per hour to drive from warehouse N to this store ?
Solution :
Let us locate the points N(50, 10) and P(50, -30) on the graph.
Step 1 :
Identify the important information.
The warehouse is located at N(50, 10) and the store is located at P(50, -30) and
A truck drives from N to P at a speed of 50 miles per hour.
Step 2 :
The line which connects N and P is parallel to y-axis.
Find the distance between N and P by adding the absolute values of the y-coordinates of the points.
Find the time it takes the truck to drive this distance by using this relationship : distance = rate · time.
Step 3 :
Add the absolute values of the y-coordinates to find the distance between point N and point P on the grid.
|10| + |-30| = 10 + 30 = 40
The store P and the warehouse N are 40 miles apart.
The truck drives 40 miles at 50 mi/h. Because 40 = 50(0.8), it takes the truck 0.8 hours or 48 minutes to travel from N to P.
(0.8 hrs = 0.8 x 60 = 48 minutes)
Justify and Evaluate :
We found the sum of the absolute values of the y-coordinates to find the vertical distance on the grid.
Then, we used the formula
Distance = Rate · Time
to find the time it takes to drive that distance.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
In this chapter / (section) a lot of lessons and problems on Travel & Distance are collected and solved to be sources, samples and templates for you.
They cover practically all aspects of Travel & Distance problems.
Read them and become familiar with the problems and the methods of their solutions.
Learn from these sources and be trained in solution of Travel & Distance problems.
After reading these lessons, your heart will belong to Math, forever !
Algebra.Com is a people’s math website. It relies on volunteers like you, who create our free content.
Creating lessons is easy! Look for other lessons and
click on ‘view source’. All you have to really know is math.
Tutors Answer Your Questions about Travel Word Problems (FREE)
Did you know that Algebra.Com OR get immediate PAID help on: |
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645, 12646..12690, 12691..12735, 12736..12780, 12781..12825, 12826..12870, 12871..12915, 12916..12960, 12961..13005, 13006..13050, 13051..13095, 13096..13140, 13141..13185, 13186..13230, 13231..13275, 13276..13320, 13321..13365, 13366..13410, 13411..13455, 13456..13500, 13501..13545, 13546..13590, 13591..13635, 13636..13680, 13681..13725, 13726..13770, 13771..13815, 13816..13860, 13861..13905, 13906..13950, 13951..13995, 13996..14040, 14041..14085, 14086..14130, 14131..14175, 14176..14220, 14221..14265, 14266..14310, 14311..14355, 14356..14400, 14401..14445, 14446..14490, 14491..14535, 14536..14580, 14581..14625, 14626..14670, 14671..14715, 14716..14760, 14761..14805, 14806..14850, 14851..14895, 14896..14940, 14941..14985, 14986..15030, 15031..15075, 15076..15120, 15121..15165, 15166..15210, 15211..15255, 15256..15300, 15301..15345, 15346..15390, 15391..15435, 15436..15480, 15481..15525, 15526..15570, 15571..15615, 15616..15660, 15661..15705, 15706..15750, 15751..15795, 15796..15840, 15841..15885, 15886..15930, 15931..15975, 15976..16020, 16021..16065, 16066..16110, 16111..16155, 16156..16200, 16201..16245, 16246..16290, 16291..16335, 16336..16380, 16381..16425, 16426..16470, 16471..16515, 16516..16560, 16561..16605, 16606..16650, 16651..16695, 16696..16740, 16741..16785, 16786..16830, 16831..16875, 16876..16920, 16921..16965, 16966..17010, 17011..17055, 17056..17100, 17101..17145, 17146..17190, 17191..17235, 17236..17280, 17281..17325, 17326..17370, 17371..17415, 17416..17460, 17461..17505, 17506..17550, 17551..17595, 17596..17640, 17641..17685, 17686..17730, 17731..17775, 17776..17820, 17821..17865, 17866..17910, 17911..17955, 17956..18000, 18001..18045, 18046..18090, 18091..18135, 18136..18180, 18181..18225, 18226..18270, 18271..18315, 18316..18360, 18361..18405, 18406..18450, 18451..18495, 18496..18540, 18541..18585, 18586..18630, 18631..18675, 18676..18720, 18721..18765, 18766..18810, 18811..18855, 18856..18900, 18901..18945, 18946..18990, 18991..19035, 19036..19080, 19081..19125, 19126..19170, 19171..19215, 19216..19260, 19261..19305, 19306..19350, 19351..19395, 19396..19440, 19441..19485, 19486..19530, 19531..19575, 19576..19620, 19621..19665, 19666..19710, 19711..19755, 19756..19800, 19801..19845, 19846..19890, 19891..19935, 19936..19980, 19981..20025, 20026..20070, 20071..20115, 20116..20160, 20161..20205, 20206..20250, 20251..20295, 20296..20340, 20341..20385, 20386..20430, 20431..20475, 20476..20520, 20521..20565, 20566..20610, 20611..20655, 20656..20700, 20701..20745, 20746..20790, 20791..20835, 20836..20880, 20881..20925, 20926..20970, 20971..21015, 21016..21060, 21061..21105, 21106..21150, 21151..21195, 21196..21240, 21241..21285, 21286..21330, 21331..21375, 21376..21420, 21421..21465, 21466..21510, 21511..21555, 21556..21600, 21601..21645, 21646..21690, 21691..21735, 21736..21780, 21781..21825, 21826..21870, 21871..21915, 21916..21960, 21961..22005, 22006..22050, 22051..22095, 22096..22140, 22141..22185, 22186..22230, 22231..22275, 22276..22320, 22321..22365, 22366..22410, 22411..22455, 22456..22500, 22501..22545, 22546..22590, 22591..22635, 22636..22680, 22681..22725, 22726..22770, 22771..22815, 22816..22860, 22861..22905, 22906..22950, 22951..22995, 22996..23040, 23041..23085, 23086..23130, 23131..23175, 23176..23220, 23221..23265, 23266..23310, 23311..23355, 23356..23400, 23401..23445, 23446..23490, 23491..23535, 23536..23580, 23581..23625, 23626..23670, 23671..23715, 23716..23760, 23761..23805, 23806..23850, 23851..23895, 23896..23940, 23941..23985, 23986..24030, 24031..24075, 24076..24120, 24121..24165, 24166..24210, 24211..24255, 24256..24300, 24301..24345, 24346..24390, 24391..24435, 24436..24480, 24481..24525, 24526..24570, 24571..24615, 24616..24660, 24661..24705, 24706..24750, 24751..24795, 24796..24840, 24841..24885, 24886..24930, 24931..24975, 24976..25020, 25021..25065, 25066..25110, 25111..25155, 25156..25200, 25201..25245, 25246..25290, 25291..25335, 25336..25380, 25381..25425, 25426..25470, 25471..25515, 25516..25560, 25561..25605, 25606..25650, 25651..25695, 25696..25740, 25741..25785, 25786..25830, 25831..25875, 25876..25920, 25921..25965, 25966..26010, 26011..26055, 26056..26100, 26101..26145, 26146..26190, 26191..26235, 26236..26280, 26281..26325, 26326..26370, 26371..26415, 26416..26460, 26461..26505, 26506..26550, 26551..26595, 26596..26640, 26641..26685, 26686..26730, 26731..26775, 26776..26820, 26821..26865, 26866..26910, 26911..26955, 26956..27000, 27001..27045, 27046..27090, 27091..27135, 27136..27180, 27181..27225, 27226..27270, 27271..27315, 27316..27360, 27361..27405, 27406..27450, 27451..27495, 27496..27540, 27541..27585, 27586..27630, 27631..27675, 27676..27720, 27721..27765, 27766..27810, 27811..27855, 27856..27900, 27901..27945, 27946..27990, 27991..28035, 28036..28080, 28081..28125, 28126..28170, 28171..28215, 28216..28260, 28261..28305, 28306..28350, 28351..28395, 28396..28440, 28441..28485, 28486..28530, 28531..28575, 28576..28620, 28621..28665, 28666..28710, 28711..28755, 28756..28800, 28801..28845, 28846..28890, 28891..28935, 28936..28980, 28981..29025, 29026..29070, 29071..29115, 29116..29160, 29161..29205, 29206..29250, 29251..29295, 29296..29340, 29341..29385, 29386..29430, 29431..29475, 29476..29520, 29521..29565, 29566..29610, 29611..29655, 29656..29700, 29701..29745, 29746..29790, 29791..29835, 29836..29880, 29881..29925, 29926..29970, 29971..30015, 30016..30060, 30061..30105, 30106..30150, 30151..30195, 30196..30240, 30241..30285, 30286..30330, 30331..30375, 30376..30420, 30421..30465, 30466..30510, 30511..30555, 30556..30600, 30601..30645, 30646..30690, 30691..30735, 30736..30780, 30781..30825, 30826..30870, 30871..30915, 30916..30960, 30961..31005, 31006..31050, 31051..31095, 31096..31140, 31141..31185, 31186..31230, 31231..31275, 31276..31320, 31321..31365, 31366..31410, 31411..31455, 31456..31500, 31501..31545, 31546..31590, 31591..31635, 31636..31680, 31681..31725, 31726..31770, 31771..31815, 31816..31860, 31861..31905, 31906..31950, 31951..31995, 31996..32040, 32041..32085, 32086..32130, 32131..32175, 32176..32220, 32221..32265, 32266..32310, 32311..32355, 32356..32400, 32401..32445, 32446..32490, 32491..32535, 32536..32580, 32581..32625, 32626..32670, 32671..32715, 32716..32760, 32761..32805, 32806..32850, 32851..32895, 32896..32940, 32941..32985, 32986..33030, 33031..33075, 33076..33120, 33121..33165, 33166..33210, 33211..33255, 33256..33300, 33301..33345, 33346..33390, 33391..33435, 33436..33480, 33481..33525, 33526..33570, 33571..33615, 33616..33660, 33661..33705, 33706..33750, 33751..33795, 33796..33840, 33841..33885, 33886..33930, 33931..33975, 33976..34020, 34021..34065, 34066..34110, 34111..34155, 34156..34200, 34201..34245, 34246..34290, 34291..34335, 34336..34380, 34381..34425, 34426..34470, 34471..34515, 34516..34560, 34561..34605, 34606..34650, 34651..34695, 34696..34740, 34741..34785, 34786..34830, 34831..34875, 34876..34920, 34921..34965, 34966..35010, 35011..35055, 35056..35100, 35101..35145, 35146..35190, 35191..35235, 35236..35280, 35281..35325, 35326..35370, 35371..35415, 35416..35460, 35461..35505, 35506..35550, 35551..35595, 35596..35640, 35641..35685, 35686..35730, 35731..35775, 35776..35820, 35821..35865, 35866..35910, 35911..35955, 35956..36000, 36001..36045, 36046..36090, 36091..36135, 36136..36180, 36181..36225, 36226..36270, 36271..36315, 36316..36360, 36361..36405, 36406..36450, 36451..36495, 36496..36540, 36541..36585, 36586..36630, 36631..36675, 36676..36720, 36721..36765, 36766..36810, 36811..36855, 36856..36900, 36901..36945, 36946..36990, 36991..37035, 37036..37080, 37081..37125, 37126..37170, 37171..37215, 37216..37260, 37261..37305
Chapter 8: Rational Expressions
8.8 Rate Word Problems: Speed, Distance and Time
Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance.
[latex]rcdot t=d[/latex]
For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.
The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:
| Who or What | Rate | Time | Distance |
|---|---|---|---|
The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.
Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Natasha | [latex]r[/latex] | [latex]text{3 h}[/latex] | [latex]text{3 h}(r)[/latex] |
| Joey | [latex]r + 2[/latex] | [latex]text{3 h}[/latex] | [latex]text{3 h}(r + 2)[/latex] |
The distance travelled by both is 30 km. Therefore, the equation to be solved is:
[latex]begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \ 3r&+&3r&+&6&=&30 \ &&&-&6&&-6 \ hline &&&&dfrac{6r}{6}&=&dfrac{24}{6} \ \ &&&&r&=&4 text{ km/h} end{array}[/latex]
This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.
Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Downstream | [latex]text{12 km/h}[/latex] | [latex]t[/latex] | [latex]text{12 km/h } (t)[/latex] |
| Upstream | [latex]text{4 km/h}[/latex] | [latex](1 — t)[/latex] | [latex]text{4 km/h } (1 — t)[/latex] |
The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:
[latex]begin{array}{rrlll} 12(t)&=&4(1&-&t) \ 12t&=&4&-&4t \ +4t&&&+&4t \ hline dfrac{16t}{16}&=&dfrac{4}{16}&& \ \ t&=&0.25&& end{array}[/latex]
This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.
Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Terry | [latex]text{20 km/h}[/latex] | [latex]t[/latex] | [latex]text{20 km/h }(t)[/latex] |
| Sally | [latex]text{80 km/h}[/latex] | [latex](t — text{6 h})[/latex] | [latex]text{80 km/h }(t — text {6 h})[/latex] |
The distance travelled by both is the same. Therefore, the equation to be solved is:
[latex]begin{array}{rrrrr} 20(t)&=&80(t&-&6) \ 20t&=&80t&-&480 \ -80t&&-80t&& \ hline dfrac{-60t}{-60}&=&dfrac{-480}{-60}&& \ \ t&=&8&& end{array}[/latex]
This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.
On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?
| Who or What | Rate | Time | Distance |
|---|---|---|---|
| Fifty-five | [latex]text{55 km/h}[/latex] | [latex]t[/latex] | [latex]text{55 km/h }(t)[/latex] |
| Forty | [latex]text{40 km/h}[/latex] | [latex](text{2.5 h}-t)[/latex] | [latex]text{40 km/h }(text{2.5 h}-t)[/latex] |
The distance travelled by both is 30 km. Therefore, the equation to be solved is:
[latex]begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \ 55t&+&100&-&40t&=&130 \ &-&100&&&&-100 \ hline &&&&dfrac{15t}{15}&=&dfrac{30}{15} \ \ &&&&t&=&2 end{array}[/latex]
This means that the time spent travelling at 40 km/h was 0.5 h.
Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.
Questions
For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.
- A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
- Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
- Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
- Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
- A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
- Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
- A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
- A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?
Solve Questions 9 to 22.
- A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
- A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
- A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
- As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
- Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
- A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
- A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
- A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
- Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
- Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
- Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
- Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
- On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
- Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.
Answer Key 8.8



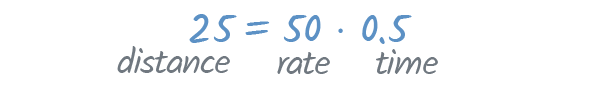
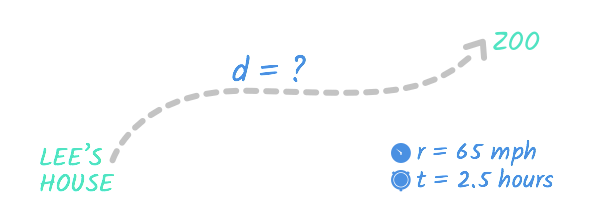
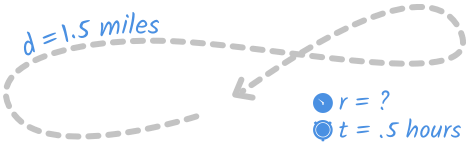

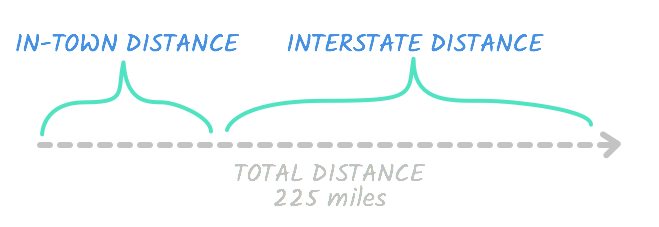

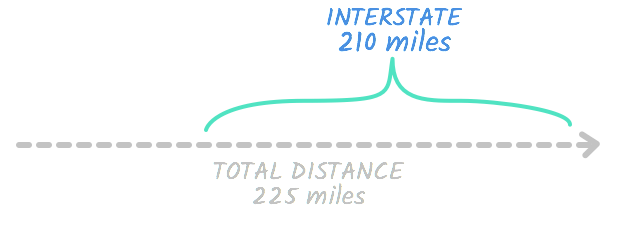

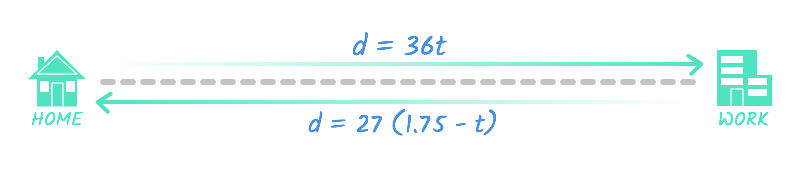

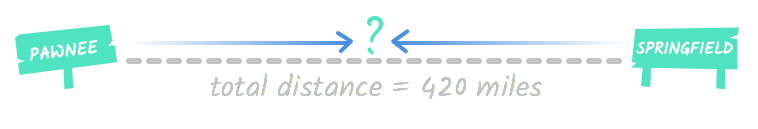



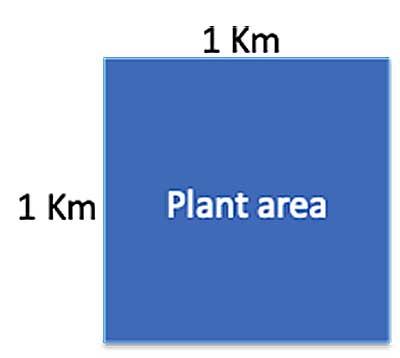
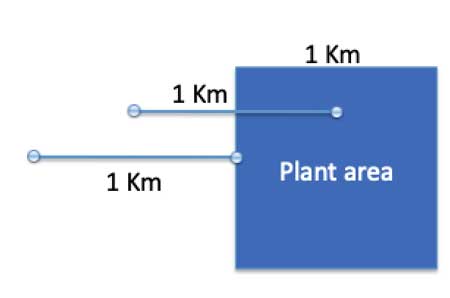
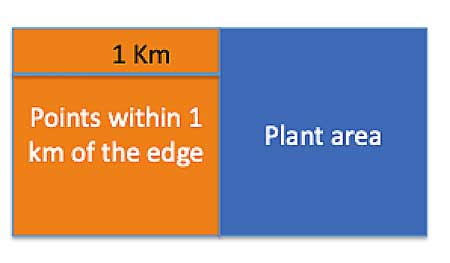
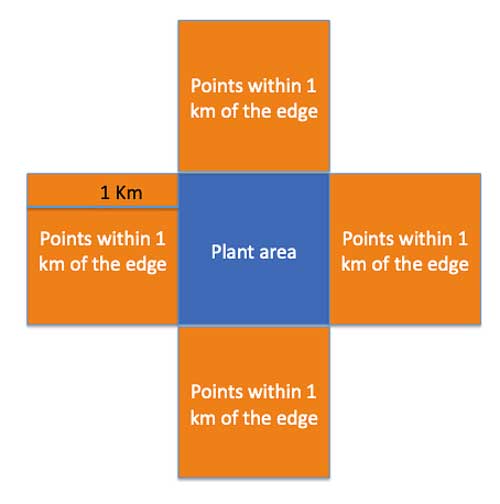
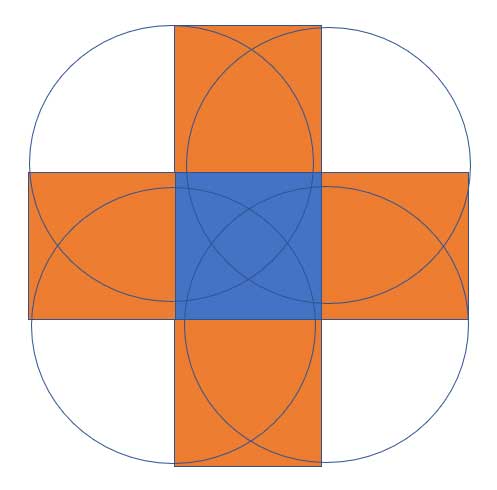


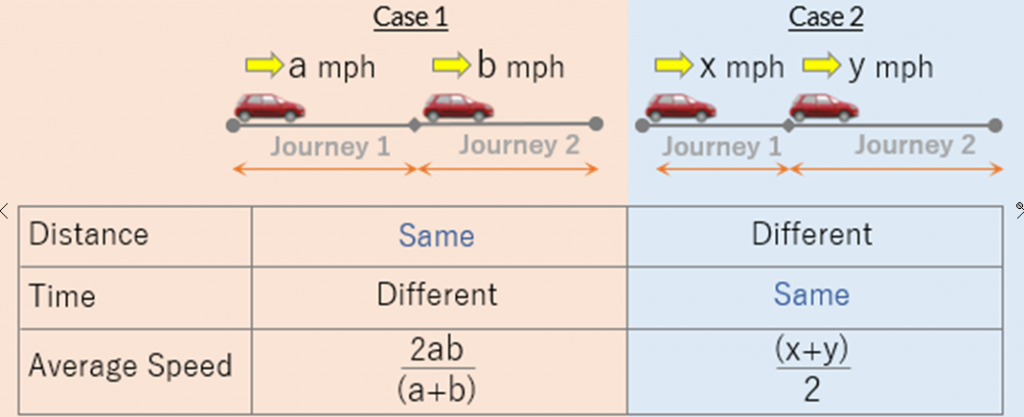
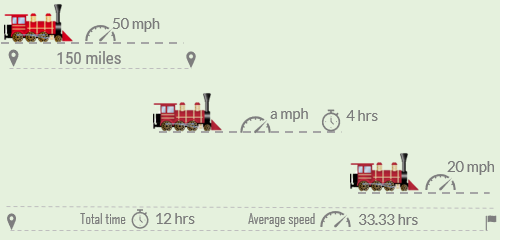






 (begin{array}{c}L=M+frac{1}{6};,,,,,5L=15M\5left( {M+frac{1}{6}} right)=15M;,,,M+frac{1}{6}=3M,,\6M+1=18M;,,,12M=1;,,M,,=frac{1}{{12}},,text{hr}text{.}\D=15left( {frac{1}{{12}}} right)=1.25,,text{miles}end{array})
(begin{array}{c}L=M+frac{1}{6};,,,,,5L=15M\5left( {M+frac{1}{6}} right)=15M;,,,M+frac{1}{6}=3M,,\6M+1=18M;,,,12M=1;,,M,,=frac{1}{{12}},,text{hr}text{.}\D=15left( {frac{1}{{12}}} right)=1.25,,text{miles}end{array})