How To Solve Age Word Problems?
If the problem involves a single person, then it is similar to an Integer Problem. Read the problem
carefully to determine the relationship between the numbers. This is shown in the examples involving a single person.
If the age problem involves the ages of two or more people then using a table would be a good idea.
A table will help you to organize the information and to write the equations. This is shown in the
examples involving more than one person.
How To Solve Age Problems Involving A Single Person?
Example:
Five years ago, John’s age was half of the age he will be in 8 years. How old is he now?
Solution:
Step 1: Let x be John’s age now. Look at the question and
put the relevant expressions above it.
Step 2: Write out the equation.
Isolate variable x
Answer: John is now 18 years old.
How To Use Algebra To Solve Age Problems?
Examples:
- Ten years from now, Orlando will be three times older than he is today. What is his current age?
- In 20 years, Kayleen will be four times older than she is today. What is her current age?
- Show Video Lesson
How To Solve Age Problems Involving More Than One Person?
Example:
John is twice as old as his friend Peter. Peter is 5 years older than Alice. In 5 years, John will be
three times as old as Alice. How old is Peter now?
Solution:
Step 1: Set up a table.
| age now | age in 5 yrs | |
|---|---|---|
| John | ||
| Peter | ||
| Alice |
Step 2: Fill in the table with information given in the question.
John is twice as old as his friend Peter. Peter is
5 years older than Alice. In 5 years, John will be three times
as old as Alice. How old is Peter now?
Let x be Peter’s age now. Add 5 to get the ages in 5 yrs.
| age now | age in 5 yrs | |
|---|---|---|
| John | 2x | 2x + 5 |
| Peter | x | x + 5 |
| Alice | x – 5 | x – 5 + 5 |
Write the new relationship in an equation using the ages in 5 yrs.
In 5 years, John will be three times as old as Alice.
2x + 5 = 3(x – 5 + 5)
2x + 5 = 3x
Isolate variable x
x = 5
Answer: Peter is now 5 years old.
Example:
John’s father is 5 times older than John and John is twice as old as his sister Alice. In two
years time, the sum of their ages will be 58. How old is John now?
Solution:
Step 1: Set up a table.
| age now | age in 2 yrs | |
|---|---|---|
| John’s father | ||
| John | ||
| Alice |
Step 2: Fill in the table with information given in the question.
John’s father is 5 times older than John and John is twice as old as his sister Alice.
In two years time, the sum of their ages will be 58. How old is John now?
Let x be John’s age now. Add 2 to get the ages in 2 yrs.
| age now | age in 2 yrs | |
|---|---|---|
| John’s father | 5x | 5x + 2 |
| John | x | x + 2 |
| Alice |
Write the new relationship in an equation using the ages in 2 yrs.
In two years time, the sum of their ages will be 58.
Answer: John is now 8 years old.
How To Solve Word Problems With Multiple Ages?
Example:
Ben is eight years older than Sarah. 10 years ago, Ben was twice as old as Sarah. Currently, how old is
Ben and Sarah?
-
Show Video Lesson
Algebra Word Problems With Multiple Ages
Example:
Mary is three times as old as her son. In 12 years, Mary’s age will be one year less than twice her
son’s age. How old is each now?
- Show Video Lesson
Algebra Word Problem With Past And Present Ages
Example:
Arun is 4 times as old as Anusha is today. Sixty years ago, Arun was 6 times as old as Anusha.
How old are they today?
- Show Video Lesson
Algebra Age Word Problem With Past, Present, And Future Ages
How to organize the data using a table and solve using a system of linear equations?
Examples:
- Sally is 3 times as old as John. 8 years from now, Sally will be twice as old as John. How old is
John? - Kim is 6 years more than twice Timothy’s age. 2 years ago, Kim was three times as old as Timothy.
How old was Kim 2 years ago? - Leah is 2 less than 3 times Rachel’s age. 3 years from now, Leah will be 7 more than twice Rachel’s
age. How old will Rachel be in 3 years from now? - Becca is twice as old as Susan and Greg is 9 years older than Susan. 3 years ago, Becca was 9 less
than 3 times Susan’s age. How old is Greg now? - Lauren is 3 less than twice Andrew’s age. 4 years from now, Sam will be 2 more than twice Andrew’s
age. 5 years ago, Sam was three times Andrew’s age. How old was Lauren 5 years ago? - Gabby is 1 year more than twice Larry’s age. 3 years from now, Megan will be 27 less than twice
Gabby’s age. 4 years ago, Megan was 1 year less than 3 times Larry’s age.
How old will Megan be 3 years from now?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Every now and then, we encounter word problems that require us to find the relationship between the ages of different people. Age word problems typically involve comparing two people’s ages at different points in time, i.e. at present, in the past, or in the future.
This lesson is divided into two parts. Part I involves age word problems that can be solved using a single variable while Part II contains age word problems that need to be solved using two variables.
Let’s get familiar with age word problems by working through some examples.
PART I: Age Word Problems Solvable with One Variable
Example 1: Tanya is 28 years older than Marcus. In 6 years, Tanya will be three times as old as Marcus. How old is Tanya now?
In this problem, we are only asked to find Tanya’s current age. However, the problem also gave us a lot of other information which can be overwhelming. To help us organize the important details, let’s create a table to list what we know so far.
Since we are only given details about their current ages and what they will be 6 years from now, we’ll go ahead and gray out the Past column.
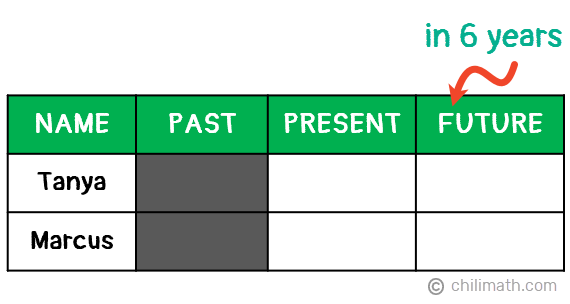
You may notice that Tanya’s current age is defined using the age of Marcus. However, Marcus’s present age is currently unknown. So let’s express Marcus’s age using the variable x. Since Tanya is 28 years older than Marcus, then Tanya’s present age must be x+28.

Next, let’s fill in the Future column which will consist of their ages in 6 years. All we have to do is add 6 to Tanya and Marcus’s present or current ages. Therefore, we have:
- Tanya: left( {x + 28} right) {color{red}+ 6} = x + 34
- Marcus: x {color{red}+ 6}

Now that our table is filled out, we can go ahead and create our equation based on the information provided. The problem states the following:
In 6 years, Tanya will be three times as old as Marcus.
Here we are trying to find the relationship between their ages in the future. We can simply say that,
Tanya’s age in 6 years = 3(Marcus’s age in 6 years)
With that in mind, we can easily construct our equation.
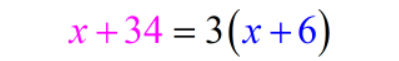
Our next step now is to solve for x. But before that, remember that our problem is asking us to find Tanya’s current age. Since Tanya’s age is defined using Marcus’s current age (which is x), we have to find his age first in order to determine what Tanya’s present age is.
Solution:
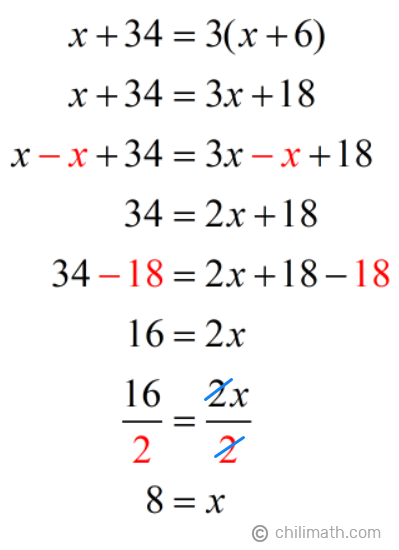
Now that we have the value for x, let’s find out what Tanya and Marcus’s current ages are. We can do this by simply replacing the x‘s with 8.
CURRENT AGES (present)
- Marcus: x = {textbf{8}} years old
- Tanya: x + 28 = {color{red}8} + 28 = {textbf{36}} years old
Going back to the problem’s question, how old is Tanya now?
Answer: Tanya is 36 years old.
Answer Check:
At this point, we are confident that our answer is correct. But, how can we be 100% sure? Well, it’s always a good idea especially in math, to check our answers so we’re certain that we got the correct values.
For this problem, we can simply verify if our answer makes our future statement true. Do you remember this statement?
In 6 years, Tanya will be three times as old as Marcus.
We know the present ages of Marcus and Tanya which are 8 and 36, respectively. Hence in 6 years, Marcus will be 14 years old while Tanya will be 42 years old.
So, will Tanya be three times as old as Marcus in 6 years? The answer is Yes.

Example 2: Bruce is 4 years younger than Hector. Twenty years ago, Hector’s age was 13 years more than half the age of Bruce. How old are they now?
By just reading the problem, we can already tell that there is a great deal of information that we have to sort through and that this problem includes a fraction. Most students easily get lost in all the given information, let alone solving equations that involve fractions. But, don’t fret! As long as you stick with the basic principles and steps on how to solve age word problems, you’ll be fine.
Right now, we don’t know Bruce or Hector’s current age. But since Bruce’s age is expressed in relation to Hector’s age, then our unknown variable will be based on Hector’s age. In other words,
- Let {textbf{textit{h}}} = Hector’s age
- {textbf{textit{h} — 4}} = Bruce’s age, since he is 4 years younger than Hector
Let’s organize all these important data into a table. We’re only given details about their present and past (20 years ago) ages so we’ll gray out the Future column.
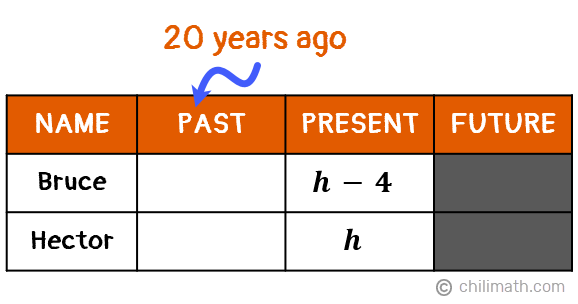
Twenty years ago, both Bruce and Hector were 20 years younger so we’ll subtract 20 from each of their present ages.
- Bruce: left( {h — 4} right) {color{red}- 20} = h — 24
- Hector: h {color{red}- 20}
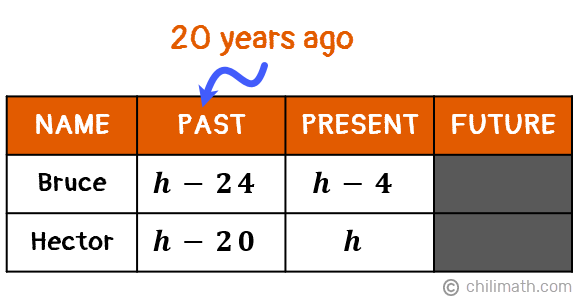
Our table is now ready so we can proceed to create our equation. As you can see under the Past column, we were able to create algebraic expressions for Bruce and Hector’s ages 20 years ago. But our problem also told us that,
Twenty years ago, Hector’s age was 13 years more than half the age of Bruce.
Since Hector’s age 20 years ago is also 13 years more than half of Bruce’s age, we can take these two algebraic expressions and set them equal to each other, to create an equation.
Hector’s age 20 years ago = Large{1 over 2}(Bruce’s age 20 years ago)+ 13
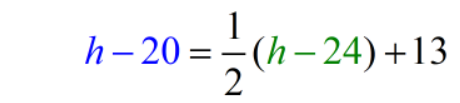
We’re now ready to solve for the unknown variable, h.
Solution:
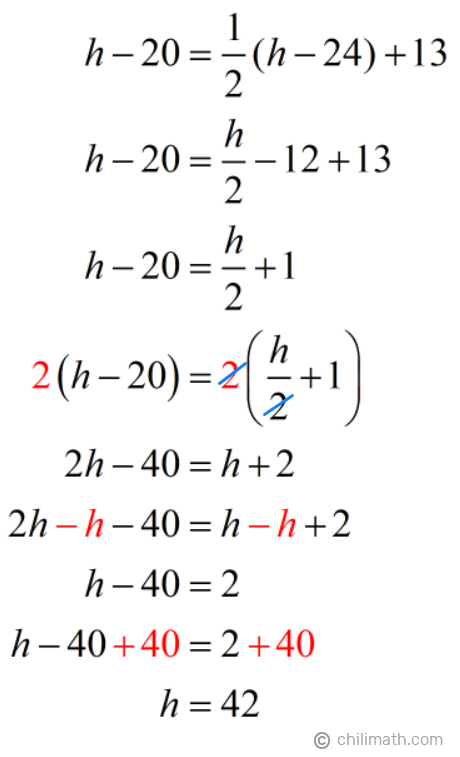
Therefore, Hector’s present age is {textbf{42}} years old.
On the other hand, you may recall that Bruce’s current age is: h — 4. Since h = 42, then Bruce’s current age is 42 — 4 = {textbf{38}}.
So, how old are they now?
Answer: Hector is 42 years old and Bruce is 38 years old.
The final step is to check our answers by substituting the unknown values into our original equation to verify if each side of the equation equals the other.
Answer Check:
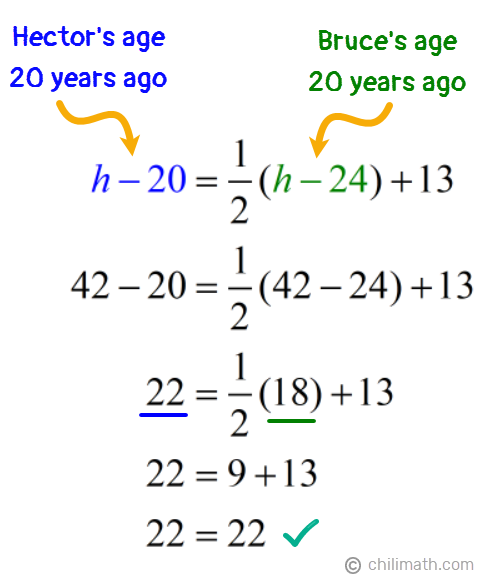
Great! Our answer checks. This just showed us that if we take Bruce’s age twenty years ago, which is 18, and divide it in half, we get 9. Adding 13 to that (9 + 13), we get 22 which was Hector’s age twenty years ago.
Therefore, we are able to confirm that twenty years ago when Hector was 22 years old and Bruce was 18 years old, Hector’s age was 13 years more than half the age of Bruce.
Example 3: Stella is 13 years younger than Kwame. Nine years from now, the sum of their ages will be 43. Find the present age of each.
This problem is a little different from our previous two examples as we are given the sum of their ages in 9 years. But right off the bat, we can see that Stella’s age is defined in terms of Kwame’s age. Therefore, we’ll select a variable to represent Kwame’s current age. In this instance, let’s use “k“.
- Let {textbf{textit{k}}} = Kwame’s age
- {textbf{textit{k} — 13}} = Stella’s age, since she is 13 years younger than Kwame

Nine years from now, both Kwame and Stella will be 9 years older. So we’ll simply add 9 to their present ages above to show their future ages.
- Kwame: k {color{red}+ 9}
- Stella: left( {k — 13} right) {color{red}+ 9} = k — 4
Let’s complete our table.

Now that we have the algebraic expressions for both their ages in 9 years, we can add these expressions to create our equation. We were given the following details:
Nine years from now, the sum of their ages will be 43.
Solution:
So we have,
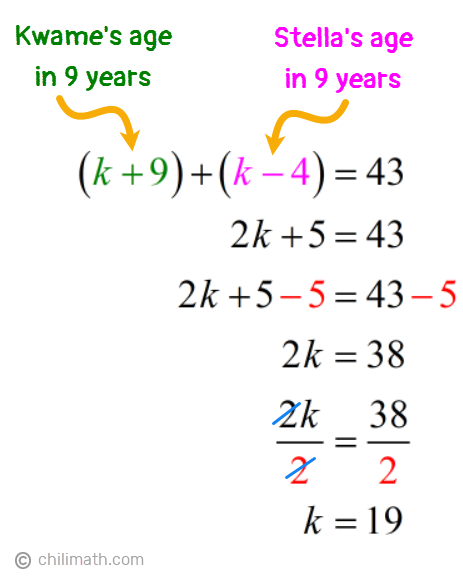
Checking back at our table, k stands for Kwame’s age. But since our problem asked us to find the current ages for both, let’s do a little bit more solving.
CURRENT AGES (present)
- Kwame: k = {textbf{19}} years old
- Stella: k — 13 = {color{red}19} — 13 = {textbf{6}} years old
Answer: Kwame is 19 years old and Stella is 6 years old.
Answer Check:
Let’s now verify if indeed the sum of Kwame and Stella’s ages in 9 years will be 43.
- Kwame’s age in 9 years: k + 9 = {color{red}19} + 9 = {textbf{28}}
- Stella’s age in 9 years: k — 4 = {color{red}19} — 4 = {textbf{15}}
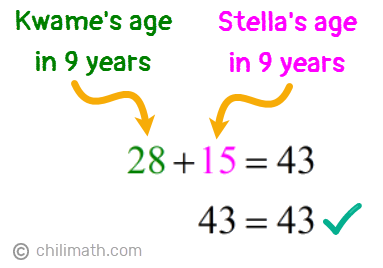
Perfect! The total of their ages nine years from now is 43 so our answers are correct.
Example 4: Mr. Cook is 34 years old. His son is 22 years younger than him. In how many years will Mr. Cook’s age be 24 years less than three times as old as his son?
We already know their current ages, so before we delve any further, let’s start filling in our table.
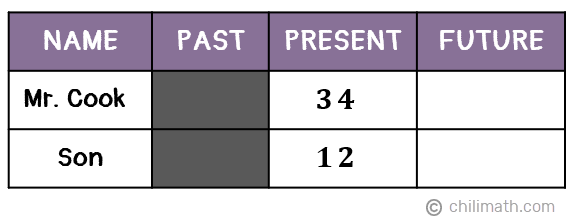
Note that since the son is 22 years younger than Mr. Cook, we subtracted 22 from 34 to get his son’s current age, 34 — {color{red}22} = 12.
This problem is unique because it’s not asking us for their ages at a certain point in time like usual. Instead, it asks us to find out the number of years when Mr. Cook’s age will meet a certain relationship with his son’s age in the future.
But at this point, we don’t know how long it will take for Mr. Cook to be 24 years less than three times as old as his son. So, let’s assign the unknown variable “x” to stand for the number of years then add x to both of their current ages to create algebraic expressions that will represent how old they will be after x years.
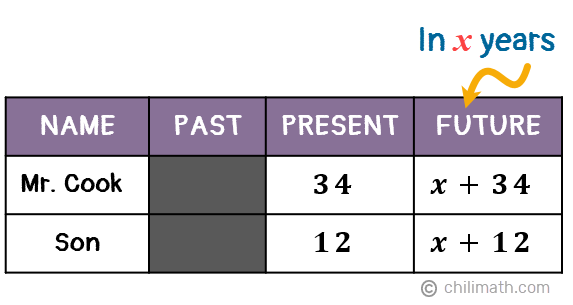
Since Mr. Cook’s age after x number of years (x + 34) will also be 24 years less than three times as old as his son, we can set these two algebraic expressions equal to each other, thus creating our equation.
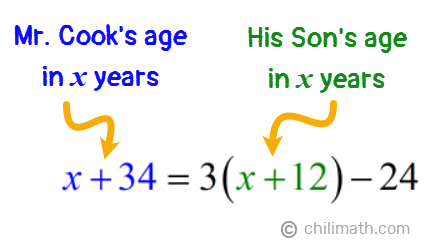
Now that we have our equation, let’s solve for x.
Solution:
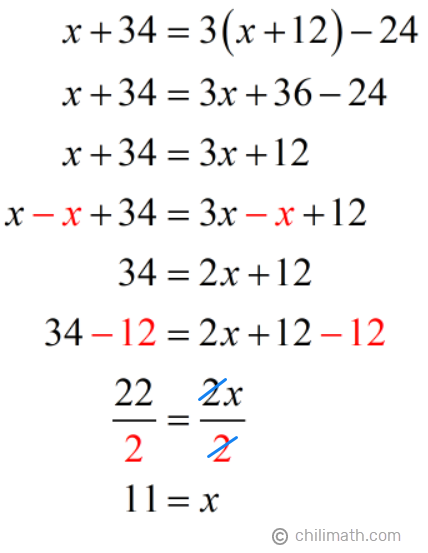
As you may recall, x stands for the number of years from now that will take for Mr. Cook to be 24 years less than three times as old as his son. Therefore,
Answer: In 11 years, Mr. Cook’s age will be 24 years less than three times as old as his son.
Answer Check:
To check if our answer is correct, we must first find out how old will Mr. Cook and his son be in 11 years. Substituting the value of x which is 11 into our algebraic expressions, we get:
- Mr. Cooks’s age in 11 years: x + 34 = {color{red}11} + 34 = {textbf{45}}
- Son’s age in 11 years: x + 12 = {color{red}11} + 12 = {textbf{23}}
So in 11 years, Mr. Cook will be 45 years old while his son will be 23 years old.
This time, I’ll leave it up to you to verify if indeed during that time, his age of 45 years old will be 24 years less than three times as old as his son. If it meets the condition, then our answer is correct.
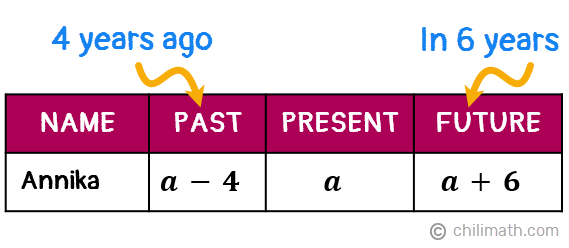
Example 5: The sum of one-fifth of Annika’s age four years ago and half of her age in six years is 33. How old is she now?
Compared to our previous exercises, this problem only involves one person. Also, instead of comparing the ages of two people at a certain point in time, we will be comparing Annika’s ages at different points in time, i.e. 4 years ago and in 6 years.
We don’t know Annika’s current age so let’s select the variable {textbf{textit{a}}} to represent this unknown value. We’ll use this variable as well to create algebraic expressions that will stand for her past and future ages.
- Let {textbf{textit{a}}} = Annika’s current age
- {textbf{textit{a} — 4}} = Annika’s age 4 years ago
- {textbf{textit{a} + 6}} = Annika’s age 6 years from now
Our problem also told us that if we add Large{1 over 5} of Annika’s age 4 years ago and Large{1 over 2} of her age 6 years from now, the sum is 33.
With this information, it’s easy for us to write our equation.

Our next step is to solve for the unknown variable, a.
Solution:
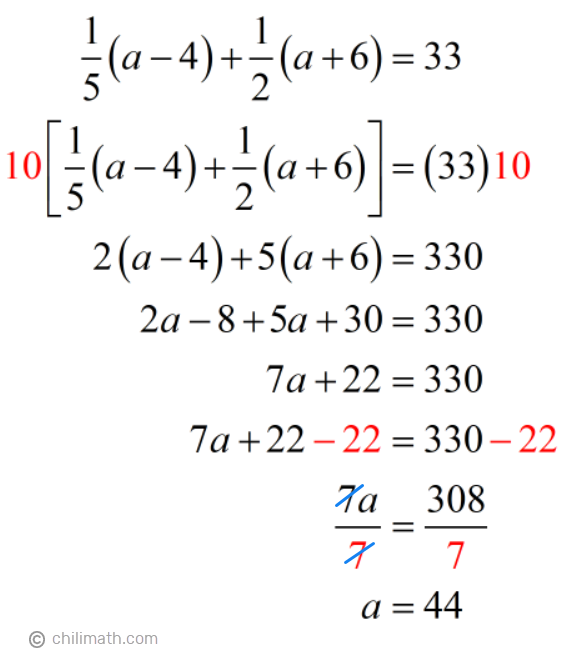
So, how old is Annika now?
Answer: Annika is currently 44 years old.
Answer Check:
As I mentioned before, it’s always a good practice to verify if you got the correct answer. To start, let’s find out what Annika’s past and future ages are.
- Annika’s age 4 years ago: a — 4 = {color{red}44} — 4 = {textbf{40}}
- Annika’s age 6 years from now: a + 6 = {color{red}44} + 6 = {textbf{50}}
Now that we know how old she was 4 years ago and how old she’ll be in 6 years, we’ll plug in these values into our original equation to see if both sides of the equation equal each other.
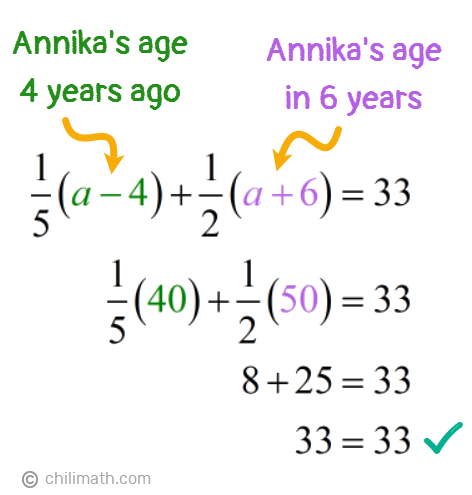
And they did! We were able to prove that the sum of Large{1 over 5} of Annika’s age 4 years ago and Large{1 over 2} of her age 6 years from now is indeed 33.
PART II: Age Word Problems Solvable with Two Variables
Example 6: The sum of Aaliyah and Harald’s ages is 28. Four years from now, Aaliyah will be three times as old as Harald. Find their present ages.
Neither Aaliyah nor Harald’s age is expressed in terms of the other. So for this problem, we will be using more than one variable to represent the unknown values. To start,
- Let {textbf{textit{a}}} be Aaliyah’s age
- Let {textbf{textit{h}}} be Harald’s age
Since they will be 4 years older in the next 4 years, we simply have to add 4 to their current ages to represent their future ages.
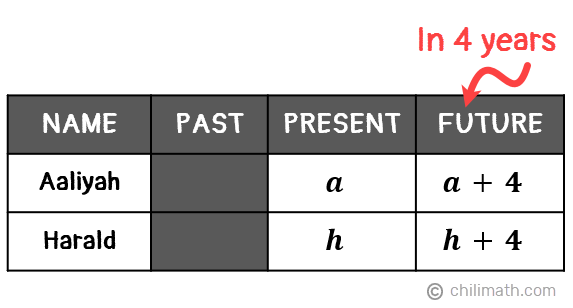
Looking back at our problem, there are two significant statements that can help us find our answers.
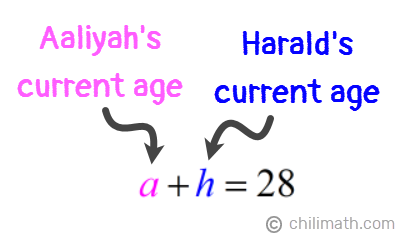
1) The sum of Aaliyah and Harald’s ages is 28.
From this statement, we can create the equation below:
2) Four years from now, Aaliyah will be three times as old as Harald.
Meanwhile, the statement above can be translated into the following equation:
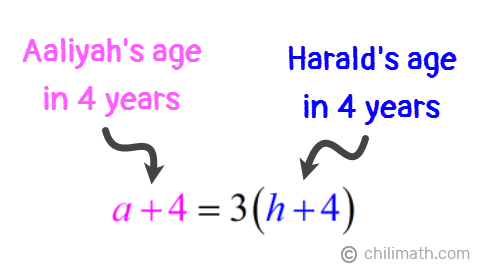
We now have two equations to solve.
- Equation 1: a + h = 28
- Equation 2: a + 4 = 3(h + 4)
First, we’ll use equation 1 to solve for a.
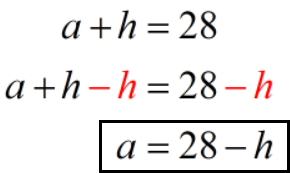
Next, we’ll replace a with 28 — h in equation 2.
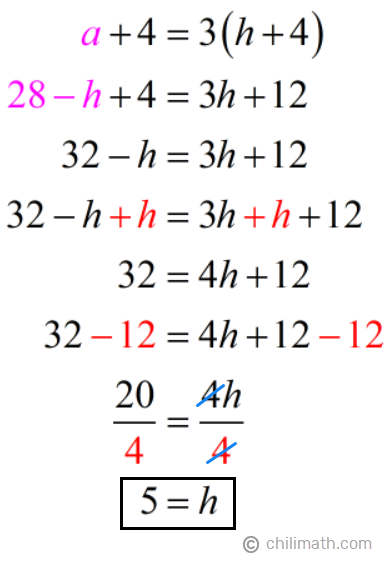
Perfect! We are able to find the values for both our unknown variables, a and h, which also stand for the present ages for Aaliyah and Harald. So we have,
- Aaliyah’s present age: a = 28 — h = 28 — {color{red}5} = {textbf{23}}
- Harald’s present age: h = {textbf{5}}
Answer: Currently, Aaliyah is 23 years old while Harald is 5 years old.
Answer Check:
I’ll leave it up to you to check if our answers are correct. But as you can see, even with just using mental computation, we can already tell that the sum of Aaliyah and Harald’s ages is 28 (23 + 5 = 28) which makes our first statement true. You may further check our answers by plugging in the values of a and h into equation 2 to verify if the left side of the equation equals the right, thus making our second statement true as well.
Example 7: The sum of the ages of Jaya and Nadia is three times Nadia’s age. Seven years ago, Jaya was three less than four times as old as Nadia. How old are they now?
This problem is similar to our previous example. However, for this one, we are not given the exact number for the sum. We first have to find out each of their current ages so we can determine what the sum is.
- Let {textbf{textit{y}}} be Jaya’s age
- Let {textbf{textit{n}}} be Nadia’s age
We then need to subtract 7 from their current ages to represent how old they were seven years ago.
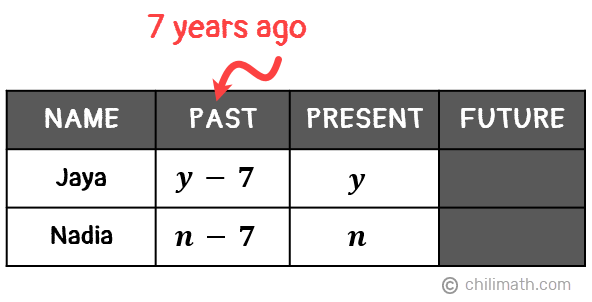
Now that we’ve organized our data, let’s go through the significant statements given in our problem and translate each into an equation.
1) The sum of the ages of Jaya and Nadia is three times Nadia’s age.
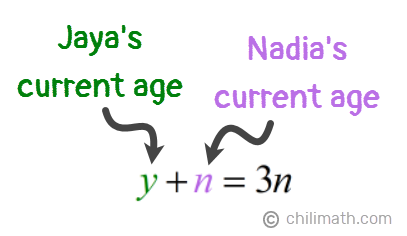
2) Seven years ago, Jaya was three less than four times as old as Nadia.
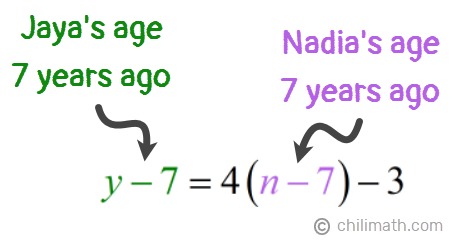
Therefore, our two equations are:
- Equation 1: y + n = 3n
- Equation 2: y — 7 = 4(n — 7) — 3
Let’s first focus on equation 1 and solve for y.
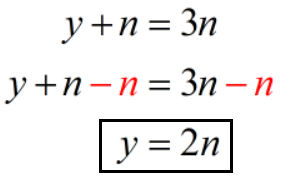
Now we’ll solve for n using the value of y from equation 1. We’ll do this by replacing y with 2n in equation 2.
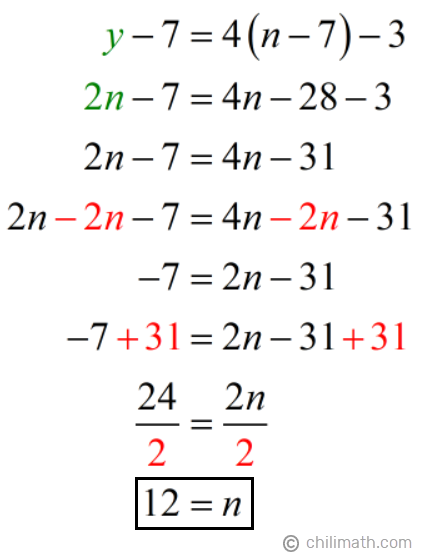
Taking the values of y and n, we have:
- Jaya’s present age: y = 2n = 2({color{red}12}) = {textbf{24}}
- Nadia’s present age: n = {textbf{12}}
So, going back to our problem. How old are they now?
Answer: Jaya is 24 years old and Nadia is 12 years old.
Answer Check:
To check our answers, we’ll replace the values of y and n in equation 1 and equation 2. Again, I’ll leave it up to you to solve both equations and verify if each side of the equation equals the other. Once you’re done with your solutions, you’ll see that we are able to prove that both statements from our problem are true.
Example 8: The difference between the ages of Penelope and her son, Zack, is 34. In six years, Penelope will be four times as old as Zack’s age two years ago. How old are they now?
It’s easy to get lost in all the information given so we’ll focus first on assigning variables that will stand for the unknown values.
- Let {textbf{textit{p}}} be Penelope’s current age
- Let {textbf{textit{z}}} be Zack’s current age
One thing that’s unique about this problem is that it involves three different points in time. We are given not only the relationship between Penelope and her son’s age in the present time but also how their ages in 6 years are related to their ages two years ago.
To show this, we’ll subtract 2 from their ages now for their ages 2 years ago then add 6 to their current ages for their ages 6 years later.
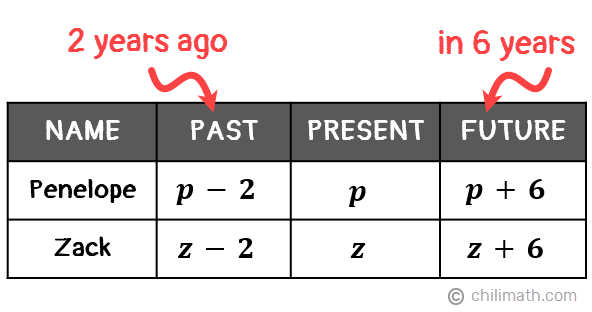
Great! We now have variables and algebraic expressions to represent Penelope and Zack’s current ages as well as their ages in the past and in the future. Moving forward, let’s go through the important details given in the problem and create an equation from each statement.
1) The difference between the ages of Penelope and her son, Zack, is 34.
Remember that Penelope is Zack’s mother so she’s definitely older than him. Therefore, we are subtracting Zack’s age from Penelope’s age to find the difference.

2) In six years, Penelope will be four times as old as Zack’s age two years ago.
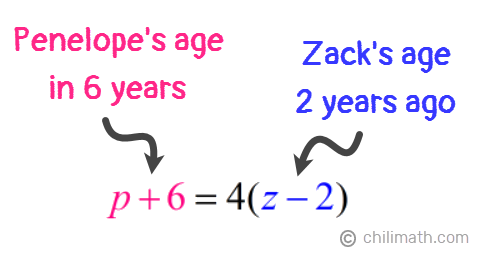
Here are our two equations:
- Equation 1: p — z = 34
- Equation 2: p + 6 = 4(z — 2)
Let’s now work on equation 1 to solve for p.
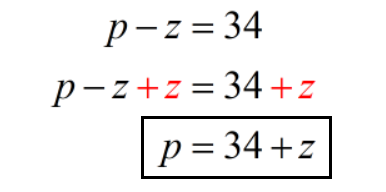
Next, we’ll replace p with 34 + z in equation 2 then solve for z.
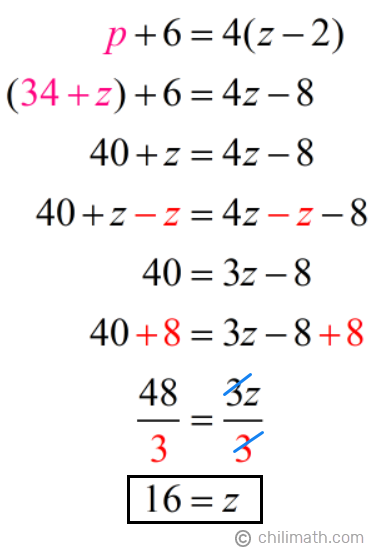
So we have,
- Penelope’s current age: p = 34 + z = 34 + ({color{red}16}) = {textbf{50}}
- Zack’s current age: z = {textbf{16}}
How about we replace the unknown values in our table and also find out what their past and future ages are?

Going back to our original question, how old are they now?
Answer: Penelope is currently 50 years old while her son, Zack, is 16 years old.
Age problems collection by Logiclike will help you train logical and algebra skills. In these
word
problems, you will deal with current, past, and future people’s ages.
How many math problems can you solve using systems of equations? And what about logical thinking
and
thinking outside the box methods?
Ten years from now, Gloria will be three times older than she is today.
What is her current age?
Mila is 5 years older than her brother, but 3 times younger than her
mother.
How old is Mila and how old is her mother, if Mila’s brother is 6 years old?
In 6 years, Bob will be 4 times as old as he is today.
How old is Bob today?
In 8 years, Mary will be 3 times as old as she is today.
How old is Mary today?
Mike is 8 years older than Alexa. 3 years ago, Mike was 5 times as old as
Alexa.
How old is Mike today?

Jennifer is 6 years older than Anna.
3 years ago, Jennifer was 4 times as old as Anna.
How old is Jennifer today?
—>
A mother is 56 years old, and her daughter is 14 years old.
In how many years will the mother be twice her daughter’s age?
How old will the mother be then? How old will your daughter be?
Six years ago, Lenny’s age was half of the age he will be in 8 years.
How old is Lenny now?
Felix is twice as old as his friend Greg.
Greg is 5 years older than Rachel.
In 5 years, Felix will be three times as old as Rachel.
How old is Greg now?
Alexa is 1 year more than twice Stella’s age.
3 years from now, Nora will be 27 less than twice Alexa’s age.
4 years ago, Nora was 1 year less than 3 times Stella’s age.
How old will Nora be 3 years from now?
Get involved with LogicLike online!
More than 550,000 parents from all over the
world are already improving thinking skills with their children.

Problem 1 :
Martin
is four times as old as his brother Luther at present. After 10 years
he will be twice the age of his brother. Find their present ages.
Solution :
Let ‘x’ and ‘y’ be the present ages of Martin and Luther respectively.
Given : Martin is four times as old as his brother Luther at present.
Then,
x = 4y —-(1)
Given : After 10 years, Martin will be twice the age of his brother Luther.
Then,
x + 10 = 2(y + 10)
x + 10 = 2y + 20
Subtract 10 from each side.
x = 2y + 10 —-(2)
From (1) and (2),
4y = 2y + 10
Subtract 2y from each side.
2y = 10
Divide each side by 2.
y = 5
Substitute 5 for y in (1).
(1)—-> x = 4(5)
x = 20
So, the present ages of martin and Luther are 20 years and 5 years respectively.
Problem 2 :
A
father is 30 years older than his son,and one year ago he was four
times as old as his son. Find the present ages of his father and his
son.
Solution :
Let ‘x’ and ‘y’ be the present ages of father and son respectively.
Given : A father is 30 years older than his son
Then,
x = y + 30 —-(1)
Given : One year ago, father was four times as old as his son.
Then,
x — 1 = 4(y — 1)
x — 1 = 4y — 4
Add 1 to each side.
x = 4y — 3 —-(2)
From (1) and (2),
y + 30 = 4y — 3
Subtract y from each side.
30 = 3y — 3
Add 3 to each side.
33 = 3y
Divide each side by 3.
11 = y
Substitute 5 for y in (1).
(1)—-> x = 11 + 30
x = 41
So, the present ages of father and son are 41 years and 11 years respectively.
Problem 3 :
The
ages of Abraham and Adam are in the ratio 5 : 7. Four years from now, the ratio of their ages will be 3 : 4. Find the present ages of them.
Solution :
Given : The ages of Abraham and Adam are in the ratio
5 : 7
Then,
age of Abraham = 5x
age of Adam = 7x
Four years from now,
age of Abraham = 5x + 4
age of Adam = 7x + 4
Given : Four years from now, the ratio of their ages will be
3 : 4
Then,
(5x + 4) : (7x + 4) = 3 : 4
(5x+4) / (7x+4) = 3 / 4
4(5x + 4) = 3(7x + 4)
20x + 16 = 21x + 12
Subtract 20x from each side.
16 = x + 12
Subtract 12 from each side.
4 = x
Then
5x = 5(4) = 20
7x = 7(4) = 28
So, the present ages of Abraham and Adam are 20 years and 28 years.
Problem 4 :
Airi’s
mother is four times as old as Airi. After five years her mother will
be three times as old as she will be then. Find their present ages.
Solution :
Let ‘x’ and ‘y’ be the present ages of Mother and Airi respectively.
Given : Airi’s mother is four times a old as Airi.
Then,
x = 4y —-(1)
Given : After five years Airi’s mother will be three times as old as Airi will be then.
Then,
x + 5 = 3(y + 5)
x + 5 = 3y + 15
Subtract 5 from each side.
x = 3y + 10 —-(2)
From (1) and (2),
4y = 3y + 10
Subtract 3y from each side.
y = 10
Substitute 10 for y in (1).
(1)—-> x = 4(10)
x = 40
So, the present ages of Airi’s mother and Airi are 40 years and 10 years respectively.
Problem 5 :
The sum of the present ages of Kiran and Kate is 60 years. If the ratio of their present ages be 7 : 8, find their present age.
Solution :
Let ‘x’ and ‘y’ be the present ages of Kiran and Kate respectively.
Given : The ratio of the present ages of Kiran and Kate is
7 : 8
Then,
present age of Kiran = 7x
present age of Kate = 8x
Given : The sum of the present ages of Kiran and Kate is 60 years.
Then,
7x + 8x = 60
15x = 60
Divide each side by 15.
x = 4
Then,
7x = 7(4) = 28
8x = 8(4) = 32
So, the present ages of Kiran and Kate are 28 years and 32 years respectively.
Problem 6 :
Andrea
is three times as old as her sister Anu. Three years ago, she was two
years less than four times the age of her sister. Find their present
ages.
Solution :
Let ‘x’ and ‘y’ be the present ages of Andrea and Anu respectively.
Given : Andrea is three times as old as her sister Anu.
x = 3y —-(1)
Given : Three years ago, Andrea was two years less than four times the age of her sister Anu.
Then,
x — 3 = 4(y — 3) — 2
x — 3 = 4y — 12 — 2
x — 3 = 4y — 14
Add 3 to each side.
x = 4y — 11 —-(2)
From (1) and (2),
3y = 4y — 11
Subtract 3y from each side.
0 = y — 11
Add 11 to each side.
11 = y
Substitute 11 for y in (1).
(1)—-> x = 3(11)
x = 33
So, the present ages of Andrea and Anu are 33 years and 11 years respectively.
Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
Setting up a system of equations is usually effective when solving age word problems involving the ages of two people. Knowing how to solve systems of equations is necessary to solve these types of problems. Other types of word problems involving systems of equations include mixture problems, money word problems, work word problems and rate word problems.
There are a lot of trick Math word problems out there and one of the types you’re probably going to run into relates to age. You’re going to be given 2 people and you’re going to be asked about their relative ages, and you’re going to be along those same lines thinking about the passage of time. So when you’re doing these problems it’s really important to keep track of their current age versus their age in the future or past depending on the problem.
Another thing to keep in mind is that if you’re adding time like if time’s going by between one equation and the next make sure you’re adding that time to the age of both people. If you only add to one person you’re going to end up with the wrong equations and the wrong answers. So there’s this all passage of time it sounds kind of like metaphysical and these like fancy stuff, that’s why you really have to be careful to show all of your work and then please check your work at the end and make sure you have a solution that makes sense in the real world.
This Lesson (OVERVIEW of lessons on age problems) was created by by ikleyn(48006)

: View Source, Show
About ikleyn:
OVERVIEW of lessons on age problems
My lessons on age word problems in this site are
— Age problems and their solutions
— HOW TO algebraize and to solve age problems?
— A fresh formulation of a traditional age problem
— Intricate age word problems
— Challenging age word problems from the archive
— Age problems for mental solution
— Age problem for three participants
— Some unusual age word problems
— Age problems with a defective sum of ages
— Miscellaneous age problems
— Entertainment age problems
— Age problem for the day of April, 1
List of lessons on age word problems with short annotations
Age problems and their solutions
Problem 1. Kevin is 4 years older than Margaret.
Next year Kevin will be 2 times as old as Margaret. How old is Kevin?
Problem 2. Ann is 2 years older than Betty.
Last year Ann was 2 times as old as Betty. How old is Ann?
Problem 3. Susan is 3 years older than Tom. Two years ago Susan was twice as old as Tom.
Find their present ages.
Problem 4. Jerry is 7 years older than Jennifer. In three years Jerry will be twice as old as Jennifer.
Find their present ages.
Problem 5. A man has a daughter and a son. The son is three years older than the daughter.
In one year the man will be six time as old as the daughter is now.
In ten years the man will be fourteen years older than the combined ages of his children at that time.
What is the man’s present age?
HOW TO algebraize and to solve age problems?
Problem 1. After 32 years from now, a young man will be 5 times as old as he was 8 years ago.
How old is the young man now?
Problem 2. Raymond is 12 years younger than Susan. Four years ago, she was 4 times as old as he was.
Find their present ages.
Problem 3. Eight years ago, Ed was ten times as old as his daughter Faith. In six years, he will be
three times as old as she. What are Ed’s and Faith’s ages now?
Problem 4. The age of the father is twice that of the elder son. Ten years hence the age of the father will be
three times that of younger son. If the difference between of ages of the two sons is 15 years, find the age of the father.
A fresh formulation of a traditional age problem
Problem 1. In a film an actor plays an «uncle», he was being criticized for marrying a woman when he is three times her age.
He then replied: «Oh, but in 20 years time I will only be twice her age.» How old are the «uncle» and the woman?
Intricate age word problems
Problem 1. A mother told her son that the son was already 10 years old when she was at his current age.
Then the mother said to the son, “I will be 88 years old when you are at my age.”
How old was the mother when her child was born?
Problem 2. A father said to his son: When I was your age, you were 2 years old.
His son replies: When I reach your age, you will be 68 years old. What is the father’s present age?
Problem 3. When A was at the age of B now, B was only 5 years old. When B become as old as A is now, A will be 71 years old.
How old are A and B now, respectively?
Problem 4. When the son will be as old as his father, their ages will add up to 126 years.
When the father was as old as the son is today, their ages added up to 38 years. Find their present age.
Problem 5. Ram is twice as old as Shyam was when Ram was as old as Shyam is now.
If the present age of Shyam is 18 years, find the present age of Ram.
Problem 6. John is twice as old as Jane was when he was as old as she is now. The sum of their age is 63. How old is John and Jane ?
Problem 7. Sum of the ages of Sam and his father is 47 years.
When Sam reaches his fathers age, the sum of their ages will be 97 years. How old is Sam?
Problem 8. Matt is half as old as James will be when Matt is twice as old as James is now.
In 5 years, the sum of Matt and James ages will be 100 years. How old are Matt and James now ?
Problem 9. Harry is 3 times as old as Louise was when Harry was as old as Louise is now.
When Louise is as old as Harry is now, they will be 28 together. How old is Harry and Louise now?
Challenging age word problems
Problem 1. Maria’s father is now twice as old as she is. 16 years ago he was four times as old as Maria was at that time. How old is each now?
Problem 2. Ali’s age now is his dad’s when Ali was 5 years old. When his dad reaches 71, Ali will be his dad’s age now.
What is the age for each of them?
Problem 3. Peter is 36 years old. Peter is twice as old as Jun was when Peter was as old as Jun is now. How old is Jun?
Problem 4. One car is seven times as old as the other. It will be 4 times as old 5 years from now.
Find the present age of each car.
Age problems for mental solution
Problem 1. Roni is 30 years old and Grace is 22 years old.
How many years ago was Roni twice as old as Grace?
Problem 2. Kres is 7 years older than Kyle. Fourteen years ago, Kres was twice as old as Kyle.
What are their present ages ?
Problem 3. Ethan is 29 years younger than Sarah. 7 years ago, Sarah’s age was 2 times Ethan’s age. How old is Ethan now?
Problem 4. Ridhima is 5 years younger than Aarav. Four years later Aarav will be twice as old as Ridhima. Find their present ages.
Problem 5. Roel is as old as the combined age of his two brothers Oski and John. But John is two years older than Oski.
The combined age of the three last year was 3/4 of their combined age at present. How old are the brothers now?
Age problem for three participants
Problem 1. Jack’s age plus Marie’s age is 27; Jack’s age plus Fred’s age is 38; Marie’s age plus Fred’s age is 33. How old is Jack?
Some unusual age word problems
Problem 1. Jenny is years old and her daughter Allyson is y years old. If Jenny lives to the age of 13y Allyson will be
years old.
How old is Allyson now?
Problem 2. If you add the square of Tom’s age to the age of Mary, the sum is 62; but if you add the square of Mary’s age
to the age of Tom, the result is 176. What is the difference between in their ages?
Problem 3. Ann, Ben and Cathy have their birthdays today. The sum of their ages is 23.
The product of their ages is 113 more than the product of their ages on their birthday last year.
What is the sum of the squares of their ages?
Problem 4. Bob’s age 4 years ago is numerically the same
as the square root of his age two years from now. Find Bob’s current age.
Problem 5. Five years from now, Jabin’s grandmother will be 3 times as old as Jabin.
The sum of the squares of their ages in 5 years is 8410. What is Jabin’s present age?
Age problems with a defective sum of ages
Problem 1. There are 4 people in Sam’s family. The sum of their ages is 73 . Sam’s father is 3 years older than his mother.
Sam’s sister is 2 years younger than him. But 4 years ago the sum of the ages of everyone in Sam’s family was 58.
How old is each of them now ?
Miscellaneous age problems
Problem 1. Xavier and Yolanda have been married for exactly 40 years. Yolanda is four years older than Xavier.
The sum of their ages is 126. How old was Yolanda when they were married ?
Problem 2. Connie is 15 years younger than Linda. When Connie got married she was two-third Linda’s age.
How old was Connie when she wed?
Problem 3. The present age of a woman is 4 times as her daughter’s age. When the woman was 29 years old, her only son,
who is two years younger than her only daughter, was born. What is the present age of the son?
Problem 4. A motor car is three times as old as its tires were when it was as old as the tires are now.
When its tires are as old as the car is now, the car will be a year older than the tires are now. What are the present ages of car and tires?
Entertainment age problems
Problem 1. How old is Jack’s grandfather? The digits of his age add to 15, his age is an even number, he is younger than 90 years.
Problem 2. Philip is twice as old as Lori. In y years he will be 1.5 times as old as Lori.
Lori’s age at present may be correctly expressed as:
y/4, 2y/3, y, 3y/2, 3y.
Problem 3. The combined age of 3 brothers is 78. The oldest brother is 26. How old is the middle and youngest brother?
Age problem for the day of April, 1
Problem 1. My brother is 3 years elder to me. My father was 28 years of age when my sister was born,
while my mother was 26 years of age when I was born. If my sister was 4 years of age when my brother was born,
what was the age of my father when my brother was born?
Problem 2. Philip is twice as old as Lori. In y years he will be 1.5 times as old as Lori.
Lori’s age at present may be correctly expressed as:
y/4, 2y/3, y, 3y/2, 3y.
Use this file/link ALGEBRA-I — YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
This lesson has been accessed 4059 times.
Chapter 7: Factoring
One application of linear equations is what are termed age problems. When solving age problems, generally the age of two different people (or objects) both now and in the future (or past) are compared. The objective of these problems is usually to find each subject’s current age. Since there can be a lot of information in these problems, a chart can be used to help organize and solve. An example of such a table is below.
| Person or Object | Current Age | Age Change |
|---|---|---|
Joey is 20 years younger than Becky. In two years, Becky will be twice as old as Joey. Fill in the age problem chart, but do not solve.
- The first sentence tells us that Joey is 20 years younger than Becky (this is the current age)
- The second sentence tells us two things:
- The age change for both Joey and Becky is plus two years
- In two years, Becky will be twice the age of Joey in two years
| Person or Object | Current Age | Age Change (+2) |
|---|---|---|
| Joey (J) | B − 20 | B − 20 + 2 B − 18 |
| Becky (B) | B | B = 2 |
Using this last statement gives us the equation to solve:
B + 2 = 2 ( B − 18)
Carmen is 12 years older than David. Five years ago, the sum of their ages was 28. How old are they now?
- The first sentence tells us that Carmen is 12 years older than David (this is the current age)
- The second sentence tells us the age change for both Carmen and David is five years ago (−5)
Filling in the chart gives us:
| Person or Object | Current Age | Age Change (−5) |
|---|---|---|
| Carmen (C) | D + 12 | D + 12 − 5 D + 7 |
| David (D) | D | D − 5 |
The last statement gives us the equation to solve:
Five years ago, the sum of their ages was 28
[latex]begin{array}{rrrrrrrrl} (D&+&7)&+&(D&-&5)&=&28 \ &&&&2D&+&2&=&28 \ &&&&&-&2&&-2 \ hline &&&&&&2D&=&26 \ \ &&&&&&D&=&dfrac{26}{2} = 13 \ end{array}[/latex]
Therefore, Carmen is David’s age (13) + 12 years = 25 years old.
The sum of the ages of Nicole and Kristin is 32. In two years, Nicole will be three times as old as Kristin. How old are they now?
- The first sentence tells us that the sum of the ages of Nicole (N) and Kristin (K) is 32. So N + K = 32, which means that N = 32 − K or
K = 32 − N (we will use these equations to eliminate one variable in our final equation) - The second sentence tells us that the age change for both Nicole and Kristen is in two years (+2)
Filling in the chart gives us:
| Person or Object | Current Age | Age Change (+2) |
|---|---|---|
| Nicole (N) | N | N + 2 |
| Kristin (K) | 32 − N | (32 − N) + 2 34 − N |
The last statement gives us the equation to solve:
In two years, Nicole will be three times as old as Kristin
[latex]begin{array}{rrrrrrr} N&+&2&=&3(34&-&N) \ N&+&2&=&102&-&3N \ +3N&-&2&&-2&+&3N \ hline &&4N&=&100&& \ \ &&N&=&dfrac{100}{4}&=&25 \ end{array}[/latex]
If Nicole is 25 years old, then Kristin is 32 − 25 = 7 years old.
Louise is 26 years old. Her daughter Carmen is 4 years old. In how many years will Louise be double her daughter’s age?
- The first sentence tells us that Louise is 26 years old and her daughter is 4 years old
- The second line tells us that the age change for both Carmen and Louise is to be calculated ([latex]x[/latex])
Filling in the chart gives us:
| Person or Object | Current Age | Age Change |
|---|---|---|
| Louise (L) | [latex]26[/latex] | [latex]26 = x[/latex] |
| Daughter (D) | [latex]4[/latex] | [latex]D = x[/latex] |
The last statement gives us the equation to solve:
In how many years will Louise be double her daughter’s age?
[latex]begin{array}{rrrrrrr} 26&+&x&=&2(4&+&x) \ 26&+&x&=&8&+&2x \ -26&-&2x&&-26&-&2x \ hline &&-x&=&-18&& \ &&x&=&18&& end{array}[/latex]
In 18 years, Louise will be twice the age of her daughter.
Questions
For Questions 1 to 8, write the equation(s) that define the relationship.
- Rick is 10 years older than his brother Jeff. In 4 years, Rick will be twice as old as Jeff.
- A father is 4 times as old as his son. In 20 years, the father will be twice as old as his son.
- Pat is 20 years older than his son James. In two years, Pat will be twice as old as James.
- Diane is 23 years older than her daughter Amy. In 6 years, Diane will be twice as old as Amy.
- Fred is 4 years older than Barney. Five years ago, the sum of their ages was 48.
- John is four times as old as Martha. Five years ago, the sum of their ages was 50.
- Tim is 5 years older than JoAnn. Six years from now, the sum of their ages will be 79.
- Jack is twice as old as Lacy. In three years, the sum of their ages will be 54.
Solve Questions 9 to 20.
- The sum of the ages of John and Mary is 32. Four years ago, John was twice as old as Mary.
- The sum of the ages of a father and son is 56. Four years ago, the father was 3 times as old as the son.
- The sum of the ages of a wood plaque and a bronze plaque is 20 years. Four years ago, the bronze plaque was one-half the age of the wood plaque.
- A man is 36 years old and his daughter is 3. In how many years will the man be 4 times as old as his daughter?
- Bob’s age is twice that of Barry’s. Five years ago, Bob was three times older than Barry. Find the age of both.
- A pitcher is 30 years old, and a vase is 22 years old. How many years ago was the pitcher twice as old as the vase?
- Marge is twice as old as Consuelo. The sum of their ages seven years ago was 13. How old are they now?
- The sum of Jason and Mandy’s ages is 35. Ten years ago, Jason was double Mandy’s age. How old are they now?
- A silver coin is 28 years older than a bronze coin. In 6 years, the silver coin will be twice as old as the bronze coin. Find the present age of each coin.
- The sum of Clyde and Wendy’s ages is 64. In four years, Wendy will be three times as old as Clyde. How old are they now?
- A sofa is 12 years old and a table is 36 years old. In how many years will the table be twice as old as the sofa?
- A father is three times as old as his son, and his daughter is 3 years younger than his son. If the sum of all three ages 3 years ago was 63 years, find the present age of the father.
Answer Key 7.9
How to approach age word problems
Age word problems are like number word problems.
You’ll still need to relate sentences in English to mathematical equations to solve for people’s ages. In this lesson we’ll look at how to do that.
One helpful way to organize these types of problems is by making a table.
Hi! I’m krista.
I create online courses to help you rock your math class. Read more.
Setting up age word problems from the information we’ve been given
Take the course
Want to learn more about Algebra 2? I have a step-by-step course for that. 
Solving age word problems
Example
In ???18??? years Sasha will be ???4??? times older than she is now. How old is she now?
Because Sasha will be four times older in ???18??? years, we can relate her age now, ???s??? to her age in ???18??? years as ???4s???.
So we can write the equation ???s+18=4s???.
We can also organize the information by making a table.
Now solve for ???s??? in the equation.
???s+18=4s???
???s-s+18=4s-s???
???18=3s???
???6=s???
Sasha is ???6??? now and in ???18??? years she’ll be ???4(6)??? or ???24??? years old.
Let’s do an example with more than one person.
One helpful way to organize these types of problems is by making a table.
Example
April is ???12??? years older than Eric. In five years, April will be twice as old as Eric. How old are Eric and April?
Because April is ???12??? years older than Eric, we can write
???A=E+12???
Because April will be twice as old as Eric in five years, we need to double Eric’s age in ???5??? years to get April’s age in five years. The next equation is
???2(E+5)=A+5???
This is a table that summarizes their ages and our equations:
Now you can substitute ???E+12??? for ???A??? into ???2(E+5)=A+5??? and simplify.
???2(E+5)=(E+12)+5???
???2E+10=E+17???
???E=7???
Substitute ???E=7??? into ???A=E+12???.
???A=7+12???
???A=19???
Right now Eric is ???7??? and April is ???19???.
Get access to the complete Algebra 2 course
Learn math
October 22, 2020
math, learn online, online course, online math, algebra, algebra 2, algebra ii, word problems, age word problems, systems of equations, solving systems, solving systems of equations, age problems
Andymath.com features free videos, notes, and practice problems with answers! Printable pages make math easy. Are you ready to be a mathmagician?
(textbf{1)}) In 10 years, Steve will be twice as old as he is today. How old is Steve today?
(textbf{2)}) 10 years ago, Jessica’s age was 1/3 the age she will be in 6 years. How old is Jessica now?
(textbf{3)}) Michael is twice as old as his brother. Five years ago he was 3 times as old as his brother. How old is Michael now?
(textbf{4)}) In 12 years, Rachel will be three times as old as she is today. How old is Rachel today?
(textbf{5)}) 8 years ago, Sam’s age was 1/4 the age he will be in 10 years. How old is Sam now?
(textbf{6)}) Emma is two times as old as her sister. Ten years ago, she was 4 times as old as her sister. How old is Emma now?
(textbf{7)}) In 18 years, Nick will be 3 times as old as he is today. How old is Nick today?
(textbf{8)}) 14 years ago, Alice’s age was 1/5 the age she will be in 10 years. How old is Alice now?
(textbf{9)}) Max is 3 times as old as his sister. In ten years, he will be 5/3 times as old as his sister. How old is Max now?
(textbf{10)}) John is 10 years younger than Morgan. Four years ago John was 3/8 as old as Morgan. How old are John and Morgan now?
(textbf{11)}) John is 15 years older than Karen. Two years ago, John was 2 times as old as Karen. How old is John?
(textbf{12)}) When I was 4, my brother was half my age. Now I am 20, and my sister is half my age. When was my sister half my brother’s age? 
See Related Pages()
(bullettext{ Word Problems- Linear Equations})
(,,,,,,,,)
(bullettext{ Word Problems- Averages})
(,,,,,,,,)
(bullettext{ Word Problems- Consecutive Integers})
(,,,,,,,,)
(bullettext{ Word Problems- Distance, Rate and Time})
(,,,,,,,,)
(bullettext{ Word Problems- Break Even})
(,,,,,,,,)
(bullettext{ Word Problems- Ratios})
(,,,,,,,,)
(bullettext{ Word Problems- Age})
(,,,,,,,,)
(bullettext{ Word Problems- Mixtures and Concentration})
(,,,,,,,,)
In Summary
Word problems involving ages are a common type of math problem that students encounter in school. These problems ask students to solve for an unknown age using information about the ages of different people. These problems often include information about the present age and the age at a specific point in the past or future. These are an important part of math education because they help students develop problem-solving skills and apply their knowledge of math concepts to real-world situations.
Word problems are typically covered in math classes for elementary and middle school students. These problems may be introduced in earlier grades as part of a lesson on basic addition and subtraction, and then become more complex as students progress.
About Andymath.com
Andymath.com is a free math website with the mission of helping students, teachers and tutors find helpful notes, useful sample problems with answers including step by step solutions, and other related materials to supplement classroom learning. If you have any requests for additional content, please contact Andy at tutoring@andymath.com. He will promptly add the content.
Topics cover Elementary Math, Middle School, Algebra, Geometry, Algebra 2/Pre-calculus/Trig, Calculus and Probability/Statistics. In the future, I hope to add Physics and Linear Algebra content.
Visit me on Youtube, Tiktok, Instagram and Facebook. Andymath content has a unique approach to presenting mathematics. The clear explanations, strong visuals mixed with dry humor regularly get millions of views. We are open to collaborations of all types, please contact Andy at tutoring@andymath.com for all enquiries. To offer financial support, visit my Patreon page. Let’s help students understand the math way of thinking!
Thank you for visiting. How exciting!









