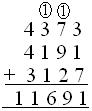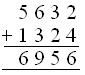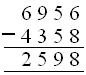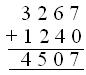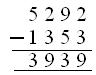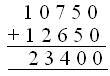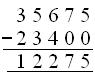Word problems involving addition and subtraction are discussed here step by step.
There are no magic rules to make problem solving easy, but a systematic approach can help to the problems easily.
Word problems based on addition are broadly of two types:
(a) When objects of two or more collections are put together.
For example:
Amy has 20 lemon sweets and 14 orange sweets. What is the total number of sweets Amy has?
(b) When an increase in number takes place.
For example:
Victor has 14 stamps. His friend gave him 23 stamps. How many stamps does Victor have in all?
The key words used in problems involving addition are:
sum; total; in all; all together.
Word problems based on subtraction are of several types:
(a) Partitioning : Take away, remove, given away.
(b) Reducing : Find out how much has been given away or how much remains.
(c) Comparison : More than / less than.
(d) Inverse of addition : How much more to be added.
The key words to look out for in a problem sum involving subtraction are:
take away; how many more ; how many less ; how many left ; greater ; smaller.
1. The girls had 3 weeks to sell tickets for their play. In the first
week, they sold 75 tickets. In the second week they sold 108 tickets and
in the third week they sold 210 tickets. How may tickets did they sell
in all?
Tickets sold in the first week = 75
Tickets sold in the second week = 108
Tickets sold in the third week = 210
Total number of tickets sold = 75 + 108 + 210 = 393
Answer: 393 tickets were sold in all.
2. Mr. Bose spent $450 for petrol on Wednesday. He spent $125 more than
that on Thursday. How much did he spend on petrol on those two days.
This problem has to be solved in two steps.
Step 1: Money spent for petrol on Thursday
450 + 125 = $575
Step 2: Money spent for petrol on both days
450 + 575 = $1025
Examples on word problems on addition and subtraction:
1. What is the sum of 4373, 4191 and 3127?
Solution:
The numbers are arranged in columns and added.
|
|
(i) Ones are added: 3 + 1 + 7 = 11 = 1 Ten + 1 one (ii) Tens are added: 1 + 7 + 9 + 2 = 19 tens = 1 hundred + 9 ten (iii) Hundreds are added: 1 + 3 + 1 + 1 = 6 Hundred (iv) Thousands are added: 4 + 4 + 3 = 11 Thousand |
Therefore, sum =11,691
2. What is the difference of 3867 and 1298?
Solution:
The numbers are arranged in columns and subtracted:
|
|
(i) Ones are subtracted: 7 < 8 1 is borrowed from 6 ten. So, 1 T or 10 + 7 = 17, 17 — 8 = 9 (ii) Tens are subtracted; 5 T < 9 T, So, 1 H or 10 T is borrowed from 8 H, 1 H = 10 T + 5 T = 15T 15T — 9T = 6 (iii) Hundreds are subtracted 7 H – 2 H = 5 H (iv) Thousands are subtracted 3 Th – 1 Th = 2 Th |
Therefore, difference = 2569
3. Subtract 4358 from the sum of 5632 and 1324.
Solution:
Sum of 5632 and 1324
|
|
Difference of 6956 and 4358
|
|
(i) 6 < 8, 1 T or 10 ones are borrowed 1 T or 10+ 6 =16, 16 — 8 = 8 (ii) 4 T < 5 T, 1 H or 10 T is borrowed 10 T + 4 T = 14 T, 14 T – 5 T = 9 T (iii) 8 H – 3 H = 5 H (iv) 6 Th – 4 Th = 2 Th |
Therefore, 2598 is the answer.
4. Find the number, which is
(i) 1240 greater than 3267.
(ii) 1353 smaller than 5292.
Solution:
(i) The number is 1240 more than 3267
Therefore, the number = 3267 + 1240 or = 4507
(ii) The number is 1353 less than 5292
Therefore, the number
= 5292 – 1353 or
= 3939
5. The population of a town is 16732. If there are 9569 males then find the number of females in the town.
Solution:
|
Population of the town Number of males Therefore, number of females |
= 1 6 7 3 2 = — 9 5 6 9 = 7 1 6 3 |
6. In a factory there are 35,675 workers. 10,750 workers come in
the first shift, 12,650 workers in the second shift and the rest come in
the third shift. How many workers come in the third shift?
Solution:
Number of workers coming in the first and second shift
= 10750 + 12650 = 23400
Therefore, number of workers coming in the third shift = 35675 — 23400 = 12275
Related Concept
● Addition
● Word
Problems on Addition
● Subtraction
● Check
for Subtraction and Addition
● Word
Problems Involving Addition and Subtraction
● Estimating
Sums and Differences
● Find the
Missing Digits
● Multiplication
● Multiply
a Number by a 2-Digit Number
● Multiplication
of a Number by a 3-Digit Number
● Multiply a Number
● Estimating Products
● Word
Problems on Multiplication
● Multiplication
and Division
● Terms Used in
Division
● Division
of Two-Digit by a One-Digit Numbers
● Division
of Four-Digit by a One-Digit Numbers
● Division
by 10 and 100 and 1000
● Dividing Numbers
● Estimating
the Quotient
● Division
by Two-Digit Numbers
● Word
Problems on Division
HOME PAGE
Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.
Related Pages
Lesson Plans and Worksheets for Grade 2
Lesson Plans and Worksheets for all Grades
More Lessons for Grade 2
Common Core For Grade 2
Common Core: 2.OA.1
Suggested Learning Target
- I can choose when to use addition and/or subtraction in a word problem
- I can represent addition and subtraction word problems using objects, drawings, and equations with unknowns in all positions.
- I can solve addition and subtraction word problems that involve two steps (doing one computation, and using that answer to perform a second computation that leads to the solution of the problem).
- I can solve word problems with unknown numbers in different positions (e.g., 5 + ? = 13, ? + 8 = 12)
- I can explore addition and subtraction with manipulatives (e.g., snap cubes, subitizing cards, tens frames, hundreds charts, number lines and empty number lines)
- I can take apart and combine numbers in a wide variety of ways
- I can use >, =, and < when comparing quantities
- I can use different thinking strategies to develop the understanding of the traditional algorithms and their processes
- I can apply properties of addition and subtraction
- I can choose the most efficient strategy to solve a problem
- I can solve various types of addition and subtraction word problems
- I can use _ or ? to represent an unknown in an equation
Take Apart and Combine Numbers
Total Unknown
Three red apples and two green apples are on the table. How many apples are on the table?
3 + 2 = ?
Addend Unknown
Five apples are on the table. Three are red and the rest are green. How many apples are green?
3 + ? = 5, 5 − 3 = ?
Both Addends Unknown
Jenny has five flowers. How many can she put in her red vase and how many in her blue vase?
5 = 0 + 5, 5 = 5 + 0
5 = 1 + 4, 5 = 4 + 1
5 = 2 + 3, 5 = 3 + 2
Compare Word Problems
Difference Unknown
(How many more?):
Jane has two oranges. Mary has five oranges. How many more oranges does Mary have than Jane?
2 + ? = 5
(How many fewer?):
Jane has two oranges. Mary has five oranges. How many fewer oranges does Jane have than Mary?
5 − 2 = ?
Smaller Unknown
(Version with more):
Mary has three more oranges than Jane. Jane has two oranges. How many oranges does Mary have?
2 + 3 = ?
(Version with fewer):
Jane has 3 fewer oranges than Mary. Jane has two oranges. How many oranges does Mary have?
3 + 2 = ?
Bigger Unknown
(Version with more):
Mary has three more oranges than Jane. Mary has five oranges. How many oranges does Jane have?
5 + 3 = ?
(Version with fewer):
Jane has 3 fewer oranges than Mary. Mary has five oranges. How many oranges does Jane have?
? + 3 = 5
One-Step Word Problems 1 — Bar Model (Part-Whole)
An effective model always has a visual model of the problem, a number sentence, and the answer to the question in a complete sentence.
Example:
Mr. Oliver had 88 pencils. He sold 27 of them. How many pencils did he have left?
- Show Video Lesson
Word Problems 2 — Bar Model (Part-Whole)
This video employs a visual way to solve world problems using bar modeling. This type of word problem uses the part-whole model. Because the part is missing, this is a subtraction problem.
Example:
There are 98 hats. 20 of them are pink and the rest are yellow. How many yellow hats are there?
- Show Video Lesson
Word Problems 3 — Bar Model (Part-Whole)
This video employs a visual way to solve world problems using bar modeling. This type of word problem uses the part-whole model. Because the whole is missing, this is an addition problem.
Example:
Mr. Gray sold 54 drinks in the morning. Mr. Frank sold 25 drinks at night. How many drinks did they sll altogether?
- Show Video Lesson
** Part-whole Word Problem**
This video shows you how to solve a word problem using bar models. This technique is one of the strategies that can be used to address Common Core math standard 2.OA.1.
Example:
Maya had some stamps. She gave 7 stamps to her younger brothers. Maya then had 14 stamps. How many stamps did Maya have at first?.
- Show Video Lesson
Comparison Word Problem
This video explains how to use bar modeling in Singapore math to solve word problems that deal with comparing. Example:
Example:
Adam has 11 fewer lollipops than Hope. If Adam has 16 lollipops, how may lollipops does Hope have?
- Show Video Lesson
Bar Model (Comparison)
This video employs a visual way to solve world problems using bar modeling. This type of word problem uses the comparison model. Because the part is missing, this is a subtraction problem.¦nbsp;
Example:
Cayla did 88 sit-ups in the morning. Nekira did 32 sit-ups at night. How many more sit-ups did Cayla do than Nekira?
- Show Video Lesson
Two-Step word problems
This video shows you how to solve two-step word problems using bar models.
Example:
50 children attended the birthday party. 13 children left during the first hour. 9 children came in during the second hour. How many children were at the birtday party then?
- Show Video Lesson
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.
We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Company | Membership | Blog | Help center | User guides | Tell us what you think | Testimonials | Careers | Contact us | Terms of service | Privacy policy
© 2023 IXL Learning. All rights reserved. Follow us
1.79
1. Much употребляется с неисчисляемыми существительными (в единственном числе), а many – с исчисляемыми во множественном числе:
I haven’t got much time.
I don’t know many of your friends.
□ Иногда much может употребляться перед исчисляемыми существительными в единственном числе:
There’s not much point in going on.
□ Many может употребляться после других определителей (the, my, its, his, her и т.п.):
Among the many unknowns after the earthquake is the extent of damage to the foundations of buildings.
The gallery is exhibiting some of his many famous paintings of ships.
2. Much и many могут употребляться как местоимения (если при этом смысл ясен):
You haven’t eaten much.
Did you find any mushrooms? — Not many.
Как правило, это звучит достаточно формально:
There is no guarantee of a full recovery. Much depends on how well she responds to treatment.
The government’s policies have done much to reduce unemployment.
Many (= many people) have argued that she is the finest poet of our generation.
Not once did I see a tiger in the jungle, although I heard many.
Перед другими определителями (the, my, this и т.п.) или местоимениями употребляется much/many of:
You can’t see much of a country in a week.
How much of the house do you want to paint this year?
I won’t pass the exam: I’ve missed too many of my lessons.
How many of you are there?
There’s not much meat left. (не ‘There’s not much of meat left’.)
Many shops open on Sunday mornings. (не ‘many of shops’ )
Of после much/many обычно не употребляется, если нет другого определителя (артикля или личного):
She didn’t eat much breakfast. (не ‘ … much of breakfast’.)
There aren’t many large glasses left. (не ‘ … many of large glasses left’.)
Но much of употребляется перед именами и географическими называниями:
I’ve seen too much of Haward recently.
Not much of Denmark is hilly.
□ Иногда возможно такое употребление:
He’s not much of a success/gentleman.
3. В разговорной речи much и many, как правило употребляются только в вопросительных и отрицательных предложениях. В утвердительных предложениях они звучат очень формально (особенно much) и вместо них употребляются другие, равнозначные по смыслу, слова и обороты:
He’s got lots of men friends, but he doesn’t know many women. (More natural than ‘He’s got many men friends…’)
Did you buy any clothes? .- Yes, lots. (не ‘Yes, many’)
How much money have you got? — I’ve got plenty. (не ‘I’ve got much’.)
a) a lot of и lots of
Эти выражения употребляются в основном в разговорной речи и могут употребляться с неисчисляемыми существительными и множественным числом исчисляемых (глагол согласуется в числе с существительным, а не с a lot of/lots of):
A lot of time is needed to learn a language.
Lots of patience is needed, too. (не ‘Lots of patience are needed, too’.)
A lot of my friends want to emigrate. (не ‘A lot of my friends wants… ’)
Lots of us think it’s time for an election.
There’s not a lot of meat left. (не ‘There’s not a lot meat left’.)
b) plenty of означает «достаточно» или «больше, чем достаточно»:
Don’t rush. There’s plenty of time.
Plenty of shops take cheques.
There’s no need to worry. We’ve got plenty of money.
Have some more coffee. — No, thank you. I’ve had plenty.
We took lots of food and drink on our walk through the hills/ …plenty of…
Jim doesn’t look well. He’s lost a lot of weight (не ‘plenty of‘)
Plenty of shops open on Sunday mornings. (не ‘Plenty shops’)
4. В более формальном стиле употребляются
a) much и many:
We have much (work) to do/many obstacles to overcome before we can claim that real progress has been achieved.
Much has been written about unemployment.
In the opinion of many economists, …
Much debate has been heard about Thornton’s new book.
There could be many explanations for this.
Much of her fiction describes women in unhappy marriages.
b) a great/good deal of, a large/considerable/substantial amount of и a large/considerable/great/substantial number of
Эти выражения звучат несколько более формально, чем a lot of и lots of:
A great/good deal of и a large amount of употребляются с неисчисляемыми существительными:
Mr. Lucas has spent a great deal of time in the Far East.
A good deal of the exhibition was devoted to her recent work.
I’ve thrown out a large amount of old clothing.
A large amount of the food was inedible/ Much of…
A large number of употребляется с существительными во множественном числе:
A large number of problems still have to be solved. (более естественно, чем
‘A large amount of problems …’ / ‘A great deal of problems …’ )
The book contains a large number of pictures, many in colour/ …many…
c) оборот many a с существительным в единственном числе:
The manager must have spent many a sleepless night worrying about his team selection.
Many a pupil at the school will be pleased that Latin is no longer compulsory.
d) обороты a good/great many:
She has a good/great many friends in New Zealand.
e) обороты far too many/ far too much (со значением «слишком много»)
Far too many students failed the end-of-year math exam.
Far too much time is wasted filling in forms.
□ Выражения с of обычно не употребляются перед такими словами как pounds, или miles:
It cost several pounds. (не ‘It cost a lot of pounds’.)
They lived many miles from the town. (не ‘They lived plenty of miles from
the town’.)
□ Обычно many (а не a lot of/lots) употребляются со словами, обозначающими время (days, minutes, months, weeks, years) и с числами + of (например: thousands of voters, millions of pounds):
We used to spend many hours driving to Melbourne and back.
He was the founder of a company now worth many millions of pounds.
□ Выражения с of могут употребляться как местоимения, если смысл ясен:
How much did it cost? — A lot. (= A lot of money.)
We should be all right for cheese — I’ve bought plenty.
He does not often speak, but when he does he says a great deal.
□ A lot и a great deal могут употребляться как наречия:
On holiday we walk and swim a lot.
The government seems to change its mind a great deal.
□ Выражения so much/many, as much/many и too much/many звучат вполне естественно в разговорной речи в утвердительных предложениях:
There was so much traffic that it took me an hour to get home.
I play as much tennis as I can.
You make too many mistakes.
She won’t drink this coffee. There’s too much sugar in it.
There was so much sugar in the coffee that she could’t drink it.
□ Much употребляется как наречие в вопросах и отрицательных предложениях:
Do you work much at weekends? I don’t travel much these days.
She’s much older than her brother.
I don’t drive much faster than you.
□ Much в формальном стиле может употребляться перед некоторыми глаголами (выражающими удовлетворение и предпочтение) в утвердительных предложениях:
I much appreciate your help.
We much prefer the country to the town.
I didn’t much enjoy the concert.
Very much употребляется как наречие (обычно не ставится перед существительным):
I very much like your new hairstyle.
Thank you very much.
There’s a whole lot of water coming under the door. (before noun) ( не ‘There’s very much water coming … ’ )
Much и many имеют степени сравнения (причем одинаковые):
George did more work/exercises than anyone else.
So he did the most work/ exercises
1.80
MORE
1. More употребляется как сравнительная степень much и many:
We need more time (не ‘ … more of time’.)
More university students are having to borrow money these days.
2. Если смысл ясен, more можно употреблять в качестве местоимения:
I’d like some more, please.
Перед другими определителями (a, the, my, this и т.п.) и местоимениями употребляется more of:
Three more of the missing climbers have been found.
Could I have some more of that smoked fish?
I don’t think any more of them want to come.
И more of употребляется перед именами и географическими названиями:
It would be nice to see more of Ray and Barbara.
Five hundred years ago, much more of Britain was covered with trees.
3. Употребляются обороты one more/ two more… и т.п..
There’s just one more river to cross.
4. More употребляется (по соответствующим правилам) для образования сравнительной степени прилагательных и наречий):
As you get older you get more tolerant.
Please drive more slowly.
5. More может употребляться как наречие:
I couldn’t agree more.
I hate this job more and more as the years go by.
1.81
MOST
1. The most употребляется как превосходная степень much и many:
Susan found the most blackberries (больше других).
The most work is often done by the quietest worker.
В разговорной речи the иногда опускается:
Who earns (the) most money in your family?
2. Most (в этом значении без артикля) означает «большинство»:
Most children like ice cream. (не ‘The most children… ’ )
Most cheese is made from cow’s milk.
Most Swiss people understand French. (не ‘Most of Swiss people…’)
Most people want a peaceful life.
Most of употребляется перед именами и географическими названиями:
I’ve read most of Shakespeare.
The Romans conquered most of England.
В этом значении most уже не превосходная степень much/many, а фактически самостоятельный определитель.
□ The majority of (=most / most of) употребляется обычно с множественным числом:
The majority of criminals are non-violent.
3. Если смысл ясен, most можно употреблять в качестве местоимения:
Some people had difficulty with the lecture, but most understood.
Перед другими определителями (a, the, my, this и т.п.) и местоимениями употребляется most of:
Most of the people here know each other.
Most of my friends live abroad. (не ‘most my friends… ’)
Most of us thought he was wrong.
He’s eaten two pizzas and most of a cold chicken.
4. (The) most употребляется (по соответствующим правилам) для образования превосходной степени прилагательных и наречий:
I wasn’t as clever as the others, but I was the most beautiful.
I work most efficiently in the early morning.
5. (The) most может употребляться как наречие (артикль часто опускается в разговорной речи):
They all talk a lot, but your little girl talks (the) most.
The truth hurts most.
Как наречие most может иметь значение «очень» в формальном стиле:
That is most kind of you.
Thank you for a most interesting afternoon.
The experience was most distressing.
□ Mostly означает «в большинстве, но не во всех случаях»
Your little girl talks the most. (не ‘…talks mostly’.)
She mostly talks about her friends.
-
#1
Which is correct:
A. How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
B. How many times more are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
I was going through a topic of probability in a textbook of elementary mathematics and found A… Think B is correct.
-
#2
You are correct. The than requires a comparative, in this case more.
-
#3
Sentence A begins:
A. How many times are the chances of getting …
This does not sound right because it has confused two different structures:
1/ What are the chances of getting (a red ball rather than a white ball?)
and
2/ How many times will we get (a red ball rather than a white ball?)
Only in structure 2 can we use «more»:
2b/ How many more times will we get (a red ball than a white ball?)
-
#4
Sentence A begins:
A. How many times are the chances of getting …
This does not sound right because it has confused two different structures:
1/ What are the chances of getting (a red ball rather than a white ball?)
and
2/ How many times will we get (a red ball rather than a white ball?)
Only in structure 2 can we use «more»:
2b/ How many more times will we get (a red ball than a white ball?)
I simply copied and pasted the sentence. It was a part of a long paragraph. Nevertheless, a sentence has to be complete in itself.
-
#5
I found the text here but I still think it is badly phrased and confusing. It is phrased as a question but does not end in a question mark:
It may be possible that the outcomes may not have equal chance of occuring unlike the cases of the coin and die. For example if a container has 5 red balls and 9 white balls and if a ball is pulled out without seeing, the chances of getting a red ball are much more. Can you see why? How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
If a comparative is to be used in your sentence it should be «less» because there are fewer red balls than white balls. There is a 5/14 chance of a red ball compared to a 9/14 chance of a white ball. Thus I would rephrase my previous suggestions:
How many less times will we get a red ball than a white ball?
or
How much less are the chances of getting a red ball than a white ball?
(answer = 4/14 = «four times out of fourteen less»)
Note: In the comparison to the previous reference (coins and dice) «more» is appropriate because each possibility on a coin is 1/2 and each possibility on a die is 1/6. The top number in both of these = 1 (ie. there is only one number 1, one number two… one heads, one tails) while there is more chance of selecting a red ball because there are five of them.
-
#6
How many less times will we get a red ball than a white ball?
We say «how many more times» not «how many much times». So, I wonder why «less» is used instead of «fewer»:
How many fewer times will we get a red ball than a white ball?
-
#7
Oh, do be careful here!
Let’s use five red balls and nine white balls. You might reasonably think that the question «how many times more are the chances of getting a white ball than a red ball?» is fine, and so it is, in a way.
You might be surprised to learn that the correct answer is «four fifths».
The problem lies in the use of «more». If A has five balls and B has six balls, few of us would argue with the person who says that B has 20% more balls than A.
If B has ten balls then he has 100% more balls than A.
If B has twenty balls then he has 300% more balls than A. 300% is the same as «three times» so B has three times more balls than A. But this sounds daft. B has twenty balls, A has five balls, and twenty is four times five, not three times five.
The problem lies in that little word «more». B has four times as many balls as A, but he has three times more balls than A.
I’ll leave you to work out for yourself how «less times» (or «times less») works out here (It is a trick question: it doesn’t)
Far better to avoid more or less in the question altogether.
What is the chance of getting a white ball compared with the chance of getting a red ball.
-
#8
Oh, do be careful here!
…
The problem lies in that little word «more». B has four times as many balls as A, but he has three times more balls than A.Far better to avoid more or less in the question altogether.
What is the chance of getting a white ball compared with the chance of getting a red ball.
This is a variation on a theme (The little word «more» is the comparative that the following thread suggests avoiding
three times longer than=three times as long as?
Last edited: Mar 14, 2018
-
#9
Thanks Unlce Jack and JulianStuart.
Let’s assume that for all my examples below there are 9 white balls and 5 red balls in the box.
______________________________________________
[Pw] — the chance of getting a white ball;
[Pr] — the chance of getting a red ball;
[Nw] — the number of white balls;
[Nr] — the number of red balls;
[A*] — how much more the chance of getting a white ball than a red ball is;
[B*] — how many times more the chance of getting a white ball than a red ball is;
[C*] — how many more times we will get a white ball than a red ball;
[Nw] = 9;
[Nr] = 5;
[Pw] = [Nw] / ([Nw] + [Nr]) = 9 / (9 + 5) = 9/14;
[Pr] = [Nr] / ([Nw] + [Nr]) = 5 / (9 + 5) = 5/14;
[A*] = [Pw] — [Pr] = 9/14 — 5/14 = 4/14;
[B*] = [A*] / [Pr] = (4/14) / (5/14) = 4/5;
[C*] = [Nw] — [Nr] = 9 — 5 = 4.
______________________________________________
You might be surprised to learn that the correct answer is «four fifths».
If I want the answer to be «four fourteenths», should I ask the question this way (the words in parentheses are optional):
1A. How much more is the chance of getting a white ball than (the chance of getting) a red ball? The answer is «four fourteenths».
2A. How much less is the chance of getting a red ball than (the chance of getting) a white ball? The answer is «four fourteenths».
1B. How much more are the chances of getting a white ball than (the chances of getting) a red ball? The answer is «four fourteenths».
2B. How much less are the chances of getting a red ball than (the chances of getting) a white ball? The answer is «four fourteenths».
How many fewer times will we get a red ball than a white ball?
Does the construction «how many fewer times»/»how many more times» make sense? For example, in these examples:
1C. If I keep taking one ball after the other until there’s nothing left in the box, then how many fewer times will I get a red ball than a white ball? The answer is «four».
2C. If I keep taking one ball after the other until there’s nothing left in the box, then how many more times will I get a white ball than a red ball? The answer is «four».
«less times» (or «times less»)
Is the word order essential?
1D. How many times more are the chances of getting a white ball than a red ball? The answer is «four fifths».
2D. How many more times are the chances of getting a white ball than a red ball? The answer is «four fifths».
1E. How many times less are the chances of getting a red ball than a white ball? The answer is «four fifths».
2E. How many less times are the chances of getting a red ball than a white ball? The answer is «four fifths».
-
#10
If I want the answer to be «four fourteenths», should I ask the question this way (the words in parentheses are optional):
1A. How much more is the chance of getting a white ball than (the chance of getting) a red ball? The answer is «four fourteenths».
2A. How much less is the chance of getting a red ball than (the chance of getting) a white ball? The answer is «four fourteenths».
1B. How much more are the chances of getting a white ball than (the chances of getting) a red ball? The answer is «four fourteenths».2B. How much less are the chances of getting a red ball than (the chances of getting) a white ball? The answer is «four fourteenths».
These all look fine to me (I see no distinction between chance and chances, though I would use the singular myself). You can also ask:
What is the difference in probability between getting a white ball and getting a red ball.
Does the construction «how many fewer times»/»how many more times» make sense? For example, in these examples:
1C. If I keep taking one ball after the other until there’s nothing left in the box, then how many fewer times will I get a red ball than a white ball? The answer is «four».
2C. If I keep taking one ball after the other until there’s nothing left in the box, then how many more times will I get a white ball than a red ball? The answer is «four».
That sounds very convoluted, and you have me puzzling over the tense of «get» and the use of «fewer», but I think both are justified and the sentences are correct.
Is the word order essential?
1D. How many times more are the chances of getting a white ball than a red ball? The answer is «four fifths».
2D. How many more times are the chances of getting a white ball than a red ball? The answer is «four fifths».
1E. How many times less are the chances of getting a red ball than a white ball? The answer is «four fifths».
2E. How many less times are the chances of getting a red ball than a white ball? The answer is «four fifths».
I would avoid all of these, to be honest. The word order doesn’t really matter («more times» and «times less» are most common, I think). The first question appears to want an answer of 1.8 and, although I said the correct answer was four fifths earlier because of the word «more», the word «times» really does confuse the issue. The second pair of questions in meaningless (though it does not stop people using the term «times less»). I would say the answer (if there is one) is «four ninths»; you have four fifths (I don’t know where you get that number from) and other people would say 1.8 (honestly!).
-
#11
The ‘more/less’, etc. complicates things unnecessarily, In My Opinion. Would you consider «What are my chances of getting a red ball rather than a white one?» as an alternative? «How much more likely am I to get a red ball than a white one?» is another alternative. Let your interlocutor figure out the mathematical odds!
Afterthought: «How much greater are my chances of getting a red ball than those of getting a white one?»
Last edited: Mar 16, 2018
-
#12
Thanks Uncle Jack and ain’ttranslationfun.
you have four fifths (I don’t know where you get that number from)
This is how I see it:
___________________________________________
Simple analogy:
___________________________________________
[A*] — the length of rope A;
[B*] — the length of rope B;
[A*] = 8;
[B*] = 2.
Rope A is [C*] times longer than rope B.
Rope B is [C*] times shorter than rope A.
[C*] = ([A*] — [B*]) / [B*] = (8 — 2) / 2 = 3.
Rope A is 3 times longer than rope B.
Rope B is 3 times shorter than rope A.
___________________________________________
Applying the above analogy to the example being discussed:
___________________________________________
[A*] — the probability of getting a white ball;
[B*] — the probability of getting a red ball;
[A*] = 9/14;
[B*] = 5/14.
The probability of getting a white ball is [C*] times more than the probability of getting a red ball.
The probability of getting a red ball is [C*] times less than the probability of getting a white ball.
[C*] = ([A*] — [B*]) / [B*] = (9/14 — 5/14) / (5/14) = (4/14) / (5/14) = 4/5.
The probability of getting a white ball is 4/5 times more than the probability of getting a red ball.
The probability of getting a red ball is 4/5 times less than the probability of getting a white ball.
___________________________________________
The first question appears to want an answer of 1.8
Would it be better to use the sentences below if I wanted either an answer of 1.8 or 0.(5)?
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
-
#13
This is how I see it:
___________________________________________
Simple analogy:
___________________________________________
[A*] — the length of rope A;
[B*] — the length of rope B;[A*] = 8;
[B*] = 2.Rope A is [C*] times longer than rope B.
Rope B is [C*] times shorter than rope A.[C*] = ([A*] — [B*]) / [B*] = (8 — 2) / 2 = 3.
Rope A is 3 times longer than rope B.
Rope B is 3 times shorter than rope A.
Which is why you really should not use «times shorter» (or «times less», as the case may be).
The difference is 6 (at least that is uncontroversial!)
A is 8 long, the difference 6 as a proportion of 8 is 75% (or three quarters or however you like to call it)
B is 75% shorter than A. This is correct English for expressing this relationship.
You might just about get away with saying that B is three-quarters times shorter than A, but this is inelegant and will leave people scratching their heads saying «why has he used ‘times’?».
What some people do say is that B is four times shorter than A. People say this, but I would never support such use. I don’t think anyone careless enough to use «times shorter» would ever consider that B was three times shorter than A, and would think you mad for saying so. They probably would not accept that A is three times longer than B, either, although this has rather more justification behind it, and would instead insist that A is four times longer than B.
This is why I say to be careful with «more» and «less» in this sort of mathematical comparison, and I recommend people avoid using any combination of «more» or «less» and «times».
Would it be better to use the sentences below if I wanted either an answer of 1.8 or 0.(5)?
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
These are horrible. Use something like «What is the ratio of the probabilities…» for the first pair. The second pair use the same construction as your sentence A at the top, which is wrong.
-
#14
Thanks Uncle Jack and ain’ttranslationfun.
This is how I see it:
…
The trouble is, a lot of people DON’T see it that way. You have been given a strong suggestion NOT to use a comparative with time or %.
This thread has vociferous arguments from both sides discussing
«Look at the following two sentences:
The rope is three times longer than that one.
The rope is three times as long as that one.
Do the two sentences mean the same?
So «X times longer than» or «X% shorter than» are seen differently by different people and if you wish to avoid ambiguity, you should avoid them. Feel free to join the discussion there
E.g., My piece of wood is three times as long as yours. If yours is 2 m long, mine is 6 m long. No ambiguity.
Same pieces of wood: My piece of wood is 4 m longer than yours. (No «times or % with comparative, just using units of measure) No ambiguity.
-
#15
Thanks Uncle Jack and JulianStuart.
The second pair use the same construction as your sentence A at the top, which is wrong.
It seems that I don’t understand what you mean. You said that my sentences 1A and 2A were good.
-
#16
It seems that I don’t understand what you mean. You said that my sentences 1A and 2A were good.
I was referring to sentence A in post #1.
-
#17
Now I see what you meant, Uncle Jack. Thanks for the clarification.
1F. How many times as much is the chance of getting a white ball as the chance of getting a red ball is? The answer is «nine fifths» or «1.8».
2F. How many times as much is the chance of getting a red ball as the chance of getting a white ball is? The answer is «five ninths» or «0.(5)».
When constructing sentences 1F and 2F, I wanted to apply the pattern of the sentence below:
How many times as many apples do I have as she does? (this link)
Can this pattern be applied somehow to the example in this thread?
1G. How many times is the chance of getting a white ball the chance of getting a red ball? The answer is «nine fifths» or «1.8».
2G. How many times is the chance of getting a red ball the chance of getting a white ball? The answer is «five ninths» or «0.(5)».
Here I wanted to use this pattern: «This house is three times the size of that house.» Can this be done?
My other attempt:
The chance of getting a white ball is 1.8 times the value of the chance of getting a red ball.
How many times is the chance of getting a white ball the value of the chance of getting a red ball?
-
#18
The trouble here is you are asking questions about probabilities, not apples or the sizes of houses, and whoever invented the English language really didn’t like probabilities, and failed to create the necessary vocabulary and syntax.
It is probably best to work backwards from a simple example. There are three red balls and one white ball.
Here are some statements that can be made about them :
- The probability of getting a red ball is 50% (or 0.5) higher than getting a white ball
- The probability of getting a white ball is 50% (or 0.5) lower than getting a red ball
- The probability of getting a red ball is three times the probability of getting a white ball
- The probability of getting a white ball is one third the probability of getting a red ball
You might also think, from all the discussion had above, that there are two other sentences that might be said:
5. The probability of getting a red ball is 200% more (or two times more) than getting a white ball
6. The probability of getting a white ball is 67% less (or two-thirds times less) than getting a white ball
but we cannot say these, because in English, «more» and «higher» are effectively synonymous (the prices in Finlay’s are 10% higher than the prices in Harrison’s), and so are «less» and «lower». Since the meanings have already been taken by (1) and (2), any attempt to try to use (5) and (6) are certain to be misunderstood. By all means replace «probability» with «chance» or «chances», but if we confine ourselves to simple English, I can think of no other valid comparison of the two probabilities than these four statements.
So, how do we ask a question to give each of the answers (1) to (4)?
A. How much higher is the probability of getting a red ball than a white ball?
Correct answers are (1) and (3)
B How much lower is the probability of getting a white ball than a red ball?
Correct answers are (2) and (4)
That might not be much help if you want to force the answer to be (1) or (2), but you could ask
C. What is the difference in probabilities between getting a red ball and getting a white ball?
In all honesty, I cannot think of a simple question which would unambiguously yield either (1) or (2) on its own, without allowing some other form of answer to be right. To force answer (3) or (4) you need to ask about the ratio of probabilities rather than the difference:
D. What is the ratio of probabilities between getting a red ball and getting a white ball?
-
#19
Thanks for the explanation, Uncle Jack.
The probability of getting a red ball is three times the probability of getting a white ball.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
-
#20
Thanks for the explanation, Uncle Jack.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
I though along those lines too, putting «is» before the first «the probability» but then could not think of a word to put where you have put the «is». You have managed to avoid this problem. Yes, it makes sense in English, but is difficult to read, and you yourself appear to have misread it, as the answer is one-third, my sentence (4), but you have quoted sentence (3).
-
#22
Which is correct:
A. How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
B. How many times more are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.I was going through a topic of probability in a textbook of elementary mathematics and found A… Think B is correct.
What you may be trying to say is:
How many times as great are the chances of getting a red ball as those of getting a white ball (probabilities for both being between 0 and 1)?
If this is the source of your sentence:
It may be possible that the outcomes may not have equal chance of occuring unlike the cases of the coin and die. For example if a container has 5 red balls and 9 white balls and if a ball is pulled out without seeing, the chances of getting a red ball are much more. Can you see why? How many times are the chances of getting a red ball than getting a white ball, probabilities for both being between 0 and 1.
then no correction to the syntax or grammar of the sentence will fix the author’s error.
I wonder if I can form the following question based on the above quoted sentence:
How many times the probability of getting a red ball is the probability of getting a white ball?
This version means the same as mine.
Two more versions of the same thing:
How many times the probability of getting a red ball is that of getting a white ball?
How many times as likely is getting a red ball compared with getting a white one?
The answer to all of these, in the context of 5 red balls and 9 white ones, is 0.55555….
If the author meant 9 white and 5 red balls, the answer would be 1.8.
Last edited: Mar 17, 2018
-
#23
Thanks for the explanation, Forero.

Donna has been a teacher, math instructional coach, interventionist, and curriculum coordinator. A frequent speaker at state and national conferences, she shares her love for math with a worldwide audience through her website, Math Coach’s Corner. Donna is also the co-author of Guided Math Workshop.
Comparison subtraction is really tricky for kids. Part of that is a lack of exposure. We typically teach subtraction as take away, and that is certainly one of the subtraction structures. But we need to move beyond that and help students understand that comparing also involves subtraction.
This post contains affiliate links, which simply means that when you use my link and purchase a product, I receive a small commission. There is no additional cost to you, and I only link to books and products that I personally use and recommend.
A common way to phrase comparison subtraction problems is how many more? There are lots of variations on that phrase: how much taller, how much more, how much faster, how many fewer, etc. Let’s look at a problem:
Marla has 5 pieces of candy. Carlos has 3 pieces of candy. How many more pieces of candy does Marla have than Carlos?
A very common error is to say 5. In other words, they just say the number that is bigger. I read, I think in Kathy Richardson’s How Children Learn Number Concepts, that children hear how much is the number that is more? instead of how many more? I thought that was really interesting.
Another way comparison subtraction can be worded is what is the difference? So the question in our candy problem would sound like What is the difference in the pieces of candy Marla has and the pieces of candy Carlos has?
So how do we help children understand comparison subtraction? Of course, it has to be concrete learning–counters, linking cubes, etc. I suggest a linear comparison, as shown in the picture. Build each number, lining them up one on top of the other. Help students to see that up to a certain point, they had the same number (3), but Martha has 2 more. Consider using a two-part question: Who has more? How many more?
To help students visualize the more part, I thought it would be helpful to cover up the part that is the same and just leave the difference showing. I made the cute little monster cards you see below, but of course, you could use an index card or even your hand.

Click here to grab a copy of the cards.
Graphing presents another great opportunity to highlight comparison subtraction. If you’re doing a daily graphing activity, like the one shown below, the numbers are already lined up for you! Click here to read more about daily graphing.
Download Article
Download Article
You can solve many real world problems with the help of math. In order to familiarize students with these kinds of problems, teachers include word problems in their math curriculum. However, word problems can present a real challenge if you don’t know how to break them down and find the numbers underneath the story. Solving word problems is an art of transforming the words and sentences into mathematical expressions and then applying conventional algebraic techniques to solve the problem.
-
1
Read the problem carefully.[1]
A common setback when trying to solve algebra word problems is assuming what the question is asking before you read the entire problem. In order to be successful in solving a word problem, you need to read the whole problem in order to assess what information is provided, and what information is missing.[2]
-
2
Determine what you are asked to find. In many problems, what you are asked to find is presented in the last sentence. This is not always true, however, so you need to read the entire problem carefully.[3]
Write down what you need to find, or else underline it in the problem, so that you do not forget what your final answer means.[4]
In an algebra word problem, you will likely be asked to find a certain value, or you may be asked to find an equation that represents a value.- For example, you might have the following problem: Jane went to a book shop and bought a book. While at the store Jane found a second interesting book and bought it for $80. The price of the second book was $10 less than three times the price of he first book. What was the price of the first book?
- In this problem, you are asked to find the price of the first book Jane purchased.
Advertisement
-
3
Summarize what you know, and what you need to know. Likely, the information you need to know is the same as what information you are asked to find. You also need to assess what information you already know. Again, underline or write out this information, so you can keep track of all the parts of the problem. For problems involving geometry, it is often helpful to draw a sketch at this point.[5]
- For example, you know that Jane bought two books. You know that the second book was $80. You also know that the second book cost $10 less than 3 times the price of the first book. You don’t know the price of the first book.
-
4
Assign variables to the unknown quantities. If you are being asked to find a certain value, you will likely only have one variable. If, however, you are asked to find an equation, you will likely have multiple variables. No matter how many variables you have, you should list each one, and indicate what they are equal to.[6]
-
5
Look for keywords.[7]
Word problems are full of keywords that give you clues about what operations to use. Locating and interpreting these keywords can help you translate the words into algebra.[8]
- Multiplication keywords include times, of, and factor.[9]
- Division keywords include per, out of, and percent.[10]
- Addition keywords include some, more, and together.[11]
- Subtraction keywords include difference, fewer, and decreased.[12]
- Multiplication keywords include times, of, and factor.[9]
Advertisement
-
1
Write an equation. Use the information you learn from the problem, including keywords, to write an algebraic description of the story.[13]
-
2
Solve an equation for one variable. If you have only one unknown in your word problem, isolate the variable in your equation and find which number it is equal to. Use the normal rules of algebra to isolate the variable. Remember that you need to keep the equation balanced. This means that whatever you do to one side of the equation, you must also do to the other side.[14]
-
3
Solve an equation with multiple variables. If you have more than one unknown in your word problem, you need to make sure you combine like terms to simplify your equation.
-
4
Interpret your answer. Look back to your list of variables and unknown information. This will remind you what you were trying to solve. Write a statement indicating what your answer means.[15]
Advertisement
-
1
Solve the following problem. This problem has more than one unknown value, so its equation will have multiple variables. This means you cannot solve for a specific numerical value of a variable. Instead, you will solve to find an equation that describes a variable.
- Robyn and Billy run a lemonade stand. They are giving all the money that they make to a cat shelter. They will combine their profits from selling lemonade with their tips. They sell cups of lemonade for 75 cents. Their mom and dad have agreed to double whatever amount they receive in tips. Write an equation that describes the amount of money Robyn and Billy will give to the shelter.
-
2
Read the problem carefully and determine what you are asked to find.[16]
You are asked to find how much money Robyn and Billy will give to the cat shelter. -
3
Summarize what you know, and what you need to know. You know that Robyn and Billy will make money from selling cups of lemonade and from getting tips. You know that they will sell each cup for 75 cents. You also know that their mom and dad will double the amount they make in tips. You don’t know how many cups of lemonade they sell, or how much tip money they get.
-
4
Assign variables to the unknown quantities. Since you have three unknowns, you will have three variables. Let
equal the amount of money they will give to the shelter. Let
equal the number of cups they sell. Let
equal the number of dollars they make in tips.
-
5
Look for keywords. Since they will “combine” their profits and tips, you know addition will be involved. Since their mom and dad will “double” their tips, you know you need to multiply their tips by a factor of 2.
-
6
Write an equation. Since you are writing an equation that describes the amount of money they will give to the shelter, the variable
will be alone on one side of the equation.
-
7
Interpret your answer. The variable
equals the amount of money Robyn and Billy will donate to the cat shelter. So, the amount they donate can be found by multiplying the number of cups of lemonade they sell by .75, and adding this product to the product of their tip money and 2.
Advertisement
Add New Question
-
Question
How do you solve an algebra word problem?
Daron Cam is an Academic Tutor and the Founder of Bay Area Tutors, Inc., a San Francisco Bay Area-based tutoring service that provides tutoring in mathematics, science, and overall academic confidence building. Daron has over eight years of teaching math in classrooms and over nine years of one-on-one tutoring experience. He teaches all levels of math including calculus, pre-algebra, algebra I, geometry, and SAT/ACT math prep. Daron holds a BA from the University of California, Berkeley and a math teaching credential from St. Mary’s College.
Academic Tutor
Expert Answer
Carefully read the problem and figure out what information you’re given and what that information should be used for. Once you know what you need to do with the values they’ve given you, the problem should be a lot easier to solve.
-
Question
If Deborah and Colin have $150 between them, and Deborah has $27 more than Colin, how much money does Deborah have?
Let x = Deborah’s money. Then (x — 27) = Colin’s money. That means that (x) + (x — 27) = 150. Combining terms: 2x — 27 = 150. Adding 27 to both sides: 2x = 177. So x = 88.50, and (x — 27) = 61.50. Deborah has $88.50, and Colin has $61.50, which together add up to $150.
-
Question
Karl is twice as old Bob. Nine years ago, Karl was three times as old as Bob. How old is each now?
Let x be Bob’s current age. Then Karl’s current age is 2x. Nine years ago Bob’s age was x-9, and Karl’s age was 2x-9. We’re told that nine years ago Karl’s age (2x-9) was three times Bob’s age (x-9). Therefore, 2x-9 = 3(x-9) = 3x-27. Subtract 2x from both sides, and add 27 to both sides: 18 = x. So Bob’s current age is 18, and Karl’s current age is 36, twice Bob’s current age. (Nine years ago Bob would have been 9, and Karl would have been 27, or three times Bob’s age then.)
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Word problems can have more than one unknown and more the one variable.
-
The number of variables is always equal to the number of unknowns.
-
While solving word problems you should always read every sentence carefully and try to extract all the numerical information.
Show More Tips
Advertisement
References
About This Article
Article SummaryX
To solve word problems in algebra, start by reading the problem carefully and determining what you’re being asked to find. Next, summarize what information you know and what you need to know. Then, assign variables to the unknown quantities. For example, if you know that Jane bought 2 books, and the second book cost $80, which was $10 less than 3 times the price of the first book, assign x to the price of the 1st book. Use this information to write your equation, which is 80 = 3x — 10. To learn how to solve an equation with multiple variables, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 56,462 times.
Reader Success Stories
-
James Carson
Sep 13, 2019
«I think this is amazing because it explains how and what you need to do.This helped me in algebra, and I recommend…» more
Did this article help you?
Enjoy learning English online with Puzzle English for free
It is clear where the confusion can arise between the words many and much: in Russian they have the same meaning. Both words convey the idea of plurality and indicate a large number of those objects to which they refer.
What, then, is the difference between them? And when is many used, and when is much? In order not to confuse these two words with each other, you need to remember small rules.
Countable and uncountable nouns
The words much and many each refer to the object that follows it. The choice of one of these two words depends on the type of the subsequent noun.
All nouns can be divided into two groups: countable and uncountable. The division into these two classes is based on the ability to count objects. Let’s look at this principle with an example: take the word chair.
It has both singular and plural forms: chair — chairs. If we imagine a set of chairs, we can count how many items it contains: one chair, two chairs, and so on.
If we take another noun, for example, snow (snow), then we will not be able to count what elements a lot of snow consists of.
Nouns of the first type that behave like chair are called countable, and nouns of the second type, like snow, are called uncountable.
Many and much: the rule of thumb
How much and many have to do with this? The most direct: the category of calculability of a noun determines which of these words will be used. Let’s turn to the examples we are already familiar with. Chair is a countable item, so many will be used with it. Snow is an uncountable noun, which means that if we want to convey the idea of a large number, we will use much with it.
I need many chairs for the party — I need many chairs for the holiday.
There is much snow in the city — There is a lot of snow in the city.
Thus, for many or much, the rule can be deduced: many appears with countable nouns, and much with uncountable nouns.
Source: https://puzzle-english.com/directory/muchmany
When to use a lot of and many. The use of much — many — a lot of in English — video tutorial
Hello, people! In this article, we will analyze in detail the rules for using the words «much», «many» and «a lot of» in English, find out the differences between them, discuss the nuances of using them in speech, and also show examples for clarity.
Translation and transcription: much — a lot, very, a lot, significantly, very;
Use: is used in a sentence when we mean a large number of uncountable nouns, i.e. those that cannot be counted by the piece;
Example:
there is much black paint left in the garage.
Left in the garage lotblack paint.
Also, it is usually used in negative or interrogative sentences:
Chris does not have muchchange. Only a few five dollar bills.
Chris doesn’t have a lot of money to trade. Just a few five dollar bills.
In affirmative sentences, «much» is sometimes used when a more formal and formal style is implied.
For example:
there is much concern about genetically modified food in the UK.
In the UK the question is acuterelatively genetically modified food.
Many
Transcription and Translation: like “much”, “many” [“menɪ] translates to“ many ”;
Use: used exclusively with countable plural nouns;
Example:
However, despite manymany problems remain unsolved.
However, despite Significantefforts, many problems remain unresolved.
В denials и issues with countable nouns «many» also occurs quite often:
How manyquail eggs are in this salad?
How many quail eggs in this salad? Anthony does not have many bottlesof winein his own private bar. At least that »s what he» s saying.
Anthony’s slightlybottles wine in his own bar. At least that’s what he says.
Can be used in affirmative offer when you need a shade formalities.
There were manyscientific articles taken into account to make a decision.
It was taken into account many scientific articles to make a decision.
A lot of
Transcription and translation: by meaning «a lot of» [ə lɔt ɔf] is similar to «much» and «many» and implies the same translation — a lot;
Use: used with both countable plural and uncountable nouns, mainly in colloquial and informal speech.
Example:
Jack had a lot ofpeanutbutter left in the jar.
Jack has left lotpeanutpastes in the bank.
The equivalent of «a lot of» is «lots of«(Even more informal form).
Lots of teenagers learn Korean because they are into k-pop.
ManyTeens are learning Korean because they are into the K-pop music genre.
Table: Difference between much, many and a lot
| WORD | Use | Value |
| countable nouns (plural) / negation + question / statement = formal style | ||
| uncountable nouns / negation + question / statement = formal style | ||
| more / more | ||
| The most | uncountable + countable nouns / adjectives | most / most |
| A lot (of) | uncountable + countable nouns / informal style | |
| lots (of) | uncountable + countable nouns / extremely informal style |
The use of the words much, many, a lot of often causes some difficulties due to the fact that in the Russian language the word “many” is universal. In English, these words have the following rules:
1. Many: many and much
Much is used with uncountable nouns, usually in negative sentences and questions.
I don’t have much money.
/ I don’t have a lot of money. /
In addition, the word much has the meanings «very», «much», «significant», «much».
«But it doesn» t matter much, «thought Alice.
«/ But it’s not so important,» thought Alice. /
He did it much sooner than she expected.
/ He did it much sooner than she expected. /
Alice was not much surprised at this.
/ This did not surprise Alice. /
Many also means «many,» but is used with countable nouns, often in negative sentences and questions (but not limited to), and in phrases with the words «many of».
I have scarcely spoken of the customs of the Kukuanas, many of which are exceedingly quaint.
/ I hardly talked about the customs of the Kukuanas, many of which are extremely strange. /
Have you been to many countries?
/ Have you been to many countries? /
Many is used, for example, when we say many days, many years, many hours, many times.
We have known each other for many years.
/ We have known each other for many years. /
Also, many can mean many (people).
Though he was a great help in his father’s business, there were many who doubted that he would become the heir to it.
/ Although he was very helpful to his father in his business, many doubted that he would become his heir. /
The words much and many are also used in the constructions as much as / as many as, too much / too many, so much / so many, how much / how many.
Source: https://sokurnso.ru/finansy/kogda-upotreblyat-a-lot-of-i-many-upotreblenie-much-many-a-lot-of-v-angliiskom/
Lesson 7. Words-parameters. The use of much and many
Words much, many (many, many, many) can be used as an addition to a noun, or be used instead.
much used only with uncountable nouns or instead of uncountable nouns:
- How much money did he spend?
- You haven’t much time if you want to catch the bus.
- Not much was written about it.
- He doesn’t eat much.He doesn’t eat much.
Many is used only with countable nouns or instead of countable nouns:
- How many books do you have?
- How many pupils are in this class?
- Many to play football. Many people like to play football.
- Not many have heard of her.
In modern English, often instead of words much и many their synonym is used a lot of (lots of). A lot of used with both countable and uncountable nouns:
- He always makes a lot of mistakes He always makes a lot of mistakes.
- we have a lot of bags.We have a lot of bags.
If the word «a lot» is preceded by too (too much), very (very), so (So), how (as), as (also) then you need to use much и many. Using A lot of in this case is incorrect.
- I have so much work to do
- She works too much.She works too hard.
- You have made very many mistakes You made a lot of mistakes.
In this lesson, the expression a lot of not used. Only much и many.
little, few
Words little, few (little, not enough) can be used as an addition to a noun, or be used instead.
Little used only with uncountable nouns:
- we have little money We don’t have much money.
- She at very little at lunch She ate very little at lunch.
- Little has been said about this event.
- John spends little time with his family. John spent little time with his family.
Few used only with countable nouns:
- He has few friends He has few friends.
- Few managers admit their mistakes.
- He has read few books He has read few books.
- Many people were invited but few came. Many people were invited, but few came.
Pronouns little и few can be used with an indefinite article in the meaning a little, a little.
Consider in comparison:
- I have a little time. I have a little time.
- I have little time. I have little time.
- I know a few words in spanish. I know a few words in spanish.
- I know few words in spanish. I know few words in Spanish.
Parameter words
AllPartNothingPeople Objects Place Time
| everybody, everyone | somebody, someone | anybody, anyone | nobody, no one |
| everything | something something, something | anything anything, anything | nothing |
| everywhere | somewhere | anywhere anywhere, anywhere | nowhere |
| always | sometimes sometimes | never |
examples:
- He sees todo MundoHe sees everyone.
- He speaks to somebody.He is talking to someone.
- I saw him somewhere. I saw him somewhere.
- I always say the truth. I always tell the truth.
- I saw someone there. I saw someone there.
- Anyone can help you. Anyone can help you.
- We bought everything.We bought everything.
- You can buy it anywhere.You can buy this anywhere.
- you will Sometimes hear them. You will sometimes hear them.
Note time parameters the sentence usually uses before the verb… All other parameters are used more often. after the verb.
В general issues the parameter is usually used Any (anybody, anyone, anything, anywhere), a not some.
As you can see from the table, the words somebody, something, somewhere can have the same translation with the words anybody, anything, anywhere.
To understand when which word to use, you need to go from the essence of the words.
Any — any, but some — some.
I saw somebody.
It’s about someone specific, so some.
I did not see anybody (I saw nobody)
Here we are talking about any person, so any.
Consider the following question-answer: Have you seen someone? I saw someone.
Did you see anyone? I saw someone.
Therefore, in the main questions, words with any are used, and in statements with some.
examples:
- Is anybody is there anyone here?
- there is somebody here. Someone is here.
- did you see anything interesting? Did you see anything interesting?
- I see something interesting there. I see something interesting there.
Using parameters is straightforward. Except for one case where the words nobody, nothing, nowhere, and never are used to convey negation:
- I didn’t tell him anything bad.
In this case, you should not copy the structure of the Russian sentence, because double negation will be a mistake in an English sentence:
- I didn’t say anything bad to him. Note tell him nothing bad. (wrong) I told him nothing bad. (right)
Let’s consider a few more suggestions:
- there is nothing interesting here. There is nothing interesting here.
- Nobody cares about my plans.
Words anyone, anybody, anything, anywhere are not negatives, therefore in negative sentences they are used as a general rule.
- I didn’t say anything bad to him. Note tell him anything bad or I told him nothing bath.
- I didn’t see anything interesting here. Note see anything interesting here or I saw nothing interesting here.
Words todo Mundo, everyone, somebody, someone, anybody, anyone, nobody и no one in English refer to singular… Therefore, the verb with them is used in the singular.
- Someone calls you.
- Does anyone hear me? can anyone hear me?
- No one was at home. Nobody was at home.
Source: https://polyglotmobile.ru/polyglot-english-base/lesson-7/
Much and Many in English. Brief instruction
Much and many in English refer to quantitative pronouns. Pronoun many is used with countable nouns, pronoun much — with uncountable.
Yesterday he spent much money. He spent a lot of money yesterday.
Many friends came to his party. Many friends came to his party.
The quantitative pronouns much and many can be used as adjective pronouns and as noun pronouns.
Pronouns-adjectives
Here much and many will mean «many».
- In affirmative sentences, they can be used:
- With adverbs of degree. These include the frequently used adverbs so — so, so; very — very, too — too, etc. They are used with pronouns to reinforce meaning. You work too much. I found so many mistakes in your work. I found a lot of mistakes in your work.
- As definitions to the subject. Much money will be spent for your classes. A lot of money will be spent on your classes. Many students study foreign languages. Many students study foreign languages.
- In relative clauses if and whether.I’ll be glad if many children come tomorrow. I will be glad if many children come tomorrow.
- Interrogative sentences also often contain much and many: How many people were there? How many people were there? Did you find much information? Did you find a lot of information? Much becomes «how much» or «how much» — with the question how much? How much oil should I use? How much oil should I use? How much is this car?
- The pronouns much and many are also used in negative sentences meaning little (not many, not much). Not many animals live in this forest. Few animals live in this forest. I have not got much money on me. I don’t have much money with me.
Pronouns — nouns
Here many is used to mean «many» and the pronoun much is used to mean «many.» Very often here these pronouns are accompanied by the preposition of. They can be used as:
- Subject. Many study English. Many are learning English. Many of them decided not to come. Many of them decided not to come. Much happened that night. A lot happened that night. Much of what she s is not interesting for me. Much that she likes is not interesting to me.
- Supplement (answers the questions of what? Who?) They ask much of us. They demand a lot from us. We saw many in this cafe.
- Circumstance (if much refers to the predicate and answers the question how?) You sleep too much. He was very much disappointed. He was very disappointed.
Comparative and superlative
Pronouns much and many can form comparative и superlative: much / many — more — (the) most. At the same time, much can act not only as a quantitative pronoun, but also as an adverb.
Much and many are used in the comparative degree more:
- With uncountable nouns and the pronoun some. Can I have some more coffee? Can I have some more coffee?
- To reinforce meaning (followed by the pronoun much). She has much more work than I do. She has a lot more work than me.
- More is used with countable nouns to indicate the exact number (followed by a numeral). I want to buy three more books. I want to buy three more books.
- With the preposition of to concretize the statement. He needs more of this fabric. He needs more (more) such fabric.
Much and many are superlative (the) most:
- To denote most of the total or number. Moreover, most is used with a noun without an article. Most students are busy now. Most of the students are busy now. Most children to play outside. Most children love to play outside.
- To denote most of a limited quantity or number. In this case, most will be used with the preposition of and with a noun with the article the or possessive pronoun. Most of the flowers in this shop were brought from Holland. Most of the flowers in this store were sourced from Holland. Most of your friends are very polite. Most of your friends are very polite.
Article recommended by an expert: Maria Solomatina
Source: https://1hello.ru/grammatika/much-many-v-anglijskom-yazyke-kratkaya-instrukciya.html
Rules for the use of much, many, few, little, a lot of and plenty of
In English, there are words called quantifiers. They are used to indicate quantity. Unlike numerals, which denote an exact amount, these words refer to an approximate amount. In this article, we will talk about words like much, many, few, little, a lot of и plenty of.
Using much, many and a lot of
All these words are translated into Russian as «a lot». However, the use of these words depends on the type of sentence (statement, negation or question) and on which noun it refers to — countable or uncountable. The basic rules are presented in the table below:
For example:
He has a lot of books. — He has lot books.
Kate doesn’t have many DVDs. — At Kate Little DVD. (Literally: Keith doesn’t have a lot of DVDs).
Holly spends a lot of time watching TV shows. — Holly conducts lot time watching television shows.
is there much petrol in the tank? — In the tank lot gasoline?
Much and many in statements
As you can see, a lot of is mainly used in affirmative sentences, and much and many — in denials and questions. However, this rule is not strict, it is based on the frequency of use, therefore much and many can be used in assertions as well. For example:
Joe has many friends. — Joe lot friends.
Also the words much and many are used instead of a lot of in a formal business style:
Many different kinds of research require the permission of the supervisor. — Many types of research require the permission of the supervisor.
If we want to say that there is too much of something (that is, build an affirmative sentence), then instead of a lot of we will use words much and many with additional word too («too much»). For example:
There were too many people at the conference. — The conference was too much people.
Oliver ate too much ice-cream. — Oliver ate too much ice cream
Synonyms of a lot of
Synonymous with the word a lot of is lots of. It is believed that lots of more informal and more often used in colloquial speech, and a lot of on the contrary, it is more formal. Lots of can also be used with both countable and uncountable nouns. For example:
Julia eats a lot of vegetables. / Julia eats lots of vegetables. — Julia is lot vegetables.
They have done a lot of work. / they have done lots of work. — They did lot work.
Another word for a large number is the word plenty of… As a rule, it is used to mean a very large amount of something, something in abundance:
we have plenty of tea at home. — At our home lot tea.
James has brought plenty of biscuits to the office. — James brought to the office lot cookies.
As we see plenty of can also be used with both countable and uncountable nouns.
The use of few, a few, little, a little
In order to understand how these words are used, we need to know two parameters: the first — whether this word refers to a countable or uncountable noun and the second: what is the meaning of the sentence — positive or negative. Consider the table below:
examples:
Kelly has a few close friends. — Kelly has slightly close friends. (Positive value).
Kelly has few close friends. — At Kelly’s little close friends. (Negative meaning).
Bobby has a little money. — Bobby has slightly of money. (A positive value is a little, but still there).
Bobby has little money. — Bobby’s little of money. (Negative meaning).
As we can see from the examples, these words have the same translation into Russian for both countable and uncountable nouns, but a different translation depending on the meaning: with a positive meaning, we translate them as «a little», with a negative meaning, as «little.»
Other meanings of much, a lot, a little
Form a lot sometimes it is used not in the meaning of «a lot», but in the meaning of «often» or «very». For example:
Do you enjoy watching films? — Yes, a lot… — Do you like to watch movies? — Yes, very.
Also the words much и a little can be used to form the comparative degree of adjectives. For example:
Source: https://www.start2study.ru/english-grammar/quantifiers/
Greetings, my dears!
There is an opinion that the Russian language is the richest language with an immense number of beautiful words! .. But how can you agree with it when in Russian there is only one word expressing a large number — «many», and in English there are already as many as three! (in fact, there are more of them — these are just the main ones).
Of course, I will not breed debates about the beauty of the language here — and it is so clear that each language is great in its own way! And here is the «Rule many many”And a few other words that we use to express quantity, I’ll expand it today so that you don’t think to get confused and make mistakes anymore! You are ready? I have already
Let’s start with a table that will clearly show you the difference. And let’s finish with the exercises — without them, your fresh knowledge will fly into the water pipe — in about the same way as an earring that accidentally fell there flies away)).
I think everything is clear from the table. Now I will explain verbally and in more detail.
- Much / a little / little
The words Much / a little / little are used only with nouns that cannot be counted, that is, with uncountable nouns. Much means a lot of something — much sugar, much water, much money.
Little — on the contrary — very little of anything — little sugar (very little sugar), little water (little water), little money (little money).
A little means «a little», it is a cross between much and little — a little sugar (a little sugar), a little water (a little water), a little money (a little money).
- Many / a few / few
The words Many / a few / few are used only with nouns that can be counted, that is, with countable nouns. Many means a lot of something — many books, many friends, many thoughts.
Few — on the contrary — very little of anything — few books, few friends, few thoughts.
A few means «several», it is a cross between many and few — a few books (a few books), a few friends (a few friends), a few thoughts (a few thoughts).
A lot of can be used with both countable and uncountable nouns, which is very convenient. A lot of often replaces much and many in affirmative sentences, whereas much and many are more appropriate in negatives and questions.
Do you have much time?
— No, I don’t have much time. or — Yes, I have a lot of time.
By the way, there are several «subtle points» where students often make mistakes. We read and remember!
! Many people! (not much)
many clothes! (not much)
Much money! (not many)
Many fruits! or! Much fruit!
And now, as promised by me, tasks with answers at the end
Exercise 1.Insert much or many instead of dots
- Have you found information about this company?
- They spent money in a shop yesterday.
- There are so places in the world that I’d to visit.
- people nowadays use bicycles instead of cars to go to work.
- «You’ve put too salt in the soup, I can’t eat it!»
- “Don’t buy food in the supermarket, we are going out tonight”.
Exercise 2.Translate sentences into English using much, many, a little, a few, little, few, a lot of
- I have few friends in this part of town.
- The teacher said so many words, but I didn’t understand anything.
- He asked the waiter to bring some water.
- In autumn, many birds fly south.
- She doesn’t like it when there is too much sugar in her tea.
- “There is absolutely no room in the closet! You have so many clothes! ”
I hope you had absolutely mistakes few!
Well, if you have any questions, do not hesitate to ask — I will definitely answer them!
Replies
Exercise 1.
Exercise 2.
- I have few friends in this part of the city.
- A teacher said so many words but I understood nothing.
- He asked a waiter to bring a little water.
- In autumn many birds fly to the south.
- She doesn’t it when there is too much sugar in tea.
- “There is no place in a wardrobe! You’ve got so many clothes! ”
To indicate a large number of someone or something (that is, say «a lot»), in English they use quantitative much, many, a lot of and few… All these pronouns have a meaning and a direct translation into Russian “many”. Beginners, and sometimes those who continue to study English, may have difficulties with what the difference between these pronouns is and how to choose the correct one. In this article, we’ll take a closer look at the much many a lot of rule.
Rules for using much, many, a lot of (affirmative sentences)
The rules for using much and many (and lot of) are their own. All of them are translated into Russian, not only «a lot», but in English there is a big difference between them. As a rule, the first step is to find out whether a countable or uncountable noun will be paired with much and many or a lot of — this is the main difference in the use of quantitative nouns.
much
The pronoun much should only be used with uncountable nouns — liquids, bulk solids, gases, etc. That is, the sentences will contain the constructions «much milk» (a lot of milk), «much water» (a lot of water), «much oxygen» (a lot of oxygen), but you will not find «many rice» or «many juice ”(a lot of falcon).
You added too much milk — You added too much milk.
I don’t much pepper in my food— I don’t like a lot of pepper in my food.
Negative sentences
According to the rules for using much and many, the pronouns much and many are most often used in negative sentences. Negations with uncountable nouns have the form not much, and negatives with countable nouns with not many.
Not many students — Few students like history lessons.
Not many of us have elephants — Not many of us have elephants. (Few of us have elephants.)He doesn’t eat much rice — He eats some meat.
Not much weight gain during pregnancy — Slight weight gain during pregnancy.
Interrogative sentences
The rules for using many and much state that the pronouns much and many are most often used in interrogative sentences. Questions with uncountable nouns start with how much, and questions with countable nouns start with how many.
How many roses are there in Kate’s hands? — How many roses does Kate have in her hands?
How many crocodiles do you have? — How many crocodiles do you have?
How many states are there in the USA? — How many states are there in the United States?
How much pepper do you take in your fried eggs? — How much pepper do you put in your scrambled eggs?
How much money does she need for her trip around the world? How much sugar do you have? — How much sugar do you have?
How much does it cost? — How much is it?
Features and exceptions
There is one peculiarity in the rules for using many and much that needs to be mentioned. When the pronouns much and many are followed by the particle of, it means «big half». In Russian, such a construction translates as «most of something», «many of».
Many of her clients live in the village “Many of her clients live outside the city.
Much of the meat is stink
Source: https://www.fanatsporta.ru/kogda-many-a-kogda-much-much-i-many-v-angliiskom-yazyke-kratkaya-instrukciya/
Much and many. Usage rules
Details Karina Galchenko Category: BEGINNER — ELEMENTARY
: 03 June 2019
180735
: 4/5
How not to get confused using much and many? Just pay attention to the rules of use, because it is no coincidence that the English came up with two words with the same meaning. They are not interchangeable: in some cases, you only need much, and in others, you only need many. It all depends on the word itself, which will refer to much or many. Let’s figure out what’s what!
As you know, nouns are divided into countable (you can count) and uncountable (you cannot count), and this is what depends on. rules for using much and many… It is necessary to remember once and for all that many is «friends» only with countable nouns, and much — with uncountable ones.
examples:
many children — many children
much water — a lot of water
But that’s not all about much and many. The rules for using these words suggest that they are best avoided in positive sentences. That is, much and many in English should be used in negations and questions. There are exceptions when these words are part of the subject.
examples:
do you have many friends here? — Do you have many friends here? (many + countable noun).
I don’t much sugar in my tea. — I don’t like a lot of sugar in tea (much + uncountable noun).
Many people speak English. — Many people speak English (many is part of the subject — many people).
Rules for the use of many much a lot of
If your positive proposal cannot do without «a lot», then pay attention to rules for using many much a lot of… It is believed that a lot of is well suited for approval. By the way, you can use it in absolutely any context. Even if you suddenly wondered what would work for a given sentence, a lot of will always help out, since it can be used for both countable and uncountable nouns.
examples:
There are a lot of people in this room. — There are many people in this room (a lot of + countable noun).
I have a lot of work today. — I have a lot of work today (a lot of + uncountable noun).
Do i have a lot of mistakes in the test? — Do I have a lot of mistakes in the test? (interrogative sentence).
They don’t have a lot of information. — They don’t have a lot of information (negative proposal).
Rules for using many much a lot of refer specifically to nouns, you cannot use these words with verbs. But what to do when it is important to «enhance» the meaning of an action? Here a lot will do (without the preposition of).
examples:
We see our parents a lot… — We see our parents a lot (meaning «see each other often»)
Do you practice this language a lot? — Do you practice this language a lot?
Drinking how much how many
Concerning how much how many, then here, too, everything depends on the noun that will follow this or that question phrase. How much should be combined with uncountable nouns, and how many with countable nouns.
examples:
How much milk do you have to buy? — How much milk do you need to buy? (how much + uncountable noun)
How many roses did he present her? — How many roses did he give her? (how many + countable noun)
Finally, I would like to note that with the words years, weeks, days it is better to use many rather than a lot of.
Example:
I have known Mary for many years. — I have known Mary for many years.
Best wishes to you!
Source: http://fluenglish.com/stati/studentam-na-zametku/29-beginner-elementary/367-much-i-many-pravila-upotrebleniya.html
A clear rule of thumb for using much-many in English. Usage examples, exercises with answers
Hello friends! How not to get confused using much and many? Just pay attention to the rules of use, because it is no coincidence that the English came up with two words with the same meaning.
They are not interchangeable: in some cases, you only need much, and in others, you only need many. It all depends on the word itself, which will refer to much or many. Let’s figure out what’s what!
Difference between many and much
Pronoun many used when it refers to objects (animate or inanimate) that can be counted. Words denoting such objects are called countable nouns.
Example:
- many children — many children
- many people — many people
- many tigers — many tigers
use many (since they can be counted)
Pronoun much is used only with nouns that cannot be counted, that is, with uncountable nouns.
Example:
- much sugar
- much water
- much money
use much (since they cannot be counted. Much means a lot of something.)
We look at the table that will clearly show you the difference in the use of Much, Many
Much / Little Many / Few A lot of / Plenty of
| Uncountable nouns | Countable nouns | Countable and uncountable nouns |
| How much money have you got? — How much money do you have? — There is some ink left in my pen. | I have many friends. He has got few best friends. — He has a few (few) best friends. | There is a lot of sugar there. — There are plenty of plants in the garden. — There are many plants in the garden. |
Many used where items can be counted individually.
If they cannot be counted, feel free to insert the word into the sentence much.
Much / many exercises:
Exercise 1. Use much or many to express How many ?.
- how days?
- how sugar?
- how cigarettes?
- How work?
- How petrol?
- How children?
- How theaters?
- How juice?
Exercise 2. Translate sentences into English using much, many, a little, a few, little, few, a lot of
- I have few friends in this part of town.
- The teacher said so many words, but I didn’t understand anything.
- He asked the waiter to bring some water.
- In autumn, many birds fly south.
- She doesn’t like it when there is too much sugar in her tea.
- “There is absolutely no room in the closet! You have so many clothes! ”
Exercise 3. Use much or many.
Do you drink ________coffee? I reading. I read _________ books. We have _______ lessons of English this year. I can’t remember _______ from this text. Do you learn _______ new English words every day? We haven’t got ________ bread. I can’t spend ________ money on toys.
Replies
Exercise 1.
- How many days? (How many days?)
- How much sugar? (How much sugar?)
- How many cigarettes? (How many cigarettes?)
- How much work? (How much work?)
- How much petrol? (How much gasoline?)
- How many children? (How many children?)
- How many theaters? (How many theaters?)
- How much juice? (How much juice?)
Exercise 2.
- I have few friends in this part of the city.
- A teacher said so many words but I understood nothing.
- He asked a waiter to bring a little water.
- In autumn many birds fly to the south.
- She doesn’t it when there is too much sugar in tea.
- “There is no place in a wardrobe! You’ve got so many clothes! ”
Exercise 3.
Do you drink much coffee? I reading. I read many books. We have many lessons of English this year. I can’t remember much from this text. Do you learn many new English words every day? We haven’t got much bread. I can’t spend much money on toys.
Friends like us, we tried!
Source: http://englishfox.ru/pravilo-much-many-v-angliiskom.html
The use of much, many, few, little, a lot of, plenty
In order not to miss new useful materials, subscribe to site updates
Have you noticed how often we use the words «a lot», «a little», «a few» in our speech and how we do not like to give exact numbers? Secretive by nature, the English also use these words very often in speech.
When we say «a lot» in English, we use the words many, much, a lot of, plenty of, and when we say «little» — few, a few, little, a little. These words are called determiners, they indicate an indefinite amount of something.
This article will show you when and where to use much, many, few, little, a lot of, plenty of in English.
The noun plays a key role in the choice of the defining word. The determiner depends on which noun is in front of us, countable (countable) or uncountable (uncountable). Once again, we recall that we can count countable nouns and they have a plural form (a boy — boys). And uncountable nouns do not have a plural form (water — some water), and we cannot count them.
We have divided all words into three groups depending on which noun they are used with. We will consider each group separately.
Much / Little Many / Few A lot of / Plenty of
| Uncountable nouns | Countable nouns | Countable and uncountable nouns |
| How much money have you got? — How much money do you have? — There is little ink left in my pen. | I have many friends. — He has got few friends. — He has few friends. | There is a lot of sugar there. — There are plenty of plants in the garden. — There are many plants in the garden. |
Many, few, a few with countable nouns
The words many (many), few (few), a few (several) are used with countable nouns. Many denotes a large number of something: many apples (many apples), many friends (many friends), many ideas (many ideas).
The opposite of many is few: few apples, few friends, few ideas. Few often have a negative meaning: very little, not enough, so little that practically none.
A few has an intermediate meaning between many and few, translated as «a few»: a few apples (a few apples), a few friends (a few friends), a few ideas (a few ideas).
— Do you have many friends in this part of the city? — At your place lot friends in this part of town?
— No, I don’t. I have few friends in this part of the city. — I do not have little friends in this part of town. (that is, not enough, I would like more)
— I have a few friends in the city center. — I have some friends in the city center.
Much, little, a little with uncountable nouns
The words much, little, and little are used with uncountable nouns. Usually, the uncountable include liquids (water — water, oil — oil), objects that are too small that cannot be counted (sand — sand, flour — flour), or abstract concepts, since they cannot be seen or touched by hands (knowledge — knowledge, work — Work).
Much stands for a large amount of something uncountable: much sugar, much milk, much time.
The opposite of much is little: little sugar, little milk, little time. Little, like few, means that something is not enough, very little.
A little means a small amount of something that cannot be counted: a little sugar, a little milk, a little time.
— Did she put much salt in the soup? — She lot put salt in the soup?
— No, she didn’t. She put little salt in the soup. — No, she put little salt in the soup. (more could have been)
— I added a little salt in her soup. — I added slightly salt in her soup.
A lot of, plenty of — universal words
The words a lot of (many) and plenty of (many) are the most «convenient»: we can use them with both countable nouns and uncountable ones.
A lot of (lots of) replaces much and many: a lot of people (many people), lots of tea (lots of tea). Plenty of means that there is a lot of something, that is, enough or even more than necessary: plenty of people (a lot of people), plenty of tea (a lot of tea).
We bought lots of souvenirs and plenty of tea when we were on vacation in Sri Lanka. — We bought lot souvenirs and lots of tea when we were on vacation in Sri Lanka.
How to learn to use adjectives with countable and uncountable nouns correctly
The use of adjectives with countable and uncountable nouns in English has its own tricks. What are they?
There are countable and uncountable nouns in English. Most often they are combined with adjectives in the same way. But there are situations when you need to know exactly which adjectives should be used with countable and which with uncountable nouns. Let’s take a look at these rules.
General rules for the use of adjectives with nouns
In English, countable nouns are those that can form a plural form (usually with the ending -s). For example: dog — dogs, pupil — pupils, pocket — pockets.
Uncountable nouns usually do not have plural forms. For example: sky, love, trust, butter, sugar. That is why in English you cannot say: «He saw many beautiful skies.» (He saw many beautiful skies) or: «She bought two milks.» (She bought two milk).
The use of countable and uncountable nouns with adjectives is in most cases identical. For example:
- «The sky was blue.» (The sky was blue) — The noun sky (sky) is uncountable.
- «He bought a blue car.» (He bought a blue car) — Here the adjective blue is used with the countable noun car.
However, it is important to remember that with the following adjectives, the use of countable and uncountable nouns will be different:
- some / any
- much / many
- little / few
- a lot of / lots of
- a little bit of
- plenty of
- enough
- No.
Some / any
The adjectives some and any can be used with both countable and uncountable nouns. Examples:
- «There is some milk in the glass.» (There is milk in a glass).
- «Do you any music?» (Do you like music?)
- «Do you have any pets?» (Do you have pets?)
- “There are some actors on the scene.” (On stage — actors).
Much / many
The adjective much is used only with uncountable nouns. For example:
- “I gained so much weight” (I gained so much weight).
- «She drinks so much coffee.» (She drinks so much coffee.)
The adjective many is used with countable nouns.
- «Many Italians are keen on pizza.» (Many Italians love pizza.)
- “The small boy was happy to see so many animals in the zoo.” (The little boy was happy to see so many animals in the zoo).
Little / few
The adjective little is used only with uncountable nouns. For example:
- “She feels little fear alone at home.” (She’s a little scared to be home alone.)
- «He had little time to prepare for exams.» (He had little time to prepare for the exam.)
The adjective few is used with countable nouns.
- «He has few options in this situation.» (He had few options in this situation.)
- «There are few animals in the desert.» (Few animals live in the desert.)
A lot of / lots of
The expressions a lot of and lots of are analogous to the adjectives much and many, but, unlike them, they can be used with both countable and uncountable nouns.
- «They have lots of (many) fans in Europe.» (They have a lot of fans in Europe).
- «They spent a lot of (much) money in the trip.» (They spent a lot of money on the trip.)
- «The boy saw a lot of (many) animals in the zoo.» (At the zoo, the boy saw many animals).
- «He gets lots of (much) pleasure walking in the park.» (He enjoys walking in the park.)
A little bit of
The adjective a little bit of in English is used quite rarely and always accompanies uncountable nouns. For example:
- «There is a little bit of sugar in the tea.» (There is some sugar in tea.)
- «There is a little bit of butter on the plate.» (There is some butter on the plate.)
Plenty of
The adjective plenty of can be used with both countable and uncountable nouns.
- “There are plenty of tourists in Rome.” (There are many tourists in Rome).
- «She uses plenty of pepper when cooking.» (She uses a lot of peppers when cooking).
Enough
Likewise, enough can be used with all nouns.
- «She has enough money to travel by plane.» (She has enough money to travel by plane.)
- «I have enough ideas to manage the project.» (I have enough ideas to manage the project).
No
The adjective no should be used with both countable and uncountable nouns.
Source: https://skyeng.ru/articles/kak-nauchitsya-upotreblyat-prilagatelnye-s-ischislyaemymi-i-neischislyaemymi-sushchestvitelnymi-pravilno

TranscriptFAQsPractice
Hey guys! Welcome to this video tutorial on word problems involving ratios.
Ratios are what we use to compare certain number values. People everywhere use ratios. We use, or at least we should, use ratios when we cook. For example, if I were to make macaroni and cheese for a group of 6 people and I knew that a (frac{1}{2}) cup of macaroni would feed one person, then I could multiply 6 times (frac{1}{2}) to get 3. Well, 3 to 6 is my ratio, and this ratio tells me that for every 3 cups of macaroni that I have, I can serve 6 people.
But hang on. What if I told you that 1 cup of macaroni to every 2 persons is the same ratio as 3:6? Well, it’s the same ratio. 3:6 can be reduced to 1:2 because both 3 and 6 are divisible by 3, which is how we get (frac{1}{2}). So, even though these two ratios look different, they are actually the same.
Let’s take a look at a few word problems, and practice working through them.
Example Problem 1
There are 7 kids in a classroom with green shirts, 8 with red shirts, and 10 with yellow shirts. What is the ratio of people with red and yellow shirts?
- 7:10
- 8:7
- 8:10
- 4:5
Alright, so let’s look at our problem, and see what it is asking us to find, and write out the information that we have been given.
So, there are 7 kids with green shirts; so, let’s write that down. We have Green: 7. We have 8 kids with red shirts, so that is Red: 8, and we have 10 kids with yellow shirts, Yellow: 10.
Now, the question is asking us to find the ratio of kids with red and yellow shirts. This means that we don’t even need to look at our number of green shirts. We’re just looking for the ratio of red shirts to yellow shirts. Well, we have 8 red shirts, and 10 yellow shirts, which gives us a ratio of 8:10.
So now let’s look at each of our options and eliminate. It can’t be 7:10, we don’t care about the green shirts. It can’t be 8:7, because again we don’t care about the green shirts. Option C is correct; that is the exact number ratio we found. Now, look closely at D here. Is 4:5 not the same thing as 8:10? 8 and 10 are both divisible by 2, and when we reduce them both down we get 4:5, so D is also correct!
Great, now let’s look at another word problem.
Example Problem 2
A vegetable tray contains 12 baby carrots, 27 cherry tomatoes, 18 florets of broccoli, and 45 slices of red bell peppers. For every 2 baby carrots, there are 3_____.
Alright, let’s start off the same way that we did our last problem; read through the problem, write down what we know, and find out what is being asked.
So, this vegetable tray contains 12 baby carrots. It contains 27 cherry tomatoes. We have 18 broccoli florets and 45 slices of red bell peppers.
Great, we have all of our information given in the problem, but what are we looking for? It says that for every 2 baby carrots there are 3 somethings. So, we need to find what those somethings are. How do we do that? Well, look at our original number of baby carrots in the problem, it’s 12, but in this ratio, it’s been reduced down to 2. What happened to make this number 2? It was divided by 6. So, since we are dealing with a ratio we know that whatever one number in the ratio was reduced by, the other number has to be reduced in the same way. So, we can multiply 6 times our 3, and 6 times 3 is 18.
When we look at all of our information written down, we can see that we have 18 broccoli florets; so there is our answer. For every 2 baby carrots, there are 3 broccoli florets.
Another way to check and verify that these two ratios are equal is by setting them up in fraction form and cross multiplying.
(frac{2}{3}=frac{12}{18})
When we cross multiply, we get (36=36).
You can practice finding ratios anywhere you go, like finding the ratio of boys to girls in your class.
I hope that this video helped you to understand how to solve word problems with ratios.
See you guys next time!
Frequently Asked Questions
Q
How do you figure out ratios?
A
A ratio is simply a comparison between two amounts. When figuring out ratios, it is important to consider what two values are being compared. This can be expressed in fraction form, in word form, or simply by using a colon.
When writing a ratio that is comparing a “part” to the “whole”, list the “part” first, and the “whole” second. For example, if you eat (3) slices of pizza out of (10) slices total, you have eaten (3) out of (10) slices. This can be expressed as (frac{3}{10}) or (3):(10), where the part is listed first, and the whole is listed second.
Ratios can also be “part” to “part” comparisons. For example, if there are (7) boys in a class, and (9) girls in a class, the ratio of boys to girls is (7):(9). Make sure to match the order of the ratio to the order presented in the scenario.
Q
What are basic ratios?
A
Ratios are used to directly compare two amounts. Basic ratios are used in many real-world situations, which makes it a valuable skill to master. Basic ratios can be expressed as fractions, words, or by using a colon. For example, (frac{4}{5}), “four to five”, and (4):(5), all represent the same ratio.
Q
What are the 3 ways to write a ratio?
A
A ratio is the comparison between two quantities. There is more than one way to write a ratio. For example, ratios can be written using a fraction bar, using a colon, or using words.
(frac{5}{8})
(5):(8)
(text{five to eight})
Q
What are equivalent ratios?
A
Ratios that have the same value are considered equivalent ratios. For example, if you slice a cake into (10) pieces, and you eat (2) pieces, you have eaten “(2) out of (10)” pieces, or (2):(10). If you had sliced the cake into (20) pieces, and eaten (4) pieces, you would have eaten the same amount of cake. Eating “4 out of 20” pieces is the same amount as eating “2 out of 10” pieces. Equivalent ratios occur when you multiply or divide both quantities of the ratio by the same amount. (frac{50}{100}) is equivalent to (frac{5}{10}) because when you divide both quantities of the ratio by (10), the result is (frac{5}{10}).
Q
How do you find an equivalent ratio?
A
Equivalent ratios can be thought of as equivalent fractions. Two ratios are equivalent if they represent the same amount. For example (frac{1}{2}) and (frac{5}{10}) are equivalent because they represent the same amount. Equivalent ratios are found by multiplying or dividing the numerator and denominator by the same amount. For example, (3):(4) and (15):(20) are equivalent ratios because both values in (3):(4) can be multiplied by (5) in order to create the ratio (15):(20).
Q
How do you solve ratio word problems?
A
Ratios have many real-world applications. Word problems that involve ratios will usually require you to find an unknown value by finding an equivalent ratio.
For example, if you made ($170) washing (10) cars, how much money did you make per car? The ratio of dollars earned compared to cars washed is (frac{170}{10}). We can divide both of these values by (10) in order to solve for the dollars earned for washing (1) car. (frac{170div10}{10div10}=frac{17}{1}). This means that ($17) was earned per car. Many word problems involving ratios require you to create equivalent ratios. Remember, as long as you multiply or divide both values of a ratio by the same amount, you have not changed the ratio.
Q
How do you write a ratio in words?
A
Ratios are used to compare two quantities. There are generally two ways to write a ratio in word form. When a ratio is considered a “part-out-of-whole” ratio, the phrase “out of” can be used. For example, if there is a pizza with (8) slices, and you eat (2) of those slices, you have eaten “(2) out of (8)” slices. However, some ratios are considered “part-to-part” ratios. For example, when comparing (3) green marbles to (8) red marbles, the phrase “(3) to (8)” can be used.
Q
How do you explain ratios and proportions?
A
Ratios describe the relationship between two amounts. Ratios can be described as part-to-part or part-to-whole. For example, in a new litter of puppies, (4) of the pups are female and (3) of the pups are male. The part-to-part ratio (4):(3) would be used to compare female to male pups. When comparing female pups to the whole liter, the part-to-whole ratio (4):(7) would be used. Similarly, the ratio of male pups to total pups would be (3):(7). If two ratios are equivalent, they are said to be proportional. For example, if (50) meters of rope weighs (5) kilograms, and (150) meters of rope weighs (15) kilograms, the two amounts are proportional. (50):(5) is equivalent to (150):(15) because both values of the first ratio are multiplied by (3) in order to create the second ratio.
Q
What is a ratio, short answer?
A
A ratio is a comparison between two amounts. Ratios can be written using a fraction bar ((frac{3}{4})), using a colon ((3):(4)), or using words (“three to four”). Ratios can be “part-to-part” or “part-to-whole”. For example, (5) green marbles and (7) red marbles would be a “part-to-part” ratio ((5):(7)). Solving (95) problems correctly out of (100) on a math test would be a “part-to-whole” ratio ((95):(100)).
Practice Questions
Question #1:
Cross multiply in order to determine which pair of ratios are equivalent.
3:5 and 4:9
6:7 and 7:8
7:8 and 35:40
12:25 and 14:17
Show Answer
Answer:
The correct answer is 7:8 and 35:40.
We can use cross multiplication to determine if two ratios are equivalent. Let’s look at the ratios for Choice C, and let’s set these up as fractions:
(frac{7}{8}) and (frac{35}{40})
Now, cross multiply by finding the product of (8×35) and (7×40). In both cases our product is 280, so we know that the original ratios are equivalent.
Hide Answer
Question #2:
Which ratio is equivalent to (frac{36}{45})?
5:6
4:5
(frac{8}{9})
(frac{5}{7})
Show Answer
Answer:
The correct answer is 4:5.
We can simplify ratios with the same strategy that we use to simplify fractions. In the ratio (frac{36}{45}) we can divide the numerator and denominator by 9. (frac{36}{45}) now becomes (frac{4}{5}) or 4:5.
Hide Answer
Question #3:
James has a bag full of red, blue, and yellow candy. There are 10 red candies, 9 blue candies, and 11 yellow candies. What is the ratio of blue candies to total candies in the bag? Simplify the ratio if possible.
Show Answer
Answer:
The correct answer is 3:10.
The total number of blue candies is 9, and the total number of candies in the bag is 30. If we set this ratio up as a fraction, we have (frac{9}{30}). This fraction can be simplified if we divide the numerator and denominator by 3. Our final answer is (frac{3}{10}) or 3:10.
Hide Answer
Question #4:
Alex is counting the coins in his pocket, and finds that he has 14 quarters, 7 nickels, and 4 dimes. What is the ratio of quarters to nickels? Simplify if possible.
Show Answer
Answer:
The correct answer is 2:1.
We can compare the number of quarters to the number of nickels by setting up a ratio. There are 14 quarters and 7 nickels, so our ratio would be 14:7. Choice B says 14:7, but we should simplify when possible. 14:7 simplifies to 2:1.
Hide Answer
Question #5:
In Mr. Jenkin’s 4th grade class there are 14 boys and 17 girls. What is the ratio of boys to girls? Simplify if possible.
Show Answer
Answer:
The correct answer is 14:17.
We can express this comparison of boys to girls as a ratio. 14 boys and 17 girls can be described as the ratio 14:17, or the fraction (frac{14}{17}). 14 and 17 do not have any factors in common, so 14:17 is in simplest form.
Hide Answer
Return to Basic Arithmetic Videos
104804