Word problems using expressions

Rational Equations: Applications — Work

He’s not as efficient as Anya, so it takes them a little bit longer. This information right here. When both pipes are opened, they fill the pool in five hours. So we figured out Anya. Shalini can run 3 miles per hour faster than her sister Meena can walk. We are actually adding the Work they complete together and alone using formula , where the Time is 1 hour or whatever the unit is.

So the number of hours it takes Bill to paint the deck is twice as long as the number of hours it takes Anya to paint a deck. And then we know that it takes Bill twice as long as Anya. Anya and Bill stained a large porch deck in 8 hours. It takes Jill 3 hours to make sandwiches for a charity organization as many as they need. Find the average speed rate of the canoe in still water. How much part of the water melon will each get including Mary? We solve these problems directly by performing the operations.

Takes them 8 hours. Let me scroll down a little bit. In these kind of problems, we have to solve for x. The part of the house cleaned by jack is: Let t be the time taken to complete the job together. Now, let’s do another variable for Bill just like that. If the two hoses are working, and the drain is open by mistake , how long will it take to fill the swimming pool?

So we can rewrite this equation as– I’ll stick to the colors for now. Let the whole water melon be denoted by 1. So, Daniel reaches the house at The individual rates of each worker is , and when you multiply the rate by the time they work, you get.

How long would it take to fill the pool if only the slower pipe is used? But it makes sense that combined they’re going to take less time than individually. Solving Word Problems with Rational Expressions A rational expression is an expression which is expressed in the form of two polynomials.

Combined rates rational equations Video transcript Working together Anya and Bill stained a large porch deck in 8 hours. If the first painter can do the entire job in twelve hours and the second painter can do it in eight hours, then this here is the trick! So the number of hours it takes Anya to paint a deck, or A, is 12 hours. Plus– do that same color. The year before Bill painted it by himself, but took twice as long as Anya did. One pipe can fill a pool 1.

Here are some examples. For word problems with rational expressions, first we have to convert the word problem into a rational expression and then, we can easily solve the rational expression. So B is equal to 2A.

Published
August 30, 2017

An algebraic sentence when written in equation form involves algebraic expressions (which contain variables such as letters in the alphabet), constants, and an equal symbol. Each algebraic sentence may contain a combination of algebraic expressions and constants, or with just two or more algebraic expressions. Almost always, the word “is” in an algebraic sentence denotes the symbol of equality.

In our example above, the algebraic sentence, “Five more than twice a number is forty-three“, is translated and written into its equation form: 2x + 5 = 43.

But before we delve into solving word problems that involve algebraic sentences, it’s crucial that we become familiar with how to translate and write algebraic expressions.

---

Algebraic Expressions

Learning how to write and translate algebraic expressions is the foundation in writing algebraic sentences. Eventually, we will use this knowledge to write algebraic equations where we solve for the value of the unknown variable.

What is an algebraic expression?

Think of an algebraic expression as the equivalent of a phrase in the English language. It does not convey a complete thought but is an important building block in constructing a sentence. Algebraic expressions consist of numbers, variables, and arithmetic operations.

Let’s take a quick look at some math phrases that were translated and written into algebraic expressions.

• the sum of a number and 8 large{,,, to ,,,, {color{red}{c + 8}}}

• 3 less than a number large{,,, to ,,,, {color{red}{y — 3}}}

• the product of 45 and m large{,,, to ,,,,{color{red}{45m}}}

• a number divided by 2 large{,,, to ,,,,Large {color{red}{x over 2}}}

---

Translating and Writing Algebraic Sentences

Once you know how to translate math phrases into algebraic expressions, it’ll be easy for you to translate and write algebraic sentences in an equation form as well.

For instance, how do you write “the difference of 16 and k is seven” into an algebraic equation?

Let’s deconstruct this algebraic sentence.

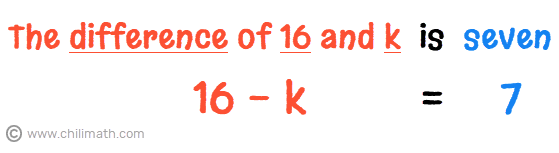
You may notice that we translated “the difference of 16 and k” into an algebraic expression, 16-k, then used the equal symbol (=) in place of the word “is”.

As I mentioned at the beginning of this lesson, the word “is” in an algebraic sentence, most of the time, signifies the equality symbol which is the case in this example.

Therefore, we can write this algebraic sentence in equation form as 16 — k = 7.

Now that we are confident in translating algebraic sentences and writing them in an equation format, it’s time for us to take one step further. We will not only translate and write algebraic sentences into algebraic equations but also proceed to solve them.

---

Examples of Algebraic Sentences Word Problems

The main key when solving word problems with algebraic sentences is to accurately translate the algebraic expressions then set up and write each algebraic equation correctly. In doing so, we can ensure that we are solving the right equation and as a result, will get the correct answer for each word problem.

Example 1: Six more than seven times a number is thirty-four. Find the number.

First, let’s deconstruct the algebraic sentence. It’s important that we identify and separate the algebraic expressions from the constants as well as determine if the problem suggests equality between the terms.

For the unknown value, we’ll use large{x} as our variable.

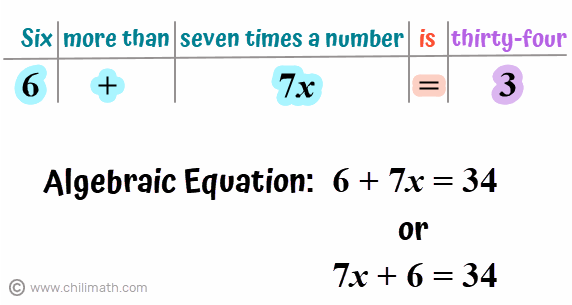
Note: Since addition is commutative, changing the order of the addends on the left side of the equation does not change the sum. Therefore, we may also write the algebraic expression as 7x+6 or the algebraic equation as 7x + 6 = 34 instead.

However, for our discussion, we will use 6 + 7x = 34 as our equation.

The original problem asks us to find the number which in this case is large{x}. So our next step is to solve for large{x} in our equation, 6 + 7x = 34.

Solution:

Now, we’ll evaluate the value of large{x = 4} to verify if the number we found satisfies the original algebraic sentence.

Remember that we are asked to find the identity of “the number” in our algebraic sentence and NOT the value of the variable large{x}. Therefore, it will be incorrect to say that large{x=4} is the answer. This is a common mistake that we always need to pay attention to.

We’ll replace the variable large{x} with the number 4 to see if the algebraic expression on the left side of the equation also results to 34.

Yes, it does! This means that number 4 is the answer.

---

Example 2: The difference between three times a number and five is sixteen. Find the number.

Right away, the word “difference” in our algebraic sentence gives us a clue that we will be using the subtraction operation. But, unlike, in addition, the order of the terms within an expression matters in subtraction. So we have to make sure that the terms in our algebraic expression are set up in the correct order.

Another keyword is “times”, which suggests that 3 is being multiplied to a number whose value is currently unknown.

This time, let’s use large{g} as our variable. Start by translating the algebraic expression correctly then continue to write the equation.

Now that we have our equation, let’s find out what the unknown value is by solving for the variable, large{g}.

Solution:

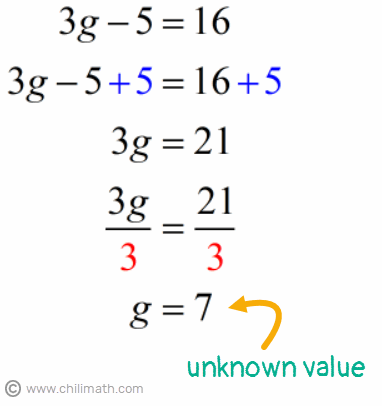
As discussed in our first example, it is important that we verify if the result of our solution makes the algebraic equation true. For this one, I will leave it up to you to evaluate the value of large{g = 7}. Remember to replace the unknown value of the variable large{g} with the number 7 to see if the left side of the equation is also equal to 16.

Since the original algebraic sentence requires us to find the number, then the answer is number 7.

---

Example 3: A number decreased by half of the number is four. Find the number.

This algebraic sentence is quite interesting because we don’t just have one unknown value, but two! First, we have the “number” (the unknown) then the “half of the number”, which means one-half of the unknown.

The keyword “half of” also indicates multiplying something by one-half while the “decreased by” tells us that we will be subtracting one term from the other.

To organize our thoughts, let’s deconstruct this algebraic sentence into its meat and potatoes.

Being able to break apart our algebraic sentence into its basic parts allows us to read the sentence thoroughly and understand the relationship between its quantities.

After setting up our algebraic equation, our next step is to solve it for large{m}.

Solution:

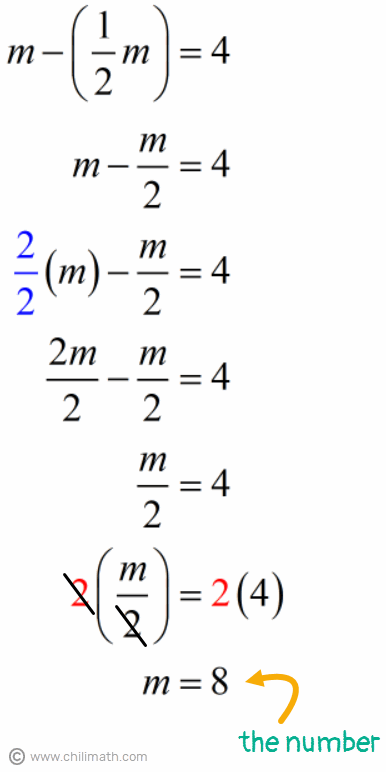
We need to evaluate the value of large{m = 8} to check if the number we got makes our algebraic equation true.

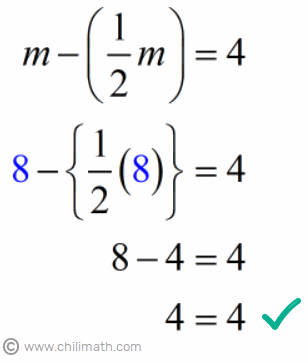
Great! The values on both sides of the equation are equal to each other. Therefore, the number 8 is the correct answer to our original algebraic sentence.

---

Example 4: Four times the sum of twice a number and six is thirty-two. Find the number.

Looking closely, we see a few keywords that would help us in translating this algebraic sentence into an equation.

• times – means that we’ll be multiplying 4 by the quantity, “sum of twice a number and six”
• sum – means that we need to add the terms, “twice a number” and six
• twice – means that a number (the unknown value) is multiplied by 2

With these in mind, let’s write our algebraic equation.

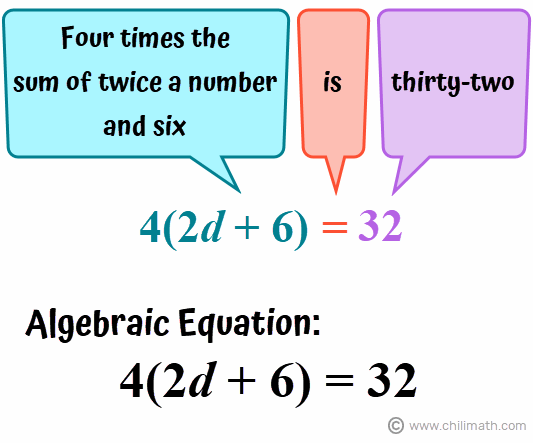
Notice that we used the variable large{d} in our equation to stand for our unknown value. Let’s now proceed and solve for large{d} and afterward, check if the value we get indeed makes the equation true.

Solution:

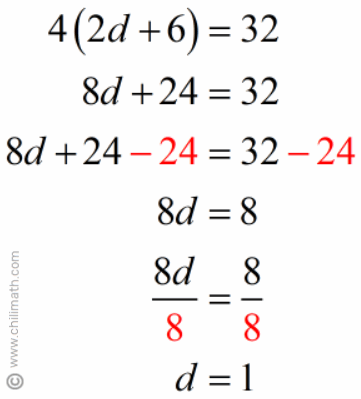
Evaluate the value of large{d = 1}:

Looks like everything checks out, so the answer to our algebraic sentence is the number 1.

---

Example 5: Two-thirds of the sum of three times a number and six is ten. What is the number?

This problem involves a fraction and an algebraic expression as you can tell. The keyword “of” indicates multiplication, so it tells us that we need to multiply the fraction large{2 over 3} by the sum of the two given quantities (“three times a number” and six).

Let’s move on and write our algebraic equation. We’ll use the variable large{y} as the placeholder for our “number” whose value is currently unknown.

Awesome! We are able to translate our algebraic sentence into an equation. It’s time for us to solve for large{y} then I’ll leave it up to you to do a check if the number we find as the value of large{y} makes the algebraic equation true.

Solution:

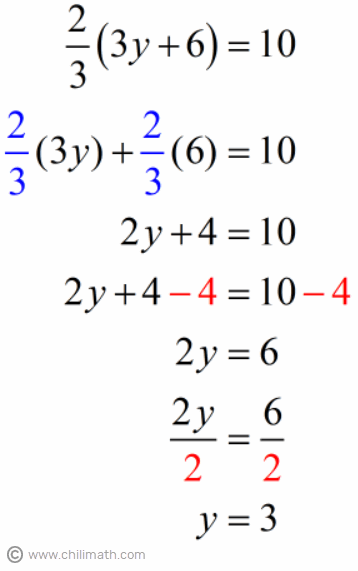
Once you evaluate large{y = 3}, you’ll see that the answer to our word problem is indeed the number 3.

---

Example 6: Twice the difference of a number and three is four more than the number. Find the number.

We have an example here that is a little different from the word problems we’ve covered so far. In this algebraic sentence, both sides of the equation contain an algebraic expression. However, the keywords present will help us translate it correctly into an equation so there’s nothing to worry about.

Keywords:

• twice – means that we will multiply the quantity (difference of a number and three) by 2
• difference – tells us to use the subtraction operation between our unknown value (“number”) and three
• more than – means that we need to add four to our unknown value

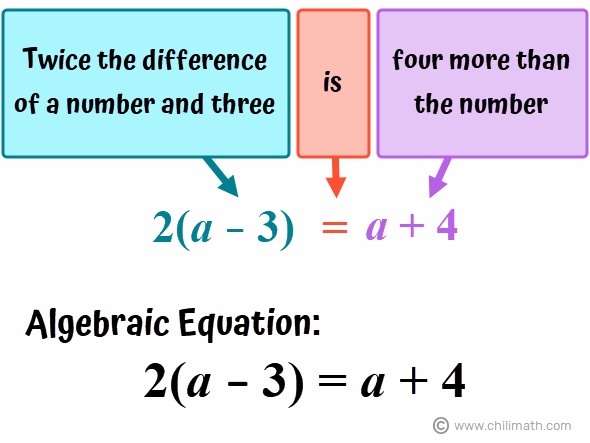
Let’s solve for our unknown value, large{a}, then verify that our result makes the algebraic equation true.

Solution:

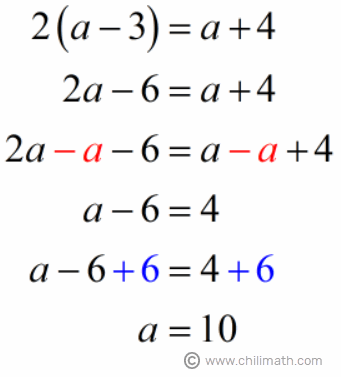
Evaluate the value of large{a = 10}:

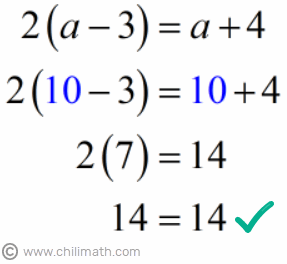
Perfect! The value we got for large{a} which is 10, made our equation equal on both sides. Thus, the answer is the number 10.

---

You might also be interested in:

Algebraic Expressions

Algebraic Expressions Worked Examples