“If Johnny has eight apples, and he gives three of them away to Sally, how many apples does he have left?” Word problems have long been met with dread by math students from all walks of life. Normally, when people think of mathematics, words are not the first visual that comes to mind; it’s numbers! However, the importance of word problems cannot be discounted. Studies on education have shown that word problems have many benefits. Of course, we at A Grade Ahead definitely see the value of word problems; our math curriculum has an emphasis on building the skills needed and completing word problems in our unique enrichment program. Let’s explore the benefits of word problems below!
Why Are Word Problems Important?
Strengthen Problem-Solving Skills
Although number-based math involves problem solving, thinking about solutions in the form of words is much more impactful and applicable to other areas of a student’s learning and cognitive development. As in life, when certain problems arise, people must be able to think about solutions in different formats in order to conjure up the best possible solution. This website offers some tips on how to help children improve their abilities to work through word problems, and therefore, improve their problem-solving skills.
[button url=”https://academy.agradeahead.com/curriculum-samples/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: chevron-circle-right” text_shadow=”0px 0px 0px #000000″]Get my FREE curriculum sample![/button]
Improve Comprehension and Analysis
Math isn’t the subject where people would imagine comprehension skills could be built, but that is just another testament to how important word problems are! Word problems offer a way to practice close reading, visualizing, interpreting, and analyzing. Students are presented with a story in a word problem. They must read closely to understand what information is important, and visualize it to gain a complete view of the goal. They must know what the question means and analyze the question for clues to how to solve the problem. All these skills are practiced before the student even begins applying any math equations!
Build Logical and Critical Thinking Skills
Students must transform numbers to visuals in their minds, and then back into numbers again – all while addressing all the logical limitations of the problem.
Including numbers in real-life scenarios makes math more interesting for students! Often, when just using math rules and not thinking critically about the problem, students can make mistakes and come up with nonsensible answers. However, because there is no scenario attached, students may not understand why such answers don’t work. For example:
Solve for x: 15x – 170= 100.
The correct answer is 18, but students who are unsure about the correct process for solving this problem could answer anything from -163 to 4 to 4,050! Without any context, these students won’t necessarily notice a logical problem with their answers. Let’s try again in the form of a word problem.
A car company must sell 100 cars each week in order to make a profit. It costs the company $170 to pay its fifteen employees each week. How many cars does each employee have to sell this week in order for the company to make a profit?
Using the scenario given, students may set up the problem as it is shown numerically and solve. However, now that we have a situation to go along with, answers like -163, 4, and 4,050 really don’t make sense, and students will be able to notice that. Word problems are important for learning because they develop a child’s logical thinking skills.
[button url=”https://academy.agradeahead.com/our-programs/math/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: pencil” text_shadow=”0px 0px 0px #000000″]Improve my child’s math skills![/button]
Develop Creativity
Becoming a word-problem master is one step toward becoming a master at life! This blog post by John Marsh gives some examples about why that is. When students can use their imaginations to visualize and explore the dimensions of various word problems, they can become more motivated to solve scenarios than if they are looking at monotonous number combinations.
Plus, this will help students when they are looking at numeric equations. They may be able to apply the word-problem thinking to come up with solutions to a math problem by imagining an equation as a word problem! Creativity is key both in the classroom and in life satisfaction, so we should probably start teaching our kids its importance through word problems!
Get Invested
One of the main struggles that teachers face in the math classroom is engaging students and making them feel excited to learn. This website gives some creative word problems that students will enjoy working on for a wide variety of math topics.
How often do you think teachers hear the question: “Why are we learning this?” (Hint: It’s a lot!) Word problems are one way to show students how they might be able to use math in their lives now, or in the future. What student doesn’t want to imagine they have 10 cookies? The bottom line is students will be more inclined to practice skills if they are convinced that it will actually be useful.
Practice, Practice, Practice!
Word problems give students a way to practice all the tools they have learned. Especially in higher levels, word problems involve multiple steps and can use many different types of math. Often, students are able to bring in concepts learned in past chapters or even past grades. This helps reinforce previously learned topics and show students the benefits of learning a concept instead of memorizing it for a test!
Demonstrate Knowledge
Word problems are a key tool in determining what material a student feels comfortable. With multiple choice problems, or even basic solving, there are many opportunities for children to get the right answer without actually understanding the process or rationale behind the math. But, with word problems, students must display the higher levels of thinking that is required, meaning that they must display that they have the knowledge needed to solve the question. Word problems make it easier to see what concepts students need extra help on.
[button url=”https://agradeahead.com/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: map-marker” text_shadow=”0px 0px 0px #000000″]Find my nearest A Grade Ahead location![/button]
After reading this, we hope you see the importance of word problems, too! If your child is struggling to apply his or her knowledge to word problems, consider an enrichment program at an academy or at home and practice the skills above.
Can you think of any more reasons that show the importance of word problems for student learning? Do you think word problems have helped your child? Let us know in the comments below!
Author: Morgan L., Writer and Teacher at A Grade Ahead; Brenna Waugaman, Writer and Teacher at A Grade Ahead
Get Notified When New Articles Post
Sign up to receive one email per week from A Grade Ahead full of parenting tips and helpful articles. Enter your information on the right hand side of our Blog page and we will add you to our list of subscribers. We also welcome your feedback and comments on our posts!
I really love doing Facebook LIVE presentations. I particularly enjoy it when I have the opportunity to talk about something that strikes a chord with homeschool parents. We did a Facebook LIVE video talking about working with students and mathematical word problems. It was like touching that third electrified rail in so far as how people feel about word problems! It would be fair to divide us into two groups:
1) Those who find word problems to be fascinating puzzles.
2) The rest of us, who really do not have an affection for word problems.
In the interest of true confession, I have never been a particular fan of mathematics. You can assign me the task of diagraming sentences all day long. In my opinion, word problems can be sometimes inscrutable.
Steve Demme (the author of Math-U-See) said to me once, “Well, Gretchen, you know when you solve math problems as an adult, they ARE word problems.” Point taken. While I would not say I love word problems to this day, I no longer have an adversarial relationship with them. One of the things I’ve always loved about Math-U-See is taking the sting out of word problems by making them a part of the daily lessons. What, however, do you do if you did not start your mathematical journey with Math-U-See?
We as parents have to be able to model for our children how to meet the challenge of word problems head on, and toward that end I want to share with you some of the tips that were shared in the Facebook LIVE video. I also have some things to say about math anxiety in adults.
You can also watch the video below, if you prefer.
Below you will find several tips to implement when working with word problems with your children. These tips are applicable, regardless of the age of your student, their mathematical experience, or even the level of Math-U-See in which they are working. As always, I am indebted to our tremendous customer service team. They are the contributors of much of my list here. You do know, of course, that being a member of the Demme Learning family means that you can call our team and ask for help if you are having a struggle. We want your success!
10 Ways to Make Word Problems Fun
1) Start With Fresh Eyes
If you are just completing a math lesson, and have already been at it for 15-20 minutes, take a break before you begin the word problems. Stand up and do some jumping jacks, have a snack, take a break. Then sit back down to the word problems.
2) Read the Word Problem All the Way Through First
Read the word problem all the way through first; don’t worry about the numbers in the word problem. Then ask yourself and your student, “do we understand what it’s all about”? Are there any new terms we are unsure of here? Are there words we don’t know?
3) Reread the Word Problem Again
Reread the word problem again; out loud is best. I know that reading out loud seems silly, but it is tremendously helpful.
4) Skip the Numbers
Sometimes in the reading out loud is it helpful to just skip the numbers altogether. Instead of reading the number, add some humor by saying “BEEP” instead of the number. Humor really DOES help learning! You can change the names of the people in the word problems to your children, their friends, or even their favorite super hero.
5) Circle Keywords
Are there keywords you can circle? “Sum”, “in all” and “all together” usually mean addition. “How many are left/remaining”, or “What is the difference” usually means subtraction. The word of is an important one as in “1/4 of 12” or “5/10 of a dollar” means you are being instructed to multiply. There are other key math words that may help you analyze a word problem – but be careful.
Depending on key words alone does not encourage students to think mathematically about a problem or use logic to reason toward a solution. Sometimes key words do not appear in problems, or additional operations may be required to find the final answer Encourage them to take the whole of the word problem in context. Make sure you both understand what the problem is asking before seeking out those individual words.
6) Rewrite the Word Problem
If word problems cause anxiety in your child, help them become the drafter of word problems. For example: 12-7= ? That is the computation. Have your student create a situation to accompany those numbers. Developing a proficiency in creating word problems really helps students develop confidence in analyzing them.
7) Word Problem Writers Are Sneaky
Remind your student that those who write word problems are a sneaky lot. They will put in information that is not necessary just to throw a student off track. If irrelevant information is a challenge for your student, try creating some word problems that contain unnecessary information. Help them become proficient in knowing what is not necessary – that is a life skill in and of itself!
 Consult the Instruction Manual
Consult the Instruction Manual
If there is a lesson in the Math-U-See curriculum that is giving you a particular challenge, make very sure you have consulted the corresponding lesson pages in the instruction manual. We always provide instruction for the how as well as the why, and often, if a family is challenged with a lesson, we find that the answers they seek can be found in the lesson manual pages.
9) Review the Questions
Word problems need to be answered in words too. Make sure that you have answered the question in words. Further, does your answer make mathematical sense? Can you plug your answer back into the word problem and work it out to to see that it is indeed correct? Remember this step. This leads to frustration for a student who has worked hard, and perhaps not found the right answer.
10) Relax
Just like any skill, learning to negotiate word problems is something that happens over time. You are not going to be an overnight success (most of the time). But if you, as the parent, can stay affirmative and encouraging, you can make a tremendous difference for your student.
In conclusion, I realize that this blog post is long. The information will be helpful to you. If you still want more, we offer more help with word problems on our parent resource page:
Word Problem Tips [PDF]
We do need to have a conversation about what our math anxiety does to our children. Look for that blog post to come in the near future. We want you and your student to have success in all your mathematical endeavors!
One important reason for studying mathematics is to nurture an aptitude for and a confidence in problem solving. To be good at problem solving, one must be able to sort through the unknown, make sense of it, persevere in it, and come away with a solution. This ability is not only critical to mathematics, but learning to solve problems successfully crosses over all aspects of life, in school and out.
George Polya’s book, How to Solve It was published in 1945. Polya, frequently referred to as “The Father of Problem Solving,” is best known for the following four basic principles of problem solving.
| George Polya’s 4 – Step Problem Solving Principles |
| 1. First Principle: Understand the problem. |
| 2. Second Principle: Devise a Plan. |
| 3. Third Principle: Carry out the plan & Solve the problem. |
| 4. Fourth Principle: Look back & Check for reasonableness & accuracy. |
These principles still stand today as reliable strategies for problem solving. Unfortunately, over time, the original significance inherent in each of Polya’s steps became less like real problem solving and more like a trick for quick calculating.
As a result unfortunately, an approach to solving word problems known as “find the magic words” was born. Instead of actually reading the problem, students just followed a scripted formula – underline numbers, find and circle magic words and Presto, put them together and problem solved. But is it?
Tracy Johnston Zager (@TracyZager), a highly respected math coach and author, shared the following two problems with her twitter followers.
First grade word problem
Lois has 16 counters.
She gets 10 more counters.
How many counters does Lois have in all?
HINT for students usually written in textbook:
Now here is another first grade word problem.
There are 20 pens.
10 pens are in each box.
How many boxes in all?
a. 1
b. 2
c. 20
d. 30
Several of the students she observed chose D. This answer proves more students are adopting the “magic words” method to problem solving. In fact, this is just a small sampling of what is now seen as routine in solving word problems; students don’t see a need to even read the words in context any longer. They simply circle the magic words; in this case, “in all,” underline the numbers; in this case 20 and 10, and then just “put them together”; in this case 20 + 10 = 30.
But 30 boxes of pencils is not a reasonable solution to this problem. The truth is, when students only use finding magic words as their method for understanding a word problem, the meaning behind the math-at-hand is missing.
Here’s another dilemma; as children get older and the problems get bigger, the magic-word approach rarely works.
When students mindlessly pull out and put together isolated words and numbers, the essence of the problem gets lost and the meaning within that context gets watered down to a few scripted steps, regardless of what the problem really means.
The acronym CUBES as a similar pick-pull-and-calculate method to problem solving is getting popular. Check out the premise behind the problem solving; circle, underline, calculate.

The problem with CUBES and similar strategies is that as students get older, the problems require more thinking, with layers that cannot be solved with a simple pull and put together method.
Without a real understanding of how to comprehend a word problem, students are not only led astray, but grow up thinking that problems are not worth investigating. In fact, students using these approaches can get the impression that problems are neat and tidy; when actually problems can get quite messy requiring logic, persistence, and creativity as trying alternative strategies can help clear the muddy waters a bit.
What’s a teacher to do?
One answer is for teachers to first spend valuable instructional time investigating and modeling what it means to actually understand a word problem.
Below you will find a sample anchor lesson for modelling how to think like a real mathematician when understanding word problems.
Anchor Lesson for what it looks like and sounds like to understand a word problem like a Real Mathematician
Purpose:
- Students will notice how a mathematician understands a word problem.
- Students will relate the skills a mathematician uses in understanding to that of a reader, scientist, historian, etc.
- Students will identify how using the strategies makes comprehension easier.
Directions:
Setting the Stage:
- Put up the following text (or something just as difficult) on Smartboard.
(Students should not have a copy of this.)
We now know that we can find equilibria solutions to a differential equation by finding values of the population for which dP/dt=0. But we also observed that the two equilibria solutions for the logistic population model differ: for equilibrium, nearby trajectories (solutions to the differential equation) are “attracted” to the equilibrium; for the other equilibrium, nearby trajectories are “repelled.” We call the first case a stable equilibrium (also called a sink) and we call the second case an unstable equilibrium (also called a source).
- Challenge your students to switch roles with you. They are now the teacher and you are the student. They will be “grading” you in how they think you did as a reader.
- Make sure you have read this ahead of time several times. Really impress the students with your oral reading. Exaggerate your reading so it sounds like you really understand the piece.
- Have the students talk to a partner and come up with a grade on how you did as a reader.
- Ask them what grade they gave you and why they gave you that grade. They will more than likely give you an “A.” (I always get one “C+” from the student who is going for the laugh.)
- Here’s the powerful part – reveal that you have no idea what you read. Share what Cris Tovanni calls “fake reading.” That is reading without thinking. Reveal that if they asked you anything about what you read, you would not be able to answer it because you really have no idea what you read. Add that real reading means you are actively involved. It takes both text and thinking.
- Let the students know the same thing happens in mathematics. Sometimes we just keep moving along in our problem solving without thinking. When that happens, we really can’t get any real meaning out of it. Sometimes we even just circle magic words and underline numbers thinking this alone will help us make meaning of the problem. But, without any real connections to what we underline, we rush into strategies without thinking and that can sometimes lead us astray.
- Ask students how many of them have ever faked their way through a math problem – they didn’t think, they just kept moving along. Raise your own hand. We’ve all done it.
Think Aloud:
- Put the following problem (or any open-ended math prompt) on your Smartboard. Students should not have a copy of the problem. That can be distracting. You want them to pay attention to your Think Aloud.
A total of 8,000 runners started a long distance race. The results of the race are listed below.
- 3/15 of the runners finished the race in less than 4 hours.
- 0.6 of the runners finished the race in 4 or more hours.
- The rest of the runners did not finish the race.
A. Calculate the number of runners who finished the race in less than 4 hours. Show and explain all your work, even if you used a calculator.
B. Calculate the number of runners who did not finish the race. Show all your work. Explain why you did each step.
- Give out the following T-Chart for students to complete during your Think Aloud. Make a copy on chart paper to use as an anchor reference in future problem solving.
| How to think & UNDERSTAND a word problem like a REAL mathematician | |
| What did you notice your teacher doing to understand a word problem like a real mathematician? | How did what you noticed help your teacher better understand the problem? |
3. Tell students that you are going to think aloud through this problem. Challenge them to notice and write anything you did to help you make meaning of the text and think like a real mathematician.
- Read the entire problem through one time (Do not read parts A or B yet). Then say, “Wow, that’s a lot of information. I think I better reread it slowly and take it apart.”
- Start over and read the first sentence. Stop and make a personal connection that helps you visualize the scenario, but get off track a little. (Use this step if you are noticing students losing focus during problem solving). Say something like, “I can make a connection to this. I went to a marathon once. I can picture that day. That was a really hot day. Oh wait, I’m getting off track. That connection is not helping me make meaning of the text. I’m going to have to ‘turn down the volume’ to that and get back to the problem. I better reread it from the beginning to get myself back on track.”
- Continue reading. Share that you first want to remove the numbers in your mind so you can connect to the story. Now replace the numbers accordingly:
- with “the total number of runners” for 8,000
- “one part” for 3/15
- “another part” for 0.6
- “a third part” for the words “the rest” in the third bullet.
- Identify there are three parts that make up the total number the runners in the race. (This will give your students a sense of the part/part/whole relationship).
- Reread the problem again, this time with the numbers included. Make a connection to 3/15 of 8,000. Say something like, “Hmmm, 3/15 of 8,000. Let me make sense of this before I move on. I know that 3/15 expressed as a friendlier fraction is 1/5. Write 1/5 in front of 3/15. Draw a visual. It can be the race (an open number line) showing what 1/5 would look like. I know in my brain that 1/5 of 8,000 is 1,600. So 1,600 runners finished the race in less than 4 hours. That’s not a lot of the runners. Point out the remaining part of the open number line (leaving four more fifths).
- Read aloud the next sentence, “0.6 of the runners finished the race in four or more hours.” Say a connection to your math class and say something like, “I remember when we were working with fractions and decimals and I found it easiest to work with either all fractions or all decimals.” Now depending on your students, you choose what you would like to do. If you want to focus on the part/part/whole relationship using fractions, say something like, “I think I’d like to continue my drawing using fractions, so I started with 1/5 and now I have 0.6 of the runners. If I think of 0.6 as a fraction, I am thinking of 6/10. Since I already am working with fifths, I’m going to rename 6/10 as 3/5.” Now draw what three more fifths would look like on your open number line. And say “If 1/5 is 1,600, then 3 times that or 3/5 would be 4,800 runners. That means most of the runners finished the race in 4 or more hours. (Purposely do not underline numbers and circle magic words. Just connect to context and meaning. Estimate and make numbers friendly and reasonable.)
- Notice that “If 1/5 finished in less than four hours, and 3/5 finished in four or more hours, that leaves 1/5 that did not finish. You know this because 1/5 + 3/5 + 1/5 = 1. (Draw as a fraction bar or show it on your open number line). That means the same amount of runners that finished in less than four hours also didn’t finish the race.
- Saying something like, “Wow, this is easy. I really understand the story in this math. I’m ready to begin reading my questions and solving my problem.”
Reflecting on Student Noticings:
- Stop and have partners share what they noticed you doing to think like a real mathematician and not just do fake math.
- Discuss with the whole class and write down what the students noticed as a T-chart on chart paper to use as a reference. Take ideas and reframe them to include good thinking strategies. Do they notice you visualizing, making connections, and looking for the mathematical patterns in the numbers; ‘turning down the volume” to connections that distract; making sense of the problem; rereading to clarify; rereading to get back on track; making a model; asking questions; using friendly numbers to help with mental math; staying in the context; and estimating?
- Challenge the students to discover how this all helped you make meaning of the text. Remember to share that is how mathematicians think. In fact, it is how scientists think, and historians, etc. Good thinking is good thinking. It crosses over content area. Students should now record their reflections on the right side of the T-Chart.
- Point out that you didn’t even begin answering the questions yet; you were making sense of the problem first.
- Do not solve the problem. It can be a problem they solve later on.
Students Give it a Go:
- Hand out copies of similar problems and have partners use active reading strategies to think through the problems out loud to each other. While one student thinks aloud, the other student notices what critical thinking habits they used to make meaning of the text.
- If you have time, they can solve the problem. Be careful not to rush into this. The focus here is how to think critically through problem solving.
A Student Resource for Math Fix-up Tools
One of the best math consultants in the country, Donna Boucher (@mathcoachcorner), and I collaborated on a list of Fix-up Tools for Mathematics. We have found this to be very useful in helping students recognize when their attention wavers and then have the tools they need to get back on track in their problem solving.
Feel free to download and share!
One of the most common refrains I hear from parents and teachers is that their kids struggle most when faced with a word problem (or story problem). This is not surprising–a problem involving a single operation, with nothing to decipher or decision to make is straightforward. If the problem says to add, you add. If it is a long division expression, you divide. But a story that uses math to model the world around us takes computation to a whole new level. And often, it causes kids to immediately freeze up. But it doesn’t have to be this way! Hopefully these word problem templates will help.
In my course on making sense of word problems, I share several meaningful ways you can help kids break down and think through word problems to solve them with confidence. And one of the things I created to go with that course is this set of word problem solving templates.
One of the biggest issues I see most kids have when it comes to word problems is that they don’t want to take time to think about the situation. In other words, what is actually happening in this story? How does it relate to the math operations that I know?
Instead, kids will pull out all the numbers and attempt to use keywords to guess at a math operation. In the early years, kids will likely just add all the numbers together.
Related: The Problem with Using Key Words to Solve Word Problems
But what if that’s not what the question is asking in this situation?
Instead, kids need to be able to visualize the problem and explain the situation in their own words so they can use the appropriate math operation to solve (and know why they used it).
How much help and support kids need to do this will vary by child, so I created a variety of problem solving templates that force them to think about the problem in several ways and make sure that the operation they use and final answer make sense.
The best part? These templates are blank (so you can use them in kindergarten all the way to high school) AND editable! So you can simply type a problem into the template and print and then your kids are ready to solve:
How to Use the Word Problem Templates:
First, decide which template you think will work best for your students (and fits your priorities in terms of what you want them to do).
These begin with a very simple template that focuses on drawing a picture or visual of some sort to model the problem, doing the actual work of computation and then writing the final answer in a complete thought.
But you may want your kids to show more of their thinking or help them to connect the dots a bit more. So there are then templates that ask them to identify the unknown or to write an equation before they do the work. Again, use whichever template works best for what you want your students to do and how much support they need.
Lastly, there are templates that include space to write a ‘plan’ for how they want to solve it and also to check their work.
Many kids rush through the actual computation without going back to make sure first that their work is accurate, but also that their answer actually answers the question.
It could be that their work is correct. They may have added or subtracted with regrouping beautifully and neatly written their final answer. But the problem may have asked a completely different question.
Altogether, there are 7 word problem templates in this download, and they are all editable, allowing you to type any word problem into the box.
Although I don’t recommend you require this much work for every single problem your students solve, it can be a useful teaching tool when you first begin. It can also be helpful if students are feeling stuck on a problem and just need a little guidance to get their thinking out of their brain and onto paper.
Get the Word Problem Solving Templates FREE!
However you are able to use these templates, I hope it provides a useful tool for kids to understand and solve word problems!
Simply fill out the form below to receive these templates right in your email inbox. 🙂
We recommend reading any word problem at least three times. By the conclusion of the third reading, you should be magically whisked away to your home in Kansas.
Read it once…
…to get a general idea of what’s going on. Is the problem about money? Height and width? Distances? Money? Yeah, we already said money, but it’s important. Can you draw a picture in the margin that helps you visualize the problem?
Twice…
…to translate from English into math. Read the problem carefully this time, figuring out which pieces of information are important and which ones aren’t. Then ignore the unnecessary bits. This may sound a bit harsh, but they’re big boys. They’ll get over it.
Three times…
…a lady. Wait, that’s not it.
…to make sure you answered the right question. To be sure, read the question one last time before drawing a box around your final answer. Even if this method of double-checking saves you only once out of every 100 times, it’ll help you in the long run. One out of 100 is better than zero out of 100, but now we’re moving into some advanced mathematics.
Sample Problem
The local department store was having a sale. Holla! Gabe bought a pair of shoes for $21, although they would’ve been cheaper if he’d bought penny loafers. He also bought some shirts that were on sale for 25% off their normal retail price of $18 each. Gabe, always the bargain hunter, spent $75 total. How many shirts did he buy? Also, does he really think any of them will go with those shoes?
Read the problem:
Once…
…for a general idea of what’s going on: Gabe went shopping and spent money. Sounds like an old familiar story. Time for an intervention, friends of Gabe. Preferably before he maxes out his Diner’s Club card.
Now we need to figure out how many shirts he bought, so we read the problem:
Twice…
…to translate from English into math. Remember, we can translate a bit at a time, sort of like how Gabe pays for some of his major purchases when he has them on layaway. Sheesh, Gabe. Get a hold of yourself.
(total amount Gabe spent) = (amount he spent on shoes) + (amount he spent on shirts)
We know he spent $75 total, of which $21 was spent on shoes. This gives us the equation:
$75 = 21 + (amount he spent on shirts)
The problem has gotten smaller. It’s depressing when that happens with cake, but great when it happens to a word problem. Now all we need to do is come up with a symbolic expression for how much Gabe spent on shirts, or the cost per shirt times the number of shirts:
(amount he spent on shirts) = (cost per shirt)(number of shirts)
Since the shirts are 25% off their normal price of $18, they cost $18 – 0.25(18) = $13.50 each. What a deal, and real polyester, too!
We need to introduce a variable for the number of shirts; s will do the trick nicely.
(amount he spent on shirts) = 13.5s
When we plug this into the earlier equation, we find that:
75 = 21 + 13.5s
Finally, we’ve reduced this thing to a super-simple-looking equation! Good riddance, vestiges of language! Begone, nouns and verbs!
Things look much nicer now, right? No worrying about shirts or shoes or prices or Gabe’s uncontrollable shopping addiction. For the moment, we can forget about the word problem and solve the equation. The answer is s = 4, by the way. In case you were interested.
Three times…
…to make sure we’re answering the right question. We want to know how many shirts Gabe bought. Is that the answer we arrived at? We found that s = 4, and s was the number of shirts Gabe bought, so we’re all done. Four new shirts for Gabe, and three of them feature a Hawaiian pattern. Gabe, if you insist on buying far more clothes than you need, can’t you at least have a decent fashion sense?
When translating from English into math, some information can be ignored. We don’t care that «the local department store was having a sale.» Gabe might, but we certainly don’t. We care about statements that tell us numbers, and statements that tell us what the question is. Any extraneous information has been placed there simply as a decoy. We’re not going to fall for that. Wait a second…two for one? We’ll grab our jacket and meet you there.
Some people find it helpful to underline the important pieces of information in a word problem. You’re like an actor highlighting in a script the lines that are important for him to remember. Unlike an actor, however, you can always look back at the original problem if you draw a blank. Also, you don’t need to wear any stage makeup.
In the problem we just did, the important bits might look something like this:
The local department store was having a sale. Gabe bought a pair of shoes for $21 and some shirts that were on sale for 25% off their normal retail price of $18 each. If Gabe spent $75 total, how many shirts did he buy?
As you practice, you’ll become better at figuring out which parts of the word problem you can ignore and which parts are important.
Or, How to Avoid Thinking in Math Class, Part 4
(See Also Parts 1, 2, and 3)
This speaks more to my naiveté as a first-year teacher than anything else, but I was shocked to find how fervently my students despised the things they called “word problems.”
“I hate these! What is this, an English lesson?”
“Can’t we do regular math?”
“Why are there words in math class?”
Their chorus: I’m okay with math, except word problems.
They treated “word problems” as some exotic and poisonous breed. These had nothing to do with the main thrust of mathematics, which was apparently to chug through computations and arrive at clean numerical solutions.
I was mystified—which is to say, clueless. Why all this word-problem hatred?
To me, the very phrase “word problems” sounds bizarre. It’s like “food meals” or “page novels.” Of course meals have food. Of course novels have pages.
And of course math problems have words!
One half of mathematics is “pure math.” It deals with abstract ideas, pursued for their own sake. It demands clear definitions and logical arguments. In short, it’s chock full of words. You don’t have trust me on this: take a look at a random research paper in pure math. There are more sentences than equations.
The other half of mathematics is “applied math.” It aims to solve real-life problems, working its fingers into fields as diverse as science, finance, design, and government. If you want to communicate about the quantitative problems in these fields (let alone solve them), well, you’d better get ready to use some words.
Word problems aren’t an invasive species. They’re the whole biosphere.
My first year, I taught students who had come through a tough, testing-driven middle school. They had bought into a simple vision of education: school is work. To them, cranking through math problems was like hammering nails or folding laundry—not necessarily a barrel of laughs, but satisfying in a familiar, workaday way. You’ve got a task. You do it. Then it’s done.
Willing to work hard? Yes; admirably.
Willing to think hard? Not necessarily.
I suspect many students share this rather joyless, overcast view of education. They may not love math, but at least they know what to expect. Word problems violate that contract; they interrupt the flow.
To see why, take an example:
Now, I look at this and think, “Ah, a problem about traveling objects.” This conjures up a whole mental map of ideas:
Brushing aside the clutter, you’ve got this basic structure to my knowledge:
The concept forms the foundation. Everyday words, mathematical symbols, whatever—those are just different languages for talking about the underlying idea. With this kind of understanding, solving the problem is pretty straightforward:
But if I’m a typical word-problem-hating student, I look at things a little differently. My knowledge is structured like this:
For a student like me, “doing math” means learning which symbols trigger which procedures. For example, the symbols “4 + 2x = 18” triggers the procedure “18 take away 4, then divide by 2,” giving an answer of 7.
These connections between symbol and procedure are mostly arbitrary. I take away 4 because… well, because that’s what I’m supposed to do. There’s no deeper reason.
And uh-oh… here come word problems.
My old triggers (the symbols “x” and “+”) are nowhere to be seen, so I don’t know which procedures to execute anymore. I need to start from scratch, learning a whole new set of cues.
And even worse, these new triggers aren’t clear and unambiguous like the old ones. They’re subtle and tenuous. They’re embedded in that messy human creation called language—full as it is of paraphrase, omission, and implication.
My teacher thinks that these “word problems” are a lot like the numerical ones, but to me, they’re a whole new breed. All my old knowledge feels useless in this unfamiliar verbal swamp.
Is it any surprise I’d rather stick to what I know?
As I wrote last week, procedural thinking is often useful (even crucial!). But it cannot replace real understanding, the kind of conceptual thinking will keep bearing fruit. Moreover, success demands connecting the two, linking concepts to procedures, ensuring always that the how is rooted in the why.
Word problems can be tricky for a lot of students, but they’re incredibly important to master. After all, in the real world, most math is in the form of word problems. “If one gallon of paint covers 400 square feet, and my wall measures 34 feet by 8 feet, how many gallons do I need?” “This sweater costs $135, but it’s on sale for 35% off. So how much is that?” Here are the best teacher-tested ideas for helping kids get a handle on these problems.
1. Solve word problems regularly
This might be the most important tip of all. Word problems should be part of everyday math practice, especially for older kids. Whenever possible, use word problems every time you teach a new math skill. Even better: give students a daily word problem to solve so they’ll get comfortable with the process.
Learn more: Teaching With Jennifer Findlay
2. Teach problem-solving routines
There are a LOT of strategies out there for teaching kids how to solve word problems (keep reading to see some terrific examples). The important thing to remember is that what works for one student may not work for another. So introduce a basic routine like Plan-Solve-Check that every kid can use every time. You can expand on the Plan and Solve steps in a variety of ways, but this basic 3-step process ensures kids slow down and take their time.
Learn more: Word Problems Made Easy
3. Visualize or model the problem
Encourage students to think of word problems as an actual story or scenario. Try acting the problem out if possible, and draw pictures, diagrams, or models. Learn more about this method and get free printable templates at the link.
Learn more: Math Geek Mama
4. Make sure they identify the actual question
Educator Robert Kaplinsky asked 32 eighth grade students to answer this nonsensical word problem. Only 25% of them realized they didn’t have the right information to answer the actual question; the other 75% gave a variety of numerical answers that involved adding, subtracting, or dividing the two numbers. That tells us kids really need to be trained to identify the actual question being asked before they proceed.
Learn more: Robert Kaplinsky
5. Remove the numbers
It seems counterintuitive … math without numbers? But this word problem strategy really forces kids to slow down and examine the problem itself, without focusing on numbers at first. If the numbers were removed from the sheep/shepherd problem above, students would have no choice but to slow down and read more carefully, rather than plowing ahead without thinking.
Learn more: Where the Magic Happens Teaching
6. Try the CUBES method
This is a tried-and-true method for teaching word problems, and it’s really effective for kids who are prone to working too fast and missing details. By taking the time to circle, box, and underline important information, students are more likely to find the correct answer to the question actually being asked.
Learn more: Teaching With a Mountain View
7. Show word problems the LOVE
Here’s another fun acronym for tackling word problems: LOVE. Using this method, kids Label numbers and other key info, then explain Our thinking by writing the equation as a sentence. They use Visuals or models to help plan and list any and all Equations they’ll use.
Learn more: Teaching With Jennifer Findlay
8. Consider teaching word problem key words
This is one of those methods that some teachers love and others hate. Those who like it feel it offers kids a simple tool for making sense of words and how they relate to math. Others feel it’s outdated, and prefer to teach word problems using context and situations instead (see below). You might just consider this one more trick to keep in your toolbox for students who need it.
Learn more: Book Units Teacher
9. Determine the operation for the situation
Instead of (or in addition to) key words, have kids really analyze the situation presented to determine the right operation(s) to use. Some key words, like “total,” can be pretty vague. It’s worth taking the time to dig deeper into what the problem is really asking. Get a free printable chart and learn how to use this method at the link.
Learn more: Solving Word Problems With Jennifer Findlay
10. Differentiate word problems to build skills
Sometimes students get so distracted by numbers that look big or scary that they give up right off the bat. For those cases, try working your way up to the skill at hand. For instance, instead of jumping right to subtracting 4 digit numbers, make the numbers smaller to start. Each successive problem can be a little more difficult, but kids will see they can use the same method regardless of the numbers themselves.
Learn more: Differentiating Math
11. Ensure they can justify their answers
One of the quickest ways to find mistakes is to look closely at your answer and ensure it makes sense. If students can explain how they came to their conclusion, they’re much more likely to get the answer right. That’s why teachers have been asking students to “show their work” for decades now.
Learn more: Madly Learning
12. Write the answer in a sentence
When you think about it, this one makes so much sense. Word problems are presented in complete sentences, so the answers should be too. This helps students make certain they’re actually answering the question being asked… part of justifying their answer.
Learn more: Multi-Step Word Problems
13. Add rigor to your word problems
A smart way to help kids conquer word problems is to, well… give them better problems to conquer. A rich math word problem is accessible and feels real to students, like something that matters. It should allow for different ways to solve it and be open for discussion. A series of problems should be varied, using different operations and situations when possible, and even include multiple steps. Visit both of the links below for excellent tips on adding rigor to your math word problems.
Learn more: The Routty Math Teacher and Alyssa Teaches
14. Use a problem-solving rounds activity.
Put all those word problem strategies and skills together with this whole-class activity. Start by reading the problem as a group and sharing important information. Then, have students work with a partner to plan how they’ll solve it. In round three, kids use those plans to solve the problem individually. Finally, they share their answer and methods with their partner and the class. Be sure to recognize and respect all problem-solving strategies that lead to the correct answer.
Learn more: Teacher Trap
Like these word problem tips and tricks? Learn more about Why It’s Important to Honor All Math Strategies.
Plus, 60+ Awesome Websites For Teaching and Learning Math.

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. Read the Entire Word Problem
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. What exactly is the question?
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd Grade Math Task Cards Bundle has word problems in almost every one of its 30 task card sets.
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

You may love GMAT word problems or you may hate them, but you can’t get around them if you want to ace the GMAT Quant section. No matter what your feelings are about this problem type, though, Magoosh’s experts have put together everything you need to know (and practice!) GMAT word problems in order to master them before test day.
Table of Contents
- What to Expect from GMAT Word Problems
- Strategy Guide: What’s the Trick to Mastering GMAT Word Problems?
- Translate from Words to Math
- Learn to Work with Variables
- Plug in Numbers (the Smart Way)
- Understand Your Strengths and Weaknesses
- GMAT Word Problem Practice Questions
- A Final Word on GMAT Word Problems
What to Expect from GMAT Word Problems
Think of GMAT word problems as questions that ask you to turn real-world situations into math problems. Of course, this can be a lot more complicated than it sounds. After all, it’s one thing to understand algebra in the abstract, and quite another to think about where the rubber meets the road.
Think about it this way: the reason human beings created algebra was to solve problems about real-world situations, and the GMAT loves asking math problems about numbers and about real-world situations, a.k.a. word problems! Even folks who can do algebra in the abstract sometimes find word problems challenging.
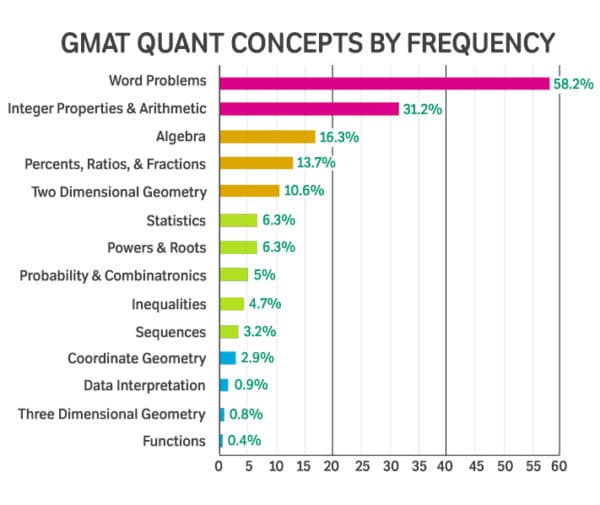
You’ll find GMAT word problems in the GMAT Quant section. How much of the GMAT is word problems? Within the Quant section, actually a whole lot! A study of official GMAT questions from actual tests show that word problems account for 58.2% of all GMAT math questions.
In other words, test-takers should anticipate a word problem cropping up (on average) in three out of every five questions you’ll see in Quant. Because of GMAT word problems’ prevalence, you can expect to see both Data Sufficiency and Problem Solving questions in this format. The question format and answer choices may look different, but the basic premise will be the same.
You may be feeling the pressure, but hang in there! If you’re worried about how to master word problems on the GMAT, keep reading for our GMAT Word Problems strategy guide.
Strategy Guide: What’s the Trick to Mastering GMAT Word Problems?
First, the disappointing news: there’s no one strategy that will work to immediately solve every word problem, every time (where would the fun in that be?). The good news: by using and combining a variety of strategies, you can put together the tools you need to ace even the most complex GMAT word problems, every single time!
With that in mind, here are the four key strategies you’ll need.
1. Translate from Words to Math
Suppose we have the following sentence in a word problem:”Three-fifths of x is 14 less than twice y squared.” How do we change words to math? Here’s a quick guide:
- The verb “is/are” is the equivalent of an equal sign; the equal sign in an equation is, in terms of “mathematical grammar,” the equivalent of a verb in a sentence. Every sentence has a verb and every equation has an equal sign.
- The word “of” means multiply (often used with fractions and percents). Ex. “26% of x” means (0.26x)
- The words “more than” or “greater than” mean addition. Ex. “5 greater than x” means (x + 5) and “7 more than y” means (y + 7)
- The words “less than” means subtraction. Ex. “8 less than Q” means (Q – 8). Notice that the first element is always subtracted: in other words, “J less than K” means (K – J).
With that in mind, let’s go back to the sentence from the hypothetical problem above.
- “three fifths of x” means [(3/5)*x]
- “is” marks the location of the equal sign
- “twice y squared” means 2(y^2)
- “14 less than twice y squared” means 2(y^2) – 14
Altogether, the equation we get is:
Using this strategy, it’s straightforward to translate from a verbal statement about numbers to an equation.
2. Learn to Work with Variables
Working with Variables Part I: Assigning Variables
Most GMAT word problem concern real world quantities and are stated in real world terms, and we need to assign algebraic variables to these real-world quantities.
Sometimes, one quantity is directly related to every other quantity in the problem. For example:
“Sarah spends 2/5 of her monthly salary on rent, 1/12 of her monthly salary on auto costs including gas and insurance, and 1/10 of her monthly salary automatically goes into saving each month. With what she has left each month, she spend she spends $800 on groceries and …”
In that problem, everything is related to “monthly salary,” so it would make a lot of sense to introduce just one variable for that, and express everything else in terms of that variable. Also, please don’t always use the boring choice of x for a variable! If we want a variable for salary, you might use the letter S, which will help you remember what the variable means! If we are given multiple variables that are all related to each other, it’s often helpful to assign a letter to the variable with the lowest value, and then express everything else in terms of this letter.
If there are two or more quantities that don’t depend directly on each other, then you may well have to introduce a different variable for each. Just remember that it’s mathematically problematic to litter a problem with a whole slew of different variables. You see, for each variable, you need an equation to solve it. If we want to solve for two different variables, we need two different equations (this is a common Word Problem scenario). If we want to solve for three different variables, we need three different equations (considerably less common). While the mathematical pattern continues to extend upward from there, more than three completely separate variables is almost unheard of on GMAT math.
When you assign variables, always be hyper-vigilant and over-the-top explicit about exactly what each variable means. Write a quick note to yourself on the scratch paper: T = the price of one box of tissue, or whatever the problem wants. What you want to avoid is the undesirable situation of solving for a number and not knowing what that number means in the problem!
Practice Question
Here’s a word problem practice question that’s a bit easier than what you might see on the GMAT!
Andrew and Beatrice each have their own savings account. Beatrice’s account has $600 less than three times what Andrew’s account has. If Andrew had $300 more dollars, then he would have exactly half what is currently in Beatrice’s account. How much does Beatrice have?
Click here for a text answer and explanation
The obvious choices for variables are A = the amount in Andrew’s account and B = the amount in Beatrice’s account. The GMAT will be good about giving you word problems involving people whose names start with a different letter so that it’s easier to assign variables. We can turn the second & third sentences into equations.
second sentence: B = 3A – 600
Both equations are solved for B, so simply set them equal.
3A – 600 = 2(A + 300)
3A – 600 = 2A + 600
A – 600 = 600
A = 1200
We can plug this into either equation to find B. (BTW, if you have time, an excellent check is to plug it into both equations, and make sure the value of B you get is the same!)
B = 3000
Thus, Andrew has $1200 in his account, and Beatrice, $3000 in hers.
Working with Variables Part II: Choosing Your Approach
When questions have variables in the answer choices, you can decide whether you’d rather take an algebraic approach or a numerical approach. Neither one of these is “better” than the other— it all depends on what works best for you.
An algebraic approach is what you most likely learned back in high school. This means that, to solve the problem, you’ll manipulate the variables according to mathematical rules. For a super-basic example, to solve ( 2x = y ), you would divide both sides by two and end up with ( x = y/2 ).
However, you could also to a numerical approach to this (and many other!) problems. This means putting numbers into both the question and the answer choices. So let’s take the previous example—which, again, is much, much easier than anything you’d see on the GMAT:
If ( 2x = y ), what is x in terms of y?
A. (y/20)
B. (y/2)
C. (4/y)
D. (20/y)
Here, you could pick a number to stand in for x in the original equation. Let’s say x is 2. If x = 2, then the original equation tells us that y = 4.
Now, plug that into the question and the answer. The question becomes: “What is 2 in terms of 4?” It’s ½, or .5. Then, look for the answer choice that gives you this answer. Plugging in the numbers, you get:
A. (y/20) = 0.2
B. (y/2) = 0.5
C. (4/y) = 1
D. (20/y) = 5
So B must be correct.
What does this look like in practice? For some harder examples, take a look over at Mike’s post on Variables in GMAT Answer Choices: 2 Approaches.
3. Plug in Numbers (the Smart Way)
If you choose to use the numerical approach described above, keep in mind that there are some key tips for plugging in numbers that you should use!
Here’s a quick summary of how to quick the best numbers for a particular problem:
- Remember that the GMAT has a broad definition of “number” that goes beyond positive integers! Zero, fractions, and negatives are all included. Work on developing number sense to help select the best numbers in a given scenario.
- For percent problems, think outside the box: GMAT test writers know lots of students pick 100. Try 500 or 1000 instead.
- Don’t try to pick numbers for questions involving more than one percent increase or decrease.
- Pay attention to units and convert them appropriately. This is particularly important in solutions and mixing problems!
- Don’t pick 1 as a number—it has too many unique properties.
A separate case involving plugging in, rather than picking, numbers: When all the answer choices are numerical, one further strategy we have at our disposal is backsolving. Using this strategy, we can pick one answer, plug it into the problem, and see whether it works. If this choice is too big or too small, it guides us in what other answer choices to eliminate. Typically, we would start with answer choice (C), but if another answer choice is a particularly convenient choice, then we would start there.
4. Understand Your Strengths and Weaknesses
With all of the above strategies at your disposal, you have everything you need to improve your answers to GMAT word problems. The most efficient way to do this is to keep an error log of word problems you’ve answered wrong in your practice, then review it. As you go through, think about the following:
- What concept or concepts was the question testing?
- What was tricky about the wording of the question?
- Were you already familiar with the methods used in the explanation video?
- Once you watched the explanation video, could you explain how to solve the problem to somebody else?
Your answers to these questions can help you craft a better strategy for GMAT Math word problems, identifying exactly what you need to review to get better!
GMAT Word Problem Practice Questions
Now that you’ve learned how to approach word problems, we’ve put together a collection of them, direct from Magoosh’s product, for you to try! Video and text answers and explanations follow each question.
- Ann and Bob planted trees on Friday. What is the ratio of the number of trees that Bob planted to the number of trees that Ann planted?
(1) Ann planted 20 trees more than Bob planted.
(2) Ann planted 10 percent more trees than Bob planted.
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 1!
Click here for a text answer and explanation to GMAT Word Problem 1!
Our task is to determine the ratio of Bob’s trees to Ann’s trees. Let’s label these numbers of trees with variables:
Bob’s trees→B, Ann’s trees→A
With these variables, we can express the ratio we want to determine:
(B/A) =?
Statement 1:
Ann planted 20 trees more than Bob planted.
Let’s translate this into an equation using A and B:
( A=B+20 )
Now we can substitute this into our ratio, replacing A:
(B/A) = ( B/(B+20) )
No matter what simplifications we make, we cannot find a numerical value for this fraction. We would need a value for B. We cannot determine the ratio. Statement 1 by itself is not sufficient.
Statement 2:
Ann planted 10 percent more trees than Bob planted.
Let’s translate this into an equation using A and B:
(A=1.10 x B )
Again, let’s substitute this in for A in our ratio:
(B/A) = ( B/(1.10B) )
= (1/1.1 )
We found a value for the ratio of Bob’s trees to Ann’s trees. Statement 2 alone is sufficient.
- The Townville museum was open for 7 consecutive days. If the number of visitors each day was 3 greater than the previous day, how many visitors were there on the first day?
(1) There were a total of 126 visitors for the 7 days.
(2) The number of visitors on the seventh day was three times the number of visitors on the first day.
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 2!
Click here for a text answer and explanation to GMAT Word Problem 2!
If x is the number of visitors on the first day, then:
x = # of visitors on the 1st day
x + 3 = # of visitors on the 2nd day
x + 6 = # of visitors on the 3rd day
x + 9 = # of visitors on the 4th day
x + 12 = # of visitors on the 5th day
x + 15 = # of visitors on the 6th day
x + 18 = # of visitors on the 7th day
1) Adding up the number of visitors gives us:
x + (x + 3) + (x + 9) + (x + 12) + (x + 15) + (x + 18) = 126
We could simplify and solve this for x. So Statement 1 is sufficient.
2) x + 18 = 3x
Again, we can simplify this and solve for x. So Statement 2 is sufficient.
Answer: (D)
- Two teachers, Ms. Ames and Mr. Betancourt, each had N cookies. Ms. Ames was able to give the same number of cookies to each one of her 24 students, with none left over. Mr. Betancourt was also able to give the same number of cookies to each one of his 18 students, with none left over. If N > 0, what is the value of N?
(1) N<100
(2) N > 50
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 3!
Click here for a text answer and explanation to GMAT Word Problem 3!
This question is really about common multiples and the LCM (note that it is different than finding the set of all multiples, though!). If Ms. Ames can give each of her 24 students k cookies, so that they all get the same and none are left over, then 24k = N. Similarly, in Mr. Betancourt’s class, 18s = N.
What are the common multiples of 18 and 24?
18 = 2×9 = 2×3×3 = 6×3
24 = 3×8 = 2×2×2×3 = 6×4
From the prime factorizations, we see that GCF = 6, so the LCM is
LCM = 6×3×4 = 72
and all other common multiples of 18 and 24 are the multiples of 72: {72, 144, 216, 288, 360, …}
Statement #1: if N<100, the only possibility is N = 72. This statement, alone and by itself, is sufficient.
Statement #2: if N > 50, then N could be 72, or 144, or 216, or etc. Many possibilities. This statement, alone and by itself, is not sufficient.
Answer = (A)
- A certain zoo has mammals and reptiles and birds, and no other animals. The ratio of mammals to reptiles to birds is 11:8:5. How many birds are in the zoo?
(1) there are twelve more mammals in the zoo than there are reptiles
(2) if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
Click here for a video answer and explanation to GMAT Word Problem 4!
Click here for a text answer and explanation to GMAT Word Problem 4!
A short way to do this problem. The prompt gives us ratio information. Each statement gives use some kind of count information, so each must be sufficient on its own. From that alone, we can conclude: answer = D. This is all we have to do for Data Sufficiency.
Here are the details, if you would like to see them.
Statement (1): there are twelve more mammals in the zoo than there are reptiles
From the ratio in the prompt, we know mammals are 11 “parts” and reptiles are 8 “parts”, so mammals have three more “parts” than do reptiles. If this difference of three “parts” consists of 12 mammals, that must mean there are four animals in each “part.” We have five bird “parts”, and if each counts as four animals, that’s 5*4 = 20 birds. This statement, alone and by itself, is sufficient.
Statement (2): if the zoo acquired 16 more mammals, the ratio of mammals to birds would be 3:1
Let’s say there are x animals in a “part”—this means there are currently 11x mammals and 5x birds. Suppose we add 16 mammals. Then the ratio of (11x + 16) mammals to 5x birds is 3:1.
(11x + 16)/(5x) = 3/1 = 3
11x + 16 = 3*(5x) = 15x
16 = 15x – 11x
16 = 4x
4 = x
So there are four animals in a “part”. The birds have five parts, 5x, so that’s 20 birds. This statement, alone and by itself, is sufficient.
Both statements are sufficient. Answer = D.
A Final Word on Word Problems
So, what is the trick to GMAT word problems? As you’ve seen in this post, there’s no one-size-fits-all trick—but there are plenty of strategies!
The strategies you’ve read about here can be used to take the given information and identify key words in a question. With them, you’ll be able to find everything from average speed to total distance traveled, from total time to total amount.
The key now is to put them into practice. Jot down these techniques or bookmark this post so you can come back as you continue your practice with GMAT word problems. You can also check out our posts on compound interest and Venn diagrams for more practice with GMAT word problems. Good luck!
This post was written with contributions from our Magoosh content creator, Rachel Kapelke-Dale.
-
Mike served as a GMAT Expert at Magoosh, helping create hundreds of lesson videos and practice questions to help guide GMAT students to success. He was also featured as «member of the month» for over two years at GMAT Club. Mike holds an A.B. in Physics (graduating magna cum laude) and an M.T.S. in Religions of the World, both from Harvard. Beyond standardized testing, Mike has over 20 years of both private and public high school teaching experience specializing in math and physics. In his free time, Mike likes smashing foosballs into orbit, and despite having no obvious cranial deficiency, he insists on rooting for the NY Mets. Learn more about the GMAT through Mike’s Youtube video explanations and resources like What is a Good GMAT Score? and the GMAT Diagnostic Test.
View all posts



 Consult the Instruction Manual
Consult the Instruction Manual