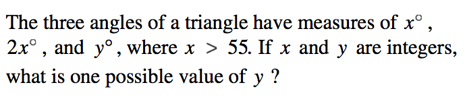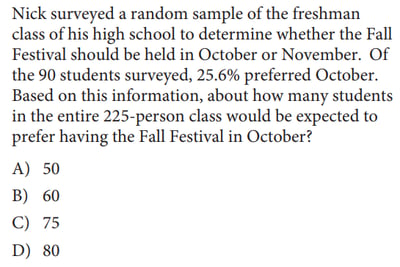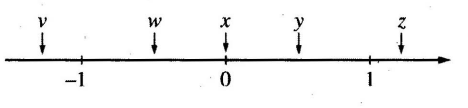About 25% of your total SAT Math section will be word problems, meaning you will have to create your own visuals and equations to solve for your answers. Though the actual math topics can vary, SAT word problems share a few commonalities, and we’re here to walk you through how to best solve them.
This post will be your complete guide to SAT Math word problems. We’ll cover how to translate word problems into equations and diagrams, the different types of math word problems you’ll see on the test, and how to go about solving your word problems on test day.
Feature Image: Antonio Litterio/Wikimedia
What Are SAT Math Word Problems?
A word problem is any math problem based mostly or entirely on a written description. You will not be provided with an equation, diagram, or graph on a word problem and must instead use your reading skills to translate the words of the question into a workable math problem. Once you do this, you can then solve it.
You will be given word problems on the SAT Math section for a variety of reasons. For one, word problems test your reading comprehension and your ability to visualize information.
Secondly, these types of questions allow test makers to ask questions that’d be impossible to ask with just a diagram or an equation. For instance, if a math question asks you to fit as many small objects into a larger one as is possible, it’d be difficult to demonstrate and ask this with only a diagram.
Translating Math Word Problems Into Equations or Drawings
In order to translate your SAT word problems into actionable math equations you can solve, you’ll need to understand and know how to utilize some key math terms. Whenever you see these words, you can translate them into the proper mathematical action.
For instance, the word «sum» means the value when two or more items are added together. So if you need to find the sum of a and b, you’ll need to set up your equation like this: a+b.
Also, note that many mathematical actions have more than one term attached, which can be used interchangeably.
Here is a chart with all the key terms and symbols you should know for SAT Math word problems:
| Key Terms | Mathematical Action |
| Sum, increased by, added to, more than, total of | + |
| Difference, decreased by, less than, subtracted from | − |
| Product, times, __ times as much, __ times as many (a number, e.g., “three times as many”) | * or x |
| Divided by, per, __ as many, __ as much (a fraction, e.g., “one-third as much”) | / or ÷ |
| Equals, is, are, equivalent | = |
| Is less than | < |
| Is greater than | > |
| Is less than or equal to | ≤ |
| Is greater than or equal to | ≥ |
Now, let’s look at these math terms in action using a few official examples:
We can solve this problem by translating the information we’re given into algebra. We know the individual price of each salad and drink, and the total revenue made from selling 209 salads and drinks combined. So let’s write this out in algebraic form.
We’ll say that the number of salads sold = S, and the number of drinks sold = D. The problem tells us that 209 salads and drinks have been sold, which we can think of as this:
S + D = 209
Finally, we’ve been told that a certain number of S and D have been sold and have brought in a total revenue of 836 dollars and 50 cents. We don’t know the exact numbers of S and D, but we do know how much each unit costs. Therefore, we can write this equation:
6.50S + 2D = 836.5
We now have two equations with the same variables (S and D). Since we want to know how many salads were sold, we’ll need to solve for D so that we can use this information to solve for S. The first equation tells us what S and D equal when added together, but we can rearrange this to tell us what just D equals in terms of S:
S + D = 209
Now, just subtract S from both sides to get what D equals:
D = 209 − S
Finally, plug this expression in for D into our other equation, and then solve for S:
6.50S + 2(209 − S) = 836.5
6.50S + 418 − 2S = 836.5
6.50S − 2S = 418.5
4.5S = 418.5
S = 93
The correct answer choice is (B) 93.
This word problem asks us to solve for one possible solution (it asks for «a possible amount»), so we know right away that there will be multiple correct answers.
Wyatt can husk at least 12 dozen ears of corn and at most 18 dozen ears of corn per hour. If he husks 72 dozen at a rate of 12 dozen an hour, this is equal to 72 / 12 = 6 hours. You could therefore write 6 as your final answer.
If Wyatt husks 72 dozen at a rate of 18 dozen an hour (the highest rate possible he can do), this comes out to 72 / 18 = 4 hours. You could write 4 as your final answer.
Since the minimum time it takes Wyatt is 4 hours and the maximum time is 6 hours, any number from 4 to 6 would be correct.
Though the hardest SAT word problems might look like Latin to you right now, practice and study will soon have you translating them into workable questions.
Typical SAT Word Problems
Word problems on the SAT can be grouped into three major categories:
- Word problems for which you must simply set up an equation
- Word problems for which you must solve for a specific value
- Word problems for which you must define the meaning of a value or variable
Below, we look at each world problem type and give you examples.
Word Problem Type 1: Setting Up an Equation
This is a fairly uncommon type of SAT word problem, but you’ll generally see it at least once on the Math section. You’ll also most likely see it first on the section.
For these problems, you must use the information you’re given and then set up the equation. No need to solve for the missing variable—this is as far as you need to go.
Almost always, you’ll see this type of question in the first four questions on the SAT Math section, meaning that the College Board consider these questions easy. This is due to the fact that you only have to provide the setup and not the execution.
To solve this problem, we’ll need to know both Armand’s and Tyrone’s situations, so let’s look at them separately:
Armand: Armand sent m text messages each hour for 5 hours, so we can write this as 5m—the number of texts he sent per hour multiplied by the total number of hours he texted.
Tyrone: Tyrone sent p text messages each hour for 4 hours, so we can write this as 4p—the number of texts he sent per hour multiplied by the total number of hours he texted.
We now know that Armand’s situation can be written algebraically as 5m, and Tyrone’s can be written as 4p. Since we’re being asked for the expression that represents the total number of texts sent by Armand and Tyrone, we must add together the two expressions:
5m + 4p
The correct answer is choice (C) 5m + 4p
Word Problem Type 2: Solving for a Missing Value
The vast majority of SAT Math word problem questions will fall into this category. For these questions, you must both set up your equation and solve for a specific piece of information.
Most (though not all) word problem questions of this type will be scenarios or stories covering all sorts of SAT Math topics, such as averages, single-variable equations, and ratios. You almost always must have a solid understanding of the math topic in question in order to solve the word problem on the topic.
Let’s try to think about this problem in terms of x. If Type A trees produced 20% more pears than Type B did, we can write this as an expression:
x + 0.2x = 1.2x = # of pears produced by Type A
In this equation, x is the number of pears produced by Type B trees. If we add 20% of x (0.2x) to x, we get the number of pears produced by Type A trees.
The problem tells us that Type A trees produced a total of 144 pears. Since we know that 1.2x is equal to the number of pears produced by Type A, we can write the following equation:
1.2x = 144
Now, all we have to do is divide both sides by 1.2 to find the number of pears produced by Type B trees:
x = 144 / 1.2
x = 120
The correct answer choice is (B) 120.
You might also get a geometry problem as a word problem, which might or might not be set up with a scenario, too. Geometry questions will be presented as word problems typically because the test makers felt the problem would be too easy to solve had you been given a diagram, or because the problem would be impossible to show with a diagram. (Note that geometry makes up a very small percentage of SAT Math.)
This is a case of a problem that is difficult to show visually, since x is not a set degree value but rather a value greater than 55; thus, it must be presented as a word problem.
Since we know that x must be an integer degree value greater than 55, let us assign it a value. In this case, let us call x 56°. (Why 56? There are other values x could be, but 56 is guaranteed to work since it’s the smallest integer larger than 55. Basically, it’s a safe bet!)
Now, because x = 56, the next angle in the triangle—2x—must measure the following:
56*2 = 112
Let’s make a rough (not to scale) sketch of what we know so far:
Now, we know that there are 180° in a triangle, so we can find the value of y by saying this:
y = 180 − 112 − 56
y = 12
One possible value for y is 12. (Other possible values are 3, 6, and 9.)
Word Problem Type 3: Explaining the Meaning of a Variable or Value
This type of problem will show up at least once. It asks you to define part of an equation provided by the word problem—generally the meaning of a specific variable or number.
This question might sound tricky at first, but it’s actually quite simple.
We know that P is the number of phones Kathy has left to fix, and d is the number of days she has worked in a week. If she’s worked 0 days (i.e., if we plug 0 into the equation), here’s what we get:
P = 108 − 23(0)
P = 108
This means that, without working any days of the week, Kathy has 108 phones to repair. The correct answer choice, therefore, is (B) Kathy starts each week with 108 phones to fix.
To help juggle all the various SAT word problems, let’s look at the math strategies and tips at our disposal.
Ready to go beyond just reading about the SAT? Then you’ll love the free five-day trial for our SAT Complete Prep program. Designed and written by PrepScholar SAT experts, our SAT program customizes to your skill level in over 40 subskills so that you can focus your studying on what will get you the biggest score gains.
Click on the button below to try it out!
SAT Math Strategies for Word Problems
Though you’ll see word problems on the SAT Math section on a variety of math topics, there are still a few techniques you can apply to solve word problems as a whole.
#1: Draw It Out
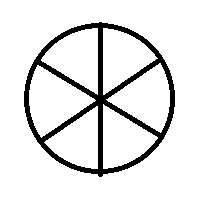
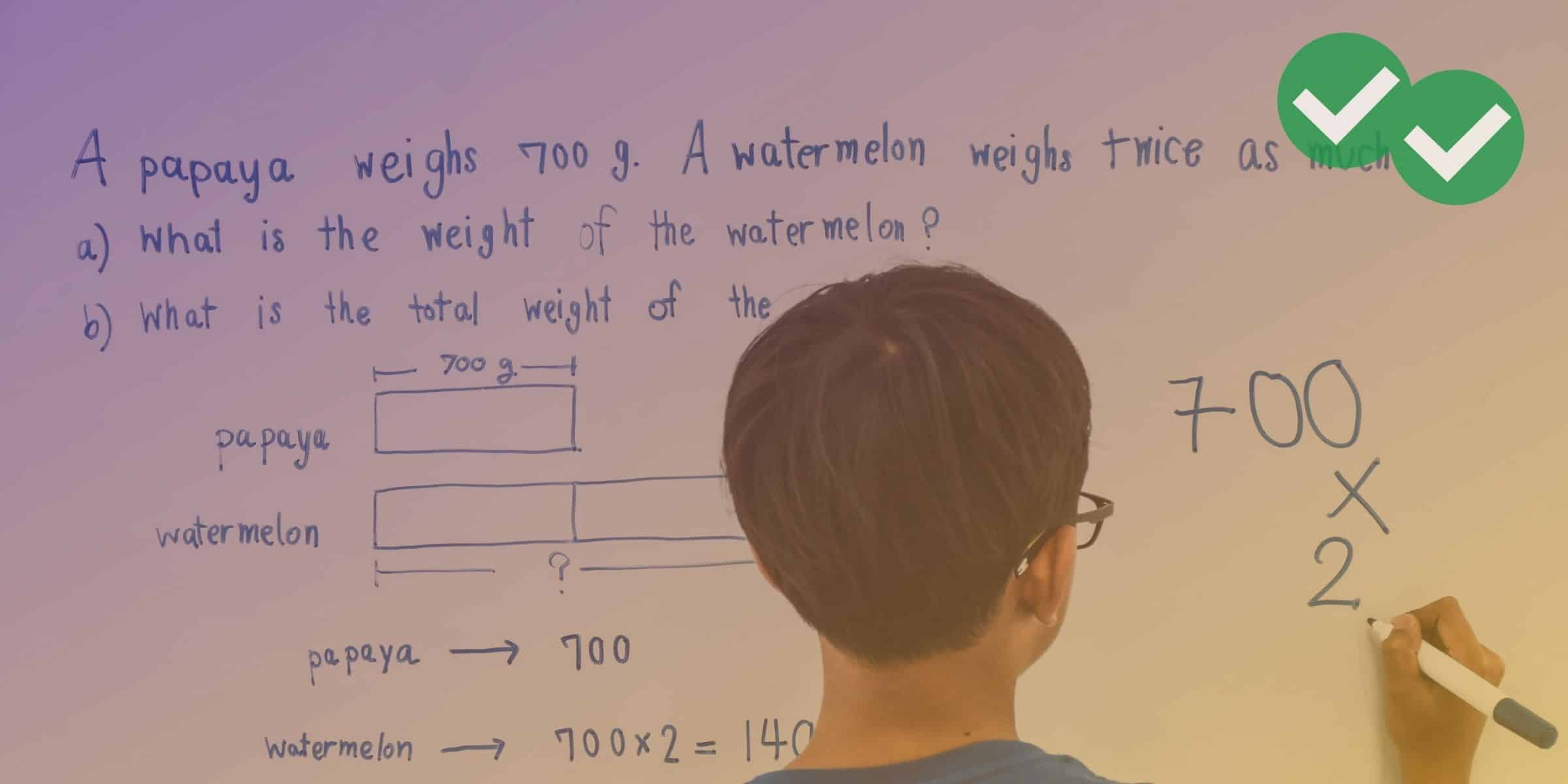
Whether your problem is a geometry problem or an algebra problem, sometimes making a quick sketch of the scene can help you understand what exactly you’re working with. For instance, let’s look at how a picture can help you solve a word problem about a circle (specifically, a pizza):
If you often have trouble visualizing problems such as these, draw it out. We know that we’re dealing with a circle since our focus is a pizza. We also know that the pizza weighs 3 pounds.
Because we’ll need to solve the weight of each slice in ounces, let’s first convert the total weight of our pizza from pounds into ounces. We’re given the conversion (1 pound = 16 ounces), so all we have to do is multiply our 3-pound pizza by 16 to get our answer:
3 * 16 = 48 ounces (for whole pizza)
Now, let’s draw a picture. First, the pizza is divided in half (not drawn to scale):
We now have two equal-sized pieces. Let’s continue drawing. The problem then says that we divide each half into three equal pieces (again, not drawn to scale):
This gives us a total of six equal-sized pieces. Since we know the total weight of the pizza is 48 ounces, all we have to do is divide by 6 (the number of pieces) to get the weight (in ounces) per piece of pizza:
48 / 6 = 8 ounces per piece
The correct answer choice is (C) 8.
As for geometry problems, remember that you might get a geometry word problem written as a word problem. In this case, make your own drawing of the scene. Even a rough sketch can help you visualize the math problem and keep all your information in order.
#2: Memorize Key Terms
If you’re not used to translating English words and descriptions into mathematical equations, then SAT word problems might be difficult to wrap your head around at first. Look at the chart we gave you above so you can learn how to translate keywords into their math equivalents. This way, you can understand exactly what a problem is asking you to find and how you’re supposed to find it.
There are free SAT Math questions available online, so memorize your terms and then practice on realistic SAT word problems to make sure you’ve got your definitions down and can apply them to the actual test.
#3: Underline and/or Write Out Important Information
The key to solving a word problem is to bring together all the key pieces of given information and put them in the right places. Make sure you write out all these givens on the diagram you’ve drawn (if the problem calls for a diagram) so that all your moving pieces are in order.
One of the best ways to keep all your pieces straight is to underline your key information in the problem, and then write them out yourself before you set up your equation. So take a moment to perform this step before you zero in on solving the question.
#4: Pay Close Attention to What’s Being Asked
It can be infuriating to find yourself solving for the wrong variable or writing in your given values in the wrong places. And yet this is entirely too easy to do when working with math word problems.
Make sure you pay strict attention to exactly what you’re meant to be solving for and exactly what pieces of information go where. Are you looking for the area or the perimeter? The value of x, 2x, or y?
It’s always better to double-check what you’re supposed to find before you start than to realize two minutes down the line that you have to begin solving the problem all over again.
#5: Brush Up on Any Specific Math Topic You Feel Weak In
You’re likely to see both a diagram/equation problem and a word problem for almost every SAT Math topic on the test. This is why there are so many different types of word problems and why you’ll need to know the ins and outs of every SAT Math topic in order to be able to solve a word problem about it.
For example, if you don’t know how to find an average given a set of numbers, you certainly won’t know how to solve a word problem that deals with averages!
Understand that solving an SAT Math word problem is a two-step process: it requires you to both understand how word problems work and to understand the math topic in question. If you have any areas of mathematical weakness, now’s a good time to brush up on them—or else SAT word problems might be trickier than you were expecting!
All set? Let’s go!
Test Your SAT Math Word Problem Knowledge
Finally, it’s time to test your word problem know-how against real SAT Math problems:
Word Problems
1. No Calculator
2. Calculator OK
3. Calculator OK
4. Calculator OK
Answers: C, B, A, 1160
Answer Explanations
1. For this problem, we have to use the information we’re given to set up an equation.
We know that Ken spent x dollars, and Paul spent 1 dollar more than Ken did. Therefore, we can write the following equation for Paul:
x + 1
Ken and Paul split the bill evenly. This means that we’ll have to solve for the total amount of both their sandwiches and then divide it by 2. Since Ken’s sandwich cost x dollars and Paul’s cost x + 1, here’s what our equation looks like when we combine the two expressions:
x + x + 1
2x + 1
Now, we can divide this expression by 2 to get the price each person paid:
(2x + 1) / 2
x + 0.5
But we’re not finished yet. We know that both Ken and Paul also paid a 20% tip on their bills. As a result, we have to multiply the total cost of one bill by 0.2, and then add this tip to the bill. Algebraically, this looks like this:
(x + 0.5) + 0.2(x + 0.5)
x + 0.5 + 0.2x + 0.1
1.2x + 0.6
The correct answer choice is (C) 1.2x + 0.6
2. You’ll have to be familiar with statistics in order to understand what this question is asking.
Since Nick surveyed a random sample of his freshman class, we can say that this sample will accurately reflect the opinion (and thus the same percentages) as the entire freshman class.
Of the 90 freshmen sampled, 25.6% said that they wanted the Fall Festival held in October. All we have to do now is find this percentage of the entire freshmen class (which consists of 225 students) to determine how many total freshmen would prefer an October festival:
225 * 0.256 = 57.6
Since the question is asking «about how many students»—and since we obviously can’t have a fraction of a person!—we’ll have to round this number to the nearest answer choice available, which is 60, or answer choice (B).
3. This is one of those problems that is asking you to define a value in the equation given. It might look confusing, but don’t be scared—it’s actually not as difficult as it appears!
First off, we know that t represents the number of seconds passed after an object is launched upward. But what if no time has passed yet? This would mean that t = 0. Here’s what happens to the equation when we plug in 0 for t:
h(0) = -16(0)2 + 110(0) + 72
h(0) = 0 + 0 + 72
h(0) = 72
As we can see, before the object is even launched, it has a height of 72 feet. This means that 72 must represent the initial height, in feet, of the object, or answer choice (A).
4. You might be tempted to draw a diagram for this problem since it’s talking about a pool (rectangle), but it’s actually quicker to just look at the numbers given and work from there.
We know that the pool currently holds 600 gallons of water and that water has been hosed into it at a rate of 8 gallons a minute for a total of 70 minutes.
To find the amount of water in the pool now, we’ll have to first solve for the amount of water added to the pool by hose. We know that 8 gallons were added each minute for 70 minutes, so all we have to do is multiply 8 by 70:
8 * 70 = 560 gallons
This tells us that 560 gallons of water were added to our already-filled, 600-gallon pool. To find the total amount of water, then, we simply add these two numbers together:
560 + 600 = 1160
The correct answer is 1160.
Aaaaaaaaaaand time for a nap.
Key Takeaways: Making Sense of SAT Math Word Problems
Word problems make up a significant portion of the SAT Math section, so it’s a good idea to understand how they work and how to translate the words on the page into a proper expression or equation. But this is still only half the battle.
Though you won’t know how to solve a word problem if you don’t know what a product is or how to draw a right triangle, you also won’t know how to solve a word problem about ratios if you don’t know how ratios work.
Therefore, be sure to learn not only how to approach math word problems as a whole, but also how to narrow your focus on any SAT Math topics you need help with. You can find links to all of our SAT Math topic guides here to help you in your studies.
What’s Next?
Want to brush up on SAT Math topics? Check out our individual math guides to get an overview of each and every topic on SAT Math. From polygons and slopes to probabilities and sequences, we’ve got you covered!
Running out of time on the SAT Math section? We have the know-how to help you beat the clock and maximize your score.
Been procrastinating on your SAT studying? Learn how you can overcome your desire to procrastinate and make a well-balanced prep plan.
Trying to get a perfect SAT score? Take a look at our guide to getting a perfect 800 on SAT Math, written by a perfect scorer.
Want to improve your SAT score by 160 points?
Check out our best-in-class online SAT prep program. We guarantee your money back if you don’t improve your SAT score by 160 points or more.
Our program is entirely online, and it customizes what you study to your strengths and weaknesses. If you liked this Math strategy guide, you’ll love our program. Along with more detailed lessons, you’ll get thousands of practice problems organized by individual skills so you learn most effectively. We’ll also give you a step-by-step program to follow so you’ll never be confused about what to study next.
Check out our 5-day free trial:
Have friends who also need help with test prep? Share this article!
About the Author
Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
By on February 23, 2021 in SAT
If the phrase “word problems” makes you want to throw your SAT prep materials at the wall, know that you’re definitely not alone. Word problems are HARD if you’re not used to translating them into numbers. And the bad news? The SAT Math section LOOOVES their word problems — they comprise 25% of the Math section!
But wait, before you actually destroy your SAT prep book or, worse, your laptop, know that anyone can become an SAT word problem master with some practice. Even if you’re a pro at making mathematical equations out of word problems, this post will cover tactics to help you solve word problems in record time.
The Different Strategies for Tackling SAT Word Problems
As if word problems weren’t hard enough, not all word problems are created equal. Some want you to create an equation, some want you to pick an equation, and some are just bent on sounding like this: If the number of apples Mary has is twice the absolute value of chocolate, how many zebras on train B will travel to San Diego on shmoople zeeple heeple?
“Huh?” is right. It’s absolutely right.
To master SAT word problems, you need to become familiar with different types of SAT word problems and what strategy — or combination of strategies — is best for the problem and easiest for you. There are three main strategies for word problems: Active Reading, Process of Elimination, and Picking Numbers.
Active Reading: You have might have learned of the active reading strategy on the SAT, which is when you go through the reading comprehension passages while underlining or taking notes to better remember and make sense of the material. But this strategy also comes in pretty handy for SAT Math word problems and can easily be combined with the strategies below. Click here to see a few examples of active reading in practice.
Process of Elimination: Process of elimination is when you plug in answer choices in the context of the problem. Obviously, it only works when there are answer choices. If you feel like active reading is going to slow you down, definitely try process of elimination — click here for an example!
Picking Numbers: Sometimes word problems have equations in the question and answer choices. If this is the case, picking numbers and plugging them into given equations is a great strategy to speed things up. To see picking numbers in action, click here.
Active Reading and SAT Math
While it may feel like it takes longer than reading passively, active reading for the right kind of SAT word problem will actually save you a ton of time in the long run. Why? Because active reading forces you to work through problems as you’re reading them and by doing so, you often find yourself at or near the answer by the time you’re done reading the question.
Don’t believe me? Check out how active reading works in this problem:
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
Yikes, even I’m getting a headache looking at it and I’ve read it already. But before we get overwhelmed by all these words, understand that the key to approaching these types of problems is a two-step process:
Step 1. Draw your attention to the numbers and what they mean in the context of the problem.
Click here to review Step 1!
In other words, what kind of equation are these numbers making? The chart below can help you figure out how to translate key words into their equivalent operators.
| Words | Their equivalent operators |
|---|---|
| Total of, added to, increased, sum | + |
| Decreased by, subtracted from, difference | — |
| Times, product | x |
| Same, equivalent, equals, is | = |
| Less than | < |
| Greater than, more than | > |
| Greater than or equal to | ≥ |
| Less than or equal to | ≤ |
Step 2. Pay close attention to what you’re supposed to answer.
Click here to review Step 2!
When I was studying for the SAT (a century ago), I had spent a lot of time beating my head on the table because I picked the answer choice for x when I really was supposed to find x + 1, or that I solved for inches instead of feet. Underlining or circling what you’re supposed to find will save you headaches… Trust. Me.
Take a look at the question again and see if you can spot any words from the chart, and highlight what you need to solve.
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
Now check out the slides below to see an example of how active reading and annotations help you get to the answer. In this example, I used both underlining and notes in the margin. Both options are good if you’re new to active reading for SAT word problems, but I prefer just writing notes in the margin because it saves time while helping me create the equation that I need to solve.
Click here to review the slides
Drawing Word Problems
If you’re still not comfortable working with equations, there’s a different type of active reading strategy you can try: sketching the situation out. In fact, for most test-takers, drawing out the problem can be faster even if you are comfortable with equations.
Let’s try it out with the same question from above:
Carrie invites some friends to a party. For every two friends who bring snacks, there are five who bring nothing with them. If the number of friends who bring nothing is 15 more than the number of friends who contribute snacks, how many friends in total arrive at the party?
By just drawing some of Carrie’s crummy friends, we’ll get there faster. (Alright, so on the actual SAT, you won’t have the luxury or the time to create such a masterpiece. You’ll just draw some circles and squares, or something similar.)
It’s pretty clear on seeing this that 2/7 of the friends have snacks and 5/7 don’t. You can also see the difference is 3/7.
Click here for the rest of the explanation
So just do a little mental highlighting and copy-pasting of that picture.
How many groups of these guys will we need to get to 15? If there are 3 people in each group, we’ll need 5 groups. Five groups of seven people total? 35 friends arrived at the party.
The takeaway? It’s a lot easier to stay focused and get your foot in the door of SAT word problems if you start sketching out the situation like this. Even if you saw the mathematical relationship pretty quickly in this example, there will almost definitely be more difficult problems on the SAT that are best drawn, at least in the beginning. And if the math becomes clear soon after, then great — the picture has served its purpose.
Simplifying SAT Word Problems by Elimination
Because the SAT is mostly multiple-choice, you don’t really have to understand how to transform word problems into equations for a lot of the questions. You can use the answers to your advantage and totally circumvent it.
Not sure where to start on a question? Did drawing the situation fall flat?
Then take a look at the answer choices. If there are concrete numbers there (and not algebraic expressions), then you should try putting some of them through the process that the word problem describes. Like drawing, the process of elimination is often faster than straightforward math.
Below is a relatively basic example. Why don’t you give it a shot first using elimination?
At 8:00 a.m., there are exactly as many chocolate donuts as there are jelly donuts on a table in the teacher’s lounge. Within five minutes, 15 of the chocolate donuts are eaten, but nobody has eaten the jelly donuts. There are then four times as many jelly donuts as there are chocolate donuts on the table. How many jelly donuts are left?
A. 5
B. 10
C. 16
D. 20
E. 40
Click here for the answer and explanation!
Answer: 20
Explanation: So, where should you start? How about with (C)? After all, Neither (A) nor (B) is divisible by four, which the answer probably will be, since the number of jelly donuts is four times that of the chocolate. And (A) is definitely too small.
In (C), there are 16 jelly donuts left, which means there must be 4 chocolate. If there are 4 chocolate donuts after the five minutes are up, there must have been 19 at the start. 19 chocolate and 16 jelly don’t match up, so that’s no good.
Let’s try (D), then, so we’ll have more jelly donuts. 20 jelly means 5 chocolate left. 5 chocolate remaining means 20 chocolate at the start. 20 and 20 match up.
As you can see with the above example, we’re done just like that. Once you’re practiced with process of elimination, you’ll find that doing it in your head is even faster!
Word Problems and Picking Numbers
Our last SAT word problems strategy is picking numbers, which is pretty straightforward. The other easy thing about picking numbers for word problems is that this strategy only works when there is a real equation in either the question or answer choice.
Check out the problem below and pick some easy numbers for h and d.
Savannah is paid $5 for each hour she works and Enrique is paid $10 for each hour he works. Between them, Enrique and Savannah work for h hours, and Enrique earns d more dollars than Savannah. Which of the following expressions gives the number of hours for which Enrique worked?
A. (frac{5h+d}{15})
B. (frac{10h-d}{15})
C. (frac{10h+5d}{2})
D. (frac{5h+15d}{25})
Click here for the answer and explanation!
Takeaway: With Practice Comes Perfect
If we’ve done our job correctly with this SAT word problems post, I hope you’re feeling a little less “huh?” and a bit more zen and that you’re itching to put some of these strategies into practice. If you liked our practice questions, there’s more of that where that came from on our SAT web app, where we give you a 100-point guarantee or your money back.
While these strategies won’t help you become a word problem master overnight, they are a great starting point to building up your active reading, elimination, and picking numbers muscle, and pretty soon, you’ll be able to put your own spin on these techniques to get to solutions faster and best suited for your learning style. Happy studying!
Thanks to Lucas Fink for his contribution to this post, especially for his enviable MS Paint skills!
-
As one of Magoosh’s Blog Editors, Anika relies on her nearly 20 years in education and youth leadership spaces to produce empowering, student-centered content across Magoosh’s blogs. Anika has a BA from Grinnell College and an MPP from Harvard University. Her experience includes serving two years as a Fulbright English Teaching Assistant in Malaysia, an SAT tutor for Kaplan, and currently, as the Executive Director of Youth Activism Project, a nonprofit that she co-founded when she was 12 years old. Anika’s work has been featured in The Washington Post, The Boston Globe, and Yahoo! Money. She has also spoken at panels and given presentations at New York University and Harvard University. If you’d like to keep up with Anika, you can check out her LinkedIn, Instagram, Twitter, and personal website.
View all posts
By the way, Magoosh can help you study for both the SAT and ACT exams. Click here to learn more!
Related Topics:
More Lessons for SAT Math
Math Worksheets
Examples, solutions, videos, activities and worksheets to help SAT students review algebra word problems.
Sample SAT Word Problems (Non-Calculator)
Questions:
1. Every year, a certain population doubles in a country. If there were 30,000 members last year, how many members will there be 5 years from now?
2. A company pays employees $10/hour if they are students and $7/hour if they are non-students. If the company hires 12 employees at a total cost of $99/hour, how many of the employees were students?
3. Mike is staying at a hotel that charges $49.95 per night plus tax for a room. A tax of 6% is applied to the room rate, and an additional one time untaxed fee of $10.00 is charged. Write down an equation that represents Mike’s total charge for staying n nights.
SAT Math Practice Question
Percentage Word Problem
Question:
In a study of goose migration habits, 180 male geese and 120 female geese have been tagged for tracking. If 80 more males are tagged, how may more female geese must be tagged such that 2/3 of the total number of geese in the study are female?
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
Welcome to AMBiPi (Amans Maths Blogs). In this article, you will get SAT 2022 Math Practice Solving Linear Equations Word Problems Questions with Answer Keys.
SAT 2022 Math Multiple Choice Practice Questions
Solving Linear Equations Word Problems Multiple Choice Questions with Answer Keys
SAT Math Practice Test Question No 1:
If 1/2 + 4x = x +2, what is the value of x?
Option A : x = 3/10
Option B : x = 1/2
Option C : x = 5/6
Option D : x = 15/2
Show/Hide Answer Key
Option A : x = 3/10
SAT Math Practice Test Question No 2:
8x + 5 = bx−7
In the equation shown above, b is a constant. For what value of b does the equation have no solutions?
Option A : -8
Option B : -7
Option C : 5
Option D : 8
Show/Hide Answer Key
Option D : 8
SAT Math Practice Test Question No 3:
If -8 – 8y = 6 – 2y, what is the value of y?
Option A : y = -3/7
Option B : y = 3/7
Option C : y = 7/3
Option D : y = -7/3
Show/Hide Answer Key
Option D : y = -7/3
SAT Math Practice Test Question No 4:
2| – v/4 | + 26 < 12
Which of the following best describes the solutions to the inequality shown above
Option A : -7 < 7
Option B : -28 < 28
Option C : No solution
Option D : All real numbers
Show/Hide Answer Key
Option C : No solution
SAT Math Practice Test Question No 5:
2/3 – 5x = bx+ 1/3
In the equation shown above, b is a constant. For what value of b does the equation no solutions?
Option A : 5
Option B : 0
Option C : -5
Option D : 2/3
Show/Hide Answer Key
Option C : -5
SAT Math Practice Test Question No 6:
If Dimitri is helping to plan the school talent show. Each performer for the talent show has 6 minutes for his or her performance, which includes transition time between performances. If the introduction for the talent show is 24 minutes long and the show will last 150 minutes, how many different performances can the talent show accommodate?
Option A : 21
Option B : 24
Option C : 25
Option D : 29
Show/Hide Answer Key
Option A : 21
SAT Math Practice Test Question No 7:
The property taxes in a town decrease as the distance from the local elementary school increases. The greatest property taxes are 4.5,and for every 10 miles from the school, property taxes decrease by 0.5 percentage points. If a house is directly east or west of the school and its property taxes are 3 what is the distance of that house from the school?
Option A : 10 miles
Option B : 20 miles
Option C : 30 miles
Option D : 40 miles
Show/Hide Answer Key
Option C : 30 miles
SAT Math Practice Test Question No 8:
If Dalia is installing a tile floor in a rectangular room. Dalia has 152 tiles available to tile the room. If each row requires 9 1/2 tiles, and 19 tiles break while Dalia is laying the floor, how many full rows of tile can she install before running out of tiles?
Option A : 12
Option B : 14
Option C : 16
Option D : 18
Show/Hide Answer Key
Option B : 14
SAT Math Practice Test Question No 9:
Phytoremediation is the use of plant growth to purify pollutants from soil, water, or air. Suppose that a crop of brake ferns can remove 15 milligrams (mg) per square meter of a particular pollutant from the soil in 20 weeks. After 20 weeks, the ferns are harvested and a new crop is planted. If cc represents the number of crops of brake ferns needed to Phytoremediation soil contaminated with 170mg per square meter of the pollutant down to healthy levels of 5mg per square meter, which equation best models the situation?
Option A : 170 − 20c = 5
Option B : 170 + 20c = 5
Option C : 170 − 15c = 5
Option D : 170 + 20c = 5
Show/Hide Answer Key
Option C : 170 − 15c = 5
SAT Math Practice Test Question No 10:
One of the rules in a public speaking contest requires contestants to speak for as close to 5 minutes (300 seconds) as possible. Contestants lose 3 points for each second they speak either over or under 5 minutes. Which expression below can be used to determine the number of points a contestant loses if she speaks for x seconds?
Option A : 3|x−300|
Option B : 5|x−300|
Option C : 3|x+300|
Option D : 3/5|x+300|
Show/Hide Answer Key
Option A: 3|x−300|
SAT Math Practice Test Question No 11:
Cara is hanging a poster that is 91 centimeters (cm) wide in her room. The center of the wall is 180cm from the right end of the wall. If Cara hangs the poster so that the center of the poster is located at the center of the wall, how far will the left and right edges of the poster be from the right end of the wall?
Option A : 225.5cm and 89cm, respectively
Option B : 271.5cm and 134.5cm, respectively
Option C : 225.5cm and 134.5cm, respectively
Option D : 271cm and 89cm, respectively
Show/Hide Answer Key
Option C : 225.5cm and 134.5cm, respectively
SAT Math Practice Test Question No 12:
Felipe is saving money for a class trip. He already has saved $250 that he will put toward the trip. To save more money for the trip, Felipe gets a job where each month he can add $350 to his savings for the trip. Let m be the number of months that Felipe has worked at his new job. If Felipe needs to save $2700 to go on the trip, which equation best models the situation?
Option A : 250m − 350 = 2700
Option B : 250m + 350 = 2700
Option C : 350m − 250 = 2700
Option D : 350m + 250 = 2700
Show/Hide Answer Key
Option D : 350m + 250 = 2700
SAT Math Practice Test Question No 13:
Camille and Hiroki have decided to start walking for exercise. Camille is going to walk 7 miles the first day and 3 miles each day after that Hiroki is too busy to walk on the first 2 days, so he decides to walk 5 miles each day until he has walked the same number of miles as Camille. If Camille and Hiroki will have walked the same number of miles, how many days will Camille have walked?
Option A : 2
Option B : 3
Option C : 5
Option D : 7
Show/Hide Answer Key
Option D : 7
SAT Math Practice Test Question No 14:
An art gallery displays a large painting in the center of a wall that is 24 feet (ft) wide. The painting is 10ft wide. Which of the following equations can be used to find the distances, x in feet, from the left end of the wall to the edges of the painting?
Option A : |x − 10| = 12
Option B : 2|x − 12| = 10
Option C : 2|x − 10| = 12
Option D : |x − 12| = 10
Show/Hide Answer Key
Option B : 2|x−12|=10
SAT Math Practice Test Question No 15:
At the county fair, the operator of a game guesses a contestant’s weight. For each pound the operator’s guess differs from the contestant’s weight, the contestant will receive $3. If a contestant received $15 when the operator guessed 120 pounds, what are the possible values for the weight of the contestant?
Option A : 105 and 115
Option B : 105 and 125
Option C : 115 and 125
Option D : 115 and 135
Show/Hide Answer Key
Option C : 115 and 125
SAT 2022 Math Grid-in Practice Questions
Solving Linear Equations and Inequalities Grid-in Choice Questions with Answer Keys
SAT Math Practice Test Question No 16:
A park shaped like a pentagon has four equal length sides and one unequal side whose length is 35 feet (ft). The perimeter of the park is 195 ft. What is the length in feet of one of the equal sides?
Show/Hide Answer Key
Correct Answer : 40
SAT Math Practice Test Question No 17:
Sasha has $2.65 in change in her pocket. The $2.65 is made up of one quarter plus an equal number of nickels and dimes. How many nickels does Sasha have in her pocket?
Show/Hide Answer Key
Correct Answer : 16
SAT Math Practice Test Question No 18:
The number of subscribers to a certain newspaper decreases by about 2,000 each year. In 2010, there were 19,000 subscribers. In what year should the newspaper expect to have approximately 7,000 subscribers?
Show/Hide Answer Key
Correct Answer : 2016
SAT Math Practice Test Question No 19:
An airplane begins its descent to land from a height of 35,000 feet (ft) above sea level. The airplane’s height changes by about −4000 ft every 3 minutes. Rounded to the nearest minute, in approximately how many minutes will the plane land?
Assume that the airport runway is at sea level.
Show/Hide Answer Key
Correct Answer : 26
SAT Math Practice Test Question No 20:
A car driving on a straight path travels about 260 feet (ft) in 3 seconds. Rounded to the nearest second, approximately how many seconds will it take for the car to travel 1 mile (mi) at the same rate? 1 mi=5,280 ft.
Show/Hide Answer Key
Correct Answer : 61
free sat math practicefree sat math practice testmath sat practicesample sat math questionssat math practice onlinesat math practice problemssat math practice testsat math practice test onlinesat math prep questionssat math questionssat math questions and answerssat math section practice testsat math test prepsat practice testsat syllabus 2022sat test prep
Question
Sanjay works as a teacher’s assistant for ($)20 per hour and tutors privately for ($)25 per hour. Last week, he made at least ($)100 working (x) hours as a teacher’s assistant and (y) hours as a private tutor. Which of the following inequalities models this situation?
- (4x+5y geq 25)
- (4x+5y geq 20)
- (5x+4y geq 25)
- (5x+4y geq 20)
Answer/Explanation
Ans: B
Question
The 2017 Wyoming state senate had 30 elected members consisting of Democrats and Republicans. Let (d) represent the number of Democrats who vote yes for a bill, and let (r) represent the number of Republicans who vote yes for a bill. For a bill to pass, more than half of the 30 senators must vote yes. Which of the following inequalities represents all possible values of (d) and (r) for a bill to pass?
- (d + r > 15)
- (d + r < 15)
- (d + r geq 15)
- (d + r leq 15)
Answer/Explanation
Ans: A
Question
The solution to which system of inequalities is represented by the shaded region of the graph?
- (y leq 7)
(y leq 2x+1) - (y leq 7)
(y geq 2x+1) - (x leq 7)
(2y leq x) - (x leq 7)
(2y geq x)
Answer/Explanation
Ans: B
Question
Aracely can spend up to a total of ($)20 on streamers and balloons for a party. Streamers cost ($)1.49 per pack, and balloons cost ($)4.39 per pack. Which of the following inequalities represents this situation, where (s) is the number of packs of streamers Aracely can buy, and (b) is the number of pack of balloons Aracely can buy? (Assume there is no sales tax.)
- (1.49s-4.39bleq 20)
- (1.49s+4.39bleq 20)
- (1.49s-4.39bgeq 20)
- (1.49s+4.39bgeq 20)
Answer/Explanation
Ans: B
Question
The coordinates of points (A),(B) and (C) are shown in the (xy)-plane above. For which of the following inequalities will each of the points (A),(B) and (C) be contained in the solution region?
- (y>-x-2)
- (ygeq -x)
- (y<x+3)
- (x<3)
Answer/Explanation
Ans: A
Question
(T(n)=80+n)
(S(n)=1,280+30n)
The given equations model the number of teachers and students in a high school from 2002 through 2017. In the equations, (n) is the number of years after 2002, where (n) is a whole number less than or equal to 15. The predicted number of teachers and students are (T(n)) and (S(n)), respectively.
Based on the model, what is the first year in which the predicted number of teachers will be greater than 90?
- 2014
- 2013
- 2012
- 2011
Answer/Explanation
Ans: B
Question
A certain elephant weighs 200 pounds at birth and gains more than 2 but less than 3 pounds per day during its first year. Which of the following inequalities represents all possible weights (w), in pounds, for the elephant 365 days after its birth?
- (400<w<600)
- (565<w<930)
- (730<w<1,095)
- (930<w<1,295)
Answer/Explanation
Ans: D
Question
(y)>4(x)
(y)<-(x)
When graphed in the (xy)-plane, what point ((x), (y)) is a solution to the given system of inequalities?
- (1,1)
- (-2,-2)
- (3,-3)
- (-4,4)
Answer/Explanation
Ans: B
Question
(c(x) = mx + 500)
A company’s total cost (c(x)), in dollars, to produce (x) shirts is given by the function above, where (m) is a constant and (x > 0). The total cost to produce 100 shirts is ($)800. What is the total cost, in dollars, to produce 1000 shirts? (Disregard the ($) sign when gridding your answer.)
Answer/Explanation
Ans: 3500
Question
Terrence’s car contains 8 gallons of fuel. He plans to drive the car (m) miles using the fuel currently in the car. If the car can drive 20 miles per gallon of fuel, which inequality gives the possible values of (m)?
- (m leq (8)(20))
- (m geq (8)(20))
- (8leq 20m)
- (8 geq 20m)
Answer/Explanation
Ans: A
Question
A clothing store is having a sale on shirts and pants. During the sale, the cost of each shirt is ($)15 and the cost of each pair of pants is ($)25. Geoff can spend at most ($)120 at the store. If Geoff buys (s) shirts and (p) pairs of pants, which of the following must be true?
- (15s+25p leq 120)
- (15s+25p geq 120)
- (25s+15p leq 120)
- (25s+15p geq 120)
Answer/Explanation
Ans: A
Question
Makayla is planning an event in a 5,400-square-foot room. If there should be at least 8 square feet per person, what is the maximum number of people that could attend this event?
- 588
- 675
- 15,274
- 43,200
Answer/Explanation
Ans: B
Question
Jonathan needs to earn at least ($)175 next week and can work at most 20 hours. He earns ($)10 per hour at his lawn service job and ($)8 per hour at his job at the gym. Which of the following systems of inequalities represents this situation in terms of the number of hours he will work at his lawn service job, (l), and the number of hours he will work at his job at the gym, (g), next week?
- (10l+8g leq 175)
(l+g leq 20) - (10l+8g leq 175)
(l+g geq 20) - (10l+8g geq 175)
(l+g leq 20) - (10l+8g geq 20)
(l+g geq 175)
Answer/Explanation
Ans: C
Question
During an ice age, the average annual global temperature was at least 4 degrees Celsius lower than the modern average. If the average annual temperature of an ice age is (y) degrees Celsius and the modern average annual temperature is (x) degrees Celsius, which of the following must be true?
- ( y = x — 4)
- ( y leq x + 4)
- ( y geq x — 4)
- ( y leq x — 4)
Answer/Explanation
Ans: D
Question
(y geq -2x+11)
(y > 3x— 9)
In the (xy)-plane, point (A) is contained in the graph of the solution set of the system of inequalities above. Which of the following could be the coordinates of point (A) ?
- (2,1)
- (4,1)
- (4, 5)
- (6, 6)
Answer/Explanation
Ans: C
Question
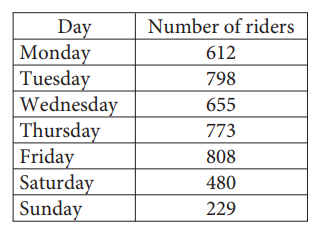
The number of people who rode a certain bus each day of a week is shown in the table below.
Which of the following is true based on these data?
- The bus had the most riders on Tuesday.
- Each day from Tuesday through Sunday, the number of riders on the bus was greater than the previous day.
- Each day from Tuesday through Sunday, the number of riders on the bus was less than the previous day.
- The two days with the fewest number of riders were Saturday and Sunday.
Answer/Explanation
Ans: D
Question
A certain colony of bacteria began with one cell, and the population doubled every 20 minutes. What was the population of the colony after 2 hours?
- 6
- 12
- 32
- 64
Answer/Explanation
Ans: D
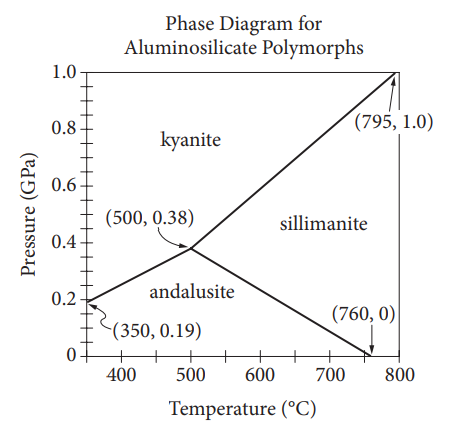
Question
During mineral formation, the same chemical compound can become different minerals depending on the temperature and pressure at the time of formation. A phase diagram is a graph that shows the conditions that are needed to form each mineral. The graph above is
a portion of the phase diagram for aluminosilicates, with the temperature (T), in degrees Celsius (°C), on the horizontal axis, and the pressure (P), in gigapascals (GPa), on the vertical axis.
Which of the following systems of inequalities best describes the region where sillimanite can form?
- (P geq 0.0021T — 0.67)
(P geq 0.0013T — 0.25) - (P leq 0.0021T — 0.67)
(P geq —0.0015T+ 1.13) - (P leq 0.0013T— 0.25)
(P geq —0.0015T+ 1.13 ) - (P leq 0.0013T— 0.25)
(P leq —0.0015T+ 1.13)
Answer/Explanation
Ans: B
Question
The gas mileage (M(s)), in miles per gallon, of a car traveling (s) miles per hour is modeled by the function below, where (20 ≤ s ≤ 75) .
(M(s)=-frac{1}{24}s^2+4s-50)
According to the model, at what speed, in miles per hour, does the car obtain its greatest gas mileage?
- 46
- 48
- 50
- 75
Answer/Explanation
Ans: B
Question
Tamika is ordering desktop computers for her company. The desktop computers cost ($)375 each, and tax is an additional 6% of the total cost of the computers. If she can spend no more than ($)40,000 on the desktop computers, including tax, what is the maximum number of computers that Tamika can purchase?
Answer/Explanation
Ans: 100
Question
Emma mows grass at a constant rate of 1.5 acres per hour. She mowed 2 acres before lunch and plans to spend (t) hours mowing after lunch. If Emma wants to mow at least 8 acres of grass today, which of the following inequalities best represents this situation?
- (1.5t geq
- (1.5t- 2 geq
- (1.5t+ 2 geq
- (2t+1.5t geq
Answer/Explanation
Ans: C
Question
The table above shows the recommended amount of potassium, in milligrams (mg) per day, for people of all ages according to the National Academy of Medicine.
Andrea’s recommended daily intake of potassium is 50% greater than that of her two-year-old brother. What is the least possible age, in years, of Andrea?
Answer/Explanation
Ans: 9
Question
(C= 10x + 4y)
The formula above gives the monthly cost (C), in dollars, of operating a delivery truck when the driver works a total of (x) hours and when (y) gallons of gasoline are used. If, in a particular month, it cost no more than ($)2,000 to operate the truck and at least 150 gallons of gas were used, what is the maximum number of hours the driver could have worked?
- 125
- 140
- 500
- 1,400
Answer/Explanation
Ans: B
Question
Students in a science lab are working in groups to build both a small and a large electrical circuit. A large circuit uses 4 resistors and 2 capacitors, and a small circuit uses 3 resistors and 1 capacitor. There are 100 resistors and 70 capacitors available, and each group must have enough resistors and capacitors to make one large and one small circuit. What is the maximum number of groups that could work on this lab project?
Answer/Explanation
Ans: 14
Question
If (m = 3), how much greater is (10m) than (6m) ?
- 3
- 4
- 12
- 30
Answer/Explanation
Ans: C
Question
A greenhouse owner purchases fertilizer in 60-gallon drums. The fertilizer is mixed with water to make several batches of solution. Each batch of solution is made by mixing 3 quarts of fertilizer with water. What is the maximum number of batches of solution that can be made from one 60-gallon drum of fertilizer? (1 gallon = 4 quarts)
- 45
- 60
- 80
- 180
Answer/Explanation
Ans: C
Question
Ryan has 1,500 yards of yarn. He wants to knit at least 2 scarves and at least 3 hats. Each scarf requires 300 yards of yarn, and each hat requires 120 yards of yarn. If (s) represents the number of scarves and (h) represents the number of hats, which of the following systems of inequalities represents this situation?
- (s + h leq 1,500)
(s geq 2)
(h geq 3) - (2s + 3h leq 1,500)
(s geq 2)
(h geq 3) - (2s + 3h leq 1,500)
(s geq 300)
(h geq 120) - (300s + 120h leq 1,500)
(s geq 2)
(h geq 3)
Answer/Explanation
Ans: D
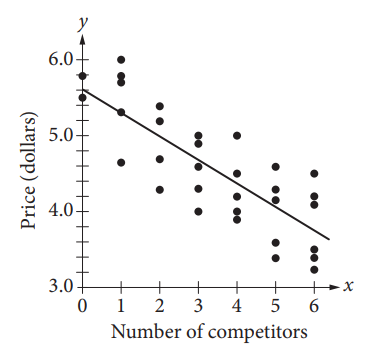
Question
A researcher is investigating the relationship between the price of a four-pack of AA batteries at a convenience store and the number of competitors the store has. She defines a store’s competitor as another similar store within a 1-mile radius of the store she selects. She selects 32 convenient stores across a state at random, and for each store, she records the number of its competitors and its price for a four-pack of AA batteries. The results are shown, along with the line of best fit, in the scatterplot below.
Another convenience store in the same state sells a four-pack AA batteries for ($)4.89. If the store’s price is more than that predicted by the line of best fit, what is the least number of competitors the store could have?
- 1
- 2
- 3
- 4
Answer/Explanation
Ans: C
Question
Every Saturday, Bob bakes loaves of bread to sell at the farmer’s market. Each loaf costs him ($)1 to make, and he sells the loaves for ($)3 each. He also pays a vendor’s fee of ($)75 every Saturday to set up his booth. What is the least number of loaves of bread Bob needs to sell every Saturday to cover the cost of the vendor’s fee?
- 38
- 37
- 25
- 19
Answer/Explanation
Ans: A
Question
Ms. Anderson currently has 550 contacts on an online professional networking site. Her goal is to have at least 1,000 contacts. If she wants to meet this goal in 25 weeks, what is the minimum number of contacts per week, on average, she should add?
- 18
- 19
- 21
- 22
Answer/Explanation
Ans: A
Question
Samantha babysat 20 different times in December. The lowest amount she earned for babysitting was ($)10, and the highest amount she earned as ($)22. Of the following, which could be the total amount she earned for babysitting during December?
- ($)190
- ($)200
- ($)320
- ($)440
- ($)640
Answer/Explanation
Ans: C
Question
The product of six consecutive integers, the least of which is 5, is how many times the product of five consecutive integers, the least of which is 5?
- 9
- 10
- 11
- 25
- 30
Answer/Explanation
Ans: B
Question
If (z) is 10 greater than (x), then (z-10) is how much greater than (x)?
- 0
- 5
- 10
- 20
- 100
Answer/Explanation
Ans: A
Question
If (2x+5<13), what is the greatest possible integer value of (x)?
Answer/Explanation
Ans: 3
Question
The height, (h) in inches, of each person in a certain population satisfies the inequality (left | frac{h-68.5}{2.7} right |leq 1). Which of the following CANNOT be the height, in inches, of a person in this population?
- 65
- 66
- 68
- 70
- 71
Answer/Explanation
Ans: A
Question
(left | p-725 right | < 107)
Harper Supply Store’s profit of (p) dollars last week satisfies the inequality above, where ($)725 is the store’s average (arithmetic mean) weekly profit. If (p) is an integer, what is the greatest possible value of (p) ?
Answer/Explanation
Ans: 831
Question
(- 5 leq a leq 5)
(1<b < 5)
In the inequalities above, (a) and (b) are integers, What is the least integer value of (frac{a}{b}) ?
- 4
- 2
- -1
- -2
- – 4
Answer/Explanation
Ans: D
Question
If (0 < 3x – 2 < 1), what is one possible value for (x) ?
Answer/Explanation
Ans: 2/3<x<1 or .666<x<1
Question
In the (xy)-plane, a circle has its center at the origin and a radius of 5. What is the length of the shortest line segment that has one endpoint on the circle and the other at (13, 0)?
Answer/Explanation
Ans: 8
Question
Set (S) consists of the positive multiples of 6 that are less than 50, and set (T) consists of the positive multiples of 8 that are less than 50. How many numbers do sets (S) and (T) have in common?
- None
- One
- Two
- Four
- Eight
Answer/Explanation
Ans: C
Question
The numbers (v,w,x,y,) and (z) are indicated on the number line above. Of the following, which quantity has the least value?
- (v)
- (vw)
- (vx)
- (vy)
- (vz)
Answer/Explanation
Ans: E
Question
If (x-5=t), then (x) is 1 more than which of the following?
- (t+4)
- (t+5)
- (t+6)
- (t+7)
- (t+8)
Answer/Explanation
Ans: A
Question
(frac{2}{x}>3)
In which of the following intervals does every value of (x) satisfy the inequality above?
- (-1<x<-frac{1}{2})
- (-frac{1}{2}<x<-frac{1}{4})
- (frac{1}{4}<x<frac{1}{2})
- (frac{1}{2}<x<frac{3}{4})
- (frac{3}{4}<x<1)
Answer/Explanation
Ans: C
Question
A gym class of 33 students is to be divided into teams of 2 or more players each. If each team must have the same number of students and every student must be on a team, what is the maximum number of teams possible?
Answer/Explanation
Ans: 11
Question
If (x) is a positive odd integer and (60<3x+8<70), what is the value of (3x+8)?
- 63
- 65
- 67
- 68
- 69
Answer/Explanation
Ans: B
Question
If (1<a<b<10) and (x=frac{a ☓ 10^5}{b ☓ 10^{-3}})
Which of the following inequalities is true?
- (10^0 <x < 10^1)
- (10^1 <x < 10^2)
- (10^2 <x < 10^3)
- (10^7 <x < 10^8)
- (10^8 <x < 10^9)
Answer/Explanation
Ans: D
Question
Prime numbers (k) and (n) are each greater than 2, and they differ by 4. If there is no prime number between (k) and (n), what is the least possible value of (k + n) ?
- 8
- 10
- 12
- 16
- 18
Answer/Explanation
Ans: E
Question
If (-1<x<0) and (0<y<1), which of the following must be true?
I. (-1<xy<0)
II. (-1<frac{x}{y}<0)
III. (y-x<1)
- I only
- II only
- III only
- I and III only
- I, II, and III
Answer/Explanation
Ans: A
Question
The integer (x) is the sum of 3 different positive integers, each less than 10. The integer (y) is the sum of 3 different positive integers, each less than 20. What is the smallest possible value of (frac{x}{y}) ?
Answer/Explanation
Ans: 1/9 or .111
Question
(6x + 3 geq a)
If the inequality above is true for the constant (a), which of the following could be a value of (x) ?
- (frac{a}{6})
- (frac{a}{6})-1
- (frac{a}{6})-3
- (frac{a-4}{6})
- (frac{a-5}{6})
Answer/Explanation
Ans: A
Question
(3<2x<11)
If (x) is an integer that satisfies the inequalities above, what is one possible value of (3x)?
Answer/Explanation
Ans: 6, 9, 12 or 15
Question
What is the greatest four-digit integer that meets the following three restrictions?
1. All of the digits are different.
2. The greatest digit is the sum of the other three digits.
3. The product of the four digits is divisible by 10 and not equal to zero.
Answer/Explanation
Ans: 8521
Question
The average (arithmetic mean) of the 3 different positive integers (x,y) and (z) is 50. If (x<y<z) and (y=30), what is the least possible value of (z)?
- 50
- 51
- 59
- 90
- 91
Answer/Explanation
Ans: E
Question
In Lewiston, 4 out of every 7 registered voters voted in the last election. If a total of 2000 votes were cast, What was the number of registered voters in Lewiston at the time of the last election?
Answer/Explanation
Ans: 3500
Question
The positive number (n) is the product of three different prime numbers greater than 2. If the sum of these three prime numbers is also prime, what is the smallest possible value of (n)?
Answer/Explanation
Ans: 165
Question
In a class consisting of 55 boys and 45 girls, 30 students have blue eyes. What is the least possible number of girls in the class who do not have blue eyes?
- 10
- 15
- 20
- 25
- 30
Answer/Explanation
Ans: B
Question
If (6y = 2x) and (y neq 0), what is the value of (frac{x}{y})?
- (frac{1}{4})
- (frac{1}{3})
- 3
- 4
- 8
Answer/Explanation
Ans: C
Question
If |(ax)- 1| (leq 1), where (a) is a positive even integer, which of the following CANNOT be a value of (x^2) ?
- 0
- (frac{1}{4})
- (frac{1}{2})
- 1
- 4
Answer/Explanation
Ans: E
Question
(k = 3w + 2)
In the equation above, if (w) is increased by 2, by how much does (k) increase?
- 2
- 3
- 5
- 6
- 8
Answer/Explanation
Ans: D
Question
(38 < 6x + 2 < 44)
What is one possible value of (x) that satisfies the inequality above?
Answer/Explanation
Ans: (6<x<7)
Question
Luis and Stacy each contributed money to pay for a trip. They contributed a total of ($)480, and Luis contributed ($)30 more than twice the amount that Stacy contributed. How much money did Luis contribute for the trip?
- ($)150
- ($)230
- ($)300
- ($)330
- ($)450
Answer/Explanation
Ans: D
Question
A marching band consists of musicians and flag bearers. The number of musicians is 4 more than twice the number of flag bearers. If there are 52 musicians, how many members does the marching band have?
- 68
- 76
- 108
- 152
- 160
Answer/Explanation
Ans: B
Question
For integers (a) and (b), where (4 leq a leq 6) and (8 leq b leq 10), what is the greatest possible value of (frac{3}{b-a})?
Answer/Explanation
Ans: 3/2, 1.5
Question
(2m geq 10)
(3m leq 21)
Which of the following is the set of all integer solutions to the system of inequalities above?
- {2,3,4}
- {3,4,5}
- {4,5,6}
- {5,6,7}
- {7,8,9}
Answer/Explanation
Ans: D
Question
(3t<41)
If (t) is an integer in the inequality above, what is the greatest possible value of (t)?
- 12
- 13
- 14
- 15
- 16
Answer/Explanation
Ans: B
Question
Lily is (x) years old. Danny’s age is 2 years less than 5 times Lily’s age. How many years old is Danny, in terms of (x)?
- 5(x)
- (x)-2
- 5((x)-2)
- 2-5(x)
- 5(x)-2
Answer/Explanation
Ans: E
Question
If (x>0) then (y=10)
If (y=10) then (z=2x)
Based on the statements in the box above, what is the value of (z) when (x)=-10?
- -20
- -5
- 10
- 20
- It cannot be determined from the information given.
Answer/Explanation
Ans: E
A typical SAT has several word problems, covering almost every math topic for which you are responsible. Expect to encounter word problems on all sorts of topics, such as: consecutive integers, fractions and percents, ratios and proportions, averages, circles, triangles, and other geometric figures. A few of these problems can be solved just with arithmetic, but most of them require basic algebra.
To solve word problems algebraically, you must treat algebra as a foreign language and learn to translate “word for word” from English into algebra, just as you would from English into French or Spanish or any other foreign language. When translating into algebra, you use some letter (often x) to represent the unknown quantity you are trying to determine. It is this translation process that causes difficulty for some students. Once the translation is completed, solving is easy using the techniques already reviewed.
Consider the pairs of typical SAT questions in Examples 1 and 2. The first ones in each pair (1A and 2A) would be considered easy, whereas the second ones (1B and 2B) would be considered harder.
Example 1A[edit | edit source]
What is 4% of 4% of 40,000?
Example 1B[edit | edit source]
In a lottery, 4% of the tickets printed can be redeemed for prizes, and 4% of those tickets have values in excess of $100. If the state prints 40,000 tickets, how many of them can be redeemed for more than $100?
Example 2A[edit | edit source]
If x + 7 = 2(x − 8), what is the value of x?
Example 2B[edit | edit source]
In 7 years, Erica will be twice as old as she was 8 years ago. How old is Erica now?
Once you translate the words into arithmetic expressions or algebraic equations, Examples 1A and 1B and 2A and 2B are clearly identical. The problem that many students have is doing the translation. It really isn’t very difficult, and you’ll learn how. First, though, look over the following English-to-algebra “dictionary.”
| English words | Mathematical meaning | Symbol |
|---|---|---|
| is, was, will be, had, has, will have, is equal to, is the same as | Equals | = |
| plus, more than, sum, increased by, added to, exceeds, received, got, older than, farther than, greater than | Addition | + |
| Minus, fewer, less than, difference, decreased by, subtracted from, younger than, gave, lost | Subtraction | − |
| Times, of, product, multiplied by | Multiplication | × |
| Divided by, quotient, per, for | Division | ÷ |
| More than, greater than | Inequality | > |
| At least | Inequality | ≥ |
| Fewer than, less than | Inequality | < |
| At most | Inequality | ≤ |
| What, how many, etc. | Unknown quantity | n (or some other variable) |
Let’s use this “dictionary” to translate some phrases and sentences.
| English sentences | Algebraic sentences |
|---|---|
| The sum of 5 and some number is 13. | 5 + n = 13 |
| John was 2 years younger than Sam. | J = S − 2 |
| Bill has at most $100. | B ≤ 100 |
| The product of 2 and a number exceeds that number by 5. | 2n = n + 5 |
In translating a statement, you first must decide what quantity the variable will represent. Often, this is obvious. Other times there is more than one possibility. Let’s translate and solve the two examples at the beginning of this section, and then look at a few new ones.
Example 1B[edit | edit source]
In a lottery, 4% of the tickets printed can be redeemed for prizes, and 4% of those tickets have values in excess of $100. If the state prints 40,000 tickets, how many of them can be redeemed for more than $100?
Solution[edit | edit source]
Let x be the number of tickets worth more than $100. Then,
x = 4% of 4% of 40,000 = 0.04 × 0.04 × 40,000 = 64,
which is also the solution to Example 1A.
Example 2B[edit | edit source]
In 7 years, Erica will be twice as old as she was 8 years ago. How old is Erica now?
Solution[edit | edit source]
Let x be Erica’s age now; 8 years ago, she was x − 8, and 7 years from now, she will be x + 7. Then,
x + 7 = 2(x − 8),
and
x + 7 = 2(x − 
Example 3[edit | edit source]
The product of 2 and 8 more than a certain number is 10 times that number. What is the number?
Solution[edit | edit source]
Let x represent the unknown number. Then,
2(8 + x) = 10x
and
2(8 + x) = 10x ⇒ 16 + 2x = 10x ⇒ 8x = 16 ⇒ x = 2
Example 4[edit | edit source]
If the sum of three consecutive integers is 20 more than the middle integer, what is the smallest of the three?
Solution[edit | edit source]
Let n represent the smallest of the three integers. Since the integers are consecutive, the middle number is n + 1, and the largest of the three numbers is n + 2. Then,
n + (n + 1) + (n + 2) = 20 + (n + 1)
and
n + (n + 1) + (n + 2) = 20 + (n + 1) ⇒ 3n + 3 = 21 + n ⇒ 2n + 3 = 21 ⇒ 2n = 18 ⇒ n = 9.
The three integers are 9, 10, and 11. Party like it’s September 10, 2011.
Most algebraic word problems on the SAT are not very difficult. If, after studying this section, you still get stuck on a question, don’t despair. In each of Examples 3 and 4, if you had been given choices, you could have back-solved, and if the questions had been grid-ins, you could have used trial and error (effectively, back-solving by making up your own choices). Here’s how.
Alternative Solution to Example 3[edit | edit source]
Pick a starting number and test (using your calculator, if necessary).
- Try 10: 8 + 10 = 18, and 2 × 18 = 36, but 10 × 10 = 100, which is much too big!
- Try 5: 8 + 5 = 13, and 2 × 13 = 26, but 10 × 5 = 50, which is still too big.
- Try 2: 8 + 2 = 10, and 2 × 10 = 20, and 10 × 2 = 20. That’s it.
Alternative Solution to Example 4[edit | edit source]
You need three consecutive integers whose sum is 20 more than the middle one. Obviously, [1, 2, 3] and [5, 6, 7] are too small; neither one even adds up to 20.
- Try [10, 11, 12]: 10 + 11 + 12 = 33, which is 22 more than 11. A bit too much.
- Try [9, 10, 11]: 9 + 10 + 11 = 30, which is 20 more than 10.
Of course, if you can do the algebra, that’s usually the best way, to handle these problems. Ongrid-ins you might have to backsolve with several numbers before zooming in on the correct answer; also, if the correct answer was a fraction, such as 
Helpful Hint[edit | edit source]
In all word problems on the SAT, remember to circle what you’re looking for. Don’t answer the wrong question!
Age Problems[edit | edit source]
In problems involving ages, remember that “years ago” means you need to subtract, and “years from now” means you need to add.
Example 5[edit | edit source]
In 1980, Judy was 3 times as old as Adam, but in 1984 she was only twice as old as he was. How old was Adam in 1990?
- C) 4
- L) 8
- I) 12
- M) 14
- B) 16
Solution[edit | edit source]
Let x be Adam’s age in 1980, and fill in the table below.
| Year | Judy | Adam |
|---|---|---|
| 1980 | 3x | x |
| 1984 | 3x + 4 | x + 4 |
Now translate: Judy’s age in 1984 was twice Adam’s age in 1984:
3x + 4 = 2(x + 4)
3x + 4 = 2(x + 4) ⇒ x + 4 = 8 ⇒ x = 4
Adam was 4 in 1980. However, 4 is not the answer to this question. Did you remember to circle what you’re looking for? The question could have asked for Adam’s age in 1980 (choice C) or 1984 (choice L) or Judy’s age in any year whatsoever (choice I is 1980, and choice B is 1984); but it didn’t. It asked for Adam’s age in 1990. Since he was 4 in 1980, then 10 years later, in 1990, he was 14 (M).
(A) ( 4)
(B) ( 
(C) ( 9)
(D) ( 10)
(E) ( 11)
Correct Answer: B
Solution 1:
Let (x) be the number of apples and the number of pears in the basket. Eric eats 5 apples, and therefore there are (x-5) apples remaining. He also eats 1 pear, and therefore there are (x-1) pears remaining. We’re told that after Eric eats there are twice as many pears as apples in the basket. We set up an equation.
[begin{array}{l c l l}
2(x-5) &=& x-1 &quad text{create equation} &(1)\
2x-10 &=& x-1 &quad text{use distributive property} &(2)\
x-10 &=& -1 &quad text{subtract} x text{from both sides} &(3)\
x &=& 9 &quad text{add} 10 text{to both sides} &(4)\
end{array}]
We’re looking for the number of pears remaining in the basket, but (x=9) is the original number of pears. Since he ate (1) pear, there are (8) pears remaining.
Solution 2:
Here, for each answer choice, we work our way backwards. We compute, based on how many pears are left, how many pears and apples there were to start with. Remember that there was the same number of apples and pears before Eric ate.
(A) If 4 pears are left, then there were 4+1=5 pears to start with.
Since there are twice as many pears remaining as apples, then there are (frac{4}{2}=2) apples left, and there were 2+5=7 apples to start with. But (5neq 7.) This is the wrong choice.
(B) If 8 pears are left, then there were 8+1=9 pears to start with.
Since there are twice as many pears remaining as apples, then there are (frac{8}{2}=4) apples left, and there were 4+5=9 apples to start with. (9=9) and therefore this is the correct answer.
(C) If 9 pears are left, then there were 9+1=10 pears to start with.
Since there are twice as many pears remaining as apples, then there are (frac{9}{2}=4.5) apples left, and there were 4.5+5=9.5 apples to start with. But (9 neq 9.5.) This is the wrong choice.
(D) If 10 pears are left, then there were 10+1=11 pears to start with.
Since there are twice as many pears remaining as apples, then there are (frac{10}{2}=5) apples left, and there were 5+5=10 apples to start with. But (10neq 11). This is the wrong choice.
(E) If 11 pears are left, then there were 11+1=12 pears to start with.
Since there are twice as many pears remaining as apples, then there are (frac{11}{2}=5.5) apples left, and there were 5.5+5=10.5 apples to start with. (10.5neq 12.) This is the wrong choice.
Incorrect Choices:
If you got this problem wrong, you should review SAT Translating Word Problems.
(A)
This wrong choice is the number of apples that remain in the basket.
(C)
If you solve for the original number of pears, you will get this wrong answer.
(D)
When accounting for the pear Eric ate, if instead of subtracting 1 from the original number of pears, you add 1, you will get this wrong answer.
(E)
When finding how many apples remain in the basket after Eric consumed 5 of them, if you add 5 to (x) instead of subtract 5 from it, you will get
[begin{array}{l c l l}
2(xfbox{+}5) &=& x-1 &quad text{mistake: added} 5 text{to} x &(1)\
end{array}]
Or, you may get this wrong answer if in step (3) of the solution you subtract 10 from both sides and you ignore the negative signs.
At 2:00 P.M. a train A leaves a station traveling at 100 mi/hr. At 4:30 P.M. train B leaves the station on a parallel route and traveling at 150 mi/hr. How far away from the station will the second train overtake the first train?
(A) ( 250) mi
(B) ( 500) mi
(C) ( 750) mi
(D) ( 800) mi
(E) ( 1500) mi
Correct Answer: C
Solution:
Tip: Distance = Rate (times) Time.
Between 2:00 P.M. and 4:30 P.M. there are 2.5 hours. This means that train A travels 2.5 hrs more than train B. If (t) denotes the hours train B travels, then train A travels ((t+2.5)) hrs. Let the distance the two trains travel be denoted by (d). Using (d=rt) we create an equation representing the distance each train traveled.
[begin{array}{l l c l l}
d&=&100(t+2.5) &quad text{train A} &(1)\
d&=&150t &quad text{train B} &(2)\
end{array}]
Since the distance the two trains traveled is the same, we set ((1)) equal to ((2).)
[begin{array}{r c l}
150t&=&100(t+2.5) &quad (1) = (2) \
150t &=& 100t + 250 &quad text{use distributive property}\
50t &=& 250 &quad text{subtract} 100t text{from both sides}\
t&=&5 text{hrs} &quad text{divide both sides by} 25\
end{array}]
So, train B travel 5 hours before it catches up with train A. But we are looking for the distance the trains have traveled when train B takes over train A. Plugging (t=5) into ((2)), we get
(5 times 150 = 750) miles.
Incorrect Choices:
(A)
This is just the sum of the speeds of the two trains.
(B)
If you find the distance train A travels from 4:30 P.M. till train B overtakes it, you will get this wrong answer.
(D)
If you think the difference between 2:00 P.M. and 4:30 P.M. is 2 hrs, you will get this wrong answer.
(E)
If you find the combined distance the trains traveled, you will get this wrong answer.
When most people hear “word problems,” they often think of the popular example of trains traveling at different speeds, or unrealistic applications of math. However, word problems represent how most people use math in everyday life, and the SAT includes these problems to test students’ ability to reason logically and solve problems.
For many students, the hardest part of a word problem is figuring out exactly what the word problem is asking of you. Not all word problems are created the same though, so we’re going to break down what you need to know so that you feel confident solving them on the SAT.
Types of Math Word Problems on the SAT
You could divide math word problem in a few different ways. You could do it by topic, for example, such as using the SAT subscores as your guide. Or you could do it by the type of solution the problem requires of you. We’re going to focus on the second way, simply because trying to divide word problems by topic would mean we’d have to cover virtually every math topic the SAT covers, which is way more than we could fit in a single post.
Creating an equation or a formula. In these problems, you’ll be given some information about a scenario and asked to come up with an equation or formula that represents that scenario. In fact, looking for the word “represents” in the question might tip you off that you’re dealing with a problem of this type. These are almost exclusively found in the multiple-choice questions, with different equations or formulas listed as the answer choices.
Solving for a value. This is the most common form of word problem. Based on the information in the word problem, you’ll need to come up with at least one specific value that satisfies the requirements of the problem. Examples include finding “how much” or “how many” of something in the problem, or finding minimums and maximum values.
Defining or interpreting. For these problems, you are often asked to interpret what a variable or a constant means in the situation described, or you might be asked what kinds of conclusions can be drawn from a survey. These types of problems often have no “math” involved, and instead ask you to think logically about a situation.
Tip: Being able to identify problems by type on the SAT is a useful prep exercise and can help you on the day you take the test. You may want to use the Math section from a free practice SAT test and circle all of the word problems. Then, read each word problem and assign it to one of the types. Doing this will help you see the commonalities between different types of questions and will allow you to spend less time on the actual test wondering what type of question you’re dealing with!
How to Approach SAT Math Word Problems
For every SAT Math word problem, there are two things to consider. The first is what we discussed above, which is to figure out what type of problem you’re dealing with to best identify what you need to do. Once you know whether you need to provide a definition, write an equation, or solve for a value, you’ve taken the first step.
The next step will be to do the math that you’ve identified you need to do based on the type of word problem. Let’s take a look at each one:
Write an equation/formula. For problems of this type and for problems that ask you to solve for a specific value, you will often need to understand how to “translate” a word problem into an equation, diagram, or graph that you can work with. Luckily, the SAT is very particular about how it uses words in its word problems, so you can always be sure that certain words are meant to relate to specific mathematical concepts. Here are some of the common phrases used by test makers to clue you in to what kind of math you’re looking for:
| Word/phrase | Mathematical meaning/symbol |
| Is, will be, is equal to, is the same as | Equals, = |
| Plus, sum, increased by, added to, received | Addition, + |
| Minus, fewer, difference, decreased by | Subtraction, – |
| Times, product, multiplied by, of | Multiplication, x |
| Divided by, quotient, per, for | Division, ÷ |
| More than, greater than | Inequality, > |
| At least, minimum | Inequality, ≥ |
| Fewer than, less than | Inequality, < |
| At most, maximum | Inequality, ≤ |
| What, how many | Variable, x (or any other letter) |
Solve for a value. With these problems, you might be given an equation as part of your information, but most likely you have to write an equation or formula and solve for the answer. You may benefit from drawing a diagram on some of these questions, especially if the word problem refers to geometric shapes but doesn’t already include one. This can help you visualize the information you’re looking for (the measure of an angle, for example) and help you focus on the right concepts to find the solution.
When translating a word problem into a diagram, make sure you follow the set-up as described in the word problem to the best of your ability, and don’t be fooled by your own diagram. For example, a problem may mention a right triangle, so you draw one. You may end up drawing a diagram that looks like a 45-45-90 triangle, but the problem is actually dealing with a 30-60-90 triangle. By labeling all of the information on your diagram and making a mental note that your drawings aren’t to scale, you can quickly make sense of most problems.
Defining and interpreting. With these types of problems, you often have the equation or formula given to you, and you just need to explain how a part of it works. If you’re not sure, consider whether you’re being asked about a constant or a variable, and eliminate any choices that don’t correspond to the type of value you’re looking at. You can also test the equation with different numbers to see how the value in question influences the equation.
Some problems involve your knowledge of statistical topics, such as understanding how to draw conclusions from surveys, or what factors affect standard deviation. For many of these problems, you’ll need to review these concepts in order to form the correct conclusion.
Examples of SAT Math Word Problems
The following example problems come from the College Board’s free SAT practice tests.
Example of Creating an Equation/Formula
How to solve: We can tell we need to come up with our own formula based on the answer choices and the word “represents” in the problem’s question. We need to find the formula that represents what the original price of a laptop was in terms of p, what Alma paid for it.
Let’s make x the original price of the laptop. In this case, x would be multiplied by .8 to get to the sales price (representing the 20% discount). The sales prices would then be multiplied by 1.08 to account for sales tax. This means that p=(1.08)(0.8)(x). We need to isolate x, so we need to divide both sides by 1.08 and 0.8. That gives us D as the correct answer.
Alternate method: Many problems requiring you to create your own equation are not too difficult, but they can get tricky when there are several steps involved or several variables. You can substitute a number for the variable you’re solving for to find the solution that way. For example, you can set $100 to be the original price of the laptop. Multiply it by .8 to find the sales price, and then by 1.08 to find the price that Alma paid. Then plug the price Alma paid into the answer choices to find the correct answer.
Example of Solving for a Value
How to solve: The word “maximum” tips us off that we are looking for a specific value and that we’ll be dealing with an inequality (see above). Given the information in the problem, we can write this inequality to start: (weight of driver) + (weight of truck) + (14x, or the weight of the boxes) ≤ 6000.
Because we’re told that the weight of the driver and the truck equals 4,500, we can replace that part of the equation: 4500 + 14x ≤ 6000. Now, all we need to do is solve for x. Subtract 4500 from both sides to get 14x ≤ 1500. Then divide both sides by 14 to get x ≤ 107.14… The answer is thus 107.
Note: Pay close attention to how you need to round when working with inequalities. Although this particular decimal probably wouldn’t have made you think to round up, if the result of the division had been 107.9999 you should still round down in this case because the number you’re looking for needs to be less than that value.
Example of Defining/Interpreting
How to solve: Again, the use of the word “interpretation” lets us know what type of problem we’re dealing with. In this case, 12 is a coefficient for the variables n and h, which are the number of landscapers and the number of hours respectively. We can thus rule out choices B and D, since those answers define 12 as a constant in place of these variables.
Since this equation is used to calculate the price of a job, we can be sure 12 represents a dollar amount as reflected in choices A and C. To figure out how things are affected, we can substitute simple numbers for n and h. When both are equal to 1 (there is one landscaper who works for one hour), then 12nh=12(1)(1)=12. When we increase both of these numbers to two, then 12nh=12(2)(2)=48. We can thus rule out C, because the price increased by more than 12 when we added another hour. Choice A is the best interpretation.
How to solve: This is an interpretation problem dealing with statistical concepts rather than interpreting an equation. To be able to “solve” you’d need to know what factors contribute to a reliable conclusion and see what was missing from this survey set-up. In this case, the correct answer is D.
In order for reliable conclusions to be drawn, a sample must be selected at random from the population to ensure that the sample is representative of the population, which in this case is the entire town. By choosing people at the same restaurant on one day, the researcher is possibly biasing their results by narrowing their sample to “people who like this one restaurant.” Because the sample is not representative, choice D identifies the factor that makes the conclusion unreliable. The other choices are factors that, given what we know from the problem, don’t negatively impact the conclusion.
SAT Math Word Problems Tips
As you may have noticed in the last example, you’ll still need to be familiar with math concepts and understand how they might show up in different situations to really feel confident taking any problem on. Here are a couple of other tips worth mentioning:
For most problems, there is more than one way to solve it. We showed this with the first example, where we provided an alternate method for solving a problem. If you find yourself stumped on a problem (we’ve all been there!), then move on to other problems and return to the one that tripped you up later. You may find that you see what you need to do more clearly.
Read carefully. The SAT test makers put a lot of care into how they write math word problems. Be sure to carefully read the question so that you don’t misread something and solve for the wrong thing. (The test makers may even include the answers that result from these common misreadings in the choices!). It’s difficult to read a question correctly once you’ve misread it. If you’re a fast reader who tends to skip over things, try mouthing the words silently as you read. It will force you to slow down just enough that you won’t miss anything, but not so much that you won’t have time to finish the test.
In general, preparing for the SAT Math section requires a multi-faceted approach. You need to be able to identify the types of questions you’re dealing with, know mathematical concepts and how to use them, and deal with other testing issues like rushing through the end or dealing with test anxiety. To help you get started, check out our free SAT Guide that includes 8 of our best test prep tips!
For more information about preparing for the SAT, check out these posts below:
30 SAT Math Formulas You Need to Know
25 Tips and Tricks for the SAT
5 Common SAT Math Mistakes to Avoid
Want to know how your SAT score/ACT score impacts your chances of acceptance to your dream schools? Our free Chancing Engine will not only help you predict your odds, but also let you know how you stack up against other applicants, and which aspects of your profile to improve. Sign up for your free CollegeVine account today to gain access to our Chancing Engine and get a jumpstart on your college strategy!