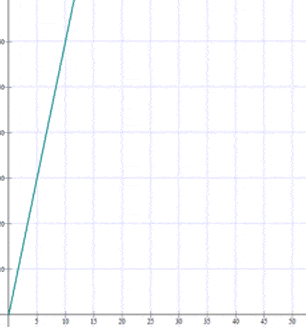
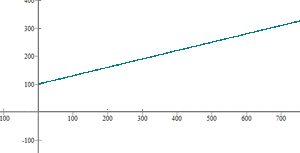
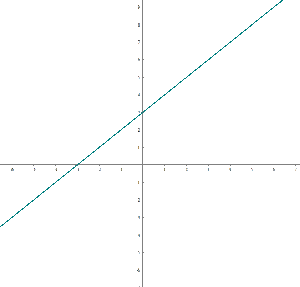
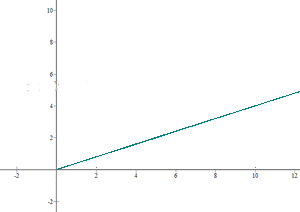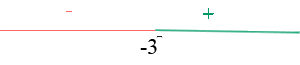Exercise 1
Three pounds of squid can be purchased at the market for dollars. Determine the equation and represent the function that defines the cost of squid based on weight.
The best Maths tutors available
5 (32 reviews)
1st lesson free!
5 (26 reviews)
1st lesson free!
4.9 (40 reviews)
1st lesson free!
5 (33 reviews)
1st lesson free!
4.9 (42 reviews)
1st lesson free!
5 (68 reviews)
1st lesson free!
5 (147 reviews)
1st lesson free!
5 (31 reviews)
1st lesson free!
5 (32 reviews)
1st lesson free!
5 (26 reviews)
1st lesson free!
4.9 (40 reviews)
1st lesson free!
5 (33 reviews)
1st lesson free!
4.9 (42 reviews)
1st lesson free!
5 (68 reviews)
1st lesson free!
5 (147 reviews)
1st lesson free!
5 (31 reviews)
1st lesson free!
Let’s go
Exercise 2
It has been observed that a particular plant’s growth is directly proportional to time. It measured when it arrived at the nursery and
exactly one week later. If the plant continues to grow at this rate, determine the function that represents the plant’s growth and graph it.
Exercise 3
A car rental charge is dollars per day plus
dollars per mile travelled. Determine the equation of the line that represents the daily cost by the number of miles travelled and graph it. If a total of
miles was travelled in one day, how much is the rental company going to receive as a payment?
Exercise 4
When digging into the earth, the temperature rises according to the following linear equation:
.
t is the increase in temperature in degrees and h is the depth in meters. Calculate:
1. What the temperature will be at depth?
2.Based on this equation, at what depth would there be a temperature of ?
Exercise 5
The pollution level in the centre of a city at is
(parts per million) and it grows in a linear fashion by
(parts per million) every hour. If
is pollution and t is the time elapsed after
, determine:
1.The equation that relates y with t.
2. The pollution level at 4 o’clock in the afternoon.
Exercise 6
A faucet dripping at a constant rate fills a test tube with of water every minute. Form a table of values for time and capacity, determine the equation and represent it graphically.
Exercise 7
For the function and
.
1. Determine the coefficients that satisfy the equation:
2. Write the equation and represent it graphically:
3. Indicate the intervals where the function has a positive and negative value.
Solution of exercise 1
Three pounds of squid can be purchased at the market for dollars. Determine the equation and represent the function that defines the cost of squid based on weight.
Since it is a directly proportional question hence, :
Solution of exercise 2
It has been observed that a particular plant’s growth is directly proportional to time. It measured when it arrived at the nursery and
exactly one week later. If the plant continues to grow at this rate, determine the function that represents the plant’s growth and graph it.
Initial height =
Weekly growth =
Solution of exercise 3
A car rental charge is dollars per day plus
dollars per mile travelled. Determine the equation of the line that represents the daily cost by the number of miles travelled and graph it. If a total of
miles was travelled in one day, how much is the rental company going to receive as a payment?
dollars
Solution of exercise 4
When digging into the earth, the temperature rises according to the following linear equation:
.
t is the increase in temperature in degrees and h is the depth in meters. Calculate:
1. What the temperature will be at depth?
2.Based on this equation, at what depth would there be a temperature of ?
Solution of exercise 5
The pollution level in the centre of a city at is
(parts per million) and it grows in a linear fashion by
(parts per million) every hour. If
is pollution and t is the time elapsed after
, determine:
1.The equation that relates y with t.
2. The pollution level at 4 o’clock in the afternoon.
10 hours have elapsed between 6 in the morning to four in the afternoon.
Solution of exercise 6
A faucet dripping at a constant rate fills a test tube with of water every minute. Form a table of values for time and capacity, determine the equation and represent it graphically.
| Time | Capacity |
|---|---|
| … | … |
Solution of exercise 7
For the function and
.
1. Determine the coefficients that satisfy the equation:
2. Write the equation and represent it graphically:
3. Indicate the intervals where the function has a positive and negative value.
Problem 1 :
The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S are functions of the mileage m; C(m) = 0.4m + 50 and S(m) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
Solution :
Total cost = C(m) + S(m)
= 0.4m + 50 + 0.03m
T(m) = 0.43 m + 50
To find the airfare for flying 1600 miles, we have to apply 1600 instead of m.
T(m) = 0.43 (1600) + 50
= 688 + 50
T(m) = 738
So, the total cost of airfare for flying 1600 miles is 738.
Problem 2 :
A salesperson whose annual earnings can be represented by the function A(x) = 30, 000 + 0.04x, where x is the rupee value of the merchandise he sells. His son is also in sales and his earnings are represented by the function S(x) = 25, 000 + 0.05x. Find (A + S)(x) and determine the total family income if they each sell Rupees 1, 50, 00, 000 worth of merchandise.
Solution :
(A + S)(x) = A(x) + S(x)
A(x) = 30, 000 + 0.04x ——-(1)
S(x) = 25, 000 + 0.05x ——-(2)
(1) + (2)
= 30, 000 + 0.04x + 25, 000 + 0.05x
A(x) + S(x) = 55000 + 0.09x
Here x = 15000000
A(x) + S(x) = 55000 + 0.09(15000000)
= 55000 + 1350000
Total income = 1405000
So, the required income is 1405000.
Problem 3 :
The function for exchanging American dollars for Singapore Dollar on a given day is f(x) = 1.23x, where x represents the number of American dollars. On the same day the function for exchanging Singapore Dollar to Indian Rupee is g(y) = 50.50y, where y represents the number of Singapore dollars. Write a function which will give the exchange rate of American dollars in terms of Indian rupee.
Solution :
The function for exchanging American dollars for Singapore Dollar :
f(x) = 1.23x
S.D = 1.23 (A.D)
Here «x» stands for American dollar and f(x) stands for Singapore dollar.
A.D = S.D/1.23 —-(1)
Exchanging Singapore Dollar to Indian Rupee is
g(y) = 50.50y
I.R = 50.50 (S.D)
S.D = I.R/50.50
Applying S.D = I.R/50.50 in(1), we get
A.D = (I.R/50.50)/1.23
A.D = I.R/62.115
I.R = 62.115 AD
So, the exchange rate of American dollars in terms of Indian rupee is I.R = 62.115 AD.
Problem 4 :
The owner of a small restaurant can prepare a particular meal at a cost of Rupees 100. He estimates that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200−x. Express his day revenue, total cost and profit on this meal as functions of x.
Solution :
Cost price of the meal = 100
Selling price = x
Number of customers = 200 — x
1 day revenue = No of customers ⋅ x
= (200 — x) ⋅ x
1 day revenue = 200 x — x2
Total cost = Cost of meal ⋅ No of customers
= 100 ⋅ (200 — x)
= 20000 — 100x
Profit = Total cost — 1 day revenue
(200 — x) ⋅ x — 100 ⋅ (200 — x)
Problem 5 :
The formula for converting from Fahrenheit to Celsius temperatures is y = (5x/9) − (160/9). Find the inverse of this function and determine whether the inverse is also a function
Solution :
y = (5x — 160)/9
9y = 5x — 160
5x = 9y + 160
x = (1/5) (9y + 160)
f-1 (x) = (1/5) (9x + 160)
f-1 (x) = (9x/5) + (160/5)
f-1 (x) = (9x/5) + 32
Inverse is also a function.
Problem 6 :
A simple cipher takes a number and codes it, using the function f(x) = 3x−4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x (by drawing the lines).
Solution :
f(x) = 3x−4
Let y = 3x — 4
3x = y + 4
x = (y + 4)/3
f-1(x) = (x + 4)/3
Inverse is also a function.
Kindly mail your feedback to v4formath@gmail.com
We always appreciate your feedback.
©All rights reserved. onlinemath4all.com
| English to Math Translation | Rate/Distance Word Problem |
| Unit Rate Problem | Profit Word Problem |
| “Find the Numbers” Word Problem | Converting Repeating Decimal to Fraction Word Problem |
| Simple Interest Rate Problem | Inequality Word Problems |
| Percent Word Problem | Integer Function Problem |
| Percent Increase Word Problem | Direct, Inverse, Joint and Combined Variation Word Problems (in that section) |
| Ratio/Proportion Word Problems | Work Word Problems (in Rational Functions and Equations) |
| Weighted Average Word Problem | Systems of Equations Word Problems (in that section) |
| Consecutive Integer Word Problem | More Word Problems using Rational Functions (in Rational Functions section) |
| Age Word Problem | Absolute Value Word Problem (in Absolute Values section) |
| Money (Coins) Word Problem | Composition of Functions Word Problems (in Advanced Functions section) |
| Mixture Word Problem, Percent Mixture Word Problem |
The algebra word problems here only involve one variable; later we’ll work on some that involve more than one, such as here in the Systems of Linear Equations and Word Problems section.
English to Math Translation for Word Problems
Doing word problems is almost like learning a new language like Spanish or French; you can basically translate word-for-word from English to Math, and here are some translations:
| English | Math | English | Math | |
| is, yields, will be | (=) | (p) percent | (displaystyle frac{p}{{100}}), or move decimal left 2 places | |
| what number, how much (look at question) | “(x)” (or any variable) | half, twice | (displaystyle frac{n}{2},,,,2n) | |
| in addition to, added to, increased by | (+) | consecutive numbers | Let (n=) first number, (n+1=) second number, (n+2=) third number… | |
| sum of (x) and (y) | (x+y) | odd/even consecutive numbers | Let (n=) first number, (n+2=) second number, (n+4=) third number…
Note: Even if you are looking for odd consecutive numbers, use (n, n+2, n+4, …). |
|
| difference of (x) and (y) | (x-y) | average of (x,y) and (z) (and so on) | (displaystyle frac{{x+y+z+…}}{{text{(how many},,text{numbers},,text{on},,text{top)}}}) | |
| product of (x) and (y) | (xtimes y) | (x) per (y), (x) to (y), (x) over (y), (x) part of (y) | (xdiv y) or (displaystyle frac{x}{y})
Example: number of girls to total people can be represented by (displaystyle frac{{text{girls}}}{{text{total}}}). |
|
| quotient of (x) and (y) | (displaystyle xdiv y,,,,,text{or },,,frac{x}{y}) | (x) per (y), as in (x) “for every” (y)
Other examples of multiplication: each hour, every hour, an hour |
Multiplication, or (xtimes y).
Example: if you drive 50 miles per hour, how many miles will you drive in 5 hours: 250 miles. |
|
| opposite of (x) | (-x) | (y) increased by (x%) | (displaystyle y+left( {ytimes frac{x}{{100}}} right)) | |
| ratio of (x) to (y) | (displaystyle xdiv y,,,,,text{or},,,,frac{x}{y}) | (y) decreased by (x%) | (displaystyle y-left( {ytimes frac{x}{{100}}} right)) | |
| a number (n) less 3 | (n-3) | (y) is at least (or no less than) (x) | (yge x) | |
| a number (n) less than 3 | (3-n) | (y) is at most (or no more than) (x) | (yle x) | |
| a number (n) reduced by 3 | (n-3) | (y) is between (x) and (z) | (xle yle z) (inclusive) (x<y<z) (exclusive) | |
| of | times |
Remember these important things:
- If you’re wondering what the variable (or unknown) should be when working on a word problem, look at what the problem is asking. This is usually what your variable is!
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
- If the problem asks for a Unit Rate, you want the ratio of the (y)-value (typically the dollar amount) to the (x)-value, when the (x)-value is 1.This is basically the slope of the linear functions. You may see feet per second, miles per hour, or amount per unit; these are all unit rates.
Here are problems that use some of the translations above. We’ll get to more difficult algebra word problems later.
Unit Rate Problem:
Problem: You buy 5 pounds of apples for $3.75. What is the unit rate of a pound of apples?
Solution: To get the unit rate, we want the amount for one pound of apples; this is when “(x)” (apples) is 1. We can set up a ratio: (displaystyle frac{{3.75}}{5}=frac{x}{1};,,,x=$.75). We also could have just divided the amount spent by the number of pounds, which makes sense.
(Another cool way to figure out what to do is to think of a simpler problem. If we buy 20 pounds of apples for $10, we “feel” the unit rate is $.50 per pound. And the math agrees with us!)
“Find the Numbers” Word Problems:
Problem: The sum of two numbers is 18. Twice the smaller number decreased by 3 equals the larger number. What are the two numbers?
Solution: We always have to define a variable, and we can look at what they are asking. The problem is asking for both the numbers, so we can make “(n)” the smaller number, and “(18-n)” the larger.
Do you see why we did this? The way I figured this out is to pretend the smaller is 10. (This isn’t necessarily the answer to the problem!) I knew the sum of the two numbers had to be 18, so I knew to take 10 and subtract it from 18 to get the other number. It is easier to think of real numbers, instead of variables when you’re coming up with the expressions.
Translate the English into math and solve:
| Problem/Math | Notes |
| The sum of two numbers is 18. Twice the smaller number decreased by 3 equals the larger number. What are the two numbers?
(displaystyle begin{align}2n-3&=18-n\2n-3,,(+n)&=18-n,,(+n)\3n,-3&=18\,,3n&=21\,frac{{3n}}{3}&=frac{{21}}{3}\n&=7,,,,,,text{(smaller number)}\18-7&=11,,,,text{(larger number)}end{align}) |
Let (n=) the smaller number, and (18-n=) the larger number.
The translation is pretty straight forward; note that we didn’t have distribute the 2 since the problem only calls for twice the smaller number, and then we subtract 3. Check our work: The sum of 7 and 11 is 18. √ Twice the smaller ((2times 7)) decreased by 3 would be (14-3=11). √ |
Another Problem:
Problem: If the product of a number and –7 is reduced by 3, the resulting number is 33 less than twice the opposite of that number. What is the number?
Solution: Define a variable, and look at what they are asking. The problem is asking for a number, so make that (n). Translate word-for-word, and remember that the “opposite” of a number just means to make it negative if it’s positive or positive if it’s negative. Thus, we can just put a negative sign in front of the variable.
If you’re not sure if you should multiply, add, or subtract, try “real numbers” to see what you should do. For example, “8 reduced by 3” is 5, so for the “reduce by 3” part, we subtract 3. Also, “33 less than 133” is 100, so for the “33 less than”, we subtract 33 at the end:
|
Problem/Math |
Notes |
| If the product of a number and –7 is reduced by 3, the resulting number is 33 less than twice the opposite of that number. What is the number?
(displaystyle begin{align}left( {-7} right)n-3&=2left( {-n} right)-33\,,,,,-7n-3&=-2n-33\-7n-3,,left( {+7n+33} right)&=-2n-33,,left( {+7n+33} right)\30&=5n\,frac{{30}}{5}&=frac{{5n}}{5}\n&=6end{align}) |
The opposite of a number means we basically just multiply the number by –1 (in our case, put a negative in front of it). Translate English to math, and, after solving, get 6 as our answer.
Check our work: If we take the product of 6 and –7 (–42) and reduce it by 3, we get –45. Is this number 33 less than twice the opposite of 6? Twice the opposite of 6 is –12, and 33 less than –12 is (-12-33=-45). We got it! √ |
Simple Interest Rate Problem:
Problem: How much money would need to be invested at 2% annual simple interest for 10 years to earn $1200? Use the formula (text{Interest}=text{Principle }times ,text{Rate},times ,text{Time}).
Solution: Using the formula (I=Prt), solve for (displaystyle P:,P=frac{I}{{rt}}=frac{{1200}}{{left( {.02} right)10}};,,,P=$6000). Note that we had to turn (2%) into a decimal: we need to get rid of the % (pretend we’re afraid of it), so we move the decimal 2 places away from it.
Note: Compound Interest problems can be found here in the Exponential Functions section.
Percent Word Problem:
(We saw similar problems in the Percentages, Ratios, and Proportions section!)
|
Percent Problem/Math |
Notes |
| 60 is 20% of what number?
(displaystyle begin{align}60&=.20times n\frac{{60}}{{.2}}&=frac{{.2n}}{{.2}}\300&=,n\n&=300end{align}) |
Translate word-for-word, and remember again that of = times, and (20%=.20=.2).
Check our work: (20%,,,text{of},,,300=.2times 300=60) √ |
Percent Increase Word Problem:
| Percent Increase Problem/Math | Notes |
| The price of a pair of shoes has increased by 15%. The original price of the shoes was $20. What is the new price? (displaystyle begin{array}{l}x=$20+left( {15%,times 20} right)\x=$20+left( {.15times 20} right)\x=$20+$3=$23\x=$23,end{array}) or (displaystyle begin{array}{l}x=$20times left( {1+15%} right)\x=$20times left( {1+.15} right)\x=$20times left( {1.15} right)\x=$23,end{array}) |
15% of the original amount (=15%times 20), since of = times. Turn the 15% into a decimal and add the product to the original amount.
The second way to do it is to multiply the original amount ($20) by (1.15,,(100%+15%)), which adds (displaystyle 15%) to the original amount before multiplying. |
Ratio/Proportion Word Problems
Relating Two Things Together: a Rate
Problem: It takes 2 minutes to print out 3 color photos on Erin’s printer. Write an equation relating the number of color photos (p) to the number of minutes (m).
Solution: This problem seems easy, but you have to think about what the problem is asking. When we are asked to relate something to something else, typically we use the last thing (the “to the” part) as the (y), or the dependent variable. I like to set up these types of problems as proportions, but what we’re looking for is actually a rate of minutes to photos, or how many minutes to print 1 photo. Remember that rate is “how many (y)” to “one (x)”, or in our case, how many “(m)” to one “(p)”. We will see later that this is like a Slope from the Coordinate System and Graphing Lines including Inequalities section. Here’s the math:
| Ratio Problem/Math | Notes |
| It takes 2 minutes to print out 3 color photos on Erin’s printer. Write an equation relating the number of color photos (p) to the number of minutes (m).
(displaystyle begin{align}frac{{text{2 minutes}}}{{text{3 color photos}}}&=frac{{text{how many minutes}}}{{text{1 color photo}}}\frac{text{2}}{text{3}}&=frac{m}{{1p}}\3m&=2p\m&=frac{2}{3}pend{align}) |
To get the rate of minutes to photos, we can set up a proportion with the minutes on the top and the photos on the bottom, and then cross-multiply.
The equation relating the number of color photos (p) to the number of minutes (m) is (displaystyle m=frac{2}{3}p). √ |
Ratio/Proportion Problem:
Problem: The ratio of boys to girls in your new class is 5 : 2. The sum of the kids in the class is 28. How many boys are in the class?
Solution: This is a rati0 problem; we learned about ratios in the Percentages, Ratios, and Proportions section. A ratio is a comparison of two numbers; a ratio of 5 to 2 (also written 5:2 or (displaystyle frac{5}{2})) means you have 5 boys for every 2 girls in your class. For example, if you had only 7 in your class, you’d have 5 boys and 2 girls. But what if you had 14? You’d have 10 boys and 4 girls, since 10 is 5 times 2, and 4 is 2 times 2. Let’s set this up in an equation, though, so we can do the algebra!
There are actually a couple of different ways to do this type of problem. Probably the most common is to set up a proportion like we did in the Percents, Ratios, and Proportions section. Let (x=) the number of boys in the class.
| Ratio Problem/Math | Notes |
| The ratio of boys to girls in your new class is 5:2. The sum of the kids in the class is 28. How many boys are in the class?
(require{cancel} displaystyle begin{align}frac{{text{boys}}}{{text{total in class}}}&=frac{x}{{28}}=frac{5}{7}\\7x&=5times 28=140\frac{{cancel{7}x}}{{cancel{7}}}&=frac{{140}}{7}\x&=20text{ boys}end{align}) |
We know that the sum of the numbers in the ratio is 7 (boys and girls: 5 + 2), and the sum of the kids in the class is 28. We also know the “boys” part of the ratio is 5.
We can set up a proportion with the same things on top or on bottom; our ratios will have “boys” on top and “total in class” on bottom. In other words, we need to see how many boys out of 28 will keep a ratio of 5 boys to 7 total in the class. Cross-multiply to get (x=20). There are 20 boys and 8 girls (28 – 20) in the new class. Check our answer: the ratio of 20 to 8 is the same as the ratio of 5 to 2. And the number of boys and girls add up to 28! √ |
There’s another common way to handle these types of problems, but this way can be a little trickier since the variable in the equation is not what the problem is asking for; we will make the variable a “multiplier” for the ratio. The advantage to this way is we don’t have to use fractions.
| Ratio Word Problem/Math | Notes |
|
The ratio of boys to girls in your new class is 5:2. The sum of the kids in the class is 28. How many boys are in the class? (begin{align}5x+2x&=28\7x=28\frac{{7x}}{7}&=frac{{28}}{7}\x&=4\\5times 4&=20,,,,text{boys}\2times 4&=8,,,,text{girls}end{align}) |
We can multiply both numbers by the same thing to keep the ratio the same – try this with some numbers to see this.
5 times a number, and 2 times that same number must equal 28. Let (x) be the multiplier – not the number of boys or girls. We get 4 as the multiplier, but we’re looking for the number of boys in the class (5 times 4 = 20) and the number of girls in the class (2 times 4 = 8). There are 20 boys and 8 girls. Check our answer: the ratio of 20 to 8 is the same as the ratio of 5 to 2 (each is divided by 4 – the multiplier!) And the number of boys and girls add up to 28! √ |
Here’s a ratio problem that’s pretty tricky; we have to do it in a lot of steps:
| Ratio Problem/Math | Notes |
| One ounce of solution X contains ingredients a and b in a ratio of 2:3. One ounce of solution Y contains ingredients a and b in a ratio of 1:2.
If solution Z is made by mixing solutions X and Y in a ratio of 3:11, then 1260 ounces of solution Z contains how many ounces of ingredient a? Solution Z: (begin{array}{c}3u+11u=1260;,,,,,u=90\3times 90=270,,,text{oz}text{. solution X}\11times 90=990,,,text{oz}text{. solution Y}end{array}) |
Work backwards on this problem, and first work with solution Z, since there are 1260 ounces of it. It’s good to start with the parts of the problems with numbers first!
Since the ratio of X and Y is 3:11 in solution Z, we can find the ratio multiplier ((u)), and find how much of solutions X and Y are in Z. There are 270 ounces of X and 990 of Y in solution Z. |
|
Solution X: (begin{array}{c}2v+3v=270;,,,,v=54\2times 54=108,,,text{oz}text{. ingredient a}\3times 54=162,,,,text{oz}text{. ingredient b}end{array}) Solution Y: (begin{array}{c}1w+2w=990;,,,,w=330\1times 330=330,,,text{oz}text{. ingredient a}\,2times 330=660,,,text{oz}text{. ingredient b}end{array}) |
From above, there are 270 ounces of solution X in solution Z. We can find out how much of ingredients a and b are in solution X by using a ratio multiplier again ((v)), since one ounce of solution X contains ingredients a and b in a ratio of 2:3. There are 108 ounces of ingredient a in solution X.
Do the same for solution Y (using ratio multiplier (w)), which contains ingredients a and b in a ratio of 1:2. There are 330 ounces of ingredient a in solution Y. |
| (108+330=438) | The problem asks for the amount of ingredient a in solution Z, so add the amounts of ingredient a in Solutions X and Y to get 438. 1260 ounces of solution Z contains 438 ounces of ingredient a. √ |
Weighted Average Word Problem:
Weighted average problems have to do with taking averages, but assigning different weights to the elements (for example, counting them more than once).
Problem: You’ve taken four tests in your Algebra II class and made an 89, 92, 78, and 83. The final is worth two test grades. What do you need to make on the final to make an A (a 90) in the class for the semester?
Solution: Define a variable, and look at what is being asked. Let (x=) what you need to make on the final. Now we have 6 test grades that will count towards our semester grade: 4 regular tests and 2 test grades that will be what you get on the final (since it counts twice, we need to add it 2 times). This is called a weighted average, since we “weighted” the final test grade twice. Use the equation for an average:
| Weighted Average Problem/Math | Notes |
| You’ve taken four tests in your Algebra II class and made an 89, 92, 78, and 83. The final is worth two test grades. What do you need to make on the final to make an A (a 90) in the class for the semester?
(require{cancel} displaystyle begin{align}frac{{89+92+78+83+x+x}}{6}&=90\frac{{89+92+78+83+2x}}{{cancel{6}}}times frac{{cancel{6}}}{1}&=90times frac{6}{1}\342+2x&=540\2x&=198\frac{{2x}}{2}&=frac{{198}}{2}\x&=99end{align}) |
The average or mean equation is just adding up all the values, and then dividing by the number of values that we just added up. For this example, divide by 6, since we have 4 tests given, and the final is worth 2 test grades.
You have to make a 99 on the final to make an A in the class! Yikes! Good luck – you can do it! Let’s see if it works: (displaystyle frac{{86+92+78+83+99+99}}{6}=frac{{540}}{6},=90,,,,,surd ) |
HINT: For any problem with weighted averages, you can multiply each value by the weight in the numerator, and then divide by the sum of all the weights that you’ve used. For example, if you had test 1 (say, an 89) counting 20% of your grade, test 2 (80) counting 40% of your grade, and test 3 (78) counting 40% of your grade, take the weighted average as in the formula below. Don’t forget to turn percentages into decimals and make sure that all the percentages that you use (the “weights”) add up to 100 (all the decimals you use as weights should add up to 1). When using decimals, your denominator should be 1:
(displaystyle frac{{left( {89times .2} right),+,left( {80times .4} right),+,left( {78times .4} right)}}{{.2+.4+.4}}=frac{{17.8+32+31.2}}{1}=81)
Consecutive Integer Word Problem:
Problem: The sum of the least and greatest of 3 consecutive integers (numbers in a row) is 60. What are the values of the 3 integers?
Solution: You’ll see these “consecutive integer” problems a lot in algebra. When you see these, you always have to assign “(n)” to the first number, “(n+1)” to the second, “(n+2)” to the third, and so on. This makes sense, since consecutive means “in a row” and we’re always adding 1 to get to the next number.
Note: If the problem asks for even or odd consecutive numbers, use “(n)”, “(n+2)”, “(n+4)”, and so on – for both even and odd numbers! It will work; trust me!
| Consecutive Integer Problem/Math | Notes |
| The sum of the least and greatest of three consecutive integers (numbers in a row) is 60. What are the values of the three integers?
(displaystyle begin{align}n+n+2&=60\2n+2&=60\2n&=58\frac{{2n}}{2}&=frac{{58}}{2}end{align}) (displaystyle n=29,,,,,,n+1=30,,,,,,n+2=31) |
Assign “(n)” to the first number, “(n+1)” to the second, and “(n+2)” to the third, since they are consecutive numbers.
Translate the English into math. The least of the three consecutive numbers is “(n)“, and the greatest is “(n+2)”. Add the least number and the greatest to get 60. The three consecutive numbers are 29, 30, and 31. Check our answer: (29+31=60,,,, surd ) |
Age Word Problem:
Problem: Your little sister Molly is one third the age of your mom. In 12 years, Molly will be half the age of your mom. How old is Molly and your mom now?
Solution: Doesn’t this one sound complicated? It’s a great one to try on your friends! It’s not that bad though – first define a variable by looking at what the problem is asking.
| Age Word Problem/Math | Notes |
| Your little sister Molly is one third the age of your mom. In 12 years, Molly will be half the age of your mom. How old is Molly and your mom now?
(begin{align}M+12&=frac{1}{2}left( {3M+12} right)\2times left( {M+12} right)&=3M+12\2M+24&=3M+12\\24-12&=3M-2M\12&=Mend{align}) (M=12,,,,,,,,,3M=36) |
Let (M=) the age of sister Molly now. From this, we know that your mom is (3M) (make it into an easier problem – if Molly is 10, your mom is 30).
Turn English into math (second sentence). Remember that we have to add 12 years to both ages ((M+12) for Molly and (3M+12) for your mom), since we’re talking about 12 years from now (unfortunately, moms have to age, too). Multiply both sides by 2 to get rid of the fraction, and then “push” the 2 through the parentheses. Get the variables to one side, and the constants to the other. Molly is 12, and your mother is 36. Let’s see if it works: In 12 years, Molly will be 24, and her mom will be 48. Aha! Molly will be half of her mom’s age in 12 years. (surd ) |
Money (Coins) Word Problem:
Note that problems like this with two variables to solve for are more easily solved with a System of Equations, which we will cover in the next section.
| Money Word Problem/Math | Notes |
| Suppose Briley has 10 coins in quarters and dimes and has a total of $1.45. How many of each coin does she have?
(displaystyle begin{align}.25Q+.10(10-Q)&=1.45\.25Q+1-.1Q&=1.45\.15Q+1&=1.45\.15Q&=.45\frac{{.15Q}}{{.15}}&=frac{{.45}}{{.15}}\Q&=3\D&=10-3=7end{align}) |
Let (Q=) the number of quarters that Briley has. Then we know that she has (10-Q) dimes (turn into easier problem – if she has 2 quarters, she has 10 minus 2, or 8 dimes).
Each quarter is worth $.25 and each dime is worth $.10; thus, the number of quarters times .25 plus the number of dimes times .10 must equal her total, or $1.45. (Again, turn into easier problem: if you have 4 quarters, you have .25 times 4 = $1.00 total). Briley has 3 quarters, and 7 dimes. Let’s see if it works: 3 quarters is $.75 and 7 dimes is $.70. If we add $.75 and $.70, we get $1.45. (surd ) |
We could have also done this problem (and many problems like these) with a table:
| Amount | Price | Total | ||
| Quarters | Q | .25 | .25 Q | Multiply across |
| Dimes | 10 – Q | .10 | .10 (10 – Q) | Multiply across |
| Total | 10 | 1.45 | Do Nothing Here | |
| Add Down | Do Nothing Here | Add Down: (.25Q+.10left( {10-Q} right)=1.45); then solve to get (Q=3,,,10-Q=7). |
Mixture Word Problem:
Mixture Word Problems are where different quantities are mixed together, and you are asked to find certain quantities. (They are also solved with multiple variables with Systems of Equations). Here is an example using one variable:
Problem: One kind of candy (jelly) sells for $5 a pound and another (chocolate) for $10 a pound. How many pounds of each should be used to make a mixture of 12 pounds of candy (both kinds) that sells for $80?
Solution: First define a variable, and it helps to use a table. Let (J=) the number of pounds of jelly candy that is used in the mixture. Then (12-J) equals the number of pounds of the chocolate candy.
| Amount | Price | Total | ||
| Jelly Candy | J | 5 | 5J | Multiply across |
| Chocolate Candy | 12 – J | 10 | 10 (12 – J) | Multiply across |
| Total | 12 | 80 | Do Nothing Here | |
| Add Down | Do Nothing Here | Add Down: (5J+10left( {12-J} right)=80); then solve to get (J=8). |
Here’s whole problem:
| Mixture Word Problem | Notes |
| One kind of candy (jelly) sells for $5 a pound and another (chocolate) for $10 a pound. How many pounds of each should be used to make a mixture of 12 pounds of candy (both kinds) that sells for $80? | From the table above:
(begin{align}5J+10(12-J)&=80\5J+120-10J&=80\-5J&=-40\J&=8end{align}) We would need 8 pounds of the jelly candy and (10-8=2) pounds of the chocolate candy. |
Percent Mixture Word Problem:
Problem: A 20% concentrate is to be mixed with a mixture having a concentration of 60% to obtain 80 liters of a mixture with a concentration of 30%. How much of the 20% concentrate and the 60% concentrate will be needed?
Solution: First define a variable, and it helps to use a table. Let (T=) the number of liters we need from the 20% concentrate, and then (80-T) will be the number of liters from the 60% concentrate. (Put in real numbers to check this).
Put this in a chart again – it’s not too bad. This one is a little more difficult since we have to multiply across for the Total row, too, since we want a 30% solution of the total.
| Amount | % Concentrate | Total | ||
| 20% Concentrate | T | .20 | .2T | Multiply across |
| 60% Concentrate | 80 – T | .60 | .60 (80 – T) | Multiply across |
|
Total (What we want) |
80 | .30 | 24 | Multiply across |
| Add Down | Do Nothing Here | Add Down: (.2T+.6left( {80-T} right)=24); then solve to get (t=60). |
Here’s the whole problem:
| Percent Mixture Word Problem | Notes |
| A 20% concentrate is to be mixed with a mixture having a concentration of 60% to obtain 80 liters of a mixture with a concentration of 30%. How much of the 20% concentrate and the 60% concentrate will be needed? | From the table above:
(begin{align}.2T+.6left( {80-T} right)&=24\.2T+48-.6T&=24\-.4T&=-24\T&=60end{align}) We would need 60 liters of the 20% solutions and (80-60=20) liters of the 60% solution. |
Remember that if the problem calls for a pure solution or concentrate, use 100% (if the percentage is that solution) or 0% (if the percentage is another solution). Here’s an example:
Problem: How many ounces of pure water must be added to 100 ounces of a 30% saline solution to make it a 10% saline solution?
Solution:
| Amount | % Saline | Total | ||
| Pure Water | W | 0% = 0 | 0W = 0 | Multiply across |
| 30% Saline (Salt) Solution | 100 | .30 | 30 | Multiply across |
|
10% Saline Solution (What we want) |
W + 100 | .10 | .1(W + 100) | Multiply across |
| Add Down | Do Nothing Here | Add Down: (0+30=.1left( {W+100} right);,,W=200). |
Don’t worry if you don’t totally get these; as you do more, they’ll get easier. We’ll do more of these when we get to the Systems of Linear Equations and Word Problems topics.
Rate/Distance Word Problem:
Distance problems have to do with how far, how fast and how long objects have travelled. Here is an example:
| Distance Word Problem/Math | Notes |
|
A train and a car start at the same place. The train is going 40 miles per hour and a car is going in the opposite direction at 60 miles per hour. How long will it be until they are 100 miles apart? (text{Distance},,=,,text{Rate},,times ,,text{Time}) Total Distance: (100=60t+40t) Solve: (begin{array}{l}100=60t+40t\100=100t;,,,,t=1end{array}) |
Always draw pictures! Remember always that (text{Distance}=text{Rate},times ,text{Time}). The rates of the train and car are 40 and 60, respectively. Usually a rate is “something per something”.
Let (t) equal the how long (in hours) it will be until the train and the car are 100 miles apart. We must figure the distance of the train and car separately, and then we can add distances together to get 100. Again, you can always add distances; look at them separately first, and then you can put them together to equal the total distance (100). The math was pretty easy on this one! In one hour, the train and the car will be 100 miles apart. |
Note that there’s an example of a System Equations Distance Problem here, and a Parametric Distance Problem here in the Parametric Equations section.
Profit Word Problem
Profit word problems have to do with the amount of money made for products or services in business. Here is an example:
Problem: Hannah paid $1.50 each for programs to her play. She sold all but 20 of them for $3 each and made a profit of $15 total. How many programs did Hannah buy? How many did she sell? Hint: Profit = Selling Price – Purchase Price
Solution: It’s easiest to a table to store the information. Let (x=) the number of programs that Hannah bought. Put in real numbers to see how we’d get the number that she sold: if she bought 100 programs and sold all but 20 of them, she would have sold 80 of them. We can see that (80=100-20), so the number sold would be (x-20).
| Number of Programs | Price | Total | ||
| Sold | x – 20 | 3.00 | 3(x – 20) | Multiply across |
| Bought | x | 1.50 | 1.5x | Multiply across |
| Profit | 15 | Total Profit Given | ||
| Do Nothing Here | Do Nothing Here | Subtract Down: To get profit, subtract Total Bought from Total Sold, and set to Profit (15): (3left( {x-20} right)-1.5x=15); solve to get (x=50). |
Here’s the whole problem:
| Profit Word Problem | Notes |
| Hannah paid $1.50 each for programs to her play. She sold all but 20 of them for $3 each and made a profit of $15 total. How many programs did Hannah buy? How many did she sell? | From the table above:
(begin{align}3left( {x-20} right)-1.5x&=15\3x-60-1.5x&=15\1.5x&=75\x&=50end{align}) Hannah bought 50 programs to make a total profit of $15. Since she sold 20 less than she bought, she sold 50 – 20 = 30 programs. |
Converting Repeating Decimal to Fraction Word Problem:
Problem: Convert (.4overline{{25}},,,(.4252525…)) to a fraction.
Solution: Converting repeating decimal to fraction problems can be easily solved with a little trick; we have to set it up as a subtraction, so the repeating part of the decimal is gone. To do this, let (x=) the repeating fraction, and then figure out ways to multiply (x) by 10, 100, and so on (multiples of 10) so we can subtract two numbers and eliminate the repeating part.
The rule of thumb is to multiply the repeating decimal by a multiple of 10 so we get the repeating digit(s) just to the left of the decimal point, and then multiply the repeating digit again by a multiple of 10 so we get repeating digit(s) just to the right of the decimal. Then subtract the two equations that we just created, and solve for (x):
| Repeating Decimal Problem/Math | Notes |
|
Convert (.4overline{{25}},,,(.4252525…)) to a fraction. (begin{array}{l},,,,,,,,,,,x=4.2525252…\text{(original repeating decimal)}\\,,,,,,,1000x=425.252525…\,,,,,,,,underline{{,,,,10x=,,,,,,4.252525…}}\,,,,,,,,,990x=421.0\,,,,,,,,,,,,,,,,,x=frac{{421}}{{990}}end{array}) |
First, let (x=.4overline{{25}}). Since (.4overline{{25}}) has repeating digits 25, we first have to figure out how to multiply (.4overline{{25}}) to get the repeating digits just to the left of the decimal place.
We can do this by multiplying (.4overline{{25}}) by 1000; we get (1000x=4underline{{25}}.252525…) Also, if we multiply (x) by 10, we get the repeating part (25) just to the right of the decimal point; we get (10x=4.underline{{25}}2525…). Now line up and subtract the two equations on the left and solve for (x); we get (displaystyle x=frac{{421}}{{990}}). Pretty cool! Let’s see if it works: Put (displaystyle frac{{421}}{{990}}) in your graphing calculator, and then hit Enter; you should something like .4252525253. √ |
Inequality Word Problems
Note that inequalities are very common in real-world situation, since we commonly hear expressions like “is less than” ((<)), “is more than” ((>)),“is no more than” ((le )), “is at least” ((ge )), and “is at most” ((le )). There are several inequality word problems the Solving Inequalities sections; here’s an example:
Problem: Erica must tutor at least 12 hour per week in order to be eligible for her work-study program at her university. She must also study 10 more hours than the time she’s tutoring, so she can keep up her grades in the program. What is the minimum number of hours Erica must study in order to be eligible for her work-study program?
Solution: First, define a variable (h), which is the number of hours that Erica must study (look at what the problem is asking). We know from above that “at least” can be translated to “(ge)”.
If Erica works, let’s say, 30 hours in her work study program, she’d have to study 40 hours (it’s easier to put in real numbers). So, the amount of time she works in her work study program would be “(h-10)”, and this number must be at least 12. Let’s set up the equation and solve:
| Inequality Word Problem/Math | Notes |
|
Erica must tutor at least 12 hour per week in order to be eligible for her work-study program at her university. She must also study 10 more hours than the time she’s tutoring, so she can keep up her grades in the program. What is the minimum number of hours Erica must study in order to be eligible for her work-study program? (begin{array}{l}h-10ge 12\underline{{,,,,,,+10ge ,,,+10}}\h,,,,,,,,,,,,ge 22end{array}) |
The algebra is simple, and we don’t have to worry about changing the sign, since we’re not multiplying or dividing by a negative number.
Erica would have to tutor at least 22 hours. Notice that 22 hours works, since the problems asked for “at least”. To check your answer, try numbers right around the answer, like 21 hours (which wouldn’t be enough), and 22 hours (which would work!) |
This inequality word problem is a little more advanced:
Problem: (displaystyle frac{4}{5}) of a number is less than 2 less than the same number. Solve the inequality and graph the results.
Solution: This is a little tricky since we have two different meanings of the words “less than”. The words “is less than” means we should use “(<)” in the problem; it’s an inequality. The words “2 less than the same number” means “(x-2)” (try it with “real” numbers).
| Inequality Word Problem/Math | Notes |
|
(displaystyle frac{4}{5}) of a number is less than 2 less than the same number. Solve the inequality and graph the results. (displaystyle begin{array}{l},,,,,,,,,,,,,,frac{4}{5}x,,,,,,,,<,,,,,,,x-2\,,,,,,,,,,,,,,,,underline{{,,,,,,-x<-x,,,,}}\,,,,,,,,,,frac{4}{5}x-x,,<,,,,,,,,-2\,,,,,,,,,,,,,,,,-frac{1}{5}x,,<,,-2\left( {-frac{1}{5}x} right)left( {-5} right),>left( {-2} right)left( {-5} right)\,,,,,,,,,,,,,,,,,,,,,,,,,,x>10,,,,,text{(watch sign!)}end{array}) |
Set up and solve inequalities like we do regular equations. Let “(x)” be the number, and translate the problem word-for-word: (displaystyle frac{4}{5}x<x-2).
Get all the “(x)”s to one side and all the “numbers” to the other sign. (We could have also multiplied both sides by 5 earlier to get rid of the fraction.) Remember to change the sign when we multiply both sides by –5, since we’re multiplying by a negative number. Once we get the answer, we can also graph the solution. Try numbers close to 10, like 9 and 11, to make sure it works. |
Rational Inequality Word Problem
Technically, this next problem contains a rational function, but it’s relatively easy to solve.
| Inequality Word Problem | Math/Notes |
| A school group wants to rent part of a bowling alley to have a party. The bowling alley costs $500 to rent, plus an additional charge of $5 per student to bowl. The group doesn’t want any student to pay more than $15 total to attend this party.
What is an inequality that could represent this situation? How many students would need to attend so each student would pay at most $15? |
Since there is a one-time cost in addition to a per-person cost, the cost per person will depend on the number of students attending the party: the more students, the lower the cost.
For (x) students attending, each would have to pay (displaystyle frac{{500}}{x}) for the bowling alley rent; try it with real numbers! In addition, each student needs to pay their $5 to bowl. Therefore, each student will need to pay (displaystyle frac{{500}}{x}+5), and since we don’t want any student to pay more than $15, the inequality that represents this situation is (displaystyle frac{{500}}{x}+5le 15). To see how many students would have to attend to keep the cost at $15 per person, solve for (x). In this example, we can multiply both sides by (x) without worrying about reversing the inequality sign, since (x) can only be positive: (displaystyle frac{{500}}{x}+5le 15;,,,frac{{500}}{x}le 10;,,,500le 10x;,,,xge 50). At least 50 students would have to attend so that each student pays no more than $15. |
Integer Function Problem (a little bit more advanced…)
Problem: The fee for hiring a tour guide to explore Italy is $1000. One guide can only take 10 tourists and additional tour guides may be hired if needed. What is the cost of hiring tour guides, as a function of the number of tourists who go on the tour? If there are 72 tourists, what is the cost of hiring guides?
Solution: Let’s think about this by using some real numbers. From 1–10 tourists the fee is (1times 1000=$1000), for 11–20 tourists, the fee is (2times 2000=$2000), and so on. Do you see how if we divide the number of tourists by 10, and go up to the next integer, we’ll get the number of tour guides we need? This is because any fraction of a set of ten tourists requires another tour guide.
To get the function we need, we can use the Least Integer Function, or Ceiling Function, which gives the least integer greater than or equal to a number (think of this as rounding up to the closest integer). The integer function is designated by (y=leftlceil x rightrceil ). (We saw a graph of a similar function, the Greatest Integer Function, in the Parent Functions and Transformations section.)
Thus, the cost of hiring tour guides is (displaystyle 1000times leftlceil {frac{x}{{10}}} rightrceil ). For 72 tourists, the cost is (displaystyle 1000times leftlceil {frac{{72}}{{10}}} rightrceil =1000times leftlceil {7.2} rightrceil =1000times 8=$8000). Makes sense!
Now, all these types of problems can get much more difficult (and we will see later how to use two variables with some of them), but it’s important to take baby steps with them. Don’t worry if they seem difficult at this time, but as long as you get the general idea of how we’re doing the translations, you’re in great shape! And don’t forget:
- When assigning variables (letters), look at what the problem is asking. You’ll typically find what the variables should be there.
- If you’re not sure how to set up the equations, use regular numbers (simple ones!) and see what you’re doing. Then put the variables back in!
Related Topics:
More Lessons for Heart of Algebra
More Lessons for SAT Math
More Resources for SAT
Algebra Tutorials
This video is for the redesigned SAT which is for you if you are taking the SAT in March 2016 and beyond.
Linear Function Word Problems
Example:
A college bookstore charges $60 for a yearly membership. The first book is free with the membership, and any book after that costs $7.60 including tax. How much money, m, does a student spend after buying b books and a yearly membership?
Go to next Question
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.


We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
by Pujan
(Ny, usa)
The value of a 1996 Mustang, in thousands of dollars, is a function of the age a of the car, in years. Let V=f(a) be the function that represents the value of the car when it is a years old. Assume V is a linear function. (a) Interpret the equation f(3)=27 in practical terms. (b) If Mustang was bought for $35,000 in 1996, find a formula for V. (c) Graph V
Need More Help With Your Algebra Studies?
Get access to hundreds of video examples and practice problems with your subscription!
Click here for more information on our affordable subscription options.
Not ready to subscribe? Register for our FREE Pre-Algebra Refresher course.
Easily See Your Progress
We track the progress you’ve made on a topic so you know what you’ve done. From the course view you can easily see what topics have what and the progress you’ve made on them. Fill the rings to completely master that section or mouse over the icon to see more details.
Make Use of Our Learning Aids
Last Viewed
Practice Accuracy
Suggested Tasks
Get quick access to the topic you’re currently learning.
See how well your practice sessions are going over time.
Stay on track with our daily recommendations.
Earn Achievements as You Learn
Make the most of your time as you use StudyPug to help you achieve your goals. Earn fun little badges the more you watch, practice, and use our service.
Create and Customize Your Avatar
Play with our fun little avatar builder to create and customize your own avatar on StudyPug. Choose your face, eye colour, hair colour and style, and background. Unlock more options the more you use StudyPug.
Company | Membership | Blog | Help center | User guides | Tell us what you think | Testimonials | Careers | Contact us | Terms of service | Privacy policy
© 2023 IXL Learning. All rights reserved. Follow us
This Lesson (Word problems on Trigonometric functions) was created by by ikleyn(48006)

: View Source, Show
About ikleyn:
Word problems on Trigonometric functions
Problem 1
Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the high temperature
of 80 degrees occurs at 5 PM and the average temperature for the day is 75 degrees. Find the temperature at 9 AM.
Solution
The amplitude is 80-75 = 5 degrees.
The period is 24 hours.
We want represent the function as the sine function.
So, we will start the period at (1/4) of 24 hours before 5 pm.
Hence, the start for the period is 11 am.
Now the general formula is
T(t) = 5*sin(2*pi*((t-11)/24)) + 75,
where t is the time (in hours) on the clock during the day in 24-hours military notation.
In particular, at t = 9 am the temperature is
T(9 am) =  =
=  =
=  =
=  =
=
=
=  =
=  = 75 - 2.5 = 72.5 degrees. ANSWER
= 75 - 2.5 = 72.5 degrees. ANSWER
Problem 2
Outside temperature over a day can be modeled as a sinusoidal function.
Suppose you know the high temperature of 96 degrees occurs at 4 PM and
the average temperature for the day is 85 degrees. Find the temperature, to the nearest degree, at 7 AM.
Solution
Our 24-hour cycle of the daily temperature change starts at 4 pm, when the temperature is maximal.
So, our sinusoidal function is, actually, the cosine function, if to start counting time from 4 pm = 16:00, or
T(t) =  +
+  where "t" is the local astronomic time in the 24-hours "military" time scale in your watch.
At 7 am next day, we have
where "t" is the local astronomic time in the 24-hours "military" time scale in your watch.
At 7 am next day, we have  of the full cycle elapsed.
It corresponds to
of the full cycle elapsed.
It corresponds to  on the unit circle, and
on the unit circle, and  = -
= -  .
So, the temperature at 7 am next day will be
.
So, the temperature at 7 am next day will be
 =
=  = 85° - 0.707*11° = 77.2°.
ANSWER. We can expect 77.2°, or 77° rounded, at 7 am next day.
= 85° - 0.707*11° = 77.2°.
ANSWER. We can expect 77.2°, or 77° rounded, at 7 am next day.
Problem 3
Outside temperature over a day can be modelled as a sinusoidal function.
Suppose you know the high temperature for the day is 90 degrees and the low temperature of 80 degrees occurs at 6 AM.
Assuming t is the number of hours since midnight, find an equation for the temperature, D(t), in terms of t.
Solution
The difference between the highest and lowest temperature is 90 - 80 = 10 degrees; hence, the midline is 85 degrees and the amplitude is= 5 degrees. Next, if x is the time starting from 6 am (x= 0 when the temperature is lowest), then OBVIOUSLY, the temperature as a function of x is D(x) =
(1) (we use the sign " - " to reflect cosinusoid about the midline, and we use the ratio x/24 to model the period of 24 hours). Now, if t is the time after midnight, then x = t-6, so the formula (1) takes the final form D(t) =
. (2) ANSWER Or, if you like to use angular degrees instead of radians, then the same formula takes an EQUIVALENT form D(t) =
. (3) ANSWER Notice that, from (2), the angular shift in the formula (2) is one fourth of the period; therefore, the formula (2) can be transformed this way D(t) =
. (4) ANSWER
Problem 4
A Ferris wheel is 20 meters in diameter and boarded from a platform that is 1 meters above the ground.
The six o’clock position on the Ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 6 minutes.
How many minutes of the ride are spent higher than 19 meters above the ground?
Solution
This Ferris wheel is a circle of the radius of 10 meters, and its center O is at the height of 11 meters above the ground. Imagine horizontal line at the level of 19 meters over the ground. It is 8 meters above the center. This horizontal line intersect the circle at two points, A and B. Consider the triangle with the vertices O, A and the point C, which is the middle of the segment AB. This triangle is a right angled triangle. Its hypotenuse is the radius OA of 10 meters long. Its leg OC is of 19-11 = 8 meters long. Hence, cos(x) == 0.8, where x is the angle AOC. It gives x = arccos(0.8) = 0.64 radians. Thus the central angle AOB is 2x = 2*0.64 = 1.28 radians. So, the time the person will be higher than 19 meters, can be found from the proportion
=
t =
=
= 1.23 minute, or about 1 minute and 14 seconds. ANSWER
Problem 5
A Ferris wheel that is 20 meters in diameter makes a revolution in 60 seconds.
If the center is 11 m above the ground, how long does it take a rider reach a height of 16 meters?
Solution
Our Ferris wheel has the radius of 20/2 = 10 meters and the lowest position at the height of 1 meter above the ground. Let's consider this Ferris wheel as rotated anti-clockwise. So, it rotates from position 6 pm (the hour hand) anti-clockwise to the position 3 pm by 90 degrees, reaching the height of 11 meters above the ground, and then rotates for some additional angle "a" anti-clockwise, such that the height is 16-11 = 5 meters above the level of the center, which is 11 meters above the ground. This angle "a" satisfies equation sin(a) == 0.5, so a = arcsin(0.5) = 30 degrees. Thus the wheel turns/rotates the angle 90 + 30 degrees = 120 degrees, total. The angular velocity of the wheel is 360 degrees in 60 seconds, or
= 6 degrees per second. So, it will take
= 20 seconds for the rider to get the height of 16 meters above the ground, starting from the lowest position. ANSWER. It will take 20 seconds.
Problem 6
A mass is suspended by a spring such that it hangs at rest 0.5 m above the ground.
The mass is raised 40 cm and released at time t = 0 seconds, causing it to oscillate sinusoidal.
If the mass returns to the high position every 1.2 seconds, derive an equation of the mass oscillations.
Solution
This problem is about deriving the formula of harmonic oscillations.
The mid-line of the sinusoid is y= 0.5 m.
The amplitude is 0.4 m.
The period is 1.2 seconds.
The time shift is such that using cosine function is preferable.
So, the equation of the mass oscillation is
y =  +
+  .
.
Problem 7
Find a possible formula for the trigonometric function whose values are in the following table.
x 0 4 8 12 16 20 24
y 3 -1 -5 -1 3 -1 -5
Solution
The minimum is -5; the maximum is 3.
Hence, the midline is -1 and the amplitude is 4.
The table dictates to use the cosine function.
The period starts from 0 and ends at 16.
So, the trigonometry function is
y =  .
Here "-1" represents the midline; the factor "4" represents the amplitude; and the factor (x/16) models the 16 units period.
.
Here "-1" represents the midline; the factor "4" represents the amplitude; and the factor (x/16) models the 16 units period.
Problem 8
State the equation for a trigonometry function of your choice
that has an amplitude of 3 units, a period of and a minimum at (0, -8).
Solution
y = -5 - 3*cos(3x). ANSWER.
EXPLANATION
The minimum value of -8 and the amplitude of 3 dictate that the midline is y = -5.
The fact that the minimum is at x= 0 dictates to use the cosine function flipped/reflected about the midline.
The argument of (3x) provides / models the period  .
.
Problem 9
Let a, b, c be three sides opposite to the angles A, B, C respectively in a triangle ABC.
Find 2ac*sin((A + C — B)/2).
Solution
First,=
=
=
. THEREFORE,
=
= cos(B). Next, due to the cosine law for triangle ABC
=
+
-
. It implies 2ac*cos(B) = a^2 + c^2 - b^2 Now we can write the final identity
= 2ac*cos(B) =
. ANSWER.
=
.
Problem 10
If p, q and r are the sides opposite to the angles P, Q and R respectively in a triangle PQR.
If =
then determine the type of the triangle PQR:
(a) Equilateral
(b) Acute Angle but not equilateral
(c) Obtuse Angle
(d) Right Angle
Solution
It is very well known fact from Geometry that for any triangle PQR with the sides p, q, r opposite to angle P,Q, R respectively, the ratios,
,
are all equal and are equal to the diameter of the circle circumscribed around the triangle PQR
=
=
= d. For the proof see, for example, lesson - Law of sines - the Geometric Proof in this site. Then from the given part of the problem, we see that
=
.
= d*d = d^2. In other words, the square of the side "r" is equal to the square of the diameter of circumscribed circle
=
. It implies r = d, i.e. the side "r" is the diameter of the circumscribed circle about triangle PQR. It means that the angle R is leaning on the diameter of the circumscribed circle, i.e. triangle PQR is a right-angled triangle with the right angle at vertex R. So, the given triangle is a right-angled triangle. ANSWER. PQR is a right-angled triangle.
My other lessons on calculating trig functions and solving trig equations in this site are
— Calculating trigonometric functions of angles
— Advanced problems on calculating trigonometric functions of angles
— Evaluating trigonometric expressions
— Solve these trigonometry problems without using a calculator
— Finding the slope of the bisector to the angle formed by two given lines in a coordinate plane
— Solving simple problems on trigonometric equations
— Solving typical problems on trigonometric equations
— Solving more complicated problems on trigonometric equations
— Solving advanced problems on trigonometric equations
— Challenging problems on trigonometric equations
— Miscellaneous problems on solving trigonometric equations
— Solving twisted trigonometric equations
— Truly elegant solution to one trigonometric equation
— Non-standard Trigonometry problems
— Proving Trigonometry identities
— Calculating the sum 1*sin(1°) + 2*sin(2°) + 3*sin(3°) + . . . + 180*sin(180°)
— Find the height
— Solving upper-league Trigonometry equations
— Math OLYMPIAD level problems on Trigonometry
— Trigonometry entertainment problems
— OVERVIEW of lessons on calculating trig functions and solving trig equations
Use this file/link ALGEBRA-II — YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 1326 times.
Students also viewed
Introduction to Linear Functions
20 termsImages
yeetimgay
Slope of a Line
20 termsImages
drrace
Unit 5: Linear Functions Word Problems (Diffi…
18 termsImages
pacingpoetTeacher
Analyzing Linear Functions
12 termsImages
Heather_StephanTeacher
Recent flashcard sets
spanish speaking test
10 terms
Joseph_Lore
dom3
21 termsImages
weraarm123
Blood vessels
15 termsImages
VictoriaElionor
Metales, no metales y metaloides
3 terms
valles_salas
Sets found in the same folder
Linear Equations: Graphing Standard Form
30 termsImages
jvybihalTeacher
Graphing Linear Inequalities and Systems of L…
70 termsImages
Smalls-2004Teacher
Function Card Sort
12 terms
Jennifer_RaabeTeacher
Linear vs. Nonlinear, Linear and Nonlinear
29 termsImages
Maggie_ElgertTeacher
Other sets by this creator
Quadratic Functions — Writing Equations
11 terms
KLRay2017Teacher
Solving Square Root Equations, Graphing Squar…
48 termsImages
KLRay2017Teacher
Two Way Tables and Venn Diagrams
9 termsImages
KLRay2017Teacher
Quadratic Word Problems
8 terms
KLRay2017Teacher
Verified questions
algebra
There are approximately 1,020,000,000 cars in the world. The number of cars in the United States is approximately 239,800,000. Compare the number of cars in the world to that available in the United States.
Verified answer
prealgebra
For this item, determine thevaue of x in the given quadrilateral.
Given: In the quadrilateral the following measures of the angles are as follows: 88 degrees, 7x+15 degrees, 13x-3 degrees and 80 degrees.
Verified answer
calculus
Evaluate ∬D1(x2+y2)n/2 dA,iint_{D}dfrac{1}{(x^2 + y^2)^{n/2}}~dA, where nn is an integer and DD is the region bounded by the circles with center the origin and radii rr and R,0<r<RR, 0 < r < R.
Verified answer
algebra2
Classify 2×3+x4+x+12 x^3+x^4+x+1 by degree.
a. quartic
b. quadratic
c. cubic
d. polynomial
Verified answer
Recommended textbook solutions
Saxon Math, Course 3
1st Edition•ISBN: 9781591418849 (1 more)Hake
4,042 solutions
Saxon Math, Course 2
1st Edition•ISBN: 9781591418351Hake, Stephen
4,848 solutions
SpringBoard Mathematics Course 2
1st Edition•ISBN: 9781457301490The College Board
2,286 solutions
Florida Math, Course 2, Back to Common Core Volume 1
1st Edition•ISBN: 9780021440849McGraw-Hill Education
959 solutions
Other Quizlet sets
Exam
50 terms
trinityqueen_13
Accounting Chapter 1 Smartlearn
89 terms
Jcedeno2021
Water, Electrolyte, and Acid-Base Balance
42 terms
serena_jones20
1
/
7