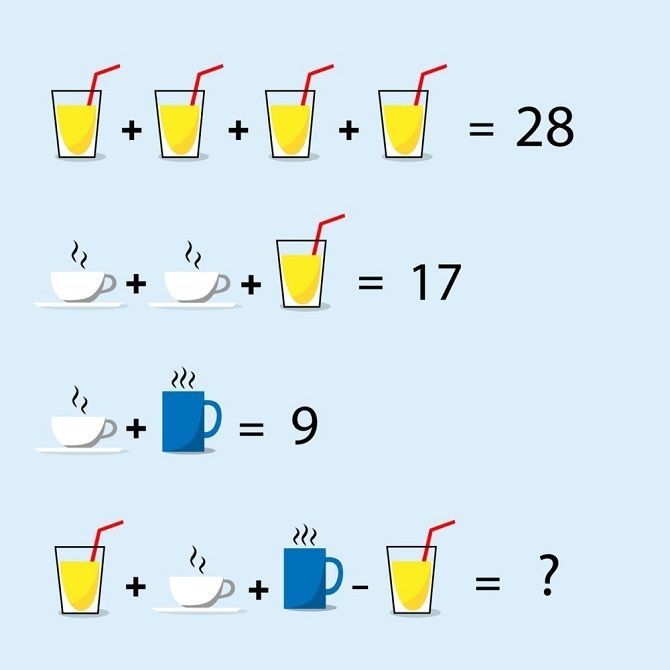
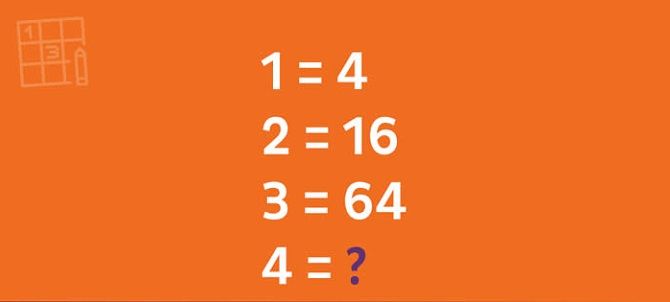Age problems collection by Logiclike will help you train logical and algebra skills. In these
word
problems, you will deal with current, past, and future people’s ages.
How many math problems can you solve using systems of equations? And what about logical thinking
and
thinking outside the box methods?
Ten years from now, Gloria will be three times older than she is today.
What is her current age?
Mila is 5 years older than her brother, but 3 times younger than her
mother.
How old is Mila and how old is her mother, if Mila’s brother is 6 years old?
In 6 years, Bob will be 4 times as old as he is today.
How old is Bob today?
In 8 years, Mary will be 3 times as old as she is today.
How old is Mary today?
Mike is 8 years older than Alexa. 3 years ago, Mike was 5 times as old as
Alexa.
How old is Mike today?

Jennifer is 6 years older than Anna.
3 years ago, Jennifer was 4 times as old as Anna.
How old is Jennifer today?
—>
A mother is 56 years old, and her daughter is 14 years old.
In how many years will the mother be twice her daughter’s age?
How old will the mother be then? How old will your daughter be?
Six years ago, Lenny’s age was half of the age he will be in 8 years.
How old is Lenny now?
Felix is twice as old as his friend Greg.
Greg is 5 years older than Rachel.
In 5 years, Felix will be three times as old as Rachel.
How old is Greg now?
Alexa is 1 year more than twice Stella’s age.
3 years from now, Nora will be 27 less than twice Alexa’s age.
4 years ago, Nora was 1 year less than 3 times Stella’s age.
How old will Nora be 3 years from now?
Get involved with LogicLike online!
More than 550,000 parents from all over the
world are already improving thinking skills with their children.

In this section, we will use familiar notations used in propositional logic. You might want to familiarize yourself with Propositional Logic first.
Like solving any other questions, we should always ask ourselves what we can and can’t do when writing out our reasoning. The first step to learn how to solve propositional logic problems is to list out what can’t be done or what is not a possibility so we can narrow down what the possible scenarios are. Remember that it is very easy to fall into an erroneous conclusion based on faulty reasoning. Take the statements below as an example, if the first statement is true, is the second statement also true?
[begin{array} &text{«If it’s raining, then I can’t play soccer».} &text{«If I can’t play soccer, then it’s raining.»} end{array}]
It is pretty clear that the issue here is: there can be other reasons why I can’t play soccer, which doesn’t necessarily depend on the weather. If we make such simple errors in reasoning when the context is very clear, just imagine what will happen when you are less certain about statements that are more vague. In the next paragraph, we will be introduced to these errors.
Converse and Inverse Errors
As a beginner, the most common mistake you can make is to assume that the converse and/or inverse of the original statement is also true. Take a look at the two sections below:
Introduction to Converse Error with erroneous reasoning:
Premise: If it’s raining, then I can’t play soccer.
Conclusion: If I can’t play soccer, then it’s raining.
Explanation: From the first statement, we are given a condition and a result: «raining» as a condition and «I can’t play soccer» as a result. The entire premise is phrased in such a way that if the condition is fulfilled, then the result will occur. However, the conclusion shows that if the result is fulfilled, then the condition will occur. This does not make sense because it is not necessary for the condition to take place if the result occurs first. This is known as a converse error.
In a general form, the argument for a converse error is as follows:
- If P occurs, then Q occurs.
- Q occurs.
- Therefore, P also occurs.
Introduction to Inverse Error with erroneous reasoning:
Premise: If it’s raining, then I can’t play soccer.
Conclusion: If it’s not raining, then I can play soccer.
Explanation: From the first statement, we are given a condition and a result: «raining» as a condition and «I can’t play soccer» as a result. The entire premise is phrased in such a way that if the condition is fulfilled, then the result will occur. However, the conclusion shows that if the condition does not occur, then the result does not occur either. This does not make sense because there can be other reasons/factors such that the result does occur. This is known as an inverse error.
In a general form, the argument for an inverse error is as follows:
- If P occurs, then Q occurs.
- P does not occur.
- Therefore, Q also does not occur.
It may now be abundantly clear that it is easy to identify we’ve made an erroneous reasoning. However, what if the statements given appear more vague? This is the reason why we introduce the two errors above (converse error and inverse error) to show that not all wrong statements are easily identifiable. Simply put, the relationship between two events do not necessarily imply that one causes the other. In short, we are pointing out the common fact that «correlation does not imply causation».
Now that we have seen these mistakes first hand, let’s do another example to remind ourselves that they are mistakes and we can hopefully avoid them in the future. Keep in mind that some of the converse/inverse statements can appear ridiculous but some do not.
We are given the following statement: If today is Sunday, then the weather is sunny. []
(qquad text{ (i)}) Write the inverse and converse of this statement.
(qquad text{(ii)}) Identify which of these statements you have made is not logical and explain why.
(text{(i)}) Inverse and Converse
- Inverse: If today is not Sunday, then the weather is not sunny.
- Converse: If the weather is sunny, then today is Sunday.
(text{(ii)}) Logical or Illogical
Though they are the inverse and converse of the original statement, we must keep in mind that they might not necessarily be an error. However, there is no harm in checking whether they are correct or not.
The inverse statement implies that the day has a direct relation on the weather being sunny or not, which is ludicrous because there can also be non-sunny days which do not fall on a Sunday.
The converse statement implies that only if the weather is sunny then the day is Sunday, which is also ludicrous because they can also have a sunny weather on days not falling on a Sunday. (_square)
Pinpoint the exact error
Now that we can identify how the errors occur, let’s take a step further and apply these techniques so that we can pinpoint exactly where the error occurs. Note that the easiest way to identify where the error arose is to convert logical statements into symbolic forms (like P implies Q). Let’s try the following example.
Taking the long view on your education, you go to the Prestige Corporation and ask what you should do in college to be hired when you graduate. The personnel director replies that you will be hired only if you major in mathematics or computer science, get a (text{B}^text{+}) average or better, and take accounting. You do, in fact, become a math major, get a (text{B}) average and take accounting. You return to Prestige Corporation, make a formal application, and are turned down. Did the personnel lie to you?
Let’s list down the requirements to be hired:
(begin{array}{r r l}
& text{(i)} & text{Major in mathematics or computer science}\
& text{(ii)} & text{Get a } text{B}^text{+} text{ average or better}\
& text{(iii)} & text{Take accounting}\
end{array})Since you became a math major, criteria (text{(i)}) is satisfied.
Since you got a (text{B}) average instead of a (text{B}^text{+}) average, criteria (text{(ii)}) is not satisfied.
Since you took accounting, criteria (text{(iii)}) is satisfied.Since you did not satisfy all the criteria and were turned down, the personnel didn’t lie to you. (_square)
Now that you’re familiar with writing out these statements and identifying possible errors, let’s try another example that uses such a property!
Insufficient information
Sharky
Satvik
Krishna
A store has been raided by looter/s, who drove away in a car. Three well-known criminals Satvik, Krishna and Sharky are brought to the police station for questioning. Inspector Aditya of the police extracts the following facts:
((1)) None other than Satvik, Krishna and Sharky was involved in the robbery.
((2)) Sharky never does a job without using Satvik (and possibly others) as accomplices.
((3)) Krishna doesn’t know how to drive.
Find the person who, in any case, is guilty.
This problem is the part of my set «Is This What You Call Logic?»
Formal terminologies
In the previous sections, we have learned the two most common errors that students will make when solving a logical reasoning problem. However, we did not formally touch on the terminologies for those terms: converse error and inverse error. Let’s begin!
Contrapositive: A statement is logically equivalent to its contrapositive. The contrapositive negates both terms in an implication and switches their positions. For example, the contrapositive of «P implies Q» is the negation of Q implies the negation of P.
-
Converse: The converse switches the positions of the terms. The converse of «P implies Q» is «Q implies P».
-
«If and only if», sometimes written as iff and known as equivalence, is implication that works in both directions. «P if and only if Q» means that both «P implies Q» and «Q implies P».
Let’s try a few examples that cover this area!
(text{ (i)}) Write down the contrapositive statement for
[text{«If you are human, then you have DNA.»}]
(text{(ii)}) Write down the two if-then statements for
[text{«A polygon is a quadrilateral if and only if the polygon has 4 sides.»}]
(text{ (i)}) contrapositive
(qquad) If you do not have DNA, then you are not human.(text{(ii)}) if-then statements
(qquad) If a polygon is a quadrilateral, then it has 4 sides.
(qquad) If a polygon has 4 sides, then it is a quadrilateral. (_square)
Simple, isn’t it? Let’s try some problems that apply the techniques we have learned above.
If Jeff does well on his next math test, then he finished his math homework.
If Jeff spends 5 hours playing video games, then he will fail his next math test.
If Jeff does not fail his next math test, then he did not spend 5 hours playing video games.
If Jeff does not finish his math homework, then he spent 5 hours playing video games.
If Jeff does not play video games, then he will do well on his next math test.
If Jeff does not finish his math homework, then he does not do well on his next math test.
If Jeff spends 2 hours playing video games, then he can finish his math homework.
If Jeff finishes his math homework, then he did not spend 5 hours playing video games.
If Jeff spends 5 hours playing video games, then he cannot finish his math homework.
If Jeff finishes his math homework, then he will do well on his next math test.
Based on this information, which of the following is logically correct?
Blue
Can’t say
Green
Yellow
Selena, Jennifer and Miley wear a blue dress, yellow dress, and green dress in an unknown order. It is known that:
1) If Selena wears blue, then Jennifer wears green.
2) If Selena wears yellow, then Miley wears green.
3) If Jennifer does not wear yellow, then Miley wears blue.
What is the color of the dress Selena is wearing?
Now that we have mastered these techniques, let’s move on to the following section for other cool proof techniques!
In this section, we will be applying some basic rules of set notations. You might want to familiarize yourself with sets and Venn diagram first.
In the previous section, we have learned the most common ways in identifying and pinpointing errors. In this section, we will apply the use of Venn Diagram as an alternative proof in solving logical reasoning problems. But what’s the benefit of this? Well, it’s simple: We do not need to verbalize these statements and we can use the visual aids to guide us to solve these problems.
Recap of set notations and Venn diagram []
Let’s do a brief recap for the application of Venn Diagrams by taking the following as an explicit example:
Consider (W,X,Y,Z) as sets, each with their own elements in them. Then by interpreting the Venn Diagram, we can obtain information like:
- All elements in set (W) is in set (Y).
- All elements in set (X) is in set (Z).
- Not all elements in set (Y) is in set (W).
- etc.
How to use Venn diagrams to solve a logical word problem []
Let us consider the following statements and deduce whether the conclusion is true or false by Venn diagram:
True or false? []
It is given that all birds have wings.
All chickens are birds.
Therefore, all chickens have wings.
Explanation: By Venn diagram, the statement «A chicken is a bird.» implies that the set «all chickens» is a subset of «all birds.» Thus we can say that all chickens have the same characteristics as a bird. Because it is given that all birds have wings (a characteristic), all chickens have wings too. Thus the conclusion is correct.
Note: We should keep in mind that this only works if the premise is true. For example, if we replace the word «wings» by «forearms» in the first statement, then the conclusion of «All chickens have forearms.» will inevitably be true despite its ridiculous claim.
Food for thought: If all phones have batteries and I have a phone, does it mean that my phone has a battery?
Careful! There are other ways of drawing out Venn diagrams!
Though it may appear very simple to set up a Venn diagram, the setup may not necessarily be unique. Let us consider a revised version of the statements above and deduce whether the conclusion is true or false by Venn diagram.
True or false? []
It is given that all birds have wings.
All chickens are birds.
Therefore, all birds are chickens.
Explanation: By Venn diagram, the statement «A chicken is a bird» implies that the set «all chickens» is a subset of «all birds.» Thus we can say that all chickens have the same characteristics as a bird. However, it is not necessarily true that all birds share the same characteristics of a chicken. (Sounds familiar? It’s converse error.) So the claim «All birds are chicken» must be false.
Note: To fix the conclusion, you should say «Some birds are chickens» instead of «All birds are chickens.»
Now that we know the fundamental applications of proof by Venn diagram, let’s apply these knowledge we learned on the following examples:
False, there might not be a pang that is a pong
False, all pangs are pongs
False, none of the pangs can be pongs
True, some pangs are pongs
True or False?
(quad) All pangs are pings.
(quad) Some pings are pongs.
(quad) Therefore, some pangs are pongs.
No, in all cases
Need more information
Yes, in all cases
Johannes has several written publications on his bookshelf. Albert notices that all of the comics are paperback books, and that some of the paperback books are manga. Are all comics manga?
Image Credit : Wikimedia Johannes Jansson
Isn’t the proof by Venn diagram fun? You don’t need to use actual words to formalize these statements. Looks very unusual, right? But it works. Speaking of unusual, is it possible to solve these logical statements if we were to spice things up by dramatizing out the statements? Yes, we can! Proof by analogy is another proof technique to solve logical problems. See the following section:
How do we solve texts that are seemingly hard to decipher?
All pangs are pings.
Some pings are pongs.
Therefore some pangs are pongs.
Consider the logical statements given above. Since we can’t relate to or identify what pangs, pings, or pongs are, it will appear that these terms are vague or all too similar. How are we supposed to solve problems like this if we have little to no clue to what is going on? Well, proof by analogy will be useful here: this is when we dramatize or caricaturize the terms used.
For example, we may call pangs as humans, pings as apes, and pongs as gorillas. With these new terms, we are able to visualize what they are. Rewriting them into the original 3 statements shows that
[text{All humans are apes. Some apes are gorillas. Therefore some humans are gorillas.}]
So the given conclusion is wrong because of the ridiculousness of the conclusion «Some humans are gorillas.»
However, an important question to ask is why this works. This is too good to be true, right? Or, are we running into some wrong argument? Why does this work?
Explanation of how this works
The reason why proof by analogy works is because we make an inference that if the objects have multiple similar characteristics, and it is given that you know one of them have an extra characteristics (call it X), then it is not a bad inference to conclude that the other object shares that same characteristic X.
To put it short, the generalized/structured form for proof by analogy is:
- P and Q has similar properties (x_1, x_2, x_3, ldots, x_n).
- We know that P has a further property (y).
- Therefore, Q probably has property (y) too.
Now let’s try a modified version of the ping-pang-pong question from earlier!
True or false? []
(qquad) All yangs are yengs and yings.
(qquad) Some yengs are yings.
(qquad) Then, all yengs are yangs.
This is false.
Let «yangs» be defined as «pets», «yengs» as «tigers», and «yings» as «cats».
So it is true (or at least still reasonable) that all pets are cats and tigers and that some tigers are cats. But it is not true that all tigers are pets. (_square)
Note: The reason why proof by analogy works best here is because we couldn’t label or identify any characteristics for yangs, yengs, and yings. Therefore, a sensible approach is to prove by analogy.
Now that you’re ready to solve logical problems by analogy, let’s try to solve the following problem again, but this time by analogy!
No, in all cases
Need more information
Yes, in all cases
Johannes has several written publications on his bookshelf. Albert notices that all of the comics are paperback books, and that some of the paperback books are manga. Are all comics manga?
Image Credit : Wikimedia Johannes Jansson
Suitability of analogy
Notice from the previous section that we’ve mentioned that «Q probably has property (y) too.» instead of «Q definitely has a property (y) too.» This is because the argument may provide what appears to be the right evidence, but the conclusion does not always follow. This subsection explains why this proof (arguemnt) might not always work.
Though it is true that we highlight or amplify parallel characteristics, the differences between things can often overwhelm their similiarities. One might note that it is always possible to extend an analogy to the point of absurdity. For illustration, take the following famous «Information Argument»:
DNA is a code.
A code requires an intelligence.
Therefore, DNA comes from an intelligence.
Yes, this will sound completely logical if we apply the implications approach. That is, it’s P implies Q and Q implies R, so P implies R. However, the argument here is not valid because the statement «DNA is a code.» is purely an analogy and thus it is not an entirely accurate statement to begin with. Thus, we have started with a wrong premise. So the merits of analogy do not hold. This is further explained in Analyzing arguments from analogy.
We can see that proof by analogy is very useful and can also be used to make incorrect conclusions. Thus, one must be careful in labeling certain characteristics when using this method. Let’s see the following examples to see how the proof by analogy backfires:
True or false? []
All squares and rectangless are convex, have four sides and form right angles at their vertices.
All squares have sides of the same length.
Therefore, all rectangles have sides of the same length.
This is obviously false because by definition, all rectangles do not have sides of the same length, but only squares have sides of the same length. We make the wrong conclusion that rectangles also have this characteristic because it is known previously that both share a number of characteristics. (_square)
Insufficient information
True
False
True or false?
It is given that Amy, Bernadette and Penny are good friends of Sheldon and Leonard.
Leslie is a good friend of Leonard.
Therefore, Leslie is a friend of Sheldon as well.
Image Credit: Wikimedia TBBT. No copyright infringement intended.
- Propositional Logic Using Algebra.
- Propositional Logic.
- Truth-tellers and Liars.
- Logic gates.
“If Johnny has eight apples, and he gives three of them away to Sally, how many apples does he have left?” Word problems have long been met with dread by math students from all walks of life. Normally, when people think of mathematics, words are not the first visual that comes to mind; it’s numbers! However, the importance of word problems cannot be discounted. Studies on education have shown that word problems have many benefits. Of course, we at A Grade Ahead definitely see the value of word problems; our math curriculum has an emphasis on building the skills needed and completing word problems in our unique enrichment program. Let’s explore the benefits of word problems below!
Why Are Word Problems Important?
Strengthen Problem-Solving Skills
Although number-based math involves problem solving, thinking about solutions in the form of words is much more impactful and applicable to other areas of a student’s learning and cognitive development. As in life, when certain problems arise, people must be able to think about solutions in different formats in order to conjure up the best possible solution. This website offers some tips on how to help children improve their abilities to work through word problems, and therefore, improve their problem-solving skills.
[button url=”https://academy.agradeahead.com/curriculum-samples/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: chevron-circle-right” text_shadow=”0px 0px 0px #000000″]Get my FREE curriculum sample![/button]
Improve Comprehension and Analysis
Math isn’t the subject where people would imagine comprehension skills could be built, but that is just another testament to how important word problems are! Word problems offer a way to practice close reading, visualizing, interpreting, and analyzing. Students are presented with a story in a word problem. They must read closely to understand what information is important, and visualize it to gain a complete view of the goal. They must know what the question means and analyze the question for clues to how to solve the problem. All these skills are practiced before the student even begins applying any math equations!
Build Logical and Critical Thinking Skills
Students must transform numbers to visuals in their minds, and then back into numbers again – all while addressing all the logical limitations of the problem.
Including numbers in real-life scenarios makes math more interesting for students! Often, when just using math rules and not thinking critically about the problem, students can make mistakes and come up with nonsensible answers. However, because there is no scenario attached, students may not understand why such answers don’t work. For example:
Solve for x: 15x – 170= 100.
The correct answer is 18, but students who are unsure about the correct process for solving this problem could answer anything from -163 to 4 to 4,050! Without any context, these students won’t necessarily notice a logical problem with their answers. Let’s try again in the form of a word problem.
A car company must sell 100 cars each week in order to make a profit. It costs the company $170 to pay its fifteen employees each week. How many cars does each employee have to sell this week in order for the company to make a profit?
Using the scenario given, students may set up the problem as it is shown numerically and solve. However, now that we have a situation to go along with, answers like -163, 4, and 4,050 really don’t make sense, and students will be able to notice that. Word problems are important for learning because they develop a child’s logical thinking skills.
[button url=”https://academy.agradeahead.com/our-programs/math/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: pencil” text_shadow=”0px 0px 0px #000000″]Improve my child’s math skills![/button]
Develop Creativity
Becoming a word-problem master is one step toward becoming a master at life! This blog post by John Marsh gives some examples about why that is. When students can use their imaginations to visualize and explore the dimensions of various word problems, they can become more motivated to solve scenarios than if they are looking at monotonous number combinations.
Plus, this will help students when they are looking at numeric equations. They may be able to apply the word-problem thinking to come up with solutions to a math problem by imagining an equation as a word problem! Creativity is key both in the classroom and in life satisfaction, so we should probably start teaching our kids its importance through word problems!
Get Invested
One of the main struggles that teachers face in the math classroom is engaging students and making them feel excited to learn. This website gives some creative word problems that students will enjoy working on for a wide variety of math topics.
How often do you think teachers hear the question: “Why are we learning this?” (Hint: It’s a lot!) Word problems are one way to show students how they might be able to use math in their lives now, or in the future. What student doesn’t want to imagine they have 10 cookies? The bottom line is students will be more inclined to practice skills if they are convinced that it will actually be useful.
Practice, Practice, Practice!
Word problems give students a way to practice all the tools they have learned. Especially in higher levels, word problems involve multiple steps and can use many different types of math. Often, students are able to bring in concepts learned in past chapters or even past grades. This helps reinforce previously learned topics and show students the benefits of learning a concept instead of memorizing it for a test!
Demonstrate Knowledge
Word problems are a key tool in determining what material a student feels comfortable. With multiple choice problems, or even basic solving, there are many opportunities for children to get the right answer without actually understanding the process or rationale behind the math. But, with word problems, students must display the higher levels of thinking that is required, meaning that they must display that they have the knowledge needed to solve the question. Word problems make it easier to see what concepts students need extra help on.
[button url=”https://agradeahead.com/” target=”blank” background=”#81BE41″ color=”#ffffff” size=”9″ center=”yes” radius=”0″ icon=”icon: map-marker” text_shadow=”0px 0px 0px #000000″]Find my nearest A Grade Ahead location![/button]
After reading this, we hope you see the importance of word problems, too! If your child is struggling to apply his or her knowledge to word problems, consider an enrichment program at an academy or at home and practice the skills above.
Can you think of any more reasons that show the importance of word problems for student learning? Do you think word problems have helped your child? Let us know in the comments below!
Author: Morgan L., Writer and Teacher at A Grade Ahead; Brenna Waugaman, Writer and Teacher at A Grade Ahead
Get Notified When New Articles Post
Sign up to receive one email per week from A Grade Ahead full of parenting tips and helpful articles. Enter your information on the right hand side of our Blog page and we will add you to our list of subscribers. We also welcome your feedback and comments on our posts!
These logical thinking problems will get your students thinking during your math problem solving time.
This is another free resource for teachers from The Curriculum Corner.
Looking to help your students practice solving logical problems?
This math problem solving strategy can be practiced with this set of resources.
The skill of solving logical problems is one that is often assessed on standardized testing.
Math Problem Solving Strategies
This is one in a series of resources to help you focus on specific problem solving strategies in the classroom.
Within this download, we are offering you a range of word problems for practice involving logical thinking.
Each page provided contains a single problem solving word problem.
Below each story problem you will find a set of four steps for students to follow when finding the answer.
For this set, the fourth step is on the second page. We have worded the pages so you can easily choose to eliminate the back page. Students might show the answer to their problem instead of writing the answer in sentence format.
We have created five different logic problems with room for students to show their work and a place for students to write their answer in complete sentences.
Ideas for using these problems
Logical thinking problems can be a good opportunity to encourage group discussions.
Let students work with a partner or in small groups.
You might also encourage students to use manipulatives. For problems such as these the manipulatives might even be note cards with names that students move around as they solve the problem.
The five included problems will give your students multiple opportunities to work on logical thinking problems.
You can download these logical thinking problems here:
Problem Solving
You might also be interested in the following free resources:
- Problem Solving Using a Table
- The answer is… Problem Solving Center
As with all of our resources, The Curriculum Corner creates these for free classroom use. Our products may not be sold. You may print and copy for your personal classroom use. These are also great for home school families!
You may not modify and resell in any form. Please let us know if you have any questions.
You may not modify and resell in any form. Please let us know if you have any questions.

3-Step System
1. Read: Read the problem and decide what the question is asking.
- Read the problem 2 times or more.
- Underline or circle key words, phrases, and numbers. Draw a line through irrelevant information.
2. Plan: Think about what the story is asking you to do. What information are you given, and what do you need to find out?
- Draw a picture.
- Circle or underline key words. (Use highlighters or crayons to color-code key numbers and phrases.)
- Write out the question in your own words.
3. Solve: What strategy could you use to find the missing information: addition, subtraction, multiplication, or division?
- Write a number sentence and solve.
- Use counters.
- Create charts.
Check your work by explaining your reasoning. Does your answer make sense?
Download this free strategy checklist from Math Fundamentals to help your child solve word problems.
Different Strategies to Solve Word Problems
Everyone learns in a different way. What makes sense to one individual often isn’t the easiest option for another. Incorporating different strategies to solve word problems can help your child discover what strategy works best for him or her. A few tips to use are:
1. Circle numbers in a story and underline key phrases.
Color coding is a fun method to incorporate to help children decide what operation the question is asking for. Assign a color to each operation and highlight the phrase that identifies it. For example, red links to addition and blue links to subtraction.
2. Incorporate a key word list.
Key word lists are best used for teaching younger children how to solve word problems. As math curriculum advances, children should not be dependent on a key word list to solve a problem. The questions get trickier.
Addition
In all
Together
Total
Altogether
Combine
Sum
Join
Subtraction
Difference
Fewer
How many more
How much more
Left
Remain
Less
3. Visuals
If your child is a visual learner, drawing a picture or using counters can help him or her understand what the problem is asking. Use number lines, charts, or counters or draw a picture.
4. Write your own word problem.
Knowing what is needed to write a word problem is the first step in identifying key words to solve a story. Take turns writing your own word problems with your child and exchange them to solve.
5. Stay organized.
It is important to write clearly and keep work space neat so children can read and follow their own computations. Many children need a separate piece of paper to allow them enough space to solve and understand their answer. Graphing paper is a great option to help students record neat work.
Download this free sample word problem from Math Fundamentals, grade 1.
How to solve a two-step word problem
In a two-step word problem children are being asking to solve two related equations. These can get tricky for children to understand when they transition from one-step to two-step problems. Help your child understand his or her relationships within two-step word problems with these strategies:
1. Circle important information.
Circle numbers and important phrases that ask questions. The number sentences needed to solve these equations are hidden in those asking questions. Identify the first and second questions needed to solve.
2. Distinguish the two parts of the problem.
First identify the first step of the first part of the word problem. Write a number sentence and solve.
3. Use the answer from the first-step solution to the whole problem.
Use the answer from the first question to help you solve the next equation. What operation does the second question require?
Check your work by explaining your reasoning. What was the question answered? Is the answer reasonable for the question being asked?
Download this free sample two-strategy word problem from Math Fundamentals, grade 2
Download this free sample multi-strategy word problem from Math Fundamentals, grade 4
Evan-Moor’s Math Fundamentals is a great resource for training students how to solve word problems in 3 simple steps. It provides step-by-step directions for solving questions and guides children with helpful visuals and key phrases.
Check out Daily Word Problems for consistent practice solving word problems.
For more fun math tips and strategies check out our Math- Ideas, Activities and Lessons Pinterest Board.
Save these tips and Pin It now!


Are you one of those who waste each free minute on scrolling in social networks? To be honest, it’s not the best activity. Another thing is when this minute or two could be spent productively!
Joy-pup.com has prepared some logic tasks that can be solved in just a few seconds, from 7 to 20. Ready for the challenge? Then go ahead!
You’ll be able to check the correct answers at the end!
Math puzzles
1. What number is encrypted?
2. How to order balls with numbers to get the number 30?
3. Which number will be the last?
Replace the question mark with the number corresponding to the equations below. Find a pattern.
Visual training for the brain
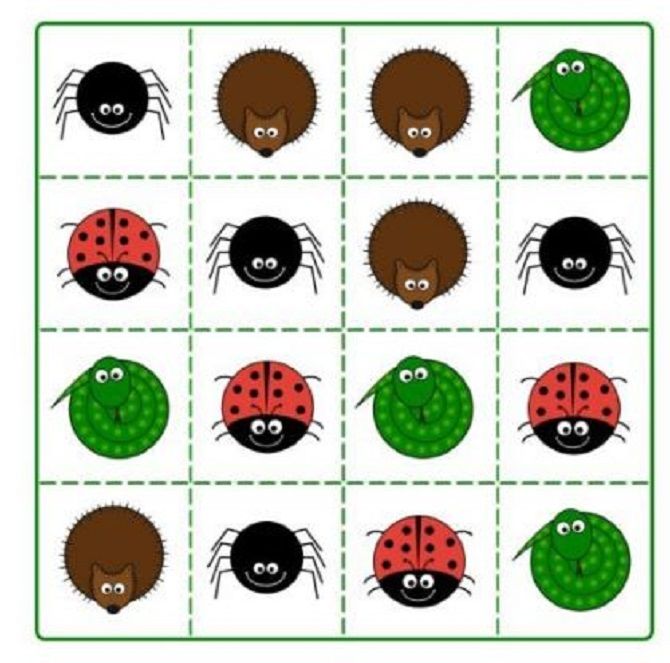
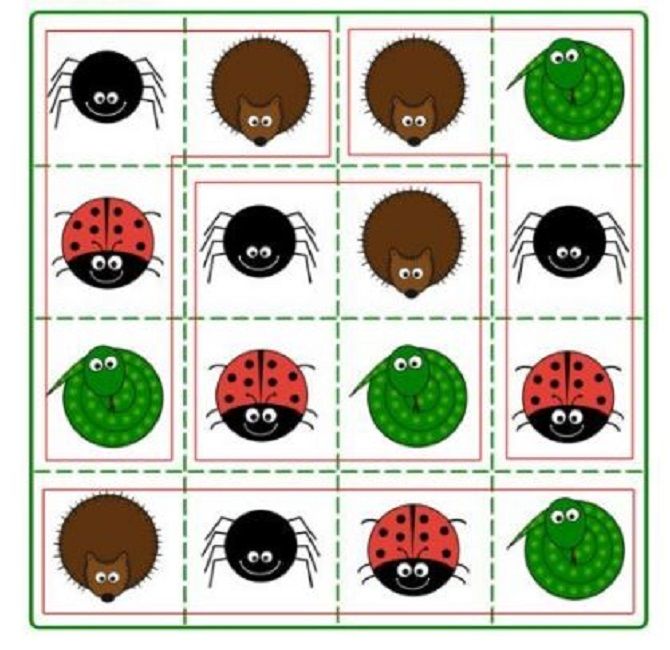
4. Divide the image into four parts that would include all types of insects:
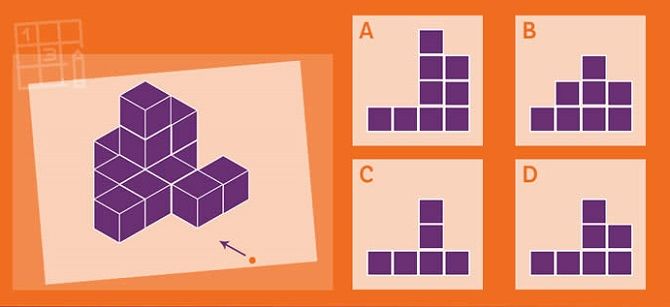
5. What is the top-down view of the tower: A, B, C or D?
6. How does a person standing at an orange spot and looking at a figure in that direction see the cubes?
7. Decide fast which fruit to add?
8. Watch carefully and guess who the thief is.
Brain teasers
9. Make a life-or-death decision. There are three doors in the room without light. There’s a poisonous snake behind the first door, a hungry lion behind the second, and the electric chair for executions behind the third. Which door is the safest to open?
10. Logical riddle. Frank’s father has 5 sons. The names of his four sons are Fefe, Fifi, Fofo, Fufu. Accordingly, what is the name of his fifth son?
11. Well known riddle: on the way to St. Ives I saw a man with 7 wives. Each wife had 7 bags. There were 7 cats in each bag. Each cat had 7 kittens. So, how many of them, including kittens, cats, bags, and wives, were heading to St. Ives?
Logical tasks
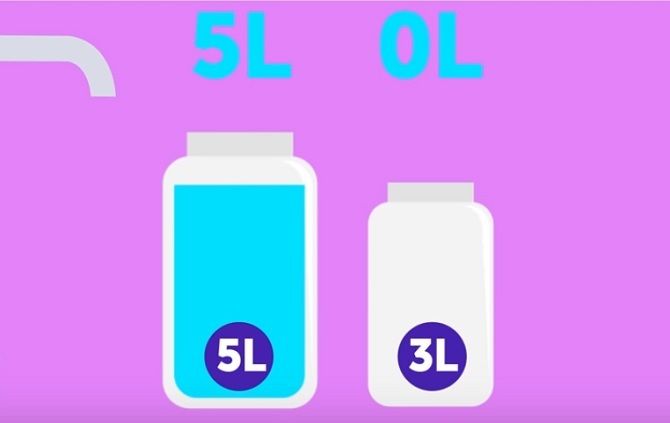
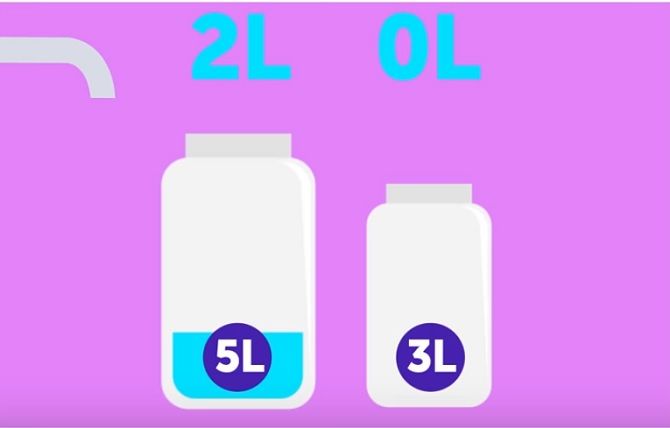
12. How to measure 4 liters of water, if there are only 5-liter and 3-liter bottles?
13. How to make the number “4”, but do not break a single stick.
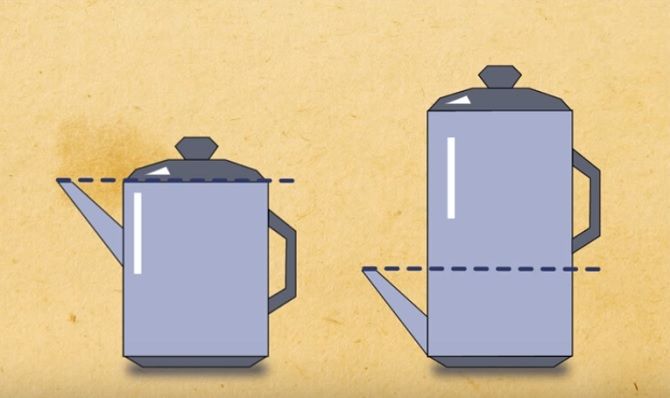
14. Which teapot has more tea?
CORRECT ANSWERS:
1. Answer: 9.
2. Answer:
This task can’t be solved mathematically because the sum of three odd numbers can’t be an even number.
But your attention is important here. If you put the balls with the numbers 11 and 13, you’ll get 24. Then, if you put the ball with the number 9, but flip it, you’ll get 24 + 6 = 30.
3. Answer:
If we know that each number obtained is a power of number 4, we get:
41 = 4
42 = 16
43 = 64
44 = 256
4. Answer:
5. Answer:
If you look at the tower from above, the top layer will be orange. So the answer is definitely not C.
The second purple layer won’t be visible from above, because it is the same size as the top layer.
And the third layer will also not be visible, because it is smaller than the two upper layers.
The fourth layer will be next visible from above around the purple layer.
The last layer will be the largest, and it is orange. Accordingly, the answer will be A.
6. Answer:
Let’s go step by step. Obviously, there are 4 blocks below.
There is a block above the rightmost one. So the answer is definitely not C.
The tallest block consists of three blocks in height.
So the answer is D.
7. Answer:
Banana, Pear, Paprica
8. Answer:
9. Answer:
Choose the room with an electric chair. The executioner will most likely go to check why there is no light, and you can escape.
10. Answer:
If Frank’s father has 5 sons, and the names of 4 sons are the same as above, then Frank is already the 5th son.
11. Answer:
Just me.
12. Answer:
1) Pour a full container of 5 liters;
2) Pour water from it to fill the 3-liter bottle and we get the remainder of 2 liters;
3) Pour 3 liters away and only 2 liters of water remain;
4) Pour it into a 3-liter bottle;
5) Fill the 5-liter bottle again
6) Pour the missing 1 liter of water into a 3-liter container and get a balance of 4 liters!
13. Answer:
14. Answer:
In the first. You should look at the position of the spout.
Did you like the training? If so, then watch another cool selection of logical tasks in our video and train your brain to the full!
Bonus! Video
The tasks proposed in this book vary considerably in both the type of their construction and the level of complexity. Some of them are close to mathematics, and for their solution it will be necessary to make a simple equation, others have nothing in common with them. Some tasks involve knowing a few simple laws of physics, some are logical exercises and puzzles, and some are just jokes, practical jokes or tricks. Some tasks are very simple — you can solve them in a matter of seconds, and above others, on the contrary, you have to pretty much smash your head. In some cases, you can not do without a pencil and paper — in others you will have to make a scheme or draw a picture. You may need a calculator or some household items. However, with all the differences between these tasks, they are similar to each other in that their solution requires a non-standard approach and the work of the imagination, which is why they are called entertaining. The solution of these problems contributes to the development of attention, memory, mental flexibility, which is also often called ingenuity, or resourcefulness.
All problems are answered and comments, but do not rush to look into them, try to find the right solution yourself. The more of these tasks you can solve, the easier and easier you will be in the future to cope with tasks of this type and even learn to compose them yourself.
The collection of tasks will help you to spend your leisure time with interest, pass the time on a long journey, find a topic of conversation or defuse a prolonged awkward pause in a conversation with unfamiliar people, as well as it will be useful in various other situations.
Task conditions
1. Each of the 10 bags contains 10 coins. Each coin weighs 10 g. But in one bag, all coins are fake — not 10 g, but 11 g. How can we determine in which bag there are fake coins (all bags are numbered from 1 to 10)? Bags can be opened and pulled out any number of coins from each.
2. The labels “Oatmeal Cookies”, “Shortcake Cookies” and “Chocolate Cookies” are mixed up on all three iron jars with cookies. Banks are closed, and you can take only one cookie from one (any) can, and then arrange the labels correctly. How to do it?
3. In your closet are 22 blue socks and 35 black socks.
You need to take a pair of socks out of the closet in complete darkness. How many socks you need to take in order to get a matching pair with a guarantee?
4. It takes 30 seconds for an old clock to break through 6 hours. In how many seconds does the clock strike 12 hours?
5. In the pond grows one leaf of lily. Every day the number of leaves doubles. On what day the pond will be half covered with lily leaves, if it is known that it will be completely covered with them in 100 days?
6. The passenger elevator rises to the fifth floor at a speed twice as large as the freight elevator, which goes to the third floor.
Which of these two elevators will come earlier: cargo to the third floor or passenger to the fifth, if they started from the first floor at the same time?
7. Flies goose. Towards him — a flock of geese. «Hello, 100 geese,» he says to them. They answer: “We are not 100 geese; Now, if there were as many of us as now, and even so much, and even half as many and a quarter as many, and even you, then there would be 100 geese. ”
How many geese fly in a flock?
8. Prove that 3 = 7. It is known that if we perform the same operation on each part of the equality, the equality will remain unchanged. We subtract five from each part of our equality: 3 — 5 = 7 — 5. It turns out: — 2 = 2. Now we will raise each part of the equation in a square: (- 2) 2 = 2 2 . It turns out: 4 = 4, therefore: 3 = 7. Find the error in this reasoning.
9. As is known, in any atom there is a nucleus whose dimensions are smaller than the size of the atom itself. If the size of the atomic nucleus is 10–12 cm, and the size of the entire atom is 10–6 cm, therefore, the nucleus is 2 times smaller than the atom itself: 12: 6 = 2. Is this statement true?
If not, how many times is the atomic nucleus smaller than an atom?
10. Is it possible to fly to the moon by plane? It is necessary to take into account that the aircraft are equipped with jet engines, like space rockets, and work on the same fuel as they.
11. Is it possible to pierce a fifty-kopeck needle with a needle?
12. A standard cup (200 g) is filled to the brim with water. How many pins can you put on it so that not a drop of water spills from a glass?
13. Ivanov has a portrait in his office. Ivanova is asked: “Who is depicted in this portrait?” Ivanov confusedly replies:
«The father depicted in the portrait is the only son of the father of the speaker.» Who is depicted in the portrait?
14. The missionary was captured by the savages who put him in a dungeon and said: “From here there are only two exits — one to freedom, the other to death; Two warriors will help you out — one always tells the truth, the other always lies, but it is unknown who is a liar and who is a truth-lover; you can ask any of them just one question. ” What question must be asked to get free?
15. In the monastery hang two ropes of rare silk. They are attached to the middle of the ceiling at a distance of one meter from each other and reach the floor. Thief-acrobat wants to steal as much rope as possible. The ceiling height is 20 m. A thief knows that if he jumps or falls from a height of more than 5 meters, he will not be able to get out of the monastery. Since he has no stairs, he can only climb on the rope. He found a way to steal both ropes almost entirely. How to do it?
16. The girl was traveling in a taxi. On the way, she talked so much that the driver was nervous. He told her that he was very sorry, but he did not hear a word, because his hearing aid does not work, he is deaf as a cork. The girl fell silent, but when they reached the place, I realized that the driver had made fun of her. How did she guess?
17. You are in the cabin of an ocean liner anchored. At midnight, the water was 4 m below the porthole and climbed 0.5 m / h. If this speed doubles every hour, then how long does the water reach the window?
18. Three travelers lay down to rest in the shade of the trees and fell asleep. While they were sleeping, the jokers smeared their foreheads with coal. Waking up and looking at each other, they began to laugh, and it seemed to each of them that the other two were laughing at each other.
Suddenly, one of them stopped laughing, because he realized that his own forehead was also dirty. How did he figure it out?
19. Shifting only one of four matches, make a square (fig. 45). Matches can neither bend nor break:
20. With the rising of the sun, the traveler began to climb a narrow, winding path to the top of the mountain. He walked faster or slower, often stopping to rest. Having come a long way, he reached the top only at sunset. After spending the night on the summit, with the rising of the sun he set off on his way back along the same path. It also descended at an uneven speed, repeatedly resting along the road, and at sunset it reached the foot of the mountain. It is clear that the average speed of descent exceeded the average speed of ascent. Is there a point on the path that the traveler passed at the same time of day, both during the ascent and during the descent?
21. The sculptor has 10 identical statues. He wants each of the four walls of the hall to have three statues. How to place them?
22. Draw, without removing the pencil from the paper, the following figures (Fig. 46):
23. One mathematician offered the merchant such a deal. The mathematician gives the merchant 100 p., And the merchant gives the mathematics in return for 1 k.
Every next day, the mathematician gives the merchant 100 p. more than the previous, that is, on the second day he gives him 200 rubles, on the third — 300 rubles. etc. And the trader gives math two times more money than the previous day, i.e. on the second day he gives him 2 k., on the third — 4 k., on the fourth — 8 k., on fifth — 16 k., etc.
To make such an exchange, they agreed within 30 days. Which of them is this exchange is profitable and why?
24. The anniversary of the October Revolution in the old style falls on October 25, and the new style — on November 7. Thus, all events in the old style for 13 days precede the same events in the new style. So, if in the new style the New Year falls on January 1, then in the old style it should fall on December 19. Why then do we celebrate the old New Year on January 14th?
25. Of the matches is made drawing glasses filled with wine (Fig. 47). Rearrange the two matches so that in the newly obtained figure the wine is out of the glass. When demonstrating the role of wine can play a match:
26. How to place six cigarettes in such a way that they all touch each other, that is, each of them touches the other five?
27. Before you are three people. One of them is Pravdolyub (speaks always the truth), the other is a Liar (always lies), and the third Diplomat (either tells the truth, then lies). You do not know who is who and ask a question to the person who stands on the left:
— Who is standing next to you?
“True love,” he says.
Then you ask the person standing in the center:
— Who are you?
“Diplomat,” he answers.
And finally, you ask the person who is standing on the right:
— Who is standing next to you?
“Liar,” he says.
Who is on the left, who is on the right, who is in the center?
28. In a ten-liter bucket is 10 liters of wine. At your disposal are two empty buckets: one — 7 liters, and the other — 3 liters. How with the help of these buckets by means of transfusions to divide 10 liters of wine into two equal parts of 5 liters each?
29. Andrei’s watch is 10 minutes behind, but he is sure that they are in a hurry for 5 minutes. He arranged to meet Katya at 8:00 by the train to go out of town. Katya is in a hurry for 5 minutes, but she thinks they are 10 minutes behind. Which of them will be the first to come to the train?
30. The 110-year-old turtle asked a dinosaur: “How old are you?” The dinosaur, which was used to expressing difficult and confusing, replied: “I am now 10 times more years old than you were when I was as old as you now». How old is the dinosaur?
31. The hijacker stole a car while trying to get to point B , but was discovered by police in point A. Departing from the chase, he began to wind, moving from A to B along the ACDB curve along the arcs of small semicircles as indicated by the arrows (Fig. 48). The policemen who pursued him started from A a moment later and, hoping to intercept the hijacker at point B , set off along the arc of the great semicircle. Will they catch up with the hijacker at point B if their speeds are exactly the same (fig. 48)?
32. Katya is twice as old as Nastya will be when Olya is as old as Katya is now. Which of them is the oldest and the youngest?
33. In one class, students divided into two groups. Some should always tell only the truth, while others should only lie. All students of the class wrote an essay on a free topic, and at the end of the essay, each student had to attribute one of the phrases: “Everything that is written here is true”, “Everything that is written here is a lie”. There were 17 truth lovers and 18 liars in the class. How many essays with a statement about the truthfulness of the written teacher counted when checking the work?
34. How many great-great-great-great-great-great-great-great-great-great-grandmothers were all your great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-grandmothers?
35. On the table lies in the unfolded handkerchief. On it in the center stands an empty glass bottle neck down. How to pull a handkerchief out of the bottle without touching it?
36. On the left side of the equality, only one dash (wand) should be put in order for the equality to be true:
5 + 5 + 5 = 550.
37. Let us prove that three times two times will be not six, but four.
Take a match, break it in half. It is one time two. Then take half and break it in half. This is the second time two. Then take the remaining half and break it in half too. This is the third time two. It turned out four. Therefore, three times two will be four, not six. Find a mistake in this reasoning.
38. How to connect nine points among themselves by four lines, without taking a pencil from paper (fig. 49)?
In the household goods store, the buyer asked:
— How much is one?
“Twenty rubles,” said the seller.
— How much is twelve?
— Forty rubles.
— Ok, give me a hundred and twelve.
— Please, from you sixty rubles.
What did the visitor buy?
40. If at 12 o’clock in the night it rains, can we expect that in 72 hours there will be sunny weather?
41. Three people paid for lunch 30 p. (each of 10 p.). After their departure, the hostess found that lunch costs not 30 rubles, but 25 rubles. and sent the boy in pursuit to return 5 p. Each of the travelers took for himself 1 p., And 2 p. they left the boy. It turns out that each of them paid not for 10 rubles, but for 9 rubles. There were three of them: 9 · 3 = 27, and two more rubles for the boy: 27 + 2 = 29. Where did the ruble go?
42. In a 1-hectare pool, 1,000,000 liters of water was poured. Can I swim in such a pool?
43. What’s more:
or
?
44. One boy lacks the cost of the 24-line ruler, and the other lacks the 2-k price. When they put their money together, they still could not buy the ruler. How much is the ruler?
45. In one parliament, deputies were divided into conservatives and liberals. The conservatives spoke only the truth in even numbers, and in odd numbers only the truth. Liberals, on the contrary, spoke only the truth in odd numbers, and in even numbers only in a lie. How with the help of one question asked to any deputy, it is possible to establish exactly what number is today: even or odd? Answers must be defined: «yes» or «no.»
46. A bottle with a cork costs 1 p. 10 k. A bottle is more expensive than a cork for 1 p. How much does a bottle cost and how much does a cork cost?
47. Katya lives on the fourth floor, and Olya lives on the second floor. Going up to the fourth floor, Katya overcomes 60 steps. How many steps does Olya need to go in order to climb to the second floor?
48. The mathematician wrote a two-digit number on a piece of paper. When he turned the paper upside down, the number decreased by 75. What number was written?
49. A rectangular sheet of paper folded in half 6 times. On a folded sheet, not on the folds, made 2 holes. How many holes will there be on a sheet?
50. Two fathers and two sons caught three birds with one stone: each one by one.
How is this possible?
51. The interviewer invites you to conceive any three-digit number. Then he asks to duplicate it to get a six-digit number. For example, you have conceived the number 389, duplicating it, get a six-digit number — 389 389; or 546 — 546 546, etc.
Next, the interlocutor offers you a six-digit number divided by 13. «Suddenly it will turn out without a trace,» he says. You make a division using a calculator (it can be done without it) and indeed your number is divisible by 13 without a remainder. Then he offers you to divide the resulting result by 11. You divide, and again it turns out without a remainder. And, finally, the interlocutor asks you to divide the resulting result by 7. The division not only goes without a trace, but also results in the very three-digit number that you have arbitrarily chosen first. How does this happen?
52. Divide the figure, consisting of three identical squares, into four equal parts (fig. 50):
53. One hundred schoolchildren simultaneously studied English and German. At the end of the course, they passed the exam, which showed that 10 schoolchildren had not mastered one or another language. Of the remaining 75, 75 people passed, and 83 passed the English exam. How many examinees are fluent in both languages?
54. How to pour exactly half of a mug, dipper, pots and any other crockery of the correct cylindrical shape, filled to the brim with water, without using any measuring devices?
55. The hour and minute hands sometimes coincide, for example, at 12 o’clock or at 24 o’clock. How many times will they coincide between 6 o’clock in the morning of one day and 10 o’clock in the evening of another day?
56. The motor ship sails from Nizhny Novgorod to Astrakhan in 5 days, it makes the return trip at the same speed in 7 days. How many days from Nizhny Novgorod to Astrakhan will the raft sail?
57. Three chickens carry three eggs in three days. How many eggs will lay 12 chickens in 12 days?
58. How to write the number 100 using five units and action signs?
59. Let’s calculate how many days a year we work and how many we have a rest. There are 365 days in a year. Eight hours a day takes everyone to sleep — it’s 122 days per year. Subtract, it remains 243 days. Eight hours a day takes rest after work, this is also 122 days a year. Subtract, 121 days left. On weekends, of which there are 52, nobody works. Subtract, it remains 69 days. Next, a four-week vacation is 28 days. Subtract 41 days left. Approximately 11 days a year occupy various holidays. Subtract, it remains 30 days. Thus, we work only one month a year.
Is this reasoning true? If not, what mistake was made in it?
60. Three rows of water-filled glasses and three empty ones stand in one row (Fig. 51). How to make so that filled and empty glasses alternate, if you can pick up only one glass?
61. If 1 worker can build a house in 12 days, then 12 workers will build it in 1 day. Consequently, 288 workers will build a house in 1 hour, 17,280 workers will build it in 1 minute, and 1,036,800 workers will be able to build a house in 1 s. Is this reasoning true? If not, what is the mistake?
62. Which word is always spelled incorrectly? (A joke task.)
63. «I guarantee,» said the seller at the pet store, «that this parrot will repeat any word he heard.» The delighted buyer bought the miracle bird, but when he came home, he found that the parrot was mute like a fish. However, the seller did not lie. How is this possible? (A joke task.)
64. The room has a candle and a kerosene lamp. What will you light first when you enter this room in the evening?
65. Peter was very tired and went to bed at 7 o’clock in the evening, setting the mechanical alarm clock at 9 o’clock in the morning. How many hours can he sleep?
66. The denial of the true sentence is a false sentence, and the negation of the false is true. However, the following example says that this is not always the case. The sentence: “This sentence contains six words,” is false, because there are not six, but five words. But the negation: “This sentence does not contain six words,” is also false, since it contains six words. How to resolve this misunderstanding?
67. How many eight-digit numbers exist, the sum of which is two digits?
68. The perimeter of a figure made up of squares is six (fig. 52). What is its area equal to?
69. What is the difference between the cube of the sum of squares of numbers 2 and 3 and the square of the sum of their cubes?
70. Half of half the number is half. What is this number?
71. With time, man will surely visit Mars. Sasha Ivanov is a man. Consequently, Sasha Ivanov will eventually visit Mars. Is this reasoning true? If not, what mistake was made in it?
72. To get an orange paint, you need to mix 6 parts of yellow paint with 2 parts of red. There are 3 g of yellow paint and 3 g of red.
How many grams of orange paint can I get in this case?
73. Of the 12 matches, 4 squares were composed (fig. 53). How do I remove 2 matches so that 2 squares remain?
74. What sign should be placed between the numbers 5 and 6 so that the resulting number is more than 5 but less than 6?
5 <5? 6 <6
75. В футбольной команде 11 игроков. Их средний возраст равен 22 годам. Во время матча один из игроков выбыл. При этом средний возраст команды стал равен 21 году. Сколько лет выбывшему игроку?
76. – Сколько лет твоему отцу? – спрашивают мальчика.
– Столько же, сколько и мне, – невозмутимо отвечает он.
– Как такое возможно?
– Очень просто: мой отец стал моим отцом только тогда, когда я родился, ведь до моего рождения он не был моим отцом, значит моему отцу столько же лет, сколько и мне.
Верно ли это рассуждение? Если нет, то какая ошибка в нём допущена?
77. В мешке 24 кг гвоздей. Каким образом можно на чашечных весах без гирь отмерить 9 кг гвоздей?
78. Peter lied from Monday to Wednesday and told the truth on other days, and Ivan lied from Thursday to Saturday and told the truth on other days. Once they said the same: “Yesterday was one of the days when I lie.” What day was yesterday?
79. Three-digit number recorded in numbers, and then — in words. It turned out that all the numbers in this number are different and increase from left to right, and all words begin with the same letter. What is this number?
80. In equality, made up of matches:
An error is made. How do you need to shift one match to make equality true?
81. How many times will a three-digit number increase if we add the same number to it?
82. Если бы не было времени, то не было бы ни одного дня. Если бы не было ни одного дня, то всегда стояла бы ночь. Но если бы всегда стояла ночь, то было бы время. Следовательно, если бы не было времени, оно было бы. В чём заключается причина данного недоразумения?
83. В каждой из двух корзин по 12 яблок. Настя взяла несколько яблок из первой корзины, а Маша взяла из второй столько, сколько осталось в первой. Сколько яблок осталось в двух корзинах вместе?
84. У одного фермера 8 свиней: 3 розовые, 4 бурые и 1 чёрная.
Сколько свиней могут сказать, что в этом небольшом стаде найдётся, по крайней мере, ещё одна свинья такой же масти, как и её собственная? (Задача-шутка.)
85. Единственный сын отца сапожника – плотник. Кем приходится сапожник плотнику?
86. Если 1 рабочий может построить дом за 5 дней, значит, 5 рабочих построят его за 1 день. Следовательно, если 1 корабль пересекает Атлантический океан за 5 дней, то 5 кораблей пересекут его за 1 день. Верно ли это утверждение? Если нет, то в чём заключается допущенная в нём ошибка?
87. Возвращаясь из школы, Петя и Саша зашли в магазин, где они увидели большие весы.
– Давай взвесим наши портфели, – предложил Петя.
Весы показали, что Петин портфель весит 2 кг, а вес Сашиного портфеля оказался равным 3 кг. Когда мальчики взвесили два портфеля вместе, весы показали 6 кг.
– Как же так? – удивился Петя. – Ведь 2 плюс 3 не равно 6.
– Ты что, не видишь? – ответил ему Саша. – У весов сдвинута стрелка.
Каков вес портфелей на самом деле?
88. Как разместить 6 кружочков на плоскости таким образом, чтобы получилось 3 ряда по 3 кружочка в каждом ряду?
89. После семи стирок длина, ширина и высота куска мыла уменьшилась вдвое. На сколько стирок хватит оставшегося куска?
90. Как от куска материи в 2/3 м отрезать 1/2 м без помощи каких-либо измерительных приборов?
91. Часто говорят, что композитором, или художником, или писателем, или учёным надо родиться. Верно ли это? Действительно ли композитором (художником, писателем, учёным) надо родиться?
(Задача-шутка.)
92. Для того чтобы видеть, совсем не обязательно иметь глаза.
Без правого глаза мы видим. Без левого тоже видим. А поскольку кроме левого и правого глаза других глаз у нас нет, то оказывается, что ни один глаз не является необходимым для зрения. Верно ли это утверждение? Если нет, то какая ошибка в нём допущена?
93. The parrot has lived for less than 100 years and can only answer yes and no questions. How many questions should he ask to find out his age?
94. Tell me how many cubes are depicted in Figure 54:
95. Three calves — how many legs? (A joke task.)
96. Один человек, попавший в неволю, рассказывает следующее: «Моя темница находилась в верхней части замка. После многодневных усилий мне удалось выломать один из прутьев в узком окне. В образовавшееся отверстие можно было пролезть, но расстояние до земли было слишком велико, чтобы просто спрыгнуть вниз. В углу темницы я обнаружил забытую кем-то верёвку. Однако она оказалась слишком короткой, чтобы можно было спуститься по ней. Тогда я вспомнил, как один мудрец удлинял слишком короткое для него одеяло, обрезав часть его снизу и пришив её сверху. Поэтому я поспешил разделить верёвку пополам и снова связать две образовавшиеся части. Тогда она стала достаточно длинной, и я благополучно спустился по ней вниз». Каким образом рассказчику удалось это сделать?
97. The interlocutor asks you to conceive any three-digit number, and then offers to write down his numbers in the reverse order, so that you get another three-digit number. For example, 528 — 825, 439 — 934, etc. Then he asks to take less from a larger number and tell him the last digit of the difference. After that, he calls the difference. How he does it?
98. Seven went — found seven rubles. If it were not for seven, but three went, would you have found much? (A joke task.)
99. Divide the drawing, consisting of seven circles, by three straight lines into seven parts so that each part has one circle:
100. Globe pulled hoop at the equator. Then the length of the hoop was increased by 10 m. At the same time, there was a small gap between the surface of the globe and the hoop. Can a man climb through this gap? The length of the earth’s equator is approximately 40,000 km.
Answers with comments
1. From the first bag you need to pull out one coin, from the second — two, from the third — three, etc. (from the tenth bag — all 10 coins).
This is followed by weighing all these coins together once. If there were no counterfeit coins among them, i.e. they would all be 10 g each, then their total weight would be 550 g. But since there are counterfeit coins (11 g each) among the weighed coins, their total weight will be greater 550 g. Moreover, if it turns out to be 551 g, then fake coins are in the first bag, because from it we took one coin, which gave one extra gram. If the total weight is 552 g, then fake coins are in the second bag, because we took two coins from it. If the total weight is 553 g, it means that the fake coins are in the third bag, etc. Thus, using only one-time weighing, you can determine exactly which bag contains the fake coins.
2. We must take the cookies from the jar with the words «Oatmeal cookies» (you can from any other). Since the bank is labeled incorrectly, it will be shortbread or chocolate. Let’s say you got the shortbread. After that, you need to swap labels «Oatmeal Cookies» and «Shortbread Cookies.» And since all the labels are mixed up by the condition, now there is oatmeal in the jar with the inscription “Chocolate Cookies”, and there is chocolate in the jar with the inscription “Oatmeal Cookies”, it means that these two labels must be interchanged.
3. From the cabinet you need to get only three socks. In this case, only 4 options are possible: all three socks are white, all three socks are black; two socks are white, one is black; two socks are black, one is white.
In each of these combinations there is one matching pair — white or black.
4. The clock strikes 12 hours in 66 seconds. When the clock strikes 6 hours, there are 5 intervals from the first strike to the last. The interval is 6 seconds (1/5 part of 30). When the clock strikes 12 hours, 11 intervals pass from the first strike to the last. Since the length of the interval is 6 s, in order to break through 12 hours, the clock takes 66 s: 11 · 6 = 66.
5. The pond will be covered with leaves of lilies by half for 99 days. By condition, the number of leaves every day doubles, and if the pond is half covered with leaves for 99 days, the next day the second half of the pond will be covered with lily leaves, that is, the pond will be completely covered with them after 100 days.
6. The path traveled to the fifth floor (four flights) by a passenger elevator is twice as long as the distance traveled to the third floor (two flights) by freight. Since the passenger elevator goes twice as fast as the freight elevator, they will pass their routes at the same time.
7. To solve this problem it is necessary to make an equation. The number of geese in a flock is x . “Now, if there were as many of us as now (i.e. x ),” said the geese, “and so much more (i.e. x ), and even half as much (i.e. 1/2 x ), and even a quarter-so much (i.e., 1/4 x ), and you (i.e. 1 goose), then we would have been 100 geese. ” It turns out the formula:
Let’s make addition in the left part of equality:
Answer: 36 geese flew in a flock.
8. The error lies in the construction of each part of the equality:
— 2 = 2, squared. It seems that the same operation is performed on each part of the equality (squaring), in fact, on each part of the equality, various operations are performed, because the left side is multiplied by –2, and the right side is multiplied by 2.
9. The statement that the atomic nucleus is two times smaller than the atom itself is, of course, not true: 10 –12 cm less than 10 –6 cm not twice, but a million times.
10. An airplane in flight is “held” in the air, so it is impossible to fly to the moon by plane, because there is no air in outer space.
11. The needle is made of steel, and the coin is made of copper. Steel is much harder than copper and therefore it is quite possible to pierce a coin with a needle.
Only manually it is impossible to do. If you try to hammer a needle into a coin with a hammer, it will also fail: the area of the sharp end of the needle is so small that its tip will vibrate and slide along the surface of the coin. In order for the needle to be stable, it is necessary to hammer it into the coin through a piece of soap, paraffin or wood: this material will give the needle a constant and right direction, and in this case it will freely pass through the copper coin.
12. In the glass you can put more than a thousand pins. In this case, not a drop of water from it will not pour out, but a small water bulge, a “hill”, is formed above the edges of the glass. According to Archimedes’ law, a body immersed in water displaces a volume of water equal to the volume of the body. The volume of one pin is so small that the volume of the water “slide” above the surface of the glass is equal to the volume of more than a thousand pins.
13. The portrait depicts the son of Ivanov. To solve the problem, you can create a simple scheme:
father (speaker);
father (pictured) = son (speaking);
son (pictured).
14. It is necessary to turn to any of the warriors with the following question: “If I ask you, does this way out lead to freedom, then you answer me“ yes ”?” With this question, the warrior who is lying all the time will be forced to tell the truth . Suppose you, showing him the way out to freedom, say: “If I ask you, does this way out lead to freedom, will you answer me“ yes ”?”
In this case it will be true if he answers “no”, but he has to lie, and therefore he is forced to say “yes”.
15. The thief tied the lower ends of the ropes together. According to one of them, he climbed to the ceiling, cut the second rope at a distance of about 30 cm from the ceiling and let it fall down. From the remaining piece of the second rope to hang, he tied a loop. Then, grasping the loop, he cut the first rope and put it in the loop. After that, he went down the double rope down and pulled the rope out of the loop.
16. If the taxi driver is deaf, as he understood where to take the girl? And again: how did he then understand that she was saying something at all?
17. Water will never reach the porthole because the liner rises with the water.
18. He reasoned like this: “Each of us may think that his own face is pure. B. is sure that his face is clean and laughs at B.’s stained forehead. But if B. had seen that my face was clean, he would have been surprised at V.’s laughter, since in this case V. would have no reason to laugh . However, B. is not surprised, so he may think that V. is laughing at me. Therefore, my face is soiled. «
19. It is necessary to move the upper match, forming a tiny square in the center of the figure.
20. A point on the path, which the traveler travels at the same time of day, both during the ascent and the descent, exists ( A ). This is easily verified with the following scheme:
The x -axis is the time of day, and the y -axis is the height of the climb. Curves are, respectively, lifting and descending graphs. The point of their intersection is exactly the same one that the traveler travels at the same time of day, both on the ascent and on the descent.
21. Statues should be arranged as follows:
22
23. Exchange is beneficial to mathematics and disadvantageous to a merchant, since the amount of money that a merchant pays, even if it is insignificant at first, increases exponentially, and the money that a mathematician pays to a merchant, increases in arithmetic progression. After 30 days, the mathematician will give the merchant about 50,000 rubles, and the merchant will owe more than 5,000,000 rubles to mathematics.
24. New Year and earlier (i.e. old style) were celebrated on January 1.
However, the old January 1 (old New Year) now, that is, the new style, falls on January 14, so there is no contradiction and misunderstanding here. The condition of the problem creates the appearance of contradiction due to the fact that different concepts are mixed up in the same words: New Year in accordance with the new style and New Year in accordance with the old style. And indeed, the New Year in a new style in the old style would fall on December 19, and the New Year in the old style in a new style falls on January 14.
25
26
27. The man who stands on the left, if he were a Truth Lover, to the question: “Who is standing next to you?” Could not answer what he said — “Truth Lover”. It means that the Pravdolyub is not on the left.
But Pravdolyub and not in the center, because, being a Pravdolyub, he could not answer the question “Who are you?” As he answered — “Diplomat”.
Hence, the Pravdolyub is on the right and, therefore, next to him, that is, in the center is the Liar, and on the left is the Diplomat.
28. The sequence of transfusions is presented in the following table. 9, where I is a bucket with a volume of 10 liters; II — 7 l bucket; III — 3 L bucket:
Thus, it is possible to divide 10 liters of wine in half, using empty buckets of 7 liters and 3 liters each, using 10 transfusions.
29. Katya will come to the train first, and Andrew, most likely, will be late for the train, as he will arrive at the station by the time when his watch will be 8 hours 05 minutes. And in fact, another 10 minutes more — 8 hours and 15 minutes. Katya will try to come by her watch by 7 hours and 50 minutes, but in reality it will be 7 hours and 45 minutes.
30. To solve this problem it is necessary to make an equation. But first, based on the dinosaur’s intricate response, the following scheme should be constructed (in the past, we will take the age of the tortoise as x ):
So, on the diagram we see that now the dinosaur is really 10 times more years than the turtle was when the dinosaur was as old as the turtle now. Since the age difference in the past and in the present remains the same, we make the equation:
Convert:
110 — x = 10 x — 110,
110 + 110 = 10 x + x
220 = 11 x
x = 220: 11 = 20.
Consequently, the turtle in the past was 20 years old, the dinosaur is now 10 times more.
The answer: a dinosaur 200 years old.
31. The sum of the diameters of small semicircles: (AC) + (CD) + (DB) is equal to the diameter of the large semicircle: AB , but since the length of the semicircle is half the product of the number π by the diameter, the distances traveled by cars will be exactly the same. Consequently, the lag of the police car from the hijacker will not decrease, and the pursuit on this site will not be crowned with success.
32. To solve this problem it is necessary to make a simple scheme (we denote the current age of Katy as x ):
It follows from the diagram that the eldest is Kate, followed by Olya and Nastya.
33. All the truthful truely asserted that everything written was true, but all liars falsely asserted that everything written by them was true. Thus, all 35 essays turned out to be a statement about the veracity of what was written.
34. Each person has 2 parents, 4 grandparents, 8 great-grandmothers and great-grandfathers, 16 great-great-grandmothers and great-great-grandparents. To find out how many great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-great-grandfathers, of course, if we exclude cases of incest, that is, marriages between different relatives.
If we take into account that one generation is about 25 years, then eight generations (discussed in the statement of the problem) correspond to 200 years, that is, 200 years ago every 256 people on Earth were relatives of each of us. For 400 years, the number of our ancestors will be: 256 · 256 = 65,536 people, that is, 400 years ago each of us had 65,536 relatives living on the planet. If you unscrew the story 1,000 years ago, it turns out that the entire population of the Earth at that time was related to each of us. So, really all people, by and large, — brothers.
35. You can try, using the inertia of the bottle, with a sharp movement to pull the scarf out from under it. But, most likely, nothing will turn out: the position of the bottle is too unstable. However, remember that the friction force decreases with vibrations. Fist one hand must be evenly and lightly knocking on the table near the bottle, and the other hand — gently pull a scarf. At a certain frequency and force of blows on the table, the handkerchief will begin to slowly slide out from under the bottle. It is important to pay attention to the fact that the edge of the scarf had a not very large edge: it, as a rule, knocks the bottle at the last moment. Therefore, it is better that the shawl is generally without an edge.
36. With the help of a single line one of the plus signs will turn into four, resulting in the equality:
545 + 5 = 550.
In this reasoning in the same words different mathematical operations are mixed: division by two and multiplication by two. The trick in the form of an outwardly correct proof of a false thought is based on this confusion.
38
39. Room for the apartment.
40. It is impossible, because after 72 hours, that is, after three days, it will be again at 12 o’clock at night, and the sun does not shine at night (if things are not happening beyond the Arctic Circle on a polar day).
41. In the hostess 25 p., The boy 2 p. Only 27 p., So those 2 p., Which the boy received, come in 27 p. And in the problem statement to 27 p. added 2 p., which the boy has, and therefore it turns out 29 p.
Need to 27 p. Do not add 2 p., And take away.
42. Looking at the turnover of the last page of the notebook in mathematics, where the system of measures and weights is given, you will see that 1 l is 1 dm 3 . Consequently, 1,000,000 dm 3 of water was poured into the pool, or 1,000 m 3 of water (since 1 m is 10 dm). Knowing the area of the basin (1 ha = 10 000 m 2 ) and the volume of water poured into it, it is easy to calculate its depth:
ABOUT: it is impossible to swim in a 10 cm deep pool.
43. To compare these values, it is necessary to bring the square root and cubic to the root of one degree. This may be the root of the sixth degree. Accordingly, the radical expressions will change. Will turn out
and
. The sixth root of nine is slightly larger than the same eight root, therefore,
more than
.
44. Denote the cost of the line as x . Then one boy lacks the cost of the ruler: x — 24 k., And the other: x — 2 k.
When adding up their money, they still could not buy a ruler.
Let’s make a simple inequality:
( x — 24) + ( x — 2) < x .
Convert:
x — 24 + x — 2 < x ,
2 x — 26 < x ,
2 x — x <26,
x <26.
So, the ruler costs less than 26 k., But more than 24 k., Since, by condition, one boy does not have enough up to its cost of 24 k.
About here: the ruler costs 25 k.
45. We need to ask any deputy: “Are you a conservative?” If he answered “yes”, then today is an even number, and if “no”, then an odd number. On even numbers, the conservatives will say the true «yes», and the liberals, speaking untruths, will also say «yes.» On odd numbers, on the contrary, the conservatives, when asked, will say no, but the liberals, who say only truth these days, will also say no.
46. At first glance it may seem that the bottle costs 1 p., And the cork 10 k., But then the bottle is more expensive than the cork by 90 k., And not by 1 p., As per the condition. In fact, a bottle costs 1 p. 05 to., And the cork costs 5 to.
47. At first glance it may seem that Olya is 30 steps down — two times less than Katya, since she lives two times lower than her. In fact, it is not. When Katya rises to the fourth floor, she overcomes 3 flights of stairs between floors. It means that there are 20 steps between two floors: 60: 3 = 20. Olya rises from the first floor to the second, therefore, she overcomes 20 steps.
48. This is the number 91, which when turned upside down turns into 16. At the same time, it decreases by 75: 91 — 16 = 75.
When solving this task, it is necessary to take into account that when turning the number, its numbers not only turn over, but also change places.
49. On the expanded sheet there will be 128 holes. It is necessary to take into account that each time a sheet is folded, the number of holes doubles.
50. Three people: grandfather, father and son — these are two fathers and two sons — they caught three birds with one stone.
51. Эффект этой задачи-фокуса заключается в том, что увеличение любого трёхзначного числа до шестизначного путём его дублирования равносильно умножению этого трёхзначного числа на 1 001. Кроме того, произведение чисел 13, 11 и 7 также равно 1 001. Следовательно, если получившееся шестизначное число разделить в любой последовательности на эти три числа (13, 11, 7), то получится исходное трёхзначное число.
52.
53. Тем или иным языком владеют 90 школьников, так как по условию 10 человек не освоили ни одного языка. Из этих 90 человек 15 не сдали немецкий, так как 75 его сдали по условию, а 7 человек не сдали английский, так как 83 его сдали по условию. Значит, всего не сдавших один из экзаменов: 15 + 7 = 22 человека из 90.
О т в е т: двумя языками овладели: 90 – 22 = 68 школьников.
54. Любая посуда правильной цилиндрической формы, если смотреть на неё сбоку, представляет собой прямоугольник. Как известно, диагональ прямоугольника делит его на две равные части. Точно так же цилиндр делится пополам эллипсом. Из наполненной водой посуды цилиндрической формы надо отливать воду до тех пор, пока поверхность воды с одной стороны не достигнет угла посуды, где её дно смыкается со стенкой, а с другой стороны края посуды, через который она выливается. В этом случае в посуде останется ровно половина воды:
55. Может показаться, что за указанный период стрелки часов совпадут всего три раза: в 12 ч дня, потом в 24 ч этого же дня и в 12 ч следующего дня. На самом же деле часовая и минутная стрелки совпадают каждый час один раз (когда минутная обгоняет часовую).
С 6 ч утра одного дня до 10 ч вечера другого дня проходит 40 ч, значит за это время часовая и минутная стрелки должны совпасть 40 раз. Но три часа из этих 40 ч составляют исключение: это 12 ч одного дня, 24 ч того же дня и 12 ч другого дня. Представим себе, что в 12 ч стрелки совпали, в следующий раз минутная стрелка догонит часовую не в первом часу, а в начале второго, т. е. с 12 ч до 1 ч (неважно – дня или ночи) совпадения стрелок не происходит. Следовательно, часовая и минутная стрелки с 6 ч утра одного дня до 10 ч вечера другого дня совпадут 37 раз.
56. Скорость теплохода примем за x , а скорость реки за у . Поскольку от Нижнего Новгорода до Астрахани теплоход плывёт по течению, то его собственная скорость и скорость реки складываются, т. е. до Астрахани он плывёт со скоростью: x + у . На обратном пути теплоход плывёт против течения, т. е. со скоростью x – у . Как известно, расстояние равно произведению скорости на время. Зная, что теплоход проделывал один и тот же путь за 5 и за 7 суток, можно составить уравнение:
5 ( x + у ) = 7 ( x – у ).
Преобразуем:
5 x + 5 y = 7 x — 7 y ,
7 y + 5 y = 7 x — 5 x ,
12 y = 2 x ,
6 y = x .
Как видим, собственная скорость теплохода в 6 раз больше скорости реки. Значит, по течению (от Нижнего Новгорода до Астрахани) он плывёт со скоростью в 7 раз большей скорости реки, ведь в этом случае скорости теплохода и реки складываются. Поскольку плот плывёт только по течению, то его скорость равна скорости реки, а значит, она в 7 раз меньше, чем скорость теплохода на пути в Астрахань. Следовательно, и времени на тот же путь плот затратит в 7 раз больше, чем теплоход: 5 · 7 = 35.
Ответ: расстояние от Нижнего Новгорода до Астрахани плот пройдёт за 35 суток.
57. Можно сходу ответить, что 12 куриц за 12 дней снесут 12 яиц.
However, it is not. Если три курицы за три дня несут три яйца, значит одна курица за те же три дня несёт одно яйцо. Следовательно, за 12 дней она снесёт: 12 : 3 = 4 яйца. Если же куриц будет 12, то за 12 дней они снесут: 12 · 4 = 48 яиц.
58. 111 – 11 = 100.
59. Конечно же, это рассуждение не верно. Видимость его правильности и убедительности создаётся за счёт того, что в нём почти незаметно смешиваются и подменяются понятия «сутки» и «день», а вернее – «рабочий день». А это совершенно разные понятия, ведь сутки – это 24 ч, а рабочий день – это 8 ч. В году 365 суток, и это то время, в которое мы и работаем, и отдыхаем, и спим. В рассуждении же понятие «365 суток» подменяется понятием «365 дней», и предполагается, что все эти дни (а на самом деле – сутки) заняты только работой. Далее из этих «365 дней» вычитается время, затрачиваемое на сон, на отдых и т. д., а это время надо вычитать не из дней (причём рабочих дней), а из суток. Тогда количество дней (рабочих) останется прежним, и недоразумения не возникнет.
60. Надо взять второй наполненный стакан слева и перелить его во второй пустой стакан справа, тогда наполненные и пустые стаканы будут чередоваться:
61. Рассуждение неверно. Говорить о том, что большее число рабочих смогут построить дом намного быстрее, можно только в пределах целых дней, т. е. если измерять время работы днями. Если же измерять это время часами, а тем более минутами и секундами, то данная закономерность (больше рабочих – быстрее работа) не действует. Ошибка рассуждения заключается в том, что в нём смешиваются различные понятия, обозначающие разные временные интервалы. Понятие «день» почти незаметно подменяется понятиями «час», «минута», «секунда», за счёт чего и создаётся видимость правильности и доказанности данного рассуждения.
62. Это слово «неправильно». Оно всегда так и пишется – «неправильно». Эффект этой задачи-шутки заключается в том, что в ней слово «неправильно» употребляется в двух разных смыслах.
63. Попугай действительно может повторять каждое услышанное слово, но он глух и не слышит ни одного слова.
64. Конечно же, спичку, так как без неё нельзя зажечь ни свечу, ни керосиновую лампу. Вопрос задачи двусмыслен, ведь его можно понимать то ли как выбор между свечой и керосиновой лампой, то ли как последовательность в зажигании чего-либо (сначала спичка, потом – от неё – всё остальное).
65. Может показаться, что Пётр будет спать 14 ч, но на самом деле он сможет поспать всего 2 ч, потому что будильник прозвонит в девять часов вечера. Простой механический будильник не различает дня и ночи и всегда звонит в то время, на которое его поставили.
Если бы это был электронный будильник компьютерного типа, который можно программировать, тогда Петру удалось бы проспать с 7 ч вечера до 9 ч утра.
66. Логическая закономерность, что отрицание истины является ложью, а отрицание лжи – истиной, действует только тогда, когда речь идёт об одном и том же предмете. В данном случае речь должна идти об одном и том же предложении. Если бы это было так, то одно утверждение обязательно было бы истинным, а другое ложным, или наоборот. Но в задаче речь идёт о двух разных предложениях. Поэтому нет ничего удивительного в том, что они оба являются ложными.
67. Сумма восьми цифр, равная двум может получиться в том случае, если одна из этих цифр двойка, а остальные – нули. Такое восьмизначное число только одно. Это 20 000 000. Но сумма восьми цифр, равная двум, также может получиться в том случае, если две из этих цифр единицы, а остальные нули. Таких восьмизначных чисел семь: 11 000 000, 10 100 000, 10 010 000, 10 001 000, 10 000 100, 10 000 010, 10 000 001.
О т в е т: существует восемь восьмизначных чисел, сумма цифр которых равна двум.
68. Периметр фигуры – это сумма длин всех её сторон. В данной фигуре 12 сторон. Если её периметр равен 6, то одна сторона равна: 6 : 12 = 0,5. Фигура состоит из 5 одинаковых квадратов, со стороной 0,5. Площадь одного квадрата равна: 0,5 · 0,5 = 0,25. Следовательно, площадь всей фигуры равна: 0,25 · 5 = 1,25.
69. Затруднение при решении может возникнуть из-за необычно сформулированного условия задачи. Сама же задача очень проста.
Требуется всего лишь записать математически то, что выражено в ней словами, т. е. распутать её словесное условие. Сумма квадратов чисел 2 и 3 – это: 2 2 + 3 2 . Куб суммы квадратов чисел 2 и 3 – это: (2 2 + 3 2 ) 3 .
Сумма кубов этих чисел – это: 2 3 + 3 3 . Квадрат этой суммы – это: (2 3 + 3 3 ) 2 . Надо найти разность первого и второго: (2 2 + 3 2 ) 3 – (2 3 + 3 3 )2 = (4 + 9) 3 – (8 + 27) 2 = 133 – 352 = 2 197 – 1 225 = 972.
70. Это число 2. Половина этого числа равна 1, а половина от половины этого числа (т. е. единицы) равна 0,5, т. е. тоже половине.
71. Рассуждение неверно. Совершено необязательно, что Саша Иванов со временем побывает на Марсе. Внешняя правильность этого рассуждения создаётся за счёт употребления в нём одного слова («человек») в двух разных смыслах: в широком (абстрактный представитель человечества) и в узком (конкретный, данный, именно этот человек).
72. Как видим по условию, для получения оранжевой краски требуется в три раза больше жёлтой краски, чем красной: 6 : 2 = 3. Значит из имеющегося количества жёлтой и красной красок надо взять в три раза больше жёлтой краски, чем красной, т. е. 3 г жёлтой и 1 г красной.
О т в е т: можно получить 4 г оранжевой краски.
73.
Можно убрать и другие 2 спички.
74. Надо поставить запятую: 5 < 5 , 6 < 6.
75. Сначала надо выяснить, каков общий возраст всех игроков команды: 22 · 11 = 242. Возраст выбывшего игрока примем за x . После того, как он выбыл общий возраст игроков команды стал равен: 242 – x . Поскольку игроков стало 10 и их средний возраст известен (21 год), можно составить уравнение:
(242 – x ) : 10 = 21,
242 – x = 210,
x = 242 – 210 = 32.
Ответ: выбывшему игроку 32 года.
76. Рассуждение, конечно же, неверно. Эффект его внешней правильности достигается благодаря употреблению понятия «возраст отца» в двух разных смыслах: возраст отца как возраст человека, который является этим отцом, и возраст отца как число лет отцовства. Кстати, во втором значении понятие «возраст», как правило, не употребляется: обычно под словосочетанием «возраст отца» понимается возраст этого человека, а не что-либо иное.
77. Сначала надо разделить 24 кг гвоздей на две равные части по 12 кг, уравновесив их на чашах весов. Затем так же разделить 12 кг гвоздей на две равные части по 6 кг. После этого отложить одну часть, а другую разделить таким же способом на части по 3 кг. Наконец к шестикилограммовой части гвоздей добавить эти 3 кг. В результате получится 9 кг гвоздей.
78. Это был четверг. В этот день Пётр правдиво сказал, что вчера (т. е. в среду) он лгал, а Иван солгал насчёт того, что вчера (т. е. в среду) он лгал, ведь по условию в среду он говорит правду.
79. Это число 147.
80
81. В 1 001 раз. Для того чтобы установить это, надо шестизначное число, полученное путём дублирования трёхзначного числа, разделить на это трёхзначное число, получится 1 001 (см. также задачу 51).
82. Ошибка данного рассуждения заключается в утверждении, что если бы не было времени, то не было бы ни одного дня, а значит, всегда стояла бы ночь. Как раз наоборот – если бы не было времени, то не могло бы быть ни одного дня и ни одной ночи, ведь понятие ночи (как и понятие дня) относится именно ко времени (и день, и ночь – это некие временные интервалы).
83. Примем число яблок, которые взяла Настя из первой корзины, за x , тогда в первой корзине осталось: 12 – x яблок. Именно столько яблок и взяла Маша из второй корзины. Значит во второй корзине осталось: 12 – (12 – x ) яблок. В двух корзинах вместе осталось: (12 – x ) + 12 – (12 – x ) = 12 – x + 12 – 12 + x = 12.
Ответ: в двух корзинах вместе осталось 12 яблок.
84. Этого не может сказать ни одна свинья, ведь свиньи, как известно, не говорят. Эта не очень серьёзная задача основана на двусмысленности вопроса: «Сколько свиней могут сказать…?» Слово «сказать» в этом вопросе можно понимать буквально – говорить членораздельной человеческой речью, а также его можно воспринимать в переносном значении – кто-то говорит от имени или за тех, которые сами говорить не могут (не умеют).
85. Сапожник и плотник – это одно лицо. В этом легко убедиться, составив простую схему:
отец (сапожника)
сапожник (сын отца сапожника) = плотник
86. Рассуждение неверно. Ошибка заключается в смешивании двух совершенно различных ситуаций в одних и тех же словах. Когда рабочие строят дом, их усилия складываются, поэтому работа идёт быстрее и выполняется за более короткий срок. Когда корабли пересекают Атлантический океан, то их «усилия» не складываются: каждый корабль преодолевает океан всё равно в одиночку, и поэтому время, затраченное на переправу через океан, не уменьшается при увеличении количества кораблей.
87. Стрелка у весов была сдвинута не вправо от нуля, а влево, т. е. весы показывали на 1 кг меньше. Значит, Петин портфель весит 3 кг, а Сашин – 4 кг. Вместе их портфели весят 7 кг. Когда они их взвесили, весы показали на 1 кг меньше, т. е. 6 кг.
88. На первый взгляд может показаться, что подобным образом можно расположить только 9 кружочков, но ведь в условии не сказано, что ряды кружочков должны быть горизонтальными или вертикальными. Они могут быть какими угодно. Расположить кружочки можно различными способами:
89. На первый взгляд может показаться, что оставшегося куска хватит на семь стирок. However, it is not. Если длина, ширина и высота куска мыла уменьшились вдвое, то его объём уменьшился не в два раза, а в восемь раз:
Если после семи стирок объём куска мыла уменьшился в восемь раз, значит оставшегося куска хватит всего на одну стирку:
90. Кусок материи в 2/3 м надо сложить пополам. Образовавшаяся линия сгиба поделит его на две равные части по 1/3 м. Затем надо сложить его ещё раз пополам. Образовавшиеся линии сгиба поделят кусок материи на четыре равные части по 1/6 м. Три таких части – это 3/6 м или искомая 1/2 метра:
91. Конечно же, композитором, равно как и художником, писателем или учёным, надо родиться, ведь если человек не родится, то он не сможет сочинять музыку, рисовать картины, писать романы или делать научные открытия. Эта шуточная задача основана на двусмысленности вопроса: «Действительно ли надо родиться?»
Данный вопрос можно понимать буквально: надо ли рождаться на свет для того, чтобы заниматься каким-либо видом деятельности; а также данный вопрос можно понимать в переносном смысле: является ли талант композитора (художника, писателя, учёного) врождённым, данным от природы или же он приобретается во время жизни упорным трудом.
92. Рассуждение, конечно же, неверно. Его внешняя правильность основана на почти незаметном исключении ещё одного варианта, который в данном рассуждении также необходимо было рассмотреть. Это вариант, когда не видит ни один глаз. Именно он и был пропущен: «Без правого глаза мы видим, без левого тоже, значит, глаза необязательны для зрения». Правильное утверждение должно быть таким: «Без правого глаза мы видим, без левого тоже видим, но без двух вместе не видим, значит, мы видим или одним глазом, или другим, или двумя вместе, но мы не можем видеть без глаз, которые, таким образом, необходимы для зрения».
93. На первый взгляд может показаться, что попугаю можно задать до 99 вопросов. На самом же деле можно обойтись гораздо меньшим числом вопросов. Спросим его так: «Тебе больше 50 лет?» Если он ответит «да», то его возраст от 51 до 99 лет; если же он ответит «нет», то ему от 1 года до 50 лет. Количество вариантов его возраста после первого же вопроса сокращается вдвое. Следующий подобный вопрос: «Тебе больше (можно спросить – меньше) 25 лет?»,
«Тебе больше (меньше) 75 лет?» (в зависимости от ответа на первый вопрос) сокращает число вариантов в четыре раза и т. д. В итоге попугаю надо задать всего 7 вопросов.
94. Этот рисунок можно видеть по-разному. Присмотритесь к нему внимательно, и вы заметите, как изображение будет переворачиваться то в одну, то в другую сторону, как бы переливаться на ваших глазах.
В одном случае мы видим шесть кубиков – три сверху, два посередине и один снизу, а в другом случае мы видим один кубик – в середине рисунка. Таким образом, всего на рисунке изображено семь кубиков.
95. Тереть телёнка можно сколь угодно долго, однако сколько телёнка ни три, у него всё равно будет четыре ноги. Эта задача-шутка основана на том, что числительное «три» имеет омоним – глагол в повелительном наклонении.
96. Рассказчик разделил верёвку не поперёк, как, скорее всего, может показаться, а вдоль, сделав из неё две верёвки одинаковой длины. Когда он связал две части вместе, верёвка стала в два раза длиннее, чем была сначала.
97. При вычитании меньшего числа из большего действует одна закономерность: сумма всех цифр разности всегда будет равна 18 (независимо от исходных чисел). Кроме того, второй цифрой разности всегда будет 9. Таким образом, зная последнюю цифру разности (или первую) можно безошибочно установить всю разность.
98. Если бы не семеро, а трое пошли, то всё равно те же самые семь рублей и нашли.
99.
100. На первый взгляд может показаться, что зазор будет настолько маленьким (ведь 10 м – это почти ничто по сравнению с 40 000 км), что в него не сможет пролезть не только человек, но даже кошка.
In fact, the size of the gap will be approximately 1.6 m, that is, a person will not only be able to crawl into it, but even pass (perhaps with a slightly bowed head).
As is known, the circumference is equal to: 2π R , where R is its radius.
So the radius of the circle is: l / 2π, where l is the length of the circle.
Thus, the circumference and its radius are in direct proportionality, but the radius is less than the length.
Increasing the length of the equatorial hoop is an increase in the circumference. Using the above formula, it is easy to establish an increase in its radius, which will be the size of the gap formed between the hoop and the surface of the globe.
Having made simple calculations, you will see that by increasing the length of the equatorial hoop by only 1 m, its radius increases by approximately 16 cm. A cat can crawl into such a gap. Increasing the length of the hoop by 10 m (as in the condition of the problem) increases the gap by about 1.6 m, and a person can enter it. If the length of the equatorial hoop increases by 100 m, then the gap will be approximately 16 m. A five-storey building will be able to “crawl” into such a gap.
Welcome to our Math Logic Problems worksheets.
All the problems on this page require children to use their reasoning and logic thinking skills to solve.
There are a range of worksheets on this page with varying levels of difficulty from 1st grade up to 5th grade.
Math Logic Problems
Logic puzzle problems are a set of problems which involve children using their reasoning and logical thinking skills.
Sometimes children who struggle in other areas of math, such as number work, find that this is an area which they excel in.
Some of the math logic problems on this page work like traditional logic puzzles with table grids to fill in, but most of the sheets
simply involve children using their thinking and resoning to solve the problems on the page.
All the logic puzzle worksheets on this page come with an answer sheet.

The problems on this page all involving solving Logic Problems.
Some of the sheets on this page include tables and way to support children with their recording and organising their work.
Some of the sheets have a space for children to record their own thinking and working out, with no support in recording.
The level of the worksheets goes from 1st grade to 5th grade (UK Years 1 to 6).
Using these sheets will help your child to:
- deveolop their reasoning and thinking skills;
- support and develop recording skills;
- solve a range of logic puzzles.
Logic Problems Worksheets
1st Grade Problems
Share the Treasure
Share the Treasure involves sharing out 20 gold bars equally into 4 piles.
The second part of the activity involves sharing out the bars using four rules.
-
Share the Treasure 1
-
Answers
Who Chose Which Shape #1
Who Chose Which Shape is a logic problem where children have to work out which salamander chose which shape from the clues given.
-
Who Chose Which Shape #1
-
Answers
2nd Grade Problems
Birthday Girl
Birthday Girl is an activity which involves finding the correct ages of all the people in the challeges using the clues that are given.
-
Birthday Girl
-
Answers
Share the Treasure #2
Share the Treasure is a logic acitivity where the aim is to share some treasure according to certain criteria.
-
Share the Treasure #2
-
Answers
Who Chose Which Shape #2
Who Chose Which Shape is a math logic problem where children have to work out which salamander chose which shape from the clues given.
-
Who Chose Which Shape #2
-
Answers
3rd Grade Problems
Color that Shape
Color that Shape is a coloring activity which uses logical thinking to work out which shape needs to be shaded which color.
-
Color that Shape
-
Answers
Join Me Up
Join Me Up is an logical puzzle where the aim is to place the numbers from 1 to 7 into the puzzle so that no consecutive numbers are next to each other.
-
Join Me Up
-
Answers
Spot the Digits
Spot the Digits is a logic activity where children have to find out the values of the letters a, b, c and d.
The values can be determined by using the 3 clues.
-
Spot the Digits
-
Answers
4th Grade Problems
Quadra’s Magic Bag Challenges
Quadra’s Magic Bag Challenges involves using thinking and reasoning skills to work out two math challenges.
The challenges also involve an element of trial and improvement, and also some addition.
-
Quadra’s Magic Bag Challenge
-
Answers
Four Dogs Problem
Four Dogs Problem is a logic problem which involves using the clues to work out the owners for each of the four dogs.
-
Four Dogs Problem
-
Answers
Who Caught the Biggest FIsh?
Who Caught the Biggest Fish is a logical number problem where you need to use trial and improvement strategies to work out
the order of size of the fish from the clues given about their weights.
-
Who Caught the Biggest Fish?
-
Answers
5th Grade Problems
Who Chose Which?
Who Chose Which is a logical number activity where you need to use the clues to work out which numbers each of the salamanders chose.
-
Who Chose Which?
-
Answers
Birthday Bonanza
Birthday Bonanza is a logic problem which requires logical thinking to work out who got which present and how old each of them was.
-
Birthday Bonanza
-
Answers
More Recommended Math Worksheets
Take a look at some more of our worksheets similar to these.
Other Word Problems by the Math Salamanders
Finding all Possibilities Problems
This is our finding all possibilities area where all the worksheets involve finding many different answers to the problem posed.
The sheets here encourage systematic working and logical thinking.
The problems are different in that, there is typically only one problem per sheet, but the problem may take quite a while to solve!
Math Real-Life Word Problems by Grade
Fraction Problems
Here you will find a range of fraction word problems to help your child apply their fraction learning.
The worksheets cover a range of fraction objectives, from adding and subtracting fractions to working out fractions of numbers.
The sheets support fraction learning from 2nd grade to 5th grade.
Ratio Problems
Here you will find a range of ratio word problems to help your child understand what a ratio is and how ratios work.
The sheets support ratio learning at a 5th grade level.
We hope you have enjoyed our Math Logic Problems on this page.
Please leave a comment at the bottom of the page if you like them!
How to Print or Save these sheets
Need help with printing or saving?
Follow these 3 easy steps to get your worksheets printed out perfectly!
-
How to Print support
How to Print or Save these sheets
Need help with printing or saving?
Follow these 3 easy steps to get your worksheets printed out perfectly!
-
How to Print support
Math-Salamanders.com
The Math Salamanders hope you enjoy using these free printable Math worksheets
and all our other Math games and resources.
We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.