Word problems in circle - Word и Excel - помощь в работе с программами

Objective: I know how to evaluate word problems that involve circles.

Fill in all the gaps, then press «Check» to check your answers. Use the «Hint» button to get a free letter if an answer is giving you trouble. You can also click on the «[?]» button to get a clue. Note that you will lose points if you ask for hints or clues!

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We hope that the free math worksheets have been helpful. We encourage parents and
teachers to select the topics according to the needs of the child. For more difficult
questions, the child may be encouraged to work out the problem on a piece of paper
before entering the solution. We hope that the kids will also love the fun stuff and
puzzles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Источник

Chapters

Exercise 1
Exercise 2
Exercise 3
Exercise 4
Exercise 5
Exercise 6
Exercise 7
Exercise 8
Exercise 9
Exercise 10
Solution of exercise 1
Solution of exercise 2
Solution of exercise 3
Solution of exercise 4
Solution of exercise 5
Solution of exercise 6
Solution of exercise 7
Solution of exercise 8
Solution of exercise 9
Solution of exercise 10

Solution of exercise 1

Anne is riding a horse which is tied to a pole with a 3.5 m piece of rope and her friend Laura is riding a donkey which is 2 m from the same center point. Calculate the distance travelled by each when they have rotated 50 times around the center.

$L_{L} = 2 cdot 3.1416 cdot 4 = 12.566$ m

$L_{A} = 2 cdot 3.1416 cdot 3.5 = 21.9912m$

Solution of exercise 2

The rope that attaches a swing to a tree is 1.8 m long and the maximum difference between trajectories is an angle of 146°. Calculate the maximum distance travelled by the seat of the swing when the swing angle is described as the maximum.

$L_{C} = frac {2 cdot pi cdot 1.8 cdot 146^0} {360^0} = 4.5 m$

Solution of exercise 3

Find the area of a circular sector whose chord is the side of the square inscribed in a circle with a 4 cm radius.

$A = frac {pi cdot 4^2 cdot 90} {360} = 12.57 cm^2$

Solution of exercise 4

Calculate the shaded area, knowing that the side of the outer square is 6 cm and the radius of the circle is 3 cm.

Area of a square =

Solution of exercise 5

In a circular park with a radius of 250 m there are 7 lamps whose bases are circles with a radius of 1 m. The entire area of the park has grass with the exception of the bases for the lamps. Calculate the lawn area.

Solution of exercise 6

Two radii (plural for radius) OA and OB form an angle of 60° for two concentric circles with 8 and 5 cm radii. Calculate the area of the circular trapezoid formed by the radii and concentric circles.

$A = frac{pi (8^2 - 5^2) cdot 60} {360} = 20.42 cm^2$

Solution of exercise 7

A circular fountain of 5 m radius lies alone in the center of a circular park of 700 m radius. Calculate the total walking area available to pedestrians visiting the park.

Solution of exercise 8

A central angle of 60° is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment between the chord joining the ends of the two radii and its corresponding arc.

$A _ {sector} = frac{pi cdot 4^2 cdot 60}{360} = 8.38 cm^2$

$h = sqrt {4^2 - 2^2} = 3.46 cm$

$A _{triangle} = frac {4 cdot 3.46}{2} = 6.93 cm^2$

$A _ {segment} = 8.38 - 6.93 = 1.45 cm^2$

Solution of exercise 9

A chord of 48 cm is 7 cm from the center of a circle. Calculate the area of the circle.

$r = sqrt {24^2 + 7^2 = 25$

Solution of exercise 10

Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of 8 m in length.

Diagonal of the square= 2R

D = 8 cm R = 4 cm

$r = frac{1}{2}$

$r = frac{sqrt{32}} {2} cm$

$A = pi cdot (4^2 - (frac{sqrt{32}} {2})^2) = pi cdot (16 - frac{32}{4}) = 25. 13 cm^2$

The platform that connects tutors and students

Did you like this article?
Rate it!

I am passionate about travelling and currently live and work in Paris. I like to spend my time reading, gardening, running, learning languages and exploring new places.

Источник

Problem 1 :

The diameter of a cart wheel is 2.1 m. Find the distance traveled when it completes 100 revolutions.

Problem 2 :

The diameter of a circular park is 98 m. Find the cost of fencing it at $4 per meter.

Problem 3 :

A wheel makes 20 revolutions to cover a distance of 66 m. Find the diameter of the wheel.

Problem 4 :

The radius of a cycle wheel is 35 cm. How many revolutions does it make to cover a distance of 81.40 m ?

Problem 5 :

The radius of a circular park is 63 m. Find the cost of fencing it at $12 per metre.

Problem 6 :

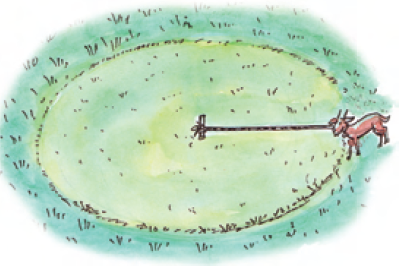
A goat is tethered by a rope 3.5 m long. Find the maximum area that the goat can graze.

Example 7 :

The circumference of a circular park is 176 m. Find the area of the park.

Problem 8 :

A silver wire when bent in the form of a square encloses an area of 121 sq. cm. If the same wire is bent in the form of a circle. Find the area of the circle.

Detailed Answer Key

Problem 1 :

The diameter of a cart wheel is 2.1 m. Find the distance traveled when it completes 100 revolutions.

Solution :

In order to find the distance covered in one revolution, we have to find the circumference of the circle.

Radius of wheel is

= 2.1 / 2

= 1.05 m

Distance traveled when 100 revolutions are completed :

= 100 x circumference of the wheel

= 100 x 2 x (22/7) x (1.05)

= 100 x 2 x 22 x 0.15

= 660 m

Problem 2 :

The diameter of a circular park is 98 m. Find the cost of fencing it at $4 per meter.

Solution :

Diameter of the circular park is 98 m.

Radius :

= 98/2

= 49 m

Cost of fencing is $4 per meter.

Length covered by fencing is equal circumference of the circular park.

Circumference of the park is

= 2πr

= 2 (22/7) x 49

= 2 x 22 x 7

= 308 m

Cost for fencing is

= 308 x 4

= $1232

Problem 3 :

A wheel makes 20 revolutions to cover a distance of 66 m. Find the diameter of the wheel.

Solution :

Given :

A wheel makes 20 revolutions to cover a distance of 66 m.

Then, the distance covered in one revolution is

= 66/20

= 33/10 m

The distance covered in one revolution is equal to circumference of the circle.

Then,

2πr = 33/10

2 x (22/7) x r = 33/10

(44/7) x r = 33/10

Multiply each side by 44/7.

r = (33/10) x (7/44)

r = 0.525

Diameter :

= 2 x radius

= 2 x 0.525

= 1.05 m

Problem 4 :

The radius of a cycle wheel is 35 cm. How many revolutions does it make to cover a distance of 81.40 m ?

Solution :

Radius is given in centimeters and the distance is given in meters.

To have all the measures in meters, we can convert the given radius measure to meters.

Radius :

= 35 cm

= 35/100 m

= 0.35 m

Let ‘n’ be the number of revolutions required to cover the distance of 81.40 m.

n x one revolution of cycle wheel = 81.40

n x 2πr = 81.40

n x 2 x (22/7) x 0.35 = 81.40

n x 2.2 = 81.40

Divide each side by 2.2

n = 81.40/2.2

n = 37

So, the cycle wheel has to revolve 37 times to cover the distance.

Problem 5 :

The radius of a circular park is 63 m. Find the cost of fencing it at $12 per metre.

Solution :

Radius of the circular park is 63 m.

Length of fencing is equal to circumference of the circular park.

Circumference of the cicular park is

= 2πr

= 2 x (22/7) x 63

= 2 x 22 x 9

= 396 m

Cost of fencing is $12 per meter.

Total cost for fencing the park is

= 396 x 12

= $4752

Problem 6 :

A goat is tethered by a rope 3.5 m long. Find the maximum area that the goat can graze.

Solution :

Radius of the circle is equal to length of the rope.

Then, the radius is

= 3.5 m

= 7/2 m

Area grazed by the goat is equal to the area of the circle with radius 7/2 m.

Maximum area grazed by the goat is

= πr²

= (22/7) x (7/2) x (7/2)

= 77/2

= 38.5 sq. m

Example 7 :

The circumference of a circular park is 176 m. Find the area of the park.

Solution :

Circumference of the circular park is 176 m (given).

Then,

2πr = 176

2 x (22/7) x r = 176

(44/7) x r = 176

Multiply each side by 7/44.

r = 176 x (7/44)

r = 28 m

Area of the circular park is

= πr²

= (22/7) x 28 x 28

= 22 x 4 x 28

= 2464 sq. m.

Problem 8 :

A silver wire when bent in the form of a square encloses an area of 121 sq. cm. If the same wire is bent in the form of a circle. Find the area of the circle.

Solution :

Area of the square is 121 sq. cm. (given)

Let a be the length of each side of the square.

Then,

a² = 121

a² = 11²

a = 11

Then, perimeter of the square is

= 4a

= 4 x 11

= 44 cm

Length of the wire is equal to perimeter of the square.

So, length of the wire is 44 cm.

If thee wire is bent in the form of a circle, then the circumference of the circle is equal to length of the wire

Circumference of a circle = 44 cm

2πr = 44

2 x (22/7) x r = 44

(44/7) x r = 44

Multiply each side by 7/44.

r = 44 x (7/44)

r = 7 cm

Area of the circle is

= πr²

= (22/7) x 7 x 7

= 154 sq. cm

Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to v4formath@gmail.com

We always appreciate your feedback.

Источник

So let’s talk about word problems, shall we? What is it about them that just messes kids up? Is it the need to read while doing math? Maybe it’s just too many words to dig through? Whatever it is, there’s just something about word problems that causes panic in my students’ eyes. That is until I started teaching them this simple word problem strategy.

Circle, Circle, Underline

So what’s the strategy? Well, it’s simple really… it’s a little chant I like to call, “Circle, Circle, Underline!” After reading the word problem, I have my students work to find the important information and underline what they want us to do (or the question). We call this “circle, circle, underline!” and I’ve found it does amazingly well at helping my beginning mathematicians make sense of all those words!

Looking for a strategy to help with multi-step word problems? Check out this post!

Introducing the Word Problem Strategy

To introduce this strategy, I first give students an example of a word problem. We talk about how all word problems have the same parts to them. They have information given and a question that needs to be answered using that information.

From there, I show them how I go through and find these important parts and “circle, circle, underline” them as I go through. I’ve found it’s best to make notes in our math interactive student notebooks (or math isns) so we can reference back to these steps anytime we need.

So, after introducing the concept whole group, I have students head back to their seats and pull out their math isns and we start gluing in some reference pages together. I tell my students, these are the pages we’ll use anytime we forget what to do!

Trying it Together

Now that we’ve had a chance to make a reference page, the students are ready to use the strategy in guided practice. Here’s where I really hit home the chant of “circle, circle, underline.” I’ve found my kids remember things when there’s a song involved. Seriously, these kids can quote me some of the most school inappropriate lyrics! So, I’m using that to my advantage and made this a chant!

For the guided practice, students work to rewrite the steps to the word problem strategy. This way they will remember it, always! Remember: writing things helps our brains remember! From there, we then work to circle, circle, underline a word problem together. This way I can guide their practice and spot check their understanding of our strategy.

Practice Time

Now that the students have made their own reference pages, they’re ready to move on to using this strategy on their own. I pass out a page for them to work on using the “circle, circle, underline” word problem strategy. Here’s where I walk around and make sure all my students are understanding how to use this strategy.

This is also a great time for students to work in pairs if needed. That collaborative discussion can help your students better understand the concept!

And that’s it… it is seriously one of the easiest strategies to teach but it is so powerful! It works so well, in fact, I taught it to my 1st-grade son who was really struggling with sorting out word problems on his math homework. Now, I hear him chanting away as he dives right in! PTL!

My students always need practice with word problems, so I love putting them in our math center tubs. Be sure to check out these Differentiated Word Problem Task Cards

Word Problem Strategy Free Download

To make it easier for you to teach this strategy to your students, be sure to grab the math isn pages I used in the form below! Just add your name and email and POOF! This little freebie will be sent right to your inbox! Don’t use math ISNs? Don’t worry! You can print out the sheets and use them as if needed!

Источник

Video of the Day

Circle Word Problems

This video covers solving word problems using sector area and arc length and the properties of circles.

Video Guide

Word problem in which you find the diameter of a circle using the arc length. This problem is solved by setting up a proportion of the arc length over circumference equaling the measure of the angle over 360 in order to find the circumference. You then use the circumference to find your diameter.

Word problem in which you find the circumference of a circle using the radius.

This problem uses the circumference formula in order to find the circumference of the circle using

the radius.

The last word problem involves a clock and how many degrees the clock travels in a certain amount of time. The solution involves finding how many degrees the hand of the clock travels per minute.

Each word problem is solved and step by step directions are given for each solution.

For more Math videos

http://www.moomoomath.com/A-Z-List-Math-Webpages.html#.UelAthvD_IU

Источник

Источник

Practice word problems that involve thinking about angles as part of a circle.

Want to join the conversation?

The clock one was the hardest. Does anyone agree?

Button navigates to signup pageComment on Anne Song’s post “The clock one was the har…”
- I agree it is hard. I got confused
  
  Comment on xirayne’s post “I agree it is hard. I got…”
Probably should have used a different term than «turns».

Button navigates to signup pageComment on robert leonard’s post “Probably should have used…”
The clock one was the hardest out of all

Button navigates to signup pageComment on prikam2538’s post “The clock one was the har…”
- It would seem as though for each one we take the number of times (it occurs) / the number of objects there are.
  In the clock problem (between 7 o’clock and 10 o’clock, there is 3 hours) we know that a clock has 12 hours which can be written as 3/12 -> 1/4. 360 / 4 = 90
  
  Comment on 雨風’s post “It would seem as though f…”
The clock problem is the one I found easiest except for the worm problem. Is this just me or…?

Button navigates to signup pageComment on asbatra’s post “The clock problem is the …”
- honestly i found the clock problem to be the hardest
  
  Comment on damionsmith8312007’s post “honestly i found the cloc…”
i kinda don’t get it but I went threw it because I tried my best!

Button navigates to signup pageComment on brittanyharris2’s post “i kinda don’t get it but …”
For me the pizza one was hardest because I can’t understand that. Anyone agrees?

Button navigates to signup pageComment on Lovish Garg’s post “For me the pizza one was …”
- It’s degrees per slice eeeezzz boi
  
  Comment on KeigoM’s post “It’s degrees per slice ee…”
This doesn’t make any sense whatsoever. It has to make at least one full turn to get to another hour. Plus another 30 degrees to get to the next hour! How is 90 degrees possible? I went through a ton of trying to solve this problem. How is 90 degrees even the answer?

Button navigates to signup pageComment on Magnolia D.’s post “This doesn’t make any sen…”
- «hour hand»
  
  Button navigates to signup page
the pizza one make it all easy. ,, half is 180 ,, thirds of 180 is 60 if u think 12 hours on a clock 6 is 180. Means every 2 hours is 60° = every hour is +30° , thanks guys. Its awesome

Button navigates to signup pageComment on Keane Trs’s post “the pizza one make it all…”
this does not make any sense!!

Button navigates to signup pageComment on Lola112’s post “this does not make any se…”
i don´t get the clock at all

Button navigates to signup pageComment on 994816103’s post “i don´t get the clock at …”
- Each hour segment is = 30degrees.
  Each segment looks like this, starting at the top of the clock, going clockwise (12 to 1=30degrees, 1 to 2 =30 degrees, 2 to 3 = 30 degrees, 3 to 4 = 30 degrees, 4 to 5 = 30 degrees…. and so on all the way around the clock.
  
  Button navigates to signup page

Источник

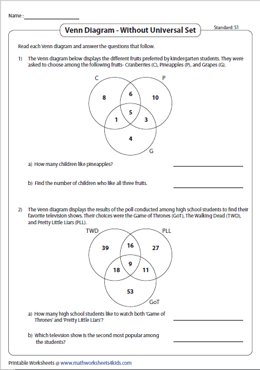
This page contains worksheets based on Venn diagram word problems, with Venn diagram containing three circles. The worksheets are broadly classified into two skills — Reading Venn diagram and drawing Venn diagram. The problems involving a universal set are also included. Printable Venn diagram word problem worksheets can be used to evaluate the analytical skills of the students of grade 6 through high school and help them organize the data. Access some of these worksheets for free!

Reading Venn Diagram — Type 1

These 6th grade pdf worksheets consist of Venn diagrams containing three sets with the elements that are illustrated with pictures. Interpret the Venn diagram and answer the word problems given below.

Reading Venn Diagram — Type 2

The elements of the sets are represented as symbols on the three circles of the Venn diagram. Count the symbols and write the answers in the space provided. Each worksheet contains two real-life scenarios.

Standard Word Problems — With Universal Set

This section features extensive collection of Venn diagram word problems with a universal set for grade 7 and grade 8 students. Real-life scenarios like doctor appointments, attractions of Niagara Falls and more are used.

Drawing Venn Diagram — Without Universal Set

Draw a venn diagram with three intersecting circles and fill in the data from the given descriptions. Also, ask 8th grade and high school students to answer questions based on union, intersection, and complement of three sets.

Draw Venn Diagram — With Universal Set

Six exclusive printable worksheets on Venn diagram word problems are included here. Draw three overlapping circles and fill in the regions using the information provided. Based on your findings, answer the word problems.

Источник